Effects of Out-of-Plane Deformation of the Base Plate on the Structural Behavior of an Exposed Column Base
Abstract
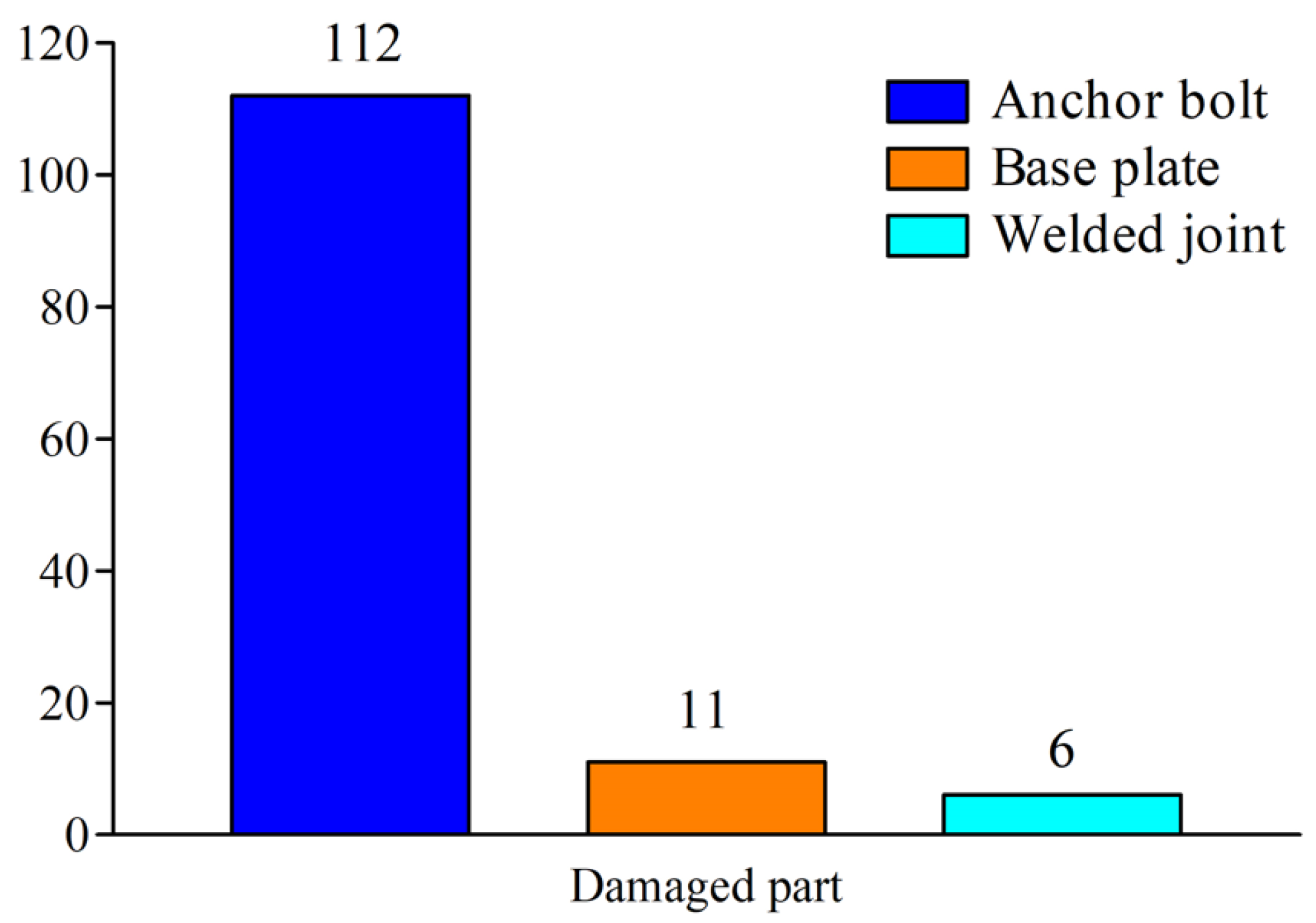
1. Introduction
2. Test Study
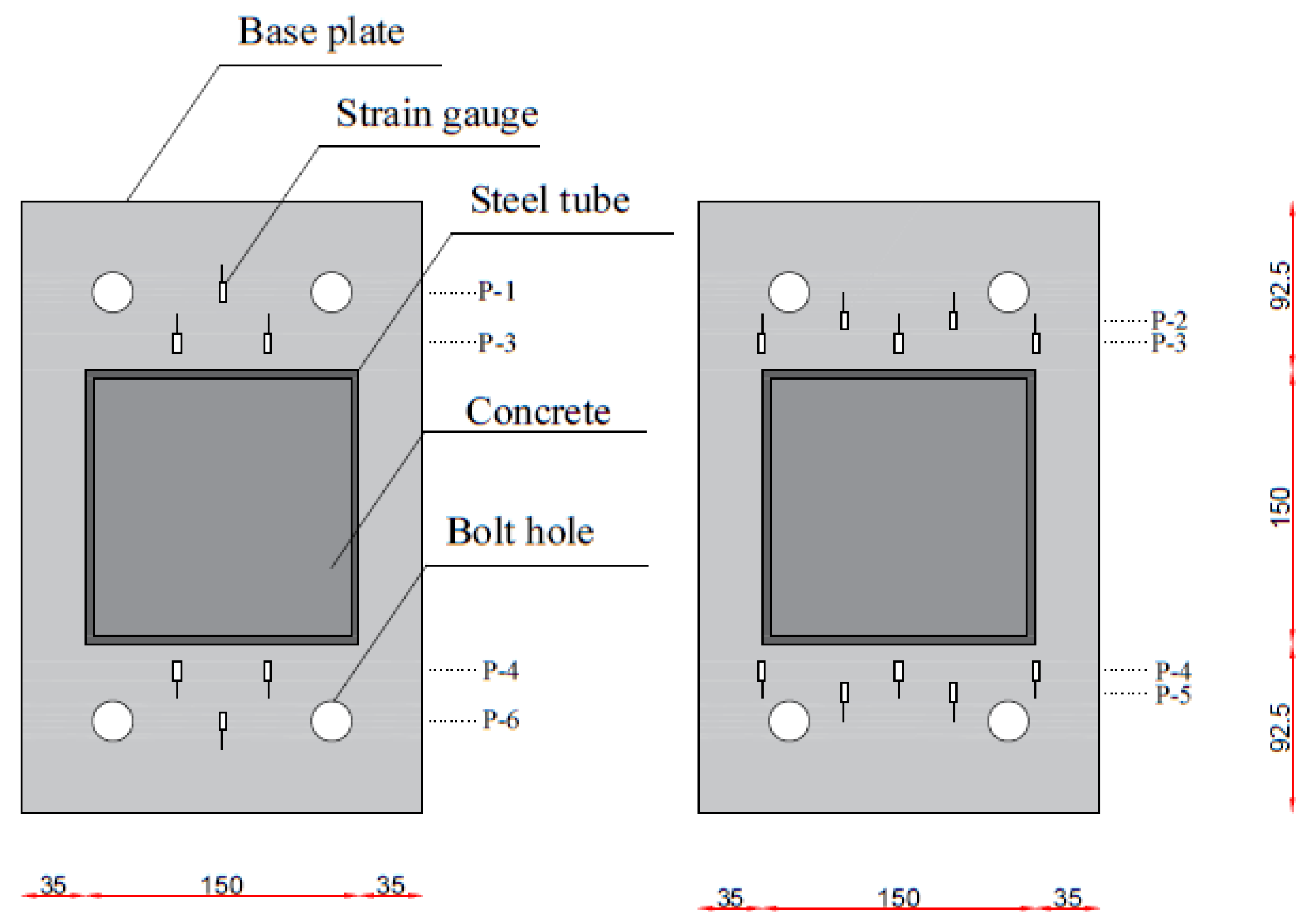
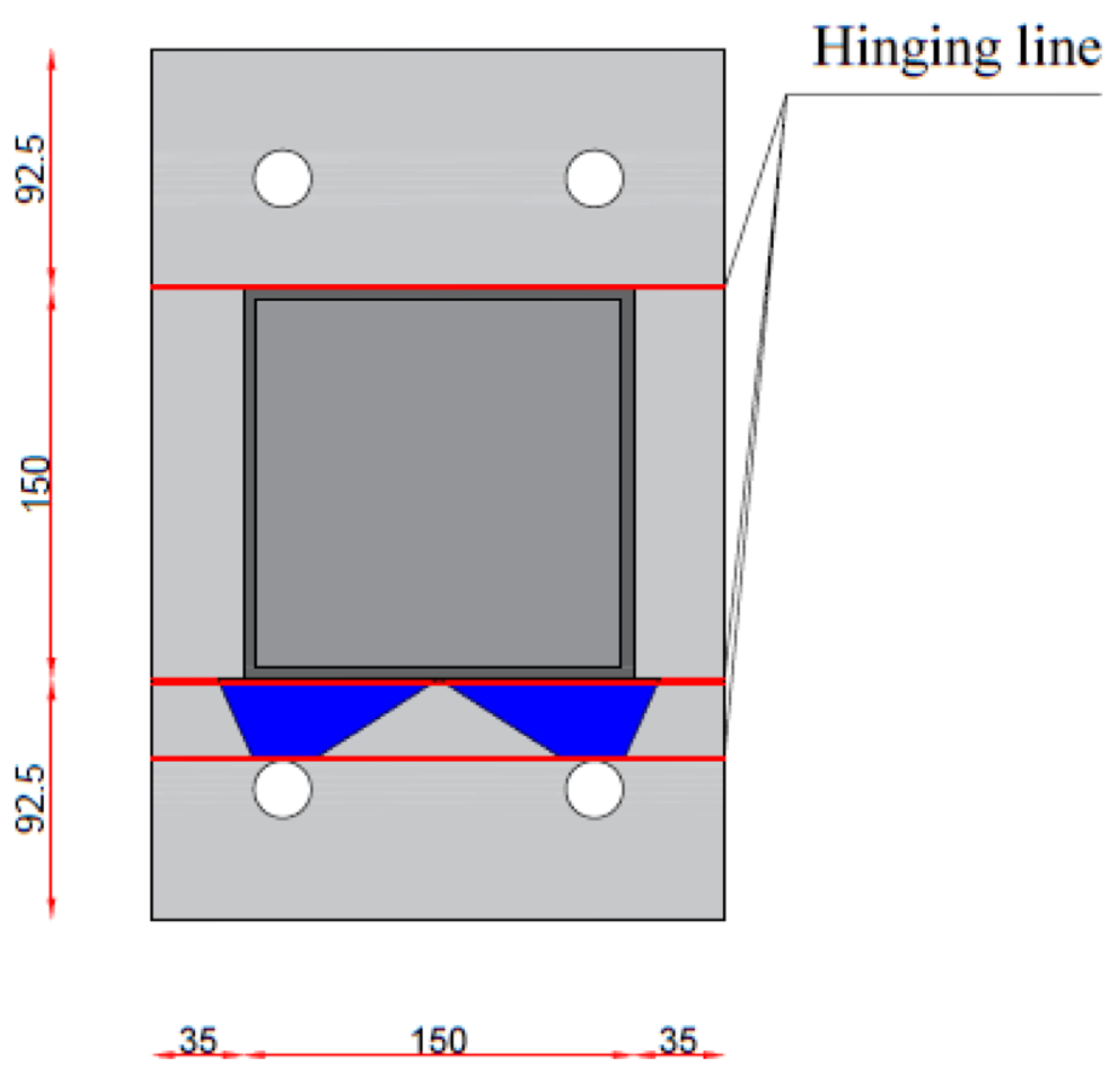
2.1. Specimens
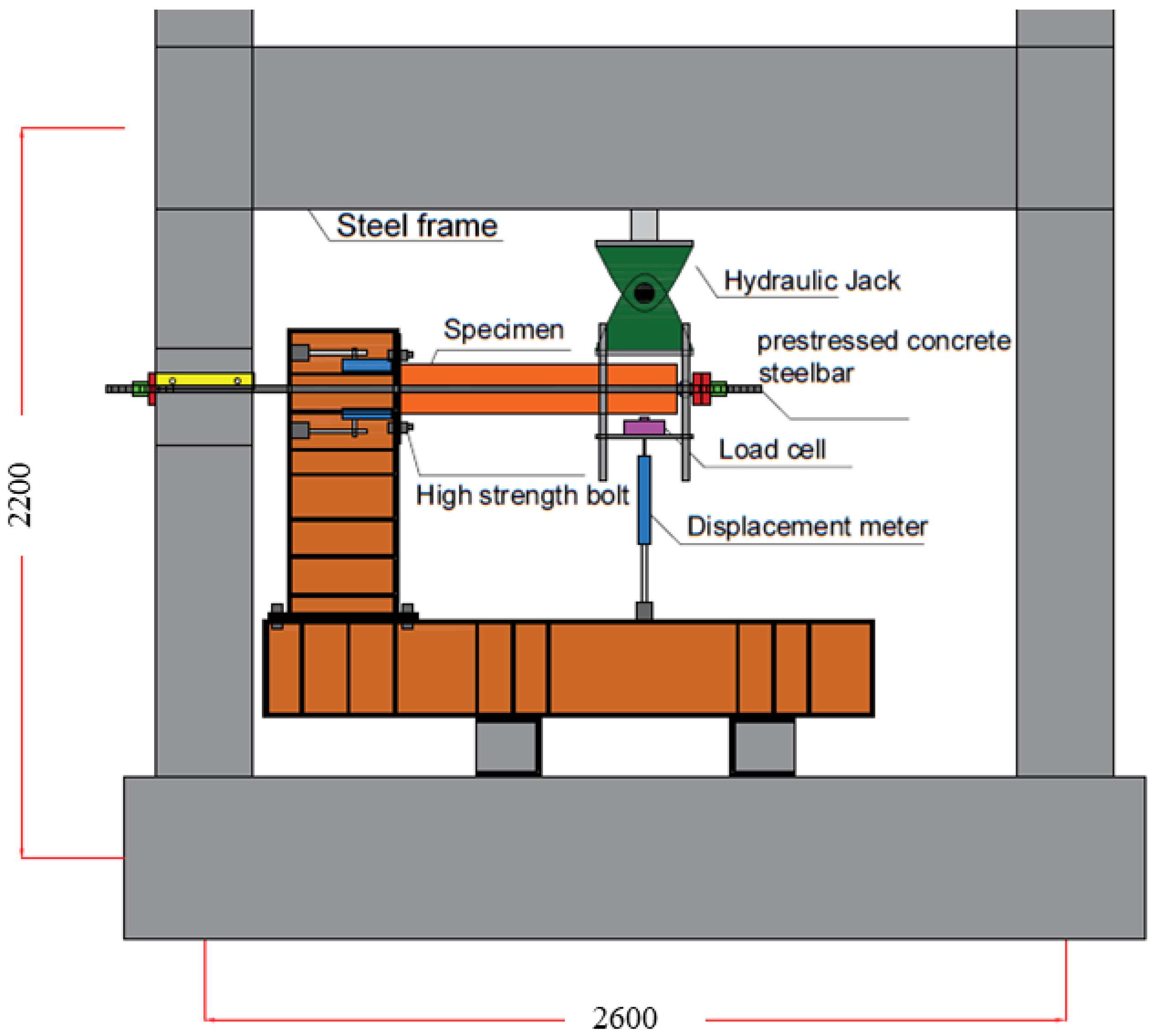
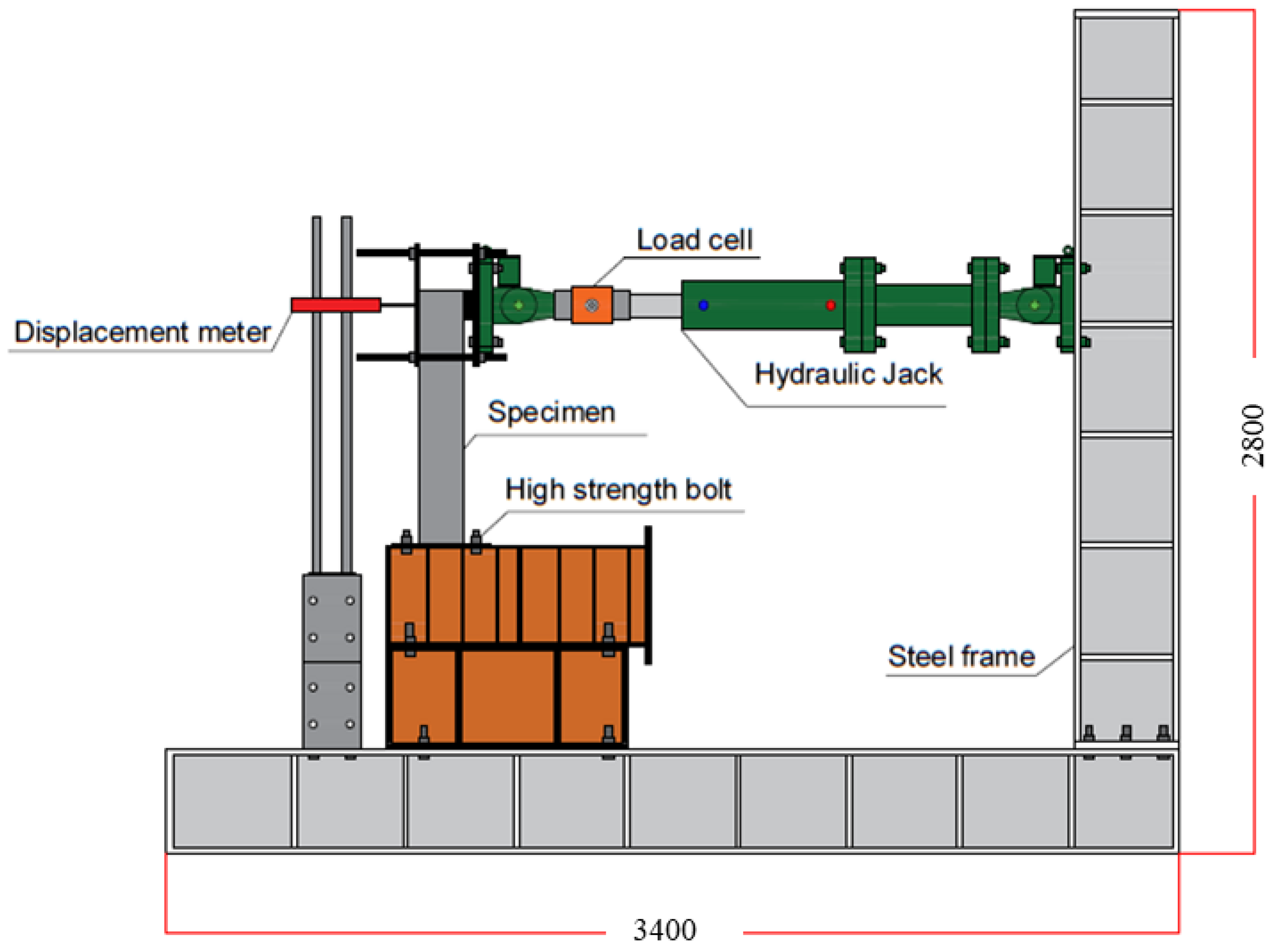
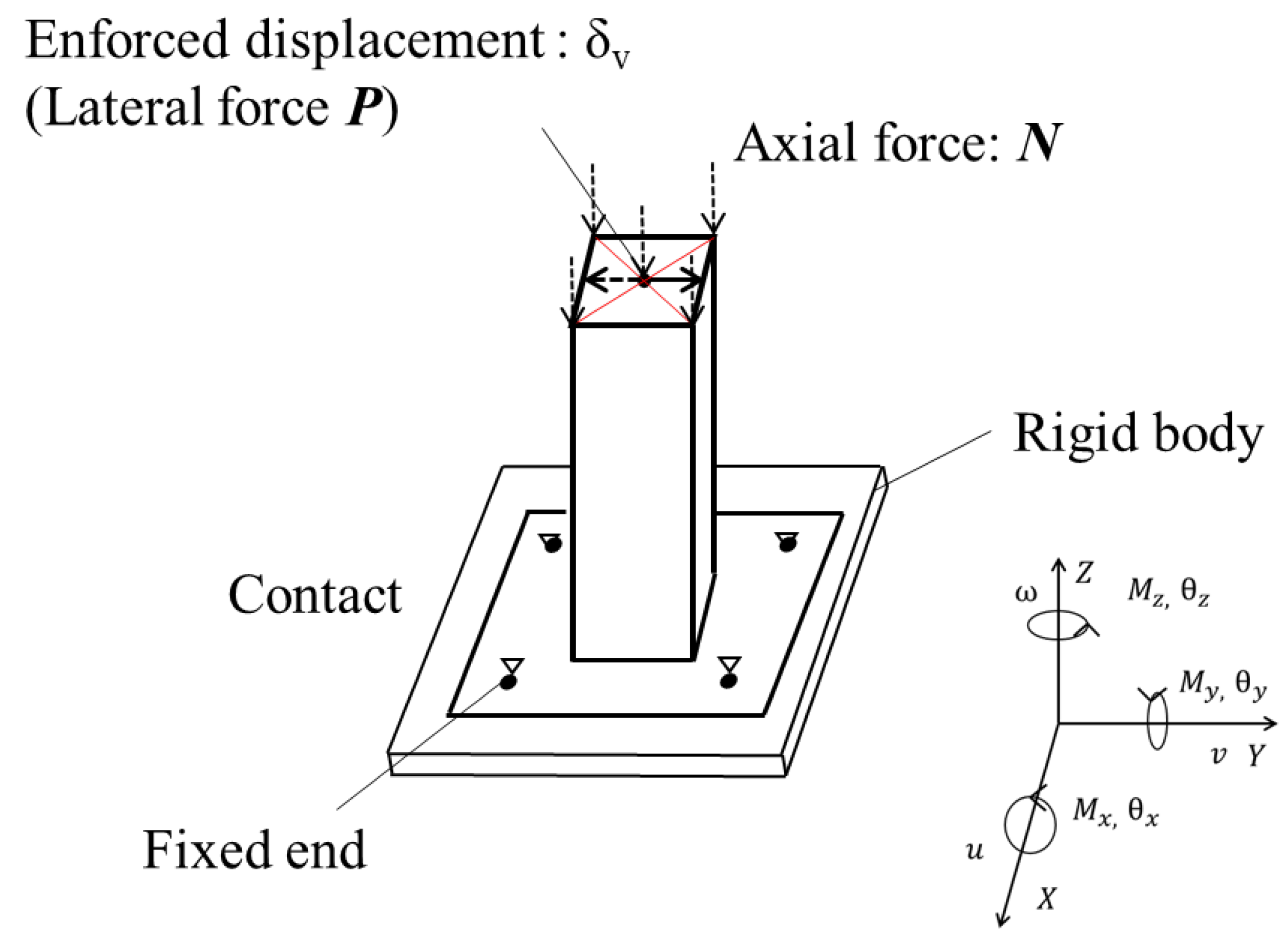
2.2. Test Setup
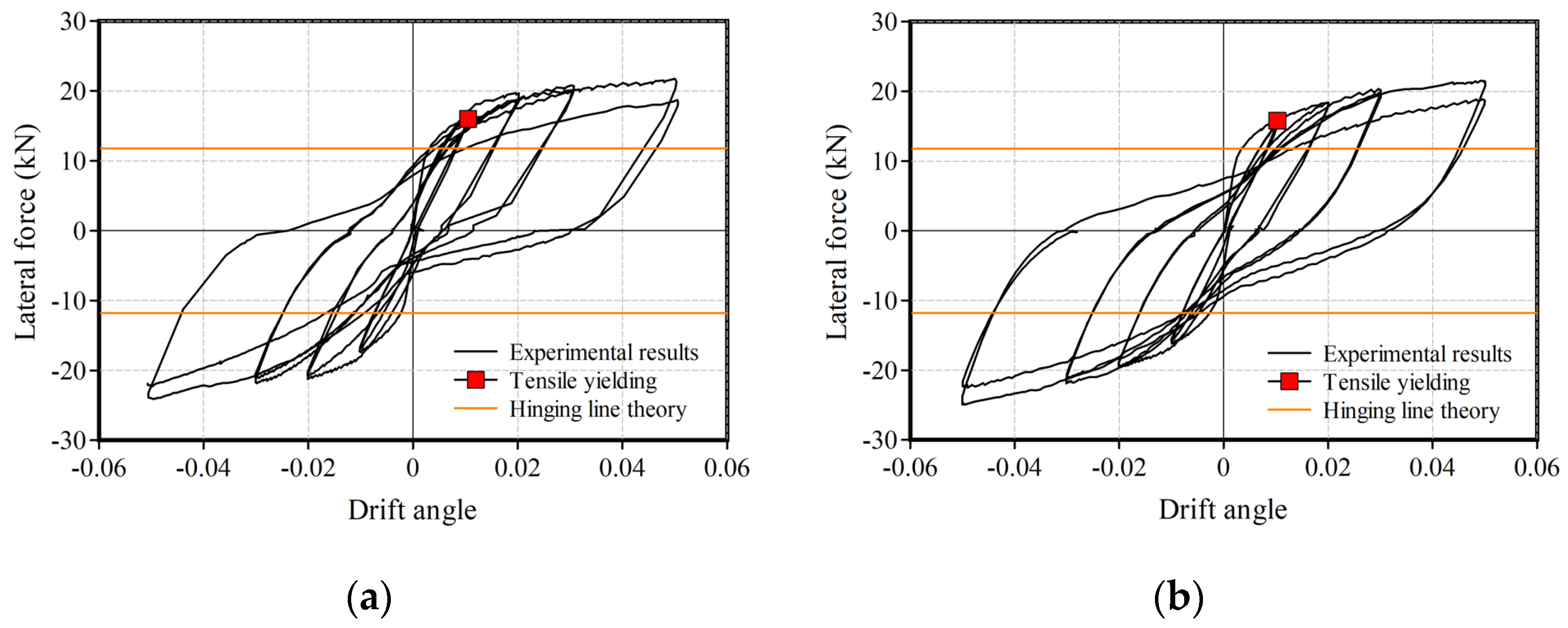
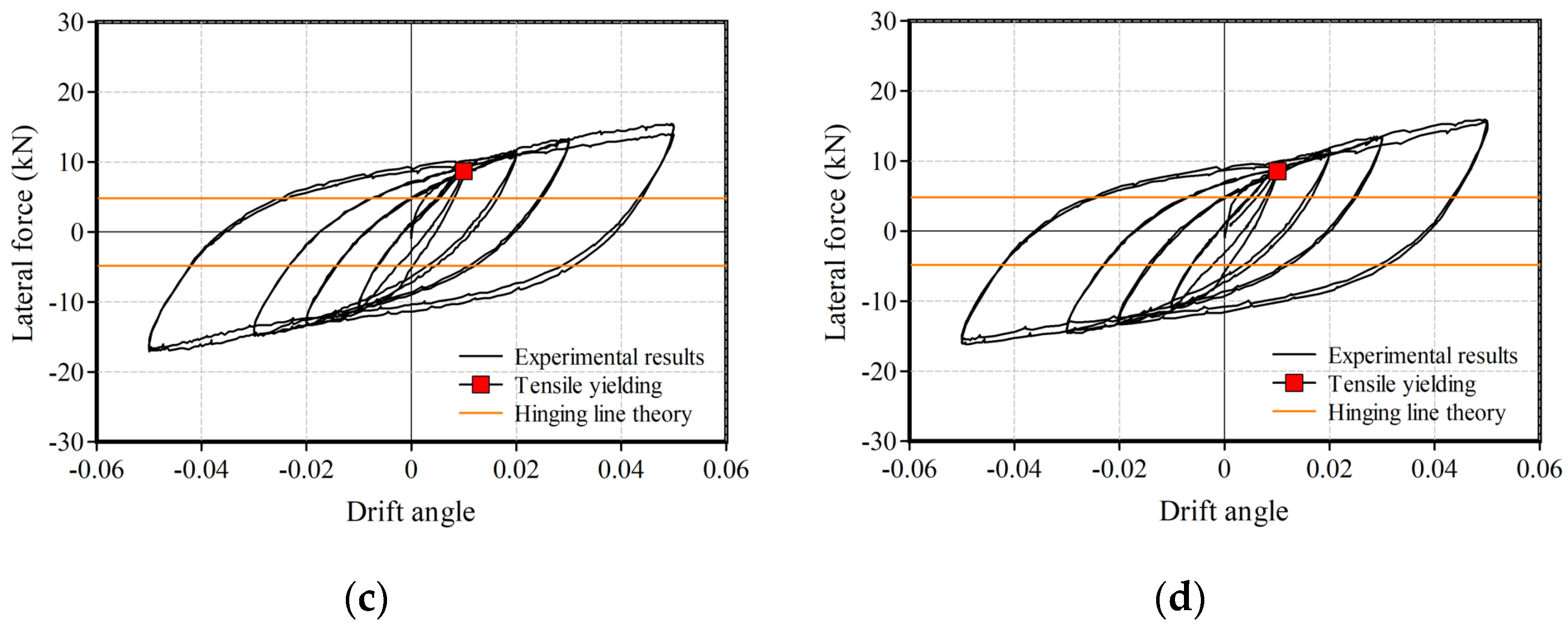
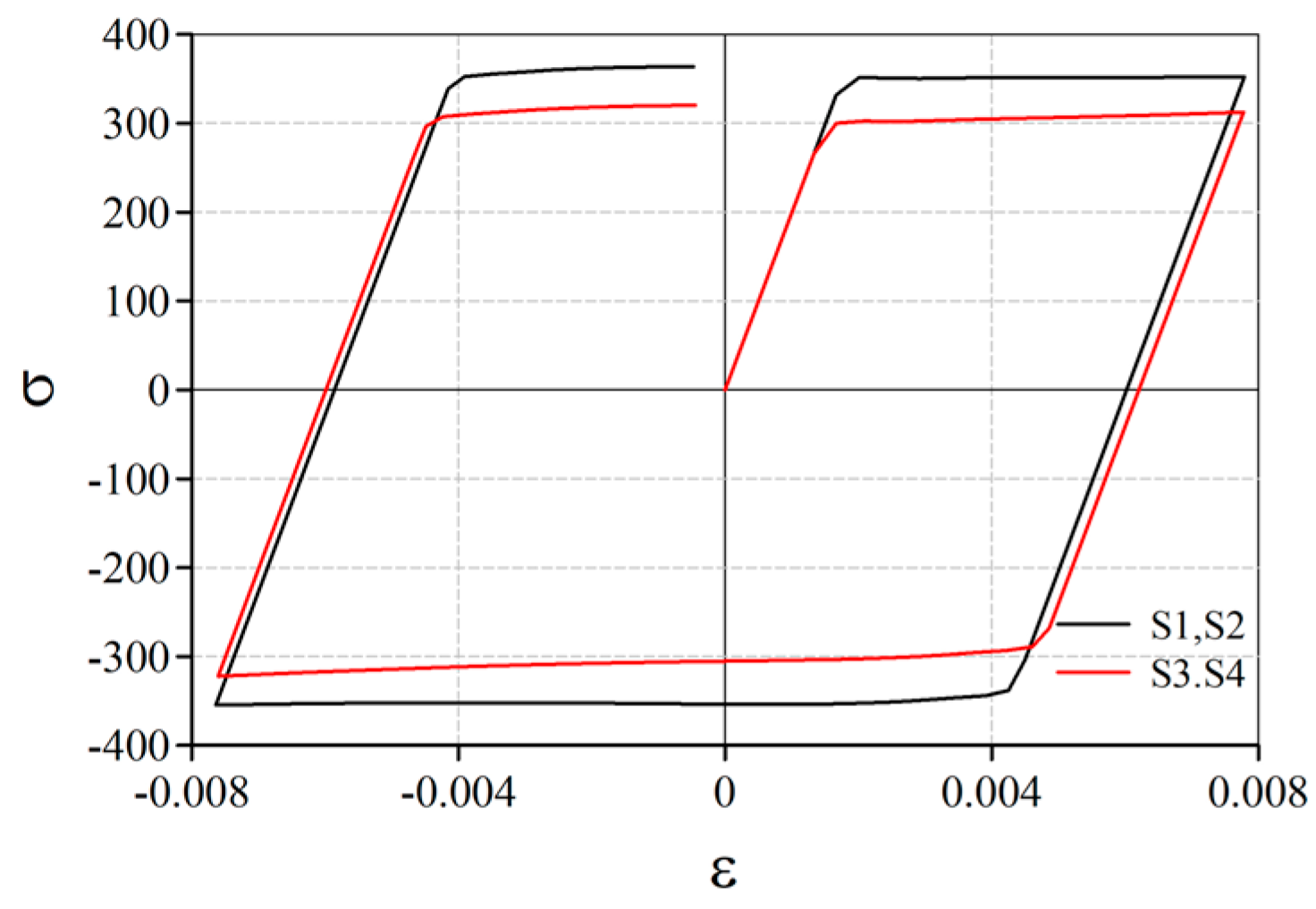
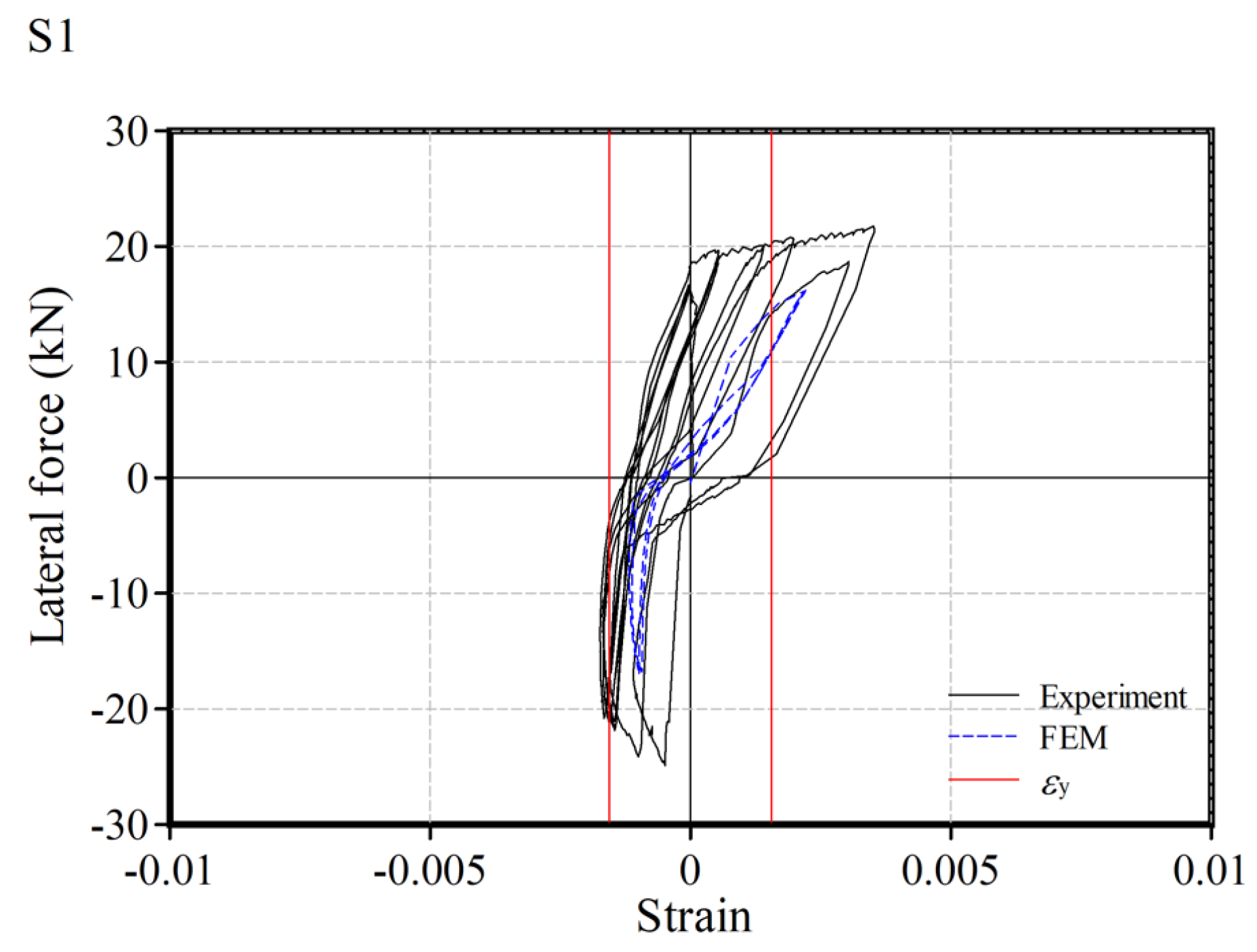
2.3. Test Results and Discussion
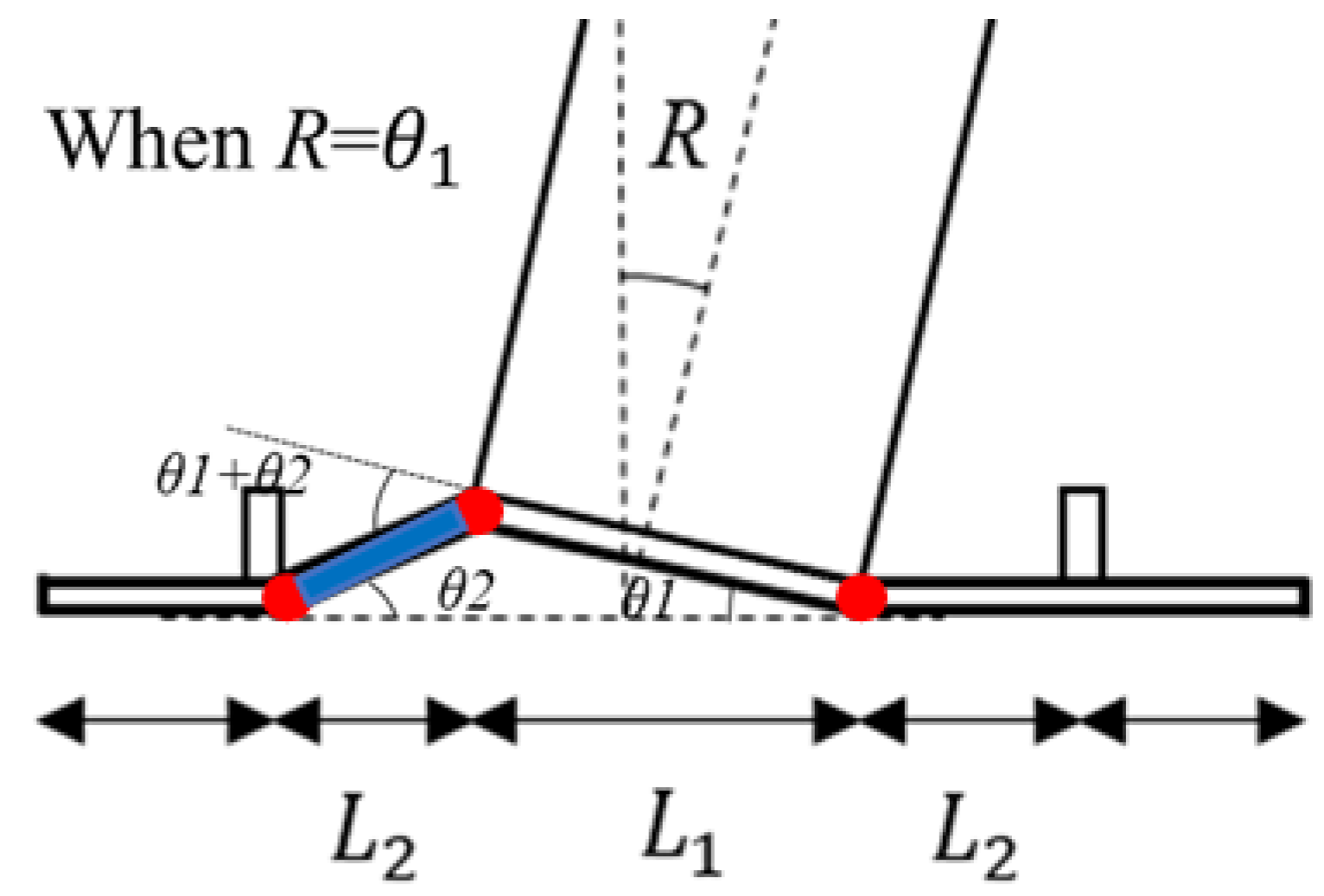
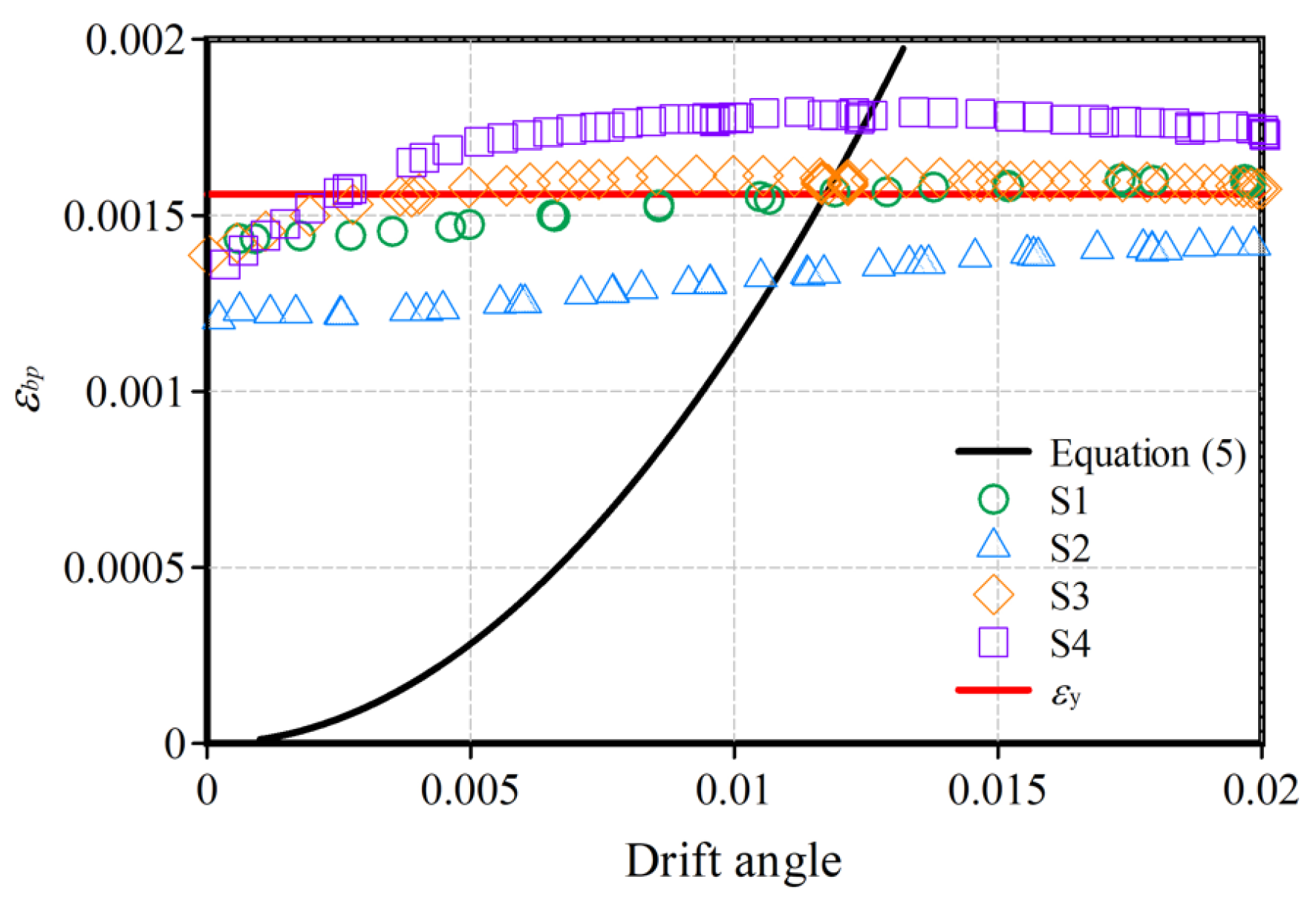
2.4. Discussion of the Deformation of the Base Plates
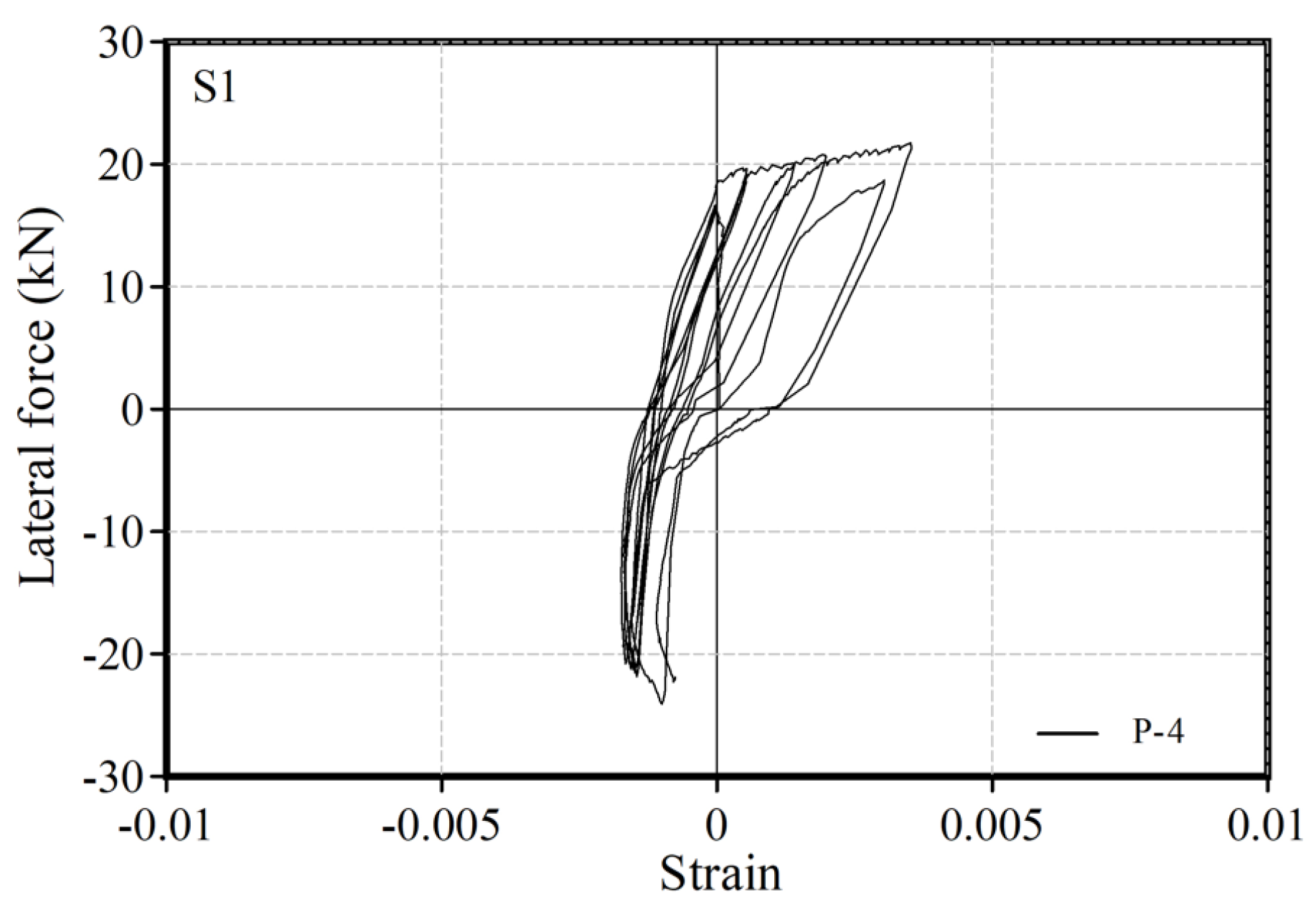
2.5. Study of the Equivalent Viscous Damping Ratio

| Specimen | heq (%) | Average heq (%) | |||||
|---|---|---|---|---|---|---|---|
| 0.01 rad | 0.02 rad | 0.03 rad | 0.05 rad | ||||
| S1 | 7.68 | 13.9 | 16.4 | 23.5 | 15.4 | 16.0 | 20.7 |
| S2 | 7.78 | 14.7 | 18.8 | 25.2 | 16.6 | ||
| S3 | 16.4 | 23.3 | 28.7 | 35.2 | 25.9 | 25.5 | |
| S4 | 15.3 | 23.5 | 28.3 | 33.2 | 25.1 | ||
3. Analysis of the Base Plate
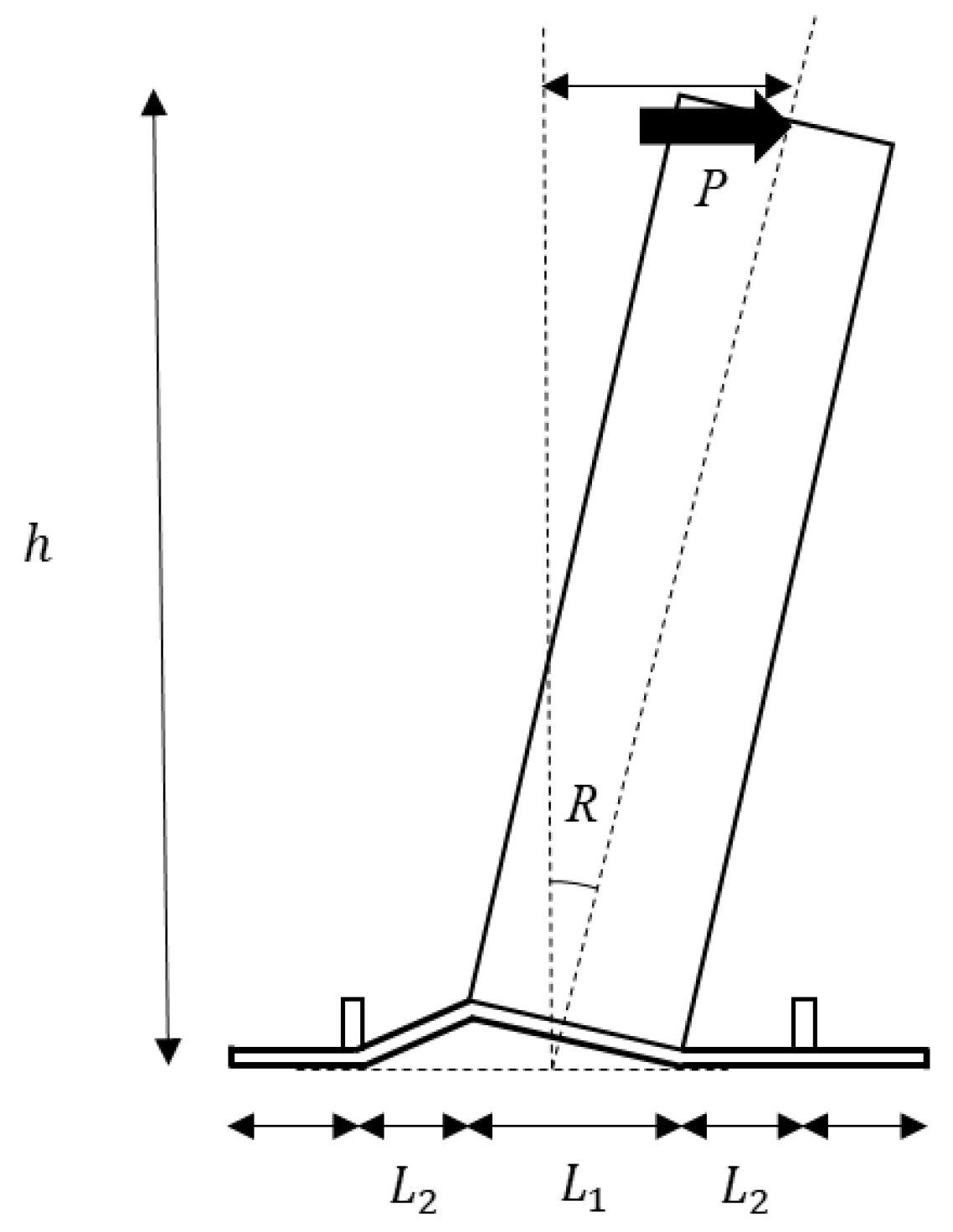
3.1. Model and Loading Process
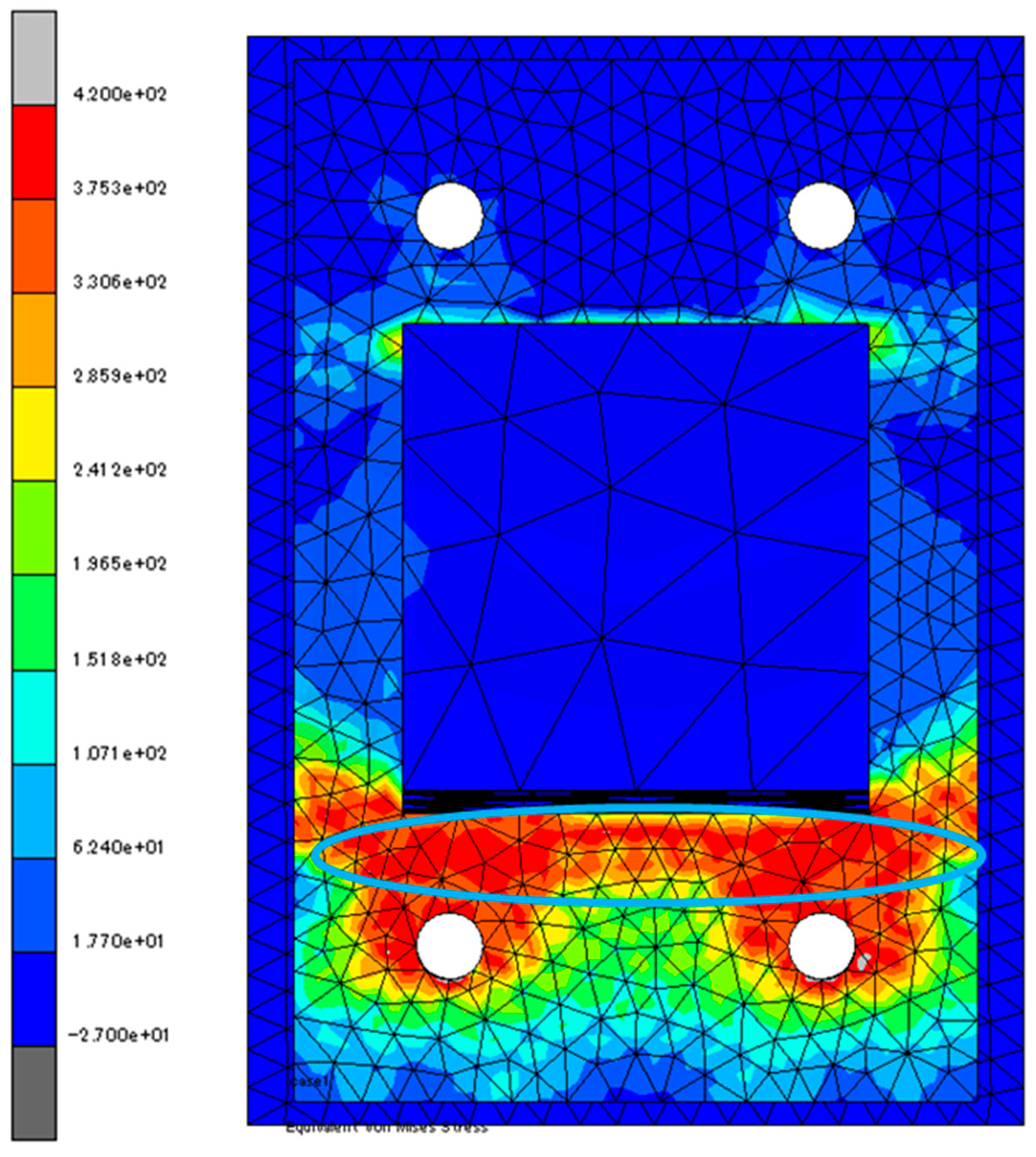
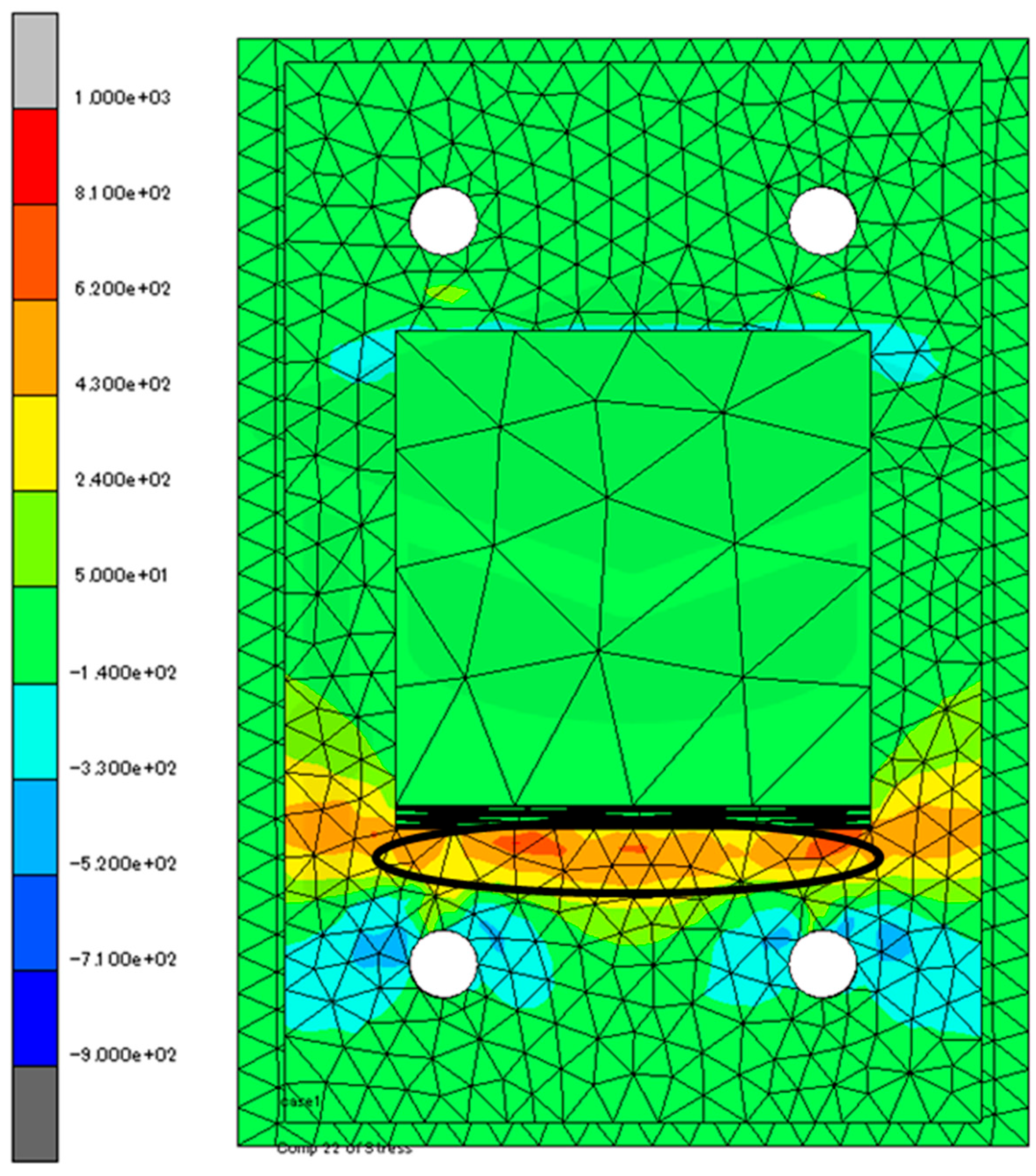
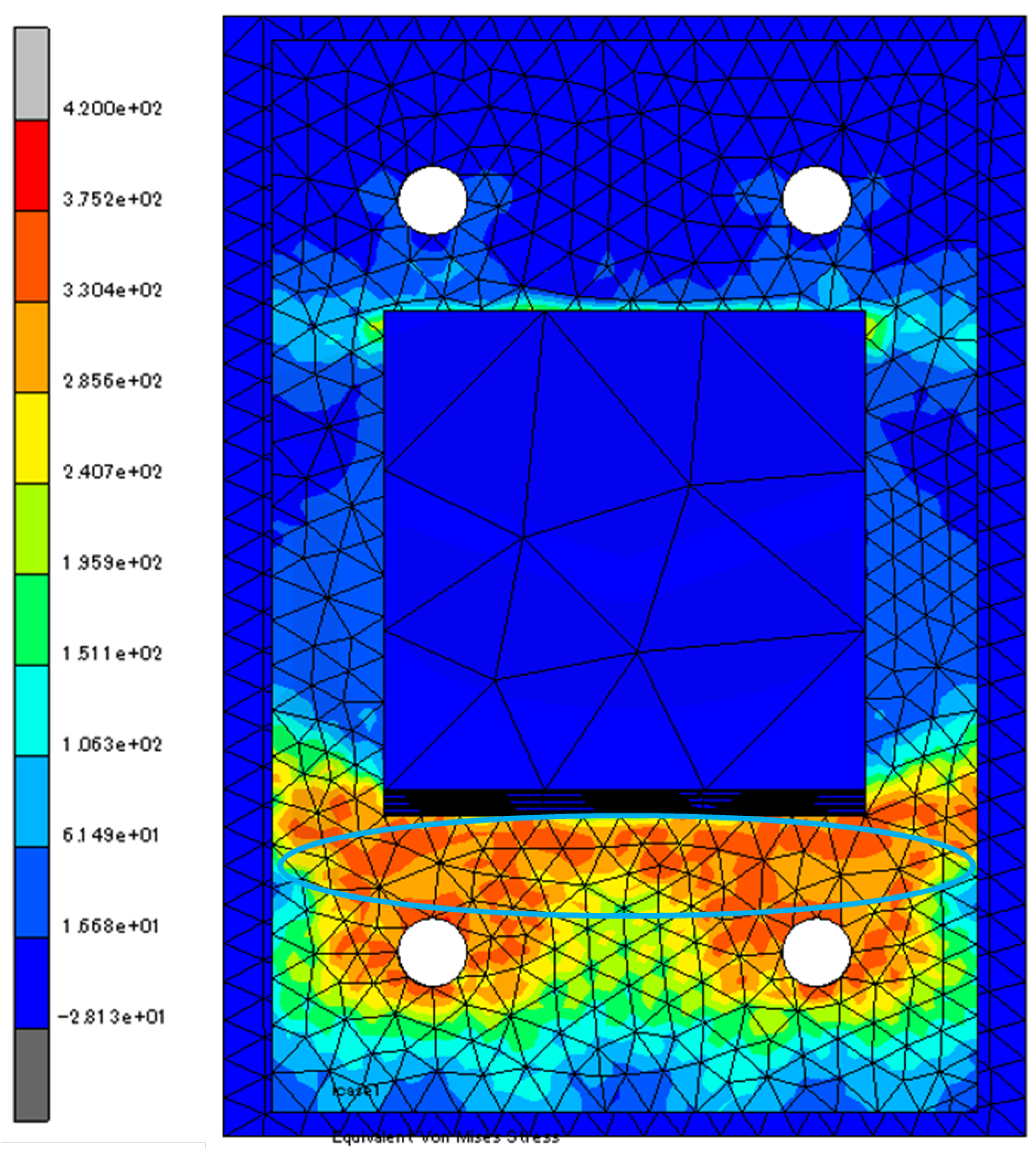
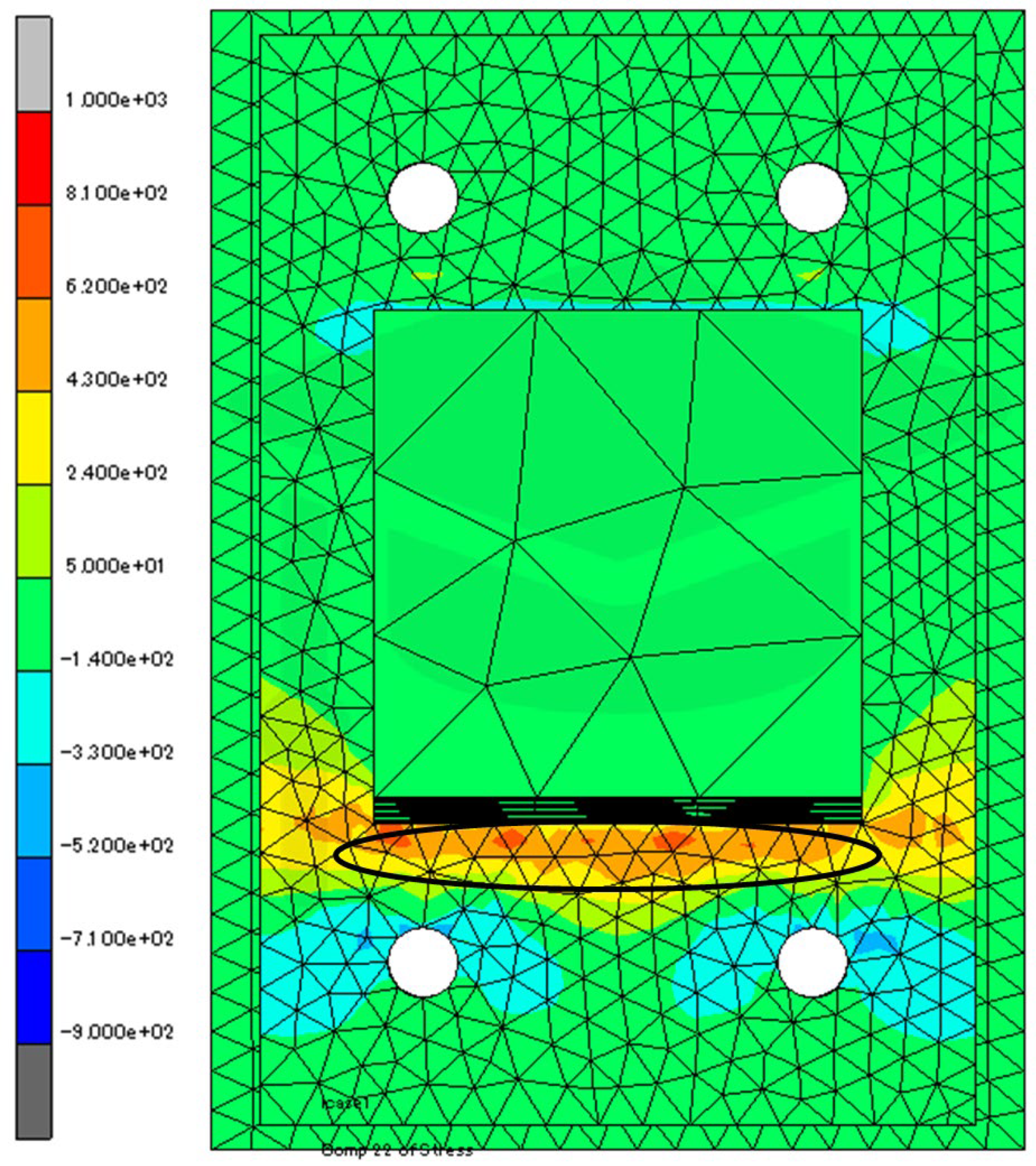
3.2. Analytical Results and Discussion
4. Simple Calculation Method for the Yielding Strength of an Exposed Column Base
5. Conclusions
- All the specimens failed in yielding at the base plates of an exposed CFST column base.
- The test results of the relationship between the lateral load and the drift angle showed stability without strength deterioration. The hysteresis characteristics of the specimens with axial force application were origin-oriented, and those of the specimens with no axial force application were spindle-shaped.
- Energy absorption capacities were estimated using the equivalent viscous damping ratio at each step of the drift angle of 0.01, 0.02, 0.03, and 0.05 rad. The ratios increased with cyclical loading. The average value was 20.7%.
- The FEM analysis traced well the test results, revealing the tensile yielding area of the base plates.
- The FEM analysis provided the stress distribution on the base plates when the load versus deformation relationship showed a significant decline at R = 0.01 rad.
- The calculation method for the tensile yielding strength of the base plate of a column base accurately evaluated each test strength. It showed that the assumption of the stress distribution area was reasonable owing to the results of the FEM analysis.
- The simple calculation method proposed in this paper demonstrated high consistency with the test results, suggesting its potential as a practical tool for structural design.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reconnaissance Report on Damage to Steel Building Structures Observed from the 1995 Hyogoken-Nanbu Earthquake; Steel Committee of Kinki Branch the Architectural Institute of Japan (AIJ): Osaka, Japan, 1995.
- Final Report of the Architectural Earthquake Investigation Committee on the 1995 Great Hanshin-Awaji Earthquake; Architectural Earthquake Investigation Committee: Tokyo, Japan, 1996.
- Damage and Lessons of Steel Structures in the Hyogoken-Nanbu Earthquake; Architectural Institute of Japan (AIJ): Tokyo, Japan, 1996.
- Cui, Y.; Wang, F.; Yamada, S. Effect of Column Base Behavior on Seismic Performance of Multi-Story Steel Moment Resisting Frames. Int. J. Struct. Stab. Dyn. 2019, 19, 1940007. [Google Scholar] [CrossRef]
- Cui, Y. Shear behavior of exposed column base connections. Steel Compos. Struct. 2016, 21, 357–371. [Google Scholar] [CrossRef]
- Kishiki, S.; Yang, X.; Ishida, T.; Tatsumi, N.; Yamada, S. Experimental study of concrete breakout failure mechanism in an exposed column base with a foundation beam. Eng. Struct. 2021, 243, 112661. [Google Scholar] [CrossRef]
- You, Y.-C.; Lee, D. Development of improved exposed column-base plate strong-axis joints of low-rise steel buildings. J. Constr. Steel Res. 2020, 169, 106062. [Google Scholar] [CrossRef]
- Recommendation for Design of Connection in Steel Structures; Architectural Institute of Japan (AIJ): Tokyo, Japan, 2021.
- You, Y.-C.; Lee, D. Effect of anchors on the seismic performance of exposed column-base plate weak-axis connections. J. Build. Eng. 2020, 32, 101803. [Google Scholar] [CrossRef]
- Yamanishi, T.; Tamai, H.; Takamatsu, T.; Matsuo, A. Elastic Rotational Rigidity of Exposed Column-base (In case of anchor bolt yield type). J. Struct. Constr. Eng. 2008, 73, 317–324. (In Japansese) [Google Scholar] [CrossRef][Green Version]
- Pan, J.; Huang, R.; Xu, J.; Wang, P.; Wang, Z.; Chen, J. Behavior of exposed column-base connections with four internal anchor bolts under seismic loading. Structures 2021, 34, 105–119. [Google Scholar] [CrossRef]
- Tamai, H.; Ichinose, N. On Deformation Capacity of Exposed Column-Base; Graduate School of Engineering, Nagasaki University: Nagasaki, Japan, 2015; Volume 45. (In Japanese) [Google Scholar]
- Lim, W.-Y.; Lee, D.; You, Y.-C. Exposed column-base plate strong-axis connections for small-size steel construction. J. Constr. Steel Res. 2017, 137, 286–296. [Google Scholar] [CrossRef]
- Akiyama, H. Seismic Design of Steel Column Bases; GIHODO SHUPPAN Co., Ltd.: Tokyo, Japan, 1985. (In Japanese) [Google Scholar]
- Yanagita, Y.; Hannuki, T.; Akiyama, H. Experimental Study on Hysteretic Behaviors of Exposed Steel Column Bases: (Part III) Experimental Formulas of Week Base-Plate Types; Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan; SC-1, Structures III, Timber Structures Steel Structures Steel Reinforced Concrete Structures; Architectural Institute of Japan (AIJ): Tokyo, Japan, 2005; pp. 651–652. (In Japanese) [Google Scholar]
- Cui, Y.; Wang, F.; Li, H.; Yamada, S. Rotational behavior of exposed column bases with different base plate thickness. Steel Compos. Struct. 2019, 32, 497–507. [Google Scholar] [CrossRef]
- Kokubo, A.; Hannuki, T.; Yanagita, Y.; Akiyama, H. Experimental Study on Hysteretic Behavior of Exposed Steel Column Bases: Part I Experimental Program and Results; Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan; C-1, Structures III, Timber Structures Steel Structures Steel Reinforced Concrete Structures; Architectural Institute of Japan (AIJ): Tokyo, Japan, 2004; pp. 721–722. (In Japanese) [Google Scholar]
- Akiyama, H.; Yamada, S.; Takahashi, M.; Katsura, D.; Kimura, K.; Yahata, S. Full scale shaking table test of the exposed column bases. J. Struct. Constr. Eng. 1998, 63, 185–192. (In Japanese) [Google Scholar] [CrossRef] [PubMed][Green Version]
- Takamatsu, T.; Douki, H. Experimental Study on Restoring Force Characteristics of Exposed-Type Column Base. Bull. Hiroshima Inst. Technol. 2001, 35, 133–140. (In Japanese) [Google Scholar]
- Inoue, K.; Suita, K. Building Steel Structure’s Theory and Design; Kajima Institute Publishing Co., Ltd.: Tokyo, Japan, 2007. (In Japanese) [Google Scholar]


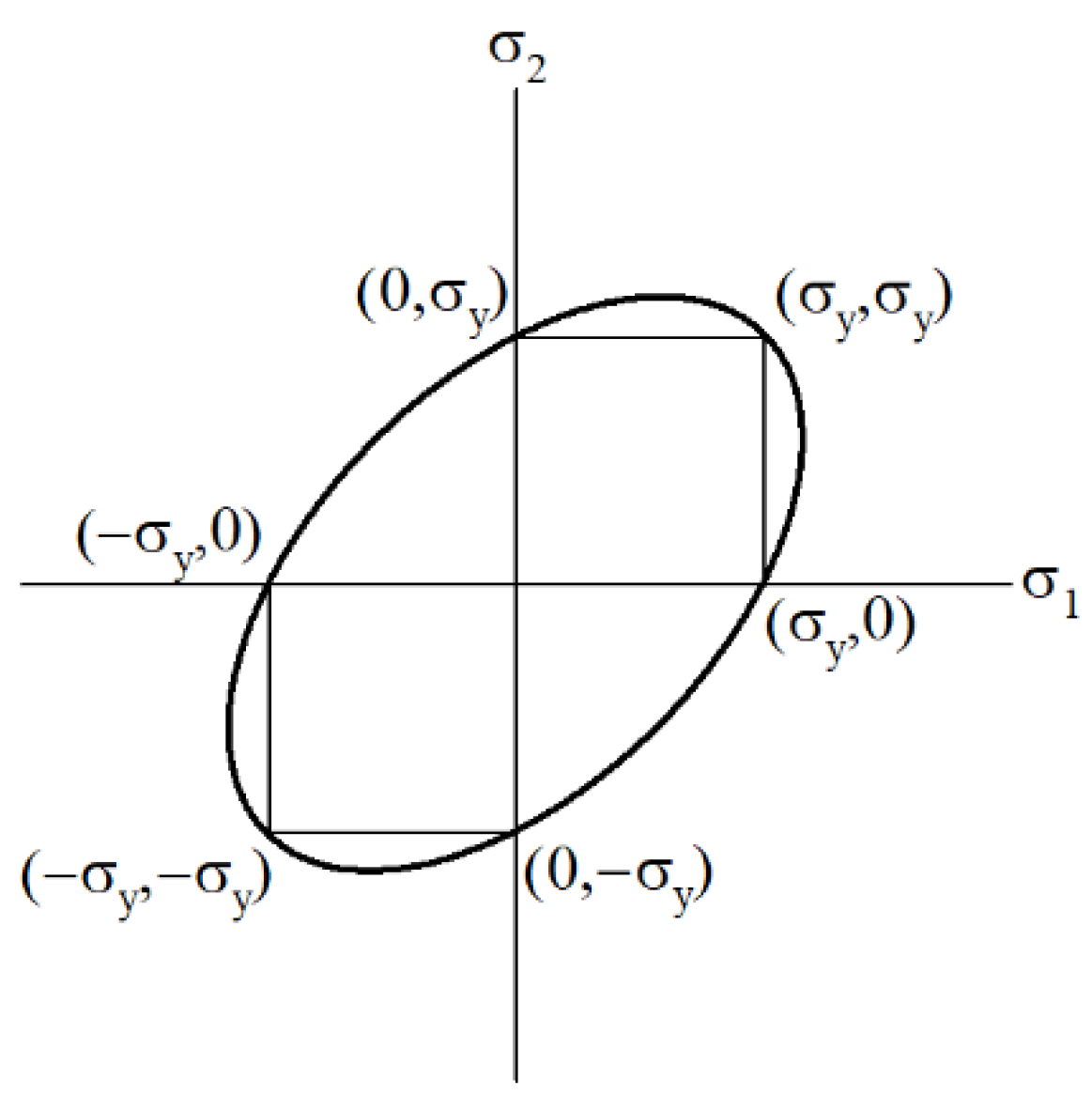


| Specimen | σy (N/mm2) | σu (N/mm2) | E (kN/mm2) |
|---|---|---|---|
| S1 | 348 | 446 | 194 |
| S2 | |||
| S3 | 352 | 449 | 205 |
| S4 |
| Specimen | BP (mm) | DP (mm) | t (mm) | σy (N/mm2) | σu (N/mm2) | E (kN/mm2) |
|---|---|---|---|---|---|---|
| S1 | 220 | 335 | 6.00 | 344 | 440 | 205 |
| S2 | ||||||
| S3 | 220 | 335 | 5.60 | 294 | 454 | 199 |
| S4 |
| Specimen | σc (N/mm2) | Ec (kN/mm2) |
|---|---|---|
| S1 | 47.6 | 31.7 |
| S2 | ||
| S3 | 49.5 | 30.2 |
| S4 |
| Test (kN) | Calculation (kN) | Analysis (kN) | Exp./Cal. (%) | Exp./Ana. (%) | |
|---|---|---|---|---|---|
| S1 | 16.0 | 16.7 | 16.8 | 95.8 | 95.2 |
| S2 | 15.8 | 16.8 | 94.6 | 94.0 | |
| S3 | 8.69 | 8.41 | 9.23 | 103 | 94.1 |
| S4 | 8.54 | 9.23 | 102 | 92.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nan, D.; Nakahara, H.; Chan, I. Effects of Out-of-Plane Deformation of the Base Plate on the Structural Behavior of an Exposed Column Base. Buildings 2024, 14, 3881. https://doi.org/10.3390/buildings14123881
Nan D, Nakahara H, Chan I. Effects of Out-of-Plane Deformation of the Base Plate on the Structural Behavior of an Exposed Column Base. Buildings. 2024; 14(12):3881. https://doi.org/10.3390/buildings14123881
Chicago/Turabian StyleNan, Ding, Hiroyuki Nakahara, and Iathong Chan. 2024. "Effects of Out-of-Plane Deformation of the Base Plate on the Structural Behavior of an Exposed Column Base" Buildings 14, no. 12: 3881. https://doi.org/10.3390/buildings14123881
APA StyleNan, D., Nakahara, H., & Chan, I. (2024). Effects of Out-of-Plane Deformation of the Base Plate on the Structural Behavior of an Exposed Column Base. Buildings, 14(12), 3881. https://doi.org/10.3390/buildings14123881






