Abstract
Rocking shallow foundations interrupt the seismic transmission path from the base of the structure and possess advantages, such as effective seismic isolation, self-resetting capabilities post-earthquake, and low costs. A numerical model of the rocking shallow foundation was developed in OpenSees (version: Opensees 3.5.0) based on field test data using numerical simulation. The effect of different parameters (column height, foundation sizes, top mass, and soil softness and stiffness) on the seismic response characteristics of rocking shallow foundations is investigated, and the seismic response characteristics of rocking shallow foundations are analyzed under the action of sinusoidal waves of different frequencies and various seismic wave types. The results of the study show that, as the height of the column increases, the bending moment decreases and settlement decreases; as the size of the foundation increases, the bending moment increases and settlement increases; as the mass of the top increases, the bending moment increases and settlement increases; and as the soil becomes softer, the bending moment decreases, and settlement increases. Inputting a sine wave that matches the structure’s natural oscillation frequency may induce resonance. This phenomenon can significantly amplify the structure’s vibrations; thus, it is essential to avoid external excitation frequencies that coincide with the foundation’s natural oscillation frequency. Under seismic loading, the rocking shallow foundation can mitigate the bending moment in the superstructure. When the displacement ratio remains within −0.5 to 0.5 percent, the foundation settlement is minimal. However, when the absolute displacement ratio exceeds 0.5 percent, the soil exhibits plastic deformation characteristics, resulting in increased foundation settlement. This study is an important contribution to the improvement of seismic performance of buildings and an important reference for improving seismic design standards and practices for buildings in earthquake-prone areas. In the future, the seismic response characteristics of rocking shallow foundations under bidirectional seismic action will be investigated.
1. Introduction
Shallow foundations are among the most commonly utilized types of foundations for houses and bridges. These foundations are employed extensively in industrial factories, medium- and low-rise residential buildings, and small to medium-span bridges. The application of shallow foundations in favorable ground conditions involves reduced design effort and is more economical. In seismic design, shallow foundations are typically assumed to be rigidly connected to the superstructure, or the interaction between foundations is considered linearly elastic, thereby neglecting the potential impacts of foundation interaction on seismic energy dissipation, isolation, and damping [1,2]. Significant redundancy exists in the actual design of shallow foundations. However, the lack of necessary seismic energy dissipation measures may lead to more severe damage to the superstructure during strong earthquakes [3]. During the 1995 Hanshin earthquake, plastic hinges were formed at the bases of the highway viaduct abutments, resulting in severe bending damage; however, the foundations and bases remained remarkably intact, with no ground deformation or cracking observed [4]. Similarly, during the 1999 Athens earthquake, a reinforced concrete building was constructed on a very rigid foundation. Although the foundation’s bearing capacity was exceptionally high, the superstructure developed plastic hinges at the ends of the columns and ultimately failed under seismic forces [5].
In response to this problem, the rocking shallow foundation was created to provide an effective solution. Rocking shallow foundation interrupts the seismic transmission path from the bottom of the structure and has the advantages of good seismic isolation, self-resetting after an earthquake and low cost [6]. Rocking shallow foundations allow the foundation to rotate during earthquakes, thereby absorbing and dissipating seismic energy to reduce the seismic response of the superstructure. This design helps prevent severe damage and collapse of the structure and provides greater safety [7,8]. Rocking shallow foundations perform better in earthquakes than conventional foundations. This is because they are able to return to their original position after an earthquake through a self-resetting mechanism and can reduce permanent deformation and damage [9]. In recent years, scholars at home and abroad have conducted a number of studies on rocking shallow foundation. Matthew J. DeJong [10] explored the fundamental behavior of swaying structures induced by horizontal ground motion. Angelo Di Egidio [11] et al. investigated the seismic response of a three-dimensional rigid body swaying on a horizontal support considering the eccentricity of the center of mass with respect to the geometric center. Mohammad G. Vetr [12] explored their efficiency as seismic systems with respect to conventional structures by numerically investigating low- and mid-rise sway structures. Ioannis E. Kavvadias [13] et al. proposed two new ground shaking spectral intensity measurements (IMs) to identify the ability of IMs to predict the rocking response under changes in block sizes by assumptions made by multiple ground motion recordings of multiple rocking rigid blocks. Jian Zhang [14] et al. investigated the rocking response of a rigid block under triangular impulses and found that the friction coefficient required to maintain the rocking rises with increasing impulse acceleration. The P. Kokkali [15] et al. study investigated the effect of shallow soil improvement on the nonlinear response of a rocking foundation when subjected to combined loading by conducting a series of centrifuge tests at the Earthquake Engineering Simulation Centre of the Rensselaer Polytechnic Institute. Wang Guobo [16] and other studies have comparatively analyzed the response of conventional foundation frame structures and sway frame structures under seismic action by means of shaking table tests and explored the effect of foundation lift-off on the seismic response of the structures. Roberto Paolucci [17] and others explored the behavior of shallow foundations in earthquakes by means of numerical simulations and shaking table tests carried out at the Public Works Research Institute in Japan. Sivapalan Gajan [18] et al. numerically simulated the soil-rocking foundation contact interface model by using OpenSees finite element software (version: Opensees 3.5.0).
In summary, numerous scholars have investigated the seismic response of rocking foundations; however, there is a scarcity of studies utilizing field test data. This paper utilizes the field test conducted by Keshab Sharma [19] as a study object, and a finite element model using OpenSees (version: Opensees 3.5.0) is developed based on this test. The seismic response characteristics of the rocking shallow foundation are examined by varying several parameters (column height, foundation dimensions, top mass, soil softness, and stiffness) and by inputting sinusoidal waves of varying frequencies, along with seismic waves of different accelerations, with the aim of providing a reference for the seismic design of rocking shallow foundations [20].
2. Numerical Modelling and Validation of Rocking Shallow Foundations
2.1. Numerical Modelling of Rocking Shallow Foundations
A simplified numerical computational model of the rocking shallow foundation was developed based on the field tests conducted by Keshab Sharma, utilizing the OpenSees finite element software, as illustrated in Figure 1 [21]. In this numerical calculation model, the superstructure is simplified as a concentrated mass, and both the intermediate columns and the foundation are simulated using elastic beam elements. The interaction between the soil and the foundation is modeled using springs. The interaction of the foundation’s base with the soil in vertical and horizontal directions is represented by Q–z springs and T–x springs, respectively, while the interaction of the foundation’s sides with the soil is represented by P–y springs. The parameter values for the Q–z, T–x, and P–y springs primarily include soil type, ultimate bearing capacity, displacement at half the ultimate bearing capacity, and radiation damping [22]. The specific parameter values for the springs in the numerical model of the rocking shallow foundation, based on the soil strength test data from field tests, are presented in Table 1, Table 2 and Table 3.
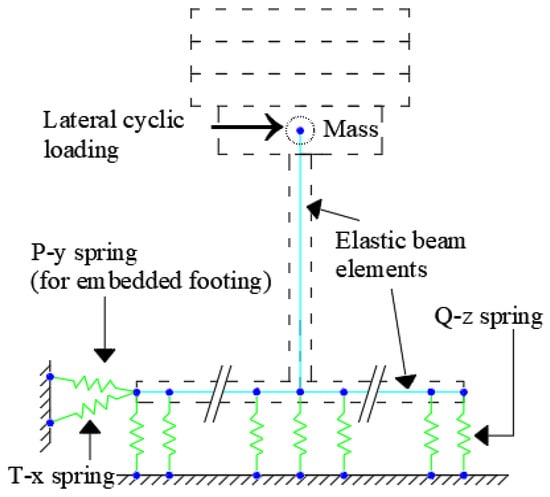
Figure 1.
Rocking Shallow Foundation OpenSees Model.

Table 1.
Parameters of P–y Spring Model.

Table 2.
Parameters of Q–z Spring Model.

Table 3.
Parameters of T–x Spring Model.
2.2. Validation of a Numerical Model of a Rocking Shallow Foundation
The reasonableness and accuracy of the numerical model for the rocking shallow foundation were verified by applying the same top displacement in the established numerical model as was utilized in the field test. Figure 2 illustrates the displacement ratio–bending moment curves, and the displacement ratio–settlement curves obtained from the numerical model calculations in comparison with the test results. Overall, the numerical model calculations exhibit general agreement with the field test results. Comparative calculations indicate that the errors of the numerical model’s bending moment for positive and negative loading compared to the field test results are 7.56% and 8.43%, respectively, while the settlement errors are 2.03% and 9.92%, respectively. The error arises because the superstructure is fixed during the field test; however, when displacement is applied, the base of the rocking foundation slips. Consequently, the bending moment and settlement results obtained from the field test are asymmetric, leading to a minor error. The error magnitude is within acceptable limits, indicating that the numerical model more accurately represents the bending moment and settlement behavior of the rocking shallow foundation.
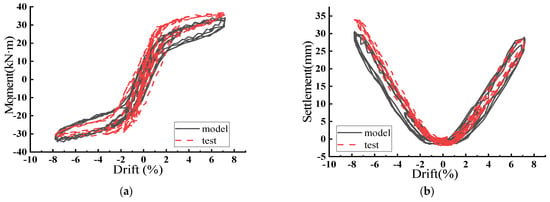
Figure 2.
Comparison of Finite Element Calculation Results with Test Results for Rocking Shallow Foundation. (a) Displacement Ratio–Moment; (b) Displacement Ratio–Foundation Settlement.
3. Analysis of the Effects of Various Parameters on Rocking Shallow Foundations
3.1. Column Height
Adopting the basic parameters of the model described in Section 2 of this paper, the height of the model columns were set to 2 m, 2.5 m, and 3 m, respectively, to obtain the settlement, as well as the bending moments of the rocking shallow foundation, as shown in Figure 3, and Table 4 and Table 5.
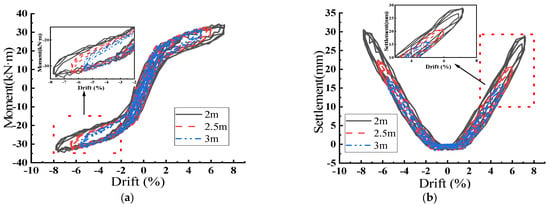
Figure 3.
Moments and Foundation Settlements for Rocking Shallow Foundations with Columns of 2m, 2.5m, 3m Heights. (a) Displacement Ratio–Moment; (b) Displacement Ratio–Foundation Settlement.

Table 4.
Maximum Moments for Models with Different Column Heights.

Table 5.
Maximum Foundation Settlements for Models with Different Column Heights.
As illustrated in Figure 3a and Table 4, the overall bending moment decreases with an increase in the column height. This phenomenon arises because a taller column experiences less displacement per unit length (displacement ratio) for the same top displacement, resulting in a reduced bending moment. When the top displacement is fixed, longer columns exhibit less curvature per unit length due to their increased flexibility, which leads to a reduction in the bending moment. As depicted in Figure 3b, when a fixed displacement is applied to the model’s top, the base sway diminishes as the column height increases. Taller columns exhibit greater flexibility, allowing them to absorb more energy for the same top displacement, resulting in reduced displacement and corresponding settlement experienced by the foundation. In a system with fixed top displacement, longer columns demonstrate increased flexibility. This implies that the displacement at the structure’s base is distributed, leading to reduced sway. As the column height increases, the application of fixed displacements at the top results in decreased bending moment and foundation sway amplitude. As the displacement ratio increases, both the bending moment and foundation sway amplitude also increase. This indicates that when the structure experiences greater lateral displacements, larger bending moments must be withstood, and the overall flexibility of the structure must be increased to effectively dissipate energy. Increasing the column height reduces the displacement ratio, thereby decreasing the bending moment and dissipating an equivalent amount of energy.
3.2. Foundation Sizes
Adopting the basic parameters of the model described in Section 2 of this paper, the size of the swing foundation is taken as 1.5 m × 1 m, 2 m × 1.5 m, and 3 m × 2 m, respectively; and the settlement, as well as the bending moments of the swing shallow foundation are obtained, as shown in Figure 4, and Table 6 and Table 7.
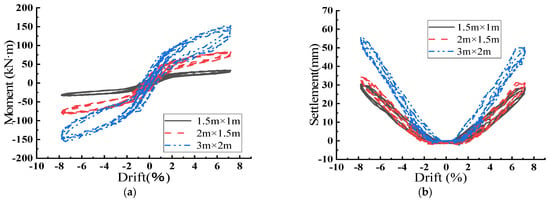
Figure 4.
Moments and Foundation Settlements for Rocking Shallow Foundations with Different Foundation Sizes. (a) Displacement Ratio–Moment; (b) Displacement Ratio–Foundation Settlement.

Table 6.
Maximum Moments for Models with Different Foundation Sizes.

Table 7.
Maximum Foundation Settlements for Models with Different Foundation Sizes.
As illustrated in Figure 4a and Table 6, the bending moment increases with an increase in foundation size. Larger foundations possess greater mass, resulting in increased inertial forces within the structure. Increased inertial forces during dynamic loading may reduce the rocking capacity of the foundation. Foundation swaying acts as an energy dissipation mechanism, allowing the structure to release energy under horizontal loading. A larger foundation size increases the overall stiffness and may inhibit swaying behavior. This occurs because a more rigid foundation is less susceptible to swaying, which diminishes energy dissipation. Furthermore, a larger foundation concentrates energy in the foundation-column cross-section rather than dispersing it through rocking. Consequently, with fixed displacement, more energy is converted into bending moments instead of being dissipated through foundation sway and soil deformation. As illustrated in Figure 4b and Table 7, base sway increases with an increase in base size. This phenomenon occurs because, when the foundation vibrates at the same angle of rotation, a larger foundation generates greater displacement, resulting in increased observed settlement values. By comparing the ratios of increase in bending moment and foundation settlement, it can be concluded that an increase in foundation size inhibits foundation sway.
3.3. Top Mass
Using the basic parameters of the model described in Section 2 of this paper, the top mass is taken as the original top mass, and two times the top mass, respectively, to obtain the settlement, as well as the bending moments of the rocking shallow foundation, as shown in Figure 5, and Table 8 and Table 9.
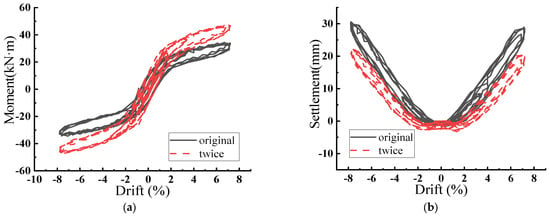
Figure 5.
Moments and Foundation Settlements for Rocking Shallow Foundations with Different Top Masses. (a) Displacement Ratio–Moment; (b) Displacement Ratio–Foundation Settlement.

Table 8.
Maximum Moments for Models with Different Top Masses.

Table 9.
Maximum Foundation Settlements for Models with Different Top Masses.
As illustrated in Figure 5a and Table 8, the bending moment increases with an increase in top mass. The increase in top mass results in a corresponding increase in inertia at the structure’s apex. Under the applied top displacement, this increased inertia results in a larger bending moment within the structure. As illustrated in Figure 5b and Table 9, the foundation settlement–displacement ratio curves are almost downward translational as the top mass increases. This phenomenon is attributed to the increase in top mass, which elevates the pressure exerted by the foundation on the underlying soil. The uplift at the foundation’s top decreases, while the downward settlement increases when subjected to top displacement. A comparison of Figure 3, Figure 4 and Figure 5 indicates that, while variations in column height, foundation size, and top mass affect the bending moment applied to the foundation, alterations in foundation size have the most significant impact. The maximum bending moment for foundation sizes of 1.5 m × 1 m and 3 m × 2 m differed by a factor of four, while the effects of other parameters were comparatively minor. This is attributable to the increased mass from the larger bottom dimensions, which significantly constrains the rocking response of the foundation. The difficulty in energy dissipation at the foundation–soil interface, along with the concentration of energy at the foundation–column joint, results in a sharp increase in the bending moment at this location.
3.4. Soil Stiffness
Adopting the basic parameters of the model described in Section 2 of this paper, the cohesion of the soil body is taken as 100 kpa, 80 kpa, and 50 kpa to simulate different soft and hard soils, and the settlement, as well as the bending moments of the swing type shallow foundation are obtained, as shown in Figure 6, and Table 10 and Table 11.
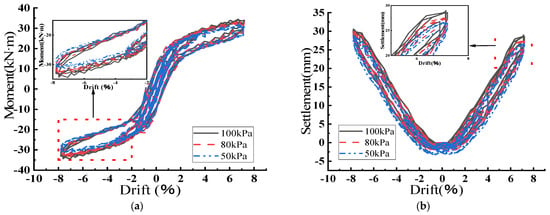
Figure 6.
Moment and Settlement Graphs for Models in Different Soft and Hard Soils. (a) Displacement Ratio–Moment; (b) Displacement Ratio–Foundation Settlement.

Table 10.
Maximum Moments in Different Soft and Hard Soils for the Model.

Table 11.
Foundation Settlements in Different Soft and Hard Soils for the Model.
4. Seismic Response Analysis of Rocking Shallow Foundations
4.1. Analysis of the Seismic Response of a Rocking Shallow Foundation Under Sinusoidal Wave Action
Resonance occurs when the frequency of an earthquake aligns with the building’s self-oscillation frequency [23]. Resonance can result in a substantial increase in the amplitude of vibrations within a building structure. This effect poses significant risks during an earthquake, potentially resulting in damage or even collapse of the building structure. In this section, a sine wave is designed to match the model’s self-oscillation frequency, while the model’s response characteristics are observed by varying the model’s self-oscillation frequency and inputting the designed sine wave.
The self-oscillation frequency of a structure is only related to stiffness and mass. It is an inherent property and is not affected by external forces. The self-oscillation frequency is calculated as:
where, “ω” is the angular frequency, “k” is the stiffness, “m” is the mass, “f” is the self-oscillation frequency, and “T” is the self-oscillation period.
The height of the column of the model described in the previous section is 2 m, at this time, the model self-oscillation period T = 0.67, self-oscillation frequency f = 1.48. When the height of the column is 1 m, the model self-oscillation period T = 0.40, self-oscillation frequency f = 2.52. When the height of the column is 4 m, the model self-oscillation period T = 1.30, self-oscillation frequency f = 0.77.
The sine wave function can be designed as:
From Figure 7, it can be seen that the frequency of the sine wave at this moment is 1.48 Hz, which is consistent with the self-oscillating frequency of the model at a column height of 2 m. By applying this sine wave to the bottom of the model, the rocking shallow foundation response obtained is shown in Figure 8.
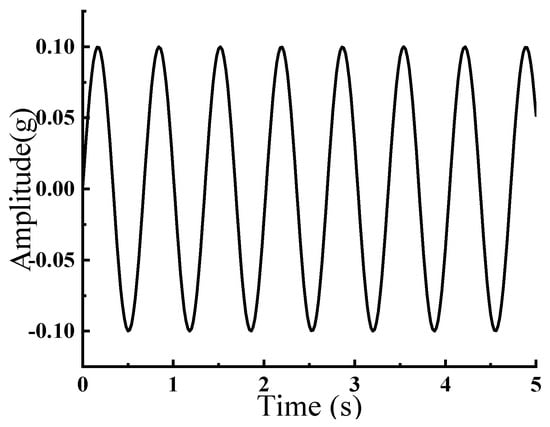
Figure 7.
Sine Wave Function Graph.
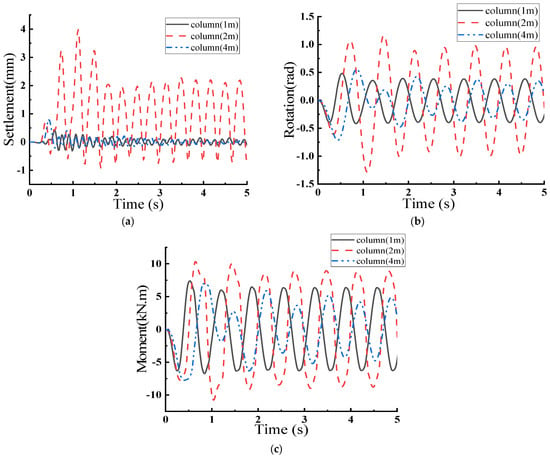
Figure 8.
Response of Rocking Shallow Foundation under the Action of Sine Wave y = 0.1sin (2.96πt). (a) Foundation Settlement–Time; (b) Top Rotation–Time; (c) Moment–Time.
As shown in Figure 8 and Table 12, the foundation settlement at a column height of 2 m is 3.98 mm, the rotation angle is 1.17, and the bending moment is 10.31 kN·m. It is significantly larger than the foundation settlement, rotation angle, and bending moments of the models at column heights of 1 m and 4 m.

Table 12.
Settlement, Rotation, and Moment for Rocking Shallow Foundation under Sine Wave Action.
The sine wave function can be designed as:
From Figure 9, it can be seen that the frequency of the sine wave at this moment is 2.52 Hz, which is consistent with the self-oscillating frequency of the model at a column height of 1 m.
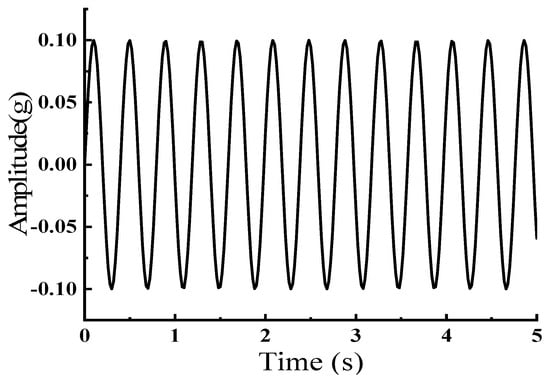
Figure 9.
Sine Wave Graph.
From Figure 10 and Table 13, it is observed that when the frequency of the sine wave coincides with the self-oscillation frequency of the model with a column height of 1 m, the foundation settlement is 2.92 mm, the rotation angle is 0.76, and the bending moment is 8.81 kN·m. Due to the resonance phenomenon, this value is significantly larger than those observed for column heights of 2 m and 4 m.
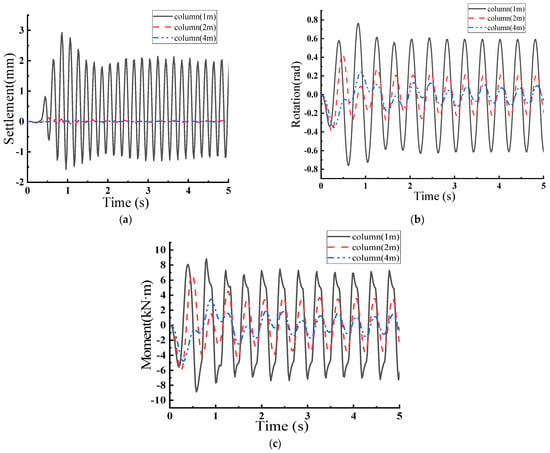
Figure 10.
Response of Rocking Shallow Foundation under the Action of Sine Wave y = 0.1sin (5.04πt). (a) Foundation Settlement–Time; (b) Top Rotation–Time; (c) Moment–Time.

Table 13.
Settlement, Rotation, and Moment for Rocking Shallow Foundation under Sine Wave y = 0.1sin (5.04πt) Action.
The sine wave function can be designed as:
From Figure 11, it can be seen that the frequency of the sine wave at this moment is 0.77 Hz, which is consistent with the self-oscillation frequency of the model with a column height of 4 m.
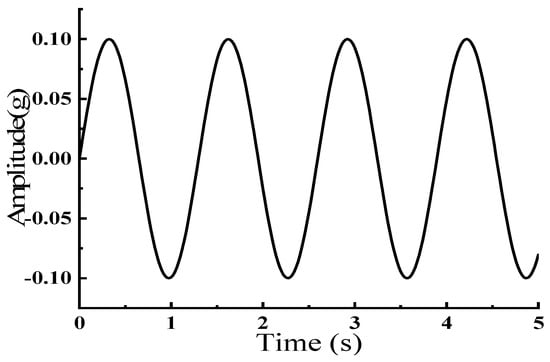
Figure 11.
Sine Wave Graph.
From Figure 12 and Table 14, it is observed that when the frequency of the sine wave coincides with the self-oscillation frequency of the model with a column height of 4 m, the foundation settlement reaches 2.6 mm, the rotation angle is 0.64, and the bending moment is 9.16 kN·m. Due to the resonance phenomenon, these values are significantly larger than those observed for column heights of 1 m and 2 m. When the frequency of the input wave coincides with the self-resonance frequency of the structure, the foundation experiences greater vertical displacement. This phenomenon occurs because vibrational energy is highly concentrated at resonance, resulting in increased forces on the foundation and thereby causing greater settlement. The increase in the rotation angle at the top of the structure is attributed to a rise in the amplitude of horizontal vibrations caused by resonance. Under resonance conditions, the top of the structure undergoes substantial lateral displacements, leading to larger corner angles. Additionally, the increase in the bending moment at resonance indicates that the structure is subjected to greater internal stresses.
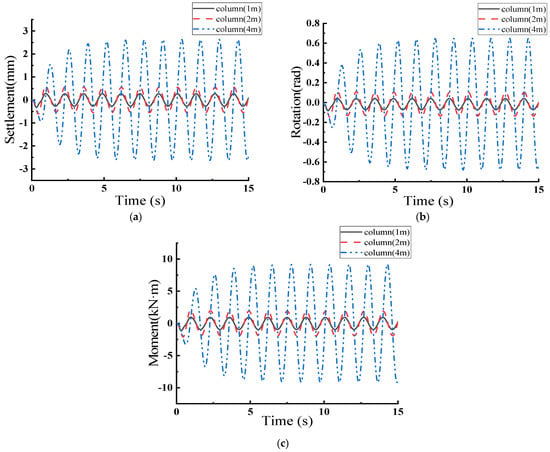
Figure 12.
Response of Rocking Shallow Foundation under the Action of Sine Wave y = 0.01sin (1.54πt). (a) Foundation Settlement–Time; (b) Top Rotation–Time; (c) Moment–Time.

Table 14.
Settlement, Rotation, and Moment for Rocking Shallow Foundation under Sine Wave y = 0.1sin (1.54πt) Action.
When the self-oscillation frequency of a structure or model coincides with the frequency of external excitation, resonance is experienced. This phenomenon results in a significant increase in the amplitude of vibration, as the structure achieves maximum amplitude at its natural frequency with minimal energy input. Thus, when the excitation frequency matches the self-oscillation frequency, foundation settlement, top rotation, and bending moment are greater than those modeled at other self-oscillation frequencies.
4.2. Seismic Response Analysis of Rocking Shallow Foundations Under Seismic Waves
The El Centro, Loma, and Taft waves are selected as input seismic waves, with their acceleration time courses and Fourier spectra presented in Figure 13, Figure 14 and Figure 15 [24,25,26]. The peak acceleration of each seismic wave is adjusted to 0.1 g, and seismic acceleration is applied at the base of the model to compare and analyze the response of the rocking shallow foundation to different seismic waves.
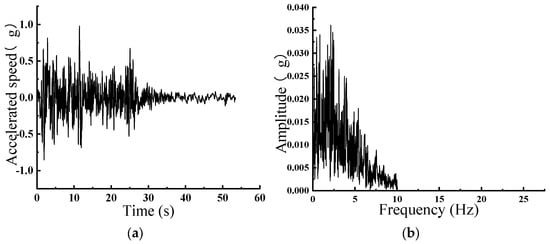
Figure 13.
1 g El Centro Earthquake Wave. (a) Acceleration Time History; (b) Fourier Spectrum.
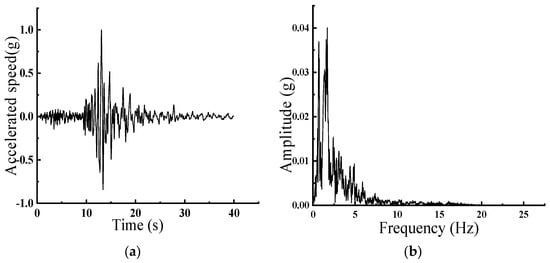
Figure 14.
1 g Loma Earthquake Wave. (a) Acceleration Time History; (b) Fourier Spectrum.
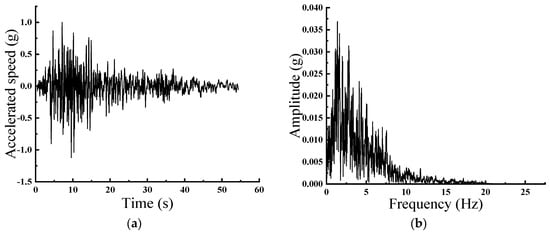
Figure 15.
1 g Taft Earthquake Wave. (a) Acceleration Time History; (b) Fourier Spectrum.
The rocking shallow foundation experiences a bending moment ranging from −8.35 kN·m to 8.84 kN·m and a displacement ratio varying from −0.73% to 0.7% under the influence of the 0.1 g El Centro wave. It can be observed in the figures that the variation of the bending moment in the middle section is predominantly linear with respect to the displacement ratio. The slopes of the bending moment curves at the ends exhibit slight changes, while the slopes of these curves diminish due to the interaction between the foundation and the soil, indicating the onset of energy dissipation. Under the action of the 0.1 g Loma wave, the bending moment of the rocking shallow foundation ranges from −10.84 kN·m to 9.0 kN·m, with a displacement ratio varying from −1.27% to 0.89%. A distinct change in the slope of the curve is evident when the displacement ratio in the negative direction is relatively large. For the 0.1 g Taft wave, the bending moment ranges from −8.47 kN·m to 9.02 kN·m, with a displacement ratio varying from −0.66% to 0.71%. The displacement ratio associated with the Taft wave is the smallest among the three scenarios, and the variation of the bending moment remains essentially linear. The magnitude of the displacement ratio reflects the degree of interaction between the foundation and the soil. A larger displacement ratio indicates a greater degree of interaction and energy dissipation, causing the bending moment curve to deviate from its original slope and exhibit non-linear growth.
From the figure, it can be concluded that the maximum settlement of the rocking shallow foundation is 1.71 mm for positive loading and 1.25 mm for negative loading under the 0.1 g El Centro wave. The figure shows that the settlement curve remains within a specific range for small absolute values of the displacement ratio, while the corresponding bending moment curve is linear. When the displacement ratio is relatively large, the settlement size increases beyond the original range, and the rate of change of the corresponding bending moment curve is reduced. This indicates that the decrease in the slope of the bending moment curve results from the interaction between the foundation and the soil. The rocking shallow foundation experiences a maximum settlement of 1.92 mm under positive loading and 3.94 mm under negative loading with a 0.1 g Loma wave. A significant decrease in the slope of the bending moment for the rocking shallow foundation during negative loading is observed in Figure 16b, corresponding to an increase in the settlement curve. The rocking shallow foundation exhibits a maximum settlement of 1.87 mm under positive loading and 1.34 mm under negative loading with a 0.1 g Taft wave. This represents the most stable behavior among the three settlement figures under the influence of a 0.1 g seismic wave. A negligible increase in edge settlement is observed in Figure 17c, which is consistent with the essentially linear response of the bending moment curve exhibited in the corresponding figure. A comparison of the three settlement diagrams reveals that the displacement ratio of the soil at the foundation ranges from −0.5% to 0.5%, which is stable in nature, while the settlement remains within a specific cyclic range. When the absolute value of the displacement ratio exceeds 0.5%, the soil exhibits characteristics of plastic deformation. The phenomenon of subsidence is no longer confined to a specific area, but rather shows a tendency to expand. The change in the bending moment applied to the upper part decreases at this time, reflecting the interaction between the foundation and the soil, as well as the dissipation of energy.
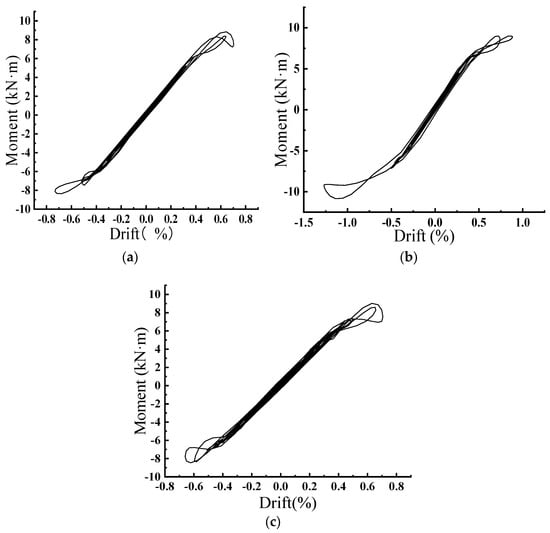
Figure 16.
Displacement Ratio–Moment Graphs under Different Earthquake Waves with a Peak Acceleration of 0.1 g. (a) Displacement Ratio–Moment under 0.1 g El Centro Wave; (b) Displacement Ratio–Moment under 0.1 g Loma Wave; (c) Displacement Ratio–Moment under 0.1 g Taft Wave.
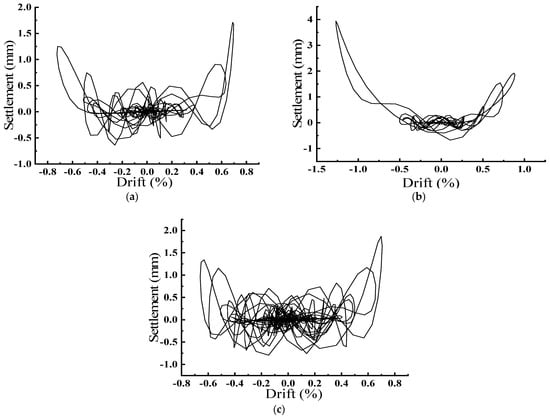
Figure 17.
Displacement Ratio–Settlement Graphs under Different Earthquake Waves with a Peak Acceleration of 0.1 g. (a) Displacement Ratio–Settlement under 0.1 g El Centro Wave; (b) Displacement Ratio–Settlement under 0.1 g Loma Wave; (c) Displacement Ratio–Settlement under 0.1 g Taft Wave.
5. Conclusions
In this paper, the method of numerical simulation is adopted. First, the computational accuracy of the numerical model is verified by comparison with experimental results. Next, the effects of various parameters on the rocking shallow foundation model are investigated. Finally, the response of the rocking shallow foundation model is analyzed under the influence of sine waves of different frequencies and three seismic waves with varying accelerations. The following basic conclusions are drawn:
- As the height of the column increases, the bending moment of the rocking shallow foundation decreases and settlement decreases; as the size of the foundation increases, the bending moment of the rocking shallow foundation increases and settlement increases; as the mass of the top increases, the bending moment of the rocking shallow foundation increases, the lifting of the foundation to the top decreases, and the settlement to the bottom increases; as the soil becomes softer, the bending moment of the rocking shallow foundation decreases, the settlement to the bottom increases, and the lifting of the foundation to the top decreases.
- By inputting a sine wave consistent with the structure’s self-oscillating frequency, it has been observed that, when the underlying self-oscillating frequency of a structure or model coincides with the frequency of an external excitation, the structure will experience resonance. Resonance phenomena may result in a substantial increase in the amplitudes of structural vibrations. This occurs because the structure can achieve maximum vibration amplitude at its natural frequency with minimal energy input. Therefore, measures should be taken to avoid the phenomenon of resonance in constructed buildings.
- A rocking shallow foundation can reduce the superstructure bending moment under seismic action. When the displacement ratio of the foundation is in the range of −0.5% to 0.5%, the settlement of the foundation is minimal. When the absolute value of the displacement ratio exceeds 0.5%, the soil is characterized by plastic deformation resulting in increased settlement.
- The bending moments and displacement ratios of rocking shallow foundations exhibit significant variations under different seismic waves. For the El Centro wave, the bending moment varies from −8.35 kN·m to 8.84 kN·m, with displacement ratios ranging from −0.73% to 0.7%. The data demonstrate a linear relationship. Under the action of Loma and Taft waves, the bending moments of rocking shallow foundation varied in the intervals from −10.84 kN·m to 9.0 kN·m and from −8.47 kN·m to 9.02 kN·m, respectively, and the bending moments varied more when the displacement ratio was negatively orientated, and the slope of the curve changes significantly.
Author Contributions
Conceptualization, J.B.; methodology, L.J.; software, J.B.; validation, Z.H. and P.P.; formal analysis, L.J.; investigation, Z.H., J.W. and P.P.; resources, J.B.; data curation, J.B.; writing—original draft preparation, J.B., Z.H. and P.P.; writing—review and editing, J.B., Z.H. and L.J.; visualization, J.B.; supervision, J.B.; project administration, J.B.; funding acquisition, J.B. and L.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (52308500); the Hunan Provincial Natural Science Foundation (2021JJ40171), China; the provincial-level college student innovation training program (S202211535086), China; and the special funding project for basic scientific research operations of the Institute of Engineering Mechanics, China Earthquake Administration (2020D15).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We are grateful to the anonymous reviewers for their constructive comments.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kannan, R.M.; James, N.; Haldar, P. Seismic Response of Rocking Shallow Foundation in RC Framed Structure: A Parametric Study. J. Vib. Eng. Technol. 2024, 12, 7121–7134. [Google Scholar] [CrossRef]
- Turner, M.M.; Ghayoomi, M.; Ueda, K.; Uzuoka, R. Performance of Rocking Foundations on Unsaturated Soil Layers with Variable Groundwater Levels. Géotechnique 2022, 72, 984–997. [Google Scholar] [CrossRef]
- Sharma, K.; Deng, L. Effects of Loading Obliquity on Field Performance of Rocking Shallow Foundations in Cohesive Soil. Géotechnique 2021, 71, 320–333. [Google Scholar] [CrossRef]
- Yashinsky, M.; Karshenas, M.J. Fundamentals of Seismic Protection for Bridges; Earthquake Engineering Research Institute (EERI): Oakland, CA, USA, 2003. [Google Scholar]
- Gazetas, G. Benefits of Unconventional Seismic Foundation Design. The 59th Rankine Lecture, British Geotechnical Association. 2019. Available online: https://www.youtube.com/watch (accessed on 26 October 2020).
- Zhou, Y.; Lv, X. State-of-the-Art on Rocking and Self-Centering Structures. J. Build. Struct. 2011, 32, 1–10. (In Chinese) [Google Scholar]
- Al-Janabi, M.A.Q.; Al-Jeznawi, D.; Bernardo, L.F.A. Modeling Techniques, Seismic Performance, and the Application of Rocking Shallow Foundations: A Review. CivilEng 2024, 5, 327–342. [Google Scholar] [CrossRef]
- Xiang, M.; Xiong, F.; Lu, Y.; Ge, Q.; Yan, H.; Ran, M. Structural Displacement Ratios for Seismic Evaluation of Structures on Rocking Shallow Foundations. Buildings 2022, 12, 174. [Google Scholar] [CrossRef]
- Lv, X.; Wu, D.; Zhou, Y. State-of-the-Art of Earthquake Resilient Structures. J. Build. Struct. 2019, 40, 1–15. (In Chinese) [Google Scholar]
- DeJong, M.J. Amplification of Rocking Due to Horizontal Ground Motion. Earthq. Spectra 2012, 28, 1405–1421. [Google Scholar] [CrossRef]
- Di Egidio, A.; Zulli, D.; Contento, A. Comparison Between the Seismic Response of 2D and 3D Models of Rigid Blocks. Earthq. Eng. Eng. Vib. 2014, 13, 151–162. [Google Scholar] [CrossRef]
- Vetr, M.G.; Nouri, A.R.; Kalantari, A. Seismic Evaluation of Rocking Structures Through Performance Assessment and Fragility Analysis. Earthq. Eng. Eng. Vib. 2016, 15, 115–127. [Google Scholar] [CrossRef]
- Kavvadias, I.E.; Papachatzakis, G.A.; Bantilas, K.E.; Vasiliadis, L.K.; Elenas, A. Rocking Spectrum Intensity Measures for Seismic Assessment of Rocking Rigid Blocks. Soil Dyn. Earthq. Eng. 2017, 101, 116–124. [Google Scholar] [CrossRef]
- Zhang, J.; Makris, N. Rocking Response of Free-Standing Blocks Under Cycloidal Pulses. J. Eng. Mech. 2001, 127, 473–483. [Google Scholar] [CrossRef]
- Kokkali, P.; Abdoun, T.; Anastasopoulos, I. Centrifuge Modeling of Rocking Foundations on Improved Soil. J. Geotech. Geoenviron. Eng. 2015, 141, 04015041. [Google Scholar] [CrossRef]
- Wang, G.; Wang, Y.; Yu, H.; Zheng, N.; Sun, F. Shaking Table Tests on Seismic Response of Rocking Frame Structure Considering Foundation Uplift. Chin. J. Geotech. Eng. 2021, 43, 2064–2074. (In Chinese) [Google Scholar]
- Paolucci, R.; Shirato, M.; Yilmaz, M.T. Seismic Behaviour of Shallow Foundations: Shaking Table Experiments vs Numerical Modelling. Earthq. Eng. Struct. Dyn. 2008, 37, 577–595. [Google Scholar] [CrossRef]
- Gajan, S.; Kayser, M. Quantification of the Influence of Subsurface Uncertainties on the Performance of Rocking Foundations During Seismic Loading. Soil Dyn. Earthq. Eng. 2019, 116, 1–14. [Google Scholar] [CrossRef]
- Sharma, K. Field Investigation and Performance-Based Seismic Design of Rocking Shallow Foundations in Cohesive Soil; University of Alberta: Edmonton, AB, Canada, 2019. [Google Scholar]
- Khamesi, S.O.; Mir Mohammad Hosseini, S.M. Numerical Investigation of the Main Factors Influencing Rocking Responses of Shallow Foundations. Proc. Inst. Civ. Eng.-Geotech. Eng. 2023, 176, 1–16. [Google Scholar] [CrossRef]
- Sharma, K.; Bin, J.; Deng, L. Performance-Based Seismic Design of Rocking Shallow Foundations in Cohesive Soil: Methodology and Numerical Validation. Soil Dyn. Earthq. Eng. 2022, 159, 107244. [Google Scholar] [CrossRef]
- Deng, L.; Kutter, B.L. Characterization of Rocking Shallow Foundations Using Centrifuge Model Tests. Earthq. Eng. Struct. Dyn. 2011, 41, 1043–1060. [Google Scholar] [CrossRef]
- Chen, S.; Liu, Q.; Zhai, C.; Wen, W. Influence of Building-Site Resonance and Building Properties on Site-City Interaction: A Numerical Investigation. Soil Dyn. Earthq. Eng. 2022, 158, 107307. [Google Scholar] [CrossRef]
- Zou, Z.; Lei, D.; Jiang, G.; Luo, B.; Chang, S.; Hou, C. Experimental Study of Bridge Foundation Reinforced with Frontand Back Rows of Anti-Slide Piles on Gravel Soil Slope under El Centro Waves. Appl. Sci. 2020, 10, 3108. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, X.; Wu, K.; Li, Z. Experimental Research on Dynamic Responses and Hydrodynamic Pressures of Deep-Water Bridge Piers under Seismic and Wave Actions. Eng. Struct. 2024, 313, 118276. [Google Scholar] [CrossRef]
- Dong, J.; Cong, X.; Ma, H.; Liu, Y.; Wang, Y. Pseudo-Dynamic Test on Composite Frame with Steel-Reinforced Recycled Concrete Columns and Steel Beams. Materials 2022, 15, 6355. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).