A Method for the Coefficient Superposition Buckling Bearing Capacity of Thin-Walled Members

Abstract

Axial compression tests were conducted on short rhombic tubes of different cross-sectional shapes. The deformation modes of the rhombic short tubes were obtained. To induce a finite element model with deformation modes consistent with the actual working conditions, buckling modes are introduced into the model as the initial imperfections of the structure. However, the buckling modes resulting from finite element buckling analyses often do not meet the needs of actual crushing modes. A coefficient superposition method of solution is proposed to derive modal characteristics consistent with the actual deformation modes by linear superposition of the buckling modes. Through the study of three aspects of theory, test, and simulation, and the comparison and verification of this method with the simulation results of related literature, the results show that the indexes derived from this method are closer to the actual circumstances and are more expandable, which provides a reference for the project.

1. Introduction

Thin-walled polygonal structures are used in important parts of a structure as the main energy absorption members, and axial compression is a common loading form [1,2]. In the early years, many scholars conducted theoretical studies on the axial compression characteristics of thin-walled structures [3,4], mostly based on the side panels of polygonal thin-walled structures, relying on the constraints imposed by the simplified boundary conditions. In actual engineering applications, thin-walled structures are often difficult to achieve in terms of idealized perfection due to their structural particularities, and the interaction between the plates causes non-ideal changes in the members, and there are unavoidable minor imperfections in the actual structure [5,6,7,8]. These inherent defects, when subjected to axial compressive loads, may contribute to the occurrence of flexural instability before the structure reaches its theoretical load-bearing capacity [9,10,11,12,13], thus posing a potential threat to the overall stability and safety of the structure. Imperfections in different locations can have different effects on the load-carrying capacity of thin-walled structures [14,15]. Therefore, the introduction of real imperfections to the finite element simulation can more accurately replay the actual working conditions.

In Abaqus 2016, the initial displacement of the structure is set as an imperfection. The initial displacements can be defined according to the following three methods: the buckling mode shapes of the structure, the displacements of the static analysis, and the direct definition of the nodal imperfections. Among them, the method of directly defining the structural node imperfection is the simplest. As early as 1983, the initial displacements of each node of the finite element model were set separately in the study of Tomas See [16], and the finite element simulation results were tested against the measured results to prove their feasibility. Subsequent studies have measured the dimensions of defects throughout the structure through high-precision instruments [17,18,19,20,21], but this method is costly and is suitable for small components. Xin et al. [22] proposed the random imperfection mode method and conformable imperfection method to introduce flexural modes to the finite element model of a dome structure, which avoids the cumbersome computational process and improves the computational efficiency. Zhang et al. [23,24], in their compression finite element simulations of thin-walled members, set multiple initial triggers at the collapse starting point of the structure to induce the buckling of the structure with different deformation modes. Tong et al. [25] created a finite element model with defects based on a combined modal defect method and verified that the defect model under a low-order multimodal combination had a high prediction accuracy. Unfortunately, the modal approach mentioned above often involves a combination of multiple algorithms with high technical complexity, which places higher requirements on personnel professionalism and is prone to misjudgment. At the same time, the introduced modes exhibit randomness and do not restore the actual failure mode of the structure well.

When performing a finite element nonlinear analysis, it is often not possible to obtain defect values for the structure as a whole. To induce a particular deformation mode in the structure, the overall buckling mode corresponding to it is generally introduced as an initial defect using modal superposition [26] and finite element calculations are performed. However, the base modes obtained based on the modal theory are due to the matrix positive definite requirement, and the flexural modes of polygonal cross-sections often do not meet the needs of the actual crushing modes. To better restore a defect model consistent with the actual deformation mode of the structure, while simplifying the modeling process, a new method is proposed in this paper to linearly superpose the known flexural modal amplitudes to derive the modal characteristics that are consistent with the actual members. The structural modes calculated by using this new superposition coefficients can well match the failure characteristics of the members. The load-carrying capacity calculated by simulation is also closer to the measured values.

2. Experiment and Parameter Design

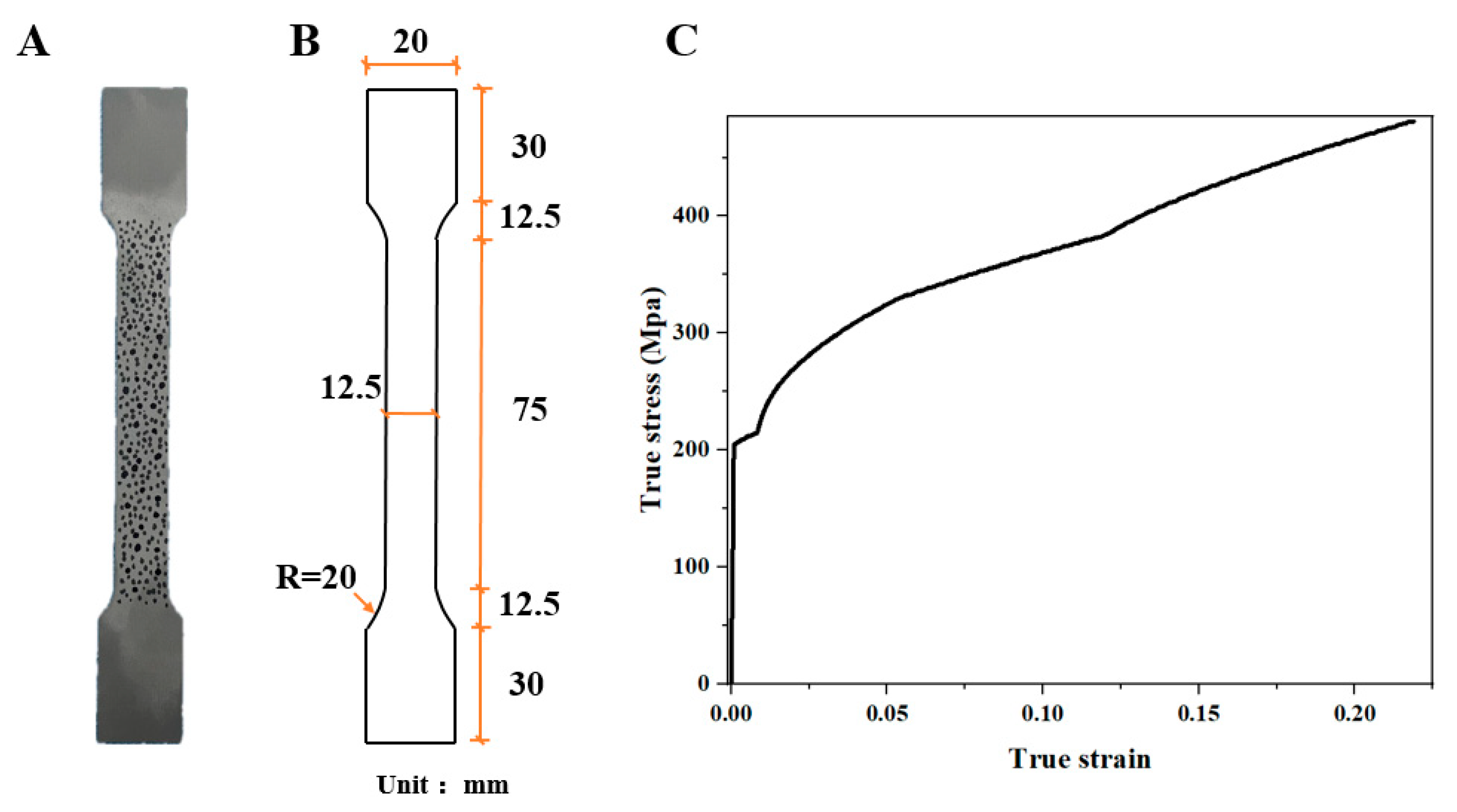
2.1. Overview of the Experiment

Axial compression tests were carried out on a set of rhombic short tubes to investigate the effect of the angle between the side plates on the compressive properties of the rhombic short tubes. The specimens used for the test were built by additive manufacturing technology and the process was layered manufacturing. The specimen is shown in Figure 1. The acute angles, ${\theta }_1,$ were 30°, 45°, 60°, and 90°. Except for the angular parameters, ${\theta }_1$ and ${\theta }_2$, the rest of the parameters remained unchanged: the height, the thickness, and the width of the plate on one side of the short tube were 30 mm, 0.6 mm, and 30 mm, respectively.

All tests in this paper were quasi-static axial compression tests. The test instrument used was an Electromechanical Universal Testing Machine produced by MTS Systems (China) Co., Ltd. (Eden Prairie, MN, USA) (in Figure 2). The model of the experimental machine was CMT5305 and the maximum loading value was 100 KN.

2.2. Material Properties

The material used for the test was stainless-steel 316 L. Since the layered fabrication process affects the mechanical properties of the members [27], tensile tests were conducted on standard tensile specimens to obtain accurate material parameters. The additively manufactured stainless-steel standard tensile flat specimen (flat specimen) and its specific dimensional parameters are plotted in Figure 3A,B, respectively [28]. A random scatter pattern was sprayed onto the surface of the specimen, and the test video was imported to GOM Correlate (GOM Software V2018), which allowed the variation in the calibrated distance of the specimen during tension to be recorded. Figure 3C plots the true stress–strain curve from the standard tensile test. According to the test data, the material parameters of the 316 L-type stainless steel used in the test can be seen: modulus of elasticity $E=218\mathrm{Gpa}$, Poisson’s ratio $\nu =0.26$, density $\rho =7592\mathrm{kg}/{\mathrm{m}}^3$, yield stress ${\mathsf{\sigma }}_{\mathrm{y}}=204\mathrm{Mpa}$, and ultimate stress ${\mathsf{\sigma }}_u=481\mathrm{Mpa}$.

3. Experimental Results

A total of four types of rhombic short tubes was tested in the compression test. Figure 4 plots the deformation of the specimen under the final moment of compression, the schematic diagram of the buckling mode, and the displacement–counterforce curve for the corresponding specimen. According to Figure 4, under axial compression, all the short rhombic tubes in the test buckled and were damaged, and 1st-order local buckling occurred in each side panel, showing different deformation modes. The difference between the buckling strength for each condition is small and much higher than the displacement values at other moments [29].

The tube can be divided into two parts: the side plate part and the folded corner part between the side plates. In the process of axial compression, the stiffness of the folded corner part is higher than that of the side plate, so the side plate buckles first, while the folded corner part can be regarded as elastic axial compression. Due to the defects of the specimen itself, the buckling of different side plates in the same specimen occurs in different directions. The buckling of the four side plates is relatively independent, which makes it possible to find an approximate linear buckling mode corresponding to any of the deformation modes in the same specimen.

4. Numerical Simulation

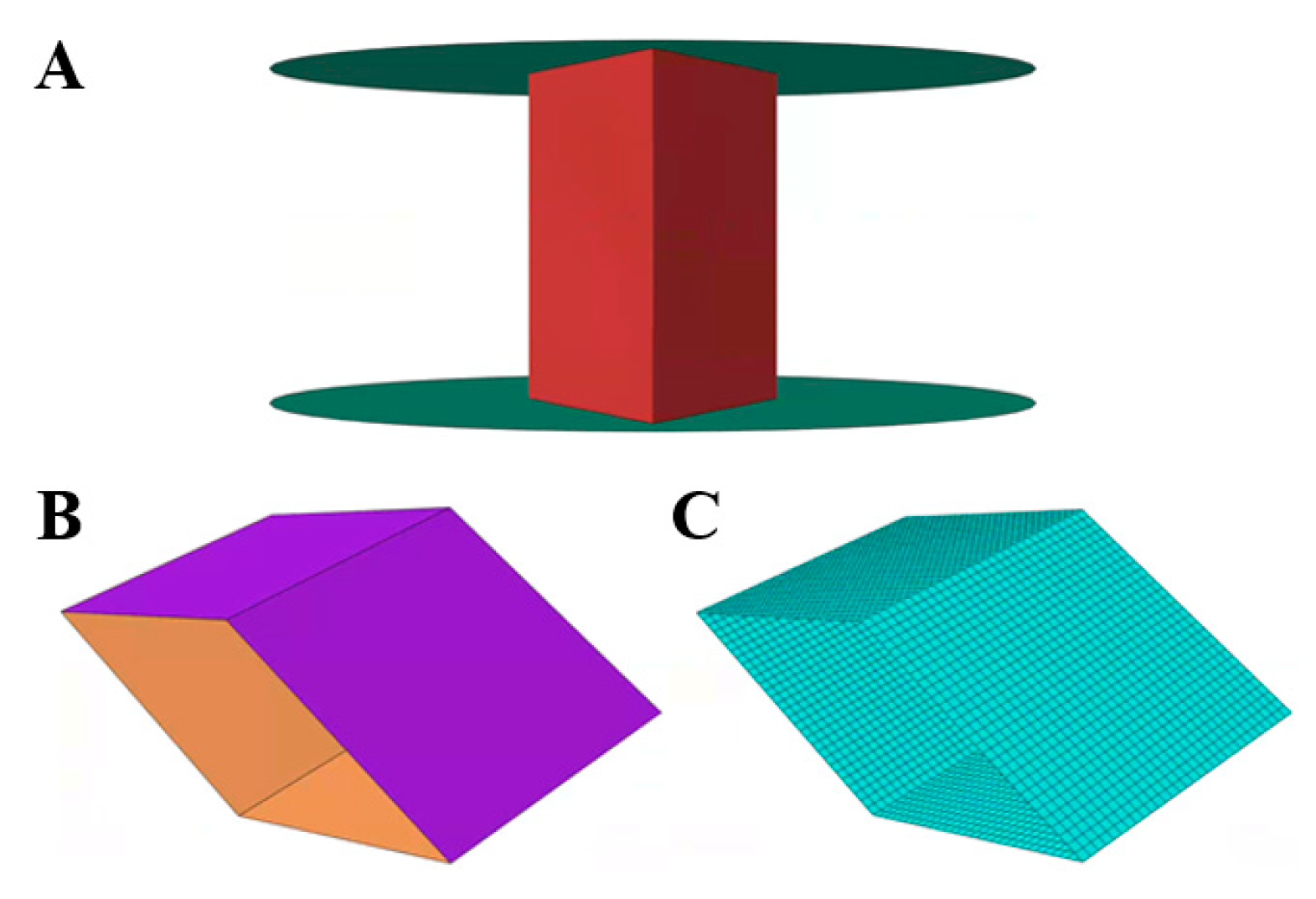
4.1. Finite Element Modeling

Finite element modeling was carried out using the finite element software Abaqus based on the dimensions of the test model. The finite element model is shown in Figure 5A. The dimensional parameters are shown in

Table 1. Superposition coefficient, ${\omega }_i$, of each working condition.

$$\mathbf{Angle}{\mathit{\theta }}_1$$ (°)	$$\mathit{\omega }$$	$$\overrightarrow{{\mathit{a}}_{\mathit{i}}}$$	$$\overrightarrow{\mathit{b}}$$	$${\mathit{\omega }}_1$$	$${\mathit{\omega }}_2$$	$${\mathit{\omega }}_3$$	$${\mathit{\omega }}_4$$
30	0.6	(1, −1, 1, −1)	(−1, −1, 1, −1)	0.3	−0.3	−0.3	0.3
		(1, 1, −1, −1)
		(1, −1, −1, 1)
		(−1, −1, −1, −1)
45		(1, −1, 1, −1)	(1, −1, −1, −1)	0	0.6	−0.6	−0.6
		(1, 1, −1, −1)
		(−1, 1, 1, −1)
		(1, 1, 1, 1)
60		(−1, 1, −1, 1)	(1, −1, 1, −1)	0.6	0	0	0
		(−1, −1, −1, −1)
		(1, 1, −1, −1)
		(1, −1, −1, 1)
90		(−1, 1, −1, 1)	(1, −1, 1, −1)	0.6	0	0	0
		(−1, −1, −1, −1)
		(1, −1, 1, −1)
		(1, 1, 1, 1)

. The negative direction of the specimen loading was set on the y-axis. The red short-pipe part in the model was the compression part, and the top and bottom two green circular plates were the loading plates. During the application of the axial compression load, the bottom loading plate stayed still and exerted full restraint. In contrast, the top loading plate exerted a displacement in the opposite direction to the y-axis. The width-to-thickness ratio, $b/t=50$, for each of the plates that make up the short tube falls into the category of thin-walled structures to simplify the computational effort of the simulation, whose position was defined as the middle. The material selected was 316 L stainless steel, and the material defines the normal positive direction of the plate shell (as shown in Figure 5B, the brown side is the positive direction and the purple side is the negative direction). We selected dynamics, explicit, and nonlinear analysis steps. For the results to converge, frictional hard contact between the plate and the upper and lower loaded ends was set, whose coefficient was set to 0.3. Tie constraints were created on the upper and lower sides of the plate to the loader. We set the global mesh seed due to the regular shape of the structure. The mesh size was set to 1 mm and the mesh delineation is shown in Figure 5C. After trial calculations, the compression results tended to converge.

4.2. Buckling Analysis

In [25], it is shown that setting initial imperfections can trigger specific deformation modes. According to the basic element method [7], the rhombic short-tube structure can be divided into four basic folding elements. The deformation mode of the folding elements predicts the overall energy absorption performance of the structure. The imperfection of adding pure local buckling modes can trigger different deformation modes—asymmetric (type I) versus symmetric (type II)—to occur in the basic folding element. In this case, the connecting strands between neighboring side panels remain straight in the buckling mode, the nodal displacements are zero, and only the buckling of the side panels is considered [30].

Buckling analysis includes linear buckling and nonlinear buckling. Linear buckling is based on the theory of small deformations and is solved once by establishing the equilibrium equations on the initial configuration of the structure without considering the structural defects, load eccentricities, etc. Its computational accuracy is poor due to ideal prerequisites and can be used to define initial defects for nonlinear buckling. Nonlinear buckling does not have the numerous preconditions of linear buckling analysis and is closer to engineering reality. In the finite element software Abaqus, linear buckling is performed through the linear regression of the buckling module to complete the calculation, while nonlinear buckling needs to use the nonlinear hydrostatic analysis to be solved. Therefore, in this buckling analysis process, firstly, linear buckling analysis is carried out by linear uptake. And secondly, the linear buckling analysis results, which are consistent with the actual experimental deformation modes, are used as the initial defects, and the defect amplitude is fixed to carry out the nonlinear static compression simulation in order to perform the nonlinear buckling analysis.

Figure 6 plots all the 1st-order results of the linear buckling modal analysis of the short rhombic tube by finite element software. There are only four results for each condition, totaling 16 linear buckling modes. However, modes corresponding to the experimental deformation modes (Figure 4) exist only for the conditions ${\theta }_1=60°$ and ${\theta }_1=90°$ (which are boxed). The results of the finite element buckling analysis fail to present the buckling modes for the remaining two conditions.

It is worth mentioning that, if the short tube structure is divided into four basic folding elements, the deformation modes of the folding elements affect the buckling modes of the overall structure. If two neighboring side panels are buckled in the same direction, there is a symmetrical basic folding element between the two panels; if they are in different directions, there is an asymmetrical basic folding element. As shown in Figure 6E, there is a difference in the displacement values of the symmetrical type of folding element concerning the asymmetrical type of folding element, mainly at the junction of the side panels. The symmetric folding element has a waveform slope of 0 at the boundary, while the waveform of the asymmetric folding element approximates a sinusoidal function. However, the overall waveforms are similar and have the same amplitude. Therefore, it can be assumed that the two waveforms are approximately the same. The side panels first buckle individually during the compression of the folding element, which then drives the overall buckling of the structure [31,32,33]. Therefore, the assumption is made that differences in the buckling modes at the side panel boundaries due to boundary conditions have little effect on the results of the induced buckling, as long as the direction of the induced local buckling of the side panels is determined.

4.3. Static Simulation of Compression

The downward pressure rate is small and falls into the quasi-static category. The explicit finite element method not only improves computational efficiency, but also effectively reduces computational non-convergence compared to static generic analyses [34,35,36,37,38]. To shorten the analysis time, dynamic analysis was chosen [39,40,41,42,43]. To minimize the impact of the shock effect generated by the loading rate on the quasi-static response, the simulated loading time was set to be 10-times the modal frequency period of the model’s 1st-order vibration modes [44]. The displacement of the loading plate is also loaded as a smooth curve (shown in Figure 7), which is second-order differentiable in the domain of definition and has zero slopes at the start and end points to reduce the oscillations generated by the stress wave [45]. To increase the computational efficiency, the mass scaling factor of the model was set to 100. The 1st-order buckling modal results were used as the initial displacements for the initial model. However, the absence of the buckling mode results in the inability to introduce buckling modes consistent with the experimental deformation modes for the model’s ${\theta }_1=30°$ and ${\theta }_1=45°$ cases.

5. Discussion

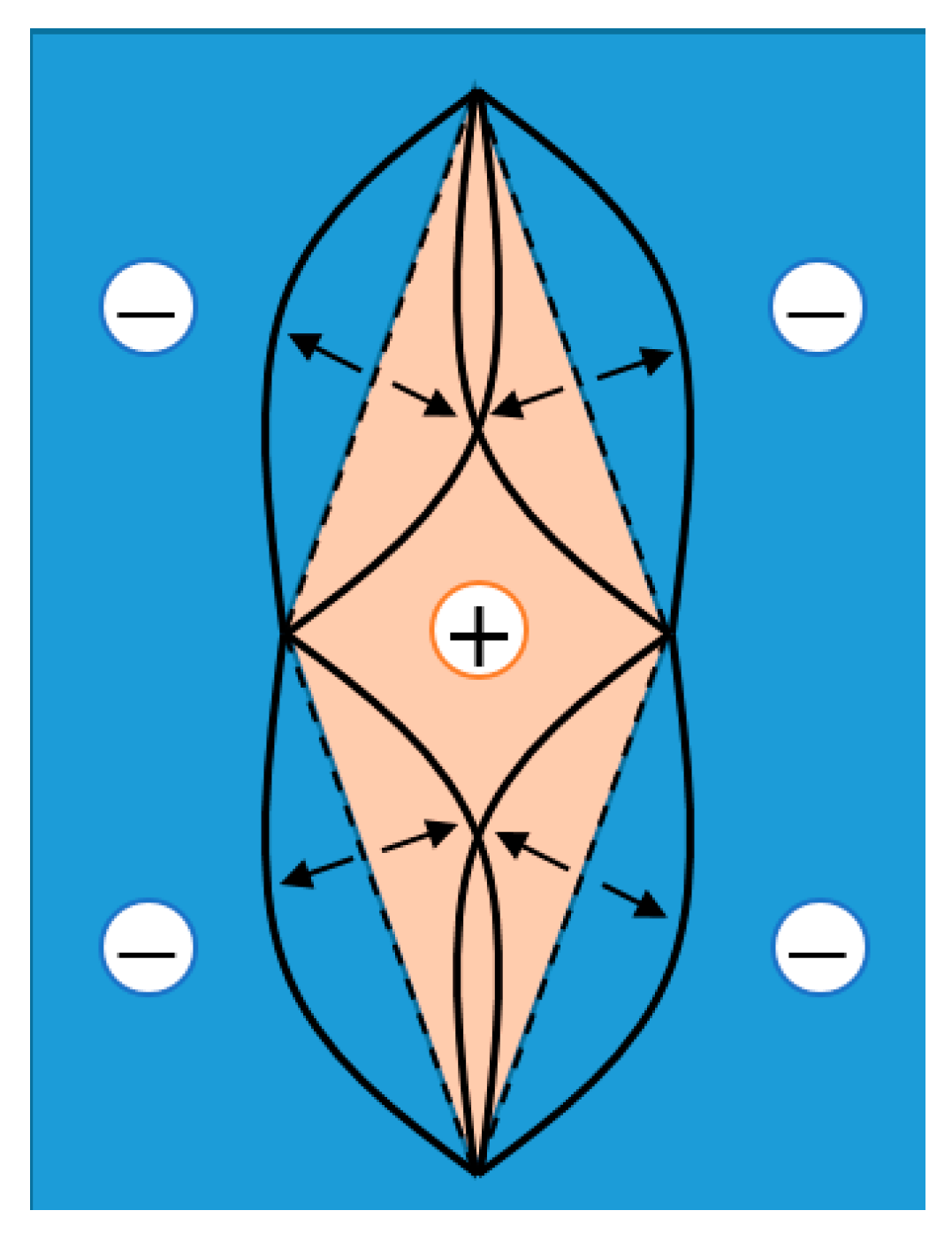
5.1. Representation of the Missing Mode

To represent the missing modes in the results of the buckling analysis, a representation of modal superposition applicable to the buckling of thin-walled structures is proposed. The results of the finite element buckling analysis were set as known modes and the buckling modes corresponding to the experimental deformation modes were set as target modes. If the structure undergoes purely local buckling in the side panels only, two $1\times 1$-type buckling modes occur in each side panel: buckling inward to the tube versus buckling outward to the tube. There is a total of four side panels for the short rhombic tube. For the structure as a whole, then, there is theoretically a total of $2^4$ locally buckling modes for the side panels of the rhombic stubs, not taking into account the equivalent case.

From the direction of the cross-section, the side panel in the upper-right corner is labeled as side panel No. 1 and is marked one by one in a clockwise order. Uniformly taking n nodes at the same location of each side panel, the initial imperfection $y\left(m\right)$ of the $m$th ($m=\mathrm{1,2},\dots ,n$) node on the NO. $j (j=\mathrm{1,2},\mathrm{3,4})$ side panel in the target buckling mode has the form:

$${\mathit{y}}_{\mathit{j}}\left(\mathit{m}\right)=\mathit{\omega }·{\mathit{\psi }}_{\mathit{j}}(\mathit{m})$$

(1)

where $\omega$ denotes the buckling scale factor of the target mode, which is set by the user according to the situation. ${\psi }_j\left(m\right)$ denotes the value of the normal displacement of the $m$th node on the $j$th side panel of the structure in the target buckling mode, whose result is provided by finite element software. Assuming that the unknown target mode is represented linearly through the four known buckling modes, the initial imperfection, $y_m$, of the target mode has the form:

$${\mathit{y}}_{\mathit{j}}\left(\mathit{m}\right)={\mathit{\omega }}_{\mathit{i}}{·\mathit{\psi }}_{\mathit{i}\mathit{j}}\left(\mathit{m}\right)={\mathit{\omega }}_1{·\mathit{\psi }}_{1\mathit{j}}\left(\mathit{m}\right)+{\mathit{\omega }}_2{·\mathit{\psi }}_{2\mathit{j}}\left(\mathit{m}\right)+{\mathit{\omega }}_3{·\mathit{\psi }}_{3\mathit{j}}\left(\mathit{m}\right)+{\mathit{\omega }}_4{·\mathit{\psi }}_{4\mathit{j}}\left(\mathit{m}\right)$$

(2)

where ${\omega }_i$ denotes the buckling scale factor for the $i$ ($i=\mathrm{1,2},\mathrm{3,4}$) known buckling mode of order 1, and ${\psi }_{ij}\left(m\right)$ denotes the value of normal displacement at node NO. $m$ for the vibration mode in the $i$th buckling mode.

Due to the symmetric, closed section, each side panel has the same boundary conditions. The four side panels have the same material, the same dimensions, and the same boundary conditions, resulting in the waveforms of the modes of the first-order local buckling of each side panel of the structure being approximately the same as those of the other side panels, with the only difference being the direction of buckling. Accordingly, a function $\psi \left(m\right)$ can be defined such that the following equation holds:

$$\mathit{\psi }\left(\mathit{m}\right)=\left|{\mathit{\psi }}_{\mathit{j}}\left(\mathit{m}\right)\right|={|\mathit{\psi }}_{\mathit{i}\mathit{j}}(\mathit{m})|$$

(3)

Define a symbolic function, $a_{ij}$, which represents the buckling orientation coefficient of side panel$j$ ($j=\mathrm{1,2},\mathrm{3,4}$) out of four side panels in the $i$th buckling mode, and takes the value of $\pm 1$, indicating the buckling orientation of the side panels. If the buckling direction is the outer side of the tube, $a_{ij}=1$, and vice versa, $a_{ij}=-1$. If no local buckling occurs in the side panel, $a_{ij}=0$; $b_j$ denotes the buckling orientation coefficient of side panel NO. $j$ in the target buckling mode (shown in Figure 8). Then, $a_{ij}$, $b_j$ can be represented as:

$$\begin{gathered} {\mathit{a}}_{\mathit{i}\mathit{j}}={\displaystyle \frac{{\mathit{\psi }}_{\mathit{i}\mathit{j}}\left(\mathit{m}\right)}{\mathit{\psi }\left(\mathit{m}\right)}} \\ {\mathit{b}}_{\mathit{j}}={\displaystyle \frac{{\mathit{\psi }}_{\mathit{i}}\left(\mathit{m}\right)}{\mathit{\psi }\left(\mathit{m}\right)}} \end{gathered}$$

(4)

where ${\psi }_{ij}\left(m\right)$ denotes the normal displacement value of the vibration mode at node $m$ of $j$ plates for the $i$th buckling mode. Similarly, $y_{jm}$ denotes the normal displacement value of the vibration mode in the target buckling mode at node NO. $m$ of plate NO. $j$. Substituting Equations (1) and (4) into Equation (2) provides:

$$\mathit{\omega }·{\mathit{b}}_{\mathit{j}}·\mathit{\psi }\left(\mathit{m}\right)={\mathit{\omega }}_{\mathit{i}}·{\mathit{a}}_{\mathit{i}\mathit{j}}·\mathit{\psi }\left(\mathit{m}\right)={\mathit{\omega }}_1·{\mathit{a}}_{1\mathit{j}}·\mathit{\psi }(\mathit{m})+{\mathit{\omega }}_2·{\mathit{a}}_{2\mathit{j}}·\mathit{\psi }(\mathit{m})+{\mathit{\omega }}_3·{\mathit{a}}_{\mathit{j}}·\mathit{\psi }(\mathit{m})+{\mathit{\omega }}_4·{\mathit{a}}_{\mathit{j}}·\mathit{\psi }(\mathit{m})$$

(5)

Simplifying the above equation gives:

$${\mathit{b}}_{\mathit{j}}={\displaystyle \frac{{\mathit{\omega }}_{\mathit{i}}}{\mathit{\omega }}}·{\mathit{a}}_{\mathit{i}\mathit{j}}={\displaystyle \frac{{\mathit{\omega }}_1}{\mathit{\omega }}}·{\mathit{a}}_{1\mathit{j}}+{\displaystyle \frac{{\mathit{\omega }}_2}{\mathit{\omega }}}·{\mathit{a}}_{2\mathit{j}}+{\displaystyle \frac{{\mathit{\omega }}_3}{\mathit{\omega }}}·{\mathit{a}}_{3\mathit{j}}+{\displaystyle \frac{{\mathit{\omega }}_4}{\mathit{\omega }}}·{\mathit{a}}_{4\mathit{j}}$$

(6)

Let $x_i={\omega }_i/\omega$, then Equation (6) can be expressed as:

$${\mathit{b}}_{\mathit{j}}={\mathit{x}}_{\mathit{i}}·{\mathit{a}}_{\mathit{i}\mathit{j}}={\mathit{x}}_1·{\mathit{a}}_{1\mathit{j}}+{\mathit{x}}_2·{\mathit{a}}_{2\mathit{j}}+{\mathit{x}}_3·{\mathit{a}}_{3\mathit{j}}+{\mathit{x}}_4·{\mathit{a}}_{4\mathit{j}}$$

(7)

The full expansion of Equation (7) is:

$$\left\{\begin{array}{c}{\mathit{b}}_1={\mathit{x}}_1·{\mathit{a}}_{11}+{\mathit{x}}_2·{\mathit{a}}_{21}+{\mathit{x}}_3·{\mathit{a}}_{31}+{\mathit{x}}_4·{\mathit{a}}_{41}\\ {\mathit{b}}_2={\mathit{x}}_1·{\mathit{a}}_{12}+{\mathit{x}}_2·{\mathit{a}}_{22}+{\mathit{x}}_3·{\mathit{a}}_{32}+{\mathit{x}}_4·{\mathit{a}}_{42}\\ {\mathit{b}}_3={\mathit{x}}_1·{\mathit{a}}_{13}+{\mathit{x}}_2·{\mathit{a}}_{23}+{\mathit{x}}_3·{\mathit{a}}_{33}+{\mathit{x}}_4·{\mathit{a}}_{43}\\ {\mathit{b}}_4={\mathit{x}}_1·{\mathit{a}}_{14}+{\mathit{x}}_2·{\mathit{a}}_{24}+{\mathit{x}}_3·{\mathit{a}}_{34}+{\mathit{x}}_4·{\mathit{a}}_{44}\end{array}\right.$$

(8)

To express the different buckling modes more simply, set the target mode vectors $\overrightarrow{b}=(b_1,b_2,b_3,b_4)$ to denote the orientation vectors of each side panel of the target buckling mode; set the known mode vectors $\overrightarrow{a_i}=(a_{i1},a_{i2},a_{i3},a_{i4})$ to denote the orientation vectors of each side panel for the known buckling modes. Then, Equation (8) can be simplified as:

$$\overrightarrow{\mathit{b}}=\left[\overrightarrow{{\mathit{a}}_1},\overrightarrow{{\mathit{a}}_2},\overrightarrow{{\mathit{a}}_3},\overrightarrow{{\mathit{a}}_4}\right]\overrightarrow{\mathit{x}}={\mathit{A}}_{4\times 4}\overrightarrow{\mathit{x}}$$

(9)

According to Figure 2, it can be seen that $\overrightarrow{b}=(1,-1,-1,-1)$ for the present operating condition, and the orientation vectors $\overrightarrow{a_i}$ for each side panel of the known modes are shown in Figure 2. Since $r\left(A_{4\times 4}\right)=r\left(A_{4\times 4}|\overrightarrow{b}\right)=4$, $\overrightarrow{x}$ has a unique solution.

Set the amplitude of the buckling mode to the side panel thickness. Based on the dimensions of the structure, define the scale factor $\omega =0.6$ for the target modes. The superposition coefficients, ${\omega }_i$, for each operating condition are shown in Table 1. Finally, the results of different linear buckling modes are simultaneously introduced into the nonlinear buckling analytical static model according to the values of the buckling superposition coefficients; simulation results consistent with the deformation patterns of the experimental results are obtained.

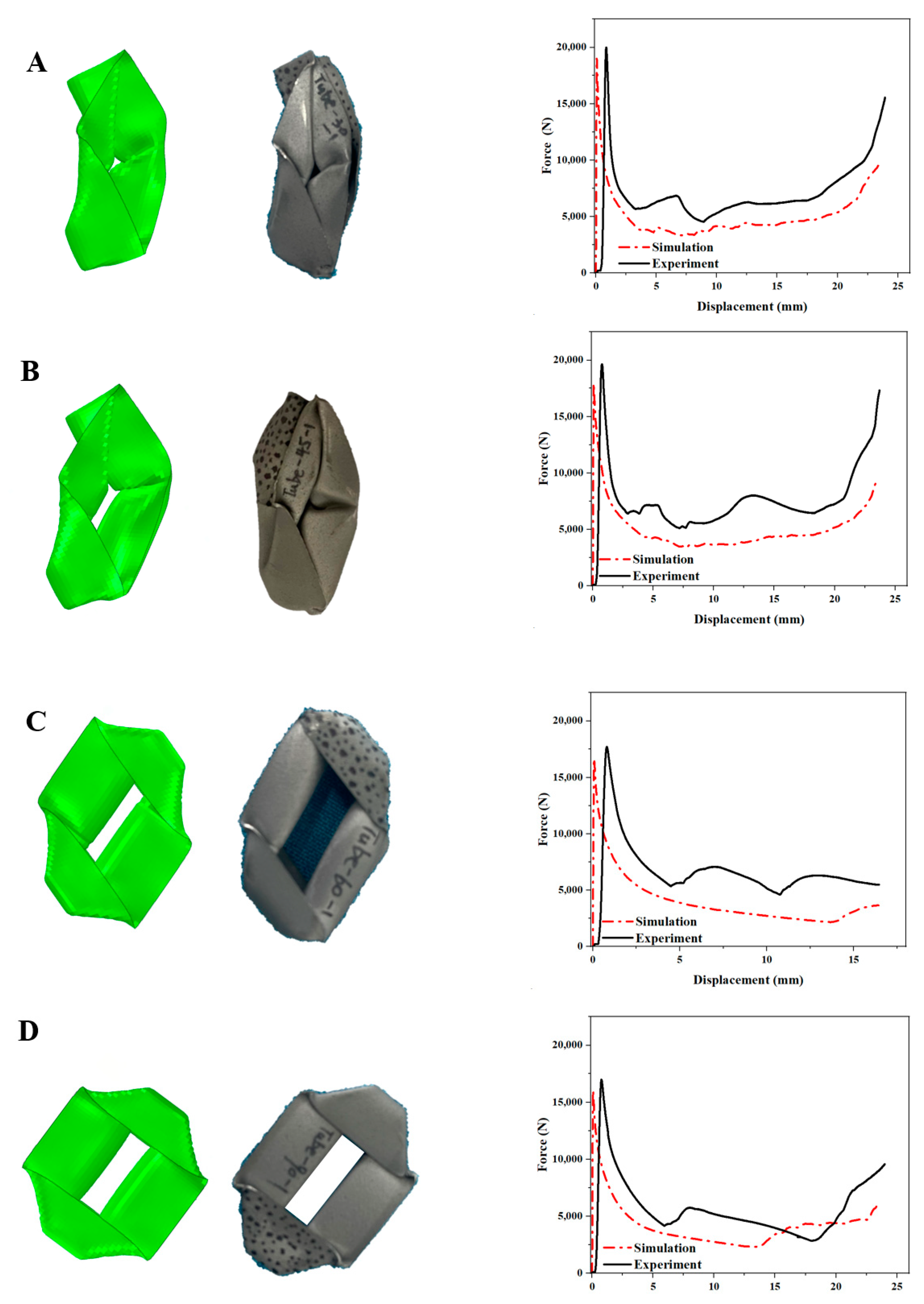
5.2. Results of the Simulation

Table 2. The comparison between the experimental value and the simulated value of the initial peak crushing force.

Serial Number	${\mathit{\theta }}_1$ (°)	$\overrightarrow{\mathit{b}}$	$\mathbf{Width}\mathit{b}$ (mm)	$\mathbf{Height}\mathit{h}$ (mm)	$\mathbf{Thickness}\mathit{t}$ (mm)	$\mathit{\omega }$	Initial Peak Crushing Force (KN)
							Experiment	Simulation
Tube30	30	(−1, −1, 1, −1)	30	30	0.6	0.6	19.990	19.005
Tube45	45	(1, −1, −1, −1)					19.644	17.933
Tube60	60	(1, −1, 1, −1)					17.711	16.642
Tube90	90	(1, −1, 1, −1)					16.993	16.018

compares the experimental and simulated values of buckling capacities for different clamping angles, ${\theta }_1$, under the working conditions with the introduction of superimposed buckling modes as the initial imperfection. Figure 9 compares the post-compression behavior of the finite element model and the experimental model after the introduction of the target modes. According to Table 2, the trend of the test values and the simulated values is the same and the results are similar; the buckling capacity decreases with the increase in the angle, ${\theta }_1$. As can be seen from Figure 9, the introduction of the target mode successfully triggers the finite element short-tube model to undergo a deformation mode consistent with the experimental short-tube model, independent of the deformation mode of the basic folding condition. The assumption that differences in buckling modes due to boundary conditions have a small effect on the results of finite elements is confirmed, as well as the feasibility of the abovementioned method of calculating the modal superposition coefficients.

5.3. Extension Form of the Method

For any thin-walled structure with $n$ $(n\ge 3)$ side panels, regardless of whether the cross-section is closed or not, with buckling scale factor $\omega$, the buckling orientation factor of the $i$th (i$=\mathrm{1,2},\dots ,n$) known buckling mode for side panel NO. $j$ ($j=\mathrm{1,2},\dots ,n$) is $a_{ij}$, and the target buckling mode orientation factor is $b_j$. Set the vectors $\overrightarrow{a_i}=(a_{i1},a_{i2},\dots ,a_{in})$, $\overrightarrow{b}=(b_1,b_2,\dots ,b_n)$, and the matrix $A_{n\times n}=[\overrightarrow{a_1},\overrightarrow{a_2},\dots ,\overrightarrow{a_n}]$. If the following conditions are satisfied:

(1)

n side panels have the same material, dimensions, and boundary conditions;

(2)

Only 1 × 1 type of local buckling or non-buckling occurs in each side panel;

(3)

At least n of these buckling modes is known and $r\left(A_{n\times n}\right)=r\left(A_{n\times n}|\overrightarrow{b}\right)=n$;

Then, any one of the other buckling modes of the short tube can be represented linearly by the known buckling modes, and the superposition coefficient ${\omega }_i$ of each mode is the solution of the following set of equations:

$${\mathit{a}}_{\mathit{i}\mathit{j}}{\mathit{\omega }}_{\mathit{i}}=\mathit{\omega }{\mathit{b}}_{\mathit{j}}$$

(10)

5.4. Finite Element Verification

Existing codes have limitations. For example, the American Iron and Steel Institute Steel Standard does not apply to sections with angles exceeding 120°. Otherwise, the calculated values of the standards tend to be conservative. To verify the extension form of the buckling modal superposition coefficient calculation method, simulations were carried out for the double-plate structure, the regular triangular stub, the regular hexagonal stub, and the regular octagonal stub. The simulation results were compared with the experimental results in the references. The dimensions of each specimen of the reference literature are shown in

Table 3. Size parameters of specimens in the references.

Author	Shape	Material	Parameters of a Side Panel			Initial Peak Crushing Force
			Width (mm)	Height (mm)	Thickness (mm)	$\mathbf{Experimental}\mathbf{Values}{\mathit{F}}_{\mathit{e}\mathit{x}\mathit{p}}$ (KN)	$\mathbf{Simulated}\mathbf{Values}{\mathit{F}}_{\mathit{s}\mathit{i}\mathit{m}}$ (KN)	$\mathbf{Simulated}\mathbf{Values}{{\mathit{F}}_{\mathit{s}\mathit{i}\mathit{m}}}^{\mathit{\prime }}\mathbf{in}\mathbf{This}\mathbf{Paper}$ (KN)
Alavi Nia [46]	Triangle	Aluminum alloy	62.8	100	1.5	31.346	31.350	32.605
Alavi Nia [46]	Hexagon	Aluminum alloy	31.4	100	1.5	36.875	25.540	31.441
Zhang [23]	Hexagon	Mid-steel Q235	40	180	1.2	59.021	65.825	58.590
Zhang [23]	Octagon	Mid-steel Q235	40	180	1.2	82.446	86.087	81.305
Fan [47]	Hexagon	Mid-steel	33.2	100	1.5	95.7	85.9	95.303
Fan [47]	Octagon	Mid-steel	24.9	100	1.5	110.2	90	100.896

. Figure 10 plots the ratio of the simulated value $F_{sim}$ and deformation modes from the references to the experimental value $F_{exp}$ that agrees with the references, as well as the ratio of the simulated value ${F_{sim}}^{’}$ of the model of the present method to the experimental value $F_{exp}$ from the references. According to Figure 10, the simulated values obtained by the method used in this paper are more stable and closer to the experimental values than the simulation results in the references.

5.5. Significance of the Method

(1)

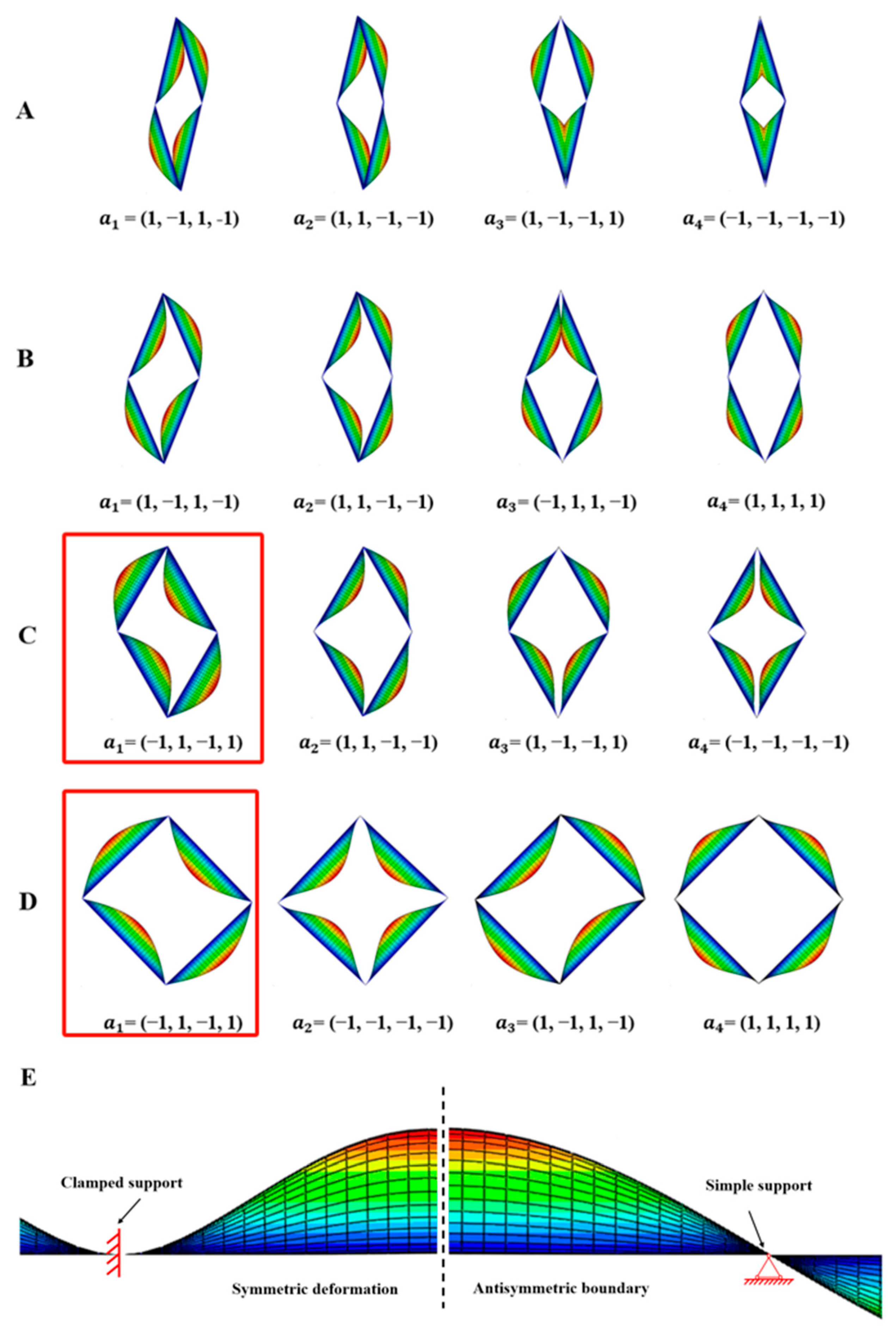
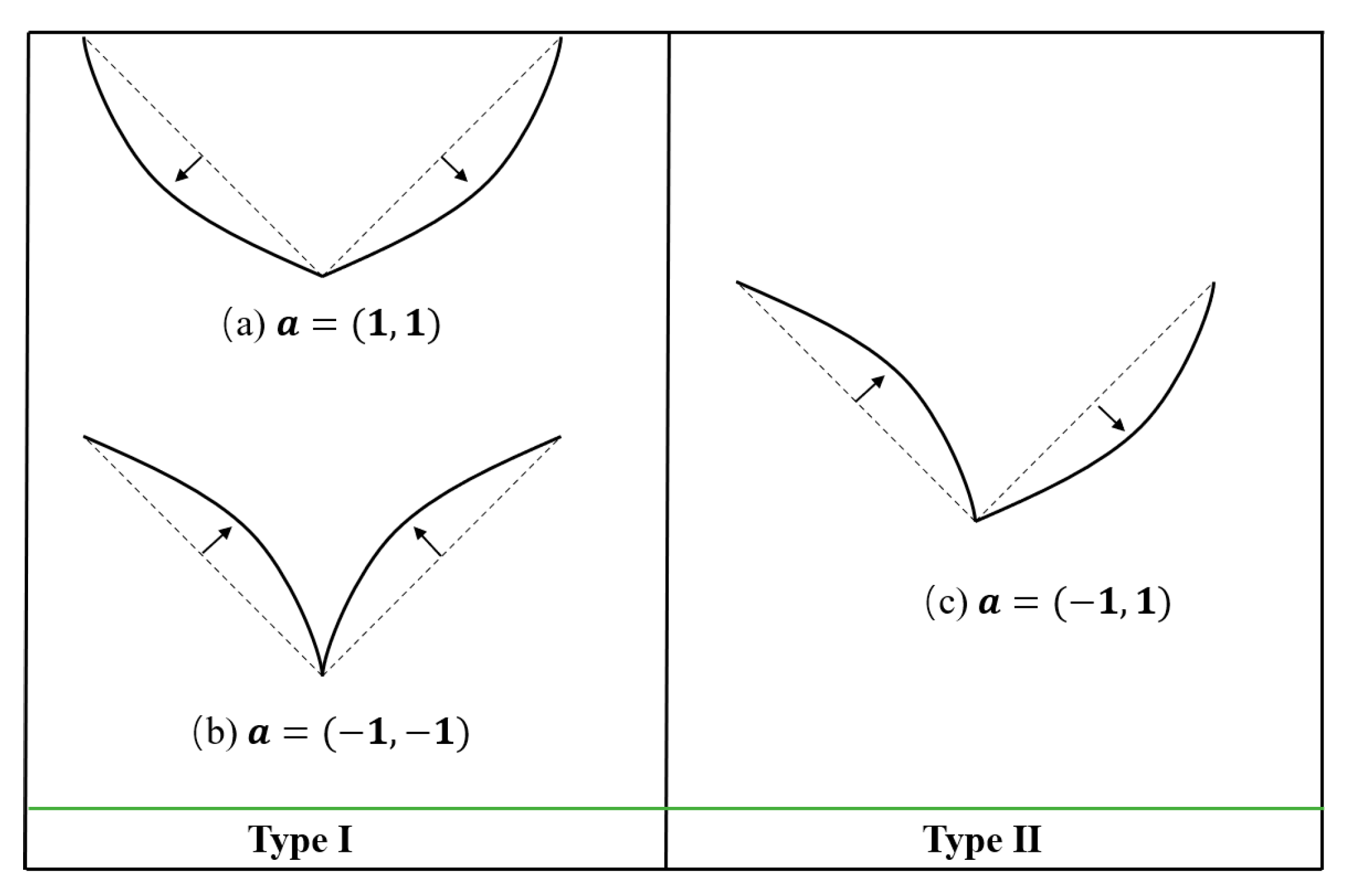
More intuitive naming rules. Due to the peculiarity of the deformation modes of the structure, the buckling mode vector of the structure can be used as the name of the structure. Compared to the previous classification of the deformation modes of the basic folding elements into asymmetric (Type I) and symmetric (Type II), the present method allows for the further classification of arbitrary deformation modes, as shown in Figure 11. Such naming provides a visual representation of the deformation mode of the structure, and the more sides there are, the more efficiently the information is conveyed. At the same time, the method is richly extensible and equally applicable to higher-order buckling.

(2)

Simpler finite element modeling. In general, to simulate the structure, the instrument is used to measure the defects of the structure and the initial displacement value is provided according to the node. This method is expensive and does not apply to large structures. This method only needs to derive the global initial defect through the boundary conditions of the structure and the displacement of the center point of each plate, which makes the modeling process simpler.

(3)

More accurate simulation results. By recording the actual buckling characteristics of the structure, this method superimposes the known modes on the basis of the random mode method, which more accurately restores the buckling characteristics of the structure, and the simulation results are more accurate.

6. Conclusions and Outlook

A set of short rhombic tubes with different angles was tested using axial compression test by an experimental loading machine, a superposed theory of buckling modes was proposed and finite element verification was carried out, and the following conclusions were finally obtained:

(1)

Through the experiments and finite element simulations of the rhombic tube (Figure 4 and Figure 6), there is a non-correspondence between the modes analyzed by finite element buckling and the crushing characteristics of the member, which indicates that the modes analyzed by finite element buckling do not fully satisfy the actual characteristic requirements of the member.

(2)

Due to the interaction between the polygonal panels, the buckling orientation of the neighboring side panels affects the buckling modes at the boundaries between the side panels. Still, it has less of an effect on the overall deformation mode of the structure.

(3)

Based on the theory of modal superposition, a method of modal correction is proposed in this paper. Based on this method, several modes are corrected by coefficients, and the modal characteristics consistent with the real deformation can be obtained. A deformation mode that matches the actual one can be obtained after superposition using this mode. It also confirms the hypothesis that differences in buckling modes due to boundary conditions have a small effect on the finite element produced results.

(4)

After the introduction of the buckling superposition factor, the experimental and simulated values of the rhombic fittings show the same trend and similar results, with the buckling capacity decreasing with the increase in the angle, θ₁.

(5)

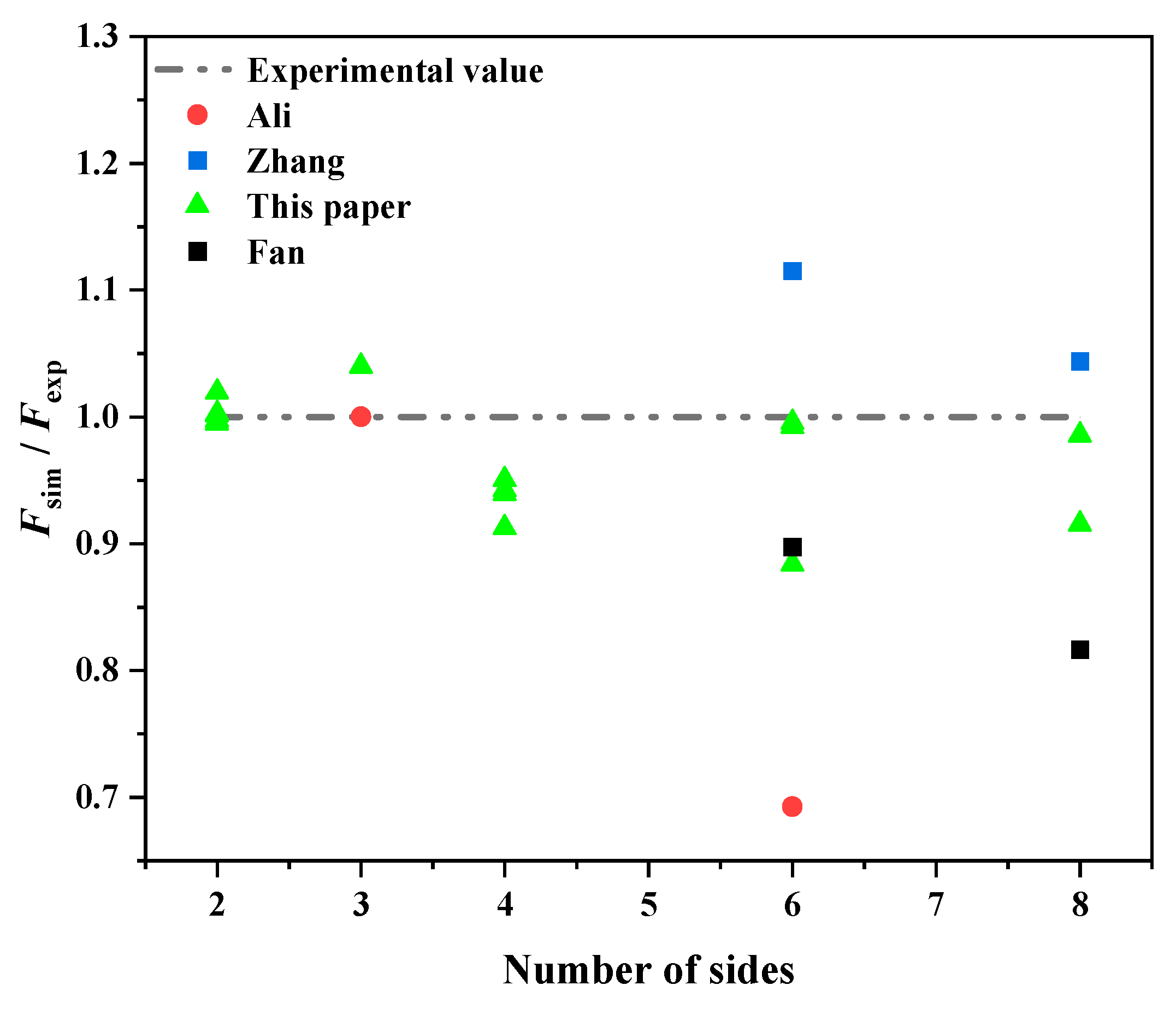
Compared with the traditional modal superposition method, the modal correction coefficients proposed in this paper can make the load-carrying capacity closer to the actual experimental value, and the results are reliable and valid, with strong expandability. With more intuitive naming rules, simpler modeling processes, and more accurate calculation results, this method has important engineering implications.

The work in this paper is still insufficient, and further research can be carried out through the following aspects:

(1)

The sample size of the experiment in this paper is too small, and only one compression experiment is carried out for each working condition. More reproducible samples with different flexion modes are yet to be carried out experimentally.

(2)

Some parameters, such as the height-to-width ratio, width-to-thickness ratio, amplitude of initial imperfection, buckling order, etc., need to be further investigated.