Abstract
This study focuses on the development of novel evaluation methods for the analysis of thin carbon reinforced concrete (CRC) structures. CRC allows for the exploration of slender components and innovative construction techniques due to its high tensile strength. In this contribution, the authors have extended the analysis of CRC shells from existing research. The internal structure of CRC specimens was explored using microtomography. The rovings within the samples were segmented from the three-dimensional tomographic reconstructions using a 3D convolutional neural network with enhanced 3D data augmentation strategies and further analyzed using image-based techniques. The main contribution is the evaluation of the manufacturing precision and the simulation of the structural behavior by measuring the carbon grid positions inside the concrete. From the segmentations, surface point clouds were generated and then integrated into a multiscale framework using a parameterized representative volume element that captures the characteristic properties of the textile reinforcement. The procedure is presented using an example covering all necessary design steps from computed tomography to multiscale analysis. The framework is able to effectively evaluate novel construction methods and analyze the linear-elastic behavior of CRC shells.
1. Introduction
Many studies have investigated carbon reinforced concrete (CRC) [1,2], and it is known that the tensile strength of carbon is significantly higher than that of steel [3,4], allowing for the construction of filigree components and further giving rise to the development of new construction methods. The research by Kalthoff et al. [5] explores such a method by using a laboratory mortar extruder (LabMorTex). They investigate impregnated glass and carbon reinforcements in various mortars and study the rheological properties of fresh concrete. Their proposed extrusion method can further deform extruded components into wave-like shapes, unlocking novel construction options [6,7]. However, such slender, shell-like structures require greater precision regarding the reinforcement compared to conventional construction methods. Furthermore, these methods necessitate the use of reliable evaluation methods with regard to their manufacturing accuracy.
To date, no guidelines exist for the design of textile-reinforced concrete components. However, numerous experimental tests have been performed to investigate the load-bearing behavior, and many different numerical methods have been used to capture the various effects that influence the load-bearing capacity. The present work focuses in particular on textile-reinforced shell structures. Within this investigation, the inner structure of such components was analyzed using a combination of state-of-the-art methods based on the findings in Mester et al. [8]. The authors proposed an approach to the analysis of CRC shells enhanced by image-based methods. In the current study, the methodology has been substantially improved in terms of automation and precision. The main contribution of this work is to study the position of the carbon grids and to simulate the load-bearing behavior of such textile-reinforced shell components. In addition, the accuracy of the extrusion process can be evaluated.
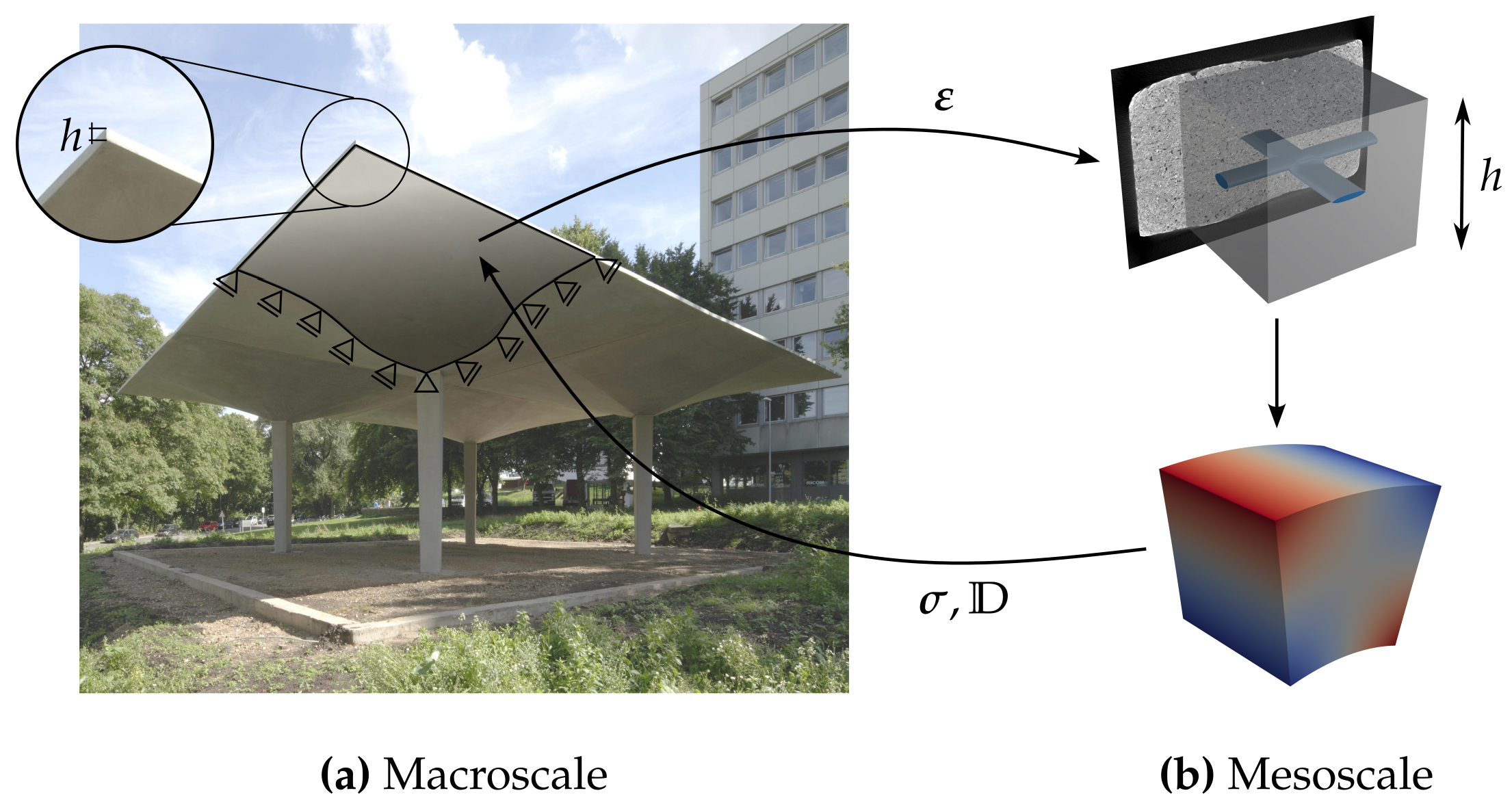
Since shell-like structures are characterized by large in-plane dimensions at small thicknesses (Figure 1), a multiscale method was used for the analysis. These methods investigate the structure at two scales: (1) the macroscopic scale, which describes the shell structure as well as its loading and boundary conditions, and (2) the mesoscopic scale, which represents the position and geometry of the textile reinforcement using a representative volume element (RVE). Figure 1 shows a textile-reinforced shell structure with an example inner structure to emphasize the large length differences (7 m span compared to only 6 cm thickness). Information on the manufacturing process and the actual reinforcement layout of this shell structure can be found in [9].
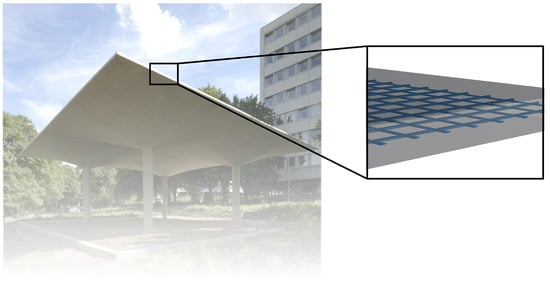
Figure 1.
Pavilion made from carbon reinforced concrete with example inner structure. The dimensions of each shell are 7 m × 7 m × 6 cm.
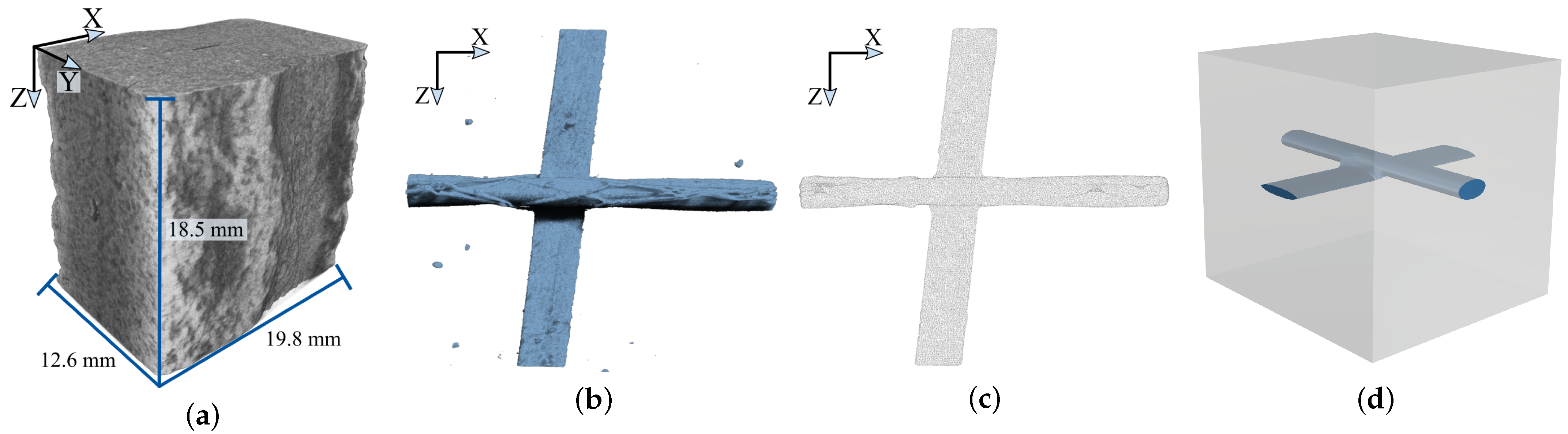
To explore the inner composition of shell structures, four distinct CRC samples presented in [5,6,7] were studied, specifically focusing on the enclosed carbon grids. First, a micro-computed tomography (µ-CT) device was used to scan the samples and to obtain digital 3D representations of them. To analyze textile-reinforced shell structures using a multiscale model, the rovings have to be segmented from the volumetric reconstructions (Figure 2a). Since this task is not easily feasible without a huge interactive effort, a 3D convolutional neural network (CNN) was used. However, such a CNN needs a lot of training data, especially in 3D, to be applicable to new CT reconstructions and the contained rovings. Therefore, based on the 2D results and software architecture presented in [10], 3D data augmentation strategies for volume segmentation have been developed. Such methods allow for the improvement of the variance of a dataset without generating new training data. In the course of this study, the augmentation methods were intensively tested on a small dataset for semantic roving segmentation [11]. However, the data structure of a 3D segmentation, such as shown in Figure 2b, is not suitable to be directly integrated into a multiscale model. Therefore, the segmentation was further processed to derive a smoothed surface represented as a point cloud (Figure 2c).
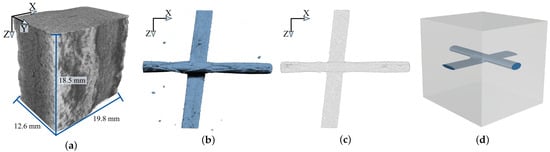
Figure 2.
From computed tomography (CT) reconstruction to representative volume element. (a) A CT reconstruction containing a carbon roving. (b) A segmentation of the roving contained in (a). (c) Point cloud representing solely the roving from (b). (d) Representative volume element including the carbon roving. (a,b) were visualized using Dragonfly 2021.1 by Object Research Systems (ORS).
The information obtained from the computed tomography images will be incorporated into the mesoscopic scale of the multiscale framework for analysis. Thus, the point cloud has to be transformed into a surface description suitable for analysis. As shown in [12,13], numerous methods have been presented for a variety of applications from different research fields. In contrast to polygonal meshes, the utilization of non-uniform rational B-splines (NURBS) for parametric surface descriptions offers the benefit of higher accuracy. Consequently, the geometric reconstruction of NURBS surfaces through imaging techniques is an important research area [14,15,16].
In the present contribution, scaled boundary isogeometric analysis (SBIGA) [17] is used for the analysis of the representative volume element. The method is boundary-oriented and utilizes NURBS surfaces, which are commonly used in computer-aided design, to describe the geometry. The use of isogeometric analysis [18,19] directly links design and analysis, which reduces approximation errors of the geometry in comparison to classical finite element methods.
2. Materials and Methods
2.1. Specimens
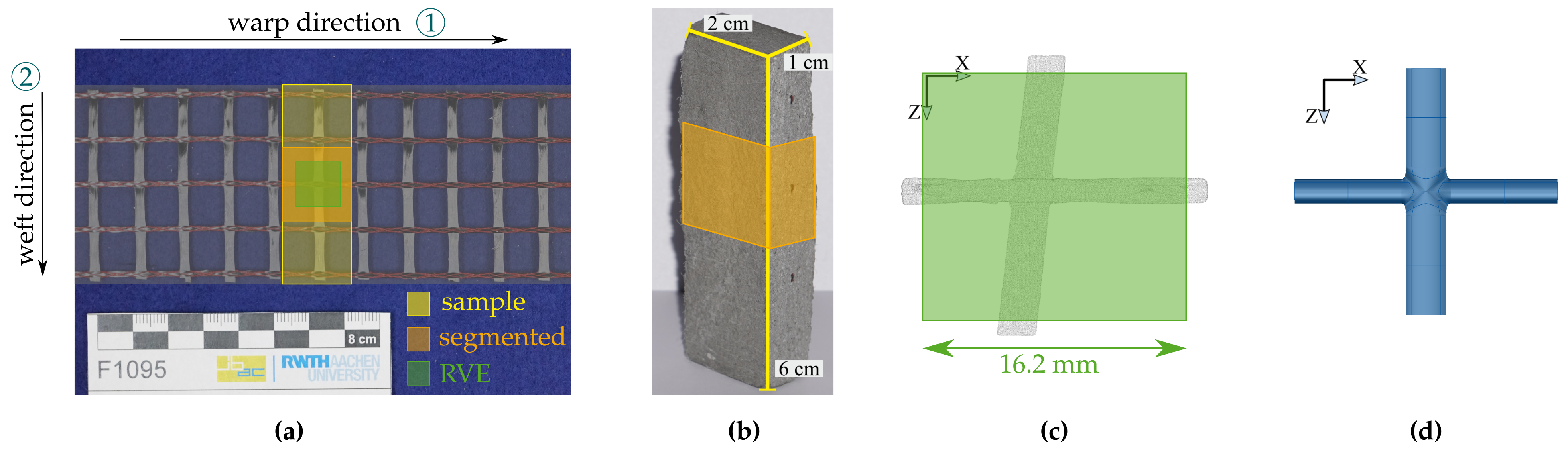
Throughout this research, the components described in [5,6,7] were utilized and studied, focusing on the positioning of grid-aligned carbon rovings (carbon fiber bundles) in various mortar matrices. Figure 3a provides a schematic illustration of one such component. The uniformity of the carbon grid and the matrix allows for the definition of a single RVE that describes the main characteristic material properties. In this study, the RVE is embedded in a homogenization framework.

Figure 3.
(a) Scheme of the cut-out region of a sample (yellow) with Grid 1 and the dimensions of a representative volume element (green). The component is indicated by the gray overlay. (b–e) From left to right: Samples A, B, C, and D with carbon reinforcement (dark spots). All samples are of roughly the same size.
The components were extruded in warp direction, resulting in varying sizes of 6 × X × 1 cm. For the investigation, a total of four samples, namely Samples A, B, C, and D (Figure 3), were extracted from four different components. All samples used in this study were uniformly cut to a size of 6 × 2 × 1 cm.
The samples contain two different carbon grids consisting of multiple continuous rovings with slightly different yarn spacings. The first reinforcement is SITgrid044 VL by the company Wilhelm Kneitz Solutions in Textile GmbH (Hof, Germany), which will be referred to as Grid 1. The second grid is GRID Q43-CCE-21-E5 by the company solidian GmbH, which will be referred to as Grid 2. Besides the yarn spacing (Figure 4), the difference is that Grid 1 was coated using polystyrene, whereas epoxy resin was used for Grid 2. Grid 1 is contained in Sample A with a yarn spacing of 16.2 mm (warp) × 14.7 mm (weft) and in Sample B with a yarn spacing of 12.5 mm in both directions. Furthermore, the rovings of Grids 1 and 2 have different cross-sections, as shown in Table 1. In Sample B, a two-layer configuration of the textile was used. Sample C as well as Sample D contained Grid 2. A sanded surface was used for Grid 2 in Sample D to improve the composite behavior.

Figure 4.
(a) Grid 1 with knitting thread (red), (b) Grid 2 with knitting thread (white), (c) Grid 2 with sanded surface.

Table 1.
Measured cross-sectional dimensions of the rovings contained in Grid 1 and Grid 2. At the intersection of the rovings in the warp and weft directions, Grid 1 has a height of ≈0.88 mm, and Grid 2 has height of ≈3.15 mm due to the coating.
2.2. Microtomography
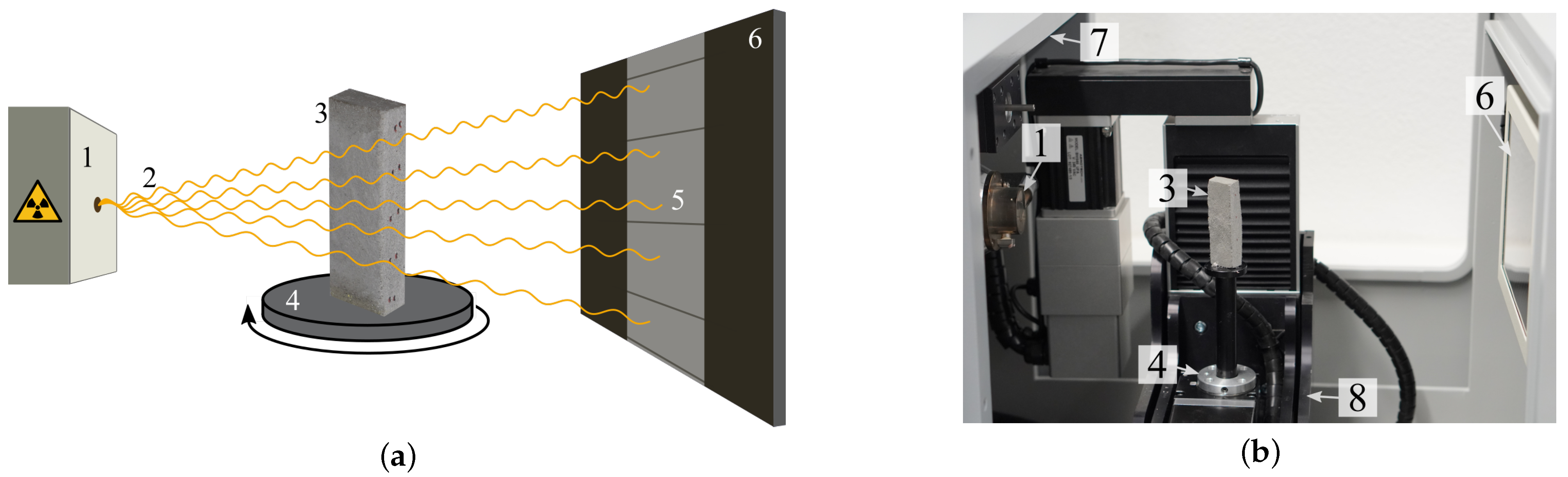
To investigate the internal characteristics of objects, a µ-CT device can be used. Such a device (Figure 5) consists of an X-ray source (1), a rotating sample plate (4), and a detector (6). During the scanning process, a sample undergoes a complete 360 rotation, and at each rotation step, it is exposed to X-ray radiation, which is typically polychromatic, meaning that the radiation contains X-rays of multiple energies (2). As the X-ray beams traverse through the object being scanned (3), the detector captures the resulting projection image (5), which is generated by recording the X-ray attenuation data. In this study, the Procon CT-XPRESS, a µ-CT device, was utilized (Figure 5b). This instrument is designed to achieve a nominal resolution as low as 5 µm per voxel [20].
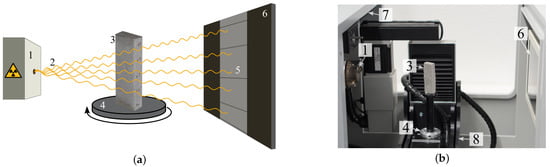
Figure 5.
Scheme and computed tomography (CT) device (Procon CT-XPRESS) with 1: X-ray source, 2: X-rays, 3: sample, 4: rotating sample plate, 5: projection on 6: X-ray detector, 7: protective cover (lead), 8: movable sample table. (a) Scheme of a CT device; (b) Photo of the test setup.
During a CT scan, the energy parameters, specifically the current and voltage, need to be adjusted based on the size of the specimen and the properties of the material being scanned. Materials with lower density and thickness require relatively little power, while denser materials necessitate higher energy levels. However, the use of higher power comes at the expense of introducing noise into the reconstructed images [21].
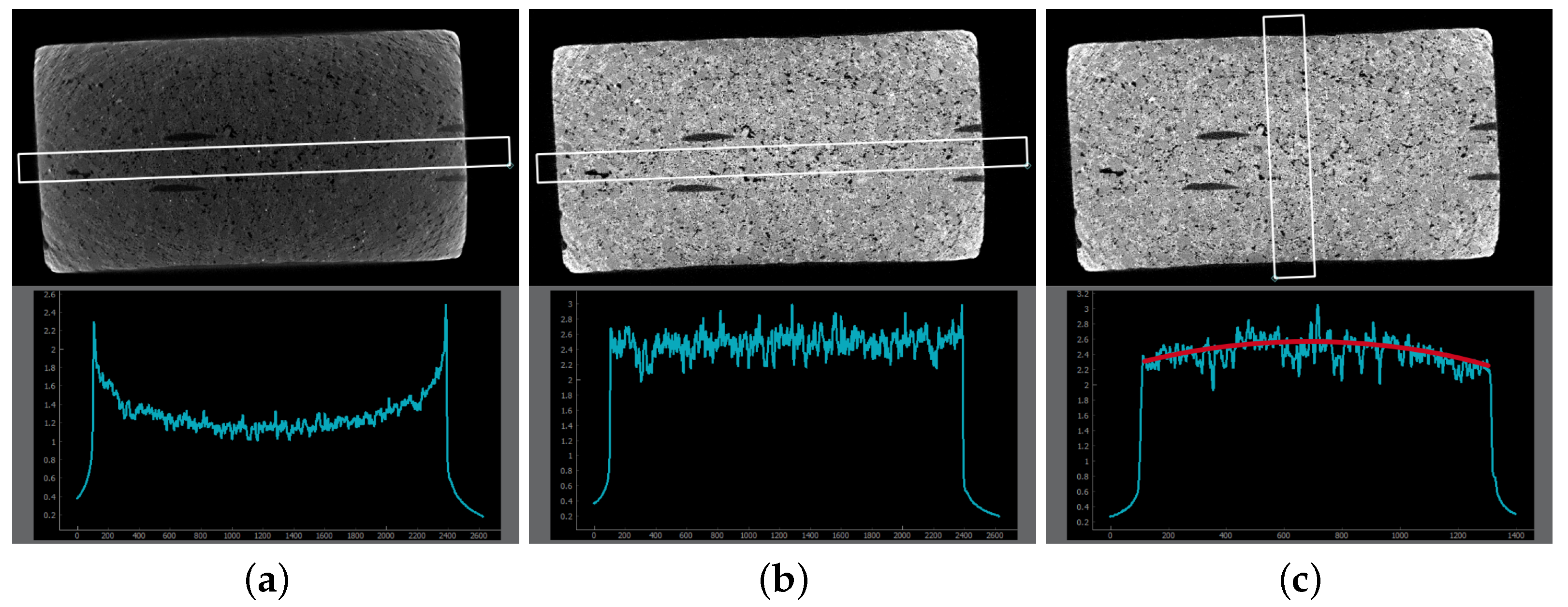
After concluding the CT scan, the gathered projection data are utilized for the reconstruction of a 3D volume using the software X-AID 2023.2 by MITOS GmbH. During the reconstruction, artifacts are likely to occur due to the physics of a CT. One error, which plays a role in this study, is the so-called beam hardening. Due to energy-dependent X-ray attenuation, the low energy X-rays (referred to as “soft X-rays”) of the generated spectrum are absorbed more quickly than the high energy X-rays (referred to as “hard X-rays”) as they pass through a sample. As a result, the number of X-ray photons reaching an X-ray detector is not directly and linearly proportional to the thickness of the penetrated material. To correct this phenomenon, most reconstruction algorithms assume linear attenuation, which leads to a difference in coloration between the outer edge and inner material of the object. This discrepancy is known as the cupping effect [22]. In essence, the cupping effect causes the outer regions to appear differently shaded compared to the inner regions due to the beam hardening phenomenon as shown in Figure 6a. In Figure 6b, a linear correction has been applied. While the profile line appears relatively flat, there is a slight increase in brightness at the edges and especially at the corners. This effect is negligible for cylindrical samples but poses a problem for non-cylindrical samples, as present in this study. Figure 6c demonstrates an instance of the introduced error. The applied correction along the long side of the sample leads to darkening of the grayscale profile at the edges of the short side, resulting in a distinct color difference between the outer and inner regions of the sample.
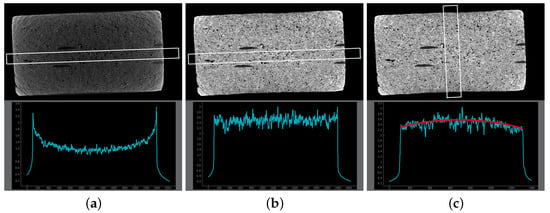
Figure 6.
Visualization of the beam hardening effect (cupping) and its correction during a computed tomography reconstruction process of Sample B using the reconstruction software X-AID 2023.2 (MITOS GmbH). Top: cross-sectional views; Bottom: grayscale profile. (a) Uncorrected reconstruction. The grayscale profile does not perfectly correlate with the specimen’s thickness. (b) Correction of the cupping effect along the long side of the sample. (c) Correction of the cupping effect along the short side of the sample using the values of (b). Due to differences in thickness between the long and short sides, the correction becomes too strong, resulting in a non-linear profile (the red line should ideally be straight).
2.3. AI-Based Segmentation
In order to analyze the inner structure, visual examination may not be sufficient. In the present work, the carbon grids are extracted to generate a representative volume element of each grid and its position in the concrete. Therefore, the reinforcement has to be segmented first. Due to the fact that carbon has a different density than concrete and thus the grayscale representation is different from concrete, one possible approach seems to be a threshold approach to extract the rovings. In Figure 7a, a histogram is shown, clearly indicating the grayscale range of a carbon reinforcement in a horizontal slice of a reconstruction (Sample B). However, as explained in Section 2.2, the gray values of a CT reconstruction are likely to be inhomogeneous. Due to cupping effects, the grayscale range of the carbon reinforcement will vary from the outer to the inner region in the volume. In Figure 7b,c, the effect is shown. The binarized roving is more porous in the center than at the edges. Furthermore, small pores and slight noise cause other components in the reconstruction to have gray values similar to those of the carbon reinforcement. Since these issues make it difficult to reliably segment the carbon rovings, and since manual extraction for multiple rovings would be very time-consuming, machine learning techniques are used to automate the process.

Figure 7.
(a) Normalized histogram of a cross-sectional image (b) of Sample B. The grayscale range of the carbon reinforcement is highlighted. (c) The horizontal slice (b) was used to calculate the histogram. A threshold was applied based on the grayscale range in (a). The result is a binarized image: all values outside the range were set to 0 (black), while all voxels inside the range were set to 255 (white).
In the domain of image segmentation, neural networks have been successfully used since 2012 [23]. In 2015, the famous U-Net [24] marked a breakthrough due to its better performance while reducing the needed computational power. Following U-Net, many other CNNs were introduced [25,26,27], and 3D versions of segment volumes were proposed [28,29,30] as well as a 3D version of the U-Net [31]. In [32], eight different architectures for deep voxel classification were compared on multiple domains. It was shown that the 3D U-Net performed best on a carbon roving segmentation task, which is the reason it was chosen in this study. The 3D U-Net consists of an encoder–decoder structure, which is very common for image and volume segmentation networks. Since it is a very well-known and simple CNN, we refer to Çiçek et al. [31] for more detailed information on the architecture. However, prior to utilizing the neural network, it has to be trained, a process carried out through supervised learning that necessitated the availability of training data.
2.3.1. Training Data
During supervised training for volume segmentation, a CNN is guided to generate a segmentation of an input volume that matches the corresponding target (“ground truth”). However, such a dataset has to be created first. Fortunately, a Carbon Rovings Segmentation Dataset was introduced in [8] and subsequently improved and made publicly available in [32] on Kaggle (link can be found in reference [11]). This dataset comprises three CT scans containing three manually segmented samples using variants (different grid spacing and impregnation) of Grid 1 with a voxel size of 9.4 µm. Figure 8 showcases the two scans used for training and validation, and a third scan designated exclusively for testing.

Figure 8.
Visualization of the Carbon Rovings Segmentation Dataset [11] with manually segmented roving targets (light blue). The upper volumes have been reduced in depth to visualize the position of the rovings. (a) Training volume of Textile 1. (b) Training volume of Textile 2. (c) Training volume of Textile 3. Volumes (a) and (b) were split into multiple subvolumes and represent the training and validation data. The volume in (c) is used for testing. All textiles are variants of Grid 1 with different yarn spacings.
For training and validation purposes, the first two volumes were manually segmented and then divided into 162 subvolumes, each measuring 256 × 256 × 128 (height × width × depth) voxels. The division in training and validation data resulted in 129 training subvolumes and 33 validation subvolumes. However, a dataset of this size is rather small, and a well-generalized CNN that can be applied to different carbon grids is not an expected outcome unless data augmentation techniques are employed.
2.3.2. Augmentation
In addition to enabling the segmentation of Grid 2, data augmentation also helps to prevent overfitting. Overfitting occurs when the CNN performs exceptionally well on the training data but fails to generalize to unseen or new data. This happens when the model becomes too complex or has too many parameters relative to the size of the training data. As a result, the model memorizes the noise and specific patterns in the training data instead of learning the underlying general patterns, leading to a lower performance on new data [33].
Data augmentation is a technique to synthetically increase the diversity and quantity of the training dataset without collecting additional real-world data. This process helps the model to learn more robust and invariant features, improving its ability to handle various real-world scenarios and reducing the risk of overfitting to the limited training samples. Most deep learning libraries include basic image transformations such as flipping, rotating, scaling, and cropping [34,35], which are commonly utilized in various applications [36,37]. The Albumentations library [34] goes a step further and provides a more extensive set of augmentation techniques specifically designed for 2D images.
In this study, two methods were used, namely offline and online augmentation. The process of applying data manipulations before the training begins is referred to as offline augmentation. In this approach, an operator maintains control over the dataset, allowing for an inspection of the augmented images and masks in advance to ensure the appropriateness of the augmentations. However, a drawback of this method is the significant increase in required storage space. With numerous possible combinations of different augmentations for each image, storing all variations becomes impractical. In contrast, online augmentation eliminates the need for additional storage space since the operations are performed dynamically on the fly [33].
In a study by Wagner et al. [10], offline and online augmentation techniques for image segmentation were examined. The findings were presented alongside a software package called AiSeg (link in Data Availability Statement), designed to facilitate the training, testing, and utilization of 2D and 3D CNNs. This software also allows for the use of optimized offline and online augmentation pipelines for 2D images, which were extended to 3D in the course of this study. In total, 13 augmentations (flip, crop, resize, rotate, squeeze, tilt, blur, noise, brightness change, contrast manipulation, random erase, sharpen, and random darken) are supported and can be chained randomly. The software also allows many fine-tuning parameters to be set with regard to these augmentations, similar to the 2D versions, as explained in [10].
During model training, the high virtual RAM usage necessitates feeding only a sub-region of a volume to the neural network in each iteration. As a result, the two augmentation approaches (offline and online) differ in their implementation. In offline augmentation, the original data are augmented, whereas in online augmentation, only a subvolume is augmented. The authors of [10] further emphasized that, for smaller datasets, offline augmentation proves beneficial, while larger datasets derive more advantages from online augmentation. The dataset used during this study is rather small, supporting the theory that offline augmentation may be beneficial. However, the creation of augmented 3D data needs a lot of storage space and therefore increases the training duration significantly compared to 2D images. Therefore, online augmentation was also investigated.
In addition to a training without any augmentation (for comparison reasons, Strategy 1), three training strategies with augmentation were tested. Strategy 2: To enhance performance on Grid 1, the training data were weakly offline augmented using only rotations. This strategy serves as a reference to [8], which used a similar approach. Strategy 3: To improve generalizability and to allow segmentation of Grid 2, strong offline augmentation was performed using suitable methods of the AiSeg software (link in Data Availability Statement). Strategy 4: To theoretically reduce training duration while increasing the dataset’s variance, the 3D online augmentation was also carried out. In Figure 9, an example of an augmented subvolume is shown. The implementation details of the 2D augmentation pipelines can be found in [10], and the software design has been adapted to 3D.

Figure 9.
Example visualization of a training subvolume of size 128 × 128 × 64 voxels (height × width × depth) before (a) and after applied online augmentation (b). From left to right: subvolume, related ground truth, and combined versions.
2.3.3. Training and Metrics
The training of a CNN involves the process of iteratively adjusting the network’s parameters to learn meaningful features from input data. At the beginning, the CNN’s weights are randomly initialized. During each training iteration, a batch of input data is fed into the network, and its output is compared to the corresponding target using a loss function (e.g., cross-entropy). When iterating over the training data, the gradients of the loss with respect to the network’s weights are then calculated through back-propagation. These gradients are used to update the weights using an optimization algorithm (e.g., stochastic gradient descent) to minimize the training loss. This process is repeated for multiple epochs until the performance of the network converges to a satisfactory level. After each epoch, the CNN in its current state is evaluated against the validation data, to estimate the validation loss on unseen data and to determine if overfitting has occurred. When both the training loss and the validation loss converge, training can be stopped, and the CNN can be used on unseen data.
Before initiating the training process, various parameters must be set, including the number of epochs, batch size, loss function, optimization algorithm, and others. These parameters, collectively known as hyperparameters, influence the model’s training and performance outcomes. Below are the parameters that differ from the original implementation and are the same in the experiments conducted.
The batch size as well as the dimensions of the inputs are constrained by the available memory of the graphics card, which is a critical consideration when dealing with 3D data due to the increased CNN parameter count. Consequently, in this study, the batch size was capped at a maximum of three and an input size of 128 × 128 × 64 (height × width × depth). As a result, group normalization was favored over batch normalization as the normalization layer. This choice is driven by the fact that group normalization demonstrates greater stability and yields improved outcomes compared to batch normalization when handling small batch sizes (<16) [38].
Performance evaluation during both the training and validation phases was performed using the binary cross-entropy loss (Equation (1)). For optimization, the Adam optimizer was used due to its robustness over a range of hyperparameter configurations [39]. The initial learning rate was set to .
where: L = Loss value
wc = Weight w of a class c
p = Predicted probability p ∈ [0, 1]
y = Target class y ∈ {0, 1}
To estimate the performance on unseen data, the DICE coefficient, also referred to as the overlap index or F1-score [40], was used. This coefficient quantifies the correspondence between the ground truth and the segmentation. Using the True Positives (TP), False Positives (FP) and False Negatives (FN), it is calculated by:
During the testing and inference (application of a CNN) phases, the volumes were partitioned into overlapping subvolumes (50% overlap), since a complete volume does not fit in the GPU memory. As a result, voxels located in overlapping regions are represented by two or more logits. A logit is the direct output of the CNN for a single voxel. In addition, due to convolutions and the inherent loss of information at the edges, the network’s output at the prediction corners is less reliable than in the central region. To mitigate this, it is common to apply a 3D Gaussian weighting [41]. In the CNN comparison (Section 2.3, [32]), a weighting of of the voxels in the center to those in the corners was used. However, for improved smoothing across overlapping regions, the corner weights were set to relative to the center weight. After applying these weights and aggregating all sub-volumes, the final prediction was generated. During a test phase, this volume was compared to the ground truth.
2.4. Roving Extraction
After successful training, the trained 3D U-Net can be used to process the 3D reconstructions obtained by tomography, as done in [8]. While the CNN is designed to accurately segment the roving, the presence of certain artifacts is likely. To address these artifacts and focus solely on extracting the roving and its surface, the authors used a connected components analysis method. This algorithm identifies clusters of adjacent voxels that are connected to each other, meaning they share a common corner or edge or that they are directly adjacent. In a single-layer carbon grid setup, the cluster consisting of the most connected voxels represents the roving. For this purpose, the authors of [8] also introduced software called the Roving Surface Extractor (link in Data Availability Statement).
Due to the fact that the knitting thread introduces unwanted complexity to the roving surface, a 3D Gaussian filter with a standard deviation of 10 was applied on the binary roving to smooth the surface and to remove possible artifacts introduced by the knitting thread. Afterwards, a point cloud describing only the surface was extracted from the smoothed 3D volume using the marching cubes algorithm [42] to significantly reduce the computational complexity of the next steps. This was used in the context of a multiscale model for the analysis of textile-reinforced shell structures.
2.5. Multiscale Modeling
Textile-reinforced shell structures are characterized by large in-plane dimensions and relatively small thicknesses, giving rise to the use of multiscale methods for analysis. These consider the structure on two scales, each of which employs different numerical methods; see Figure 10. The macroscopic scale describes the geometry, loading, and boundary conditions of the shell; see Figure 10a. The remaining characteristic properties of the structure, such as the geometry and position of the textile reinforcement, are described by a representative volume element. In the case of shell homogenization, the thickness of the RVE corresponds to the shell thickness h, as in Figure 10, which is a characteristic feature of the approach. Thus, the scale is referred to as mesoscale in the following (Figure 10b).
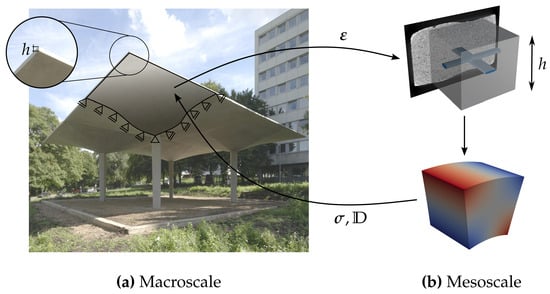
Figure 10.
Schematic homogenization procedure for shell structures using computed tomography data on the mesoscopic scale. (Adapted with permission from Ref. [43]. 2023, L. Mester.)
Multiscale methods are often referred to as computational homogenization because they aim to model the macroscopic structure as homogeneous. However, they do not intend to develop full constitutive laws for the composite material. For carbon reinforced concrete, this has been done, for example, in [44,45].
Generally, computational homogenization offers a variety of methods and possible applications, and extensive overviews can be found, for example, in [46,47]. Homogenization with application to shell structures is discussed in [48,49,50,51].
The present contribution is based on the work of Gruttmann and Wagner [51] and employed a Reissner–Mindlin kinematic for the description of the macroscopic scale, which allows transverse shear effects to be taken into account. The scaled boundary isogeometric analysis [17] was used for the analysis of the RVE. The information obtained from the extracted roving, such as the orientation and position of the textile, was incorporated into the RVE. The two components, concrete and textile, were modeled separately. This allows separate material models to be used for each component. The effective material response for each point on the macrostructure is to be determined.
The procedure can be briefly outlined in the following steps: (1) For each macroscopic integration point, the strains were applied to the RVE using appropriate boundary conditions. (2) The mesoscopic boundary value problem was solved, and (3) the obtained stresses and effective material properties were returned to the macroscopic scale. The procedure is shown schematically in Figure 10. This procedure is repeated for every macroscopic point. Here, the macroscopic shell structure is analyzed using finite elements; thus, the effective material response must be determined for each macroscopic integration point using the described procedure. Since the numerical problems on both scales are treated concurrently, the method is often referred to as FE [52].
The mesoscopic and macroscopic scales must be coupled in an energetically consistent manner. Here, the Hill–Mandel condition [53] was used, which states that the virtual internal work on the mesoscopic scale averaged over the mid-surface of the RVE is equal to the macroscopic virtual work. From this, different boundary conditions for the lateral surfaces of the RVE can be derived; see, for example, [54]. Here, periodic boundary conditions were employed due to the repetitive structure of the reinforcement. However, the coupling of a two-dimensional structural element on the macroscopic scale and a three-dimensional continuum formulation on the mesoscopic scale is not trivial. The employed boundary conditions are presented in more detail in [55]. They require the constructed RVE to be symmetric with respect to the axes in the plane, as well as being point symmetric. This is an important requirement for the construction of a representative volume element suitable for analysis using computed tomography data.
2.6. Scaled Boundary Isogeometric Analysis
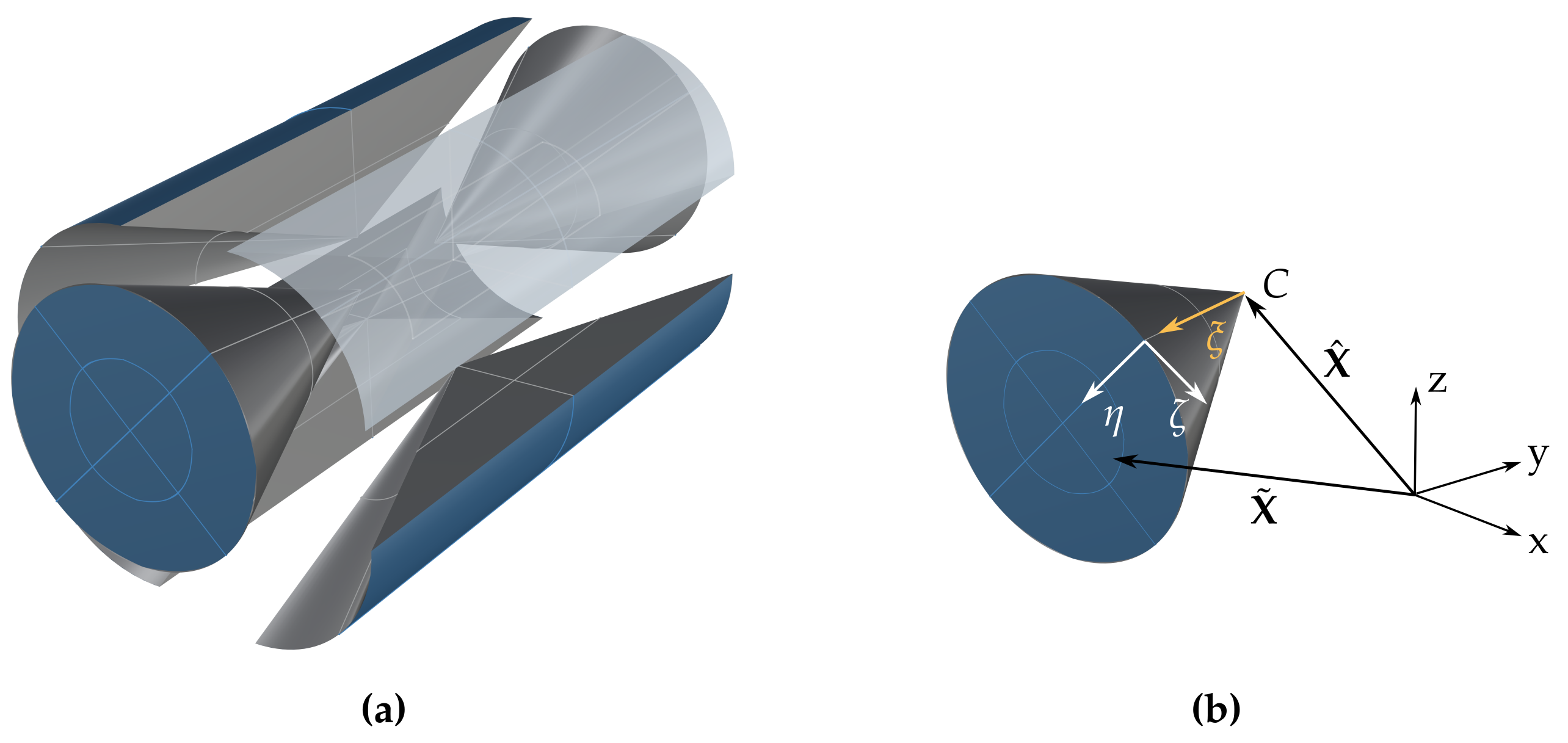
The mesoscopic representative volume element was analyzed using scaled boundary isogeometric analysis. Analogous to computer-aided design, volumes are described by means of their surfaces. Here, these were defined by NURBS, which can be used directly in the context of isogeometric analysis [18,19]. To transform the bivariate tensor product into a volumetric description, a scaling center C was introduced, using concepts known from the scaled boundary finite-element method [56]. The linear scaling direction, running from the scaling center to the boundaries, thus introduced the third direction needed for a volumetric description of a body. Thus, any volumetric body can be described by its boundary surface and a scaling center. The interior of the solid was then parameterized by a scaling parameter , which runs from the scaling center (where ) to the boundary (where ). Correspondingly, the surface was discretized with the two parameters ; see Figure 11. Therefore, any point in the domain can be described by:
where describes any point on the boundary, and denotes the position vector of the scaling center C.
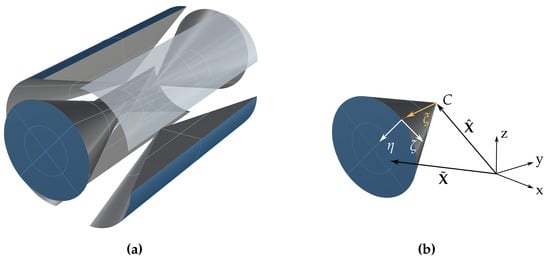
Figure 11.
(a) Exploded view of a cylinder and (b) example discretization of a section.
Classically, the scaling center needs to be positioned within the kernel of the geometry to be visible from any point on the surface. This requires the geometry to be star-shaped. Recently, efforts have been made to overcome this limitation, for example, by using curved scaling lines, such as circular arcs or parabolic lines [57,58]. Alternatively, for the two-dimensional case, it has been shown that the scaling center can be positioned outside of the kernel and even outside of the geometry [59,60,61]. However, to date, these approaches are limited to two dimensions. Therefore, complex geometries are divided into several star-shaped domains in order to apply SBIGA. Some algorithms for the subdivision have been proposed [62], but again they are limited to two-dimensional domains. Consequently, an RVE representation is employed when the subdomains are known to be star-shaped.
2.7. Parameterized RVE and Definition of Characteristic Geometric Properties
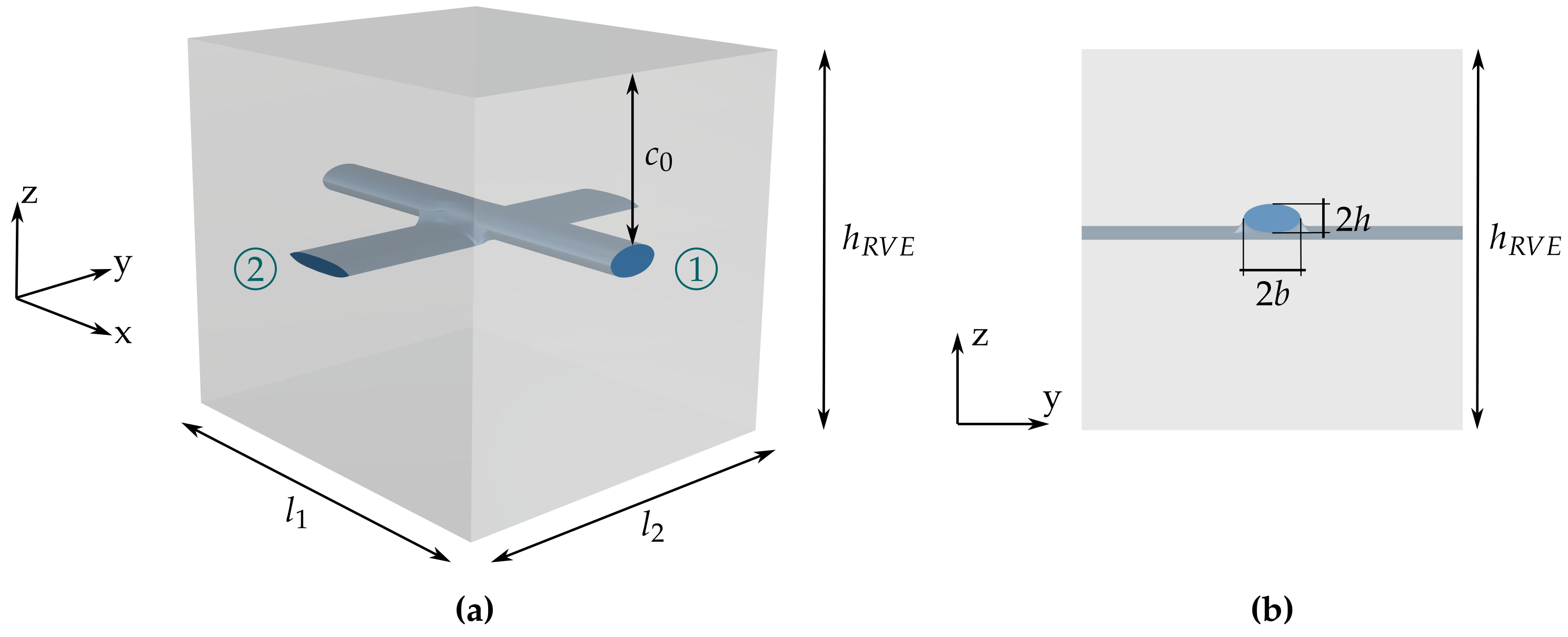
From the first-order shell homogenization approach using scaled boundary isogeometric analysis on the mesoscale, two significant restrictions on the RVE have been derived. First, the use of periodic boundary conditions requires symmetry and point symmetry of the opposing RVE boundaries. In addition, the scaled boundary isogeometric analysis requires star-shaped geometries. Therefore, a parameterized RVE geometry considering a roving intersection has been developed and is shown in Figure 12. The main characteristics of the RVE are the grid opening in warp and weft directions and , the concrete cover , the RVE height , as well as the roving dimensions that have been identified. From observations, the rovings were assumed to be elliptical, so their radii can be given by and for the weft and warp directions, respectively. Regarding their relative position, it is assumed that the lower edge of the ellipse describing the weft direction coincides with the center line of the elliptical cylinder describing the warp direction. The geometry is modeled using the Grasshopper plug-in for the computer-aided design software Rhinoceros. The parameterized model can be found on Zenodo [63].
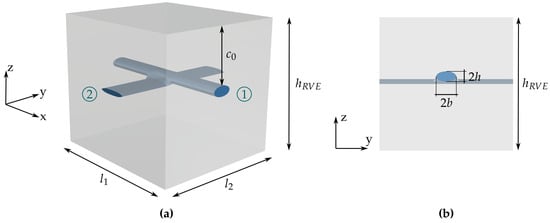
Figure 12.
(a) Perspective and (b) plane view (y–z plane) of parameterized RVE with dimensions (1: warp direction, 2: weft direction).
These characteristics were obtained from the extracted roving geometry and data provided by the manufacturer. In the following, it is explained how to obtain the characteristic values.
Note that both constituents, concrete and textile, are assumed to be homogeneous. Therefore, any air inclusions or grains in the concrete are neglected.
2.7.1. Roving Dimensions and
The roving geometry was approximated as elliptical with the radii and in the warp and weft directions, respectively. The width of the approximated roving is described as , and corresponds to the height of the roving, as shown in Figure 12b.
To determine the radii, an averaged cross-sectional area was determined for each roving using the extracted 3D surface point cloud, as described in Section 2.4. A number of slices were evaluated along each roving axis, where each slice corresponds to a 2D image. Figure 13a shows an example of a cross-sectional image from computed tomography. From the extracted 3D point cloud describing the surface of the rovings, a 2D point cloud describing the outline of the roving was obtained for each cross-section. The concave hull algorithm, based on [64], was used to derive a polygon describing the outline of the roving. Figure 13b,c show the boundary point cloud from the roving extraction and its concave hull for the 2D image in Figure 13a.

Figure 13.
(a) Example cross-sectional image of Sample A with magnification of roving. (b) Corresponding point cloud and concave hull. (c) Magnification of point cloud and concave hull.
From this, the centroid of each cross-section and the two radii were determined. The averaged properties of the roving are then obtained as:
In general, it was not necessary to consider all slices obtained from CT data. The number of slices considered should be large enough to ensure a correct mean value. The area where two rovings intersect was not considered, since in these areas the point cloud describes the outline of both rovings.
From the averaged radii, the aspect ratio was obtained as . Using the averaged cross-sectional area and the aspect ratio, the radii of the approximating ellipse can be determined from:
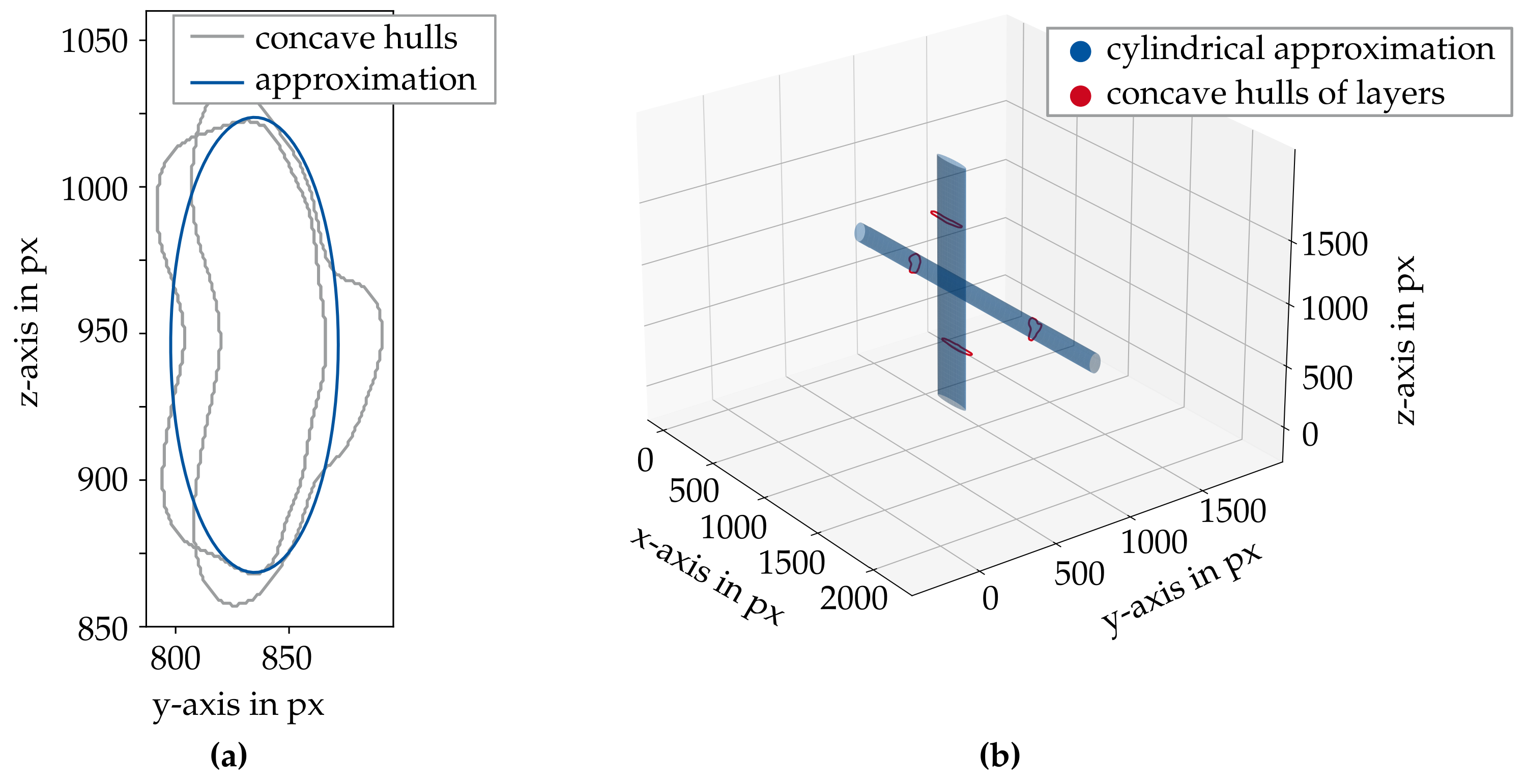
From these dimensions, the ellipse describing the cross-section of the roving was determined, with its centroid corresponding to the averaged centroid. Figure 14a shows the derived ellipse from only two concave hulls in plane view, while Figure 14b shows the perspective view of the derived cylindrical approximation and two used concave hulls.
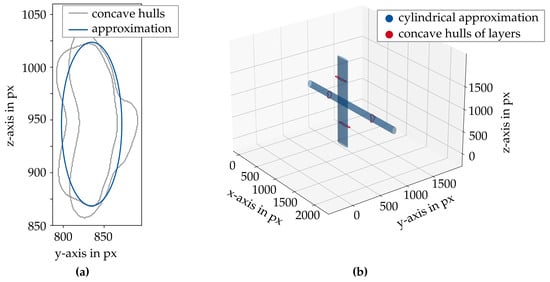
Figure 14.
(a) Plane view of approximated ellipse from two concave hulls describing the roving. (b) Perspective view of derived elliptical cylinders with concave hulls used for approximation.
2.7.2. In-Plane Dimensions
For the application of periodic boundary conditions in the framework of the homogenization approach, periodically repeating RVEs are assumed. Since only one intersection of the rovings was considered, the in-plane dimensions of the RVE can be directly correlated with the grid properties of the textile. Therefore, the dimensions and were taken from the data sheet of the manufacturer and correspond to the thread spacing (the distance between the center lines) in the warp and weft directions, respectively. For visualization, the in-plane RVE dimensions are depicted in Figure 3a.
2.7.3. Shell Thickness
The RVE height corresponds to the thickness of the concrete shell. It was determined prior to production. The average shell thickness of the scanned concrete sample can also be determined using computed tomography data. This can be beneficial for the evaluation of novel production methods, such as extrusion [5].
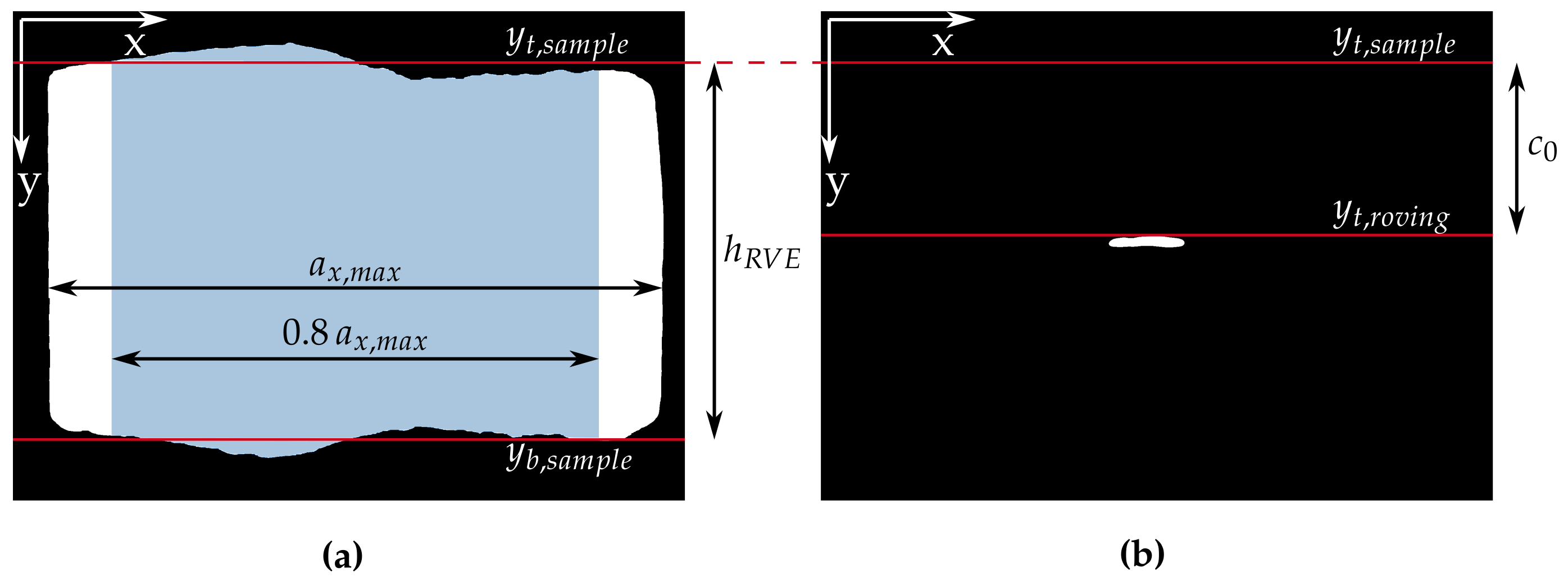
For this purpose, the cross-sectional images were binarized using a range-based threshold (e.g., as in Section 2.3, Figure 7) and the flood fill algorithm, i.e., all pixels within the boundary of the sample are set to 255 (white), and all pixels outside are set to 0 (black). The height was determined by measuring the distance between the averaged upper () and lower () boundaries of the sample, indicated by the two red lines in Figure 15a. Note that of the sample was neglected on each side. This choice was driven by the fact that the sample is not perfectly rectangular due to production imperfections. This procedure can be repeated for multiple images along the z-direction to determine an average thickness.
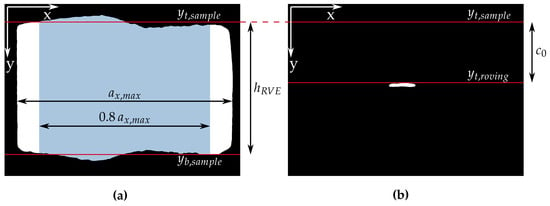
Figure 15.
(a) Binary image of Sample A (pixels belonging to sample have value 255 (white)). (b) Binary image of the roving contained in Sample A (pixels belonging to extracted roving have value 255 (white)).
2.7.4. Concrete Cover
Similar to the shell thickness, the concrete cover of the textile depends on the manufacturing process. Verification using CT data is important not only for the evaluation of new production processes, but also because the positioning of the textile within the shell is of interest for the load-bearing behavior, especially for thin shells. Due to the production process, the position of the textile can vary, for example, due to lifting or settling of the textile.
Again, the position can be determined using binary images. The procedure is similar to the one used for determining the shell thickness (Section 2.7.3). The pixels belonging to the roving have the value 255 (white), and others have the value 0 (black), as shown in Figure 15b. The concrete cover was estimated using the distance from the averaged upper boundary (upper red line in Figure 15a) to the first white pixel in the y-direction (lower red line in Figure 15b). Again, this procedure was repeated for multiple 2D images along the sample to determine an average concrete cover.
2.7.5. Concluding Assumptions
To conclude, the assumptions made for the characterization of a representative volume element are briefly summarized:
- Rovings are orthogonal to each other.
- Only one intersection of rovings is considered.
- Rovings are approximated as elliptical cylinders.
Although the present work examines extruded textile-reinforced specimens, the assumptions presented are also valid for other carbon reinforced concrete structures using grid-aligned carbon textile reinforcement, regardless of the construction technique. The main feature that justifies the assumptions is the periodically repeating textile reinforcement. Generally, any textile grid can be investigated; however, the chosen multiscale technique requires the RVE to be symmetric as well as point symmetric (see Section 2.5). Therefore, in the first step, the approach is limited to orthogonal reinforcement geometries.
3. Results and Discussion
3.1. Microtomography
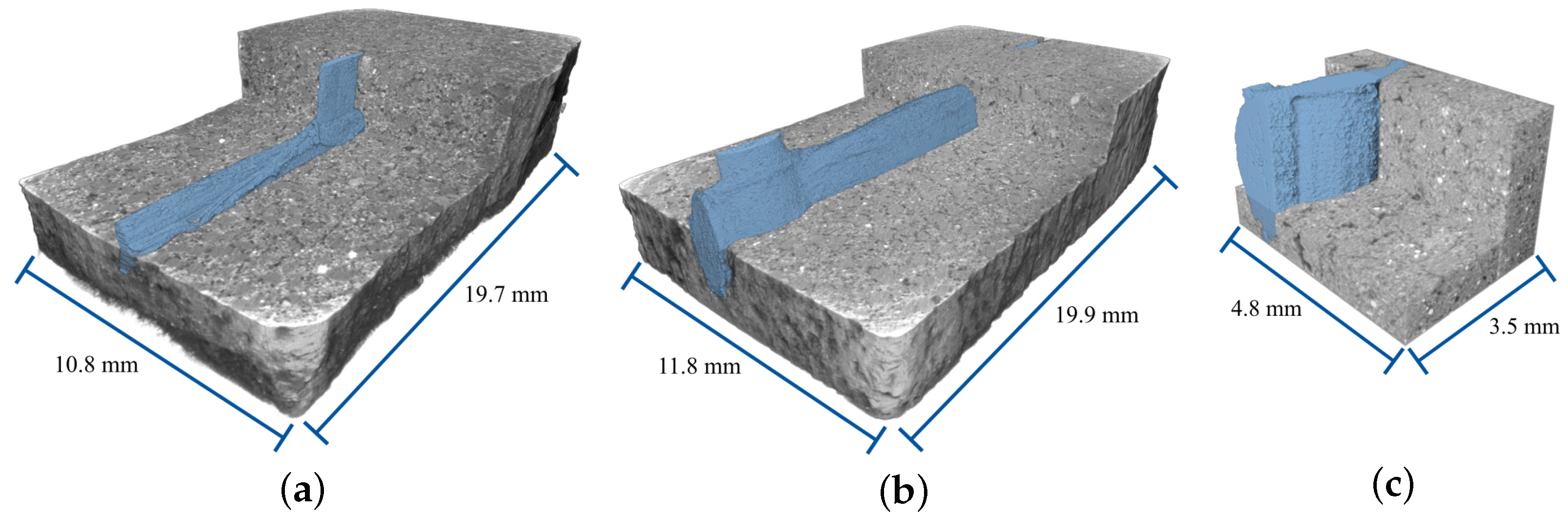
The Procon CT-XPRESS (Section 2.2) was used to scan the four samples. The scanned region varies depending on the reconstruction settings and the placement of the samples relative to the X-ray source and detector. Figure 16 shows the the volumetric reconstructions of the four samples. Furthermore, Figure 17 displays cross-sectional images of Sample A, revealing a slight shift in the carbon grid introduced during the extrusion process. Figure 18 includes cross-sectional slices of all samples, indicating that more coating was used for Grid 2 compared to Grid 1. The coating is generally barely distinguishable from the roving. In Sample D, the coating is used to fix the sand to the surface.

Figure 16.
(a) Sample A (voxel size: 9.5 µm). (b) Sample B (voxel size: 8.9 µm). (c) Sample C (voxel size: 9.4 µm). (d) Sample D (voxel size: 9.4 µm). The dark spots in the reconstructions are the carbon grids. (e) Schematic of the scanned region.

Figure 17.
Cross-sectional images of a computed tomography reconstruction of Sample A. (a) Sample A with marked image positions. (b) X–Y-view with roving. (c) X–Z-view with roving. (d) Y–Z-view with roving.

Figure 18.
Cross-sectional images of Samples B, C, and D along with magnifications. (a) Sample B contains a two-layer configuration of Grid 1. (b) Sample C contains Grid 2 with a lot of coating. The roving is highlighted within the yellow contours. The coating is indicated by the red arrow. (c) Sample D contains Grid 2 with a sanded surface, clearly visible in the computed tomography scan.
3.2. Deep Learning
To extract the rovings, it is necessary to segment the four reconstructions using a trained 3D U-Net. As explained in Section 2.3.2, the network was trained using four strategies: (1) training with the standard dataset, (2) training with weak offline augmentation, (3) training with strong offline augmentation, and (4) training with online augmentation. The following methods were allowed during the augmentation:
- Weak offline augmentation:
- –
- Rotation around X, Y, and Z;
- Strong offline augmentation:
- –
- Rotation (around X, Y, and Z), resizing, flipping, tilting, squeezing, noise addition, blurring, sharpening, contrast manipulation, brightness manipulation;
- Online augmentation:
- –
- Offline: rotation around X and Y due to the difference in input height (128), width (128) and depth (64);
- –
- Online: rotation (around Z), resizing, flipping, tilting, squeezing, noise addition, blurring, sharpening, contrast manipulation, brightness manipulation.
Training 3D convolutional neural networks (CNNs) with various augmentation methods demands considerable computational resources due to the three-dimensional nature of the datasets. Therefore, this section starts by describing the hardware configuration. Subsequently, the results of the training experiments are provided.
3.2.1. Hardware and Training Duration
The 3D U-Net was trained on a high-performance computing (HPC) system. Throughout the training phases of Strategies 1, 2, and 3, 12 cores, 60 GB RAM, and 8 NVIDIA A100-SXM4 GPUs (40 GB VRAM each) were allocated. Since the online augmentation involved parallel batch processing, 24 cores (the maximum per node) were used. The training runs for the four strategies according to Section 2.3.2 were initially instructed to train the CNNs for 100 epochs. However, the online augmentation increased the variance of the datasets to such an extent that 200 epochs were required for the CNN to converge.
Table 2 shows the training time for all strategies. These training times are not representative for any other machine, but they do provide a rough comparison between these approaches. In [10], the online augmentation was as fast as a training without augmentation. However, in this study, 8 GPUs were used instead of 1. Therefore, with only 24 cores in total, each GPU had only three parallel processes to load and augment the input batches, which is clearly not enough for 3D.

Table 2.
Computational time required to process 100 epochs, depending on the augmentation strategy. The dataset used for online augmentation has been increased as explained in Section 2.3.2.
3.2.2. Training Results
In total, four CNNs were trained, each using a different strategy. The final results are shown in Table 3. As mentioned in Section 2.3.1, the dataset consists exclusively of variations of Grid 1. Therefore, high DICE coefficients and validation accuracies are expected. The accuracy represents the ratio of correctly classified voxels to all voxels in the validation dataset. The DICE values in Table 3 show that the generalization ability using Strategy 1 was the worst compared to the other strategies, even though the test data represent the same grid type.

Table 3.
Training results of testing DICE and validation metrics.
Training with strong offline augmented data achieved the highest DICE, the highest validation accuracy, and the lowest validation loss. Strategy 4 has the highest loss but still a high accuracy, which means that the CNN generates many small errors.
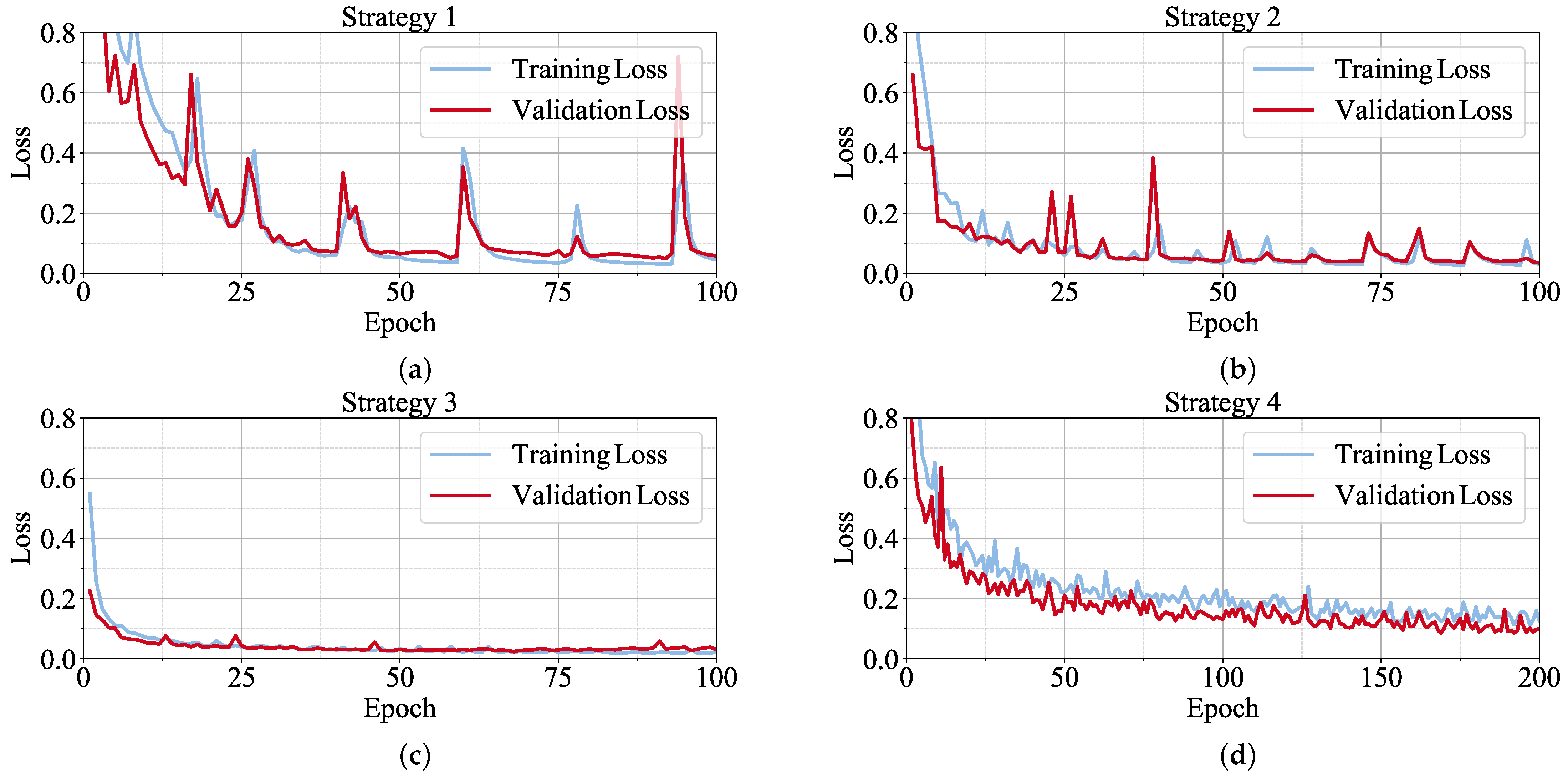
Due to the high similarity between the training and validation data, no direct overfitting could be observed for all strategies during the training phases, as shown in Figure 19. The similarity is further emphasized by the convergence behavior of Strategies 1 to 3, since the validation loss was almost identical to the training loss. Therefore, splitting the dataset into training, validation, and test data seems to be ineffective.
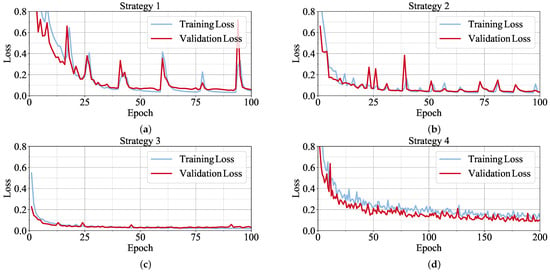
Figure 19.
Training and validation loss for all four strategies. (a) Strategy 1: No augmentation. (b) Strategy 2: Weak offline augmentation. (c) Strategy 3: Strong offline augmentation. (d) Strategy 4: Online augmentation.
A closer inspection of the graphs suggests that the CNNs using Strategies 1 and 2 may exhibit a tendency to overfit specifically on Grid 1 variations due to the strong correlation with the loss graphs. This may also be true for Strategy 3 but cannot be said with certainty. In contrast, only Strategy 4 introduced enough variability into the training data to create a notable distinction from the validation data. Consequently, the validation loss diverged from the training loss in this case, and both losses were higher when compared to Strategies 1 to 3.
However, the results lack information on the generalization ability of the networks with respect to different carbon grids.
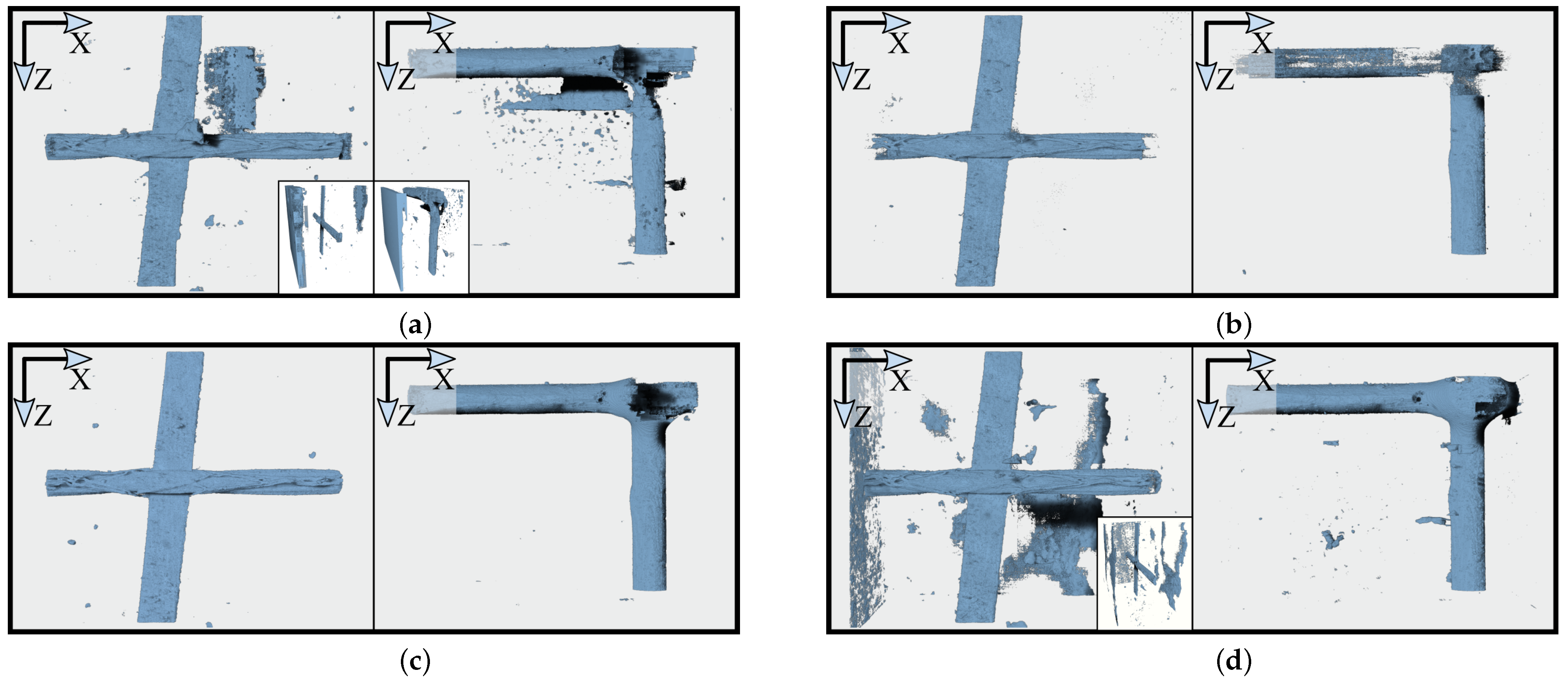
For the reasons mentioned above, the CNN trained on Strategies 1 and 2 may not perform well on Grid 2 at all. For Strategies 3 and 4, it remains unclear which CNN performs best on different grids, although Strategy 3 may have overfitted on variants of Grid 1 as well. For comparison, all networks were used to segment both Sample A and Sample C, as visualized in Figure 20. Except for the CNN without data augmentation (Figure 20a), all networks were able to preserve the shape of the roving of Sample A. However, the CNN trained with Strategy 2 failed on Grid 2 (Figure 20b). The 3D U-Net models trained with Strategies 3 and 4 were able to segment Grid 2 (Figure 20c,d), with Strategy 4 slightly outperforming Strategy 3 in the overlap region of the rovings (Figure 20d right). The heavily augmented dataset resulted in fewer artifacts (Figure 20c), although there were still gaps in the segmentation within the overlap region of the rovings in Sample C. For Sample B, all networks performed well. Sample D could only be segmented using the online augmentation approach. However, the segmentation contained many errors and was not usable. These results disproved the assumption that Strategy 3 also strongly overfitted to the Grid 1 variants but confirmed that Strategy 4 increased the variance of the datasets the most.

Figure 20.
Segmentation of Sample A (left in all subimages) and Sample C (right in all subimages) using each of the four strategies. (a) Strategy 1: No augmentation with removed artifacts in frontal views and full segmentation as miniatures. (b) Strategy 2: Weak offline augmentation. (c) Strategy 3: Strong offline augmentation. (d) Strategy 4: Online augmentation with removed artifacts in Sample A (frontal view) and full segmentation as miniatures.
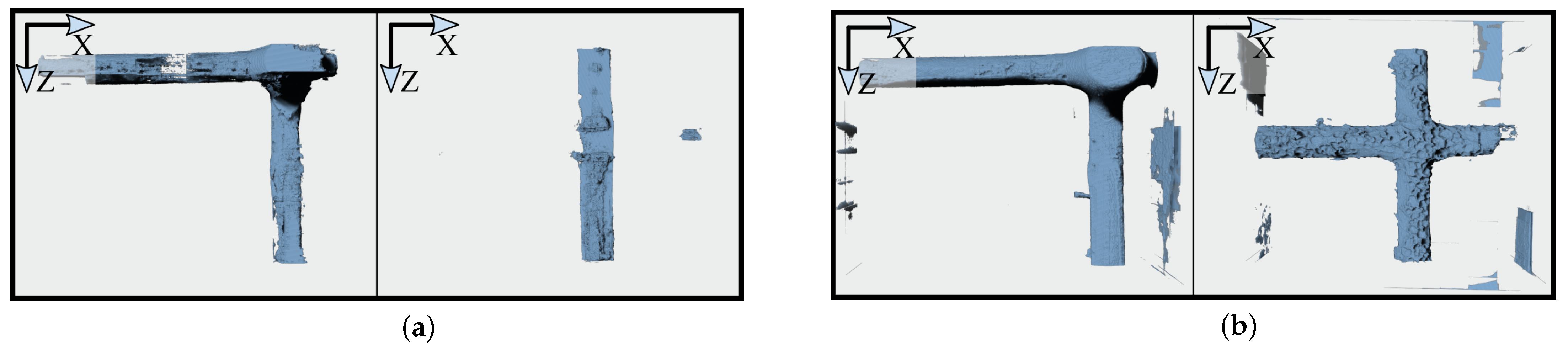
From the observations, both CNNs (Strategies 3 and 4) failed only in regions where they “saw” only voxels related to the roving and air. This suggests a potential solution: by resizing the volumes or scanning with larger voxel sizes, the CNN will be able to segment Grid 2 as well. This hypothesis was tested on Samples C and D, with the results visualized in Figure 21. The reconstructions were resized to a voxel size of 18.8 µm (scale factor of 0.5). The CNN trained with Strategy 3 exhibited significant performance degradation when confronted with resizing. This discrepancy can be explained by the fact that the offline augmented dataset could not achieve the same variability as that created by the online augmentation, as mentioned above. The online augmentation allowed the CNN to learn the underlying features more effectively so that it could segment the roving at larger voxel sizes. However, the CNN cannot distinguish the coating from the roving, and thus the extracted rovings were too large (see Figure 18b).
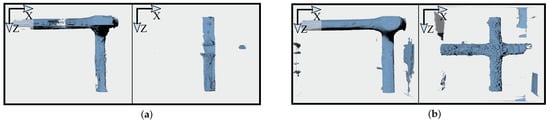
Figure 21.
Test of Strategies 3 and 4 on resized versions of Samples C and D (scale factor: 0.5, voxel size: 18.8 µm). (a) Strategy 3 on resized Samples C (left) and D (right). (b) Strategy 4 on resized Samples C (left) and D (right).
For Grid 1, Strategy 3 produced the best visual segmentation, followed by the online augmentation approach, despite the presence of additional artifacts (Figure 20d, left). However, the remaining noise is eliminated during post-processing in the roving extraction phase. With respect to Grid 2 and the general applicability, online augmentation proved to be the most effective strategy. Therefore, the 3D U-Net with online augmentation was preferred for the following steps, as it performed best overall.
3.3. Roving Extraction
The 3D U-Net trained with Strategy 4 was used to extract all rovings, as it visually performed best in the roving segmentation task. Although this strategy contains many artifacts, the Roving Surface Extractor (link in Data Availability Statement) was able to remove them, and only the rovings (and coating) were obtained (Figure 22). The rovings of Samples A, B, and C were extracted almost perfectly, while in Sample D, a small fraction (≈3 mm) is missing.
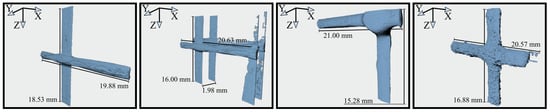
Figure 22.
Post-processed rovings using the 3D U-Net trained with Strategy 4. From left to right: Samples A, B, C, and D.
3.4. Parameterized RVE and Definition of Characteristic Geometric Properties
Of the four extracted samples, Samples C and D contained too much coating, resulting in incorrect roving dimensions; see Figure 18. Sample B contained two layers of textile and two roving intersections and was therefore not suitable as an introductory example. Therefore, the characteristic properties for Sample A were derived.
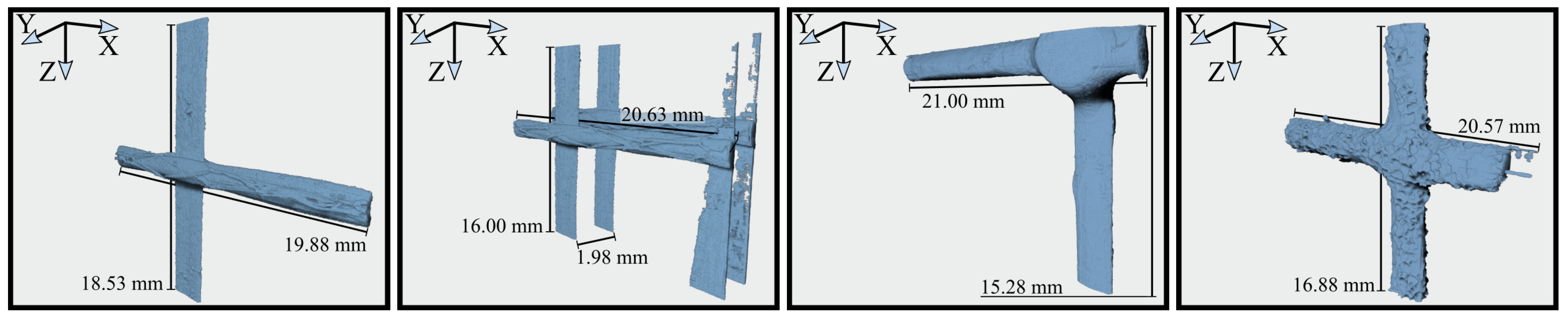
Figure 23a illustrates the sample size and the size of the RVE that was modeled. Figure 23b shows Sample A. Figure 23c depicts the point cloud of the extracted roving. Finally, Figure 23d shows the obtained surface model of the roving that will be embedded in the RVE. For an illustration of the complete modeling process from CT reconstruction to parameterized RVE, refer to Figure 2.
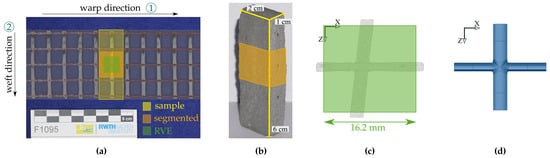
Figure 23.
(a) Textile of Sample A indicating the sample, segmented size, and size of representative volume element (RVE). (b) Sample A with highlighted scanned region. (c) Point cloud representing the roving in (a), RVE size indicated. (d) Surface model of the roving from the parameterized RVE.
The segmented area had the dimensions of 19.88 mm (warp) × 18.53 mm (weft). Further, it can also be seen that both rovings were not orthogonal to each other; see Figure 23c. The roving in the weft direction was not parallel to the z-axis but rotated by approximately . The voxel size of Sample A was 9.5 µm.
3.4.1. Roving Dimensions and
To approximate the roving dimensions of the textile in Sample A, the method described in Section 2.7.1 was used for the x- and z-directions, respectively. The number of slices used for the evaluation is crucial.
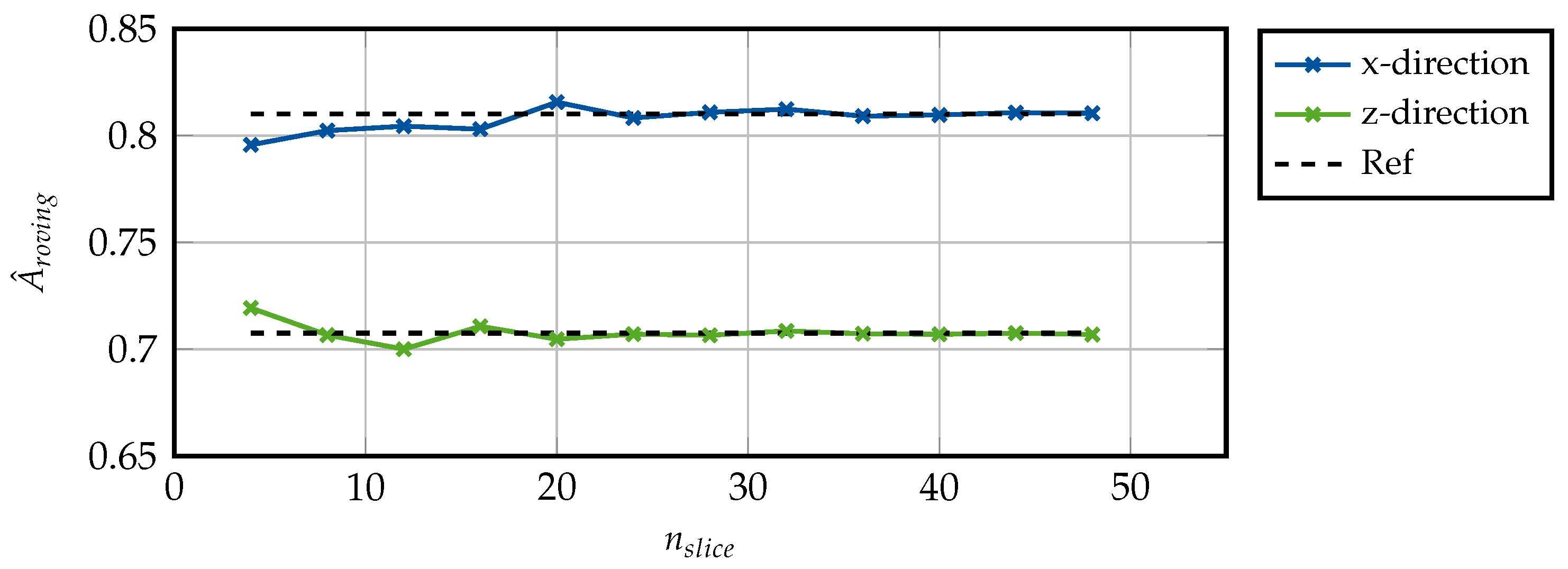
For each slice, the concave hull algorithm was used to derive a polygon representing the area described by the point cloud. The area of the polygon corresponds to the cross-sectional area of the roving for the respective slice. The analysis was carried out for a varying number of slices, and the results for the obtained averaged cross-sectional areas are depicted in Figure 24. The reference solution (plotted as a dashed line) was obtained with . It was observed that, for an increasing number of slices, the averaged cross-sectional area converged to a fixed value.
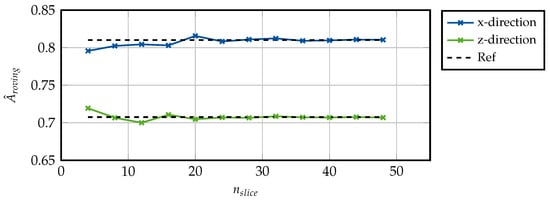
Figure 24.
Obtained cross-sectional area of roving for varying number of slices for each direction of Sample A.
In the following, was chosen to derive the roving geometry. Applying the concave hull algorithm to the point cloud of the extracted roving and using Equation (4), the averaged properties for each roving (in x- and z-directions) were obtained. Following Equation (5), the dimensions of the ellipse approximating the rovings were derived and are summarized in Table 4.

Table 4.
Derived cross-sectional dimensions of cylindrical approximation of roving using .
Since the roving in the weft direction was not perfectly parallel to the z-axis (see Figure 2c), the derived dimensions may be inaccurate. To investigate this issue, the extracted surface was rotated by around the y-axis. Again, the width, height, and cross-sectional areas of the rovings in both directions were obtained. The maximum difference amounts to for the width of the roving (weft direction). In the civil engineering context, this is considered negligible.
The textile used in Sample A was SITgrid 044 VL with yarn spacings of 16.20 mm (warp) × 14.70 mm (weft) (Section 2.1). According to the manufacturer, the cross-sectional area of the textile is 35.25 mm/m. From this, cross-sectional areas of 0.57 mm (warp) and 0.52 mm (weft) were derived, which is a significant difference compared to the results in Table 4. The deviation can be explained by the coating of the rovings and the knitting thread (shown in red in Figure 4a). Because the training dataset also contained the knitting thread as ground truth, and since the grayscale value and structure of the knitting thread and coating are similar to those of the roving, the segmentation could not distinguish between them. Figure 17b illustrates the problem. The knitting thread runs along the x-axis below the roving and is repeatedly interrupted, but the grayscale value is indistinguishable from that of the roving itself. The same applies to the coating.
However, since the textile was fully impregnated and the impregnation and textile were fully bonded, we used the values obtained from computed tomography data for further calculations.
3.4.2. In-Plane Dimensions
The in-plane dimensions depend on the textile and can be obtained from the manufacturer’s data sheet. It was taken as the distance between the center lines of the rovings in the warp and weft directions. For the present example (Sample A), the dimensions were
as mentioned in Section 2.1. The in-plane RVE size, in comparison to the sample size and the segmented area, is shown in Figure 3a.
3.4.3. Shell Thickness
The sample was produced using the Laboratory Mortar Extruder (LabMorTex) [5]. The employed mouthpiece had an opening height of ; however, due to the extrusion process, the thickness of the extruded components was larger than the mouthpiece opening.
Using 2D binary images describing the sample at 35 locations along the scanning direction (z-axis), an averaged shell thickness was obtained using the procedure described in Section 2.7.3. Again, was chosen; however, five images were discarded since they depicted the intersection of the two rovings.
For the present example, the shell thickness derived from the computed tomography images was obtained as mm. The deviation between the expected height, corresponding to the mouthpiece opening, and the derived thickness from computed tomography originates from the extrusion process and is discussed in more detail in Kalthoff et al. [5].
3.4.4. Concrete Cover
The concrete cover depends on the sample. Here, the textile was positioned at the center of the component [5]. Especially for thin structures, the position of the textile within the shell is an important characteristic, which is why a verification using computed tomography images is useful.
Using the same 35 locations along the scan direction that have been used for the determination of the shell thickness, the average concrete cover is derived using the method from Section 2.7.4 and is obtained as .
For validation, the theoretical concrete cover was calculated using the derived roving dimensions and shell thickness for the case of a perfectly centrally aligned roving as:
It can be concluded that the textile was successfully placed at the center of the component during the production process, since .
3.4.5. Example
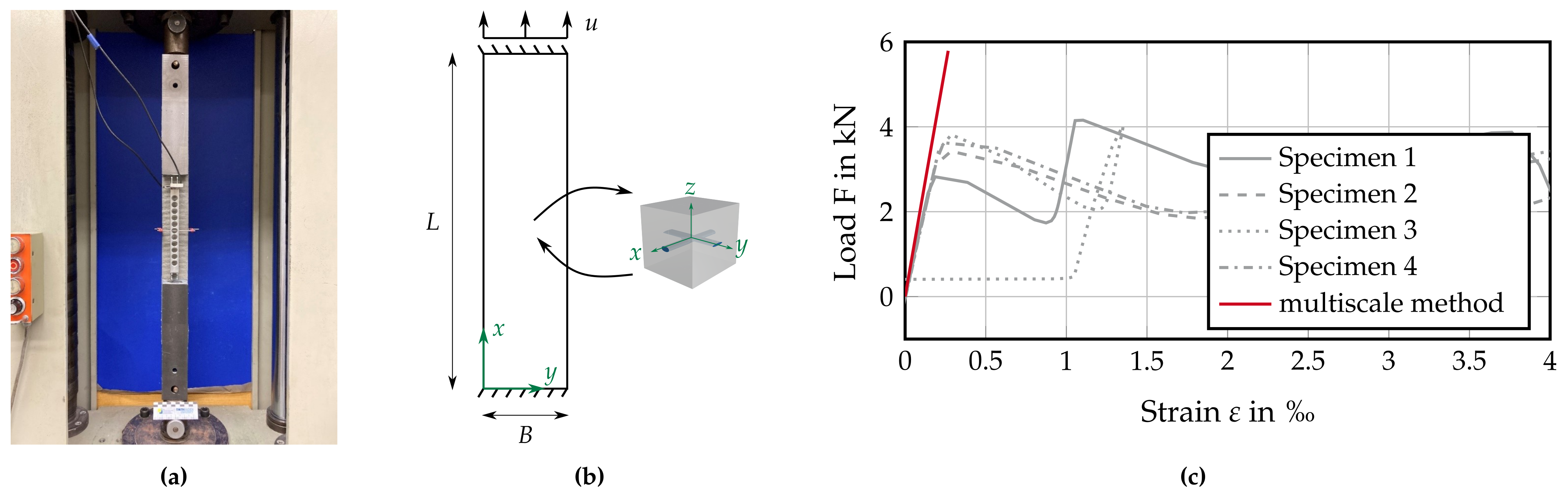
Sample A was taken from an extruded concrete specimen, which was experimentally tested in a tensile test [5]. The setup is depicted in Figure 25a. The free length is given by mm, and the width of the specimen is mm. These dimensions characterize the macroscopic shell; see Figure 25b (left). The example has been presented in [65]. In contrast, here the geometric properties of the RVE were derived according to Section 3.4.1, Section 3.4.2, Section 3.4.3 and Section 3.4.4. The constructed representative volume element was embedded in a multiscale framework; see Figure 25b. The material parameters are given in Table 5 and were chosen according to [5]. Here, for an initial comparison, only linear-elastic material behavior was assumed. Following the experimental test, the analysis was conducted using displacement control, where mm/m. The 3D model of the RVE used for analysis is published on Zenodo [63].
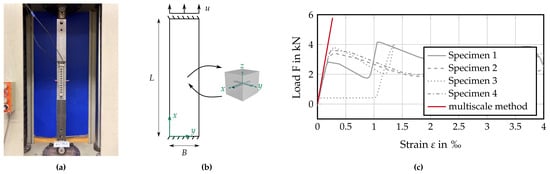
Figure 25.
(a) Experimental setup. (b) Adaptation for multiscale approach. (c) Load-strain curve for tensile test. (Adapted with permission from Ref. [65]. 2023, L. Mester).

Table 5.
Material parameters for tension test.
Figure 25c shows the load-strain curve for four tested extruded specimens and the proposed multiscale approach. Good agreement in the linear-elastic regime can be observed. This proves the applicability of the multiscale approach for the analysis of textile-reinforced concrete structures. Furthermore, it is shown that the derived geometric properties yield the correct volume fractions between textile and concrete. In the future, more examples need to be considered that take the positioning of the textile within the concrete into account, e.g., in bending-dominated examples. The non-linear effects, such as degradation of the concrete and debonding between roving and concrete, need to be considered in future work. Kikis et al. [43] have presented a microplane-damage model in the context of a shell homogenization approach, which is able to represent the nonlinear material behavior of concrete. Here, the material parameters have been taken from [5]; in the future, these should be calibrated and validated by means of multiple examples. The use of a more advanced material model will then allow for evaluation of the load-bearing behavior of textile-reinforced concrete structures.
3.4.6. Assumptions
Finally, the assumptions made in Section 2.7.5 are evaluated with regard to their applicability to the selected example.
- Orthogonality: From Figure 2c, it is clear that the rovings in warp and weft directions were not perfectly orthogonal to each other. However, the rotation of the extracted roving led to only small deviations in the derived geometric properties. Additionally, the distortion was introduced by the extrusion process. Using classical production methods, the distortion of the textile is less distinct. Thus, the assumption of orthogonal rovings is valid.
- A single roving intersection is sufficient for the RVE. This assumption is valid as long as manufacturing errors, which could lead to varying shell thicknesses or concrete covers, can be excluded. Ideally, the segmented area is greater than or equal to the RVE size in order to properly approximate the roving dimensions.
- Elliptical cross-sections are assumed for both rovings. Analysis of the cross-sectional images revealed that small height-to-width ratios should be considered for the roving. In the context of the presented linear-elastic tensile test, the shape approximation proved to be satisfactory.
For the selected example, the assumptions made are valid. In general, the assumption of the rovings being orthogonal to each other only holds as long as the warp and weft direction of the textile are orthogonal. For other textile geometries, the parameterized RVE has to be adapted. Note that the employed periodic boundary conditions in the multiscale approach require the RVE to be symmetric and point symmetric. Thus, a non-symmetric RVE requires different boundary conditions for the homogenization process. A possible solution is discussed in [65].
The investigation of only a single roving intersection is sufficient as long as it is periodically repeating and representative of the whole structure. If the reinforcement layout changes within the structure, e.g., multiple layers of textile in highly stressed areas, multiple RVEs have to be defined. These can be used for homogenization of the corresponding areas.
The assumption of elliptical roving geometries may not be sufficient if debonding or friction are to be investigated. That would require a different algorithm to define the roving geometries; one possibility is presented in Zhang et al. [66] for modeling arteries. Due to the limitations imposed by the scaling center, e.g., star-shapedness, automation is not trivial. Again, the chosen homogenization process requires symmetry and point symmetry, which further complicates the possible description of an RVE.
4. Conclusions
A multiscale method for the analysis of thin structures enhanced by image-based methods was presented. It can be used for the evaluation of novel construction methods and for the structural analysis of textile-reinforced concrete shells.
The entire process, ranging from the generation of computed tomography data to the segmentation and derivation of characteristic geometric properties for the multiscale method, was demonstrated on an extruded concrete specimen. The computed tomography images were processed using a 3D convolutional neural network to obtain a volumetric reconstruction of the grid-aligned rovings within the mortar matrix. Four different augmentation strategies were presented, and the efficiency of the trained CNNs was compared. The derived grid properties were validated by comparison with values from existing literature. A linear-elastic benchmark example showed the validity of the multiscale approach.
However, there is still room for improvement.
In terms of roving extraction, the CNN training dataset can be extended with different textiles and/or the implementation of an unpaired volume-to-volume translation for the training data generation based on [67].
For the structural analysis of concrete specimens, further validation using more complex examples is required to validate the derived geometric properties. For the analysis of specimens with multiple reinforcement layers, the proposed parameterized RVE can be used multiple times on top of one another, so that an extension is straightforward. The analysis of specimens where the weft and warp directions of the employed textile are not orthogonal to each other requires the definition of an adapted parameterized RVE and, consequently, may require different boundary conditions within the multiscale framework. To evaluate the non-linear material behavior of concrete, a microplane damage model can be used [43]. The calibration and validation of the respective material parameters using several different experimental examples is part of future work. At this stage, a full bond between concrete and roving is assumed. However, when investigating debonding behavior, the assumption of an elliptical shape of the roving may not be sufficient. For these cases, it may be beneficial to incorporate the exact roving geometry in the RVE. However, this cannot necessarily be incorporated directly into the multiscale framework.
Author Contributions
Conceptualization, F.W. and L.M.; methodology, F.W. and L.M.; software, F.W. and L.M.; validation, F.W. and L.M.; formal analysis, F.W. and L.M.; investigation, F.W. and L.M.; resources, H.-G.M. and S.K.; data curation, F.W. and L.M.; writing—original draft preparation, F.W., L.M., H.-G.M., and S.K.; writing—review and editing, F.W., L.M., H.-G.M., and S.K.; visualization, F.W. and L.M.; supervision, H.-G.M. and S.K.; project administration, H.-G.M. and S.K.; funding acquisition, H.-G.M. and S.K. All authors have read and agreed to the published version of the manuscript.
Funding
The research work presented in the publication has been funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—SFB/TRR 280; Project-ID: 417002380.
Data Availability Statement
Software available at: https://gitlab.com/fra-wa/aiseg (AiSeg for CNN training, accessed on 17 September 2023); https://gitlab.com/fra-wa/roving_surface_extractor (Roving Surface Extractor, accessed on 17 September 2023). CNN training data available at: https://doi.org/10.34740/KAGGLE/DS/2920892 (Roving Segmentation Dataset, accessed on 17 September 2023). Parameterized RVE model available at: https://doi.org/10.5281/zenodo.8340828 (accessed on 15 September 2023).
Acknowledgments
The authors are grateful to the Center for Information Services and High Performance Computing [Zentrum für Informationsdienste und Hochleistungsrechnen (ZIH)] at TUD Dresden University of Technology for providing its facilities for high throughput calculations.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| CNN | Convolutional neural network |
| CRC | Carbon reinforced concrete |
| CT | Computed tomography |
| LabMorTex | Laboratory Mortar Extruder |
| NURBS | Non-uniform rational B-splines |
| RVE | Representative volume element |
| SBIGA | Scaled boundary isogeometric analysis |
References
- Scheerer, S.; Zobel, R.; Müller, E.; Senckpiel-Peters, T.; Schmidt, A.; Curbach, M. Flexural Strengthening of RC Structures with TRC—Experimental Observations, Design Approach and Application. Appl. Sci. 2019, 9, 1322. [Google Scholar] [CrossRef]
- Beckmann, B.; Bielak, J.; Bosbach, S.; Scheerer, S.; Schmidt, C.; Hegger, J.; Curbach, M. Collaborative research on carbon reinforced concrete structures in the CRC/TRR 280 project. Civ. Eng. Des. 2021, 3, 99–109. [Google Scholar] [CrossRef]
- Bielak, J.; Kollegger, J.; Hegger, J. Shear in Slabs with Non-Metallic Reinforcement. Ph.D. Thesis, Lehrstuhl und Institut für Massivbau, RWTH Aachen University, Aachen, Germany, 2021. [Google Scholar] [CrossRef]
- Morales Cruz, C. Supplementary Data to Crack-distributing Carbon Textile Reinforced Concrete Protection Layers. Ph.D. Thesis, Lehrstuhl für Baustoffkunde–Bauwerkserhaltung, RWTH Aachen University, Aachen, Germany, 2022. [Google Scholar] [CrossRef]
- Kalthoff, M.; Raupach, M.; Matschei, T. Investigation into the Integration of Impregnated Glass and Carbon Textiles in a Laboratory Mortar Extruder (LabMorTex). Materials 2021, 14, 7406. [Google Scholar] [CrossRef]
- Kalthoff, M.; Raupach, M.; Matschei, T. Extrusion and Subsequent Transformation of Textile-Reinforced Mortar Components—Requirements on the Textile, Mortar and Process Parameters with a Laboratory Mortar Extruder (LabMorTex). Buildings 2022, 12, 726. [Google Scholar] [CrossRef]
- Kalthoff, M.; Bosbach, S.; Backes, J.G.; Morales Cruz, C.; Claßen, M.; Traverso, M.; Raupach, M.; Matschei, T. Fabrication of lightweight, carbon textile reinforced concrete components with internally nested lattice structure using 2-layer extrusion by LabMorTex. Constr. Build. Mater. 2023, 395, 132334. [Google Scholar] [CrossRef]
- Mester, L.; Wagner, F.; Liebold, F.; Klarmann, S.; Maas, H.G.; Klinkel, S. Image-Based Modelling and Analysis of Carbon-Fibre Reinforced Concrete Shell Structures. In Proceedings of the Concrete Innovation for Sustainability, Oslo, Norway, 12–16 June 2022; Volume 6, pp. 1631–1640. [Google Scholar]
- Scholzen, A.; Chudoba, R.; Hegger, J. Dünnwandiges Schalentragwerk aus textilbewehrtem Beton. Beton- Und Stahlbetonbau 2012, 107, 767–776. [Google Scholar] [CrossRef]
- Wagner, F.; Eltner, A.; Maas, H.G. River water segmentation in surveillance camera images: A comparative study of offline and online augmentation using 32 CNNs. Int. J. Appl. Earth Obs. Geoinf. 2023, 119, 103305. [Google Scholar] [CrossRef]
- Wagner, F. Carbon Rovings Segmentation Dataset. 2023. Available online: https://www.kaggle.com/datasets/franzwagner/carbon-rovings (accessed on 22 August 2023).
- Berger, M.; Tagliasacchi, A.; Seversky, L.M.; Alliez, P.; Guennebaud, G.; Levine, J.A.; Sharf, A.; Silva, C.T. A Survey of Surface Reconstruction from Point Clouds. Comput. Graph. Forum 2017, 36, 301–329. [Google Scholar] [CrossRef]
- Huang, Z.; Wen, Y.; Wang, Z.; Ren, J.; Jia, K. Surface Reconstruction from Point Clouds: A Survey and a Benchmark. arXiv 2022, arXiv:2205.02413. [Google Scholar] [CrossRef]
- Vukicevic, A.M.; Çimen, S.; Jagic, N.; Jovicic, G.; Frangi, A.F.; Filipovic, N. Three-dimensional reconstruction and NURBS-based structured meshing of coronary arteries from the conventional X-ray angiography projection images. Sci. Rep. 2018, 8, 1711. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, L.; Qu, J.; Xia, Z.; Deng, X. Isogeometric analysis based on geometric reconstruction models. Front. Mech. Eng. 2021, 16, 782–797. [Google Scholar] [CrossRef]
- Grove, O.; Rajab, K.; Piegl, L.A. From CT to NURBS: Contour Fitting with B-spline Curves. Comput.-Aided Des. Appl. 2010, 7, 1–19. [Google Scholar] [CrossRef]
- Chasapi, M.; Mester, L.; Simeon, B.; Klinkel, S. Isogeometric analysis of 3D solids in boundary representation for problems in nonlinear solid mechanics and structural dynamics. Int. J. Numer. Methods Eng. 2021. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Cottrell, J.A.; Bazilevs, Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef]
- Cottrell, J.A.; Hughes, T.J.R.; Bazilevs, Y. Isogeometric Analysis: Toward Integration of CAD and FEA; John Wiley and Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- ProCon X-Ray GmbH. PXR PROCON X-RAY. 2020. Available online: https://procon-x-ray.de/ct-xpress/ (accessed on 17 September 2023).
- Millner, M.R.; Payne, W.H.; Waggener, R.G.; McDavid, W.D.; Dennis, M.J.; Sank, V.J. Determination of effective energies in CT calibration. Med Phys. 1978, 5, 543–545. [Google Scholar] [CrossRef]
- Tan, Y.; Kiekens, K.; Welkenhuyzen, F.; Kruth, J.; Dewulf, W. Beam hardening correction and its influence on the measurement accuracy and repeatability for CT dimensional metrology applications. In Proceedings of the 4th Conference on Industrial Computed Tomography (iCT), Wels, Austria, 19–21 September 2012; Volume 17, pp. 355–362. [Google Scholar]
- Ciresan, D.; Giusti, A.; Gambardella, L.; Schmidhuber, J. Deep Neural Networks Segment Neuronal Membranes in Electron Microscopy Images. Adv. Neural Inf. Processing Syst. 2012, 25, 1–9. Available online: https://papers.nips.cc/paper_files/paper/2012/hash/459a4ddcb586f24efd9395aa7662bc7c-Abstract.html (accessed on 22 August 2023).
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Handa, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Robust Semantic Pixel-Wise Labelling. arXiv 2015, arXiv:1505.07293. [Google Scholar] [CrossRef]
- Xiao, T.; Liu, Y.; Zhou, B.; Jiang, Y.; Sun, J. Unified Perceptual Parsing for Scene Understanding. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 432–448. [Google Scholar] [CrossRef]
- Peng, C.; Zhang, X.; Yu, G.; Luo, G.; Sun, J. Large Kernel Matters—Improve Semantic Segmentation by Global Convolutional Network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; IEEE Computer Society: Los Alamitos, CA, USA, 2017; pp. 1743–1751. [Google Scholar] [CrossRef]
- Yu, L.; Cheng, J.Z.; Dou, Q.; Yang, X.; Chen, H.; Qin, J.; Heng, P.A. Automatic 3D Cardiovascular MR Segmentation with Densely-Connected Volumetric ConvNets. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2017. MICCAI 2017; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2017; Volume 10434, pp. 287–295. [Google Scholar] [CrossRef]
- Bui, T.D.; Shin, J.; Moon, T. Skip-connected 3D DenseNet for volumetric infant brain MRI segmentation. Biomed. Signal Process. Control. 2019, 54, 101613. [Google Scholar] [CrossRef]
- Chen, S.; Ma, K.; Zheng, Y. Med3D: Transfer Learning for 3D Medical Image Analysis. arXiv 2019, arXiv:1904.00625. [Google Scholar] [CrossRef]
- Çiçek, Ö.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning Dense Volumetric Segmentation from Sparse Annotation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2016, Athens, Greece, 17–21 October 2016; Ourselin, S., Joskowicz, L., Sabuncu, M.R., Unal, G., Wells, W., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 424–432. [Google Scholar] [CrossRef]
- Wagner, F.; Maas, H.G. A Comparative Study of Deep Architectures for Voxel Segmentation in Volume Images. In Proceedings of the ISPRS Geospatial Week 2023, Cairo, Egypt, 2–7 September 2023. [Google Scholar]
- Shorten, C.; Khoshgoftaar, T.M. A survey on Image Data Augmentation for Deep Learning. J. Big Data 2019, 6, 60. [Google Scholar] [CrossRef]
- Buslaev, A.; Iglovikov, V.I.; Khvedchenya, E.; Parinov, A.; Druzhinin, M.; Kalinin, A.A. Albumentations: Fast and Flexible Image Augmentations. Information 2020, 11, 125. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the Neural Information Processing Systems (NIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; pp. 8026–8037. Available online: https://proceedings.neurips.cc/paper_files/paper/2019/file/bdbca288fee7f92f2bfa9f7012727740-Paper.pdf (accessed on 22 August 2023).
- Alam, M.; Wang, J.F.; Guangpei, C.; Yunrong, L.V.; Chen, Y. Convolutional Neural Network for the Semantic Segmentation of Remote Sensing Images. Mob. Netw. Appl. 2021, 26, 200–215. [Google Scholar] [CrossRef]
- Xu, H.; He, H.; Zhang, Y.; Ma, L.; Li, J. A comparative study of loss functions for road segmentation in remotely sensed road datasets. Int. J. Appl. Earth Obs. Geoinf. 2023, 116, 103159. [Google Scholar] [CrossRef]
- Wu, Y.; He, K. Group Normalization. Int. J. Comput. Vis. 2020, 128, 742–755. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015; Conference Track Proceedings. Bengio, Y., LeCun, Y., Eds.; Cornel University Press: Ithaca, NY, USA, 2017. [Google Scholar] [CrossRef]
- Taha, A.A.; Hanbury, A. Metrics for evaluating 3D medical image segmentation: Analysis, selection, and tool. BMC Med. Imaging 2015, 15, 29. [Google Scholar] [CrossRef]
- Cardoso, M.J.; Li, W.; Brown, R.; Ma, N.; Kerfoot, E.; Wang, Y.; Murrey, B.; Myronenko, A.; Zhao, C.; Yang, D.; et al. MONAI: An open-source framework for deep learning in healthcare. arXiv 2022, arXiv:2211.02701. [Google Scholar] [CrossRef]
- Lorensen, W.E.; Cline, H.E. Marching Cubes: A High Resolution 3D Surface Construction Algorithm. In Proceedings of the ACM SIGGRAPH Computer Graphics; Association for Computing Machinery: New York, NY, USA, 1987; Volume 21, SIGGRAPH ’87; pp. 163–169. [Google Scholar] [CrossRef]
- Kikis, G.; Mester, L.; Spartali, H.; Chudoba, R.; Klinkel, S. Analyse des Trag- und Bruchverhaltens von Carbonbetonstrukturen im Rahmen des SFB/TRR 280/Analysis of the load-bearing and fracture behavior of carbon concrete structures as part of the SFB/TRR 280. Bauingenieur 2023, 98, 218–226. [Google Scholar] [CrossRef]
- Platen, J.; Zreid, I.; Kaliske, M. A nonlocal microplane approach to model textile reinforced concrete at finite deformations. Int. J. Solids Struct. 2023, 267, 112151. [Google Scholar] [CrossRef]
- Valeri, P.; Fernàndez Ruiz, M.; Muttoni, A. Tensile response of textile reinforced concrete. Constr. Build. Mater. 2020, 258, 119517. [Google Scholar] [CrossRef]
- Schröder, J. A numerical two-scale homogenization scheme: The FE2-method. In Plasticity and Beyond: Microstructures, Crystal-Plasticity and Phase Transitions; Springer: Vienna, Austria, 2014; pp. 1–64. [Google Scholar] [CrossRef]
- Saeb, S.; Steinmann, P.; Javili, A. Aspects of Computational Homogenization at Finite Deformations: A Unifying Review From Reuss’ to Voigt’s Bound. Appl. Mech. Rev. 2016, 68, 050801. [Google Scholar] [CrossRef]
- Coenen, E.; Kouznetsova, V.; Geers, M. Computational homogenization for heterogeneous thin sheets. Int. J. Numer. Methods Eng. 2010, 83, 1180–1205. [Google Scholar] [CrossRef]
- Hii, A.K.; El Said, B. A kinematically consistent second-order computational homogenisation framework for thick shell models. Comput. Methods Appl. Mech. Eng. 2022, 398, 115136. [Google Scholar] [CrossRef]
- Börjesson, E.; Larsson, F.; Runesson, K.; Remmers, J.J.; Fagerström, M. Variationally consistent homogenisation of plates. Comput. Methods Appl. Mech. Eng. 2023, 413, 116094. [Google Scholar] [CrossRef]
- Gruttmann, F.; Wagner, W. A coupled two-scale shell model with applications to layered structures. Int. J. Numer. Methods Eng. 2013, 94, 1233–1254. [Google Scholar] [CrossRef]
- Feyel, F.; Chaboche, J.L. FE2 multiscale approach for modelling the elastoviscoplastic behaviour of long fibre SiC/Ti composite materials. Comput. Methods Appl. Mech. Eng. 2000, 183, 309–330. [Google Scholar] [CrossRef]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Miehe, C.; Koch, A. Computational micro-to-macro transitions of discretized microstructures undergoing small strains. Arch. Appl. Mech. Ingenieur Arch. 2002, 72, 300–317. [Google Scholar] [CrossRef]
- Mester, L.; Klarmann, S.; Klinkel, S. Homogenization assumptions for the two-scale analysis of first-order shear deformable shells. Comput. Mech. 2023. [Google Scholar]
- Song, C. The Scaled Boundary Finite Element Method; John Wiley & Sons, Ltd.: Chichester, UK, 2018. [Google Scholar] [CrossRef]
- Jüttler, B.; Maroscheck, S.; Kim, M.S.; Youn Hong, Q. Arc fibrations of planar domains. Comput. Aided Geom. Des. 2019, 71, 105–118. [Google Scholar] [CrossRef]
- Trautner, S.; Jüttler, B.; Kim, M.S. Representing planar domains by polar parameterizations with parabolic parameter lines. Comput. Aided Geom. Des. 2021, 85, 101966. [Google Scholar] [CrossRef]
- Chin, E.B.; Sukumar, N. Scaled boundary cubature scheme for numerical integration over planar regions with affine and curved boundaries. Comput. Methods Appl. Mech. Eng. 2021, 380, 113796. [Google Scholar] [CrossRef]
- Sauren, B.; Klarmann, S.; Kobbelt, L.; Klinkel, S. A mixed polygonal finite element formulation for nearly-incompressible finite elasticity. Comput. Methods Appl. Mech. Eng. 2023, 403, 115656. [Google Scholar] [CrossRef]
- Reichel, R.; Klinkel, S. A non–uniform rational B–splines enhanced finite element formulation based on the scaled boundary parameterization for the analysis of heterogeneous solids. Int. J. Numer. Methods Eng. 2023, 124, 2068–2092. [Google Scholar] [CrossRef]
- Bauer, B.; Arioli, C.; Simeon, B. Generating Star-Shaped Blocks for Scaled Boundary Multipatch IGA. In Isogeometric Analysis and Applications 2018; van Brummelen, H., Vuik, C., Möller, M., Verhoosel, C., Simeon, B., Jüttler, B., Eds.; Lecture Notes in Computational Science and Engineering; Springer International Publishing: Cham, Switzerland, 2021; Volume 133, pp. 1–25. [Google Scholar] [CrossRef]
- Mester, L.; Klinkel, S. Parameterized Representative Volume Element (RVE) for Textile-Reinfoced Composites. 2023. Available online: https://zenodo.org/record/8340828 (accessed on 22 August 2023).
- Park, J.S.; Oh, S.J. A new concave hull algorithm and concaveness measure for n-dimensional datasets. J. Inf. Sci. Eng. 2012, 28, 587–600. [Google Scholar]
- Mester, L.; Klarmann, S.; Klinkel, S. Homogenisation for macroscopic shell structures with application to textile–reinforced mesostructures. PAMM 2023, 22. [Google Scholar] [CrossRef]
- Zhang, Y.; Bazilevs, Y.; Goswami, S.; Bajaj, C.L.; Hughes, T.J.R. Patient-Specific Vascular NURBS Modeling for Isogeometric Analysis of Blood Flow. Comput. Methods Appl. Mech. Eng. 2007, 196, 2943–2959. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired Image-to-Image Translation Using Cycle-Consistent Adversarial Networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2242–2251. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).