Investigation on Behaviours along Weak Axes of Steel Beam under Low Velocity Impact Loading: Experimental and Numerical
Abstract
1. Introduction
2. Experimental Study
2.1. Material Properties
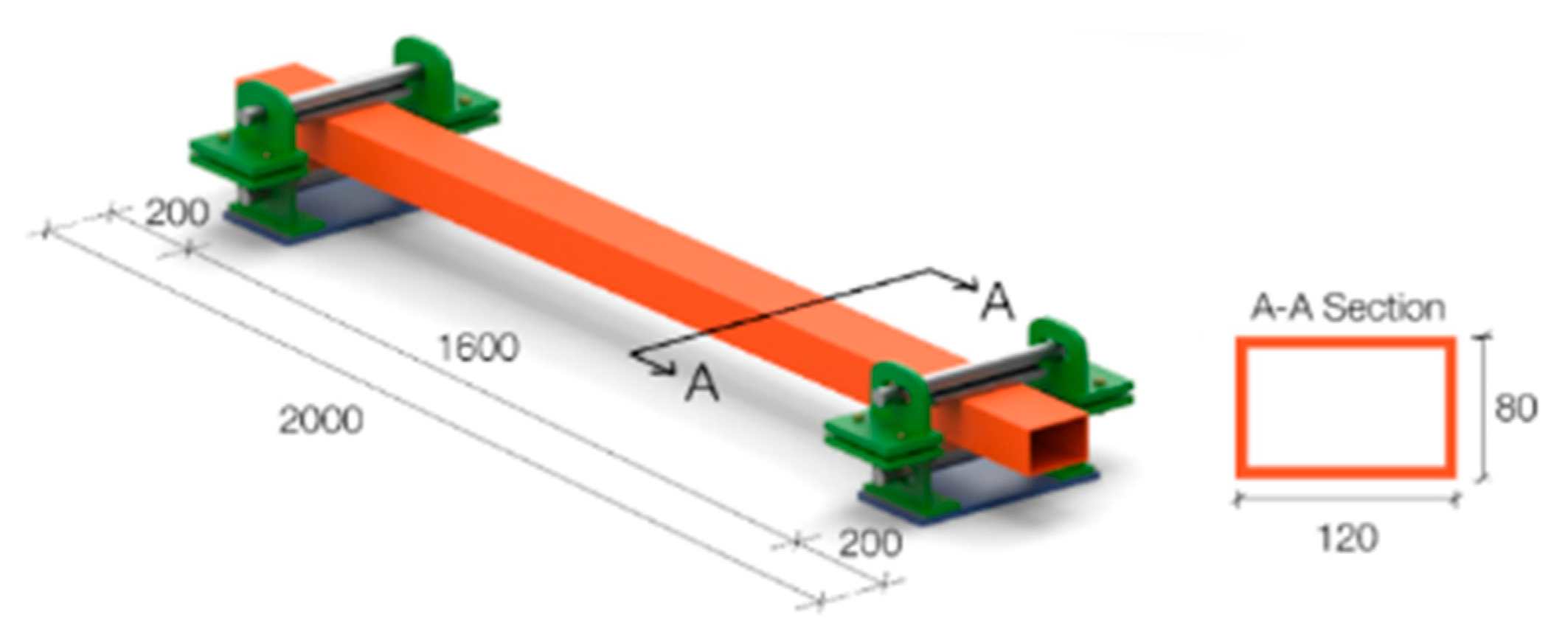
2.2. Specimen Geometry
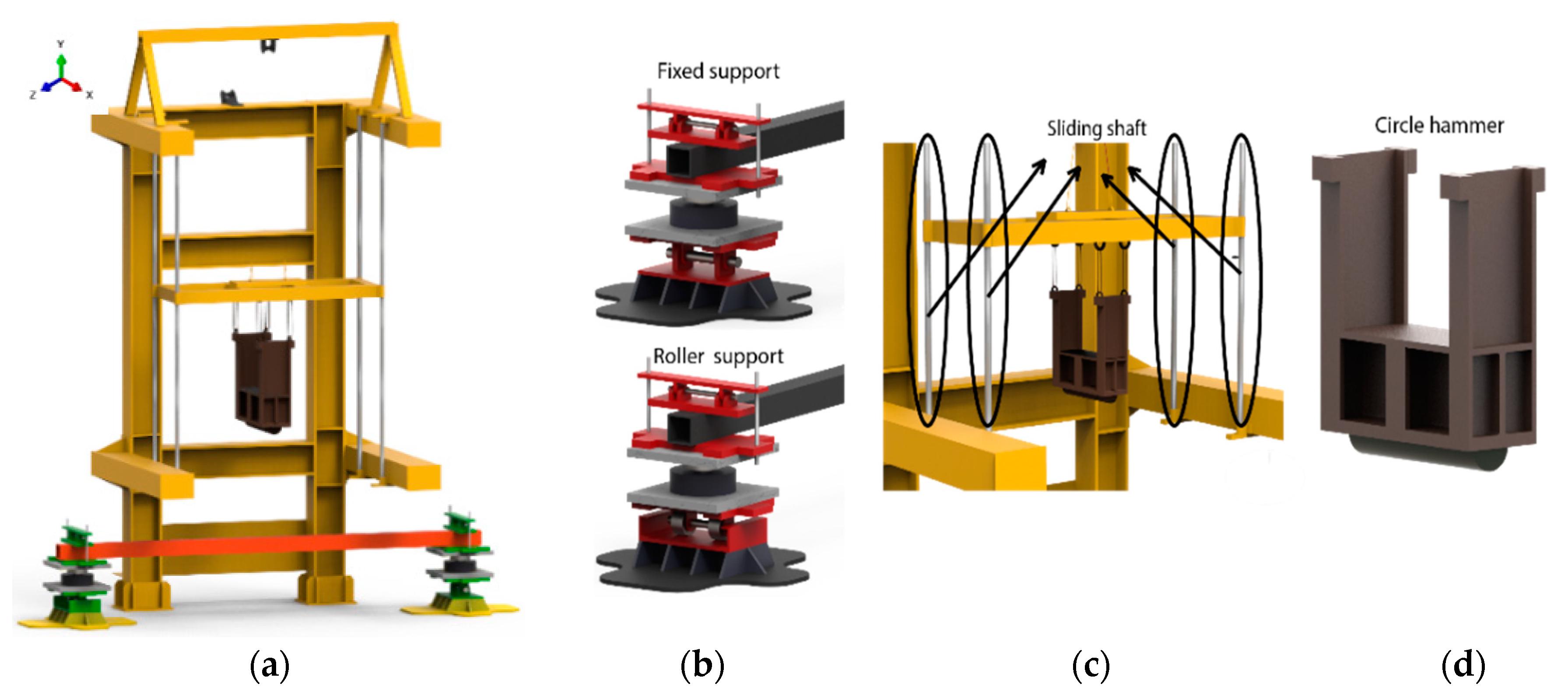
2.3. Test Setup and Measurement
3. Numerical Studies
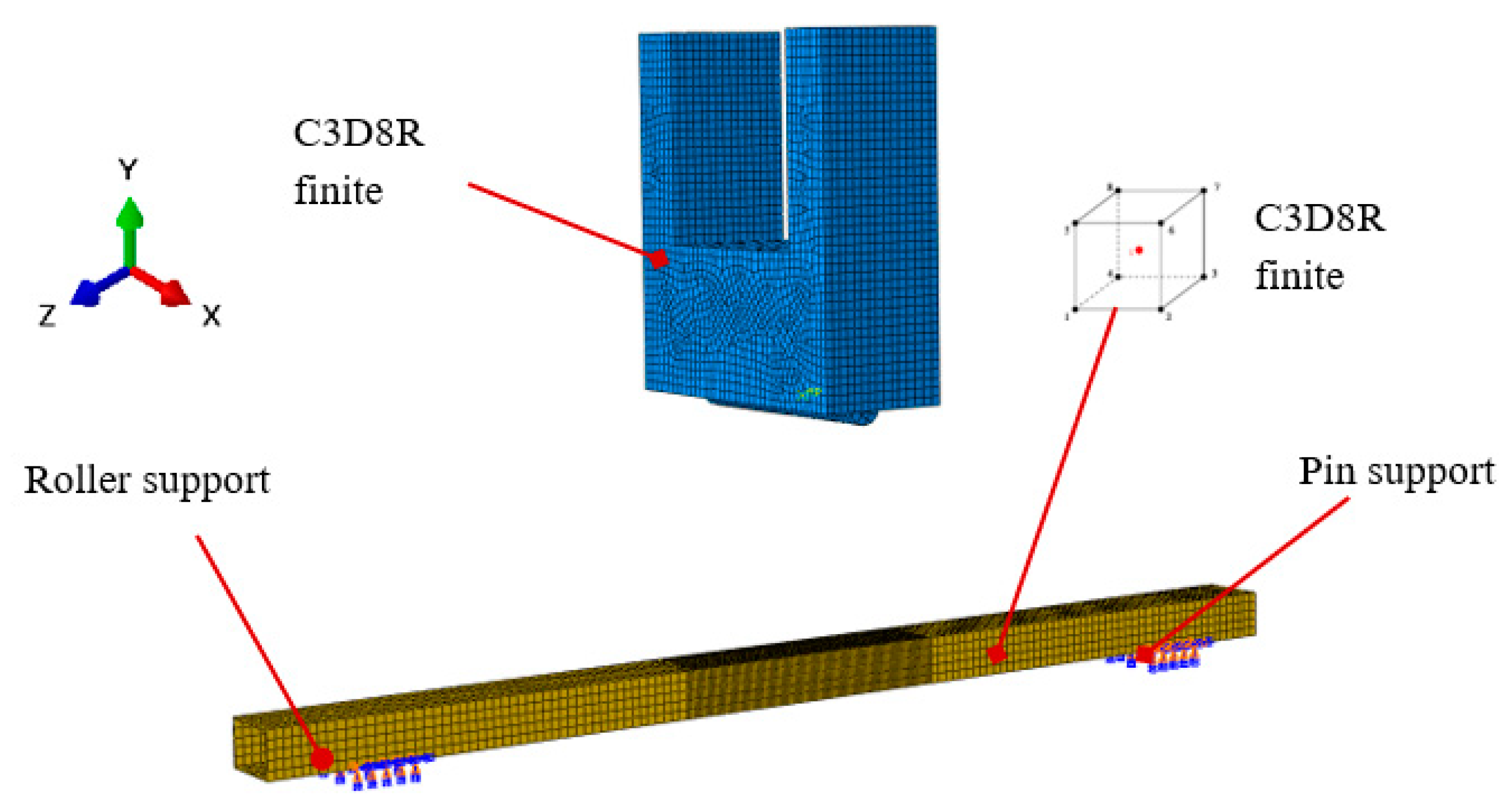
3.1. Finite Element Modeling
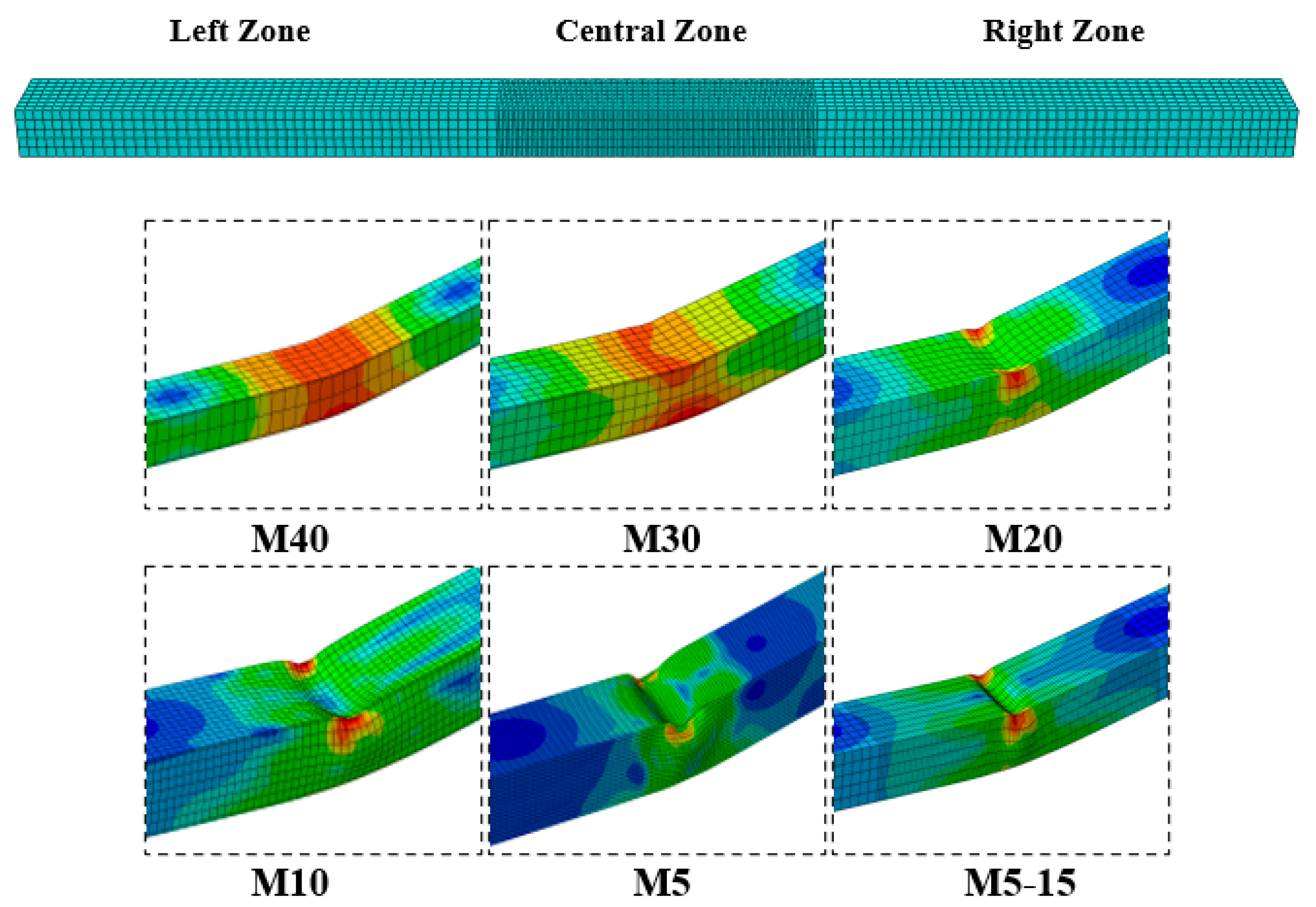
3.2. Mesh Convergence Studies
4. Results and Discussion
4.1. Experimental Results
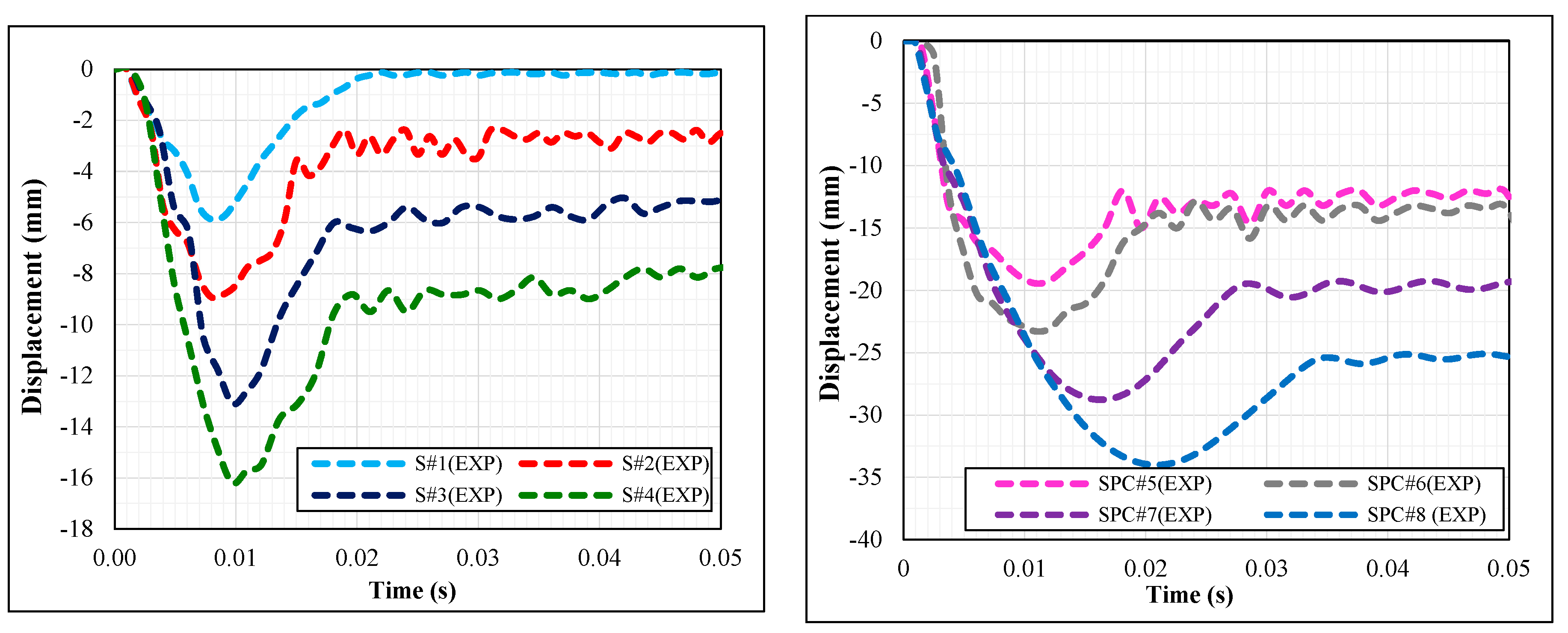
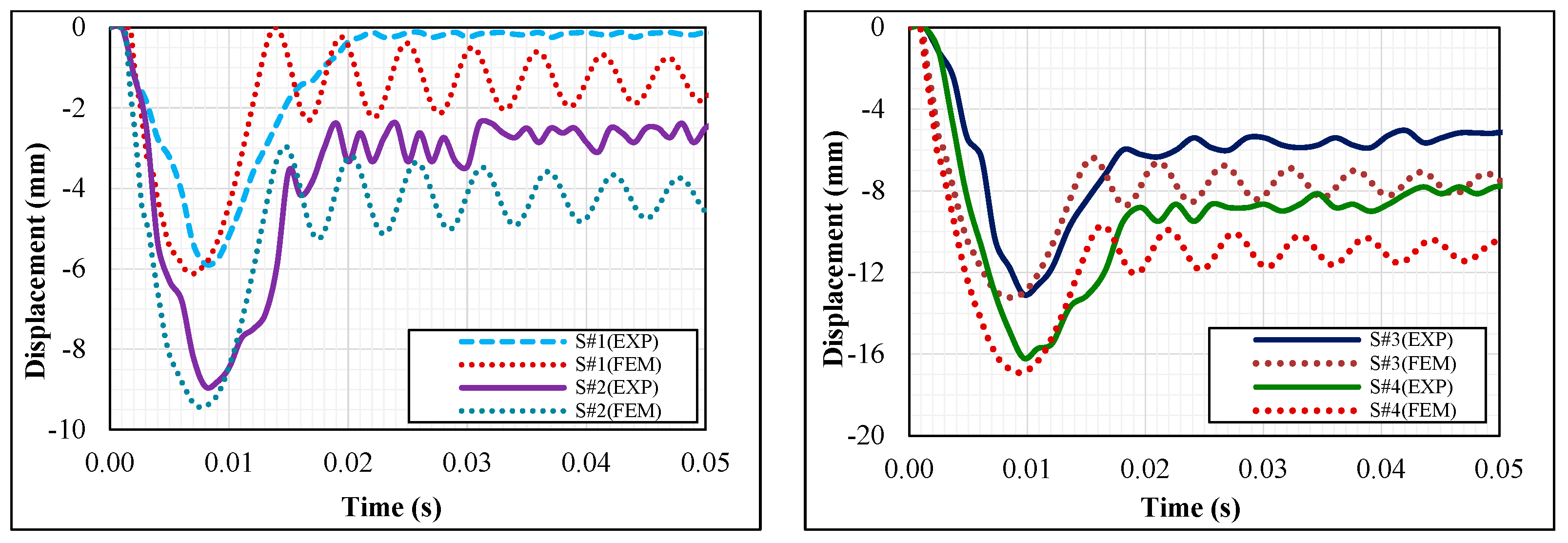
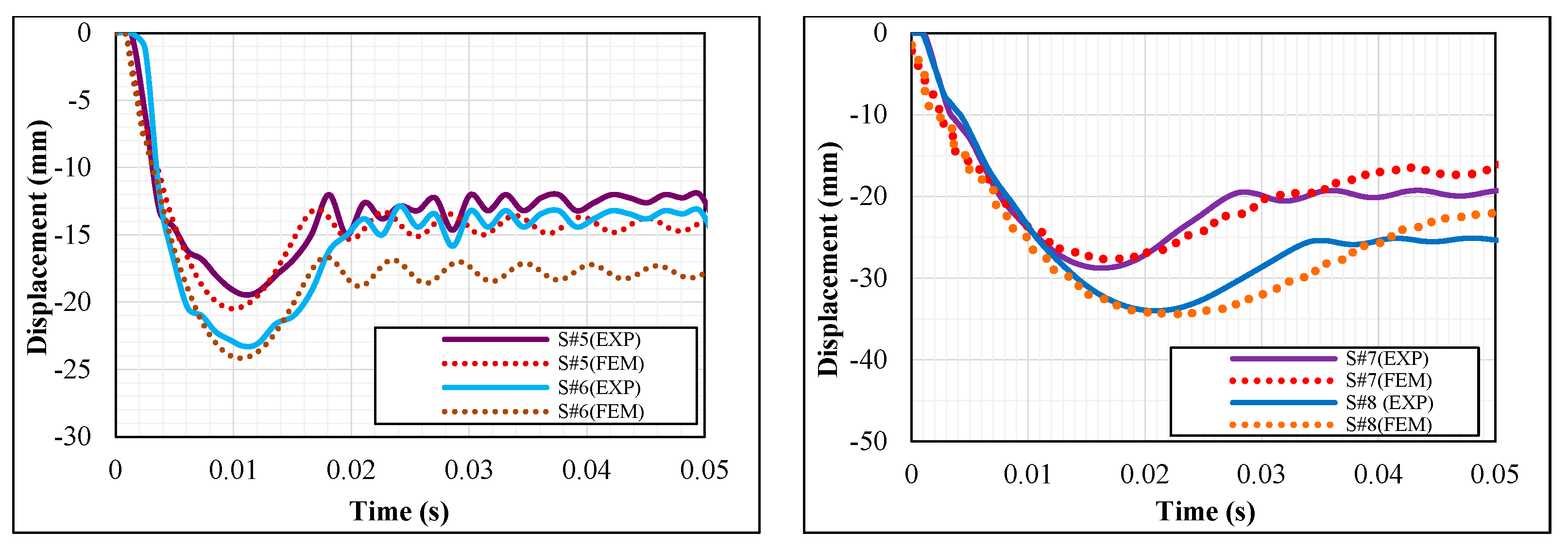
4.1.1. Displacement-Time Responses and Damage Status
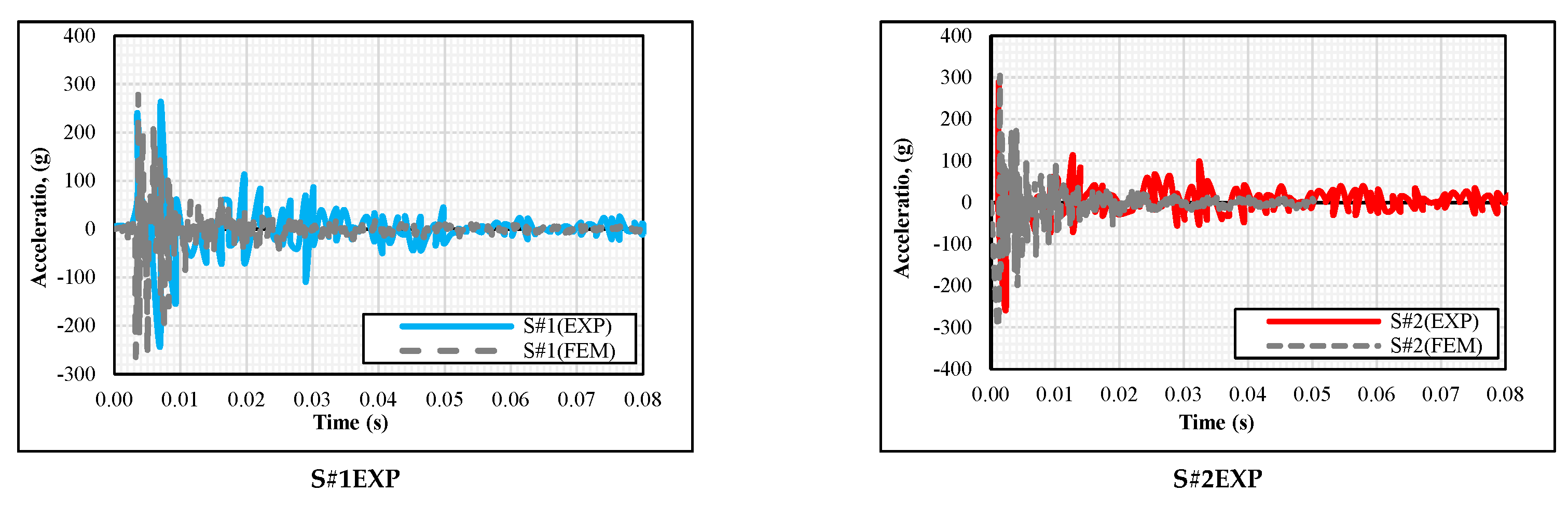
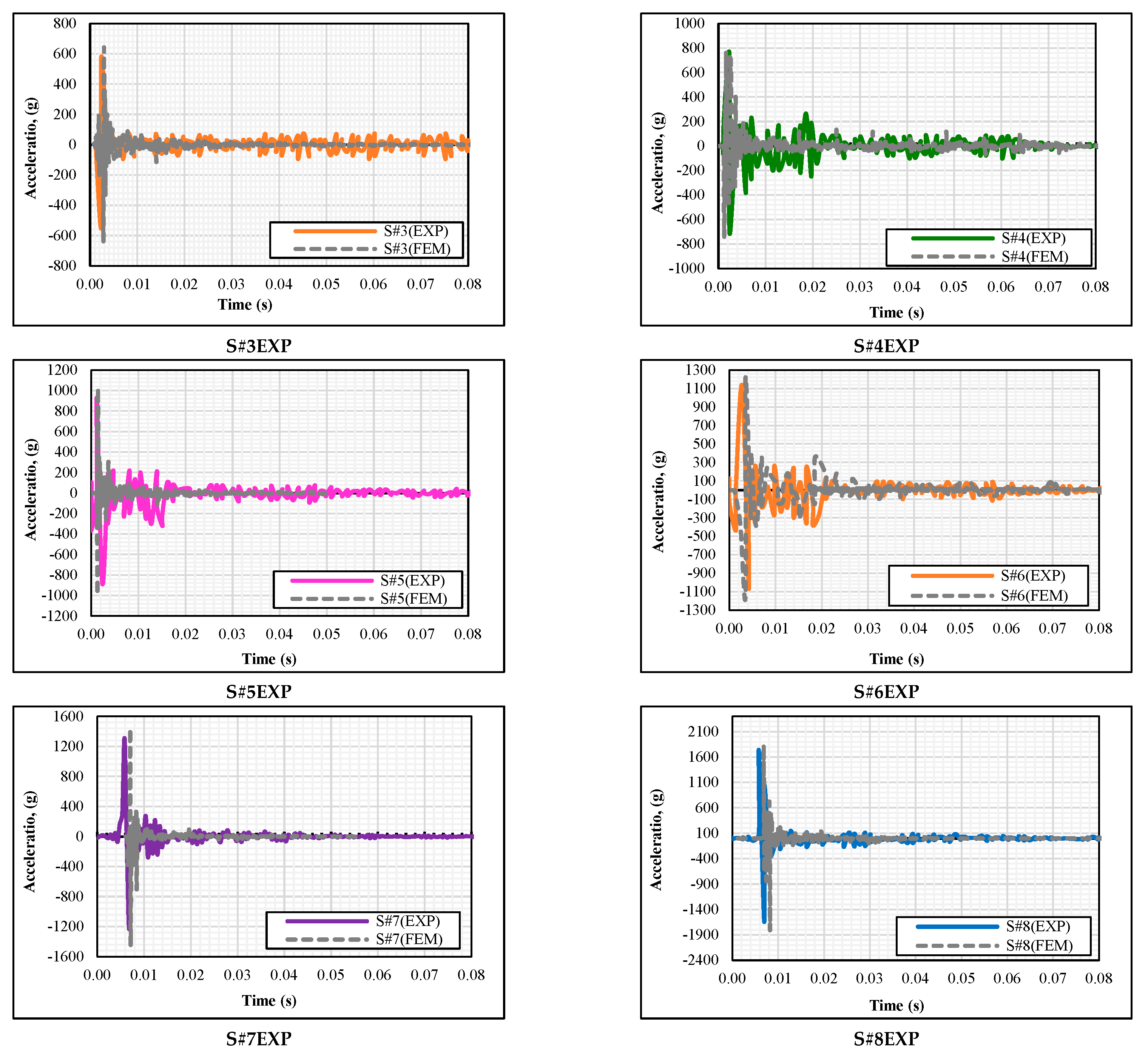
4.1.2. Acceleration-Time
4.1.3. Impact Force
4.1.4. Impact Load Factors for Static Analysis
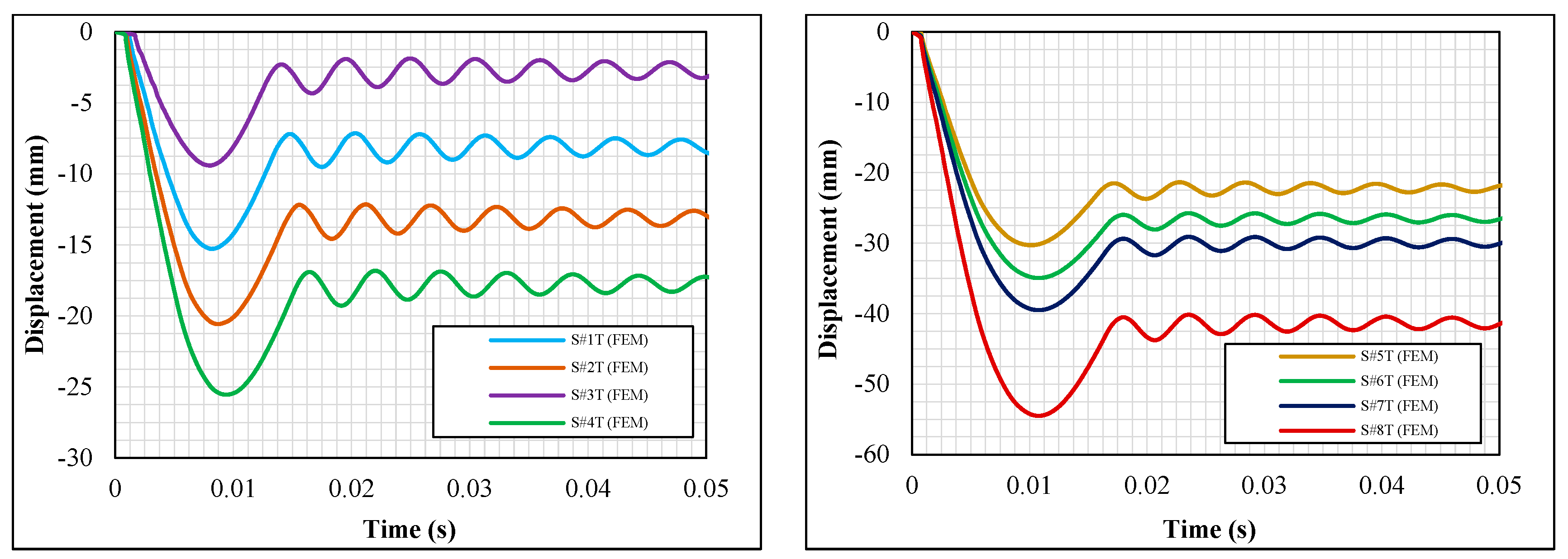
4.2. Numerical Results and Discussion
5. Conclusions
- In mesh convergence studies under impact loading on a rectangular hollow section (RHS) beam along its weak axis, the differences between the experimental and numerical results were calculated in the midpoint displacement as 35.02% for M40, 27.04% for M30, 16.43% for M20, 7.29% for M10, 3.52% for M5 and 1.12% for M5-15, respectively. It means that the optimum mesh size could not be the smallest one and directly affected the midspan displacement and out-of-plane plastic denting of the RHS steel beam along its weak axis.
- Test series A samples, which had 183.94–735.75 J energy, experienced a 16.19 mm residual deformation and were within the elastic deformation region, while test series B samples, which were exposed to 919.69–1471.50 J energy, experienced a 19.44 mm residual deformation and were within plastic deformation zone. This means that with an increase in the impact energy, the deformation went from the elastic region to the plastic region.
- The maximum displacement at the midpoint of the S#1EXP (test series A) sample was recorded as 5.88 mm, while it was recorded as 33.9 mm for sample S#8EXP (test series B). Although the amount of impact energy on S#8EXP was 8 times more than S#1EXP, the deflection was almost 5.8 times bigger. It can be inferred that in beams that are placed along their weak axes, the deflection increment coefficient was not equal to that of the energy.
- In addition, the accelerations generated due to the impact energy, which were 260 g for S#1EXP (183.94 J energy) and 1760 g for S#8EXP (1471.5 J energy), were compared. Similar to the deflection, the amount of the increase in acceleration was not equivalent to the amount of the increase in energy since there was an 8 times increase in energy, but only a 6.5 times increase could be observed in acceleration.
- Using D’Alembert dynamic equations, the impact forces were estimated where the maximum impact force was seen in S#8EXP (388.18 kN) and the minimum impact force was seen in S#1EXP (71.80 kN). The inertial force values were obtained from the accelerometers, and the sum of the reaction forces was estimated from the load cell.
- As the loading was changing from static to dynamic, the reaction forces estimated using the impact factor coefficient had differences ranging from 4% to 30% with the reaction forces estimated experimentally. It is worth mentioning that the difference tended to increase as the impact factor coefficient value increased.
- The maximum difference in the acceleration values obtained experimentally and numerically was recorded in S#2, which was 12.28%, while the biggest differences in the maximum deflection and residual displacement were seen in S#1 (5.7%) and S#8 (16%), respectively. As the supports experienced some partial damage in the experimental study and the situation was ideal in finite element analysis, the difference in the residual displacement was higher.
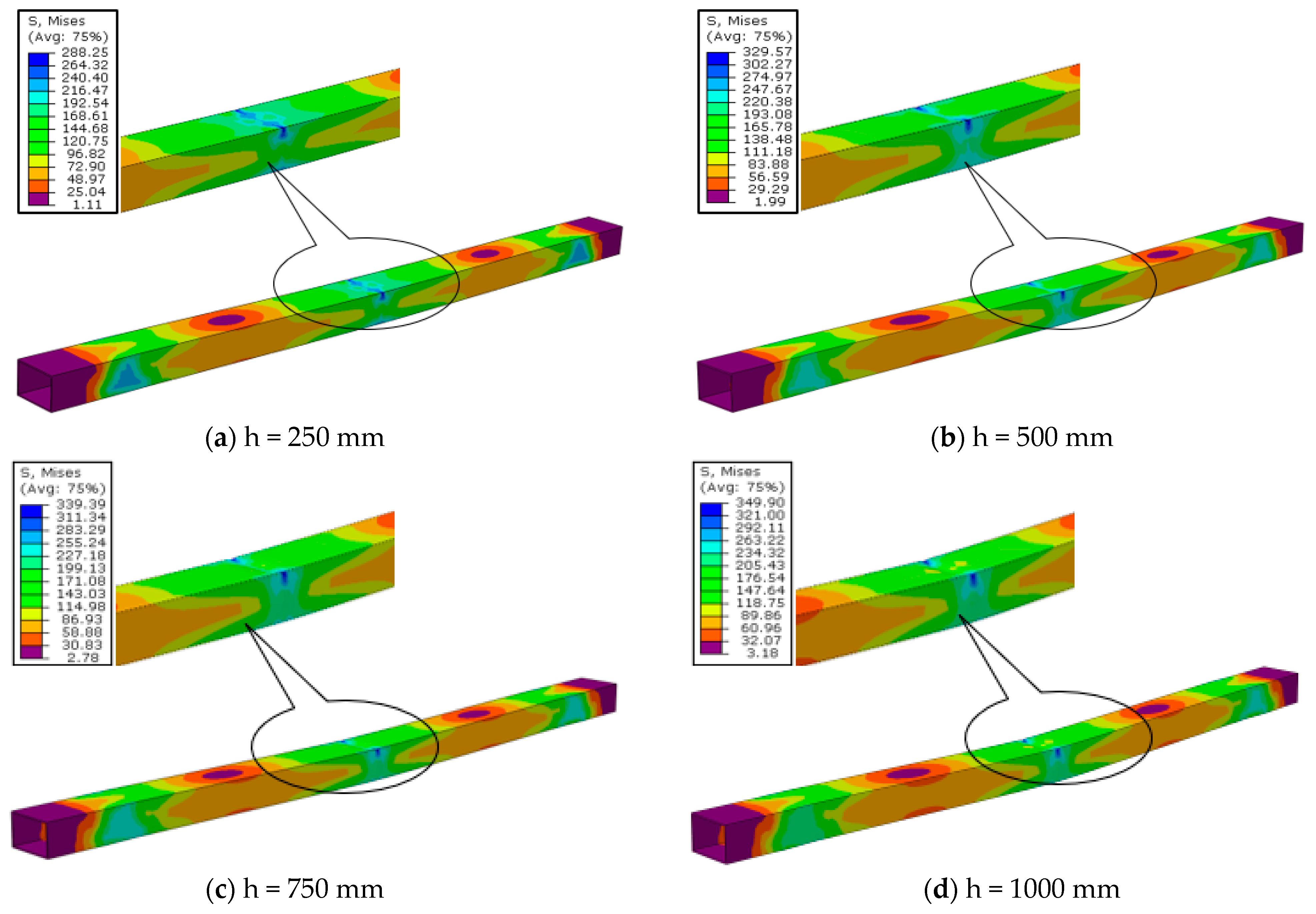
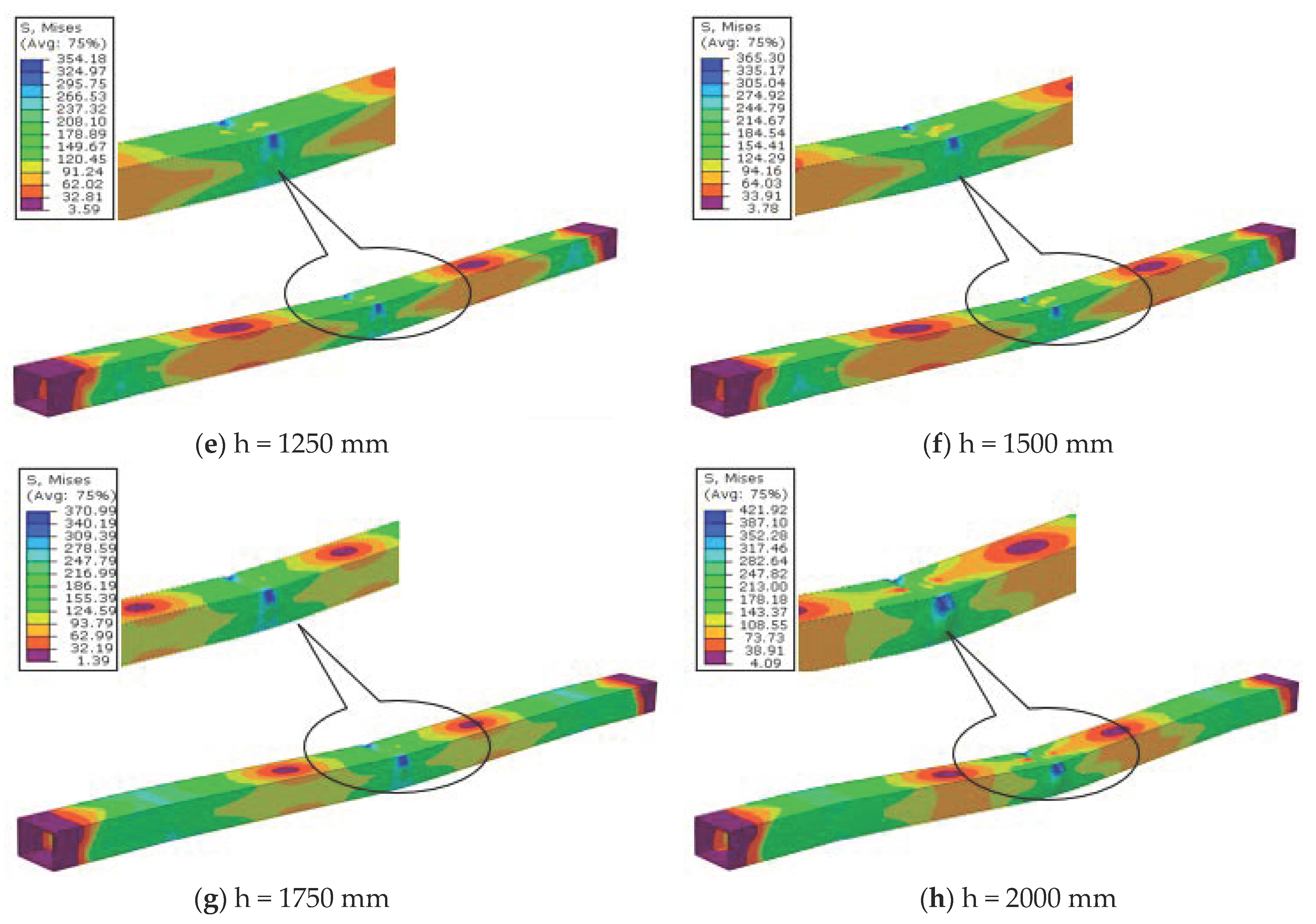
- Moreover, the stresses in the finite element analysis were estimated using Von Misses stress distributions for all eight samples (both test series A and B). The minimum stress was observed in S#1FEM, which was 288 Mpa, and the maximum stress was observed in S#8FEM, which was 421 Mpa. With the amount of energy increased by 8 times, the amount of stress only increased by 45.80%. This means that in beams that are placed along their weak axes, the Von Misses stress distribution increment coefficient is not equal to that of the energy.
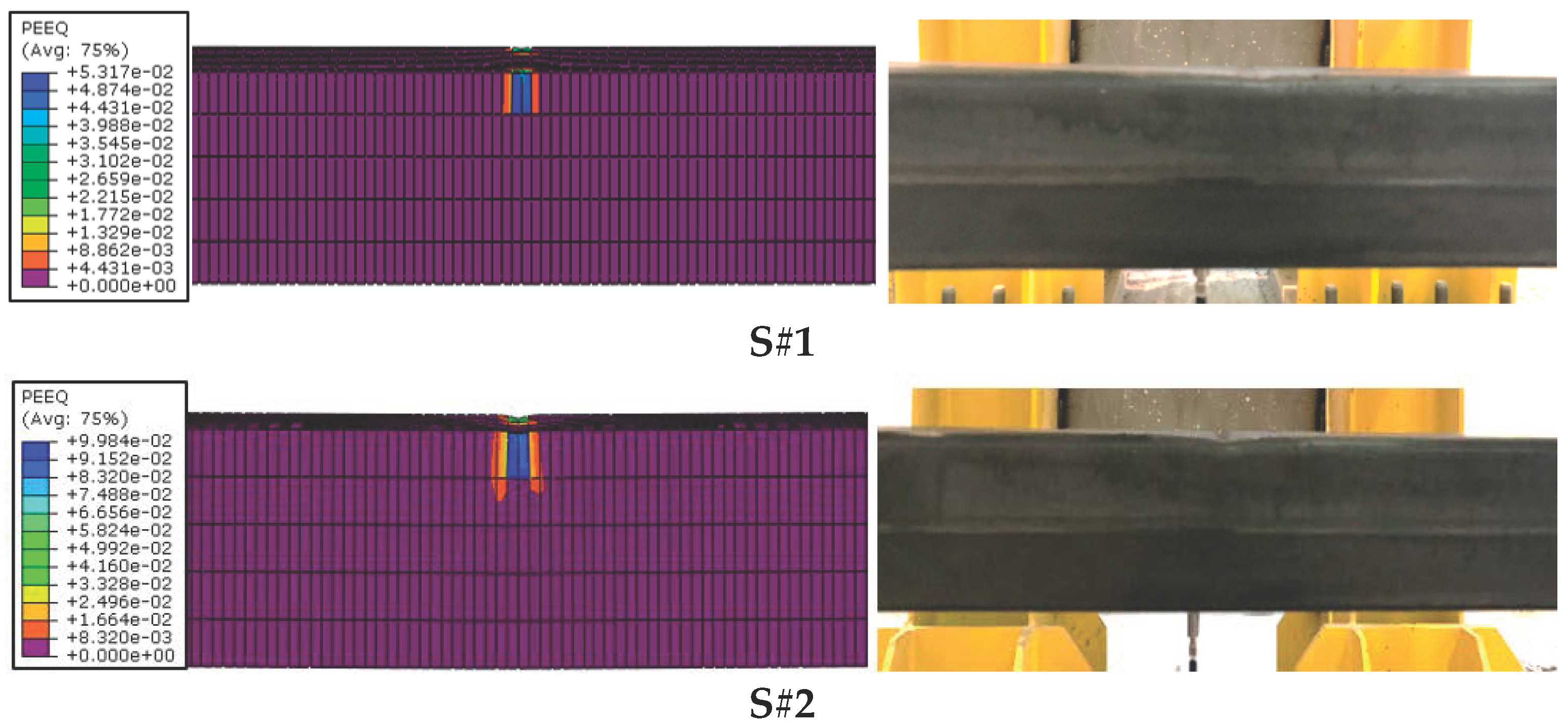
- Furthermore, as the equivalent plastic strain deformation was calculated using FE analysis, it was revealed that the lowest plastic deformation occurred in model S#1FEM, which was 0.531 mm, and the highest plastic deformation occurred in S#8FEM with a value of 2.56 mm.
- To sum up, based on our experimental and FEM studies, it was concluded that the increases in the drop height of the impact force (particularly low-velocity impact) and the amount of energy in beams that are placed on their weak axes would increase the amount of acceleration, maximum deflection at beam midpoint, internal stress, residual displacement, and plastic deformation in such beams.
- The plastic deformation on the top of the sample S#1EXP had a very small value (3.28 mm) at the first impact; however, the deformation that would occur on the beam element if the load were to be exerted repeatedly might result differently. For instance, the repetitive, very low-impact loading that is exerted on the beam of an offshore structure during stoppage is a real situation such as this. Thus, it is highly recommended to examine such a situation for a better understanding of the beam behaviors.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Watson, A.R.; Reid, S.R.; Johnson, W.; Thomas, S.G. Experimental study of the crushing of circular tubes by centrally applied opposed wedge-shaped indenters. Int. J. Mech. Sci. 1976, 18, 387–397. [Google Scholar] [CrossRef]
- ASTM E23; ASTM Standard Test Methods for Notched Bar Impact Testing of Metallic Materials. American Society for Testing and Materials (ASTM): Filadelfia, PA, USA, 2002.
- Det Norske Veritas (DNV). Design Against Accidental Loads, Recommended Practice DNV-682 RP-C204. 2010. Available online: https://rules.dnvgl.com/servicedocuments/dnv (accessed on 16 July 2022).
- Li, G.Q.; Zhang, Y.; Yang, T.C.; Jiang, J.; Lu, Y.; Chen, S.W. Effect of blast-induced column failure pattern on collapse behavior of steel frames. Adv. Steel Constr. 2018, 14, 376–390. [Google Scholar]
- Yu, H.X.; Liew, J.R. Steel framed structures subjected to the combined effects of blast and fire-Part 1: State-of-the-art review. Adv. Steel Constr. 2005, 1, 67–84. [Google Scholar]
- Yu, H.X.; Liew, J.R. Steel framed structures subjected to the combined effects of blast and fire: Part 2: Case study. Adv. Steel Constr. 2005, 1, 85–104. [Google Scholar]
- Teixeira, F.B.; Caldas, R.B.; Grilo, L.F. Influence of different shapes of geometric imperfections on the structural behavior of beams with large web openings. Adv. Steel Constr. 2020, 16, 272–278. [Google Scholar]
- Kantar, E.; Erdem, R.T.; Anıl, Ö. Nonlinear finite element analysis of impact behavior of concrete beam. Math. Comput. Appl. 2011, 16, 183–193. [Google Scholar] [CrossRef]
- Wang, Y.; Qian, X.; Liew, J.R.; Zhang, M.H. Experimental behavior of cement filled pipe-in-pipe composite structures under transverse impact. Int. J. Impact Eng. 2014, 72, 1–16. [Google Scholar] [CrossRef]
- He, X.; Soares, C.G. Experimental study on the dynamic behavior of beams under repeated impacts. Int. J. Impact Eng. 2021, 147, 103724. [Google Scholar] [CrossRef]
- Zeinoddini, M.; Parke, G.A.R.; Harding, J.E. Axially pre-loaded steel tubes subjected to lateral impacts: An experimental study. Int. J. Impact Eng. 2002, 27, 669–690. [Google Scholar] [CrossRef]
- Zeinoddini, M.; Harding, J.E.; Parke, G.A.R. Axially pre-loaded steel tubes subjected to lateral impacts (a numerical simulation). Int. J. Impact Eng. 2008, 35, 1267–1279. [Google Scholar] [CrossRef]
- Merwad, A.M.; El-Sisi, A.A.; Mustafa, S.A.; Sallam, H.E.D.M. Lateral Impact Response of Rubberized-Fibrous Concrete-Filled Steel Tubular Columns: Experiment and Numerical Study. Buildings 2022, 12, 1566. [Google Scholar] [CrossRef]
- Saatci, S. Structures Subjected to Impact Loads. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2007. [Google Scholar]
- Batarlar, B. Behavior of Reinforced Concrete Slabs Subjected to Impact Loads. Master’s Thesis, Izmir Institute of Technology, Izmir, Turkey, 2013. [Google Scholar]
- Gu, S.; Zhao, J.; Li, J.; Peng, F.; Kong, C.; Yang, L. Application of Fractal Theory to the Analysis of Failure Characteristics of Low-Velocity-Impact Concrete Slabs. Buildings 2023, 13, 2190. [Google Scholar] [CrossRef]
- Husem, M.; Cosgun, S.I.; Sesli, H. Finite element analysis of RC walls with different geometries under impact loading. Comput. Concr. Int. J. 2018, 21, 583–592. [Google Scholar]
- Kezmane, A.; Chiaia, B.; Kumpyak, O.; Maksimov, V.; Placidi, L. 3D modelling of reinforced concrete slab with yielding supports subject to impact load. Eur. J. Environ. Civ. Eng. 2017, 21, 988–1025. [Google Scholar] [CrossRef]
- Breen, C.; Guild, F.; Pavier, M. Impact of thick CFRP laminates: The effect of impact velocity. Compos. Part A Appl. Sci. Manuf. 2005, 36, 205–211. [Google Scholar] [CrossRef]
- Zhang, R.; Zhi, X.D.; Fan, F. Plastic behavior of circular steel tubes subjected to low-velocity transverse impact. Int. J. Impact Eng. 2018, 114, 1–19. [Google Scholar] [CrossRef]
- Nasery, M.M.; Ağcakoca, E.; Yaman, Z. Experimental and numerical analysis of impactor geometric shape effects on steel beams under impact loading. Structures 2020, 27, 1118–1138. [Google Scholar] [CrossRef]
- Anil, Ö.; Kantar, E.; Yilmaz, M.C. Low velocity impact behavior of RC slabs with different support types. Constr. Build. Mater. 2015, 93, 1078–1088. [Google Scholar] [CrossRef]
- Allan, J.D.; Marshall, J. The Effect of Ship Impact in the Load Carrying Capacity of Steel Tubes; ETDEWEB: London, UK, 1992. [Google Scholar]
- Frieze, P.A.; Cho, S.R. Impact damage and assessment of offshore tubulars. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 3–6 May 1993. [Google Scholar]
- Qu, H.; Huo, J.; Xu, C.; Fu, F. Numerical studies on dynamic behavior of tubular T-joint subjected to impact loading. Int. J. Impact Eng. 2014, 67, 12–26. [Google Scholar] [CrossRef]
- Kharazan, M.; Sadr, M.H.; Kiani, M. Delamination growth analysis in composite laminates subjected to low velocity impact. Steel Compos. Struct. 2014, 17, 387–403. [Google Scholar] [CrossRef]
- Zhao, W.; Guo, Q.; Dou, X.; Zhou, Y.; Ye, Y. Impact response of steel-concrete composite panels: Experiments and FE analyses. Steel Compos. Struct. 2018, 26, 255–263. [Google Scholar]
- Chen, Z.H.; Yang, J.G.; Liu, Z.S. Experimental and numerical investigation on upheaval buckling of free-span submarine pipeline. Adv. Steel Constr. 2019, 15, 323–328. [Google Scholar]
- Zhang, S.; Pedersen, P.T.; Ocakli, H. Collisions damage assessment of ships and jack-up rigs. Ships Offshore Struct. 2015, 10, 470–478. [Google Scholar] [CrossRef][Green Version]
- Baaskaran, N.; Ponappa, K.; Shankar, S. Assessment of dynamic crushing and energy absorption characteristics of thin-walled cylinders due to axial and oblique impact load. Steel Compos. Struct. 2018, 28, 179–194. [Google Scholar]
- Kadhim, M.M.; Wu, Z.; Cunningham, L.S. Experimental study of CFRP strengthened steel columns subject to lateral impact loads. Compos. Struct. 2018, 185, 94–104. [Google Scholar] [CrossRef]
- Kang, X.J.; Liu, Y.H.; Zhao, L.; Yu, Z.X.; Zhao, S.C.; Tang, H. Dynamic response analysis method for the peak value stage of concrete-filled steel tube beams under lateral impact. Adv. Steel Constr. 2019, 15, 329–337. [Google Scholar]
- Behinaein, P.; Cotsovos, D.M.; Abbas, A.A. Behaviour of steel-fibre-reinforced concrete beams under high-rate loading. Comput. Concr. 2018, 22, 337–353. [Google Scholar]
- Ağcakoca, E.; Bıyıklıoğlu, E. Experimentally and numerically investigating the performances of aramid fiber-reinforced steel beams under impact loadings. Arab. J. Sci. Eng. 2020, 45, 8053–8068. [Google Scholar] [CrossRef]
- Wu, Q.J.; Zhi, X.D.; Guo, M.H. Finite element analysis for the progressive failure of FRP-reinforced steel component under low-velocity impact. Adv. Steel Constr. 2019, 15, 267–273. [Google Scholar]
- Ding, X.; Fan, Y.; Kong, G.; Zheng, C. Wave propagation in a concrete filled steel tubular column due to transient impact load. Steel Compos. Struct. Int. J. 2014, 17, 891–906. [Google Scholar] [CrossRef]
- ASTM A370-13; ASTM Standard Test Methods and Definitions for Mechanical Testing of Steel Products A370-13. American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 2010.
- Han, F.; Wang, Y.; Zhang, T.; Li, Q.; Song, Y. Effect of different roll forming processes on material properties of square tubes. Adv. Steel Constr. 2020, 16, 181–190. [Google Scholar]
- ABAQUS/CAE, version 6.12; Dassault Systemes Simulia Corp.: Providence, RI, USA, 2016.
- Richardson, M.O.W.; Wisheart, M.J. Review of low-velocity impact properties of composite materials. Compos. Part A Appl. Sci. Manuf. 1996, 27, 1123–1131. [Google Scholar] [CrossRef]
- Hibbitt, H.; Karlsson, B.; Sorensen, P. ABAQUS Analysis User’s Manual, Version 6.11; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2011.
- Nasery, M.M.; Ağcakoca, E.; Yaman, Z. Inspecting the mesh size effects in finite element modelling of steel beams under impact loading. In Proceedings of the International Science and Engineering Applications Symposium on Hazards, Karabuk, Turkey, 25–27 July 2019. [Google Scholar]
- Ellinas, C.P. Damage on Offshore Tubular Bracing Member. In Proceedings of the IABSE Colloquium, Copenhagen, Denmark, 30 May–2 June 1983. [Google Scholar]
- Soleimani, S.M.; Banthia, N. A novel drop weight impact setup for testing reinforced concrete beams. Exp. Tech. 2014, 38, 72–79. [Google Scholar] [CrossRef]
- Pham, T.M.; Hao, H. Plastic hinges and inertia forces in RC beams under impact loads. Int. J. Impact Eng. 2017, 103, 1–11. [Google Scholar] [CrossRef]
- Soleimani, S.M.; Banthia, N.; Mindess, S. Behavior of RC beams under impact loading: Some new findings. In Proceedings of the Sixth International Conference on Fracture Mechanics of Concrete and Concrete Structures, Catania, Italy, 17–22 June 2007. [Google Scholar]
- Biggs, J.M.; Biggs, J. Introduction to Structural Dynamics; McGraw-Hill College: Chicago, IL, USA, 1964. [Google Scholar]
- Pytel, A.; Kiusalaas, J. Mechanics of Material; Brooks/Cole-Thomson Learning: Belmont, CA, USA, 2003. [Google Scholar]
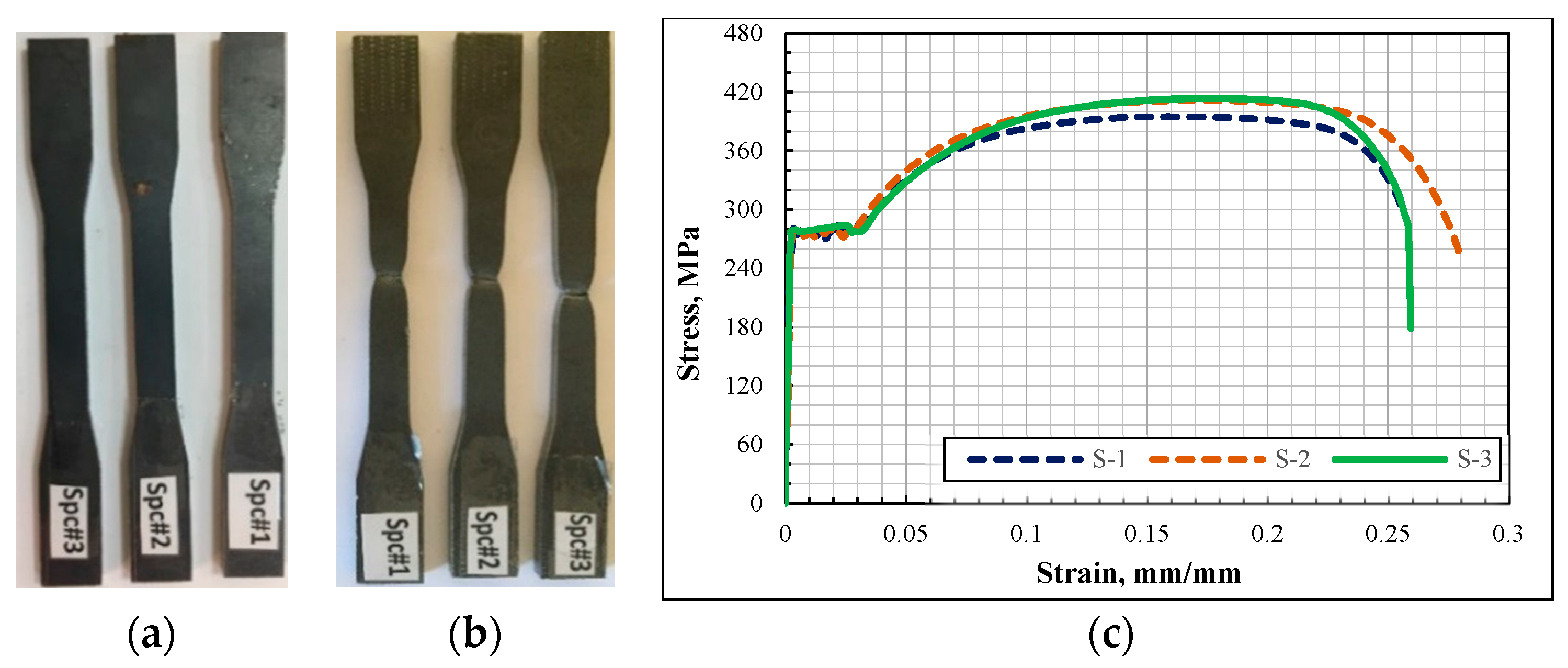
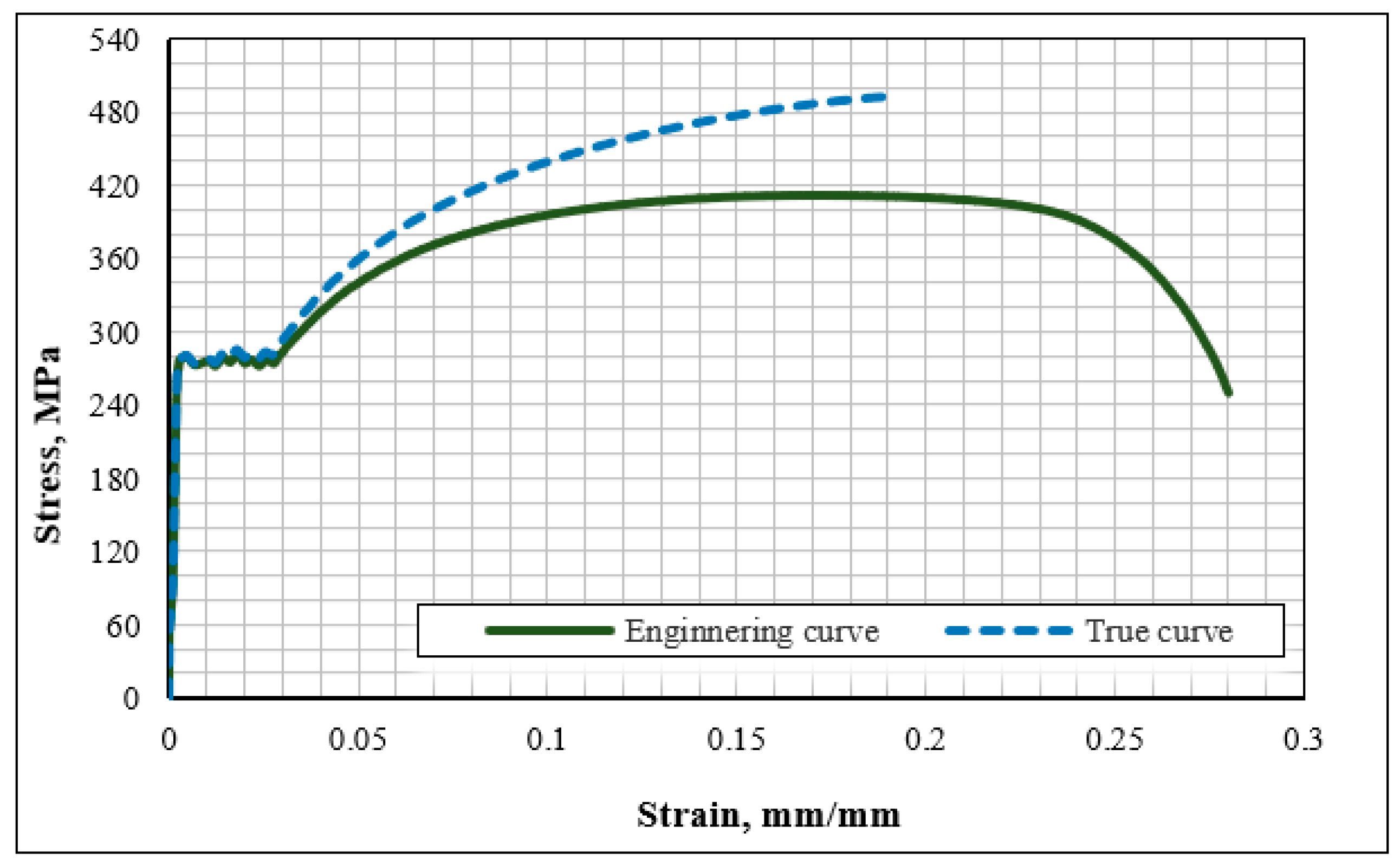






| Sample Code | Yield Stress (MPa) | Tensile Stress (MPa) | Elongation (%) | Elastic Modulus (GPa) |
|---|---|---|---|---|
| S-1 | 268.74 | 392.15 | 24.94 | 174.88 |
| S-2 | 276.97 | 409.32 | 23.74 | 176.38 |
| S-3 | 272.67 | 411.41 | 23.82 | 177.66 |
| Codes | Dimensions (mm) | Length (mm) | Cross Sectional Area (mm²) | Weight of the Beam (kg/m) | Moment of İnertia about the Strong Axes (104 × mm4) | Moment of İnertia about the Weak Axis (104 × mm4) | Drop Height (mm) | Hammer Weight (kg) | Impact Energy (J) | |
|---|---|---|---|---|---|---|---|---|---|---|
| Series A | S#1 | 120 × 80 × 3 | 2000 | 1140 | 8.9 | 230 | 123 | 250 | 75 | 183.94 |
| S#2 | 120 × 80 × 3 | 2000 | 1140 | 8.9 | 230 | 123 | 500 | 75 | 367.88 | |
| S#3 | 120 × 80 × 3 | 2000 | 1140 | 8.9 | 230 | 123 | 750 | 75 | 551.81 | |
| S#4 | 120 × 80 × 3 | 2000 | 1140 | 8.9 | 230 | 123 | 1000 | 75 | 735.75 | |
| Series B | S#5 | 120 × 80 × 3 | 2000 | 1140 | 8.9 | 230 | 123 | 1250 | 75 | 919.69 |
| S#6 | 120 × 80 × 3 | 2000 | 1140 | 8.9 | 230 | 123 | 1500 | 75 | 1103.63 | |
| S#7 | 120 × 80 × 3 | 2000 | 1140 | 8.9 | 230 | 123 | 1750 | 75 | 1287.56 | |
| S#8 | 120 × 80 × 3 | 2000 | 1140 | 8.9 | 230 | 123 | 2000 | 75 | 1471.50 |
| Model Name | Beam Regions | FEM Displacement (mm) | Experimental Displacement (mm) | %Difference of Experimental and FEM Displacements | ||
|---|---|---|---|---|---|---|
| Right | Central | Left | ||||
| M40 | 40 × 40 | 40 × 40 | 40 × 40 | 21.86 | 16.19 | 35.02 |
| M30 | 30 × 30 | 30 × 30 | 30 × 30 | 20.64 | 27.49 | |
| M20 | 20 × 20 | 20 × 20 | 20 × 20 | 18.85 | 16.43 | |
| M10 | 10 × 10 | 10 × 10 | 10 × 10 | 17.37 | 7.29 | |
| M5 | 5 × 5 | 5 × 5 | 5 × 5 | 16.76 | 3.52 | |
| M5-15 | 15 × 15 | 5 × 15 | 15 × 15 | 16.01 | 1.12 | |
| Test Series | Sample Code | Drop Height (mm) | Max. Midpoint Displacement (mm) | Max. Midpoint Acceleration (g) | Impact Energy (J) |
|---|---|---|---|---|---|
| Series A | S#1EXP | 250 | 5.88 | 260 | 183.94 |
| S#2EXP | 500 | 8.93 | 290 | 367.88 | |
| S#3EXP | 750 | 13.08 | 570 | 551.81 | |
| S#4EXP | 1000 | 16.19 | 743 | 735.75 | |
| Series B | S#5EXP | 1250 | 19.44 | 910 | 919.69 |
| S#6EXP | 1500 | 23.28 | 1120 | 1103.63 | |
| S#7EXP | 1750 | 28.77 | 1306 | 1287.56 | |
| S#8EXP | 2000 | 33.99 | 1706 | 1471.50 |
| Sum of Maximum Reaction Forces (kN) | Maximum İnertia Force (kN) | Maximum İmpact Force (kN) | |
|---|---|---|---|
| S#1(EXP) | 34.72 | 37.08 | 71.80 |
| S#2(EXP) | 49.69 | 46.22 | 95.91 |
| S#3(EXP) | 61.94 | 89.71 | 151.65 |
| S#4(EXP) | 72.65 | 116.43 | 189.08 |
| S#5(EXP) | 82.94 | 132.05 | 214.99 |
| S#6(EXP) | 92.78 | 172.43 | 265.21 |
| S#7(EXP) | 102.16 | 205.21 | 307.37 |
| S#8(EXP) | 121.05 | 267.13 | 388.18 |
| Specimen Code | Static Deflection | Impact Factor (η) | Impact Factor Total Reaction Force (kN) (Pmax) | Exp. Total Reaction Force (kN) | Diff. between Impact Factor and Experiment Forces (%) |
|---|---|---|---|---|---|
| S#1 | 25.5 | 45.29 | 33.32 | 34.72 | 4.20 |
| S#2 | 25.5 | 63.63 | 46.82 | 49.69 | 6.13 |
| S#3 | 25.5 | 77.70 | 57.17 | 61.94 | 8.34 |
| S#4 | 25.5 | 89.57 | 65.90 | 72.65 | 10.24 |
| S#5 | 25.5 | 100.02 | 73.59 | 82.94 | 12.71 |
| S#6 | 25.5 | 109.47 | 80.54 | 92.78 | 15.19 |
| S#7 | 25.5 | 118.16 | 86.94 | 102.16 | 17.50 |
| S#8 | 25.5 | 126.25 | 92.89 | 121.05 | 30.31 |
| Specimen Code | Max. Displacement on the Bottom Face of the Beam (EXP) (mm) | Max. Displacement on the Bottom Face of the Beam (FEM) (mm) | Differences on the Bottom Face (%) | Max. Displacement on the Top Face of the Beam (FEM) (mm) | Difference between the Top and Bottom Face of the FEM (%) | Vertical Denting (FEM) (mm) | Percentage of the Vertical Plastic Denting (%) |
|---|---|---|---|---|---|---|---|
| S#1 | 5.88 | 6.12 | 4.08 | 9.40 | 53.59 | 3.28 | 4.10 |
| S#2 | 8.93 | 9.43 | 5.59 | 15.27 | 61.93 | 5.84 | 7.31 |
| S#3 | 13.08 | 13.23 | 1.15 | 20.56 | 55.40 | 7.33 | 9.16 |
| S#4 | 16.19 | 16.91 | 4.45 | 25.53 | 50.97 | 8.62 | 10.78 |
| S#5 | 19.44 | 20.48 | 5.35 | 30.27 | 47.80 | 9.79 | 12.24 |
| S#6 | 23.28 | 24.15 | 3.74 | 34.94 | 44.68 | 10.79 | 13.49 |
| S#7 | 28.77 | 27.65 | 3.89 | 39.49 | 42.82 | 11.84 | 14.80 |
| S#8 | 33.99 | 34.45 | 1.35 | 54.50 | 58.20 | 20.05 | 25.06 |
| Specimen Number | Drop Height of Hammer (mm) | Hammer Weight (N) | Max. Displacement (mm) | Residual Displacement (mm) | Acceleration (g) | Reaction Forces (kN) | Von Mises Stress (MPa) | PEEQ (Equivalent Plastic Strain) (10−1) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EXP | Dif (%) | FEM | EXP | Dif (%) | FEM | EXP | Dif (%) | FEM | EXP | Dif (%) | Mathematically | FEM | FEM | |||
| S#1 | 250 | 750 | 5.88 | 4.08 | 6.12 | 0.12 | - | 1.78 | −233 | 6.90 | −258 | 34.72 | 4.03 | 33.32 | 288 | 0.531 |
| 260 | 278 | |||||||||||||||
| S#2 | 500 | 750 | 8.93 | 5.60 | 9.43 | 2.38 | 12.60 | 2.68 | −258 | 3.79 | −308 | 49.69 | 5.78 | 46.82 | 329 | 0.998 |
| 290 | 301 | |||||||||||||||
| S#3 | 750 | 750 | 13.08 | 1.11 | 13.23 | 3.23 | 13.93 | 3.68 | −540 | 12.28 | −624 | 61.94 | 7.70 | 57.17 | 339 | 1.26 |
| 570 | 640 | |||||||||||||||
| S#4 | 1000 | 750 | 16.19 | 4.45 | 16.91 | 4.60 | 28.04 | 5.89 | −700 | 2.29 | −740 | 72.65 | 9.28 | 65.91 | 349 | 1.45 |
| 743 | 760 | |||||||||||||||
| S#5 | 1250 | 750 | 19.44 | 5.35 | 20.48 | 14.64 | 29.99 | 19.03 | −880 | 7.95 | −950 | 82.94 | 11.27 | 73.59 | 354 | 1.57 |
| 910 | 1015 | |||||||||||||||
| S#6 | 1500 | 750 | 23.28 | 3.74 | 24.15 | 15.84 | 6.57 | 14.80 | −1056 | 7.95 | −1140 | 92.78 | 13.19 | 80.54 | 365 | 1.72 |
| 1120 | 1218 | |||||||||||||||
| S#7 | 1750 | 750 | 28.77 | 3.89 | 27.65 | 19.52 | 30.03 | 13.60 | −1230 | 8.35 | −1402 | 102.16 | 14.90 | 86.94 | 370 | 2.16 |
| 1306 | 1415 | |||||||||||||||
| S#8 | 2000 | 750 | 33.99 | 1.35 | 34.45 | 25.33 | 15.99 | 29.38 | −1636 | 7.85 | −1801 | 121.05 | 23.26 | 92.89 | 421 | 2.56 |
| 1706 | 1840 | |||||||||||||||
| Max. Differences (%) | 5.60 | 30.33 | 12.28 | 23.26 | ||||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nasery, M.M. Investigation on Behaviours along Weak Axes of Steel Beam under Low Velocity Impact Loading: Experimental and Numerical. Buildings 2023, 13, 2331. https://doi.org/10.3390/buildings13092331
Nasery MM. Investigation on Behaviours along Weak Axes of Steel Beam under Low Velocity Impact Loading: Experimental and Numerical. Buildings. 2023; 13(9):2331. https://doi.org/10.3390/buildings13092331
Chicago/Turabian StyleNasery, Mohammad Manzoor. 2023. "Investigation on Behaviours along Weak Axes of Steel Beam under Low Velocity Impact Loading: Experimental and Numerical" Buildings 13, no. 9: 2331. https://doi.org/10.3390/buildings13092331
APA StyleNasery, M. M. (2023). Investigation on Behaviours along Weak Axes of Steel Beam under Low Velocity Impact Loading: Experimental and Numerical. Buildings, 13(9), 2331. https://doi.org/10.3390/buildings13092331






