Abstract
The paper is devoted to a review of recent achievements in the field of dynamic analysis of structures and structural elements, such as beams and plates, with embedded viscoelastic (VE) dampers and/or layers. The general characteristics of VE materials, their rheological models, and methods of parameters identification are discussed. New formulations of dynamic problems for systems with VE elements are also reviewed. The methods of determination of dynamic characteristics, together with the methods of analysis of steady-state and transient vibrations of such systems, are also discussed. Both linear and geometrically non-linear vibrations are considered. The paper ends with a review of the methods of sensitivity and uncertainty analysis, and the methods of optimization, for structures with VE elements.
1. Introduction
Vibrations are undesirable in structures due to the requirements of structural stability, durability, particularly against fatigue, general performance, and noise reduction. Excessive vibrations represent an important problem in many types of civil engineering structures, aircraft, and machinery, as well as small electronic equipment and devices. They can be reduced by increasing the damping capacity of the considered system and/or by increasing its stiffness. Damping capacity can be changed using various types of vibration control systems. All the structural control systems can be categorized into four main types: active, semi-active, passive, and hybrid. The above-mentioned systems were discussed in earlier reviews [1,2,3,4,4,5,6,7,8,9,10].
Passive control systems are among the most suitable types of control systems for reducing structural vibrations because of their advantages: their lack of an external source of energy required to activate them, simplicity of design, construction, and maintenance, and ease of installation. The lower cost of such systems in comparison with the cost of active and semi-active control systems is also a very important asset. There are many types of passive control systems, for instance, tuned mass dampers [3], metallic dampers [8], friction dampers [11], viscous dampers [3], and viscoelastic (VE) dampers [3,10]. The latter are used very often and with great success. Recently, conventional damping control systems have been complemented with a new type of device, called inerters [12,13].
For a few decades, viscous and VE dampers have been extensively used for the seismic response control in buildings. Such devices are exploited with good results in newly erected structures and also in retrofit projects, as described in recent publications and books [14,15,16].
VE dampers are able to dissipate energy at all deformation levels and can, therefore, be used in structures exposed to both strong winds and earthquakes. Moreover, VE dampers are often used for retrofitting of structures. The buildings where VE dampers were installed include Suqian Communication Building, Chaoshan Xinhe Building, Petrol Hotel Building in Xi’an, and Suqian Transportation Building in Jiangsu [5,17] in China; US Steel Tower in Pittsburgh [9], Columbia Center Building, and Two Union Square Building in Seattle in the USA; YC Condominiums in Canada; and the Chientan railroad station roof in Taiwan, where the VE coupling damper system was applied. Another important field of application of VE dampers is in bridge engineering [18,19]. In a typical configuration of a VE damper, the VE material is bonded between steel plates to dissipate oscillation energy. An advantage of VE dampers is that they are able to dissipate energy at all levels of excitation forces. It is therefore evident that VE dampers are among the most efficient vibration control devices in strengthening of existing structures, and the design of new structures, against actions of wind and earthquakes.
In recent decades, many studies have been presented concerning the reduction in structural vibrations based on the use of passive damping control techniques by means of surface treatments with VE materials. A survey of different subjects on the VE treatments can be found in [20]. Another type of VE passive control system incorporates layered elements, such as beams, plates, and shells, consisting of VE layers embedded between elastic layers [21]. Such elements are widely used in many fields of engineering, e.g., aerospace, automobile, nuclear, and biomedical. Such elements have advantageous properties: high load capacity, high stiffness, and lightness. The VE layers feature the property of dissipating a large amount of energy, which is why they can significantly reduce vibrations and noise, thereby avoiding fatigue failure. In this type of control system, a free damping layer and/or a constrained damping layer are added to the structural system. In the case of the free layer damping, the VE layer is glued onto a vibrating metallic base and the whole system can be considered in the context of the flexural behavior of a two-layered element. In the constrained layer damping case, the VE core subjected mainly to shear deformation is embedded between two layers, usually elastic. Vibration energy is then dissipated mainly due to the shear deformation of the VE layer. Constrained layer damping is the most popular passive damping mechanism used in structural vibration control.
It should be noted that all the types of VE control devices reviewed in this paper are typical and widely used in engineering. Among these, the beams, plates, and shells with VE layers are used in numerous engineering fields, whereas the applications of the VE dampers are mainly found in civil engineering. The basic concepts, research status of theoretical description, and engineering applications of all those VE control systems are summarized and their advantages and disadvantages are discussed. Thus, this paper may serve as a reference source for applications and for new research. It should also be emphasized that this survey paper places emphasis on theoretical achievements in the field of VE control systems developed in the last few decades.
The aim of the paper is to present recent achievements in the field of dynamics of structures which are partially built from VE materials. The rest of paper is organized as follows. General characteristics of VE materials are presented in Section 2 together with a discussion of newly introduced VE materials. Rheological models of VE materials and dampers, together with recent methods for identification of models’ parameters, are the subject of Section 3. In Section 4, the influence of temperature on parameters in the VE models is discussed and recent papers devoted to this problem are briefly presented. Discussion of existing formulations of dynamics problems for VE structural elements, together with methods of solving equations of motion, mainly in the cases of free or steady-state vibration, is contained in Section 5. The analysis of dynamic characteristics of VE systems often leads to the non-linear eigenvalue problem. The existing methods of solving such problems are reviewed in Section 6. In many cases, during the numerical integration of equations of motion for systems with VE elements, the history of vibrations must be taken into account. For this reason, special time-integration methods are needed. The achievements in this field are briefly discussed in Section 7. Sensitivity and uncertainty analysis in the dynamics of VE structures are relatively new problems. Recent achievements in this field are presented in Section 8. Section 9 presents some new results in the domain of optimization of structures with VE dampers. Final conclusions are formulated in Section 10.
2. General Characteristics of VE Materials and New VE Materials Used in Dampers and Layers
VE materials dissipate energy through forces related to the velocity of motion. Moreover, damping occurs for different levels of excitations. Fluid and solid VE materials are applied in the passive control systems. Various highly viscous fluids, such as Polydimethylsiloxane (C2H6OSi) (see [22]), as well as magnetorheological and electrorheological fluids, are used in the fluid dampers [1,3,15]. Typically, these dampers have the form of a cylinder filled with a VE fluid and a perforated piston. Its movement causes the liquid to flow through its orifices and thus the damping force is generated. In the case of magnetorheological or electrorheological fluids, the magnetic or electric field is applied when the fluid flows through the orifices. However, magnetorheological dampers and beams or plates with magnetorheological layers are components of semi-active or active control systems because the magnetic field is applied to the VE layers in order to change their rheological properties very quickly in time. The literature concerning mechanical problems for these types of systems is very broad and is outside the scope of the present review. Interested readers can consult the review papers [23,24] where an introduction to this problem and an overview of the literature are presented.
Many types of polymeric materials, classified as solid VE, exhibit a damping behavior. In [25], one can find a list of several categories of polymers available for manufacturing of stable material damping systems. Polymers are materials composed of long, intertwined and cross-linked molecular chains. Elastomers are an important class of polymers and they are very often used in VE damping devices. Many types of rubbers represent an important subclass. Elastomers exhibit the capability of reversible deformation under an action of mechanical forces, while maintaining the structural continuity. When subjected to loading, an elastomer can deform in a wide displacement range and can dissipate energy through shear deformation, both axial and rotational [26]. Each solid VE material exhibits two fundamental rheological phenomena, i.e., creep and stress relaxation [25,26]. Creep is the tendency to undergo a slow increase in deformation under the action of a constant mechanical stress. It occurs as a result of a long-term exposure to high levels of stress which are still below the yield strength of the material. Relaxation is a phenomenon which is characterized by decreasing the existing stress when the material is subjected to a constant state of strain. In dynamics, the most important mechanical properties of solid VE materials are the storage modulus, which characterizes the stiffness of the material, and the loss modulus and the loss factor, which are the measures of damping properties. All these parameters are dependent on the excitation frequency, temperature, and magnitude of vibration amplitudes, if the amplitudes are large enough. A general trend is that the storage modulus and the loss factor increase with increasing excitation frequencies. The impact of ambient temperature on the properties of solid VE materials is a more complex problem. At low ambient temperature conditions, called the glassy region, the polymer molecules are frozen and the VE material has a high stiffness, a large storage modulus, and a small loss factor. As the temperature increases some of the polymer molecules begin to wiggle around. This range of temperature is called the transition region. In the transition region, the storage modulus decreases with temperature but the loss factor reaches its maximum at a certain value of temperature. With the further increase in temperature, the VE materials enter the rubbery region. Now, both the storage modulus and the loss factor decrease with temperature. These tendencies are schematically illustrated in Figure 1. The combination of properties of VE materials in the transition region is most appropriate for the dissipation of energy and is exploited in VE dampers and layers. Moreover, the temperature of VE materials can increase due to self-heating, which was experimentally and numerically studied, for example, in [27,28].
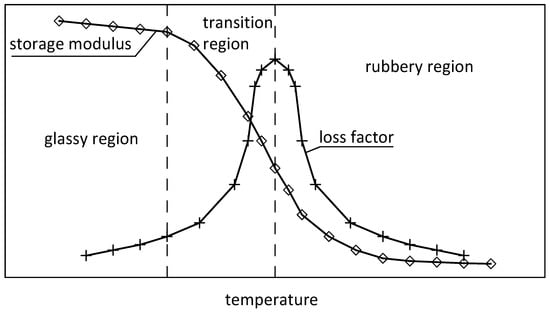
Figure 1.
Temperature dependence of the storage modulus and the loss factor.
In Figure 1, the curves of the storage modulus and the loss factor versus temperature are only shown schematically and do not represent any specific experimental data. However, qualitatively similar experimental results can be found, for example, in the papers [29,30].
VE materials used in dampers and layers must satisfy some specific requirements. First of all, they must feature a large loss factor. They must also be characterized by high heat dissipation and low heat generation properties. Another requirement is a stable working performance in a wide range of temperatures. The VE material should also be durable, i.e., resistant to corrosion, oxidation, and fatigue. All these requirements are not easily satisfied by real VE materials. For this reason, modified rubbers are often used in VE dampers. Fillers, such as silica, silicate, clay, and carbon black, which is most popular, are used for improving the properties of rubber. A high damping rubber with a high deformation capacity produced in China was investigated by Chen et al. in [31]. Wu et al. [32] found that the addition of small organic molecules to rubber can greatly improve its loss factor. Several types of VE materials with various types of matrices based on nitrile butadiene rubber and silicone rubber were proposed for dampers in [33]. Experimental results showed that such VE materials had a high energy dissipation capacity and featured stable performance. A high damping acrylate-based VE material was described by Xu et al. in [34], who investigated the dynamic properties of acrylate VE dampers at different temperatures, frequencies, and amplitudes. Experimental results showed that these dampers had an excellent damping capacity. The feasibility of using a blended rubber matrix to enlarge the working temperature range of VE materials was investigated in [35]. It was found that the loss factor was almost doubled in comparison with a single rubber matrix. In the paper by Ge et al. [36], results of an experimental study of nitrile-butadiene rubber with different damping modifiers were presented. The obtained VE material was found to possess excellent damping properties. Moreover, in [37], some other papers about the modification of rubbers were reviewed. The influence of aging on some VE materials used in dampers was experimentally investigated in [37]. Experimental results concerning the dynamic properties of the VE material were also presented by Xu et al. [38]. Very recently, the feasibility of using a novel hyperelastic and high-damping rubber material was experimentally investigated in [39] in order to determine its damping ratio, compressibility, and elasticity behavior under axial dynamic load. The results showed that the considered material could provide a high damping ratio between 10% and 13%. An elastomer compound with a high damping capacity and a relatively low stiffness was tested by He et al. [40]. The obtained results indicated that the tested VE material had excellent deformability with a strain amplitude of over 500% combined with a high-stress strength. Moreover, the examined VE material featured a superior energy dissipation capacity with a maximum viscous damping ratio of up to 30%. Low frequency dependence under cyclic dynamic loading and a better energy dissipation capacity at high loading frequency were also observed. Results from the dynamic testing of a thermoplastic elastomer of the olefin-styrene series were presented in [41]. The considered material exhibited a low temperature dependence. The mechanical properties of the VE material and their dependence on the amplitude and frequency of excitation of the material, as well as on its temperature, were determined.
3. Models of VE Materials and Identification of Theirs Parameters
Various studies on materials with rheological properties were conducted in the 19th century by Ludwig Boltzmann, James Clark Maxwell, and Lord Kelvin [42]. The linear theory of viscoelasticity is founded on the Boltzmann superposition principle, according to which each load step makes an independent contribution to the final state [43]. This principle is most often used to formulate the integral representation of linear viscoelasticity. However, the more common way of describing linear viscoelasticity is the differential approach, where the rheological properties are represented by an appropriate combination of simple mechanical elements: springs and dashpots. The spring is a symbol of a purely elastic solid obeying Hooke’s law, whereas the dashpot, as a damping element, symbolizes the properties of an ideal Newtonian viscous fluid. A number of individual mechanical elements and the way they can be connected are illustrated graphically in Figure 2.
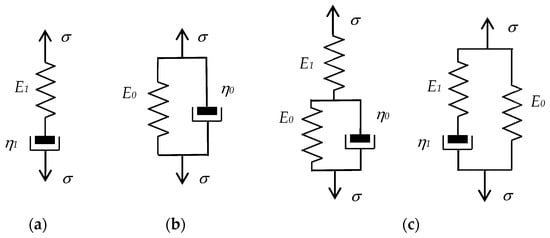
Figure 2.
Basic classical mechanical models of VE materials: (a) Maxwell model, (b) Kelvin–Voigt model, (c) standard three-parameter models.
The basic classical mechanical models of VE materials are composed of an elastic spring and a viscous damping element connected in series for the Maxwell model (see Figure 2a) or in parallel for the Kelvin–Voigt model (Figure 2b). In Figure 2, stands for stress, is the coefficient of elasticity, and is the coefficient of viscous damping.
However, the basic models are insufficient to fully describe the dynamic behavior of VE materials and they are only effective in a small frequency range. The Maxwell model fails to reproduce the phenomenon of creep [43], whereas the Kelvin–Voigt model does not describe the relaxation behavior well and represents the rheological properties poorly, even for uncomplicated materials such as rubbers [44].
By connecting a spring in series with a Kelvin–Voigt element or in parallel with a Maxwell element, the three-element elastic models [45], also called standard linear solid models, are obtained; see Figure 2c. These models are also referred to as standard three-parameter Voigt and Maxwell models [46] or standard linear Kelvin and Maxwell solid models [47], respectively. They both exhibit the same mechanical behavior although their structure is different. According to the principle of conversion, one model can be replaced with another and they can be described by the same equation [47,48].
In the classical approach to modeling of linear VE behavior, the stress–strain equation can be represented in a general form by differential operators [49].
where ) and ) are the functions of stress and strain varying in time t, and are the model coefficients, and M and N are the corresponding numbers of the series components.
More complex four-parameter classical models are formed as a combination of basic models. The Burgers model [50] is built from the Kelvin–Voigt model connected in series with the Maxwell model. On the other hand, a parallel connection leads to the standard model, also known as the Zener model [51]. These models more realistically represent rheological properties of a VE material with a good trade-off between complexity and accuracy [44]. The Burgers model is widely used in road construction engineering because it best describes the creep and the relaxation characteristics of asphalt composite concrete [52].
Three- or four-element models can describe the dynamic behavior of VE materials with a good approximation only for selected small ranges of temperature and vibration frequencies. Representation of rheological properties of VE materials over a wider temperature or frequency range requires models with a large or even infinite number of mechanical elements, i.e., springs and dashpots [43,53].
By combining a much larger number of basic models, generalized series/parallel models are obtained, which have two forms: the generalized Maxwell-type models, useful for the analysis of VE fluids and rubber-like materials, and the generalized Voigt-type models, which should be used for VE solids [42]. If a spring is added in parallel to the generalized Maxwell model, as in Figure 3, an extended model is obtained that is suitable for solving problems in the dynamics of solids, including VE materials [46,54].
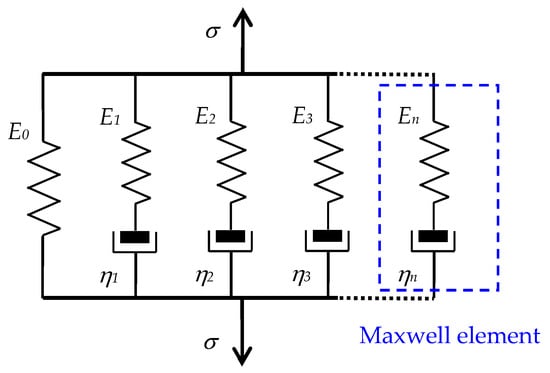
Figure 3.
The generalized Maxwell model with an additional spring.
A highly versatile and accurate model can be built by combining basic and generalized models in an arbitrary way. For any model composed of springs and dashpots, the constitutive relation can be written in a form of a differential equation. The advantage of the differential equations approach is that each model can be easily understood and interpreted physically. The disadvantage is that more advanced models are described by a higher-order differential equation, which complicates the calculations, and it is very difficult or sometimes impossible to identify the parameters of the model adopted for the real material [44,55].
A way to overcome the aforementioned problems is to use fractional calculus to describe rheological phenomena [56,57]. Dashpots used in the classical rheological models can be replaced with the so-called spring-pot elements, i.e., the Scott-Blair elements, for which the constitutive equation includes a non-integer derivative [58,59]. At the turn of the 20th century, many definitions of fractional derivatives appeared, given by Liouville, Riemann, Grunwald, and Letnikov. Currently, one of the most commonly used definitions of the fractional derivative is the Caputo derivative [60]. It can be proved that fractional models using a limited number of parameters make it possible to describe the behavior of VE materials at various frequencies, excitation amplitudes, and temperatures with acceptable accuracy [61,62]. The constitutive equation for such a model can be derived from Equation (1) by adopting the appropriate orders of derivatives smaller than unity (i.e., or/and ).
In the case of more complex models, it is also desirable to establish a relationship between the mechanical performance and the micro-configurations of the VE material, since changes in the rheological properties of the VE materials are attributed to a change in the microstructure [26,63]. In [62] it was shown that the higher-order fractional derivative model modified with the theory of internal variables and the principle of temperature–frequency equivalence is sufficiently accurate in describing the dynamic behavior of VE materials with varying frequencies and displacement amplitudes. Non-linear models are created when it is assumed that the resistance force depends on the velocity and amplitude of deformation [64].
The VE properties are exhibited by various polymeric materials, such as adhesives, elastomers, and rubber. In order to accurately describe the dynamic behavior of a real VE material, it is essential to select a proper rheological model and correctly identify its parameters. Usually, the identification of model parameters requires a series of appropriate and relevant experiments and then, via a proper mathematical description of the physical behavior in the test, the results of the experiments are fitted to the mathematical model [65]. There are many methods for evaluating the performance of VE damping materials, which can be grouped in different ways.
In the context of the type of experimental tests, we can distinguish uniaxial tests [66], shear dynamic modulus tests [67], creep tests, stress relaxation tests [68,69], and beam bending tests [70]. All these tests can be dynamic [71] or pseudo-static, and they typically involve the measurement and acquisition of time histories of forces and displacements, which are then processed numerically [72].
In the case of static experiments, creep data are usually only available and the identification scheme is used to determine the parameters of the retardation function from the creep data [73]. The retardation function can then be transformed into a relaxation function. The relaxation experiment can be simulated by forcing a strain in the material and measuring the stress generated [69]. Studying the creep and the relaxation curves of materials is an effective method for dynamic testing at low frequencies, as the material needs time to respond to excitation [53].
In the vast majority of cases, experimental data are obtained by Dynamic Mechanical Analysis (DMA) [66,67]. DMA involves forcing the material to oscillate at a certain frequency and measuring its strain and stress beyond the resonant frequencies of the test stand. By varying the frequency, a transfer function can be built between the stress and strain over its wide range. This type of test is most suitable to acquire information on the frequency-dependent behavior [53].
With more advanced measurement technologies such as Digital Image Correlation (DIC) and Digital Volume Correlation (DVC), it is possible to obtain local information contained in full-field displacement/deformation data [74]. The use of DIC measurements in dynamic experimental tests can be subject to quality problems such as loss of grid points during loading, inaccessible measurements close to the boundary, and non-Gaussian noise.
Depending on how the experimental data are processed, identification methods can be divided into two categories—direct and inverse identification methods [75]. In the direct methods, experimental dynamic data can be converted directly to dynamic stress–strain data or, equivalently, to the dynamic modulus at a specified frequency or strain rate [66]. The direct methods are not suitable for measuring dynamic mechanical properties of adhesives at lap joints with adherents because it is very difficult to distinguish between the elastic effects of the adherents and the adhesives [75].
In the category of inverse methods for identifying properties of VE materials, an inverse problem solving is used. For example, methods based on updating a FE model can be used. A numerical model of a structure with VE material is created. Then the parameters of the adopted material model are adjusted so that the response of the real structure measured in the experiment coincides with the results obtained from the finite element simulation [76]. Differences between measured and calculated values can be minimized using a gradient-based optimization algorithm to estimate the true values of the VE material model parameters [75,77].
The majority of identification cases are based on a cantilever beam specimen, where only damping of the VE material is included in the analytical model, whereas damping of the clamped specimen and air damping are usually ignored [78]. The results of some analyses show that the loss factor of VE materials would be overestimated if only material damping were included in the analysis model [79].
In the context of the fitting methods, stochastic techniques [80], evolution strategies [22,81], and optimization procedures [73,76,82,83] can be considered. Although no gradient information is needed in most of these methods, their performance is poor [65]. In addition, the process of parameter identification is an inverse problem that is determined, and it can be ill-conditioned due to noise present in the experimental data [22]. The choice of testing and fitting method also depends on the number of parameters present in the model that must be identified. Direct identification from time-domain or frequency-domain data is generally a difficult task, especially when more sophisticated models are required to achieve sufficient accuracy in relatively broad domains [84]. Some approaches to overcome these problems, illustrated by four identification methods, are described in [73].
When the number of model parameters is small, such as in the classical Kelvin or Maxwell models, appropriate algebraic operations can lead to formulae that determine the model parameters directly from the experiment results [85].
The hysteretic model allows the definition of a stress–strain or a load–displacement relationship using a closed-form expression that does not require any iterative algorithm to fully characterize the response [86]. The constitutive parameters represent physical properties that can be directly related to quantities deduced from experimental data [83].
Stochastic identification techniques have an advantage over deterministic methods in their ability to account for uncertainty associated with established models, which can be caused by varying material properties, as well as their spatial distribution, measurement or modeling errors, and insufficient information available [80].
The Ant Colony Optimization algorithm can be used to solve the inverse problem of identifying unknown constitutive parameters in homogeneous/regionally inhomogeneous fractional VE fields [81].
Very recently, a computational homogenization framework for VE composites within the framework of non-ordinary state-based peridynamic theory was presented in [87]. The proposed framework was used to calculate the effective properties in both time and frequency domains of two VE matrix-inclusion composite systems—one with an elastic inclusion and VE matrix, and the other one with VE inclusion and an elastic matrix.
4. Influence of Temperature on VE Parameters and Behavior of VE Systems
The influence of temperature on the material behavior in the structures with VE elements is a very interesting problem. The temperature changes may occur due to the changing ambient temperature and due to the self-heating resulting from conversion of the dynamic energy into heat during damping of vibrations. The temperature rise in the VE material leads to substantial changes in its mechanical properties.
The problem of self-heating was considered in the papers [88,89,90], where formulae for the calculation of the temperature rise in fluid dampers were derived for different forcing functions. The temperature-rise formulae for small-amplitude motion induced by wind loads were presented in [89], and those for large-amplitude motion due to seismic loading were presented in [88]. Those theoretical considerations were supported by experimental studies [91]. The results of theoretical and experimental studies on the effect of self-heating on the mechanical characteristics of VE materials were presented in [28]. The paper [92] was dedicated to a stochastic finite element analysis of a three-layer sandwich plate containing a VE layer. The dependence of the behavior of the VE materials on frequency and temperature was taken into account. The paper [93] contains a description of the modeling methodology of structural systems supported by VE mounts or joints based on the frequency response function coupling technique.
The majority of contributions in the field of ambient temperature influence rely on the assumption of the so-called rheologically simple material for which the frequency–temperature superposition rule [94,95] can be used. The dependence of the VE behavior on frequency and temperature is considered by using the complex modulus approach and the concept of reduced frequency and shift factor; see Figure 4. Among several proposals aiming at the computation of the shift factors, the Williams–Landel–Ferry (WLF) formula [94] is most frequently applied to compute the horizontal shift aT (see Figure 4), whereas the vertical shift bT is usually neglected.
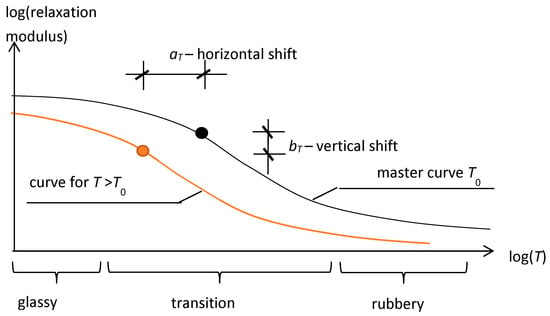
Figure 4.
Illustration of the frequency–temperature superposition rule.
In (2), T is the current temperature, T0 is the reference temperature, and c1, c2 are the material parameters, which should be obtained from experiments.
The analysis of sensitivity of complex frequency response functions to geometrical characteristics and temperature developed for plates with passive constrained damping layers was presented in [96]. The paper [97] described an extended VE model, based on isothermal models, where the temperature–frequency superposition effect was directly considered. The model was used for experimental data analysis in order to identify a set of global parameters which were able to represent the effect of frequency and varying temperatures. The paper [98] was devoted to experimental studies on the sensitivity of the cyclic behavior of elastomeric isolators to ambient temperature variations. The results of experimental investigation, which was intended to study the temperature effect on frequencies, mode shapes, and damping ratios of VE layered beams, were presented in [99].
The influence of temperature on damping properties of VE materials was widely investigated. This problem for slab-column structures with VE dampers was examined in [100,101]. The papers [102,103] reported results of research concerning plates with VE damping layers and the temperature effect on parameters of a VE material model was taken into account.
In the paper [104], Diani et al. presented the experimental study of torsion-loaded elements. They took into account the phenomenon of shape memory of polymer networks. The temperature influence was considered using the frequency–temperature superposition and the shift was computed using the WLF formula. The frequency range considered was from 0.01 to 63 Hz. The VE properties of the material were modeled using the 12-parameter generalized Maxwell model.
Arikoglu in [105] carried out the analysis of VE material behavior with the use of the nested Zener fractional model. The parameters of the model were obtained from the Wicket plot using the genetic algorithm method and the relaxation time followed from the experiments. The temperature influence was included using frequency–temperature superposition. Interestingly, two methods of shift computation were compared—the notorious WLF formula and the modified Kaelble approach, which also allows analysis of the temperatures below the glass transition limit.
In a series of papers, Xu et al. [38,106,107] analyzed the behavior of a VE damper. The damper was tested experimentally and it was successfully modeled using the equivalent fractional Kelvin, fractional Maxwell, and Prony series material models. The frequency–temperature superposition was used and the shift coefficients were obtained using the WLF formula with the coefficients proposed by Lakes in [108].
Later, the same group of researchers analyzed the VE plate with the temperature-dependent properties under the action of a moving heat source [109]. The thermodynamic analysis was performed for the material, including non-local effects. In the recent paper [110], those authors tested the VE material in the form of nitrile rubber with small molecule additives under the varying temperature conditions. The modified fractional Kelvin model was used to describe the VE properties, wherein the supramolecular interaction was considered. The temperature shift in the frequency–temperature superposition was introduced using the WLF formula.
The problem of flutter suppression in the supersonic flow for VE layered plates was analyzed by Cunha-Filho et al. in [103]. The effect of temperature was introduced directly into expressions for the complex dynamic modulus using the frequency–temperature superposition rule. The shift factor was computed using the Drake–Soovere [111] proposal, which is more complex than the WLF formula because it also contains the terms depending on the square of temperature difference. This approach can be used for temperatures within the range of 210–360 K, which is of practical importance in aeronautics.
The problem of wave propagation in the thermo-VE material subjected to thermal loading was considered by Sheoran et al. in [112]. That work was related to the thermo-visco-elasticity theory and included the thermal variation of the model parameters, as well as the self-heating.
In [113], Wei et al. considered the dynamics of rail pads made from three different VE materials. The data from experiments carried out in temperatures from the range of −45 to +20 °C were fitted using the fractional Kelvin VE material model combined with the frequency–temperature superposition, and the shift factor was computed using the WLF formula.
Pettermann and De Simone [114] considered the anisotropic thermo-VE material subjected to elastic relaxation and thermal expansion creep. The constitutive law was based on the relaxation tensor introduced in the form of Prony series expansion. The frequency–temperature superposition rule was applied and the shift factor was computed using the WLF formula. The formulation for plane states and the 3D case was presented and implemented in the finite element method.
The non-linear time-history response of multi-degree of freedom structures with VE dampers under the action of seismic loading was considered in [115]. The VE properties of the damper were described using the recursive-parameter material model in the form of an extension of the Nakamura proposal [116]. The extension to model the temperature dependence embedded in the formulation was based on the WLF formula. The proposed approach was found to be more reliable than that employing the standard Kelvin–Voigt material model.
Li et al. [117] proposed a combined thermo-VE model based on the fractional VE constitutive law merged with the frequency–temperature superposition rule and the WLF formula used to compute the shift parameter. The model was verified experimentally in the tensile test and DMA. It was found that the model remained valid for a wide range of frequencies spanning 10 orders of magnitude.
The analysis of plates made of VE materials was performed in [118,119]. The free vibrations in the geometrically linear case and geometrically non-linear harmonic vibrations were considered. The VE material was described using the fractional Zener model. The temperature influence was introduced using the frequency–temperature superposition rule and the shift factor was computed using the WLF formula. Based on the results from [61], the shift was applied only to the relaxation time value.
Dai et al. [120] analyzed a 10-story frame with VE dampers under the action of seismic loading based on the record of historical earthquakes. The material of damper was described by the fractional Zener model. The influence of ambient temperature was introduced using the frequency–temperature superposition rule and the shift factor was computed from the WLF formula. In the numerical simulations, optimum ranges of temperature were found from the point of view of vibration reduction. The same authors continued the analysis of seismically loaded structures with dampers in [121]. They proposed the rational polynomial form of the VE constitutive law, which is the generalization of all the popular VE material models including various variants of Kelvin, Maxwell, and Zener models. The temperature influence was included in the WLF shift factor.
The influence of temperature on dynamic characteristic, i.e., natural frequencies, damping ratios, and modes of vibration, for frames with VE dampers, was investigated in [122]. The frequency–temperature correspondence principle was used and the resulting non-linear eigenvalue problem was solved via the homotopy method and the incremental-iterative procedure.
In [123], Zhang et al. proposed a simple fractional temperature spectrum model to describe the behavior of the VE material in various temperature conditions. The model was based on the five-parameter fractional viscoelasticity combined with the frequency–temperature superposition, including both horizontal and vertical shifting of complex modulus function vs. the frequency logarithm. The model was successfully verified and calibrated to match the experimental data obtained from testing of two rubber materials.
5. Formulation of Equations of Motion and Their Solution for Beams and Frames with VE Elements
5.1. Linear Vibrations
The dynamics of structural elements, such as beams, plates, or shells, including geometric non-linearity, made from or incorporating fragments of VE materials, is an important research topic due to the practical importance of these elements in many fields of engineering. For over the past 20 years, this subject has gained importance and, consequently, there are many research reports related to it.
Equations of free vibrations for three-layered plates with a VE core were derived in [124] using the principle of virtual work. The resulting eigenvalue problem was numerically solved for the complex eigenvalues to yield the dynamic characteristics. The authors considered the general case and several simplified scenarios.
The finite element formulation of the free vibration of damped sandwich beams was considered in [125]. The authors formulated the equation of motion in the discretized form using the Galerkin finite element, which included the VE material treated as an elastic material with the substituted complex shear modulus and featuring the constant shear stress distribution. The non-linear eigenvalue problem was solved using the developed iterative method to yield the frequencies and loss factors.
The eigenfrequency problem of laminated beams and plates with a VE material was solved in [126]. The finite element method was used to formulate the discrete non-linear equations of motion and the high-order Newton–Raphson method combined with the homotopy procedure was used in the solution process.
A four-node facet-type quadrangular shell finite element, based on a layer-wise theory, developed for static and dynamic modeling of laminated structures with VE damping layers in the linear range, was derived in [127]. The sandwich structure was divided into layers treated individually as thick plates. The equations of free vibrations were formulated using the Hamilton principle. The solutions of the standard eigenvalue problem were presented for the plates and shells with elastic orthotropic layers.
A VE sandwich beam modeled with the Zener material and a fractional derivative was analyzed in [128]. The governing equation of motion for the linear transient vibrations was formulated directly in the finite element discretized version and solved using a direct time-integration method based on the implicit Newmark scheme.
Free vibrations of a three-layered sandwich beam were analyzed in [129]. The beam was considered to be a combination of Rayleigh beam theory for the elastic faces and a Timoshenko beam for the core. The equations of motion were derived from the Hamilton principle. They were solved analytically using the extensive symbolic algebra operations. The natural frequencies and vibration modes were obtained from the Wittrick–Williams algorithm.
In [130], Cortés et al. presented a homogenized finite element formulation for the transient dynamic analysis of beams with asymmetric and symmetric unconstrained layer damping. The VE material was characterized by a five-parameter fractional derivative model. The derivation of a fractional matrix equation of motion was based on the Galerkin weighted residual method. The application of the Grünwald–Letnikov definition of the fractional derivatives allowed the fractional equation to be solved numerically using two different implicit formulations.
The vibrations of sandwich composite beams were considered in [131]. The problem was described by the approximated simplified fourth-order beam theory and the equation of motion was formulated using the Hamilton principle. A higher-order sandwich beam model was employed to obtain the estimates of the frequency-dependent bending stiffness and shear modulus of the equivalent Bernoulli–Euler and Timoshenko models. The predicted eigenfrequencies and transfer accellerance functions resulting from the analytical solution were compared to the data obtained from the higher-order model and from experimental measurements.
A finite element model for the analysis of the linear vibrations of sandwich VE beams was developed in [132]. The model was formed by elastic frame elements, one VE plate element, and four rigid connectors. Assessment of a time-domain formulation for numerical modeling of VE materials was conducted using the Golla–Hughes method based on a second-order time-domain realization of Laplace-domain motion equations. The parameters used in the model of the VE material were obtained experimentally.
In the paper [133], an overview of the kinematic theories to model the three-layered composite beam with a VE core was presented. The authors considered the classical laminate theories, first- and higher-order shear deformation theories, and zig-zag theories, and proposed one universal formulation. Based on the numerous static and dynamic analyses in the linear range, it was concluded that the models based on the zig-zag theories yielded more accurate results, especially in the cases featuring a high ratio of stiffness values between the core and the faces.
Another overview of zig-zag theories used to analyze the laminate structures, including plates and shells was given by Carrera in [134]. The same author recently developed a unified formulation called Carrera Unified Formulation (CUF). The advantage of CUF is that it represents a generalized framework from which virtually every theory of structures can be obtained as a degenerated case of an arbitrary expansion of the generalized unknown. CUF was successfully employed, among other applications, to analyze a beam that contains layers or inclusions made of a VE material described with the Maxwell and standard linear solid models, in [135]. The viscoelasticity was modeled using the integral form of the constitutive law. The Hamilton principle was used to formulate the equations of motion. The solution in the frequency domain after the Laplace transformation was then inverted to the time domain using the numerical inversion methods.
CUF has also been generalized to allow for different expansion orders and descriptions for individual displacement components, leading to the Generalized Unified Formulation (GUF), as well as to groups of plies, i.e., the sublaminates, to yield the Sublaminate Generalized Unified Formulation (SGUF). The latter was used in [136] to analyze free and forced vibrations of sandwich beams and plates including an arbitrary number of damping cores. The equations of motion were derived using the Hamilton principle. They were solved by the computationally efficient Ritz method, which allowed any type of boundary conditions to be taken into account.
Damped free vibrations of thick composite and sandwich composite plates were considered in [137]. The third-order shear deformation theory was applied and the equations of motion were derived using the Hamilton principle. The modal damping was assumed and the dynamic characteristics followed from the solution of the eigenvalue problem.
Alvelid [138] analyzed the free and harmonically forced linear vibrations of the sandwich cantilever beam. The VE core was modeled using the fractional linear solid material. The governing equations were formulated for the Timoshenko beam theory and the resulting sixth-order differential equation was solved analytically to obtain the natural frequencies and the amplitude–frequency response curves.
Free and forced vibrations of symmetric sandwich structures with a VE core were analyzed in [139]. A damped beam finite element for three-layered symmetric straight damped sandwich structures was derived using the Hamilton principle. The damping was assumed to be proportional to mass and stiffness matrices, and the resulting complex-valued linear eigenvalue problem was solved to obtain the dynamic characteristics. The response curves were determined classically from the corresponding complex-valued ordinary set of equations.
Wang et al. [140] considered vibrations of a five-layer composite beam made of elastic, piezoelectric, and VE materials, where the latter were described using the Golla–Hughes–McTavish model. The layers’ kinematics were defined using the Euler–Bernoulli assumptions and the VE layer had an additional enhancement in the form of the shear angle associated with transverse shear. The Hamilton principle was used to formulate the equations of motion. The use of the second-order Anelastic Displacement Fields approach with three fields to implement the VE material model enabled the straightforward development of time-domain and frequency-domain finite elements.
Free vibrations of orthotropic multilayer sandwich structures with a VE core leading to high damping were studied in [141]. The aim was to establish numerical tools for the design of multilayer composite structures with high damping. The equations of motion were formulated using the principle of virtual work. A finite element model to solve the problem was derived from the classical zig-zag model with shear deformation in the VE layer.
Geometrically linear free vibrations of VE Mindlin plates with ambient temperature influence were considered in [118]. The governing equations were derived in the Laplace domain and, after the finite element discretization, the non-linear eigenvalue problem was obtained using the principle of virtual work. It was solved for the dynamic characteristics via a novel approach which simplified the procedure, reducing it to a combination of one linear eigenvalue problem and one simple algebraic non-linear equation with one unknown.
Free vibrations of laminated VE composite plates on Pasternak VE medium with simply supported edge conditions were investigated in [142]. The plate was made of linear VE polymeric matrix reinforced by transversely isotropic elastic fibers. The Boltzmann superposition principle was used to describe the time-dependent stiffness coefficients of laminates. The coupled integro-PDEs of motions were derived based on the third-order shear deformation theory, the Laplace transformation, and the Hamilton principle. Complex frequencies and closed-form solutions for transient response were computed by the weighted residual method, an iterative numerical algorithm, and the Fourier transform.
Vibration characteristics of laminated composite beams with magnetorheological layers were investigated using layer-wise theory in [143]. In the three-layered beam, each layer was considered to be a thick Reissner–Mindlin plate strip divided into several layers. Each of these was described using the first-order shear theory. The Hamilton principle was used to formulate the equations of motion. The natural frequencies were calculated via frequency sweeping with the stiffness matrix of the beam recalculated at each frequency value.
Dynamic behavior of free layer damping plates with thick unconstrained VE layer was analyzed in [144]. The Kirchhoff–Love thin plate formulation was adapted to take the shear stiffness into account by using a substitute equivalent frequency-dependent flexural stiffness. The results of free and forced vibrations analyses were obtained using the symbolic algebra program MATLAB. This approach was then extended to the cases of constrained VE layers in [145].
Linear free vibration analysis of asymmetric VE annular and circular plates was considered in [146]. The first-order shear deformation theory was used and the VE behavior in shear was assumed in the form of the standard linear solid model. The Hamilton principle was employed to formulate the governing equations, which were solved analytically using the perturbation technique and the Fourier series.
Free vibrations of a three-layer composite sandwich plate with a frequency-dependent VE core modeled using the Biot material were considered in [147]. The equations of motion in the finite element discretized form were obtained using the Hamilton principle. They were decoupled and transformed from the second-order differential type to the first-order state equation. The resulting non-linear eigenvalue problem was solved using the MATLAB program.
In the paper [148], the displacement-based refined zig-zag theory (RZT) was used for the first time to determine the dynamic characteristics of composite sandwich plates made from elastic and VE layers. This was a development of the approach proposed in [149] by the same authors, and was devised to analyze the layered beams. The use of RZT allowed the introduction of an efficient and simple description of the layered structures’ kinematics. Its accuracy was ensured by the properties of the zig-zag function introduced in [150,151]. It was assumed that its distribution was piecewise linear with gradient discontinuities at the layers’ interfaces and vanishing at the upper and lower plate surface. The graphical illustration of this function, denoted by for a plate with thickness h, consisting of N layers, is presented in Figure 5. For the k-th layer it has the following form:
where the quantities with a tilda indicate the values of the zig-zag function at the layers’ interfaces (see Figure 5), and the local co-ordinate
is introduced with the help of the layer thickness hk and z co-ordinate zu(k) of the upper limit of the k-th layer. When compared to the single-layer theories, the introduction of only one additional degree of freedom for beams, or two additional degrees of freedom for plates, at each finite element node yielded a very low computational cost. The equations of motion were derived using the principle of virtual work. The resulting non-linear eigenvalue problem was solved using the continuation method.
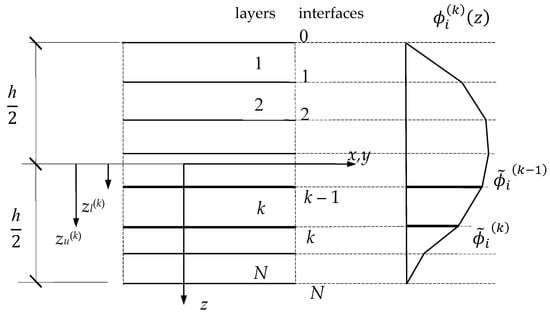
Figure 5.
Layered plate layout and the zig-zag function.
A finite element formulation for vibration and damping analysis of sandwich plates with a moderately thick VE core was proposed in [152]. The mixed layer-wise theory was applied where the VE core was modeled using a general high-order deformation theory. The viscoelasticity was described as a quasi-three-dimensional solid. Quadrilateral finite elements were developed and dynamic equations were formulated using the Hamilton principle in the variational form. An iterative procedure was introduced to solve the non-linear eigenvalue problem.
Free and forced vibrations of VE plates were considered in [153]. The governing equations of the Kirchhoff plate with Kelvin–Voigt viscoelasticity were derived and solved analytically.
Dang et al. [154] used a variable fractional derivative model to describe the vibrations of the circular plate with varying thickness. The method was used to formulate a ternary variable fractional differential equation of the plate. The shifted-Chebyshev-polynomials algorithm was introduced to numerically solve the complex equation directly in the time domain.
Linear vibration analysis of adaptive sandwich plates resting on a VE medium was presented in [155]. The sandwich plates with a fiber-reinforced layer, two magnetostrictive actuators, and VE faces were considered. The Kelvin–Voigt model was used. Based on the unified plate theory, the governing equation of motion for the system was formulated using the Hamilton principle. The solution was obtained analytically using the Navier method.
The natural frequencies of functionally graded composite VE plate on the visco-Pasternak foundation were examined in [156]. The higher-order shear deformation theory was used. The Kelvin–Voigt viscoelasticity model was employed. The equations of motion were formulated using the Hamilton principle. The analytical solution was obtained using the Navier method and a semi-analytical method founded on the generalized differential quadrature method.
5.2. Geometrically Non-Linear Vibrations
Xia and Łukasiewicz [157] analyzed non-linear forced vibrations of sandwich panels with the core modeled as the Kelvin–Voigt VE material. The equations of motion were formulated using the principle of virtual work and solved using the harmonic balance method with one harmonic assumed.
Kim and Kim [158] used the hereditary model of VE material within the solution of non-linear free vibrations of laminated plates. The equations of motion were derived using the Hamilton principle. The discretized problem was solved using the multiple scales method. It was shown that, for small non-linearities, the non-linear analysis and VE analysis can be carried out separately by considering decaying amplitude obtained from the linear VE analysis within the conventional elastic non-linear analysis.
The non-linear vibrations of VE sandwich beams were considered in [159]. In the kinematic model, it was assumed that two elastic layers remained parallel and that the shear strain was constant across the VE core, which was modeled using a general linear VE constitutive law. The amplitude equation was obtained from the principle of virtual work. It was solved via coupling the harmonic balance method with the one-mode Galerkin analysis.
Non-linear natural frequencies for vibrations of beams made from the Kelvin–Voigt VE material were analyzed in [160]. The Hamilton principle was used to formulate the equations of motion. They were solved analytically using the combination of the perturbation and Galerkin methods. The used multiple scale approach was found to be restricted to small non-linearities.
Jacques et al. [161] used the principle of virtual work to formulate the equations of motion for the non-linear vibrations of sandwich beams, where VE material was modeled with hereditary integrals. The solution was obtained via the harmonic balance method with one harmonic term and the exponential representation of the solution. The finite element method was used to discretize the problem. The similar approach was used by Bilasse et al. [162,163] to analyze the linear and non-linear vibrations of sandwich beams with various frequency-dependent models of viscoelasticity.
VE plates with high-order shear deformation theory were considered in [164]. The equations of motion were formulated as the integro-partial differential equations. They were converted to an explicit matrix form in the spatial domain using the matrix formulae of the differential quadrature method, the special matrix product, and the domain decoupled technique. This approach allowed the investigation of numerous non-linear phenomena including a transition to chaos.
Non-linear vibrations of Kelvin–Voigt VE beams with additional non-linear spring support during axial movement were analyzed in [165,166]. The equations of motion were derived using Newton’s law of motion and they were solved analytically using the multiple scale perturbation approach.
Active damping of non-linear vibrations by piezoelectric composites in laminate plates with viscoelasticity modeled using the Golla–Hughes–McTavish (GHM) material was analyzed in [167,168]. The first-order shear deformation theory was applied. The principle of virtual work was used to formulate the equations of motion, which were discretized using the finite element method and solved in the time domain. The similar approach was used in [169] to solve the problem of geometrically linear vibrations of thin laminated plates with a three-dimensional fractional derivative model of viscoelasticity. Based on similar tools, in [170,171] the same group of authors further considered the transient non-linear vibrations of skew laminated composite plates and non-linear thin panels with piezoelectric active constrained layer damping patches or layers. Finally, the functionally graded and smart plates with piezoelectric layers for active constraining were considered in [172,173].
Non-linear forced vibrations of symmetric laminated beams with a VE core were the subject of the paper [174]. The principle of virtual work and the harmonic balance method coupled with the one-mode Galerkin approach were used to formulate and solve the problem analytically.
An interesting version of the harmonic balance method combined with the residue homotopy continuation was applied to solve the non-linear vibrations of arches by Leung et al. in [175]. The governing differential equations were derived for the primary resonance and the Galerkin method was used to discretize the problem.
In [176], Mahmoudkhani et al. analyzed the non-linear free and forced vibrations of sandwich plates where the VE core was made from a Green–Rivlin material. The obtained results were compared with those for various other non-linear models. The equations of motion were formulated using the Hamilton principle. They were solved using the fifth-order multiple-scales method, and the resulting differential equations were in turn solved by the method of eigenfunction expansion.
Free vibrations of composite beams containing elastic and VE layers were considered in [177]. The four-parameter rheological model with a fractional derivative was applied to describe the mechanical properties of VE layers. The principle of virtual work and the finite element method together with the Laplace transform were used to formulate the equation of motion in the frequency domain. The dynamic characteristics were computed as the solution to a non-linear eigenvalue problem obtained using the continuation method.
Non-linear vibrations of simply supported plates with geometric imperfections, made from a Kelvin–Voigt VE material, were considered in [178]. The equations of motion were formulated based on the expressions for potential and kinematic energy. Their discretized version was solved using the arc-length continuation and collocation methods.
The problem of harmonic vibrations of VE plates was analyzed in [179,180]. The VE material was described by the classical and fractional Zener models. The equations of motion were formulated for the geometrically non-linear plate kinematics using the principle of virtual work. The harmonic balance method was used to solve the problem, where the orders of the approximation of the solution were varied from 1 to 2 for different parts of the kinematic description to match the kinematic relations of the Mindlin plates. The resulting non-linear amplitude equations were discretized using the finite element method and solved by the arc-length curve following approach.
The flutter of a sandwich circular cylindrical shell with the fractional order Zener constitutive relationship was considered in [181]. The formulation of the sandwich cylinder was obtained basing on the Donnell–Mushtari theory for facing layers and the first-order shear deformation theory for the VE layer. The Lagrange method and the Rayleigh–Ritz method were implemented to derive and solve the governing equations. The obtained set of ordinary differential equations was solved to determine the stability margin of the three-layered cylinder.
Shafei et al. [182] proposed an efficient iso-geometric formulation for non-linear vibrations of VE plates. The generalized multi-axial Maxwell model was used to express the VE constitutive equations. The plate formulation was based on a higher-order shear deformation theory. The governing equations of motion were derived using the Hamilton principle. The solution in the time domain was obtained by the use of the Newmark constant average acceleration method.
5.3. Structural Elements on Viscoelastic Foundations
Viscoelastic foundations are another means of reducing undesired vibrations of structures and their elements. The topic is especially important in the case of micro- and nanoscale objects which, in addition to their uses at the nanoscale, are also often used in the manufacture of larger-scale elements with an intricate internal structure having a functionally graded (FG) type, or as layered composites. Consequently, recent years have seen an enormous scientific effort and numerous contributions to the general knowledge and understanding of the behavior of beams, plates, and shells at various scales resting on substrates with time-dependent materials.
The task of discussing and presenting all of these is certainly beyond the scope of this paper. This topic itself would deserve a separate dedicated review paper. Actually, an excellent overview of the subject of viscoelastic foundations, together with an extensive review of papers devoted to it, was presented by Younessian et al. [183]. This compilation includes a thorough description of the existing theoretical models describing the behavior of time-dependent substrates. A separate chapter is devoted to modeling of various structural elements resting on VE foundation. The possible methods of solutions are also discussed and the problems are illustrated by selected practical applications. That review summarizes the state of the art in this subject until 2019. Thus, it was decided to focus the attention in this paper on the research results published after that time.
The vast majority of those recent contributions are devoted to the analysis of free vibrations and parametric analyses of the dependence of dynamic characteristics in systems on various details of the model, see e.g., [184,185,186,187,188,189,190,191,192,193,194,195,196,197,198,199,200,201,202,203,204,205,206,207,208,209,210,211,212,213]. The second large group of papers concerns the harmonic forced vibrations, both linear [155,214,215,216] and geometrically non-linear [217,218,219,220,221,222,223,224,225,226,227,228,229]. The other group of contributions focuses on the vibrations forced by a moving load or a moving mass, e.g., [193,230,231,232].
A large variety of types of structural elements is considered, including beams [187,194,195,206,213,228,232], plates [193,202,203,214,218,220,227], shells [204], composite beams [186,198,201,207,211,215,224,225], composite plates [155,185,191,199,200,210,212,222,223,226], composite shells [190,216,219,221], nanobeams [184,189,196], FG nanoplates [192,197,208,229,230,231], and FG nanoshells/nanopanels [188,209,217].
The overview of the literature indicates that the majority of recent contributions deal with structural elements resting on the Pasternak foundation with VE properties modeled using the Kelvin–Voigt description. This is the case in [155,184,185,189,190,191,192,194,196,197,198,199,200,201,204,205,206,207,209,210,212,217,225,226,231], where a classical linear version of the model was applied. In the paper [208], the VE foundation was represented using the variable Kelvin–Voigt description. The version of the Kelvin–Voigt description with non-linear elastic properties was considered in [210,219,222,223,228]. It is known that the use of fractional derivatives significantly improves the properties of VE models. Following this knowledge, this type of mathematical description of Kelvin–Voigt material was introduced in several papers [203,227].
The possibility of applying a simpler foundation model, i.e., the Winkler model with a Kelvin–Voigt viscoelastic component, is also commonly investigated, as in [187,188,215,230,231] using the linear description, or in [213,218,224] with the non-linear elastic element. The fractional derivative within this model was considered in [193,214].
There are also attempts to model the foundation in the Pasternak configuration combined with standard linear solid viscoelasticity in its fractional variant [195,202,227,232].
Finally, research has also reported on more elaborate foundation types, such as the Kerr foundation with a double VE layer, including in the papers [186,211], whereas, in [221], the influence of the foundation with the Hetenyi shear layer was analyzed.
6. Determination of Dynamic Characteristics of Systems with VE Elements
Dynamic characteristics, i.e., the natural frequencies, the non-dimensional damping ratios, and the modes of vibrations, are extremely important parameters as they enable one to understand the dynamic response of structures. Information about their values is crucial in the process of designing and optimizing systems, as well as for understanding their behavior under dynamic influences. Mathematical models of systems with VE materials or containing VE elements must take into account the fact that dissipative forces depend on the time history. The equation describing the eigenvalue problem for systems with VE damping can be formulated in a general form [233] as follows:
where M and K represent the mass matrix and the stiffness matrix of the system, respectively. is the displacement vector and denotes the damping kernel functions matrix. Mathematically, any function can be assumed for provided the energy dissipation functional is non-negative. Examples of these functions for the classical VE models can be found in [54,233], whereas for the fractional models, they can be found in [234]. In the Laplace domain, (5) reads as follows:
where s is the Laplace variable, is the Laplace transform of , and D(s) is referred to as the dynamic stiffness matrix
and is the matrix of damping kernel functions in the Laplace domain.
To find the dynamic characteristics of the considered system, it is necessary to solve the non-linear eigenvalue problem formulated in the matrix form (6). The number of solutions depends on the adopted VE model. It is well known, that for a linear eigenvalue problem, the number of solutions is n, where n is the dimension of matrices involved in the non-linear eigenvalue problem. However, when the viscous or the simple classical or fractional Kelvin model is used and the system is sub-critically damped, the number of solutions to the eigenproblem (6) is 2n and they have the complex conjugate format. If the system is super-critically damped, then multiple real solutions may appear. In other words, when a more complex model is applied, the number of solutions is 2n + p with additional p real solutions. The 2n conjugate complex eigenvalues are referred to as the elastic modes, whereas the p eigenvalues are called the damping modes. This is a fundamental difference between VE and elastic systems, where only n solutions exist.
Many methods can be found in the literature that can be applied to solve the non-linear eigenvalue problem describing systems with multiple degrees of freedom. A review of the methods applicable to solving eigenproblems also occurring in systems with VE damping can be found in, among others, [235,236]. In many papers, relatively simple systems with one or just a few degrees of freedom are considered that include damping elements described in a general way, so that the formulations can also be applied to VE elements. In [126,237], a method based on asymptotic perturbation theory was presented. The papers [238,239] demonstrated how a system with multiple degrees of freedom can be transformed into a linear system which can be solved using a state-space approach. The Biot model was considered in these works. In [240], a system with VE dampers was also considered, where a simplified model consisting of a mass, a stiffness corresponding to the structural stiffness, and stiffness and damping coefficients of the dampers was adopted. Analytical solutions were presented for both the deterministic and stochastic formulations of the eigenproblem. Furthermore, in [241], a proposal was made to replace a VE continuous system with a system composed of a spring, a damper, and a mass. Single-degree-of-freedom systems with fractional derivative damping were also investigated in [242,243]. In the latter paper, the system was additionally connected to an inerter.
The papers [233,244] presented a solution to the eigenvalue problem based on the first- and second-order Taylor series expansion of the modal damping function. The solutions included both complex and real eigenvalues. In [245,246], a recursive numerical procedure based on the fixed-point theorem was presented. The method involved a formulation of recursive functions that allow for the iterative determination of eigenvalues and eigenvectors. The eigenvalues were the fixed points of these functions. In the papers [247,248], an iterative procedure was described, which started with solving the eigenvalue problem for the undamped system and then approximated the eigenvalues and eigenvectors using finite increments, utilizing the derivatives of the eigenvector and the Rayleigh quotient. In [249], an iterative method was presented, which allowed for simultaneous estimation of eigenvalues and left and right eigenvectors. The application of the proposed method to discrete and continuous systems with VE elements was demonstrated. Another iterative method was proposed in [250] for systems in which damping was described by the Biot model. A closed-form analytical solution for determining complex eigenvalues of non-proportionally damped systems was presented in [251]. An expression was derived in order to illustrate how the eigenvalues depended on the damping parameters, which required solving only the eigenvalue problem for the undamped system.
The above-mentioned iterative and analytical methods were presented for relatively simple systems with VE elements, but they are not limited to them. In the literature, one can also find numerous studies that involve modifications of the previously described methods or entirely new approaches, which are applied to realistic structural systems with VE materials or VE elements, such as layers or dampers.
In the first group of papers, studies related to linear VE systems are reported. Among the early works, one can find [252,253], which also considered the non-linear eigenvalue problem. Linear VE systems were also discussed in the previously mentioned papers [234,240]. Considerations of linear VE systems were included in [118,254,255]. They were dedicated to determining the dynamic characteristics of frames and plates made of VE materials, described using both classical and fractional rheological models. By utilizing proportional damping, the solution of the non-linear eigenvalue problem arising in such structures could be reduced to solving an eigenvalue problem for the elastic system, followed by solving a single non-linear algebraic equation with one unknown. The influence of temperature was also taken into account in [118,255]. In [146], an analytical solution for VE circular and annular plates was presented, whereas the solution for non-linear vibrations was presented in [256] for a VE plate with material properties described by fractional derivatives.
In the second group of papers, methods for solving non-linear eigenproblems occurring in the dynamics of systems with VE elements were described. A system of two buildings connected by a VE damper was analyzed in [257]. An analytical solution was derived assuming that the buildings were treated as homogeneous beams.
In the papers [61,258], a method was presented for analyzing frames with dampers, whose behavior was described using fractional derivatives. A recursive numerical method was applied based on an artificial perturbation parameter governing damping. In the work [61], the influence of temperature on the dynamic characteristics was also included using the temperature–frequency superposition principle.
The application of the continuation method, also known as the homotopy method, yielded very good results in calculation of the dynamic characteristics of systems with VE elements described by both classical and fractional rheological models. In [259], dynamic characteristics of frames with built-in VE dampers were determined, and in [122], the influence of temperature was additionally taken into account. In the papers [149,177], beams with VE layers were analyzed; [260] reported the results for plates with VE layers, and in [261], reticulated domes built from composite elastic/VE rods were studied. In the continuation method, the initial solution is known and derived from solving the eigenvalue problem for the undamped system. Then, by introducing a homotopy parameter, a solution trajectory is constructed by gradually modifying this parameter in an iterative-incremental procedure. Graphical interpretation of the continuation method in the case of one degree of freedom system is presented in Figure 6. Here, is a sought quantity and is the homotopy parameter. The continuation method is used to simultaneously determine the eigenvalue and eigenvector for the selected mode.
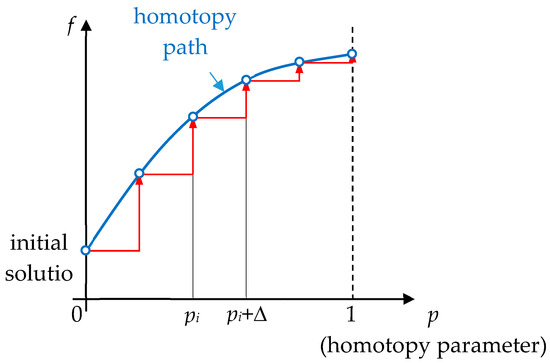
Figure 6.
Illustrative explanation of the continuation method.
The application of the subspace iteration method to systems with VE elements was presented in [262,263]. This method allowed for the simultaneous determination of several initial eigenvalues and their corresponding eigenvectors. It was particularly useful for systems with multiple degrees of freedom, where solving the entire non-linear eigenvalue problem would require significant computational effort or was practically impossible. In the former paper, classical models of damping elements were considered and an additional reduced eigenproblem was solved using the state space formulation. In the latter, fractional models were also considered and the reduced eigenvalue problem was solved using the continuation method.
Due to the wide application of structures with VE layers in civil engineering, aerospace and aviation, automotive, and energy industries, several studies emerged in recent years where methods for determining the dynamic characteristics of such structures were developed. Besides the previously mentioned layered beams, they were analyzed in [264], where the order-reduction iteration method was applied to find a solution to the non-linear eigenvalue problem. In [136], the Ritz method was used to determine the dynamic characteristics of a sandwich beam. In [144], an iterative method was proposed to solve the non-linear eigenproblem for a sandwich plate, involving updating the complex stiffness matrix at each step. The paper [143] presented an approximate solution for a VE composite plate resting on a visco-Pasternak foundation using the Galerkin method. The Rayleigh–Ritz method was employed for a sandwich cylindrical shell in [265]. Non-linear vibrations in sandwich beams and plates were analyzed using the harmonic balance method in the papers [162,163]. In [164], four numerical procedures were compared: real eigenmodes, improved real eigenmodes, approached complex eigenmodes, and exact complex eigenmodes, whereas in [163] dynamic characteristics were found using the asymptotic numerical method in conjunction with automatic differentiation techniques. The method proposed in [266] allowed for the calculation of dynamic characteristics of beams and frames with VE layers described by a fractional model. A plate with a VE layer was also analyzed in [267]. The authors proposed a method to solve the non-linear eigenvalue problem, which depended not only on frequency but also on a selected design parameter. A continuous solution was obtained as a function of the parameter describing the orientation of the fibers in the orthotropic layers of the sandwich plate, but it was also possible to study the influence of other parameters, such as layer thickness or temperature.
In recent years, an increasing number of studies have been carried out that analyze VE structures modeled using the nonlocal theory. This was useful for describing nanostructures because it took into account that the behavior at a particular point was not only influenced by its immediate neighborhood. In the papers [268,269,270], the nonlocal theory was applied to analyze a VE Euler–Bernoulli beam using the finite element method. The main difference with respect to the previous considerations was that nodes far from the considered element affected the energy expression and, consequently, the damping matrix. Those papers presented solutions to the resulting eigenvalue problem. Two solutions to the eigenvalue problem were proposed for the considered VE Timoshenko beam in [271]. The first solution was a semi-analytical method in which the Galerkin method was used in the first step, followed by solving the differential equations using a direct numerical procedure. The second solution was a numerical method, whose accuracy was verified by a comparison with the first method. In the paper [272], a solution was presented for a VE beam using the Galerkin method in combination with the state-space formulation. The natural vibrations of a VE beam described by a generalized Maxwell model were analyzed in [273], whereas the papers [274,275] presented a solution for a fractional model. Solutions to the eigenvalue problem for VE plates described by the Maxwell and Zener models, respectively, were demonstrated in [276,277].
Dynamic characteristics of systems with VE damping can also be determined approximately using the modal strain energy method. This approach enables an efficient estimation, which can be particularly useful for complex geometries or large systems. In the paper [278], systems with VE layers were analyzed and solutions were presented for beams, plates, and rings. The study [279] considered frames with VE dampers. It was demonstrated that the damping coefficients calculated using the modal strain energy method were approximately equal to the actual values if they were not greater than 20% of the critical damping value. A similar conclusion was presented in the work [280], where the authors also analyzed frames with VE dampers and investigated, among other factors, the influence of neglecting the effect of imaginary mode shapes. A modification of the classical modal strain energy method was proposed to eliminate assumptions that lead to the overestimation of damping coefficients for systems with damping above 20% of the critical damping value. The frame with dampers was also analyzed in [281], where three methods were compared: complex mode superposition, direct integration, and the modal strain energy method. An analysis was also conducted to examine how the matrix condensation method affected the accuracy of the obtained results and the computation time. The modal strain energy method was applied in the paper [282] to a rectangular plate with VE boundary supports. In the study [283], laminated beams with VE layers were analyzed for which the dynamic characteristics were determined using the modal strain energy method at various temperatures. The modal strain energy method was applied in the analysis of cylindrical shells with a VE layer in [284,285]. In [286], the authors proposed a modification of this method for the analysis of structures with a VE layer by introducing a coefficient that varied with the amplitude of the modal loss factor.
7. Methods of Numerical Integration of Motion Equations of Systems with VE Elements
In the previous sections it was shown that the time-domain equations of motion of structures with VE dampers and/or layers treated as the discrete systems can be written in the form of differential equations or differential-integral equation. They can include ordinary or fractional derivatives. Earlier in this paper, solutions to the equations of motion for systems executing free or steady state vibration were reviewed. Here, solutions to the equations of motion for arbitrary transient loads are discussed.
If the classical rheological models, such as the Kelvin, Maxwell, or Zener models, are used to describe VE dampers or layers, the equations of motion have the form of ordinary differential equations. The well-known time-integration methods can be used to solve them. The Newmark method was used in [287,288,289]. The state-space formulation which transforms the equations of motion from the second-order differential equations to the first-order differential equation, together with the direct time-domain integration method, was used in [290]. In particular, as in [288], the exponential damping model was considered. The modal approach and the original numerical procedure were presented in [291,292] and used for the analysis of transient vibration of buildings equipped with VE dampers. In the paper [293], the dynamic response analysis method for non-viscously damped systems was derived basing on the Newmark assumption of acceleration. In the proposed direct time-integration method, the convolution integral term was calculated directly using the trapezoidal rule. The semi-analytical methods and implicit Runge–Kutta methods were adopted and compared in [294], where they were used to integrate equations with Prony series describing the linear viscoelasticity problems. The central difference method was used in [295] to determine the dynamic response of non-viscously damped structures using the explicit methods. Patlashenko et al. [296] developed the time-stepping schemes for the linear Volterra-type systems of integro-differential equations, which may arise in the semi-discrete finite element model of dynamic viscoelasticity. The modal reduction method, together with the method similar to the so-called precise integration method, was presented in [297,298] for the analysis of transient vibrations of VE systems with multiple damping models. The Laplace method was used in [299] to analyze transient vibration of VE composite beams, where the Biot model was used to describe the properties of a VE layer.
In the case of the equations of motion with the fractional derivatives, their non-local character must be taken into account. For this reason, special methods are needed to numerically integrate the equations of motion. Very often the numerical approximation of fractional derivatives is employed via the Grünwald–Letnikov approximation. In connection with the Newmark method, this approach was first used by Padovan in [300] and later also in the papers [128,130,301,302,303,304,305,306,307,308,309]. Due to their non-local character, the numerical evaluation of fractional derivatives requires a high number of computations. In this case, all the fractional derivatives need to be evaluated at any instant of time. In doing so, the whole time history of system variables must be taken into consideration. In the case of a multiple-degrees-of-freedom system described by the in-time fractional differential equations that are solved numerically by time integration, the numerical effort and the storage requirements are huge. Therefore, new methods for the numerical calculation of fractional derivatives were developed with the aim of considerably reducing the numerical effort. Following the suggestion presented in [310], the reduction in numerical effort can be achieved by adopting a certain temporal resolution. The idea was motivated by the fact that, as the time integration proceeds, previous values of variables had a decreasing influence on the current value of the fractional derivative. An efficient numerical method to integrate the constitutive response of fractional order viscoelasticity was developed in [311]. The method could be used for variable time steps. To overcome the problem of the increasing amount of data that had to be stored and used in each time step, the sparse quadrature was introduced.
A time-marching procedure based on a composite explicit method was proposed in [312] for non-viscous damping systems. In that method, an improved integral approximation scheme applicable to any causal kernel function was developed to enhance the convolution solution accuracy. The papers [295,313,314] described an explicit computational method of dynamic response for non-viscously damped structure systems. The explicit formula was derived using the differential property of convolution and the central difference formula of acceleration. Moreover, a time-integration method based on the weak-form Galerkin method was proposed in [315] for non-viscous damping systems with a convolution damping model.
8. Methods of Sensitivity and Uncertainty Analysis of Structures with Viscoelastic Elements
The concept of sensitivity and uncertainty analysis is depicted in Figure 7. Uncertainties in the input parameters (p1, …pi, …, pn) of the considered model result in the presence of uncertainty in the response function of the structure. Uncertainty analysis enables the determination of the uncertainty in the response function, as indicated by the shading in the figure, while sensitivity analysis helps identify the parameters that have the greatest influence on the structural response.
Figure 7.
Concept of sensitivity and uncertainty analysis.
Sensitivity analysis is one of the most important tools that allows for the evaluation of the influence of design parameters on the dynamic response of a structure. It is useful during project optimization, parameter identification, structural health monitoring, model updating, and damage detection. The methods of sensitivity analysis of eigenvalues and corresponding eigenvectors can be divided into three groups. The first is the modal method, which requires the determination of all or almost all the modes, and is therefore inefficient. For systems where damping can be described as viscoelastic, this approach was applied in [316]. The second method, introduced by Nelson, is more efficient as it requires only the determination of the eigenvalue and its corresponding eigenvector, for which sensitivity is to be determined. It was developed in [317] and applied to non-viscously damped systems. In the third group of methods, algebraic approaches are included, among which the direct differentiation method (DDM) and adjoint variables method (AVM) can be distinguished. DDM was presented in [318,319], where it was applied to systems with non-viscous damping. This involved solving a system of algebraic equations, where the unknowns were the sensitivities of eigenvalues and their corresponding eigenvectors. The system of equations consisted of a differentiated equation describing the eigenvalue problem and a differentiated normalization condition. In [320], extended analysis was carried out for the second-order sensitivity. In [321], a method was presented for determining sensitivities of repeated eigenvalues and their corresponding eigenvectors, whereas in [322], both distinct and repeated eigenvalues were considered. AVM is more advantageous than DDM in some cases, especially when the number of design parameters is large and the number of constraints is small. AVM involves adopting an objective function in terms of eigenvalue, eigenvector, and design parameters. Then, the augmented function formulated using the eigenvalue problem and the normalization condition is differentiated. This method was applied in [323] to systems where damping was described by fractional derivatives.
Both DDM and AVM were applied in [324] to determine the sensitivity of eigenvalues and eigenvectors for frames with VE dampers described by classical and fractional rheological models. DDM was also extended to the second-order sensitivity analysis. In [325], DDM was applied to calculate the sensitivity of eigenvalues and eigenvectors in composite beams with VE layers described by fractional derivatives. The sensitivity of dynamic characteristics of composite systems with VE layers was also analyzed in [326,327]. The paper [328] was devoted to the determination of the sensitivity of eigenvalues for beams supported by VE supports. In the paper [329], frames and beams with VE elements were analyzed. The second-order sensitivity analysis using DDM, AVM, and a hybrid method were presented and the effectiveness of those methods was compared.
Both DDM and AVM can also be applied to calculate the sensitivity of transient-response and frequency-response functions. The sensitivity analysis of transient response for non-viscously damped systems was presented in [330]. The authors used AVM for this purpose. AVM was also applied in [331] to compute the sensitivity of transient response. Two solution schemes were discussed and compared: discretize-then-differentiate and differentiate-then-discretize. In [332], a new and more efficient state-space-based discretize-then-differentiate method was proposed for calculating the sensitivity of transient response. In the study [333], the application of DDM to the sensitivity of the first and second order was discussed. In [334], a method based on model order reduction techniques was proposed for sensitivity analysis of transient response. First- and second-order sensitivities were determined and it was demonstrated that good results can be achieved with reduced computation time.
Both DDM and AVM were used in [335] to calculate the sensitivity of the frequency response function (FRF). The sensitivity of eigenvalue solutions was also considered. In [336], the sensitivity of FRF and amplitudes of steady-state vibrations were analyzed using DDM. The authors examined a frame with VE dampers described by fractional derivatives. The sensitivity of FRF was also analyzed in [96,337] for structures with VE layers. The analysis was performed using DDM due to changes in structural parameters and temperature variations. In [338], a method for calculating higher-order eigenvalues was presented to find the harmonic response of a structure.
Sensitivity analysis is widely used in studies dedicated to topology optimization. In the context of systems with VE elements, sensitivity calculated with respect to a change in design parameters using the adjoint variable approach was applied in [339,340,341,342]. Practical application of sensitivity analysis can also be found in [343,344], where it was used to solve the inverse problems.
In design and analysis of systems subjected to dynamic loads, considering the uncertainties of design parameters is also a crucial aspect. Uncertainties arise from modeling inaccuracies, measurement errors, manufacturing errors, and other factors. One of the early works on modeling uncertainties in VE systems was [345]. It provided an overview of methods and presented the question of parameter uncertainties as a convex optimization problem.
The methods where uncertainties of design variables are considered can be categorized into three groups. The first group includes probabilistic methods, where parameters are treated as random variables and their distributions are approximated based on available data. The second group consists of methods based on the fuzzy theory, which is particularly useful when there is lack of sufficient data regarding parameter variability. The next group comprises methods where parameters are modeled as intervals with values allowed to vary within the specified bounds. It should be noted that hybrid methods can also be devised, which combine the three basic approaches.
Numerous papers were dedicated to solving dynamic problems with design parameters modeled as random variables. In [346], a stochastic finite element approach was presented for modeling a sandwich beam with a VE layer. Random parameters were represented using the Karhunen–Loève expansion and free vibration was approximated using generalized polynomial chaos expansion. Both geometric and material parameters were considered to be uncertain. Similar uncertainties were investigated in [347], where the calculations were performed using Monte Carlo simulations. In [348], the authors analyzed the dynamic characteristics of a three-layered structure with a VE layer described by a fractional model. In the study [349], an iterative method was proposed to reduce the non-linear eigenvalue problem that arose after considering uncertainties, aiming to approximate complex eigenmodes. The authors studied a sandwich beam with a VE layer. In [350], sandwich plates and cylindrical structures were analyzed using a stochastic collocation method.
The probabilistic approach is also widely used for computing frequency response functions. In [351], two approaches were proposed—one based on an ensemble of equivalent damping functions and the other based on random matrix theory. The frequency response function for a sandwich structure with a VE layer was calculated in [92] using the stochastic finite element method. Random parameters were discretized using the Karhunen–Loève expansion. In [352,353], the adaptive sparse grid collocation method was applied to analyze the frequency response function of structures with a VE layer. It was demonstrated that the proposed method accurately predicted the response variability while improving computational efficiency. In the papers [354,355,356,357], non-parametric probabilistic approaches and random matrix theory were applied for stochastic analysis, where parameter uncertainties were introduced. Reliability analysis for layered systems with randomly described uncertain parameters was presented in [358], and for systems with dampers in [359]. The paper [360], focused on the study of dynamic damage in layered systems with uncertain parameters.
The second group of methods is based on the fuzzy theory. In papers such as [361,362], frames with VE dampers were analyzed and a stochastic model of the dampers was presented.
The third approach employing interval representation of uncertain parameters was proposed for VE systems in [363]. The authors applied non-probabilistic convex modeling to analyze forced vibrations of VE beams. In [364], interval analysis and Taylor series expansion were used for analyzing frames with VE dampers. Similarly, an algorithm based on Taylor series expansion was proposed to determine critical combinations of uncertain design parameters for structures with VE dampers in [365], and for a sandwich beam with VE layers in [366]. The paper [367] focused on the reliability analysis of structures with dampers, where the parameters were described by interval numbers. The dampers in [365,367] were modeled using fractional derivatives. In [368], interval analysis was applied to solve the identification problem of parameters described as fuzzy.
9. Optimization of Structures with VE Elements
Devices used in passive damping systems, including VE dampers, have to be tuned, i.e., their parameters need to be properly designed. The second important factor that determines their effectiveness is the proper configuration, i.e., their arrangement in the structure. Usually, the chosen combination of parameters and location for VE dampers is considered optimal when the effectiveness in mitigating earthquake- or wind-induced vibrations is best. However, the parameters that define this effectiveness can vary and, depending on the type of structure, one can use displacement values, inter-story drifts, internal force values or accelerations [369]. Consequently, different optimization strategies and different objective functions are adopted [370]: maximum inter-story drifts, the sum of inter-story drifts [371,372,373], absolute acceleration [374], displacement [374,375], base shear [374], an energy-based damage index [376], and base moments [377], as well as the combinations of some structural performance functions; see Figure 8.
Figure 8.
Selected examples of optimization strategies and optimization methods.
Various methods can be used to determine the optimal location of dampers in a structure. They can be divided into three main groups: evolutionary methods, analytical methods, and heuristic methods [16].
Typically, in evolutionary approaches, such as the genetic algorithm (GA) [378,379,380], the artificial bee colony algorithm (ABCA) [376], or particle swarm optimization (PSO) [71,381], different starting points are selected and then the best solution is searched for sequentially. Such a search without calculating the gradient can lead to local optima, especially when there is little variation in the value of the cost function in the domain of design variables. Evolutionary methods are regarded as simple, practical, and highly effective [375], but there is no confirmation that the solution found represents the global optimum.
The following examples of methods belonging to the second group of analytical approaches [369] can be considered: gradient-based algorithm (GBA) [370,382], inverse problem approach (IPA) [372], steepest direction search algorithm (SDSA) [383], and fully stressed design algorithm (FSDA) [384].
In the approaches using a gradient-based algorithm (GBA), the optimization is usually of the first-order type. The constraints on the various normalized responses of the structure with dampers are condensed to a single constraint on their maximum value and the required gradient is effectively derived analytically using the adjoint analytical method. Therefore, a computational effort at the order of a single additional analysis is required, regardless of the number of design variables considered or the responses to be constrained [370,384]. A possible weakness of GBA is that its objective is achieved by minimizing the sum of the performance index instead of the peak value, which is commonly considered to be a better damage indicator. The gradient-based evolutionary optimization technique developed using the Lagrange multiplier optimization technique made it possible to satisfy the optimality criterion for the distribution of VE dampers and the limitation of the supporting member forces [382].
In the approach involving an incremental formulation of the inverse problem (IPA), the amplitude of the transfer function expressed as the sum of inter-story drifts at the fundamental natural frequency can be minimized with a reduction in the total amount of damping [370,372]. The advantage of this approach is that the algorithm is simple and the result obtained is independent of the input ground motions [383]. The approach using IPA is not as simple as the direct one; this method requires a considerable effort to develop the needed programming script.
The performance indicator of FSDA is the inter-story drift, which is the main limitation of this method. The advantage is that it takes into account the variability of earthquake data [369].
The third group consists of heuristic methods, among which one can list the following: sequential search algorithm (SSA) [385], pattern search algorithm (PSA) [380], uniform distribution (UD) [386], proportional story shear distribution (SSPD) algorithm [387], story shear strain energy distribution procedure (SSSE, SSSEES), first-story damping system (FSDS), and proportional stiffness distribution (SPD).
The SSA method is assigned to the group of repetitive methodologies because of its reasonable physical significance and simplicity, as dampers are added one by one to achieve the performance goal. In addition, the SSA method is suitable for controlling the inter-story drift, but it is not effective in reducing the floor acceleration, especially in buildings with non-uniform floor stiffness [388].
The UD method for frame structures where one damper per floor is assumed was typically used for comparison with other approaches that yield a more optimal damper placement [380,386].
The SSPD method was based on the fact that inter-story velocities on upper floors tend to be lower than on lower floors and, therefore, dampers can be distributed according to story shear stiffness [387]. However, this relatively simple approach is not cost-effective for practical applications.
The basic idea of the PSA method is to use steps of a certain magnitude to sample variables and reduce their size when the variation of the function value is stopped [380]. This method is suitable for problems in which the function cannot be differentiated or is not continuous. The PSA method can handle a large number of variables without involving significant computational resources, but it can converge to local minima and various initial values lead to different optimization results.
In some cases, more desirable results for optimizing damping systems in structures may result from including damage cost as an optimization objective [389]. However, a separate issue then requiring analysis is the determination of the damage measure [390].
It is worth mentioning that it is possible, and sometimes even necessary, to use a multi-objective optimization strategy, in which there are several objectives. For example, in papers [378,391], a genetic algorithm approach was developed to allow the evaluation of a Pareto front, in which inter-story drifts and total accelerations served as objectives.
10. Concluding Remarks
The presented extensive literature review proves significant progress in development of theories describing dynamic behavior of systems with embedded VE elements. Based on it, the following conclusions can be drawn:
- (i)
- Significant progress has been gained in the field of designing of rubber-like materials with high damping properties; some new materials have the maximum damping ratio of up to 30% (see [36]);
- (ii)
- Advanced rheological models (both classical and fractional) are now adopted to characterize dynamic properties of VE elements and sophisticated identification procedures are developed to determine the parameters of those models;
- (iii)
- The identification procedures are quite complicated and need further improvements in the future; a nonlinear model of dampers which takes into account the influence of vibration amplitude in dampers is very much desired;
- (iv)
- Currently, the influence of ambient temperature on parameters of VE elements and overall dynamic behavior of systems with these elements is taken into account only for the case of rheologically simple materials, usually adopting the frequency–temperature superposition principle and the shifting techniques; studies concerning the influence of ambient temperature on parameters of rheologically complex materials are required;
- (v)
- Non-linear dynamic analysis of beams and plates with VE layers became a highly popular research subject due to its practical importance; in particular, very recently, the refined zig-zag theory was successfully applied to the analysis of free and steady-state vibrations; see also the very recent papers [392,393];
- (vi)
- Solution of an eigenvalue problem, in many cases a non-linear one, is required to determine dynamic characteristics of systems with VE elements; there are several methods available to solve this problem efficiently;
- (vii)
- Numerical integration methods for solving the equation of motion of systems with VE elements must take into account a complete history of the considered dynamic process, which significantly complicates the numerical procedure and for which further improvements aiming at the reduction in the total time of integration of equations of motion are very much desired;
- (viii)
- Recent achievements in sensitivity analysis and uncertainty quantification of design parameters involve the refinement of advanced methods to assess the influence of the parameter variability on the dynamic response of systems with VE elements; in the case of uncertain parameters, it is crucial to develop efficient methods because the recently proposed methods are computationally complex and involve multiple analyses to obtain reliable results;
- (ix)
- Heuristic methods are often used in optimization problems because of their reasonable physical relevance and simplicity, as dampers are added one by one with an even distribution or according to a certain pattern; however, their effectiveness is lower for asymmetrical structures or those featuring varying stiffness.
Author Contributions
Conceptualization, R.L., P.L., M.Ł.-P. and Z.M.P.; methodology, R.L., P.L., M.Ł.-P. and Z.M.P.; validation, R.L., P.L., M.Ł.-P. and Z.M.P.; formal analysis, R.L., P.L., M.Ł.-P. and Z.M.P.; investigation, R.L., P.L., M.Ł.-P. and Z.M.P.; resources, R.L., P.L., M.Ł.-P. and Z.M.P.; data curation, R.L., P.L., M.Ł.-P. and Z.M.P.; writing—original draft preparation, R.L., P.L., M.Ł.-P. and Z.M.P.; writing—review and editing, R.L., P.L., M.Ł.-P. and Z.M.P.; visualization, R.L. and Z.M.P.; supervision, R.L.; project administration, P.L. and Z.M.P.; funding acquisition P.L., Z.M.P. and M.Ł.-P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Poznan University of Technology, Grant No. 0411/SBAD/0008.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Spencer, B.F.; Nagarajaiah, S. State of the art of structural control. J. Struct. Eng. 2003, 129, 845–856. [Google Scholar] [CrossRef]
- Saaed, T.E.; Nikolakopoulos, G.; Jonasson, J.E.; Hedlund, H. A state-of-the-art review of structural control systems. J. Vib. Control 2015, 21, 919–937. [Google Scholar] [CrossRef]
- Housner, G.W.; Bergmann, L.A.; Caughey, T.K.; Chassiakos, A.G.; Claus, R.O.; Masri, S.F.; Skelton, R.E.; Soong, T.T.; Spencer, B.F.; Yao, J.T.P. Structural control: Past, present, and future. J. Eng. Mech. 1997, 123, 897–971. [Google Scholar] [CrossRef]
- Symans, M.D.; Charney, F.A.; Whittaker, A.S.; Constantinou, M.C. Energy dissipation systems for seismic applications: Current practice and recent developments. J. Struct. Eng. 2008, 134, 3–21. [Google Scholar] [CrossRef]
- Li, H.; Huo, L. Advances in structural control in civil engineering in China. Math. Probl. Eng. 2010, 2010, 936081. [Google Scholar] [CrossRef]
- El-Khoury, O.; Adeli, H. Recent advances on vibration control of structures under dynamic loading. Arch. Comput. Methods Eng. 2013, 20, 353–360. [Google Scholar] [CrossRef]
- Korkmaz, S. A review of active structural control: Challenges for engineering informatics. Comput. Struct. 2011, 89, 2113–2132. [Google Scholar] [CrossRef]
- Javanmardi, A.; Ibrahim, Z.; Ghaedi, K.; Ghadim, H.B.; Hanif, M.U. State-of-the-Art Review of Metallic Dampers: Testing, Development and Implementation. Arch. Comp. Meth. Eng. 2020, 27, 455–478. [Google Scholar] [CrossRef]
- Soong, T.T.; Spencer, B.F. Supplemental energy dissipation: State-of-the-art and state-of-the-practice. Eng. Struct. 2002, 24, 243–259. [Google Scholar] [CrossRef]
- Alhasan, A.A.; Vafaei, M.; Alih, S.C. Viscoelastic dampers for protection of structures against seismic actions. Innov. Infrastruct. Solut. 2022, 7, 309. [Google Scholar] [CrossRef]
- Jaisee, S.; Yue, F.; Ooi, Y.H. A state-of-the-art review on passive friction dampers and their applications. Eng. Struct. 2021, 235, 112022. [Google Scholar] [CrossRef]
- Ma, R.; Bi, K.; Hao, H. Inerter-based structural vibration control: A state-of-the-art review. Eng. Struct. 2021, 243, 112655. [Google Scholar] [CrossRef]
- Wagg, D.J. A review of the mechanical inerter: Historical context, physical realisations and nonlinear applications. Nonlinear Dyn. 2021, 104, 13–34. [Google Scholar] [CrossRef]
- Christopoulos, C.; Filiatrault, A. Principles of Passive Supplemental Damping and Seismic Isolation; IUSS Press: Pavia, Italy, 2006. [Google Scholar]
- Soong, T.T.; Dargush, G.F. Passive Energy Dissipation Systems in Structural Engineering; John Wiley: Chichester, UK; New York, NY, USA, 1997. [Google Scholar]
- De Domenico, D.; Ricciardi, G.; Takewaki, I. Design strategies of viscous dampers for seismic protection of building structures: A review. Soil Dyn. Earthq. Eng. 2019, 118, 144–165. [Google Scholar] [CrossRef]
- Xu, Z.D.; Wang, D.X.; Shi, C.F. Model, tests and application design for viscoelastic dampers. J. Vib. Control 2010, 17, 1359–1370. [Google Scholar] [CrossRef]
- Choo, J.F.; Koh, H.M.; Kang, S.C.; Kim, B.S. Vibration control of long-span high-speed railway bridges under periodic moving loading using viscoelastic dampers. In Structures for High-Speed Railway Transportation; International Association for Bridge and Structural Engineering: Antwerp, Belgium, 2003. [Google Scholar]
- Moliner, E.; Museros, P.; Martinez-Rodrigo, M.D. Retrofit of existing railway bridges of short to medium spans for high-speed traffic using viscoelastic dampers. Eng. Struct. 2012, 40, 519–528. [Google Scholar] [CrossRef]
- Cortés, F.; Martinez, M.; Elejabarrieta, M.J. Viscoelastic Surface Treatments for Passive Control of Structural Vibration; Nova Publishers: New York, NY, USA, 2012. [Google Scholar]
- Sandeep, S.H.; Srinivasa, C.V. Hybrid sandwich panels: A review. Int. J. Appl. Mech. Eng. 2020, 25, 64–85. [Google Scholar] [CrossRef]
- Lewandowski, R.; Słowik, M.; Przychodzki, M. Parameters identification of fractional models of viscoelastic dampers and fluids. Struc. Eng. Mech. 2017, 63, 181–193. [Google Scholar] [CrossRef]
- Eshaghi, M.; Sedaghati, R.; Rakheja, S. Dynamic characteristics and control of magnetorheological/electrorheological sandwich structures: A state-of-the-art review. J. Intell. Mater. Syst. Struct. 2016, 27, 2003–2037. [Google Scholar] [CrossRef]
- Osial, M.; Pregowska, A.; Warczak, M.; Giersig, M. Magnetorheological fluids: A concise review of composition, physicochemical properties, and models. J. Intell. Mater. Syst. Struct. 2023, 34, 1045389X231157357. [Google Scholar] [CrossRef]
- Jones, D.I.G. Handbook of Viscoelastic Vibration Damping; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Shu, Z.; You, R.; Zhou, Y. Viscoelastic materials for structural dampers: A review. Constr. Build. Mater. 2022, 342, 127955. [Google Scholar] [CrossRef]
- Shu, Z.; Ning, B.; Li, S.; Li, Z.; Gan, Z.; Xie, Y. Experimental and numerical investigations of replaceable moment-resisting viscoelastic damper for steel frames. J. Constr. Steel Res. 2020, 170, 106100. [Google Scholar] [CrossRef]
- De Cazenove, J.; Rade, D.A.; de Lima, A.M.G.; Araujo, C.A. A numerical and experimental investigation on self-heating effects in viscoelastic dampers. Mech. Sys. Sig. Proc. 2012, 27, 433–445. [Google Scholar] [CrossRef]
- Chakraborty, B.C.; Ratna, D. Polymers for Vibration Damping Applications; Elsevier: Cambridge, MA, USA, 2020. [Google Scholar]
- Shedbale, N.; Muley, P.V. Review on Viscoelastic Materials used in Viscoelastic Dampers. Int. Res. J. Eng. Technol. 2017, 4, 7. [Google Scholar]
- Chen, Y.; Chen, C.; Ma, Q.; Jang, H.; Wan, Z. Study on mechanical properties of high damping viscoelastic dampers. Adv. Struct. Eng. 2019, 22, 2925–2936. [Google Scholar] [CrossRef]
- Wu, C.; Otani, Y.; Namiki, N.; Emi, H.; Nitta, K. Phase modification of acrylate rubber/chlorinated polypropylene blends by a hindered phenol compound. J. Polym. 2001, 33, 322–329. [Google Scholar] [CrossRef]
- Xu, Z.D.; Liao, Y.X.; Ge, T.; Xu, C. Experimental and theoretical study on viscoelastic dampers with different matrix rubbers. J. Eng. Mech. 2016, 142, 04016051. [Google Scholar] [CrossRef]
- Xu, Z.D.; Ge, T.; Liu, J. Experimental and theoretical study of high-energy dissipation-viscoelastic dampers based on acrylate-rubber matrix. J. Eng. Mech. 2020, 146, 04020057. [Google Scholar] [CrossRef]
- Xu, Z.D.; Yang, Y.; Zhu, Y.N.; Ge, T. Experimental study and mathematical modeling of viscoelastic dampers with wider temperature range based on blended rubber matrix. J. Build. Eng. 2023, 70, 106414. [Google Scholar] [CrossRef]
- Ge, T.; Xu, Z.D.; Yuan, F.G. Development of viscoelastic damper based on NBR and organic small-molecule composites. J. Mater. Civ. Eng. 2022, 34, 04022192. [Google Scholar] [CrossRef]
- Ge, T.; Xu, Z.D.; Yuan, F.G. Predictive model of dynamic mechanical properties of VE damper based on acrylic rubber–graphene oxide composites considering aging damage. J. Aero. Eng. 2022, 35, 04021132. [Google Scholar] [CrossRef]
- Xu, Y.S.; Xu, Z.D.; Guo, Y.Q.; Ge, T.; Xu, C.; Huang, X. Theoretical and experimental study of viscoelastic damper based on fractional derivative approach and micromolecular structures. J. Vib. Acoust. 2019, 141, 031010. [Google Scholar] [CrossRef]
- Teh, T.W.; Tan, C.G.; Jumaat, M.Z. Feasibility evaluation of novel high-damping rubbers as energy-dissipation material under axial dynamic load for damper devices. Buildings 2022, 12, 1917. [Google Scholar] [CrossRef]
- He, Z.; Shi, F.; Lin, Z.; Zhang, C.; Zhou, Y.; Zhao, F. Experimental characterization on cyclic stability behavior of a high-damping viscoelastic damper. Constr. Build. Mater. 2023, 371, 130749. [Google Scholar] [CrossRef]
- Nakamura, Y.; Hanzawa, T.; Nomura, T.; Takada, T. Performance-based placement of manufactured viscoelastic dampers for design response spectrum. Front. Built Environ. 2016, 2, 10. [Google Scholar] [CrossRef]
- Shitikova, M.V.; Krusser, A.I. Models of viscoelastic materials: A review on historical development and formulation. In Theoretical Analyses, Computations, and Experiments of Multiscale Materials; Giorgio, I., Placidi, L., Barchiesi, E., Abali, B.E., Altenbach, H., Eds.; Springer: Cham, Switzerland, 2022; Volume 175. [Google Scholar] [CrossRef]
- Genovese, A.; Carputo, F.; Maiorano, A.; Timpone, F.; Farroni, F.; Sakhnevych, A. Study on the generalized formulations with the aim to reproduce the viscoelastic dynamic behavior of polymers. Appl. Sci. 2020, 10, 2321. [Google Scholar] [CrossRef]
- Vasques, C.M.A.; Moreira, R.A.S.; Rodrigues, J.D. Viscoelastic damping Technologies—Part I: Modeling and finite element implementation. J. Adv. Res. Mech. Eng. 2010, 1, 76–95. [Google Scholar]
- Bland, D.R. The Theory of Linear Viscoelasticity; Pergamon Press: Oxford, UK, 1960. [Google Scholar]
- Tschoegl, N.W. Representation of Linear Viscoelastic Behavior by Series-Parallel Models. In The Phenomenological Theory of Linear Viscoelastic Behavior; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar] [CrossRef]
- Steinmann, P.; Runesson, K. The Catalogue of Computational Material Models: Basic Geometrically Linear Models in 1D; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Lin, C.-Y. Rethinking and researching the physical meaning of the standard linear solid model in viscoelasticity. Mech. Adv. Mater. Struct. 2023, 1–16, in print. [Google Scholar] [CrossRef]
- Park, S.W. Analytical modeling of viscoelastic dampers for structural and vibration control. Int. J. Solids Struct. 2001, 38, 8065–8092. [Google Scholar] [CrossRef]
- Burgers, J.M. First and Second Report on Viscosity and Plasticity; Academy of Sciences at Amsterdam: Amsterdam, NY, USA, 1935. [Google Scholar]
- Zener, C. Elasticity and Anelasticity of Metals; University of Chicago Press: Chicago, IL, USA, 1948. [Google Scholar]
- Huang, C.; Gao, D.; Meng, T.; Yang, C. Investigation into Viscoelastic Properties of Fiber-Reinforced Asphalt Composite Concrete Based on the Burgers Model. Buildings 2023, 13, 449. [Google Scholar] [CrossRef]
- Renaud, F.; Dion, J.L.; Chevallier, G.; Tawfiq, I.; Lemaire, R. A new identification method of viscoelastic behavior: Application to the generalized Maxwell model. Mech. Syst. Signal Process. 2011, 25, 991–1010. [Google Scholar] [CrossRef]
- Lewandowski, R.; Bartkowiak, A.; Maciejewski, H. Dynamic analysis of frames with viscoelastic dampers: A comparison of damper models. Struct. Eng. Mech. 2012, 41, 113–137. [Google Scholar] [CrossRef]
- Ottosen, N.; Ristinmaa, M. The Mechanics of Constitutive Modeling; Elsevier: Amsterdam, NY, USA, 2005. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. Fractional calculus—A different approach to the analysis of viscoelastically damped materials. AIAA J. 1983, 21, 741–748. [Google Scholar] [CrossRef]
- Rossikhin, Y.A.; Shitikova, M.V. A new method for solving dynamic problems of fractional derivative viscoelasticity. Int. J. Eng. Sci. 2001, 39, 149–176. [Google Scholar] [CrossRef]
- Pritz, T. Five-parameter fractional derivative model for polymeric damping materials. J. Sound Vib. 2003, 265, 935–952. [Google Scholar] [CrossRef]
- Lewandowski, R.; Chorążyczewski, B. Identification of the parameters of the Kelvin–Voigt and the Maxwell fractional models, used to modeling of viscoelastic dampers. Comp. Struct. 2010, 88, 1–17. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose is almost frequency independent-II. Geophys. J. R. Astron. Soc. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Lewandowski, R.; Przychodzki, M. Approximate method for temperature-dependent characteristics of structures with viscoelastic dampers. Arch. Appl. Mech. 2018, 88, 1695–1711. [Google Scholar] [CrossRef]
- Xu, Y.; He, Q.; Guo, Y.-Q.; Huang, X.-H.; Dong, Y.-R.; Hu, Z.-W.; Kim, J. Experimental and theoretical investigation of viscoelastic damper by applying fractional derivative method and internal variable theory. Buildings 2023, 13, 239. [Google Scholar] [CrossRef]
- Tang, S.; Greene, M.S.; Liu, W.K. Two-scale mechanism-based theory of nonlinear viscoelasticity. J. Mech. Phys. Solids 2012, 60, 199–226. [Google Scholar] [CrossRef]
- Vasile, O.; Bugaru, M. A New Modeling Approach for Viscous Dampers Using an Extended Kelvin–Voigt Rheological Model Based on the Identification of the Constitutive Law’s Parameters. Computation 2023, 11, 3. [Google Scholar] [CrossRef]
- Ghobadi, E.; Shutov, A.; Steeb, H. Parameter Identification and Validation of Shape-Memory Polymers within the Framework of Finite Strain Viscoelasticity. Materials 2021, 14, 2049. [Google Scholar] [CrossRef]
- Zhang, L.H.; Yao, X.H.; Zang, S.G.; Han, Q. Temperature and strain rate dependent tensile behavior of a transparent polyurethane interlayer. Mater. Des. 2015, 65, 1181–1188. [Google Scholar] [CrossRef]
- Martinez-Agirre, M.; Illescas, S.; Elejabarrieta, M.J. Characterisation and modelling of prestrained viscoelastic films. Int. J. Adhes. Adhes. 2014, 50, 183–190. [Google Scholar] [CrossRef]
- Chen, T. Determining a Prony Series for a Viscoelastic Material from Time Varying Strain Data; Technical Report; NASA: Washington, DC, USA, 2000. [Google Scholar]
- Rothermel, R.; Panfilenko, W.; Sharma, P.; Wald, A.; Schuster, T.; Jung, A.; Diebels, S. A method for determining the parameters in a rheological model for viscoelastic materials by minimizing Tikhonov functionals. Appl. Math. Sci. Eng. 2022, 30, 141–165. [Google Scholar] [CrossRef]
- Najib, M.F.; Nobari, A.S.; Nikbin, K. Modification and evaluation of a FRF-based model updating method for identification of viscoelastic constitutive models for a nonlinear polyurethane adhesive in a bonded joint. Int. J. Adhes. Adhes. 2017, 74, 181–193. [Google Scholar] [CrossRef]
- Pawlak, Z.M.; Denisiewicz, A. Identification of the fractional Zener model parameters for a viscoelastic material over a wide range of frequencies and temperatures. Materials 2021, 14, 7024. [Google Scholar] [CrossRef]
- Vasques, C.M.A.; Moreira, R.A.S.; Rodrigues, J. Viscoelastic damping technologies—Part II: Experimental identification procedure and validation. J. Adv. Res. Mech. Eng. 2010, 1, 96–110. [Google Scholar]
- Gerlach, S.; Matzenmiller, A. Comparison of numerical methods for identification of viscoelastic line spectra from static test data. Int. J. Numer. Meth. Eng. 2005, 63, 428–454. [Google Scholar] [CrossRef]
- Marino, E.; Flaschel, M.; Kumar, S.; de Lorenzis, L. Automated identification of linear viscoelastic constitutive laws with EUCLID. arXiv 2022, arXiv:2212.10969. [Google Scholar] [CrossRef]
- Najib, M.F.; Nobari, A.S. Nonlinear viscoelastic constitutive model identification for a polyurethane adhesive in a bonded joint using structural dynamic model updating. Mech. Mater. 2016, 100, 72–85. [Google Scholar] [CrossRef]
- Kim, S.-Y.; Lee, D. Identification of fractional-derivative-model parameters of viscoelastic materials from measured FRFs. J. Sound Vib. 2009, 324, 570–586. [Google Scholar] [CrossRef]
- Naraghi, T.; Nobari, A.S. Identification of the dynamic characteristics of a viscoelastic, nonlinear adhesive joint. J. Sound Vib. 2015, 352, 92–102. [Google Scholar] [CrossRef]
- Sun, W.; Wang, Z.; Liu, R.; Yan, X. Inverse Identification of the frequency-dependent mechanical parameters of a viscoelastic core layer based on the vibration response. Appl. Sci. 2017, 7, 455. [Google Scholar] [CrossRef]
- Sun, W.; Wang, Z.; Yan, X.; Zhu, M. Inverse identification of the frequency-dependent mechanical parameters of viscoelastic materials based on the measured FRFs. Mech. Syst. Signal Process. 2018, 98, 816–833. [Google Scholar] [CrossRef]
- Mehrez, L.; Kassem, E.; Masad, E.; Little, D. Stochastic Identification of Linear-Viscoelastic Models of Aged and Unaged Asphalt Mixtures. J. Mater. Civ. Eng. 2015, 27, 04014149. [Google Scholar] [CrossRef]
- Xiao, Z.; Haitian, Y.; Yiqian, H. Identification of constitutive parameters for fractional viscoelasticity. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 311–322. [Google Scholar] [CrossRef]
- Deng, R.; Davies, P.; Bajaj, A.K. Flexible polyurethane foam modelling and identification of viscoelastic parameters for automotive seating applications. J. Vib. Acoust. 2003, 262, 391–417. [Google Scholar] [CrossRef]
- Sessa, S.; Vaiana, N.; Paradiso, M.; Rosati, L. An inverse identification strategy for the mechanical parameters of a phenomenological hysteretic constitutive model. Mech. Syst. Signal Process. 2020, 139, 106622. [Google Scholar] [CrossRef]
- Grosso, P.; de Felice, A.; Sorrentino, S. A method for the experimental identification of equivalent viscoelastic models from vibration of thin plates. Mech. Syst. Signal Process. 2021, 153, 107527. [Google Scholar] [CrossRef]
- Lewandowski, R.; Chorążyczewski, B.; Wasilewicz, P. Evaluation of parameters of viscous fluid and viscoelastic dampers. Vib. Phys. Syst. 2006, 22, 223–228. [Google Scholar]
- Vaiana, N.; Sessa, S.; Marmo, F.; Rosati, L. An accurate and computationally efficient uniaxial phenomenological model for steel and fiber reinforced elastomeric bearings. Compos. Struct. 2019, 211, 196–212. [Google Scholar] [CrossRef]
- Galadima, Y.K.; Oterkus, S.; Oterkus, E.; Amin, I.; El-Aassar, A.-H.; Shawky, H. A nonlocal method to compute effective properties of viscoelastic composite materials based on peridynamic computational homogenization theory. Compos. Struct. 2023, 319, 117147. [Google Scholar] [CrossRef]
- Makris, N.; Roussos, Y.; Whittaker, A.S.; Kelly, J.M. Viscous heating of fluid dampers, II: Large-amplitude motions. J. Eng. Mech. 1998, 124, 1217–1223. [Google Scholar] [CrossRef]
- Kasai, K.; Sato, D. A constitutive rule for viscoelastic material considering heat conduction and heat transfer. In Proceedings of the Second International Conference on Urban Earthquake Engineering, Tokyo, Japan, 7–8 March 2005; pp. 459–466. [Google Scholar]
- Guo, J.W.; Daniel, Y.; Montgomery, M.; Christopoulos, C. Thermal-mechanical model for predicting the wind and seismic response of viscoelastic dampers. J. Eng. Mech. 2016, 142, 04016067. [Google Scholar] [CrossRef]
- Black, C.J.; Makris, N. Viscous heating of fluid dampers under small and large amplitude motions: Experimental studies and parametric modeling. J. Eng. Mech. 2007, 133, 566–577. [Google Scholar] [CrossRef]
- De Lima, A.M.G.; Rade, D.A.; Bouhaddi, N. Stochastic modeling of surface viscoelastic treatments combined with model condensation procedures. Shock Vib. 2010, 17, 429–444. [Google Scholar] [CrossRef]
- De Lima, A.M.G.; Rade, D.A.; Lepore-Neto, F.P. An efficient modeling methodology of structural systems containing viscoelastic dampers based on frequency response function substructuring. Mech. Syst. Sig. Process. 2009, 23, 1272–1281. [Google Scholar] [CrossRef]
- Brinson, H.F.; Brinson, L.C. Polymer Engineering Science and Viscoelasticity: An Introduction; Springer: New York, NY, USA, 2008. [Google Scholar]
- Shaw, M.T. Introduction to Polymer Rheology; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- De Lima, A.M.G.; Stoppa, M.H.; Rade, D.A.; Steffen, V., Jr. Sensitivity analysis of viscoelastic structures. Shock Vib. 2006, 13, 545–558. [Google Scholar] [CrossRef]
- Moreira, R.A.S.; Corte-Real, J.D.; Dias Rodrigues, J. A generalized frequency-temperature viscoelastic Model. Shock Vib. 2010, 17, 407–418. [Google Scholar] [CrossRef]
- Cardone, D.; Gesualdi, G.; Nigro, D. Effects of air temperature on the cyclic behavior of elastomeric seismic isolators. Bull. Earthq. Eng. 2011, 9, 1227–1255. [Google Scholar] [CrossRef]
- Park, H.-I.; Min, C.-H. Temperature effect on vibration characteristics of viscoelastic laminated beam. Int. J. Offshore Polar Eng. 2010, 20, 118–124. [Google Scholar]
- Tsai, C.S. Temperature effect of viscoelastic dampers during earthquakes. J. Struct. Eng. 1994, 120, 394–409. [Google Scholar] [CrossRef]
- Chang, K.C.; Soong, T.T.; Oh, S.-T.; Lai, M.L. Seismic behavior of steel frame with added viscoelastic dampers. J. Struct. Eng. 1995, 121, 1418–1426. [Google Scholar] [CrossRef]
- De Lima, A.M.G.; Rade, D.A.; Lacerda, H.B.; Araújo, C.A. An investigation of the self-heating phenomenon in viscoelastic materials subjected to cyclic loadings accounting for prestress. Mech. Syst. Sig. Process 2015, 58–59, 115–127. [Google Scholar] [CrossRef]
- Cunha-Filho, A.G.; de Lima, A.M.G.; Donadon, M.V.; Leao, L.S. Flutter suppression of plates using passive constrained viscoelastic layers. Mech. Syst. Sig. Process. 2016, 79, 99–111. [Google Scholar] [CrossRef]
- Diani, J.; Gilormini, P.; Frédy, C.; Rousseau, I. Predicting thermal shape memory of crosslinked polymer networks from linear viscoelasticity. Int. J. Solids Struct. 2012, 49, 793–799. [Google Scholar] [CrossRef]
- Arikoglu, A. A new fractional derivative model for linearly viscoelastic materials and parameter identification via genetic algorithms. Rheol. Acta 2014, 53, 219–233. [Google Scholar] [CrossRef]
- Xu, Z.-D.; Xu, C.; Hu, J. Equivalent fractional Kelvin model and experimental study on viscoelastic damper. J. Vib. Control 2015, 21, 2536–2552. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, Z.-D.; Guo, Y.-Q.; Huang, X.; Dong, Y.; Li, Q. Dynamic properties and energy dissipation study of sandwich viscoelastic damper considering temperature influence. Buildings 2021, 11, 470. [Google Scholar] [CrossRef]
- Lakes, R.S. Viscoelastic Materials; Cambridge University Press: London, UK, 2009. [Google Scholar]
- Xu, Y.; Xu, Z.-D.; Guo, Y.-Q.; Huang, X.; Zhang, Z.; Sun, B.; Kim, J. Thermodynamic behaviors of a viscoelastic plate for vibration control with nonlocal effect and temperature-dependent properties when subjected to a moving heat source. J. Eng. Mech. 2022, 148, 04022022. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, Z.-D.; Guo, Y.-Q.; Sarwar, W.; She, W.; Geng, Z.-F. Study on viscoelastic materials at micro scale pondering supramolecular interaction impacts with DMA tests and fractional derivative modelling. J. Appl. Polym. Sci. 2023, 140, e53660. [Google Scholar] [CrossRef]
- Drake, M.L.; Soovere, J. A Design Guide for Damping of Aerospace Structures. In Proceedings of the Vibration Damping Workshop, Long Beach, CA, USA, 27–29 February 1984; Air Force Wright Aeronautical Laboratories, Wright-Patterson Air Force Base: Greene County, OH, USA, 1984. AFWAL-TR-84-3064. pp. VV-1–VV-10. [Google Scholar]
- Sheoran, S.S.; Kalkal, K.K.; Deswal, S. Fractional order thermo-viscoelastic problem with temperature dependent modulus of elasticity. Mech. Adv. Mater. Struct. 2016, 23, 407–414. [Google Scholar] [CrossRef]
- Wei, K.; Yang, Q.; Dou, Y.; Wang, F.; Wang, P. Experimental investigation into temperature- and frequency-dependent dynamic properties of high-speed rail pads. Constr. Build. Mater. 2017, 151, 848–858. [Google Scholar] [CrossRef]
- Pettermann, H.E.; de Simone, A. An anisotropic linear thermo-viscoelastic constitutive law. Elastic relaxation and thermal expansion creep in the time domain. Mech. Time-Depend. Mater. 2018, 22, 421–433. [Google Scholar] [CrossRef]
- Ghaemmaghami, A.R.; Kwon, O.-S. Nonlinear modeling of MDOF structures equipped with viscoelastic dampers with strain, temperature and frequency-dependent properties. Eng. Struct. 2018, 168, 903–914. [Google Scholar] [CrossRef]
- Nakamura, N. Improved methods to transfer frequency-dependent complex stiffness to time domain. Earthq. Eng. Struct. Dyn. 2006, 35, 1037–1050. [Google Scholar] [CrossRef]
- Li, Z.L.; Qin, Y.; Sun, B.; Jia, C.L.; Zhang, W.J.; Yan, B.J.; Shi, Q.L. A fractional approach to the time-temperature dependence of dynamic viscoelastic behaviour. J. Mech. Sci. Technol. 2019, 33, 139–147. [Google Scholar] [CrossRef]
- Litewka, P.; Lewandowski, R. Dynamic characteristics of viscoelastic Mindlin plates with influence of temperature. Comput. Struct. 2020, 229, 106181. [Google Scholar] [CrossRef]
- Litewka, P.; Lewandowski, R. Temperature influence on non-linear harmonic vibrations of plates made of viscoelastic materials. Eng. Trans. 2020, 68, 159–176. [Google Scholar]
- Dai, J.; Xu, Z.-D.; Gai, P.-P.; Yan, X. Seismic performance of viscoelastically damped structures at different ambient temperatures. J. Vib. Control 2021, 27, 2819–2834. [Google Scholar] [CrossRef]
- Dai, J.; Gai, P.-P.; Xu, Z.-D.; Chen, Z.Q. A reduced-order improved rational polynomial method for viscoelastically damped structures considering ambient temperature effect. Soil Dyn. Earthq. Eng. 2022, 159, 107315. [Google Scholar] [CrossRef]
- Lewandowski, R. Influence of temperature on the dynamic characteristics of structures with viscoelastic dampers. J. Struct. Eng. 2019, 145, 04018245. [Google Scholar] [CrossRef]
- Zhang, H.; Li, S.; Zhang, Z.; Luo, H.; Wang, Y. A five-parameter fractional derivative temperature spectrum model for polymeric damping materials. Polym. Test. 2020, 89, 106654. [Google Scholar] [CrossRef]
- Cupiał, P.; Nizioł, J. Vibration and damping analysis of three-layered composite plate with a viscoelastic mid-layer. J. Sound Vib. 1995, 183, 99–114. [Google Scholar] [CrossRef]
- Sainsbury, M.G.; Zhang, Q.J. The Galerkin element method, applied to the vibration of damped sandwich beams. Comput. Struct. 1999, 71, 239–256. [Google Scholar] [CrossRef]
- Duigou, L.; Daya, E.M.; Potier-Ferry, M. Iterative algorithms for non-linear eigenvalue problems. Application to vibrations of viscoelastic shells. Comput. Methods Appl. Mech. Eng. 2003, 192, 1323–1335. [Google Scholar] [CrossRef]
- Moreira, R.A.S.; Rodrigues, J.D. A layerwise model for thin soft core sandwich plates. Comput. Struct. 2006, 84, 1256–1263. [Google Scholar] [CrossRef]
- Galucio, A.C.; Deü, J.-F.; Ohayon, R. Finite element formulation of viscoelastic sandwich beams using fractional derivative operators. Comput. Mech. 2004, 33, 282–291. [Google Scholar] [CrossRef]
- Banerjee, J.R.; Sobey, A.J. Dynamic stiffness formulation and free vibration analysis of a three-layered sandwich beam. Int. J. Solids Struct. 2005, 42, 2181–2197. [Google Scholar] [CrossRef]
- Cortés, F.; Elejabarrieta, M.J. Homogenised finite element for transient dynamic analysis of unconstrained layer damping beams involving fractional derivative models. Comput. Mech. 2007, 40, 313–324. [Google Scholar] [CrossRef]
- Backstrom, D.; Nilsson, A.C. Modeling the vibration of sandwich beams using frequency-dependent parameters. J. Sound Vib. 2007, 300, 589–611. [Google Scholar] [CrossRef]
- Barbosa, F.S.; Farage, M.C.R. A finite element model for sandwich viscoelastic beams: Experimental and numerical assessment. J. Sound Vib. 2008, 317, 91–111. [Google Scholar] [CrossRef]
- Hu, H.; Belouettar, S.; Potier-Ferry, M.; Daya, E.M. Review and assessment of various theories for modeling sandwich composites. Compos. Struct. 2008, 84, 282–292. [Google Scholar] [CrossRef]
- Carrera, E. Historical review of Zig-Zag theories for multilayered plates and shells. Appl. Mech. Rev. ASME 2003, 56, 287–308. [Google Scholar] [CrossRef]
- Kiasat, S.; Filippi, M.; Nobari, A.S.; Carrera, E. Layer-wise dynamic analysis of a beam with global and local viscoelastic contributions using an FE/Laplace transform approach. Acta Mech. 2022, 233, 4747–4761. [Google Scholar] [CrossRef]
- D’Ottavio, M.; Krasnobrizha, A.; Valot, E.; Polit, O.; Vescovini, R.; Dozio, L. Dynamic response of viscoelastic multiple-core sandwich structures. J. Sound Vib. 2021, 491, 115753. [Google Scholar] [CrossRef]
- Plagianakos, T.S.; Saravanos, D.A. High-order layerwise finite element for the damped free-vibration response of thick composite and sandwich composite plates. Int. J. Numer. Methods Eng. 2009, 77, 1593–1626. [Google Scholar] [CrossRef]
- Alvelid, M. Sixth order differential equation for sandwich beam deflection including transverse shear. Compos. Struct. 2013, 102, 29–37. [Google Scholar] [CrossRef]
- Won, S.G.; Bae, S.H.; Cho, J.R.; Bae, S.R.; Jeong, W.B. Three-layered damped element for forced vibration analysis of symmetric sandwich structures with a viscoelastic core. Finite Elem. Anal. Des. 2013, 68, 39–51. [Google Scholar] [CrossRef]
- Wang, Y.; Inman, D.J. Finite element analysis and experimental study on dynamic properties of a composite beam with viscoelastic damping. J. Sound Vib. 2013, 332, 6177–6191. [Google Scholar] [CrossRef]
- Akoussan, K.; Boudaoud, H.; Daya, E.M.; Carrera, E. Vibration Modeling of Multilayer Composite Structures with Viscoelastic Layers. Mech. Adv. Mater. Struct. 2015, 22, 136–149. [Google Scholar] [CrossRef]
- Zamani, H.A.; Aghdam, M.M.; Sadighi, M. Free vibration analysis of thick viscoelastic composite plates on visco-Pasternak foundation using higher-order theory. Compos. Struct. 2017, 182, 25–35. [Google Scholar] [CrossRef]
- Naji, J.; Zabihollah, A.; Behzad, M. Vibration characteristics of laminated composite beams with magnetorheological layer using layerwise theory. Mech. Adv. Mater. Struct. 2018, 25, 202–211. [Google Scholar] [CrossRef]
- Zarraga, O.; Sarría, I.; García-Barruetabeña, J.; Cortés, F. Dynamic analysis of plates with thick unconstrained layer damping. Eng. Struct. 2019, 201, 109809. [Google Scholar] [CrossRef]
- Zarraga, O.; Sarría, I.; García-Barruetabeña, J.; Elejabarrieta, M.J.; Cortés, F. General homogenised formulation for thick viscoelastic layered structures for finite element applications. Mathematics 2020, 8, 714. [Google Scholar] [CrossRef]
- Alavi, S.H.; Eipakchi, H. An analytical approach for free vibrations analysis of viscoelastic circular and annular plates using FSDT. Mech. Adv. Mater. Struct. 2020, 27, 250–264. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, X.; Wu, N.; Chu, F.; Luo, D. The finite element modeling and experimental study of sandwich plates with frequency-dependent viscoelastic material model. Materials 2020, 13, 2296. [Google Scholar] [CrossRef]
- Lewandowski, R.; Litewka, P.; Wielentejczyk, P. Free vibrations of laminate plates with viscoelastic layers using the refined zig-zag theory. Part 1 Theoretical background. Compos. Struct. 2021, 278, 114547. [Google Scholar] [CrossRef]
- Lewandowski, R.; Litewka, P.; Wielentejczyk, P. Dynamic characteristics of multi-layered viscoelastic beams using the refined zig-zag theory. Composite Struct. 2021, 259, 113212. [Google Scholar] [CrossRef]
- Tessler, A.; di Sciuva, M.; Gherlone, M. A refined zigzag beam theory for composite and sandwich beams. J. Compos. Mater. 2009, 43, 1051–1081. [Google Scholar] [CrossRef]
- Tessler, A.; di Sciuva, M.; Gherlone, M. A consistent refinement of first-order shear-deformation theory for laminated composite and sandwich plates using improved zigzag kinematics. J. Mech. Mater. Struct. 2010, 5, 341–367. [Google Scholar] [CrossRef]
- Ren, S.; Zhao, G.; Zhang, S. A layerwise finite element formulation for vibration and damping analysis of sandwich plate with moderately thick viscoelastic core. Mech. Adv. Mater. Struct. 2020, 27, 1201–1212. [Google Scholar] [CrossRef]
- Rouzegar, J.; Vazirzadeh, M.; Heydari, M.H. A fractional viscoelastic model for vibrational analysis of thin plate excited by supports movement. Mech. Res. Commun. 2020, 110, 103618. [Google Scholar] [CrossRef]
- Dang, R.; Cui, Y.; Qu, J.; Yang, A.; Chen, Y. Variable fractional modeling and vibration analysis of variable-thickness viscoelastic circular plate. Appl. Math. Modell. 2022, 110, 767–778. [Google Scholar] [CrossRef]
- Zenkour, A.M.; El-Shahrany, H.D. Vibration of viscoelastic magnetostrictive plates embedded in viscoelastic foundations in hygrothermal environments. Acta Mech. Sin. 2023, 39, 522305. [Google Scholar] [CrossRef]
- Huang, W.; Ren, J.; Forooghi, A. Vibrational frequencies of FG-GPLRC viscoelastic rectangular plate subjected to different temperature loadings based on higher-order shear deformation theory and utilizing GDQ procedure. Mech. Based Des. Struct. Mach. 2023, 51, 1775–1800. [Google Scholar] [CrossRef]
- Xia, Z.Q.; Lukasiewicz, S. Nonlinear damped vibrations of simply-supported rectangular sandwich plates. Nonlinear Dyn. 1995, 8, 417–433. [Google Scholar] [CrossRef]
- Kim, T.-W.; Kim, J.-H. Nonlinear vibration of viscoelastic laminated composite plates. Int. J. Solids Struct. 2002, 39, 2857–2870. [Google Scholar] [CrossRef]
- Daya, E.M.; Azrar, L.; Potier-Ferry, M. An amplitude equation for the non-linear vibration of viscoelastically damped sandwich beams. J. Sound Vib. 2004, 271, 789–813. [Google Scholar] [CrossRef]
- Mahmoodi, S.N.; Khadem, S.E.; Kokabi, M. Non-linear free vibrations of Kelvin-Voigt visco-elastic beams. Int. J. Mech. Sci. 2007, 49, 722–732. [Google Scholar] [CrossRef]
- Jacques, N.; Daya, E.M.; Potier-Ferry, M. Nonlinear vibration of viscoelastic sandwich beams by the harmonic balance and finite element methods. J. Sound Vib. 2010, 329, 4251–4265. [Google Scholar] [CrossRef]
- Bilasse, M.; Daya, E.M.; Azrar, L. Linear and nonlinear vibrations analysis of viscoelastic sandwich beams. J. Sound Vib. 2010, 329, 4950–4969. [Google Scholar] [CrossRef]
- Bilasse, M.; Azrar, L.; Daya, E.M. Complex modes based numerical analysis of viscoelastic sandwich plates vibrations. Comput. Struct. 2011, 89, 539–555. [Google Scholar] [CrossRef]
- Li, J.-J.; Cheng, C.-J. Differential quadrature method for analyzing nonlinear dynamic characteristics of viscoelastic plates with shear effects. Nonlinear Dyn. 2010, 61, 57–70. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Nonlinear forced dynamics of an axially moving viscoelastic beam with an internal resonance. Int. J. Mech. Sci. 2011, 53, 1022–1037. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Nonlinear dynamic response of a simply-supported Kelvin-Voigt viscoelastic beam, additionally supported by a nonlinear spring. Nonlinear Anal. Real World Appl. 2012, 13, 1319–1333. [Google Scholar] [CrossRef]
- Sarangi, S.K.; Ray, M.C. Active damping of geometrically nonlinear vibrations of laminated composite plates using vertically reinforced 1–3 piezoelectric composites. Acta Mech. 2011, 222, 363–380. [Google Scholar] [CrossRef]
- Kumar, R.S.; Ray, M.C. Active constrained layer damping of geometrically nonlinear vibrations of smart laminated composite sandwich plates using 1–3 piezoelectric composites. Int. J. Mech. Mater. Des. 2012, 8, 359–380. [Google Scholar] [CrossRef]
- Datta, P.; Ray, M.C. Three-dimensional fractional derivative model of smart constrained layer damping treatment for composite plates. Compos. Struct. 2016, 156, 291–306. [Google Scholar] [CrossRef]
- Kanasogi, R.M.; Ray, M.C. Control of geometrically nonlinear vibrations of skew laminated composite plates using skew or rectangular 1–3 piezoelectric patches. Int. J. Mech. Mater. Des. 2013, 9, 325–354. [Google Scholar] [CrossRef]
- Shivakumar, J.; Ashok, M.H.; Ray, M.C. Active control of geometrically nonlinear transient vibrations of laminated composite cylindrical panels using piezoelectric fiber reinforced composite. Acta Mech. 2013, 224, 1–15. [Google Scholar] [CrossRef]
- Kumar, A.M.S.; Panda, S.; Chakraborty, D. Piezo-viscoelastically damped nonlinear frequency response of functionally graded plates with a heated plate-surface. J. Vib. Control 2016, 22, 320–343. [Google Scholar]
- Kumar, R.S.; Ray, M.C. Smart damping of geometrically nonlinear vibrations of functionally graded sandwich plates using 1–3 piezoelectric composites. Mech. Adv. Mater. Struct. 2016, 23, 652–669. [Google Scholar] [CrossRef]
- Youzera, H.; Meftah, S.A.; Challamel, N.; Tounsi, A. Nonlinear damping and forced vibration analysis of laminated composite beams. Compos. Part B 2012, 43, 1147–1154. [Google Scholar] [CrossRef]
- Leung, A.Y.T.; Yang, H.X.; Zhu, P.; Guo, Z.J. Steady state response of fractionally damped nonlinear viscoelastic arches by residue harmonic homotopy. Comput. Struct. 2013, 121, 10–21. [Google Scholar] [CrossRef]
- Mahmoudkhani, S.; Haddadpour, H.; Navazi, H.M. The effects of nonlinearities on the vibration of viscoelastic sandwich plates. Int. J. Non-Linear Mech. 2014, 62, 41–57. [Google Scholar] [CrossRef]
- Lewandowski, R.; Baum, M. Dynamic characteristics of multilayered beams with viscoelastic layers described by the fractional Zener model. Arch. Appl. Mech. 2015, 85, 1793–1814. [Google Scholar] [CrossRef]
- Amabili, M. Nonlinear vibrations of viscoelastic rectangular plates. J. Sound Vib. 2016, 362, 142–156. [Google Scholar] [CrossRef]
- Litewka, P.; Lewandowski, R. Nonlinear harmonically excited vibrations of plates with Zener material. Nonlinear Dyn. 2017, 89, 691–712. [Google Scholar] [CrossRef]
- Litewka, P.; Lewandowski, R. Steady-state non-linear vibrations of plates using Zener material with fractional derivative. Comput. Mech. 2017, 60, 333–354. [Google Scholar] [CrossRef]
- Mokhtari, M.; Permoon, M.R.; Haddadpour, H. Aeroelastic analysis of sandwich cylinder with fractional viscoelastic core described by Zener model. J. Fluids Struct. 2019, 85, 1–16. [Google Scholar] [CrossRef]
- Shafei, E.; Faroughi, S.; Rabczuk, T. Nonlinear transient vibration of viscoelastic plates: A NURBS-based isogeometric HSDT approach. Comput. Math. Appl. 2021, 84, 1–15. [Google Scholar] [CrossRef]
- Younesian, D.; Hosseinkhani, A.; Askari, H.; ·Esmailzadeh, E. Elastic and viscoelastic foundations: A review on linear and nonlinear vibration modeling and applications. Nonlinear Dyn. 2019, 97, 853–895. [Google Scholar] [CrossRef]
- Sarparast, H.; Ebrahimi-Mamaghani, A.; Safarpour, M.; Ouakad, H.M.; Dimitri, R.; Tornabene, F. Nonlocal study of the vibration and stability response of small-scale axially moving supported beams on viscoelastic-Pasternak foundation in a hygro-thermal environment. Math. Meth. Appl. Sci. 2020, 1–12, early view. [Google Scholar] [CrossRef]
- Amir, S.; Arshid, E.; Maraghi, Z.K. Free vibration analysis of magneto-rheological smart annular three-layered plates subjected to magnetic field in viscoelastic medium. Smart Struct. Syst. 2020, 25, 581–592. [Google Scholar] [CrossRef]
- Keshtegar, B.; Motezaker, M.; Kolahchi, R.; Trung, N.-T. Wave propagation and vibration responses in porous smart nanocomposite sandwich beam resting on Kerr foundation considering structural damping. Thin Wall. Struct. 2020, 154, 106820. [Google Scholar] [CrossRef]
- Patil, M.A.; Kadoli, R. Influence of Winkler and viscoelastic foundation on free vibration of functionally graded beam integrated with Terfenol-D layer. J. Braz. Soc. Mech. Sci. 2020, 42, 591. [Google Scholar] [CrossRef]
- Ghabussi, A.; Ashrafi, N.; Shavalipour, A.; Hosseinpour, A.; Habibi, M.; Moayedi, H.; Babaei, B.; Safarpour, H. Free vibration analysis of an electro-elastic GPLRC cylindrical shell surrounded by viscoelastic foundation using modified length-couple stress parameter. Mech. Based Des. Struct. Mach. 2021, 49, 738–762. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, M.; Wang, Z.; Lei, Y. Thermo-electro-mechanical vibration of piezoelectric nanobeams resting on a viscoelastic foundation. J. Phys. Conf. Ser. 2021, 1759, 012029. [Google Scholar] [CrossRef]
- Kargar, J.; Arani, A.G.; Arshid, E.; Rahaghi, M.I. Vibration analysis of spherical sandwich panels with MR fluids core and magneto-electro-elastic face sheets resting on orthotropic viscoelastic foundation. Struct. Eng. Mech. 2021, 78, 557–572. [Google Scholar] [CrossRef]
- Li, H.; Gao, Z.; Zhao, J.; Ma, H.; Han, Q.; Liu, J. Vibration suppression effect of porous graphene platelet coating on fiber reinforced polymer composite plate with viscoelastic damping boundary conditions resting on viscoelastic foundation. Eng. Struct. 2021, 237, 112167. [Google Scholar] [CrossRef]
- Souad, H.; Ismail, M.; Hichem, A.; Noureddine, E. Vibration analysis of viscoelastic FGM nanoscale plate resting on viscoelastic medium using higher-order theory. Period. Polytech. Civ. Eng. 2021, 65, 255–275. [Google Scholar] [CrossRef]
- Praharaj, R.K.; Datta, N. Dynamic response of plates resting on a fractional viscoelastic foundation and subjected to a moving load. Mech. Based Des. Struct. Mach. 2022, 50, 2317–2332. [Google Scholar] [CrossRef]
- Bensaid, I.; Saimi, A. Dynamic investigation of functionally graded porous beams resting on viscoelastic foundation using generalised differential quadrature method. Aust. J. Mech. Eng. 2023, 21, 1440–1459. [Google Scholar] [CrossRef]
- Li, M.-L.; Wei, P.-J.; Zhou, X.-L. Wave propagation and free vibration of a Timoshenko beam mounted on the viscoelastic Pasternak foundation modelled by fraction-order derivatives. Mech. Time-Depend. Mat. 2022, 1–15. [Google Scholar] [CrossRef]
- Ghali, D.; Ismail, M.; Hichem, A.; Noureddine, E.; Belaid, M. Investigating the free vibration of viscoelastic FGM Timoshenko nanobeams resting on viscoelastic foundations with the shear correction factor using finite element method. Mech. Based Des. Struct. Mach. 2022, 1–26, in print. [Google Scholar]
- Van Tuyen, B. Free Vibration Behaviors of Nanoplates Resting on Viscoelastic Medium. Arab. J. Sci. Eng. 2023, 48, 11511–11524. [Google Scholar] [CrossRef]
- Al Mukahal, F.H.H.; Sobhy, M. Wave propagation and free vibration of FG graphene platelets sandwich curved beam with auxetic core resting on viscoelastic foundation via DQM. Arch. Civ. Mech. Eng. 2022, 22, 12. [Google Scholar] [CrossRef]
- Mei, M.; Alamri, S.; Turki Jalil, A.; Hadrawi, S.K.; Khan, I.; Baghaei, S. Wave propagation and vibration analysis of sandwich structure with a bio-based flexible core and composite face sheets subjected to visco-Pasternak foundation and magnetic field. Compos. Struct. 2022, 300, 116132. [Google Scholar] [CrossRef]
- Foroutan, K.; Carrera, E.; Ahmadi, H. Nonlinear hygrothermal vibration and buckling analysis of imperfect FG-CNTRC cylindrical panels embedded in viscoelastic foundations. Eur. J. Mech. A-Solid 2021, 85, 104107. [Google Scholar] [CrossRef]
- Zhang, P.; Schiavone, P.; Qing, H. Unified two-phase nonlocal formulation for vibration of functionally graded beams resting on nonlocal viscoelastic Winkler-Pasternak foundation. Appl. Math. Mech. 2023, 44, 89–108. [Google Scholar] [CrossRef]
- Song, P.; Wei, P.; Zhou, X. Vibration of rectangular plate on fractional order viscoelastic foundation subjected to standing and moving loads. Mech. Time-Depend. Mat. 2023, 1–21, in print. [Google Scholar] [CrossRef]
- Song, P.; Wei, P.; Zhou, X.; Bi, X. Free vibration of fully clamped rectangular plate on fractional viscoelastic Pasternak foundations. Chin. Q. Mech. 2022, 43, 681–690. [Google Scholar] [CrossRef]
- Zamani, H.A. Frequency analysis of FG-CNT–reinforced composite doubly curved panels on visco-Pasternak medium. Adv. Compos. Hybrid Mater. 2021, 4, 830–844. [Google Scholar] [CrossRef]
- Zamani, H.A.; Salehi, M. Free vibration of foam plates on viscoelastic foundations considering thickness stretching. Mech. Time-Depend. Mat. 2023, 1–18, in print. [Google Scholar] [CrossRef]
- Yu, Y.; Fu, Y.; Zhang, W. Analysis of transverse natural frequency of two-span continuous Timoshenko beam on viscoelastic Pasternak foundation. J. Vib. Shock 2023, 42, 1–10. [Google Scholar] [CrossRef]
- Wu, D.; Lei, Y.; Wang, Z.; Yu, B.; Zhang, D. Free vibration analysis of carbon-nanotube reinforced beams resting on a viscoelastic Pasternak foundation by the nonlocal Eshelby–Mori–Tanaka method. Mech. Compos. Mater. 2023, 59, 479–494. [Google Scholar] [CrossRef]
- Pham, Q.H.; Tran, V.K.; Tran, T.T.; Nguyen, V.C.; Zenkour, A.M. Nonlocal higher-order finite element modeling for vibration analysis of viscoelastic orthotropic nanoplates resting on variable viscoelastic foundation. Compos. Struct. 2023, 318, 117067. [Google Scholar] [CrossRef]
- Ghandourah, E.E.; Daikh, A.A.; Khatir, S.; Alhawsawi, A.M.; Banoqitah, E.M.; Eltaher, M.A. A dynamic analysis of porous coated functionally graded nanoshells rested on viscoelastic medium. Mathematics 2023, 11, 2407. [Google Scholar] [CrossRef]
- Alazwari, M.A.; Zenkour, A.M. A quasi-3d refined theory for the vibration of functionally graded plates resting on visco-Winkler-Pasternak foundations. Mathematics 2022, 10, 716. [Google Scholar] [CrossRef]
- Zenkour, A.M.; El-Shahrany, H.D. Hygrothermal vibration control of cross-ply magneto-viscoelastic beams resting on Kerr’s foundations. J. Eng. Math. 2023, 140, 2. [Google Scholar] [CrossRef]
- Zaitoun, M.W.; Chikh, A.; Tounsi, A.; Sharif, S.; Al-Osta, M.A.; Al-Dulaijan, S.U.; Al-Zahrani, M.M. An efficient computational model for vibration behaviour of a functionally graded sandwich plate in a hygrothermal environment with viscoelastic foundation effects. Eng. Comput. 2023, 39, 1127–1141. [Google Scholar] [CrossRef]
- Alimoradzadeh, M.; Tornabene, F.; Esfarjani, S.M.; Dimitri, R. Finite strain-based theory for the superharmonic and subharmonic resonance of beams resting on a nonlinear viscoelastic foundation in thermal conditions, and subjected to a moving mass loading. Int. J. Non-Linear Mech. 2023, 148, 104271. [Google Scholar] [CrossRef]
- Praharaj, R.K.; Datta, N. On the transient response of plates on fractionally damped viscoelastic foundation. Comput. Appl. Math. 2020, 39, 256. [Google Scholar] [CrossRef]
- Kiarasi, F.; Asadi, A.; Babaei, M.; Asemi, K.; Hosseini, M. Dynamic analysis of functionally graded carbon nanotube (FGCNT) reinforced composite beam resting on viscoelastic foundation subjected to impulsive loading. J. Comput. Appl. Mech. 2022, 53, 1–22. [Google Scholar] [CrossRef]
- Xiao, C.; Zhang, G.; Hu, P.; Yu, Y.; Mo, Y.; Mohammadi, R. Vibration suppression of the viscoelastic sandwich doubly-curved shells using magnetostrictive layers subjected to Kerr’s foundation. Int. J. Struct. Stab. Dyn. 2022, 22, 2250058. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Hosseini, S.H.S. Investigation of flexoelectric effect on nonlinear forced vibration of piezoelectric/functionally graded porous nanocomposite resting on viscoelastic foundation. J. Strain Anal. 2020, 55, 53–68. [Google Scholar] [CrossRef]
- Salawu, S.A.; Sobamowo, G.M.; Sadiq, O.M. Forced vibration analysis of isotropic thin circular plate resting on nonlinear viscoelastic foundation. Iran. J. Sci. Technol. Trans. Civ. Eng. 2020, 44 (Suppl. S1), 277–288. [Google Scholar] [CrossRef]
- Aris, H.; Ahmadi, H. Combination resonance analysis of imperfect functionally graded conical shell resting on nonlinear viscoelastic foundation in thermal environment under multi-excitation. J. Vib. Control 2022, 28, 2121–2144. [Google Scholar] [CrossRef]
- Moayeri, M.; Darabi, B.; Sianaki, A.H.; Adamian, A. Third order nonlinear vibration of viscoelastic circular microplate based on softening and hardening nonlinear viscoelastic foundation under thermal loading. Eur. J. Mech. A-Solid 2022, 95, 104644. [Google Scholar] [CrossRef]
- Jahangiri, R.; Rezaee, M.; Manafi, H. Nonlinear and chaotic vibrations of FG double curved sandwich shallow shells resting on visco-elastic nonlinear Hetenyi foundation under combined resonances. Compos. Struct. 2022, 295, 115721. [Google Scholar] [CrossRef]
- Foroutan, K.; Dai, L. Nonlinear dynamic responses of porous FG sandwich cylindrical shells with a viscoelastic core resting on a nonlinear viscoelastic foundation. Mech. Adv. Mater. Struct. 2023, 30, 3184–3203. [Google Scholar] [CrossRef]
- Foroutan, K.; Ahmadi, H. Nonlinear vibration of SSMFG cylindrical shells with internal resonances resting on the nonlinear viscoelastic foundation. Struct. Eng. Mech. 2022, 84, 767–782. [Google Scholar] [CrossRef]
- Alimoradzadeh, M.; Akbas, S.D. Nonlinear vibration analysis of carbon nanotube-reinforced composite beams resting on nonlinear viscoelastic foundation. Geomech. Eng. 2023, 32, 125–135. [Google Scholar] [CrossRef]
- Alimoradzadeh, M.; Akbas, S.D. Nonlinear thermal vibration of FGM beams resting on nonlinear viscoelastic foundation. Steel Compos. Struct. 2022, 44, 557–567. [Google Scholar] [CrossRef]
- Khani Arani, H.; Shariyat, M. Nonlinear 2D-DQ volume-preservative global–local dynamic analysis of composite sandwich plates with soft hyperelastic cores and viscoelastic Winkler-Pasternak foundations. Structures 2023, 55, 727–746. [Google Scholar] [CrossRef]
- Shitikova, M.V.; Kandu, V.V.; Krusser, A.I. On nonlinear vibrations of an elastic plate on a fractional viscoelastic foundation in a viscoelastic medium in the presence of the one-to-one internal resonance. J. Sound Vib. 2023, 549, 117564. [Google Scholar] [CrossRef]
- Javidi, R.; Rezaei, B.; Zand, M.M. Nonlinear dynamics of a beam subjected to a moving mass and resting on a viscoelastic foundation using optimal homotopy analysis method. Int. J. Struct. Stab. 2023, 23, 2350084. [Google Scholar] [CrossRef]
- Zhao, Y.; Hou, X.; Zhang, S.; Sun, T.; Du, L.; Deng, Z. Nonlinear forced vibration of thermo-electro-elastic piezoelectric graphene composite nanoplate based on viscoelastic foundation. Acta Mech. Sin. 2023, 39, 522228. [Google Scholar] [CrossRef]
- Liu, G.; Wu, S.; Shahsavari, D.; Karami, B.; Tounsi, A. Dynamics of imperfect inhomogeneous nanoplate with exponentially-varying properties resting on viscoelastic foundation. Eur. J. Mech. A-Solid 2022, 95, 104649. [Google Scholar] [CrossRef]
- Hai, T.; Al-Masoudy, M.M.; Alsulamy, S.; Hechmi El Ouni, M.; Ayvazyan, A.; Kumar, A. Moving load analysis on cross/angle-ply laminated composite nanoplates resting on viscoelastic foundation. Compos. Struct. 2023, 305, 116540. [Google Scholar] [CrossRef]
- Bi, X.; Wei, P.; Zhou, X.; Song, P. Dynamic response of Timoshenko beams fixed at both ends on a fractional-order viscoelastic Pasternak foundation. Chin. Q. Mech. 2023, 44, 122–132. [Google Scholar] [CrossRef]
- Adhikari, S.; Pascual, B. Eigenvalues of linear viscoelastic systems. J. Sound Vib. 2009, 325, 1000–1011. [Google Scholar] [CrossRef]
- Chang, T.; Singh, M.P. Seismic analysis of structures with a fractional derivative model of viscoelastic dampers. Earthq. Eng. Eng. Vib. 2002, 1, 251–260. [Google Scholar] [CrossRef]
- Ruhe, A. Algorithms for the nonlinear eigenvalue problem. SIAM J. Numer. Anal. 1973, 10, 674–689. [Google Scholar] [CrossRef]
- Voss, H. Nonlinear eigenvalue problems. In Handbook of Linear Algebra 164; Chapman and Hall/CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Daya, E.M.; Potier-Ferry, M. A numerical method for nonlinear eigenvalue problems application to vibrations of viscoelastic structures. Comput. Struct. 2001, 79, 533–541. [Google Scholar] [CrossRef]
- Muravyov, A.; Hutton, S.G. Closed-form solutions and the eigenvalue problem for vibration of discrete viscoelastic systems. J. Appl. Mech. 1997, 64, 684–691. [Google Scholar] [CrossRef]
- Menon, S.; Tang, J. A state-space approach for the dynamic analysis of viscoelastic systems. Comput. Struct. 2004, 82, 1123–1130. [Google Scholar] [CrossRef]
- Hryniewicz, Z. Dynamic analysis of systems with deterministic and stochastic viscoelastic dampers. J. Sound Vib. 2004, 278, 1013–1023. [Google Scholar] [CrossRef]
- Gürgöze, M.; Doğruoğlu, A.N.; Zeren, S. On the eigencharacteristics of a cantilevered visco-elastic beam carrying a tip mass and its representation by a spring-damper-mass system. J. Sound Vib. 2007, 301, 420–426. [Google Scholar] [CrossRef]
- Wang, P.; Wang, Q.; Xu, X.; Chen, N. Fractional critical damping theory and its application in active suspension control. Shock Vib. 2017, 2017, 2738976. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, J.; Tai, Y.; Xu, X.; Chen, N. Critical damping design method of vibration isolation system with both fractional-order inerter and damper. Mech. Adv. Mater. Struct. 2022, 29, 1348–1359. [Google Scholar] [CrossRef]
- Adhikari, S.; Pascual, B. Iterative methods for eigenvalues of viscoelastic systems. J. Vib. Acoust. 2011, 133, 021002-1–021002-7. [Google Scholar] [CrossRef]
- Lázaro, M.; Pérez-Aparicio, J.L.; Epstein, M. Computation of eigenvalues in proportionally damped viscoelastic structures based on the fixed-point iteration. Appl. Math. Comput. 2012, 219, 3511–3529. [Google Scholar] [CrossRef][Green Version]
- Lázaro, M. Eigensolutions of nonviscously damped systems based on the fixed-point iteration. J. Sound Vib. 2018, 418, 100–121. [Google Scholar] [CrossRef]
- Cortés, F.; Elajabarrieta, M.J. An approximate numerical method for the complex eigenproblem in systems characterized by a structural damping matrix. J. Sound Vib. 2006, 296, 166–182. [Google Scholar] [CrossRef]
- Cortés, F.; Elejabarrieta, M.J. Computational methods for complex eigenproblems in finite element analysis of structural systems with viscoelastic damping treatments. Comput. Methods Appl. Mech. Eng. 2006, 195, 6448–6462. [Google Scholar] [CrossRef]
- Singh, K.V. Eigenvalue and eigenvector computation for discrete and continuous structures composed of viscoelastic materials. Int. J. Mech. Sci. 2016, 110, 127–137. [Google Scholar] [CrossRef]
- Lin, R.M.; Ng, T.Y. An iterative method for exact eigenvalues and eigenvectors of general nonviscously damped structural systems. Eng. Struct. 2019, 180, 630–641. [Google Scholar] [CrossRef]
- Lázaro, M. Closed-form eigensolutions of nonviscously, nonproportionally damped systems based on continuous damping sensitivity. J. Sound Vib. 2018, 413, 368–382. [Google Scholar] [CrossRef]
- Bailey, P.B.; Chen, P.J. Natural modes of vibration of linear viscoelastic circular plates with free edges. Int. J. Solids Struct. 1987, 23, 785–795. [Google Scholar] [CrossRef]
- Segalman, D.J. Calculation of damping matrices for linearly viscoelastic structures. J. Appl. Mech. 1987, 54, 585–588. [Google Scholar] [CrossRef]
- Lewandowski, R.; Wielentejczyk, P. Free vibration of frame structures made of Zener type viscoelastic material. MATEC WEB of Conferences. In Proceedings of the 16th Symposium of Structural Dynamics (DYNKON 2019), Kombornia, Poland, 22–24 May 2019; Volume 285, p. 00009. [Google Scholar] [CrossRef]
- Lewandowski, R.; Wielentejczyk, P. Analysis of dynamic characteristics of viscoelastic frame structures. Arch. Appl. Mech. 2020, 90, 147–171. [Google Scholar] [CrossRef]
- Rossikhin, Y.A.; Shitikova, M.V. Analysis of free non-linear vibrations of a viscoelastic plate under the conditions of different internal resonances. In. J. Non-Linear Mech. 2006, 41, 313–325. [Google Scholar] [CrossRef]
- Tubaldi, E. Dynamic behavior of adjacent buildings connected by linear viscous/viscoelastic dampers. Struct. Control Health Monit. 2015, 22, 1086–1102. [Google Scholar] [CrossRef]
- Lewandowski, R. Approximate method for determination of dynamic characteristics of structures with viscoelastic dampers. Vib. Phys. Syst. 2016, 27, 219–226. [Google Scholar]
- Pawlak, Z.; Lewandowski, R. The continuation method for the eigenvalue problem of structures with viscoelastic dampers. Comput. Struct. 2013, 125, 53–61. [Google Scholar] [CrossRef]
- Litewka, P.; Lewandowski, R.; Wielentejczyk, P. Free vibrations of laminate plates with viscoelastic layers using the refined zig-zag theory—Part 2. Numerical analysis. Compos. Struct. 2021, 278, 114550. [Google Scholar] [CrossRef]
- Lewandowski, R.; Kawa, O.; Studziński, R. Dynamic characteristics of reticulated domes built of composite elastic/viscoelastic rods modeled by the fractional Zener model. Buildings 2022, 12, 1999. [Google Scholar] [CrossRef]
- Fischer, P. Eigensolution of nonclassically damped structures by complex subspace iteration. Comput. Methods Appl. Mech. Eng. 2000, 189, 149–166. [Google Scholar] [CrossRef]
- Łasecka-Plura, M.; Lewandowski, R. The subspace iteration method for nonlinear eigenvalue problems occurring in the dynamics of structures with viscoelastic elements. Comput. Struct. 2021, 254, 106571. [Google Scholar] [CrossRef]
- Chen, X.; Chen, H.L.; Hu, X.L. Damping predication of sandwich structures by order-reduction-iteration approach. J. Sound Vib. 1999, 222, 803–812. [Google Scholar] [CrossRef]
- Mokhtari, M.; Permoon, M.R.; Haddadpour, H. Dynamic analysis of isotropic sandwich cylindrical shell with fractional viscoelastic core using Rayleigh-Ritz method. Compos. Struct. 2018, 186, 165–174. [Google Scholar] [CrossRef]
- Lázaro, M.; Pérez-Aparicio, J.L. Dynamic analysis of frame structures with free viscoelastic layers: New closed-form solutions of eigenvalues and a viscous approach. Eng. Struct. 2013, 54, 69–81. [Google Scholar] [CrossRef]
- Akoussan, K.; Boudaoud, H.; Daya, E.M.; Koutsawa, Y.; Carrera, E. Numerical method for nonlinear complex eigenvalues problems depending on two parameters: Application to three-layered viscoelastic composite structures. Mech. Adv. Mater. Struct. 2018, 25, 1361–1373. [Google Scholar] [CrossRef]
- Friswell, M.I.; Adhikari, S.; Lei, Y. Non-local finite element analysis of damped beams. Int. J. Solids Struct. 2007, 44, 7564–7576. [Google Scholar] [CrossRef]
- Friswell, M.I.; Adhikari, S.; Lei, Y. Vibration analysis of beams with non-local foundations using the finite element method. Int. J. Numer. Methods Eng. 2007, 71, 1365–1386. [Google Scholar] [CrossRef]
- Lei, Y.; Murmu, T.; Adhikari, S.; Friswell, M.I. Dynamic characteristics of damped viscoelastic nonlocal Euler-Bernoulli beams. Eur. J. Mech. A Solids 2013, 42, 125–136. [Google Scholar] [CrossRef]
- Ansari, R.; Oskouie, M.F.; Sadeghi, F.; Bazdid-Vahdati, M. Free vibration of fractional viscoelastic Timoshenko nanobeams using the nonlocal elasticity theory. Phys. E Low-Dimens. Syst. Nanostructures 2015, 74, 318–327. [Google Scholar] [CrossRef]
- Elyasi, P.; Neya, B.N.; Firoozjaee, A.R. Free vibration of viscoelastic nonlocally damped tapered axially functionally graded beams using the state-space formulation. Eng. Struct. 2023, 288, 116183. [Google Scholar] [CrossRef]
- Naghinejad, M.; Ovesy, H.R. Viscoelastic free vibration behavior of nano-scaled beams via finite element nonlocal integral elasticity approach. J. Vib. Control 2019, 25, 445–459. [Google Scholar] [CrossRef]
- Cajić, M.; Karličiś, D.; Lazarević, M. Nonlocal vibration of a fractional order viscoelastic nanobeam with attached nanoparticle. Theor. Appl. Mech. 2015, 42, 167–190. [Google Scholar] [CrossRef]
- Martin, O. Nonlocal effects on the dynamic analysis of a viscoelastic nanobeam using a fractional Zener model. Appl. Math. Model. 2019, 73, 637–650. [Google Scholar] [CrossRef]
- Rajabi, K.; Hosseini-Hashemi, S. Application of the generalized Hooke’s law for viscoelastic materials (GHVMs) in nonlocal free damped vibration analysis of viscoelastic orthotropic nanoplates. Int. J. Mech. Sci. 2017, 124–125, 158–165. [Google Scholar] [CrossRef]
- Rajabi, K.; Hosseini-Hashemi, S. Application of the generalized Hooke’s law for viscoelastic materials (GHVMs) in nanoscale mass sensing applications of viscoelastic nanoplates: A theoretical study. Eur. J. Mech. A Solids. 2018, 67, 71–83. [Google Scholar] [CrossRef]
- Johnson, C.D.; Kienholz, D.A. Finite element prediction of damping in structures with constrained viscoelastic layers. AIAA J. 1982, 20, 1284–1290. [Google Scholar] [CrossRef]
- Shen, K.L.; Soong, T.T. Seismic behaviour of reinforced concrete frame with added viscoelastic dampers. Eng. Struct. 1995, 17, 372–380. [Google Scholar] [CrossRef]
- Tsai, M.H.; Chang, K.C. A study of the modal strain energy method for viscoelastically damped structures. J. Chin. Inst. Eng. 2001, 24, 311–320. [Google Scholar] [CrossRef]
- Lee, D.G.; Hong, S.; Kim, J. Efficient seismic analysis of building structures with added viscoelastic dampers. Eng. Struct. 2002, 24, 1217–1227. [Google Scholar] [CrossRef]
- Fan, Z. Transient vibration and sound radiation of a rectangular plate with viscoelastic boundary supports. Int. J. Numer. Methods Eng. 2001, 51, 619–630. [Google Scholar] [CrossRef]
- Rao, M.D.; Echempati, R.; Nadella, S. Dynamic analysis and damping of composite structures embedded with viscoelastic layers. Compos. B 1997, 28, 547–554. [Google Scholar] [CrossRef]
- Saravanan, C.; Ganesan, N.; Ramamurti, V. Study on energy dissipation pattern in vibrating fluid filled cylindrical shells with a constrained viscoelastic layer. Comput. Struct. 2000, 75, 575–591. [Google Scholar] [CrossRef]
- Saravanan, C.; Ganesan, N.; Ramamurti, V. Vibration and damping analysis of multilayered fluid filled cylindrical shells with constrained viscoelastic damping using modal strain energy method. Comput. Struct. 2000, 75, 395–417. [Google Scholar] [CrossRef]
- Sun, B.; Wang, J.; Li, Z.I.; Qin, Y.; Liu, S.Z.; Tomker, D. Modified modal strain energy method for analyzing the dynamic damping behavior of constrained viscoelastic structures. J. Eng. Sci. Technol. 2017, 10, 174–180. [Google Scholar] [CrossRef]
- Aprile, A.; Benedetti, A. Implicit dynamic analysis of VE-damped structures using Maxwell parallel systems. Eng. Comp. 1999, 16, 374–396. [Google Scholar] [CrossRef]
- Cortés, F.; Mateos, M.; Elejabarrieta, M.J. A direct integration formulation for exponentially damped structural systems. Comp. Struct. 2009, 87, 391–394. [Google Scholar] [CrossRef]
- Puthanpurayil, A.M.; Carr, A.J.; Dhakal, R.P. A generic time domain implementation scheme for non-classical convolution damping models. Eng. Struct. 2014, 71, 88–98. [Google Scholar] [CrossRef]
- Adhikari, S.; Wagner, N. Direct time-domain integration method for exponentially damped linear systems. Comp. Struct. 2004, 82, 2453–2461. [Google Scholar] [CrossRef]
- Palmeri, A.; Muscolino, G.A. numerical method for the time-domain dynamic analysis of buildings equipped with viscoelastic dampers. Struct. Control Health Monit. 2011, 18, 519–539. [Google Scholar] [CrossRef]
- Palmeri, A.; Ricciardelli, F.; de Luca, A.; Muscolino, G. State space formulation for linear viscoelastic dynamic systems with memory. J. Eng. Mech. 2003, 129, 715–724. [Google Scholar] [CrossRef]
- Liu, Q. Computational method of the dynamic response for nonviscously damped structure systems. J. Eng. Mech. 2014, 140, 04014085. [Google Scholar] [CrossRef]
- Sorvari, J.; Hämäläinen, J. Time integration in linear viscoelasticity—A comparative study. Mech. Time-Depend Mater. 2010, 14, 307–328. [Google Scholar] [CrossRef]
- Liu, Q. Explicit computational method of dynamic response for non-viscously damped structure systems. Mech. Res. Commun. 2016, 71, 48–55. [Google Scholar] [CrossRef]
- Patlashenko, I.; Givoli, D.; Barbone, P. Time-stepping schemes for systems of Volterra integro-differential equations. Comp. Meth. Appl. Mech. Eng. 2001, 190, 5691–5718. [Google Scholar] [CrossRef]
- Ding, Z.; Li, L.; Kong, J.; Qin, L. A modal projection-based reduction method for transient dynamic responses of viscoelastic systems with multiple damping models. Comp. Struct. 2018, 194, 60–73. [Google Scholar] [CrossRef]
- Ding, Z.; Li, L.; Hu, Y. A modified precise integration method for transient dynamic analysis in structural systems with multiple damping models. Mech. Syst. Signal Process. 2018, 98, 613–633. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, G.T. The Biot Model and its application in viscoelastic Composite structures. J. Vib. Acoust. 2007, 129, 533–540. [Google Scholar] [CrossRef]
- Padovan, J. Computational algorithms fir FE formulations involving fractional operators. Comp. Mech. 1987, 2, 271–287. [Google Scholar] [CrossRef]
- Enelund, M.; Olsson, P. Damping described by fading memory—Analysis and application to fractional derivative models. Int. J. Solids Struct. 1999, 36, 939–970. [Google Scholar] [CrossRef]
- Enelund, M.; Lesieutre, G.A. Time domain modeling of damping using anelastic displacement fields and fractional calculus. Int. J. Solids Struct. 1999, 36, 4447–4472. [Google Scholar] [CrossRef]
- Schmidt, A.; Gaul, L. Finite element formulation of viscoelastic constitutive equations using fractional time derivatives. Nonlinear Dyn. 2002, 29, 37–55. [Google Scholar] [CrossRef]
- Schmidt, A.; Lotsch, M.; Gaul, L. Implementation of a new method for the computation of fractionally damped structures into the finite element method. Shock Vib. 2010, 17, 419–428. [Google Scholar] [CrossRef][Green Version]
- Cortés, F.; Elejabarrieta, M.J. Finite element formulations for transient dynamic analysis in structural systems with viscoelastic treatments containing fractional derivative models. Int. J. Numer. Meth. Eng. 2007, 69, 2173–2195. [Google Scholar] [CrossRef]
- Datta, P.; Ray, M.C. Fractional order derivative model of viscoelastic layer for active damping of geometrically nonlinear vibrations of smart composite plates. Comp. Mater. Cont. 2015, 49–50, 47–80. [Google Scholar] [CrossRef]
- Bucher, C.; Pirrotta, A. Dynamic finite element analysis of fractionally damped structural systems in the time domain. Acta Mech. 2015, 226, 3977–3990. [Google Scholar] [CrossRef]
- Singh, M.P.; Chang, T.S.; Nandan, H. Algorithms for seismic analysis of MDOF systems with fractional derivatives. Eng. Struct. 2011, 33, 2371–2381. [Google Scholar] [CrossRef]
- Cortés, F.; Brun, M.; Elejabarrieta, M.J. A finite element formulation for the transient response of free layer damping plates including fractional derivatives. Comp. Struct. 2023, 282, 107039. [Google Scholar] [CrossRef]
- Schmidt, A.; Gaul, L. On the numerical evaluation of fractional derivatives in multi-degree-of-freedom systems. Signal Proc. 2006, 86, 2592–2601. [Google Scholar] [CrossRef]
- Adolfsson, K.; Enelund, M.; Larsson, S. Adaptive discretization of fractional order viscoelasticity using sparse time history. Comp. Meth. Appl. Mech. Eng. 2004, 193, 4567–4590. [Google Scholar] [CrossRef]
- Liu, T.; Wen, W.; Wang, P.; Feng, F. A time-marching procedure based on a sub-step explicit time integration scheme for non-viscous damping systems. Eng. Comp. 2023, 1–21, in print. [Google Scholar] [CrossRef]
- Shen, R.; Qian, X.; Zhou, J. Direct integration for non-viscous structural systems and its simplification. Mech. Res. Comm. 2019, 95, 8–15. [Google Scholar] [CrossRef]
- Xu, J.; Li, J. Stochastic dynamic response and reliability assessment of controlled structures with fractional derivative model of viscoelastic dampers. Mech. Syst. Signal Process. 2016, 72–73, 865–896. [Google Scholar] [CrossRef]
- Shen, R.; Qian, X.; Zhou, J.; Lee, C. A time integration method based on the weak form Galerkin method for non-viscous damping systems. Mech. Syst. Signal Process. 2021, 151, 107361. [Google Scholar] [CrossRef]
- Adhikari, S. Derivative of eigensolutions of nonviscously damped linear systems. AIAA J. 2002, 40, 2061–2069. [Google Scholar] [CrossRef]
- Adhikari, S.; Friswell, M.I. Calculation of eigensolution derivatives for nonviscously damped systems using Nelson’s method. AIAA J. 2006, 44, 1799–1806. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y.J.; Wang, X.L.; Ling, L. Computation of eigensolution derivatives for nonviscously damped systems using the algebraic method. AIAA J. 2012, 50, 2282–2284. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y.; Wang, X.; Ling, L. Eigensensitivity analysis for asymmetric nonviscous systems. AIAA J. 2013, 51, 738–741. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y.; Wang, X. Design sensitivity and Hessian matrix of generalized eigenproblems. Mech. Syst. Signal Process. 2014, 43, 272–294. [Google Scholar] [CrossRef]
- Wang, P.; Dai, H. Eigensensitivity analysis for symmetric nonviscously damped systems with repeated eigenvalues. J. Vibroengineering 2014, 16, 4065–4076. [Google Scholar]
- Li, L.; Hu, Y.; Wang, X. A study on design sensitivity analysis for general nonlinear eigenproblems. Mech. Syst. Signal Process. 2013, 34, 88–105. [Google Scholar] [CrossRef]
- Kobelev, V. Sensitivity analysis of the linear nonconservative systems with fractional damping. Struct. Multidiscipl. Optim. 2007, 33, 179–188. [Google Scholar] [CrossRef]
- Lewandowski, R.; Łasecka-Plura, M. Design sensitivity analysis of structures with viscoelastic dampers. Comput. Struct. 2016, 164, 95–107. [Google Scholar] [CrossRef]
- Łasecka-Plura, M.; Lewandowski, R. Sensitivity analysis of dynamic characteristics of composite beams with viscoelastic layers. Procedia Eng. 2017, 199, 366–371. [Google Scholar] [CrossRef]
- Akoussan, K.; Boudaoud, H.; Daya, E.M.; Koutsawa, Y.; Carrera, E. Sensitivity analysis of the damping properties of viscoelastic composite structures according to the layers thicknesses. Compos. Struct. 2016, 149, 11–25. [Google Scholar] [CrossRef]
- Lampoh, K.; Charpentier, I.; Mostafa, D.E. Eigenmode sensitivity of damped sandwich structures. Comptes Rendus Mécanique 2014, 342, 700–705. [Google Scholar] [CrossRef]
- Cha, P.D.; Carbon, K.C.; Hsieh, R. Eigenvalues and eigenvalue sensitivities of a beam supported by viscoelastic solids. J. Vib. Acoust. 2014, 136, 021017. [Google Scholar] [CrossRef]
- Łasecka-Plura, M. A comparative study of the sensitivity analysis for systems with viscoelastic elements. Arch. Mech. Eng. 2023, 70, 5–25. [Google Scholar] [CrossRef]
- Yun, K.S.; Youn, S.K. Design sensitivity analysis for transient response of non-viscously damped dynamic systems. Struct. Multidiscipl. Optim. 2017, 55, 2197–2210. [Google Scholar] [CrossRef]
- Ding, Z.; Li, L.; Li, X.; Kong, J. A comparative study of design sensitivity analysis based on adjoint variable method for transient response of non-viscously damped systems. Mech. Syst. Signal Process. 2018, 110, 390–411. [Google Scholar] [CrossRef]
- Ding, Z.; Zhang, L.; Gao, Q.; Lia, W.H. State-space based discretize-then-differentiate adjoint sensitivity method for transient responses of non-viscously damped systems. Comput. Struct. 2021, 250, 106540. [Google Scholar] [CrossRef]
- Ding, Z.; Li, L.; Zou, G.; Kong, J. Design sensitivity analysis for transient response of non-viscously damped systems based on direct differentiate method. Mech. Syst. Signal Process. 2019, 121, 322–342. [Google Scholar] [CrossRef]
- Ding, Z.; Shi, J.; Gao, Q.; Huang, Q.; Liao, W.H. Design sensitivity analysis for transient responses of viscoelastically damped systems using model order reduction techniques. Struct. Multidiscipl. Optim. 2020, 64, 1501–1526. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y.; Wang, X. Design sensitivity analysis of dynamic response of nonviscously damped systems. Mech. Syst. Signal Process. 2013, 41, 613–638. [Google Scholar] [CrossRef]
- Łasecka-Plura, M.; Lewandowski, R. Design sensitivity analysis of frequency response functions and steady-state response for structures with viscoelastic dampers. Vib. Phys. Syst. 2014, 26, 129–136. [Google Scholar]
- De Lima, A.M.G.; Faria, A.W.; Rade, D.A. Sensitivity analysis of frequency response functions of composite sandwich plates containing viscoelastic layers. Compos. Struct. 2010, 92, 364–376. [Google Scholar] [CrossRef]
- Martinez-Agirre, M.; Elejabarrieta, M.J. Higher order eigensensitivities-based numerical method for the harmonic analysis of viscoelastically damped structures. Int. J. Numer. Methods Eng. 2011, 88, 1280–1296. [Google Scholar] [CrossRef]
- Huang, X.; Zhou, S.; Sun, G.; Li, G.; Xie, Y.M. Topology optimization for microstructures of viscoelastic composite materials. Comput. Methods Appl. Mech. Eng. 2015, 283, 503–516. [Google Scholar] [CrossRef]
- Yun, K.S.; Youn, S.K. Topology optimization of viscoelastic damping layers for attenuating transient response of shell structures. Finite Elem. Anal. Des. 2018, 141, 154–165. [Google Scholar] [CrossRef]
- James, K.A.; Waisman, H. Topology optimization of viscoelastic structures using a time-dependent adjoint method. Comput. Methods Appl. Mech. Eng. 2015, 285, 166–187. [Google Scholar] [CrossRef]
- Pingaro, M.; Venini, P. A fast approach to analysis and optimization of viscoelastic beams. Comput. Struct. 2016, 168, 46–55. [Google Scholar] [CrossRef]
- Jamshidi, B.; Hematiyan, M.R.; Mahzoon, M.; Shiah, Y.C. Load identification for a viscoelastic solid by an accurate meshfree sensitivity analysis. Eng. Struct. 2020, 203, 109895. [Google Scholar] [CrossRef]
- Chongshuai, W.; Yiqian, H.; Haitian, Y. A SBFEM and sensitivity analysis based algorithm for solving inverse viscoelastic problems. Eng. Anal. Bound. Elem. 2019, 106, 588–598. [Google Scholar] [CrossRef]
- Elishakoff, I. Essay on uncertainties in elastic and viscoelastic structures: From A. M. Freudenthal’s criticism to modern convex modeling. Comput. Struct. 1995, 56, 871–895. [Google Scholar] [CrossRef]
- Sepahvand, K.; Marbur, S. On uncertainty quantification in sandwich structures with spatial random damping behavior. In Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014, Porto, Portugal, 30 June–2 July 2014. [Google Scholar]
- Hernández, W.P.; Castello, D.A.; Ritto, T.G. Uncertainty propagation analysis in laminated structures with viscoelastic core. Comput. Struct. 2016, 164, 23–37. [Google Scholar] [CrossRef]
- Hernández, W.P.; Castello, D.A.; Ritto, T.G. Stochastic fields to analyze uncertainties in laminated structures with viscoelastic core. J. Comput. Interdiscip. Sci. 2018, 9, 195–204. [Google Scholar] [CrossRef]
- Silva, V.A.C.; de Lima, A.M.G.; Bouhaddi, N.; Lacerda, H.B. Uncertainty propagation and experimental verification of nonlinear viscoelastic sandwich beams. Mech. Syst. Signal Process. 2019, 132, 654–669. [Google Scholar] [CrossRef]
- Wang, T.; Xu, C.; Hamdaoui, M.; Guo, N.; Gu, L. Uncertainty propagation in modal analysis of viscoelastic sandwich structures using a stochastic collocation method. J. Sandw. Struct. 2021, 23, 1141–1165. [Google Scholar] [CrossRef]
- Adhikari, S. On the quantification of damping model uncertainty. J. Sound Vib. 2007, 306, 153–171. [Google Scholar] [CrossRef]
- Wang, T.; Xu, C.; Guo, N. A novel frequency-labeled adaptive sparse grid collocation method for uncertainty quantification of the frequency response of general viscoelastic damping structures. Int. J. Mech. Sci. 2021, 193, 106168. [Google Scholar] [CrossRef]
- Wang, T.; Xu, C.; Guo, N.; Hamdaoui, M.; Daya, E.I. Uncertainty propagation of frequency response of viscoelastic damping structures using a modified high-dimensional adaptive sparse grid collocation method. Mech. Adv. Mater. Struct. 2022, 29, 506–524. [Google Scholar] [CrossRef]
- Soize, C.; Poloskov, I.E. Time-domain formulation in computational dynamics for linear viscoelastic media with model uncertainties and stochastic excitation. Comput. Math. With Appl. 2012, 64, 3594–3612. [Google Scholar] [CrossRef]
- Capillon, R.; Desceliers, C.; Soize, C. Uncertainty quantification for viscoelastic composite structures in computational linear structural dynamics. In Proceedings of the ISMA2016-USD2016, Leuven, Belgium, 19–24 September 2016. [Google Scholar]
- Capillon, R.; Desceliers, C.; Soize, C. Uncertainty quantification in computational linear structural dynamics for viscoelastic composite structures. Comput. Methods Appl. Mech. Eng. 2016, 305, 154–172. [Google Scholar] [CrossRef]
- Capillon, R.; Desceliers, C.; Soize, C. Model uncertainties in computational viscoelastic linear structural dynamics. Procedia Eng. 2017, 199, 1210–1215. [Google Scholar] [CrossRef]
- Guerdi, M.; Lima, A.M.G.; Bouhaddi, N.; Rade, D.A. Robust design of viscoelastic structures based on stochastic finite element models. Mech. Syst. Signal Process. 2010, 24, 59–77. [Google Scholar] [CrossRef]
- Guo, A.X.; Xu, Y.L.; Wu, B. Seismic reliability analysis of hysteretic structure with viscoelastic dampers. Eng. Struct. 2002, 24, 373–383. [Google Scholar] [CrossRef]
- Gonçalves, L.K.S.; Rosa, U.L.; de Lima, A.M.G. Fatigue damage investigation and optimization of a viscoelastically damped system with uncertainties. J. Brazilian Soc. Mech. 2019, 41, 382. [Google Scholar] [CrossRef]
- Nasab, M.S.E.; Kim, J. Fuzzy analysis of a viscoelastic damper in seismic retrofit of structures. Eng. Struct. 2022, 250, 113473. [Google Scholar] [CrossRef]
- Nasab, M.S.E.; Guo, Y.Q.; Kim, J. Seismic retrofit of a soft first-story building using viscoelastic dampers considering inherent uncertainties. J. Build. Eng. 2022, 47, 103866. [Google Scholar] [CrossRef]
- Elishakoff, I.; Elisseeff, P.; Glegg, S.A.L. Nonprobabilistic, Convex-Theoretic modeling of scatter in material properties. AIAA J. 1994, 32, 843–849. [Google Scholar] [CrossRef]
- Fujita, K.; Takewaki, I. An efficient methodology for robustness evaluation by advanced interval analysis using updated second-order Taylor series expansion. Eng. Struct. 2011, 33, 3299–3310. [Google Scholar] [CrossRef]
- Łasecka-Plura, M.; Lewandowski, R. Dynamic characteristics and frequency response function for frame with dampers with uncertain design parameters. Mech. Based Des. Struct. Mach. 2017, 45, 296–312. [Google Scholar] [CrossRef]
- Łasecka-Plura, M. Dynamic characteristics of a composite beam with viscoelastic layers under uncertain-but-bounded design parameters. Appl. Sci. 2023, 13, 6473. [Google Scholar] [CrossRef]
- Sofi, A.; Muscolino, G.; di Paola, M. Reliability analysis of structures controlled by external fractional viscoelastic dampers with interval parameters. Acta Mech. Sin. 2023, 39, 722486. [Google Scholar] [CrossRef]
- Peng, R.; He, Y.; Yang, H. An efficient numerical method to solve inverse fuzzy-uncertain viscoelastic problems of identification. Inverse Probl. Sci. Eng. 2021, 29, 920–943. [Google Scholar] [CrossRef]
- Kookalani, S.; Shen, D.; Zhu, L.L.; Lindsey, M. An Overview of Optimal Damper Placement Methods in Structures. Iran. J. Sci. Technol. Trans. Civ. Eng. 2022, 46, 1785–1804. [Google Scholar] [CrossRef]
- Takewaki, I. Building Control with Passive Dampers: Optimal Performance-Based Design for Earthquakes; John Wiley & Sons (Asia) Pte. Ltd.: Singapore, 2009. [Google Scholar] [CrossRef]
- Takewaki, I. Optimal damper placement for planar building frames using transfer functions. Struct. Multidiscip. Optim. 2000, 20, 280–287. [Google Scholar] [CrossRef]
- Sánchez, W.E.D.; Avila, S.M.; de Brito, J.L.V. Optimal placement of damping devices in buildings. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 337. [Google Scholar] [CrossRef]
- Takewaki, I. Optimal damper placement for minimum transfer functions. Earthq. Eng. Struct Dyn. 1997, 26, 1113–1124. [Google Scholar] [CrossRef]
- Cimellaro, G.P. Simultaneous stiffness-damping optimization of structures with respect to acceleration, displacement and base shear. Eng. Struct. 2007, 29, 2853–2870. [Google Scholar] [CrossRef]
- Sonmez, M.; Aydin, E.; Karabork, T. Using an artificial bee colony algorithm for the optimal placement of viscous dampers in planar building frames. Struct. Multidiscip. Optim. 2013, 48, 395–409. [Google Scholar] [CrossRef]
- Lavan, O.; Levy, R. Optimal design of supplemental viscous dampers for irregular shear-frames in the presence of yielding. Earthq. Eng. Struct. Dyn. 2005, 34, 889–907. [Google Scholar] [CrossRef]
- Aydin, E. Optimal damper placement based on base moment in steel building frames. J. Constr. Steel Res. 2012, 79, 216–225. [Google Scholar] [CrossRef]
- Lavan, O.; Dargush, G.F. Multi-objective evolutionary seismic design with passive energy dissipation systems. J. Earthq. Eng. 2009, 13, 758–790. [Google Scholar] [CrossRef]
- Xie, Z.; Shepard, W.; Woodbury, K. Design Optimization for Vibration Reduction of Viscoelastic Damped Structures Using Genetic Algorithms. Shock Vib. 2009, 16, 455–466. [Google Scholar] [CrossRef]
- Pricopie, A.; Costache, A. Viscous Damper Distribution Using Genetic Algorithms and Pattern Search Optimization. In The 1940 Vrancea Earthquake. Issues, Insights and Lessons Learnt; Vacareanu, R., Ionescu, C., Eds.; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Lenartowicz, A.; Przychodzki, M.; Guminiak, M.; Garbowski, T. Optimal placement of viscoelastic vibration dampers for Kirchhoff plates based on PSO method. Materials 2021, 14, 6616. [Google Scholar] [CrossRef] [PubMed]
- Fujita, K.; Moustafa, A.; Takewaki, I. Optimal placement of visco-elastic dampers and supporting members under variable critical excitations. Earthq. Struct. 2010, 1, 43–67. [Google Scholar] [CrossRef]
- Akehashi, H.; Takewaki, I. Comparative investigation on optimal viscous damper placement for elastic-plastic MDOF structures: Transfer function amplitude or double impulse. Soil Dynam. Earthq. Eng. 2020, 130, 105987. [Google Scholar] [CrossRef]
- Lavan, O. Optimal Design of Viscous Dampers and Their Supporting Members for the Seismic Retrofitting of 3D Irregular Frame Structures. J. Struct. Eng. 2015, 141, 04015026. [Google Scholar] [CrossRef]
- Lopez-Garcia, D.; Soong, T.T. Efficiency of a simple approach to damper allocation in MDOF structures. J. Struct. Control 2002, 9, 19–30. [Google Scholar] [CrossRef]
- Hussien, O.S.; Elamy, M.I. Optimal placement of dampers on multistorey frames using dynamic analysis. Strength Mater. 2020, 52, 470–479. [Google Scholar] [CrossRef]
- Hwang, J.S.; Lin, W.C.; Wu, N.J. Comparison of distribution methods for viscous damping coefficients to buildings. Struct. Infrastruct. Eng. 2013, 9, 28–41. [Google Scholar] [CrossRef]
- Singh, M.P.; Moreschi, L.M. Optimal seismic response control with dampers. Earthq. Eng. Struct. Dyn. 2001, 30, 553–572. [Google Scholar] [CrossRef]
- Rayegani, A.; Nouri, G. Seismic collapse probability and life cycle cost assessment of isolated structures subjected to pounding with smart hybrid isolation system using a modified fuzzy based controller. Structures 2022, 44, 30–41. [Google Scholar] [CrossRef]
- Gong, W.; Xiong, S. Probabilistic seismic risk assessment of modified pseudonegative stiffness control of a base-isolated building. Struct. Infrastruct. Eng. 2016, 12, 1295–1309. [Google Scholar] [CrossRef]
- Rayegani, A.; Nouri, G. Application of Smart Dampers for Prevention of Seismic Pounding in Isolated Structures Subjected to Near-fault Earthquakes. J. Earthq. Eng. 2022, 26, 4069–4084. [Google Scholar] [CrossRef]
- Lewandowski, R.; Litewka, P. Nonlinear harmonic vibrations of laminate plates with viscoelastic layers using refined zig-zag theory. Part 1—Theoretical background. Compos. Struct. 2023, 320, 117200. [Google Scholar] [CrossRef]
- Lewandowski, R.; Litewka, P. Nonlinear harmonic vibrations of laminate plates with VE layers using refined zig-zag theory. Part 2—Numerical solution. Compos. Struct. 2023, 319, 117062. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).