Early Shrinkage Modeling of Complex Internally Confined Concrete Based on Capillary Tension Theory
Abstract
:1. Introduction
2. Experimental Design
2.1. Concrete Mixing Ratio
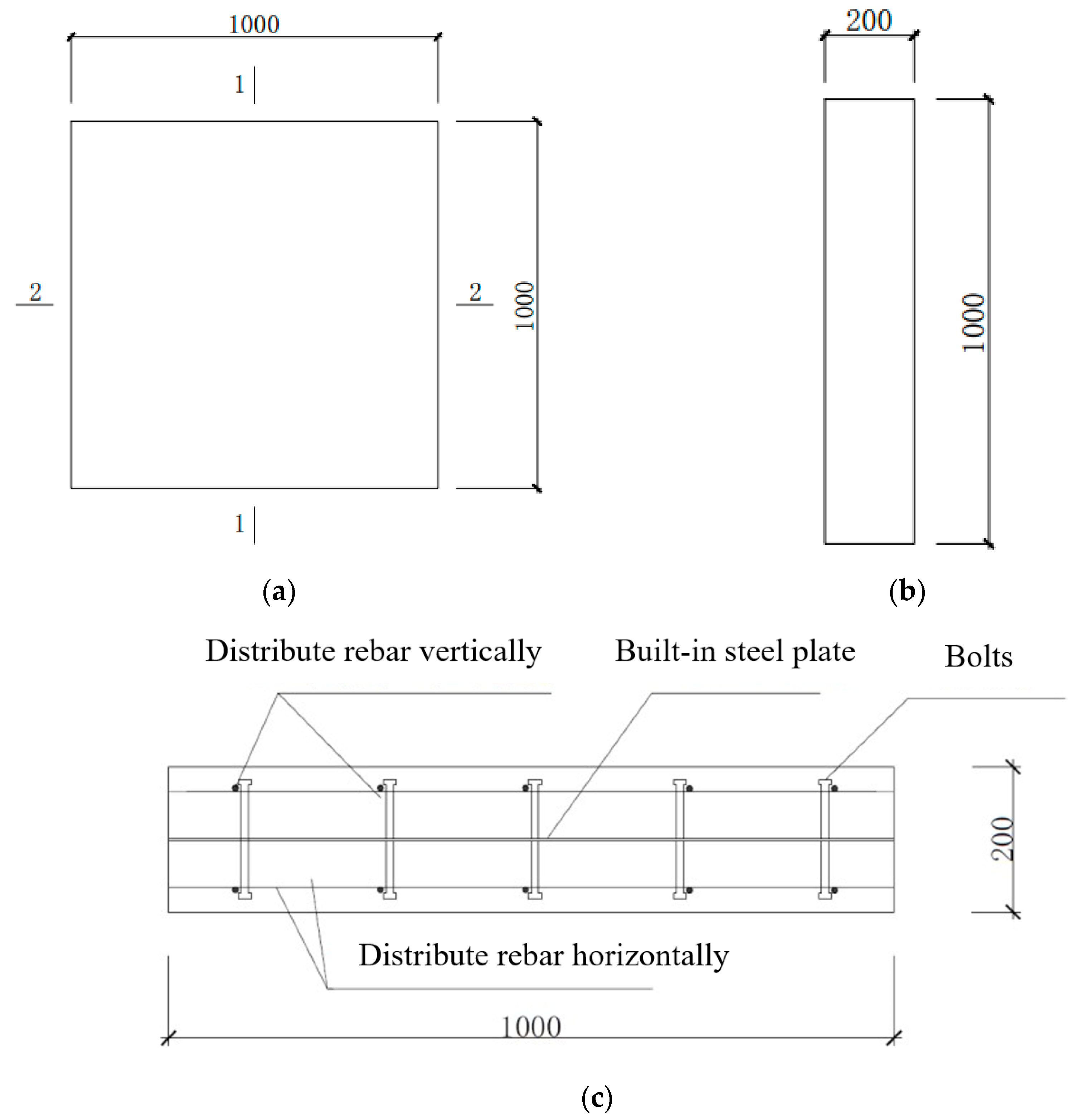
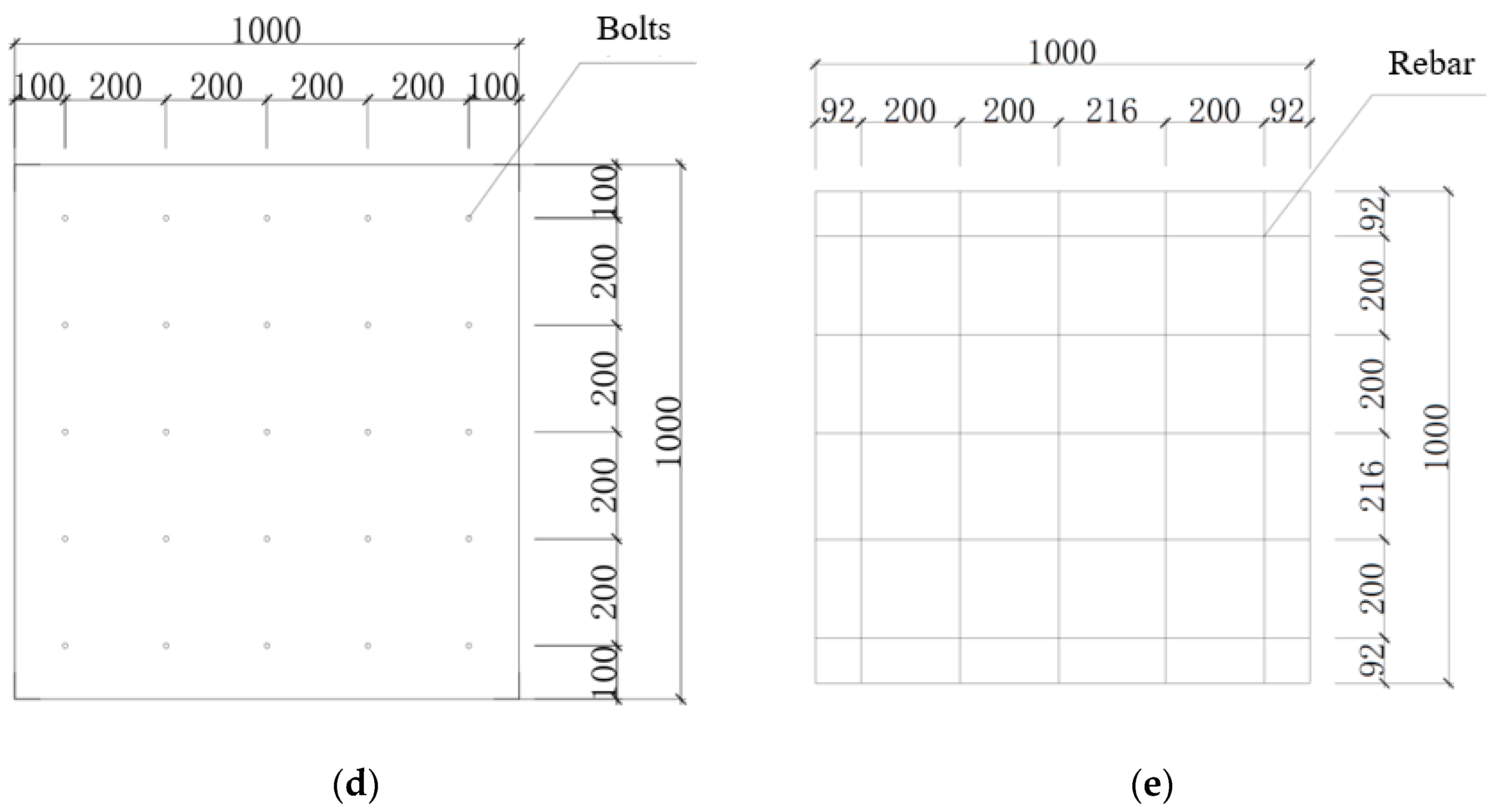
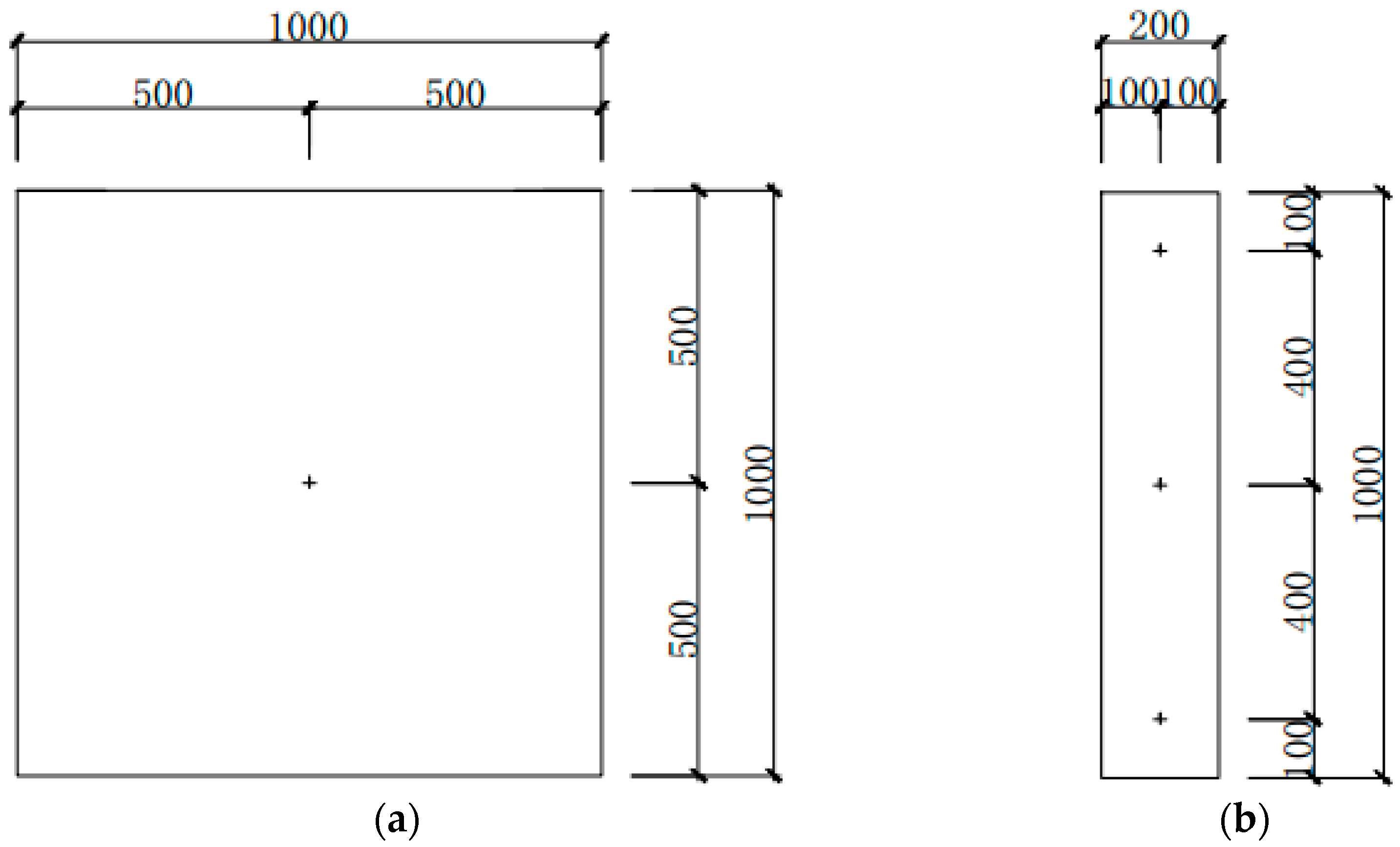
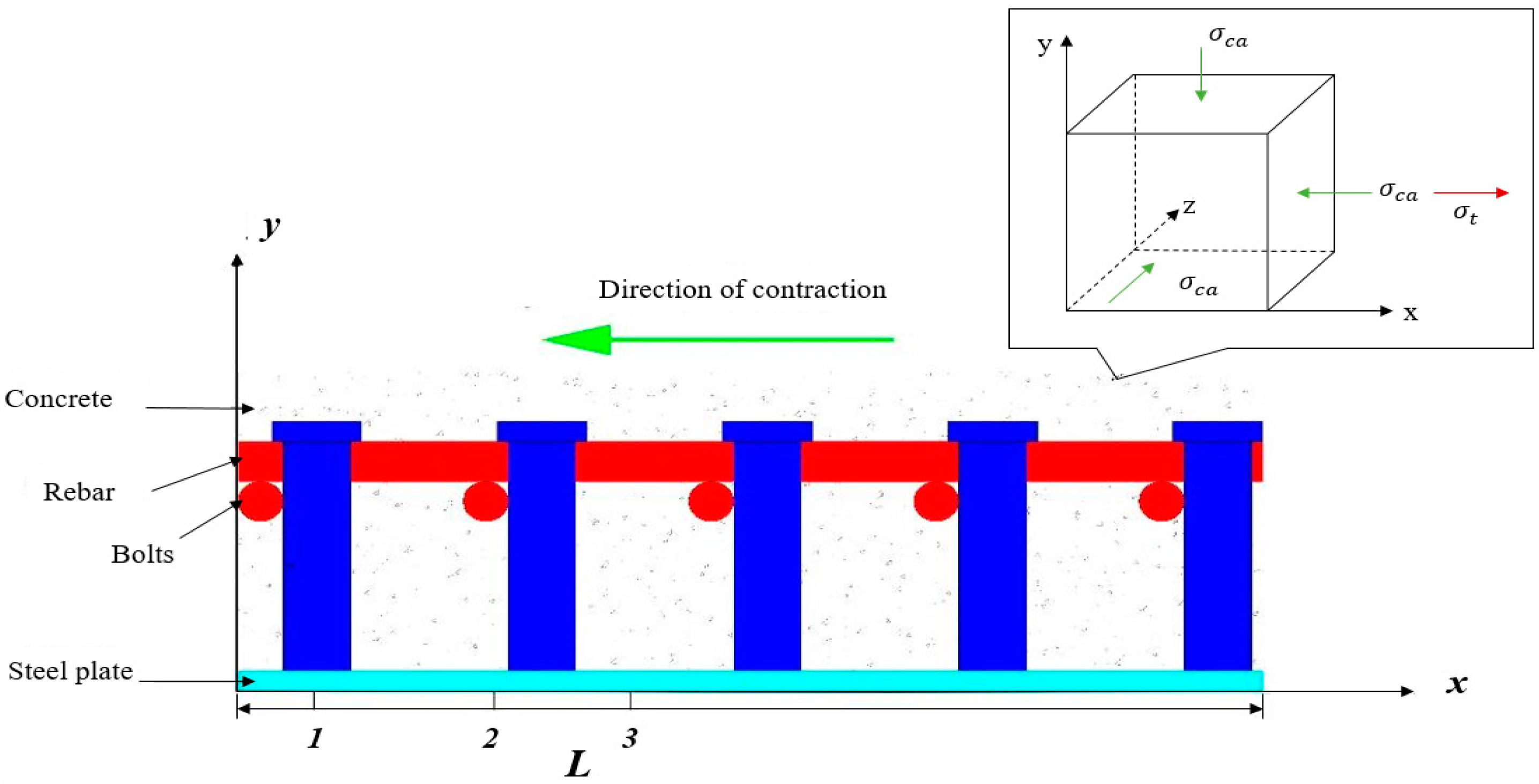
2.2. Specimen Design
- Steel strength is Q235B, and thickness is 10 mm;
- The diameter of the bolts is 16 mm, the length is 80 mm, and it is welded on both sides of the steel plate in a square arrangement, as shown in Figure 1d;
- Horizontal distribution reinforcement is Φ10@200, and longitudinal horizontal reinforcement is Φ10@200. These are bidirectionally arranged along the test specimen in two layers, with the same diameter of reinforcement in both directions. The studs are passed through the distribution reinforcement mesh, as shown in Figure 1c,e.
2.3. Performance Testing
2.3.1. Mechanical Properties Testing
2.3.2. Concrete Restraint Shrinkage Test
2.3.3. Concrete Pore Structure Test
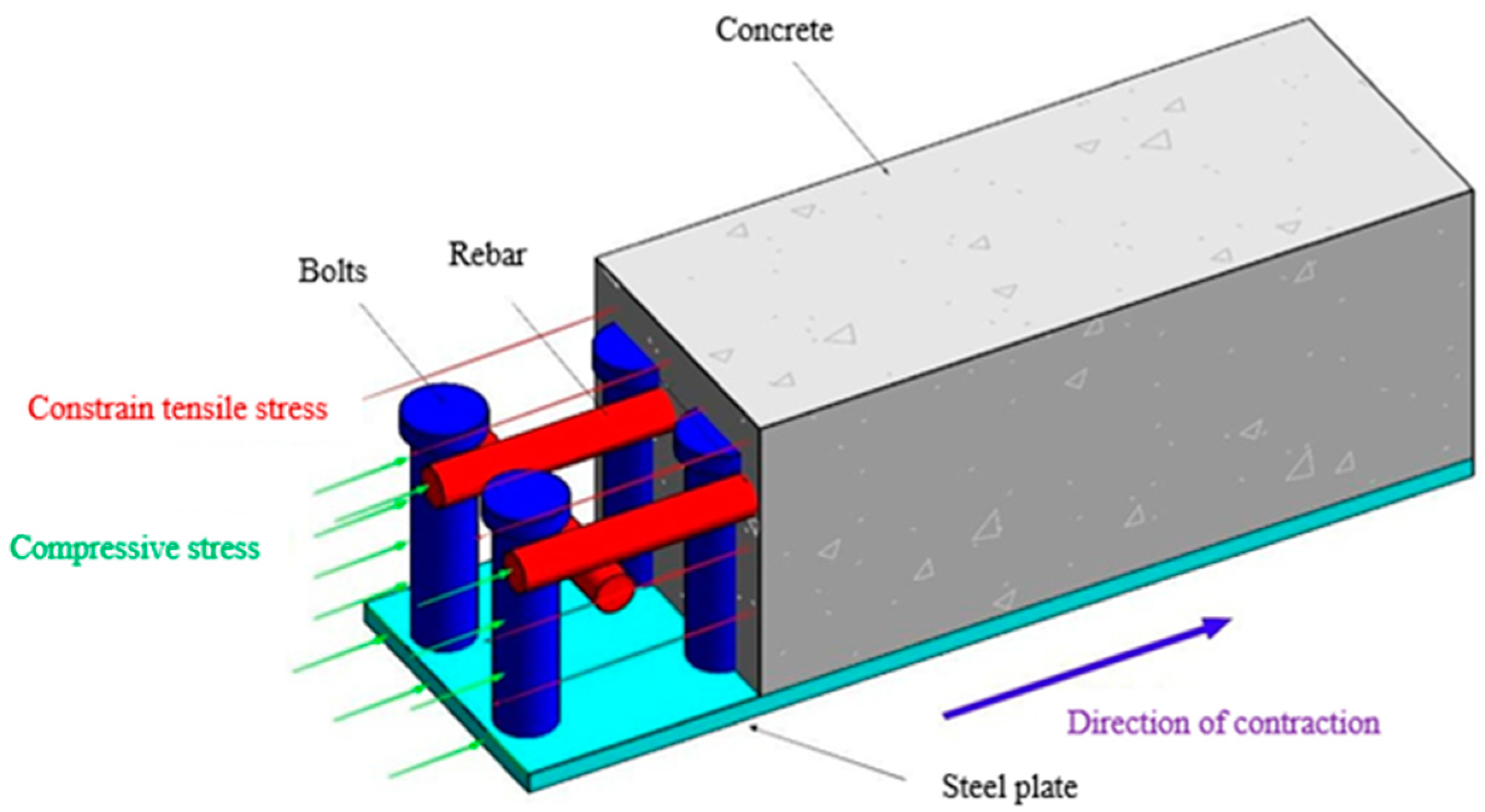
3. Shrinkage Modeling of Concrete with Complex Internal Constraints Based on Capillary Tension Theory
3.1. Shrinkage Modeling of Concrete with Complex Internal Constraints
4. Hole Structures in Complex Internally Confined Concrete
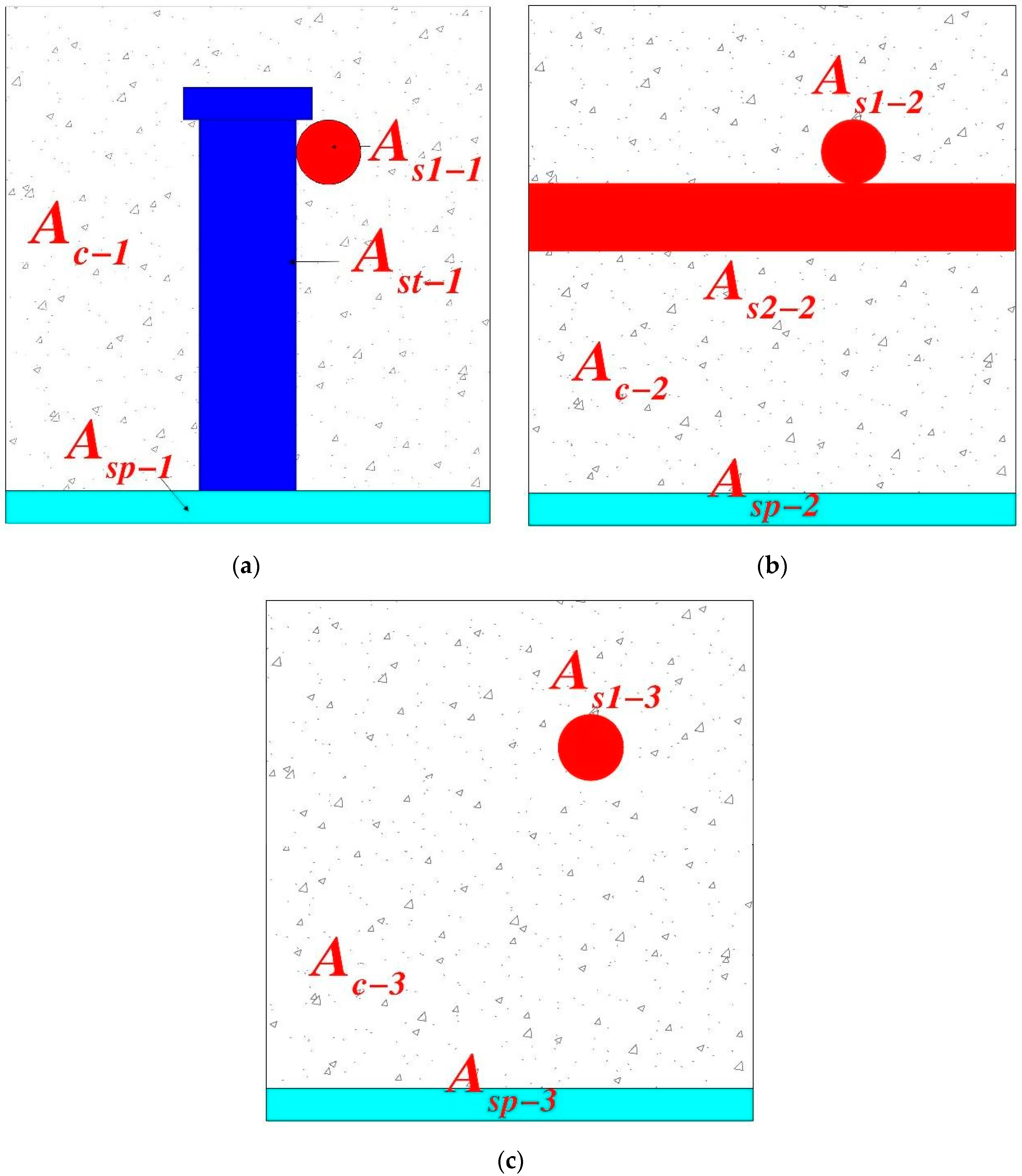
4.1. Confinement Factor of Concrete by Steel Plates, Pins, and Reinforcement Bars
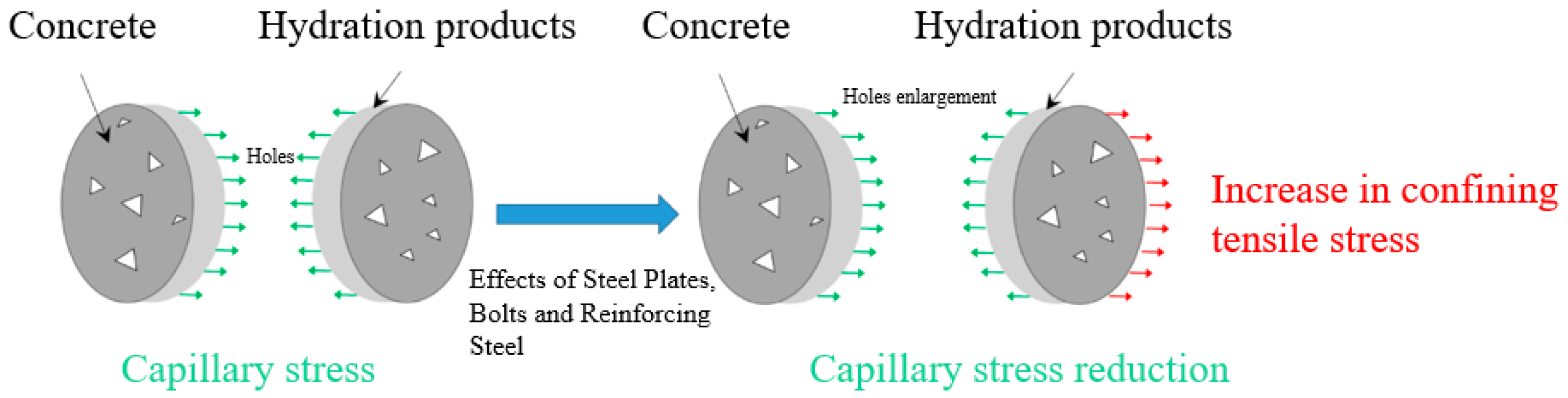
4.2. Influence of Steel Plates, Pins, and Reinforcement on the Structure of Concrete Holes
5. Shrinkage of Complex Internally Confined Concrete
5.1. Effect of Constraint Factor on Concrete Shrinkage
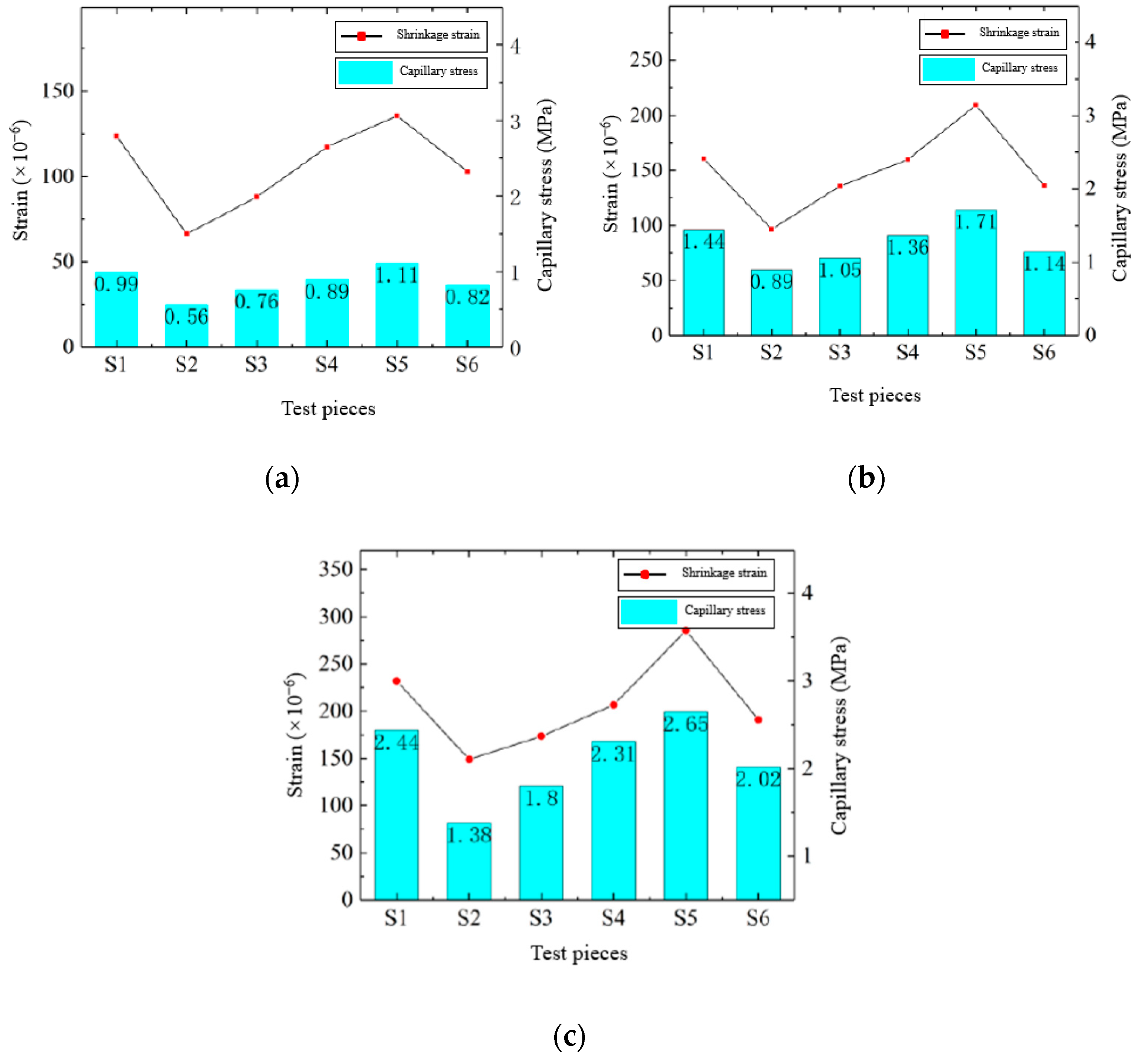
5.2. Effect of Constraint Coefficient on Capillary Pore Stresses
5.3. Effect of Capillary Pore Stress on Concrete Shrinkage
5.4. Shrinkage Prediction of Complex Internally Confined Concrete
6. Conclusions
- The degree of the restraining of concrete by the steel plate, studs, and reinforcement is expressed by the restraining coefficient λ. The larger the restraining coefficient, the stronger the restraining effect. The constraint coefficient increases with the increase in the steel plate thickness, reinforcement diameter, stud diameter, and stud height, and increases with the decrease in stud spacing.
- Steel plates, studs, and reinforcement have an important effect on concrete shrinkage, which decreases with the increase in the thickness of the steel plate, diameter of the reinforcement, diameter of the studs, and the height of the studs and increases with the increase in the stud spacing. This effect is not only due to the coordination of the deformation of the steel plate, studs, and reinforcement but also because the increase in the corresponding parameter increases the constraint coefficient. Moreover, the constraint factor will lead to a reduction in the capillary pore stress, which leads to a decrease in the shrinkage of the concrete.
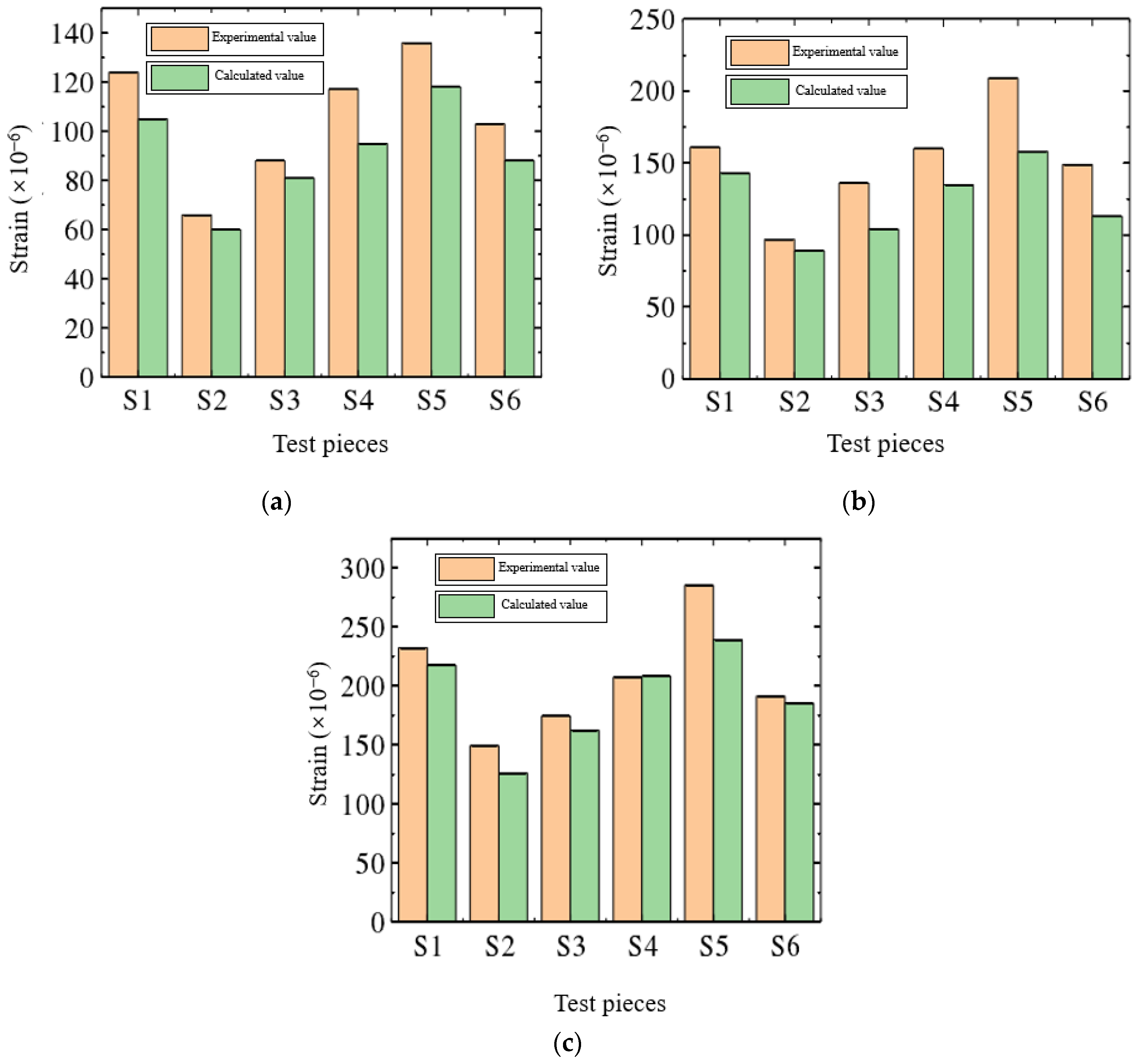
- Comparing the measured shrinkage strain values of restrained concrete at the ages of 3, 7, and 28 d with the predicted values of the shrinkage model revealed that the average error predicted during each age was below 15%. This proves that the shrinkage model is feasible for predicting the shrinkage strain of concrete under the joint constraints of steel plates, bolts, and steel bars.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, D.; Ma, Y.; Zhao, G.; Zhang, M.; Qiu, J. Seismic behavior of steel-plate encased concrete shear wall with paralleled circular CFST columns: Laboratory test and numerical simulation. Structures 2023, 49, 240–255. [Google Scholar] [CrossRef]
- Wang, W.; Ren, Y.; Lu, Z.; Song, J.; Han, B.; Zhou, Y. Experimental study of the hysteretic behaviour of corrugated steel plate shear walls and steel plate reinforced concrete composite shear walls. J. Constr. Steel Res. 2019, 160, 136–152. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Cao, W.; Yu, C. Seismic behavior of composite shear walls incorporating high-strength materials and CFST boundary elements. Eng. Struct. 2020, 220, 110994. [Google Scholar] [CrossRef]
- Li, B.; Li, J.; Xu, W. Dynamic Time Analysis of the Composite Shear Wall on the Grid-Tube-Type Double Steel Plate Wall with Infilled Concrete; IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; p. 012008. [Google Scholar]
- Ge, W.; Zhang, Z.; Xu, W.; Ashour, A.; Jiang, H.; Sun, C.; Song, S.; Cao, D. Seismic response of grid tubular-double steel plate concrete composite shear walls and combined system subjected to low reversed cyclic loading. Eng. Struct. 2022, 256, 114028. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, W.; Ge, W.; Abbas, E.M.A.; Jiang, H.; Wang, Y.; Yao, S. Seismic performance of grid tubular-double steel plate concrete composite shear wall. J. Constr. Steel Res. 2022, 189, 107077. [Google Scholar] [CrossRef]
- Xiang, T.; Liu, J.; Lv, Z.; Wei, F.; Liu, Q.; Zhang, Y.; Ren, H.; Zhou, S.; Chen, D. The effect of silicon-based waterproof agent on the wettability of superhydrophobic concrete and enhanced corrosion resistance. Constr. Build. Mater. 2021, 313, 125482. [Google Scholar] [CrossRef]
- Wang, L.; Yu, Z.; Liu, B.; Zhao, F.; Tang, S.; Jin, M. Effects of Fly Ash Dosage on Shrinkage, Crack Resistance and Fractal Characteristics of Face Slab Concrete. Fractal Fract. 2022, 6, 335. [Google Scholar] [CrossRef]
- Safiuddin, M.; Kaish, A.B.M.A.; Woon, C.-O.; Raman, S.N. Early-Age Cracking in Concrete: Causes, Consequences, Remedial Measures, and Recommendations. Appl. Sci. 2018, 8, 1730. [Google Scholar] [CrossRef]
- Shen, D.; Kang, J.; Liu, C.; Li, M.; Wei, Y.; Zhou, L. Effect of temperature rise inhibitor on early-age behavior and cracking resistance of high strength concrete under uniaxial restrained condition. J. Build. Eng. 2023, 64, 105588. [Google Scholar] [CrossRef]
- Ali, B.; Hawreen, A.; Ben Kahla, N.; Talha Amir, M.; Azab, M.; Raza, A. A critical review on the utilization of coir (coconut fiber) in cementitious materials. Constr. Build. Mater. 2022, 351, 128957. [Google Scholar] [CrossRef]
- Shang, M.; Qiao, H.; He, Z.; Zhang, Y.; Liu, X.; Zhang, Y.; Wang, J. Study on the shrinkage mechanism and prediction model of high-strength specified density concrete based on the internal curing micro-pump effect of MSW incineration tailings. Constr. Build. Mater. 2023, 372, 130804. [Google Scholar] [CrossRef]
- Shen, D.; Li, C.; Liu, C.; Li, M.; Kang, J. Experimental investigations on early-age tensile creep of internally cured high strength concrete under different initial stress/strength ratios. Constr. Build. Mater. 2020, 265, 120313. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Banthia, N.; Yoon, Y.-S. Effectiveness of shrinkage-reducing admixture in reducing autogenous shrinkage stress of ultra-high-performance fiber-reinforced concrete. Cem. Concr. Compos. 2015, 64, 27–36. [Google Scholar] [CrossRef]
- Shen, D.; Jiang, J.; Shen, J.; Yao, P.; Jiang, G. Influence of curing temperature on autogenous shrinkage and cracking resistance of high-performance concrete at an early age. Constr. Build. Mater. 2016, 103, 67–76. [Google Scholar] [CrossRef]
- Negahban, E.; Bagheri, A.; Sanjayan, J. One-Year study of restrained shrinkage and creep behaviours of geopolymer concrete. Constr. Build. Mater. 2023, 376, 131057. [Google Scholar] [CrossRef]
- Khan, I.; Xu, T.; Castel, A.; Gilbert, R.I. Early-age tensile creep and shrinkage-induced cracking in internally restrained concrete members. Mag. Concr. Res. 2019, 71, 1167–1179. [Google Scholar] [CrossRef]
- Gao, Z. Research on Evaluation Technique of Concrete Cracking Performance under Restraint Condition. For. Chem. Rev. 2022, 1034–1041. Available online: https://www.forestchemicalsreview.com/index.php/JFCR/article/view/986 (accessed on 1 August 2023).
- Huang, L.; Hua, J.; Kang, M.; Luo, Q.; Zhou, F. Influence of Steel Plates and Studs on Shrinkage Behavior and Cracking Potential of High-Performance Concrete. Materials 2019, 12, 342. [Google Scholar] [CrossRef]
- Chen, L.; Chen, Z.; Zhang, Y.; Liu, Y.; Osman, A.; Farghali, M.; Hua, J.; Al-Fatesh, A.; Ihara, I.; Rooney, D.; et al. Artificial intelligence-based solutions for climate change: A review. Environ. Chem. Lett. 2023. [Google Scholar] [CrossRef]
- Chen, L.; Huang, L.; Hua, J.; Chen, Z.; Wei, L.; Osman, A.; Fawzy, S.; Rooney, D.; Dong, L.; Yap, P. Green construction for low-carbon cities: A review. Environ. Chem. Lett. 2023, 21, 1627–1657. [Google Scholar] [CrossRef]
- Chen, L.; Msigwa, G.; Yang, M.; Osman, A.; Fawzy, S.; Rooney, D.; Yap, P. Strategies to achieve a carbon neutral society: A review. Environ. Chem. Lett. 2022, 20, 2277–2310. [Google Scholar] [CrossRef] [PubMed]
- JGJT380-2015; Technical Specification for Steel Plate Shear Walls. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2016.
- GB50010-2010; Concrete Structural Design Code. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2015.
- JGJ3-2010; Technical Specification for High-Rise Buildings with Concrete Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2010.
- JGJ138-2016; Combined Structural Design Specification. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2016.
- GB50011-2010; Seismic Design Code for Buildings. Ministry of Housing and Urban-Rural Development of the People’s Republic of China and General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2016.
- GBT50081-2019; Test Methods of Physical and Mechanical Properties of Concrete. Ministry of Housing and Urban-Rural Development of the People’s Republic of China and the State Administration of Market Supervision and Administration of the People’s Republic of China: Beijing, China, 2019.
- GB50017-2017; Steel Structure Design Standard. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2017.




| Water to Binder Ratio | Cement | Course Aggregate | Sand | Water | Fly Ash | Additive |
|---|---|---|---|---|---|---|
| 0.29 | 482 | 1064 | 680 | 154 | 48 | 12.7 |
| No. | Section Size (mm) | Plate Thickness (mm) | Distribution Rebar Straight Diameter (mm) | Bolt Diameter (mm) | Bolt Height (mm) | Bolt Spacing (mm) | Curing Condition |
|---|---|---|---|---|---|---|---|
| P | 1000 × 200 | 0 | 0 | 0 | 0 | 0 | Sealed |
| S1 | 1000 × 200 | 10 | 10 | 16 | 80 | 200 | Sealed |
| S2 | 1000 × 200 | 12 | 10 | 16 | 80 | 200 | Sealed |
| S3 | 1000 × 200 | 10 | 10 | 16 | 80 | 100 | Sealed |
| S4 | 1000 × 200 | 10 | 10 | 19 | 80 | 200 | Sealed |
| S5 | 1000 × 200 | 10 | 10 | 16 | 70 | 200 | Sealed |
| S6 | 1000 × 200 | 10 | 12 | 16 | 80 | 200 | Sealed |
| Basic Properties | Age (Days) | |||
|---|---|---|---|---|
| 3 | 7 | 14 | 28 | |
| Cube compressive strength (MPa) | 42.8 | 48.2 | 56.4 | 61.0 |
| Splitting tensile strength (MPa) | 3.8 | 4.1 | 4.5 | 5.2 |
| Elastic modulus (Gpa) | 30.0 | 32.3 | 35.0 | 35.5 |
| No. | Constraint Factor (×104 MPa) | ||
|---|---|---|---|
| 3 Days | 7 Days | 28 Days | |
| S1 | 3.75 | 3.87 | 4.04 |
| S2 | 4.15 | 4.27 | 4.44 |
| S3 | 3.96 | 4.08 | 4.26 |
| S4 | 3.79 | 3.91 | 4.09 |
| S5 | 3.72 | 3.84 | 4.01 |
| S6 | 3.85 | 3.97 | 4.14 |
| No. | Capillary Stress (MPa) | ||
|---|---|---|---|
| 3 Days | 7 Days | 28 Days | |
| S1 | 0.99 | 1.44 | 2.44 |
| S2 | 0.56 | 0.89 | 1.38 |
| S3 | 0.76 | 1.05 | 1.80 |
| S4 | 0.89 | 1.36 | 2.31 |
| S5 | 1.11 | 1.71 | 2.65 |
| S6 | 0.82 | 1.14 | 2.02 |
| No. | 3 Days | 7 Days | 28 Days | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Tested Values | Calculated Values | Relative Error | Tested Values | Calculated Values | Relative Error | Tested Values | Calculated Value | Relative Error | |
| S1 | 124 | 105 | 15.0% | 161 | 143 | 10.9% | 232 | 220 | 5.3% |
| S2 | 66 | 60 | 9.5% | 97 | 89 | 8.4% | 149 | 125 | 16.3% |
| S3 | 88 | 81 | 7.7% | 136 | 104 | 23.4% | 174 | 162 | 6.8% |
| S4 | 117 | 95 | 19.1% | 160 | 135 | 15.7% | 207 | 208 | 0.9% |
| S5 | 136 | 118 | 13.2% | 209 | 169 | 19.2% | 285 | 239 | 16.4% |
| S6 | 103 | 88 | 14.9% | 136 | 113 | 16.8% | 191 | 182 | 4.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, F.; Jiang, H.; Huang, L.; Hu, Y.; Xie, Z.; Zeng, Z.; Liu, M.; Wang, B.; Zhou, X. Early Shrinkage Modeling of Complex Internally Confined Concrete Based on Capillary Tension Theory. Buildings 2023, 13, 2201. https://doi.org/10.3390/buildings13092201
Zhou F, Jiang H, Huang L, Hu Y, Xie Z, Zeng Z, Liu M, Wang B, Zhou X. Early Shrinkage Modeling of Complex Internally Confined Concrete Based on Capillary Tension Theory. Buildings. 2023; 13(9):2201. https://doi.org/10.3390/buildings13092201
Chicago/Turabian StyleZhou, Fengbin, Hao Jiang, Lepeng Huang, Ying Hu, Zhuolin Xie, Zhikai Zeng, Maoyi Liu, Bo Wang, and Xingyang Zhou. 2023. "Early Shrinkage Modeling of Complex Internally Confined Concrete Based on Capillary Tension Theory" Buildings 13, no. 9: 2201. https://doi.org/10.3390/buildings13092201
APA StyleZhou, F., Jiang, H., Huang, L., Hu, Y., Xie, Z., Zeng, Z., Liu, M., Wang, B., & Zhou, X. (2023). Early Shrinkage Modeling of Complex Internally Confined Concrete Based on Capillary Tension Theory. Buildings, 13(9), 2201. https://doi.org/10.3390/buildings13092201






