Research on Lateral Performance of Corrugated Steel Plate Shear Walls Connected with Beams Only under Horizontal Loads
Abstract
1. Introduction
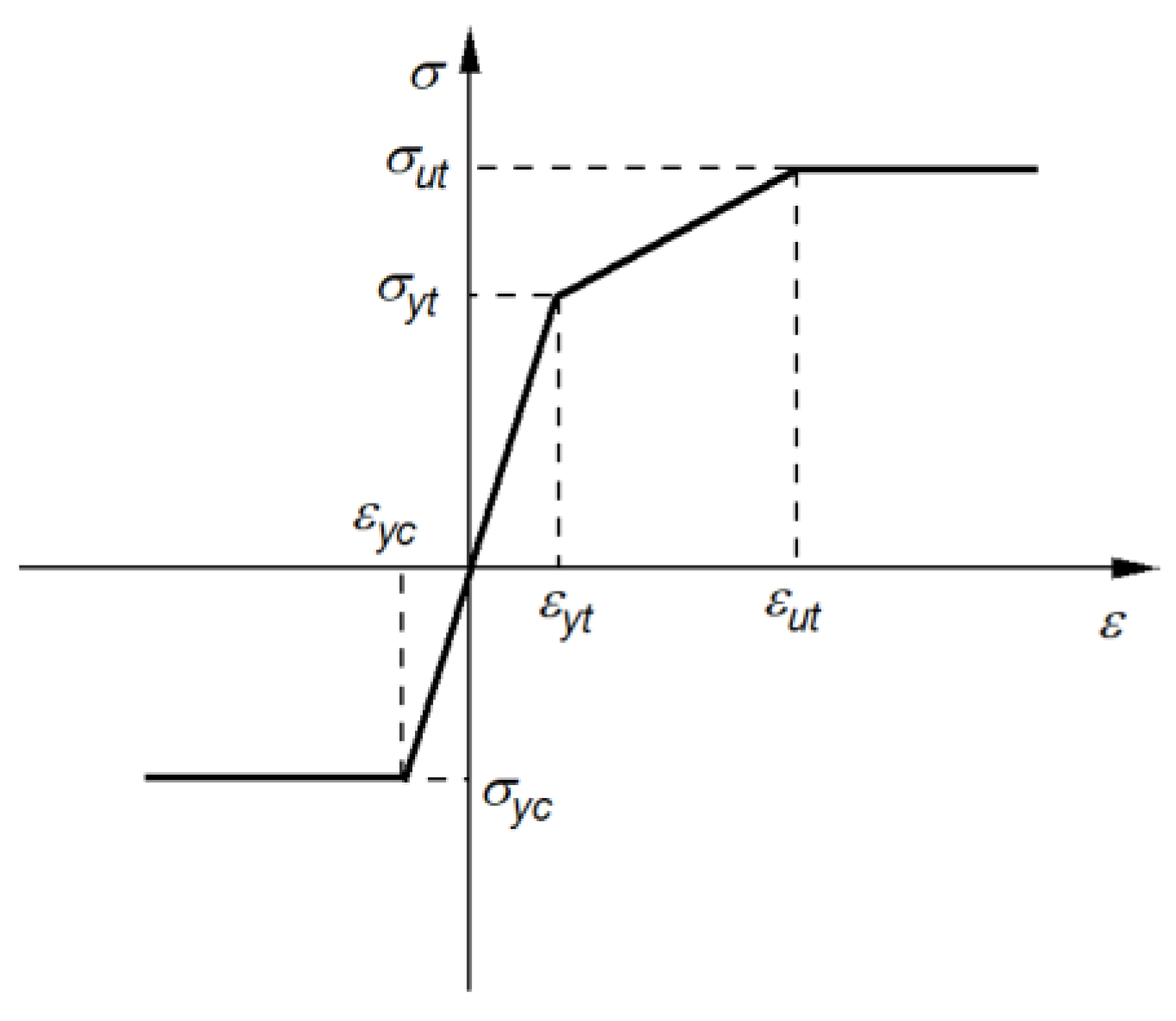
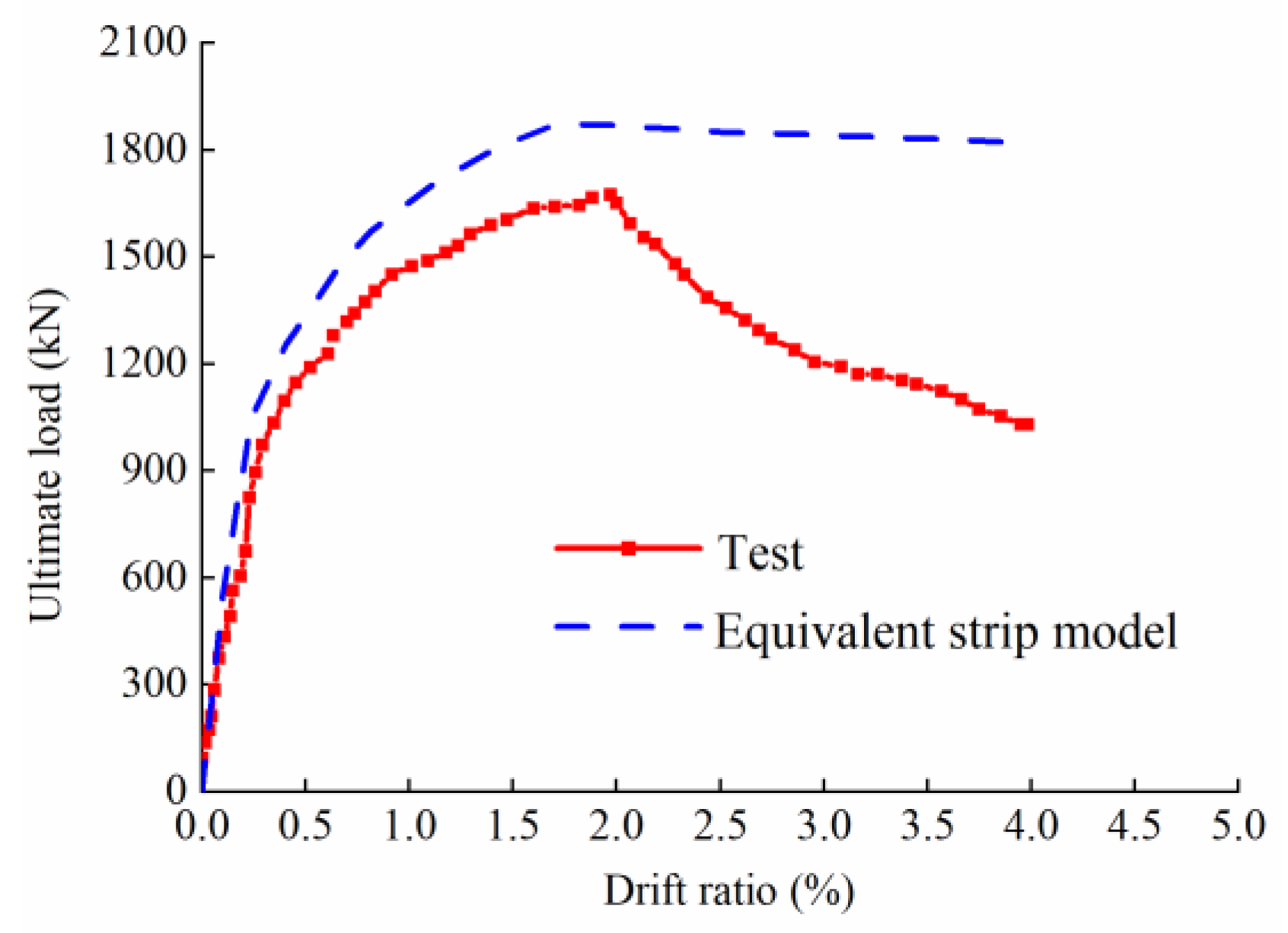
2. Finite Element (FE) Model and Verification
3. Parametric Analyses and Discussions
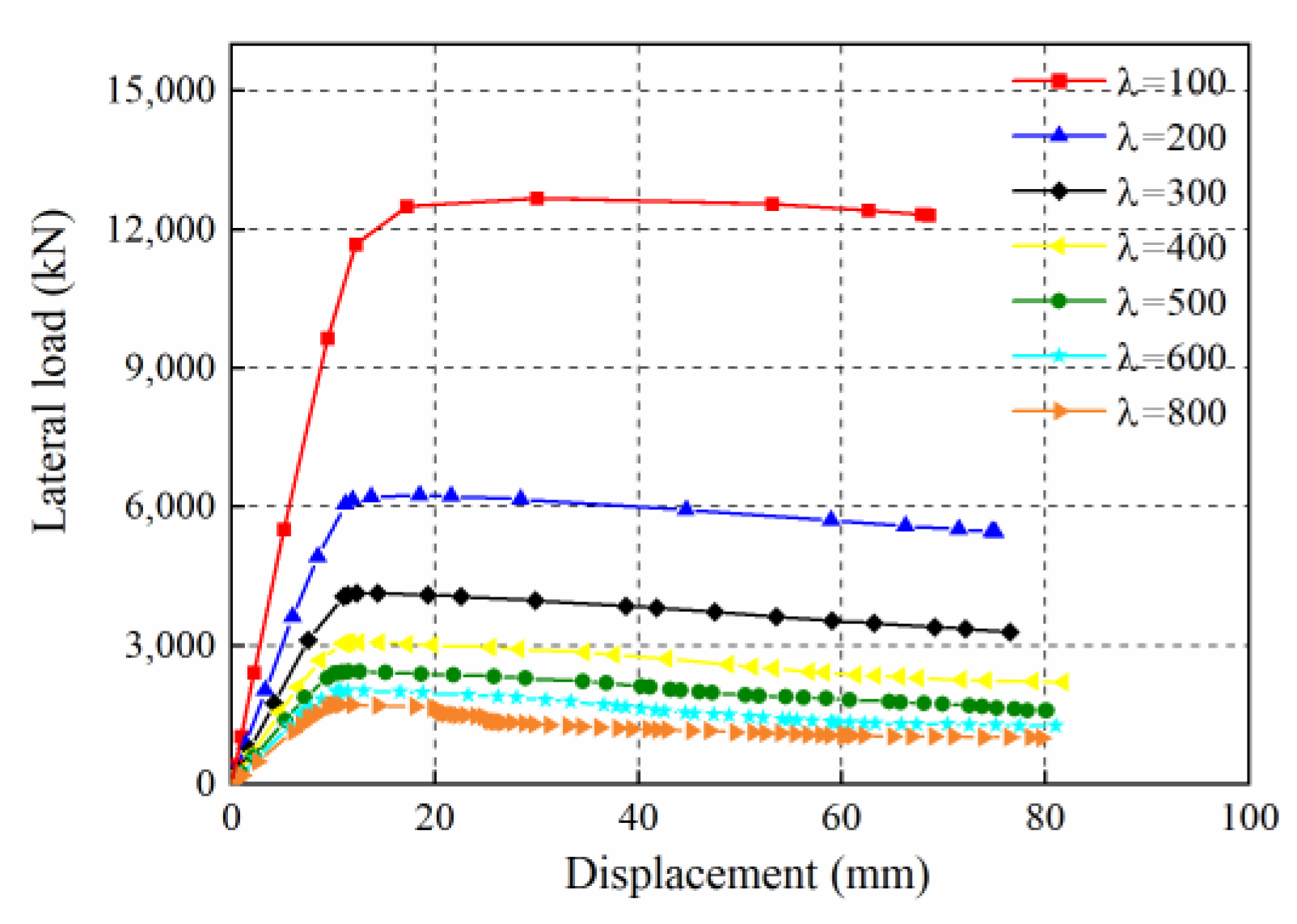
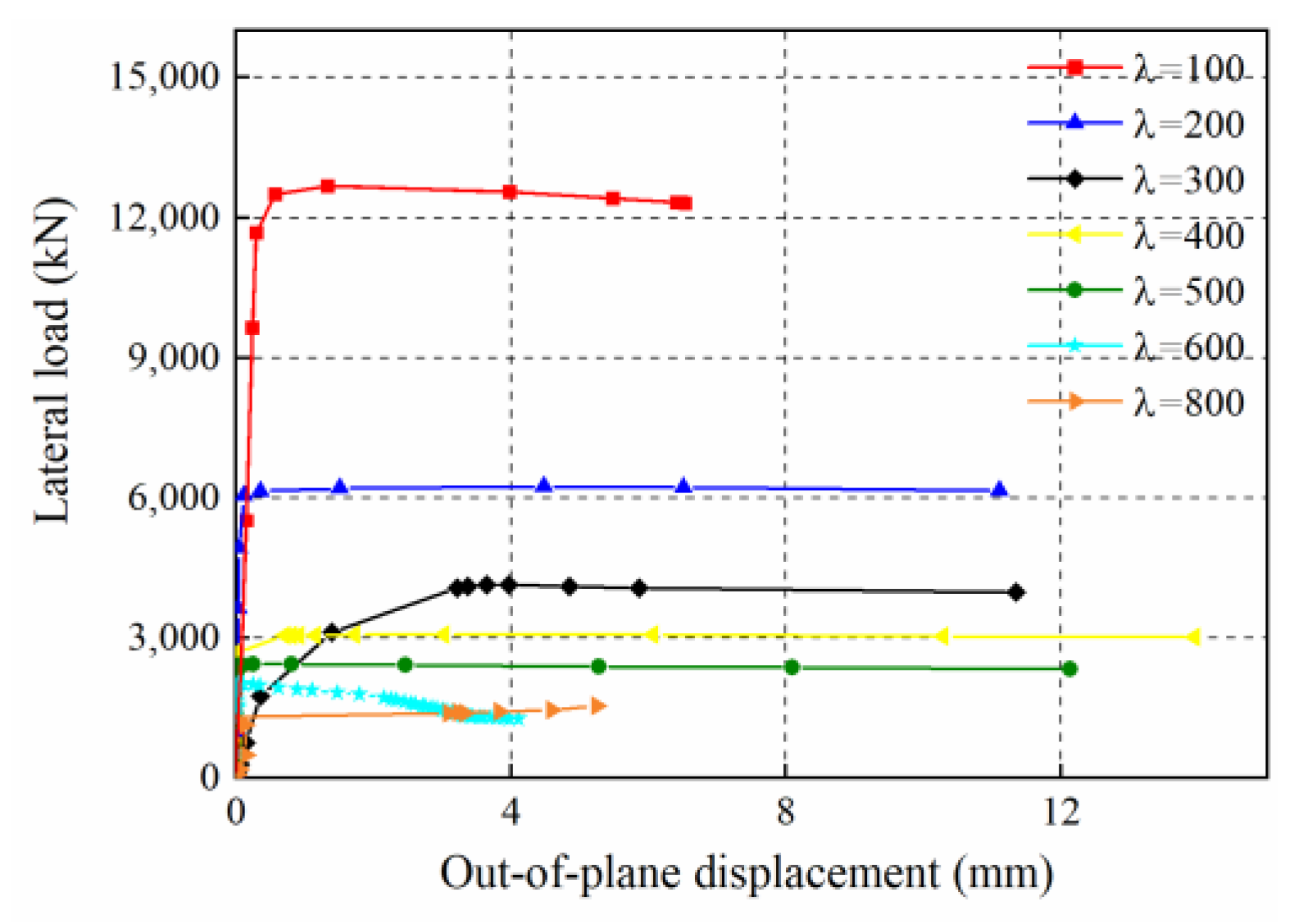
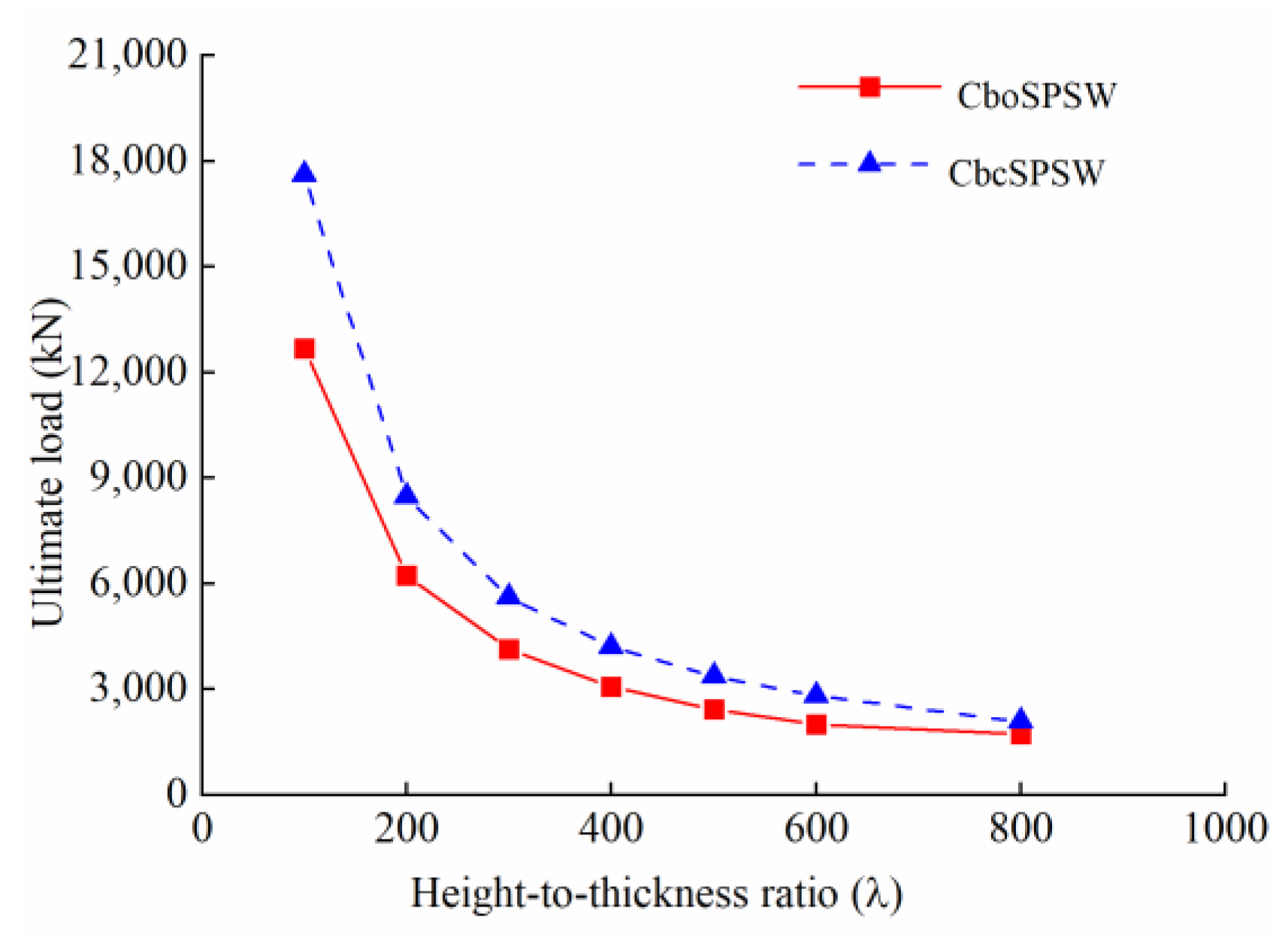
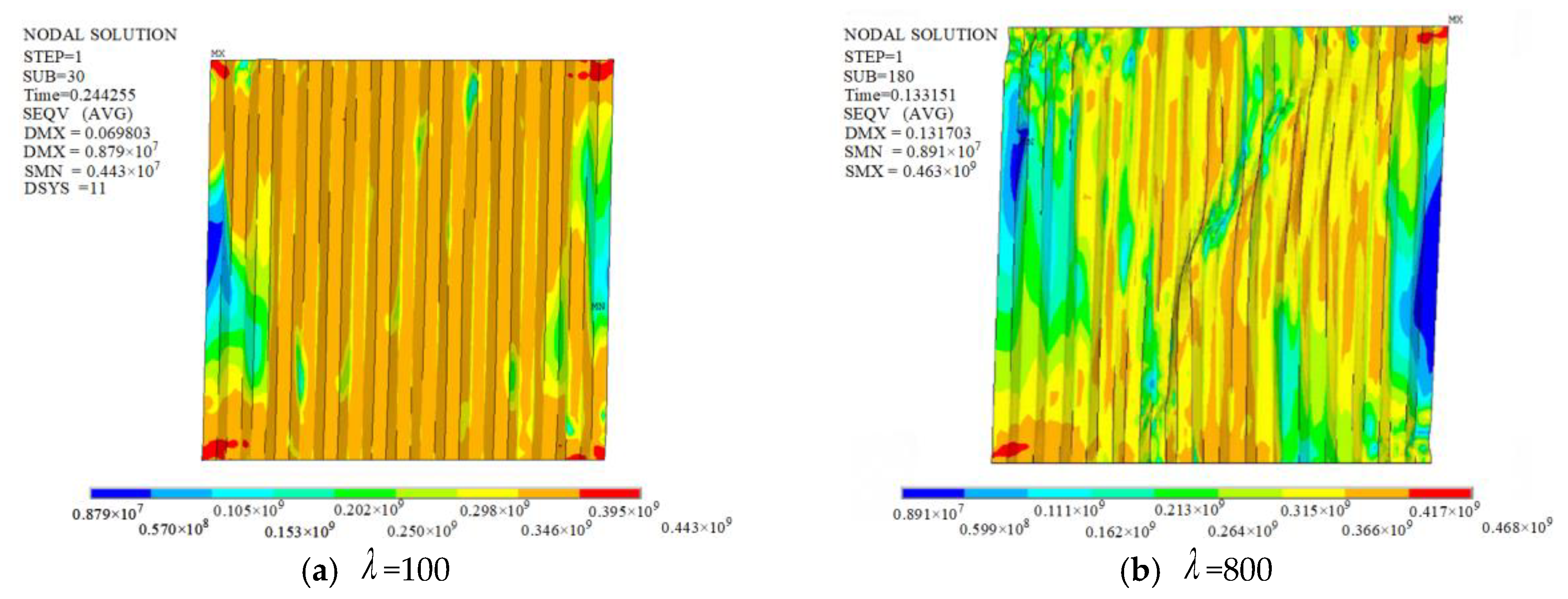
3.1. Height–Thickness Ratio Effect
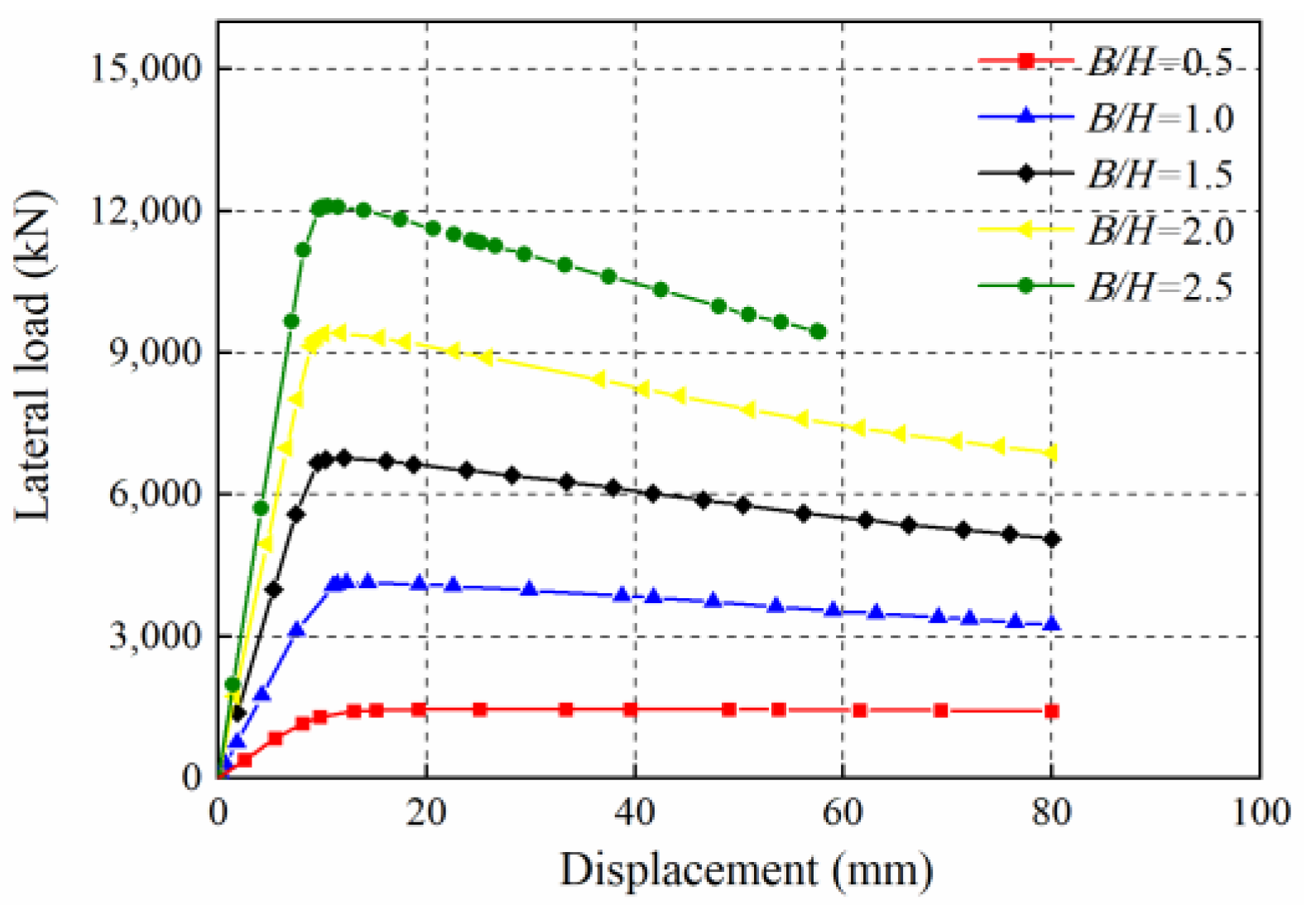
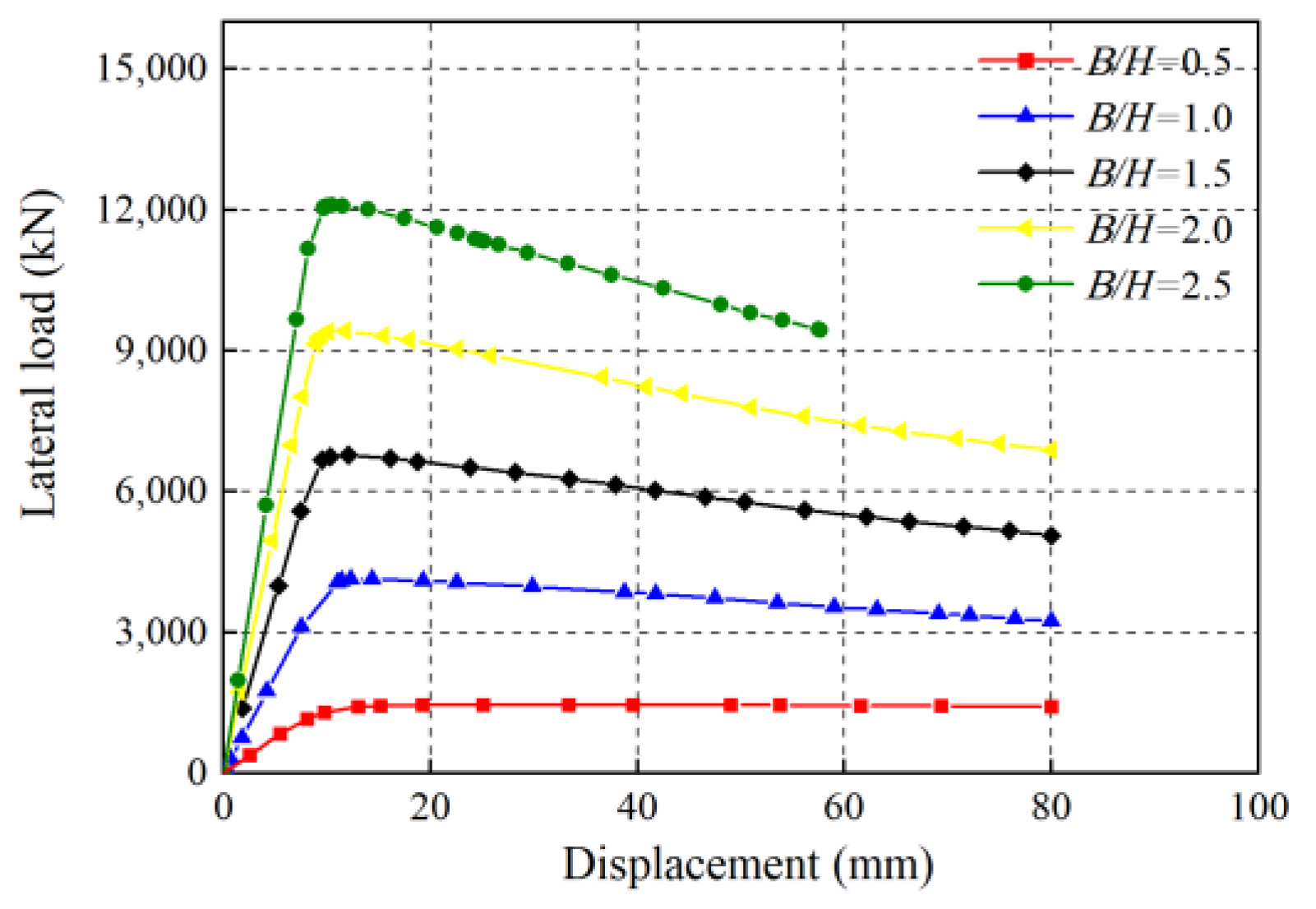
3.2. Aspect Ratio Effect
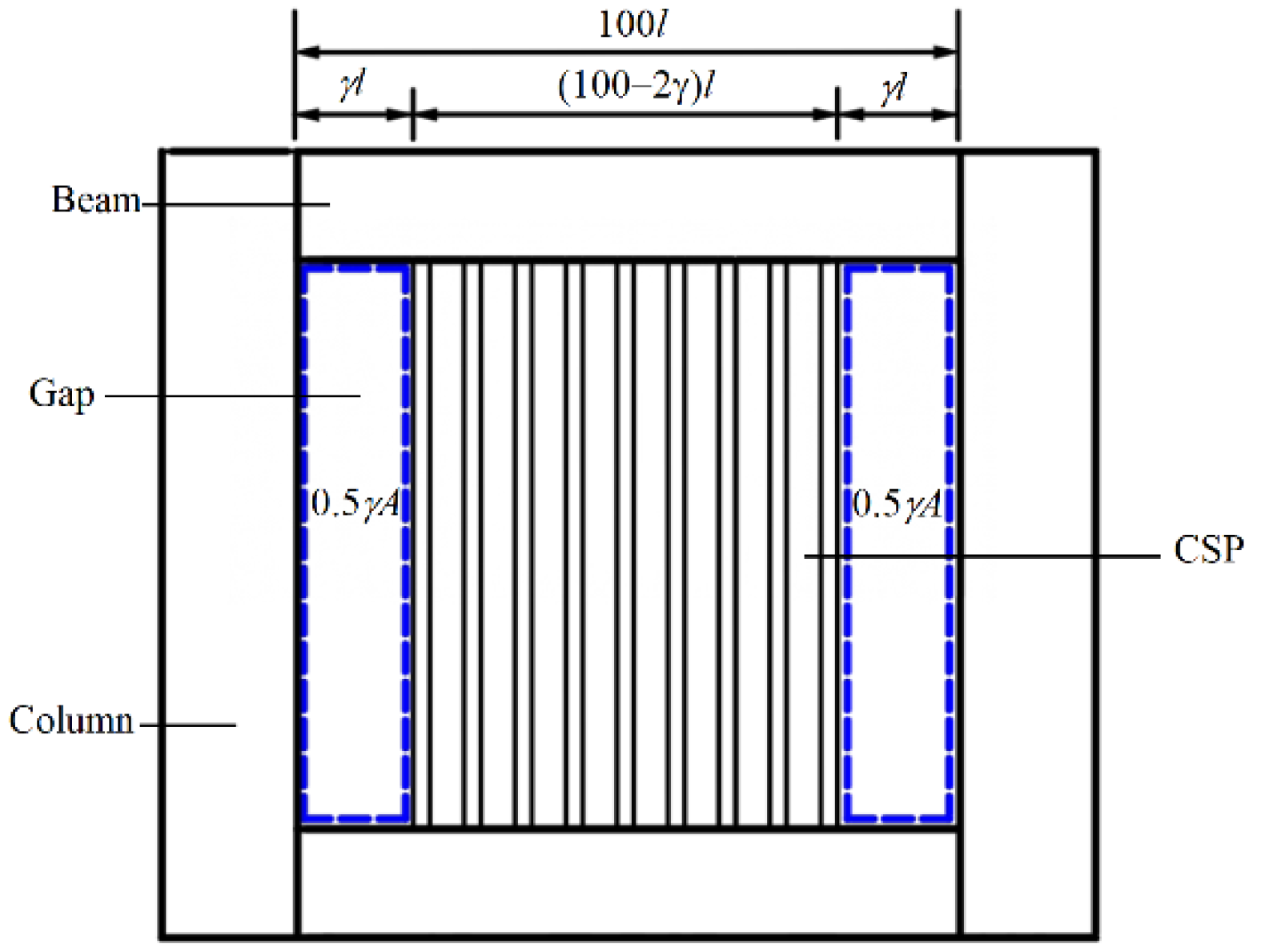
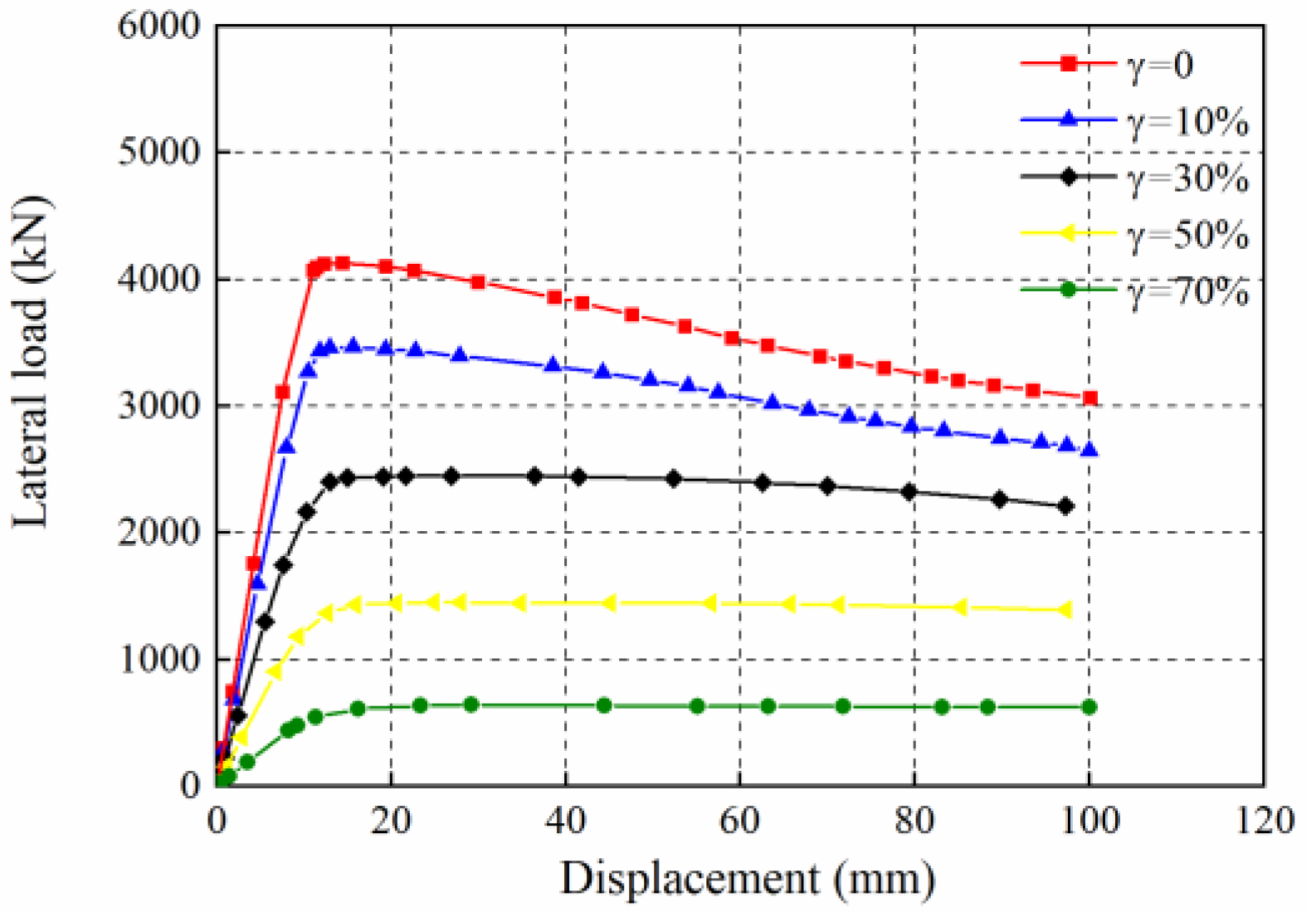
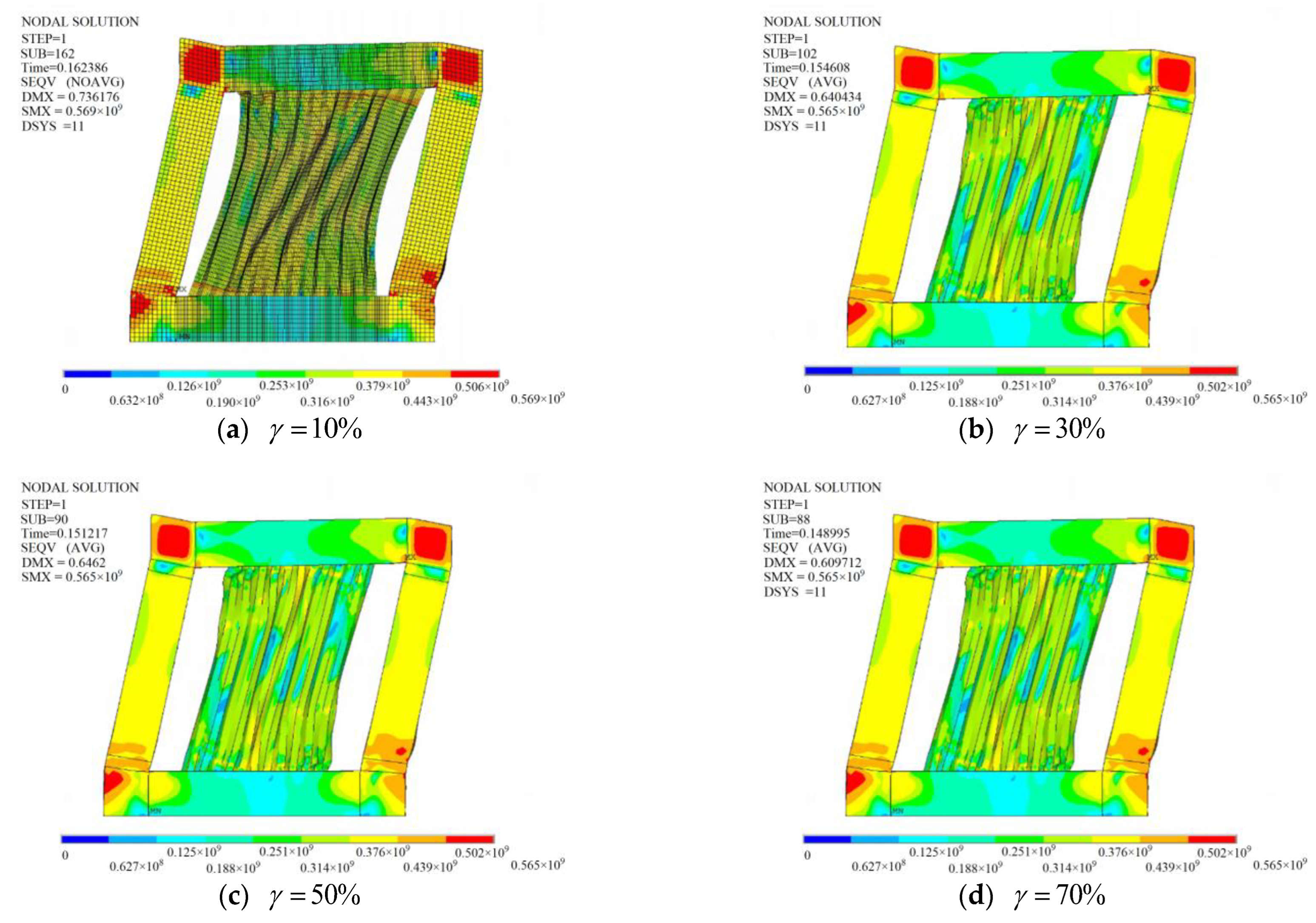
3.3. Opening Rate Effect
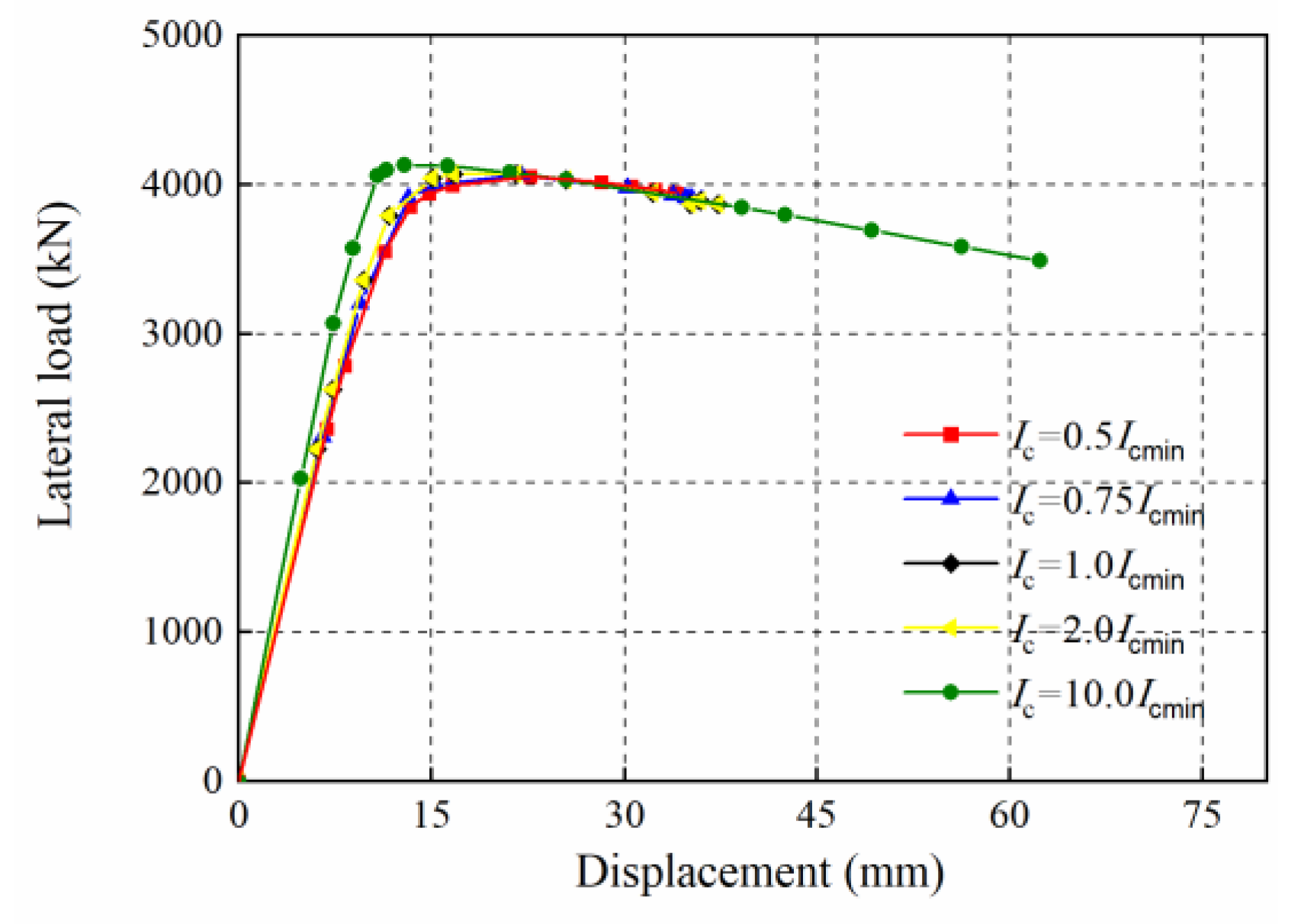
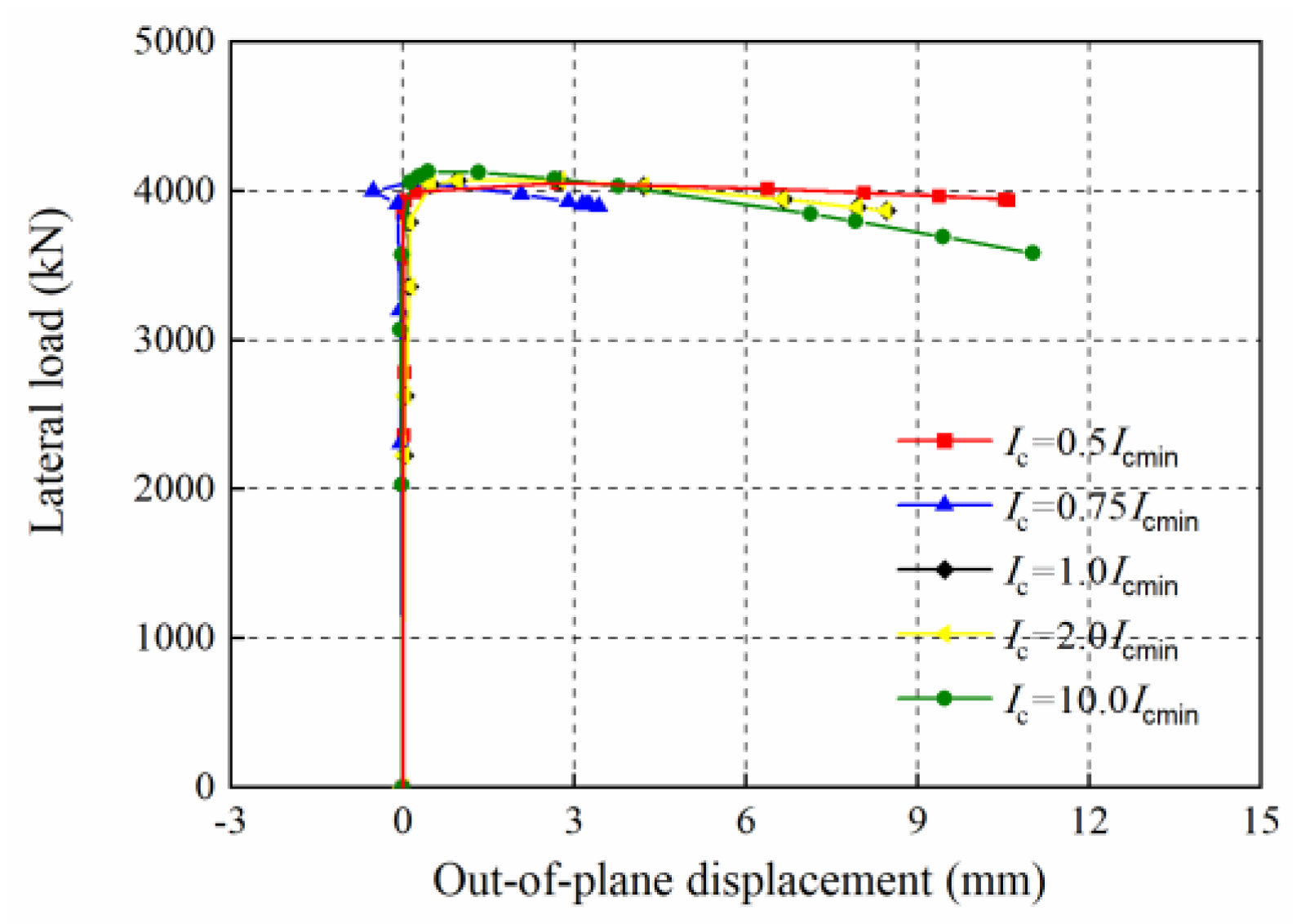
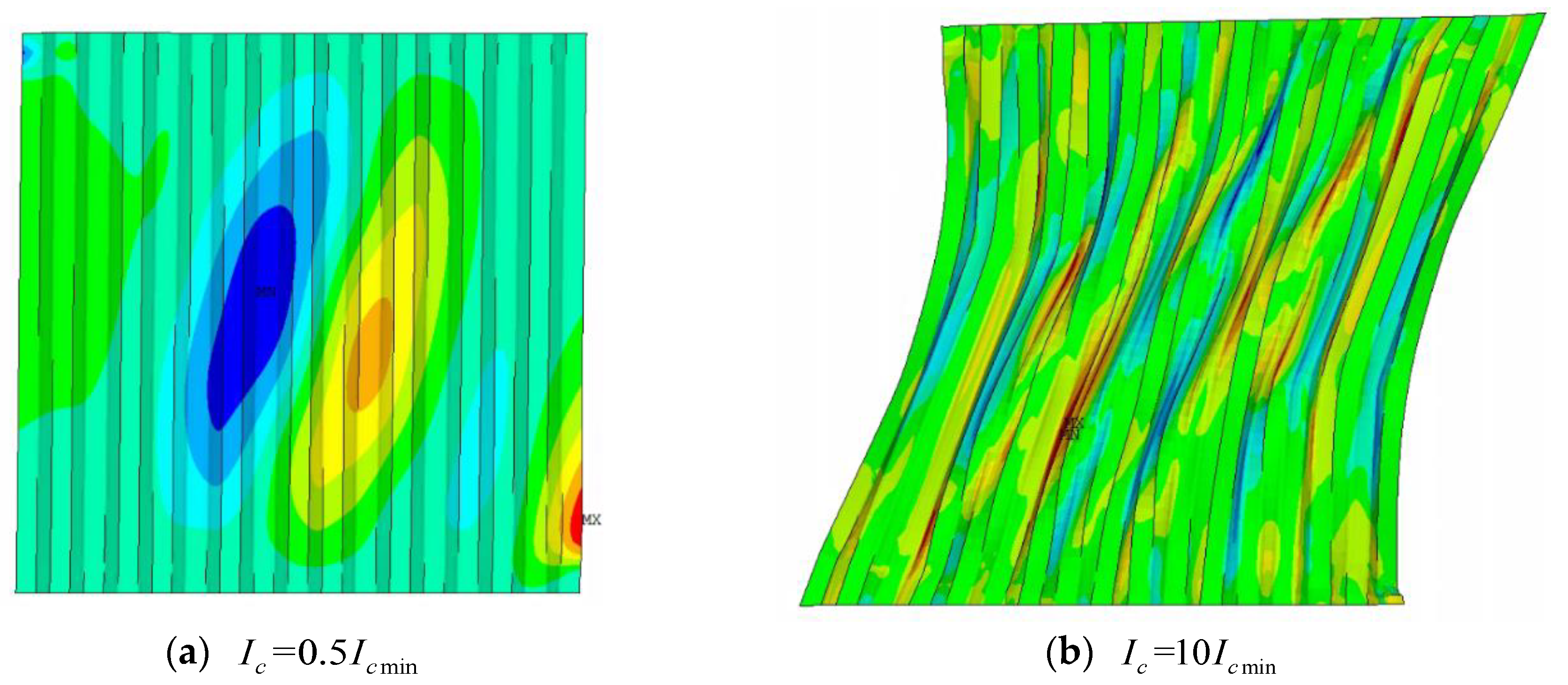
3.4. Surrounding Frame Stiffness Effect
4. Simplified Analytical Model
5. Conclusions
- (1)
- The initial stiffness and strength have a negative relationship with the height–thickness ratio. In contrast with the strength of the CSPs in CbcSPSWs, the strength of CSPs in CboSPSWs is lesser. When the height–thickness ratio increases from 100 to 800, the ultimate loads of the CSPs in the CboSPSWs decrease from 19% to 28% compared to those of the CbcSPSWs. The initial stiffnesses of the CboSPSWs decrease from 26% to 33% compared to those of the CbcSPSWs.
- (2)
- The free edges of CSPs under compression are easy to buckle and deform, and this is the reason the mechanical properties of the CSPs in the CboSPSWs are not fully utilized. Moreover, the corners of the CSPs are the first parts to be destroyed. It is suggested that the free edges of CSPs should be strengthened by adding stiffeners on one side or two sides of the CSPs in practical projects.
- (3)
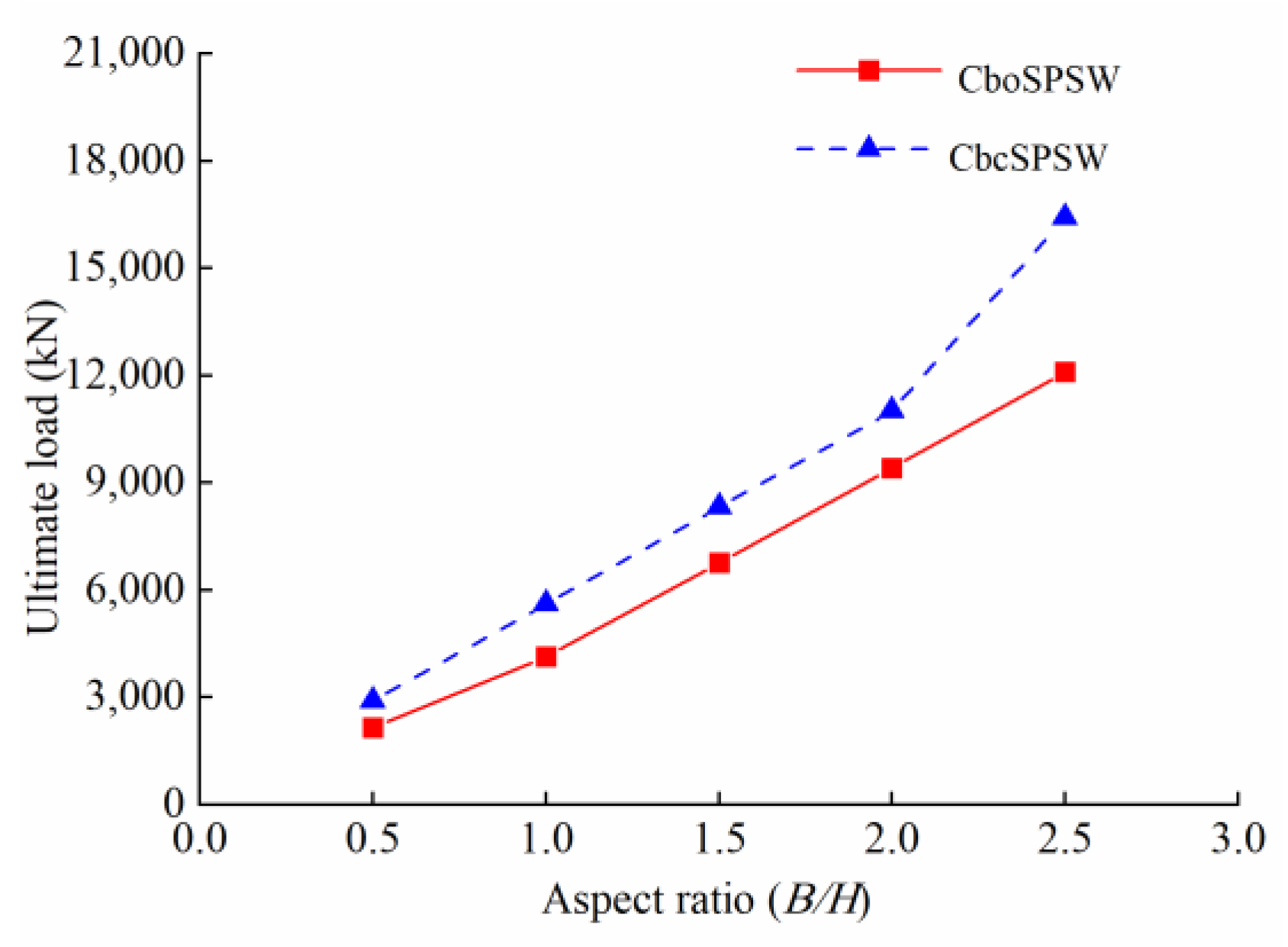
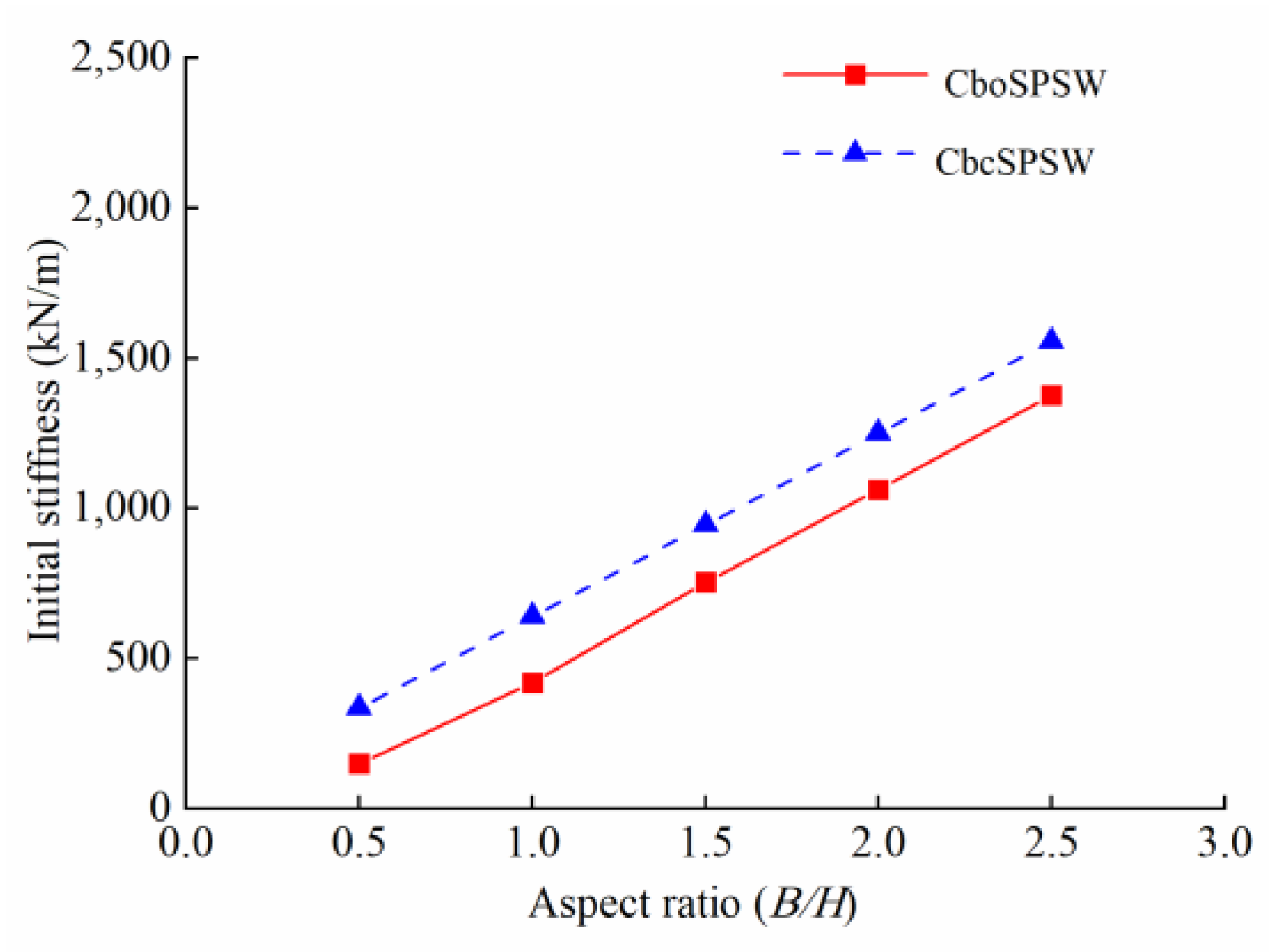
- The initial stiffnesses and ultimate loads of the CboSPSWs increase with the increase of the aspect ratio. The initial stiffnesses and ultimate loads of the CboSPSWs are lower than those of the CbcSPSWs. When the aspect ratio increases from 0.5 to 2.5, due to the connections with beams only, the strengths of the CboSPSWs decrease 15–27% compared to those of the CbcSPSWs, and the initial stiffnesses of the CboSPSWs decrease from 15% to 27% compared to those of the CbcSPSWs. It is suggested that the aspect ratio should be controlled less than 2.0 for a strength decrease of the CSPs.
- (4)
- The ultimate capacities and initial stiffness have a linear decrease relationship with the opening rate. When the opening rates are 50% and 70%, the CSPs show bending and compressive performance, which is similar to performance of the columns. Therefore, the opening rate should be less than 50% in the design of CboSPSWs.
- (5)
- The modified equivalent strip model for the CboSPSW was developed to simplify the elasto-plastic analysis. The results show that the modified equivalent strip model can simulate the shear behavior of the CboSPSW well.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Opening area | |
| Whole area of the CSP | |
| Section areas of the tension and compressive members in the strip model | |
| Horizontal subpanel width of the corrugated steel plate | |
| Width of the corrugated plate | |
| Single wavelength of the corrugated plate | |
| Horizontal projection of the inclined panel width | |
| Center-to-center distance of adjacent beams | |
| Center-to-center distance between adjacent columns | |
| Elastic modulus of the CSP material | |
| Elastic modulus of the tension member | |
| Elastic modulus of the CSP material | |
| Yield stress of a corrugated steel plate | |
| Shear yield stress of a corrugated steel plate | |
| Shear modulus of a corrugated steel plate | |
| Corrugation depth of the corrugated plate | |
| Height of corrugated steel plate | |
| Minimum area moment of inertia of a surrounding column | |
| Initial stiffness of the CboSPSW | |
| Initial stiffness of the corrugated steel plate | |
| Length of the opening in equivalent strip model | |
| Thickness of the corrugated steel plate | |
| Lateral force of the CSPSW | |
| Ultimate shear load of a CboSPSW with an opening rate | |
| Ultimate shear load of a CboSPSW with no opening | |
| Yield load of a corrugated steel plate | |
| Compressive load of a corrugated steel plate | |
| Compressive displacement of a corrugated steel plate | |
| Displacement corresponding to the ultimate load of a corrugated steel plate | |
| Poisson’s ratio of steel | |
| Corrugation angle | |
| Yield stress of the tension member in the strip model | |
| Yield stress of the compression member | |
| Ultimate tensile stress of the compression member | |
| Uniformity coefficient of shear load along CSP width | |
| Inclination angle of the tension field in the corrugated steel plate | |
| Reduction coefficient of the lateral stiffness of a CSP | |
| Height–thickness ratio | |
| Opening rate | |
| Yield stress of a corrugated steel plate | |
| Compressive stress of a corrugated steel plate | |
| Compressive strain of a tension member in the strip model | |
| Ultimate tensile strain corresponding to the ultimate load of the tension member |
References
- Wang, W.; Ren, Y.; Lu, Z.; Song, J.; Han, B.; Zhou, Y. Experimental study of the hysteretic behaviour of corrugated steel plate shear walls and steel plate reinforced concrete composite shear walls. J. Constr. Steel Res. 2019, 160, 136–152. [Google Scholar] [CrossRef]
- Kalali, H.; Hajsadeghi, M.; Zirakian, T.; Alaee, F.J. Hysteretic performance of SPSWs with trapezoidally horizontal corrugated web-plates. Steel Compos. Struct. 2015, 19, 277–292. [Google Scholar] [CrossRef]
- Fadhil, H.; Ibrahim, A.; Mahmood, M. Effect of corrugation angle and direction on the performance of corrugated steel plate shear walls. Civ. Eng. J. 2018, 4, 2667. [Google Scholar] [CrossRef]
- Berman, J.; Bruneau, M. Experimental investigation of self-centering steel plate shear wall. Struct Eng. 2005, 131, 259–267. [Google Scholar] [CrossRef]
- Dou, C.; Pi, Y.L.; Gao, W. Shear resistance and post-buckling behavior of corrugated panels in steel plate shear walls. Thin-Walled Struct. 2018, 131, 816–826. [Google Scholar] [CrossRef]
- Wang, W.; Quan, C.; Li, Y.; Zhen, G.K.; Zhao, H.T. Experimental study and numerical simulation analysis on seismic performance of corrugated steel-plate shear wall with replaceable bottom corner dampers. Soil Dyn. Earthq. Eng. 2022, 152, 107061. [Google Scholar] [CrossRef]
- Farzampour, A.; Hu, J. Mansouri. Seismic Behaviour Investigation of the Corrugated Steel Shear Walls Considering Variations of Corrugation Geometrical Characteristics. Int. J. Steel Struct. 2018, 18, 1297–1305. [Google Scholar] [CrossRef]
- Gholizadeh, M.; Yadollahi, Y. Comparing Steel Plate Shear Wall Behavior with Simple and Corrugated Plates. Appl. Mech. Mater. 2012, 1599, 80–85. [Google Scholar] [CrossRef]
- Emami, F.; Mofid, M.; Vafai, A. Experimental study on cyclic behaviour of trapezoidally corrugated steel shear walls. Eng. Struct. 2013, 48, 750–762. [Google Scholar] [CrossRef]
- Edalati, S.A.; Yadollahi, Y.; Pakar, I.; Emadi, A.; Bayat, M. Numerical study on the performance of corrugated steel shear walls. Wind. Struct. 2014, 19, 405–420. [Google Scholar] [CrossRef]
- Shon, S.; Yoo, M.; Lee, S. An experimental study on the shear hysteresis and energy dissipation of the steel frame with a trapezoidal-corrugated steel plate. Materials 2017, 10, 261. [Google Scholar] [CrossRef]
- Bahrebar, M.; Kabir, M.Z.; Hajsadeghi, M.; Zirakian, T.; Lim, J.B. Structural performance of steel plate shear walls with trapezoidal corrugations and centrally-placed square perforations. Int. J. Steel Struct. 2016, 16, 845–855. [Google Scholar] [CrossRef]
- Dou, C.; Jiang, Z.; Pi, Y.; Guo, Y. Elastic shear buckling of sinusoidally corrugated steel plate shear wall. Eng. Struct. 2016, 121, 146–156. [Google Scholar] [CrossRef]
- Tong, J.; Guo, Y. Shear resistance of stiffened steel corrugated shear walls. Thin-Walled Struct. 2018, 127, 76–79. [Google Scholar] [CrossRef]
- Zhang, W.; Mahdavian, M.; Li, Y.; Yu, C. Experiments and simulations of cold-formed steel wall assemblies using corrugated steel sheathing subjected to shear and gravity loads. Struct. Eng. 2017, 143, 04016193. [Google Scholar] [CrossRef]
- Tong, J.Z.; Guo, Y.L. Elastic buckling behavior of steel trapezoidal corrugated shear walls with vertical stiffeners. Thin-Walled Struct. 2015, 95, 31–39. [Google Scholar] [CrossRef]
- Feng, L.; Sun, T.; Ou, J. Elastic buckling analysis of steel-strip-stiffened trapezoidal corrugated steel plate shear walls. J. Constr. Steel Res. 2021, 184, 106833. [Google Scholar] [CrossRef]
- Zhao, Q.; Qiu, J.; Zhao, Y.; Cheng, Y. Performance-Based Seismic Design of Corrugated Steel Plate Shear Walls. KSCE J. Civ. Eng. 2022, 26, 3486–3503. [Google Scholar] [CrossRef]
- Zhao, Q.; Qiu, J.; Li, N.; Li, Z. Experimental study on seismic performance of trapezoidally corrugated steel plate shear walls. Jianzhu Jiegou Xuebao/J. Build. Struct. 2018, 39, 112–120. [Google Scholar]
- Cao, Q.; Huang, J.; Zhao, L.; Fang, Z.; Zhang, Z. Research on shear performance of corrugated steel plate shear walls with inelastic buckling of infilled plates under lateral loads. J. Build. Eng. 2022, 52, 104406. [Google Scholar] [CrossRef]
- Farzampour, A.; Laman, J. Behavior prediction of corrugated steel plate shear walls with openings. J. Constr. Steel Res. 2015, 114, 258–268. [Google Scholar] [CrossRef]
- Emami, F.; Mofid, M. On the hysteretic behavior of trapezoidally corrugated steel shear walls. Struct. Des. Tall Spec. Build. 2014, 23, 94–104. [Google Scholar] [CrossRef]
- Zhao, Q.; Qiu, J.; Li, Y.; Yu, C. Lateral behavior and PFI model of sinusoidal corrugated steel plate shear walls. J. Constr. Steel Res. 2023, 203, 107812. [Google Scholar] [CrossRef]
- Deng, E.F.; Zong, L.; Wang, H.P.; Shi, F.W.; Ding, Y. High efficiency analysis model for corrugated steel plate shear walls in modular steel construction. Thin-Walled Struct. 2020, 156, 106963. [Google Scholar] [CrossRef]
- Tong, J.-Z.; Guo, Y.-L.; Zuo, J.-Q. Elastic buckling and load-resistant behaviors of double-corrugated-plate shear walls under pure in-plane shear loads. Thin-Walled Struct. 2018, 130, 593–612. [Google Scholar] [CrossRef]
- Deng, R.; Yang, J.D.; Gao, Y.; Wang, Y.H.; Li, Q.Q. Behaviour of double-corrugated steel plates under cyclic in-plane shear loading: An experimental study. Eng. Struct. 2023, 276, 115327. [Google Scholar] [CrossRef]
- Wang, W.; Song, J.; Hou, M.; Liu, G.; Wang, W. Experimental study and numerical simulation of replaceable corrugated steel plate-concrete composite shear walls. Soil Dyn. Earthq. Eng. 2019, 127, 105827. [Google Scholar] [CrossRef]
- Huang, S. Experimental Study on Seismic Behavior of Corrugated Steel Shear Walls. Ph.D. Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2019. [Google Scholar]
- Wang, W.; Zhao, H.T.; Quan, C.C.; Song, H.L.; Li, Y.; Zhou, Y.X. Shear bearing capacity of vertical corrugated steel plate shear wall with replaceable toe. Zhejiang Daxue Xuebao (Gongxue Ban) 2021, 55, 1407–1418. [Google Scholar]
- Feng, L.; Sun, T.; Qu, J. Method of determining the minimum number of stiffeners for stiffened corrugated steel walls. Structures 2021, 34, 3487–3500. [Google Scholar] [CrossRef]
- Zhao, Q.; Qiu, J.; Hao, B. Lateral behaviour of vertically-corrugated Steel plate shear walls connected with beams only. J. Tianjin Univ. (Sci. Technol.) 2019, 2, 46–53. (In Chinese) [Google Scholar]
- Qiu, M. Seismic Performance Analysis of Corrugated Steel Plate Shear Wall Connected at Both Sides. Master’s Thesis, Dalian University of Technology, Dalian, China, 2020. (In Chinese). [Google Scholar]
- Kashan, S.M.G.; Maleki, S. Cyclic Performance of Corrugated Steel Plate Shear Walls with Beam-Only-Connected Infill Plates. Adv. Civ. Eng. 2021, 2021, 554623. [Google Scholar]
- Montgomery, C.J.; Medhekar, M.; Lubell, A.S.; Prion, H.G.; Ventura, C.E.; Rezai, M. Unstiffened steel plate shear wall performance under cyclic loading. Structure. Eng. 2001, 127, 973–975. [Google Scholar] [CrossRef]
- CAN/CSA-S1601; Limits States Design of Steel Structures. Canadian Standards Association: Mississauga, ON, Canada, 2001.
- ANSI/AISC 341-05; Seismic Provision for Structural Steel Buildings. American Institute of Steel Construction: Chicago, IL, USA, 2005.
- Berman, J.; Bruneau, M. Plastic Analysis and Design of Steel Plate Shear Walls. J. Struct. Eng. 2003, 129, 695–697. [Google Scholar] [CrossRef]
- Shishkin, J.; Ver, R.; Grondin, G. Analysis of Steel Plate Shear Walls Using the Modified Strip Model; Department of Civil and Environmental Engineering, University of Alberta: Edmonton, AB, Canada, 2005. [Google Scholar]
- Gb 50011; Code for Seismic Design of Buildings 2010. China Ministry of Construction: Beijing, China, 2010. (In Chinese)
- Qu, L.; Zhuang, Y.; Shao, H. Form factor for shear and its calculation Tables. J. Build. Struct. 1986, 8, 37–53. (In Chinese) [Google Scholar]
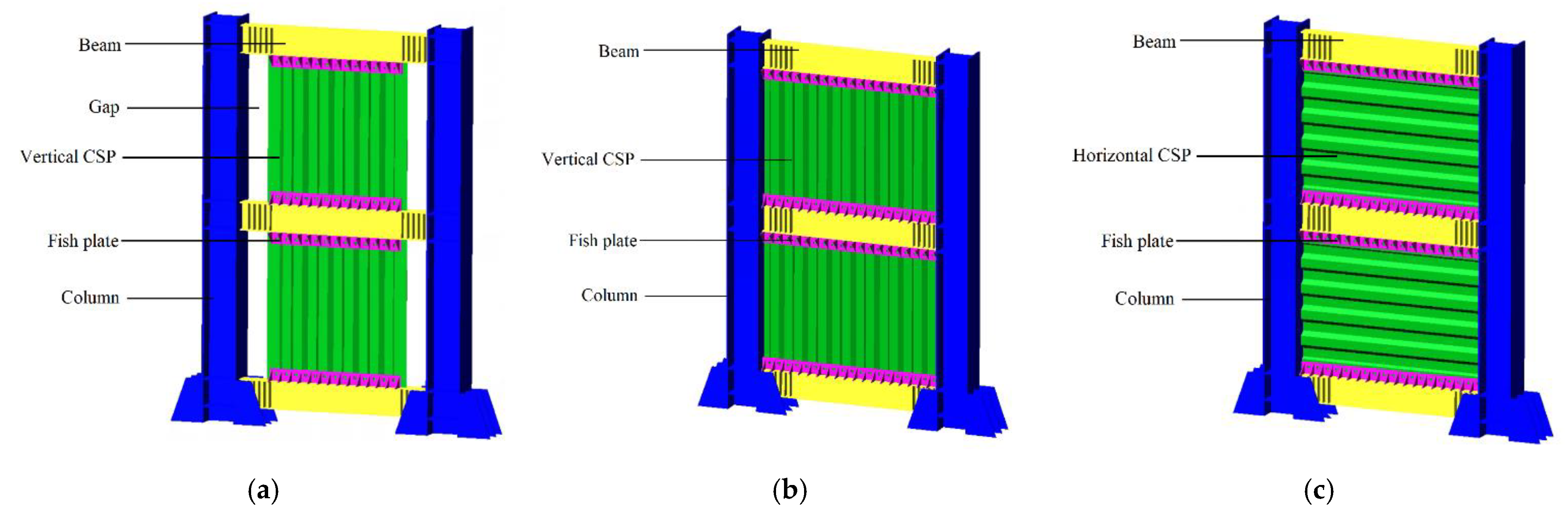
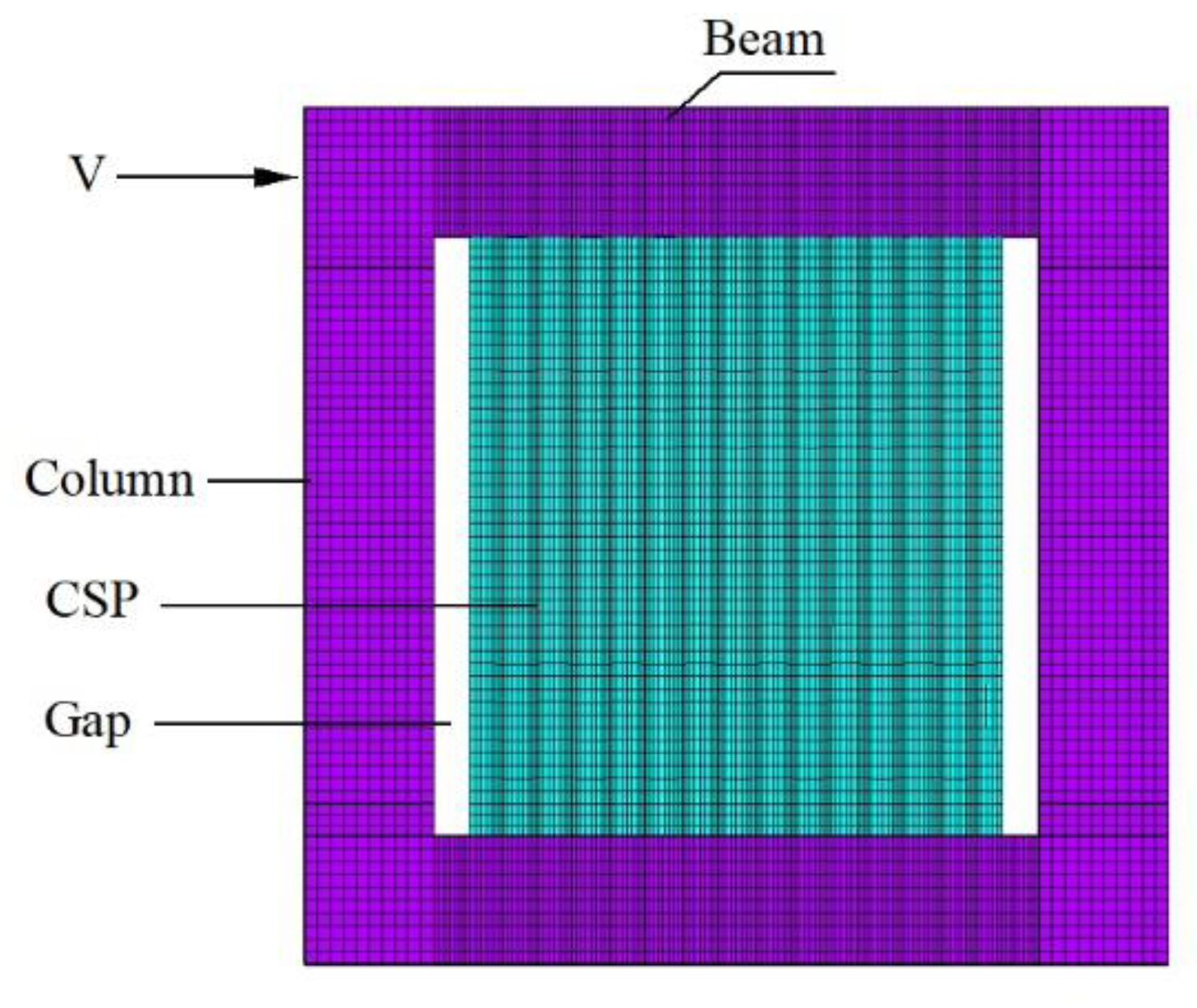
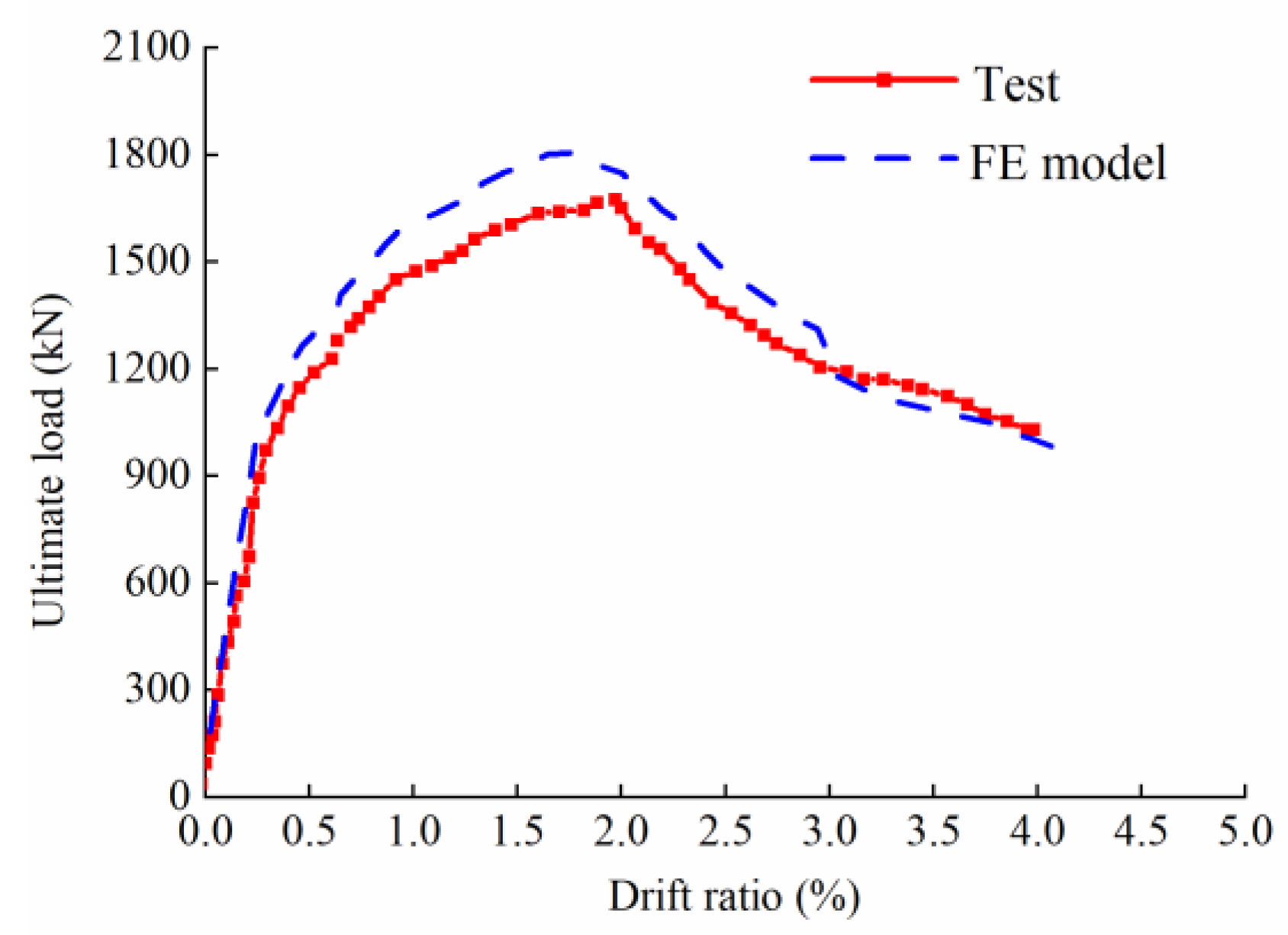
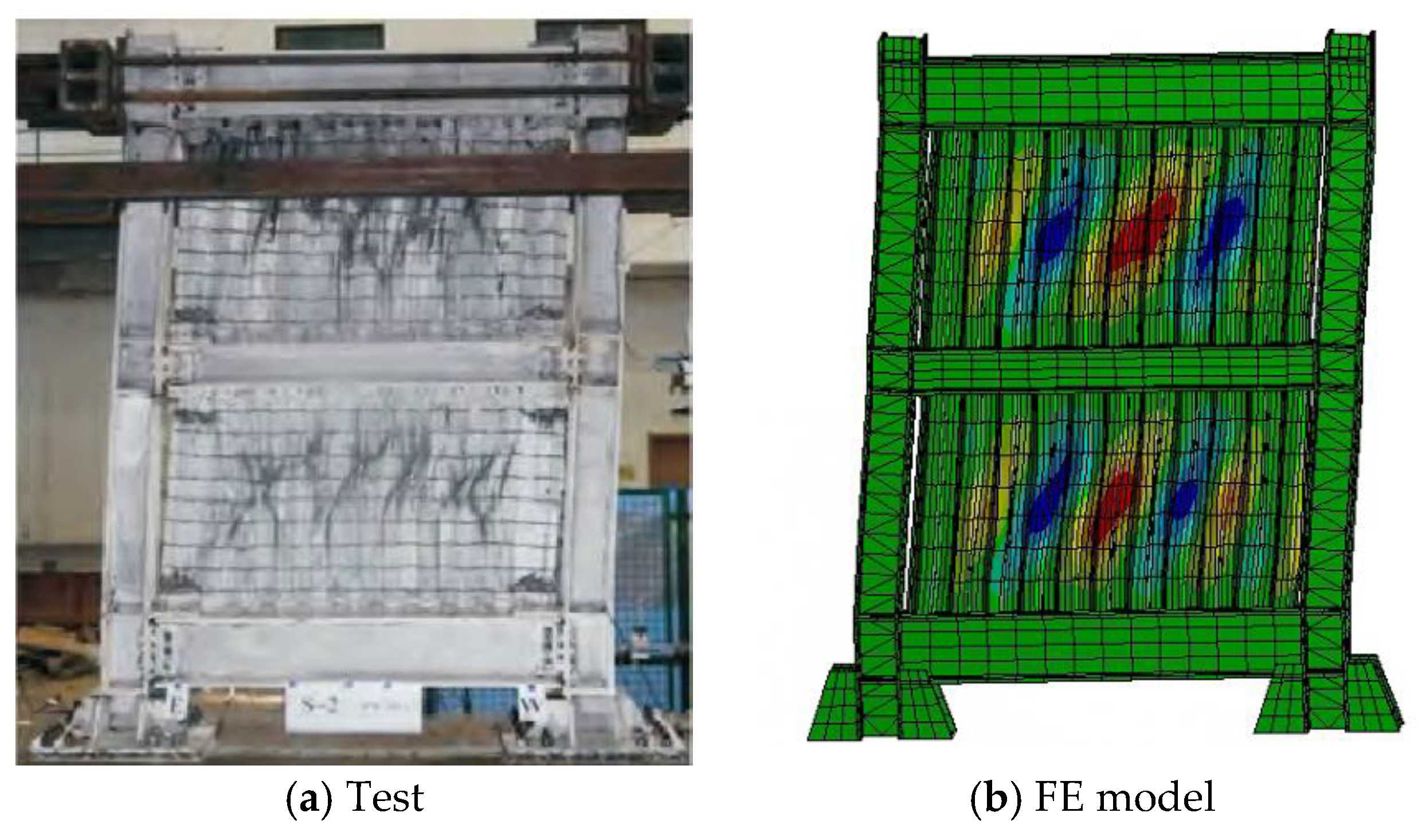








| Member | CSP Section | Frame Section | ||||||
|---|---|---|---|---|---|---|---|---|
| (mm) | (mm) | (mm) | (mm) | (mm) | Column (mm) | Beam (mm) | ||
| CboW1 | 100 | 2800 | 2800 | 70 | 100 | 70 | H-600 × 600 × 60 × 60 | H-600 × 600 × 60 × 60 |
| CboW2 | 200 | 2800 | 2800 | 70 | 100 | 70 | H-600 × 600 × 60 × 60 | H-600 × 600 × 60 × 60 |
| CboW3 | 300 | 2800 | 2800 | 70 | 100 | 70 | H-600 × 600 × 60 × 60 | H-600 × 600 × 60 × 60 |
| CboW4 | 400 | 2800 | 2800 | 70 | 100 | 70 | H-600 × 600 × 60 × 60 | H-600 × 600 × 60 × 60 |
| CboW5 | 500 | 2800 | 2800 | 70 | 100 | 70 | H-600 × 600 × 60 × 60 | H-600 × 600 × 60 × 60 |
| CboW6 | 600 | 2800 | 2800 | 70 | 100 | 70 | H-600 × 600 × 60 × 60 | H-600 × 600 × 60 × 60 |
| CboW7 | 800 | 2800 | 2800 | 70 | 100 | 70 | H-600 × 600 × 60 × 60 | H-600 × 600 × 60 × 60 |
| CboW8 | 300 | 2800 | 1400 | 70 | 100 | 70 | H-970 × 970 × 97 × 97 | H-970 × 970 × 97 × 97 |
| CboW9 | 300 | 2800 | 4200 | 70 | 100 | 70 | H-970 × 970 × 97 × 97 | H-970 × 970 × 97 × 97 |
| CboW10 | 300 | 2800 | 5600 | 70 | 100 | 70 | H-970 × 970 × 97 × 97 | H-970 × 970 × 97 × 97 |
| CboW11 | 300 | 2800 | 7000 | 70 | 100 | 70 | H-970 × 970 × 97 × 97 | H-970 × 970 × 97 × 97 |
| CboW12 | 300 | 2800 | 2800 | 70 | 100 | 70 | H-300 × 300 × 30 × 30 | H-300 × 300 × 30 × 30 |
| CboW13 | 300 | 2800 | 2800 | 70 | 100 | 70 | H-320 × 320 × 32 × 32 | H-320 × 320 × 32 × 32 |
| CboW14 | 300 | 2800 | 2800 | 70 | 100 | 70 | H-350 × 350 × 35 × 35 | H-350 × 350 × 35 × 35 |
| CboW15 | 300 | 2800 | 2800 | 70 | 100 | 70 | H-380 × 380 × 38 × 38 | H-380 × 380 × 38 × 38 |
| CboW16 | 300 | 2800 | 2800 | 70 | 100 | 70 | H-620 × 620 × 62 × 62 | H-620 × 620 × 62 × 62 |
| Member | CSP Section | Frame Section | |||||||
|---|---|---|---|---|---|---|---|---|---|
| (mm) | (mm) | (mm) | (mm) | (mm) | Opening Rate | Column (mm) | Beam (mm) | ||
| CboW17 | 300 | 2800 | 2800 | 70 | 100 | 70 | 0 | 600 × 600 × 60 × 60 | 600 × 600 × 60 × 60 |
| CboW18 | 300 | 2800 | 2800 | 70 | 100 | 70 | 10% | 600 × 600 × 60 × 60 | 600 × 600 × 60 × 60 |
| CboW19 | 300 | 2800 | 2800 | 70 | 100 | 70 | 30% | 600 × 600 × 60 × 60 | 600 × 600 × 60 × 60 |
| CboW20 | 300 | 2800 | 2800 | 70 | 100 | 70 | 50% | 600 × 600 × 60 × 60 | 600 × 600 × 60 × 60 |
| CboW21 | 300 | 2800 | 2800 | 70 | 100 | 70 | 70% | 600 × 600 × 60 × 60 | 600 × 600 × 60 × 60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Q.; Huang, J.; Gu, B. Research on Lateral Performance of Corrugated Steel Plate Shear Walls Connected with Beams Only under Horizontal Loads. Buildings 2023, 13, 1996. https://doi.org/10.3390/buildings13081996
Cao Q, Huang J, Gu B. Research on Lateral Performance of Corrugated Steel Plate Shear Walls Connected with Beams Only under Horizontal Loads. Buildings. 2023; 13(8):1996. https://doi.org/10.3390/buildings13081996
Chicago/Turabian StyleCao, Qiang, Jingyu Huang, and Baonan Gu. 2023. "Research on Lateral Performance of Corrugated Steel Plate Shear Walls Connected with Beams Only under Horizontal Loads" Buildings 13, no. 8: 1996. https://doi.org/10.3390/buildings13081996
APA StyleCao, Q., Huang, J., & Gu, B. (2023). Research on Lateral Performance of Corrugated Steel Plate Shear Walls Connected with Beams Only under Horizontal Loads. Buildings, 13(8), 1996. https://doi.org/10.3390/buildings13081996




