The Quality Assessment of Timber Structural Joints Using the Coaxial Correlation Method

Abstract

With the growing popularity of timber structures, the requirement for reliable and non-destructive methods to assess the quality and condition of structural joints becomes increasingly essential. A novel coaxial correlations method is investigated to assess the degradation of panel-to-panel moment joints in timber structures. The method involves analysing the response data obtained from accelerometers placed on both sides of the joint and comparing the readings to evaluate the joint’s condition. A specific joint solution to simulate the degradation of the moment joint in laboratory conditions is selected based on its simplicity and the ease with which its degradation can be simulated. The joint consists of angle brackets joined with timber screws and bolts to plywood panels. Gradually unscrewing the timber screws reduces the joint’s stiffness to simulate wear and tear over time. The experimental setup includes static loading and finite element modelling (FEM) to determine the rotational stiffness of the investigated joint at each degradation level. A dynamic experiment using vibration loading with sweep signal in the frequency range of 10 Hz to 2000 Hz is conducted to assess the quality of the joint. The conducted research provides valuable insights into the behaviour of timber panel-to-panel connections. The findings highlight the relationship between joint stiffness, vertical displacements, and the proposed dimensionless parameter, volume root mean square value (RMS_vol), which offers a more comprehensive assessment of the joint’s condition in three spatial directions. As a result of the research, it has been established that, in the case of linear-type connections, unlike point-type joints, there is a possibility of signal scattering, so it is recommended that power comparisons and evaluations of the response signals from both accelerometers at the initial stage of applying the coaxial correlations method are performed.

1. Introduction

Timber structures have gained significant attention recently due to their sustainable and environmentally friendly nature [1,2,3]. Buildings and construction account for approximately 40% of global energy consumption and contribute 33% of greenhouse gas emissions [4]. With the growing interest in sustainable construction practices, timber has emerged as a viable alternative to conventional building materials. Timber offers numerous advantages, such as a low carbon footprint, renewable resource availability, and aesthetic appeal [5,6]. As a result, the use of timber in construction has witnessed a resurgence, with an increasing number of multi-story timber buildings being designed and built [7,8].

However, ensuring timber structures’ structural integrity and long-term performance presents unique challenges [9,10]. Timber is susceptible to various degradation mechanisms, including moisture, fungal decay, and mechanical damage, which can compromise strength and stiffness [11,12]. Therefore, the quality control of timber structures is of the utmost importance to ensure their safety, durability, and reliability throughout their service life.

Traditionally, quality control in timber structures has relied on destructive testing methods, which involve extracting samples or subjecting the structure to load tests until failure. While these methods provide valuable information, they are invasive, time-consuming, and expensive. Moreover, destructive testing is not feasible for in-service structures or those with complex joint configurations.

Non-destructive quality control methods have emerged as a promising alternative to overcome these limitations. Non-destructive testing (NDT) techniques allow for the evaluation of structural conditions without causing damage to the timber elements or the overall structure [13]. NDT methods enable timely and cost-effective assessment of civil engineering structures, facilitating preventive maintenance, timely repairs, structural health monitoring, and the determination of the residual resources of buildings [14,15].

Various techniques have been employed to evaluate timber structures in the field of non-destructive quality control. These techniques include visual inspection, ultrasound testing, infrared thermography, acoustic emission, resistography, moisture-content tests, vibration-based methods, and others [16,17,18,19,20]. Each technique offers unique advantages and limitations, and their effectiveness depends on factors such as the type of defect, accessibility, and the size and configuration of the timber elements.

Among the non-destructive techniques, vibration-based methods have gained prominence due to their sensitivity to changes in stiffness and dynamic characteristics of the structure [14,21,22,23]. Vibration-based methods involve exciting the structure with a known input signal and analysing the response to extract information about its stiffness, damping, and natural frequencies. By monitoring changes in the structure’s dynamic behaviour, it is possible to identify defects, degradation, and changes in the mechanical properties of timber elements.

A growing interest has recently arisen in developing non-destructive quality control methods tailored explicitly for timber structures [24,25]. Researchers have focused on investigating the behaviour of timber connections, which play a critical role in the overall performance and stability of timber structures [8,11,26,27]. The stiffness of a joint directly influences how internal forces and deformations are distributed within a structure [28,29]. The joints in timber structures are typically classified as pinned or moment joints (Figure 1). Understanding the degradation mechanisms and evaluating the condition of timber connections is essential for ensuring the safety and reliability of the entire structure.

This study presents a novel non-destructive evaluation method, the coaxial correlations method, for assessing the degradation of panel-to-panel moment joints in timber structures. By incorporating static loading, finite element modelling (FEM), and dynamic vibration testing, the authors aim to simulate and assess the behaviour of panel-to-panel moment joints under varying degradation levels.

The proposed method offers several advantages over existing techniques, comprehensively assessing the joint’s condition in three spatial directions. Using vibration-based methods combined with numerical modelling enhances the understanding of the joint’s stiffness, displacements, and the proposed dimensionless parameter, volume root mean square value (RMS_vol). These findings contribute to more accurately evaluating the quality and integrity of panel-to-panel moment joints in timber structures.

Overall, this study contributes to the growing body of research on non-destructive quality control methods for timber structures and provides valuable insights into the behaviour of timber connections. By offering a non-invasive and efficient approach to assess the quality of structural joints, the coaxial correlations method can potentially improve the safety and durability of timber structures, thus promoting their wider adoption in sustainable construction practices.

2. Materials and Methods

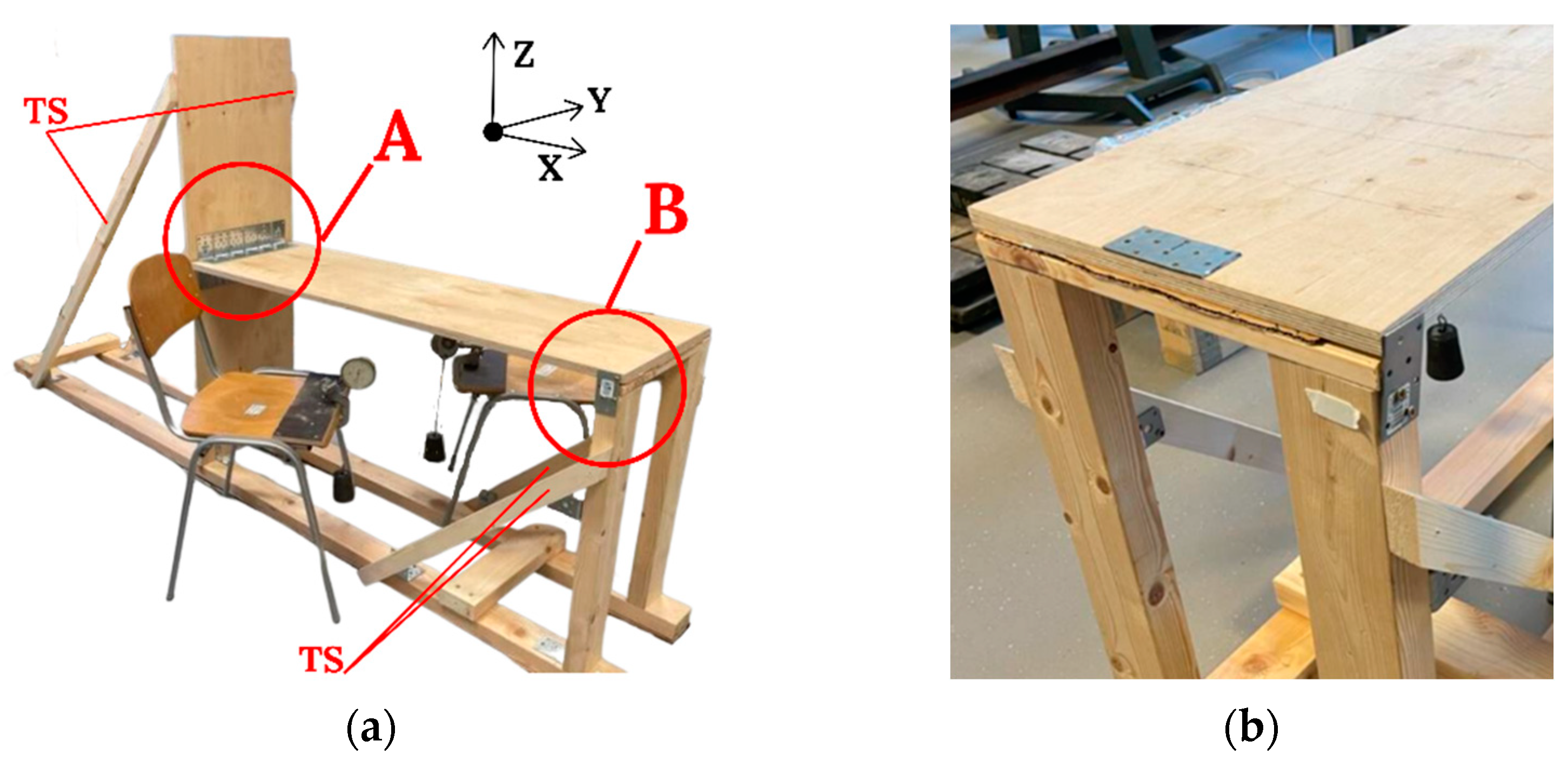
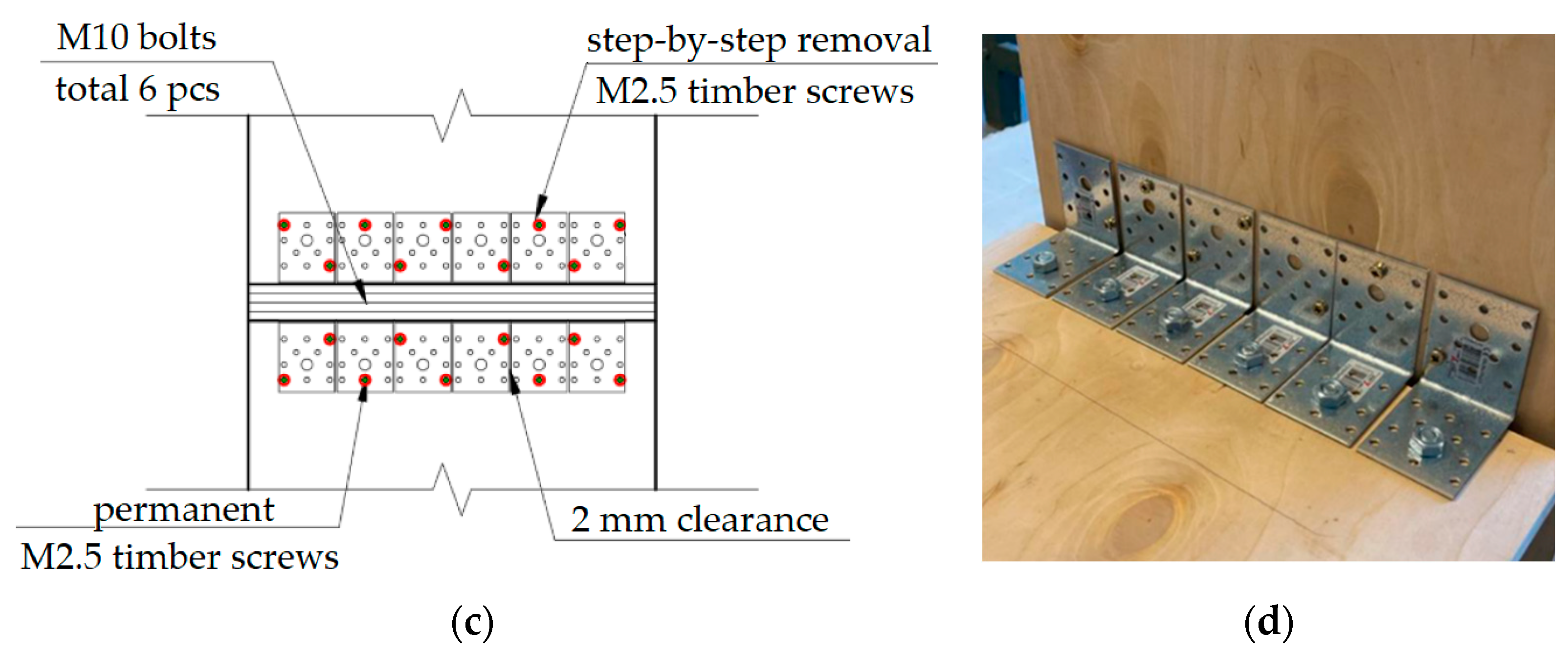
2.1. Choice of the Object of Investigation

This study focused on simulating real timber structure connections without destructive testing methods [30]. A panel-to-panel moment joint consisting of steel angles joined with timber screws and bolts to plywood panels was carefully selected as the subject of investigation. This joint solution was chosen for its simplicity and the ease with which the degradation of a moment-resisting connection in timber multi-storey buildings can be replicated under laboratory conditions. By loosening bolts, we can effectively reduce the joint’s stiffness and emulate the behaviour during the degradation of a moment-resisting joint, such as the wall-to-floor panel connection in timber multi-storey buildings.

The objective was to create a versatile joint configuration capable of absorbing a wide range of bending moments, allowing for various adjustment possibilities. The experiment involves designing and fabricating a specialised testing stend specifically tailored to simulate the behaviour of multi-storey timber floor structures at various degrees of joint degradation. This stend incorporates the selected adjustable panel-to-panel moment joint (Figure 2). The range of adjustment possibilities allows us to evaluate the joint’s performance under various loading conditions, making the findings more applicable to diverse timber construction scenarios. This approach of simulating joint degradation by loosening bolts eliminates the need for destruction and provides a controlled and replicable environment for studying joint behaviour over time.

The stend consists of two Riga Ply plywood panels of grade IV according to EN 635-2 with dimensions of 1250 mm × 400 mm and a thickness of 18 mm and additional timber supports. Riga Ply, produced by Latvijas Finieris Group, comprises 13 cross-bonded birch veneer layers. Additional timber supports play a vital role in ensuring the stability of both the vertical plywood panel and the vertical support under the free-end connection of the horizontal plywood panel. The timber supports provide the possibility to represent investigated connection as analogous to the connection between a wall and floor panel in a larger structure. By incorporating the additional timber supports, the stend is fortified against unwanted movements that may arise due to its relatively small size. These supports effectively minimise potential structural instabilities, making the stend more robust and reliable.

The experimental setup includes two types of connections shown in Figure 2a: a free-end connection (B) and a panel-to-panel moment joint (A). The free-end connection allows for the vertical (Z-axis) and longitudinal (X-axis) movements of the plywood panel while preventing transversal (Y-axis) movements with steel plates on both sides of the connection. The moment joint is made of angle brackets with dimensions 70 mm × 55 mm × 2 mm, and Fortis-produced fasteners—timber screws and bolts following the European standard EN 1995-1-1, which outlines the general principles and rules for designing joints in timber structures. Angle brackets produced by Arras CF are one-piece non-welded three-dimensional nailing plates designed for use in timber-to-timber connections. Used angle brackets are made from pre-galvanised steel DX51D + Z275 according to EN 10346:2015, with a steel yield strength of at least 250 MPa and tensile strength of at least 330 MPa. The angle brackets are placed in two rows at the top and bottom of the horizontal panel, with 6 pieces on each side. M2.5 timber screws with a length of 15 mm are used to fasten each row of angle brackets to the vertical plywood panel. We use 8.8-grade M10 hexagon head bolts with thread up to the head, a tensile strength of at least 800 MPa, and a yield strength of at least 640 MPa to connect the angle brackets and the horizontal plywood panel. The total amount of used fasteners is 9 timber screws per one steel angle row (18 timber screws in total for investigated connection) and 6 bolts.

The structural joint considered during the current study is the moment one which can take up the bending moment. The load-carrying capacities of the considered joint are defined by the parameters of the strengthening details and fasteners by their amounts. The degradation of the connections during the structure’s service life is simulated by the unscrewing of timber screws on the top row of steel angles and measurement, thereby simulating the wear and tear of the connection over time. The assumption is that there is a functional relationship between the connection joint’s stiffness and the structure’s vibrational characteristics.

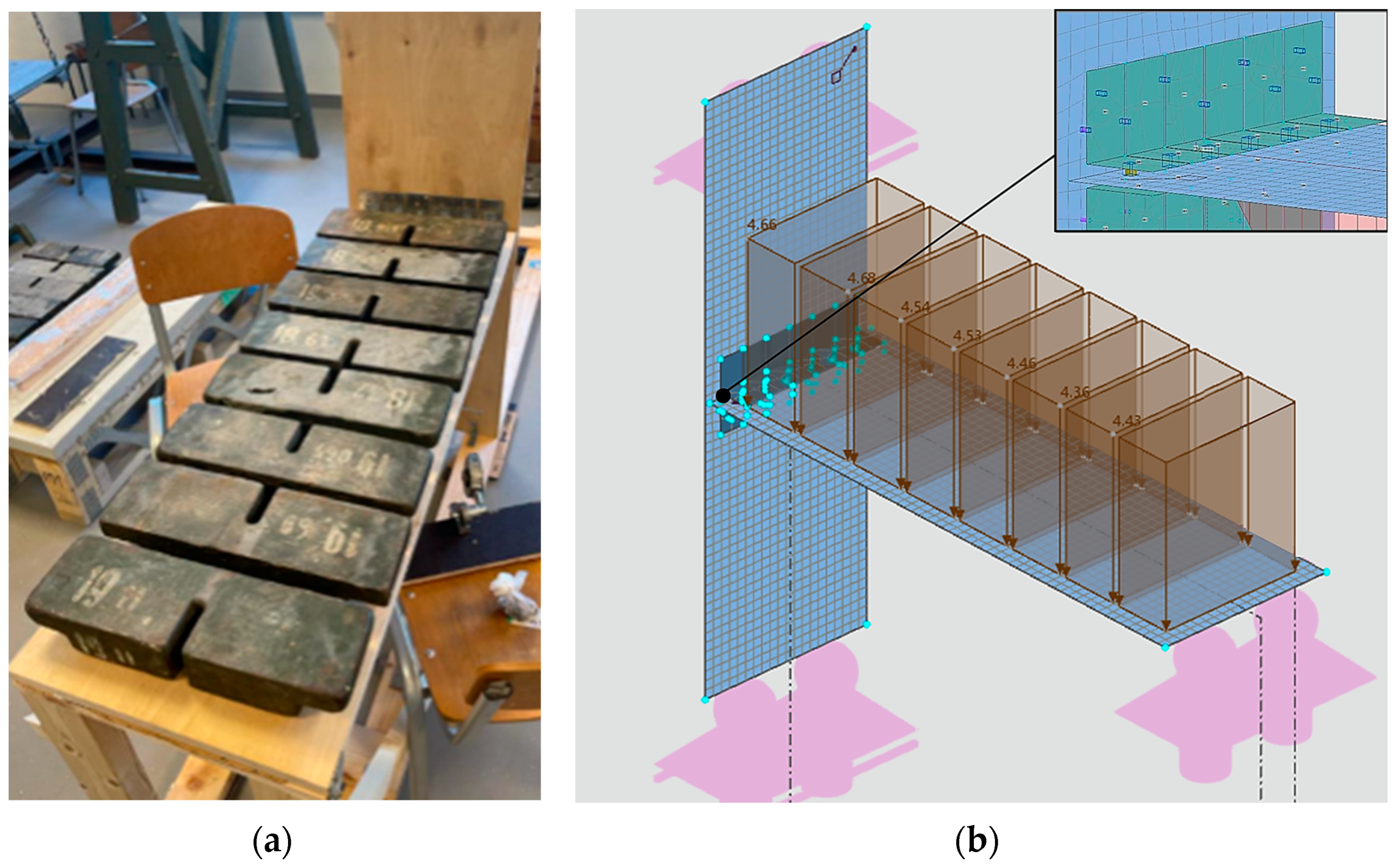
2.2. Evaluation of Stiffness of Investigated Joint Using Static Loading

To determine the stiffness of the investigated joint at each degradation level, the static loading of the stend and its modelling based on the finite element method are carried out. The panel-to-panel moment joint degradation process was modelled by changing the number of screws in the angle brackets row at the top of the horizontal panel from 9 to 0 under a static load equal to 151.8 kg. Zero timber screws on the top row of angle brackets represent the case when the investigated connection cannot carry the bending moment, and the horizontal plywood panel is simply supported. The loading was carried out by adding steel pieces with the weight changing within limits from 17 kg to 21 kg. The placement of the steel pieces during loading is shown in Figure 3.

Numerical models of the investigated joint were developed with the structural analysis program RFEM. This part of the investigation is the determination of the rotation stiffness of the investigated joint at various degrees of joint degradation by calibrating a numerical model to further determine the relationship between the joint’s stiffness and the structure’s vibrational characteristics. The failure stage of the investigated connection is not of interest. Only the linear behaviour of materials is investigated. The orthotropic elastic material model was used for plywood elements, and the linear elastic material model was used for modelling angle brackets and fasteners.

There were two unknown characteristics of the investigated joint to be determined—the mean elastic modules of the plywood and the joint’s rotational stiffness during the modelling, so the two models have been developed differently. The surface type finite element with rectangular mesh and a target length of 0.02 m was used to model the plywood panels for both developed models. This mesh size provided accurate results (reducing the mesh fineness did not change the results significantly) and good calculation speed. During the first modelling approach, angle brackets were modelled using surface-type finite elements and the fasteners were modelled using beam elements as full pipe profiles. The number of fasteners corresponded to the real assembly for each degradation grade. The modulus of elasticity of the plywood was determined via the iterative calibration of the numerical model with laboratory experiment data. The joint degradation was simulated via the step-by-step deletion of timber screws at each new iteration. A total of 10 bolt variations were tested for each load (starting with a non-degraded assembly with 9 timber screws in the top row of the angle brackets to a fully degraded assembly without timber screws in the top row of the angle brackets).

During the second modelling approach, the panel-to-panel connection was modelled using a line hinge function (without modelling fasteners separately) with a defined value of the joint’s rotational stiffness. Using the iterative calibration of the developed second approach model with laboratory experiment data, the rotational stiffness of the moment joint was determined for each degradation step.

The maximum vertical displacements of the horizontal panel were determined with laboratory testing using the mechanical deflectometers with a precision of 0.01 mm and numerical models developed in the software RFEM 6 version 6.01.0019.

2.3. Coaxial Correlation Method for Structural Joint Quality Evaluation

The evaluation method proposed for assessing the degradation of structural joints has demonstrated promising results, particularly in the case of two beams joining at right angles both for timber and steel structures [31,32] and steel beam slip connections [33].

A dynamic vibration-based experiment was conducted to evaluate the quality of the timber panel-to-panel moment joint during its degradation. The coaxial correlation method involved generating a signal using specialised software, transmitting the signal through an electrodynamic actuator, capturing the signal with accelerometers placed on both sides of investigated joint, and analysing the differences in the readings to assess the condition of the joint. The experimental setup included an electrodynamic actuator, which produced signals in the frequency range of 10 Hz to 2000 Hz, and two sensors capable of measuring 6D acceleration.

The experimental procedure involved running the sweep-type signals with a duration of 0.5 s in the frequency range of 10 Hz to 2000 Hz applied to the end of the free supported horizontal panel in direction Z according to Figure 4, checking the signals’ compatibility with the accelerometer’s range, saving the appropriate signals, simulating degradation via the step-by-step removal of timber screws from the upper row of connections, and repeating the experiment until no fasteners remained in the upper row.

The structure’s response is measured in three spatial directions: X, Y, and Z, using two 3D accelerometers. The signal is initially detected with an accelerometer A1 affixed to the horizontal element (as a reference point) and subsequently with an accelerometer A2 affixed to the vertical element (Figure 4). The accelerometer readings correspond precisely to an idealised scenario where the joint is perfectly rigid. However, suppose the joint undergoes loss of rigidity during operation. In that case, the accelerometer readings will deviate (indicating energy absorption by the compromised joint), enabling conclusions to be drawn regarding the joint’s condition. The obtained signals are transmitted to a computer for further post-processing (Figure 5).

It was concluded in the previous study [33] that the nature of the root mean square (RMS) during the degradation of the joint may change in different axes, and wrongly chosen axes may lead to wrong conclusions regarding the state of the investigated joint, especially in the case of complex joints. During this study, the data post-processing process described in [33] has been enhanced and simplified by introducing one parameter for evaluating joint degradation in three directions at once, thus obtaining a more complete picture of the state of the joint. The proposed dimensionless parameter is obtained using the equation which calculates the volume root square value (RMS_vol):

$${\mathrm{RMS}}_{\mathrm{vol}}=\sqrt{{\mathrm{RMS}}_{\mathrm{x}}^2+{\mathrm{RMS}}_{\mathrm{y}}^2+{\mathrm{RMS}}_{\mathrm{z}}^2}$$

(1)

where RMS_x, RMS_y, and RMS_z are RMS values from the processed signal convolution as a measure of the similarity between two signals in directions X, Y, and Z, correspondingly.

In addition to the newly introduced parameter, the evaluation of the joint with the proposed coaxial correlations method was carried out under a loaded stand of 151.8 kg.

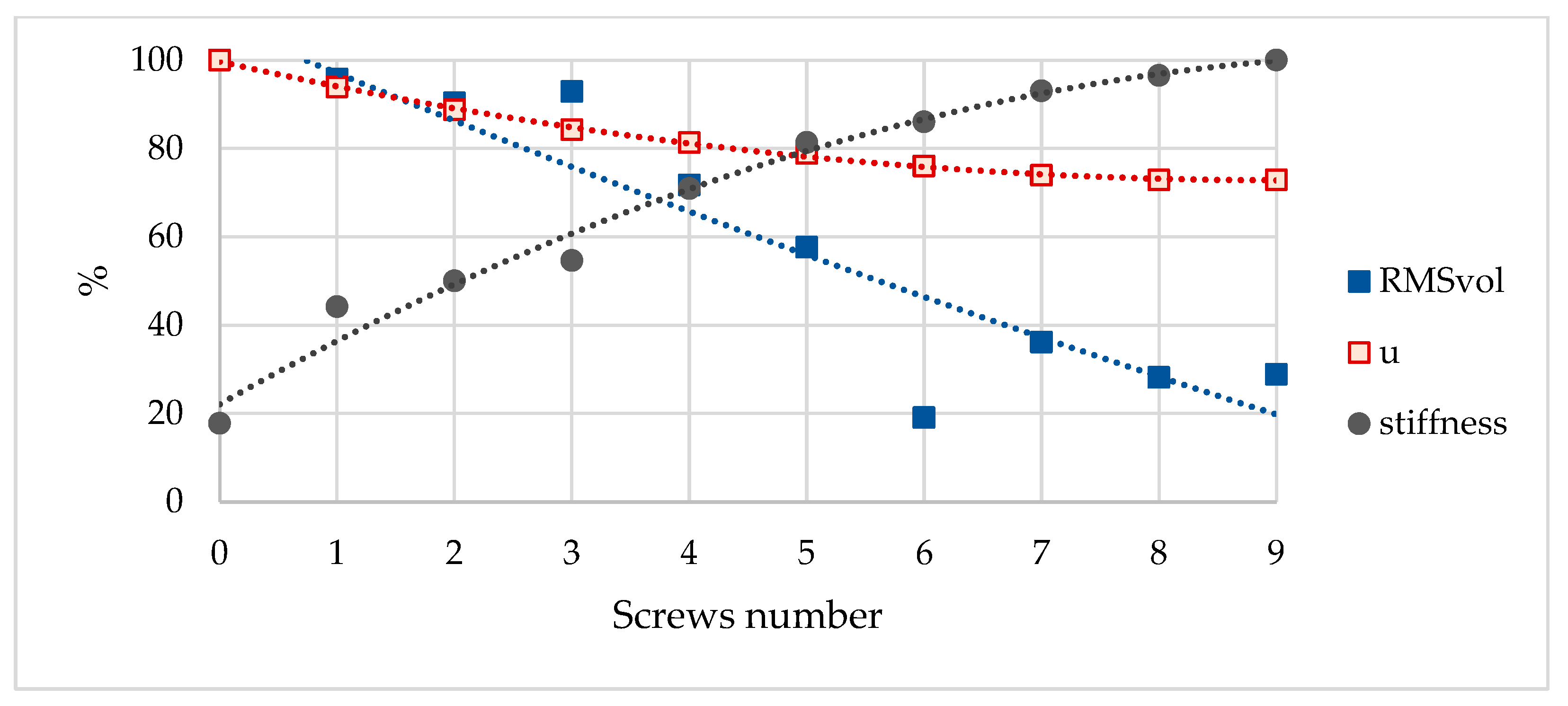
3. Results and Discussion

In the framework of static loading with 151.8 kg, ten measurements were made by removing one timber screw from the joint model at each stage. The numerical model, including the modelling of each screw in the investigated joint, was validated with laboratory experiment data. The results obtained for the stend modelling panel-to-panel moment joint are given in

Table 1. Vertical displacements and rotational stiffness obtained via static loading and numerical models.

Nr.	Screws Number	Displacement, mm		Difference, %	Rotational Stiffness of the Investigated Joint Obtained by the 2nd Numerical Model, [kNm × rad−1 × m−1]
		uexp	uFEM,1
1	9	17.85	18.3	2.46	8.60
2	8	17.83	18.5	3.65	8.30
3	7	18.10	18.6	2.69	8.00
4	6	18.61	18.9	1.56	7.40
5	5	19.30	19.1	1.05	7.00
6	4	19.90	19.7	1.02	6.10
7	3	20.63	20.6	0.15	4.70
8	2	21.73	20.9	3.95	4.30
9	1	22.99	21.4	7.43	3.80
10	0	24.48	23.9	2.43	1.53

.

The modulus of elasticity of the plywood was estimated at 6800 MPa by comparing the maximum vertical displacements of the stend horizontal panel obtained via the laboratory experiment (u_exp) and the first-type numerical model (u_FEM,1) with modelled fasteners.

The rotational stiffness of the investigated moment joint for the stages differed with the number of screws determined by the second-type numerical model, in which the studied joint is remodelled as a linear support. The rotational stiffness of the linear support is determined iteratively based on the displacements obtained in the laboratory experiment and the modulus of elasticity obtained via validation of the first-type numerical model. The obtained rotational stiffness of the moment joint is used for its quality assessment using the coaxial correlation method.

The post-processing of collected raw response signals F1 and F2 from the A1 and A2 accelerometers includes the removal of offsets. As a result, signals with a mean value of zero are obtained. As a next step, both signals are concatenated to save the scale relationships between two signals in the same axis direction. The concatenated signal pairs’ normalisation is completed to further compare the signal pairs in all three directions. The signal pairs after normalisation in the X, Y, and Z directions are shown in Figure 6.

The signal pairs are split after normalisation to the F1* and F2*. The similarity comparison of the obtained signals F1* and F2* is made with the RMS of the signals’ convolution in three directions and by determining the proposed dimensionless parameter—volume root mean square value. Obtained volume root square values are given in

Table 2. RMS of signals’ convolution in three directions and proposed volume root mean square parameter.

Nr.	Screws Number	RMSx	RMSy	RMSz	RMSvol
1	9	1.5739	4.2289	6.0235	7.5262
2	8	2.5188	2.7883	6.3096	7.3437
3	7	3.7834	2.2017	8.3543	9.4316
4	6	1.0254	3.8577	2.9503	4.9636
5	5	0.9018	5.4463	13.9686	15.0199
6	4	2.6823	5.8421	17.5589	18.6986
7	3	4.7522	4.2519	23.3603	24.2150
8	2	0.9565	4.3896	23.1195	23.5519
9	1	2.2475	4.2156	24.4985	24.9599
10	0	7.4473	4.4542	24.5854	26.0720

.

Figure 7 describes the obtained behaviour of the joint during its degradation. As can be seen, a decrease in moment joint rotational stiffness increases maximal vertical displacements and the proposed parameter—volume root mean square. RMS_vol shows the changes in the joint more clearly than maximal vertical displacements. For example, when the joint rotational stiffness decreases by two times, the maximal vertical displacement only increases by 22%, while the RMS_vol increases by 213%.

On the one hand, the dependence between the proposed parameter RMS_vol and joint stiffness is obtained. On the other hand, it is the opposite compared to the direct relationships obtained in the previous research [31,32,33]. The physic-mechanical clarification of the increased RMS_vol with the degradation of the joint stiffness can be explained with the configuration and type of the investigated joint. Figure 6 shows a significant difference in the power of the collected response signals from both accelerometers A1 and A2, indicating signal scattering in this kind of panel-to-panel connection. The transmitted signal is dispersed in multiple directions in the horizontal panel due to various factors, leading to signal degradation in the vertical panel, measured with A2. During the loss of joint stiffness, the horizontal panel becomes more free and can be more exposed to vibrations from the input signal. Based on this, the response signal of the horizontal panel measured with A1 increases in its power and can lead to an overall increase in the RMS of both signals from A1 and A2 convolution.

4. Conclusions

The coaxial correlation method, which includes the processing of response data from coaxially placed accelerometers on either side of the joint, is applied to assess panel-to-panel moment joint degradation in timber structures. The dependence between the proposed new dimensionless parameter, volume root mean square value (RMS_vol), and the joint’s rotational stiffness is obtained during the research. The following results and conclusions are obtained and made:

• There is a clear relationship between joint stiffness, vertical displacements, and the RMS_vol parameter, as well as the RMS_vol parameter more sensitively reflecting changes in the joint’s condition compared to maximal vertical displacements.
• In the case of the input signal as a sweep signal in the frequency range of 10 Hz to 2000 Hz and the placement of the accelerometer pair symmetrically on either side of the joint, aligned with its axis, an inverse correlation between the calculated RMS_vol values of convolution signals and the panel-to-panel moment joint rotational stiffness is obtained.
• The reason for the opposite direction of the relation mentioned above can be signal scattering.
• The changes in the RMS_vol parameter can be used for monitoring the system’s condition during operation as a reference point using determined parameters at the initial stage, with an approved design stiffness condition. But, it is recommended that, at the stage of the reference measurement, it should be determined whether the input signal is well transferred through the joint by comparing the power of the response signals from both sides of the joint of interest to save a more user-friendly interpretation of the results.

The obtained findings provide valuable insights into the behaviour of timber panel-to-panel connections and offer a non-destructive method for assessing the quality of structural joints. This investigation aims to approve the conception of the existence of the dependence between RMS_vol and joint degradation level, and additional research is required to adopt the proposed technique for on-site non-destructive testing.