New Interaction Formulae for Plastic Resistances of Z-Sections under Combinations of Bending Moments My,Ed, Mz,Ed and Bimoment BEd
Abstract
:Highlights
- -
- Exact interaction curves for the plastic resistances of Z-sections taking into account the combination of three internal forces, i.e., My,Ed, Mz,Ed and BEd, are presented.
- -
- Approximate interaction formulas for Z-section plastic resistances taking into account three internal forces, i.e., My,Ed, Mz,Ed and BEd, is presented.
Abstract
1. Introduction
1.1. Overview of the Former Investigations
1.2. Calculation of the Factor ξ
- Method A, which divides the section into elements. The unknowns are the stresses in each element;
- Method B, which divides the section into three parts (two flanges and the web). In each part, the unknowns are the axial force and the bending moment about the strong axis.
1.2.1. Method A (According to Osterrieder et al. [24])
1.2.2. Method B (Kindmann and Frickel [12])
1.3. Research Significance
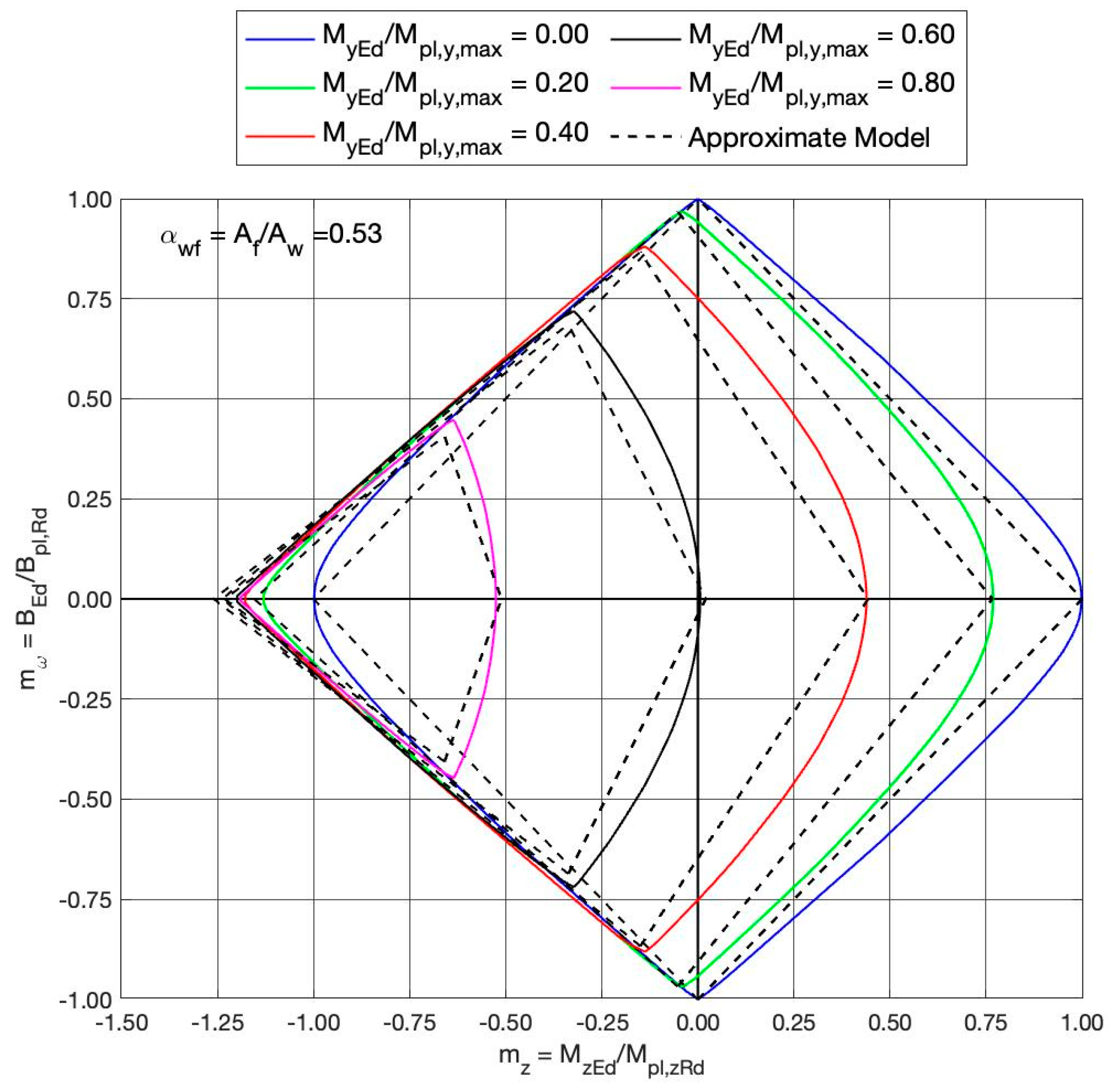
2. Interaction Formulae of the Authors’ Proposal (Approximate Curves)
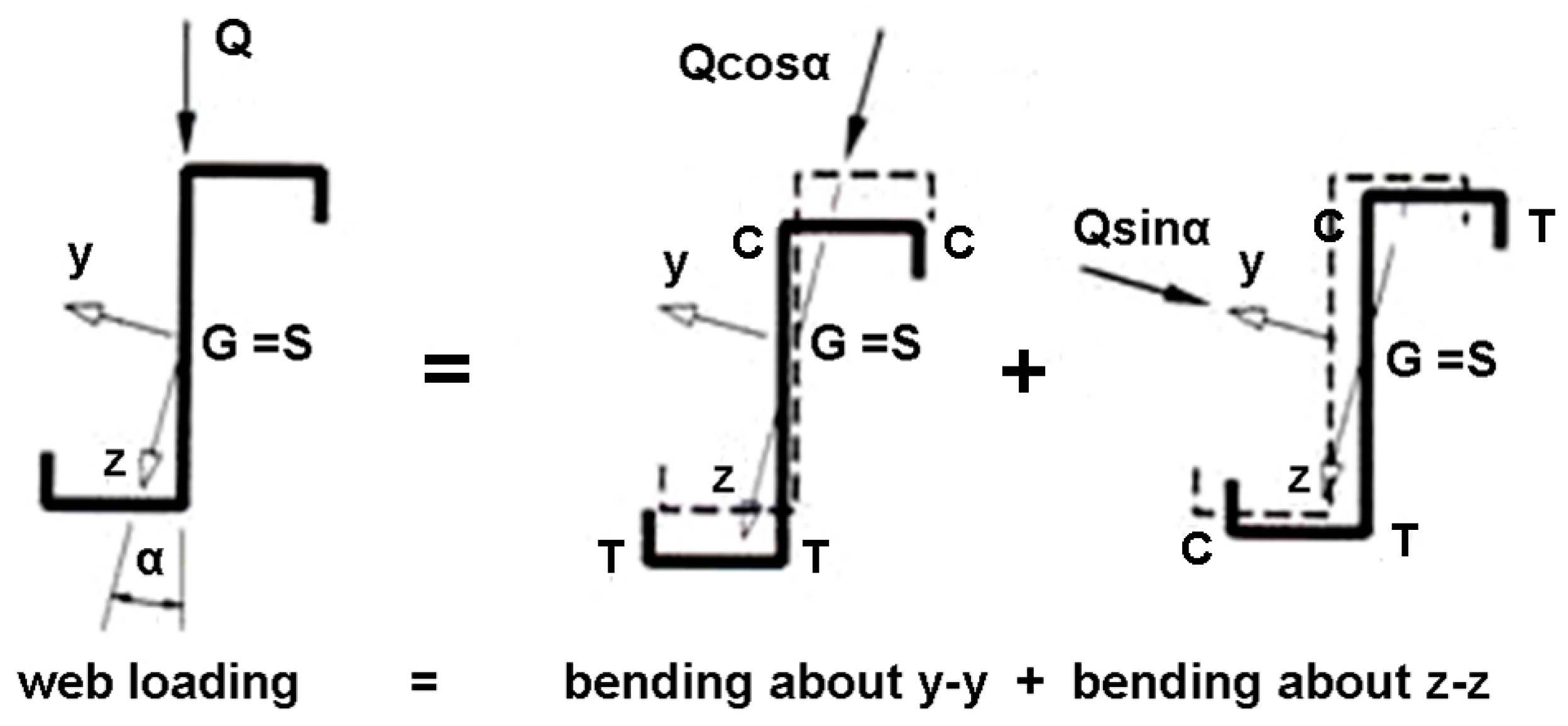
3. Importance of Z-Section Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature: (Alphabetically)
| BEd | design value of the bimoment |
| Bpl,Rd | design value of the plastic bimoment resistance |
| b | width of a cross-section |
| fy | yield stress |
| h | depth of a cross-section |
| hw | web depth |
| MBfl,z,Ed | design value of the bending moment of the bottom flange about the z-axis |
| MBfl,z,Rd | design value of the plastic bending moment resistance of the bottom flange about the z-axis |
| Mfl,z,Rd | design value of the plastic bending moment resistance of the flange about the z-axis |
| Mpl,y,Rd, Mpl,Rd | design value of the plastic moment resistance about the y-axis |
| Mpl,z,Rd | design value of the plastic moment resistance about the z-axis |
| MTfl,z,Ed | design value of the bending moment of the top flange about the z-axis |
| MTfl,z,Rd | design value of the plastic bending moment resistance of the top flange about the z-axis |
| Mw,pl,y,Rd | design value of the plastic moment resistance of the web about the y-axis |
| Mw,y,Ed | design value of the bending moment of the web about the y-axis |
| Mw,y,Rd | design value of the plastic bending moment resistance of the web about the y-axis |
| My,Ed | design value of the bending moment about the y-axis |
| Mz,Ed | design value of the bending moment about the z-axis |
| NBfl,Ed | design value of the axial force of the bottom flange |
| NBfl,Rd | design value of the plastic axial force resistance of the bottom flange |
| NTfl,Ed | design value of the axial force of the top flange |
| NTfl,Rd | design value of the plastic axial force resistance of the top flange |
| Nw,Ed | design value of the axial force of the web |
| Nw,Rd | design value of the plastic axial force resistance of the web |
| Tt,Ed | design value of internal St. Venant torsional moment |
| Tw,Ed | design value of internal warping torsional moment |
| tf | flange thickness |
| tw | web thickness |
| Vy,Ed | design value of the shear force in direction of the y-axis |
| Vz,Ed | design value of the shear force in direction of the z-axis |
| y, z | section coordinates along the y- and z-axes |
| γM0 | partial safety factor for the resistance of cross-section whatever the class is |
| σ | normal stress |
| τ | shear stress |
| ω | warping function |
References
- Agüero, A.; Baláž, I.; Koleková, Y.; Moroczová, L. New interaction formula for the plastic resistance of I- and H-sections under combinations of bending moments My,Ed, Mz,Ed and bimoment BEd. Structures 2021, 29, 577–585. [Google Scholar] [CrossRef]
- Agüero, A.; Baláž, I.; Koleková, Y.; Lázaro, M. New interaction formula for plastic resistance of channel sections under combinations of bending moments My, Ed, Mz, Ed and bimoment BEd. Structures 2022, 44, 594–602. [Google Scholar] [CrossRef]
- Davison, B.; Owens, G.W. (Eds.) Steel Designers Manual, 7th ed.; SCI, Wiley Blackwell: Chichester, UK, 2016. [Google Scholar]
- Yu, W.-W. Cold-Formed Steel Design, 2nd ed.; John Wiley & Sons. Inc.: New York, NY, USA, 1991. [Google Scholar]
- Sputo, T.; Turner, J.L. Bracing Cold-Formed Structures. A Design Manual; ASCE, SEI: Reston, VA, USA, 2006. [Google Scholar]
- CEN. EN 1993-1-3:2006 and Corrigendum AC (2009) and Amendment A1; Eurocode 3: Design of Steel structures. Part 1-3: General Rules—Supplementary Rules for Cold-Formed Members and Sheeting; CEN: Brussels, Belgium, 2015. [Google Scholar]
- CEN. EN 1993-1-1:2005 and Corrigendum AC (2006) and Corrigendum AC (2009) and Amendment A1; Eurocode 3: Design of Steel Structures. Part 1.1: General Rules and Rules for Buildings; CEN: Brussels, Belgium, 2014. [Google Scholar]
- Walsh, D. Structural Stability Research Council. In Proceedings of the 50th Anniversary Conference, SSRC, Bethlehem, PA, USA, 21–22 June 1994. [Google Scholar]
- Desautels, P. Elastic-Plastic Torsion of Thin-Walled Members. Master’s Thesis, McGill University, Montreal, Canada, June 1980. [Google Scholar]
- Daddazio, R.P.; Bieniek, M.P.; DiMaggio, F.L. Yield surface for thin Bars with warping restraint. J. Eng. Mech. 1983, 109, 450–465. [Google Scholar] [CrossRef]
- Debski, H.; Samborski, S.; Rozylo, P.; Wysmulski, P. Stability and load-carrying capacity of thin-walled FRP composite Z-profiles under eccentric compression. Materials 2020, 13, 2956. [Google Scholar] [CrossRef] [PubMed]
- Kindmann, R.; Frickel, J. Elastische und Plastische Querschnittstragfähigkeit Grundlagen, Methoden, Berechnungsverfahren, Beispiele. Mit CD-ROM: RUBSTAHL Lehr- und Lernprogramme; Ernst & Sohn, A Wiley Company: Berlin, Germany, 2002. [Google Scholar]
- QST-TSV-3Blech. Übersicht zu den RUBSTAHL-Programme. 2002. Available online: https://www.kindmann.de/software-neu (accessed on 4 May 2023).
- Programm SHAPE-THIN 8 (German Name DUENQ), version 8.13.01.140108 x64; Dlubal Software GmbH: Tiefenbach, Germany, 2018.
- Agüero, A.; Gimenez, F. Software Thinwallres. Available online: https://labmatlab-was.upv.es/webapps/home/thinwallresopenclosed.html (accessed on 4 May 2023).
- Agüero, A.; Gimenez, F. Software ThinwallresNMyMzB. Available online: https://labmatlab-was.upv.es/webapps/home/ThinWallResNMyMzB.html (accessed on 4 May 2023).
- Martincek, M. Software GEPARD. Available online: https://sites.google.com/view/gepard/?pli=1 (accessed on 4 May 2023).
- Vayas, I.; Charalampakis, A.; Koumousis, V. Inelastic resistance of angle sections subjected to biaxial bending and normal forces. Steel Constr. 2009, 2, 138–146. [Google Scholar] [CrossRef]
- DIN. DIN 1027 2004-4, SZS, Round Edged Hot Rolled Zee Section (Z30—Z200); DIN: Berlin, Germany, 2004. [Google Scholar]
- ADM. ADM 2015 (Z 1.3/4 x 1.3/4 x 1.09–Z5 x 3.1/4 x 6.19); ADM: Chicago, IL, USA, 2010. [Google Scholar]
- Baláž, I.; Koleková, Y.; Agüero, A. Elastic and plastic resistance of thin walled HVH sections. In Proceedings of the 7th World Conference in Multidisciplinary Civil Engineering-Architecture-Urban Planning Symposium (WMCAUS 2022), Prague, Czech Republic, 5–9 September 2022. [Google Scholar]
- Baláž, I.; Koleková, Y.; Agüero, A. Plastic resistance of Z-sections under various internal forces. In Proceedings of the 7th World Conference in Multidisciplinary Civil Engineering-Architecture-Urban Planning Symposium (WMCAUS 2022), Prague, Czech Republic, 5–9 September 2022. [Google Scholar]
- Baláž, I.; Koleková, Y.; Agüero, A. Plastic resistance of channel sections under various internal forces. In Proceedings of the 20th International Conference in Numerical Analysis and Applied Mathematics, Heraklion, Greece, 19–25 September 2022. [Google Scholar]
- Osterrieder, P.; Kretzschmar, J. First-hinge analysis for lateral buckling design of open thin-walled steel members. J. Constr. Steel Res. 2006, 62, 35–43. [Google Scholar] [CrossRef]
- Broer, G.; Martin-Bullmann, R. Kaltprofile, 4th ed.; Verlag Stahleisen mbH: Düsseldorf, Germany, 1993; 258p. [Google Scholar]
- Wetzell, O.W. (Ed.) Wendehorst Bautechnische Zahlentafeln, 33rd ed.; Springer Vieweg: Berlin/Heidelberg, Germany, 2009; 1560p, Available online: https://link.springer.com/book/10.1007/978-3-8348-8613-2 (accessed on 4 May 2023).
- Schneider, K.J. Bautabellen mit Berechnungshinweisen und Beispielen, 9th ed.; Werner-Verlag: Köln, Germany, 1990. [Google Scholar]
- Rhodes, J.; Lawson, R.M. Design of Structures Using Cold Formed Steel Sections: Section Properties and Member Capacities; SCI Publication 089; The Steel Construction Institute: Ascot, UK, 1992; 149p. [Google Scholar]
- American Iron and Steel Institute. Cold-Formed Steel Design Manual, 1986 ed.; Addendum, AISI: Washington, DC, USA, 1989. [Google Scholar]
- Structx, Shape Formulas. Available online: https://www.structx.com/Shape_Formulas_007.html (accessed on 4 May 2023).
- RoofingSheets, Purlin. Available online: https://www.roofingsheets.co.uk/z-purlin.html (accessed on 4 May 2023).
- RoofingSheetsByRhino, Purlin. Available online: https://www.roofingsheetsbyrhino.com/z-purlin/ (accessed on 4 May 2023).
- PurlinMill, Purlins Dimensions. Available online: https://www.thepurlinmill.com/z-purlins-dimensions (accessed on 4 May 2023).
- ThakkaGroup, Purlin Data Sheet. Available online: https://www.thakkargroup.com/z_purlin_specification.html (accessed on 4 May 2023).
- TigerProfile, Purlin Data Sheet. Available online: http://www.tigerprofiles.com/media/98530/z-purlin-data-sheet.pdf (accessed on 4 May 2023).
- Aespan, Structural Section. Available online: https://www.aepspan.com/wp-content/uploads/PS201_Structural-Sections.pdf (accessed on 4 May 2023).
- Metroll, Standard Purlins Girts. Available online: https://www.metroll.com.au/wp-content/uploads/metroll_standard_purlins_girts.pdf (accessed on 4 May 2023).
- Flefospan, Section Properties. Available online: https://www.flexospan.com/cadfiles/purlins-girts/SECTION%20PROPERTIES1-ZEE%20PROP.pdf (accessed on 4 May 2023).
- OrangeBook, Section Dimensions Properties. Available online: https://orangebook.arcelormittal.com/design-data/uk-na/cold-formed-sections/z/section-properties-dimensions-properties/ (accessed on 4 May 2023).
- Metsec, Z-Section Dimensions Properties. Available online: https://www.metsec.com/products/purlins-side-rails/technical-details/components-accessories/z-section-dimensions-properties/ (accessed on 4 May 2023).
- ClackDietrich, Girt Section Properties. 2021. Available online: https://www.clarkdietrich.com/sites/default/files/imce/pdf/20_Products/23_ExtFraming/z-girt/CD_Z-Girt_Section_Properties_9-20-21.pdf (accessed on 4 May 2023).
- Beams, Channels and Merchant Bars, Sales Programme, Arcelor Sections Commercial s.a., Arcelor Group, 240p. Available online: https://sections.arcelormittal.com/ (accessed on 4 May 2023).
- Fritz Walter Stahlkatalog, 228p. Available online: https://www.fritzwalter.de/fileadmin/user_upload/gesamt_72dpi.pdf (accessed on 4 May 2023).
- Agüero, A.; Baláž, I.; Koleková, Z. Improved interaction formula for the plastic resistance of I- and H-sections under a combination of bending moments My,Ed, Mz,Ed, and bimoment BEd. Appl. Sci. 2022, 12, 7888. [Google Scholar] [CrossRef]

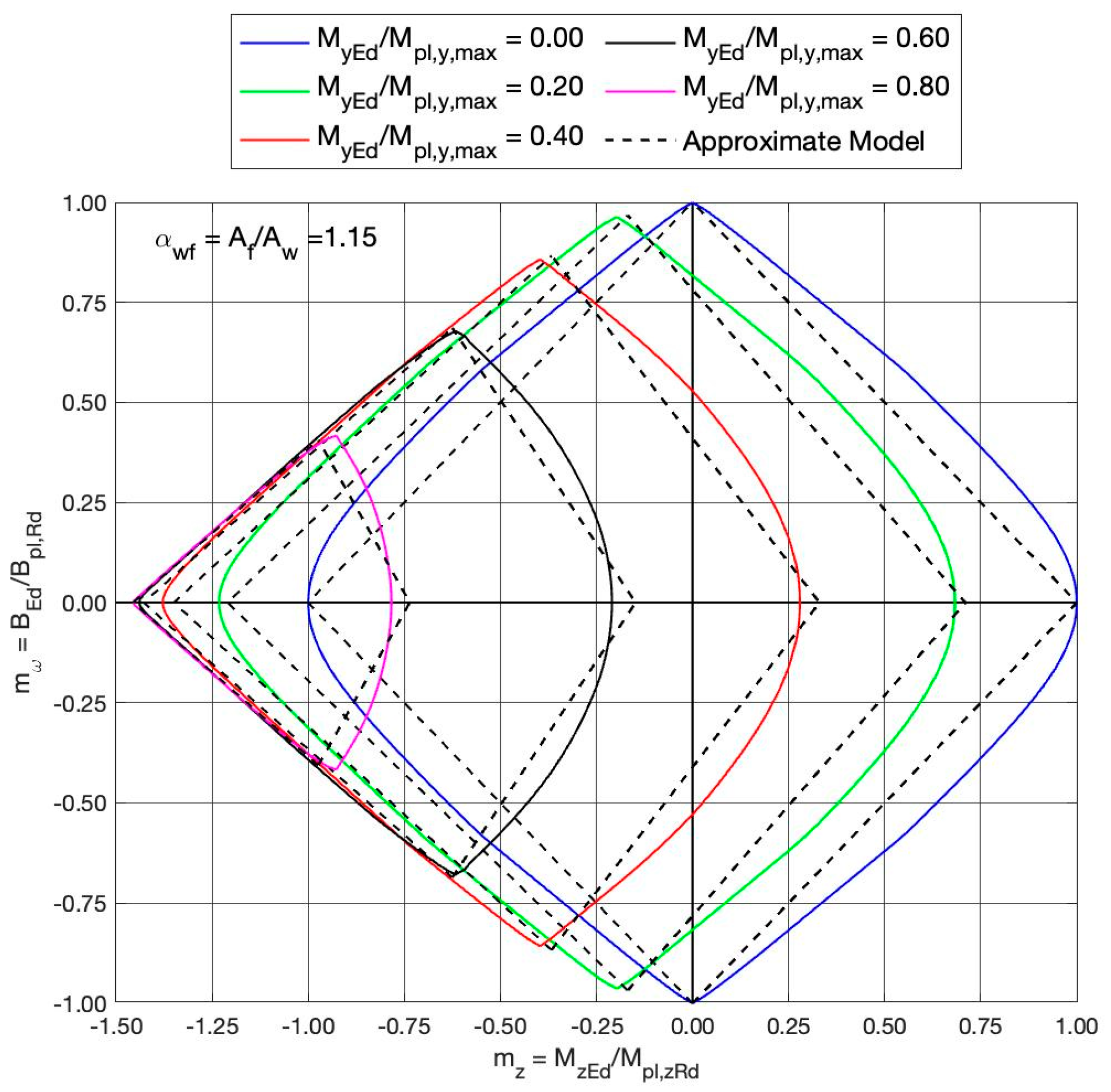
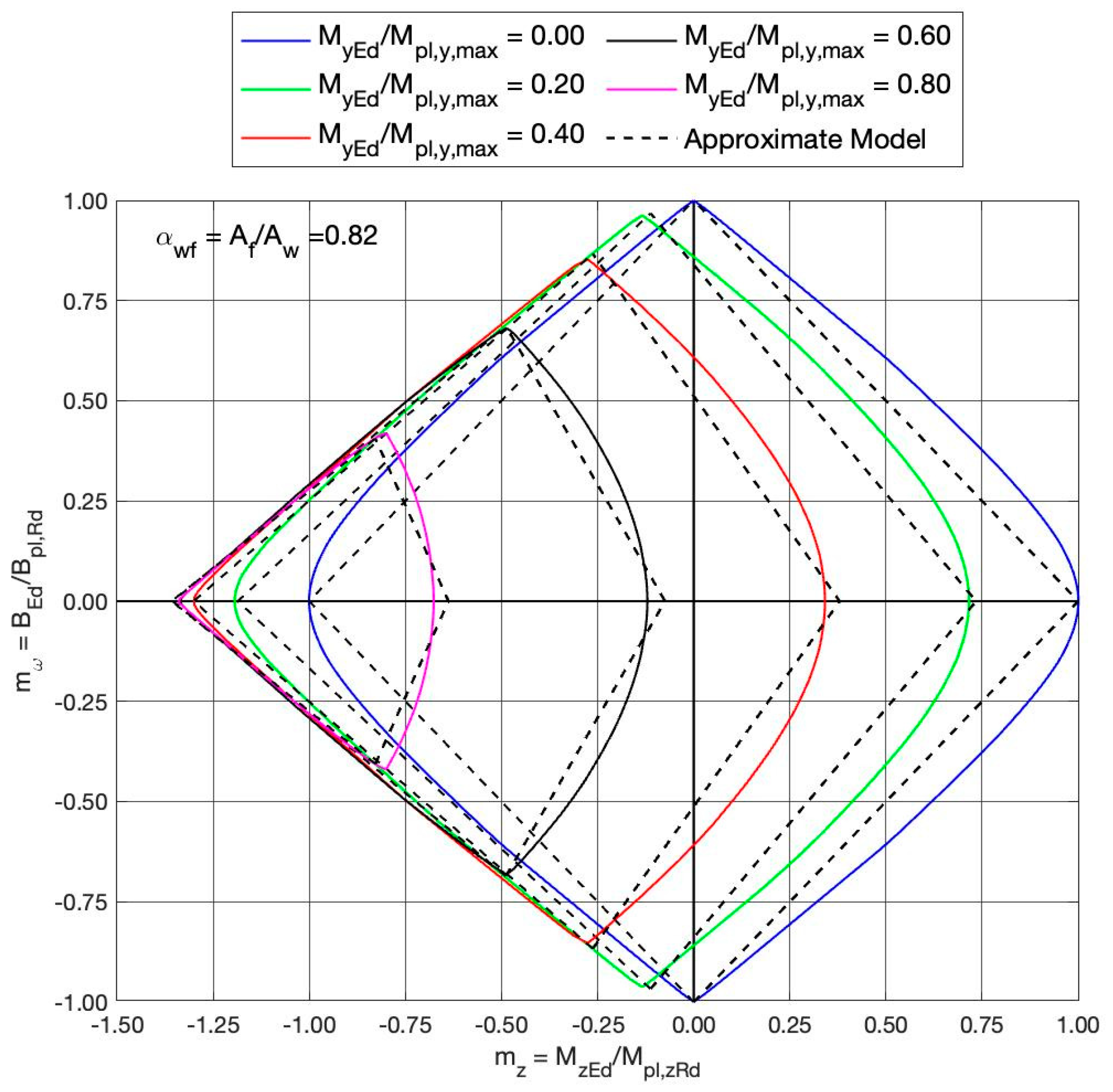
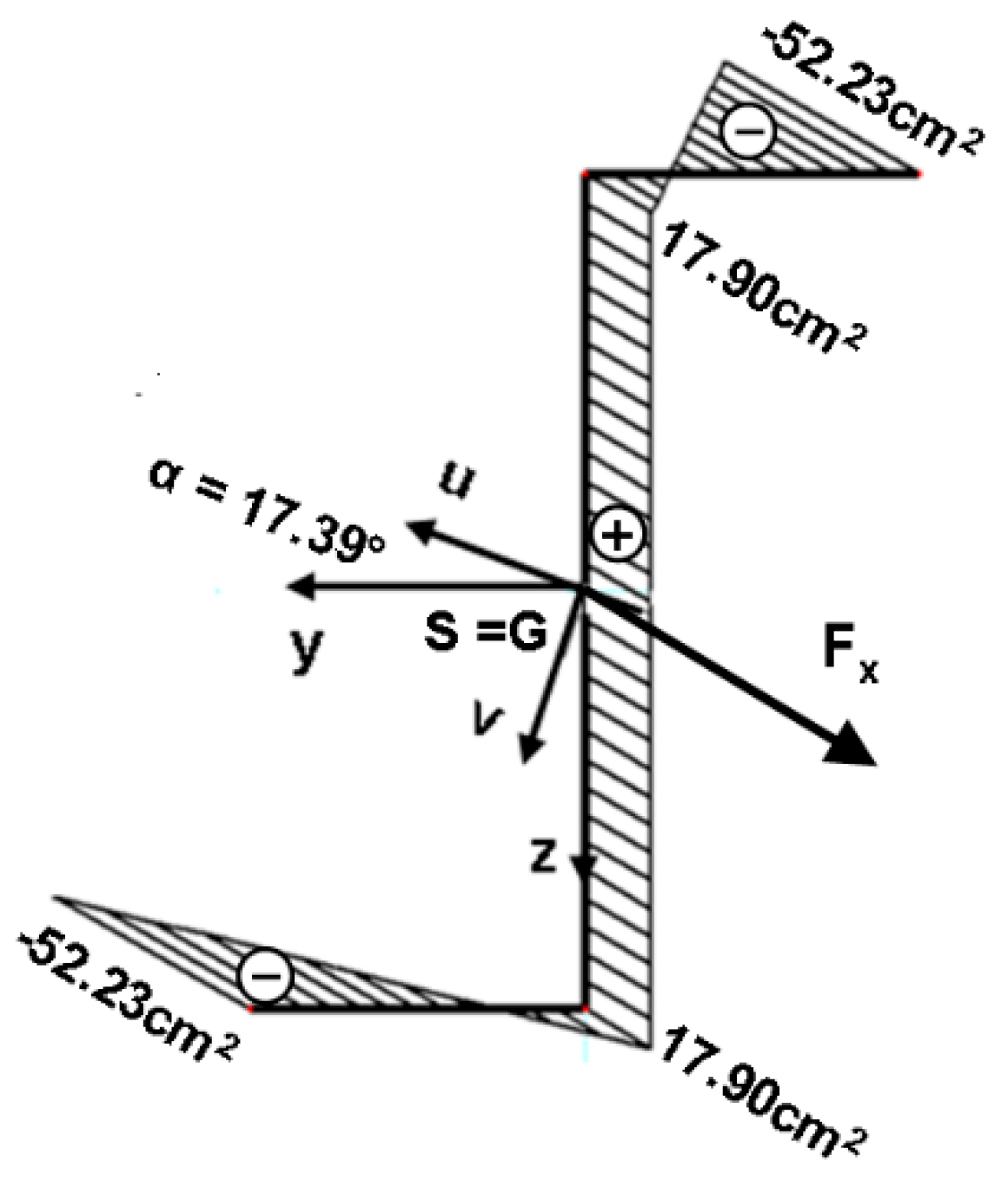
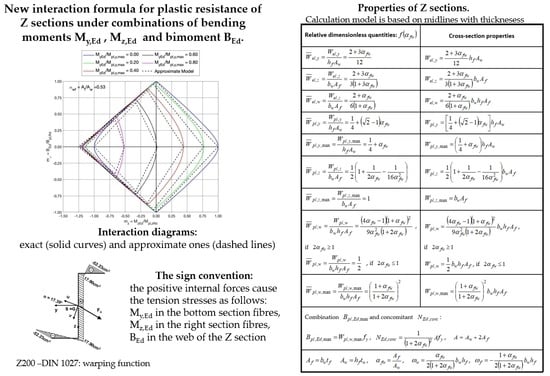
| Relative Dimensionless Quantities: | Cross-Section Properties |
|---|---|
| , if , if | , if , if |
| Combination of and concomitant : , , | |
| , , , , | |
| 0.000 | 0.200 | 0.400 | 0.600 | 0.800 | |
|---|---|---|---|---|---|
| 1.161 | 1.020 | 0.925 | 0.863 | 0.824 | |
| 1.000 | 0.810 | 0.616 | 0.419 | 0.215 | |
| 1.161 | 1.372 | 1.698 | 2.229 | 3.185 | |
| 1.000 | 1.180 | 1.327 | 1.376 | 1.146 | |
| A | 1.000 | 0.879 | 0.797 | 0.744 | 0.710 |
| B | 1.000 | 1.014 | 0.986 | 0.937 | 0.874 |
| C | −1.000 | −1.182 | −1.463 | −1.920 | −2.744 |
| D | 1.000 | 0.906 | 0.648 | 0.039 | −1.402 |
| Section | Z30 | Z40 | Z50 | Z60 | Z80 | Z100 | Z120 | Z140 | Z160 | Z180 | Z200 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DIN 1027 | 3.97 | 6.75 | 10.5 | 14.9 | 27.3 | 44.4 | 67.0 | 96.6 | 132 | 178 | 230 | |
| Table 1 | 1.47 | 2.57 | 4.13 | 5.87 | 11.3 | 18.7 | 28.5 | 42.4 | 58.4 | 80.1 | 103.9 | |
| DIN 1027 | 3.80 | 4.66 | 5.88 | 7.09 | 10.1 | 14.0 | 18.8 | 24.3 | 31.0 | 38.4 | 47.6 | |
| Table 1 | 2.28 | 2.89 | 3.76 | 4.55 | 6.74 | 9.46 | 12.8 | 16.9 | 21.7 | 27.4 | 33.9 |
| Cross-section geometrical properties | ||||||||
| mm | mm | mm | mm | mm | mm | cm2 | cm2 | cm2 |
| 200 | 80 | 10 | 13 | 187 | 75 | 9.75 | 18.70 | 38.20 |
| Relative dimensionless quantities as a function of | ||||||||
| 0.297 | 0.463 | 0.276 | 0.466 | 0.771 | 0.865 | 1.000 | 0.5027 | 0.555 |
| Physical properties of the cross-section | ||||||||
| cm3 | cm3 | cm4 | cm3 | cm3 | cm3 | cm3 | cm4 | cm4 |
| 103.86 | 33.88 | 377.71 | 162.94 | 269.75 | 63.22 | 73.125 | 687.47 | 758.48 |
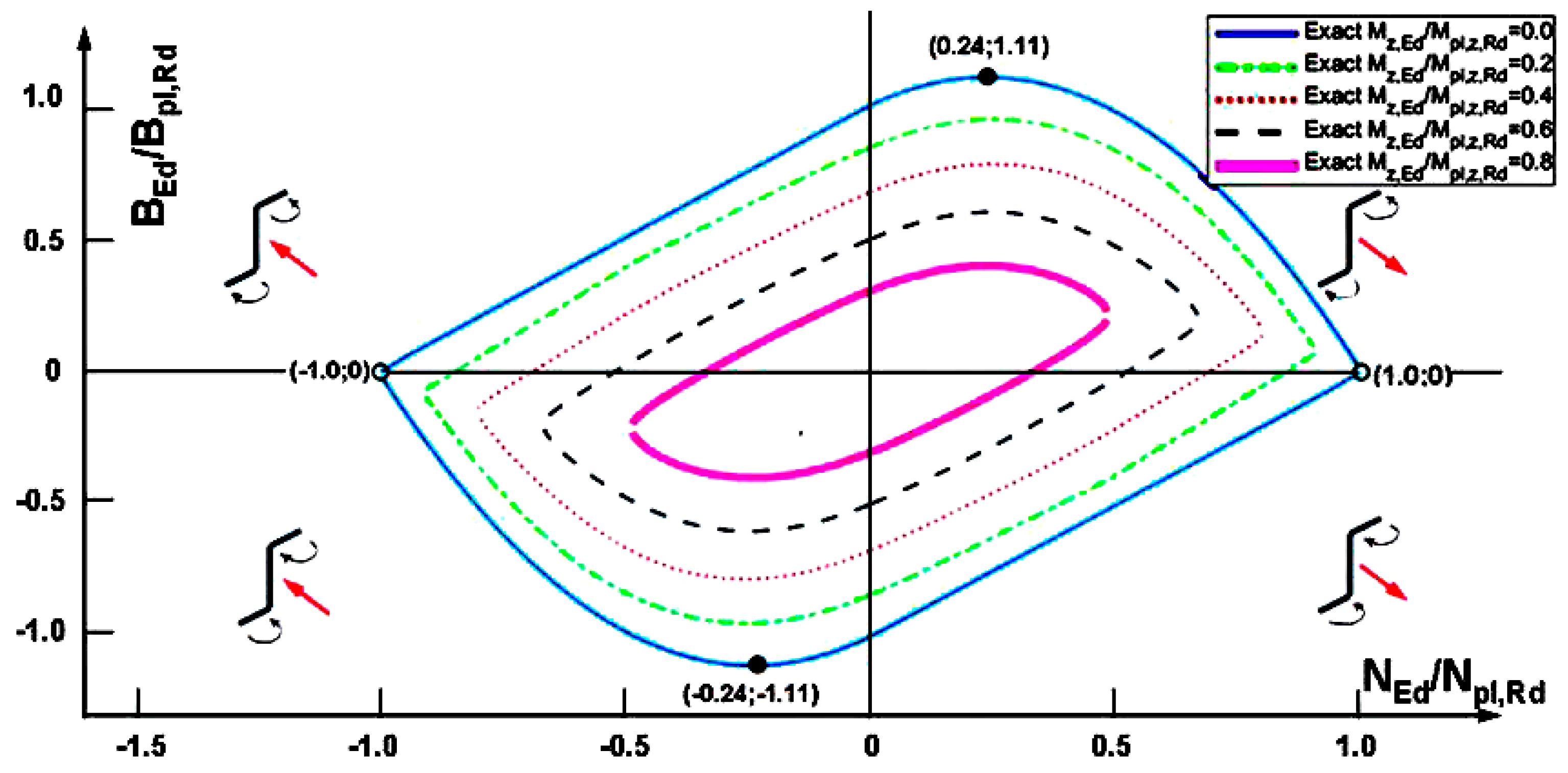
| Bimoment–Axial Force Combination Example in Figure 3 | |||||
|---|---|---|---|---|---|
| kNm2 | kNm2 | kN | kN | - | - |
| 1.782 | 1.605 | 215.12 | 897.70 | 0.24 | 1.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agüero, A.; Baláž, I.; Koleková, Y.; Lázaro, M. New Interaction Formulae for Plastic Resistances of Z-Sections under Combinations of Bending Moments My,Ed, Mz,Ed and Bimoment BEd. Buildings 2023, 13, 1778. https://doi.org/10.3390/buildings13071778
Agüero A, Baláž I, Koleková Y, Lázaro M. New Interaction Formulae for Plastic Resistances of Z-Sections under Combinations of Bending Moments My,Ed, Mz,Ed and Bimoment BEd. Buildings. 2023; 13(7):1778. https://doi.org/10.3390/buildings13071778
Chicago/Turabian StyleAgüero, Antonio, Ivan Baláž, Yvona Koleková, and Mario Lázaro. 2023. "New Interaction Formulae for Plastic Resistances of Z-Sections under Combinations of Bending Moments My,Ed, Mz,Ed and Bimoment BEd" Buildings 13, no. 7: 1778. https://doi.org/10.3390/buildings13071778
APA StyleAgüero, A., Baláž, I., Koleková, Y., & Lázaro, M. (2023). New Interaction Formulae for Plastic Resistances of Z-Sections under Combinations of Bending Moments My,Ed, Mz,Ed and Bimoment BEd. Buildings, 13(7), 1778. https://doi.org/10.3390/buildings13071778