Analysis of the Seismic Performance of Rectangular Recycled Aggregate Concrete Columns with Different Parameters
Abstract
:1. Introduction
2. Experimental Data Collection
2.1. Theoretical Derivation
2.2. Data Selection
2.3. Characteristic Point Data Collection
2.4. Tests Description
3. Parameters Analysis
3.1. Skeleton Curve Analysis
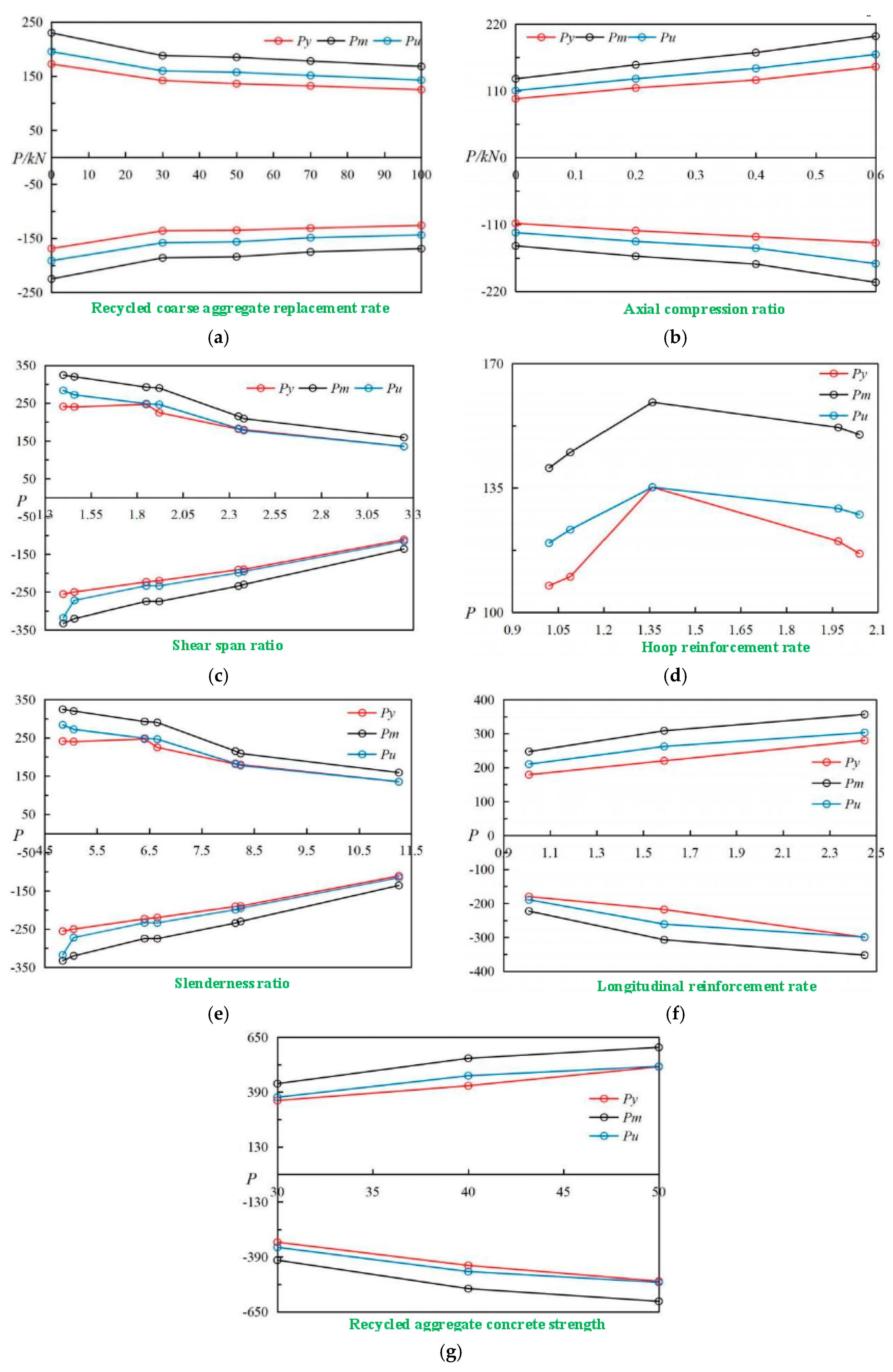
3.2. Load-Bearing Capacity Analysis
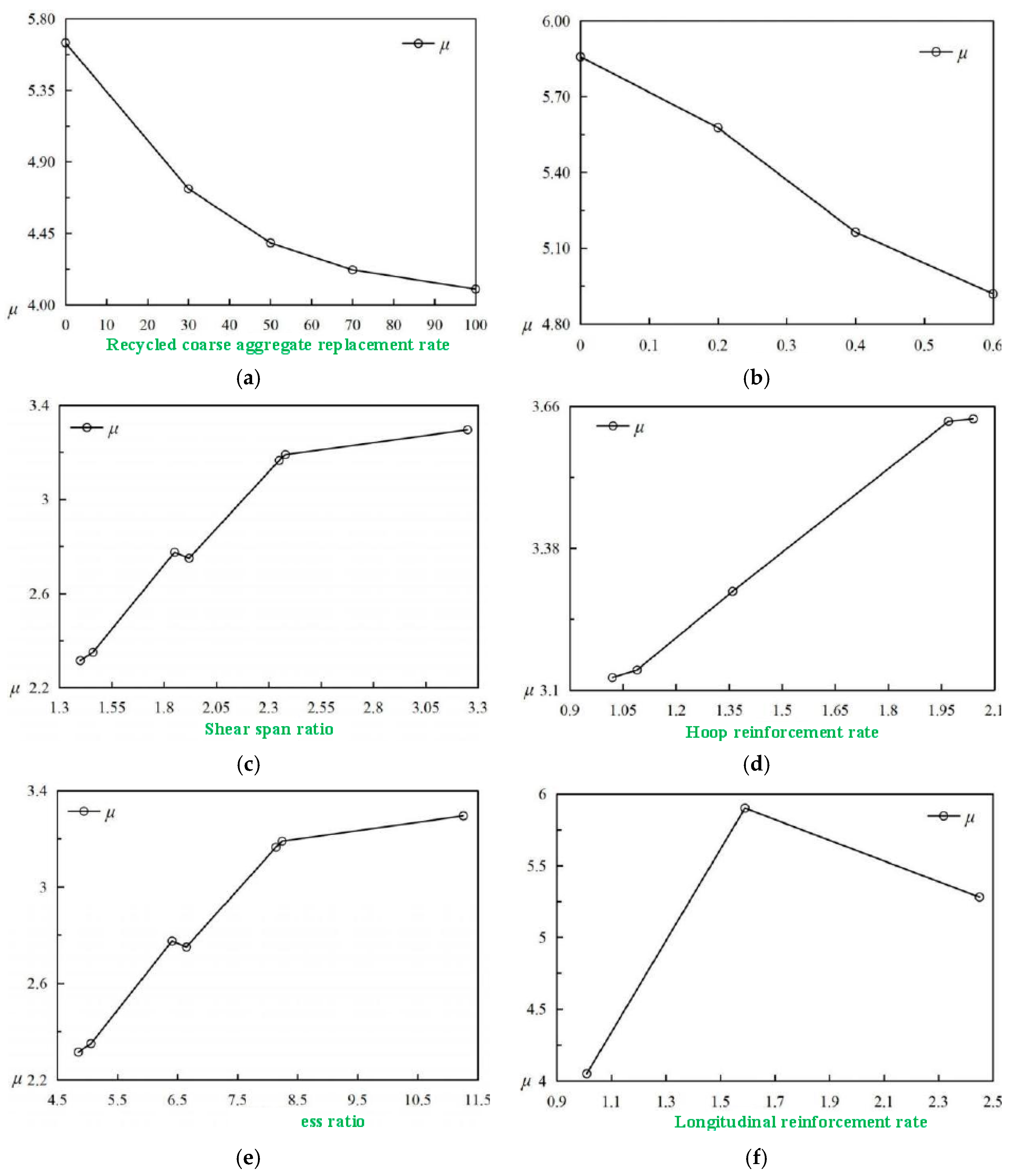
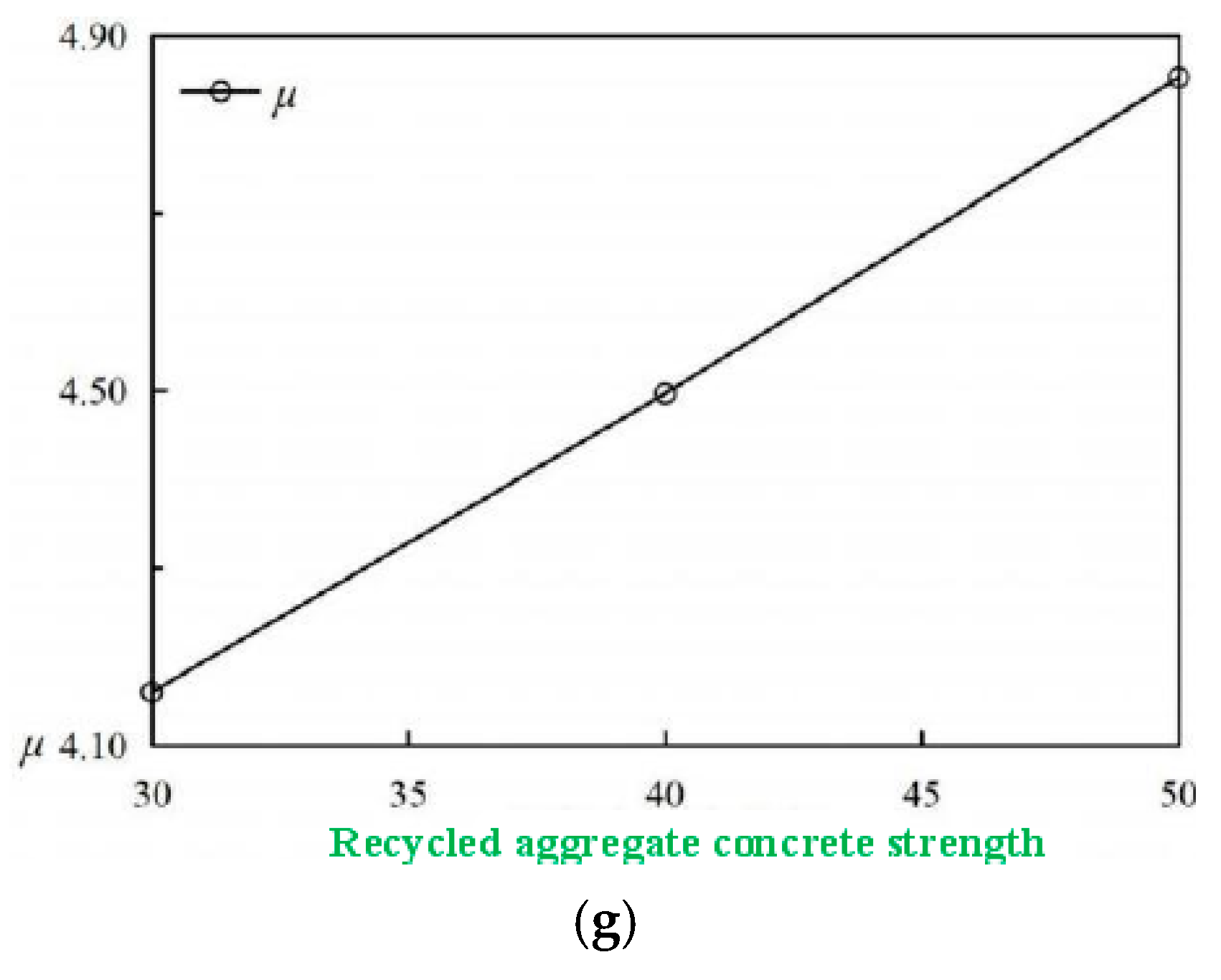
3.3. Ductility Performance Analysis
4. Conclusions
- (1)
- For the seismic design of rectangular recycled aggregate concrete columns, it is recommended to adopt a replacement rate of recycled coarse aggregate ranging from 0% to 30%, a slenderness ratio between 6.65 and 8.24, an axial compression ratio ranging from 0.2 to 0.4, a shear span ratio between 1.92 and 2.38, and a recycled aggregate concrete strength of either C40 or C50 to ensure satisfactory bearing capacity and ductility performance.
- (2)
- As the longitudinal reinforcement rate increases, the bearing capacity of the specimen also increases, while the ductility performance exhibits an initial improvement followed by a subsequent reduction. The optimal longitudinal reinforcement rate for the seismic design of rectangular recycled aggregate concrete columns is recommended to be around 1.59%.
- (3)
- As the hoop reinforcement rate enhances, the ductility performance of the specimen also improves, while the bearing capacity exhibits an initial increase followed by a subsequent decrease. The best hoop reinforcement rate for the seismic design of rectangular recycled aggregate concrete columns is recommended to be approximately 1.36%.
- (4)
- The sensitivity of different parameters to the seismic performance of the structure varies. The sensitivity of longitudinal reinforcement rate, slenderness ratio, shear span ratio, concrete strength grade, and axial compression ratio is stronger, while the sensitivity of hoop reinforcement rate and recycled coarse aggregate replacement rate is poor. To attain the best performance of the structure, engineers must take economic rationality into account and alter the fewest factors. Therefore, it is recommended to change the longitudinal reinforcement rate, slenderness ratio, shear span ratio, concrete strength grade, and axial compression ratio of the specimen to improve the seismic performance of the structure.
- (5)
- In this study, the seismic design limitations and boundary conditions are γ ∈ [0, 100%], n0 ∈ [0, 0.9], λ0 ∈ [5.06, 18.479], λ ∈ [1.09, 3.93], ρsl ∈ [1.01%, 2.45%], ρsv ∈ [1.4%, 5.33%], and f ∈ [C30, C50].
- (6)
- This study reviewed and collected a large amount of data from the literature, and the conclusions are very effective, but there are still certain aspects to be improved. For instance, when the hoop reinforcement rate is around 1.36% and the longitudinal reinforcement rate is about 1.59%, the data and the seismic performance of the structure need to be supplemented and further studied. In addition, the scope of the parameters needs to be widened to make the conclusions more general. The aforementioned will be added and improved in future research.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiao, J.; Wang, C.; Ding, T.; Akbarnezhad, A. A recycled aggregate concrete high-rise building: Structural performance and embodied carbon footprint. J. Clean. Prod. 2018, 199, 868–881. [Google Scholar] [CrossRef]
- Xiao, J.Z.; Xia, B.; Xiao, X.W. Theoretical framework for sustainability design of engineering structures. China Civ. Eng. J. 2020, 53, 1–12. [Google Scholar]
- Ding, T.; Xiao, J.Z.; Tam, V.W. A closed-loop life cycle assessment of recycled aggregate concrete utilization in China. Waste Manag. 2016, 56, 367–375. [Google Scholar] [CrossRef] [PubMed]
- Cao, W.L.; Zhao, Y.X.; Ye, T.P. A review of recent advances in the long-term working characteristic of recycled concrete structure. J. Harbin Inst. Technol. 2019, 51, 1–17. [Google Scholar]
- Dong, H.; Song, Y.; Cao, W.; Sun, W.; Zhang, J. Flexural bond behavior of reinforced recycled aggregate concrete. Constr. Build. Mater. 2019, 213, 514–527. [Google Scholar] [CrossRef]
- Ollivier, J.R.; Maso, J.C.; Bourdette, B. Interfacial transition zone in concrete. Adv. Cem. Based Mater. 1995, 2, 30–38. [Google Scholar] [CrossRef]
- Liu, C.; Fan, J.; Bai, G.; Quan, Z.; Fu, G.; Zhu, C.; Fan, Z. Cyclic load tests and seismic performance of recycled aggregate concrete (RAC) columns. Constr. Build. Mater. 2019, 195, 682–694. [Google Scholar] [CrossRef]
- Gaurav, G.; Singh, B. Experimental investigation for splice strength of deformed steel bars in normal-, medium- and high-strength recycled aggregate concrete. Constr. Build. Mater. 2021, 266, 121185. [Google Scholar] [CrossRef]
- Yuan, C.M.; Cai, J.; Chen, Q.J.; Liu, X.; Huang, H.; Zuo, Z.; He, A. Experimental study on seismic behaviour of precast recycled fine aggregate concrete columns with pressed sleeve connections. Structures 2023, 48, 1373–1390. [Google Scholar] [CrossRef]
- Cai, R.; Zhang, J.; Liu, Y.; Tao, X. Seismic behavior of recycled concrete columns reinforced with ultra-high-strength steel bars. Eng. Struct. 2023, 279, 115633. [Google Scholar] [CrossRef]
- Ma, H.; Xue, J.; Zhang, X.; Luo, D. Seismic performance of steel-reinforced recycled concrete columns under low cyclic loads. Constr. Build. Mater. 2013, 48, 229–237. [Google Scholar] [CrossRef]
- Zhang, Y.D. Experimental study on the seismic behavior of recycled concrete short columns with different stirrup ratios. Build. Struct. 2011, 41, 272–276. [Google Scholar]
- Zhang, Y.Q.; Cao, W.L.; Zhang, J.W. An experimental study on the seismic behavior of recycled concrete short columns with crossed reinforcing bars. Technol. Earthq. Disaster Prev. 2010, 5, 89–98. [Google Scholar]
- Yin, H.P.; Cao, W.L.; Zhang, Y.J.; Zhang, J. An Experimental study on the seismic behavior of recycled concrete columns with different reinforcement ratio. Technol. Earthq. Disaster Prev. 2010, 5, 99–107. [Google Scholar]
- Yin, H.P.; Cao, W.L.; Zhang, Y.J.; Zhang, J. An experimental study on the seismic behavior of recycled concrete columns with different recycled aggregate substitution ratios. World Earthq. Eng. 2010, 26, 57–63. [Google Scholar]
- Peng, Y.K.; Wu, H.; Gao, Q.C. Experimental study on seismic behavior of recycled concrete slender columns. J. Southeast Univ. 2013, 43, 576–581. [Google Scholar]
- Bai, G.; Liu, C.; Zhao, H.; Yao, F.; Zhu, L. Experimental research on seismic behavior of recycled concrete frame columns. J. Earthq. Eng. Eng. Vib. 2011, 31, 61–66. [Google Scholar]
- Peng, S.; Liu, G.; Xiong, Z.; Wang, J.; Li, G. Effect of confinement materials and damage degree on the seismic behavior of RRACFST columns. J. Build. Eng. 2022, 57, 104938. [Google Scholar] [CrossRef]
- Peng, S.; Xiong, Z. Experimental study on the seismic behavior of CFRP-strengthened seismic-damaged recycled aggregate concrete-filled rectangular steel tube frame columns. J. Build. Eng. 2022, 45, 103422. [Google Scholar] [CrossRef]
- GB50010-2010; Code for Design of Concrete Structures. China Architecture and Building Press: Beijing, China, 2010. (In Chinese)
- Peng, S.; Xiong, Z.; Zeng, X.G. A restoring force model for CFRP seismic-damaged RACFST columns: Theoretical, experimental, and simulation analysis. Structures 2022, 40, 273–283. [Google Scholar] [CrossRef]
- Ai, L.; Soltangharaei, V.; Ziehl, P. Evaluation of ASR in concrete using acoustic emission and deep learning. Nucl. Eng. Des. 2021, 380, 111328. [Google Scholar] [CrossRef]
- Ai, L.; Soltangharaei, V.; Ziehl, P. Developing a heterogeneous ensemble learning framework to evaluate Alkali-silica reaction damage in concrete using acoustic emission signals. Mech. Syst. Signal Process. 2022, 172, 108981. [Google Scholar] [CrossRef]
- Peng, S.; Xu, C.; Lu, M.; Yang, J. Experimental research and finite element analysis on seismic behavior of CFRP-strengthened seismic-damaged composite steel-concrete frame columns. Eng. Struct. 2018, 155, 50–60. [Google Scholar] [CrossRef]
- Soltangharaei, V.; Ai, L.; Anay, R.; Bayat, M.; Ziehl, P. Implementation of information entropy, b-value, and regression analyses for temporal evaluation of acoustic emission data recorded during ASR cracking. Pract. Period. Struct. Des. Constr. 2021, 26, 04020065. [Google Scholar] [CrossRef]
- Soltangharaei, V.; Anay, R.; Ai, L.; Giannini, E.R.; Zhu, J.; Ziehl, P. Temporal evaluation of ASR cracking in concrete specimens using acoustic emission. J. Mater. Civ. Eng. 2020, 32, 04020285. [Google Scholar] [CrossRef]
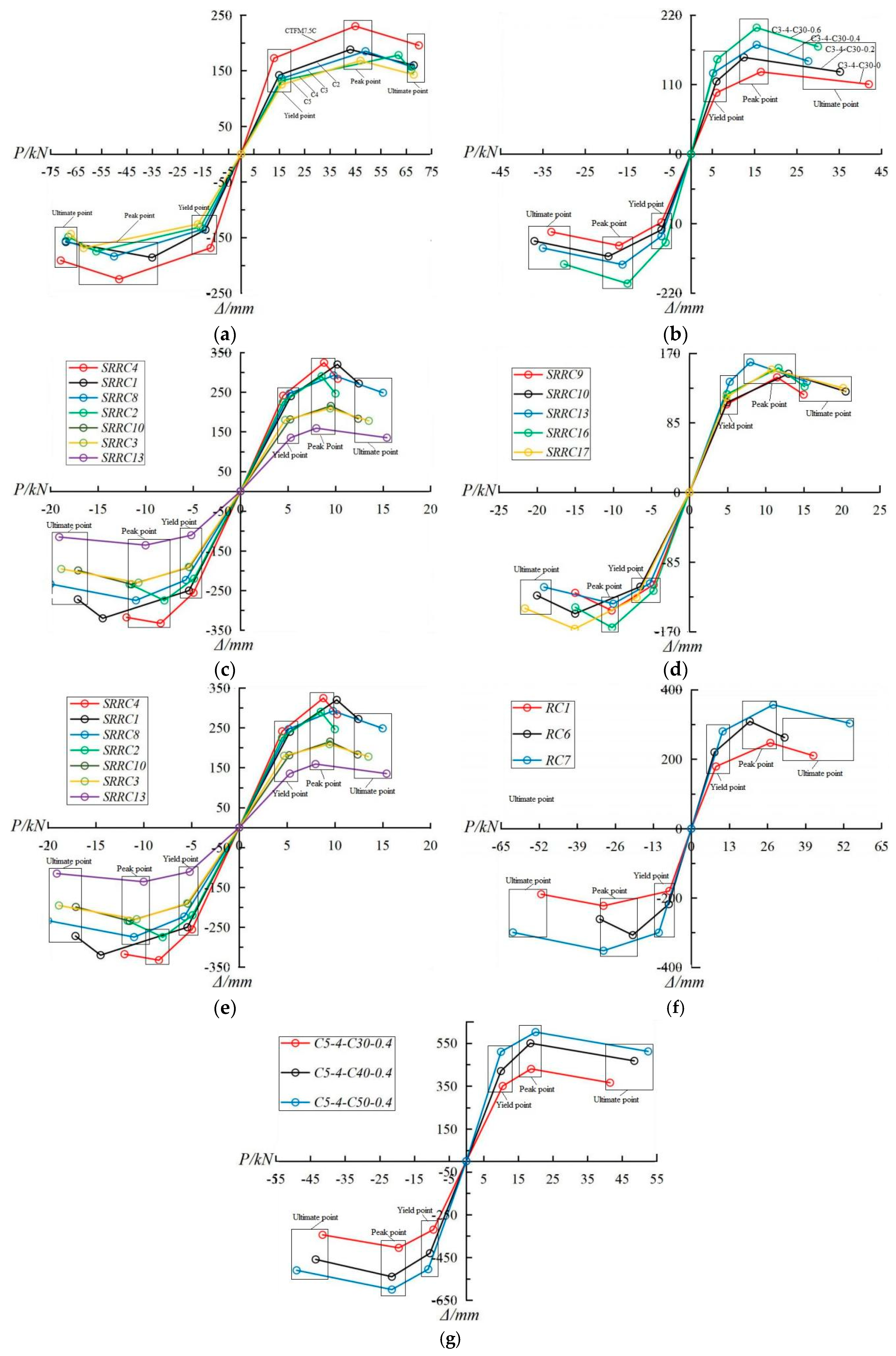
| Reference | Specimen | γ/% | Lw*Lh*t*H/mm | n0 | λ0 | λ | ρsv/% | ρsl/% | f |
|---|---|---|---|---|---|---|---|---|---|
| Wu [20] | RC1 | 30 | 400*400*4*1200 | 0.3 | 3.00 | 3 | 3.93 | 1.59 | C35 |
| RC2 | 30 | 400*400*4*1200 | 0 | 3.00 | 3 | 3.93 | 1.59 | C35 | |
| RC3 | 30 | 400*400*4*1200 | 0.15 | 3.00 | 3 | 3.93 | 1.59 | C35 | |
| RC4 | 30 | 400*400*4*1200 | 0.45 | 3.00 | 3 | 3.93 | 1.59 | C35 | |
| RC5 | 30 | 400*400*4*1200 | 0.6 | 3.00 | 3 | 3.93 | 1.59 | C35 | |
| RC6 | 30 | 400*400*4*1200 | 0.3 | 3.00 | 3 | 3.93 | 1.01 | C35 | |
| RC7 | 30 | 400*400*4*1200 | 0.3 | 3.00 | 3 | 3.93 | 2.45 | C35 | |
| RC8 | 0 | 400*400*4*1200 | 0.3 | 3.00 | 3 | 3.93 | 1.59 | C35 | |
| RC9 | 70 | 400*400*4*1200 | 0.3 | 3.00 | 3 | 3.93 | 1.59 | C35 | |
| RC10 | 30 | 400*400*4*1200 | 0.15 | 3.00 | 3 | 3.93 | 1.59 | C35 | |
| Bai et al. [17] | SRRC1 | 100 | 180*240*4*350 | 0.6 | 1.46 | 1.46 | 1.36 | 1.42 | C40 |
| SRRC2 | 100 | 180*240*4*460 | 0.6 | 1.92 | 1.92 | 1.36 | 1.42 | C40 | |
| SRRC3 | 100 | 180*240*4*570 | 0.6 | 2.38 | 2.38 | 1.36 | 1.42 | C40 | |
| SRRC4 | 0 | 180*240*4*780 | 0.6 | 3.25 | 3.25 | 1.36 | 1.42 | C40 | |
| SRRC5 | 50 | 180*240*4*780 | 0.6 | 3.25 | 3.25 | 1.36 | 1.42 | C40 | |
| SRRC6 | 100 | 180*240*4*780 | 0.6 | 3.25 | 3.25 | 1.36 | 1.42 | C40 | |
| SRRC7 | 100 | 180*240*4*780 | 0.4 | 3.25 | 3.25 | 1.36 | 1.42 | C40 | |
| SRRC8 | 100 | 180*240*4*780 | 0.8 | 3.25 | 3.25 | 1.36 | 1.42 | C40 | |
| SRRC9 | 100 | 180*240*4*780 | 0.6 | 3.25 | 3.25 | 1.09 | 1.42 | C40 | |
| SRRC10 | 100 | 180*240*4*780 | 0.6 | 3.25 | 3.25 | 1.97 | 1.42 | C40 | |
| SRRC11 | 100 | 180*240*4*780 | 0.6 | 3.25 | 3.25 | 1.36 | 1.42 | C50 | |
| SRRC12 | 100 | 180*240*4*780 | 0.6 | 3.25 | 3.25 | 1.36 | 1.42 | C60 | |
| SRRC13 | 100 | 180*240*4*780 | 0.6 | 3.25 | 3.25 | 1.36 | 1.42 | C40 | |
| SRRC14 | 100 | 180*240*4*780 | 0.6 | 3.25 | 3.25 | 1.36 | 1.42 | C40 | |
| Ma et al. [11] | SRRC1 | 0 | 180*240*4*335 | 0.6 | 1.40 | 1.4 | 1.36 | 1.42 | C40 |
| SRRC2 | 30 | 180*240*4*335 | 0.6 | 1.40 | 1.4 | 1.36 | 1.42 | C40 | |
| SRRC3 | 70 | 180*240*4*335 | 0.6 | 1.40 | 1.4 | 1.36 | 1.42 | C40 | |
| SRRC4 | 100 | 180*240*4*335 | 0.6 | 1.40 | 1.4 | 1.36 | 1.42 | C40 | |
| SRRC5 | 100 | 180*240*4*335 | 0.3 | 1.40 | 1.4 | 1.36 | 1.42 | C40 | |
| SRRC6 | 100 | 180*240*4*335 | 0.9 | 1.40 | 1.4 | 1.36 | 1.42 | C40 | |
| SRRC7 | 100 | 180*240*4*335 | 0.6 | 1.40 | 1.4 | 1.02 | 1.42 | C40 | |
| SRRC8 | 100 | 180*240*4*335 | 0.6 | 1.40 | 1.4 | 2.04 | 1.42 | C40 | |
| SRRC9 | 100 | 180*240*4*445 | 0.6 | 1.85 | 1.85 | 1.36 | 1.42 | C40 | |
| SRRC10 | 100 | 180*240*4*565 | 0.6 | 2.35 | 2.35 | 1.36 | 1.42 | C40 | |
| SRRC11 | 0 | 180*240*4*780 | 0.6 | 3.25 | 3.25 | 1.36 | 1.42 | C40 | |
| SRRC12 | 70 | 180*240*4*780 | 0.6 | 3.25 | 3.25 | 1.36 | 1.42 | C40 | |
| SRRC13 | 100 | 180*240*4*780 | 0.6 | 3.25 | 3.25 | 1.36 | 1.42 | C40 | |
| SRRC14 | 100 | 180*240*4*780 | 0.3 | 3.25 | 3.25 | 1.36 | 1.42 | C40 | |
| SRRC15 | 100 | 180*240*4*780 | 0.9 | 3.25 | 3.25 | 1.36 | 1.42 | C40 | |
| SRRC16 | 100 | 180*240*4*780 | 0.6 | 3.25 | 3.25 | 1.02 | 1.42 | C40 | |
| SRRC17 | 100 | 180*240*4*780 | 0.6 | 3.25 | 3.25 | 2.04 | 1.42 | C40 | |
| Peng et al. [16] | C2 | 30 | 300*300*7.5*1600 | 0.4 | 5.33 | 5.33 | 3.77 | 1.5 | C30 |
| C3 | 50 | 300*300*7.5*1600 | 0.4 | 5.33 | 5.33 | 3.77 | 1.5 | C30 | |
| C4 | 70 | 300*300*7.5*1600 | 0.4 | 5.33 | 5.33 | 3.77 | 1.5 | C30 | |
| C5 | 100 | 300*300*7.5*1600 | 0.4 | 5.33 | 5.33 | 3.77 | 1.5 | C30 | |
| Gaurav et al. [8] | CTFM7.5C | 0 | 300*300*7.5*1600 | 0.4 | 5.33 | 5.33 | 3.77 | 1.5 | C30 |
| Yuan et al. [9] | C3-4-C30-0 | 0 | 300*300*4*1200 | 0 | 4.00 | 4 | 1.89 | 1.51 | C30 |
| C3-4-C30-0.2 | 0 | 300*300*4*1200 | 0.2 | 4.00 | 4 | 1.89 | 1.51 | C30 | |
| C3-4-C30-0.4 | 0 | 300*300*4*1200 | 0.4 | 4.00 | 4 | 1.89 | 1.51 | C30 | |
| C3-4-C30-0.6 | 0 | 300*300*4*1200 | 0.6 | 4.00 | 4 | 1.89 | 1.51 | C30 | |
| C5-4-C30-0.4 | 0 | 500*500*4*2000 | 0.4 | 4.00 | 4 | 1.89 | 1.51 | C30 | |
| C5-4-C40-0.4 | 0 | 500*500*4*2000 | 0.4 | 4.00 | 4 | 1.89 | 1.51 | C40 | |
| C5-4-C50-0.4 | 0 | 500*500*4*2000 | 0.4 | 4.00 | 4 | 1.89 | 1.51 | C50 |
| Reference | Specimen | Load Type | Yield Point | Peak Point | Ultimate Point | μ | |||
|---|---|---|---|---|---|---|---|---|---|
| Py | Δy | Pm | Δm | Pu | Δu | ||||
| Wu [20] | RC1 | + | 220 | 8.44 | 308.55 | 27 | 262.27 | 41.72 | 5.9 |
| - | 218 | 7.48 | 307.19 | 30 | 261.11 | 51.28 | |||
| RC2 | + | 104 | 6.9 | 147.91 | 10 | 125.72 | 72.98 | 9.45 | |
| - | 140 | 9.17 | 170.89 | 60 | 145.26 | 76.39 | |||
| RC3 | + | 195 | 8.88 | 273.59 | 29 | 232.55 | 53.89 | 6.06 | |
| - | 217 | 9.98 | 271.37 | 30 | 230.66 | 60.34 | |||
| RC4 | + | 250 | 6.27 | 347.91 | 14 | 295.72 | 26.09 | 4 | |
| - | 252 | 7.07 | 308.31 | 20 | 262.06 | 27.13 | |||
| RC5 | + | 250 | 6.41 | 354.81 | 13 | 301.59 | 20.81 | 3.72 | |
| - | 260 | 6.75 | 326.82 | 20 | 277.8 | 28.25 | |||
| RC6 | + | 179 | 7.91 | 247.12 | 20 | 210.05 | 31.88 | 4.05 | |
| - | 180 | 7.68 | 222.79 | 20 | 189.37 | 31.26 | |||
| RC7 | + | 280 | 10.71 | 356.56 | 28 | 303.08 | 54.17 | 5.28 | |
| - | 300 | 11.1 | 352.19 | 30 | 299.36 | 60.95 | |||
| RC8 | + | 220 | 6.79 | 281.35 | 19 | 239.15 | 40.71 | 5.26 | |
| - | 215 | 7.56 | 268.88 | 20 | 228.55 | 34.14 | |||
| RC9 | + | 245 | 9.6 | 299.43 | 26 | 254.52 | 49.18 | 5.49 | |
| - | 220 | 9.29 | 257.18 | 20 | 218.6 | 54.44 | |||
| RC10 | + | 180 | 9.04 | 250.81 | 25 | 213.19 | 53.69 | 7.2 | |
| - | 190 | 8.79 | 211.94 | 21 | 180.15 | 74.34 | |||
| Bai et al. [17] | SRRC1 | + | 240 | 4.49 | 320 | 8.8 | 272 | 10.24 | 2.35 |
| - | 250 | 4.94 | 320 | 8.4 | 272 | 12 | |||
| SRRC2 | + | 245 | 5.3 | 290 | 10.2 | 246.5 | 12.46 | 2.75 | |
| - | 220 | 5.42 | 275 | 14.5 | 233.75 | 17.13 | |||
| SRRC3 | + | 180 | 5.17 | 209 | 9.8 | 177.65 | 15 | 3.19 | |
| - | 190 | 5.75 | 230 | 11 | 195.5 | 20 | |||
| SRRC4 | + | 130 | 5.1 | 160 | 9 | 136 | 15 | 3.49 | |
| - | 80 | 4.21 | 140 | 13.4 | 119 | 17 | |||
| SRRC5 | + | 100 | 3.89 | 155 | 10 | 131.75 | 13 | 3.36 | |
| - | 100 | 3.85 | 152 | 9.8 | 127.5 | 13 | |||
| SRRC6 | + | 125 | 4.28 | 150 | 7 | 127.5 | 12.5 | 3.31 | |
| - | 100 | 4.34 | 140 | 10 | 119 | 16 | |||
| SRRC7 | + | 103 | 6.08 | 130 | 14 | 110.5 | 34 | 5.21 | |
| - | 115 | 6 | 148 | 19 | 125.8 | 29 | |||
| SRRC8 | + | 148 | 5.87 | 175 | 8 | 148.75 | 11.8 | 2.18 | |
| - | 130 | 5.5 | 170 | 9.5 | 144.5 | 13 | |||
| SRRC9 | + | 110 | 4.87 | 145 | 11.5 | 123.25 | 15 | 3.14 | |
| - | 115 | 4.7 | 148 | 10.2 | 125.8 | 15 | |||
| SRRC10 | + | 120 | 4.94 | 152 | 13 | 129.2 | 20.5 | 3.63 | |
| - | 120 | 6.45 | 165 | 15 | 140.25 | 20 | |||
| SRRC11 | + | 135 | 4.87 | 175 | 8 | 148.75 | 13 | 3.1 | |
| - | 105 | 4.25 | 148 | 12 | 125.8 | 15 | |||
| SRRC12 | + | 140 | 4 | 178 | 8 | 151.3 | 13.8 | 3 | |
| - | 125 | 6.27 | 150 | 11.8 | 127.5 | 16 | |||
| SRRC13 | + | 150 | 5.34 | 180 | 8 | 153 | 14 | 2.98 | |
| - | 118 | 4.79 | 150 | 12 | 127.5 | 16 | |||
| SRRC14 | + | 160 | 4.11 | 200 | 7.5 | 170 | 12 | 2.65 | |
| - | 150 | 6.47 | 170 | 11.5 | 144.5 | 15 | |||
| Ma et al. [11] | SRRC1 | + | 250.5 | 3.68 | 328.2 | 8.35 | 279 | 10.21 | 2.66 |
| - | 249.8 | 3.77 | 322.7 | 8.3 | 274.3 | 9.62 | |||
| SRRC2 | + | 266.9 | 3.71 | 343.4 | 7.57 | 291.9 | 8.93 | 2.60 | |
| - | 259.2 | 3.67 | 327.3 | 8.08 | 303.3 | 10.25 | |||
| SRRC3 | + | 274.7 | 4.58 | 334 | 7.92 | 286.8 | 10.6 | 2.35 | |
| - | 262.7 | 4.77 | 328.3 | 8.48 | 279 | 11.4 | |||
| SRRC4 | + | 241.2 | 4.47 | 324.5 | 8.53 | 283.8 | 10 | 2.32 | |
| - | 255.5 | 4.89 | 332.6 | 8.01 | 317.6 | 11.67 | |||
| SRRC5 | + | 215.8 | 3.98 | 306.2 | 10.7 | 260.3 | 17.87 | 4.07 | |
| - | 258.9 | 4.39 | 331 | 8.39 | 281.4 | 15.98 | |||
| SRRC6 | + | 299.6 | 4.97 | 403.7 | 7.29 | 347.2 | 8.63 | 2.04 | |
| - | 268.4 | 3.28 | 357 | 7.48 | 319.4 | 7.67 | |||
| SRRC7 | + | 269.4 | 4.61 | 324.8 | 7.64 | 304.4 | 9.28 | 2.18 | |
| - | 266 | 3.44 | 312.6 | 6.31 | 292.6 | 8.1 | |||
| SRRC8 | + | 245.7 | 4.48 | 332.4 | 10.4 | 311.1 | 12.97 | 2.76 | |
| - | 323.4 | 4.2 | 377.2 | 7.89 | 365 | 11 | |||
| SRRC9 | + | 246.8 | 5.23 | 292.4 | 9.5 | 248.6 | 12.39 | 2.78 | |
| - | 223.3 | 5.37 | 274.7 | 11.5 | 233.5 | 17.09 | |||
| SRRC10 | + | 181.3 | 4.7 | 215.3 | 9.44 | 183 | 13.51 | 3.17 | |
| - | 190.9 | 5.45 | 234.3 | 10.7 | 199.2 | 18.86 | |||
| SRRC11 | + | 125.7 | 4.75 | 148 | 7.01 | 125.8 | 13.89 | 3.47 | |
| - | 112.8 | 4.58 | 145.8 | 10.8 | 123.9 | 18.39 | |||
| SRRC12 | + | 117.5 | 4.31 | 153.3 | 9.98 | 130.3 | 14.32 | 3.34 | |
| - | 118.3 | 4.25 | 155.9 | 9.37 | 132.5 | 14.31 | |||
| SRRC13 | + | 135.2 | 5.29 | 159.1 | 7.98 | 135.2 | 15.41 | 3.30 | |
| - | 111 | 5.18 | 135.9 | 9.99 | 115.5 | 19.08 | |||
| SRRC14 | + | 100.2 | 5.75 | 127.8 | 14.2 | 108.6 | 32.18 | 5.22 | |
| - | 112.6 | 6.19 | 143.6 | 16.1 | 122 | 29.98 | |||
| SRRC15 | + | 146.1 | 5.52 | 169.4 | 8.5 | 144 | 11.16 | 2.19 | |
| - | 143 | 5.42 | 168.3 | 8.43 | 143 | 12.82 | |||
| SRRC16 | + | 107.5 | 4.93 | 140.6 | 11.7 | 119.5 | 15.12 | 3.13 | |
| - | 112.6 | 4.71 | 144.2 | 10.2 | 122.6 | 14.98 | |||
| SRRC17 | + | 116.5 | 4.85 | 150 | 10.8 | 127.5 | 20.18 | 3.64 | |
| - | 128.3 | 6.94 | 166.5 | 15.1 | 141.5 | 21.59 | |||
| Peng et al. [16] | C2 | + | 142 | 15 | 188 | 43 | 159.8 | 68 | 4.73 |
| - | 136 | 14 | 186 | 35 | 158.1 | 69 | |||
| C3 | + | 136 | 16 | 185 | 49 | 157.25 | 67 | 4.39 | |
| - | 135 | 15 | 184 | 50 | 156.4 | 69 | |||
| C4 | + | 132 | 16 | 178 | 62 | 151.3 | 67 | 4.22 | |
| - | 131 | 16 | 175 | 57 | 148.75 | 68 | |||
| C5 | + | 125 | 16 | 168 | 47 | 142.8 | 68 | 4.10 | |
| - | 126 | 17 | 169 | 62 | 143.65 | 67 | |||
| Gaurav et al. [8] | CTFM7.5C | + | 172.5 | 13 | 230 | 45 | 195.5 | 70 | 5.65 |
| - | 168.75 | 12 | 225 | 48 | 191.25 | 71 | |||
| Yuan et al. [9] | C3-4-C30-0 | + | 97 | 6 | 130 | 16.5 | 110.5 | 42 | 5.86 |
| - | 108 | 7 | 145 | 17 | 123.25 | 33 | |||
| C3-4-C30-0.2 | + | 115 | 6 | 153 | 12.5 | 130.05 | 35.2 | 5.58 | |
| - | 120 | 7 | 162 | 19.5 | 137.7 | 37 | |||
| C3-4-C30-0.4 | + | 128 | 5.2 | 173 | 15.5 | 147.05 | 27.7 | 5.16 | |
| - | 130 | 7 | 175 | 16.2 | 148.75 | 35 | |||
| C3-4-C30-0.6 | + | 150 | 6.2 | 200 | 15.5 | 170 | 30 | 4.92 | |
| - | 140 | 6 | 205 | 15 | 174.25 | 30 | |||
| C5-4-C30-0.4 | + | 350 | 10.5 | 430 | 18.7 | 365.5 | 41.5 | 4.16 | |
| - | 320 | 9.5 | 405 | 19.5 | 344.25 | 41.5 | |||
| C5-4-C40-0.4 | + | 420 | 10 | 550 | 18.5 | 467.5 | 48.5 | 4.50 | |
| - | 430 | 10.5 | 540 | 21.5 | 459 | 43.5 | |||
| C5-4-C50-0.4 | + | 510 | 10 | 602 | 20 | 511.7 | 52.5 | 4.85 | |
| - | 505 | 11 | 600 | 21.5 | 510 | 49 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, H.; Peng, S.; Xu, C.; Zhu, Y.; Sun, J.; Luo, S.; Deng, N.; He, L.; Han, Y.; Wu, C. Analysis of the Seismic Performance of Rectangular Recycled Aggregate Concrete Columns with Different Parameters. Buildings 2023, 13, 1761. https://doi.org/10.3390/buildings13071761
Ma H, Peng S, Xu C, Zhu Y, Sun J, Luo S, Deng N, He L, Han Y, Wu C. Analysis of the Seismic Performance of Rectangular Recycled Aggregate Concrete Columns with Different Parameters. Buildings. 2023; 13(7):1761. https://doi.org/10.3390/buildings13071761
Chicago/Turabian StyleMa, Haoran, Sheng Peng, Chengxiang Xu, Yide Zhu, Jie Sun, Siyu Luo, Nianchun Deng, Li He, Yunfei Han, and Cai Wu. 2023. "Analysis of the Seismic Performance of Rectangular Recycled Aggregate Concrete Columns with Different Parameters" Buildings 13, no. 7: 1761. https://doi.org/10.3390/buildings13071761
APA StyleMa, H., Peng, S., Xu, C., Zhu, Y., Sun, J., Luo, S., Deng, N., He, L., Han, Y., & Wu, C. (2023). Analysis of the Seismic Performance of Rectangular Recycled Aggregate Concrete Columns with Different Parameters. Buildings, 13(7), 1761. https://doi.org/10.3390/buildings13071761






