Abstract
This work presents a new approach to investigating water conduction properties in real three-dimensional (3D) voids of asphalt mixtures. Three different molding methods were employed for the same grade of asphalt mixture, and the three asphalt mixture specimens were scanned using X-ray Computerized Tomography (CT) to identify the real 3D void structure distribution inside the mixture. The real 3D behavior of void moisture conduction inside the mixture was simulated using the discrete lattice Boltzmann method and the BGK collision model. Three different molding methods were used to study the behavior of mesoscopic seepage inside the specimen. The results show that water conduction varies substantially in real 3D voids inside diverse molded objects. Regardless of flow and flow velocity, the Superpave Gyratory Compactor (SGC) method is extraordinarily close to the conduction qualities of the actual field core material. It shows that the Marshall molding method is inconsistent with the actual pavement molding method, and the SGC method can not only ensure that the reasonable void ratio is conducive to the thermal expansion and cold shrinkage space of the asphalt mixture but also prevents rainwater from entering the asphalt mixture. This work provides a new perspective for the study of water damage resistance and medium transmission characteristics of asphalt mixtures.
1. Introduction
The specimen molding procedure for designing asphalt mixes is crucial to the road performance of the asphalt mixtures. Currently, the Marshall molding method or SGC method is commonly utilized in asphalt mixture design [1,2]. Variable molding methods affect the particle distribution of the asphalt mixture, resulting in variable void distributions [3]. As a consequence, the conduction path of water in the void is radically different. The structure of the asphalt mixture’s internal voids and their connectedness influence whether the internal held water can be distributed in time [4,5].
The primary cause of water damage to asphalt pavement is the flushing and transfer of water in the asphalt mixture [6]. On the one hand, water flushing decreases the bonding strength of asphalt mortar and aggregate, making the aggregate prone to spalling [7]. On the other hand, repeated vehicle loads result in dynamic water flushing inside the meso-gap, causing meso-damage to the asphalt pavement [8,9]. The transmission and seepage behavior of water in the voids of the asphalt mixture contributed to the deterioration of the material microstructure, which significantly decreases the service life of asphalt pavement. As a result, investigating the seepage characteristics of the asphalt mixture void structure is essential for understanding the mechanism of water damage and enhancing pavement durability.
Previously, researchers primarily used the homogeneous material concept to analyze the seepage features of asphalt mixtures [10,11]. However, the mesoscopic void structure of an asphalt mixture is complex, the void scale is extensive, and the spatial distribution is diverse. The research approach ignores the heterogeneous characteristics of asphalt mixture voids, resulting in a considerable difference between the predicted water conduction characteristics and the seepage characteristics of real asphalt pavement. Therefore, it is necessary to investigate the effect of mesoscopic complex void structural features on the internal water conduction behavior of asphalt mixes.
In recent years, the development of non-destructive detection technology for civil engineering materials has served as a technological foundation for the extraction and characterization of asphalt mixture mesostructure characteristics. Researchers used X-ray CT technology to detect the mesostructure of asphalt mixtures, extracted and modeled complex void structure characteristics, tracked mesoscale water conduction characteristics, and preliminarily realized the description of water distribution and seepage characteristics at the mesoscale [12,13,14]. As a consequence, it is an essential way of precisely describing the mesoscopic seepage behavior in complicated void structures by applying mesoscopic detection technology to investigate the mesoscopic structural features and seepage behavior of the asphalt mixes. As a consequence of this, the transmission channel of water in the complicated voids of asphalt mixes with various compaction methods was investigated, and the features of flow rate and flow velocity in different parts of specimens were evaluated, beginning with the mesostructure characteristics of voids. On this basis, the micro-void morphology seepage flow characteristics have been investigated with the goal of acquiring a detailed knowledge of the water flow transmission behavior in asphalt mixes under different compaction processes.
However, due to the complex mesostructure of the asphalt mixture, there is a lack of an appropriate characterization approach for the conduction of water in the specimen’s accurate 3D void structure. The internal distribution of voids for the same type of graded asphalt mixture under different compaction molding methods is completely different, as is the conduction of water in its interior, causing the study of mesoscopic seepage characteristics based on void characteristics. It is challenging to fully describe the seepage features and explain the seepage behavior in real asphalt pavement construction [15,16,17].
In summary, different specimen molding methods in the design of asphalt mixtures would result in entirely different internal void distributions of asphalt mixtures, which would impact water conduction in the void of asphalt mixtures. Water flow transmission behavior in the asphalt mixture is the primary source of moisture damage in asphalt pavements. Because of the constraints of the homogenous material concept in asphalt mixture seepage research, the non-uniform distribution and transmission behavior of water flow in mesostructure cannot be effectively characterized.
The development of X-ray CT technology provides a technological approach for studying the mesoscopic structural properties of voids. As a consequence, this work applied X-ray CT technology to investigate the mesoscopic void morphology of asphalt mixtures. Different molding methods of asphalt mixture specimens (Marshall, SGC, and Field core) were scanned to obtain the real mesoscopic structural distribution within the mixture. Using the discrete lattice Boltzmann model [18], a water conduction simulation of the flow of fluid within the mixture was performed, and the mesoscopic seepage behavior of the inner voids of the specimen under different molding methods was looked into. Explaining the mesoscopic seepage characteristics of asphalt mixtures provides a theoretical foundation for investigating the water damage resistance and medium transmission characteristics of asphalt mixtures.
2. Materials and Methods
2.1. Raw Materials and Gradation
2.1.1. Aggregates
The diabase gravel aggregate was used, and the aggregate technical specifications are shown in Table 1.

Table 1.
Aggregate specification.
2.1.2. Asphalt
SBS modified asphalt was used, Table 2 shows the specifications of the asphalt.

Table 2.
Specifications of the asphalt.
2.1.3. Gradation
The SMA-13 gradation was used, and the gradation is shown in Table 3.

Table 3.
SMA-13 gradation.
2.2. Specimen Preparation
To investigate the impact of different molding methods on moisture conduction in real 3D internal voids of asphalt mixture, the SMA-13 (Stone Mastic Asphalt with NMAS (nominal maximum aggregate size) of 13 mm) was taken directly from the construction location, and the Marshall and SGC tests were performed as soon as it was delivered. The Marshall test specimens were compacted with 75 blows per side in accordance with the parameters; the number of SGC was 100 times; the rotation angle was 1.16°; the pressure was 600 kPa; and the asphalt mixture specimen was created. After the paving and rolling of the road portion had been completed and cooled, the core sample was drilled at the location, and the three specimens are shown in Figure 1.

Figure 1.
Three different kinds of compaction molding specimens.
2.3. Asphalt Mixture Specimen Parameters
The volume parameters and mechanical properties of asphalt mixes formed using three different molding methods were measured. The field core has the largest density and the lowest porosity, as shown in Table 4. The capacity of the asphalt mixture sample to endure the failure load under specified circumstances is referred to as its stability. The Marshall stability test of the asphalt mixture reveals that the field core has the largest stability value, followed by the gyratory compaction specimen, and the Marshall specimen has the lowest.

Table 4.
Specimen parameters.
2.4. CT Scan and 3D Reconstruction
CT imaging technology was developed in 1971 and first used in medicine [19]. Because of its perspective characteristics, it is valued by researchers in various fields [20]. Since the late 1990s, CT technology has been steadily used to study the interior microstructure of asphalt mixes [21,22]. Nowadays, high-precision industrial CT has become one of the most important means to obtain 3D images of things.
In this study, the tomographic pictures of the asphalt mixture were acquired using the AX-5000CT open high-precision industrial CT of Ahoying Precision Instruments (Shanghai) Co., Ltd. The latest 3D visualization analysis software, VGStudio MAX3.0 of Volume Graphics Company in Germany, was selected to reconstruct the cross-sectional images of the asphalt mixture and extract the voids. VGStudio MAX3.0 is widely used in medical and industrial fields because of its high precision, many data processing functions, strong image segmentation function, good image filtering optimization function, and ability to make unique 3D films and observe the internal structure of objects from any perspective.
The asphalt mixture is made up of coarse and fine aggregate mortar as well as voids. Because of the different densities of the three, they have different CT numbers. The X-ray attenuation coefficient is also different, so it has different gray values. In the CT image, the aggregate density is the largest and the gray value is the lowest, which is white or gray-white in the CT image; the maximum gray value of voids is black, and the gray value of asphalt mortar is gray between voids and aggregates. Asphalt mortar, aggregates, and voids can be extracted based on different gray values [23,24]. The acquired tomographic picture was reconstructed in three dimensions using a cone beam filtering back projection technique. Figure 2 shows a 3D reconstruction picture of the asphalt mixture.

Figure 2.
Three-dimensional reconstruction of asphalt mixture.
3. Modeling Methodology
Some studies have computed the permeability of porous media by constructing an analogous random network of cylinders or tubes, modeling microstructures based on mesoscopic geometric models of voids, and numerically solving fluid flow equations [25,26]. To some degree, these numerical models can demonstrate the impact of porous medium microstructure on permeability. However, the asphalt mixture is a very complicated, heterogeneous structural system. There are still significant variations between the idealized structural model used to approximate the internal water conduction mechanisms and the real situation.
Because of its ease of processing complicated boundary conditions and high parallel computing performance, the lattice Boltzmann method (LBM) has seen widespread use in the field of porous media [27]. This approach develops a discrete model at the mesoscopic particle size to determine macroscopic variables such as density and flow rate. The lattice approach takes advantage of a computer’s tremendous processing capacity to better examine seepage issues in complex porous media [28,29].
3.1. Basic Principle of LBM
A cubic lattice with a side length of (lattice step) separates the computational domain in the lattice Boltzmann technique. A particle distribution function has been defined for each lattice point to reflect the quantity of fluid particles moving in the same path as the location (). At each distinct time step (), the particles travel to the closest lattice point with a discrete velocity and clash with other particles at this lattice point. The distribution function of the particles will be adjusted after the collision [18]. The process is known as migration and collision, and it is described mathematically as
In the formula, is the particle distribution function, is the position, s the direction of motion, t is time, is the time step, is the collision operator, which describes how fluid particles collide. Fluid particles progressively gravitate to an equilibrium distribution due to the continual cycle of migration and collision. The BGK collision model is expressed as follows [30]:
In the formula, represents the specific stability distribution function, and is the without dimensions relaxation time. The D3Q19 discrete velocity model is employed in this work [31]. The distribution function and associated parameters are as follows:
h is the lattice side length, represents the lattice’s velocity, represents the lattice sound velocity, represents the weight coefficient, represents the density of liquid, is the macro velocity.
The macroscopic density , velocity and pressure of the model are defined as follows:
In addition, the relationship between the kinematic viscosity coefficient of the fluid and the dimensionless relaxation time and the lattice parameters is
In principle, the LBM D3Q19 model can only be used to simulate the flow of compressible fluids. The number of fluid flow must be smaller than 0.1 to ensure that the numerical solution of LBM converges to the Navier–Stokes equation of incompressible fluid [32]. The is defined as follows:
In the formula, is the maximum velocity of the fluid. In LBM, for the convenience of calculation, all units are generally treated dimensionlessly, that is, lattice units are used. The ratio of lattice unit to physical unit is a fixed reference quantity, the change rule of the lattice unit is completely consistent with that of the physical unit.
In this paper, for convenience, the physical quantities related to the DEM model use physical units, and the physical quantities related to LBM simulation use lattice units, such as watershed size , flow rate , permeability .
3.2. Boundary Conditions
The embedded boundary condition was applied in this simulation. The pressure differential between the intake and exit drove the fluid flow direction along the positive Z axis. The pressure boundary is dealt with utilizing the Zou/He boundary method [33]. The non-slip fluid–solid borders around the model and the solid particle surface were addressed in rebound format [30].
3.3. Simulation of Moisture Conduction in the Mixture
The embedded boundary condition was chosen. The total flow rate applied between the inlet and exit planes was 8.0 × 10−8 m3/s. At 20 °C, the kinematic viscosity was 0.001 Pa/s. The highest number of iterations was 25,000, and the convergence error was 1.0 × 10−6. Finally, three asphalt mixture specimens’ water conduction streamline diagrams were obtained. The 3D distributions of internal voids in all three kinds of asphalt mixes were produced and compared with the water conduction streamline diagram using the 3D void extraction method of the asphalt mixture specimen mentioned in Section 2.3 above.
4. Results and Discussion
4.1. Water Distribution Position Analysis
The colorful lines in Figure 3 show the streamlines of the water flow within the specimen. The depiction of the distribution of the water conduction channel inside the mixture reveals the following differences:

Figure 3.
Three-dimensional flow lines of asphalt mixture specimens: (a) Marshall compaction specimen (b) Superpave Gyratory Compactor specimen (c) Field Core.
- (1)
- Figure 3a shows that the internal water conduction channel of the Marshall compacted specimen is mostly distributed in the middle of the specimen, with no water retention at the higher and lower ends. This is due to the fact that the Marshall compacted specimen’s massive voids are primarily dispersed in the center of the specimen, indicating that the water is primarily trapped inside the Marshall specimen and is difficult to release. For a lengthy period of time, the water retained inside the mixture is submerged in the asphalt mixture, causing the asphalt to peel away from the aggregate surface, decreasing the asphalt mixture’s bonding strength, and damaging the pavement’s longevity.
- (2)
- Figure 3b,c show that for the water conduction simulation of the field core specimen and the SGC specimen, the water is mostly distributed towards the top end of the specimen, with reduced water retention in the center of the specimen. The fundamental explanation for this is because the effective porosity in the middle area of these two specimens is small, while the proportion of effective porosity at the upper end of the specimen is substantial. It demonstrates that the majority of the water just remains in the gap on the surface of the specimen and does not create retention within the specimen. Moisture on the surface of asphalt pavement evaporates quickly into the air, causing little water damage to the asphalt mixture. It demonstrates that the moisture in the specimen’s internal void conduction path from the SGC method is very close to the actual pavement rolling molding method, confirming that the SGC method can not only ensure a reasonable void ratio but also prevent rainwater from entering the asphalt mixture specimen.
4.2. Analysis of Flow Variation in Different Sections
Each specimen’s flow across each portion was calculated. Figure 4 shows the variation in flow with depth.

Figure 4.
Variation in flow pattern with specimen depth: (a) Marshall compaction specimen; (b) Superpave Gyratory Compactor specimen (c) Field core.
The flow in the center of the SGC and Field Core specimens is almost zero, indicating that there is practically no water movement in the specimen. This is due to the high effective porosity at both ends of the SGC specimen and the surface layer coring specimen, while the effective porosity in the middle position is modest; consequently, the flow at both ends of the specimen is much larger than the flow in the middle position of the specimen. Little water flowed through the top layer of the Field Core specimen at its 5–20 mm location, showing that the center section of the two compacted specimens is dense and impenetrable.
4.3. Analysis of Flow Rate Variation in Different Sections
The variations in water conduction velocity in Figure 5 show that:
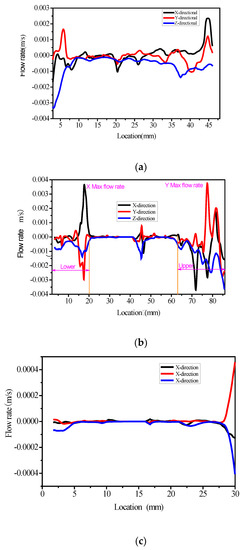
Figure 5.
Flow rate variation law with specimen depth: (a) Marshall compaction specimen (b) Superpave Gyratory Compactor specimen (c) Field core.
The flow rate in the specimen’s vertical direction, as well as Z direction, is not zero, indicating that water flows from top to bottom through the whole Marshall specimen; at a position of 10–30 mm in the middle of the specimen, the water flow velocity of the specimen in both vertical and horizontal directions (X, Y, and Z) is maintained reasonably steadily, with little fluctuation. The water flow velocity in the top section of the specimen then begins to increase, but it remains lower than the water flow velocity at the bottom of the specimen. This is because the specimen has a large effective porosity at the bottom and a relatively small effective porosity in the middle.
The SGC specimen’s flow velocity distribution is mostly at the two ends of the specimen, such as the horizontal direction of the bottom section of the specimen (0–20 mm). The flow velocity varies substantially in all three directions, with the X direction reaching its highest at 17 mm. The flow velocity in the horizontal and vertical directions changes significantly towards the top end of the specimen (63–86 mm), owing to the high effective void ratio and substantial void connectivity. However, the rate of flow in three directions is quite low within the center of the specimen, and the fluctuation is not significant even when the flow velocity is zero, showing that there is no water retention in this location.
The water flow velocity in the field core is primarily concentrated in the top section of the specimen. The water flow velocity in the three directions is almost zero in most of the middle places of the specimen. It shows that asphalt pavement compaction is appropriate throughout the process of construction and makes the asphalt pavement dense and impermeable and prevents rainfall from entering the interior of the pavement resulting in long-term retention and less moisture damage.
5. Conclusions
In this study, X-ray CT technology was used to model water conduction inside mixed specimens for three different compaction modes of the SMA-13. The distribution of water conduction locations within the mixture, as well as the flow and velocity changes of distinct sections were investigated.
- The Marshall compacted specimen has a large and high effective void ratio. Moisture easily enters the specimen via the surface gaps. The SGC specimen’s effective gap is small, and the percentage is low. The internal water conduction channel is mostly concentrated in the top half of the specimen, and water cannot easily enter the specimen through the upper gap. The water conduction channel is mostly focused on the top end of the specimen; the intermediate position is less concentrated, the distribution is sparse, and the water is primarily concentrated in the upper surface layer of the specimen.
- It has been thoroughly shown that the SGC method is quite close to the real road rolling molding process, both in terms of flow and flow velocity. The SGC method not only ensures adequate porosity but also keeps rainfall out of the asphalt mixture specimen. Specifically, since SGC may greatly improve the voids in asphalt mixtures, the void values of each part of the SGC specimen are decreased to varied degrees when compared to the Marshall compaction specimen. The asphalt mixture specimen created by SGC will be staggered throughout the compaction process owing to rotation, resulting in a more equal distribution of aggregates, more reasonable voids, and a more stable structure. As a result, the SGC specimen outperforms the Marshall compaction specimen and pavement in terms of road performance.
- This study provides a new perspective when comparing the internal water conduction behavior of asphalt mixture specimens with different molding methods, analyzing the water retention characteristics in the voids, and clarifying the meso-seepage characteristics of asphalt mixtures under void morphological characteristics. It provides a theoretical basis for the investigation of asphalt mixtures’ water damage resistance and medium transmission properties. More research will be performed in the future to investigate the interior permeability behavior of asphalt mixture specimens.
Author Contributions
C.W., Q.Y. and X.Z. conceived and designed the experiments; Q.Y. performed the experiments; C.W. and Q.Y. analyzed the data; Q.Y. contributed materials/analysis tools; and C.W. wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This publication was funded by the National Natural Science Foundation of China (No. 52068005).
Data Availability Statement
The data presented in this study are available on request from the authors.
Acknowledgments
The authors thank all those who contributed to the experimental part of this study, South China University of Technology, and Di Zhang for their technical support and assistance in the experimental activities.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jiang, Y.J.; Zhang, Y.; Xu, J.S.; Deng, C.Q.; Tian, T. Performance of stone mastic asphalt mixtures fabricated by different compaction methods. Appl. Sci. 2020, 10, 2523. [Google Scholar] [CrossRef]
- Dong, Y.M.; Tan, Y.Q.; Yang, L.Y. Evaluation of performance on crumb-rubber-modified asphalt mixture. J. Test. Eval. 2012, 40, 1089–1093. [Google Scholar] [CrossRef]
- Li, Y.P.; Jiang, W.; Shan, J.H.; Li, P.F.; Lu, R.; Lu, B.W. Characteristics of void distribution and aggregate degradation of asphalt mixture specimens compacted using field and laboratory methods. Constr. Build. Mater. 2021, 270, 121488. [Google Scholar] [CrossRef]
- Geng, J.G.; Chen, M.Y.; Shang, T.; Li, X.; Kim, Y.R.; Kuang, D.L. The Performance of super absorbent polymer (sap) water-retaining asphalt mixture. Materials 2019, 12, 1964. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Harvey, J.T.; Holland, T.J.; Kayhanian, M. The use of reflective and permeable pavements as a potential practice for heat island mitigation and stormwater management. Environ. Res. Lett. 2013, 8, 049501. [Google Scholar] [CrossRef]
- Xu, H.N.; Xing, C.; Zhang, H.Y.; Li, H.Z.; Tan, Y.Q. Moisture seepage in asphalt mixture using X-ray imaging technology. Int. J. Heat Mass Transfer. 2019, 131, 375–384. [Google Scholar] [CrossRef]
- Wu, H.N.; Li, P.; Nian, T.F.; Zhang, G.H.; He, T.; Wei, X.Y. Evaluation of asphalt and asphalt mixtures’ water stability method under multiple freeze-thaw cycles. Constr. Build. Mater. 2019, 228, 117089. [Google Scholar] [CrossRef]
- Wang, W.T.; Wang, L.B.; Xiong, H.C.; Luo, R. A review and perspective for research on moisture damage in asphalt pavement induced by dynamic pore water pressure. Constr. Build. Mater. 2019, 204, 631–642. [Google Scholar] [CrossRef]
- Xu, H.N.; Tan, Y.Q.; Yao, X.G. X-ray computed tomography in hydraulics of asphalt mixtures: Procedure, accuracy, and application. Constr. Build. Mater. 2016, 108, 10–21. [Google Scholar] [CrossRef]
- Zhang, Q.S.; Ji, T.J.; Wang, Z.Q.; Xiao, L. Experimental study and calculation of a three-dimensional finite element model of infiltration in drainage asphalt pavement. Materials 2020, 13, 3909. [Google Scholar] [CrossRef]
- Ji, T.J.; Xiao, L.; Chen, F. Parametric analysis of the drainage performance of porous asphalt pavement based on a 3D FEM method. J. Mater. Civ. Eng. 2020, 32, 04020383. [Google Scholar] [CrossRef]
- Chen, J.; Yin, X.J.; Wang, H.; Ma, X.; Ding, Y.M.; Liao, G.Y. Directional distribution of three-dimensional connected voids in porous asphalt mixture and flow simulation of permeability anisotropy. Int. J. Pavement Eng. 2020, 21, 1550–1562. [Google Scholar] [CrossRef]
- Xu, H.N.; Guo, W.; Tan, Y.Q. Internal structure evolution of asphalt mixtures during freeze–thaw cycles. Mater. Des. 2015, 86, 436–446. [Google Scholar] [CrossRef]
- Xu, H.N.; Guo, W.; Tan, Y.Q. Permeability of asphalt mixtures exposed to freeze–thaw cycles. Cold Reg. Sci. Technol. 2016, 123, 99–106. [Google Scholar] [CrossRef]
- Li, H.Z.; Xu, H.N.; Chen, F.C.; Liu, K.D.; Tan, Y.Q.; Leng, B.B. Evolution of water migration in porous asphalt due to clogging. J. Cleaner Prod. 2022, 330, 129823. [Google Scholar] [CrossRef]
- Yang, B.; Li, H.; Zhang, H.J.; Xie, N.; Zhou, H.N. Laboratorial investigation on effects of microscopic void characteristics on properties of porous asphalt mixture. Constr. Build. Mater. 2019, 213, 434–446. [Google Scholar] [CrossRef]
- Chu, L.J.; Fwa, T.F. A functional approach for determining skid resistance threshold state of porous pavement. Int. J. Pavement Eng. 2019, 20, 481–489. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Hounsfield, G.N. Computerized transverse axial scanning (tomography): Part 1. Description of system. Br. J. Radiol. 1973, 46, 1016–1022. [Google Scholar] [CrossRef]
- Radon, J. On the determination of functions from their integral values along certain manifolds. IEEE Trans. Med. Imaging 1986, 5, 170–176. [Google Scholar] [CrossRef]
- Wu, W.L.; Wang, D.Y.; Zhang, X.N. Estimating the gradation of asphalt mixtures using X-ray computerized tomography and stereology method. Road Mater. Pavement Des. 2011, 12, 699–710. [Google Scholar] [CrossRef]
- Zhang, X.N.; Wan, C.; Wang, D.; He, L.F. Numerical simulation of asphalt mixture based on three-dimensional heterogeneous specimen. J. Cent. South Univ. Technol. 2011, 18, 2201–2206. [Google Scholar] [CrossRef]
- Zhang, L.; Zheng, G.P.; Zhang, K.; Wang, Y.F.; Chen, C.M.; Zhao, L.T.; Xu, J.Q.; Liu, X.Q.; Wang, L.Q.; Tan, Y.Q.; et al. Study on the Extraction of CT Images with Non-Uniform Illumination for the Microstructure of Asphalt Mixture. Materials 2022, 15, 7364. [Google Scholar] [CrossRef] [PubMed]
- Cong, L.; Shi, J.C.; Wang, T.J.; Yang, F.; Zhu, T.T. A method to evaluate the segregation of compacted asphalt pavement by processing the images of paved asphalt mixture. Constr. Build. Mater. 2019, 224, 622–629. [Google Scholar] [CrossRef]
- Adler, P.M.; Jacquin, C.G.; Quiblier, J.A. Flow in simulated porous media. Int. J. Multiph. Flow 1990, 16, 691–712. [Google Scholar] [CrossRef]
- Lock, P.A.; Jing, X.; Zimmerman, R.W.; Schlueter, E.M. Predicting the permeability of sandstone from image analysis of pore structure. J. Appl. Phys. 2002, 92, 6311–6319. [Google Scholar] [CrossRef]
- Succi, S.; Foti, E.; Higuera, F. Three-dimensional flows in complex geometries with the lattice Boltzmann method. Europhys. Lett. 1989, 10, 433–438. [Google Scholar] [CrossRef]
- Pan, C.; Hilpert, M.; Miller, C.T. Pore-scale modeling of saturated permeabilities in random sphere packings. Phys. Rev. E 2001, 64, 066702. [Google Scholar] [CrossRef]
- Qian, N.G.; Wang, D.Y.; Li, D.N.; Shi, L.W. Three-dimensional mesoscopic permeability of porous asphalt mixture. Constr. Build. Mater. 2020, 236, 117430. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A model for collision processes in gases. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Qian, Y.H.; d’Humières, D.; Lallemand, P. Lattice BGK models for Navier-Stokes equation. Europhys. Lett. 1992, 17, 479–484. [Google Scholar] [CrossRef]
- Feng, Y.T.; Han, K.; Owen, D.R.J. Coupled lattice Boltzmann method and discrete element modelling of particle transport in turbulent fluid flows: Computational issues. Int. J. Numer. Meth. Eng. 2007, 72, 1111–1134. [Google Scholar] [CrossRef]
- Zou, Q.S.; He, X.Y. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys. Fluids 1997, 9, 1591–1598. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).