Abstract
In recent decades, precast concrete buildings have undergone significant development, attracting considerable academic attention to their mechanical performances. Unlike cast-in-situ buildings, precast buildings are assembled on site by connecting precast components using mechanical devices or on-site casted joints, which makes the connections particularly important for overall structural performances. This study presents a comprehensive review of the mechanical performances of precast buildings, with a specific focus on various types of connections and their structural properties. This study reviews the mechanical performances of building connections using dry, wet, and/or hybrid methods between pre-manufactured components, e.g., beam–column joints, wall–panel connections, and column/wall–foundation connections. Both experimental and numerical investigations are reviewed. The paper provides a valuable reference regarding the mechanical performances of precast concrete buildings.
1. Introduction
Precast concrete buildings are constructed by assembling pre-manufactured components, such as beams, columns, and shear walls, using connections on site. In recent decades, precast buildings have become increasingly widely used due to their extraordinary advantages, e.g., efficient construction, reduced labor requirements, easier quality control, lower environmental dependency, and reduced pollution [1]. As a result, precast concrete buildings have garnered attention from the academic community.
Precast buildings require careful consideration in structural engineering due to the fact that their mechanical performances are different from those of cast-in-place buildings under extreme loading conditions, e.g., earthquakes and hurricanes. It is difficult to ensure a precast building with the same integrity as the cast-in-situ buildings, because failures may develop along connections to components. While Architectural Design Codes such as ACI 550 and EN 13369 provide guidance for the design and construction of precast structures, they cannot provide an assurance of the safety of precast buildings during earthquakes. The unsatisfactory presence of connections in critical positions can lead to brittle failure or even the progressive collapse of the precast buildings [2]. For example, during the L’Aquila earthquake in 2009, structural failures were observed due to insufficient anchorage against forces at connections, which was caused by the absence of mortar infilling [3], further resulting in shed beam connections failing and elements around steel dowels losing support. The survey conducted on the 2011 earthquake in Turkey [4] found that connections that lack moment-resisting capacity can cause joint damage and result in the collapse of a structure. During the Emilia earthquake in 2012, the sliding frictions at connections caused significant damage, leading to a loss of support for the horizontal structural components [5]. Therefore, it is essential to guarantee connections with adequate load-bearing capacities. Moreover, the rapid pace of technological advancements and the utilization of high-performance materials have rendered the existing engineering codes inadequate for addressing current scenarios, which make it necessary to conduct research on their mechanical performances.
To date, there has been a considerable amount of research on connections for precast building. The connections can be broadly categorized into three types based on their construction methods, i.e., dry connections, wet connections, and hybrid connections. Dry connections utilize mechanical fasteners and connectors to join components together, which enables fast construction. Wet connections, on the other hand, use cast-in-situ materials to connect components, which provides superior integrity for precast buildings and can even match the integrity of cast-in-situ buildings. Hybrid connections possess the advantages of dry and wet connections, enabling faster construction while maintaining superior integrity. Additionally, these connections provide enhanced long-term mechanical performances.
Furthermore, the details of the connections vary based on their particular location. For example, when it comes to beam–column joints, construction is highly complex due to factors such as reinforcement bending, embedding, and overlapping. As a result, stress distribution and cracking are intricate. A well-designed joint is crucial in order to ensure sufficient bending and shear capacities. In contrast, wall–panel connections have relatively simple constructions, and their stress distribution and cracking are also less complex, which makes them easier to analyze. The column/wall–foundation connections exhibit similarities with beam–column joints, but are subject to the highest levels of stress in structures. Reinforcing the connections between columns/walls and foundations is often required in order to maintain the safety of a structure.
This paper summarizes the dry/wet/hybrid connections of the beam–column joints, wall–panel connections, column/wall–foundation connections, and the structural performances of precast buildings. Both experimental and numerical studies pertaining to mechanical properties are summarized, which provides a useful reference for the study of precast buildings.
2. Dry Connections of Beam–Column Joints
The beam–column joint is a critical component of precast buildings that has garnered significant academic attention. This is because the joint plays a pivotal role in ensuring the integrity of a structure during earthquakes. Additionally, its intricate construction makes it the most demanding aspect of the building process.
Over the past decade, researchers have proposed various beam–column joints and have aimed to enhance the mechanical performances of the structures. This section provides a review of dry connections, which typically employ mechanical fasteners and connectors to join different structural components. Dry connections have attractive merits, as they enable the rapid assembly of precast components by eliminating the need for a curing time, thus enabling fast construction. Dry connections facilitate faster modular offsite constructions, thanks to their quick assembly and ability to be dismantled easily. In addition, their mechanical nature enables their easy disassembly and reusability in other structures. However, since dry connections do not establish a monolithic bond between precast elements, the integrity of the structure may be reduced. Researchers have proposed various design proposals to find a connection type with enhanced mechanical performances, aiming to achieve a comparable mechanical performance to cast-in-situ joints. Each of the proposed dry connection types was tested to evaluate their mechanical properties, including their load-bearing capacity, stiffness, durability, seismic resistance, and other relevant factors.
2.1. Dry Connections Using Steel Plates and Bolts
One commonly used dry connection method involves utilizing pre-embedded steel plates and bolts to connect beams and columns. Ye et al. [6] used I-sectional steel plates, high-strength bolts, and cladding steel plates to create beam–column joints, as shown in Figure 1. The test results indicated that the joint could mitigate the stress concentration. The bearing capacity and energy dissipation were found to be dependent on the length of the cladding plates.
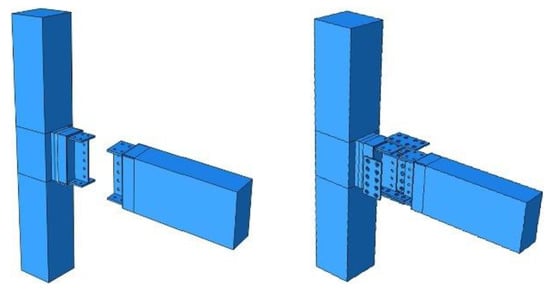
Figure 1.
Joint proposed by Ye et al. (reprinted from [6]).
Nzabonimpa et al. [7] used steel connectors embedded in the beam and column to build the joint. They tested the joint in both RC frames and steel–concrete composite frames, as shown in Figure 2. The beam end plates and the couplers cast in the column were connected by high-strength bolts. The construction speed of this joint remains comparable to that of steel frames.
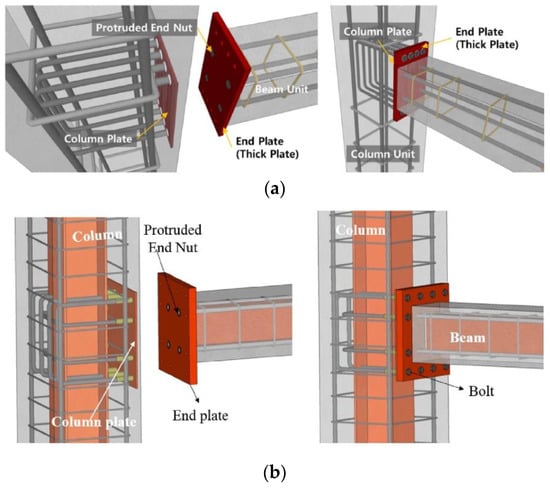
Figure 2.
Joints for different types of buildings proposed by Nzabonimpa et al. (reprinted from [7]). (a) Construction of reinforced concrete buildings, (b) construction of composite steel–concrete buildings.
Furthermore, a numerical study in which the finite element method (FEM) was used was conducted in order to analyze the proposed joint, as shown in Figure 3 [8]. All the components were modeled using solid elements. A hardening material was designated for steel parts, and a damaged plasticity material was designated for concrete parts. Between the two surfaces, the frictionless assumption was employed in the tangential direction, while a rigid contact model with a linear penalty was utilized in the normal direction.
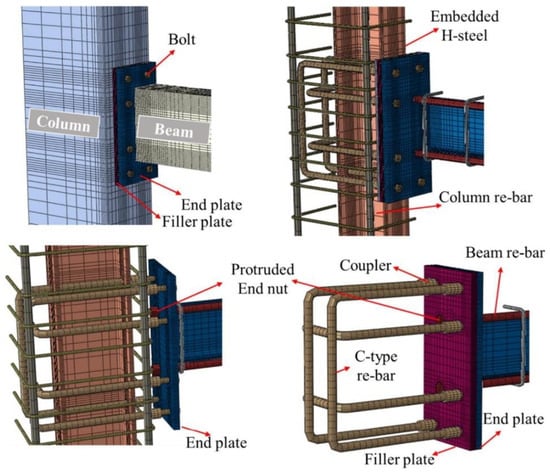
Figure 3.
FEM model for the joints proposed by Nzabonimpa et al. (reprinted from [8]).
In the work by Aninthaneni et al. [9], rebars were used to anchor the beam and the column together. The rebars passed through the slotted holes in the column, with one side secured to an end plate of the beam and the other side secured to the backing plate of the column, as shown in Figure 4. Gussets or stiffeners were welded to the end steel plates to increase their moment capacity and rotational stiffness. Based on the test results, the joint had a stiffness comparable to that of a monolithic concrete joint.
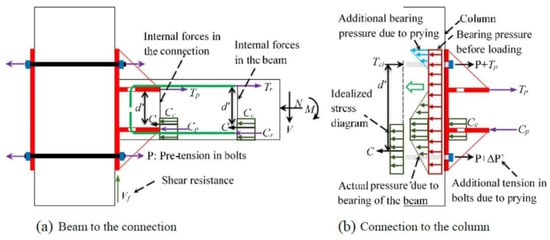
Figure 4.
Joint proposed by Aninthaneni et al. (reprinted from [9]).
2.2. The Use of Other Devices Together with Steel Plates and Bolts
Moreover, some other devices can also be introduced in dry connections. By incorporating dampers between the steel plates, the energy dissipation capacity of the joint can be enhanced. Additionally, by connecting the steel plates for different components using hinge pins, hinge joints can be created. Yang et al. [10] proposed a rotational friction dissipative joint for the purpose of dissipating energy, as shown in Figure 5. A friction pad was fixed between the column connector and beam connector using pre-tensioned bolts and a pin. This joint provided simple details, adjustable performances, and desirable seismic performances. Its nonlinear behavior was determined by the frictional hinge. The material, quantity, and geometric properties of the friction pads or the pretension load of the bolts can adjust the frictional hinge. According to the test, the rotational load–displacement relationship of the joint demonstrates its ability to exhibit ideal elastoplastic behavior.
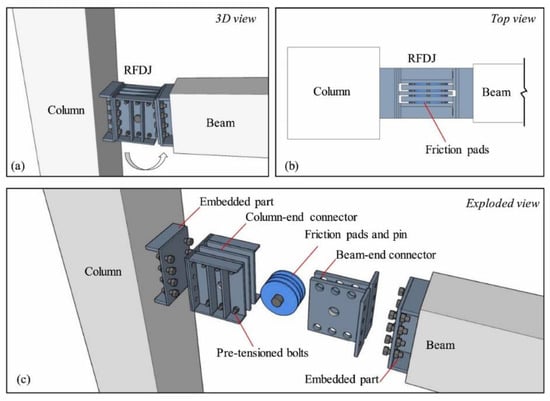
Figure 5.
Joint proposed by Yang et al. (reprinted from [10]). (a) 3D view, (b) Top view, (c) Exploded view.
Li and Qi [11] used steel connectors equipped with dampers, lugs, and high-strength hinge pins in the joints, as illustrated in Figure 6. Perforated steel plates were used as dampers, which were connected to steel plates. The proposed steel joint provided several benefits, including sufficient initial stiffness and an excellent capacity for energy dissipation. Experimental tests confirmed that this joint could ensure the plastic hinge occurring in the beam, and exhibited a better hysteretic performance, higher energy dissipation, and greater ductility than a monolithic joint.
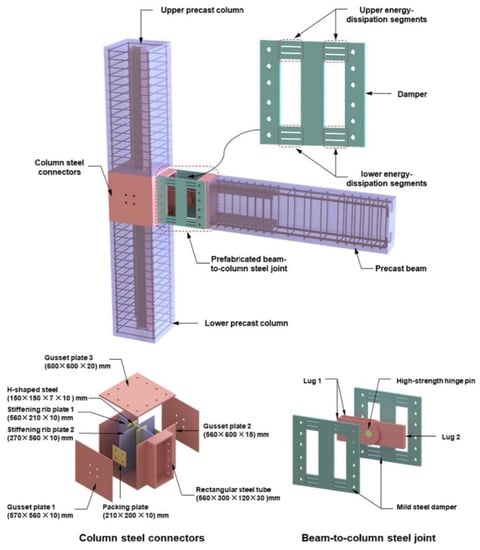
Figure 6.
Joint proposed by Li and Qi (reprinted from [11]).
2.3. Dry Connections Using Corbel and Dowels
An additional option involves the use of corbels to support beams on columns. Zhang et al. [12] utilized a corbel, as illustrated in Figure 7. The beams were connected to the column using connectors, dowel bars, and high-yield reinforcement bars. This joint was easy to assemble and disassemble, allowing for efficient component upgrading and replacement. According to the tests, the failure modes of the joint satisfied the strong-column weak-beam principle.
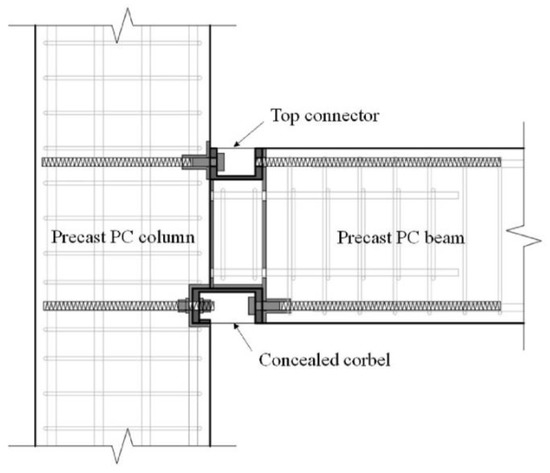
Figure 7.
Joint proposed by Zhang et al. (reprinted from [12]).
Some researchers [13,14,15] have tested corbel-connected beam–column joints, and used lap-splice bars to connect the T-section beam and column, as illustrated in Figure 8. The experimental results showed that the potential plastic hinge was formed at the beam ends near the column faces, preventing the failures of the column and joint. Post-tension rebars could enhance the connection strengths and stiffnesses under the cyclic inelastic loads that simulated ground excitations during earthquakes.
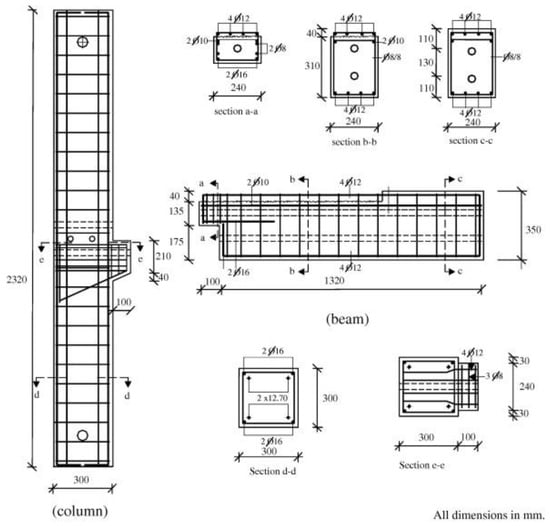
Figure 8.
Joint proposed by Kaya and Arslan (reprinted from [13]).
Additionally, the FEM model was also adopted to analyze the joint using a corbel. Ding et al. [14] used solid elements to model bolts and steel plates while using linear truss elements to model reinforcing bars. They simulated the dynamic responses of the joint in order to analyze its mechanical performances under earthquake conditions. The model is shown in Figure 9, as follows.
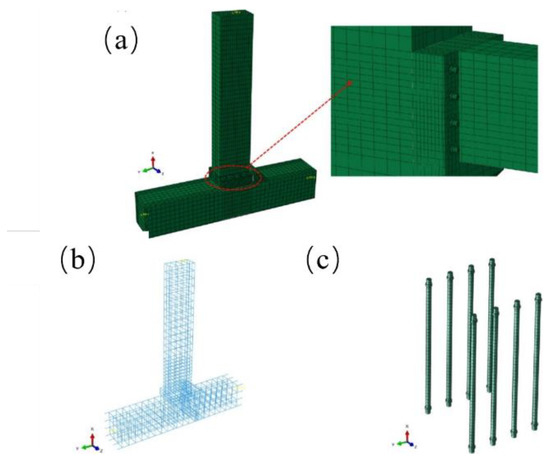
Figure 9.
FEM model of Ding et al.: (a) concrete mesh; (b) rebar mesh; (c) bolt mesh (reprinted from [14]).
Elsanadedy et al. [15] built a model of the specimen tested in their experiment. By taking advantage of its symmetrical properties, the model was built in half, as shown in Figure 10. Solid elements were used for modeling all the components, but rebars were modeled using truss elements. The smeared crack model was designated for concrete. The steel plates and angles at the beam–column connections were constructed using a designated isotropic hardening material. The steel rebars were modeled using a piecewise linear plasticity model.
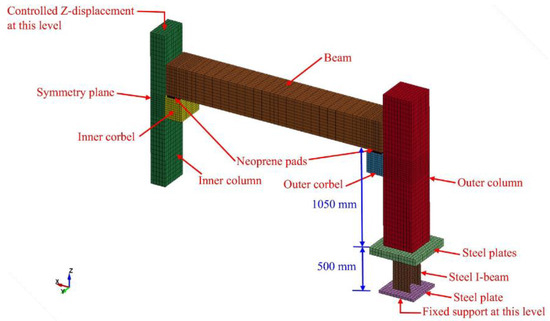
Figure 10.
FEM model by Elsanadedy et al. (reprinted from [15]).
3. Wet Connections of Beam–Column Joints
This section reviews wet connections, which require the use of cast-in-situ materials for connecting structural components. Wet connections cast concrete on site and use grout sleeves to connect components. Sometimes, high-performance materials such as ECC or UHPC are employed as substitutes for concrete in order to enhance the strength and deformation capabilities of the joint. Unlike dry connections, wet connections avoid the stress concentration phenomena caused by the presence of welding, bolts, or holes. In addition, the use of cast-in-situ materials provides the structure with better integrity. For wet connections, researchers are dedicated to optimizing the methods used to design materials and enhancing their properties in order to improve their mechanical and structural performances, including their load-bearing capacity, durability, seismic resistance, and so on. Furthermore, researchers are devoted to developing and refining simulation methods that can be used to predict the performances of wet connections under various loading and environmental conditions.
3.1. Wet Connections
Deng et al. [16] used cast-in-situ concrete to connect precast beams and bottom precast columns, as shown in Figure 11. The longitudinal bars of the beam had a 90-degree hook, which was intended to be cast in the joint. Steel sleeves were utilized to connect the protruding steel from the joint, thereby connecting the upper column and the joint. In different specimens, joints were cast using highly ductile fiber-reinforced concrete and normal concrete in order to study the impact of material strength on the failure modes. The test results showed that the utilization of highly ductile fiber-reinforced concrete in precast concrete beam–column connections improved both their shear capacity and damage-tolerance capacity significantly.
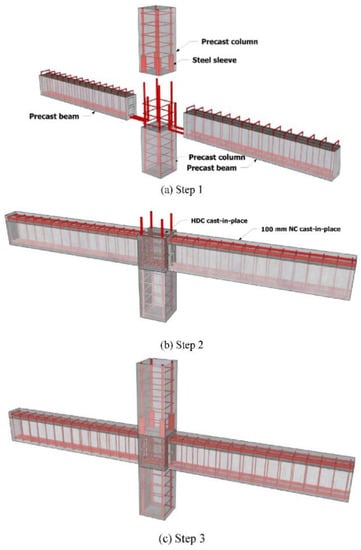
Figure 11.
Joint proposed by Deng et al. (reprinted from [16]).
To improve the shear capacity of the joint at the interface, Xue et al. [17] inserted shear keys at the bottom of the upper precast columns and the top of the bottom core areas, as shown in Figure 12. Moreover, Ultra-High Performance Concrete (UHPC) was used in the study to enhance the integrity of the joint due to its high strength and durability, demonstrating an effective method for improving the mechanical and structural performances of the joint.
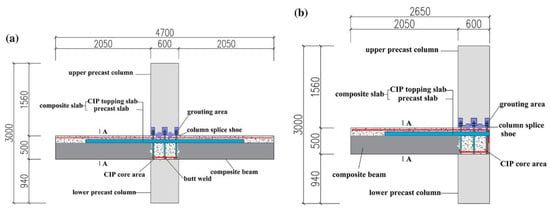
Figure 12.
Joint proposed by Xue et al. (reprinted from [17]). (a) Interior connection; (b) Exterior connection.
Breccolotti et al. [18] used fiber-reinforced concrete to connect beams and columns in the joint. A comparison was made between the structural behaviors of the joint and a cast-in-situ joint, and comparable mechanical performances were found between the two types of joints. Yan et al. [19] studied a joint with beams installed in two directions. Specifically, one beam was installed on the bottom column continuously, where the protruding reinforcement from the bottom column passed through the pre-reserved holes of the beam, as shown in Figure 13. High-performance grout was poured into the holes. In the orthogonal direction, concrete was cast on site to connect the beams and column, where the reinforcement bars were connected by sleeves. The upper precast column was connected to the joint by using grouted sleeves. The test results showed that the joint exhibited good seismic performance on par with that of cast-in-situ connections. Furthermore, the grout sleeve, cast-in-situ region, and rebar holes were found to significantly impact both the plastic hinge and the core regions’ seismic behaviors.
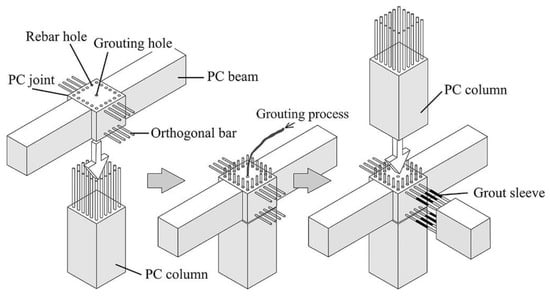
Figure 13.
Joint proposed by Yan et al. (reprinted from [19]).
Lv et al. [20] employed U-shaped beam shells at the end of precast beams to facilitate construction, as shown in Figure 14. Additionally, the mechanical behavior of the joint was investigated and compared to joints without U-shaped beam shells. They conducted quasi-static cyclic experiments to evaluate its load-bearing capacities, such as its strength, stiffness, ductility, capacity for energy dissipation, and cracking propagation. Their study indicated that the mechanical and structural performances of the joints with and without U-shaped beam shells were similar.
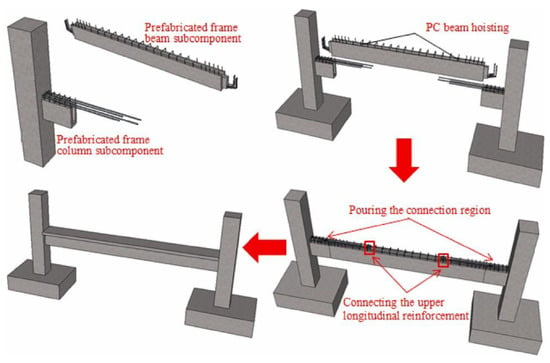
Figure 14.
Joint proposed by Lv et al. (reprinted from [20]).
Gou et al. [21] conducted further research on the use of U-shaped beam shells by utilizing ultra-ductile, low-shrinkage Engineered Cementitious Composite (ECC), as shown in Figure 15. The use of ECC effectively controlled the drying shrinkage while preserving the high ductility and multi-cracking characteristics. Partially substituting concrete with low shrinkage ECC can notably enhance the seismic performance and damage tolerance of beam–column joints, while also simplifying reinforcement details in the joint zone.
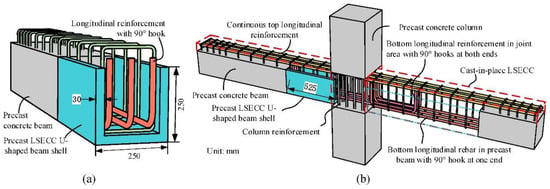
Figure 15.
Joint proposed by Gou et al. (reprinted from [21]). (a) precast LSECC/RC composite beam and (b) beam-column assemblage.
For the wet connections, researchers have also developed some numerical methods to predict their mechanical performance. However, because the integrity of the joint is compatible with the monolithic joint, their numerical simulation method is also similar. Feng et al. [22] utilized FEM to analyze the specimens in their experiment. The beams were manufactured using a U-shaped beam shell, as illustrated in Figure 16. The numerical models were divided into four parts, i.e., precast beams, precast columns, cast-in-situ concrete, and an interface layer. Solid elements were used to model the components, except for reinforcement bars, which were modeled using truss elements.
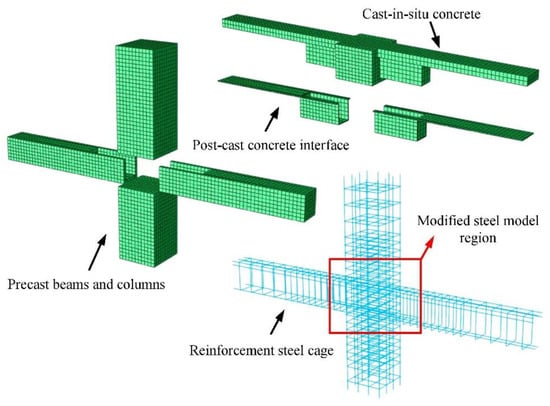
Figure 16.
FEM model by Feng et al. (reprinted from [22]).
By using FEM in a parametric study, Xu et al. [23] studied the mechanical properties of the joint, including the load-carrying capacity, deformation capacity, plastic hinge length, and rotation caused by bond slip. Li et al. [24,25] used constant-stress solid elements to model the concrete and interface layer and used beam elements called Hughes–Liu elements to model the sleeves and rebars. They compared the dynamic responses of monolithic and precast concrete joints under impact loads. In addition, parametric analyses were performed, in which factors such as the impact energy, the inclination angle of the drop weight, and concrete strength were considered.
3.2. Study of Grouted Sleeves
In wet connections, the grouted sleeve is the most commonly used device to splice steel bars. The mechanical performance of grouted sleeves is of significant importance in ensuring the quality of the joint. Many researchers have conducted in-depth research on this device via experiments or numerical simulations. In general, grouted sleeves can be divided into half-grouted sleeves and full-grouted sleeves.
Firstly, the research is summarized on half-grouted sleeves. Half-grouted sleeve connections are designed using a half-threaded end to facilitate the connection of threaded rebars. Meanwhile, the other rebar extends into the sleeve and is fixed by filling the remaining space with grouted material. Yuan et al. [26] conducted a study on the tensile properties of half-grouted sleeve connections, as shown in Figure 17. Additionally, they proposed a simple analytical model to predict the load-carrying capacity of specimens for the structure. The test showed that three distinct failure modes occurred in the experiment, namely rebar fracture, bond failure, and thread failure. The ultimate tensile capacity was determined as the mode with the lowest load-carrying capacity among the three failure modes observed.
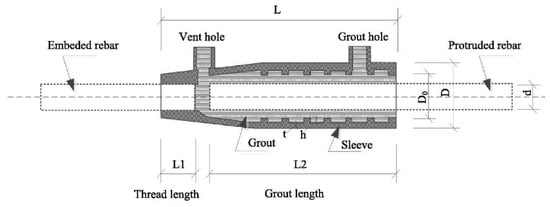
Figure 17.
Half-grouted sleeve (reprinted from [26]).
Ma et al. [27] investigated the mechanical properties of semi-grouting sleeves via pull-out tests. Varying parameters were studied, which included the steel bar diameter, anchorage length, and grouting material strength. The results showed that increasing the steel bar diameter led to an increase in the ultimate bearing capacity. Xu et al. [28] tested 126 half-grouted sleeve connection specimens to examine the influence of various defects on the bond behaviors, e.g., grouting, longitudinal, circumferential, and inclined defects, based on which a bond stress–slip constitutive relationship was proposed. The study indicated that the defect level of insufficient grouting impacts the bond properties and failure modes, while the grouting configuration has little effect. A 30% volume ratio was crucial for determining the bonding properties, with different failure modes occurring below and above this threshold. As the volume ratio increased, the peak bond stress decreased. Zhang et al. [29] studied the mechanical properties of half-grouted sleeves under varying temperatures. The experiment was conducted using a static testing method. The results showed that the bond strength between the grout and rebar decreased with higher temperatures.
On the other hand, the literature on full-grouted sleeves is reviewed. In the case of full-grouted sleeves, the rebars of two components are effectively connected to the sleeve by filling it with grouted material. Guo et al. [30] studied the mechanical performances of fully-grouted sleeve connectors with grouting defects by testing 42 specimens. The configuration of the specimen is shown in Figure 18. The results presented two failure modes, i.e., the fracture of the reinforcing bar and the anchor failure of reinforcing bars.
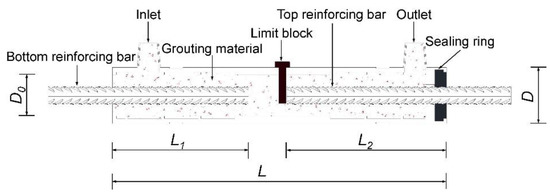
Figure 18.
Full-grouted sleeve by Guo et al. (reprinted form [30]).
Yin et al. [31] tested a series of fully-grouted specimens to investigate the dynamic behaviors of joints under varying rates of dynamic loading. The results showed that an increase in the loading rate increased both the bearing capacity and maximum strain. Lu et al. [32] investigated the mechanical properties of grouted sleeves with wedges and grouted sleeves with wedges and threads under uniaxial tension. The results revealed that the tensile capacity of the splice increased with the increasing diameter of the anchorage segment of the spliced bar, as well as the length and slope of the wedge at both ends of the sleeve. The addition of threads to the sleeve did not significantly improve its tensile capacity. Qiu et al. [33] investigated the use of UHPC grout for the sleeve connection of assembled precast elements. The study involved testing precast specimens with UHPC-grouted sleeve connections under flexural loading. The results indicated that the failure modes of the specimens with the UHPC-grouted sleeve connections were comparable to those observed in cast-in-situ specimens. Additionally, Liu et al. [34] investigated fully-grouted sleeves by using both experimental and numerical methods. In their study, only rebar fracture failure was observed, with significant grout fracture appearing at the end of the grouted sleeve. The grouted sleeve demonstrated perfect elastic behavior and good splice performance under uniaxial tension.
4. Hybrid Connections of Beam–Column Joints
The following section reviews hybrid connections, which are a type of structural connection that combines the features of wet and dry connections. Hybrid connections have superior long-term mechanical performances compared to dry and wet connections, because the presence of the grout or concrete material used in wet connections can help to reduce the stress concentrations that appear in dry connections, while using a limited amount of this material can reduce the effects of shrinkage and creep. In addition, hybrid connections can provide overall structural integrity compared with dry connections. The combination of mechanical fasteners and cast-in-situ materials enables the connections to achieve high-load-carrying capacities, while also allowing structures to absorb and dissipate more seismic energy during earthquakes. On the other hand, hybrid connections have a higher construction speed compared with wet connections. Since the use of mechanical fasteners and connectors helps to provide immediate stability and strength to the connection, construction can proceed before the cast-in-situ concrete has been fully cured. Hybrid connections can also provide improved control over tolerances and alignments compared to wet connections.
A study by Lacerda et al. [35] investigated a hybrid joint in which the precast beams were supported by corbels attached to the column. The vertical gap between the corbel and beam was filled with a layer of grout, aiming to provide cushioning, as depicted in Figure 19. The continuity reinforcement bars of the beam were designed to enhance the integrity of the joint. According to the test results, the joint demonstrated satisfactory load capacities, surpassing the ultimate load predicted by conventional designs for reinforced concrete rectangular sections.
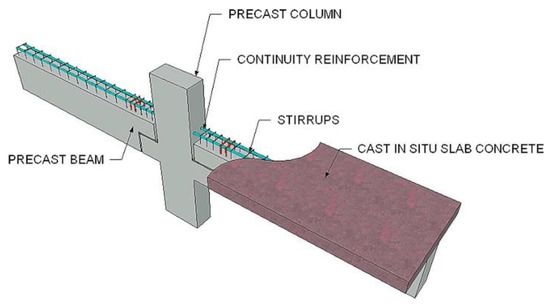
Figure 19.
Joint proposed by Lacerda et al. (reprinted from [35]).
Yuksel et al. [36] conducted a study on a hybrid connection in industrial buildings. In this connection, beams were welded to steel plates that were set on the corbel of the column. The joint and the topping of the beam were filled with concrete on site, as shown in Figure 20.
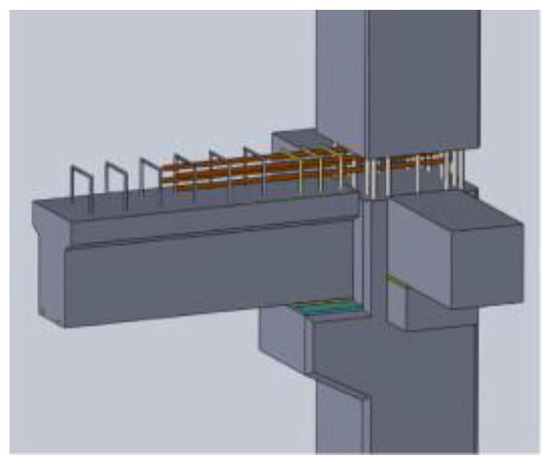
Figure 20.
Joint proposed by Yuksel et al. (reprinted from [36]).
Breccolotti et al. [37] proposed a hybrid joint, in which the beam ends were gradually widened and two rectangular prismatic elements called “shoulders” were created. The shoulders were positioned on the brackets of the column, and then fixed by pouring fiber-reinforced concrete into the space between the shoulders, as shown in Figure 21. The use of loop splices and cast-in-situ concrete with steel fibers improved the ductility of the wet joint, while also ensuring high strength and simplicity in construction. Moreover, FEM was adopted for the numerical study. Solid elements were used to model concrete, and truss elements were used to model reinforcement bars. Since the joint exhibits excellent integrity, no specific constraints were introduced in order to model the contact between the various components.
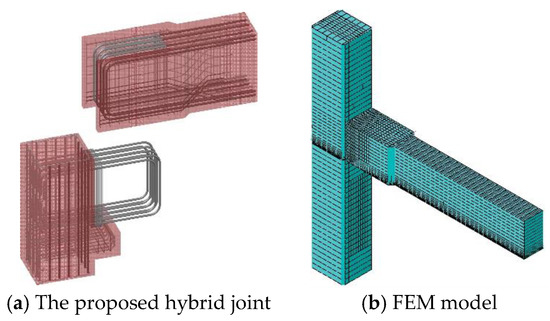
Figure 21.
Joint proposed by Breccolotti et al. (reprinted from [37]).
Fan et al. [38] proposed a similar hybrid joint using a U-shaped beam shell at the end of the beam, supported on the corbels of the precast column, as shown in Figure 22.
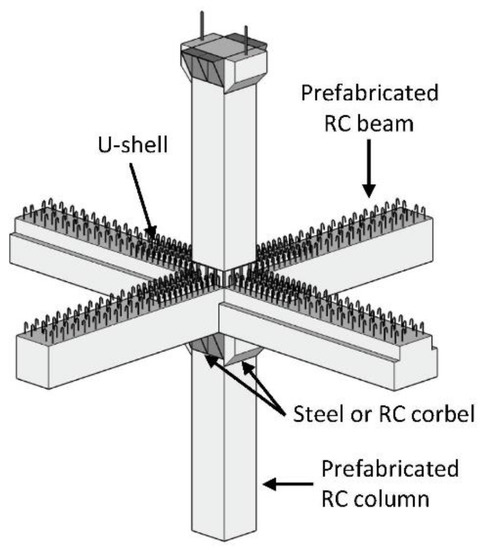
Figure 22.
Joint proposed by Fan et al. (reprinted from [38]).
Certain hybrid connections have utilized more intricate construction techniques. Ghayeb et al. [39] proposed a hybrid joint using steel couplers. According to the protruding steel tubes and plates, the columns and beams were assembled and then cast together. The lower column was connected to the beam using gusset plates and steel bolts, while the upper column was connected using a steel tube and grouted steel couplers. Shear links were also installed in the connection area. The remaining uncast areas of the joint were filled using cast-in-situ concrete. The connection exhibited a good performance with regard to strength, ductility, energy dissipation, and stiffness, as shown in Figure 23.
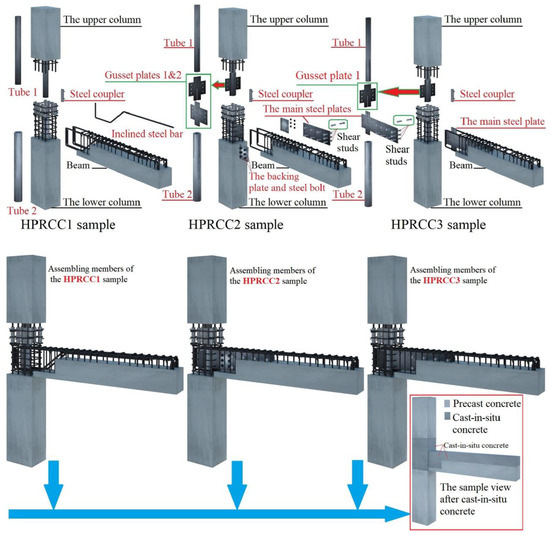
Figure 23.
Joint proposed by Ghayeb et al. (reprinted from [39]).
Esmaeili and Ahooghalandary [40] proposed a hybrid connection comprising a dry type for the lower part and a semi-monolithic type for the upper part, as shown in Figure 24. A steel box with a stiffener was utilized in the precast column to prevent out-of-plane buckling. The beam comprised two segments, i.e., the lower precast segments and the upper in situ segments. The precast portions were anchored to the concrete of the beam end using headed studs. After installation, the upper part of the beam was cast. Its dimensions were suitable for transportation and installation, making it practical for on-site assembly. For this joint, seat plates were easy to assemble, without the need for tight tolerances to achieve precise results in construction.
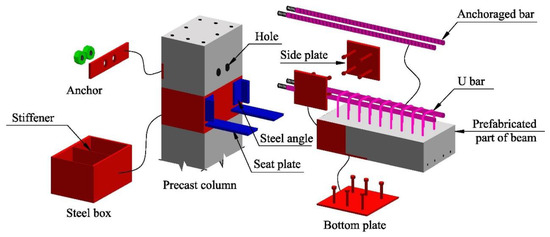
Figure 24.
Joint proposed by Esmaeili and Ahooghalandary (reprinted from [40]).
Zhang et al. [41] used connection steel plates, I-shaped steel connectors, and steel fiber concrete to create the hybrid joint, as shown in Figure 25. The steel skeleton was embedded in the precast column and fastened by high-strength bolts. Then, the concrete was cast into the region. The joint displayed high strength, cumulative energy dissipation, and minimized damage and stiffness deterioration, achieved via the deformation of weakened flange cover plates to enhance energy dissipation and transfer failure to the connection region.
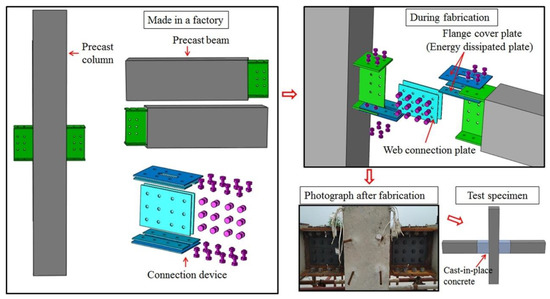
Figure 25.
Joint proposed by Zhang et al. (reprinted from [41]).
Ketiyot and Hansapinyo [42] incorporated a T-section steel insert into a beam embedded in precast beam ends. The protruding part of the T-section steel could be seated on the edge of the column, and the depth of the top beam was reduced to enable lap-splice bars to connect both beams via the beam–column joint. Finally, concrete was poured into the joint to complete the assembly. One advantage of incorporating T-section steel inserts into precast beam–column joints is the enhanced seismic performance it provides.
Furthermore, researchers have investigated the use of dampers in precast buildings and examined the energy dissipation characteristics of buildings equipped with such devices during seismic events. For instance, Morgen and Kurama [43] examined the use of friction dampers in unbonded post-tensioned precast concrete buildings. These dampers enabled large nonlinear lateral displacements while minimizing damage to the structure, but they may also result in unacceptable levels of displacement. However, since damper devices are not the main object of this work, only a brief description is provided.
5. Wall–Panel Connections
This section reviews the literature on wall–panel connections. Shear walls are significant structural elements in high-rise buildings that require reliable connections between wall panels. Sufficient connection strength and stiffness are necessary to ensure the safety of the overall structure. As shear walls have unique characteristics, wall–panel constructions also differ from beam–column joints. Wall–panel connections can also be roughly divided into dry, wet and hybrid connections.
For dry connections, Malla et al. [44] conducted experiments to test the mechanical performances of wall panels connected by bolts for dry connections. Their specimens were assembled using steel components such as blocks, gusset plates, steel bolts, and nuts, as shown in Figure 26. In addition, their study utilized the FEM method to analyze the specimens, predominantly relying on tetrahedral meshing for the model while implementing hexahedral meshing for the areas situated near the joints. In the FEM model, concrete was designated using a cracking model and steel was designated using an isotropic hardening model.
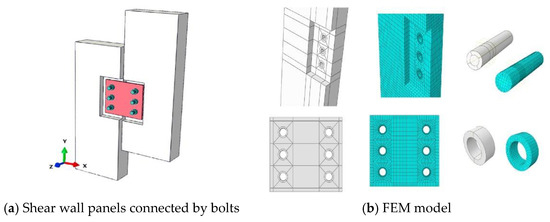
Figure 26.
Connections proposed by Malla et al. (reprinted from [44]).
Sun et al. [45] utilized H-shaped steel connectors and high-strength bolts to connect adjacent wall panels, as shown in Figure 27. The system comprised top and bottom steel units that were cast onto the wall, with the vertical steel bars welded to the inner side of the steel units before casting. Precision bolt holes were positioned on the side plates of these units. Through these bolt holes, pre-tensioned bolts were installed in order to attach the walls to the H-shaped steel connector. This system offered the benefits of maximizing the structural integrity against seismic loads and maintaining a favorable assembly efficiency. Bolted connection installations and mounting tolerances should adhere to technical specifications for high-strength bolt connections in steel structures.
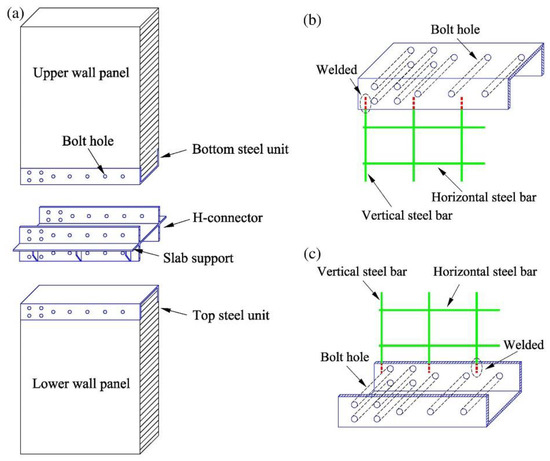
Figure 27.
Connections proposed by Sun et al. (reprinted from [45]). (a) assembling of upper and lower walls, (b) top steel unit, and (c) bottom steel unit.
Naserpour et al. [46] employed steel plates and bolts in order to connect precast wall panels, as shown in Figure 28. Frames were incorporated into the system to improve its mechanical strength and durability. In addition, the FEM method was utilized in order to analyze the system, implementing solid elements with a damaged plastic model for concrete and an isotropic and kinematic hardening elasto-plastic material model for steel members. The demountable shear walls with a rocking column system utilized a jointed rocking base connection in order to protect the columns at their bases. Additionally, a set of slit steel dampers attached via bolting enhanced the lateral resistance and energy dissipation capacity of the column system by absorbing energy through flexural–shear deformation resulting from the column’s rocking movement.
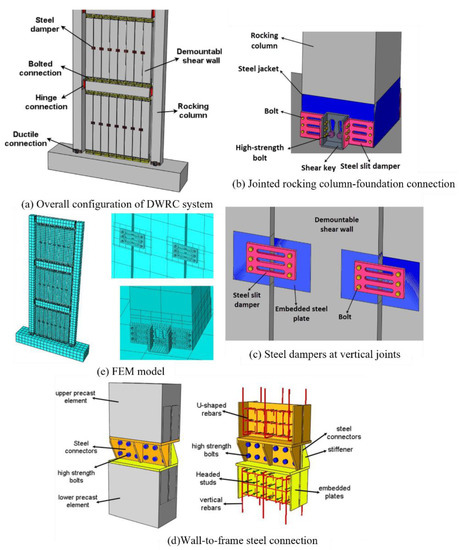
Figure 28.
Connections proposed by Naserpour et al. (reprinted from [46]).
Similarly, Naserpour et al. [47] examined a rocking wall–frame system. The wall panels at both ends were connected to the surrounding frame using unbonded pre-tensioned tendons, while O-shaped steel dampers were applied to the corners of these walls. The frame was adopted to improve the mechanical performances of the system. Steel angles were used to connect the beams and columns, as well as the columns and foundation. Meanwhile, FEM was used to conduct numerical analysis. The models utilized solid elements to model the components. Surface-to-surface contact constraints were assigned between the wall and beam, as well as the wall and foundation. The constraints allowed for gap opening while providing hard contact during compression along the normal direction, with a designated friction mechanism in the tangential direction.
Wet connections are also commonly used for connecting wall panels. For instance, Peng et al. [48] used grouted sleeves to connect wall panels, as shown in Figure 29. The system comprised a cylindrical steel sleeve with an infusion pipe and a checking pipe, embedded in the bottom zone of the shear wall. After erecting and fixing the precast wall in the field, all longitudinal steel bars in the lower shear wall were inserted into their respective steel sleeves in the upper shear wall. Finally, the mortar was poured into the steel sleeve through the infusion pipe until it overflowed from the checking pipe. To achieve rapid construction, longitudinal steel bars in the precast shear walls could be connected using a steel sleeve embedded with mortar.
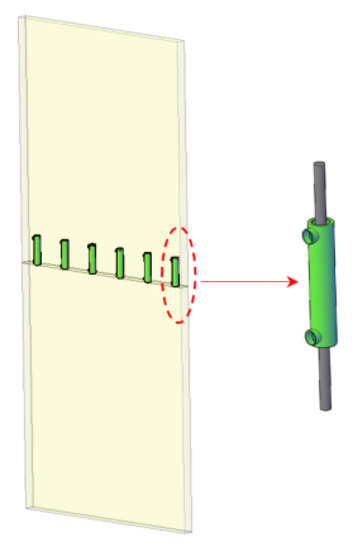
Figure 29.
Connection proposed by Peng et al. (reprinted from [48]).
In addition, Ling et al. [49] took an additional step to enhance the bond performance of the sleeve by welding four steel bars onto the inner surface of the pipe at each end. This provided an interlocking mechanism that enabled the grout to effectively bond with the spliced bars. Meanwhile, Solak [50] employed epoxy to anchor the connections. According to the results, the ductility of the specimens with the connections was significantly lower than the monolithic specimens. Lu et al. [51] proposed a joint-connected beam that utilized cast-in-situ concrete to create connections, enabling continuous reinforcement splicing, as shown in Figure 30. The reinforcing bars in the restrained edge members extended from the walls and were bent to form closed rectangular steel rings. Closed rectangular stirrups were inserted into the spacings of the steel rings where the top and bottom walls overlapped. Longitudinal bars were utilized to create the framework of the boundary beam. After setting up support templates, concrete could be poured into the joint connected beam to connect the top and bottom walls.

Figure 30.
Connection proposed by Ling et al. (reprinted from [50]).
6. Column/Wall–Foundation Connections
Structures are subjected to significant forces at their foundations, making the performances of connections at this location crucial. The connections between columns/walls and foundations are especially important for preventing collapse. Poor connections between columns and foundations can compromise the lateral stability of a structure, increasing its vulnerability to damage from lateral forces such as wind or seismic events. Therefore, the connections to the foundation are usually strengthened to ensure the safety and stability of the structure. This section provides a review of the study on the connections to the foundation.
Nascimbene and Bianco [52] proposed hybrid bolted connections, in which a connector called column shoe was used. The device is shown in Figure 31. According to the column shoes, the load could be transformed between the column and foundation. The use of nuts and washers to fasten anchor bolts provides a means of regulating the vertical position, height level, and connection fixity of the column. The column–foundation connections used in this system exhibited a reliable stiffness and bearing capacity, as well as the strong capacity for energy compared to conventional systems.
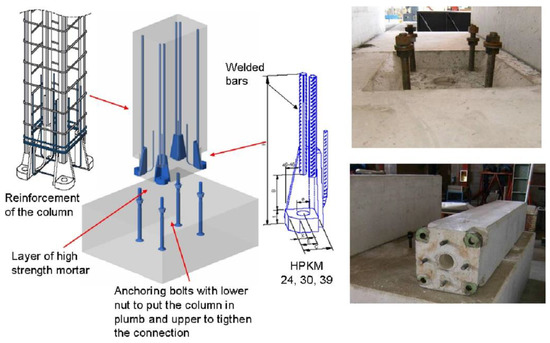
Figure 31.
Connections proposed by Nascimbene and Bianco (reprinted from [52]).
Metelli et al. [53] used the grouted sleeve to connect the column and foundation. The steel bars were extended from the column and anchored in the foundation. Steel plates and studs were designed to locate the column steel bars. During the assembling phase, threaded bars were tightened to the bushes of the column, and leveling steel plates were fixed to the longitudinal bars. The bars were then connected to the studs embedded in the foundation using leveling plates for stability during grout injection and curing. Once installed, steel formwork was added at the column base and high-strength grout was cast to fill the gaps at the column–footing interface. The connection utilizing threaded high-strength steel bars in the grouted sleeves exhibited favorable behaviors, including strength, ductility, cyclic stability, and energy dissipation.
On the other hand, wet connections are more commonly used for column/wall–foundation connections. Liu et al. [54] investigated the use of grouted sleeves for the column–foundation connection. The study involved testing two cast-in-situ specimens and four precast specimens. The results indicated that the sleeve connections provided a satisfactory lateral deformation capacity and ductility for the precast specimens. However, the strengths of the sleeve connections were found to be lower than those of their cast-in-situ counterparts. Xu et al. [55] utilized ECC to improve the strengths of the column–foundation connections. The grouted sleeves were embedded in ECC to connect the protruding steel bars of the foundation. In addition, there was a 20 mm in height grouting layer on the footing of the column, as shown in Figure 32.
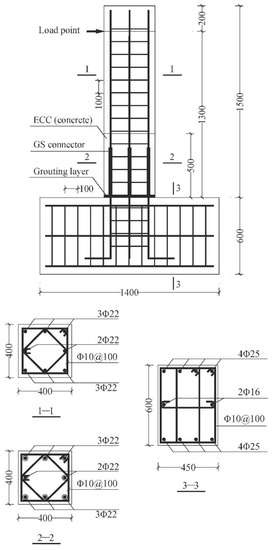
Figure 32.
Connection proposed by Xu et al. (reprinted from [55]).
Aragon et al. [56] used a connection that comprised a single bar embedded in either a tapered or straight steel sleeve, with optional surface corrugations. In addition, they used a finite element model to simulate a wall–foundation connection, as shown in Figure 33. In the model, the energy-dissipating bar in each connection was modeled using a discrete uniaxial truss element, with a multi-linear stress–strain relationship for steel defined for each energy-dissipating bar based on the data from the experimental program. The grout inside the connector sleeve was modeled using three-dimensional four-node stress/displacement solid elements and the fracture–plastic concrete constitutive material mode. The model utilized the bond stress versus slip relationship to investigate the slip of the energy-dissipating bar from the grout.
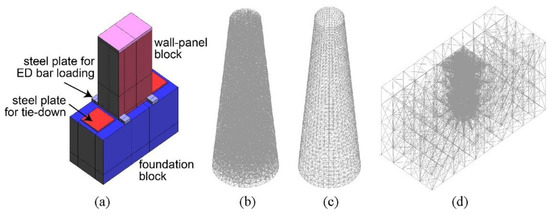
Figure 33.
Connections proposed by Aragon et al.: (a) rendering; (b) grout; (c) grout–sleeve interface; (d) foundation (reprinted from [56]).
Similarly, Ding et al. [57] used three-dimensional finite element models to validate the failure modes and mechanical behaviors of specimens under cyclic loading, as shown in Figure 34. Solid elements were used to model the concrete, while truss elements were used to model the reinforcement bars. The grouted sleeves were simplified as cylindrical steel shells and modeled using four-node quadrilateral surface shell elements with reduced integration. Four-node bond–slip elements were also adopted to consider the influence of bond-slips between rebars and concrete. Additionally, the damage plastic model was used to model concrete. The recovery factor was used to describe the changes in stiffness and strength that occur when the stress state shifts between tension and compression. The grouted sleeve was assigned elastic material, which was embedded in concrete. Surface-to-surface contacts were used to simulate the contact behaviors of the precast column and precast footing.
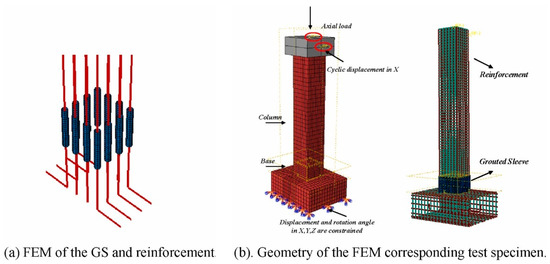
Figure 34.
Connection proposed by Ding et al. (reprinted from [57]).
Torra-Bilal et al. [58] used solid elements with a damage plastic model to simulate concrete. For steel angle–column and steel rods–angles interactions, surface-to-surface interaction was used with hard contact for normal behavior and penalty friction for tangential behavior. Tie constraint was adopted for the interaction between the steel angle and the beam, as well as some connections between the steel angle and the embedded steel plates in the beam. Each reference point was connected to equivalent point nodes using a tie connection. The embedded region command was used to simulate the interactions of all reinforcement bars with the beam and column while adding a bond–slip effect to all defined embedded regions of reinforcement. Sookree et al. [59] devised an embedded horizontal dry connection that utilizes a square-shaped ring connector, high-strength hex nuts, flat washers, and grout for assembling precast concrete shear walls. They also simulated the wall–column joint using FEM, with a contact constraint to connect the wall and foundation. Furthermore, a parametric study was conducted on the thickness and grade of the ring connector, the grade of the vertical steel bars, the number of ring connectors, and the diameter of the vertical steel bars at the connection joints. This simulation method was also used by Du et al. [60]. They introduced a novel self-centering concrete shear wall system that incorporates slip–friction energy-dissipating devices at the wall base, as shown in Figure 35. During earthquakes, the corner joints of the walls are open and close, causing the slip–friction connectors to generate frictional energy dissipation. Moreover, they created a precise numerical model to evaluate the seismic performance of the self-centering concrete wall and also analyzed the impact of different design parameters on the performance of the wall based on the numerical model.
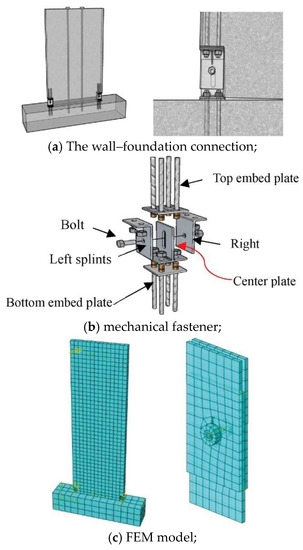
Figure 35.
Connection and its FEM model proposed by Du et al. (reprinted from [60]).
7. Study on Performances of Structural Connections
After presenting various connections between the components, this section provides a comprehensive overview of the research on entire precast buildings, focusing on the dynamic responses of the entire structures during earthquakes. Researchers have conducted numerous experimental tests to explore the propagation of localized damage throughout the entire structure. Additionally, these studies also examined the effects of redistributing resisting forces on the structural dynamic responses. While research on a structural level is less common compared to the component level, some researchers have achieved promising outcomes.
Priestley et al. [61] tested a frame–shear wall building to simulate a five-story precast concrete building at a 60% scale. The shear wall was arranged in one direction. Damage in the wall direction was minimal, with only minor spalling and fine cracking observed, whereas damage in the frame direction was less than expected for an equivalent reinforced concrete structure subjected to the same drift levels. The prestressed frame performed particularly well, with only minor damage to the covering concrete and fiber grout pads. In contrast, the non-prestressed frame showed more damage in gap connections, and beam rotation about the longitudinal axis was noted at high levels of response displacements. The low residual drift was a characteristic of the unbonded prestressing system used to provide strength in the wall direction, which was also apparent in the prestressed frame. Simple analytical models provided accurate predictions of the responses of the building. Dal Lago et al. [62] tested a three-story full-scale precast building, where floor-to-beam connections were connected by a large diameter dowel (see Figure 36). The roof utilized dowels for diaphragm actions, while the lower stories used welded connections to increase the stiffness. The columns had corbels for beam connections. The structure remained elastic under a PGA of 0.15 g, but severe damage and failure occurred at the frame–wall connection when subjected to a PGA of 0.3 g.

Figure 36.
Experiment conducted by Dal Lago et al. (reprinted from [62]). (a) loading apparatus, (b) specimen.
Zhang and Li [63] proposed the rapid installation of dry energy-dissipating connections in their study, as shown in Figure 37. This type of connection used inclined soft steel strips and steel plates pulled by high-strength bolts. To facilitate energy dissipation, aluminum plates were placed between the soft steel strips and the shear wall. The horizontal connections employed steel plates anchored on the concealed columns and tensioned by high-strength bolts. Aluminum plates were used here to achieve friction energy dissipation. Additionally, four inclined braces were installed perpendicularly to the shear wall to ensure out-of-plane stiffness. A bolted connection was utilized between the precast wall and the slab. They tested two 2/3-scale precast shear wall structures, i.e., one with the proposed dry energy-dissipating connection and the other with a cast-in-situ concrete connection, to compare their seismic capacity. The results validated the proposed dry energy-dissipating connection, which had a similar structural performance to the traditional cast-in-situ concrete connection.

Figure 37.
Experiment conducted by Zhang and Li (reprinted from [63]).
He et al. [64] proposed a dry bolt connection using an enclosed angle steel frame to prevent local concrete damage caused by high stresses, as shown in Figure 38. A full-scale two-story precast concrete structure model was tested, consisting of four floor slabs, two roof slabs, and eight wall panels connected via the method they proposed using steel plates and high-strength bolts. The results demonstrated that the precast concrete sandwich wall–panel structure exhibited high lateral stiffness, large safety margins, and high strength reserves.
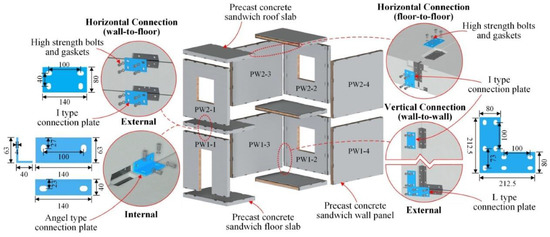
Figure 38.
Experiment conducted by He et al. (reprinted from [64]).
Guo et al. [65] proposed a low-rise precast wall–panel structure using bolts, as shown in Figure 39. The system utilized dry connections between concrete walls to create a box structure that transferred both gravity and lateral loads. A 1/2-scaled three-story model was constructed for the shaking table test. The findings indicated that high-strength bolt connections are crucial for initial stiffness and dynamic responses. The structure exhibited minimal damage, with most components remaining elastic. The sliding of the floor slab was significant, while precast walls showed minimal lateral deformations. Fragility curves were derived for different damage limit states, indicating a low probability of structure collapse. It is recommended bolt connections are improved and the structural system is optimized in order to reduce acceleration responses and potential economic losses.
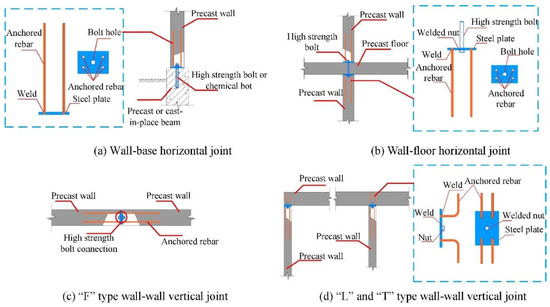
Figure 39.
Connection details of the experiment by Guo et al. (reprinted from [65]).
When it comes to numerical simulations on the structural level, the methods used to simulate column–foundation and wall–panel connections are quite similar. In structural analysis, refined models are often difficult to work with due to their high computational requirements. Structural elements, such as shell and beam–column elements, are commonly used in the modeling. Structures assembled using wet connections, which behave similarly to cast-in-situ structures, do not require the special treatment of connections and can be simulated using conventional techniques for cast-in-situ structures. However, structures assembled using dry connections behave differently. In the following section, some simple structural elements for dry connections are presented. El-Sheikh et al. [66] proposed two models, i.e., a fiber model and a spring model, to simulate the dry connections, as shown in Figure 40. In the fiber model, rigid end zones are employed to model the joint panel zone that is connected to the beam–column elements. A zero-length spring element is introduced to capture the panel zone shear deformations. Furthermore, truss elements and two rigid links are utilized to simulate unbonded post-tensioning steel. The spring model utilizes a zero-length rotational spring element to simulate the nonlinear behaviors of the unbonded post-tensioned precast beam–column connection, replacing the fiber and truss elements used in the fiber model.
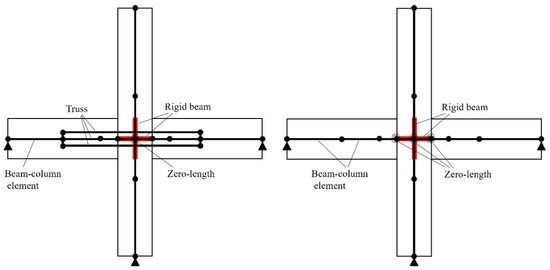
Figure 40.
Numerical simulation method proposed by EI-Sheikh et al.
Kim et al. [67] proposed two types of nodes to simulate the “beam growth” in precast buildings, as shown in Figure 41. In the first model, the joint is modeled using seven nodes, while the connecting section of the beam is modeled using four nodes. Six nodes are rigidly linked to the central node C4 for the joint. The model does not account for joint deformations. To transfer the moment using axial forces, a tri-linear model was used to link the beam and column at the interface. Node B2 and Node C2 are linked with horizontal springs, as well as Node B3 and Node C3. Additionally, very stiff vertical springs at Nodes B1–C1 are utilized to transfer the shear force across the interface in the vertical direction. The second model simplifies the first model by replacing three nodes and elements with a rotational spring at the interface. Similarly, Ozden and Ertas [68] also utilized a tri-linear idealization to model the interface of the beam–column connection.
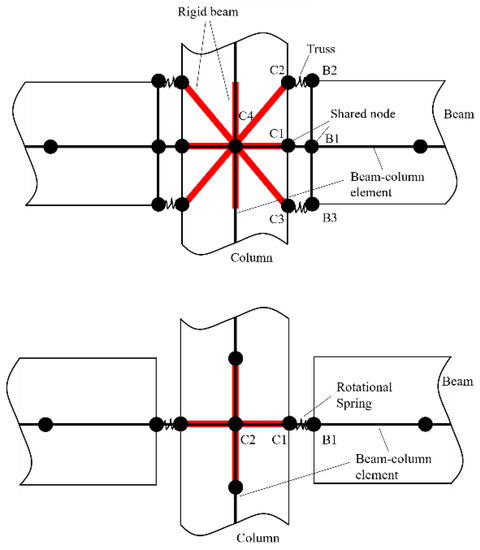
Figure 41.
Joint element proposed by Kim et al.
For the wall–panel connections, Xu et al. [69] utilized structural elements in their simulations, as shown in Figure 42. The shear wall specimens were numerically simulated using a multi-layer shell element model. Truss elements were used at the boundaries to simulate grout-filled sleeve connections.
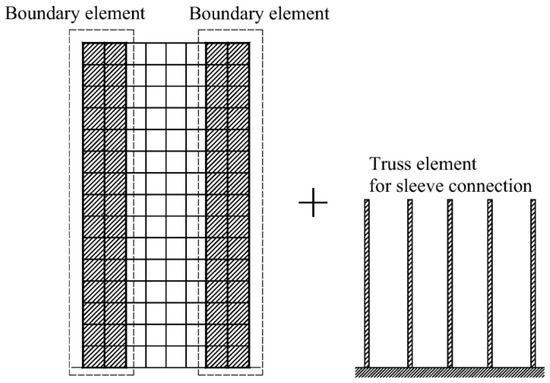
Figure 42.
FEM model proposed by Xu et al. (reprinted from [69]).
Cao et al. [70,71] examined the dynamic and probabilistic seismic performances of precast prestressed-reinforced concrete frames with a particular emphasis on the influence of slabs. They employed the FEM method to analyze the structural behaviors under seismic conditions, evaluated the dynamic responses, and conducted probabilistic analyses. The results indicated that slabs significantly affect seismic performances, with better performances in moderate damage states but worse performances in severe states. In addition, Zhang et al. [72] proposed a multiscale modeling strategy for wet connection joints in the Finite Element Method (FEM). The model incorporated wet-type features such as grouted splice sleeves, bond–slips, and concrete interfaces. The implementation of the approach was realized in OpenSees. Tests were conducted at both the member and structural levels to compare and verify the effectiveness of their method in predicting the seismic behaviors of precast RC beam–column connections. According to the results neglecting the joint panel effect in higher stories, the computational efficiency improved by approximately 50% for ground motions.
8. Conclusions
This study presents a review of the mechanical and structural performances of precast buildings, with a particular focus on connections due to their significant impact on the precast building system. Various types of connections used in precast buildings are introduced, including dry/wet/hybrid connections for beam–column joints, wall–panel connections, and column/wall–foundation connections. Both experimental and numerical methods are discussed regarding the assessment of their structural performances. Dry connections can enable rapid construction but cannot provide integrity as monolithic buildings can, prompting the development of new connecting methods to improve the integrity. Wet connections, on the other hand, offer better structural integrity by using cast-in-situ materials to connect components. Hybrid connections combine the features of dry and wet connections, providing both improved mechanical performances and a faster construction speed. Moreover, the paper also reviews the structural-level performances of precast buildings, which exhibit excellent seismic performances when possessing reliable connections. The paper serves as a valuable resource for quickly referencing precast concrete buildings.
Author Contributions
Conceptualization, Q.G. and R.C.; investigation, Q.G., N.Z. and R.C.; resources, Q.G.; data curation, R.C.; writing—original draft preparation, Q.G. and R.C.; writing—review and editing, Q.G. and N.Z.; visualization, R.C.; supervision, Q.G. and N.Z.; project administration, Q.G.; funding acquisition, Q.G. All authors have read and agreed to the published version of the manuscript.
Funding
The authors gratefully acknowledge the financial support from the National Natural Science Foundation of China (51978591 and 51578473).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Polat, G. Precast concrete systems in developing vs. industrialized countries. J. Civ. Eng. Manag. 2010, 16, 85–94. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, Z.; Cheng, X.; Li, Y.; Diao, M.; Sun, H. Experimental and numerical investigation of the progressive collapse of precast reinforced concrete frame substructures with wet connections. Eng. Struct. 2022, 256, 114010. [Google Scholar] [CrossRef]
- Toniolo, G.; Colombo, A. Precast concrete structures: The lessons learned from the L’Aquila earthquake. Struct. Concr. 2012, 13, 73–83. [Google Scholar] [CrossRef]
- Ozden, S.; Akpinar, E.; Erdogan, H.; Atalay, H.M. Performance of precast concrete structures in October 2011 Van earthquake, Turkey. Mag. Concr. Res. 2014, 66, 543–552. [Google Scholar] [CrossRef]
- Magliulo, G.; Ercolino, M.; Petrone, C.; Coppola, O.; Manfredi, G. The Emilia earthquake: Seismic performance of precast reinforced concrete buildings. Earthq. Spectra 2014, 30, 891–912. [Google Scholar] [CrossRef]
- Ye, M.; Jiang, J.; Chen, H.; Zhou, H.; Song, D. Seismic behavior of an innovative hybrid beam-column connection for precast concrete structures. Eng. Struct. 2021, 227, 111436. [Google Scholar] [CrossRef]
- Nzabonimpa, J.D.; Hong, W.K.; Park, S.C. Experimental investigation of dry mechanical beam–column joints for precast concrete based frames. Struct. Des. Tall Spec. Build. 2017, 26, e1302. [Google Scholar] [CrossRef]
- Nzabonimpa, J.D.; Hong, W.K.; Kim, J. Nonlinear finite element model for the novel mechanical beam-column joints of precast concrete-based frames. Comput. Struct. 2017, 189, 31–48. [Google Scholar] [CrossRef]
- Aninthaneni, P.K.; Dhakal, R.P.; Marshall, J.; Bothara, J. Nonlinear cyclic behaviour of precast concrete frame sub-assemblies with “dry” end plate connection. In Proceedings of Structures; Elsevier: Amsterdam, The Netherlands, 2018; pp. 124–136. [Google Scholar]
- Yang, C.; Li, A.; Xie, L. Development of design method for precast concrete frame with dry-connected rotational friction dissipative beam-to-column joints. J. Build. Eng. 2022, 45, 103563. [Google Scholar] [CrossRef]
- Li, Z.; Qi, Y.; Teng, J. Experimental investigation of prefabricated beam-to-column steel joints for precast concrete structures under cyclic loading. Eng. Struct. 2020, 209, 110217. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, Y.; Li, A.; Yang, T. Experimental study on a new type of precast beam-column joint. J. Build. Eng. 2022, 51, 104252. [Google Scholar] [CrossRef]
- Kaya, M.; Arslan, A.S. Analytical modeling of post-tensioned precast beam-to-column connections. Mater. Des. 2009, 30, 3802–3811. [Google Scholar] [CrossRef]
- Ding, K.; Ye, Y.; Ma, W. Seismic performance of precast concrete beam-column joint based on the bolt connection. Eng. Struct. 2021, 232, 111884. [Google Scholar] [CrossRef]
- Elsanadedy, H.M.; Almusallam, T.H.; Al-Salloum, Y.A.; Abbas, H. Investigation of precast RC beam-column assemblies under column-loss scenario. Constr. Build. Mater. 2017, 142, 552–571. [Google Scholar] [CrossRef]
- Deng, M.; Ma, F.; Song, S.; Lü, H.; Sun, H. Seismic performance of interior precast concrete beam-column connections with highly ductile fiber-reinforced concrete in the critical cast-in-place regions. Eng. Struct. 2020, 210, 110360. [Google Scholar] [CrossRef]
- Xue, W.; Bai, H.; Dai, L.; Hu, X.; Dubec, M. Seismic behavior of precast concrete beam-column connections with bolt connectors in columns. Struct. Concr. 2021, 22, 1297–1314. [Google Scholar] [CrossRef]
- Li, D.; Wu, C.; Zhou, Y.; Luo, W.; Lie, W. A precast beam-column connection using metallic damper as connector: Experiment and application. J. Constr. Steel Res. 2021, 181, 106628. [Google Scholar] [CrossRef]
- Yan, Q.; Chen, T.; Xie, Z. Seismic experimental study on a precast concrete beam-column connection with grout sleeves. Eng. Struct. 2018, 155, 330–344. [Google Scholar] [CrossRef]
- Lv, X.; Yu, Z.; Shan, Z. Seismic behaviour of frame structures with assembly of prefabricated concrete beam. J. Build. Eng. 2021, 40, 102765. [Google Scholar] [CrossRef]
- Gou, S.; Ding, R.; Fan, J.; Nie, X.; Zhang, J. Experimental study on seismic performance of precast LSECC/RC composite joints with U-shaped LSECC beam shells. Eng. Struct. 2019, 189, 618–634. [Google Scholar] [CrossRef]
- Feng, D.; Wu, G.; Lu, Y. Finite element modelling approach for precast reinforced concrete beam-to-column connections under cyclic loading. Eng. Struct. 2018, 174, 49–66. [Google Scholar] [CrossRef]
- Xu, L.; Pan, J.; Guo, L. Mechanical performance of precast RC columns with grouted sleeve connections. Eng. Struct. 2022, 252, 113654. [Google Scholar] [CrossRef]
- Li, H.; Chen, W.; Hao, H. Dynamic response of precast concrete beam with wet connection subjected to impact loads. Eng. Struct. 2019, 191, 247–263. [Google Scholar] [CrossRef]
- Li, H.; Chen, W.; Huang, Z.; Hao, H.; Ngo, T.T.; Pham, T.M.; Yeoh, K.J. Dynamic response of monolithic and precast concrete joint with wet connections under impact loads. Eng. Struct. 2022, 250, 113434. [Google Scholar] [CrossRef]
- Yuan, H.; Zhenggeng, Z.; Naito, C.J.; Weijian, Y. Tensile behavior of half grouted sleeve connections: Experimental study and analytical modeling. Constr. Build. Mater. 2017, 152, 96–104. [Google Scholar] [CrossRef]
- Ma, J.; Bai, G.; Liang, L.; Wang, L.; Su, N. Mechanical behavior of semi-grouting sleeve and steel bar connection. Struct. Concr. 2023. [Google Scholar] [CrossRef]
- Xu, F.; Wang, K.; Wang, S.; Li, W.; Liu, W.; Du, D. Experimental bond behavior of deformed rebars in half-grouted sleeve connections with insufficient grouting defect. Constr. Build. Mater. 2018, 185, 264–274. [Google Scholar] [CrossRef]
- Zhang, W.; Deng, X.; Zhang, J.; Yi, W. Tensile behavior of half grouted sleeve connection at elevated temperatures. Constr. Build. Mater. 2018, 176, 259–270. [Google Scholar] [CrossRef]
- Guo, T.; Yang, J.; Wang, W.; Li, C. Experimental investigation on connection performance of fully-grouted sleeve connectors with various grouting defects. Constr. Build. Mater. 2022, 327, 126981. [Google Scholar] [CrossRef]
- Yin, F.; Yin, S.; Cheng, Z.; Chen, N.; Wang, Y. Experimental research on dynamic mechanical properties of fully-grouted sleeve connections. Constr. Build. Mater. 2021, 288, 123125. [Google Scholar] [CrossRef]
- Lu, Z.; Huang, J.; Li, Y.; Dai, S.; Peng, Z.; Liu, X.; Zhang, M. Mechanical behaviour of grouted sleeve splice under uniaxial tensile loading. Eng. Struct. 2019, 186, 421–435. [Google Scholar] [CrossRef]
- Qiu, M.; Shao, X.; Zhu, Y.; Hussein, H.H.; Liu, Y. Tensile and flexural tests on ultrahigh performance concrete grouted sleeve connection. Struct. Concr. 2023, 24, 703–720. [Google Scholar] [CrossRef]
- Liu, C.; Pan, L.; Liu, H.; Tong, H.; Yang, Y.; Chen, W. Experimental and numerical investigation on mechanical properties of grouted-sleeve splices. Constr. Build. Mater. 2020, 260, 120441. [Google Scholar] [CrossRef]
- Lacerda, M.S.; da Silva, T.J.; Alva, G.S.; de Lima, M.V. Influence of the vertical grouting in the interface between corbel and beam in beam-to-column connections of precast concrete structures—An experimental analysis. Eng. Struct. 2018, 172, 201–213. [Google Scholar] [CrossRef]
- Yuksel, E.; Karadogan, H.F.; Bal, I.E.; Ilki, A.; Bal, A.; Inci, P. Seismic behavior of two exterior beam–column connections made of normal-strength concrete developed for precast construction. Eng. Struct. 2015, 99, 157–172. [Google Scholar] [CrossRef]
- Breccolotti, M.; Gentile, S.; Tommasini, M.; Materazzi, A.L.; Bonfigli, M.F.; Pasqualini, B.; Colone, V.; Gianesini, M. Beam-column joints in continuous RC frames: Comparison between cast-in-situ and precast solutions. Eng. Struct. 2016, 127, 129–144. [Google Scholar] [CrossRef]
- Fan, J.; Wu, G.; Feng, D.; Zeng, Y.; Lu, Y. Seismic performance of a novel self-sustaining beam-column connection for precast concrete moment-resisting frames. Eng. Struct. 2020, 222, 111096. [Google Scholar] [CrossRef]
- Ghayeb, H.H.; Razak, H.A.; Sulong, N.R. Seismic performance of innovative hybrid precast reinforced concrete beam-to-column connections. Eng. Struct. 2020, 202, 109886. [Google Scholar] [CrossRef]
- Esmaeili, J.; Ahooghalandary, N. Introducing an easy-install precast concrete beam-to-column connection strengthened by steel box and peripheral plates. Eng. Struct. 2020, 205, 110006. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, C.; Rong, X.; Yang, H.; Li, Y. Development and experimental investigation of hybrid precast concrete beam–column joints. Eng. Struct. 2020, 219, 110922. [Google Scholar] [CrossRef]
- Ketiyot, R.; Hansapinyo, C. Seismic performance of interior precast concrete beam-column connections with T-section steel inserts under cyclic loading. Earthq. Eng. Eng. Vib. 2018, 17, 355–369. [Google Scholar] [CrossRef]
- Morgen, B.; Kurama, Y. A friction damper for post-tensioned precast concrete beam-to-column joints. PCI J. 2004, 49, 112–133. [Google Scholar] [CrossRef]
- Malla, P.; Xiong, F.; Cai, G.; Xu, Y.; Larbi, A.S.; Chen, W. Numerical study on the behaviour of vertical bolted joints for precast concrete wall-based low-rise buildings. J. Build. Eng. 2021, 33, 101529. [Google Scholar] [CrossRef]
- Sun, J.; Qiu, H.; Jiang, H. Experimental study and associated mechanism analysis of horizontal bolted connections involved in a precast concrete shear wall system. Struct. Concr. 2019, 20, 282–295. [Google Scholar] [CrossRef]
- Naserpour, A.; Fathi, M.; Dhakal, R.P. Demountable shear wall with rocking boundary columns for precast concrete buildings in high seismic regions. In Proceedings of Structures; Elsevier: Amsterdam, The Netherlands, 2022; pp. 1454–1474. [Google Scholar]
- Naserpour, A.; Fathi, M. Numerical study of a multiple post-tensioned rocking wall-frame system for seismic resilient precast concrete buildings. Earthq. Eng. Eng. Vib. 2022, 21, 377–393. [Google Scholar] [CrossRef]
- Peng, Y.; Qian, J.; Wang, Y. Cyclic performance of precast concrete shear walls with a mortar–sleeve connection for longitudinal steel bars. Mater. Struct. 2016, 49, 2455–2469. [Google Scholar] [CrossRef]
- Ling, J.; Abd. Rahman, A.B.; Ibrahim, I.S.; Abdul Hamid, Z. An experimental study of welded bar sleeve wall panel connection under tensile, shear, and flexural loads. Int. J. Concr. Struct. Mater. 2017, 11, 525–540. [Google Scholar] [CrossRef]
- Solak, A.; Tama, Y.S.; Yılmaz, S.; Kaplan, H. Experimental study on behavior of anchored external shear wall panel connections. Bull. Earthq. Eng. 2015, 13, 3065–3081. [Google Scholar] [CrossRef]
- Lu, X.; Wang, L.; Wang, D.; Jiang, H. An innovative joint connecting beam for precast concrete shear wall structures. Struct. Concr. 2016, 17, 972–986. [Google Scholar] [CrossRef]
- Nascimbene, R.; Bianco, L. Cyclic response of column to foundation connections of reinforced concrete precast structures: Numerical and experimental comparisons. Eng. Struct. 2021, 247, 113214. [Google Scholar] [CrossRef]
- Metelli, G.; Beschi, C.; Riva, P. Cyclic behaviour of a column to foundation joint for concrete precast structures. Eur. J. Environ. Civ. Eng. 2011, 15, 1297–1318. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, B.; Cai, J.; Lee, D.; Deng, X.; Feng, J. Experimental study on seismic behavior of precast concrete column with grouted sleeve connections considering ratios of longitudinal reinforcement and stirrups. Bull. Earthq. Eng. 2018, 16, 6077–6104. [Google Scholar] [CrossRef]
- Xu, L.; Pan, J.; Cai, J. Seismic performance of precast RC and RC/ECC composite columns with grouted sleeve connections. Eng. Struct. 2019, 188, 104–110. [Google Scholar] [CrossRef]
- Aragon, T.C.; Kurama, Y.C.; Meinheit, D.F. Numerical modeling and behavior of ductile short-grouted reinforcing bar-to-foundation connections for precast concrete structures. Eng. Struct. 2021, 233, 111900. [Google Scholar] [CrossRef]
- Ding, M.; Xu, W.; Wang, J.; Chen, Y.; Du, X.; Fang, R. Seismic performance of prefabricated concrete columns with grouted sleeve connections, and a deformation-capacity estimation method. J. Build. Eng. 2022, 55, 104722. [Google Scholar] [CrossRef]
- Torra-Bilal, I.; Mahamid, M.; Baran, E. Cyclic behaviour of precast beam-to-column connections: An experimental and numerical investigation. In Proceedings of Structures; Elsevier: Amsterdam, The Netherlands, 2022; pp. 939–957. [Google Scholar]
- Sookree, E.; Huang, Z.; Wang, Z. A Numerical Study on the Seismic Performance of a Horizontal Dry Connection for Precast Concrete Shear Walls. KSCE J. Civ. Eng. 2023, 27, 1617–1639. [Google Scholar] [CrossRef]
- Du, X.; Wang, Z.; Liu, H.; Liu, M. Research on seismic behavior of precast self-centering concrete walls with dry slip-friction connectors. J. Build. Eng. 2021, 42, 102668. [Google Scholar] [CrossRef]
- Priestley, M.; Sritharan, S.; Conley, J.; Pampanin, S. Preliminary results and conclusions from the PRESSS five-story precast concrete test building. PCI J. 1999, 44, 42–67. [Google Scholar] [CrossRef]
- Dal Lago, B.; Muhaxheri, M.; Ferrara, L. Numerical and experimental analysis of an innovative lightweight precast concrete wall. Eng. Struct. 2017, 137, 204–222. [Google Scholar] [CrossRef]
- Zhang, R.; Li, A. Experimental study on the performance of damaged precast shear wall structures after base isolation. Eng. Struct. 2021, 228, 111553. [Google Scholar] [CrossRef]
- He, J.; Xu, Z.; Zhang, L.; Lin, Z.; Hu, Z.; Li, Q.; Dong, Y. Shaking table tests and seismic assessment of a full-scale precast concrete sandwich wall panel structure with bolt connections. Eng. Struct. 2023, 278, 115543. [Google Scholar] [CrossRef]
- Guo, W.; Zhai, Z.; Cui, Y.; Yu, Z.; Wu, X. Seismic performance assessment of low-rise precast wall panel structure with bolt connections. Eng. Struct. 2019, 181, 562–578. [Google Scholar] [CrossRef]
- El-Sheikh, M.; Sause, R.; Pessiki, S.; Lu, L. Seismic behavior and design of unbonded post-tensioned precast concrete frames. PCI J. 1999, 44, 54–71. [Google Scholar] [CrossRef]
- Kim, J.; Stanton, J.; MacRae, G. Effect of beam growth on reinforced concrete frames. J. Struct. Eng. 2004, 130, 1333–1342. [Google Scholar] [CrossRef]
- Ozden, S.; Ertas, O. Modeling of pre-cast concrete hybrid connections by considering the residual deformations. Int. J. Phys. Sci. 2010, 5, 781–792. [Google Scholar]
- Xu, G.; Wang, Z.; Wu, B.; Bursi, O.S.; Tan, X.; Yang, Q.; Wen, L. Seismic performance of precast shear wall with sleeves connection based on experimental and numerical studies. Eng. Struct. 2017, 150, 346–358. [Google Scholar] [CrossRef]
- Cao, X.; Feng, D.; Beer, M. Consistent seismic hazard and fragility analysis considering combined capacity-demand uncertainties via probability density evolution method. Struct. Saf. 2023, 103, 102330. [Google Scholar] [CrossRef]
- Cao, X.; Xiong, C.; Feng, D.; Wu, G. Dynamic and Probabilistic Seismic Performance Assessment of Precast Prestressed Rcfs Incorporating Slab Influence Through Three-Dimensional Spatial Model. Bull. Earthq. Eng. 2021, 20, 6705–6739. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, Z.; Sun, B. A practical multiscale modeling strategy to model wet-type beam–column connections for seismic analysis of precast RC frame structures. Soil Dyn. Earthq. Eng. 2023, 168, 107824. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).