Comparative Analysis of ANN and LSTM Prediction Accuracy and Cooling Energy Savings through AHU-DAT Control in an Office Building
Abstract
1. Introduction
1.1. Background
1.2. Scope
2. Machine Learning-Based Prediction Model: Concept and Formulation
2.1. Artificial Neural Network
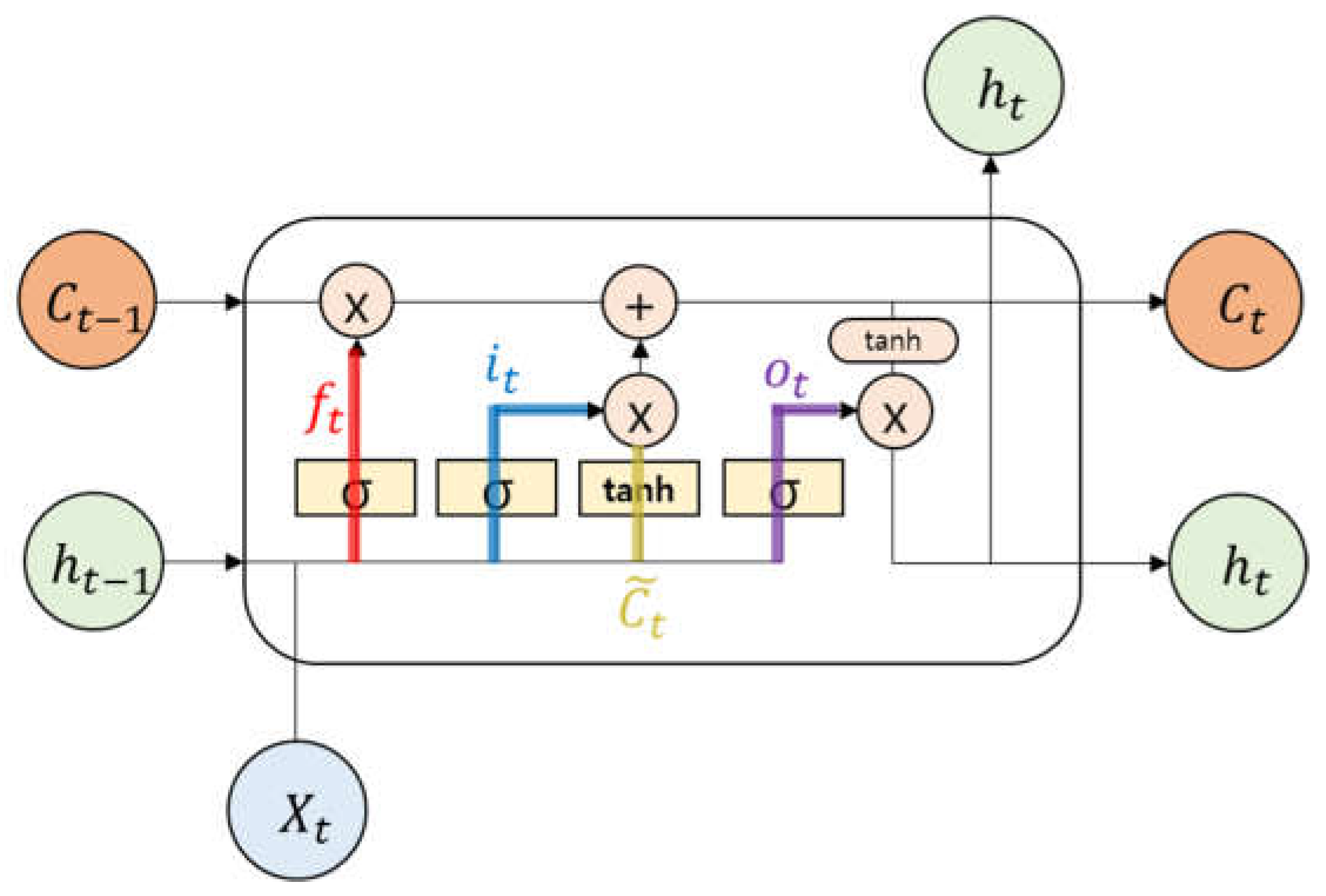
2.2. Long Short-Term Memory
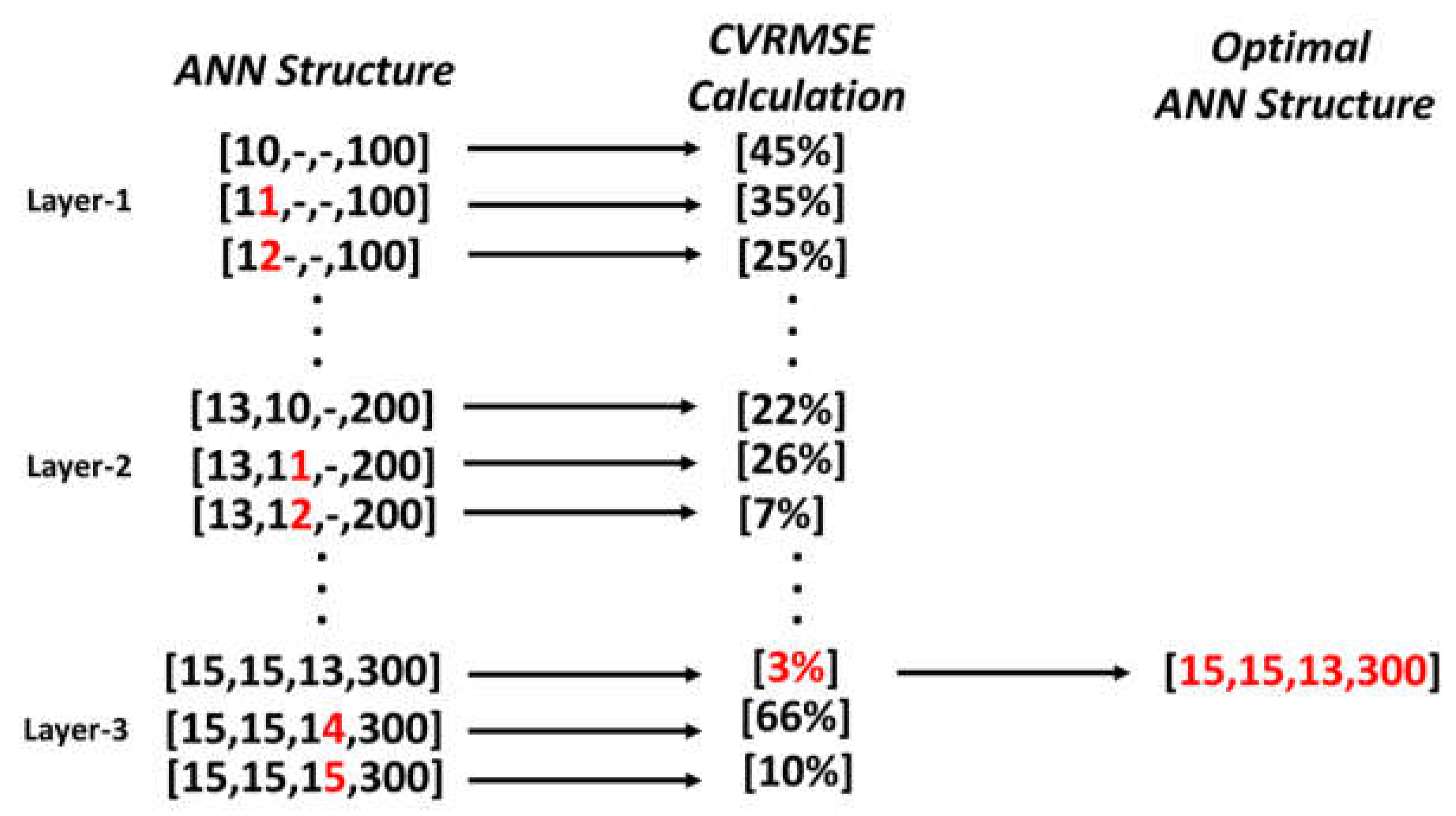
2.3. Development Process of ML Models
2.4. A Comparative Method for Evaluating the Accuracy of Prediction Models
3. Simulation Study
3.1. Simulation Program
3.2. Target Building and Simulation Model
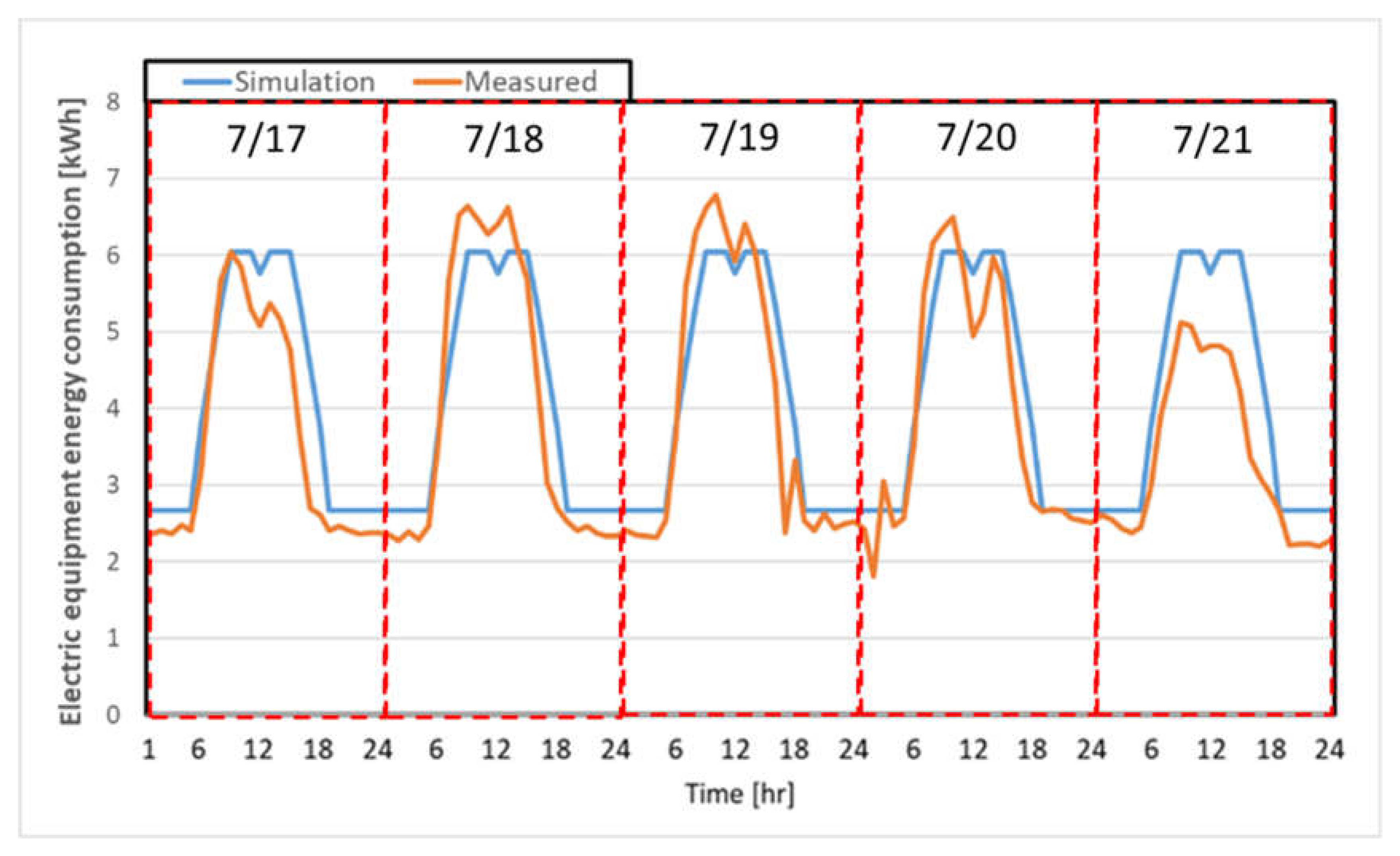
3.3. Calibration Process
4. Case Study
4.1. Simulation Cases
4.2. ML-Based HVAC Control Methods
5. Analysis and Results
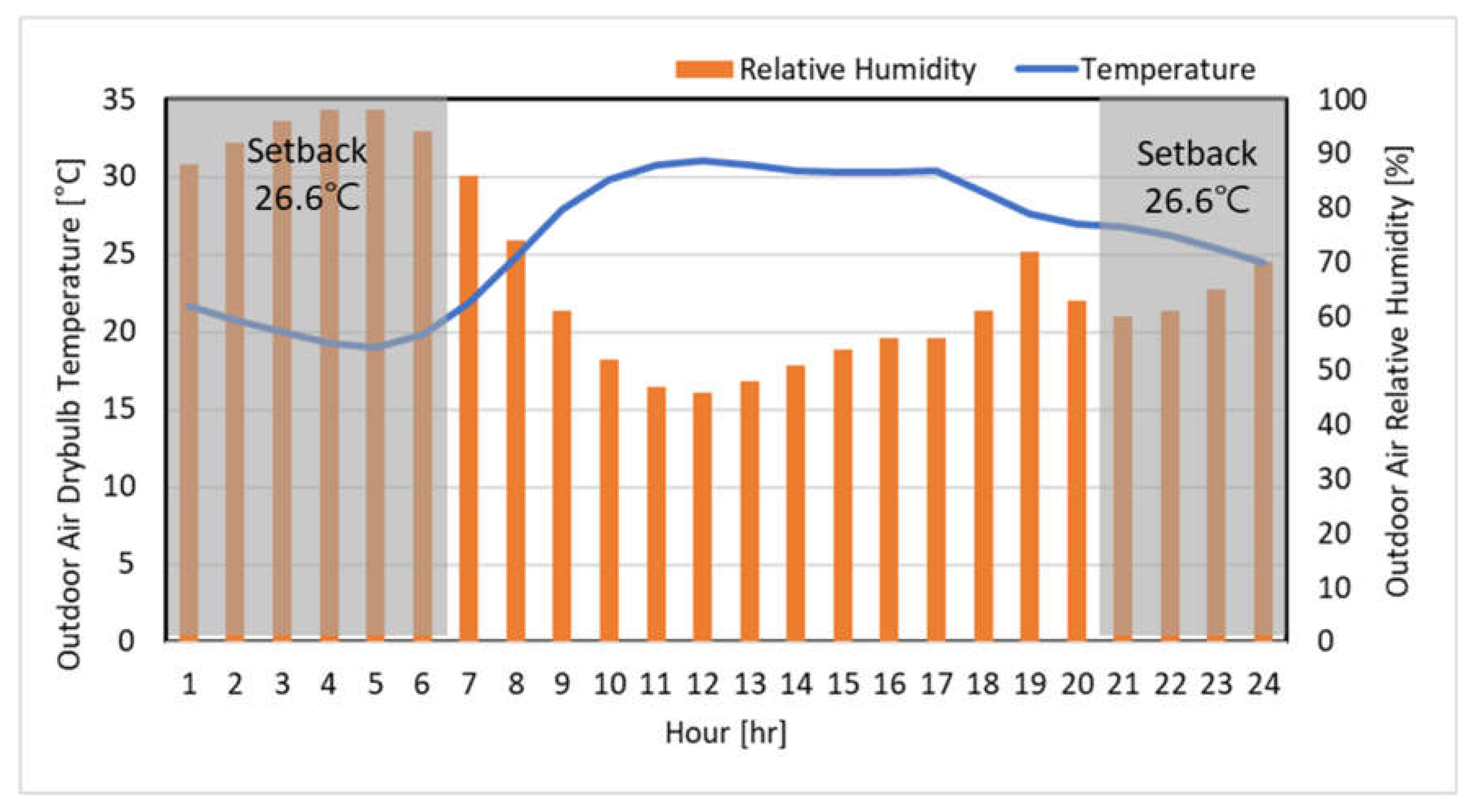
5.1. Weather Conditions
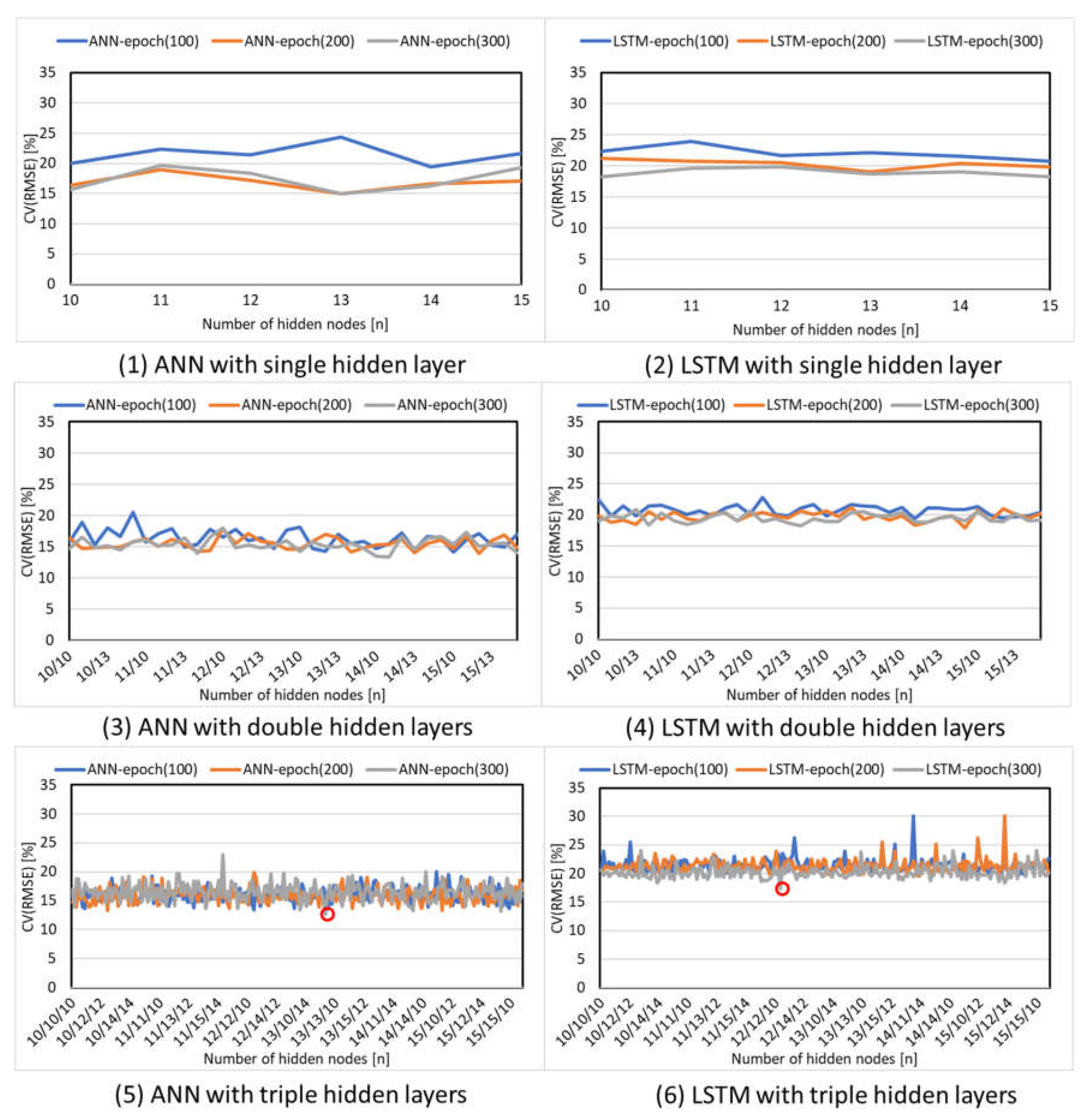
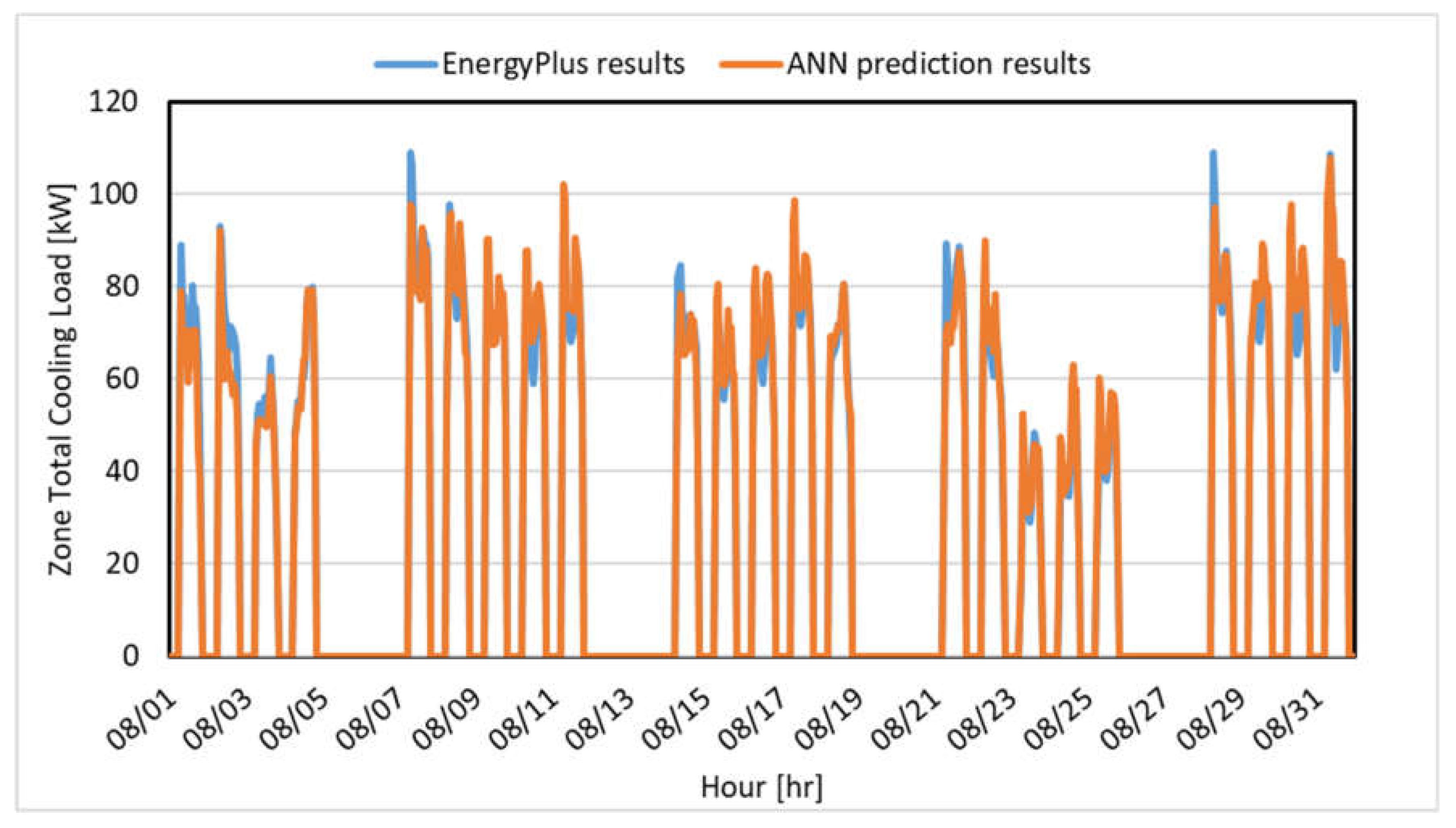
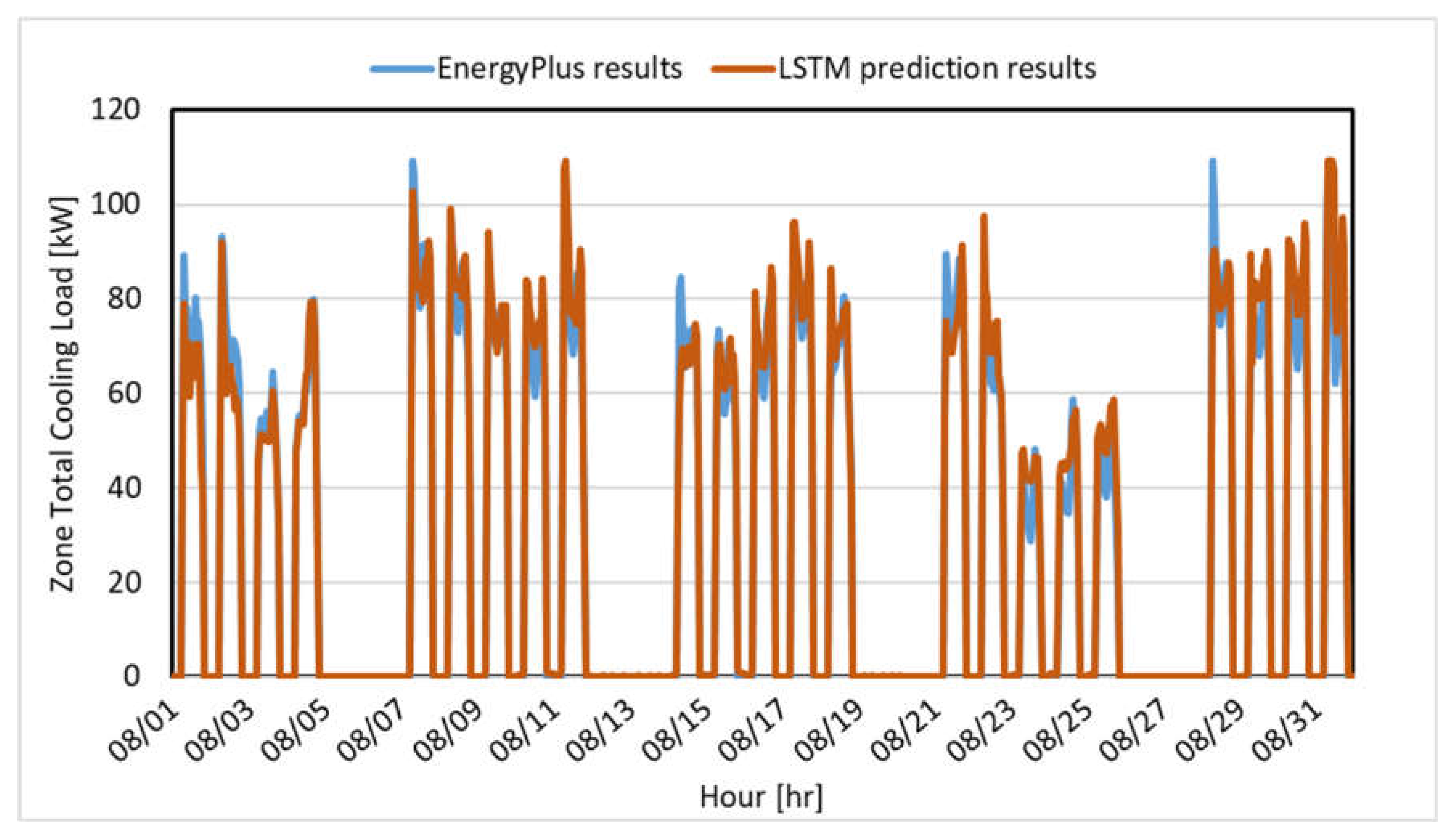
5.2. Evaluation of Cooling Load Prediction Model Accuracy
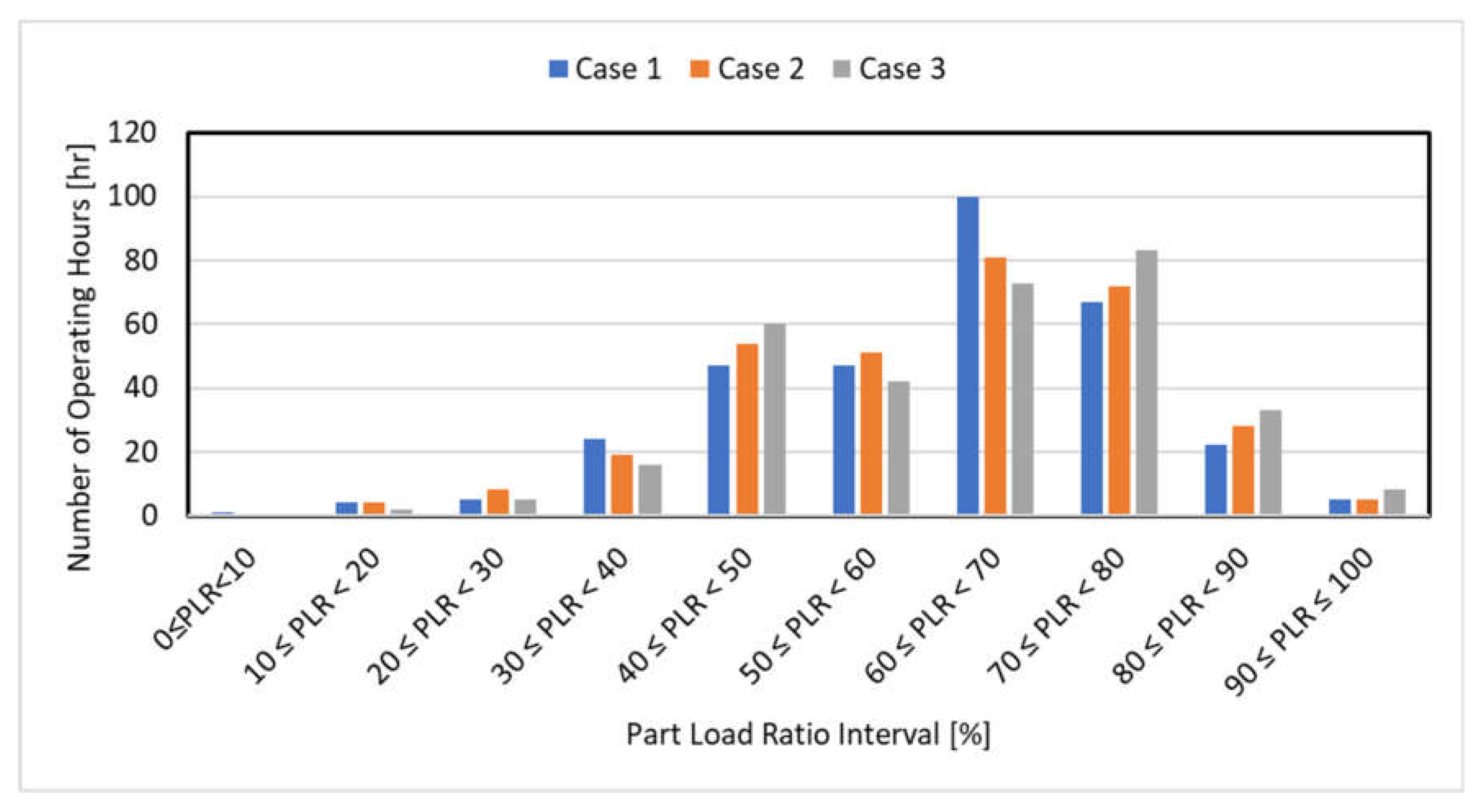
5.3. AHU-DAT Operating Scenarios Comparison
5.4. Weather Conditions on the Representative Day
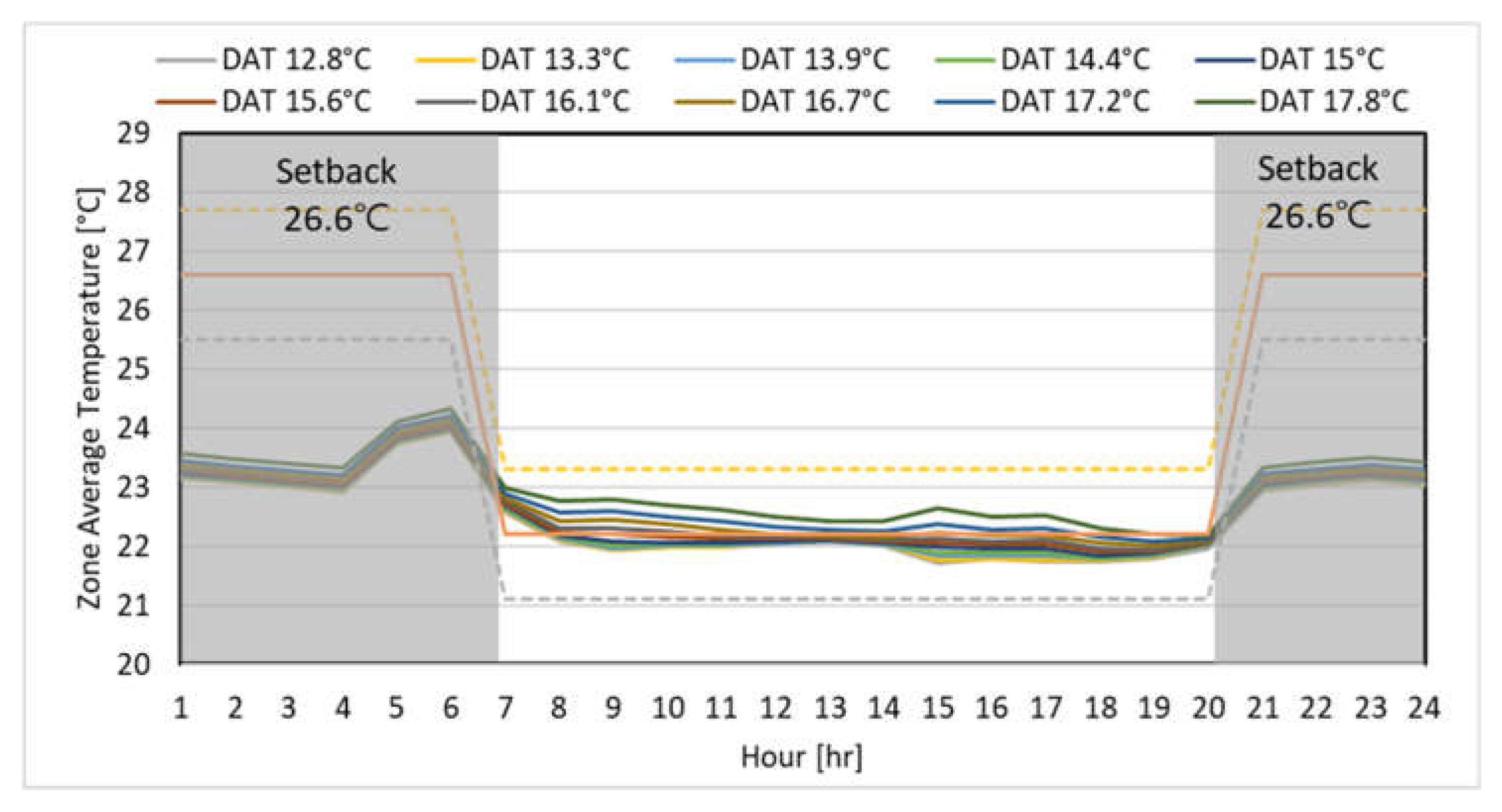
5.5. Sensitivity Analysis of Zone Mean Air Temperature According to AHU-DAT Change on the Representative Day
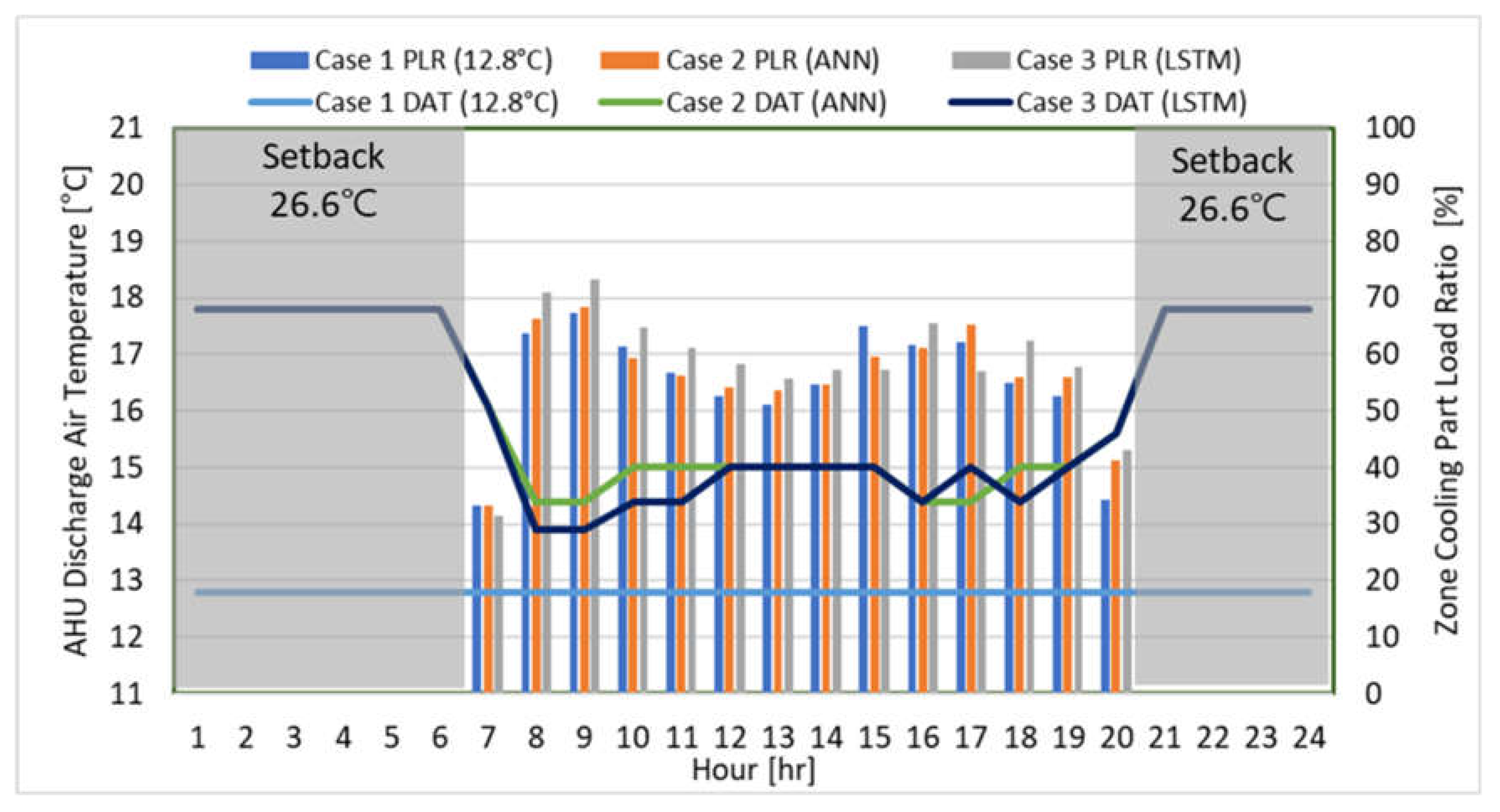
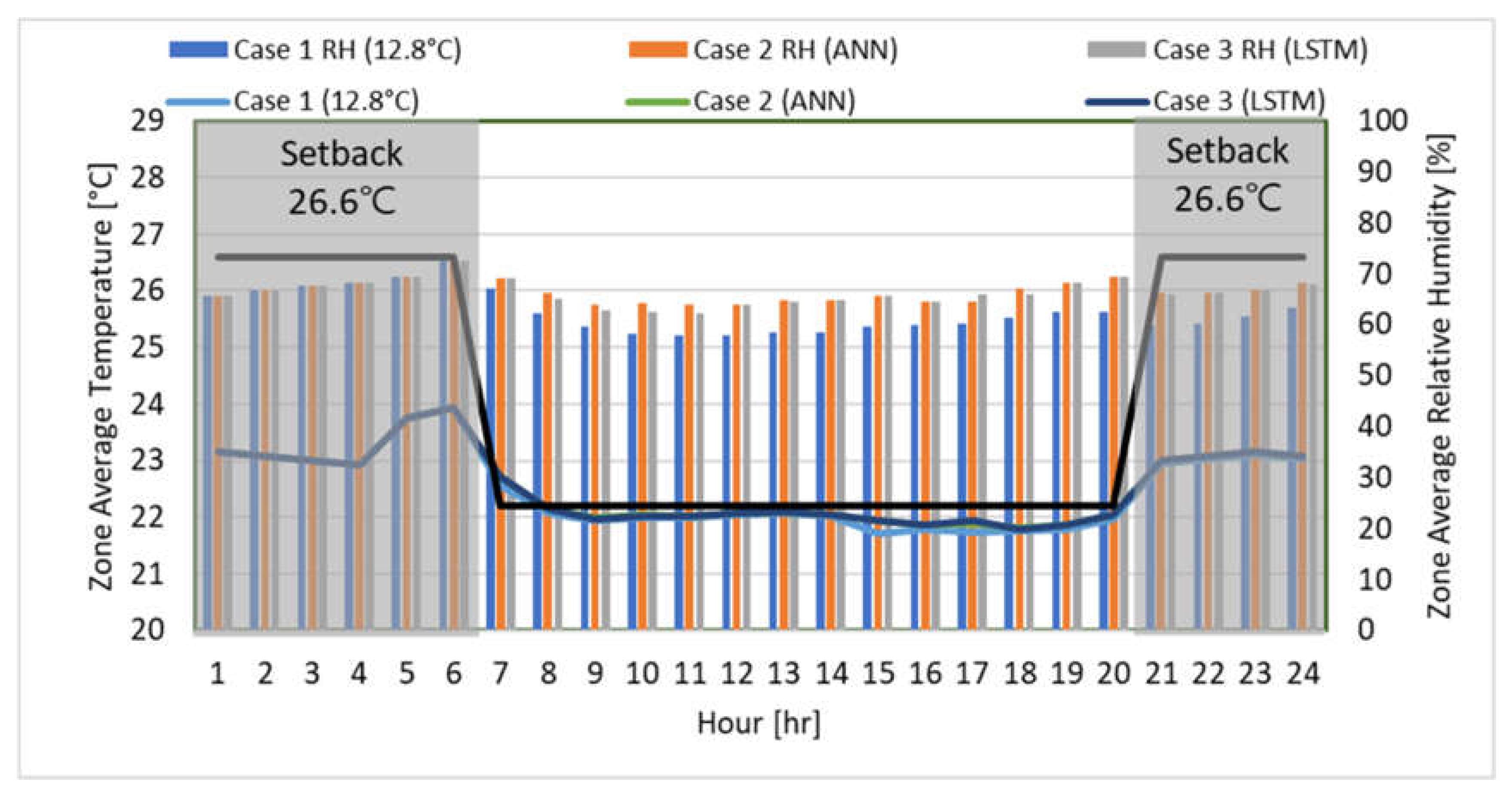
5.6. Comparison of AHU-DAT Pattern on the Representative Day
5.7. Comparison of Total Cooling Energy Consumption on the Representative Day
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- U.S Energy Information Administration (EIA). Annual Energy Outlook 2019. 2019. Available online: https://www.eia.gov/todayinenergy/detail.php?id=38112 (accessed on 17 April 2023).
- International Energy Agency (IEA). The Future of Cooling. 2018. Available online: https://www.iea.org/reports/the-future-of-cooling (accessed on 17 April 2023).
- Yeon, S.; Yu, B.; Seo, B.; Yoon, Y.; Lee, K.H. ANN based automatic slat angle control of venetian blind for minimized total load in an office building. Sol. Energy 2019, 180, 133–145. [Google Scholar] [CrossRef]
- Seo, B.M.; Yoon, Y.B.; Song, S.; Cho, S. ANN-based thermal load prediction approach for advanced controls in building energy systems. In Proceedings of the Conference for ARCC 2019 International Conference, Toronto, ON, Canada, 29 May–1 June 2019. [Google Scholar]
- Lee, J.M.; Hong, S.H.; Seo, B.M.; Lee, K.H. Application of artificial neural networks for optimized AHU discharge air temperature set-point and minimized cooling energy in VAV system. Appl. Therm. Eng. 2019, 153, 726–738. [Google Scholar] [CrossRef]
- Qian, F.; Gao, W.; Yang, Y.; Yu, D. Potential analysis of the transfer learning model in short and medium-term forecasting of building HVAC energy consumption. Energy 2020, 193, 116724. [Google Scholar] [CrossRef]
- Moon, J.W.; Yang, Y.K.; Choi, E.J.; Choi, Y.J.; Lee, K.-H.; Kim, Y.-S.; Park, B.R. Development of a control algorithm aiming at cost-effective operation of a VRF heating system. Appl. Therm. Eng. 2019, 149, 1522–1531. [Google Scholar] [CrossRef]
- Park, B.R.; Choi, E.J.; Hong, J.; Lee, J.H.; Moon, J.W. Development of an energy cost prediction model for a VRF heating system. Appl. Therm. Eng. 2018, 140, 476–486. [Google Scholar] [CrossRef]
- Mtibaa, F.; Nguyen, K.-K.; Dermardiros, V.; Cheriet, M. Context-aware Model Predictive Control framework for multi-zone buildings. J. Build. Eng. 2021, 42, 102340. [Google Scholar] [CrossRef]
- Sendra-Arranz, R.; Gutiérrez, A. A long short-term memory artificial neural network to predict daily HVAC consumption in buildings. Energy Build. 2020, 216, 109952. [Google Scholar]
- Mba, L.; Meukam, P.; Kemajou, A. Application of artificial neural network for predicting hourly indoor air temperature and relative humidity in modern building in humid region. Energy Build. 2016, 121, 32–42. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, X. A hybrid method of dynamic cooling and heating load forecasting for office buildings based on artificial intelligence and regression analysis. Energy Build. 2018, 174, 293–308. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F.; Fung, A.S.; Raahemifar, K. Artificial neural network (ANN) based model predictive control (MPC) and optimization of HVAC systems: A state of the art review and case study of a residential HVAC system. Energy Build. 2017, 141, 96–113. [Google Scholar] [CrossRef]
- Jang, J.; Han, J.; Leigh, S.-B. Prediction of heating energy consumption with operation pattern variables for non-residential buildings using LSTM networks. Energy Build. 2022, 255, 111647. [Google Scholar] [CrossRef]
- Faiq, M.; Tan, K.G.; Liew, C.P.; Hossain, F.; Tso, C.-P.; Lim, L.L.; Wong, A.Y.K.; Shah, Z.M. Prediction of energy consumption in campus buildings using long short-term memory. Alex. Eng. J. 2023, 67, 65–76. [Google Scholar] [CrossRef]
- Fang, Z.; Crimier, N.; Scanu, L.; Midelet, A.; Alyafi, A.; Delinchant, B. Multi-zone indoor temperature prediction with LSTM-based sequence to sequence model. Energy Build. 2021, 245, 111053. [Google Scholar] [CrossRef]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Optimal Deep Learning LSTM Model for Electric Load Forecasting using Feature Selection and Genetic Algorithm: Comparison with Machine Learning Approaches†. Energies 2018, 11, 1636. [Google Scholar] [CrossRef]
- Somu, N.; Ramamritham, G.R.K. A deep learning framework for building energy consumption forecast. Renew. Sustain. Energy Rev. 2021, 137, 110591. [Google Scholar]
- Peng, C.; Tao, Y.; Chen, Z.; Zhang, Y.; Sun, X. Multi-source transfer learning guided ensemble LSTM for building multi-load forecasting. Expert Syst. Appl. 2022, 202, 117194. [Google Scholar] [CrossRef]
- Rashid, T. Make Your Own Neural Network; CreateSpace Independent Publishing Platform: North Charleston, SC, USA, 2016. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Mittal, A. Understanding RNN and LSTM. 2019. Available online: https://towardsdatascience.com/understanding-rnn-and-lstm-f7cdf6dfc14e (accessed on 17 April 2023).
- Zarzycki, K.; Lawrynczuk, M. LSTM and GRU Neural Networks as Models of Dynamical Processes Used in Predictive Control: A Comparison of Models Developed for Two Chemical Reactors. Sensors 2021, 21, 5625. [Google Scholar] [CrossRef] [PubMed]
- Olah, C. Understanding LSTM Networks. 2015. Available online: https://colah.github.io/posts/2015-08-Understanding-LSTMs/ (accessed on 17 April 2023).
- Jung, M.; Mendes, P.R.d.C.; Önnheim, M.; Gustavsson, E. Model Predictive Control when utilizing LSTM as dynamic models. Eng. Appl. Artif. Intell. 2023, 123, 106226. [Google Scholar] [CrossRef]
- Keras. Available online: https://keras.io/about/ (accessed on 17 April 2023).
- Falk, R.F.; Miller, N.B. A Primer for Soft Modeling; University of Akron Press: Akron, OH, USA, 1992. [Google Scholar]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation Coefficients: Appropriate Use and Interpretation. Anesth Analg. 2018, 126, 1763–1768. [Google Scholar] [PubMed]
- ASHRAE. Guideline 14-2014. 2014. Measurement of Energy and Demand Savings; American Society of Heating, Refrigerating, and Air Conditioning Engineers: Atlanta, GA, USA, 2014. [Google Scholar]
- North Carolina Environmental Quality, Energy Saving Fact Sheet: Chillers. 2010. Available online: https://www.deq.nc.gov/environmental-assistance-and-customer-service/ias-energy-efficiency/opportunities/chillers/download (accessed on 26 April 2023).
- International Performance Measurement & Verification Protocol (IPMVP). Concepts and Options for Determining Energy and Water Savings. Volume 1, Section 3.4.4.2. 2002. Available online: https://www.nrel.gov/docs/fy02osti/31505.pdf (accessed on 26 April 2023).
- Federal Energy Management Program (FEMP). M&V Guidelines: Measurement and Verification for Performance-Based Contracts Version 4.0, Section 4.5.3. 2015. Available online: https://www.energy.gov/femp/articles/mv-guidelines-measurement-and-verification-performance-based-contracts-version-40 (accessed on 26 April 2023).









| Correlation Factor with Cooling Load | Outdoor Air Temperature (°C) | Outdoor Air Relative Humidity (%) | Diffuse Solar Radiation (W/m²) | Direct Solar Radiation (W/m²) | Lighting Schedules (%) | Electric Equipment Schedules (%) | People Schedules (%) | Day and Hour Type (-) |
|---|---|---|---|---|---|---|---|---|
| r | 0.5621 | −0.5022 | 0.4737 | 0.4863 | 0.8694 | 0.8353 | 0.9061 | 0.9446 |
| r² | 0.3159 | 0.2522 | 0.2243 | 0.2365 | 0.7558 | 0.6977 | 0.8210 | 0.8923 |
| Division | Hyperparameter Range | |
|---|---|---|
| ANN | LSTM | |
| Number of hidden layers [n] | 1, 2, 3 | |
| Number of hidden nodes [n] | 10~15 | |
| Epochs [n] | 100, 200, 300 | |
| Batch size [n] | 24 | |
| Optimizer | Adam | |
| Activation Function | Sigmoid and Rectified linear unit | |
| Zone | |
|---|---|
| Break Room | 5.0 |
| Closed Office | 12.1 |
| Open Office | 12.1 |
| Conference | 12.1 |
| IT Room | 12.1 |
| Lobby | 9.3 |
| Corridor | 9.3 |
| Mechanical Room | 14.0 |
| Stair | 12.1 |
| Rest Room | 14.9 |
| Storage | 14.0 |
| Construction | U-Value (W/m2 K) | Visible Transmittance | Solar Heat Gain Coefficient |
|---|---|---|---|
| Exterior Wall | 0.232 | X | X |
| Interior Wall | 2.867 | X | X |
| Roof | 0.174 | X | X |
| Exterior window | 1.65 | 0.60 | 0.31 |
| Class | AHU-DAT (°C) | Case 1 | Class | AHU-DAT (°C) | Cases 2 and 3 |
|---|---|---|---|---|---|
| Interval | Interval | ||||
| 1 | 12.8 | 0% ≤ PLR < 10% | 1 | 17.8 | 0% ≤ PLR < 10% |
| 2 | 12.8 | 10% ≤ PLR < 20% | 2 | 17.2 | 10% ≤ PLR < 20% |
| 3 | 12.8 | 20% ≤ PLR < 30% | 3 | 16.7 | 20% ≤ PLR < 30% |
| 4 | 12.8 | 30% ≤ PLR < 40% | 4 | 16.1 | 30% ≤ PLR < 40% |
| 5 | 12.8 | 40% ≤ PLR < 50% | 5 | 15.6 | 40% ≤ PLR < 50% |
| 6 | 12.8 | 50% ≤ PLR < 60% | 6 | 15.0 | 50% ≤ PLR < 60% |
| 7 | 12.8 | 60% ≤ PLR < 70% | 7 | 14.4 | 60% ≤ PLR < 70% |
| 8 | 12.8 | 70% ≤ PLR < 80% | 8 | 13.9 | 70% ≤ PLR < 80% |
| 9 | 12.8 | 80% ≤ PLR < 90% | 9 | 13.3 | 80% ≤ PLR < 90% |
| 10 | 12.8 | 90% ≤ PLR ≤ 100% | 10 | 12.8 | 90% ≤ PLR ≤ 100% |
| Division | ANN | LSTM |
|---|---|---|
| Optimized Values | Optimized Values | |
| Number of Hidden Layers [n] | 3 | 3 |
| Number of Hidden Neurons Layer 1 [n] | 13 | 12 |
| Number of Hidden Neurons Layer 2 [n] | 12 | 12 |
| Number of Hidden Neurons Layer 3 [n] | 11 | 12 |
| Epochs [n] | 300 | 300 |
| CV(RMSE) [%] | 12.7 | 17.3 |
| Class | AHU-DAT (°C) | Case 1 | AHU-DAT (°C) | Case 2 | Case 3 | |||
|---|---|---|---|---|---|---|---|---|
| Interval | Number of Hours (h) | Interval | Number of Hours (h) | Interval | Number of Hours (h) | |||
| 1 | 12.8 | 0% ≤ PLR < 10% | 1 | 17.8 | 0% ≤ PLR < 10% | - | 0% ≤ PLR < 10% | - |
| 2 | 12.8 | 10% ≤ PLR < 20% | 4 | 17.2 | 10% ≤ PLR < 20% | 4 | 10% ≤ PLR < 20% | 2 |
| 3 | 12.8 | 20% ≤ PLR < 30% | 5 | 16.7 | 20% ≤ PLR < 30% | 8 | 20% ≤ PLR < 30% | 5 |
| 4 | 12.8 | 30% ≤ PLR < 40% | 24 | 16.1 | 30% ≤ PLR < 40% | 19 | 30% ≤ PLR < 40% | 16 |
| 5 | 12.8 | 40% ≤ PLR < 50% | 47 | 15.6 | 40% ≤ PLR < 50% | 54 | 40% ≤ PLR < 50% | 60 |
| 6 | 12.8 | 50% ≤ PLR < 60% | 47 | 15.0 | 50% ≤ PLR < 60% | 51 | 50% ≤ PLR < 60% | 42 |
| 7 | 12.8 | 60% ≤ PLR < 70% | 100 | 14.4 | 60% ≤ PLR < 70% | 81 | 60% ≤ PLR < 70% | 73 |
| 8 | 12.8 | 70% ≤ PLR < 80% | 67 | 13.9 | 70% ≤ PLR < 80% | 72 | 70% ≤ PLR < 80% | 83 |
| 9 | 12.8 | 80% ≤ PLR < 90% | 22 | 13.3 | 80% ≤ PLR < 90% | 28 | 80% ≤ PLR < 90% | 33 |
| 10 | 12.8 | 90% ≤ PLR ≤ 100% | 5 | 12.8 | 90% ≤ PLR ≤ 100% | 5 | 90% ≤ PLR ≤ 100% | 8 |
| Total hours (h) | 322 | 322 | 322 | |||||
| Case 1 | Case 2 | Case 3 | |
|---|---|---|---|
| CHW used (MJ/day) | 3060.0 | 2870.2 | 2875.7 |
| TOR (ton-hour/day) | 241.7 | 226.7 | 227.1 |
| CHW electricity consumption (kWh/day) based on COP 5 (0.7 kW/ton) | 169.2 | 158.7 | 159.0 |
| CHW Pump electricity consumption (kWh/day) | 12.3 | 10.7 | 10.8 |
| Fan electricity consumption (kWh/day) | 10.8 | 16.7 | 16.1 |
| Total cooling electricity consumption (CHW+CHW pump+fan) [kWh/day] | 192.3 | 186.1 | 185.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seo, B.; Yoon, Y.; Lee, K.H.; Cho, S. Comparative Analysis of ANN and LSTM Prediction Accuracy and Cooling Energy Savings through AHU-DAT Control in an Office Building. Buildings 2023, 13, 1434. https://doi.org/10.3390/buildings13061434
Seo B, Yoon Y, Lee KH, Cho S. Comparative Analysis of ANN and LSTM Prediction Accuracy and Cooling Energy Savings through AHU-DAT Control in an Office Building. Buildings. 2023; 13(6):1434. https://doi.org/10.3390/buildings13061434
Chicago/Turabian StyleSeo, Byeongmo, Yeobeom Yoon, Kwang Ho Lee, and Soolyeon Cho. 2023. "Comparative Analysis of ANN and LSTM Prediction Accuracy and Cooling Energy Savings through AHU-DAT Control in an Office Building" Buildings 13, no. 6: 1434. https://doi.org/10.3390/buildings13061434
APA StyleSeo, B., Yoon, Y., Lee, K. H., & Cho, S. (2023). Comparative Analysis of ANN and LSTM Prediction Accuracy and Cooling Energy Savings through AHU-DAT Control in an Office Building. Buildings, 13(6), 1434. https://doi.org/10.3390/buildings13061434







