Flexural Behavior of Cold-Formed Steel Composite Floor Infilled with Desert Sand Foamed Concrete
Abstract
:1. Introduction
2. Experimental Program
2.1. Specimen Details and Fabrication
2.2. Material Properties
2.3. Test Set-Up and Procedure
3. Experimental Results and Discussion
3.1. Failure Phenomena and Modes
3.1.1. CF-1
3.1.2. CF-2
3.1.3. CF-3
3.1.4. CF-4
3.1.5. Comparison and Discussion
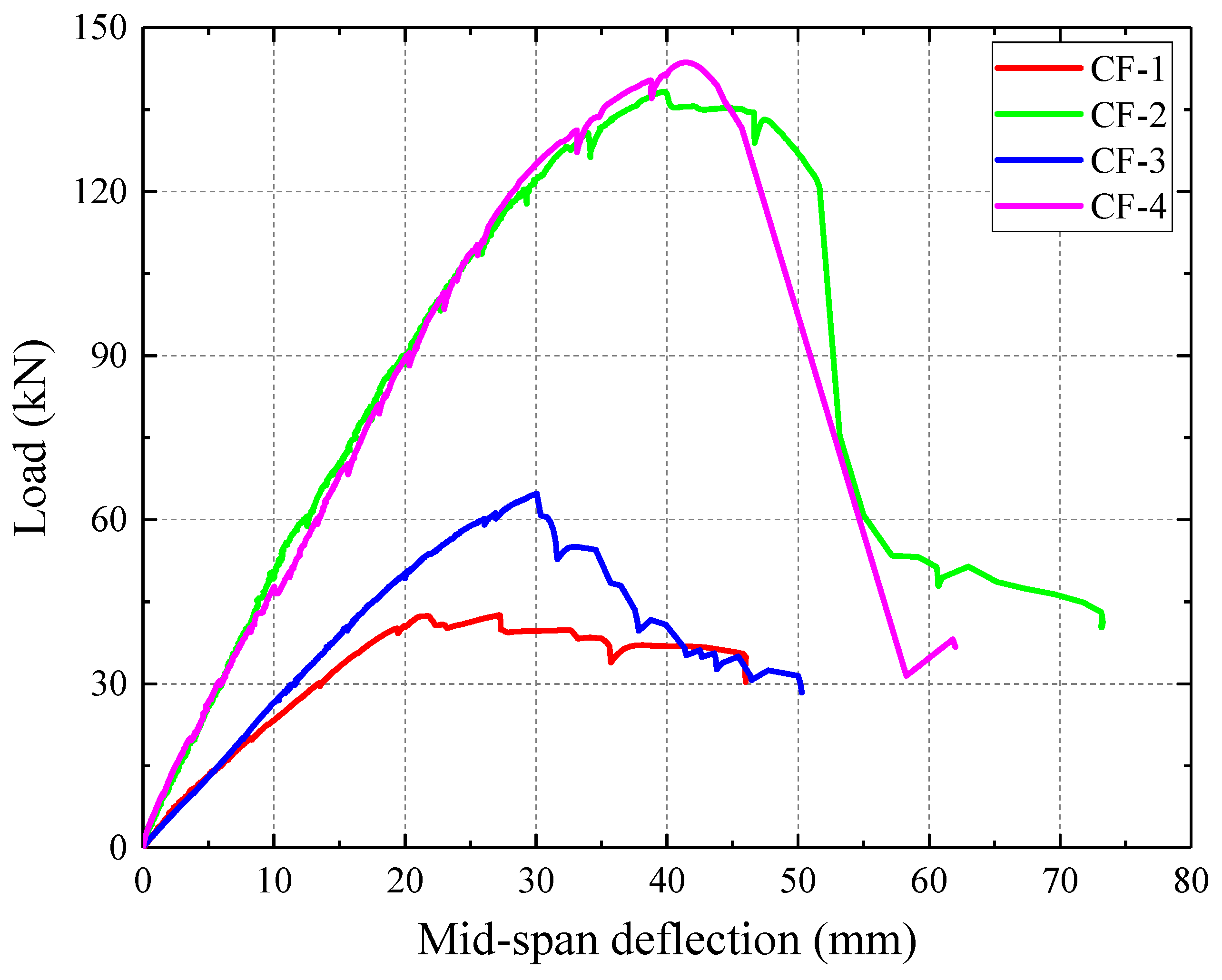
3.2. Load vs. Mid-Span Deflection Curves
- (1)
- The introduction of foamed concrete filling significantly enhanced the flexural stiffness and ultimate capacity of the floor. The flexural stiffness K increased by 117.6% and 73.6% for the specimens without holes and with holes, respectively, while Fp increased by 224.9% and 121.8%, respectively.
- (2)
- The specimens without holes (CF-1 and CF-2) displayed a more gradual decrease in bearing capacity after reaching the peak load, indicating better ductility. For specimen CF-2, the foamed concrete was compressed and compacted after reaching the peak load, which showed good ductility, and the load dropped sharply until the compression strain was too large and the CFS buckled and failed.
- (3)
- The presence of holes increased the ultimate capacity of the composite floor. For the specimens without foamed concrete filling (CF-1 and CF-3), Fp increased significantly by up to 52.2%. In general, the presence of holes weakens the cross-section of the CFS joists, reducing their capacity regardless of whether the final failure mode is local buckling or web crippling under the loading point. However, due to the high strength and poor ductility of the LQ550 grade cold-formed thin-walled steel used in this study, the deformation of CFS sections without holes was limited, and a tearing failure occurred at the cold-formed position before the full development of deformation. For the specimens infilled with foamed concrete (CF-2 and CF-4), Fp only increased by 3.9%. The presence of holes improved the bond–slip behavior between foamed concrete and CFS, increasing the degree of composite action and making better use of the compression strength of the foamed concrete. However, the presence of holes also weakened the web section, causing a tensile fracture of the steel joist from the bottom flange to the hole edge, resulting in a strength failure. Consequently, the impact of holes on the ultimate capacity of specimens infilled with foamed concrete was not significant.
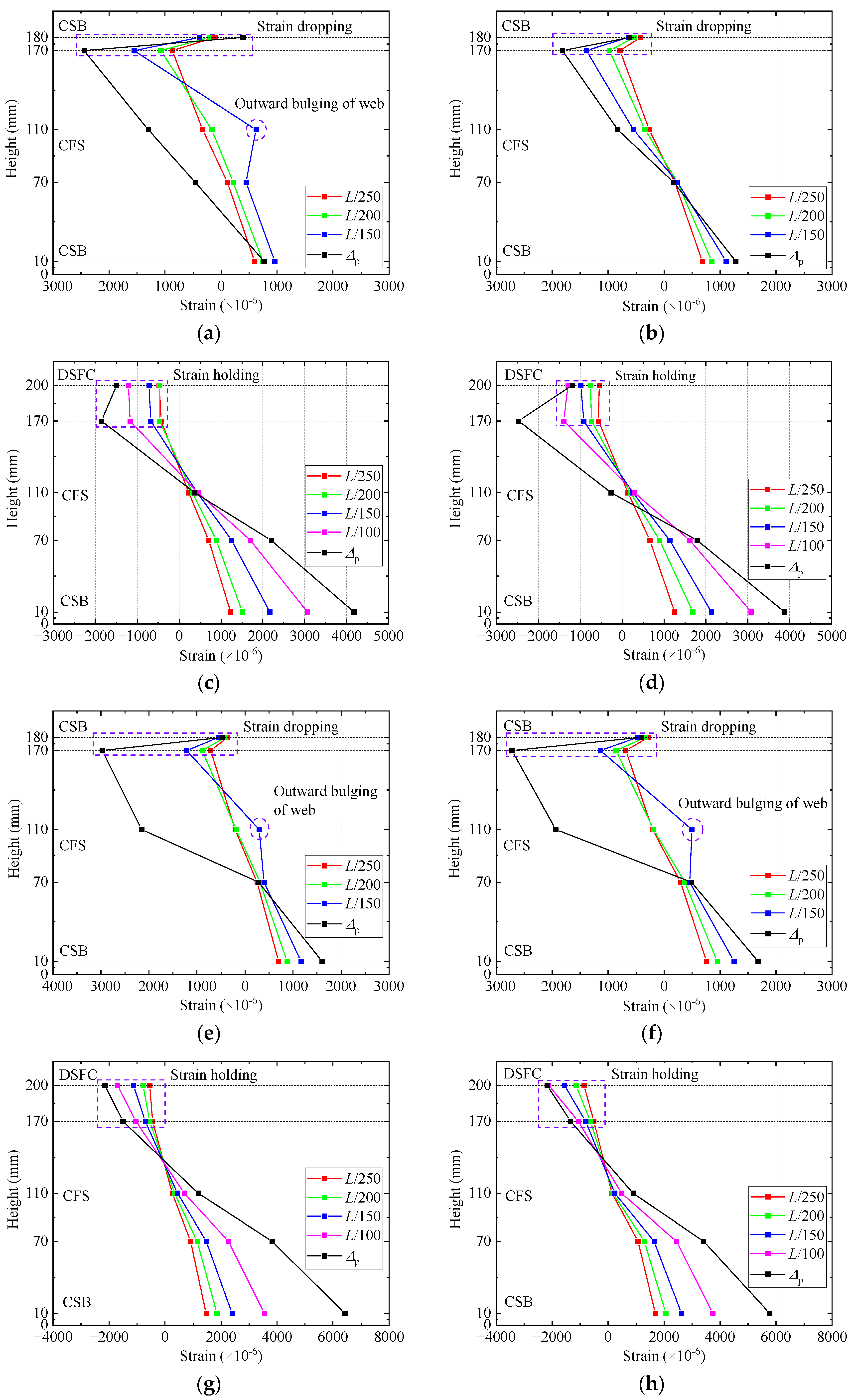
3.3. Strain Distribution at Mid-Span Section
- (1)
- Foamed concrete was effective in constraining the buckling deformation of cold-formed steel. For the specimens without foamed concrete filling (CF-1 and CF-3), the CFS satisfied the plane section assumption during the initial loading stage (Δ = L/250; Δ = L/200). As the load approached the ultimate capacity (Δ = L/150), abnormal tensile strains occurred at the height of 110 mm due to local buckling deformation that caused outward bulging. When load reached the peak (Δ = Δp), very large compressive strains occurred at the height of 110–170 mm due to the web crippling failure. For the specimens infilled with foamed concrete (CF-2 and CF-4), the foamed concrete prevented web crippling failure and effectively constrained the buckling deformation of CFS joists throughout the entire length, so that the CFS satisfied the plane section assumption during the entire loading process.
- (2)
- Self-drilling screws had difficulty in achieving effective load transfer and coordinated deformation between the CSB and CFS. By comparing the strains at the CFS web (height of 170 mm) and the top surface of the CSB (height of 180 mm) for specimens CF-1 and CF-3, it can be found that as the load increased, the compressive strain of the CFS kept increasing, while the compressive strain of the CSB remained almost unchanged at a low level. Instead, local damage occurred at the stress concentration point where the self-drilling screws were connected to the CSB. This indicated that self-drilling screw connections struggled to achieve effective load transfer and coordinated deformation between the CSB and CFS.
- (3)
- Partial composite action was achieved by the bonding effect between foamed concrete and CFS. By comparing the strains at the CFS web (height of 170 mm) and the top layer of the foamed concrete (height of 200 mm) for specimens CF-2 and CF-4, it can be found that as the load increased, the compressive strain of the CFS and the foamed concrete both kept increasing. For the specimen without holes (CF-2), the strain growth of the foamed concrete was relatively low, and only partial coordinated deformation was achieved. Moreover, the degree of composite action significantly decreased in the later loading stage due to the separation between the foamed concrete and CFS. For the specimen with holes (CF-4), the enhancement from the bond–slip behavior under holes resulted in a higher growth rate in the foamed concrete strain throughout the entire loading process, achieving fully coordinated deformation, and the section basically satisfied the plane section assumption.
- (4)
- The strain distribution on the left and right sides of the CF-1 specimen was significantly different, which is consistent with its failure mode of only right-side crippling and buckling of the CFS joist.
4. Nonlinear Finite Element Analysis
4.1. Finite Element Modeling
4.2. Verification of Finite Element Model
4.3. Parametric Analyses
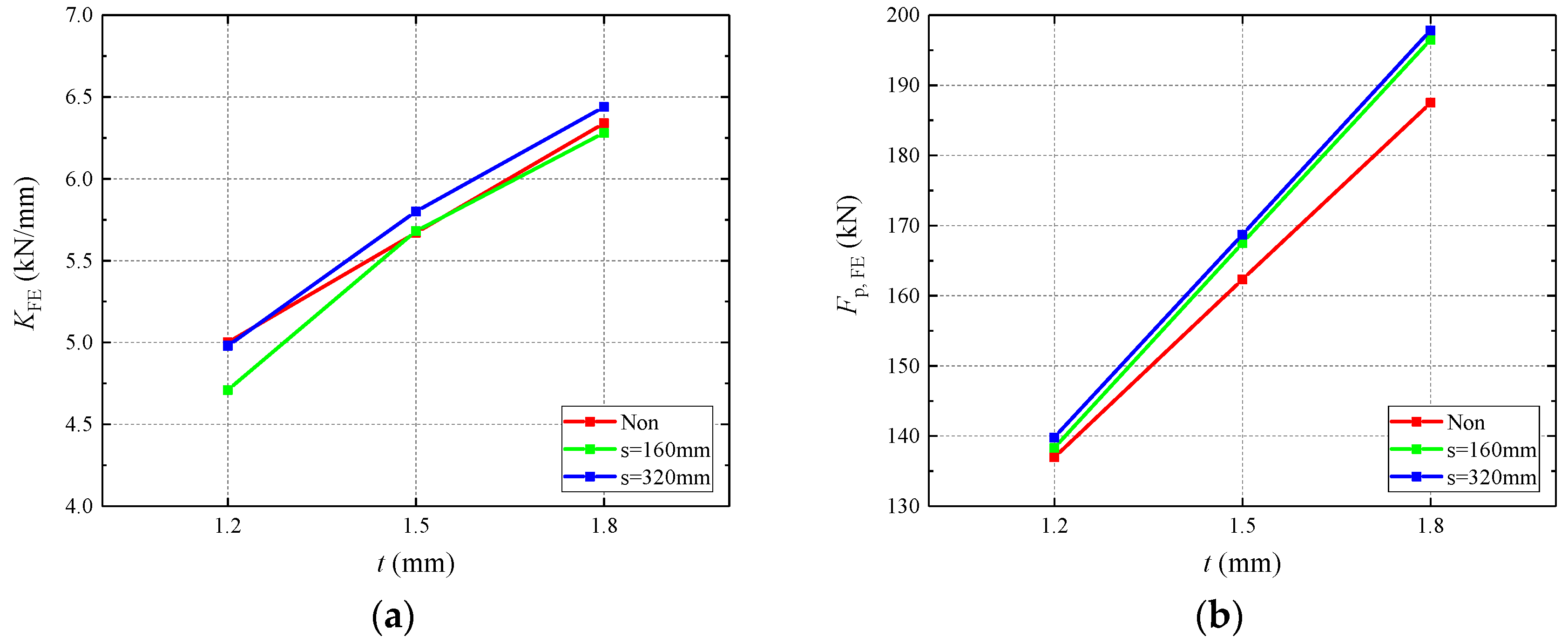
4.3.1. Influence of CFS Thickness
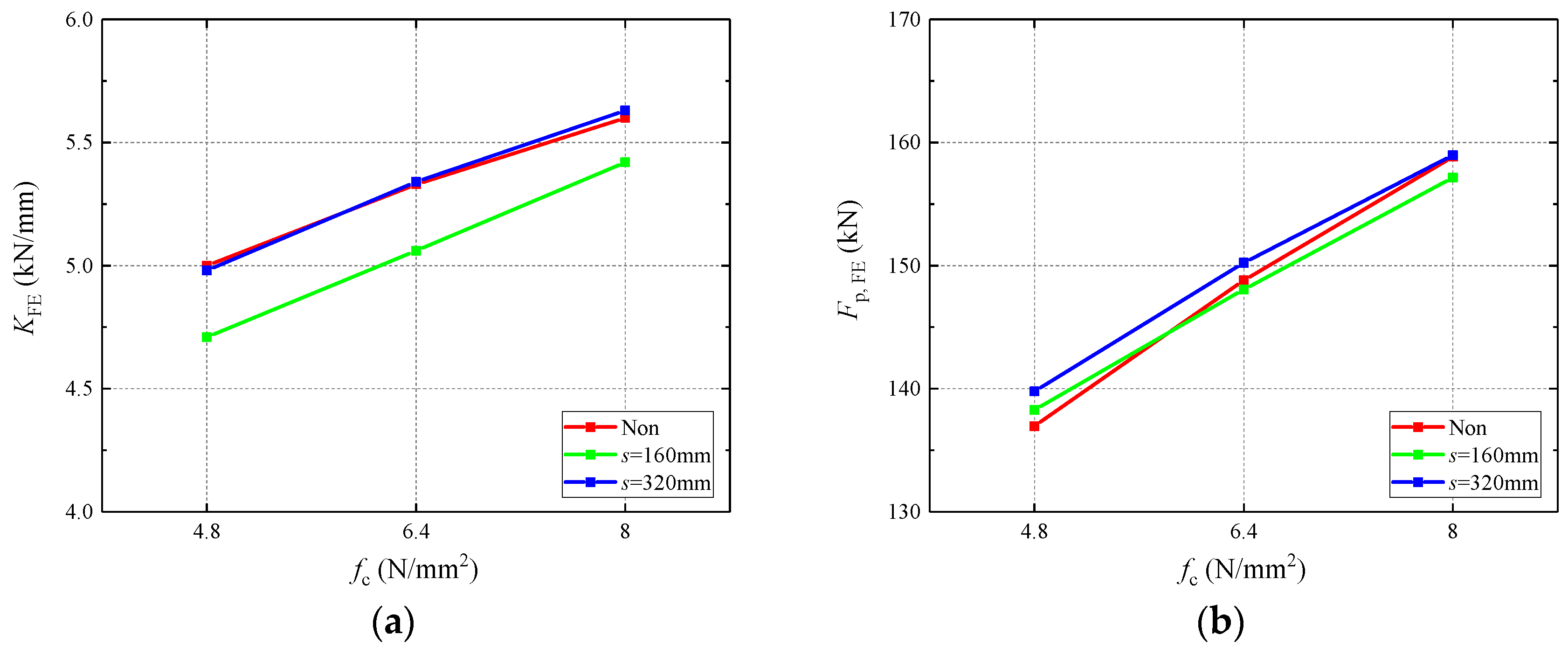
4.3.2. Influence of Foamed Concrete Strength
4.3.3. Influence of Hole Spacing
5. Conclusions
- (1)
- For specimens without foamed concrete filling, the failure mode was web crippling of cold-formed thin-walled steel joists under concentrated loads. The presence of holes weakened the section stiffness, allowing the deformation of LQ550 steel to fully develop. For specimens infilled with foamed concrete, the presence of holes changed the failure mode from tensile fracture to local buckling of CFS and crushing of constrained foamed concrete.
- (2)
- Foamed concrete resisted compression in the compression zone and effectively constrained the buckling deformation of cold-formed thin-walled steel to improve the bearing capacity and stiffness of the composite floor.
- (3)
- Self-drilling screw connections struggled to achieve effective load transfer and coordinated deformation between CSB and CFS. The bonding effect between DSFC and CFS achieved partial composite action, and the degree of composite action increased with the improvement in the bond–slip behavior from holes.
- (4)
- The flexural behavior was improved with the increase in CFS thickness and foamed concrete strength. The impact of the holes was not obvious for specimens infilled with holes.
6. Future work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hanaor, A. Tests of composite beams with cold-formed sections. J. Constr. Steel Res. 2000, 54, 245–264. [Google Scholar] [CrossRef]
- Hosseinpour, M.; Zeynalian, M.; Ataei, A.; Daei, M. An experimental study on structural performance of U-shaped shear connector in composite cold-formed steel floor joists. Eng. Struct. 2021, 249, 113379. [Google Scholar] [CrossRef]
- Hosseinpour, M.; Zeynalian, M.; Ataei, A.; Daei, M. Push-out tests on bolted shear connectors in composite cold-formed steel beams. Thin-Walled Struct. 2021, 164, 107831. [Google Scholar] [CrossRef]
- Hosseinpour, M.; Zeynalian, M.; Daei, M.; Ataei, A. Numerical study on behavior of bolted shear connector used in composite cold-formed steel beams. Thin-Walled Struct. 2022, 177, 109377. [Google Scholar] [CrossRef]
- Hsu, C.-T.T.; Punurai, S.; Punurai, W.; Majdi, Y. New composite beams having cold-formed steel joists and concrete slab. Eng. Struct. 2014, 71, 187–200. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J.; Xiao, Y.; Wang, W. Experimental and analytical assessments on flexural behaviour of CTLST composite beams. Thin-Walled Struct. 2019, 138, 15–31. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Xiao, Y.; Guo, L. Cyclic behavior tests and evaluation of CFS truss composite floors. J. Build. Eng. 2020, 35, 101974. [Google Scholar] [CrossRef]
- Lakkavalli, B.S.; Liu, Y. Experimental study of composite cold-formed steel C-section floor joists. J. Constr. Steel Res. 2006, 62, 995–1006. [Google Scholar] [CrossRef]
- Güldür, H.; Baran, E.; Topkaya, C. Experimental and numerical analysis of cold-formed steel floor trusses with concrete filled compression chord. Eng. Struct. 2021, 234, 111813. [Google Scholar] [CrossRef]
- Xu, L.; Tangorra, F. Experimental investigation of lightweight residential floors supported by cold-formed steel C-shape joists. J. Constr. Steel Res. 2007, 63, 422–435. [Google Scholar] [CrossRef]
- Zhou, X.; Shi, Y.; Xu, L.; Yao, X.; Wang, W. A simplified method to evaluate the flexural capacity of lightweight cold-formed steel floor system with oriented strand board subfloor. Thin-Walled Struct. 2018, 134, 40–51. [Google Scholar] [CrossRef]
- Kyvelou, P.; Gardner, L.; Nethercot, D.A. Composite Action Between Cold-Formed Steel Beams and Wood-Based Floorboards. Int. J. Struct. Stab. Dyn. 2015, 15, 1540029. [Google Scholar] [CrossRef]
- Li, Y.; Shan, W.; Shen, H.; Zhang, Z.-W.; Liu, J. Bending resistance of I-section bamboo–steel composite beams utilizing adhesive bonding. Thin-Walled Struct. 2015, 89, 17–24. [Google Scholar] [CrossRef]
- Tian, L.-M.; Kou, Y.-F.; Hao, J.-P.; Zhao, L.-W. Flexural performance of a lightweight composite floor comprising cold-formed steel trusses and a composite mortar slab. Thin-Walled Struct. 2019, 144, 106361. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, K.; Guan, Y.; Yao, X.; Xu, L.; Zhang, H. The flexural behavior of cold-formed steel composite beams. Eng. Struct. 2020, 218, 110819. [Google Scholar] [CrossRef]
- Guettala, S.; Mezghiche, B. Compressive strength and hydration with age of cement pastes containing dune sand powder. Constr. Build. Mater. 2011, 25, 1263–1269. [Google Scholar] [CrossRef]
- Luo, F.J.; He, L.; Pan, Z.; Duan, W.H.; Zhao, X.L.; Collins, F. Effect of very fine particles on workability and strength of concrete made with dune sand. Constr. Build. Mater. 2013, 47, 131–137. [Google Scholar] [CrossRef]
- Bouziani, T. Assessment of fresh properties and compressive strength of self-compacting concrete made with different sand types by mixture design modelling approach. Constr. Build. Mater. 2013, 49, 308–314. [Google Scholar] [CrossRef]
- Yan, W.; Wu, G.; Dong, Z. Optimization of the mix proportion for desert sand concrete based on a statistical model. Constr. Build. Mater. 2019, 226, 469–482. [Google Scholar] [CrossRef]
- Zhang, M.; Zhu, X.; Shi, J.; Liu, B.; He, Z.; Liang, C. Utilization of desert sand in the production of sustainable cement-based materials: A critical review. Constr. Build. Mater. 2022, 327, 127014. [Google Scholar] [CrossRef]
- Shi, Z. Green manufacturing of silicate materials using desert sand as a raw-material resource. Constr. Build. Mater. 2022, 338, 127539. [Google Scholar] [CrossRef]
- GB/T 228-2021; Metallic Materials-Tensile Testing at Ambient Temperature. China Architecture & Building Press: Beijing, China, 2021. (In Chinese)
- JG/T 266-2011; Foamed Concrete. Standards Press of China: Beijing, China, 2011. (In Chinese)
- JGJ/T 421-2018; Technical Standard for Cold-Formed Thin-Walled Steel Multi-Storey Residential Buildings. China Architecture & Building Press: Beijing, China, 2018. (In Chinese)
- Dai, S.; Zuo, Y.; Zhao, X.; Li, P. Research on effect of axial compression ratio on lightweight steel-foam concrete shear wall. Earthq. Resist. Eng. Retrofit. 2021, 43, 32–36. (In Chinese) [Google Scholar]
- Yu, C. Cold-formed steel flexural member with edge stiffened holes: Behavior, optimization, and design. J. Constr. Steel Res. 2012, 71, 210–218. [Google Scholar] [CrossRef]
- Zhao, J.; Sun, K.; Yu, C.; Wang, J. Tests and direct strength design on cold-formed steel channel beams with web holes. Eng. Struct. 2019, 184, 434–446. [Google Scholar] [CrossRef]
- Chen, B.; Roy, K.; Uzzaman, A.; Lim, J.B. Moment capacity of cold-formed channel beams with edge-stiffened web holes, un-stiffened web holes and plain webs. Thin-Walled Struct. 2020, 157, 107070. [Google Scholar] [CrossRef]
- Chen, B.; Roy, K.; Fang, Z.; Uzzaman, A.; Chi, Y.; Lim, J.B. Web crippling capacity of fastened cold-formed steel channels with edge-stiffened web holes, un-stiffened web holes and plain webs under two-flange loading. Thin-Walled Struct. 2021, 163, 107666. [Google Scholar] [CrossRef]
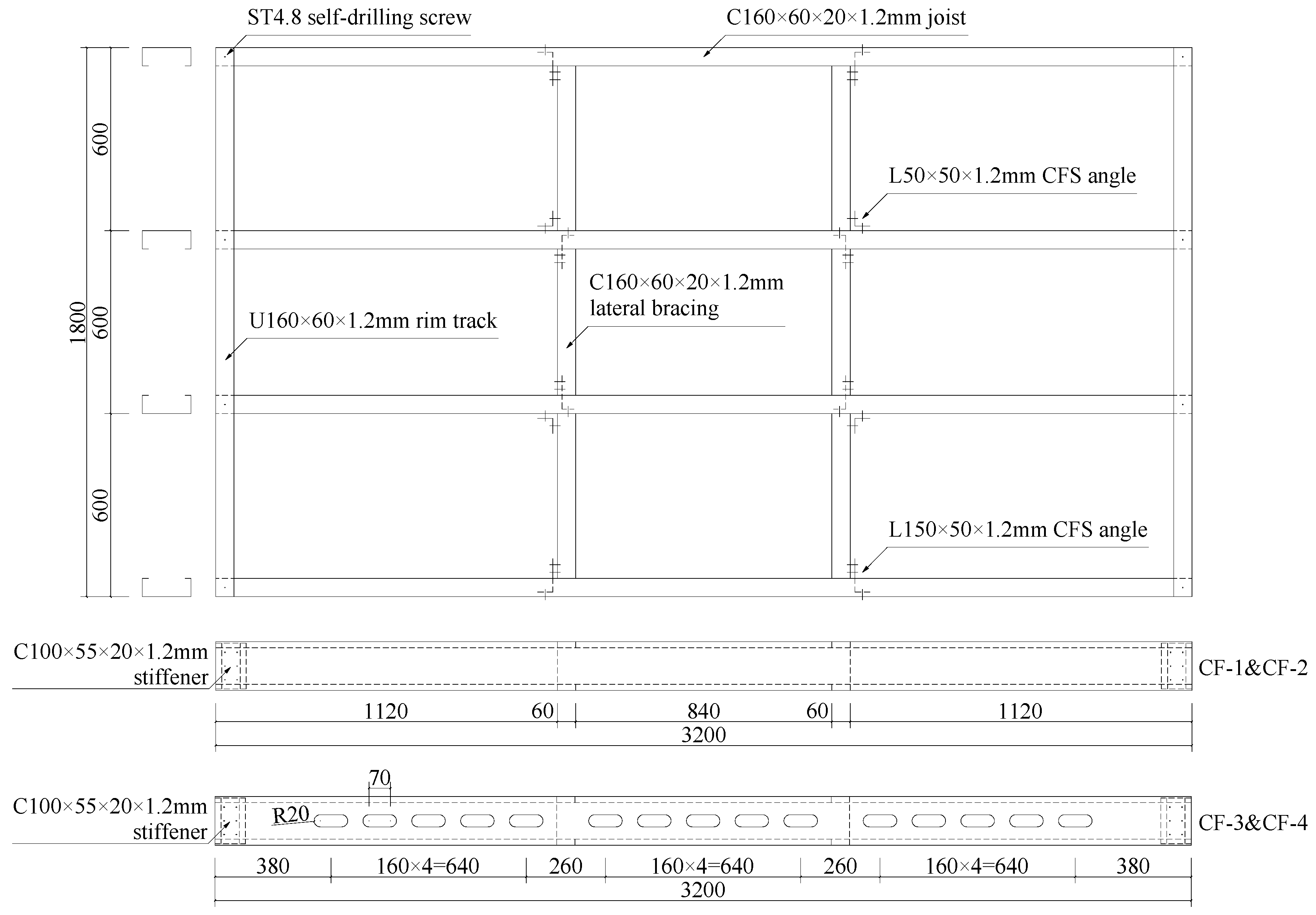







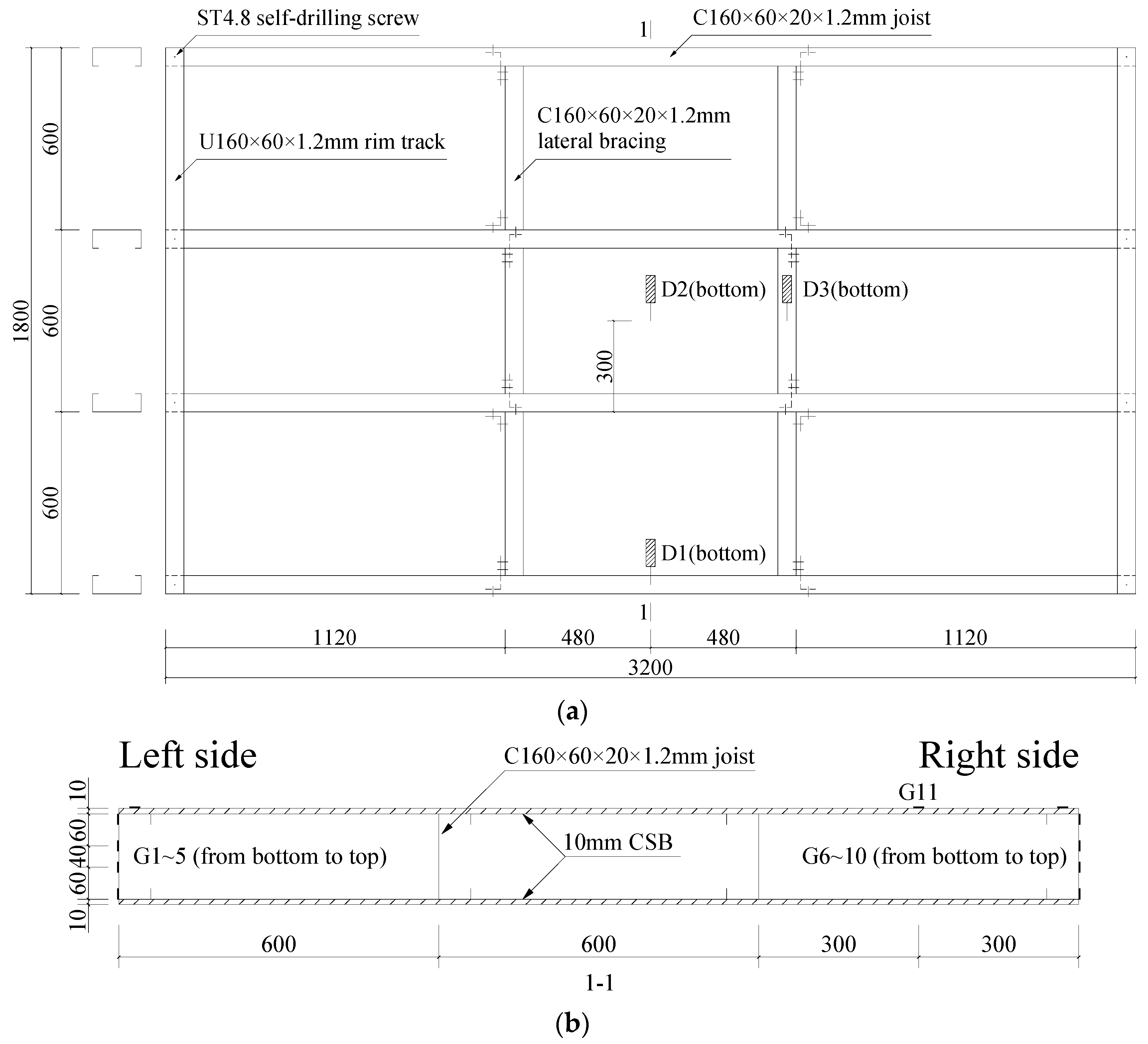











| Specimen | Span (mm) | Width (mm) | Height (mm) | Component |
|---|---|---|---|---|
| CF-1 | 3200 | 1800 | 180 | CFS joists + CSBs |
| CF-2 | 180 | CFS joists + CSBs + DSFC | ||
| CF-3 | 200 | CFS joists with holes + CSBs | ||
| CF-4 | 200 | CFS joists with holes + CSBs + DSFC |
| Thickness (mm) | Elastic Modulus (MPa) | Yield Stress (MPa) | Ultimate Stress (MPa) | Elongation (%) |
|---|---|---|---|---|
| 1.2 | 2.12 × 105 | 594.36 | 601.75 | 16.1 |
| Particle size (μm) | 600 | 300 | 150 | <150 |
| Residue on sieve (%) | 24.4 | 23.4 | 49.2 | 3.0 |
| Cement (g) | Desert Sand (g) | Water (g) | Foam Volume (L) | Water-Reducing Agents (g) | Polypropylene Fiber (g) | Water-Cement Ratio |
|---|---|---|---|---|---|---|
| 450 | 150 | 126 | 1 | 3.6 | 0.9 | 0.28 |
| Density (kg·m−3) | Compressive Strength (MPa) | Elastic Modulus (MPa) |
|---|---|---|
| 1042.0 | 4.80 | 3243.3 |
| Thickness (mm) | Density (g·cm−3) | Flexural Strength (MPa) |
|---|---|---|
| 10.0 | 1.32 | 11.9 |
| Specimen | L/250 (mm) | K (kN/mm) | F250 (mm) | Fp (kN) | Δp (mm) |
|---|---|---|---|---|---|
| CF-1 | 12 | 2.27 | 27.35 | 42.55 | 27.22 |
| CF-2 | 4.94 | 59.33 | 138.25 | 39.77 | |
| CF-3 | 2.61 | 31.43 | 64.76 | 30.06 | |
| CF-4 | 4.53 | 54.45 | 143.64 | 41.50 |
| Dilation Angle | Flow Potential Eccentricity | fb0/fc0 | K | Viscosity Parameter |
|---|---|---|---|---|
| 30° | 0.1 | 1.16 | 0.6667 | 0.0005 |
| Specimen | KFE | RK,t | RK,fc | Fp,FE | RF,t | RF,fc |
|---|---|---|---|---|---|---|
| CF-1.2t-4.8fc | 5.00 | 1.00 | 1.00 | 136.97 | 1.00 | 1.00 |
| CF-1.5t-4.8fc | 5.67 | 1.13 | \ | 162.32 | 1.19 | \ |
| CF-1.8t-4.8fc | 6.34 | 1.27 | \ | 187.51 | 1.37 | \ |
| CF-1.2t-6.4fc | 5.33 | \ | 1.07 | 148.80 | \ | 1.09 |
| CF-1.2t-8.0fc | 5.60 | \ | 1.12 | 158.85 | \ | 1.16 |
| CF-160s-1.2t-4.8fc | 4.71 | 1.00 | 1.00 | 138.28 | 1.00 | 1.00 |
| CF-160s-1.5t-4.8fc | 5.68 | 1.21 | \ | 167.50 | 1.21 | \ |
| CF-160s-1.8t-4.8fc | 6.28 | 1.33 | \ | 196.52 | 1.42 | \ |
| CF-160s-1.2t-6.4fc | 5.06 | \ | 1.07 | 148.06 | \ | 1.07 |
| CF-160s-1.2t-8.0fc | 5.42 | \ | 1.15 | 157.16 | \ | 1.14 |
| CF-320s-1.2t-4.8fc | 4.98 | 1.00 | 1.00 | 139.78 | 1.00 | 1.00 |
| CF-320s-1.5t-4.8fc | 5.80 | 1.16 | \ | 168.72 | 1.21 | \ |
| CF-320s-1.8t-4.8fc | 6.44 | 1.29 | \ | 197.83 | 1.42 | \ |
| CF-320s-1.2t-6.4fc | 5.34 | \ | 1.07 | 150.23 | \ | 1.07 |
| CF-320s-1.2t-8.0fc | 5.63 | \ | 1.13 | 158.98 | \ | 1.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, B.; Shi, Y.; Wang, W.; Wang, Q.; Hu, Z. Flexural Behavior of Cold-Formed Steel Composite Floor Infilled with Desert Sand Foamed Concrete. Buildings 2023, 13, 1217. https://doi.org/10.3390/buildings13051217
Yao B, Shi Y, Wang W, Wang Q, Hu Z. Flexural Behavior of Cold-Formed Steel Composite Floor Infilled with Desert Sand Foamed Concrete. Buildings. 2023; 13(5):1217. https://doi.org/10.3390/buildings13051217
Chicago/Turabian StyleYao, Bin, Yu Shi, Weiyong Wang, Qiang Wang, and Zhiyou Hu. 2023. "Flexural Behavior of Cold-Formed Steel Composite Floor Infilled with Desert Sand Foamed Concrete" Buildings 13, no. 5: 1217. https://doi.org/10.3390/buildings13051217
APA StyleYao, B., Shi, Y., Wang, W., Wang, Q., & Hu, Z. (2023). Flexural Behavior of Cold-Formed Steel Composite Floor Infilled with Desert Sand Foamed Concrete. Buildings, 13(5), 1217. https://doi.org/10.3390/buildings13051217





