Experimental Research on the Mechanical Properties of MURSP-Type Steel-Concrete Composite Beams in Negative-Moment Region

Abstract

To verify the effectiveness of uplift-restricted and slip-permitted (URSP) connectors in alleviating crack formation in the negative-moment region of steel-concrete composite beams (SCCBs) and improve the engineering adaptability of URSP connectors, this paper proposes a modified uplift-restricted and slip-permitted (MURSP) connector. Static load tests and theoretical analysis were conducted on two overhanging beams with MURSP connectors and ordinary studs to analyze the influence of different stud forms on the deflection, crack, and slip of SCCBs in the negative-moment region. Finally, a nonlinear finite element modeling method for MURSP-type steel-concrete composite beams was developed, and a finite element model was established. The results showed that the use of MURSP connectors could effectively alleviate the concrete cracking problem in the negative-moment zone of SCCBs. Compared with the common stud SCCB, the crack load of the MURSP-type SCCB was higher, the maximum crack width was lower, and the crack distribution was more uniform; however, the overall flexural stiffness of the overhanging beam with MURSP connectors was reduced by 3.08%. The interface slip of the overhanging beam with the MURSP connectors increased suddenly in the initial stage of loading, whereas the increase was more gradual in the later stage. The SCCB model established in this study was in good agreement with the results of experimental beams. The finite element analysis results showed that the ordinary stud and MURSP connector exhibited different stress and deformation states in the negative-moment region of SCCBs, and the deformation states changed from bending type to shear type.

1. Introduction

Steel-concrete composite beams (SCCBs) are widely used in bridge structures, particularly in small- and medium-span bridges owing to their excellent mechanical properties. However, the concrete slab is subjected to tension in the negative-moment region of a continuous beam. The concrete in the negative-moment region easily undergoes cracking, which seriously affects the stiffness and durability of bridges.

In order to solve the cracking problem of concrete in the negative-moment region of SCCBs, Nie et al. [1,2] proposed the concept of an uplift-restricted and slip-permitted connector (URSP), wherein a low-elastic modulus material is wrapped around the web and flange of T-shaped steel. Chen et al. [3] studied the slip and mechanical properties of URSP screw-shaped connectors by performing extrapolation tests. The study [4,5,6,7,8] showed that the application of a URSP connector improved the crack resistance and had little influence on the bearing capacity and stiffness. Experimental studies have shown that the relative slip between a concrete slab and a steel beam is high at the bottom of the screw but low at the nut [3]. Since the main function of the low-elastic modulus material is to release the constraint of concrete slip, and the slip at the nut is very small, a modified URSP (MURSP) connector (Figure 1d) is proposed in this paper by wrapping foamed plastics only around the screw and not around the nut. In this paper, the cracking behavior and bending stiffness of MURSP-type SCCBs in the negative-moment region were studied experimentally, and the experimental results were verified by theoretical analysis and finite element calculation.

Figure 1. Structure of the overhanging SCCBs. (a) Negative moment region of a continuous beam. (b) Overturned simply supported beam. (c) Overhanging beam. (d) Dimensions of the test specimen.

In terms of experimental research, many scholars have conducted experimental studies on the mechanical properties of SCCBs in the negative-moment region [9,10,11,12,13,14]. In these studies, simply supported beams were subjected to mid-span reverse loading to simulate the stress state in the negative-moment region(Figure 1b). In this paper, an overhanging beam(Figure 1c) was used to simulate the mechanical behavior in the negative-moment region of the composite beam, and it was considered that this method was more consistent with the actual stress state.

In terms of theoretical analysis and finite element analysis, Alexandre Rossi [15] numerically analyzed the buckling and post-buckling using the ABAQUS software to evaluate the behavior of an SCCB under the influence of a hogging moment. Lou [16] established a nonlinear model of a two-span prestressed steel-concrete composite beam, evaluated its flexural performance, and quantified its secondary bending moment. Zhu [17] studied the transverse performance of a composite box girder considering compressive membrane action and proposed a new calculation method to evaluate the load capacity of a composite box girder with different boundary conditions. Based on the principle of virtual work and the variational method, Dezi et al. [18] proposed a theoretical model l for analyzing the shear-lag effect in composite beams. At present, these research projects focus more on the mechanical properties of composite beams and less on the connectors between steel beams and concrete slab.

In order to verify that the proposed MURSP connector could increase the cracking moment of concrete in composite beams, static tests were carried out on two steel-concrete composite overhanging beams, one of which was made of ordinary studs and the other of MURSP connectors. This study kept a watchful eye on the influence of different connectors on crack propagation and stiffness variation in the negative moment zone of composite beams. The experimental results were verified by theoretical analysis, and calculation methods of both the cracking moment and bending stiffness in the negative-moment region of MURSP composite beams are proposed. Furthermore, an elaborate finite element model of the test beam was established, and the mechanical properties of the MURSP connector were analyzed.

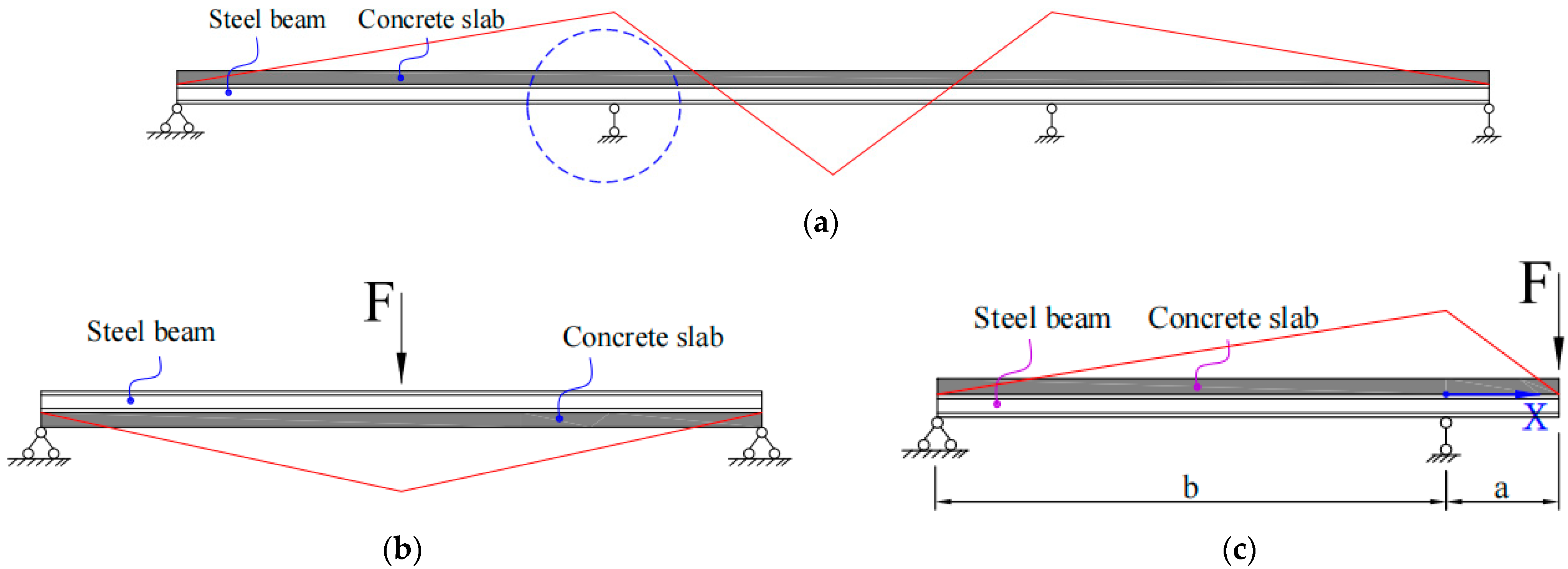
2. Test Design

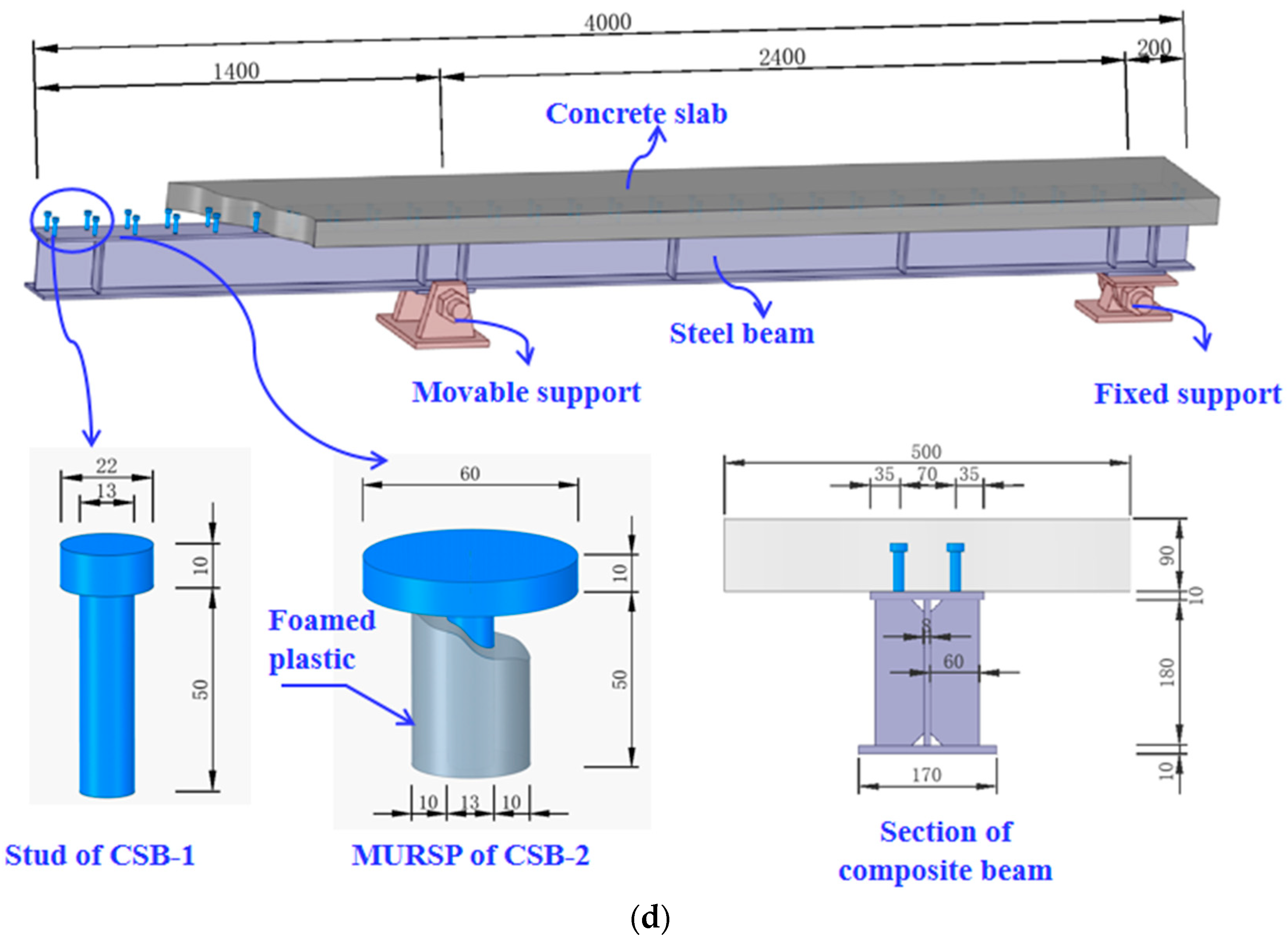
2.1. Test Specimens

In this study, two steel-concrete composite overhanging beams were designed, numbered CSB-1 and CSB-2. Ordinary studs were used in CSB-1, and MURSP connectors were used in CSB-2. Figure 1d shows the specimens. The diameter of the internal longitudinal reinforcement was 10 mm, and the distance was 75 mm. The diameter of the transverse reinforcement was 6 mm, and the distance was 100 mm. The concrete slab and the steel beam were connected by studs, with a longitudinal distance of 140 mm and a transverse distance of 70 mm. It should be noted that although CSB-1 and CSB-2 use different connectors, their dimensions are the same, as shown in Figure 1d.

2.2. Material Properties

The strength grades of the concrete used for slabs were C50. Three groups (nine blocks in total) of 150 mm × 150 mm × 150 mm test cubes were kept to measure the compressive strength of the concrete. Six blocks of 150 mm × 150 mm × 300 mm prismatic test blocks were kept for measuring the elastic modulus of concrete, and three blocks of 150 mm × 150 mm × 550 mm test blocks were kept for measuring the tensile strength of concrete, see Figure 2. After pouring, the test beams and test blocks were cured in high-temperature steam under the same conditions. The concrete used for the two test beams was poured simultaneously. Table 1 presents the measured properties of the concrete material [19].

Figure 2. Mechanical property test of concrete. (a) Cube compressive strength. (b) Bending and tensile strength. (c) Elastic Modulus.

Table 1. Mechanical properties of concrete.

Component	Material	Elastic Modulus EC/MPa	Cube Compressive Strength fcu/MPa	Bending and Tensile Strength ft/MPa
Concrete	C50	4.113 × 104	53.95	4.728

Table 2 presents the measured properties of the steel bar and steel [20,21]. The strength grade of the steel beams in the specimen was Q345D, and the strength grade of longitudinal reinforcement and transversal reinforcement were HPB400 and HRB300, respectively. The connectors were made of ML15 steel, which is produced and welded in accordance with Chinese specifications [22,23].

Table 2. Mechanical properties of the steel bar and steel beam.

Component	Material	Thickness or Diameter/mm	Yield Strength fy/MPa	Ultimate Tensile Strength fu/MPa	Elongation
Steel beam	Q355D	10	415	536	30%
		8	441	571	25.5%
Steel bar	HRB400	10	451	668	21%
	HPB300	6	334	478	25%

2.3. Loading Procedure

The test beam was supported at moving support and fixed support. The concentrated load was applied to the end of the overhanging beam. Figure 3 illustrates the loading device at the test site. In order to simulate the force condition in the negative-moment region of the composite beam as truly as possible, a fixed support was used at the end of the beam, and a movable support was used at the other position. The fixed support limited the displacement of the beam in three directions but did not limit the rotation, while the moveable support only limited the vertical movement of the beam. When the overhanging end was loaded, the composite beam inclined downward, and the concrete top surface was no longer horizontal. A loading device was designed using fixed support at the loading point to make the load more uniform. When loading, the fixed support could rotate with the tilt of the overhanging end so that the applied load was always kept vertically down.

Figure 3. Experimental setup.

2.4. Test Procedure

In this test, the mechanical properties of SCCBs in the negative-moment region were mainly studied. Gauges of deflection, slip, and strain were arranged in the negative-moment region, as shown in Figure 4, where P represented the measurement point of interface slip, D represented the measurement point of vertical displacement, and W represented the measuring point of stud strain. Strain gauges of concrete, steel beam, and steel bar were arranged at Sections 2-2, 3-3, and 4-4. Figure 4b only shows the arrangement of gauges for Section 2-2, and the arrangement of the other two sections is the same as that of Section 2-2, where C represents the measuring point of concrete strain, S stands for the measuring point of steel beam strain, and R represents the measuring point of reinforcement strain.

Figure 4. Instrumentation arrangement on a specimen. (a) Gauges of deflection, slip, and strain of studs. (b) Strain gauges of concrete, steel beam, and steel bar at Section 2-2.

3. Experimental Results and Theoretical Derivation

3.1. Test Phenomena

3.1.1. Test Phenomena of CSB-1

At the beginning of the formal loading of CSB-1, the deflection of the overhanging end increased gradually with increasing load. When the load was 34 kN, the first crack appeared in the concrete slab at the top of the movable support. With the increasing load, the length and number of cracks increased. After loading to 180 kN, the lower flange of the steel beam gradually buckled. Further, the displacement of the overhanging end increased gradually while the load increased a small amount. Finally, the load could not be increased, and the test was over.

3.1.2. Test Phenomena of CSB-2

At the beginning of the formal loading of CSB-2, there was a tearing sound, indicating that the bond at the interface between the concrete and steel beam had been broken at this time. When the load was 48 kN, the first crack appeared in the concrete slab at the top of the movable support. With increasing load, the length and number of cracks continued to expand, and the cracks were gradually connected; however, the crack width increased gradually. During the test, the deflection of the overhanging end increased gradually with the increase of the load, and the concrete slab did not lift. When the load was increased to 170 kN, the deflection of the overhanging end reached 45 mm, which is unsuitable for continuous loading. At this point, the loading was terminated.

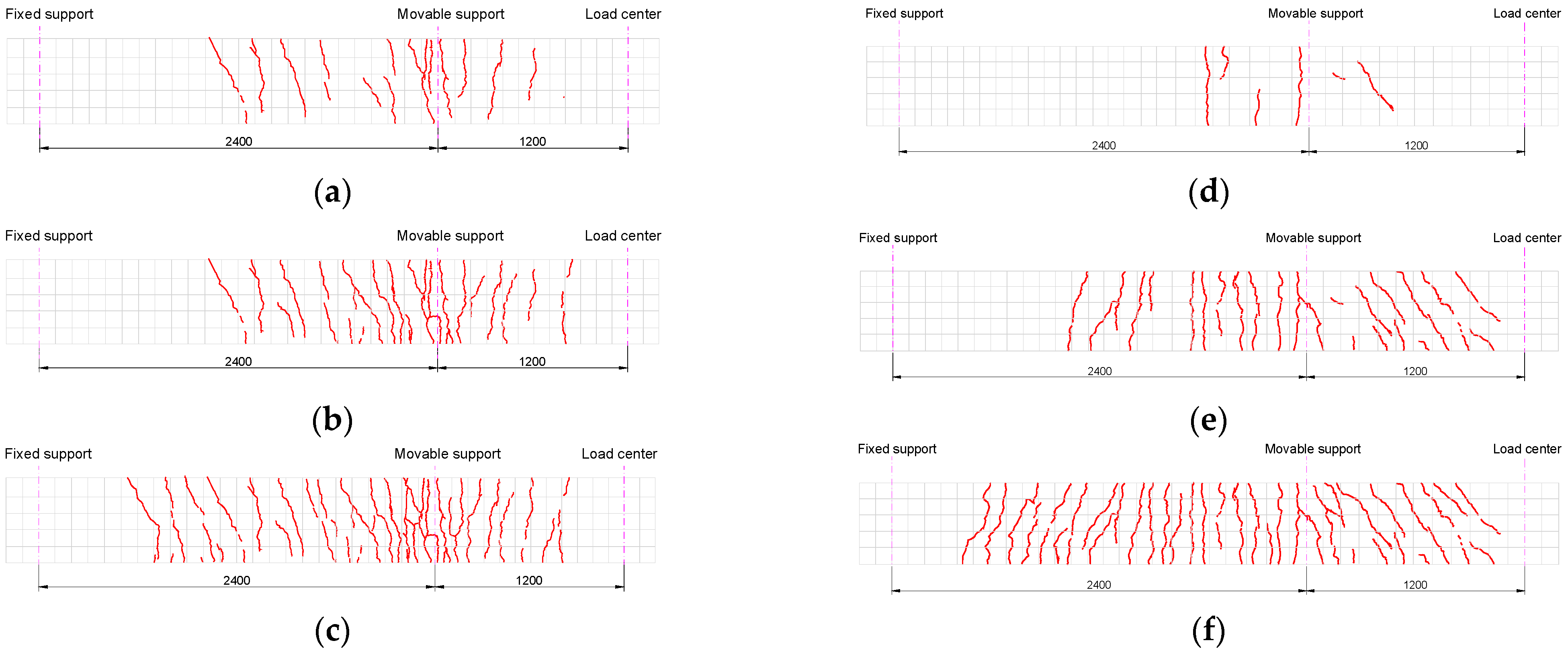
3.2. Crack Analysis

Figure 5 shows the crack distribution at each stage of loading. The cracks in the two beams gradually extended from the top of the movable support to both sides. At the end of loading, the cracks in CSB-1 were concentrated at the top of the movable support. The cracks in CSB-1 gradually expanded and connected, forming a dense fracture network at the top of the moveable support. In contrast, the crack distribution of CSB-2 was more uniform, and the crack spacing was approximately 100 mm.

Figure 5. Crack distribution. (a) CSB-1 60 kN. (b) CSB-1 100 kN. (c) CSB-1 170 kN. (d) CSB-2 60 kN. (e) CSB-2 100 kN. (f) CSB-2 170 kN.

When CSB-1 was loaded to 34 kN, the first crack appeared in the concrete slab at the top of the movable support, and then the number of cracks gradually increased. CSB-2 was loaded to 48 kN with the first crack at the top of the movable support. The crack load of CSB-2 was approximately 14 kN greater than that of CSB-1. According to the test results, the cracking moment of concrete in the negative bending moment region could be increased by 41% by using the MURSP connector. Theoretically, the derivation of the cracking moment of the common stud composite beam and MURSP composite beam was conducted in Section 3.5.1, and the same conclusion was obtained as in the test.

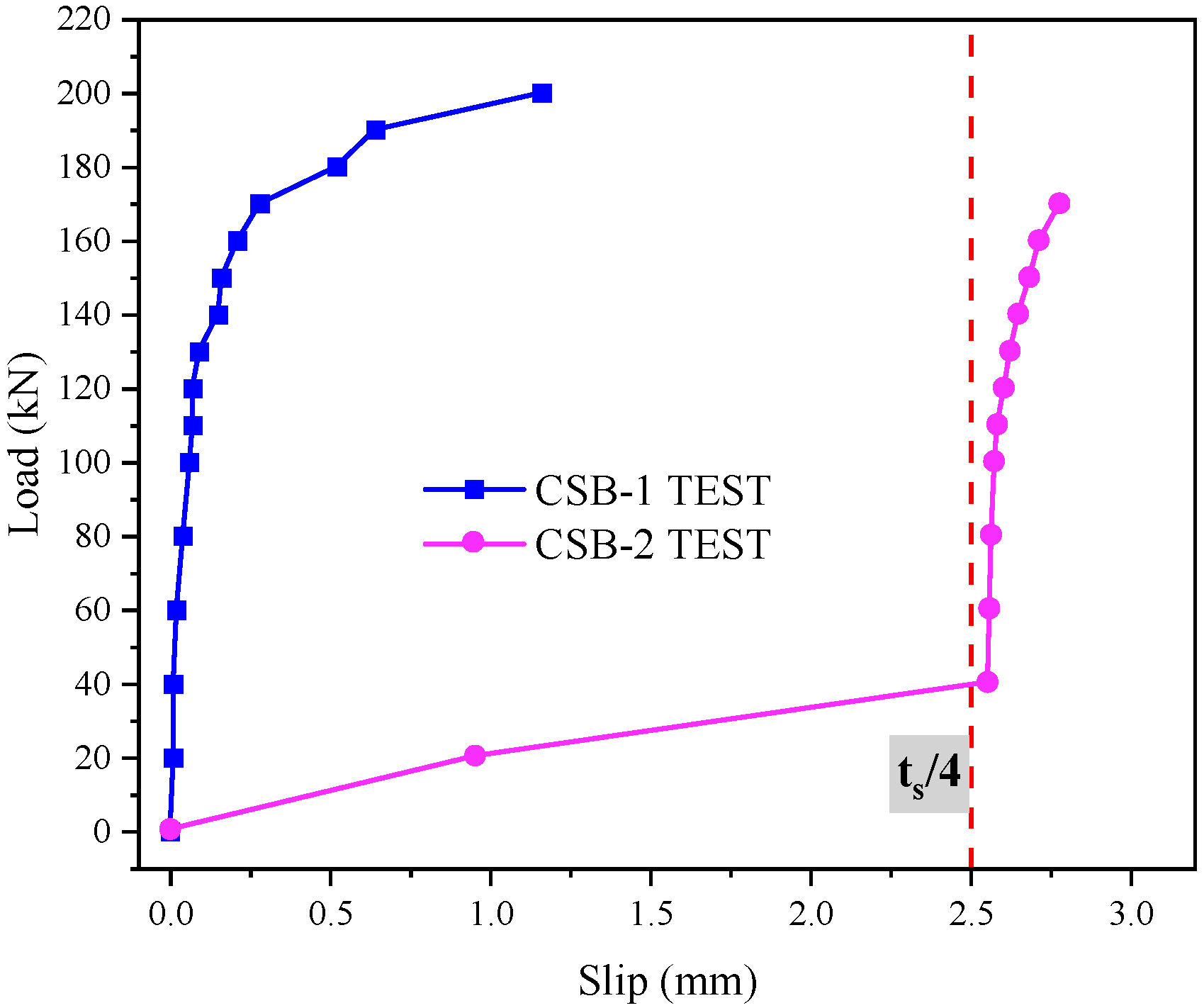
3.3. Interface Slip Analysis

Figure 6 shows the slip values at the overhanging ends of CSB-1 and CSB-2. In the initial stage of loading, there was a small slip in CSB-1, and the slip was in a linear relationship with the load. When the load was 130 kN, the slip value was only 0.09 mm. In the middle stage of loading, the steel beam gradually yielded, the slip increased significantly, and the slip value no longer maintained a linear relationship with the load. In the late loading stage, the slip value increased rapidly, and the test beam entered the strengthening stage. CSB-2 had a different slip rule from CSB-1. In the initial stage of loading (approximately 30 kN), a tearing sound could be heard, and the interface slip speed increased rapidly. When the load was 40 kN, the slip value reached 2.56 mm. This phenomenon has also been experimentally observed by Nie [24]. Subsequently, with increasing load, the slip value increased gradually. When the load was 170 kN, the slip value was 2.785 mm.

Figure 6. Load–slip curves.

For CSB-2, the load–slip curve is roughly consistent with the model proposed by Han SW [25]. The whole curve includes four stages: (1) Elastic stage (δ ⩽ δ₀), (2) Slip stage (δ₀ < δ ⩽ t_s/4), (3) Stud-like stage (t_s/4 < δ ⩽ δ_u), and (4) Ultimate stage (δ_u < δ < δ_f), where t_s represents the thickness of foamed plastics. In the first stage of loading, the shear stress on the interface between the concrete and steel beam was borne by the bond between the two. There is a linear relationship between load and slip, but the duration of this stage was very short. In the second stage, the bond between the steel beam and the concrete slab was broken, and the interface slid significantly. In this stage, due to the wrapping of the low elastic mold material, there is a large slip between the concrete and the steel beam, and the stud does not bear the shear force. The maximum slip value was about 1/4 of the thickness of the foam plastic. Therefore, in the initial stage of loading (approximately 30 kN), a tearing sound could be heard, indicating that the bond at the interface between the concrete and steel beam had been broken at this time. At the third stage, the foamed plastics could no longer be compressed, and the interface slip increased slowly with the increase of load. The slip growth law of this stage was similar to that of the initial stage of CSB-1. In the fourth stage, the stress of the stud gradually reached the shear strength and the stud was cut off.

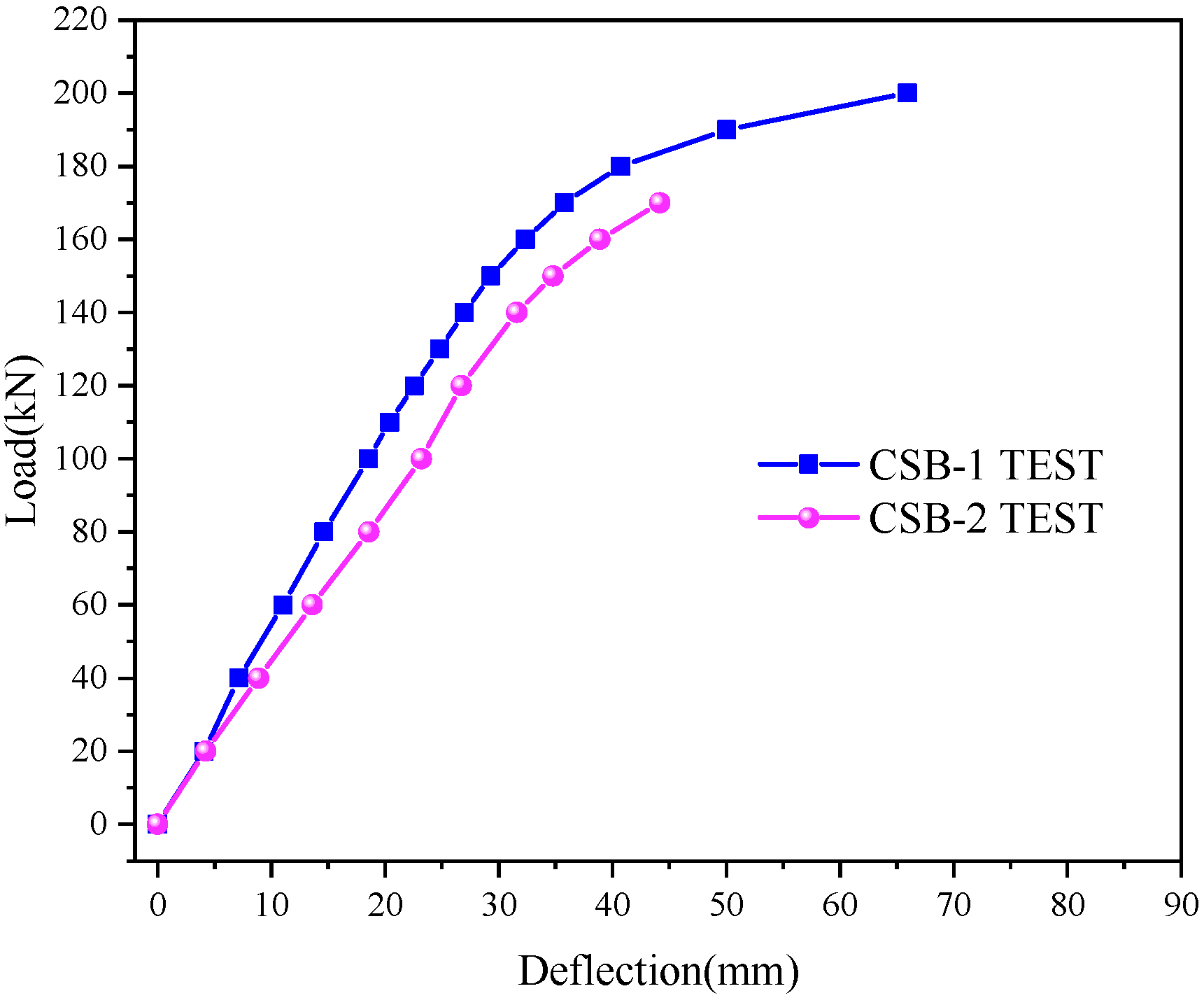
3.4. Load–Deflection Curves

Figure 7 shows the relationship between the load and the deflection of the overhanging end of the two test beams. Based on the test results, the loading process can be divided into three stages: elastic stage, yield stage, and strengthening stage. In the first stage, no cracks were formed in the concrete slab, and the load and deflection increased linearly. In the yield stage, cracks appeared in the concrete, the load and deflection were no longer linear, and the stiffness of the composite beams decreased to a certain extent. In the third stage, the bottom flange of the steel beam gradually buckled, and the deflection increased rapidly. As shown in Figure 7, the secant slopes of CSB-1 and CSB-2 were 4.87 and 4.72 in the initial stage, respectively. The overall bending stiffness of CSB-2 decreased by 3.08% compared with that of CSB-1. When the load was 140 kN, the secant slopes of CSB-1 and CSB-2 were 5.09 and 4.68, respectively, and the overall stiffness of CSB-2 was reduced by 8.06% compared with that of CSB-1. In general, the application of the MURSP connector had little influence on the stiffness of the composite beam [5]. The main reason for the reduction of the stiffness of CSB-2 is the increase of the interface slip between the steel beam and the concrete slab, which will be verified by theoretical derivation in Section 3.5.2.

Figure 7. Load–deflection curves.

It should be noted that the failure states of composite beams were different. At the end of the static load test of CSB-1, the bottom flange of the steel beam appeared to be buckling, and the load at this time was 210 kN, as shown in Figure 8. At the end of the static load test of CSB-2, the load was 170 kN, and the deflection of overhanging end reached 45 mm, which is unsuitable for further loading.

Figure 8. Buckling of the bottom flange of CSB-1.

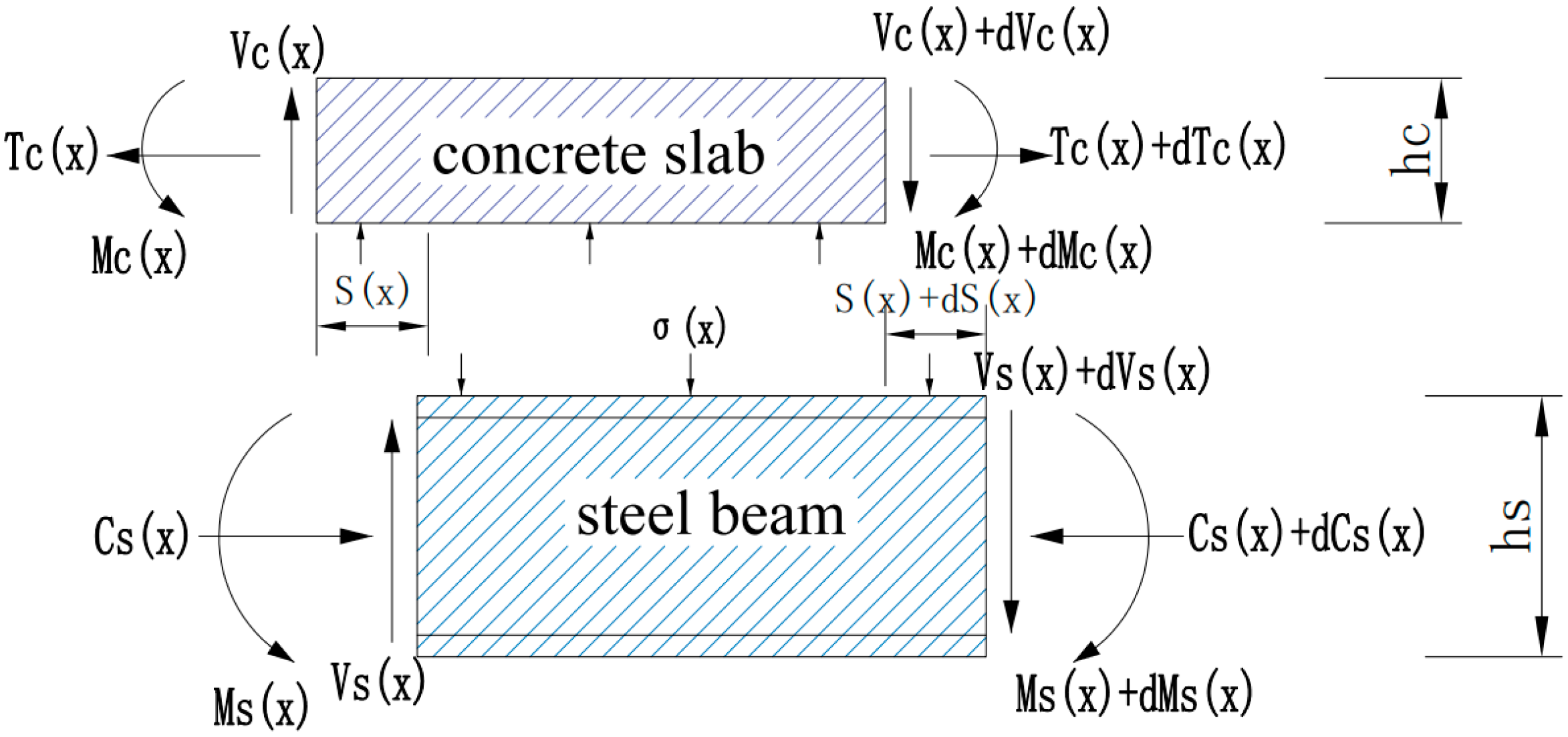
3.5. Theoretical Derivation

In order to analyze the interface slip, crack, and deformation of MURSP-type steel-concrete composite beams in the negative-moment region, the interface slip model of the composite beam was established, as shown in Figure 9.

Figure 9. Internal force distribution in a microsegment of the beam.

According to the mechanical equilibrium relationship of the x-direction of the microsegment, the following equation can be obtained.

$$d{T}_c(x)=0$$

(1)

$$d{C}_s(x)=0$$

(2)

where $T_c$ is the tension on the section of the concrete slab and $C_s$ is the pressure on the section of the steel beam. Because $T_c(a)=T_c(-b)=0$ and $C_s(a)=C_s(-b)=0$, $T_c(x)=C_s(x)=0$.

The curvature of the steel beam and concrete slab can be expressed using the following formula:

$${\varphi }_1(x)=\frac{M_c(x)}{E_c{I}_c}=\frac{M_s(x)}{E_s{I}_s}=\frac{M(x)}{E_s{I}_0}$$

(3)

where $M\left(x\right)$ is the bending moment at the coordinate x, $M_c$ is the bending moment of the concrete slab, $M_s$ is the bending moment of the steel beam, and $I_0$ is the cross-section equivalent moment of inertia.

The longitudinal strain at the bottom of the concrete slab and the top of the steel beam can be calculated by the bending moment and axial force of the section and expressed as follows:

$${\epsilon }_{cb}(x)=-\frac{M_c(x)h_c}{2E_c{I}_c}+\frac{T_c(x)}{E_c{A}_C}=-\frac{h_c}{2}\varphi (x)$$

(4)

$${\epsilon }_{st}(x)=\frac{M_s(x)h_s}{2E_s{I}_s}-\frac{C_s(x)}{E_s{A}_s}=\frac{h_s}{2}\varphi (x)$$

(5)

where $A_c$ is the sectional area of the concrete slab and $A_s$ is the sectional area of the steel beam.

The relative slip strain between the concrete slab and the steel beam can be calculated by the following formula:

$${\epsilon }_s(x)=\frac{dS(x)}{dx}={\epsilon }_{st}(x)-{\epsilon }_{cb}(x)=\frac{h}{2}\varphi (x)$$

(6)

where $S\left(x\right)$ is the relative slip at the interface between concrete and the steel beam.

Assuming that the vertical force exerted by the overhanging end is F, the bending moment of the test beam can be expressed as:

$$\left\{\begin{array}{l}-b\le x\le 0\hspace{0.33em}\hspace{0.33em}M(x)=\frac{Fa}{b}(b+x)\\ 0\le x\le a\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}M(x)=F(a-x)\end{array}\right.$$

(7)

By substituting the bending moment into Equation (6) and integrating, the interface slip is:

$$\left\{\begin{array}{l}-b\le x\le 0\hspace{0.33em}\hspace{0.33em}S(x)=\frac{hFa}{4b{E}_s{I}_0}(2bx+x^2)+A_1\\ 0\le x\le a\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}S(x)=\frac{hF}{4E_s{I}_0}(2ax-x^2)+A_2\end{array}\right.$$

(8)

The boundary conditions can be expressed as follows:

$$\left\{\begin{array}{l}S(x){|}_{x=0^{+}}=S(x){|}_{x=0^{-}}\\ S(x){|}_{x=-0.423b}=0\end{array}\right.$$

(9)

Substituting Equation (9) into Equation (8), the following equation is obtained:

$$A_1=A_2=\frac{0.667hFab}{4E_s{I}_0}$$

(10)

By substituting Equation (10) into Equation (8) and then substituting Equation (8) into Equation (6), the following equation can be obtained:

$$\left\{\begin{array}{l}-b\le x\le 0\hspace{0.33em}{\epsilon }_s=\frac{d{S}_1(x)}{dx}=\frac{h{F}_{1}a}{2b{E}_s{I}_0}(b+x)\\ 0\le x\le a\hspace{0.33em}\hspace{0.33em}\hspace{0.17em}{\epsilon }_s=\frac{d{S}_1(x)}{dx}=\frac{h{F}_1}{2E_s{I}_0}(a-x)\end{array}\right.$$

(11)

3.5.1. Cracking Moment of Concrete

The longitudinal strain at the top of the concrete slab above the movable support of CSB-2 can be expressed as:

$${\epsilon }_{ct}(0)=\frac{M_c(0)h_c}{2E_c{I}_c}=\frac{M(0)h_c}{2E_s{I}_0}=\frac{Fa{h}_c}{2E_s{I}_0}$$

(12)

Assuming that the ultimate tensile strain of concrete is ${\epsilon }_{cr}$, the cracking moment of concrete of CSB-2 can be expressed as:

$$M_{cr}=\frac{2E_s{I}_0{\epsilon }_{cr}}{h_c}$$

(13)

The longitudinal strain at the top of the concrete slab above the movable support of CSB-1 can be calculated according to [20]:

$${\epsilon }_{ct}(0)=\frac{M(0)h_c}{2E_s{I}_0}+\frac{T_c(0)}{E_c{A}_c}$$

(14)

The cracking moment of concrete of CSB-1 can be expressed as:

$$M_{cr}=\frac{2E_s{I}_0}{h_c}({\epsilon }_{cr}-\frac{T_c(0)}{E_c{A}_c})$$

(15)

The cracking moment calculated by Equations (13) and (15) is shown in Table 3. The following conclusions can be drawn from Table 3:

Table 3. Comparison of the cracking moment.

Number of the Test Beams	Test Value of Cracking Moment (kN·m)	Calculated Value of Cracking Moment (kN·m)	Percentage Difference
CSB-1	40.8	38.7	5.147%
CSB-2	57.6	49.33	14.41%

(1)

The calculated values are in good agreement with the test values, indicating that the method proposed in this paper can accurately calculate the cracking moment in the negative moment region of the composite beam.

(2)

Compared with the composite beam with ordinary studs, the cracking moment of concrete can be improved by using MURSP connectors in the negative bending moment region.

3.5.2. Additional Deflection

According to the mechanics of materials, the relation between the additional deflection and the slip strain of the section can be expressed as:

$$\frac{d^2\Delta f(x)}{d{x}^2}=\frac{\Delta M\left(x\right)}{E_s{I}_0}=\frac{{\epsilon }_s(x)}{h}$$

(16)

where $\Delta f(x)$ is the additional deflection due to relative slip.

By substituting Equation (11) into Equation (16) and integrating twice, the additional deflection of CSB-2 is obtained, as shown in Equation (17):

$$\left\{\begin{array}{l}-b\le x\le 0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\Delta f(x)=\frac{Fa}{12b{E}_s{I}_0}(3b{x}^2+x^3)+E_{1}x+E_2\\ 0\le x\le a\hspace{0.33em}\hspace{0.17em}\hspace{0.33em}\hspace{0.33em}\Delta f(x)=\frac{F}{12E_s{I}_0}(3a{x}^2-x^3)+E_{3}x+E_4\end{array}\right.$$

(17)

The following boundary conditions are considered:

$$\left\{\begin{array}{l}\Delta f(x){|}_{x=0}=0\\ \frac{d\Delta f(x)}{dx}{|}_{x=0^{-}}=\frac{d\Delta f(x)}{dx}{|}_{x=0^{+}}\\ \Delta f(x){|}_{x=-b}=0\end{array}\right.$$

(18)

Substituting Equation (18) into Equation (17), the following equation is obtained:

$$\left\{\begin{array}{l}{E}_1=E_3=\frac{Fab}{6E_s{I}_0}\\ E_2=E_4=0\end{array}\right.$$

(19)

Additional deflection of CSB-1 can be calculated according to [20].

The deflection in the negative moment region of composite beams considering concrete cracking and interface slip can be expressed as follows. The linear stiffness reduction method proposed in reference [20] is used to consider the influence of concrete cracking when calculating $f(x)$.

$$f_a(x)=f(x)+\Delta f(x)$$

(20)

Figure 10 shows a comparison between the test and calculated values of deflection. Before the load value of CSB-1 is 180 kN, and before the load value of CSB-2 is 160 kN, the calculated deflection is in good agreement with the test deflection. After that, the composite beam enters the strengthening stage, the steel beam gradually bends, and the test value differs greatly from the calculated value. This method can be used to calculate the deflection of composite beams in normal service conditions because the nonlinear properties of materials are not considered in the calculation.

Figure 10. Comparison of calculated and tested deflection of the overhanging end. (a) CSB-1. (b) CSB-2.

4. Numerical Analyses

4.1. Analysis Step

To ensure the reliability of the test results and to further study the mechanical properties of the MURSP connectors, 3D finite element models were established. Considering the nonlinearity of the material, geometry and contact, a static analysis of the composite beams was conducted. The steps of numerical analysis are as follows:

(1)

Establish the solid models of steel beam, MURSP connectors, concrete slab and reinforcements according to the dimensions of the test beam.

(2)

Assign the material properties of steel beam, MURSP connectors, concrete slab and reinforcements, respectively.

(3)

Divide all solid models into finite elements.

(4)

Determine the contact between reinforcement and concrete, MURSP connectors and concrete, and concrete and steel beam.

(5)

Apply the load to the overhanging end of the overhanging beam and then calculate.

(6)

Compare the calculation results with the test results to verify the accuracy of the finite element model.

(7)

Analyze the mechanical properties of the MURSP connectors.

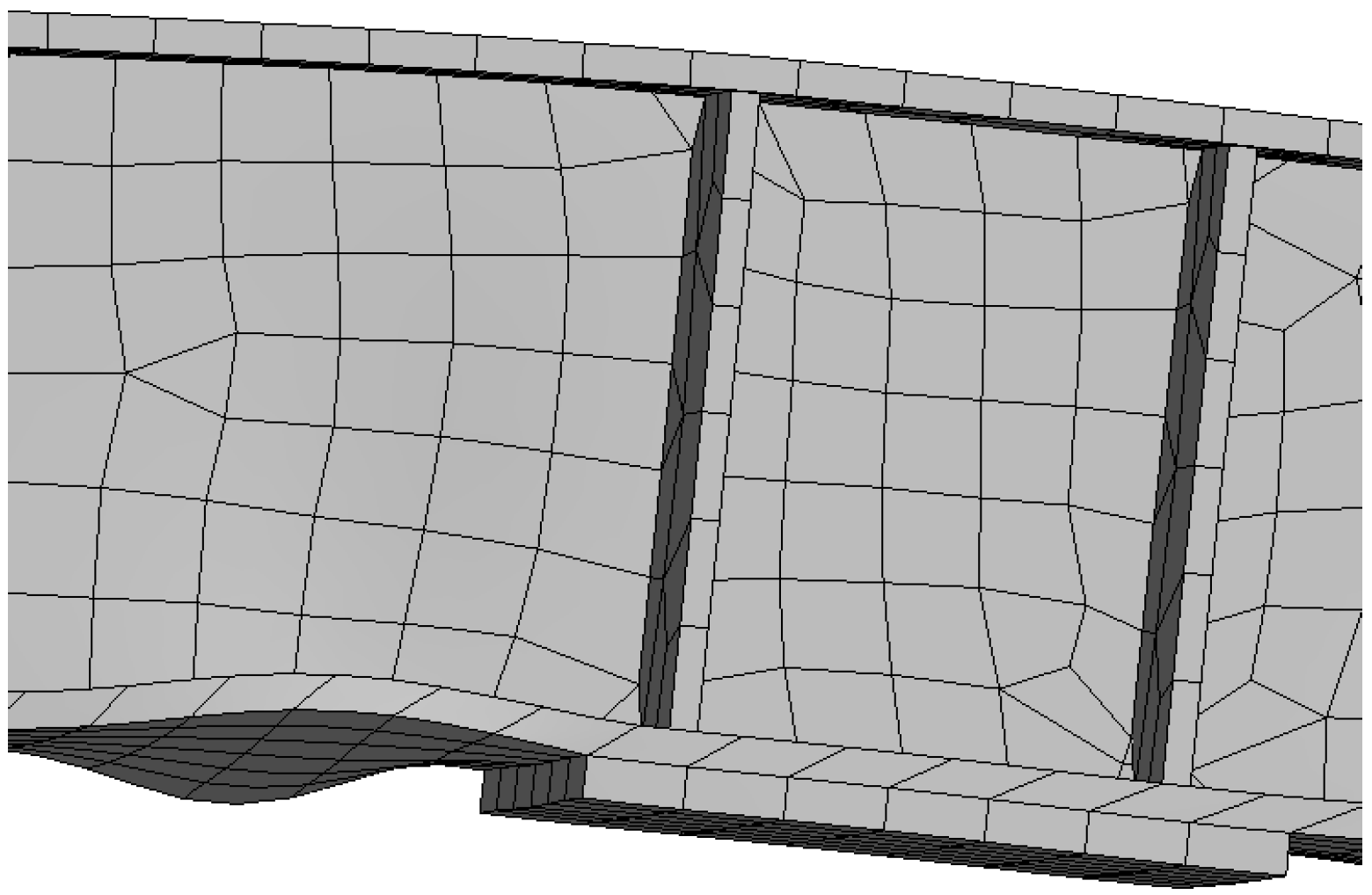
4.2. Finite Element Model

4.2.1. Element Types

Three-dimensional FE models of CSB-1 and CSB-2 were developed using the commercial software ANSYS. Concrete slab, steel beam, support, and studs were simulated by solid elements SOLID186/187. The steel bars were simulated by BEAM188.

In order to obtain the correct calculation results, the convergence of the mesh was analyzed, and the deflection of the overhang and the stress of the stud under different mesh were compared, as shown in Table 4. By comparison, when the size of the concrete element was less than 24 mm, and the size of the stud element was less than 12 mm, a stable calculation result could be obtained. In this paper, the size of the concrete elements was 20 mm, the size of the steel beam elements was 30 mm, and the size of the stud elements was 10 mm.

Table 4. Comparison of calculation results when the load is 100kN.

Size of the Elements	Concrete 28 mm Studs 14 mm	Concrete 24 mm Studs 12 mm	Concrete 20 Studs 10 mm
Deflection of the overhang/mm	22.156	23.532	23.724
Maximum strain of stud/(με)	1.745 × 10−3	1.924 × 10−3	1.987 × 10−3

4.2.2. Material Properties

The uniaxial compression and uniaxial tensile stress-strain curves of concrete specified in Chinese standard (GB 50010-2010) were adopted as the constitutive relation curve of concrete [26], as shown in Figure 11. The multilinear kinematic hardening criterion was adopted as the constitutive relationship of concrete, and the parameters are shown in Table 1. It was considered that steel is an ideal uniform material, so the bilinear kinematic (BKIN) model was adopted for the steel beams, steel bars and studs. Table 2 presents the specific parameters.

Figure 11. Stress-strain curve of concrete. (a) The compressive stress-strain curve. (b) The tensile stress-strain curve.

The foamed plastics were simulated using Mooney–Rivlin’s three-parameter elastomer model. The elastic strain energy can be expressed as in Equation (1), and the parameters were C₁₀ = 59.27 MPa, C₀₁ = −44.74 MPa, C₁₁ = 8.99 MPa and D₁ = 5.26 × 10⁻⁴ MPa⁻¹ [27,28].

$$W=C_{10}\left({\overline{I}}_1-3\right)+C_{01}\left({\overline{I}}_2-3\right)+C_{11}\left({\overline{I}}_1-3\right)\left({\overline{I}}_2-3\right)+\frac{1}{D_1}{\left(J-1\right)}^2$$

(21)

4.2.3. Contact

The relationship between the adjacent parts of the FE model was set by “contact” in ANSYS. “Frictional” contact was used between the bottom of the steel beam and the roller shaft at the top of the movable support [29,30,31]. The friction coefficient was set to 0.2, and hard contact was adopted in the normal direction to ensure no penetration between each other. “Frictional” contact was used to simulate the relationship between concrete and studs, and the friction coefficient was set to 0.2. The bottom of the concrete slab and the top of the steel beam were also simulated by “Frictional” contact. The steel bar and concrete were considered to be bound together, and the slip between them was ignored. Therefore, “Bonded” contact was used to describe the relationship between steel and concrete. “Bonded” contact was also used to simulate the relationship between foamed plastics and studs. “Frictionless” contact was used to simulate the relationship between the nut and the upper flange of the steel beam.

4.2.4. Boundary Condition and Loading Application

The displacement in the three directions was constrained at the fixed support, and the vertical displacement was constrained at the movable support. In order to make the calculation result converge more easily, a vertical displacement was applied to the overhanging end of the beam. Both material nonlinearity and geometric nonlinearity were considered in the calculation. The experimental loading through the hydraulic actuator on the beam was applied by increasing the displacement of the overhanging end (acting vertically downwards) until complete specimen failure.

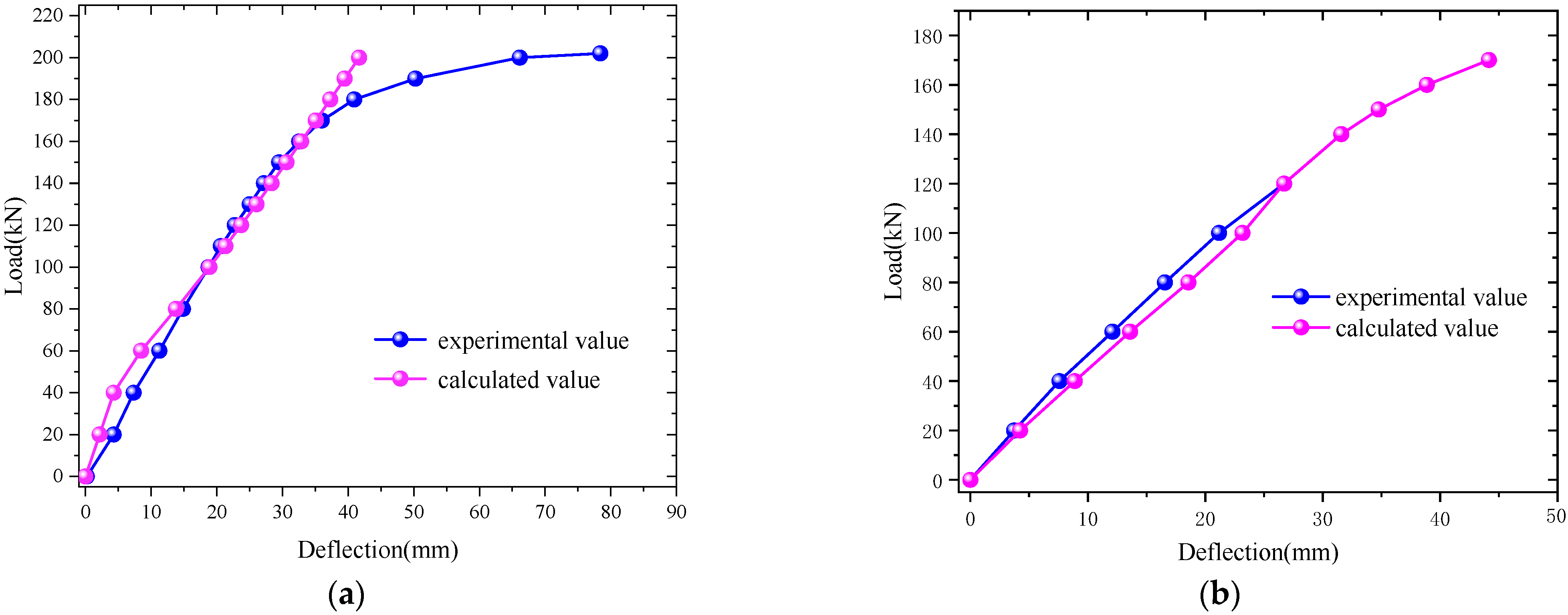
4.3. Comparison of Calculation Results

4.3.1. Failure Mode

Figure 12 shows the failure mode of CSB-1 by finite element calculation. The bottom flange of the steel beam of the two models gradually yielded from the loading of 180 kN. The failure mode of the finite element model is exactly the same as the experimental results (Figure 8).

Figure 12. Buckling of the steel beam of CSB-1.

4.3.2. Load–Deflection Curves

Figure 13 shows the load–deflection curves of the finite element models and the test beams. Clearly, the load–deflection curves of the finite element model were in good agreement with the experimental values, proving the accuracy of the established finite element model.

Figure 13. The overhanging end deflection of test value and FEM calculated value of CSB-2.

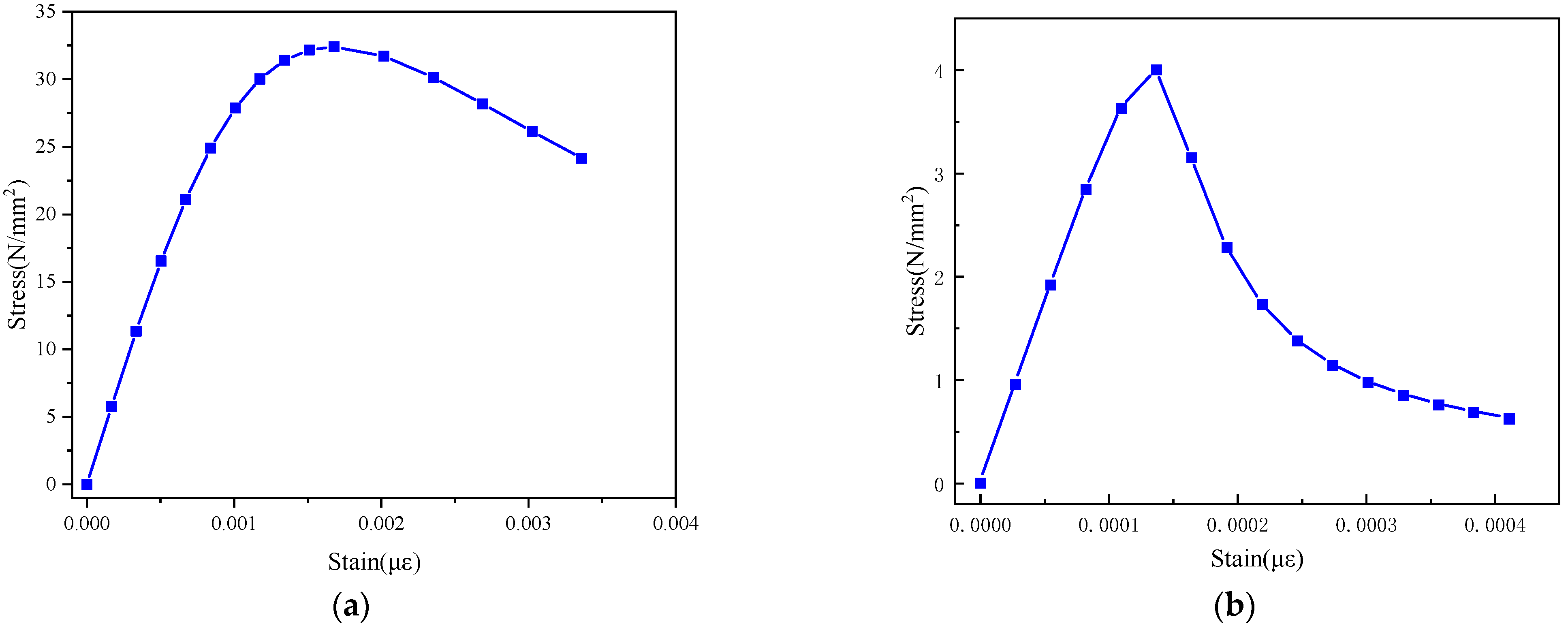
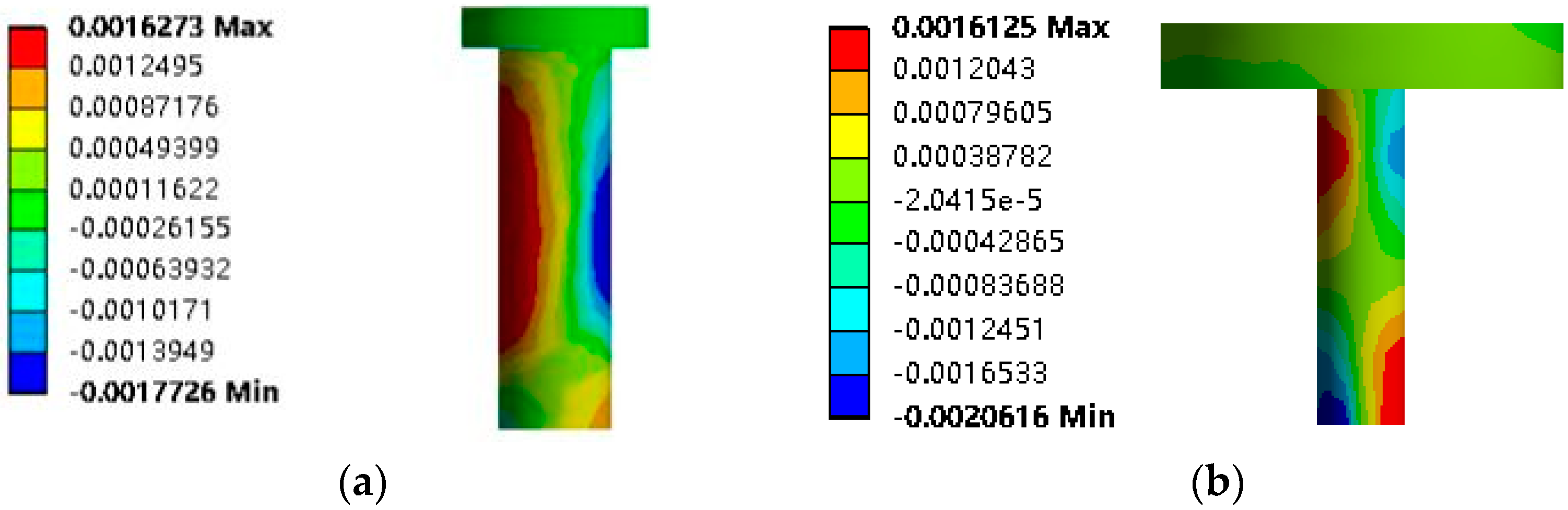
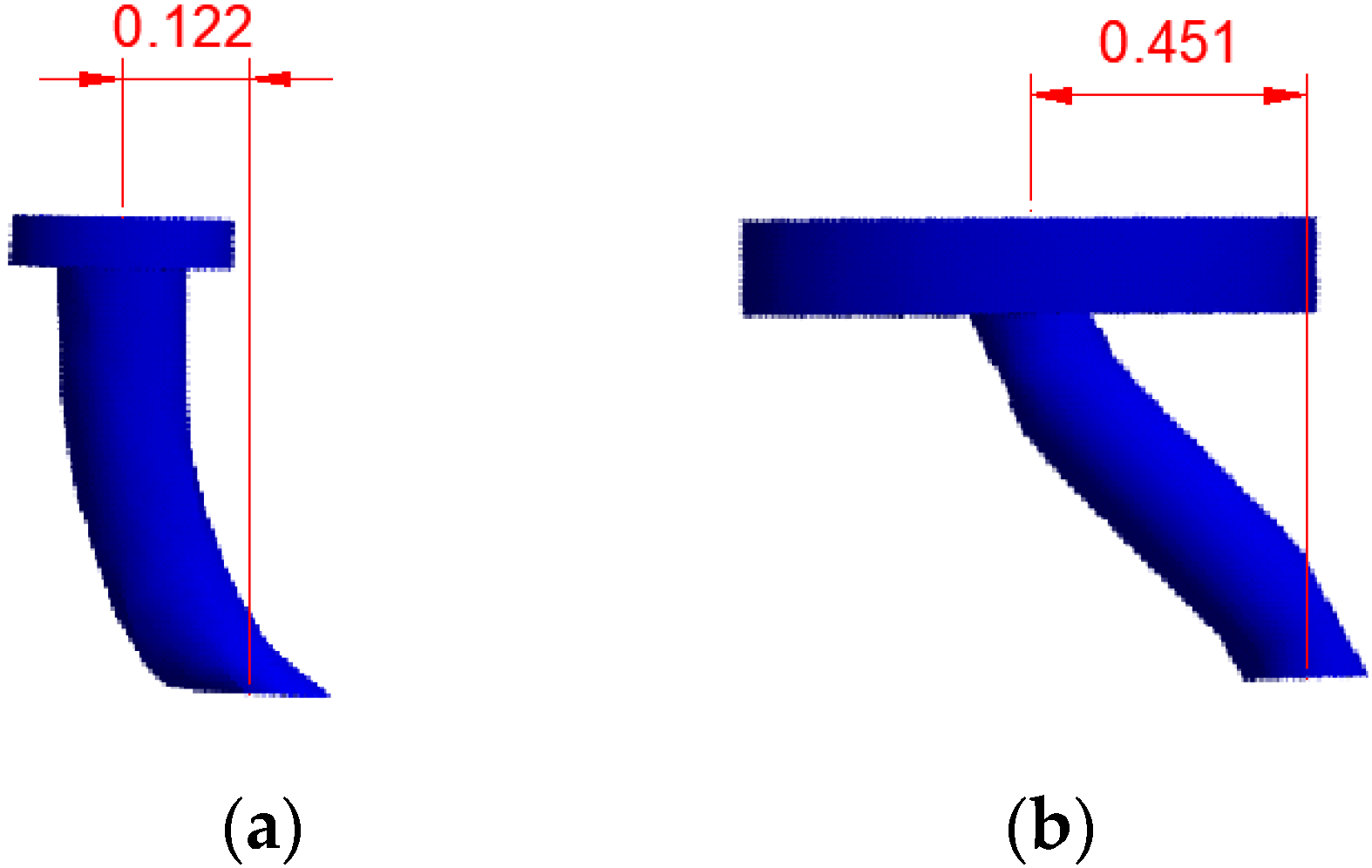
4.4. Mechanical Morphology Analysis of the Studs

In order to study the mechanical properties of the studs, the finite element model of the studs was established using the solid elements. In CSB-1, since the stud was welded onto the steel beam, the lower part of the stud and the upper flange of the steel beam were connected by common joints. The screw and nut could slide with the concrete; therefore, the two were made to contact with the concrete by “Frictional” contact. In CSB-2, the lower part of the stud was connected to the upper flange of the steel beam by common joints, the foamed plastics were bonded to the screw (it was assumed that the screw and foamed plastics would not disengage), and the nut and the concrete were connected by “Frictional.”

Figure 14 shows the axial strain of the studs at Section 2-2 calculated by FEM when the load was 160 kN. By comparing the stud strain at the same position of the two test beams, it is evident that the maximum strains of CSB-1 and CSB-2 were similar, but the strain distribution was different. In the middle of the ordinary stud, one side was compressive stress, and the other side was tensile stress. For the MURSP connector, the axial stress in the middle of the stud was very low. At the top and bottom of the MURSP connector, one side was the compressive stress, and the other side was the tensile stress.

Figure 14. Axial strain of the studs at Section 2-2 (με). (a) CSB-1. (b) CSB-2.

Figure 15 shows the displacement difference between the top and bottom of the studs in Section 2-2 calculated by FEM under a load of 160 kN. The figure clearly shows that the displacement difference of the ordinary stud was 0.122 mm, while that of the MURSP connector was 0.451 mm, which was 3.7 times that of the ordinary stud. This may be the reason for the high strain in the MURSP connector.

Figure 15. Displacement difference between the top and bottom of the studs at Section 2-2 (mm). (a) CSB-1. (b) CSB-2.

In terms of the deformation form, the MURSP connector was closer to shear deformation, while the ordinary stud was closer to bending deformation. The main reason is that the nut area of the MURSP connector was larger than that of the ordinary stud. The nut could not move or rotate under the restriction provided by concrete, and the bottom of the stud was welded together with the steel beam. When there was a displacement difference in the MURSP due to interface slip, the screw exhibited shear deformation under the constraint of both ends. The nut of the ordinary stud had a small area, and the concrete could not effectively constrain the rotation of the nut; therefore, bending deformation occurred under the effect of a displacement difference.

5. Conclusions

Through experiments and numerical analysis, the performance of the negative-moment region of steel-concrete composite beams with MURSP connectors was studied. The following conclusions can be drawn:

(1)

The proposed composite beam with MURSP connectors could effectively release the tensile stress of concrete, thereby increasing the crack load.

(2)

Compared with composite beams with common studs, the slip composite beams with MURSP connectors increased significantly in the negative-bending moment region, and the slip mainly occurred in the early loading stage. The use of MURSP connectors weakened the bond between the steel beam and the concrete slab. During the loading process, the center axis appeared in the concrete slab of the composite overhanging beam with MURSP connectors, while the neutral axis did not appear in the concrete slab of the ordinary composite overhanging beam.

(3)

The overall flexural stiffness of the overhanging beam with MURSP connectors proposed in this paper was reduced by 3.08% compared with that of ordinary studs.

(4)

Accurate finite element models of the overhanging beams with ordinary studs and MURSP connectors were established while fully considering the nonlinearity of the materials and the contact relationships between the components, and the mechanical properties of the test beams were analyzed. The accuracy of the finite element models was proven by comparing the results.

(5)

The finite element analysis showed that the ordinary stud and the MURSP connector exhibited different stress and deformation states in the negative-moment region of the composite beams. The ordinary stud exhibited bending deformation, while the MURSP exhibited shear deformation. Under the same load, the displacement difference between the top and bottom of the latter was approximately 3.7 times that of the former.

6. Further Research

In this paper, the bending stiffness, the concrete cracks, and interface slip in the negative moment region of composite beams with MURSP connectors are studied. The research results can provide a reference for the design of composite beams. It is necessary to further study the influence of parameters such as the thickness of foamed plastic on the mechanical properties of this composite beam.

The composite beam is under static load in this study, while the actual bridge is under cyclic load. It is necessary to study the mechanical properties of the composite beam under fatigue load, which is being conducted.