Recycling Textile Waste to Enhance Building Thermal Insulation and Reduce Carbon Emissions: Experimentation and Model-Based Dynamic Assessment

Abstract

By enhancing the thermal properties of cement-based building materials, energy consumption and carbon dioxide (CO₂) emissions related to space conditioning in buildings can be alleviated. This study aims to present cement-based composites reinforced by textile fibers for application in building and construction. Several lightweight coating mortars were produced by partially replacing the sand in the mix with different percentages of textile waste. Mechanical and thermal characterizations of the reinforced cementitious composites were performed. The results showed that the thermal conductivity of cementitious compounds decreased as the proportion of reinforcing material in the mixture increased. In terms of mechanical properties, the textile slightly reduced the compressive strength of cementitious mortar, while it improved the flexural strength. A numerical study was then performed to derive the actual impact of these reinforced materials on the thermal behavior of a building element using COMSOL Multiphysics. Numerous configurations of walls coated with different mortar mixtures were studied. The results showed that coating both sides of a building wall with 20 mm of textile-reinforced mortar reduced the internal temperature by 1.5 °C. Thus, the application of these thermally improved mortars as coating mortars appears to be a relevant solution to enhance the thermal performance of buildings.

1. Introduction

Due to population growth and improving living standards in general, the consumption of textiles has increased worldwide, which has led to an increase in textile production. The textile industry presents a consumption of clothing and textiles of 7 kg per year per capita, and more than 49 million tons of products are produced every year [1]. Meanwhile, the textile industry is one of the most worrying supply chains, having catastrophic social and environmental impacts worldwide [2]. In 2020, textile consumption in Europe had, on average, the fourth-highest impact on the environment and climate change [3]. Moreover, increases in textile global production result in the creation of a high amount of textile waste. Accordingly, the implementation of a circular model in the textile sector, taking into account the recycling of textile waste, is essential to ensure sustainability and mitigate the environmental impacts of this sector. There are two types of textile waste: reusable waste (production offcuts, reel offcuts, etc.) and recyclable waste (filament, etc.). The last category, in turn, is divided into two main categories: one of high value and the other of low value. It is estimated that 1/4 of textile waste consists of pure fibers: cotton, synthetics, and others. In Tunisia, there were more than 3000 companies in the textile and clothing industry in 2019 [4]. The total textile waste in Tunisia was about 31.1 kilotons, divided into 6.3 kilotons of reusable waste and 24.8 kilotons of recyclable waste. The latter, in turn, is divided into 9.8 kilotons in high value and 15.0 kilotons of low value waste [3].

The textile industry is not the only one with disastrous social and environmental impacts. The building sector has many drawbacks in terms of energy consumption and carbon dioxide (CO₂) emissions [5]. According to the International Energy Agency (IEA), the residential and industrial building sectors represent more than a third of global final energy consumption and nearly 40% of total direct and indirect carbon dioxide (CO₂) emissions [6]. Most residential and industrial buildings require high-energy consumption to ensure acceptable thermal comfort for their occupants. Therefore, the implementation of an energy-saving program in buildings by improving the thermal performance of construction elements has become a necessity, with the application of thermal insulation being a promising way to reduce energy losses [7,8,9]. The commonly used technique to improve the insulation capacity of walls is to embed the insulation layer in the erected foundation wall, which increases the thickness of the wall and delays the construction time [10]. To overcome these design disadvantages, several researchers are focusing on the integration of insulators in building materials such as plaster [11], concrete [12,13], mortar [14,15,16], and construction bricks [17,18,19]. Fibers are among the most widely studied insulators for use in cementitious materials and have proven to be an excellent solution for mitigating heat loss. In fact, several studies have been carried out in this field of research to study new cement-based composites reinforced with fibers such as wool fiber [20], Acaï [21], palm fiber [22,23], agricultural fiber wastes [24], coconut fiber [25], rice straw fibers [26], recycled brass fibers [27], and basalt fiber [28].

The past decades have witnessed a growing interest in textile-reinforced mortar (TRM), and it has become one of the most important fiber-reinforced materials due to its promising textile properties. Based on a review of the literature, the use of textile fiber as a reinforcing material has only been explored in a limited number of applications. Generally, textiles have mainly been incorporated into cement-based materials to improve their mechanical strength, ductility, toughness, and durability [29,30,31,32,33,34,35,36,37,38]. Sadrolodabaee et al. [39] investigated the mechanical and durability properties of cement composites reinforced with two types of textile waste, either a fraction of short fibers or non-woven fabric. Flexural strength, toughness, stiffness, and drying shrinkage developed composites were evaluated. A composite reinforced with six layers of non-woven fabric showed optimal performance with a flexural strength of 15.5 MPa and a toughness of 9.7 kJ/m². Gulinelli et al. [40] studied the performance of various wall configurations strengthened with textile-reinforced mortar. The structural performance was evaluated experimentally and numerically by conducting diagonal compression tests. The findings indicated that, compared to a simple wall, the reinforcement systems lead to a substantial improvement in both load-bearing capacity and rigidity. Abbas et al. [41] investigated the potential of using 16 different textile fabrics for structural applications. A series of tests, including microscopic analysis, mass per unit area, and tensile strength, were carried out on specimens made of textile-reinforced mortar to determine the most suitable fabric. The results showed that the mass per unit area of the tested fabrics varied between 117 and 1145 g/m². It was noticed that the tensile strength was greater in the warp direction compared to the weft direction, owing to the increased number of yarns in the warp direction. Moreover, it was found that plain weave fabrics had higher strength compared to twill weave fabrics. Plain weave was deemed to be the most suitable among the 16 selected fabrics for use in textile-reinforced mortar applications, due to its adequate spacing and alternating arrangement of yarns, leading to a stronger bond with the matrix and higher tensile strength. Regarding thermal performance studies, few authors have experimentally investigated the integration of textile fibers in cementitious mortars to enhance building thermal insulation [42]. Oliveira et al. [1], for example, experimentally investigated the effect of fabric shavings on the thermal and mechanical properties of mortars. The results showed that the mechanical strength of the fabric-yarns-reinforced mortar was lower than that of the reference mortar. Despite this reduction, the minimum values set by the standards for compressive and flexural strengths were met. Furthermore, when the textile-reinforced mortar was thermally tested at 60 °C, its internal surface temperature was about 12 °C lower than that of the reference. This property is extremely important for questions of durability, as it protects structures and walls from expansion and contraction movements. Briga et al. [43] also investigated the potential of using textile fibers in building construction applications. The thermal characterization of the developed composites was performed by analyzing the heat flows, internal surface temperatures, heat transfer coefficients, and infrared thermal imaging. The authors affirmed that increasing the proportion of textile fibers in the mix resulted in higher thermal stability. Moreover, the developed composite showed promising results compared to traditional building materials.

Only a few studies have focused on the incorporation of textile fibers as thermal reinforcing in cementitious mortars. Since the results were promising, a more concise understanding and exploration of the overall thermal performance of these composites is required. Thus, this study aims to evaluate the potential of incorporating recycled industrial textile waste into building components to enhance their thermal properties and reduce energy consumption in buildings. Several lightweight coating mortars were produced by partially replacing the sand in the mix with different percentages of textile waste as reinforcement material. The mechanical and thermo-physical characterizations of these composites were carried out. A numerical investigation was then performed to examine the thermal efficiency of the developed materials using COMSOL Multiphysics 5.5 software. Numerous configurations of walls coated with different coating mortar mixtures were studied. The study suggests using textile-reinforced cement-based materials as coating mortars to enhance the thermal performance of buildings and reduce energy consumption and CO₂ emissions.

2. Textile Reinforced Mortar: Preparing and Testing Methods

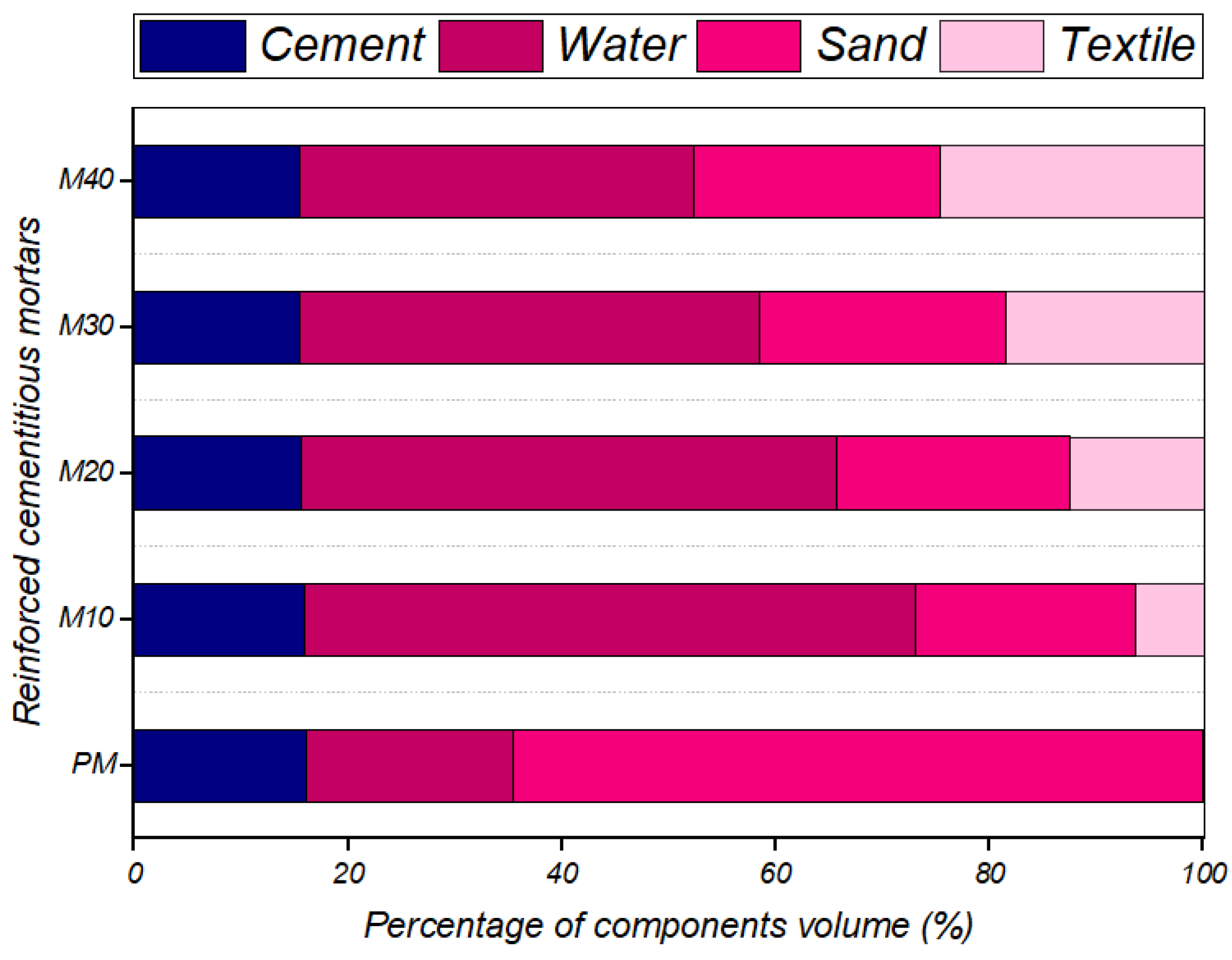
2.1. Samples Preparation

Fiber-reinforced mortars were prepared by replacing the sand of cement mortar with volume fractions of 0% (PM), 10% (M10), 20% (M20), 30% (M30), and 40% (M40) of textile. The cement used in this study was Portland cement in accordance with the terminology of the European standard EN-197-1 [44] and was supplied by Cementos Molins Industrial S.A. A natural sand AF-R-0/2-S was used as a fine aggregate. The textile fiber added as a reinforcing material is a waste generated at the end of the textile spinning process.

Table 1. Thermal properties of textile-reinforced mortar components.

Material	Thermal Conductivity [W/m∙K]	Thermal Diffusivity [mm2/s]	Volumetric Heat Capacity [MJ/m3 K]
Cement	0.140	0.201	0.694
Sand	0.335	0.278	0.278
Textile fibers	0.082	0.418	0.196

summarizes the thermal properties of the fibers used. Before mixing the mortar, the fiber was dispersed by injecting compressed air. Mortar mixes were prepared using a cement-to-sand volume ratio of 1:4 and the mix design is shown in

Table 2. Mixture designs for tested mortar samples, mass for 1 m³.

Materials	PM	M10	M20	M30	M40
Cement	215	215	215	215	215
Sand	1540	1386	1232	1078	924
Textile	0	5.26	10.52	15.78	21.04

and Figure 1. The mortar mixing procedure was carried out according to the European standard EN 1015-2 [45]. Finally, the mixed slurry was poured into prismatic molds with dimensions of 40 × 40 × 160 mm (Figure 2). The blend was cast in two stages, each layer set being first tapped with a steel bar and then vibrated until the fresh mortar was completely leveled. Three samples of each mixture were made. The samples were left in the molds for 24 h at a laboratory temperature of 20 °C. After demolding, some of the specimens were cured in water for 7 days and others for 28 days.

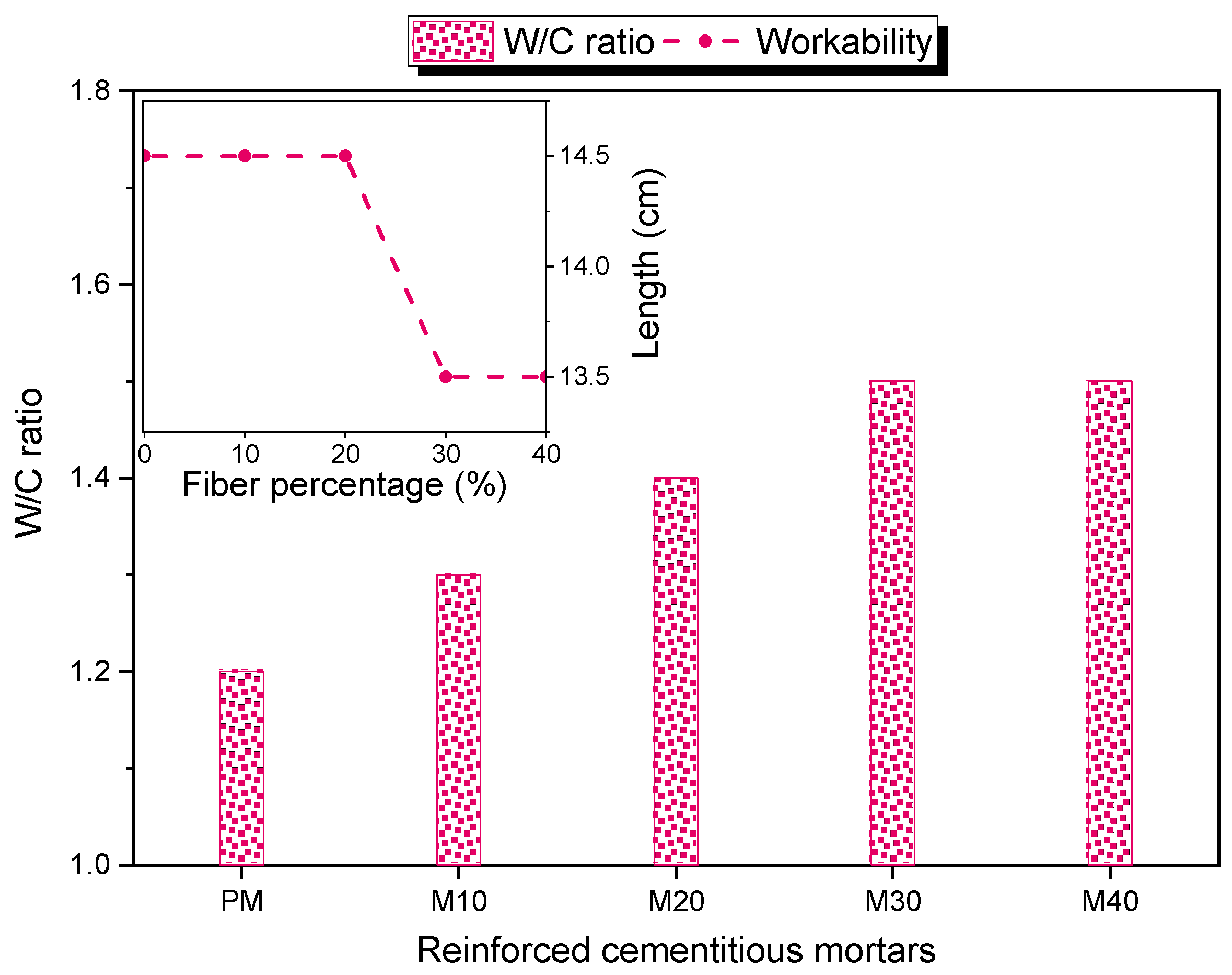
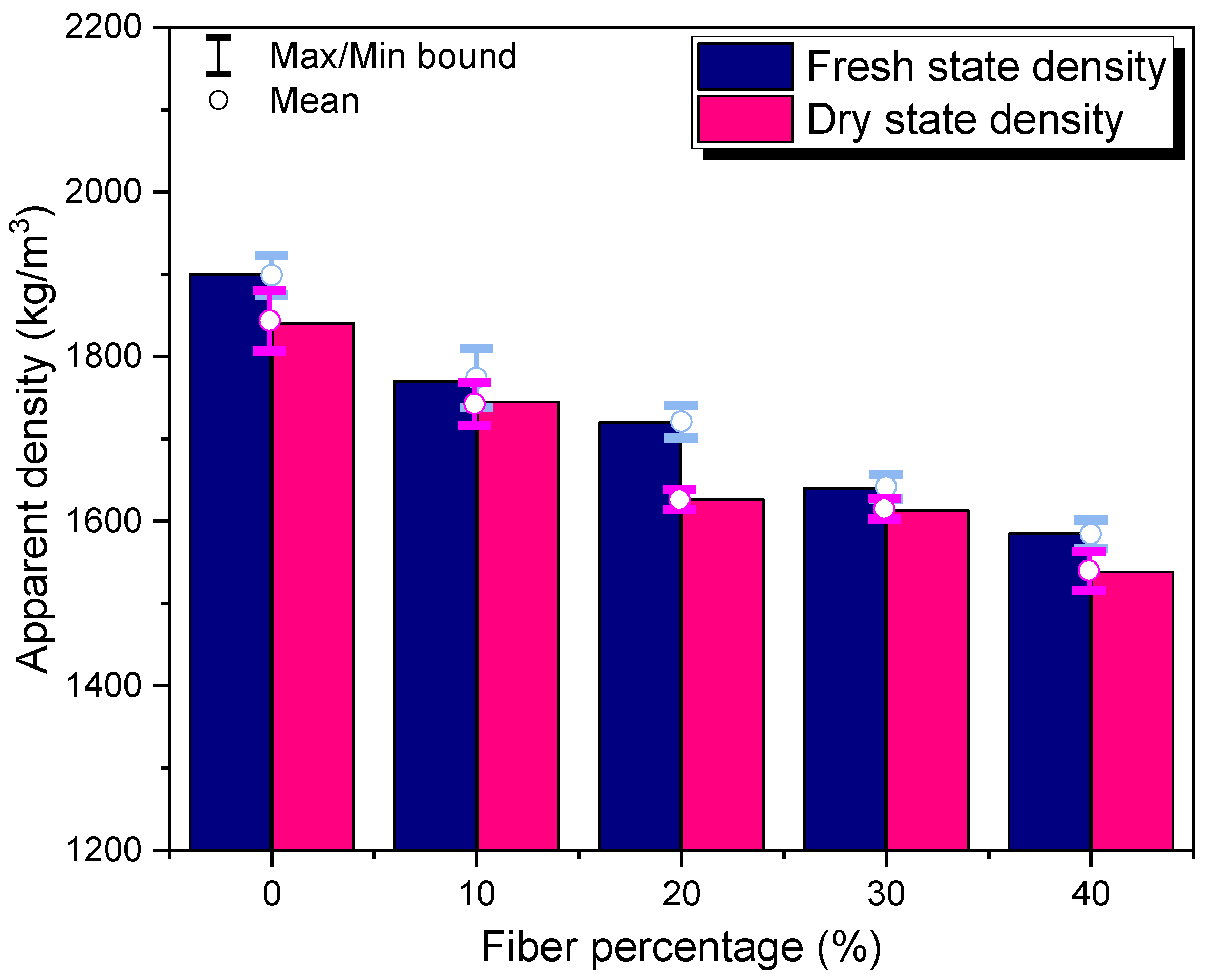
2.2. Workability and Density Measurement

Both the flow behavior and the bulk density were tested in the fresh state. The fluidity of the cementitious mortar, which is expressed by the workability, was evaluated immediately after the mixing process using a flow table test (Figure 3a) in accordance with the standard EN 1015-3 [46]. The fresh bulk density was quantified by the European standard EN 1015-6 [47]. In the hardened state, the dry bulk density of the reinforced mortars was studied in accordance with the EN 1015-10 standard [48].

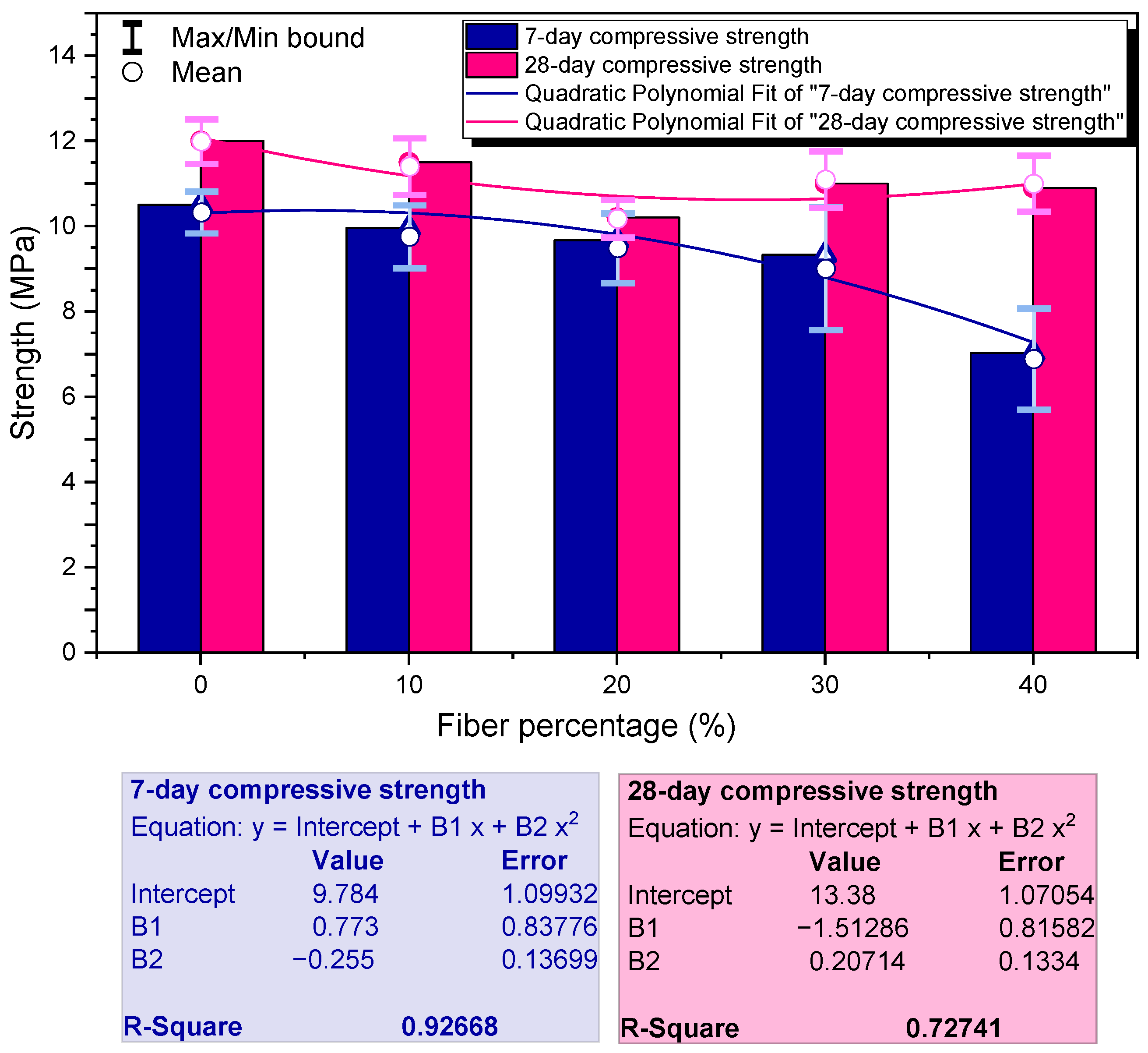
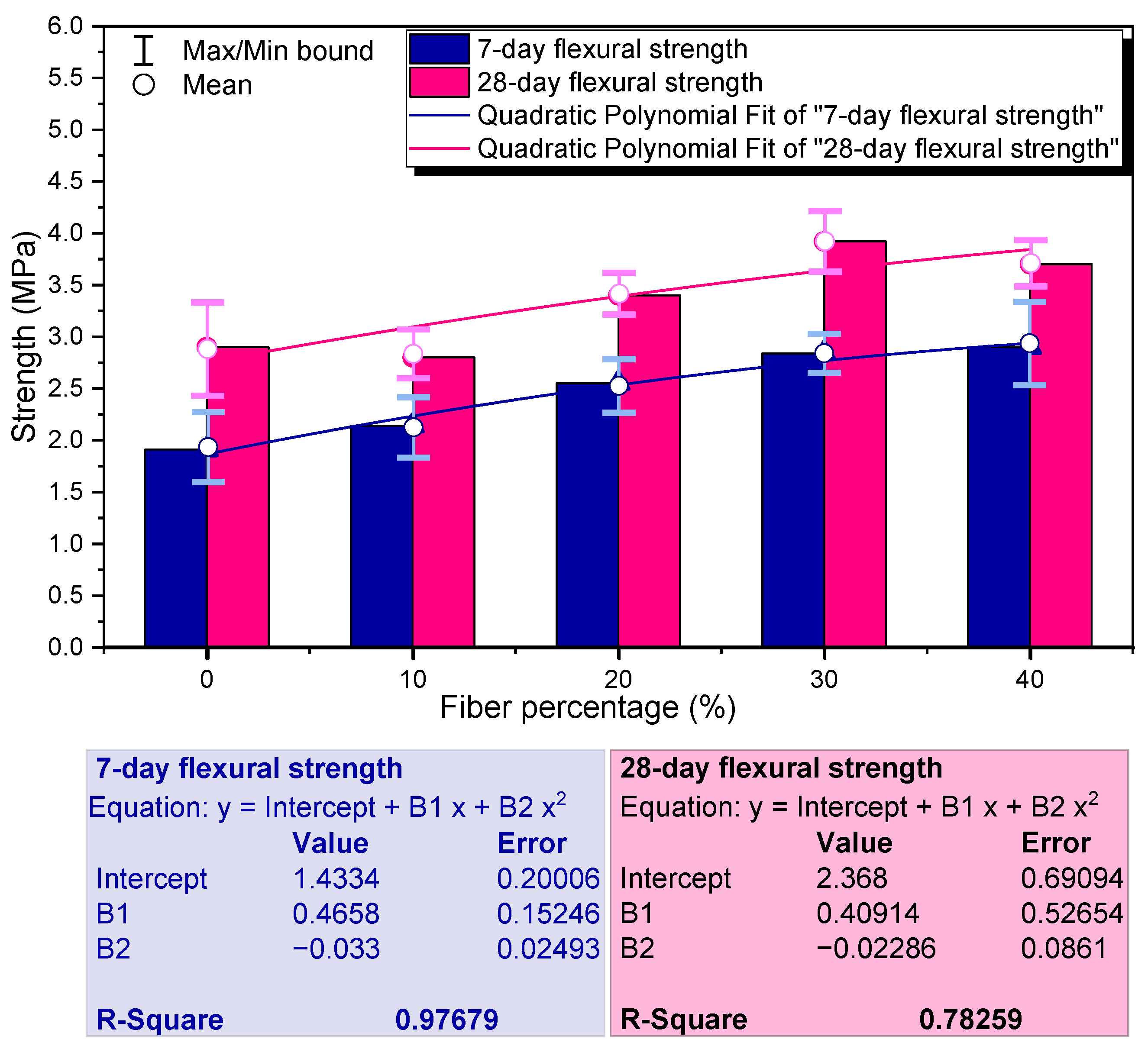
2.3. Mechanical Characterization

For the mechanical characterization of the hardened cementitious composites, flexural and compressive strength tests were carried out according to the EN 1015-11 standard [49]. A COINSA Controls Industrial servo-controlled testing machine with two different heads, one for flexure testing and the other for compression testing, as shown in Figure 4, was used to test the reinforced cementitious mortars. To assess the bending strength, a three-point flexion test was carried out with a load rate of 50 ± 10 N/s. The compressive strength tests were carried out following the flexion tests using one of the two resulting fragments with a loading rate of 2400 ± 200 N/s. The two tests were carried out until the fracture of the prismatic specimen and the breaking load were recorded.

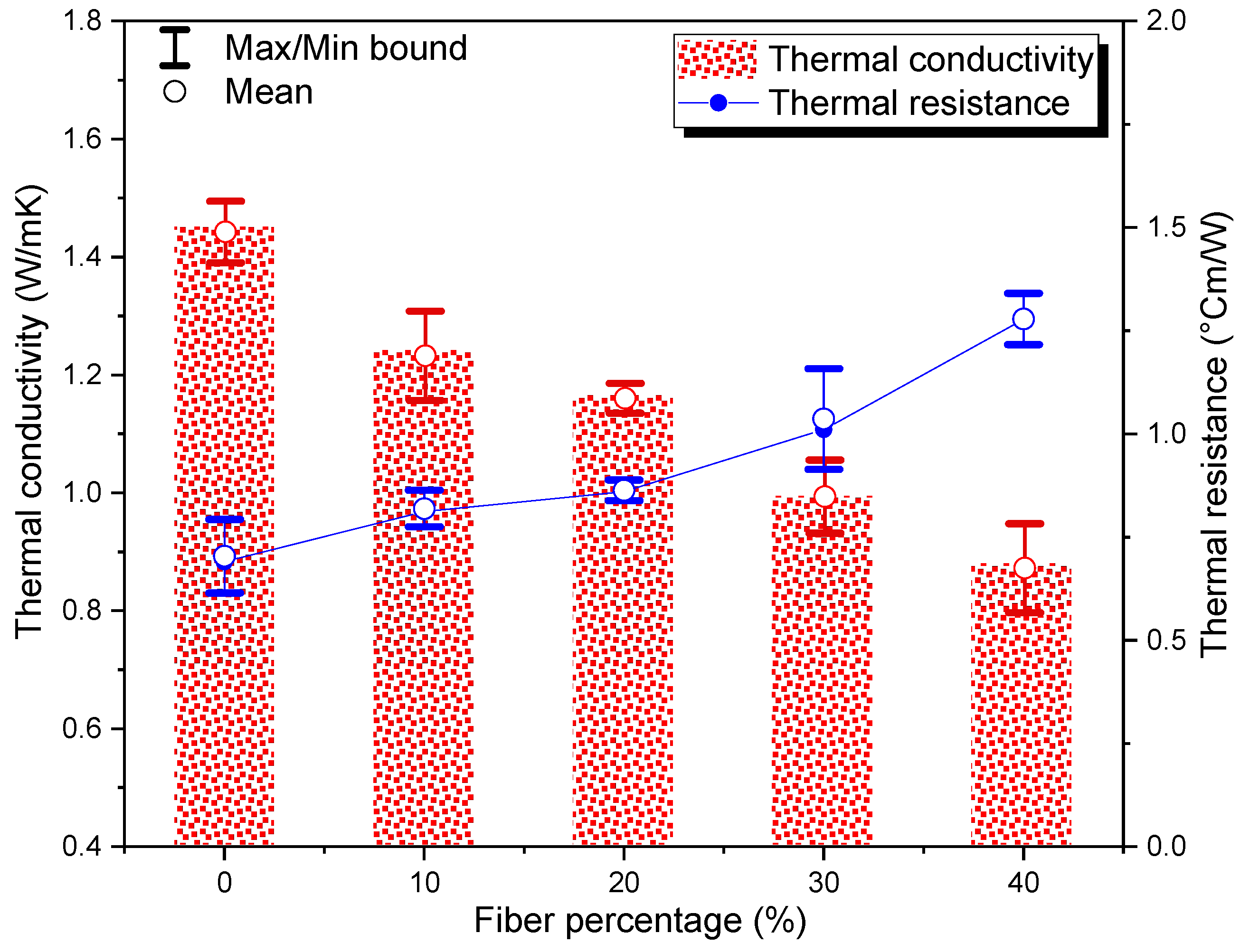
2.4. Thermal Characterization

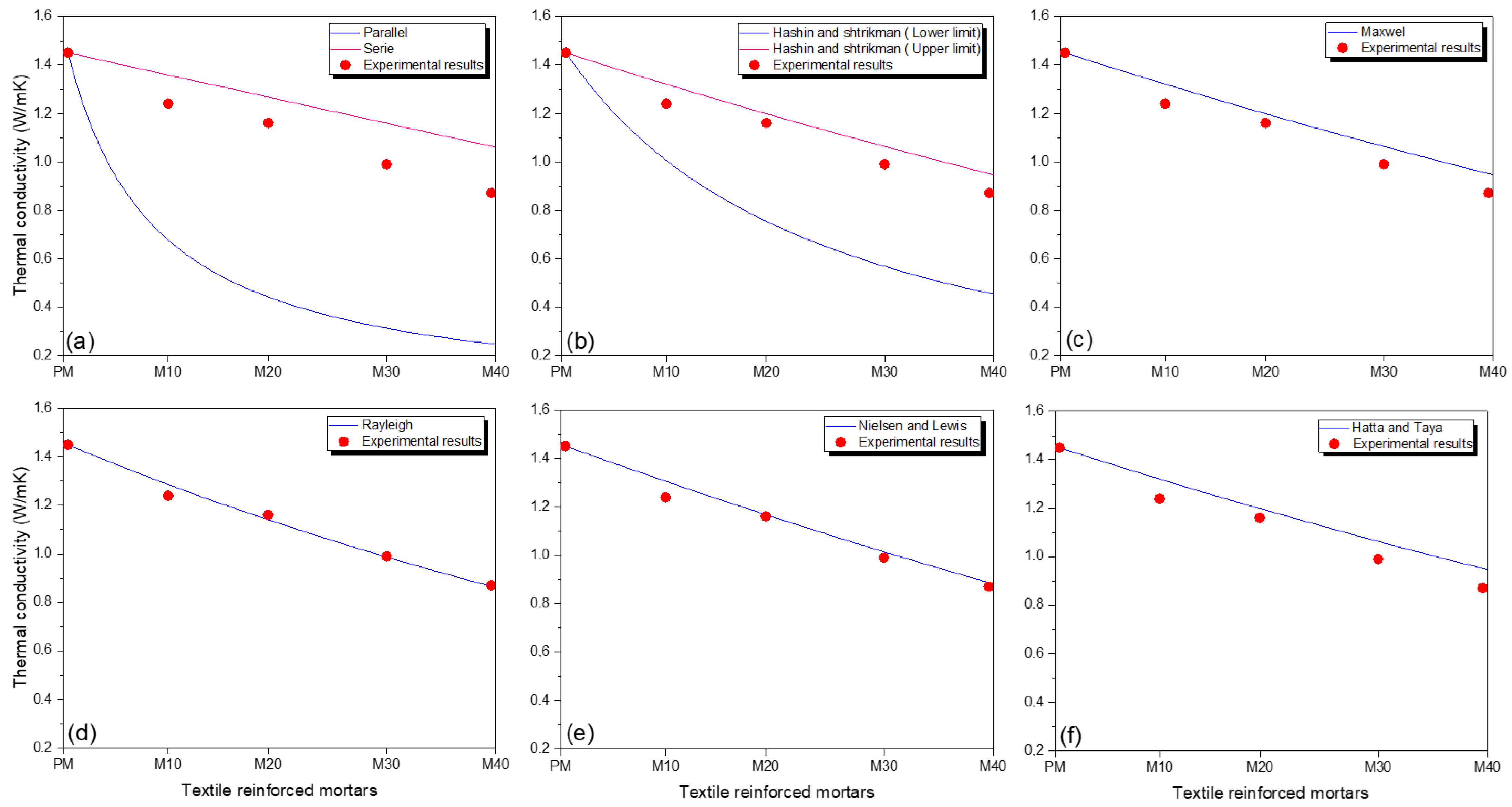
2.4.1. Analytical Prediction of Composite Thermal Conductivity

As a bulk property, the thermal conductivity of composite material can be predicted by several theoretical models. Starting with Maxwell [50], numerous analytical investigations [51,52,53] have been performed to solve the problem of thermal conduction in heterogeneous materials. The suggested models are mathematical expressions that determine the effective thermal conductivity of a composite material based on the thermal conductivities of its components as well as the shape and proportion of the reinforcing material. The suitability of a particular model is established by the underlying assumptions made during its development. Thus far, various analytical solutions are available to predict thermal conductivity for the most common composite structures, including dispersion compounds. In this work, several theoretical models were presented, which assume that the reinforcing material consists of randomly dispersed spherical units within the matrix, for comparison with the experimental results. In all of the models, we considered a composite material with thermal conductivity Kc, consisting of spherical units with thermal conductivity Krf embedded in a continuous matrix with thermal conductivity Kmx at a volume fraction φ.

• Series and Parallel models: Figure 5 shows the two plain theoretical methodologies that have been followed to predict the effect of adding a reinforcing material on the thermal conductivity of a matrix. The first approach focuses on individually considering the contribution of each component to model the thermal conductivity of the composite through the application of the percolation theory [54]. Based on the electrical analogy, this model is called a series model. In this case, the effective thermal conductivity of the composite material is given by [55,56,57]:

Kc = (1 − φ) Kmx + φ Krf

(1)

The second approach assumes that the composite reacts as a homogeneous material. This model follows the arrangement of parallel electric circuits, which is represented by the following expression:

Kc = 1/(((1 − φ))/Kmx + φ/Krf)

(2)

The aforementioned models present upper (interactive model) and lower bounds (non-interactive model) of the effective thermal conductivity that the data encompass [55,56,57].

• Maxwell model: This model was developed to define the electrical conductivity of a heterogeneous medium composed of dispersed spheres. The development of this model provides an accurate solution for the effective thermal conductivity of arbitrarily distributed homogeneous spherical particles without interaction in a homogeneous matrix [56]:

Kc = Kmx (2 Kmx + Krf − 2 (Kmx − Krf) φ)/(2 Kmx + Krf + (Kmx − Krf) φ)

(3)

The main limitation of this model is its limited applicability to only low concentrations of reinforcing particles. However, it has served as a base for creating new, advanced models that account for additional parameters related to the various components involved [57].

• Rayleigh model: This model was adapted to predict the effect of cylindrical reinforcement materials on the thermal conductivity of a matrix. The equation below allows for the effective thermal conductivity to be calculated [58]:

Kc = Kmx (Kmx + Krf − (Kmx − Krf) φ)/(Kmx + Krf + (Kmx − Krf) φ)

(4)

• Hashin and Shtrikman model: Following the approach of Maxwell and using the perturbation hypothesis, Hashin and Shtrikman developed a model to predict the thermal conductivity of randomly scattered units in a continuous matrix. This model provides upper and lower limits of the effective thermal conductivity rather than deriving an equation for it. Moreover, it is shown that, in the case of composite material, these limits are the most restrictive that one can obtain in terms of volume fractions of charge and conductivity [59]. Equations (5) and (6) indicate the lower and upper limits of the conductivity [55]:

Kc_min = Kmx (1 + (p − 1) D φ)/(1 − D φ)

(5)

Kc_max = Kmx (Krf (1+ (p − 1) (1 − φ) d)/(Kmx (1 − (1 − φ) d)

(6)

where

D = (Krf − Kmx)/(Krf + (p − 1) Kmx)

(7)

d = (Kmx − Krf)/(Kmx + (p − 1) Krf)

(8)

and p is a parameter involving the morphology of the particles, in the case of a spherical dispersion p = 3 and for a cylindrical dispersion p = 2.

• Hatta and Taya model: Hatta and Taya developed a model to predict the thermal conductivity of a composite consisting of short fibers with different orientations [60,61] based on the analogy of Eshelby [62]. This approach is based on predicting the steady-state equivalent thermal conductivity of the composite by considering the shape and interactions between the additions with different orientations. The equation they arrived at is [55]:

Kc = Kmx + (φ Kmx)/(S (1 − φ) + Kmx ⁄ ((Krf − Kmx)))

(9)

where S = 1/3 for spherical particles.

• Nielsen and Lewis model: Nielsen and Lewis derived a semi-theoretical model for predicting thermal conductivity [63,64], based on the Halpin-Tsai equation [65]. They adjusted the model to handle non-spherical additives using a coefficient, which depends on the shape and orientation of the particles. Moreover, Nielsen and Lewis’s model considers the effect of the maximum fraction of the additive, φmax. The semi-empirical model developed is as follows [66]:

Kc = Kmx (1+ C E φ)/(1 − β E φ)

(10)

where:

E = (Krf ⁄ Kmx − 1)/(Krf/Kmx + C)

(11)

β = 1+ ((1 − φmax) φ)/(φmax)²

(12)

For spherical additive randomly dispersed in the matrix, C = 1.5 and φmax = 0.637 [57].

2.4.2. Experimental Characterization

To study the thermal properties of reinforced mortars, The TEMPOS thermal properties analyzer was used on the remaining fragment from the flexion test. As shown in Figure 6, the samples must be drilled first with a rotary hammer and then cleaned with compressed air. Before inserting the sensor needle, the hole must be filled with thermal grease. Good thermal contact between the sensor and the sample is critical for accurate measurements; therefore, it is important to ensure that the sensor fits tightly into the hole. Finally, the thermal conductivity and thermal resistance were measured in the climatic chamber at a temperature of around 20 °C.

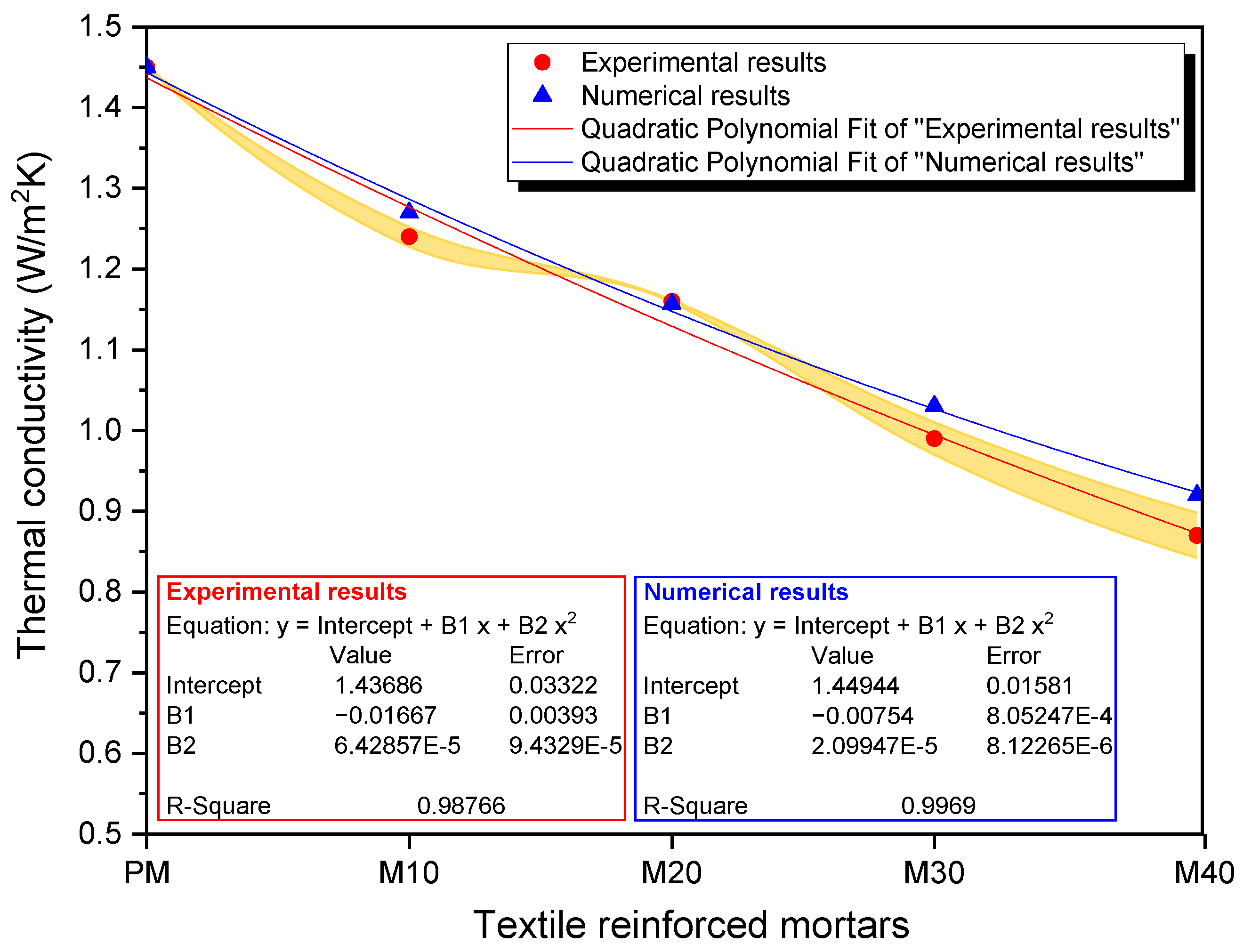
2.4.3. Numerical Characterization

A numerical study was performed to investigate the thermal properties of the textile-reinforced mortars using COMSOL Multiphysics software. The first crucial step for a successful simulation is to generate an appropriate geometry for the problem. In this case, a three-dimensional model featuring a rectangular block defining the mortar matrix and spherical units representing the reinforcement material was used to conduct the thermal analysis on the composite materials with varying additive concentrations. In this steady-state heat conduction problem, the heat flux was only considered along the x-direction. The faces that were perpendicular to the direction of the heat flow were considered isothermal. One surface was set at 15 °C and the other at 40 °C. The other faces that were parallel to the x-direction were all considered adiabatic. The thermal conductivities that were predicted by this model were compared and validated with the experimental results. After validation of the model, it was be used to predict the thermal diffusivity and the volumetric heat capacity of the textile-reinforced mortars.

3. Evaluation of Characterization Results

In order to assess the influence of textile fibers on cement-based mortars, several tests were carried out on the fresh and hardened states of the mixtures. Each measurement was repeated three times to guarantee repeatability, and the mean value was reported.

3.1. Workability Testing

The amount of water added to the dry mix was adjusted differently for each percentage of textile waste added to achieve acceptable workability. The details of the modified cementitious mortar mix proportions are summarized in Figure 1. The Water to Cement (W/C) ratio values with different fiber percentages are illustrated in Figure 7. The measured flow diameter of the control mixture without fibers was 145 mm. In this test program, the flow rate for all of the mortar mixtures was kept at a specified value of 140 ± 5 mm, in order to obtain a fluid and workable consistency. As can be seen, fiber-reinforced mortars showed a higher water requirement in order to achieve similar workability to plain mortar. This was due to the high water absorption of the fibers.

3.2. Bulk Density Testing

Figure 8 shows the variation in apparent density of the samples in both fresh and dry states versus the reinforcing material percentage. The fiber-free cement mortar had a fresh apparent density of 1900 kg/m³. After adding varying amounts of textile fibers, the fresh state apparent density dropped to a value of 1585 kg/m³, exhibiting a difference of around 315 kg/m³. For the M40 sample, in the hardened state, the density diminished to 1538 kg/m³. with a difference of around 302 kg/m³ compared to the plain mortar PM. Thus, it can be deduced that the incorporation of the fibers into the cementitious mortar is accompanied by a loss of density. This lightness is due to the low fiber density.

3.3. Mechanical Characterization

Coating mortars must have a sufficient mechanical strength to withstand the multiple impacts to which they may be subjected during their lifetime. Accordingly, the mechanical performance of the textile waste-reinforced mortars was investigated at 7 and 28 days of curing. Figure 9 illustrates the failure modes of the textil-ized mortars during the mechanical tests after 7 and 28 days, respectively. The visual inspection of the defective samples (Figure 9a) confirmed that the mortars containing more textile fibers showed more severe damage under the applied load. This predicts that increasing fiber content will cause a dramatic drop in sample stiffness and a subsequent reduction in compressive strength. Figure 10 and Figure 11 show the average compressive and flexural strength results, respectively. Based on the graphs, increasing the curing period significantly enhances mechanical performance. For the compressive strength testing, the increasing percentage between the 7th day and the 28th day was approximately 35% for the M40 sample. Compared to the 7-day flexural strength, the increase in the 28-day strength was 34% for the PM sample and 22% for the M40 sample. It is worth noting that, as the amount of textile increased, the flexural strength gained over the curing period was affected. As can be seen, the plain mortar PM had the highest compressive and flexural strength regardless of the curing period. In adding the textile fibers, a decrease in the compressive strength of mortars occurs. Figure 10 shows that the seven-day compressive strength for the M40 sample decreased by approximately 33% compared to ordinary mortar PM. However, the compression resistance of the samples after 28 days of curing slightly decreased until reaching a difference of 15 % for the M40 mix compared to the PM sample. This diminution in mechanical strength for the textile-reinforced mortars could be attributed to the low strength and high compressibility of the textile fibers. Despite the reduction in compressive strength, all of the reinforced mortars met the requirement for use as a coating mortar in building construction according to EN 998-1 [67]. Concerning Figure 11, regardless of the curing period, the flexural strength of the mortars increased as the percentage of reinforcing material increased. The increase in the seven-day flexural strength was about 11%, 25%, 33%, and 34% for the M10, M20, M30, and M40 samples, respectively, compared to the control sample. The 28-day flexural strength increased to 3.7 MPa, which corresponds to an increase of approximately 22% compared to the textile-free mortar.

3.4. Thermal Characterization

Figure 12 illustrates the variation in thermal conductivity and thermal resistance of the reinforced mortars under climatic chamber conditions. As can be seen, the thermal conductivity shows a clear downward trend with an increasing proportion of reinforcement material. With 10% fibers incorporated, the thermal conductivity decreased by 15% compared to the plain mortar. By increasing the amount of textile, the thermal conductivity was further decreased until a value of about 0.87 W/m∙K was reached, which is about 42% lower than the PM sample. Accordingly, the addition of textile fibers increased the thermal resistance of the cement mortar to approximately 1.27 m∙K/W. This improvement in the thermal properties of mortars is attributed to the low thermal conductivity of the textile fiber.

Figure 13 shows a comparison between the experimentally measured thermal conductivities of the reinforced mortars and those predicted using the models mentioned above. Both the experimental data and theoretical data show a similar trend. An increase in the proportion of the reinforcing material corresponds to a decrease in the thermal conductivity of cementitious mortar. The results showed that the experimental outcomes fall within the bounds of the series and parallel models and Hashin–Strikman model. The other analytical models had similar results with minor variations. Since the reinforcing materials are assumed to be spherical particles dispersed in the cementitious matrix, the Hata and Taya model coincides with the Maxwell model. Although the experimental thermal conductivity was close to the results of these two models, a slight discrepancy can be observed. This difference is due to the fact that the model only considers the thermal conductivity of the constituent materials of the composite. The Rayleigh model exhibited the best agreement with the experimental data, especially for the samples with high percentages of reinforcing materials. These results demonstrate that the textile fibers were well-dispersed in the matrix, resulting in homogeneous composites.

Figure 14 shows a comparison of the numerical and experimental results of the thermal conductivity of textile-reinforced mortars. Both results show the same tendency, with an error interval marked by the orange area. For the samples with a higher textile content, the margin of error between the predicted and experimental results increased slightly. The experimental values of thermal conductivity are lower than those predicted. This can be explained by the uncontrolled phenomena, which can occur during the preparation and which are not taken into account by the model, such as the porosity and the contact resistance between components. In general, the results indicate the effectiveness of the computational model.

Thermal diffusivity quantifies the speed at which heat is transferred through materials from a hot to a cold end. It is calculated by dividing the thermal conductivity of the material by its density and specific heat capacity at a constant pressure. The mathematical expression of thermal diffusivity is as follows:

α = K/ρCp

(13)

where K is the thermal conductivity; Cp is the specific heat capacity; ρ is the density. Moreover, ρCp is the volumetric heat capacity.

Figure 15 shows the numerically predicted thermal diffusivity and volumetric heat capacity of the mortars reinforced with textile waste. The addition of fibers to the cementitious mortar reduced both thermal diffusivity and volumetric heat capacity. With a low content of textile fibers, the thermal diffusivity and the volumetric heat capacity of textilized mortars marginally diminished until 1.13 mm²/s and 1.12 MJ/m³·K, respectively. As well, by increasing the proportion of textile fibers to 40 %, the thermal diffusivity and volumetric heat capacity were decreased to 0.97 mm²/s and 0.91 MJ/m³·K, respectively. The addition of the textile fiber waste into the cementitious mortar reduced the thermal diffusivity and the volumetric heat capacity in correlation with the drop in thermal conductivity. Compared to the PM sample, a 40% decrease in thermal conductivity for the M40 sample caused drops of 21% and 23% in thermal diffusivity and volumetric heat capacity, respectively.

4. Case Study: Numerical Investigation of a Hollow Brick Wall Coated with Textile-Reinforced Mortar

As the textile-reinforced mortars showed better thermal potential than an ordinary cementitious mortar with acceptable mechanical behavior, the application of these composites as a coating mortar appears to be a relevant solution to reducing energy consumption and carbon dioxide (CO₂) emissions. Thus, a transient heat transfer analysis was conducted using the COMSOL Multiphysics software to predict the effect of adding textile fibers on the thermal performance of buildings.

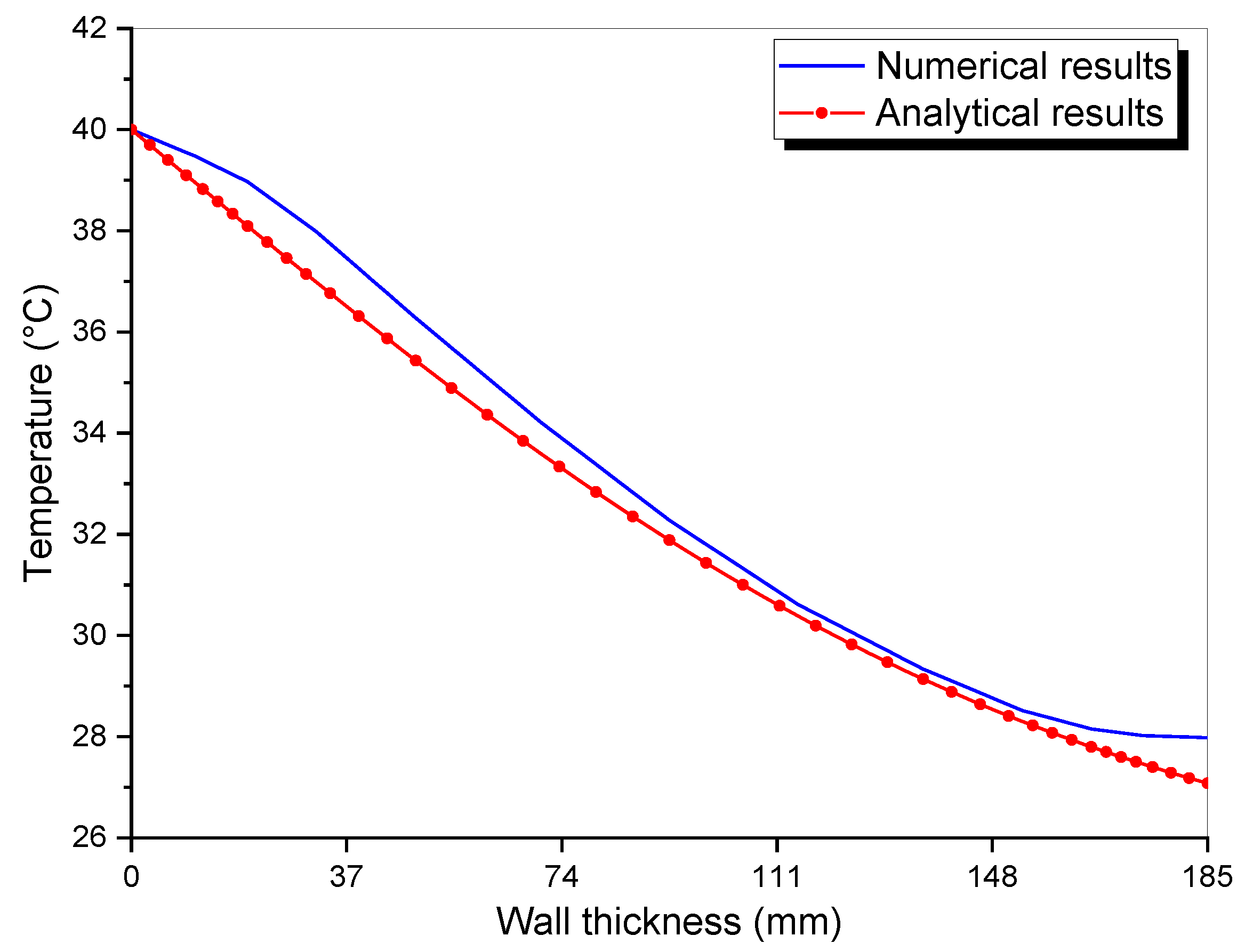
4.1. Numerical Model and Validation

The developed numerical model is intended to investigate the thermal response of a building wall after the application of thermal excitation on the outer surface. The investigated wall consisted of hollow bricks measuring 15 × 20 × 30 cm and contained 12 cavities. The bricks were joined horizontally and vertically with ordinary mortar (PM) with a thickness of 10 mm. Moreover, the wall was coated on both sides with a 20 mm-thick layer of cement mortar in three different scenarios, as shown in Figure 16. The impact of changing the type of coating mortar was analyzed numerically based on the temperature change on the inner surface of each wall configuration after imposing a temperature of 40 °C on the outer surface. To solve this heat transfer problem, the heat conduction in solids and heat convection in air cavities were considered, while the radiative heat transfer through air cavities was excluded. Before starting the simulation, the model was meshed using tetrahedral elements, resulting in a mesh with 492,357 elements. The validation of the aforementioned model involved comparing its predictions with the analytical solution of a transient heat transfer problem. The analytical solution was obtained by transforming the partial differential equation into an ordinary differential equation (Equation (14)) using the Gaussian error function [68].

T (x,t) = Tc − (Tc − Tin) (erf((x)/√((4kt)))

(14)

where T is the temperature, Tc is the imposed heat temperature, Tin is the initial temperature, x is the location of calculation, k is the thermal conductivity, and t is the time.

To evaluate the performance of the proposed model, the Root Mean Squared Error (RMSE) was calculated as follows:

$$\mathrm{RMSE}=\sqrt{{\displaystyle \sum }_{j=1}^n{\left(mj-pj\right)}^2/n}$$

(15)

where mj and pj are, respectively, the average of the measured and predicted parameters, and n is the number of variables.

In order to validate the numerical model mentioned above, the result of case study 1, where the wall was coated with ordinary mortar on both sides, was compared with the analytical results. Figure 17 shows a comparison of the numerically predicted and the analytically calculated change in the internal surface temperature as a function of the wall thickness. As can be seen, the numerical and analytical thermal behaviors illustrate a similar tendency, with a root mean square error (RMSE) of 0.59. This consistency of results demonstrates the effectiveness of the numerical model in studying heat transfer through the brick wall.

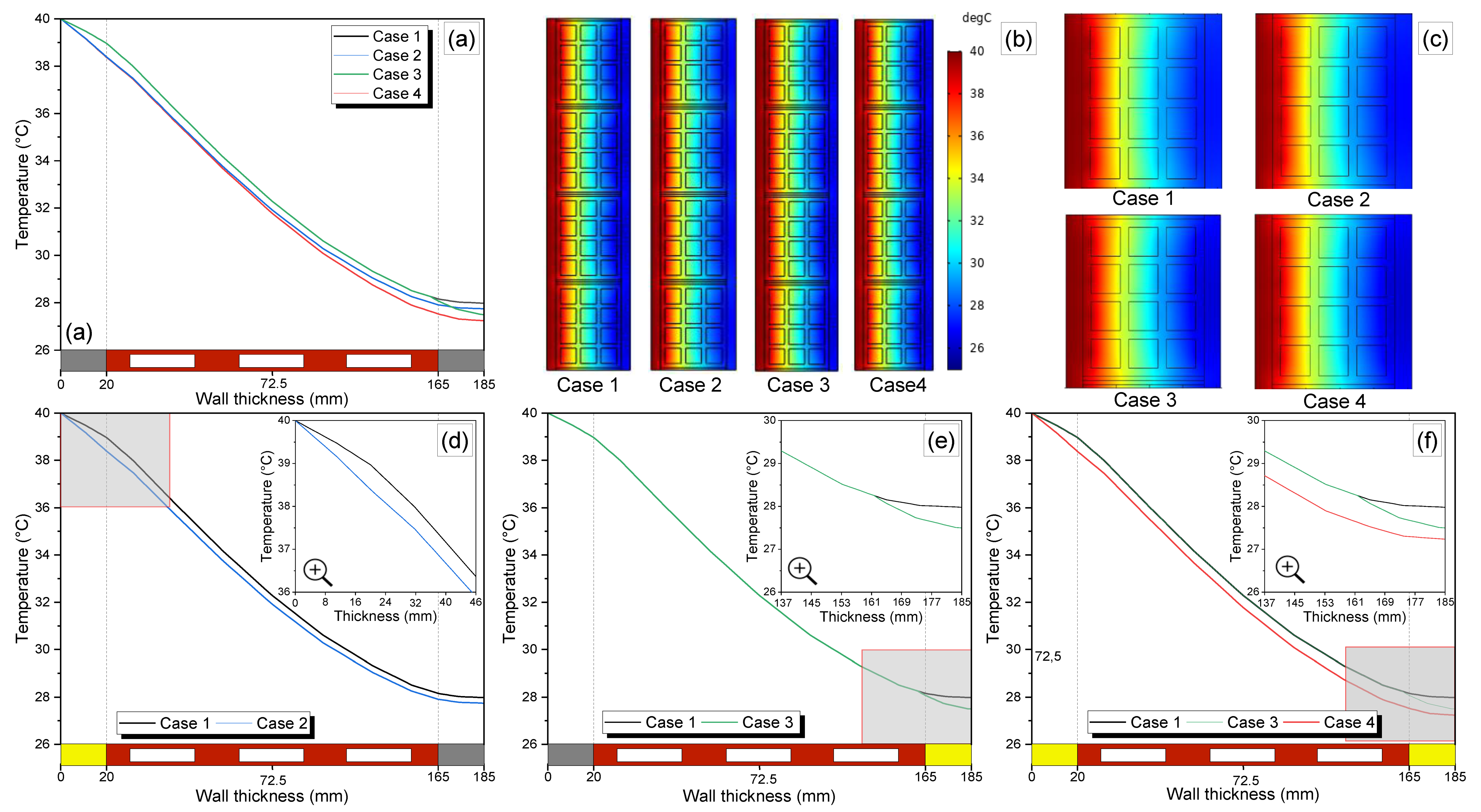
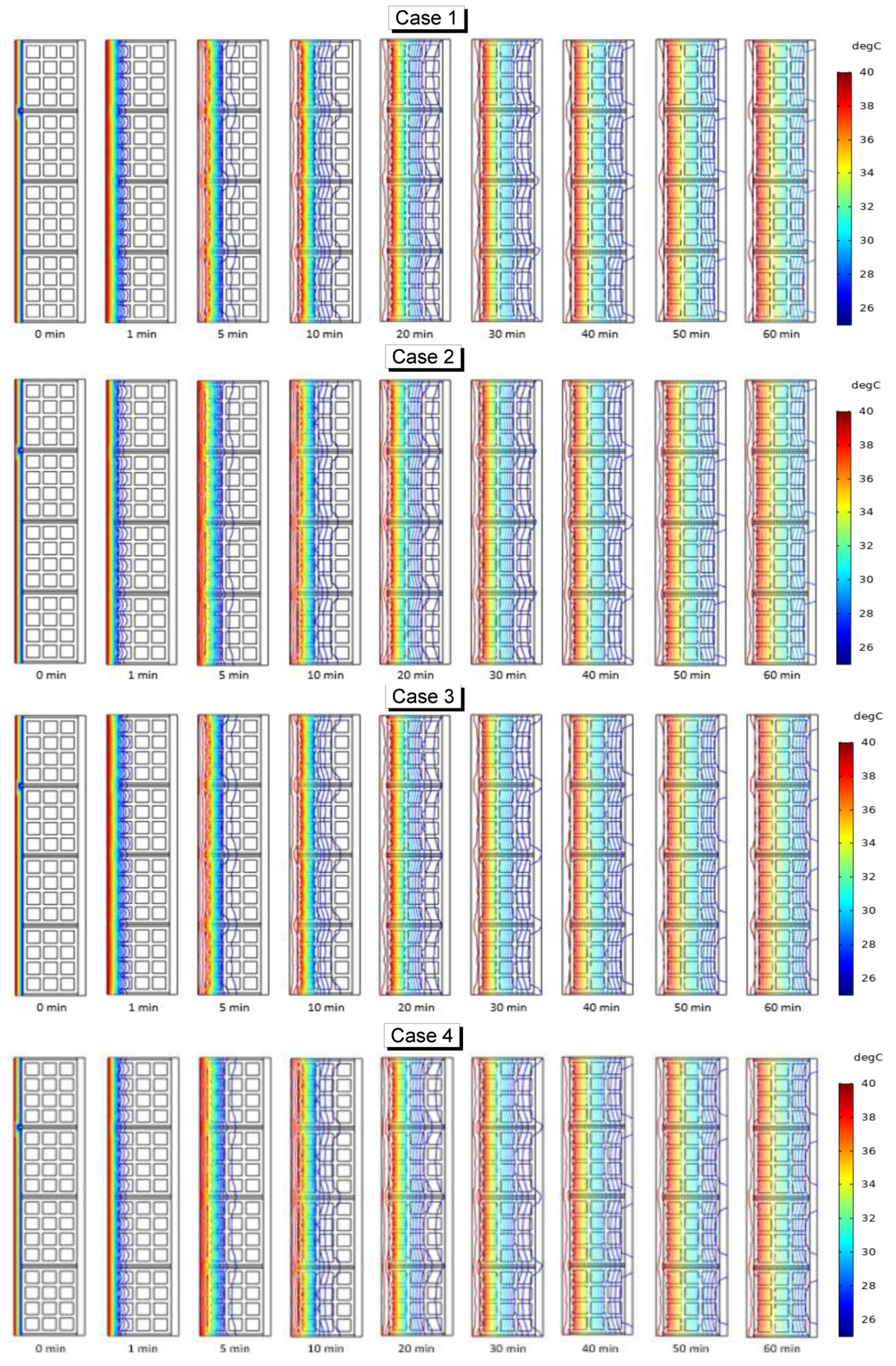
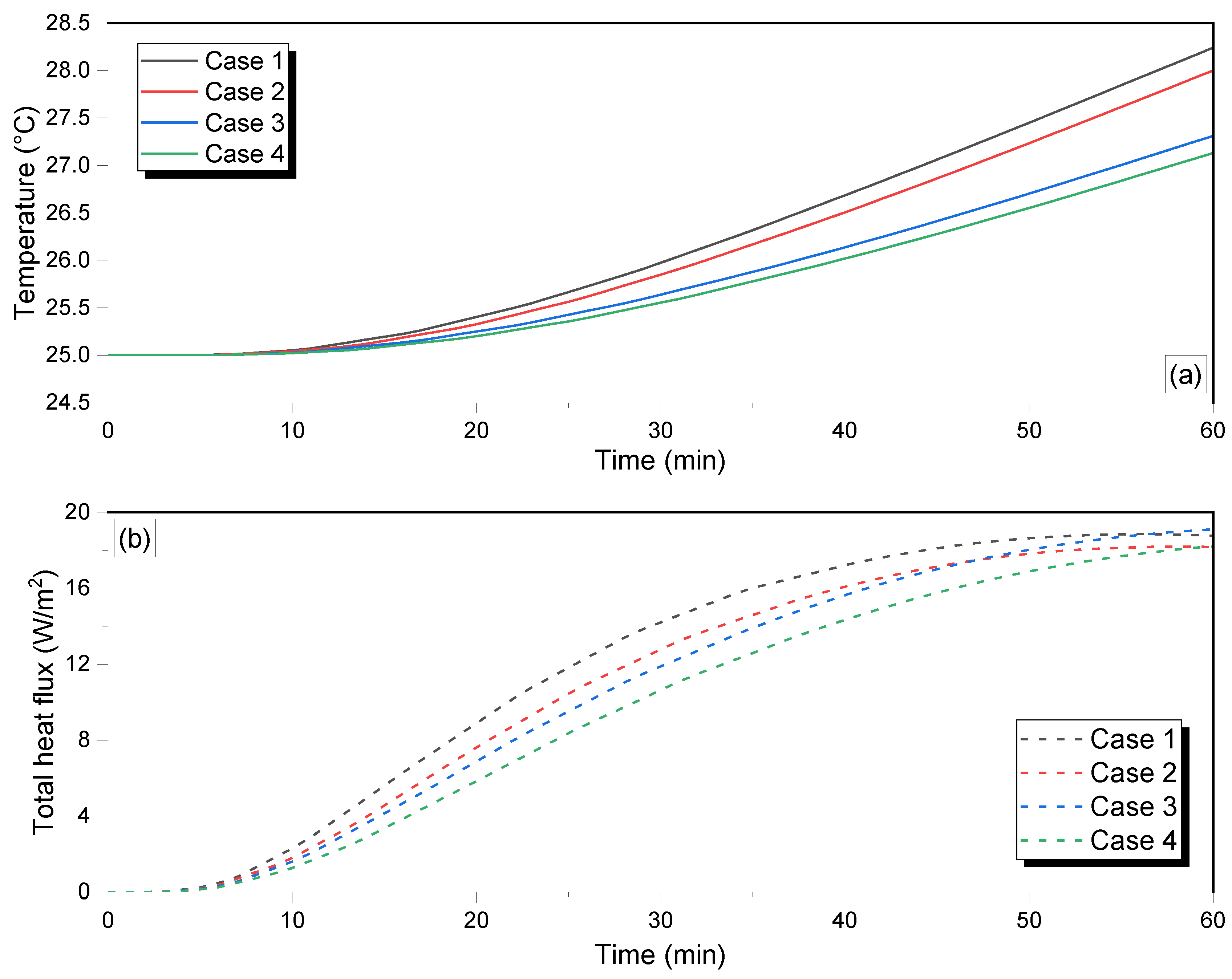
4.2. Computational Assessment of a Textile Reinforced Wall

Figure 18 summarizes the numerical results of the spatial variation in temperature after 50 min of thermal excitation for the different wall configurations. Figure 18d shows the temperature change along the wall thickness for both the first and second cases. As the graph shows, the temperature propagation in the wall of case 2, coated with textile-reinforced mortar on the outside and plain mortar on the inside, was slower than in the wall coated with ordinary mortar on both sides. Comparing case 1 and case 3, the temperature propagation along the first parts of the walls shows the same tendency since the outer coating layers consist of the same material. However, the integration of the textile into the inner layer of the wall of case 3 slowed down the spread of temperature, as shown in Figure 18e. The application of a textile-reinforced mortar as an inner coating material leads to a greater decrease in temperature than insulation applied to the external mortar layer. Figure 18f illustrates the effect of coating a wall with fiber-reinforced mortar on both sides. The use of textile mortar as a coating mortar on both sides showed the best results for reducing the temperature spread.

Figure 19 and Figure 20 present the variation in heat fluxes and inner surface temperatures versus time after the thermal excitation on the outer surface. As expected, the temperature profile of a wall depends on the thermal conductivity and, consequently, the thermal resistance of its components. As shown in Figure 19, the integration of the textile into the coating mortar reduced the temperature spread in the wall. In fact, the insulation of the outer surface caused a slight decrease in temperature, while the integration of the textile in the inner surface of the wall improved the thermal performance by almost 4% compared to case 1. However, the optimal values were obtained by the fourth case, where the wall was coated on both sides with textile-reinforced mortar. The temperature of the inner surface may decrease by approximately 1.5 °C using the textilized composite. The variation in heat flux, as shown in Figure 20b, also corroborates the results presented for the variation in inner surface temperature. Lower transmitted heat flux values were achieved when the reinforced mortar was incorporated into the investigated wall.

5. Conclusions and Perspective

The incorporation of recycled materials into building components is not only promoted for ecological reasons, but can also improve certain properties of building materials. Therefore, the objective of this study was to develop thermally enhanced cement-based materials by incorporating textile fiber waste as a replacement for sand in varying ratios. The results showed that textile fiber-reinforced mortars can be promising coating mortars due to their improved thermal properties and acceptable mechanical strength. In fact, replacing 40% of the sand with textile fibers caused drops in thermal conductivity, thermal diffusivity, and volumetric heat capacity by about 40%, 21%, and 23%, respectively, compared to ordinary cement mortar. Furthermore, the integration of textile fibers improved the flexural strength of cementitious mortar. Although the reinforcement of the mortar with textile fibers decreased the compressive strength, it still met the requirement for use as a coating mortar. Since the textile-reinforced mortar has a high potential to be used as a coating mortar, a numerical study was performed to study its impact on the thermal behavior of a hollow brick wall. The examined wall was coated with the reinforced mortar in different arrangements. The results showed that coating a wall with a 20 mm layer of textile-reinforced mortar on both sides improved the overall thermal performance.

This work sheds light on the influence of incorporating textile fiber waste as a thermal reinforcement material into cementitious mortar on both its thermal and mechanical properties and, thus, on its impact on a building element. The results highlighted the significant potential of using textile fibers in the development of more energy-efficient and environmentally-friendly building materials and practices as a means to minimize energy consumption and alleviate the environmental effects of widespread waste materials. Further research can be carried out to investigate the impact of textile fibers on the durability and long-term characteristics of cement mortars. Moreover, it would be beneficial to assess the influence of incorporating these materials on the thermal efficiency of entire buildings, beyond simply analyzing their effect on a single wall.