On Interpolative Meshless Analysis of Orthotropic Elasticity
Abstract
1. Introduction
2. Basics of Three Interpolative Meshless Shape Functions
2.1. Radial Point Interpolation Method (RPIM)
2.2. Improved Interpolating Moving Least-Squares Method (IMLSM)
2.3. Improved Interpolating Moving Least-Squares Method (IIMLSM)
3. The Establishment of Discrete Equations
4. Numerical Examples
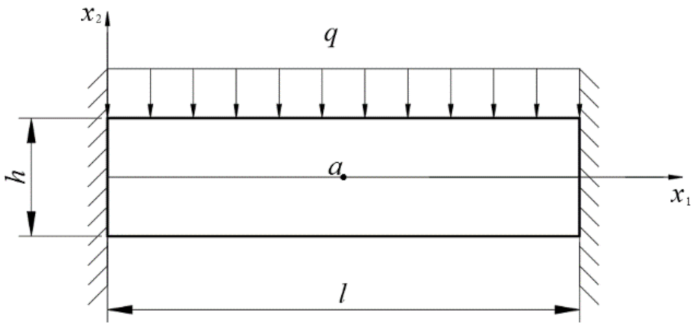
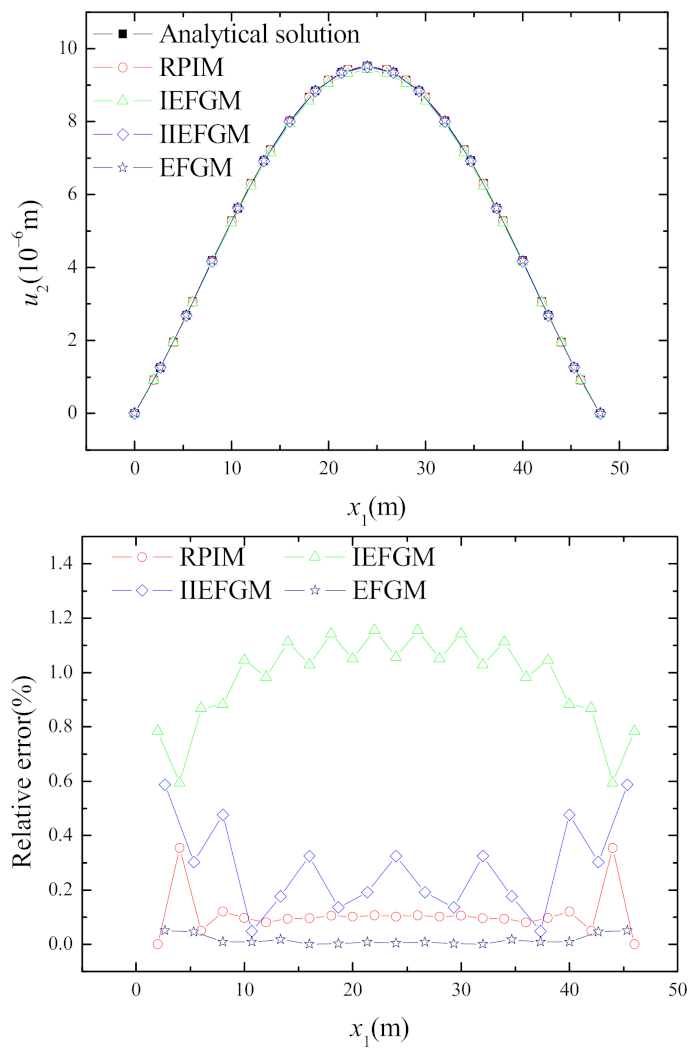
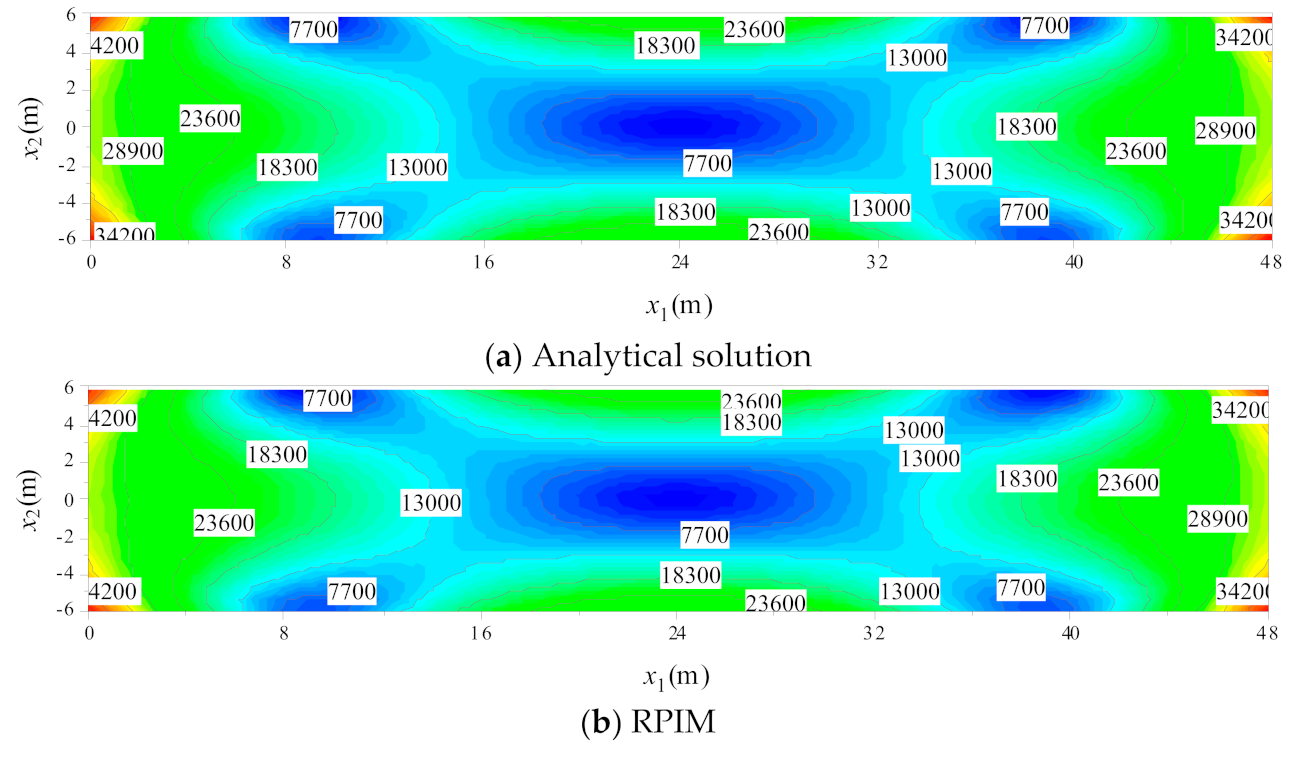
4.1. Clamped-Clamped Beam Subjected to Uniformly Distributed Load
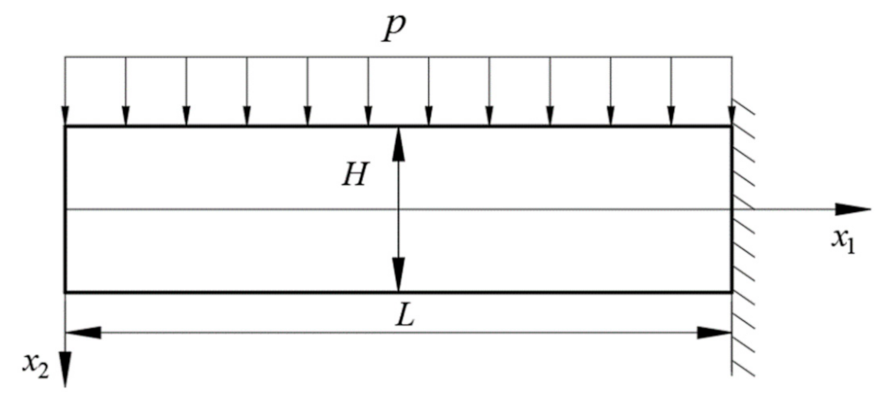
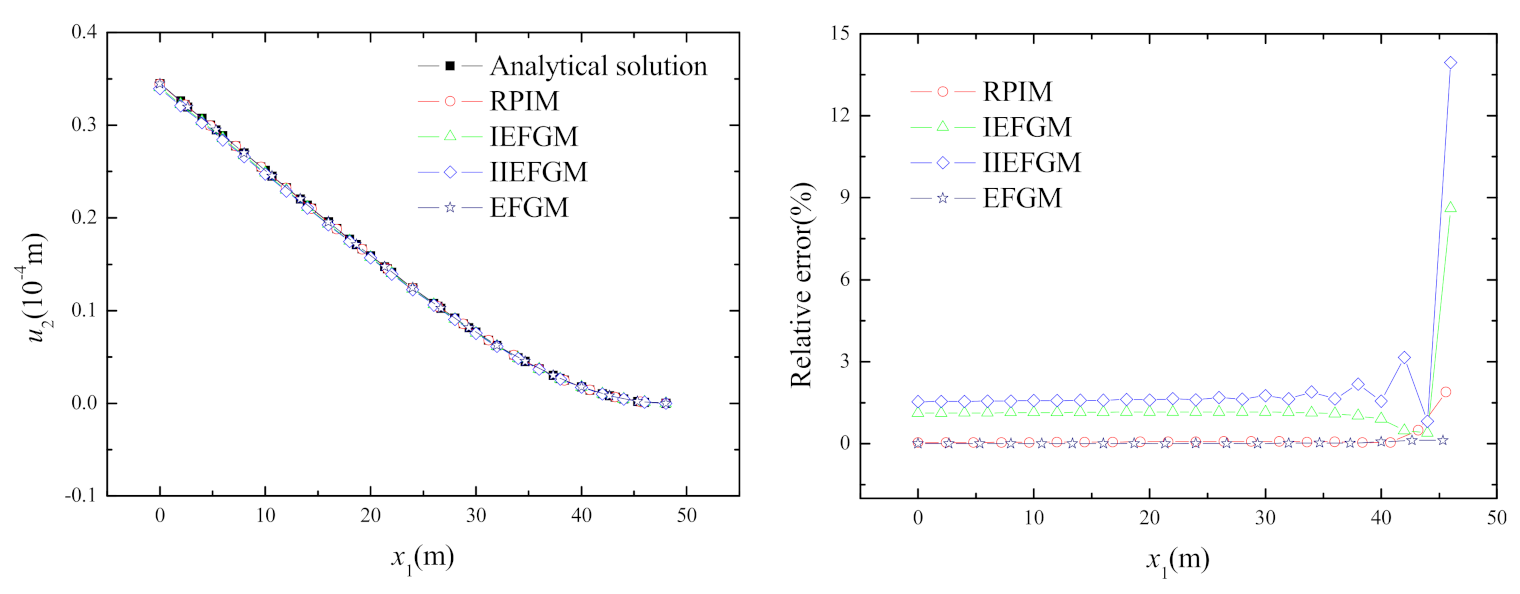
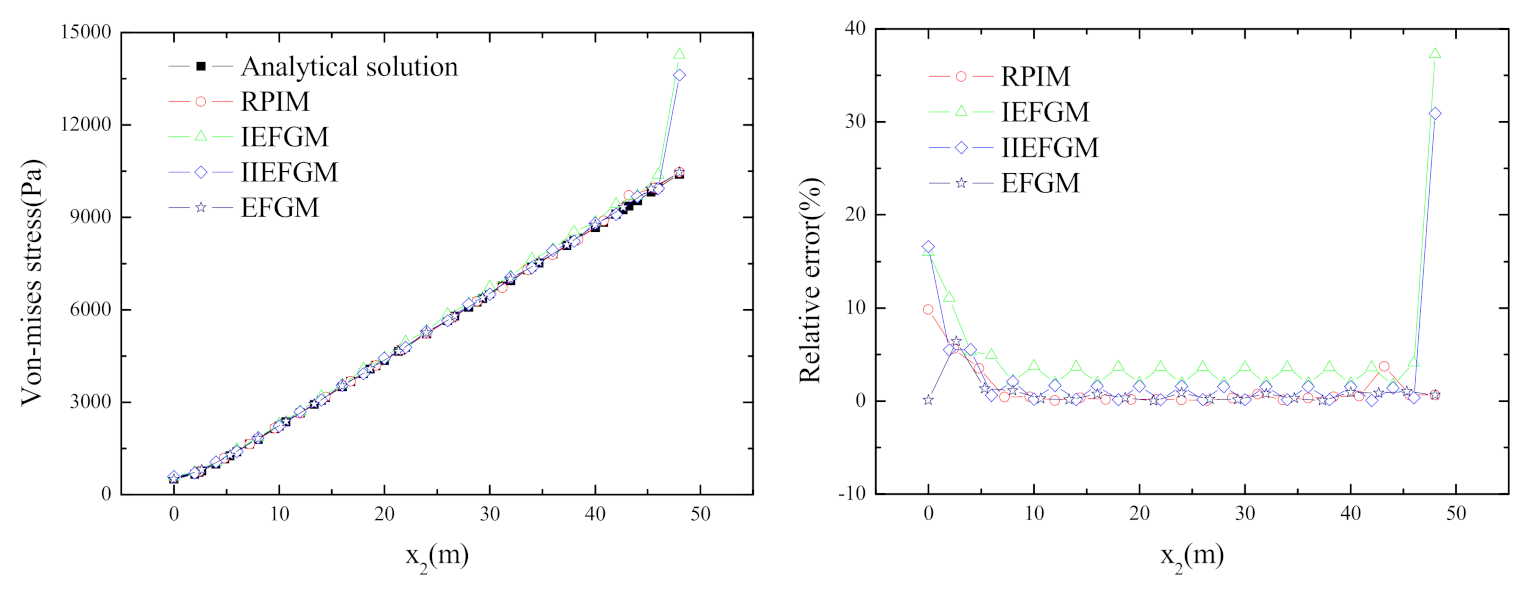
4.2. Cantilever Beam Subjected to a Uniform Load
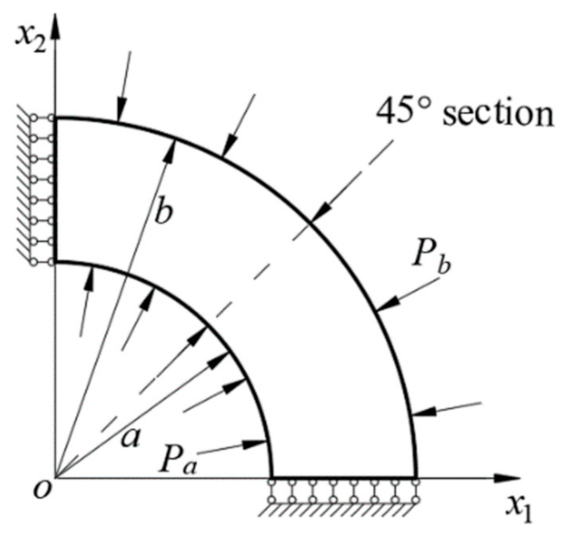
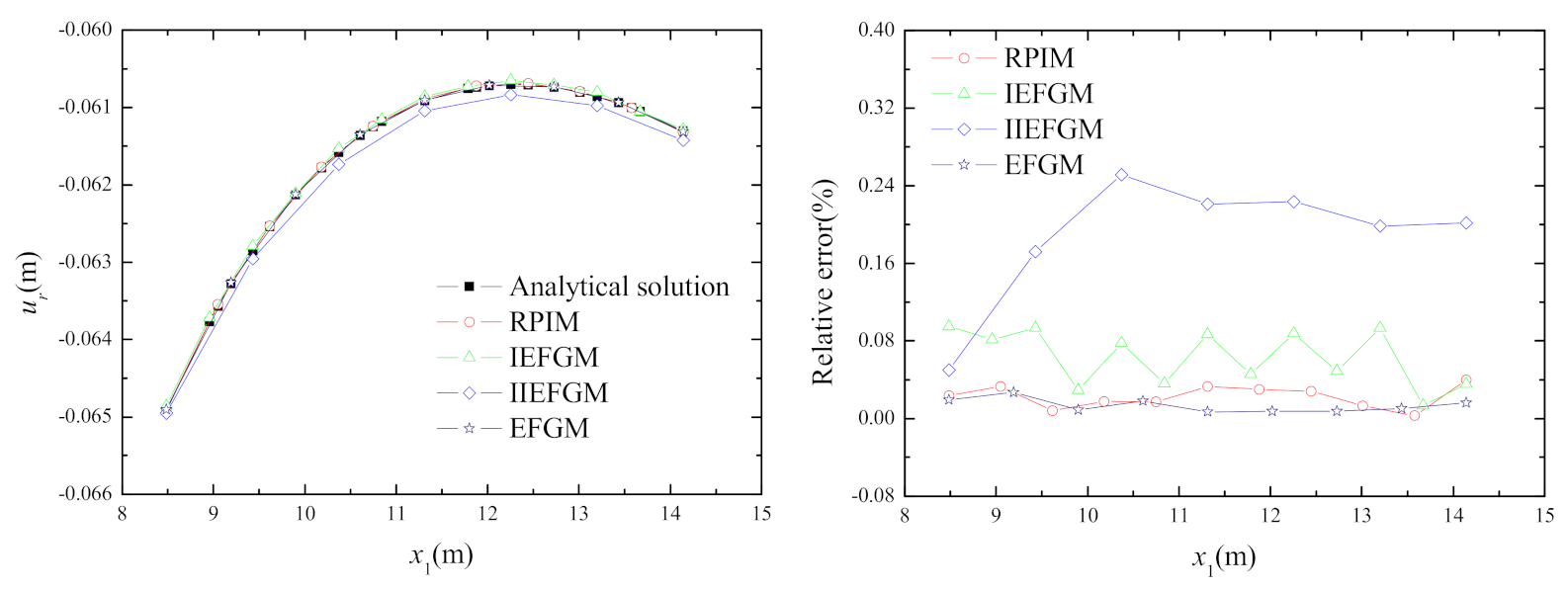
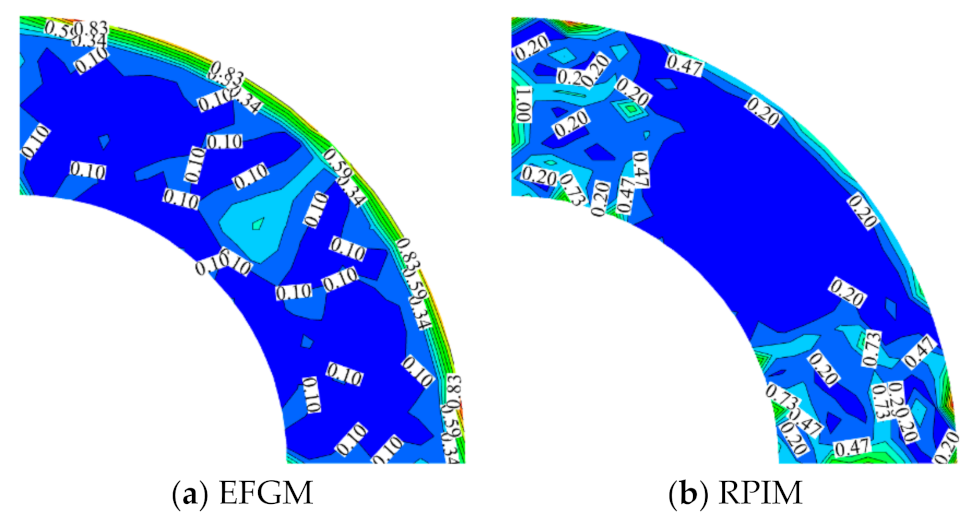
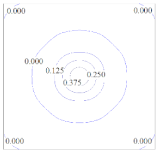
4.3. Ring under Pressures Applied Both Internally and Externally
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Belytschko, T.; Lu, Y.Y.; Gu, L. Element-free Galerkin methods. Int. J. Numer. Methods Eng. 2010, 37, 229–256. [Google Scholar] [CrossRef]
- Liu, W.K.; Jun, S.; Zhang, Y.F. Reproducing kernel particle methods. Int. J. Numer. Methods Fluids 1995, 20, 1081–1106. [Google Scholar] [CrossRef]
- Li, D.M.; Featherston, C.A.; Wu, Z.M. An element-free study of variable stiffness composite plates with cutouts for enhanced buckling and post-buckling performance. Comput. Methods Appl. Mech. Eng. 2020, 371, 113314. [Google Scholar] [CrossRef]
- Li, D.M.; Kong, L.H.; Liu, J.H. A generalized decoupling numerical framework for polymeric gels and its element-free implementation. Int. J. Numer. Methods Eng. 2020, 121, 2701–2726. [Google Scholar] [CrossRef]
- Chen, J.S.; Pan, C.H.; Wu, C.T.; Liu, W.K. Reproducing Kernel Particle Methods for large deformation analysis of non-linear structures. Comput. Methods Appl. Mech. Eng. 1996, 139, 195–227. [Google Scholar] [CrossRef]
- Li, D.M.; Tian, L.R. Large deformation analysis of gel using the complex variable element-free Galerkin method. Appl. Math. Model. 2018, 61, 484–497. [Google Scholar] [CrossRef]
- Li, D.M.; Liu, J.H.; Nie, F.H.; Featherston, C.A.; Wu, Z.M. On tracking arbitrary crack path with complex variable meshless methods. Comput. Methods Appl. Mech. Eng. 2022, 399, 115402. [Google Scholar] [CrossRef]
- Pan, J.H.; Li, D.M.; Luo, X.B.; Zhu, W. An enriched improved complex variable element-free Galerkin method for efficient fracture analysis of orthotropic materials. Theor. Appl. Fract. Mech. 2022, 121, 103488. [Google Scholar] [CrossRef]
- Liew, K.M.; Sun, Y.Z.; Kitipornchai, S. Boundary element-free method for fracture analysis of 2-D anisotropic piezoelectric solids. Int. J. Numer. Methods Eng. 2007, 69, 729–749. [Google Scholar] [CrossRef]
- Rabczuk, T.; Belytschko, T. Cracking particles: A simplified meshfree method for arbitrary evolving cracks. Int. J. Numer. Methods Eng. 2004, 61, 2316–2343. [Google Scholar] [CrossRef]
- Liu, G.R.; Gu, Y.T. A point interpolation method for two-dimensional solids. Int. J. Numer. Methods Eng. 2001, 50, 937–951. [Google Scholar] [CrossRef]
- Wang, J.G.; Liu, G.R. A point interpolation meshless method based on radial basis function. Int. J. Numer. Methods Eng. 2002, 54, 1623–1648. [Google Scholar] [CrossRef]
- Ren, H.P.; Cheng, Y.M. The interpolating element-free Galerkin method for two-dimensional elasticity problems. Int. J. Appl. Mech. 2011, 3, 735–758. [Google Scholar] [CrossRef]
- Lancaster, P.; Salkauskas, K. Surface generated by moving least squares methods. Math. Comput. 1981, 37, 141–158. [Google Scholar] [CrossRef]
- Wang, J.F.; Sun, F.X.; Cheng, Y.M. An improved interpolating element-free Galerkin method with a nonsingular weight function for two-dimensional potential problems. Chin. Phys. B 2012, 21, 090204. [Google Scholar] [CrossRef]
- Deng, Y.J.; He, X.Q. An improved interpolating complex variable meshless method for bending problem of Kirchhoff plates. Int. J. Appl. Mech. 2017, 9, 1750089. [Google Scholar] [CrossRef]
- Zhang, T.; Li, X.L. A variational multiscale interpolating element-free Galerkin method for convection-diffusion and Stokes problems. Eng. Anal. Bound. Elem. 2017, 82, 185–193. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, W.; Feng, Y.T.; Ma, G.; Cheng, Y.G.; Chang, X.L. An adaptive orthogonal improved interpolating moving least-square method and a new boundary element-free method. Appl. Math. Comput. 2019, 353, 347–370. [Google Scholar] [CrossRef]
- Singh, R.; Singh, K.M. Interpolating meshless local Petrov-Galerkin method for steady state heat conduction problem. Eng. Anal. Bound. Elem. 2019, 101, 56–66. [Google Scholar] [CrossRef]
- Bourantas, G.; Zwick, B.F.; Joldes, G.R.; Wittek, A.; Miller, K. Simple and robust element-free Galerkin method with almost interpolating shape functions for finite deformation elasticity. Appl. Math. Model. 2021, 96, 284–303. [Google Scholar] [CrossRef]
- Wang, L.; Qian, Z. A meshfree stabilized collocation method (SCM) based on reproducing kernel approximation. Comput. Methods Appl. Mech. Eng. 2020, 371, 113303. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Y.; Zou, Y.; Yang, F. A gradient reproducing kernel based stabilized collocation method for the static and dynamic problems of thin elastic beams and plates. Comput. Mech. 2021, 68, 709–739. [Google Scholar] [CrossRef]
- Qian, Z.; Wang, L.; Gu, Y.; Zhang, C. An efficient meshfree gradient smoothing collocation method (GSCM) using reproducing kernel approximation. Comput. Methods Appl. Mech. Eng. 2021, 374, 113573. [Google Scholar] [CrossRef]
- Quintero MA, M.; Tam CP, T.; Li, H.T. Structural analysis of a Guadua bamboo bridge in Colombia. Sustain. Struct. 2022, 2, 000020. [Google Scholar]
- Ponzo, F.C.; Antonio, D.C.; Nicla, L.; Nigro, D. Experimental estimation of energy dissipated by multistorey post-tensioned timber framed buildings with anti-seismic dissipative devices. Sustain. Struct. 2021, 1, 000007. [Google Scholar]
- Liew, K.M.; Lei, Z.X.; Yu, J.L.; Zhang, L.W. Postbuckling of carbon nanotube-reinforced functionally graded cylindrical panels under axial compression using a meshless approach. Comput. Methods Appl. Mech. Eng. 2014, 268, 1–17. [Google Scholar] [CrossRef]
- Wu, Z.M.; Raju, G.; Weaver, P.M. Optimization of postbuckling behaviour of variable thickness composite panels with Variable Angle Tows: Towards 'buckle-free' design concept. Int. J. Solids Struct. 2018, 132–133, 66–79. [Google Scholar] [CrossRef]
- Dinis LM, J.S.; Jorge RM, N.; Belinha, J. A 3D shell-like approach using a natural neighbour meshless method: Isotropic and orthotropic thin structures. Compos. Struct. 2010, 92, 1132–1142. [Google Scholar] [CrossRef]
- Njiwa, R.K. Isotropic-BEM coupled with a local point interpolation method for the solution of 3D-anisotropic elasticity problems. Eng. Anal. Bound. Elem. 2011, 35, 611–615. [Google Scholar] [CrossRef]
- Bui, T.Q.; Nguyen, M.N. A novel meshfree model for buckling and vibration analysis of rectangular orthotropic plates. Struct. Eng. Mech. 2011, 39, 579–598. [Google Scholar] [CrossRef]
- Fallah, N.; Nikrafter, N. Meshless finite volume method for the analysis of fracture problems in orthotropic media. Eng. Fract. Mech. 2018, 204, 46–62. [Google Scholar] [CrossRef]
- Lohit, S.K.; Gaonkar, A.K.; Gotkhindi, T.P. Interpolating Modified Moving Least Squares based element free Galerkin method for fracture mechanics problems. Theor. Appl. Fract. Mech. 2022, 122, 103569. [Google Scholar] [CrossRef]
- Luo, X.B.; Li, D.M.; Liu, C.L.; Pan, J.H. Buckling analysis of variable stiffness composite plates with elliptical cutouts using an efficient RPIM based on naturally stabilized nodal integration scheme. Compos. Struct. 2022, 302, 116243. [Google Scholar] [CrossRef]
- Hardy, R.L. Theory and applications of the multiquadrics-Biharmonic method (20 years of discovery 1968–1988). Comput. Math. Appl. 1990, 19, 163–208. [Google Scholar] [CrossRef]
- Lekhnit︠s︡kii, S.G. Anisotropic Plates; Gordon and Breach: Philadelphia, PA, USA, 1968. [Google Scholar]



| n1 × n2 | l1 × l2 | dmax | Others | |
|---|---|---|---|---|
| EFGM | 19 × 11 | 12 × 8 | 3.5 | = 3 × 1014 |
| RPIM | 25 × 11 | 12 × 8 | 4.5 | q = 2.5, c = 1.0 |
| IEFGM | 25 × 13 | 12 × 8 | 2.5 | = 6.0 |
| IIEFGM | 19 × 13 | 12 × 8 | 1.5 | — |
| MLS | RPIM | IMLS | IIMLS | |
|---|---|---|---|---|
 |  |  |  | |
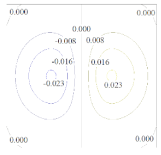 |  |  | 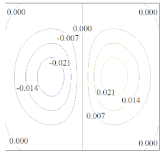 | |
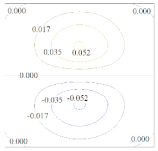 | 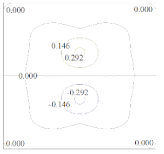 |  |  |
| n1 × n2 | l1 × l2 | dmax | Other Parameters | |
|---|---|---|---|---|
| EFGM | 19 × 13 | 12 × 8 | 3.5 | = 3 × 1014 |
| RPIM | 21 × 7 | 12 × 8 | 4.5 | q = 2.5, c = 1.0 |
| IEFGM | 25 × 13 | 12 × 8 | 1.5 | = 6.0 |
| IIEFGM | 25 × 13 | 12 × 8 | 1.5 | — |
| n1 × n2 | l1 × l2 | dmax | Other Parameters | |
|---|---|---|---|---|
| EFGM | 9 × 25 | 6 × 24 | 2.5 | = 2 × 108 |
| RPIM | 11 × 25 | 6 × 24 | 3.5 | q = 1.5, c = 1.0 |
| IEFGM | 13 × 25 | 6 × 24 | 1.5 | = 4.0 |
| IIEFGM | 7 × 25 | 6 × 24 | 1.5 | — |
| EFGM | RPIM | IEFGM | IIEFGM | |
|---|---|---|---|---|
| Radial displacement | 0.0001 | 0.000005 | 0.00085 | 0.0043 |
| Von Mises stress | 0.07225 | 0.0545 | 0.391 | 0.9947 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Y.-Y.; Tian, Y.-C.; Li, D.M.; Luo, X.-B.; Liu, B. On Interpolative Meshless Analysis of Orthotropic Elasticity. Buildings 2023, 13, 387. https://doi.org/10.3390/buildings13020387
Zou Y-Y, Tian Y-C, Li DM, Luo X-B, Liu B. On Interpolative Meshless Analysis of Orthotropic Elasticity. Buildings. 2023; 13(2):387. https://doi.org/10.3390/buildings13020387
Chicago/Turabian StyleZou, You-Yun, Yu-Cheng Tian, D. M. Li, Xu-Bao Luo, and Bin Liu. 2023. "On Interpolative Meshless Analysis of Orthotropic Elasticity" Buildings 13, no. 2: 387. https://doi.org/10.3390/buildings13020387
APA StyleZou, Y.-Y., Tian, Y.-C., Li, D. M., Luo, X.-B., & Liu, B. (2023). On Interpolative Meshless Analysis of Orthotropic Elasticity. Buildings, 13(2), 387. https://doi.org/10.3390/buildings13020387







