Study of Heat Recovery Equipment for Building Applications

Abstract

Nowadays, heat exchangers find widespread use across various applications in different fields, particularly in the field of heat recovery. This paper provides a detailed explanation of a plate heat exchanger counter-flow model developed in Simulink/Matlab. Water was employed in simulations for both circuits, although the thermal properties of other fluids can be investigated by modifying them. The “Tanks in series” method was used for simulation purposes. The developed model enables users to explore the impact of various parameters on heat exchanger functionality, such as altering the number of plates, the material or thickness of the plates, and the nature of thermal agents (gaseous or liquid). These models play a crucial role not only in simulating and sizing heat exchangers but also in achieving parametric optimization. Parameter variations can be employed to examine the operation of existing equipment under conditions different from their design specifications. The Simulink/Matlab proposed model, featuring a variable number of finite volumes to ensure high accuracy, was compared to the classical design method for plate heat exchangers. The results revealed good accuracy, with relative errors for heat transfer rate remaining below 2.6%. This research also considered the study of the number of finite volumes necessary for achieving accurate results. For the 40 finite volumes model, the relative error for heat transfer rate is less than 10%. Dividing the mesh into 50 finite volumes along the fluid flow direction resulted in relative errors ranging from 1.6% to 1.7%, indicating that a finer mesh was not necessary. To validate the conceived model, experimental data from the literature were compared. The relative errors for heat transfer rate between the Matlab/Simulink model’s results and experimental data ranged from 1.58% to 11.92%, demonstrating a strong agreement between the conceived model and the experimental values.

1. Introduction

Heat exchangers are used for a wide array of applications, with various types and sizes available on the market [1,2,3]. Almost every household is equipped with such devices, operating with different fluids on the primary and secondary circuits. The progression of these systems is characterized by the incorporation of novel technologies and materials, along with the utilization of dynamic simulation models for the purpose of optimization and performance evaluation. The advancement of these models, specifically for plate heat exchangers, has been significantly aided by software tools such as Simulink and Matlab, which allow for thorough examination and enhancement under different operational circumstances [4,5,6].

The interest in developing dynamic simulation models lies in implementing heat transfer equations in a simulation environment that facilitates the creation of a fast and user-friendly model. The modeled heat exchanger in this study is of the counter-flow type, using a plate surface and employing the “tanks in series” method for meshing [7,8]. This method involves a mesh structure that can be optimized to ensure acceptable computing times.

Literature studies have focused on modeling tube-in-tube heat exchangers using refrigerant cycles, particularly for the evaporator and condenser of mechanical compression cooling machines [9]. Given that every mechanical compression machine incorporates at least two heat exchangers, the significance of these devices and their dynamic simulations becomes evident. Adsorption machines used for cooling purposes feature four heat exchangers, using different cooling agents and fluids at varying temperatures in either vapor or liquid states [10,11]. Each aspect is crucial for the sizing and design of heat exchangers, employing diverse approaches and dynamic simulation tools.

Other simulation models for heat exchangers address steady-state conditions, offering faster simulation times. Optimizations of the number of channels, passes, and various configurations are analyzed and refined [12]. Additionally, variable inlet parameters play a key role in simulating real conditions encountered in applications with heat exchangers (such as variable seawater temperature, outside air temperature, or well water temperature). The purpose of these simulations is to explore the optimal configuration of the parameters described above and to understand the influence of a constant or variable overall heat transfer coefficient.

Papers addressing malfunctions in the operation of heat exchangers are particularly interesting in cold climates [13]. These exchangers are commonly used for air cooling in cooling batteries within air handling units, frequently found in numerous office buildings. In marine applications, these heat exchangers utilize air-to-water fluids. Malfunctions may occur due to freezing water, which can partially or completely block the heat exchanger. Therefore, it is crucial to input the water temperature at the inlet of the heat exchanger into the model, considering that seawater temperature can vary, sometimes reaching freezing conditions depending on the depth of aspiration.

The Laplace transform was employed as a simulation tool in Matlab/Simulink software R2015b, and validation results are also presented. The heat exchanger in question is a cross-flow unit, and the discretization uses the Laplace transform to incorporate bi-dimensional modeling.

A similar simulation model explored water-to-water heat exchangers developed in the Matlab/Simulink environment, a user-friendly simulation platform with a useful library featuring numerous examples of different component types that can be connected to create the desired model for study [14]. The implementation involved differential finite equations, and various parameter variations are presented. The mathematical model is iterative, with variable simulation times for different solvers, offering the flexibility of using either fixed or variable steps based on the equations implemented in the design.

Matlab/Simulink simulation software presents significant advantages, being a well-known tool with ample online resources for assistance, including a comprehensive presentation of similar topics on the developer’s website. It comprises two distinct software components, with Matlab serving as a classic computer programming tool, while Simulink operates as block connection software featuring blocks with diverse functions, ranging from simple to more complex.

The results presented [14] used a discretization with just five elementary cells due to the required computing time, considering both summer and winter sea water temperatures in steady-state conditions with water properties derived from the Black Sea. This research provides numerical results at each node without optimizing the discretization or comparing them with experimental data. Future work should involve the incorporation of variable inlet parameters, such as water temperature and flow, along with a comparison with experimental data and optimization of the model’s discretization.

Over the past few years, there has been an increasing use and modeling of a specific heat exchanger: the vertical ground heat exchanger. Due to the prevalence of heat pumps, particularly the ground-to-water type, optimizing and designing such a heat exchanger becomes crucial for long-term usage. Dedicated software applications exist for this purpose, as well as experimental tests that play a vital role in simulation and sizing [15,16,17]. For buildings requiring a substantial number of wells and ground heat exchangers, their quantity is of great significance for economic reasons [18,19,20]. The Thermal Response Test (TRT) experimental method is a widely employed measurement in such applications. It involves measuring the properties of the soil in a specific location to provide essential data for simulations and design capacities of ground heat exchangers, especially for heat pumps in large buildings.

In pursuit of energy efficiency and a higher fresh air rate, air-to-soil heat exchangers are also used in large building applications with significant airflow requirements. These systems involve placing a special type of plastic pipe, typically containing silver ions for bacteriological reasons, into the ground. This setup heats and cools the indoor air needed for the building’s Air Handling Units, recovering energy freely from the ground. Commonly referred to as a Canadian well or Provençal well, such a heat exchanger can also be designed for cooling purposes in warm climates [21,22,23]. The performance of this heat exchanger depends on various factors, such as soil nature, airflow, humidity, meteorological conditions, groundwater depth, and the depth of the grounded heat exchanger.

The diverse heat exchangers described above have broad applications in our lives and are available in various types on the market. The present work focuses on the simulation and optimization of a plate heat exchanger’s meshing into several elementary cells. As a prospective step, besides comparing the fundamentals of heat transfer theory, an experimental setup would be valuable. A comparison between modeling in Matlab/Simulink and measured values is presented and discussed [24]. The model used consists of three partial differential equations (PDEs) employing the finite volume method. Due to the short fluid residence time and limited dynamics of the inlet temperatures in this work, only one cell volume was used in the simulations. A good agreement was found with the experimental results, validating the simulated model.

Another study presents dynamic simulations of a counter-flow heat exchanger [25]. The results of this study are presented and compared to experimental data found in the literature to validate the results. Simulations include inlet temperatures for both fluids and changes in the mass flow rate. The numerical method in this case is based on the analytical solution of the energy equation, a model that, according to the authors, offers a fast computing time.

An interesting and similar work are presented in [26] with a simplified plate heat exchanger model, compared and validated with experimental data. The Orthogonal Collocation Method (OCM) is used for discretization, and the accuracy and comparison with experimental data are reported to be very good.

Studies on heat transfer involving 3D nanofluids (water-based) are presented in [27]. Another mathematical model concerning fluid flow through a porous and stretching sheet is analytically simulated, including mass transfer, thermal radiation, and Hall current [28]. Detailed mathematical approaches concern hybrid nanofluid flow energy transfer through a permeable vertically rotating surface [29] and other numerical models of heat transfer, including convergence of the studied models [30,31]. These nanofluids have demonstrated promising capabilities in enhancing thermal conductivity and heat transfer efficiency. The investigation of Al₂O₃-water nanofluids has been conducted to assess their impact on the efficiency of cross-flow microheat exchangers, revealing notable enhancements in heat transfer capabilities [32,33,34,35,36]. Furthermore, the incorporation of heat exchangers into intricate systems, such as solar thermal heat pump hybrid systems, has been subjected to modeling in order to enhance energy preservation in buildings. This analysis underscores the significance of heat exchangers in sustainable energy alternatives [37].

An interesting study presents an investigation on how ultrasonic excitation affects heat transfer rates in a fin-and-flat tube heat exchanger [38]. Parameters such as ambient temperature, flow rate, air passing velocity, Reynolds number, and Nusselt number were varied. Results show that reducing flow rate, ambient temperature, and air passing velocity enhances ultrasonic effects, with the highest heat transfer enhancement reaching 70.11%. The findings offer valuable insights for optimizing the design of ultrasonic vibrating fin-and-tube heat exchangers.

Studies investigate how nanofluid concentration influences heat transfer in an ultrasonic finned tube heat exchanger using a Multi-Walled Carbon Nanotube (MWCN) [39]. This research validates results and assesses uncertainties, exploring parameters like ambient temperature and MWCNT concentration. Findings indicate enhanced heat transfer with increased nanofluid concentration, proposing a promising avenue for combining nanofluid and ultrasonic benefits in optimal conditions.

Recent studies explore the heat performance of a Multi-Layered Oscillating Heat Pipe Heat Exchanger (ML-OHPHE) for heat recovery in HVAC systems [40]. Experimental tests under different conditions were conducted and compared with simulations using Honeywell’s UniSim^® Design Suite software. The results suggest that the ML-OHPHE could effectively serve as a passive heat transfer device for HVAC heat recovery [40].

Metal additive manufacturing (AM) with SUS316L material to create oscillating heat pipes was considered in recent studies [41]. Experiments on printing parameters and thermal performance were conducted. Suitable laser parameters produced oscillating heat pipes with good compactness and minimal dimensional error. This study also investigated the impact of inter-channel spacing on thermal performance, revealing that reducing thermal interaction can enhance the oscillation effect, resulting in improved equivalent thermal conductivity. The experiments demonstrated higher equivalent thermal conductivity at low power with reduced thermal interaction [41].

In summary, the ongoing investigation and progress in heat exchanger technology, which encompasses a range of kinds and applications, plays a vital role in the progression of energy systems. The incorporation of novel materials, computer modeling, and optimization methods plays a crucial role in augmenting the effectiveness and sustainability of heat exchangers. This, in turn, contributes to worldwide endeavors aimed at conserving energy and safeguarding the environment.

The novelty of this paper lies in the detailed explanation of a counter-flow plate heat exchanger model developed using Simulink/Matlab. Water was employed in simulations for both circuits, although the thermal properties of other fluids can be investigated by modifying them. The “Tanks in series” method was utilized for simulation purposes. The developed model enables users to explore the impact of various parameters on heat exchanger functionality, such as altering the number of plates, the material or thickness of the plates, and the nature of thermal agents (gaseous or liquid). The results of the proposed Simulink/Matlab model were compared to the classical design method for plate heat exchangers and experimental data from the literature.

2. Materials and Methods

This study aim was to describe by numerical simulations heat transfer between two fluids crossing a plate heat exchanger. Heat transfer equations were solved using Matlab/Simulink mathematical modeling software. The Matlab/Simulink model was tested under the same conditions as a heat exchanger designed with a classical algorithm from the literature [31]. The input parameters were the same for the Matlab/Simulink model, and for the classical calculated method, the output temperatures for both fluids obtained with both methods were compared. Also, the heat flow values were compared. Relative errors were calculated between the two methods, both for fluids’ outlet temperatures and heat flow. Experimental data from the literature [31] were taken for the plate heat exchanger, and the conceived Matlab/Simulink model was tested for the same conditions. The purpose of both comparisons with the conceived model was to express the good agreement of our model with two very different methods of validation.

The conceived model can be used by engineers to determine heat exchanger working parameters for other conditions than the ones presented in the technical report of an equipment, being very useful and user-friendly. As well, changing the number of plates or the type of plate can be of interest to a heat exchanger designer. Generally, the working parameters are given for testing conditions, but real-life situations differ from those conditions. So, easily determining the correct value for heat flow for different inlet/outlet temperatures is often very useful for thermal engineers. All parameters are introduced by the model user in a panel, a “mask.”

2.1. Overall Heat Transfer Coefficient and Plate Heat Exchanger Calculation

The first step in our study was to calculate the overall heat transfer coefficient and plate heat exchanger design according to [31], as described hereafter. The input data for the heat exchanger were: both fluids were water; the primary fluid’s temperatures vary between 90 °C and 104 °C; and the two fluids’ temperatures vary between 60 °C and 80 °C. The exchanger’s heat transfer rate was 168 kW. The heat exchanger was made of stainless-steel plates, each one having 0.2 m² surface area. The plate’s thickness was 5.5 mm. Plate thickness is not a usual one, but we considered it to test the model limitations under very different conditions.

The heat balance equation written for a heat exchanger is as follows:

$$\varnothing =\mathsf{\eta } {\mathsf{\rho }}_{\mathrm{a}1}{\mathrm{V}}_{\mathrm{a}1}{\mathrm{c}}_{{\mathrm{p}}_{\mathrm{a}1}}\left({\mathrm{T}}_{\mathrm{a}1 \mathrm{in}}-{\mathrm{T}}_{\mathrm{a}1 \mathrm{out}}\right)={\mathsf{\rho }}_{\mathrm{a}2}{\mathrm{V}}_{\mathrm{a}2}{\mathrm{c}}_{{\mathrm{p}}_{\mathrm{a}2}}\left({\mathrm{T}}_{\mathrm{a}2 \mathrm{in}}-{\mathrm{T}}_{\mathrm{a}2 \mathrm{out}}\right)=\mathrm{U} \mathrm{S} ∆{\mathrm{T}}_{\log }$$

(1)

where: $\varnothing$ is the heat flow [W]; $\mathsf{\eta }$ is the thermal isolation efficiency, ${\mathsf{\rho }}_{\mathrm{a}1}$ and ${\mathsf{\rho }}_{\mathrm{a}2}$ are the fluids’ density at mean temperature [kg/m³]; ${\mathrm{V}}_{\mathrm{a}1}$ and ${\mathrm{V}}_{\mathrm{a}2}$ are the volumetric flows for both fluids [m³/s]; ${\mathrm{c}}_{{\mathrm{p}}_{\mathrm{a}1}}\mathrm{a}\mathrm{n}\mathrm{d} {\mathrm{c}}_{{\mathrm{p}}_{\mathrm{a}2}}$ are the fluids’ heat capacity at mean temperature [J/(kg·K)]; ${\mathrm{T}}_{\mathrm{a}1 \mathrm{i}\mathrm{n}} \mathrm{a}\mathrm{n}\mathrm{d} {\mathrm{T}}_{\mathrm{a}1 \mathrm{o}\mathrm{u}\mathrm{t}}$ the inlet and outlet temperature for primary fluid [K]; ${\mathrm{T}}_{\mathrm{a}2 \mathrm{i}\mathrm{n}} \mathrm{a}\mathrm{n}\mathrm{d} {\mathrm{T}}_{\mathrm{a}2 \mathrm{o}\mathrm{u}\mathrm{t}}$ the inlet and outlet temperature for secondary fluid [K]; U is the overall heat transfer coefficient [W/(m²·K)]; S is the total surface of all thermally effective plates [m²]; $∆{\mathrm{T}}_{\mathrm{l}\mathrm{o}\mathrm{g}}$ is the logarithmic mean temperature difference [K], calculated for counter-flow arrangements.

According to the heat balance Equation (1) and fluids’ thermal properties, the mass flow rate for each fluid can be calculated. From the third part of the same equation, the total surface area of all thermally effective plates can be estimated as a first step. For this, the logarithmic mean temperature difference can be calculated using the input data and an overall heat transfer coefficient estimated in a custom range for a plate heat exchanger (in our case, between 3000 and 7000 W/m²·K). The plate’s characteristics depend on the manufacturer we considered the following for our study: stainless steel plates, each having a 0.2 m² surface area and a 5.5 mm thickness.

The effective number of plates is:

$$\left({\mathrm{N}}^{\prime }-2\right)=\frac{{\mathrm{S}}^{\prime }}{\mathrm{s}}$$

(2)

where N′ is the preliminary total number of plates and S′ is the total surface of all thermally effective plates [m²].

The hydraulic diameter of the channel d_h (Equation (3)), channel flow area, flow rates (obtained from Equation (1)), and thermodynamic fluid properties at their mean temperature are used to calculate the first flow speed and the heat transfer coefficient.

$${\mathrm{d}}_{\mathrm{h}}=\frac{4 \mathrm{channel} \mathrm{flowarea} \mathrm{area}}{\mathrm{wetted} \mathrm{perimeter}}=\frac{4 \mathrm{g}\mathrm{L}}{2\left(\mathrm{g}+\mathrm{L}\mathsf{\phi }\right)}\approx \frac{2 \mathrm{g}}{\mathsf{\phi }}$$

(3)

where g is the channel spacing, L is the plate’s width, and $\mathsf{\phi }$ is the surface enlargement factor, defined as the ratio of the actual effective area given by the manufacturer to the projected plate area.

The mass flow rate per channel, mass velocity, and Reynolds number for cold and hot fluids can be calculated afterwards. Heat transfer coefficients strongly depend on a large number of parameters, like chevron inclination angle relative to flow direction, corrugation profile, channel spacing, surface enlargement factor ($\mathsf{\phi })$, thermodynamic temperature-dependent fluids’ properties, etc. Parts of these parameters are not completely presented by the manufacturer. The conventional approach for heat transfer coefficient employs a correlation between the Nusselt number and Reynolds number based on the hydraulic diameter of the channel (Equation (3)) [24].

The overall heat transfer coefficient, which also considers the heat exchanger’s fouling, can be estimated as:

$$\mathrm{U}=\frac{1}{{\mathrm{h}}_{\mathrm{h}\mathrm{o}\mathrm{t} \mathrm{f}\mathrm{l}\mathrm{u}\mathrm{i}\mathrm{d}}}+\frac{1}{{\mathrm{h}}_{\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{d} \mathrm{f}\mathrm{l}\mathrm{u}\mathrm{i}\mathrm{d}}}+\frac{{\mathsf{\delta }}_{\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e}}}{{\mathsf{\lambda }}_{\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e}}}+{\mathrm{R}}_{\mathrm{f}\mathrm{o}\mathrm{u}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{c}\mathrm{o}\mathrm{l}\mathrm{d} \mathrm{s}\mathrm{i}\mathrm{d}\mathrm{e}}+{\mathrm{R}}_{\mathrm{f}\mathrm{o}\mathrm{u}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{h}\mathrm{o}\mathrm{t} \mathrm{s}\mathrm{i}\mathrm{d}\mathrm{e}}$$

(4)

where: h _{hot fluid} and h _{cold fluid} are the heat transfer coefficients for hot and cold fluid (W/m² K), ${\mathsf{\delta }}_{\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e}}$ is the plate thickness (m), ${\mathsf{\lambda }}_{\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e}}$ is the thermal conductivity of the plate material (W/m K), ${\mathrm{R}}_{\mathrm{f}\mathrm{o}\mathrm{u}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{c}\mathrm{o}\mathrm{l}\mathrm{d} \mathrm{s}\mathrm{i}\mathrm{d}\mathrm{e}}$ and ${\mathrm{R}}_{\mathrm{f}\mathrm{o}\mathrm{u}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{h}\mathrm{o}\mathrm{t} \mathrm{s}\mathrm{i}\mathrm{d}\mathrm{e}}$ are the fouling resistance on cold and hot sides (m² K/W). For our calculus, the fouling was neglected on both sides.

After the overall heat transfer is calculated, if the difference between the calculated value and the estimated one used as a preliminary one is less than 3%, the design step is finished. Otherwise, the next iteration is started using the last calculated overall heat transfer coefficient, and the iterations are continued until a less than 3% error is obtained.

The process specifications and construction data for the plate heat exchanger are presented in

Table 1. The process specification data for the plate heat exchanger.

Parameter	Hot Fluid	Cold Fluid
Fluids	Wastewater	Cooling water
Mass flow rates (kg/s)	2.88	2.01
Inlet temperature (°C)	104	60
Outlet temperature (°C)	90	80
Specific heat (J/g K)	4.21	4.19
Viscosity (s/m2)	0.284 × 10−6	0.415 × 10−6
Thermal conductivity (W/m K)	0.6836	0.6676
Density (kg/m3)	955.4	977.7
Nusselt (-)	195	168.7
Heat transfer coefficient (W/m2 K)	12,090	10,238

.

Table 2. The constructional data for the plate heat exchanger.

Parameter	Value	U.M.
Plate material	Stainless Steel	(-)
Thermal conductivity of plate material	17	W/m K
Plate surface	0.2	m2
Plate thickness	5.5	mm
Plate height	989	mm
Plate width	242	mm
Plate material density	7850	kg/m3
Plate material-specific heat	0.49	J/g K
Chevron angle	60	degrees
Enlargement factor	1.19	-
Effective number of plates	10	-

presents the calculated parameters for the heat exchanger, based on the described method and the value from the last iteration. These values are further used in simulations in Matlab/Simulink.

2.2. Heat Exchanger Simulation in Matlab/Simulink

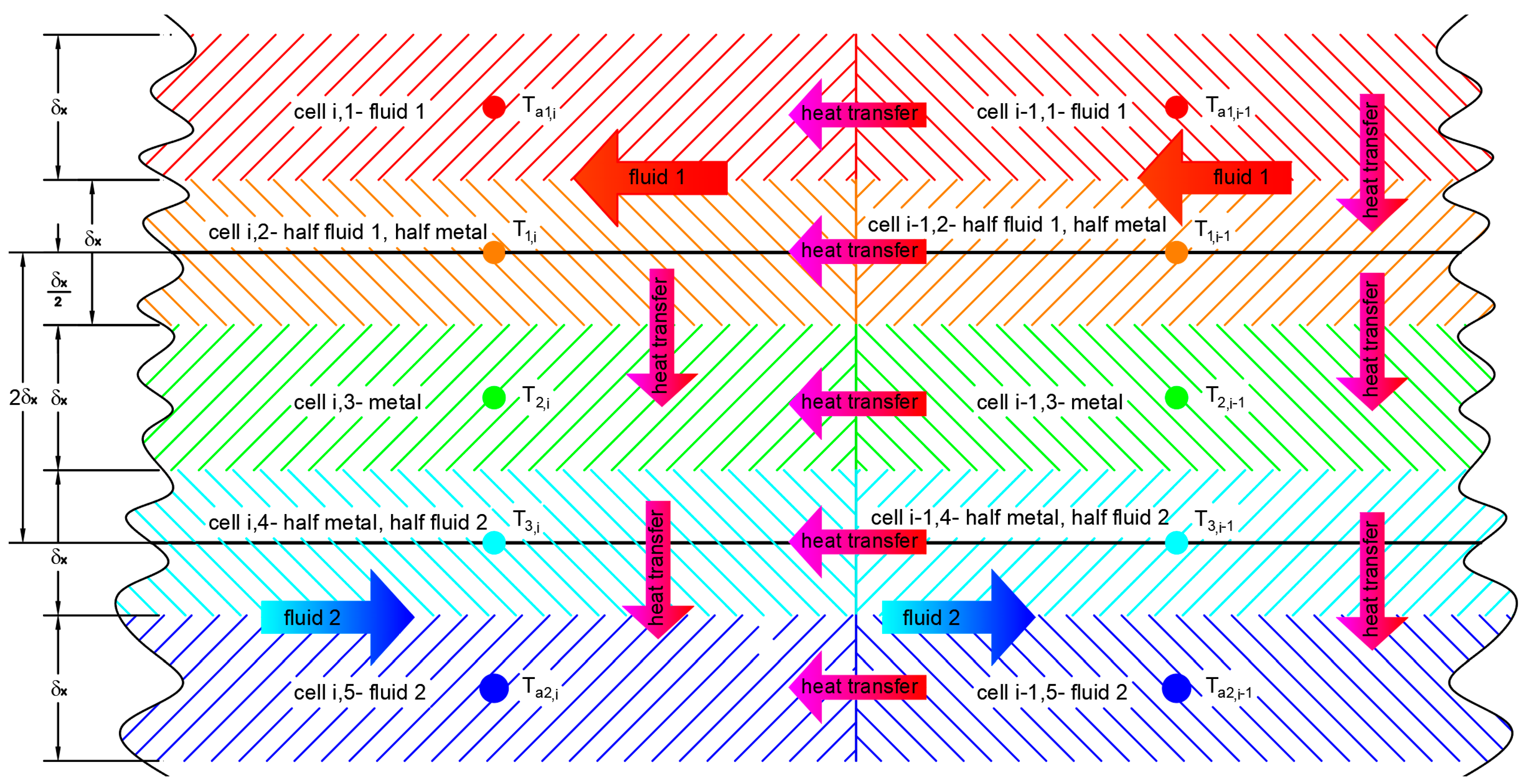
Each system’s element to be modeled is represented by a block containing either the equations’ characteristics or blocks that represent the system’s sub-elements. Those blocks can also be pre-programmed elements representing different operators, like integration, sum, product, etc., or different software functionalities, like visualization of results, for example. Whatever their nature, the blocks are connected to each other in the graphic interface to assemble the system’s equations and reproduce its operating dynamics.

The heat transfer algorithm based on the heat transfer equations is presented in Figure 1 for two simulation elementary cells, cell “i” and cell “i − 1”.

In order to describe the heat transfer, five elementary cells were considered in the heat transfer rate direction. For each cell, a heat transfer equation was considered based on previous research experience [41,42], as follows:

• Cell _i,1, which describes fluid 1 temperature variation, is noted with “T_a1”. Fluid 1 is the one with the highest temperature. This cell is placed in the fluid 1 zone, with forced convection heat transfer being considered.

$${\mathsf{\rho }}_{\mathrm{a}1}{\mathrm{V}}_{\mathrm{a}1}{\mathrm{c}}_{{\mathrm{p}}_{\mathrm{a}1}}\frac{\mathrm{d}{\mathrm{T}}_{\mathrm{a}1}}{\mathrm{d}\mathrm{t}}={\mathrm{h}}_{\mathrm{T}1}{\mathrm{A}}_{\mathrm{s}}\left({\mathrm{T}}_1-{\mathrm{T}}_{\mathrm{a}1}\right)+{\mathrm{w}}_{\mathrm{a}1}{\mathrm{c}}_{{\mathrm{p}}_{\mathrm{a}1}}\left({\mathrm{T}}_{\mathrm{a}1\mathrm{i}\mathrm{n}}-{\mathrm{T}}_{\mathrm{a}1}\right)$$

(5)

where: ${\mathsf{\rho }}_{\mathrm{a}1}$ is the primary fluid’s density at mean temperature [kg/m³]; ${\mathrm{V}}_{\mathrm{a}1}$ is the primary fluid volumetric flow [m³/s]; ${\mathrm{c}}_{{\mathrm{p}}_{\mathrm{a}1}}$ is the primary fluid’s heat capacity at mean temperature [J/(kg·K)]; ${\mathrm{T}}_{\mathrm{a}1} \mathrm{i}\mathrm{s}$ the cell i,1 temperature for primary fluid [K]; ${\mathrm{T}}_{\mathrm{a}1 \mathrm{i}\mathrm{n}}$ is the cell_i,1 inlet temperature for primary fluid [K]; h_T1 is the heat transfer coefficient for primary fluid [W/(m²·K)], ${\mathrm{A}}_{\mathrm{s}}$ is cell _i,1 heat surface [m²], ${\mathrm{T}}_1$ is the cell _i,2 temperature [K]; ${\mathrm{w}}_{\mathrm{a}1}$ is the primary fluid mass flow [kg/s].

• Cell i,2, which describes the plate temperature variation on the side of fluid 1, is noted with “T₁”. Half of this cell dimension in the heat transfer rate direction is placed in the fluid 1 zone, and the other half is in the plate thickness. The plate thickness is, as presented in Figure 1, “2δ_x”. Each elementary cell has a “ δ_x” thickness. The thickness of the cell is its dimension in the heat transfer rate direction. Heat transfer inside this cell is obtained by forced convection in the fluid layer and conduction in the metal layer.

$${\mathsf{\rho }}_{\mathrm{m}}\frac{{\mathsf{\delta }}_{\mathrm{x}}}{2}{\mathrm{c}}_{{\mathrm{p}}_{\mathrm{m}}}\frac{{\mathrm{d}\mathrm{T}}_1}{\mathrm{d}\mathrm{t}}=\frac{{\mathsf{\lambda }}_{\mathrm{m}}}{{\mathsf{\delta }}_{\mathrm{x}}}\left({\mathrm{T}}_2-{\mathrm{T}}_1\right)+{\mathrm{h}}_{\mathrm{T}1}\left({\mathrm{T}}_{\mathrm{a}1}-{\mathrm{T}}_1\right)$$

(6)

where: ${\mathsf{\rho }}_{\mathrm{m}}$ is the metal density [kg/m³]; “ δ_x” cell’s thickness [m]; ${\mathrm{c}}_{{\mathrm{p}}_{\mathrm{m}}}$ is the metal’s heat capacity [J/(kg·K)]; ${\mathrm{T}}_1$ is the cell _i,2 temperature [K]; ${\mathsf{\lambda }}_{\mathrm{m}}$ is the metal’s thermal conductivity [W/(m·K)]; ${\mathrm{T}}_2$ is the cell _i,3 temperature [K]; h_T1 is the heat transfer coefficient for primary fluid [W/(m² K)]; ${\mathrm{T}}_{\mathrm{a}1} \mathrm{i}\mathrm{s}$ the cell _i,1 temperature for primary fluid [K].

• Cell i,3, which describes the plate temperature variation at its half thickness, is noted with “T₂”. The entire cell is made of metal, so heat transfer by conduction is considered.

$${\mathsf{\rho }}_{\mathrm{m}}{\mathsf{\delta }}_{\mathrm{x}}{\mathrm{c}}_{{\mathrm{p}}_{\mathrm{m}}}\frac{{\mathrm{d}\mathrm{T}}_2}{\mathrm{d}\mathrm{t}}=\frac{{\mathsf{\lambda }}_{\mathrm{m}}}{{\mathsf{\delta }}_{\mathrm{x}}}\left({\mathrm{T}}_1-{\mathrm{T}}_2\right)-\frac{{\mathsf{\lambda }}_{\mathrm{m}}}{{\mathsf{\delta }}_{\mathrm{x}}}\left({\mathrm{T}}_2-{\mathrm{T}}_3\right)$$

(7)

where: ${\mathsf{\rho }}_{\mathrm{m}}$ is the metal density [kg/m³]; “ δ_x” cell’s thickness [m]; ${\mathrm{c}}_{{\mathrm{p}}_{\mathrm{m}}}$ is the metal’s heat capacity [J/(kg·K)]; ${\mathrm{T}}_2$ is the cell _i,3 temperature [K]; ${\mathsf{\lambda }}_{\mathrm{m}}$ is the metal’s thermal conductivity [W/(m·K)]; ${\mathrm{T}}_1$ is the cell _i,2 temperature [K]; ${\mathrm{T}}_3 \mathrm{i}\mathrm{s}$ the cell _i,4 temperature [K].

• Cell i,4, which describes the plate temperature variation on the side of fluid 2, is noted with "T₃." Half of this cell dimension in the heat transfer rate direction is placed in the fluid 2 zone, and the other half is in the plate thickness. Heat transfer inside this cell is obtained by forced convection in the fluid layer and conduction in the metal layer.

$${\mathsf{\rho }}_{\mathrm{m}}\frac{{\mathsf{\delta }}_{\mathrm{x}}}{2}{\mathrm{c}}_{{\mathrm{p}}_{\mathrm{m}}}\frac{{\mathrm{d}\mathrm{T}}_3}{\mathrm{d}\mathrm{t}}=\frac{{\mathsf{\lambda }}_{\mathrm{m}}}{{\mathsf{\delta }}_{\mathrm{x}}}\left({\mathrm{T}}_2-{\mathrm{T}}_3\right)+{\mathrm{h}}_{\mathrm{T}2}\left({\mathrm{T}}_{\mathrm{a}2}-{\mathrm{T}}_3\right)$$

(8)

where: ${\mathsf{\rho }}_{\mathrm{m}}$ is the metal density [kg/m³]; “ δ_x” cell’s thickness [m]; ${\mathrm{c}}_{{\mathrm{p}}_{\mathrm{m}}}$ is the metal’s heat capacity [J/(kg·K)]; ${\mathrm{T}}_3$ is the cell _i,4 temperature [K]; ${\mathsf{\lambda }}_{\mathrm{m}}$ is the metal’s thermal conductivity [W/(m·K)]; ${\mathrm{T}}_2$ is the cell _i,3 temperature [K]; h_T2 is the heat transfer coefficient for secondary fluid [W/(m² K)]; ${\mathrm{T}}_{\mathrm{a}2}$ is the cell _i,1 temperature for secondary fluid [K].

• Cell i,5, which describes fluid 2 temperature variation, is noted with “T_a2”. Fluid 2 is the one with the lowest temperature. This cell is placed in the fluid 2 zone; forced convection heat transfer is being considered.

$${\mathsf{\rho }}_{\mathrm{a}2}{\mathrm{V}}_{\mathrm{a}2}{\mathrm{c}}_{{\mathrm{p}}_{\mathrm{a}2}}\frac{\mathrm{d}{\mathrm{T}}_{\mathrm{a}2}}{\mathrm{d}\mathrm{t}}={\mathrm{h}}_{\mathrm{T}2}{\mathrm{A}}_{\mathrm{s}}\left({\mathrm{T}}_3-{\mathrm{T}}_{\mathrm{a}2}\right)+{\mathrm{w}}_{\mathrm{a}2}{\mathrm{c}}_{{\mathrm{p}}_{\mathrm{a}2}}\left({\mathrm{T}}_{\mathrm{a}2\mathrm{i}\mathrm{n}}-{\mathrm{T}}_{\mathrm{a}1}\right)$$

(9)

where: ${\mathsf{\rho }}_{\mathrm{a}2}$ is the secondary fluid’s density at mean temperature [kg/m³]; ${\mathrm{V}}_{\mathrm{a}2}$ is the secondary fluid volumetric flow [m³/s]; ${\mathrm{c}}_{{\mathrm{p}}_{\mathrm{a}2}}$ is the secondary fluid’s heat capacity at mean temperature [J/(kg·K)]; ${\mathrm{T}}_{\mathrm{a}2} \mathrm{i}\mathrm{s}$ the cell_i,5 temperature for secondary fluid [K]; h_T2 is the heat transfer coefficient for secondary fluid [W/(m² K)]; ${\mathrm{A}}_{\mathrm{s}}$ is cell _i,5 heat surface [m²],${\mathrm{T}}_3$ is the cell _i,4 temperature [K]; ${\mathrm{w}}_{\mathrm{a}2}$ is the secondary fluid mass flow [kg/s]; ${\mathrm{T}}_{\mathrm{a}2\mathrm{i}\mathrm{n}}$ is the cell _i,5 inlet temperature for secondary fluid [K].

The heat exchanger “tanks in series” model was performed in five elementary cells along the heat transfer direction and one or more cells along the fluid flow. For the first model, only one cell along the fluid flow was considered. Thus, in order to verify the model’s convergence, after this step, the number of elementary cells along the fluid flow was increased in order to obtain its influence on the results, until little influence was observed. 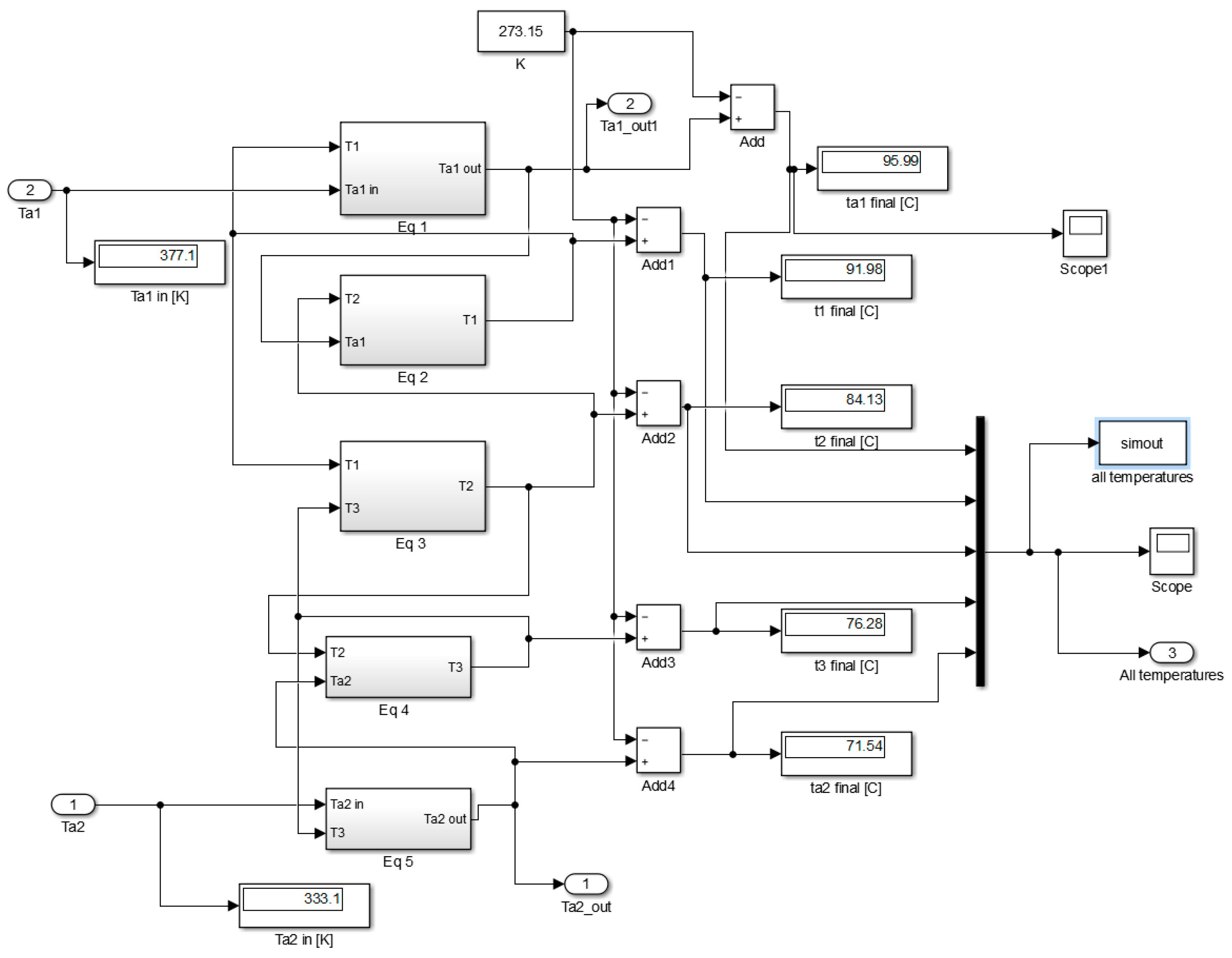Figure 2 presents a block diagram corresponding to the second level of modeling in Matlab/Simulink.

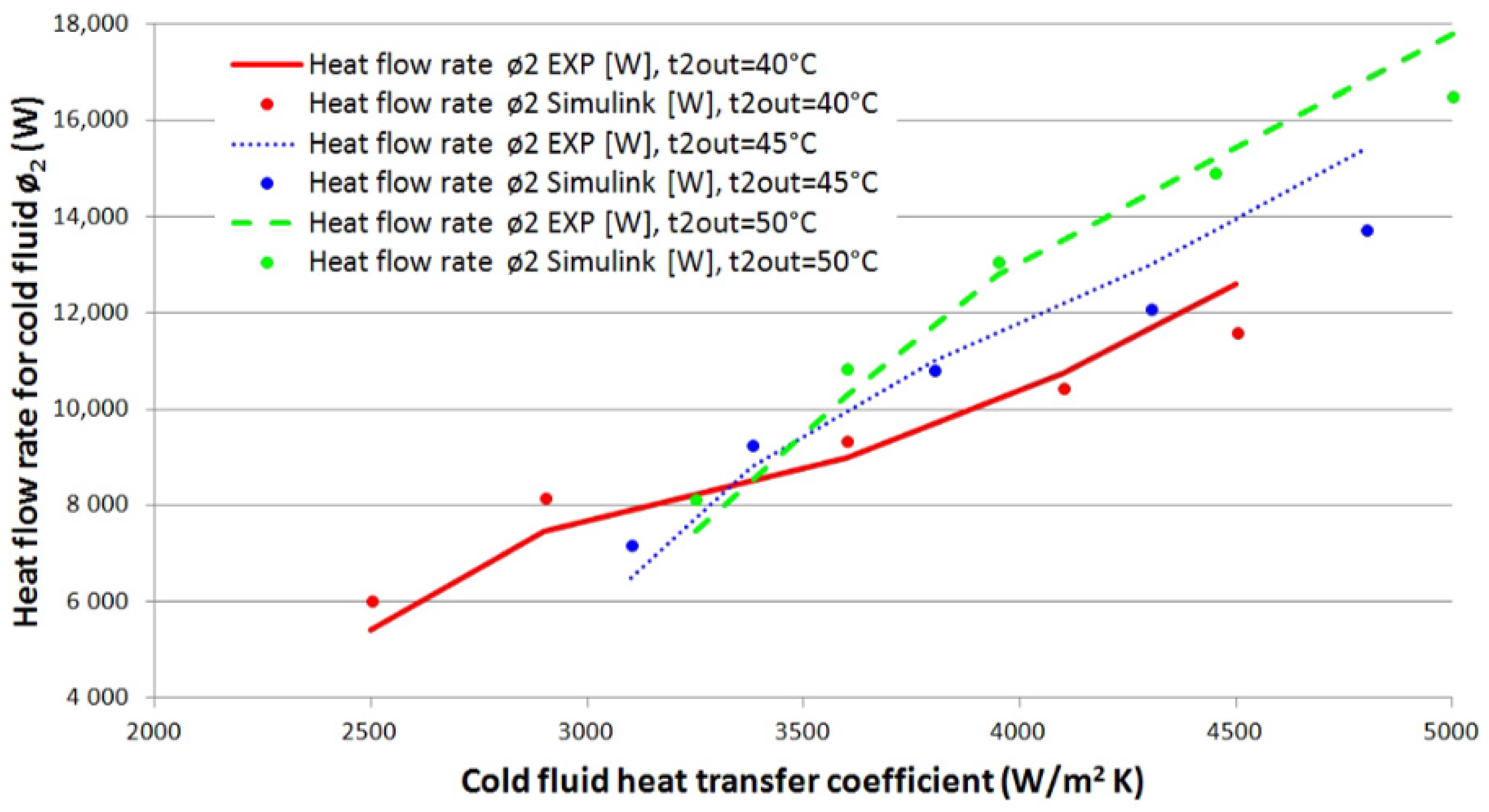
For the model evaluation, data obtained following the heat transfer steps for the plate heat exchanger were used. The primary fluid’s temperatures vary between 90 °C and 104 °C, and the fluid’s temperatures vary between 60 °C and 80 °C. Both fluids were water. The exchanger’s heat transfer rate was 168 kW. The heat exchanger was made of 10 middle plates made of stainless steel, each one having 0.2 m² surface area. The plate’s thickness was 5.5 mm. According to the values presented, the heat transfer coefficient by convection for fluid one was calculated to be equal to 12,090 W/m²K, and the heat transfer coefficient by convection for fluid two was equal to 10,238 W/m²K. The calculated parameters were used in Matlab/Simulink in order to verify the differences between the two calculation methods.

Figure 3 shows the second heat transfer equation, written for “T₁” temperature from the 3rd level of modeling in Matlab/Simulink.

3. Results and Discussion

In Figure 2, where the second level of modeling from Matlab/Simulink is presented, the five temperatures can be observed. The outlet temperature of fluid one obtained with Matlab/Simulink is 95.99 °C, and the outlet temperature of fluid two is 71.54 °C, with relative errors of −6.66% and 10.58% between the two calculation variants for primary fluid and secondary fluid outlet temperatures, respectively. Concerning the relative errors calculated between the heat flow transferred from the primary fluid and received by the secondary one, with respect to the design theme, 42.8% and 42.3% values were respectively obtained. These errors are induced by the coarse model mesh along the fluid flow. In order to observe the impact of model mesh along the fluid flow, results from models having 1, 10, 20, 30, 40, and 50 cells along the fluid flow are compared in

Table 3. Modeled values and calculated errors with respect to the values given by the design theme for outlet temperatures of the two fluids and heat transfer rates.

Parameter	1 Cell	10 Cells	20 Cells	30 Cells	40 Cells	50 Cells	Reference
ta1 out [°C]	95.99	93.12	92.29	91.74	90.6	90.37	90
ta2 out [°C]	71.54	75.68	76.87	77.66	79.31	79.64	80
Relative error for ta1 out [%]	−6.66	−3.47	−2.54	−1.93	−0.67	−0.41
Relative error for ta2 out [%]	10.58	5.40	3.91	2.93	0.86	0.45
(ta1 in–ta1 out) [°C]	8.01	10.88	11.71	12.26	13.4	13.63	14
(ta2 out–ta2 in) [°C]	11.54	15.68	16.87	17.66	19.31	19.64	20
ø1 [kW]	97.1	131.9	142.0	148.7	162.5	165.3	169.7
ø2 [kW]	97.1	131.9	141.9	148.6	162.5	165.2	168.3
Relative error for ø1 [%]	42.8	22.3	16.4	12.4	4.3	2.6
Relative error for ø2 [%]	42.3	21.6	15.7	11.7	3.4	1.8

. Modeled values and calculated errors with respect to the given values by the design theme for outlet temperatures, temperature difference between inlet and outlet, and heat transfer rates for both fluids are presented in Table 3. In Figure 4, the second level from Matlab/Simulink for the 50-cell model is presented for three consecutive cells. Each of the 50 cells contains under the mask the five equations presented in Figure 2 and explained before (Equations (5)–(9)).

The results presented in Table 3 show that there is a strong correlation between the Matlab/Simulink obtained results and the calculated results by means of stationary heat transfer equations for plate heat exchangers. The relative error calculated for primary agent outlet temperature varies from −6.66% to −0.41% between the 1 cell model and the 50 cells model. For the secondary agent outlet temperature, the relative error varies from 10.58% to 0.45% between the 1 cell model and the 50 cells model. The relative error calculated between the heat transfer rate obtained in Matlab/Simulink and the design theme varies between 42.8% and 2.6% for the primary fluid and 42.3% and 1.8% for the secondary fluid. It can be noticed that with the 40-cell model, the relative error for heat transfer rate is less than 10%, the relative error accepted in engineering. Dividing the mesh into 50 cells along the flow direction, the relative errors vary by 1.6–1.7%, meaning that a finer mesh is not necessary.

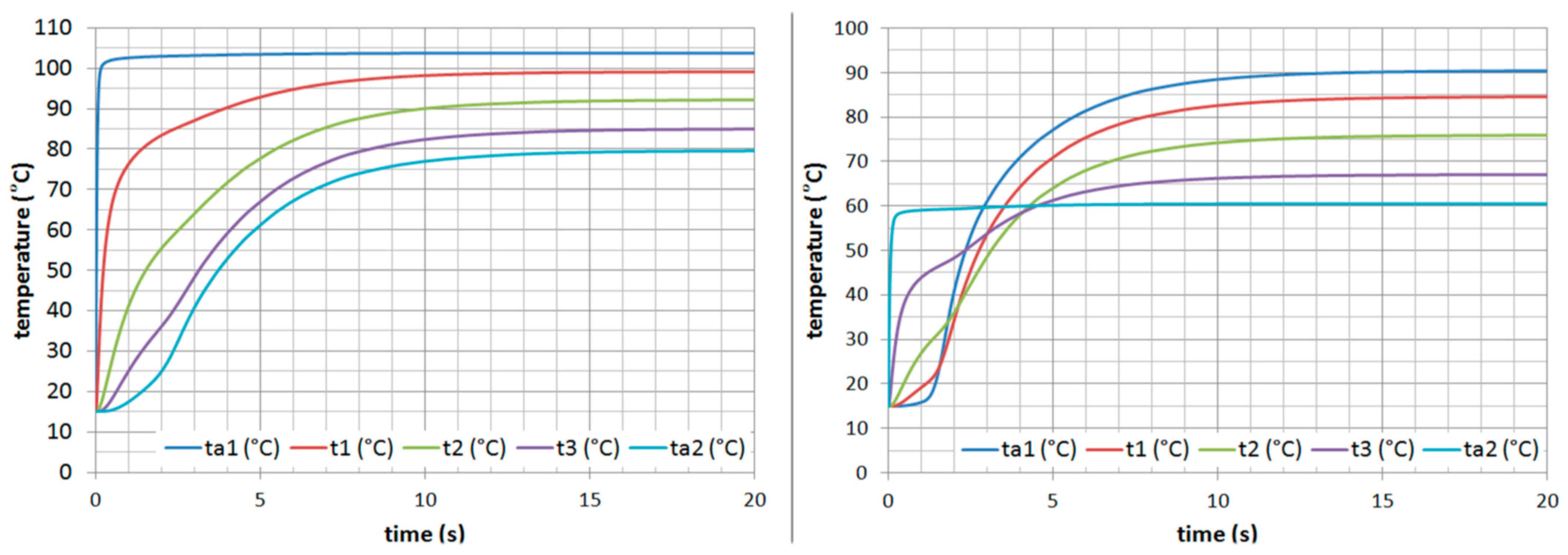
Figure 5 presents the transitory part of the temperature distribution of the extreme cells for the first and 50th cells of the model. The constant of time for the system is more than 15 s, when equilibrium is reached for all the elementary cells in the heat exchanger. In this figure, we can notice the primary fluid’s temperature for the first cell is 104 °C and around 90 °C (90.37 °C) for the last one. The counter-flow, the secondary fluid, has an outlet temperature of around 80 °C (79.64 °C) after the first cell, at its outlet, and of 60 °C after the 50th cell, at its inlet. All temperature distributions represented have an initial temperature of 15 °C for the system, which is assumed to be the ambient temperature around and inside the heat exchanger before being heated and can be modified according to environmental conditions.

From a physical point of view, the temperatures’ variations presented in Figure 5 are in good correlation with the heat transfer phenomena. If we compare the temperature difference between the primary agent and the plate’s temperature on its side and the temperature difference between the secondary agent and the plate’s temperature on its side, we can see that on the primary agent side, the temperature difference is smaller as the convective heat transfer coefficient is higher. If we compare the temperature difference between the primary fluid and the plate’s temperature on its side with the temperature difference between the plate’s outside and its middle, we can notice that the first one is smaller as the convective heat transfer coefficient is higher than the conductive one. The plate thickness of 5.5 mm is not a common one for plate heat exchangers, being chosen to verify the model’s limitations.

4. Model Validation with Experimental Data

Experimental data from the literature were used in order to validate the conceived Simulink model for heat exchangers. [31] performed an experimental study on plate heat exchangers for different outlet temperatures of secondary fluid, like 40 °C, 45 °C, and 50 °C, and different mass flow rates of the same fluid, like 3,4,5,6 and 7 lpm. Fluid heat transfer properties and heat exchanger properties (as a plate’s surface, number of plates, plate thickness, material, etc.) were used in the Simulink model to compare the simulation results with the experimental ones taken from the literature [31]. Fluid heat transfer coefficients found in the literature [31] were used in the Simulink model, and heat flow rates obtained in Simulink were compared with those experimentally determined by [31]. In Figure 6, a comparison between the heat flow rate on the cold side of the fluid obtained with the Simulink model and the heat flow rate experimentally determined by [31], as a function of the cold fluid heat transfer coefficient, for three levels of outlet temperature for the cold fluid is presented.

Relative errors for heat flow rate were calculated between simulated results and experimental ones with the help of Equation (10), and the values vary from 1.58% to 11.92%, showing a good agreement between the conceived model and the experimental values [31].

$$\mathrm{R}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e} \mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}\left[\%\right]=\frac{\left|\mathrm{S}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}-\mathrm{E}\mathrm{x}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{l} \mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}\right|}{\mathrm{E}\mathrm{x}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{l} \mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}\times 100$$

(10)

The good agreement between the Simulink model and the experimental values demonstrates that the model is valid and can be used by engineers to quickly evaluate one parameter impact on heat transfer by using a model instead of the usual heat transfer design calculus.

5. Conclusions

Unsteady heat transfer equations were used in order to describe temperatures’ variation inside a plate heat exchanger using Matlab/Simulink. The results obtained in Matlab/Simulink were compared with calculated ones using steady state criterion equations of heat transfer used by engineers to design plate heat exchangers. Heat transfer coefficients for both fluids obtained with steady state equations were used in the Matlab/Simulink model, together with heat exchange surface, fluids’, and metals’ thermal properties. Good validation was obtained for the steady-state zone between the Matlab/Simulink 50 cell model and the results obtained by using the heat transfer equations for the plate heat exchanger. The relative error decreased from 6.66% to 0.41% between the 1-cell model and the 50-cell model for the outlet temperature of the primary fluid. The relative error decreased from 10.58% to 0.45% between the 1-cell model and the 50-cell model for the outlet temperature of secondary fluid. The relative error calculated between the heat transfer rate obtained in Matlab/Simulink and the design theme varies between 42.8% and 2.6% for the primary fluid and 42.3% and 1.8% for the secondary fluid. It can be noticed that with the 40-cell model, the relative error for heat transfer rates is less than 10%, the relative error accepted in engineering. Dividing the mesh into 50 cells along the flow direction, the relative errors vary by 1.6–1.7%, meaning that a finer mesh is not necessary.

The developed model offers engineers a user-friendly tool to determine heat exchanger working parameters under various conditions, extending beyond those specified in technical equipment reports. Unlike classical methods, our Simulink/Matlab-based approach provides rapid numerical results with good convergence, enabling visualization of transient zones and easy modification of variables like plate material or thickness. Experimental validation [31] showed a 1.58% to 11.92% error range in heat flow rate, affirming the model’s accuracy. This versatile Matlab/Simulink model simulates the impact of different parameters in various heat exchanger applications, including geothermal probes and air-water exchangers, with the capability to adjust for fluid and metal properties. Future improvements aim to incorporate phase changes and mass transfer considerations into the model.