An Explainable Evaluation Model for Building Thermal Comfort in China
Abstract
:1. Introduction
2. Data Preparation
2.1. Dataset Filtering
- The thermal sensation scale is based on the ASHRAE Standard 55-2020 [32] 7-point voting scale, from −3 (cold) to 3 (hot). The thermal comfort scale is a 6-point scale from 0 (very comfortable) to 5 (very uncomfortable). The thermal acceptability scale is a 4-point scale from −1 (unacceptable) to 1 (acceptable).
- Clothing Insulation: Respondents were prompted to select the clothing type that matched their attire at the time of taking the survey. In instances where their specific clothing type was not listed, they were guided to choose the closest alternative. The insulation value for individual clothing items was determined based on ASHRAE 55-2020 [32]. For outfits composed of multiple garments, the total insulation value was computed by aggregating the insulation values of each individual piece.
- Metabolic Rate: The dataset features metabolic rate values for the Chinese population across various activity states. These values were ascertained in [33] using indirect calorimetry. The participants’ activities at the time of completing the questionnaire were documented and subsequently translated into metabolic rate values. The corresponding values are sitting (0.9 met), sitting while typing (1.0 met), sitting with document filing (1.2 met), standing in an office setting (1.1 met), standing with document filing (1.3 met), and walking at a pace of 2 km/h (2.1 met).
2.2. Feature Selection
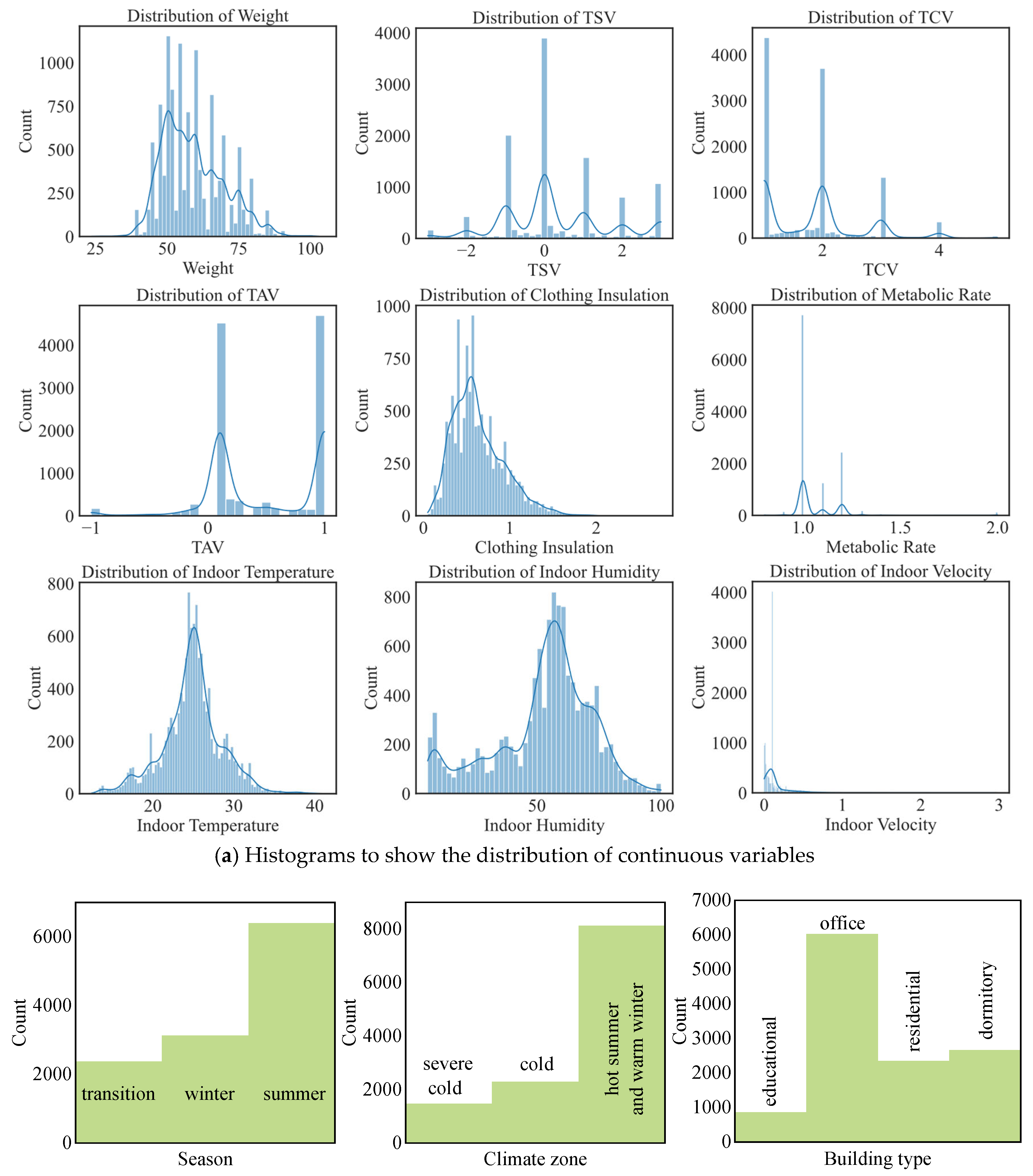
- Exclusion of Irrelevant Features: The primary objective of any modelling endeavor is to capture the underlying patterns in the data that are pertinent to the prediction or classification task at hand. Hence, the first step in our feature selection process is to remove any feature that does not have a direct or meaningful relationship with the evaluation indicators. Features that do not contribute significant information or might introduce noise into the system are systematically identified and excluded. This ensures that our model remains focused on pertinent information and is not swayed by irrelevant data.
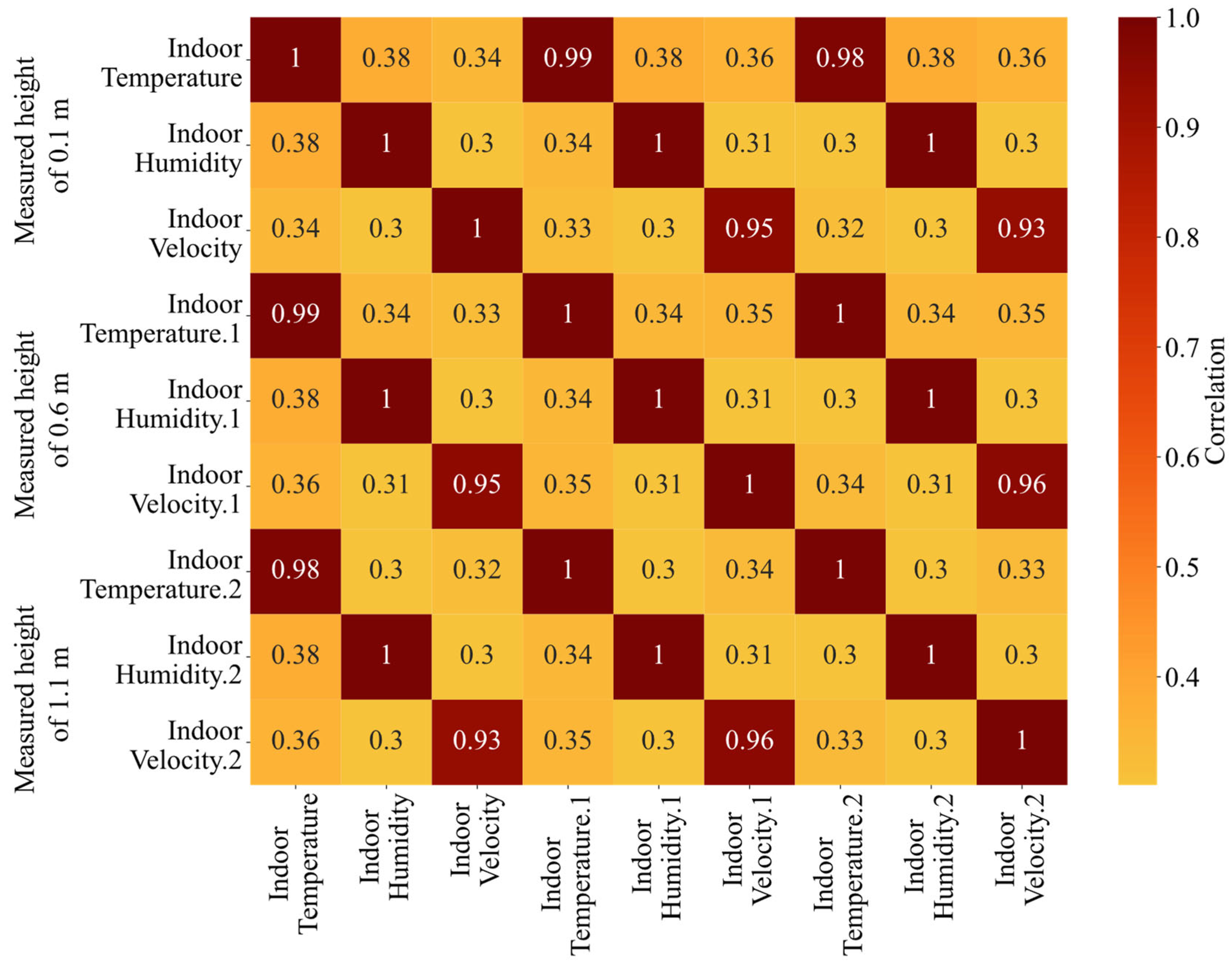
- Addressing Feature Collinearity: The presence of highly correlated or collinear features can introduce instability in certain models and can also make the model’s interpretations more challenging. When two or more features convey similar information, they are, in essence, redundant, and the inclusion of all these features does not necessarily improve the predictive power of the model but certainly increases the computational burden. In our methodology, if a set of features exhibit high collinearity (i.e., they are highly related), we adopt a conservative approach by retaining only a few representative features from that set and discarding the rest. This approach ensures that our model remains efficient without a compromise in its predictive capability.
- For the TSV evaluation model, the related input features are building type, building function, thermal operation mode, clothing insulation, metabolic rate, and indoor air temperature.
- For the TCV evaluation model, the related input features are seasons, city, building type, building function, thermal operation mode, clothing insulation, metabolic rate, indoor air temperature, indoor relative humidity, and indoor air velocity.
- For the TAV evaluation model, the related input features are city, climate zoom, weight, clothing insulation, metabolic rate, indoor air temperature, and indoor air velocity.
3. Model Establishment
3.1. LightGBM Model
3.2. Bayesian-Optimized Hyperparameters
3.3. Model Training
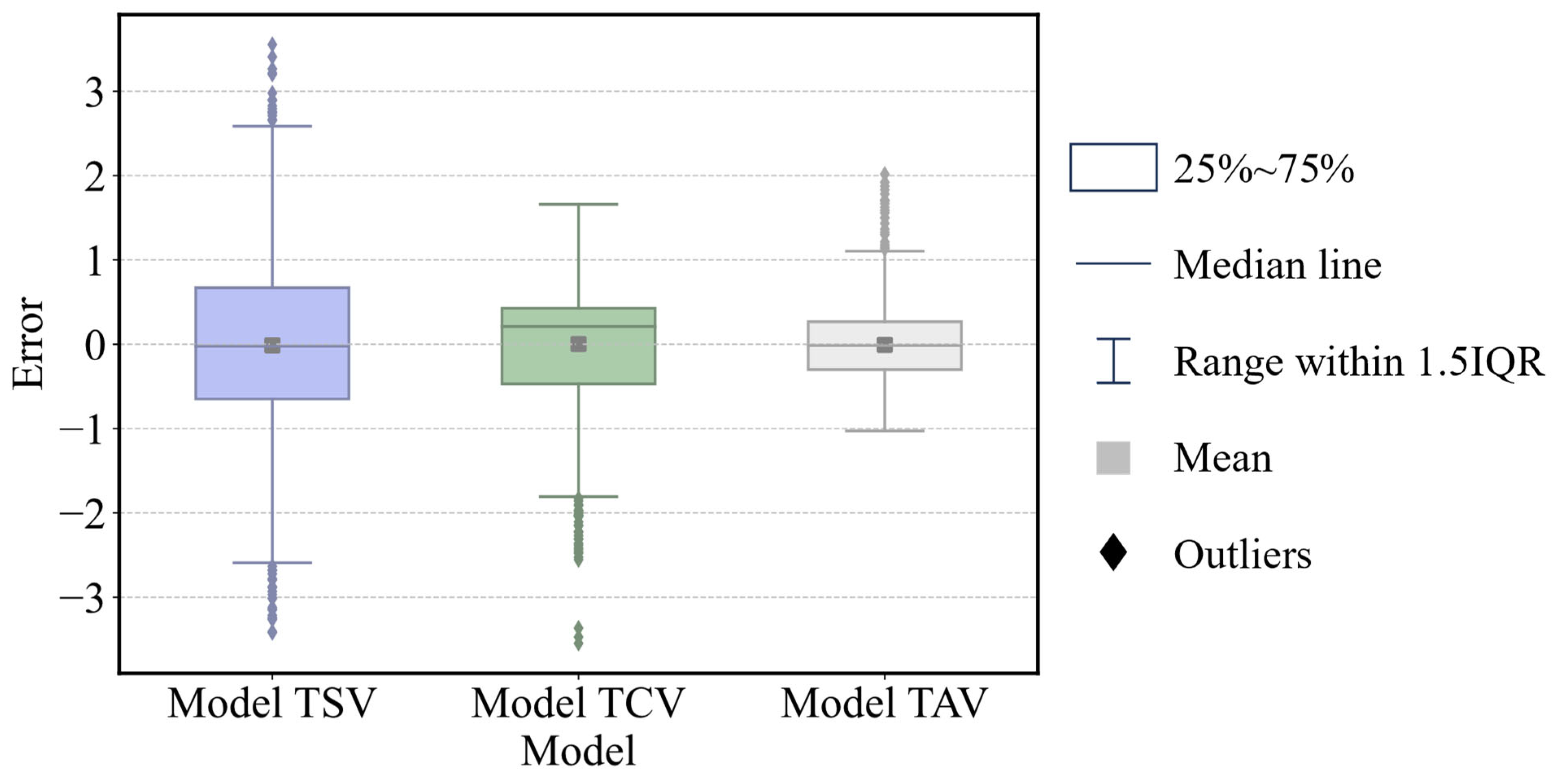
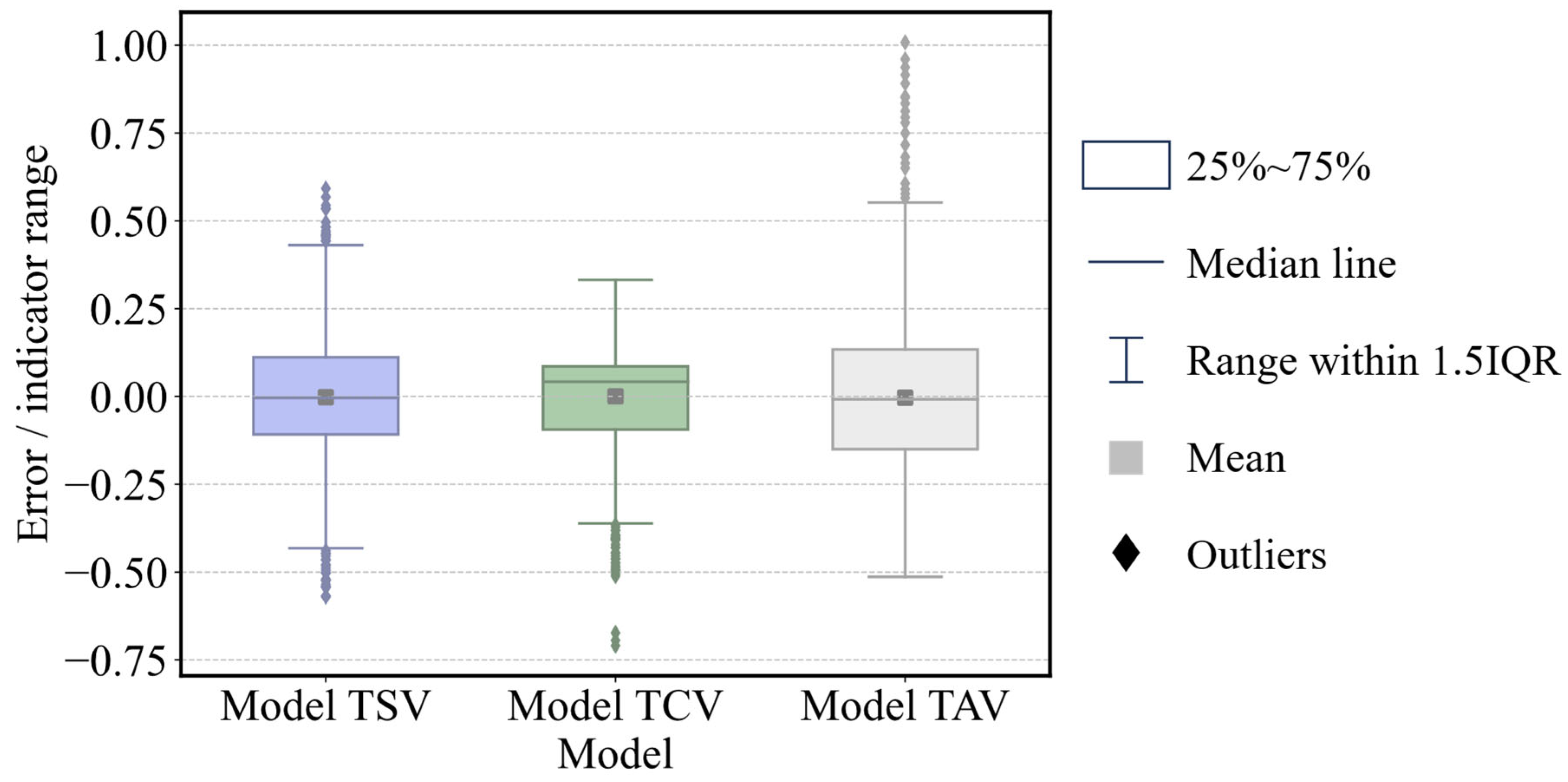
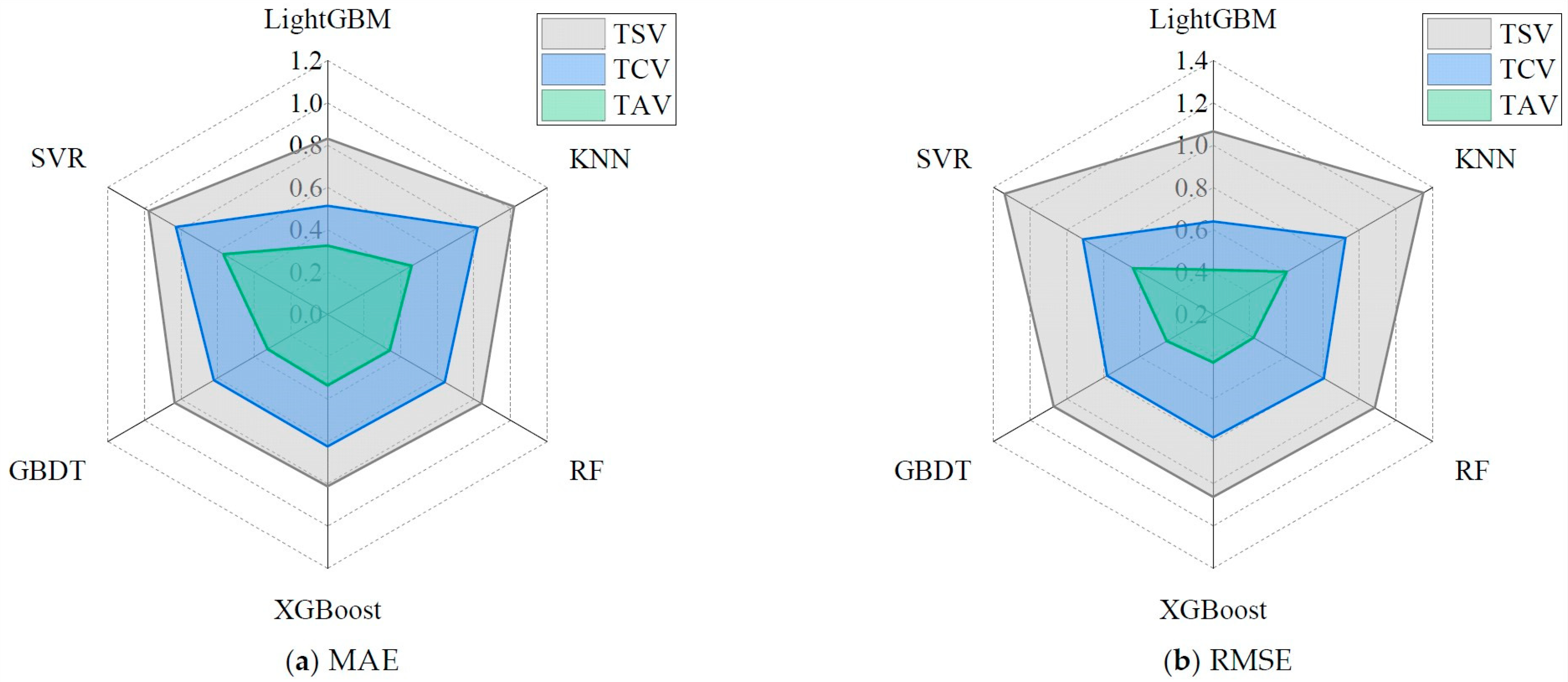
4. Model Performance
5. Model Interpretation
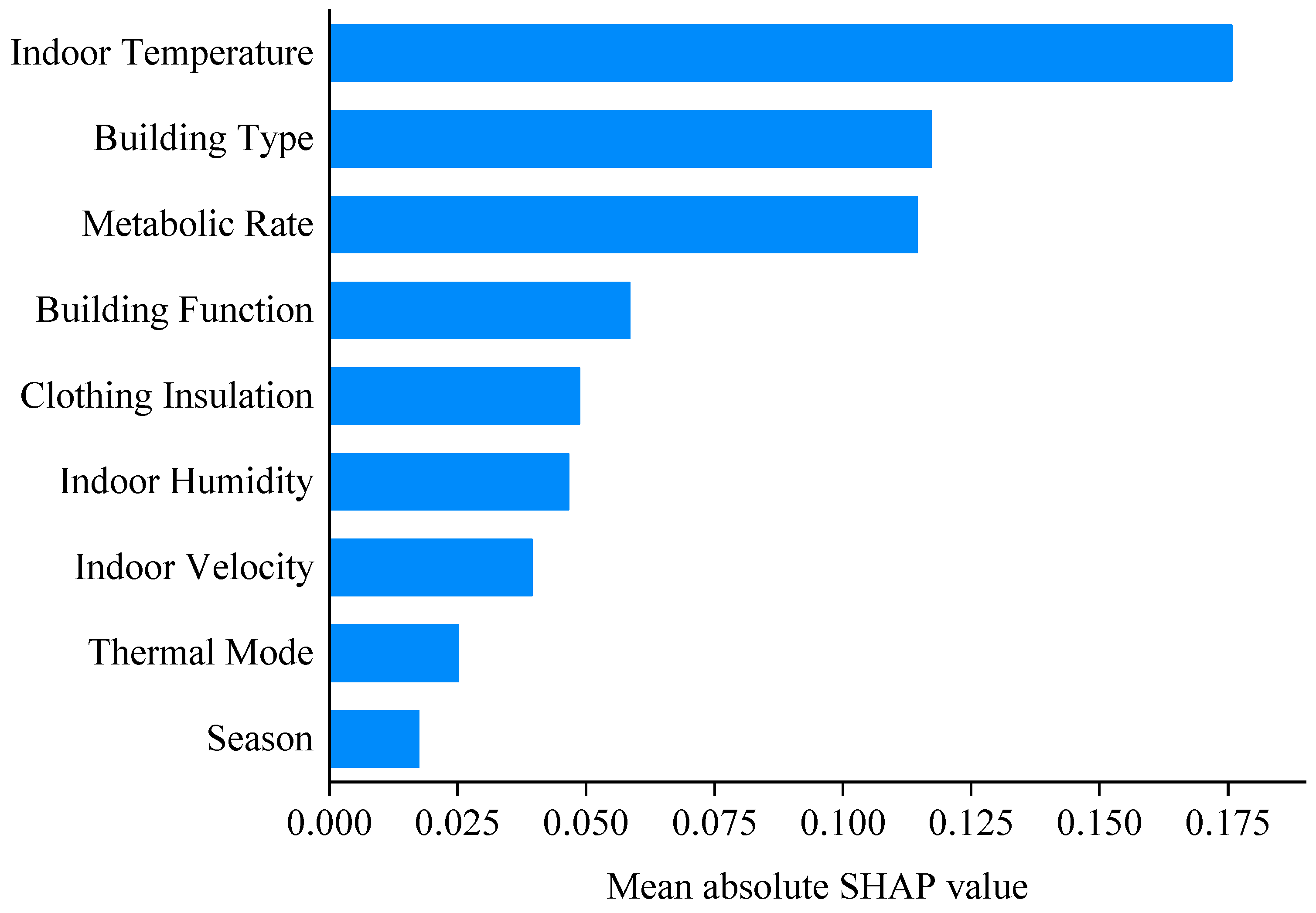
5.1. Influence Weights
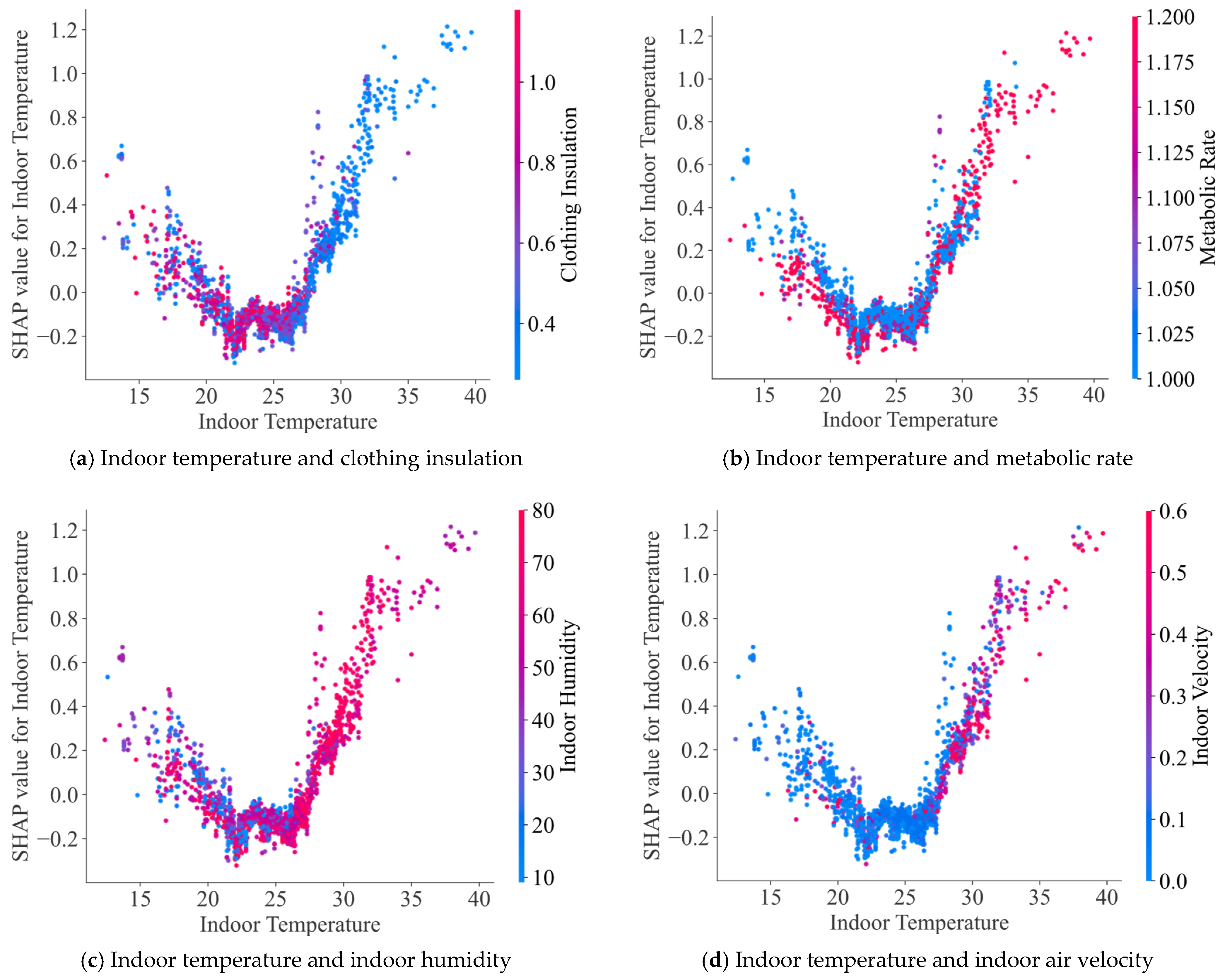
5.2. Marginal Effects
5.3. Interactive Mechanism
6. Conclusions
- (1)
- Our model has demonstrated commendable accuracy in evaluating thermal comfort, with SHAP analysis providing granular insights into the model’s internal workings. The ability of the model to generalize across the test set with high precision suggests its potential for widespread application in smart building management systems.
- (2)
- The study underscores the paramount influence of indoor temperature on thermal comfort voting, reiterating the necessity for precise temperature control in the pursuit of occupant comfort. The notable impacts of building type and metabolic rate highlight the significance of architectural design and human physiological activity in thermal comfort perception.
- (3)
- The insights gleaned from our analysis have significant policy implications. They can inform the development of energy-efficient thermal comfort standards and regulations that are sensitive to regional climatic diversity and personalized occupant needs. Accurate predictions of thermal comfort can aid substantially in the optimization of energy usage, aligning with the objectives of sustainable development and carbon neutrality. The model’s ability to delineate the influence of distinct factors enables the design of energy-efficient and occupant-centric thermal environments.
- (4)
- The research paves the way for future studies to incorporate additional variables, such as clothing adaptability, occupant behaviour, and building occupancy patterns. Such expansions could yield a holistic thermal comfort model that is both predictive and prescriptive, aiding stakeholders in creating energy-efficient, comfortable, and health-promoting built environments.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Houghton, J. Global warming. Rep. Prog. Phys. 2005, 68, 1343. [Google Scholar] [CrossRef]
- Quadros, B.; Mizgier, M. Urban green infrastructures to improve pedestrian thermal comfort: A systematic review. Urban For. Urban Green. 2023, 88, 128091. [Google Scholar] [CrossRef]
- EU Directive. 31/EU of the European Parliament and of the Council of 19 May 2010 on the Energy Performance of Buildings. Off. J. Eur. Union 2010, 153, 13–35. [Google Scholar]
- Yuan, D.; Jiang, W.; Sha, A.; Xiao, J.; Wu, W.; Wang, T. Technology method and functional characteristics of road thermoelectric generator system based on Seebeck effect. Appl. Energy 2023, 331, 120459. [Google Scholar] [CrossRef]
- Jiang, W.; Yuan, D.; Shan, J.; Ye, W.; Lu, H.; Sha, A. Experimental study of the performance of porous ultra-thin asphalt overlay. Int. J. Pavement Eng. 2022, 23, 2049–2061. [Google Scholar] [CrossRef]
- Jiang, W.; Li, P.; Sha, A.; Li, Y.; Yuan, D.; Xiao, J.; Xing, C. Research on Pavement Traffic Load State Perception Based on the Piezoelectric Effect. IEEE Trans. Intell. Transp. Syst. 2023, 24, 8264–8278. [Google Scholar] [CrossRef]
- Vergés, R.; Gaspar, K.; Forcada, N. Assessment of the energy implications adopting adaptive thermal comfort models during the cooling season: A case study for Mediterranean nursing homes. Energy Build. 2023, 299, 113598. [Google Scholar] [CrossRef]
- Yue, L.; Zhongqing, C. Seasonal thermal comfort and adaptive behaviours for the occupants of residential buildings: Shaoxing as a case study. Energy Build. 2023, 292, 113165. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, C.; Zhao, Y.; Li, J.; Ma, Y.; Zhu, C. A systematic review on thermal environment and thermal comfort studies in Chinese residential buildings. Energy Build. 2023, 291, 113134. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). Global Status Report for Buildings and Construction; IEA: Paris, France, 2019. [Google Scholar]
- Ma, Z.; Wang, J.; Ye, S.; Wang, R.; Dong, F.; Feng, Y. Real-time indoor thermal comfort prediction in campus buildings driven by deep learning algorithms. J. Build. Eng. 2023, 78, 107603. [Google Scholar] [CrossRef]
- Uddin, M.N.; Lee, M.; Ni, M. The impact of socio-demographic factors on occupants’ thermal comfort and sensation: An integrated approach using statistical analysis and agent-based modeling. Build. Environ. 2023, 346, 110974. [Google Scholar] [CrossRef]
- Wu, Y.; Cao, B.; Zhu, Y. Development of an automatic personal comfort system (APCS) based on real-time thermal sensation prediction. Build. Environ. 2023, 246, 110958. [Google Scholar] [CrossRef]
- Ma, S.; Deng, W.; Lu, J.; Zhou, T.; Liu, B. Investigation of thermal comfort and preferred temperatures for healthcare staff in hospitals in Ningbo, China. J. Build. Eng. 2023, 80, 108029. [Google Scholar] [CrossRef]
- Lee, J.; Cha, S.H.; Hong, T.; Koo, C. Empirical investigation of occupant-centric thermal comfort in hotel guestrooms. Renew. Sustain. Energy Rev. 2024, 189, 114046. [Google Scholar] [CrossRef]
- ANSI/ASHRAE Standard 55-2017; Thermal Environmental Conditions for Human Occupancy. ASHRAE: Peachtree Corners, GA, USA, 2017.
- ISO 7730:2005; Ergonomics of the Thermal Environment—Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the PMV and PPD Indices and Local Thermal Comfort Criteria. ISO: Geneva, Switzerland, 2005.
- Fanger, P.O. Thermal Comfort: Analysis and Applications in Environmental Engineering; Danish Technical Press: Copenhagen, Denmark, 1970. [Google Scholar]
- De Dear, R.J.; Brager, G.S. Thermal comfort in naturally ventilated buildings: Revisions to ASHRAE Standard 55. Energy Build. 2002, 34, 549–561. [Google Scholar] [CrossRef]
- Kramer, T.; Garcia-Hansen, V.; Omrani, S.; Zhou, J.; Chen, D. Personal differences in thermal comfort perception: Observations from a field study in Brisbane, Australia. Build. Environ. 2023, 245, 110873. [Google Scholar] [CrossRef]
- Su, X.; Yuan, Y.; Wang, Z.; Liu, W.; Lan, L.; Lian, Z. Human thermal comfort in non-uniform thermal environments: A review. Energy Built Environ. 2023, in press. [CrossRef]
- Wu, Y.; Jiang, A.; Liu, H.; Li, B.; Wang, W.; Zheng, X. Effect of the mood of indoor activities on thermal comfort after winter commutes with different metabolic levels. Energy Build. 2023, in press. [CrossRef]
- Zhang, J.; Lu, J.; Deng, W.; Beccarelli, P.; Lun, I.Y.F. Thermal comfort investigation of rural houses in China: A review. Build. Environ. 2023, 235, 110208. [Google Scholar] [CrossRef]
- Deng, M.; Fu, B.; Menassa, C.C.; Kamat, V.R. Learning-Based personal models for joint optimization of thermal comfort and energy consumption in flexible workplaces. Energy Build. 2023, 298, 113438. [Google Scholar] [CrossRef]
- Arowoiya, V.A.; Moehler, R.C.; Fang, Y. Digital Twin Technology for Thermal Comfort and Energy Efficiency in Buildings: A State-of-the-Art and future directions. Energy Built Environ. 2023, in press. [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4768–4777. [Google Scholar]
- Strumbelj, E.; Kononenko, I. Explaining prediction models and individual predictions with feature contributions. Knowl. Inf. Syst. 2014, 41, 647–665. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should I trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Yang, Y.; Yuan, Y.; Han, Z.; Liu, G. Interpretability analysis for thermal sensation machine learning models: An exploration based on the SHAP approach. Indoor Air 2022, 32, e12984. [Google Scholar] [CrossRef]
- Iban, M.C. An explainable model for the mass appraisal of residences: The application of tree-based Machine Learning algorithms and interpretation of value determinants. Habitat Int. 2022, 128, 102660. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, S.; Zhai, Y.; Gao, S.; Wang, F.; Lian, Z.; Duanmu, L.; Zhang, Y.; Zhou, X.; Cao, B.; et al. The Chinese thermal comfort dataset. Sci. Data 2023, 10, 662. [Google Scholar] [CrossRef] [PubMed]
- ASHRAE Standard 55-2020; Thermal Environmental Conditions for Human Occupancy. ASHRAE: Atlanta, GA, USA, 2020.
- Zhai, Y.C.; Li, M.; Gao, S.; Yang, L.; Zhang, H.; Arens, E.; Gao, Y. Indirect calorimetry on the metabolic rate of sitting, standing and walking office activities. Build. Environ. 2018, 145, 77–84. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3149–3157. [Google Scholar]
- Jin, D.; Lu, Y.; Qin, J.; Cheng, Z.; Mao, Z. SwiftIDS: Real-time intrusion detection system based on LightGBM and parallel intrusion detection mechanism. Comput. Secur. 2020, 97, 101984. [Google Scholar] [CrossRef]
- Liang, W.; Luo, S.; Zhao, G.; Wu, H. Predicting hard rock pillar stability using GBDT, XGBoost, and LightGBM algorithms. Mathematics 2020, 8, 765. [Google Scholar] [CrossRef]
- Mangalathu, S.; Hwang, S.H.; Jeon, J.S. Failure mode and effects analysis of RC members based on machine-learning-based SHapley Additive exPlanations (SHAP) approach. Eng. Struct. 2020, 219, 110927. [Google Scholar] [CrossRef]
- Nor, A.K.M.; Pedapati, S.R.; Muhammad, M.; Leiva, V. Abnormality detection and failure prediction using explainable Bayesian deep learning: Methodology and case study with industrial data. Mathematics 2022, 10, 554. [Google Scholar] [CrossRef]
- Parsa, A.B.; Movahedi, A.; Taghipour, H.; Derrible, S.; Mohammadian, A. Toward safer highways, application of XGBoost and SHAP for real-time accident detection and feature analysis. Accid. Anal. Prev. 2020, 136, 105405. [Google Scholar] [CrossRef] [PubMed]
- Wen, X.; Xie, Y.; Wu, L.; Jiang, L. Quantifying and comparing the effects of key risk factors on various types of roadway segment crashes with LightGBM and SHAP. Accid. Anal. Prev. 2021, 159, 106261. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.D.; LaFave, J.M.; Lee, Y.J.; Shin, M. Rapid seismic damage-state assessment of steel moment frames using machine learning. Eng. Struct. 2022, 252, 113737. [Google Scholar] [CrossRef]
- Li, Z.; Lei, H.; Ma, E.; Lai, J.; Qiu, J. Ensemble technique to predict post-earthquake damage of buildings integrating tree-based models and tabular neural networks. Comput. Struct. 2023, 287, 107114. [Google Scholar] [CrossRef]
- Zafarmandi, S.; Matzarakis, A.; Norford, L. Effects of clothing’s thermal insulation on outdoor thermal comfort and thermal sensation: A case study in Tehran, Iran. Sustain. Cities Soc. 2024, 100, 104988. [Google Scholar] [CrossRef]
- Abdollahzadeh, S.M.; Heidari, S.; Einifar, A. Evaluating thermal comfort and neutral temperature in residential apartments in hot and dry climate: A case study in Shiraz, Iran. J. Build. Eng. 2023, 76, 107161. [Google Scholar] [CrossRef]



| Categories | Features |
|---|---|
| General and building information | Seasons, city, climate zoom, building type, building function, thermal operation mode |
| Subject’s personal information | Gender, age, height, weight |
| Subjective thermal comfort information | Thermal sensation voting scale (TSV), thermal comfort voting scale (TCV), thermal acceptability voting scale (TAV), clothing insulation, metabolic rate |
| Indoor physical parameters | Measured from different heights above the floor (0.1 m, 0.6 m, 1.1 m): Air temperature, relative humidity, air velocity |
| Outdoor environment parameters | Mean daily outdoor temperature |
| Categories | Features |
|---|---|
| General and building information | Seasons, climate zoom, building type, building function, thermal operation mode |
| Subject’s personal information | Weight |
| Subjective thermal comfort information | Clothing insulation, metabolic rate |
| Indoor physical parameters | Measured from 0.6 m above the floor: Air temperature, relative humidity, air velocity |
| Hyperparameters | Searching Space | The Optimal Value for TSV Evaluation | The Optimal Value for TCV Evaluation | The Optimal Value for TAV Evaluation |
|---|---|---|---|---|
| num_leaves | [24, 45] | 28 | 25 | 43 |
| feature_fraction | [0.1, 0.9] | 0.86 | 0.59 | 0.57 |
| bagging_fraction | [0.8, 1.0] | 0.84 | 0.83 | 0.83 |
| max_depth | [5, 15] | 14 | 13 | 14 |
| lambda_l1 | [0, 1] | 0.69 | 0.12 | 0.42 |
| lambda_l2 | [0, 1] | 0.22 | 0.85 | 0.71 |
| min_split_gain | [0.001, 0.1] | 0.07 | 0.06 | 0.001 |
| n_estimators | [100, 1000] | 329 | 466 | 339 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Ma, E. An Explainable Evaluation Model for Building Thermal Comfort in China. Buildings 2023, 13, 3107. https://doi.org/10.3390/buildings13123107
Liu H, Ma E. An Explainable Evaluation Model for Building Thermal Comfort in China. Buildings. 2023; 13(12):3107. https://doi.org/10.3390/buildings13123107
Chicago/Turabian StyleLiu, Haiyang, and Enlin Ma. 2023. "An Explainable Evaluation Model for Building Thermal Comfort in China" Buildings 13, no. 12: 3107. https://doi.org/10.3390/buildings13123107
APA StyleLiu, H., & Ma, E. (2023). An Explainable Evaluation Model for Building Thermal Comfort in China. Buildings, 13(12), 3107. https://doi.org/10.3390/buildings13123107





