Lateral Load-Carrying Capacity of Low-Rise Reinforced Concrete Walls in Nuclear Safety-Related Structures
Abstract
:1. Introduction
2. Experimental Program
2.1. Test Specimens
2.2. Test Results
- (1)
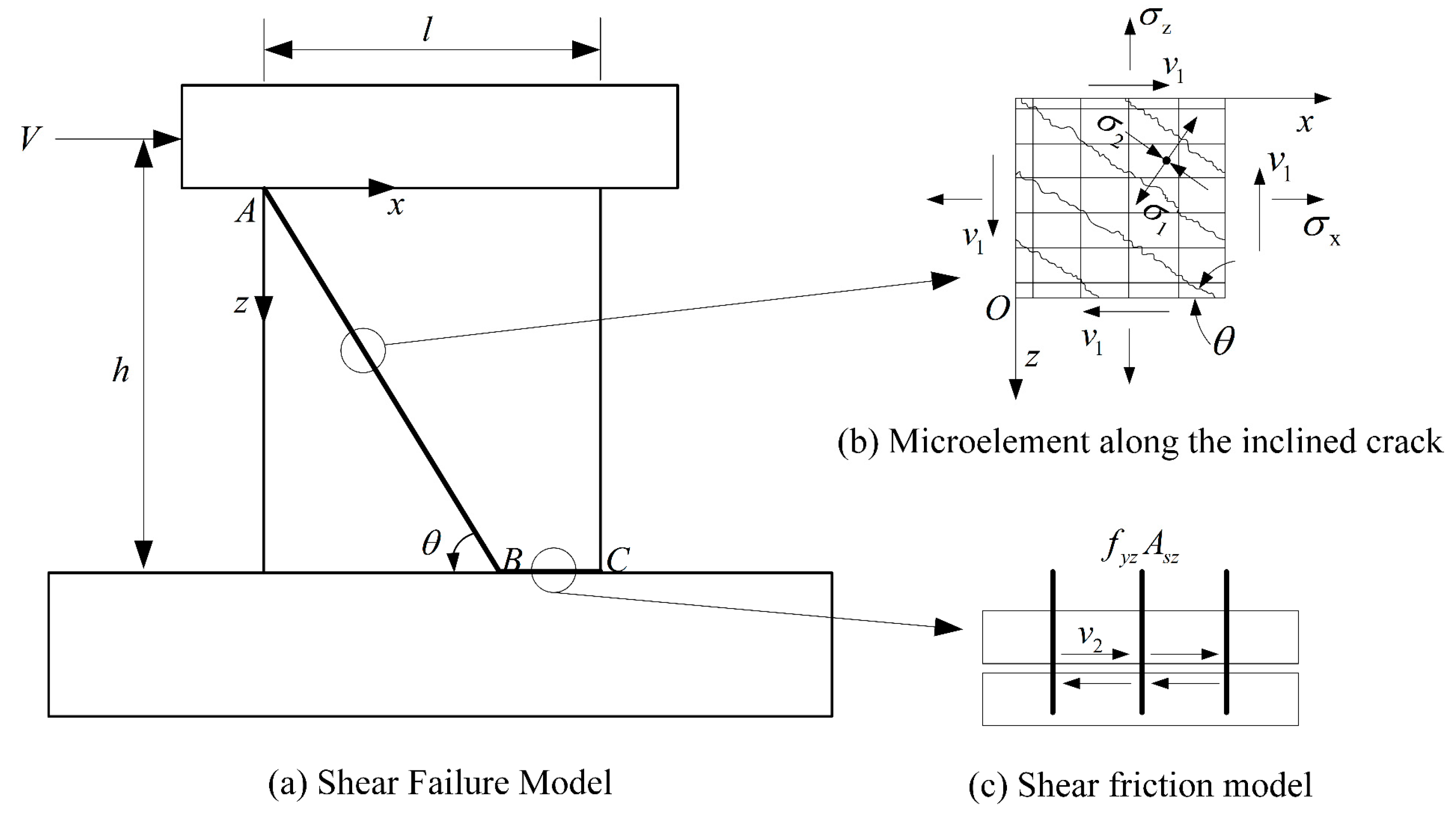
- The response of LRC walls significantly differs from high-rise reinforced concrete walls designed for flexural failure control. For low-rise walls with an aspect ratio of less than 1 and subjected to constant axial pressure, inclined cracks initially appear under increased lateral loads. As the load continues to increase, these inclined cracks extend to the interface between the web wall and basement beams, forming an inclined crack–shear friction failure mechanism.
- (2)
- The lateral load-carrying capacity of LRC walls is influenced by the aspect ratio, axial compression ratio, and reinforcement ratio. Among these factors, the aspect ratio exerts the most significant influence on the lateral load-carrying capacity of LRC walls. For LRC walls of equal height, a smaller aspect ratio corresponds to a higher lateral load-carrying capacity, with the length of shear friction along the base interface of the wall increasing accordingly.
3. Mechanical Model and Basic Equation of the Lateral Load-Carrying Capacity
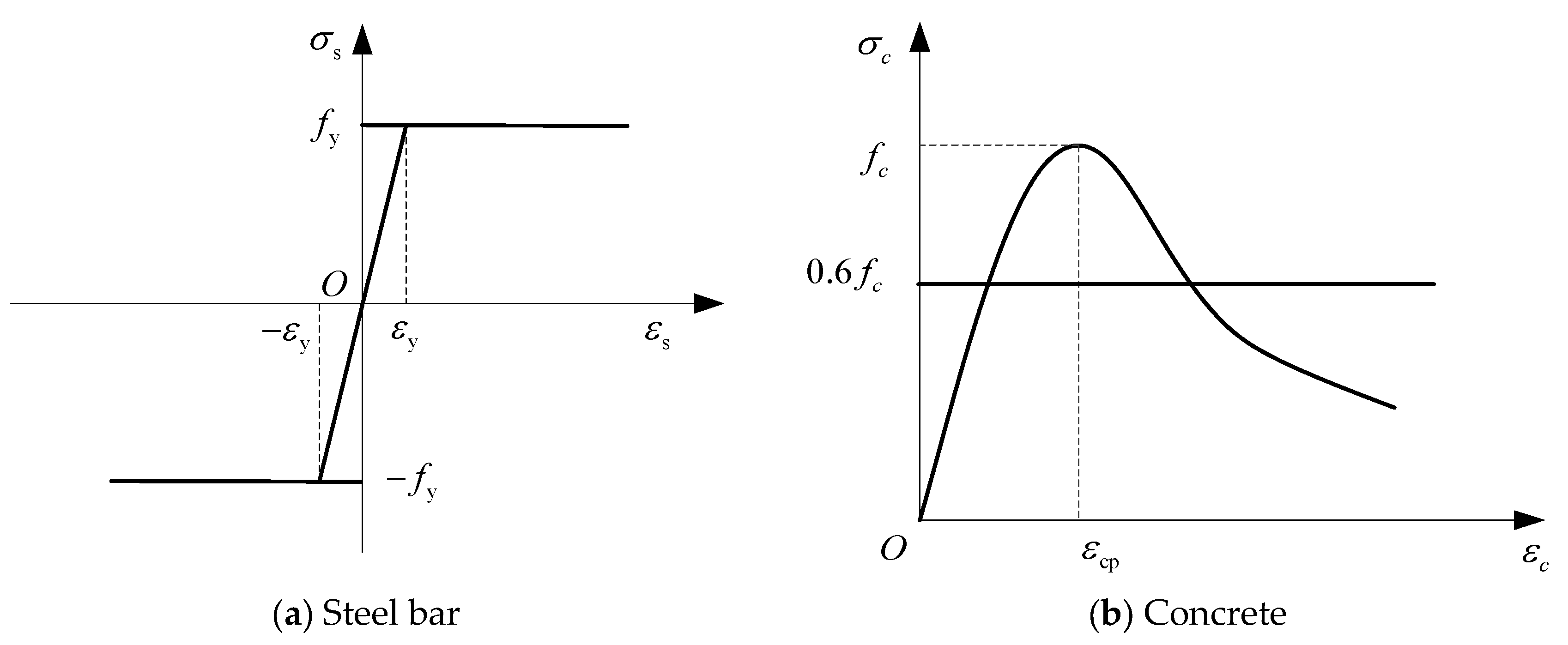
3.1. Mechanical Model
3.2. Shear Force Carried by Inclined Crack Plane
3.3. Shear Force Carried by Shear Friction Crack Plane
3.4. Total Lateral Load-Carrying Capacity of Walls
4. Simplification and Calibration of Equation
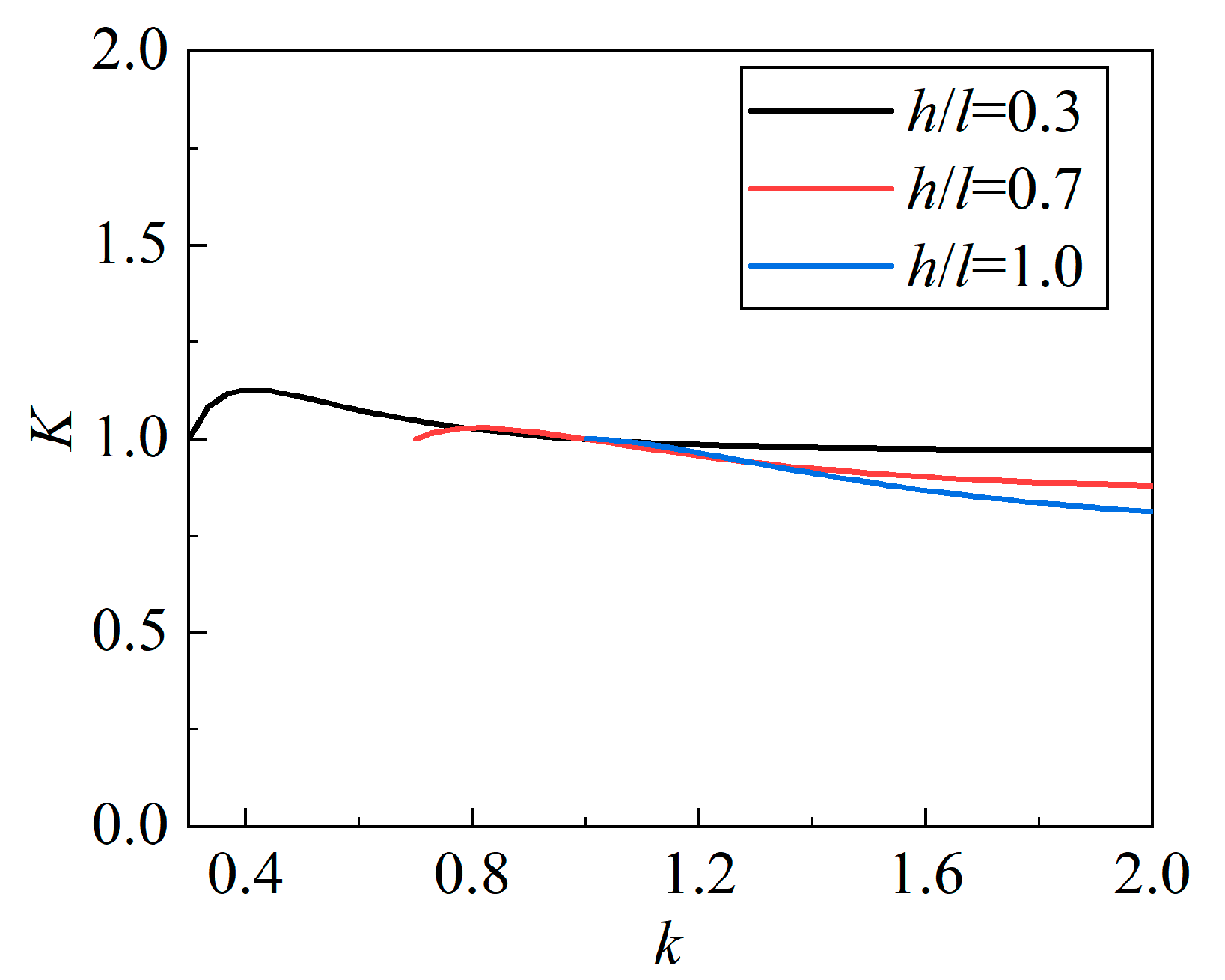
4.1. Simplification of Equation Denominator
4.2. Simplification of Equation Numerator
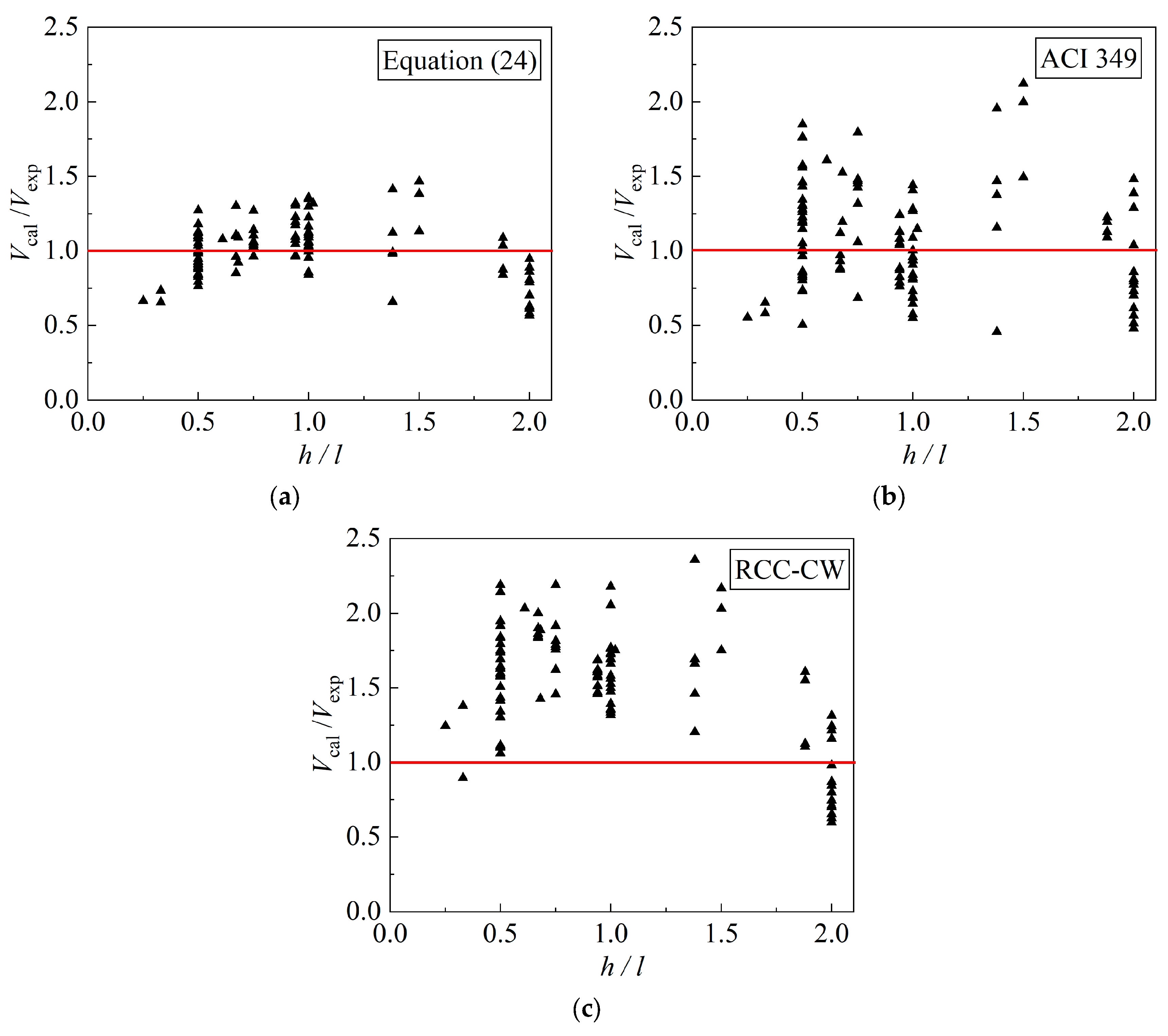
5. Comparison with Test Results and Equations in Current Codes
6. Lateral Load-Carrying Capacity under Axial Tensile Force
7. Conclusions
- (1)
- The experimental results indicate that the inclined crack appears and extends to the wall base and bottom beam interfaces under constant axial compressive force and horizontal loading for LRC walls with an aspect ratio between 0.33 and 1. The failure mode of LRC walls can be recognized as a combination of inclined crack and shear friction crack. The aspect ratio has a dominant effect on the lateral load-carrying capacity of LRC walls. The smaller the aspect ratio, the longer the length of the shear friction interface along the wall base.
- (2)
- The equation proposed in this study accurately predicts the lateral load-carrying capacity of 106 LRC walls under axial compressive force. The proposed equation provides an average calculated-to-experimental ratio of 0.996 and a minimum coefficient of variation (COV) of 0.203. It was found that both equations in ACI 349 and RCC-CW overestimate the lateral load-carrying capacity by 8% and 53%, with coefficients of variation (COV) of 0.341 and 0.250, respectively.
- (3)
- The proposed equation is also applicable to LRC walls subjected to axial tensile force and horizontal loads, with minor modifications. For 25 LRC walls under axial tensile force collected from the literature, it provides an average calculated-to-experimental ratio of 1.000, with a coefficient of variation (COV) of 0.206. In comparison to the prediction results from the equations in ACI 349 and RCC-CW, the proposed equation demonstrates greater accuracy. The equation in ACI 349 underestimates the lateral load-carrying capacity by nearly 25%, while the equation in RCC-CW overestimates it by approximately 77%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivations of Shear Strength of RC Micro-Element
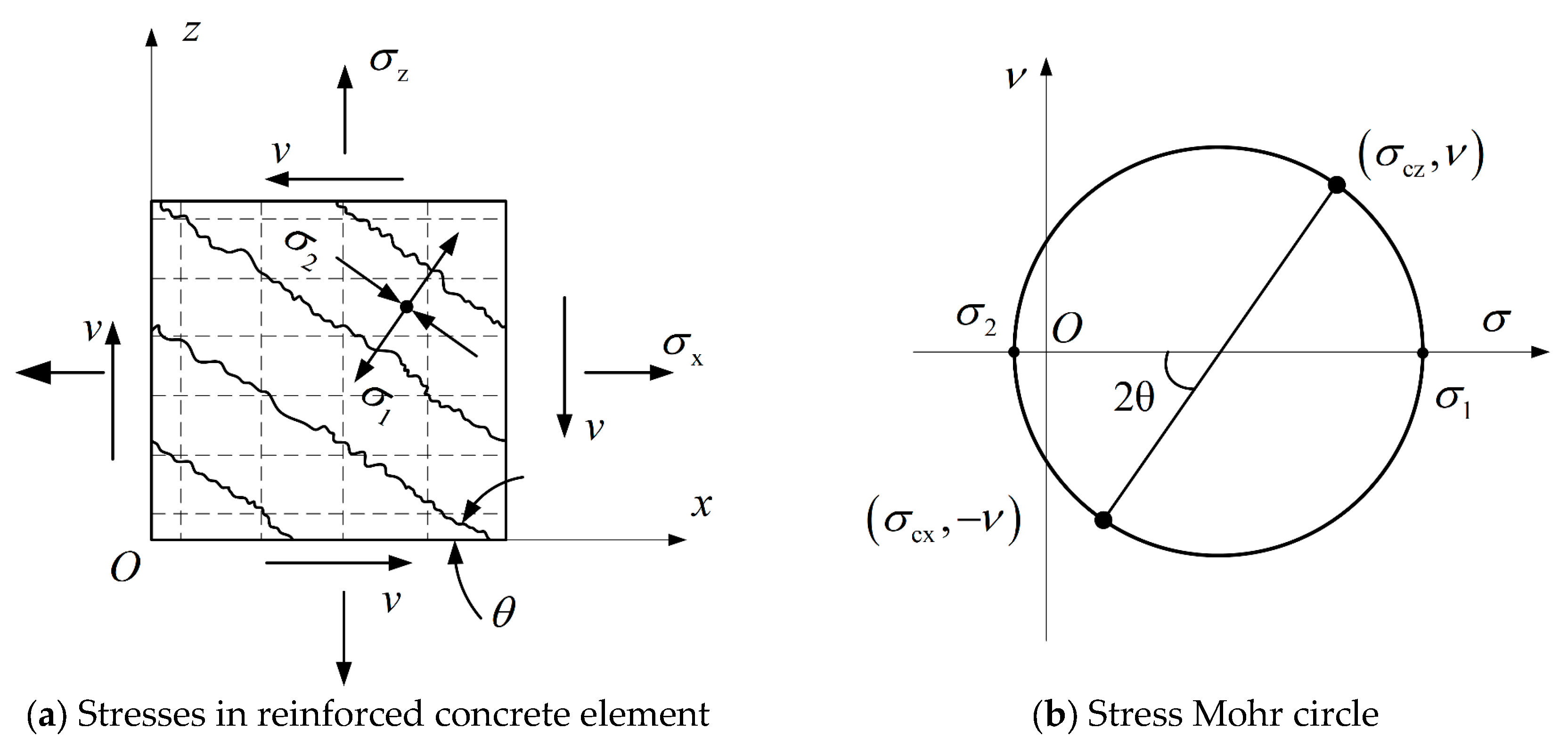
Appendix A.1. Yield Criteria and Orthogonal Condition
Appendix A.2. Compatibility and Kinematic Condition
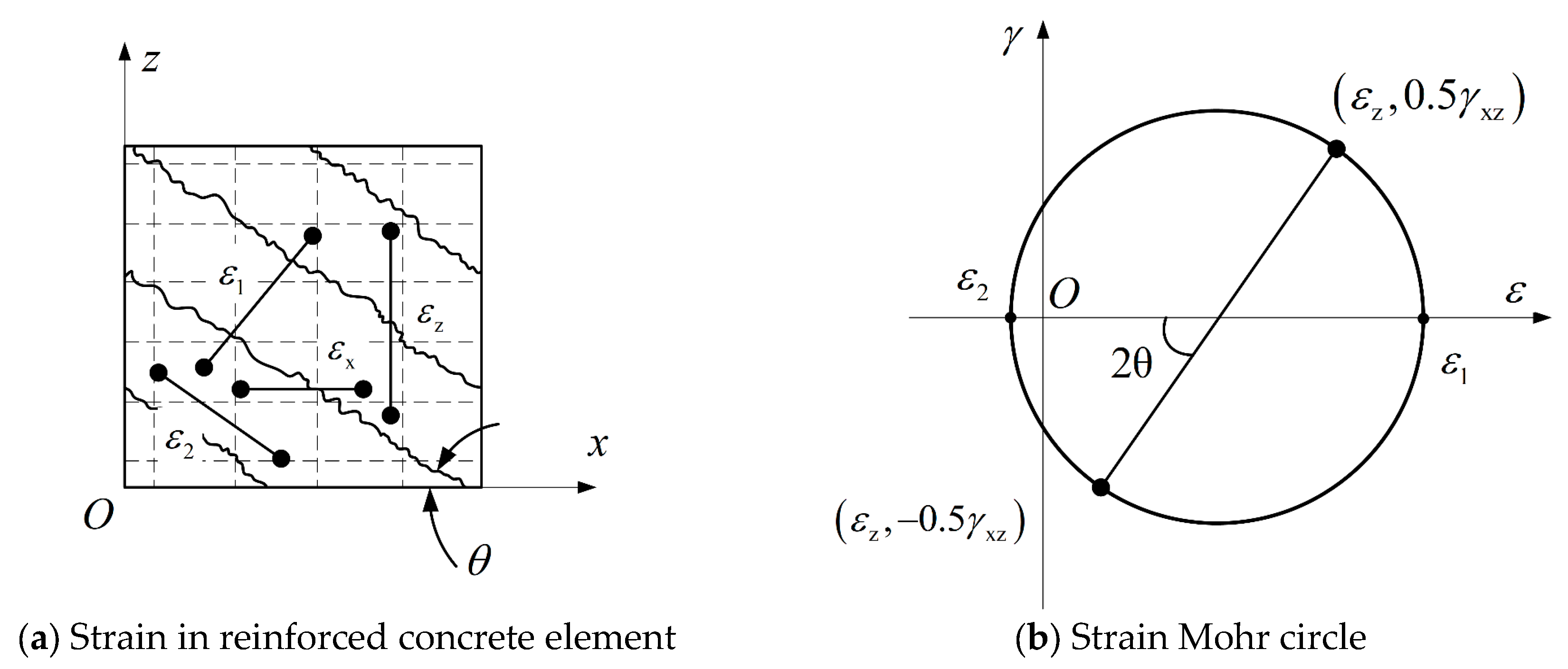
Appendix A.3. Shear Strength of RC Element
References
- Li, X.; Gong, J. Probabilistic Evaluation of the Leak-Tightness Function of the Nuclear Containment Structure Subjected to Internal Pressure. Reliab. Eng. Syst. Saf. 2024, 241, 109684. [Google Scholar] [CrossRef]
- Barda, F.; Hanson, J.M.; Corley, W.G. Shear Strength of Low-Rise Walls with Boundary Elements; American Concrete Institute: Farmington Hills, MI, USA, 1977; ACI Special Publication, SP-053; pp. 149–202. [Google Scholar]
- ASCE 43-05; Seismic Design Criteria for Structures, Systems, and Components in Nuclear Facilities. American Society of Civil Engineers: Reston, VA, USA, 2005.
- RCC-CW-15; Rules for Design and Construction of PWR Nuclear Civil Works. AFCEN: Paris, France, 2015.
- NB/T 20256-13; Seismic Design Code of Nuclear Safety Related Structure. National Energy Administration: Beijing, China, 2013.
- Gulec, C.K.; Whittaker, A.S.; Stojadinovic, B. Shear Strength of Squat Rectangular Reinforced Concrete Walls. ACI Struct. J. 2008, 105, 488–497. [Google Scholar] [CrossRef]
- ASCE 43-19; Seismic Design Criteria for Structures, Systems, and Components in Nuclear Facilities. American Society of Civil Engineers: Reston, VA, USA, 2019.
- ACI 349-13; Code Requirements for Nuclear Safety-Related Concrete Structures and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2014.
- ACI 318-08; Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2008.
- Gulec, C.K.; Whittaker, A.S. Performance-Based Assessment and Design of Squat Reinforced Concrete Shear Walls; State University of New York at Buffalo: Buffalo, NY, USA, 2009. [Google Scholar]
- Hsu, T.T.C.; Mo, Y.L. Softening of Concrete in Low-Rise Shear Walls. J. Am. Concr. Inst. 1985, 82, 883–889. [Google Scholar] [CrossRef]
- Kassem, W. Shear Strength of Squat Walls: A Strut-and-Tie Model and Closed-Form Design Formula. Eng. Struct. 2015, 84, 430–438. [Google Scholar] [CrossRef]
- Hwang, S.; Lee, H. Strength Prediction for Discontinuity Regions by Softened Strut-and-Tie Model. J. Struct. Eng. 2002, 128, 1519–1526. [Google Scholar] [CrossRef]
- Gulec, C.K.; Whittaker, A.S. Empirical Equations for Peak Shear Strength of Low Aspect Ratio Reinforced Concrete Walls. ACI Struct. J. 2011, 108, 80–89. [Google Scholar] [CrossRef]
- Gong, J.; Sun, Y.; Zhang, N. Study on In-Plane Shear of RC Walls in Nuclear Power Plant Based on the Plastic Limit Theory. Build. Struct. 2018, 48, 44–50. [Google Scholar] [CrossRef]
- Luna, B.N.; Whittaker, A.S. Peak Strength of Shear-Critical Reinforced Concrete Walls. ACI Struct. J. 2019, 116, 257–266. [Google Scholar] [CrossRef]
- Salonikios, T.N. Analytical Prediction of the Inelastic Response of RC Walls with Low Aspect Ratio. J. Struct. Eng. 2007, 133, 844–854. [Google Scholar] [CrossRef]
- Salonikios, T.N.; Kappos, A.J.; Tegos, I.A.; Penelis, G.G. Cyclic Load Behavior of Low-Slenderness Reinforced Concrete Walls: Failure Modes, Strength and Deformation Analysis, and Design Implications. ACI Struct. J. 2000, 97, 132–141. [Google Scholar] [CrossRef]
- GB 50010; Code for Design of Concrete Structures. China Architecture and Building Press: Beijing, China, 2010.
- JGJ 2015; Specification of Testing Methods for Earthquake Resistant Building. China Ministry of Construction: Beijing, China, 2015.
- Nielsen, M.P.; Hoang, L.C. Limit Analysis and Concrete Plasticity, 3rd ed.; Taylor & Francis: Abingdon, UK, 2010; ISBN 9781439803967. [Google Scholar]
- EN 1992-1-1:2004; Eurocode 2: Design of Concrete Structures-Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- Nie, X.; Wang, J.; Tao, M.; Fan, J.; Mo, Y.L.; Zhang, Z. Experimental Study of Shear Critical Reinforced Concrete Shear Walls under Tension Bending Shear Combined Cyclic Load. J. Struct. Eng. 2020, 146, 04020047. [Google Scholar] [CrossRef]
- Ji, X.; Cheng, X.; Xu, M. Coupled Axial Tension-Shear Behavior of Reinforced Concrete Walls. Eng. Struct. 2018, 167, 132–142. [Google Scholar] [CrossRef]
- Ren, C. Experimental Study on Tension-Shear Performance of Reinforced Concrete Shear Wall; China Academy of Building Research: Beijing, China, 2018. [Google Scholar]
- Lai, T. Experimental Research on Mechanical Behavior of Concrete Shear Walls under Tension and Shear. Master’s Thesis, Tianjin University, Tianjin, China, 2015. [Google Scholar]
- Bentz, E.C.; Vecchio, F.J.; Collins, M.P. Simplified Compression Field Theory for Calculating Shear Strength of Reinforced Concrete Elements. ACI Struct. J. 2006, 103, 614–624. [Google Scholar] [CrossRef]
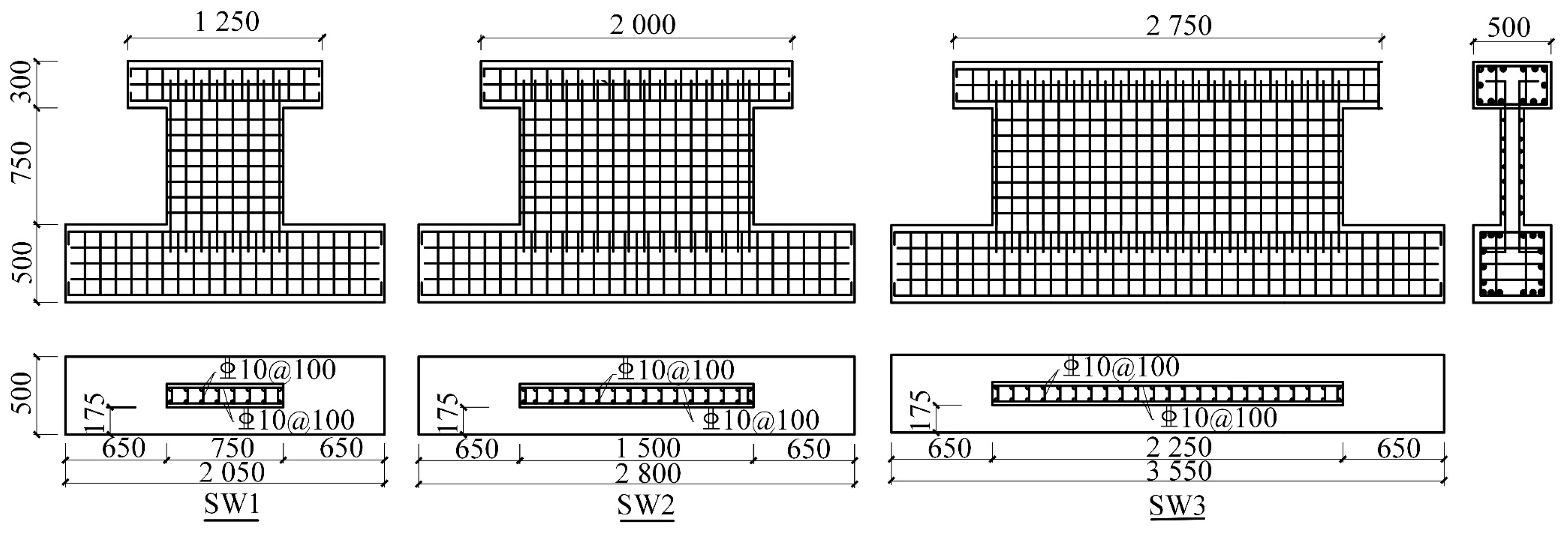





| Specimen | b/mm | h/mm | l/mm | Steel Bars | /% | /% | n |
|---|---|---|---|---|---|---|---|
| SW1 | 150 | 750 | 750 | D10@100 | 1.12 | 0.98 | 0.1 |
| SW2 | 150 | 750 | 1500 | D10@100 | 1.12 | 0.98 | 0.1 |
| SW3 | 150 | 750 | 2250 | D10@100 | 1.07 | 0.98 | 0.1 |
| SW4 | 150 | 750 | 750 | D10@100 | 1.12 | 0.98 | 0.3 |
| SW5 | 150 | 750 | 1500 | D8@100 | 0.71 | 0.63 | 0.1 |
| SW6 | 150 | 750 | 2250 | D8@100 | 0.69 | 0.63 | 0.1 |
| Specimens | SW1 | SW2 | SW3 | SW4 | SW5 | SW6 |
|---|---|---|---|---|---|---|
| Ve/kN | 347.8 | 1221.1 | 2300.9 | 477.1 | 1042.0 | 2051.2 |
| Specimen | SW1 | SW2 | SW3 | SW4 | SW5 | SW6 |
|---|---|---|---|---|---|---|
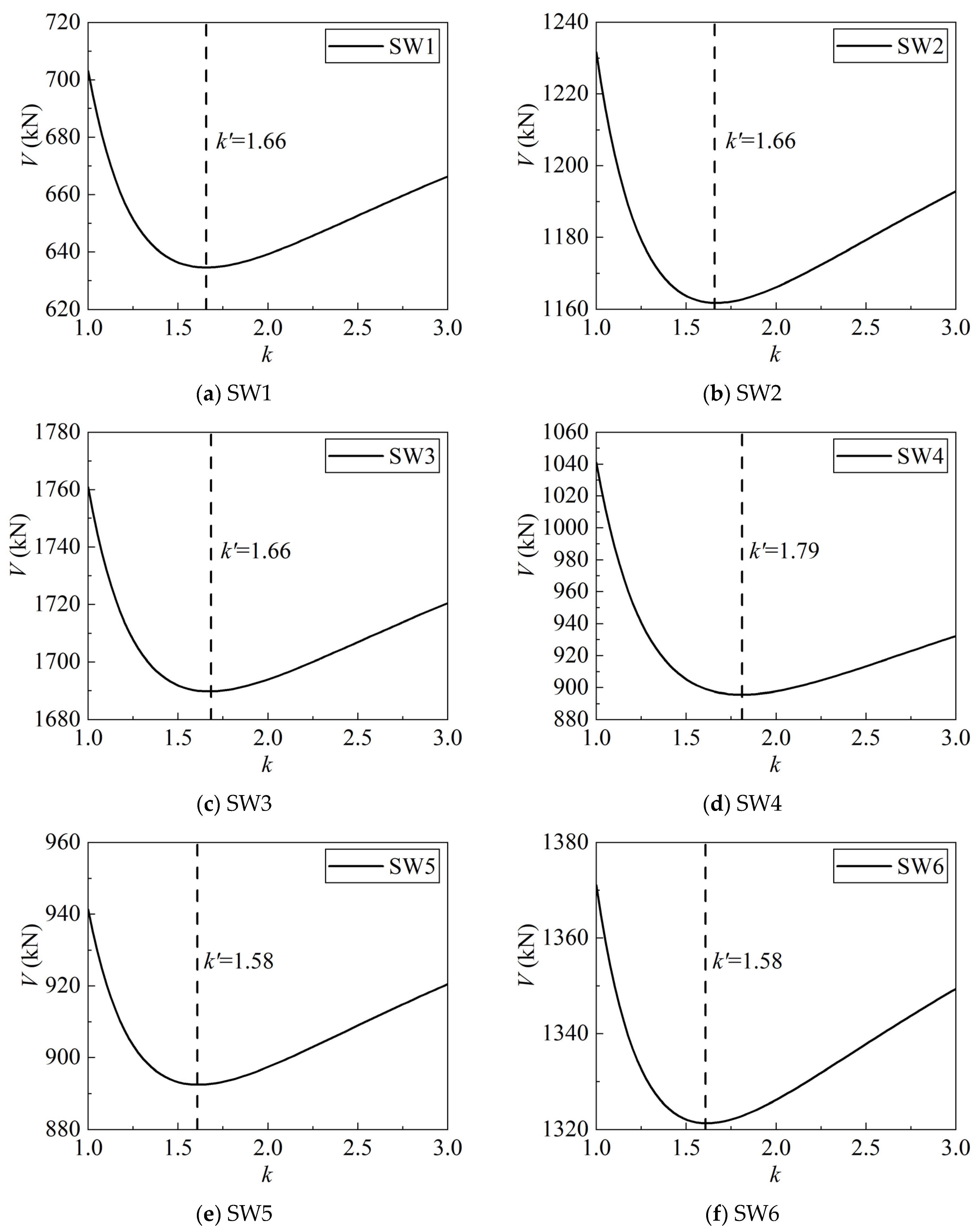
| k | 1.67 | 1.67 | 1.69 | 1.83 | 1.65 | 1.65 |
| V/kN | 634.7 | 1162.9 | 1691.4 | 901.3 | 896.0 | 1324.7 |
| Ve/kN | 347.8 | 1221.1 | 2300.9 | 477.1 | 1042.0 | 2051.2 |
| A | B | |
|---|---|---|
| 1 | 0 | |
| 0 | 1 |
| Mean | Standard Deviation | COV | Minimum | Median | Maximum | |
|---|---|---|---|---|---|---|
| Equation (24)/Vexp | 0.996 | 0.203 | 0.204 | 0.566 | 1.029 | 1.468 |
| Vn2/Vexp | 1.077 | 0.367 | 0.341 | 0.459 | 1.048 | 2.124 |
| Vn3/Vexp | 1.529 | 0.382 | 0.250 | 0.597 | 1.600 | 2.360 |
| Mean | Standard Deviation | COV | Minimum | Median | Maximum | |
|---|---|---|---|---|---|---|
| Equation (30)/Vexp | 1.000 | 0.206 | 0.206 | 0.722 | 0.966 | 1.573 |
| Vn2/Vexp | 0.750 | 0.344 | 0.459 | 0.307 | 0.695 | 1.614 |
| Vn3/Vexp | 1.777 | 0.717 | 0.404 | 0.958 | 1.572 | 4.065 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, S.; Li, X.; Gong, J. Lateral Load-Carrying Capacity of Low-Rise Reinforced Concrete Walls in Nuclear Safety-Related Structures. Buildings 2023, 13, 3090. https://doi.org/10.3390/buildings13123090
Guo S, Li X, Gong J. Lateral Load-Carrying Capacity of Low-Rise Reinforced Concrete Walls in Nuclear Safety-Related Structures. Buildings. 2023; 13(12):3090. https://doi.org/10.3390/buildings13123090
Chicago/Turabian StyleGuo, Shuheng, Xinbo Li, and Jinxin Gong. 2023. "Lateral Load-Carrying Capacity of Low-Rise Reinforced Concrete Walls in Nuclear Safety-Related Structures" Buildings 13, no. 12: 3090. https://doi.org/10.3390/buildings13123090
APA StyleGuo, S., Li, X., & Gong, J. (2023). Lateral Load-Carrying Capacity of Low-Rise Reinforced Concrete Walls in Nuclear Safety-Related Structures. Buildings, 13(12), 3090. https://doi.org/10.3390/buildings13123090





