Experimental Study on Bond Behavior between CFRP and Concrete with a Convex-Circular Arc Interface
Abstract
:1. Introduction
2. Experimental Program
2.1. Specimen’s Design
2.2. Material Properties
2.3. Preparation of Bonding Specimens
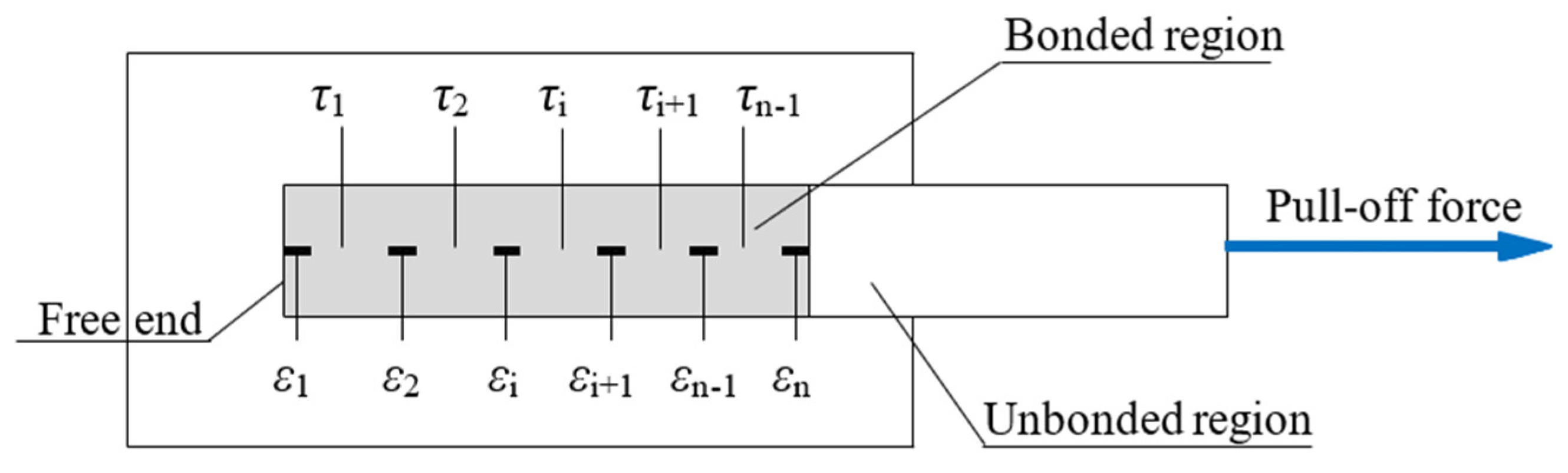
2.4. Single Shear Test Method
3. Results and Analysis
3.1. Failure Pattern
3.2. Ultimate Bearing Capacity
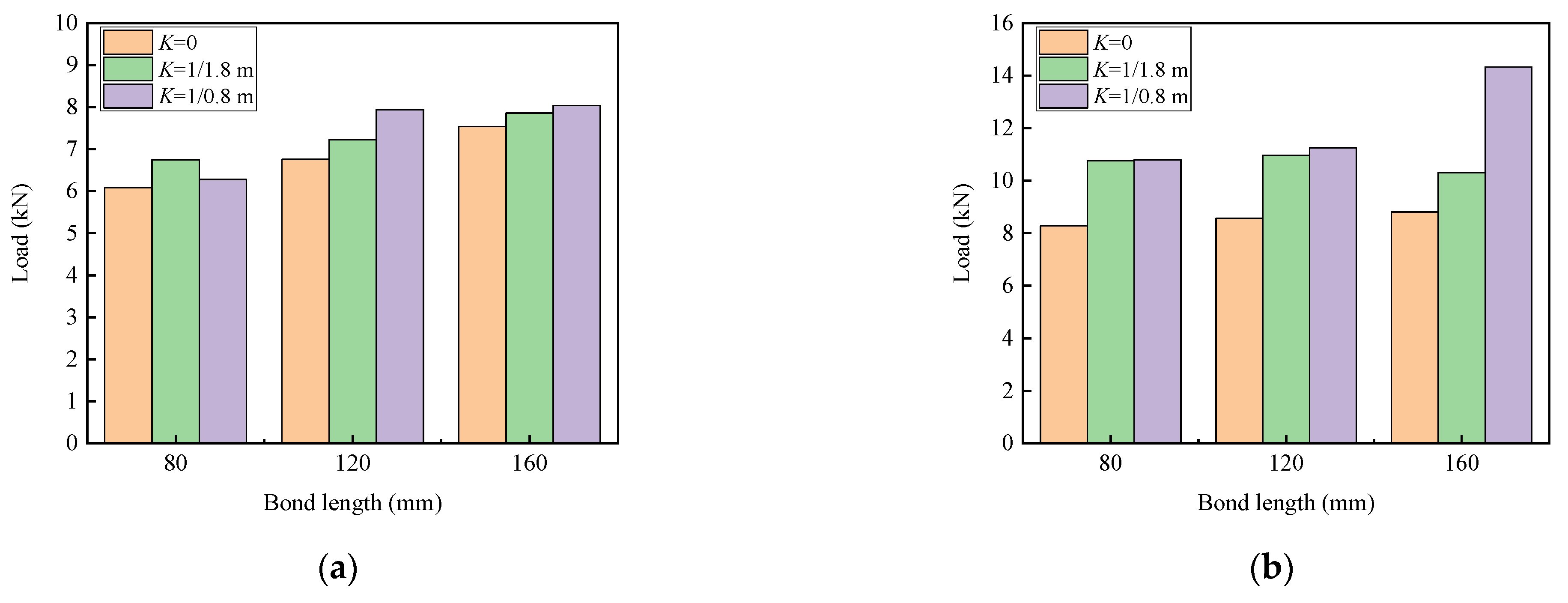
3.2.1. Effect of Bond Length and Layers of CFRP Laminates
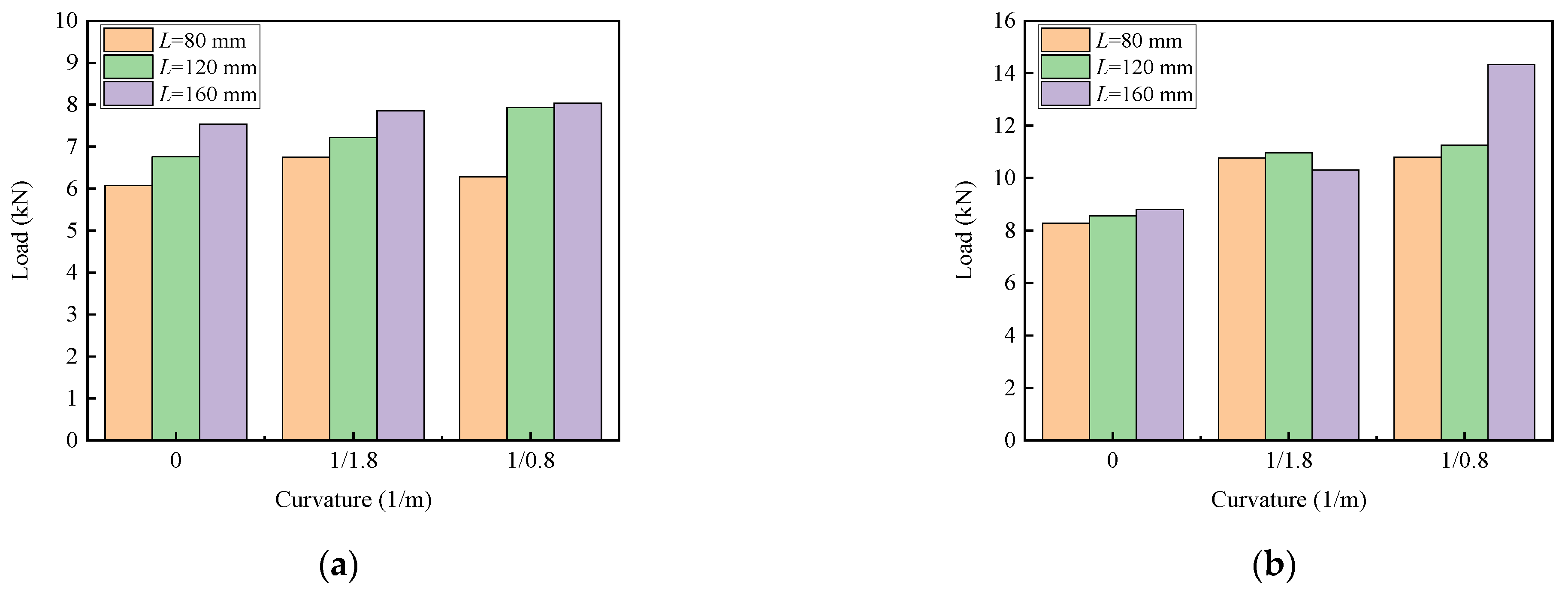
3.2.2. Effect of Bond Surface Curvature of Concrete
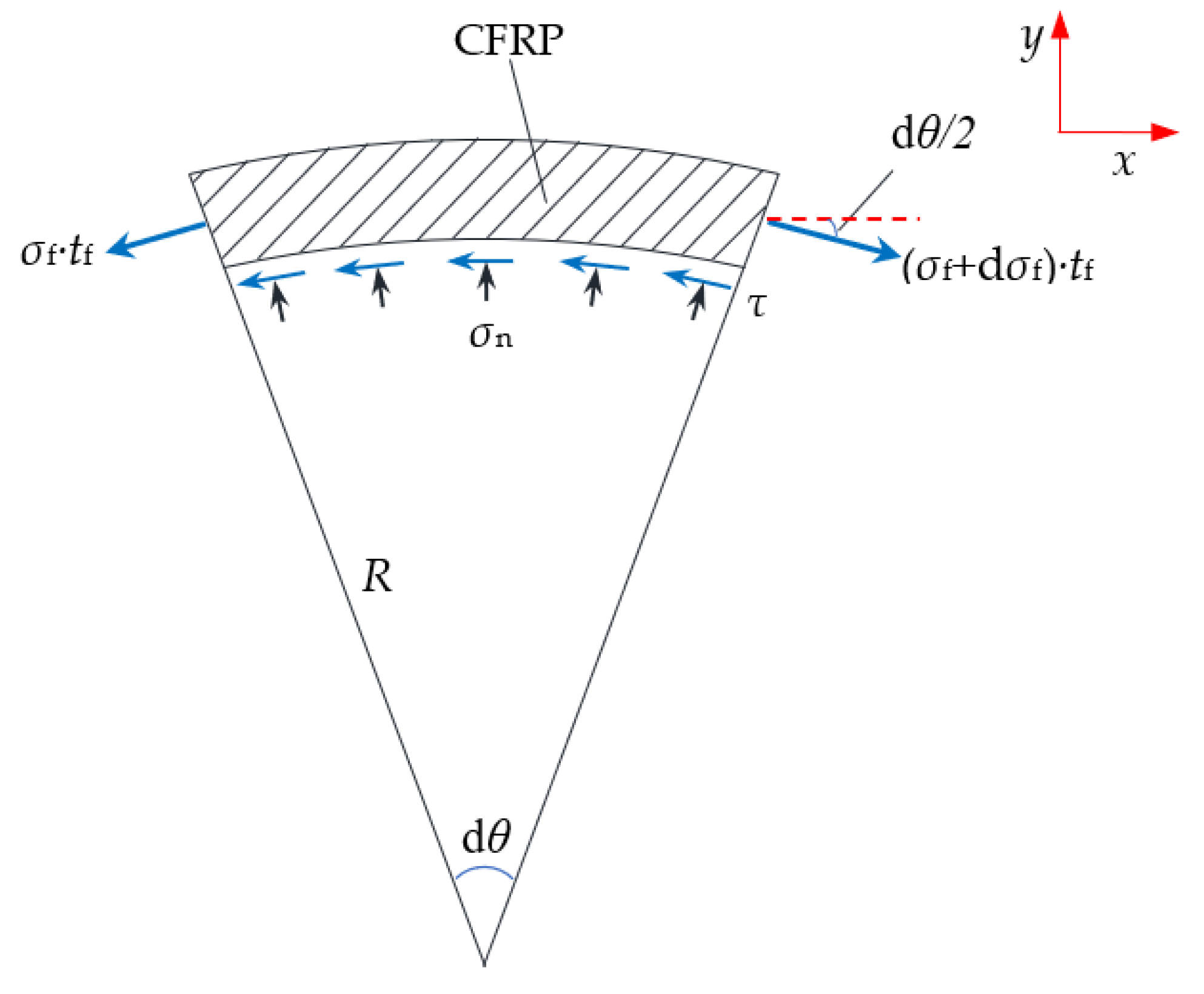
3.2.3. Calculation Model
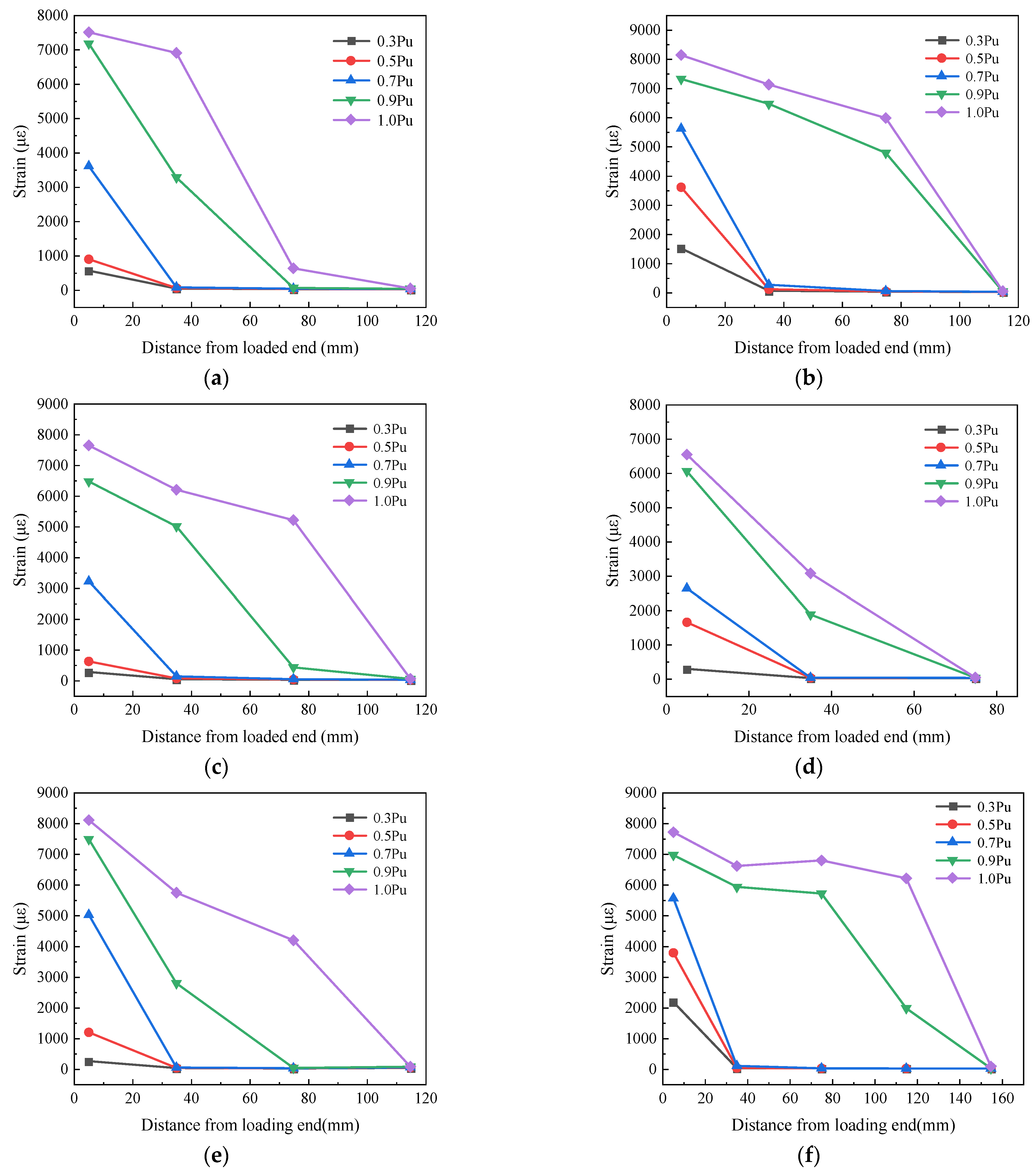
3.3. CFRP Strains
3.4. Bond–Slip Constitutive Model
4. Conclusions
- (1)
- The peeling of CFRP was the main failure pattern of the bonding specimens. With the increase in the concrete interface curvature from 0 to 1/(0.8 m), the bond capacity had an increase of about 9% for the one-layer CFRP specimens, while it had an increase of about 42% for the two-layer CFRP specimens.
- (2)
- Considering the influence of the concrete interface curvature, the calculation formula of the bond capacity of CFRP to concrete is proposed, and the curvature influence coefficient is obtained through the regression of the experimental data. The applicability of the formula was verified by comparing the calculated values with the experimental results.
- (3)
- The variation in the CFRP strain during the loading process was analyzed. The local bond–slip curve of each specimen was calculated through the differential analysis of the tested CFRP strains. A two-stage model is proposed for simulating the interface relationship. In comparison with the three existing bond–slip models, the model proposed in this study is closest to the test results.
- (4)
- It should be noted that the scope of the present research has been limited to CFRP–concrete bonded specimens with a convex-circular arc surface as well as a flat surface. The present work can be applied to externally bonded CFRP laminates on strengthening concrete pipes and other concrete structural members with a convex curved surface. Further efforts can be carried out on the bond behavior of CFRP to concrete with more complex curved interfaces.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gravina, R.J.; Smith, S.T. Flexural behaviour of indeterminate concrete beams reinforced with FRP bars. Eng. Struct. 2008, 30, 2370–2380. [Google Scholar] [CrossRef]
- Li, F.; Zhang, J.; Hou, P.; Qu, F. Experimental study on reinforcing corroded reinforced concrete beams with adhesive steel plates. Concrete 2013, 35, 9–12. [Google Scholar]
- Qu, F.; Meng, J.; Li, F. Numerical analysis of corroded reinforced concrete reinforced by adhesive steel reinforcement. Concrete 2016, 38, 8–11. [Google Scholar]
- Isleem, H.F.; Wang, D.Y.; Wang, Z.Y. A new numerical model for polymer-confined rectangular concrete columns. Proc. Inst. Civ. Eng. Struct. Build. 2019, 172, 528–544. [Google Scholar] [CrossRef]
- Isleem, H.F.; Wang, Z.Y.; Wang, D.Y.; Smith, S.T. Monotonic and cyclic axial compressive behavior of CFRP-confined rectangular RC columns. J. Compos. Constr. 2018, 2, 04018023. [Google Scholar] [CrossRef]
- Tahir, M.; Wang, Z.Y.; Ali, K.M.; Isleem, H.F. Shear behavior of concrete beams reinforced with CFRP laminate strip stirrups using wet-layup technique. Structures 2019, 22, 43–52. [Google Scholar] [CrossRef]
- Razaqpur, A.G.; Lamberti, M.; Ascione, F. Debonding evolution in nonlinear FRP-retrofitted RC beams with cohesive interface. Compos. Struct. 2020, 236, 111858. [Google Scholar] [CrossRef]
- Isleem, H.F.; Wang, D.Y.; Wang, Z.Y. Modeling the axial compressive stress-strain behavior of CFRP-confined rectangular RC columns under monotonic and cyclic loading. Compos. Struct. 2018, 185, 229–240. [Google Scholar] [CrossRef]
- Wang, H.; Li, C.; Song, S.; Wang, Y.; Meng, Q.; Li, F. Flexural performance of cracked reinforced concrete beams strengthened with prestressed CFRP laminates under repeated loads. Buildings 2023, 13, 2115. [Google Scholar] [CrossRef]
- Smith, S.T.; Teng, J. Shear-bending interaction in debonding failures of FRP-plated RC beams. Adv. Struct. Eng. 2003, 6, 183–199. [Google Scholar] [CrossRef]
- Cao, S.; Chen, J.; Pan, J.; Sun, N. ESPI measurement of bond-slip relationships of FRP-concrete interface. J. Compos. Constr. 2007, 11, 149–160. [Google Scholar] [CrossRef]
- Aydin, H.; Gravina, R.J.; Visintin, P. A partial-interaction approach for extracting FRP-to-concrete bond characteristics from environmentally loaded flexural tests. Compos. Part B Eng. 2018, 132, 214–228. [Google Scholar] [CrossRef]
- Monti, G.; Liotta, M. Tests and design equations for FRP-strengthening in shear. Constr. Build. Mater. 2007, 21, 799–809. [Google Scholar] [CrossRef]
- Colotti, V. Effectiveness factors for bond strength in FRP shear-strengthened RC beams. Mater. Struct. 2016, 49, 5031–5049. [Google Scholar] [CrossRef]
- Razaqpur, A.G.; Lamberti, M.; Ascione, F. A nonlinear semi-analytical model for predicting debonding of FRP laminates from RC beams subjected to uniform or concentrated load. Constr. Build. Mater. 2020, 233, 117838. [Google Scholar] [CrossRef]
- Ascione, F.; Lamberti, M.; Napoli, A.; Razaqpur, A.G.; Realfonzo, R. Modeling SRP-concrete interfacial bond behavior and strength. Eng. Struct. 2019, 187, 220–230. [Google Scholar] [CrossRef]
- Lamberti, M.; Ascione, F.; Napoli, A.; Razaqpur, G.; Realfonzo, R. Nonlinear analytical procedure for predicting debonding of laminate from substrate subjected to monotonic or cyclic load. Materials 2022, 15, 8690. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Wang, Y.; Qu, F.; Guo, X.; Li, Y.; Cheng, S. Bonded behavior of hybrid-bonded CFRP to heat-damaged concrete interface. Buildings 2023, 13, 2736. [Google Scholar] [CrossRef]
- Teng, J.; Smith, S.T.; Yao, J.; Chen, J. Intermediate crack-induced debonding in RC beams and slabs. Constr. Build. Mater. 2003, 17, 447–462. [Google Scholar] [CrossRef]
- Kabir, M.I.; Shrestha, R.; Samali, B. Effects of applied environmental conditions on the pull-out strengths of CFRP-concrete bond. Constr. Build. Mater. 2016, 114, 817–830. [Google Scholar] [CrossRef]
- Van Gemert, D. Force transfer in epoxy-bonded steel-concrete joints. Int. J. Adhes. Adhes. 1980, 1, 67–72. [Google Scholar] [CrossRef]
- Chen, J.; Teng, J. Anchorage strength models for FRP and steel plates bonded to concrete. J. Struct. Eng. 2001, 127, 784–791. [Google Scholar] [CrossRef]
- Bizindavyi, L.; Neale, K.W. Transfer lengths and bond strengths for composites bonded to concrete. J. Compos. Constr. 1999, 3, 153–160. [Google Scholar] [CrossRef]
- Jawdhari, A.; Semendary, A.; Fam, A.; Khoury, I.; Steinberg, E. Bond characteristics of CFRP rod panels adhered to concrete under bending effects. J. Compos. Constr. 2019, 23, 04018077. [Google Scholar] [CrossRef]
- Liu, K.; Wu, Y. Analytical identification of bond-slip relationship of EB-FRP joints. Compos. Part B Eng. 2012, 43, 1955–1963. [Google Scholar] [CrossRef]
- Ceroni, F.; Garofano, A.; Pecce, M. Bond tests on tuff elements externally bonded with FRP materials. Mater. Struct. 2015, 48, 2093–2110. [Google Scholar] [CrossRef]
- Yang, Y.; Yue, Q.; Hu, Y. Experimental study on bond performance between carbon fiber laminates and concrete. J. Build. Struct. 2001, 22, 36–42. [Google Scholar]
- Moghaddas, A.; Mostofinejad, D.; Saljoughian, A.; Ilia, E. An empirical FRP-concrete bond-slip model for externally-bonded reinforcement on grooves. Constr. Build. Mater. 2021, 281, 122575. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Z.; Yang, Q.; Chen, W. On shear bond strength of FRP-concrete structures. Eng. Struct. 2010, 32, 897–905. [Google Scholar] [CrossRef]
- Lu, X.; Teng, J.; Ye, L.; Jiang, J. Bond–slip models for FRP laminates/plates bonded to concrete. Eng. Struct. 2005, 27, 920–937. [Google Scholar] [CrossRef]
- Liu, G.; Qu, F.; Zhao, S.; Zhang, H. Experimental study on the adhesion properties of CFRP fabric to post-temperature concrete. J. Build. Struct. 2019, 40, 156–162. [Google Scholar]
- Leone, M.; Matthys, S.; Aiello, M.A. Effect of elevated service temperature on bond between FRP EBR systems and concrete. Compos. Part B Eng. 2009, 40, 85–93. [Google Scholar] [CrossRef]
- Jia, D.; Gao, W.; Duan, D.; Yang, J.; Dai, J. Full-range behavior of FRP-to-concrete bonded joints subjected to combined effects of loading and temperature variation. Eng. Fract. Mech. 2021, 254, 107928. [Google Scholar] [CrossRef]
- Arruda, M.R.T.; Firmo, J.P.; Correia, J.R.; Tiago, C. Numerical modelling of the bond between concrete and CFRP laminates at elevated temperatures. Eng. Struct. 2016, 110, 233–243. [Google Scholar] [CrossRef]
- Li, Y.; Chen, J.; Yang, Z.; Esmaeeli, E.; Sha, W.; Huang, Y. Effects of concrete heterogeneity on FRP-concrete bond behaviour: Experimental and mesoscale numerical studies. Compos. Struct. 2021, 275, 114436. [Google Scholar] [CrossRef]
- Li, W.; Yan, Z.; Cao, Z.; Pan, J. Effect of concrete surface roughness on the bonding performance between the CFRP and concrete. J. Shenzhen Univ. Sci. Eng. 2007, 24, 13–17. [Google Scholar]
- Pan, J.; Leung, C.K. Effect of concrete composition on FRP/concrete bond capacity. J. Compos. Constr. 2007, 11, 611–618. [Google Scholar] [CrossRef]
- De Lorenzis, L.; Teng, J.G. Near-surface mounted FRP reinforcement: An emerging technique for strengthening structures. Compos. Part B Eng. 2007, 38, 119–143. [Google Scholar] [CrossRef]
- Qu, F.; Xu, Z.; Yu, T.; Song, K. Experimental study on bonding performance of embedded carbon fiber reinforced composite panel-concrete interface. J. N. China Univ. Water Resour. Electric Power (Nat. Sci. Ed.) 2020, 41, 65–69. [Google Scholar]
- Zhai, K.; Fang, H.; Fu, B.; Wang, F.; Hu, B. Mechanical response of externally bonded CFRP on repair of PCCPs with broken wires under internal water pressure. Constr. Build. Mater. 2020, 239, 117878. [Google Scholar] [CrossRef]
- Zhai, K.; Fang, H.; Guo, C.; Ni, P.; Wu, H.; Wang, F. Full-scale experiment and numerical simulation of prestressed concrete cylinder pipe with broken wires strengthened by prestressed CFRP. Tunn. Undergr. Space Technol. 2021, 115, 104021. [Google Scholar] [CrossRef]
- Coronado, C.A.; Lopez, M.M. Damage approach for the prediction of debonding failure on concrete elements strengthened with FRP. J. Compos. Constr. 2007, 11, 391–400. [Google Scholar] [CrossRef]
- Mazzotti, C.; Savoia, M.; Ferracuti, B. An experimental study on delamination of FRP plates bonded to concrete. Constr. Build. Mater. 2008, 22, 1409–1421. [Google Scholar] [CrossRef]
- Liu, G.; Li, B.; Bao, J.; Cheng, S.; Meng, Q.; Zhao, S. Case study on prestressed CFRP plates applied for strengthening hollow-section beam removed from an old bridge. Polymers 2023, 15, 549. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Zhang, F.; Liu, J.; Lu, X. Whole-process bond characteristics of FRP-to-concrete joint under pressure. KSCE J. Civ. Eng. 2018, 22, 5114–5122. [Google Scholar] [CrossRef]
- Feng, D.; Liu, Z.; Wang, X.; Chen, Y.; Chang, J.; Wei, D.; Jiang, Z. Machine learning-based compressive strength prediction for concrete: An adaptive boosting approach. Constr. Build. Mater. 2020, 230, 117000. [Google Scholar] [CrossRef]
- Jia, Z.; Wang, W.; Zhang, J.; Li, H. Contact high-temperature strain automatic calibration and precision compensation research. J. Artif. Intell. Technol. 2022, 2, 69–76. [Google Scholar]
- Du, H.; Du, S.; Li, W. Probabilistic time series forecasting with deep non-linear state space models. CAAI Trans. Intell. Technol. 2023, 8, 3–13. [Google Scholar] [CrossRef]
- Isleem, H.F.; Peng, F.; Tayeh, B.A. Confinement model for LRS FRP-confined concrete using conventional regression and artificial neural network techniques. Compos. Struct. 2022, 279, 114779. [Google Scholar] [CrossRef]
- Dai, J.; Ueda, T.; Sato, Y. Development of the nonlinear bond stress-slip model of fiber reinforced plastics laminate-concrete interfaces with a simple method. J. Compos. Constr. 2005, 9, 52–62. [Google Scholar] [CrossRef]
- Ferracuti, B.; Savoia, M.; Mazzotti, C. Interface law for FRP–concrete delamination. Compos. Struct. 2007, 80, 523–531. [Google Scholar] [CrossRef]
- Biscaia, H.; Chastre, C.; Silva, M. Bond-slip model for FRP-to-concrete bonded joints under external compression. Compos. Part B Eng. 2015, 80, 246–259. [Google Scholar] [CrossRef]
- Yuan, H.; Teng, J.; Seracino, R.; Wu, Z.; Yao, J. Full-range behavior of FRP-to-concrete bonded joints. Eng. Struct. 2004, 26, 553. [Google Scholar] [CrossRef]
- Au, C.; Büyüköztürk, O. Debonding of FRP plated concrete: A tri-layer fracture treatment. Eng. Fract. Mech. 2006, 73, 348–365. [Google Scholar] [CrossRef]
- Wu, Z.; Yuan, H.; Niu, H. Stress transfer and fracture propagation in different kinds of adhesive joints. J. Eng. Mech. 2002, 128, 562–573. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, Y.; Yun, Y. Analytical modeling of the bond-slip relationship at FRP-concrete interfaces for adhesively-bonded joints. Compos. Part B Eng. 2010, 41, 423–433. [Google Scholar] [CrossRef]
- Liu, G.; Dou, X.; Qu, F.; Shang, P.; Zhao, S. Bond behavior of steel bars in concrete confined with stirrups under freeze–thaw cycles. Materials. 2022, 15, 7152. [Google Scholar] [CrossRef]
- Monti, G.; Renzelli, M.; Luciani, P. FRP adhesion in uncracked and cracked concrete zones. In Proceedings of the 6th International Symposium on FRP Reinforcement for Concrete Structures, Singapore, 8–10 July 2003. [Google Scholar]
- Nakaba, K.; Kanakubo, T.; Furuta, T.; Yoshizawa, H. Bond behavior between fiber-reinforced polymer laminates and concrete. ACI Struct. J. 2001, 98, 359–367. [Google Scholar]
- Savoia, M.; Ferracuti, B.; Mazzotti, C. Non-linear bond-slip law for FRP-concrete interface. In Proceedings of the 6th International Symposium on FRP Reinforcement for Concrete Structures, Singapore, 8–10 July 2003. [Google Scholar]
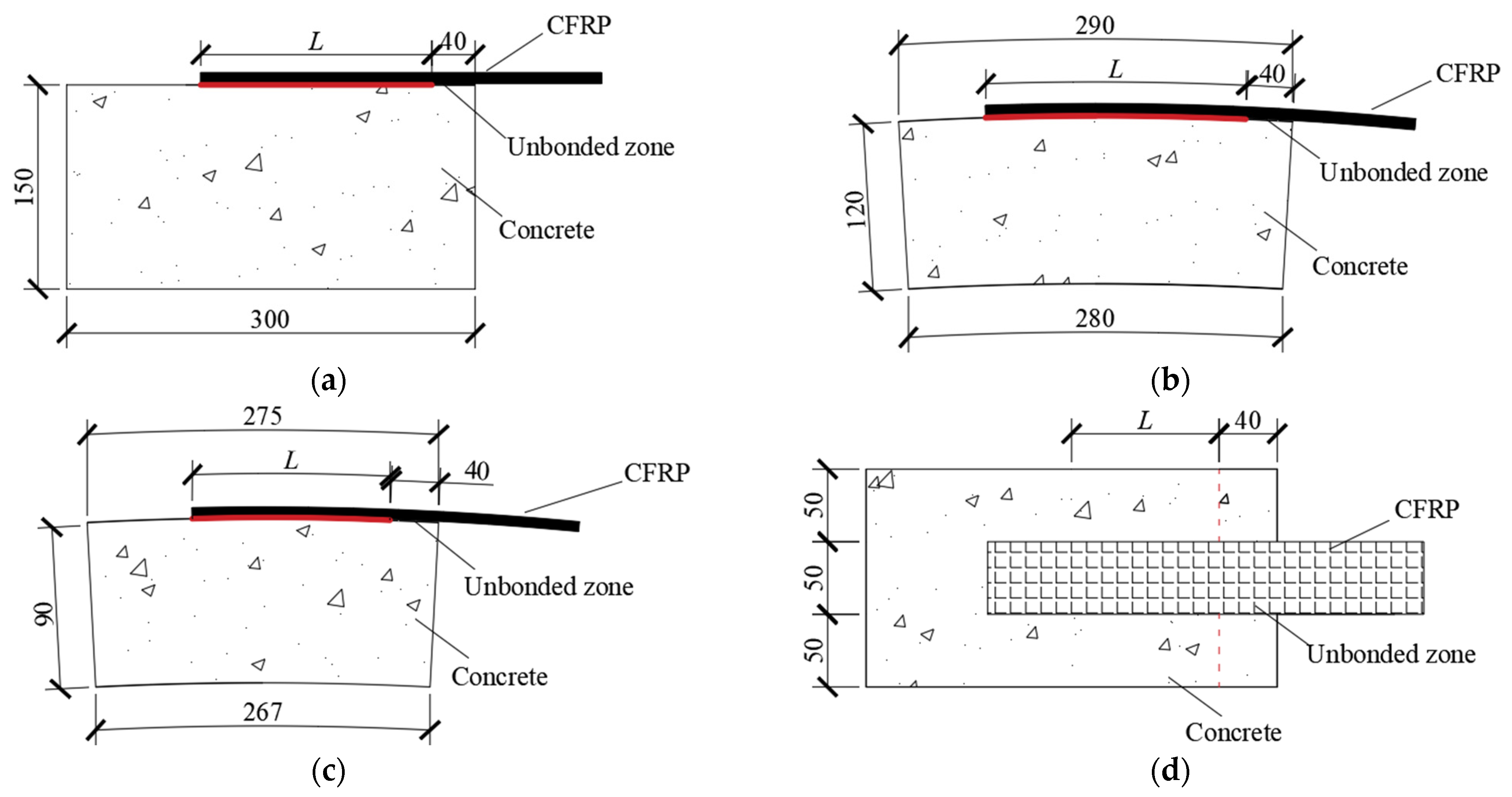



| Water | Cement | Fly Ash | Fine Aggregate | Coarse Aggregate | Water Reducer |
|---|---|---|---|---|---|
| 141 | 360 | 64 | 698 | 1188 | 6.36 |
| Bond Length (mm) | x1 | x2 | x3 | x4 | x5 |
|---|---|---|---|---|---|
| 80 | 5 | 35 | 75 | - | - |
| 120 | 5 | 35 | 75 | 115 | - |
| 160 | 5 | 35 | 75 | 115 | 155 |
| Group No. | fcu (N/mm2) | K (1/m) | tf (mm) | L (mm) | Test Result (kN) | Calculated Value (kN) | Calculated/Test Result |
|---|---|---|---|---|---|---|---|
| K1L80P1 | 66.71 | 0 | 0.167 | 80 | 6.08 | 6.70 | 1.10 |
| K2L80P1 | 66.71 | 1/1.8 | 0.167 | 80 | 6.75 | 6.96 | 1.03 |
| K3L80P1 | 66.71 | 1/0.8 | 0.167 | 80 | 6.28 | 7.29 | 1.16 |
| K1L120P1 | 51.62 | 0 | 0.167 | 120 | 6.76 | 6.29 | 0.93 |
| K2L120P1 | 51.62 | 1/1.8 | 0.167 | 120 | 7.22 | 6.53 | 0.90 |
| K3L120P1 | 51.62 | 1/0.8 | 0.167 | 120 | 7.94 | 6.84 | 0.86 |
| K1L160P1 | 69.13 | 0 | 0.167 | 160 | 7.54 | 6.76 | 0.90 |
| K2L160P1 | 69.13 | 1/1.8 | 0.167 | 160 | 7.86 | 7.03 | 0.89 |
| K3L160P1 | 69.13 | 1/0.8 | 0.167 | 160 | 8.04 | 7.35 | 0.91 |
| K1L80P2 | 69.13 | 0 | 0.334 | 80 | 8.28 | 8.89 | 1.07 |
| K2L80P2 | 69.13 | 1/1.8 | 0.334 | 80 | 10.76 | 10.13 | 0.94 |
| K3L80P2 | 69.13 | 1/0.8 | 0.334 | 80 | 10.80 | 11.67 | 1.08 |
| K1L120P2 | 69.13 | 0 | 0.334 | 120 | 8.56 | 9.56 | 1.12 |
| K2L120P2 | 69.13 | 1/1.8 | 0.334 | 120 | 10.97 | 10.89 | 0.99 |
| K3L120P2 | 69.13 | 1/0.8 | 0.334 | 120 | 11.26 | 12.55 | 1.11 |
| K1L160P2 | 61.20 | 0 | 0.334 | 160 | 8.81 | 9.28 | 1.05 |
| K2L160P2 | 61.20 | 1/1.8 | 0.334 | 160 | 10.31 | 10.57 | 1.02 |
| K3L160P2 | 61.20 | 1/0.8 | 0.334 | 160 | 14.33 | 12.18 | 0.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, F.; Wei, H.; Lu, H.; Feng, D.; Meng, Q.; Zhao, S. Experimental Study on Bond Behavior between CFRP and Concrete with a Convex-Circular Arc Interface. Buildings 2023, 13, 3077. https://doi.org/10.3390/buildings13123077
Qu F, Wei H, Lu H, Feng D, Meng Q, Zhao S. Experimental Study on Bond Behavior between CFRP and Concrete with a Convex-Circular Arc Interface. Buildings. 2023; 13(12):3077. https://doi.org/10.3390/buildings13123077
Chicago/Turabian StyleQu, Fulai, Hexiang Wei, Hailu Lu, Dakuo Feng, Qingxin Meng, and Shunbo Zhao. 2023. "Experimental Study on Bond Behavior between CFRP and Concrete with a Convex-Circular Arc Interface" Buildings 13, no. 12: 3077. https://doi.org/10.3390/buildings13123077
APA StyleQu, F., Wei, H., Lu, H., Feng, D., Meng, Q., & Zhao, S. (2023). Experimental Study on Bond Behavior between CFRP and Concrete with a Convex-Circular Arc Interface. Buildings, 13(12), 3077. https://doi.org/10.3390/buildings13123077







