Simulation of the Hygro-Thermo-Mechanical Behavior of Earth Brick Walls in Their Environment
Abstract
:1. Introduction
2. Materials and Methods
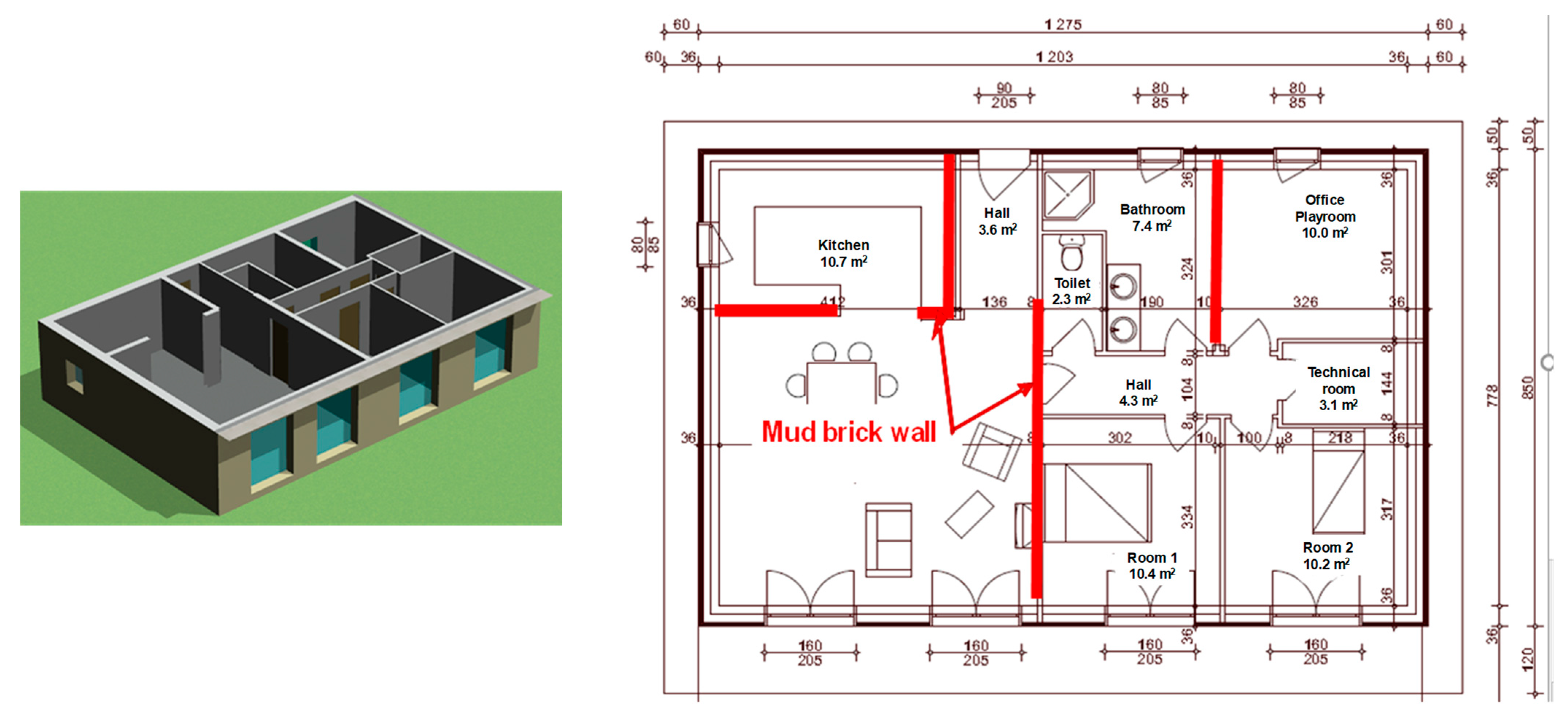
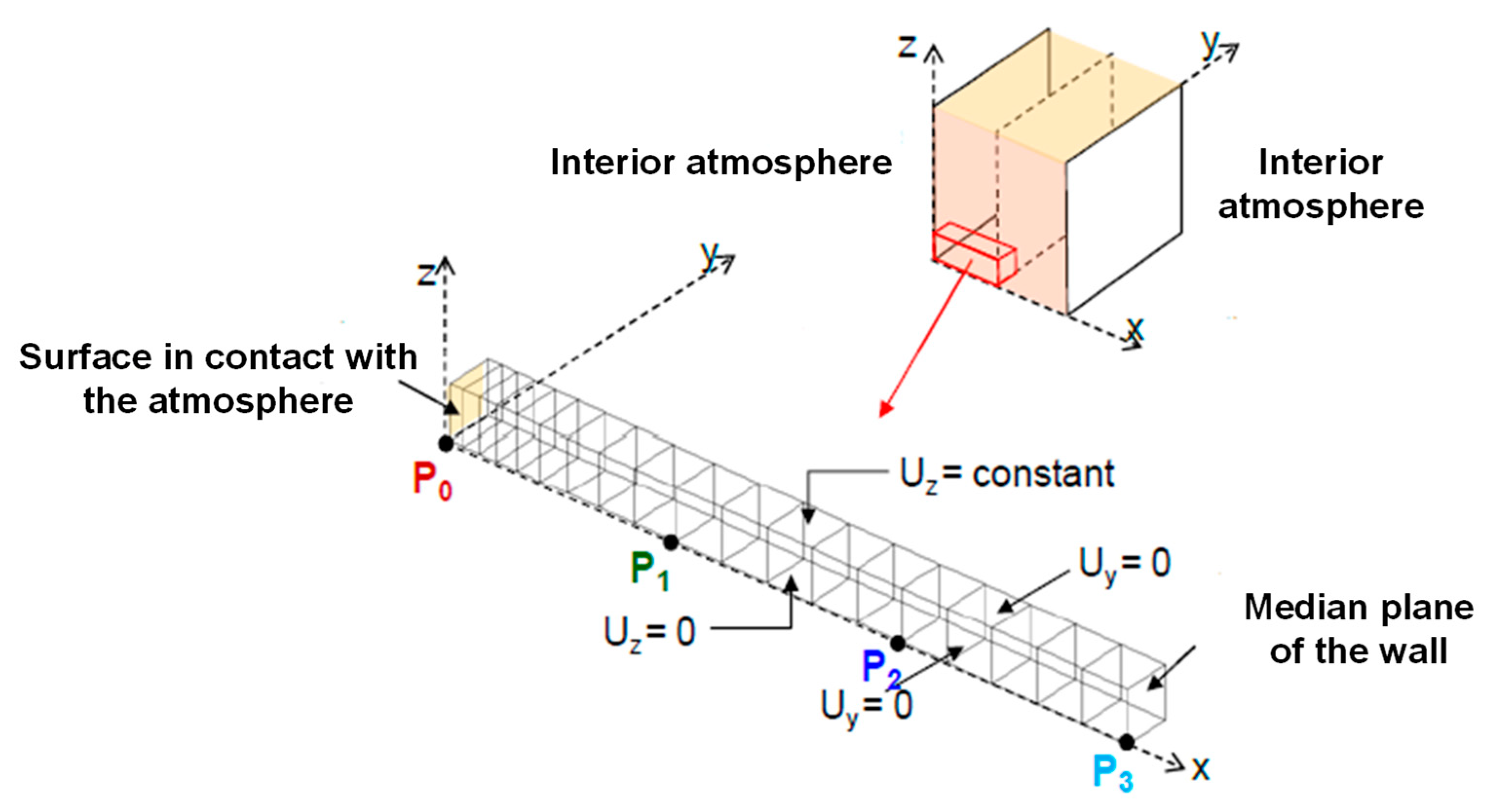
2.1. Description of the Simulated Dwelling
- In the so-called “basic” version, all partition walls in the dwelling are lightweight plasterboard walls on a metal frame. The cladding on all walls is considered to be vapor impermeable; also, the hygroscopic properties of the furnishings and textiles in the home are neglected.
- In the “earth” version, the earth brick wall replaces certain partition walls over a surface area of 30.8 m², with the other assumptions remaining identical to the basic version.
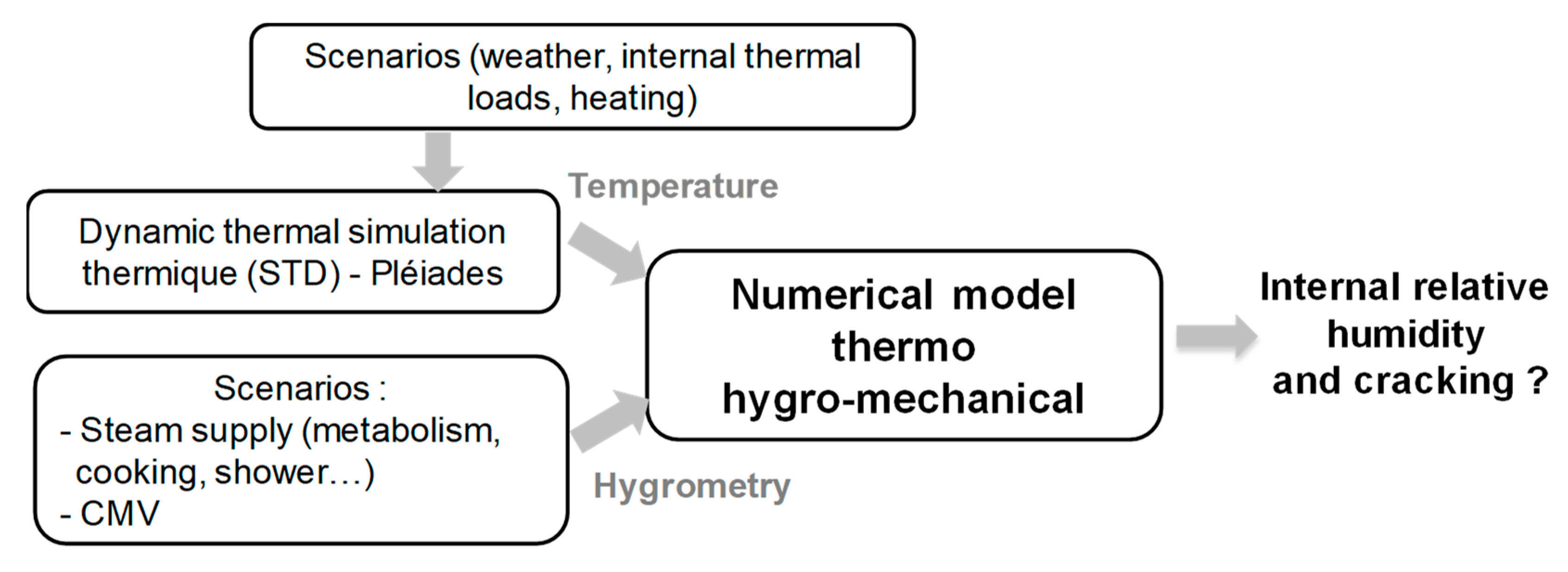
2.2. Numerical Model
2.2.1. State-of-the-Art
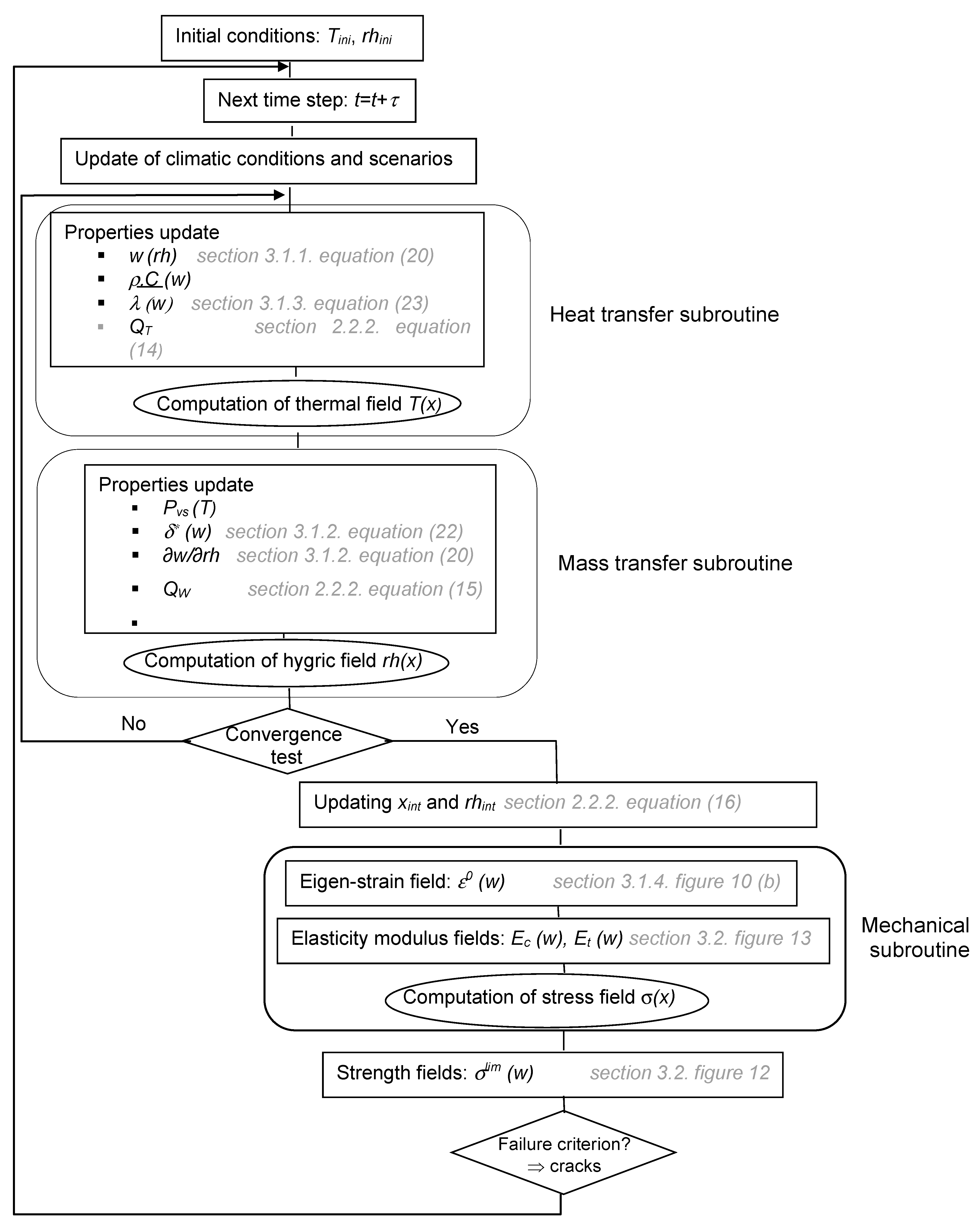
2.2.2. Description of the Numerical Model Developed
- : specific humidity of the indoor air at time t [kg water/kg dry air]
- : specific humidity of the indoor air at time t+ζ [kg water/kg dry air]
- : time step [s]
- : dry density of indoor air (kg/m3)
- : interior volume of the zone [m3]
- : mass flow rate of the internal water vapor inputs from occupants and processes [kg/s]
- : mass flow rate of water vapor supplied by the CMV. This value is estimated using Equation (17).
- : extracted air volume flow rate [m3/h]
- and : specific humidity of outdoor and indoor air [kg water/kg dry air]
- : mass flow rate of water vapor transferred from the wall to the environment [kg/s]. This value is calculated according to Equation (18).
- : mass flow of water vapor leaving the surface Smod of the model [kg/s]
- : exchange surface area of the model [m²]
- : total exchange surface area of the actual wall (including both faces) [m²]
2.2.3. Simulation of Coupled Behavior
3. Determination of Model Input Parameters
3.1. Characterization of Thermal and Hydric Properties
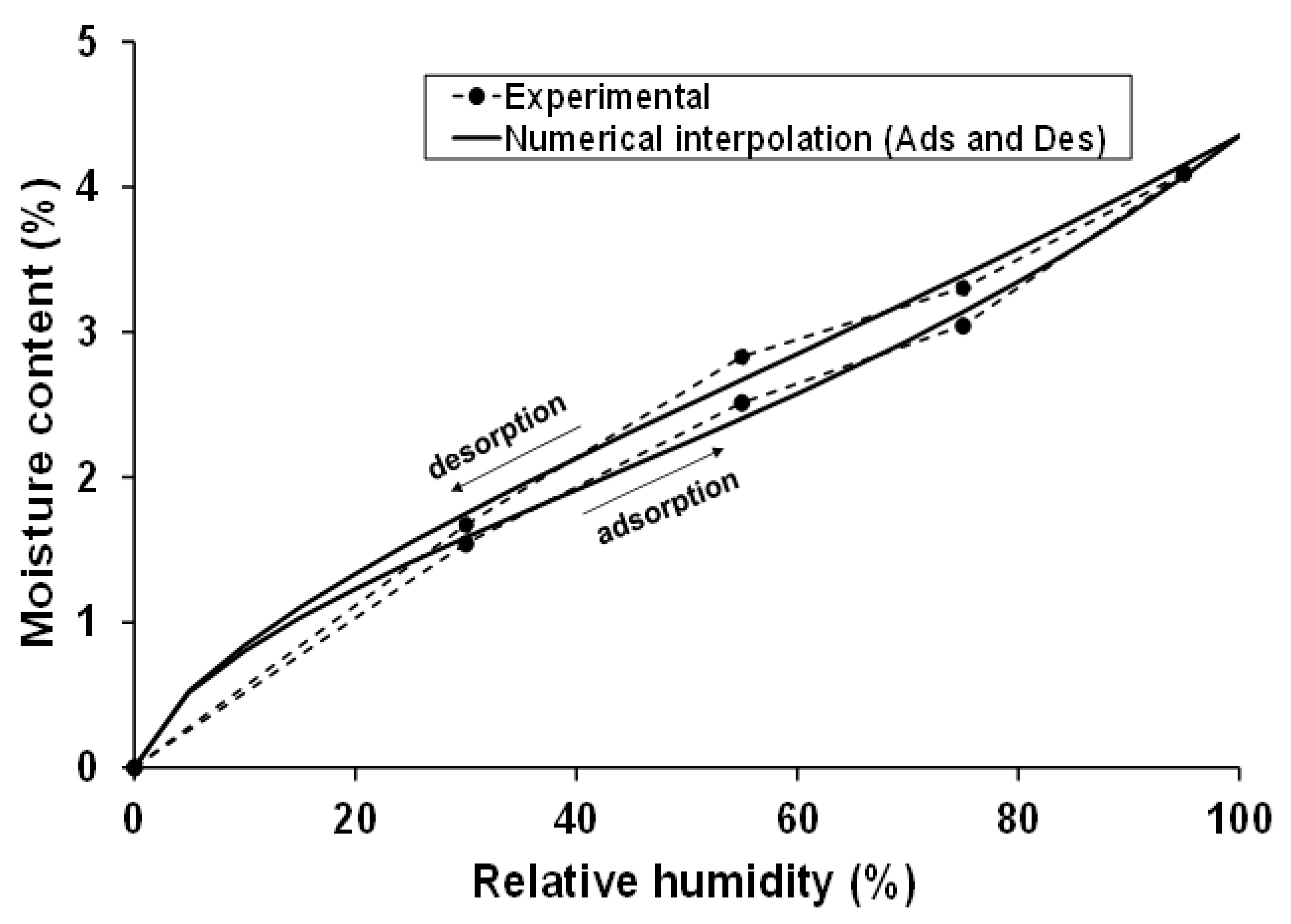
3.1.1. Sorption Isotherm and Moisture Capacity
- Adsorption: ws = 4.35%, aa = 0.67, φa = 0.68
- Desorption: ws = 4.35%, ad = 0.30, φd = 0.69
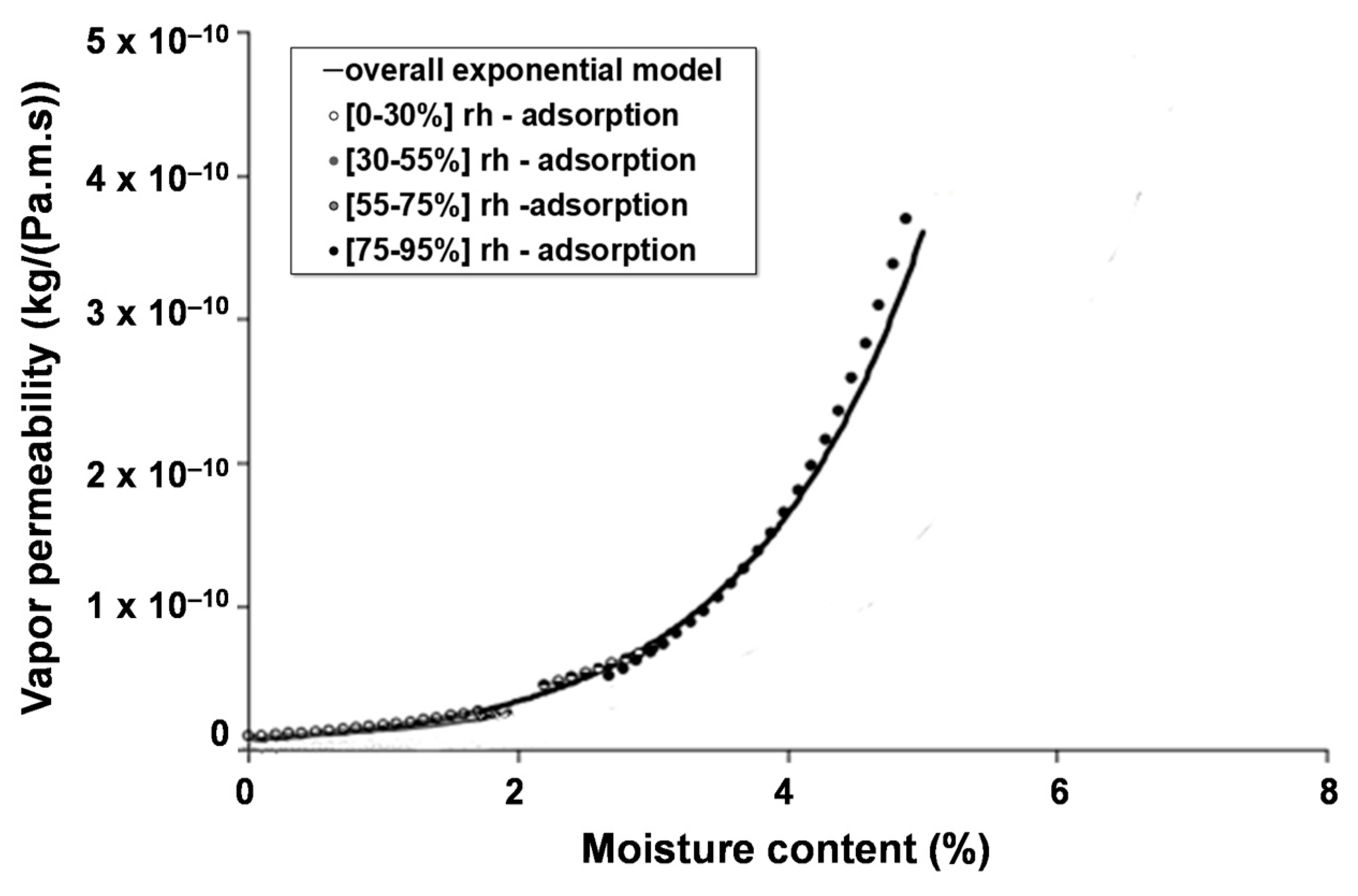
3.1.2. Apparent Vapor Permeability
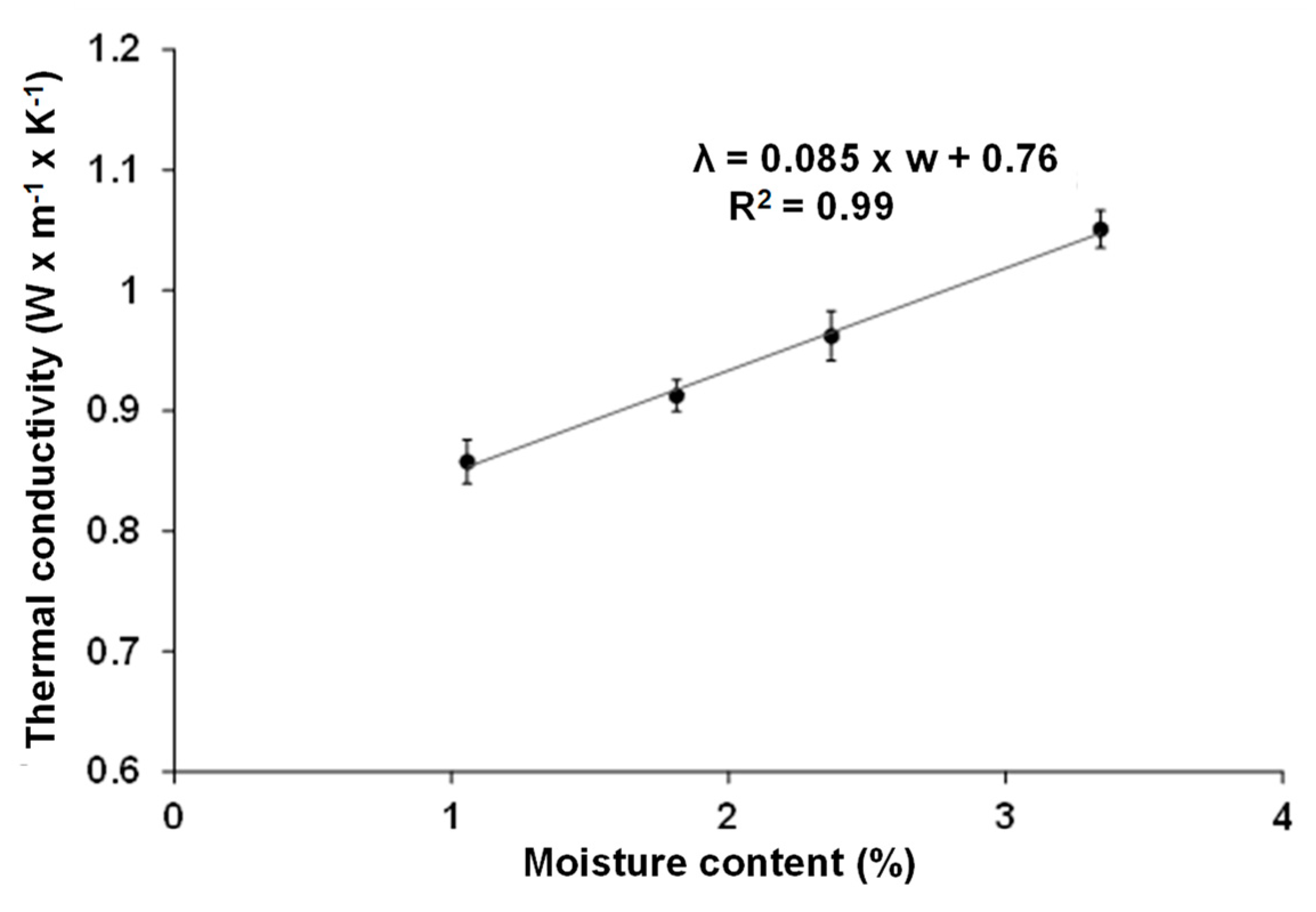
3.1.3. Thermal Conductivity
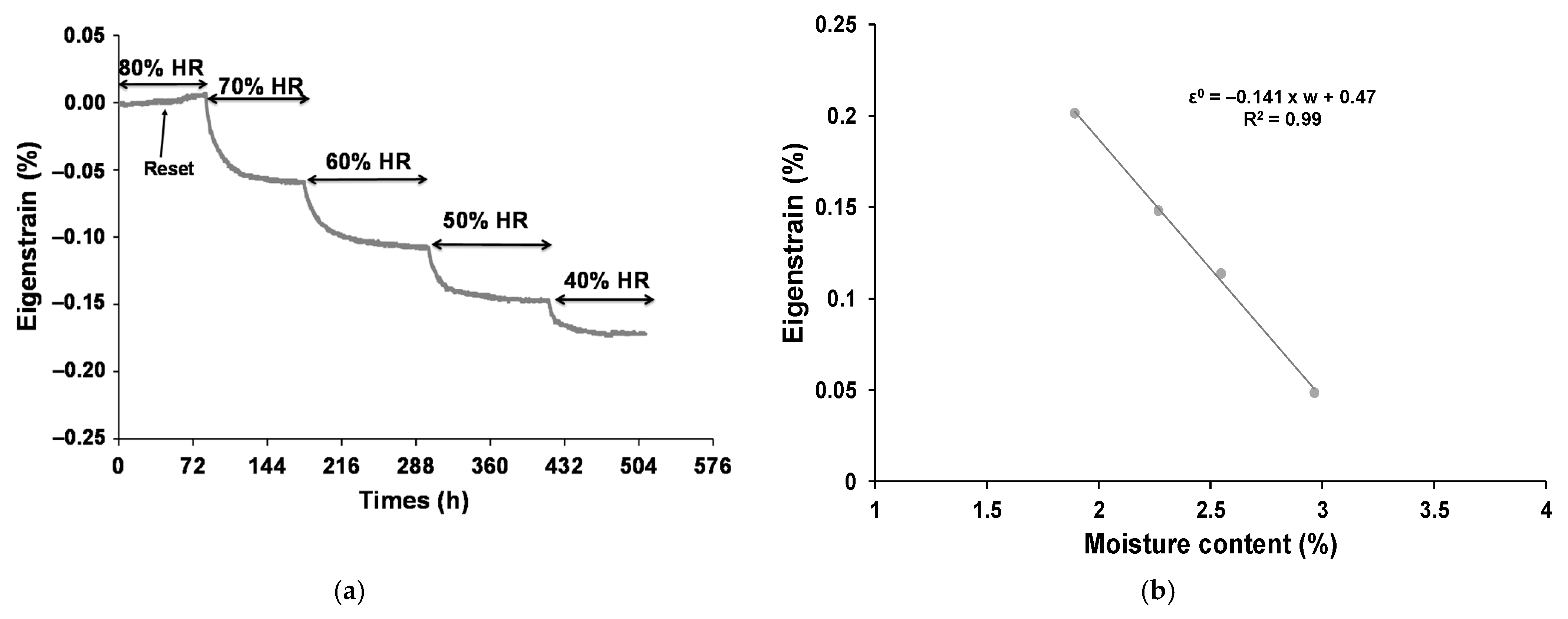
3.1.4. Calculation of the Water-Induced Eigenstrain Field
3.2. Characterization of Hygro-Mechanical Properties
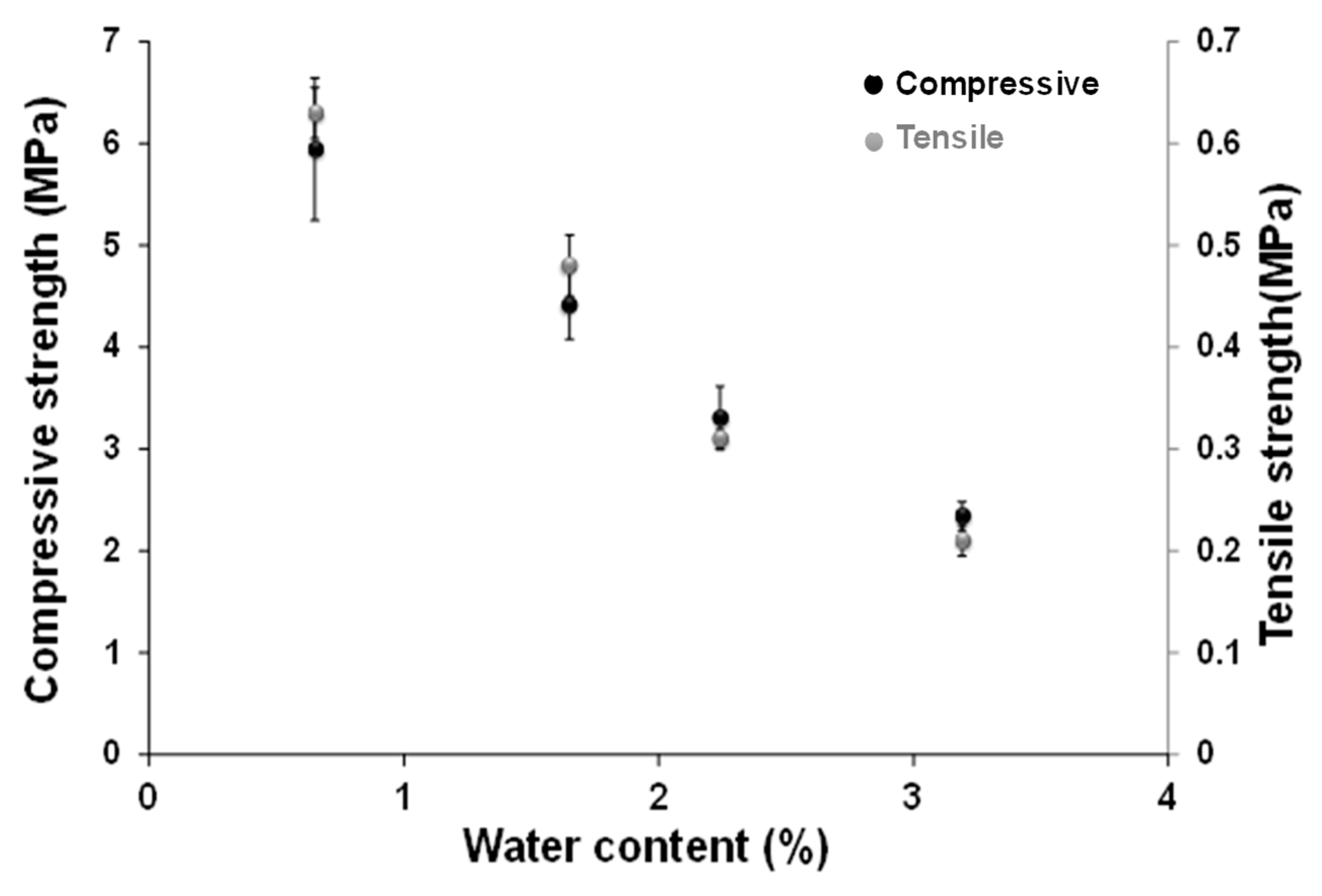
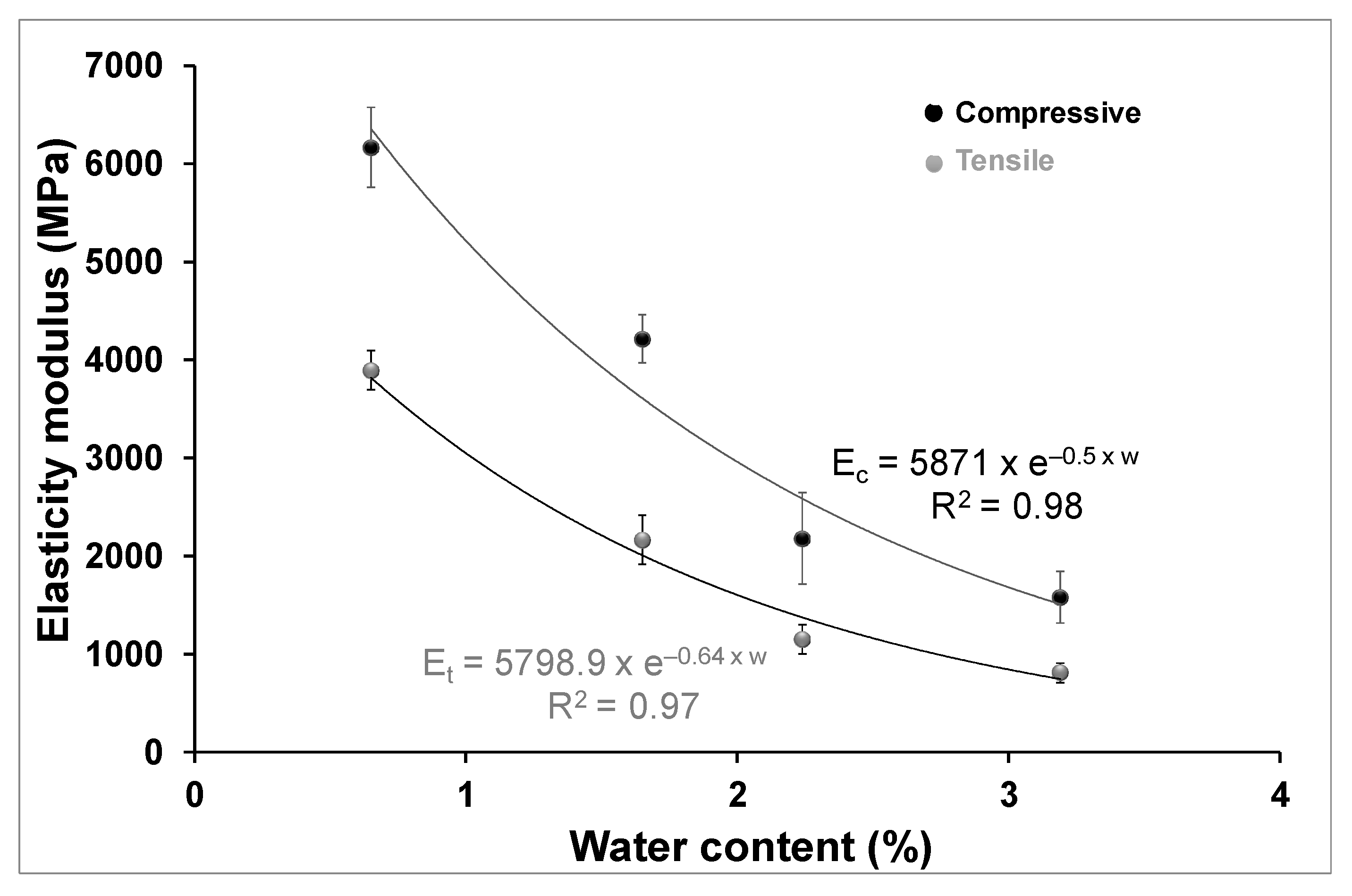
3.2.1. Compression Test
3.2.2. Tensile Test (Brazilian)
4. Numerical Results
4.1. Annual Study
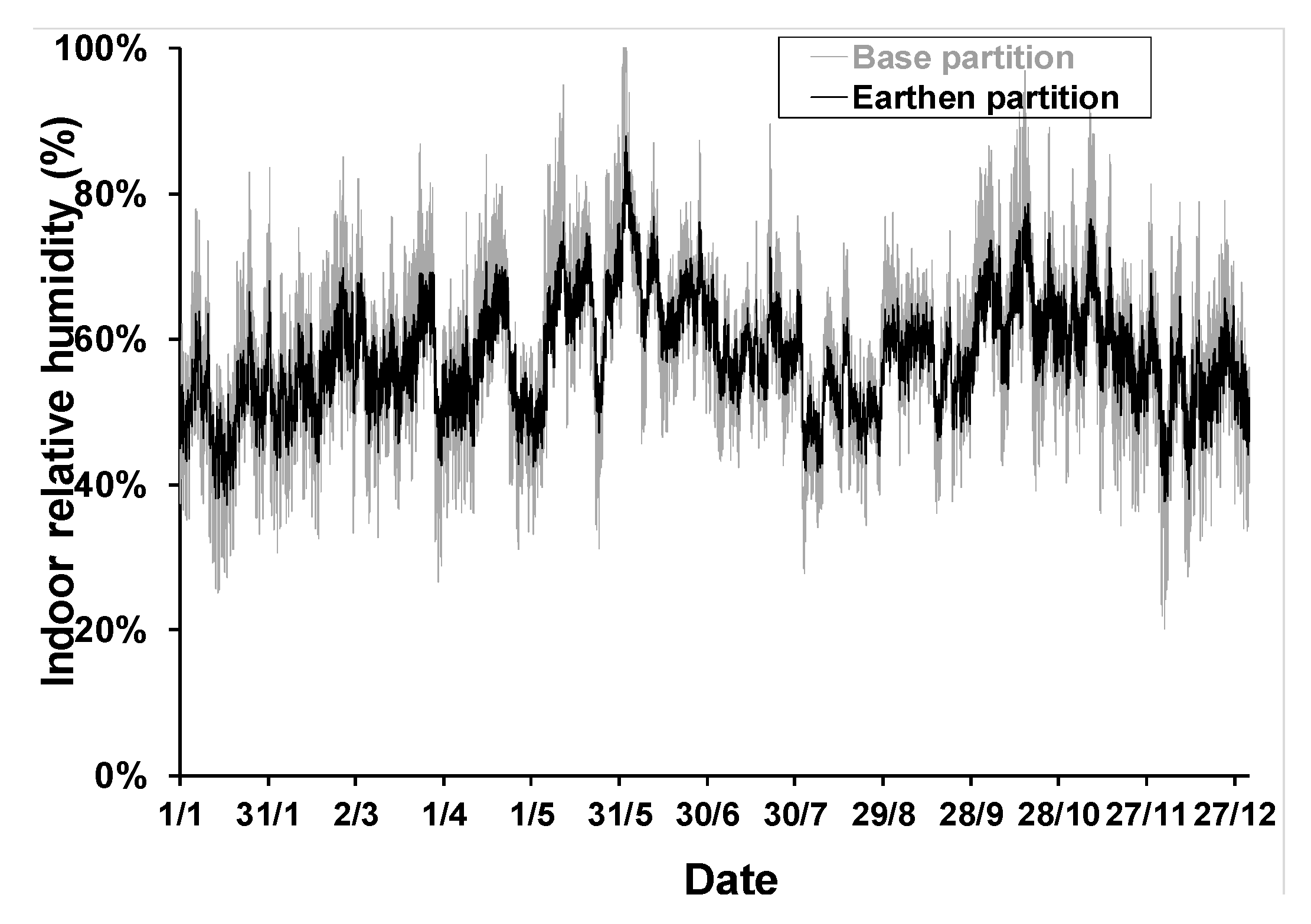
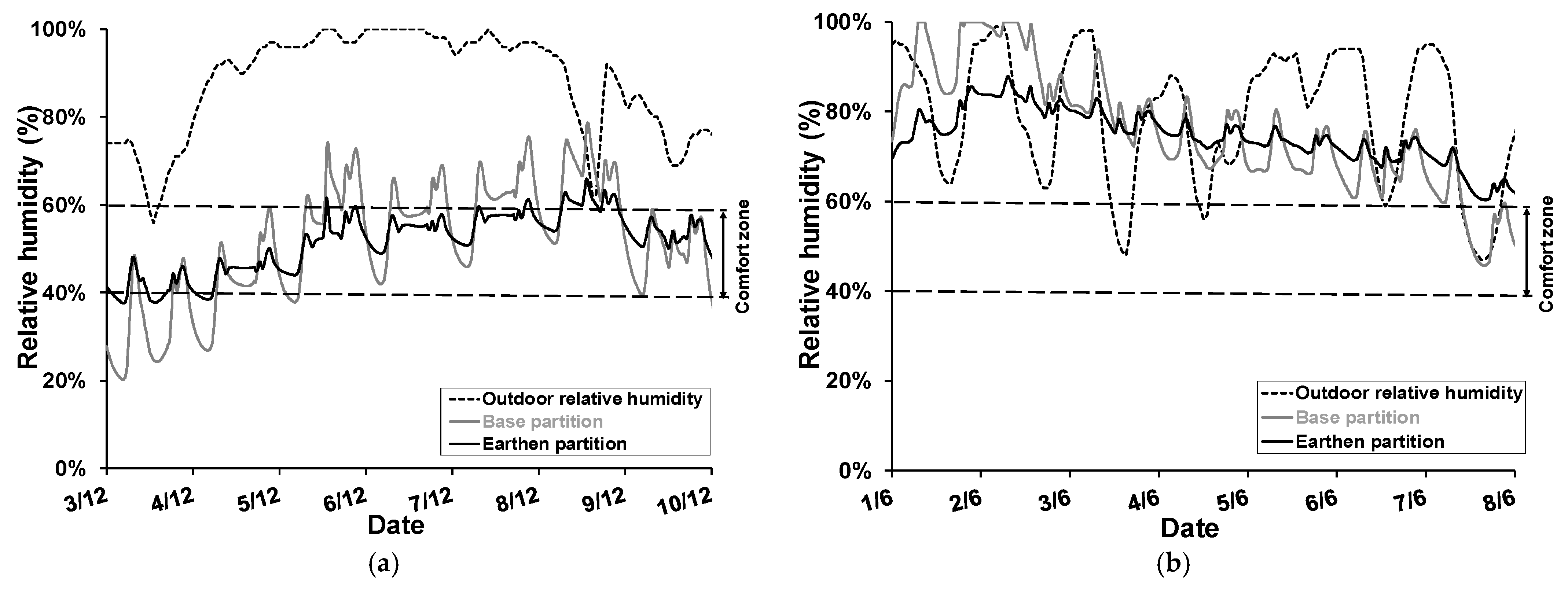
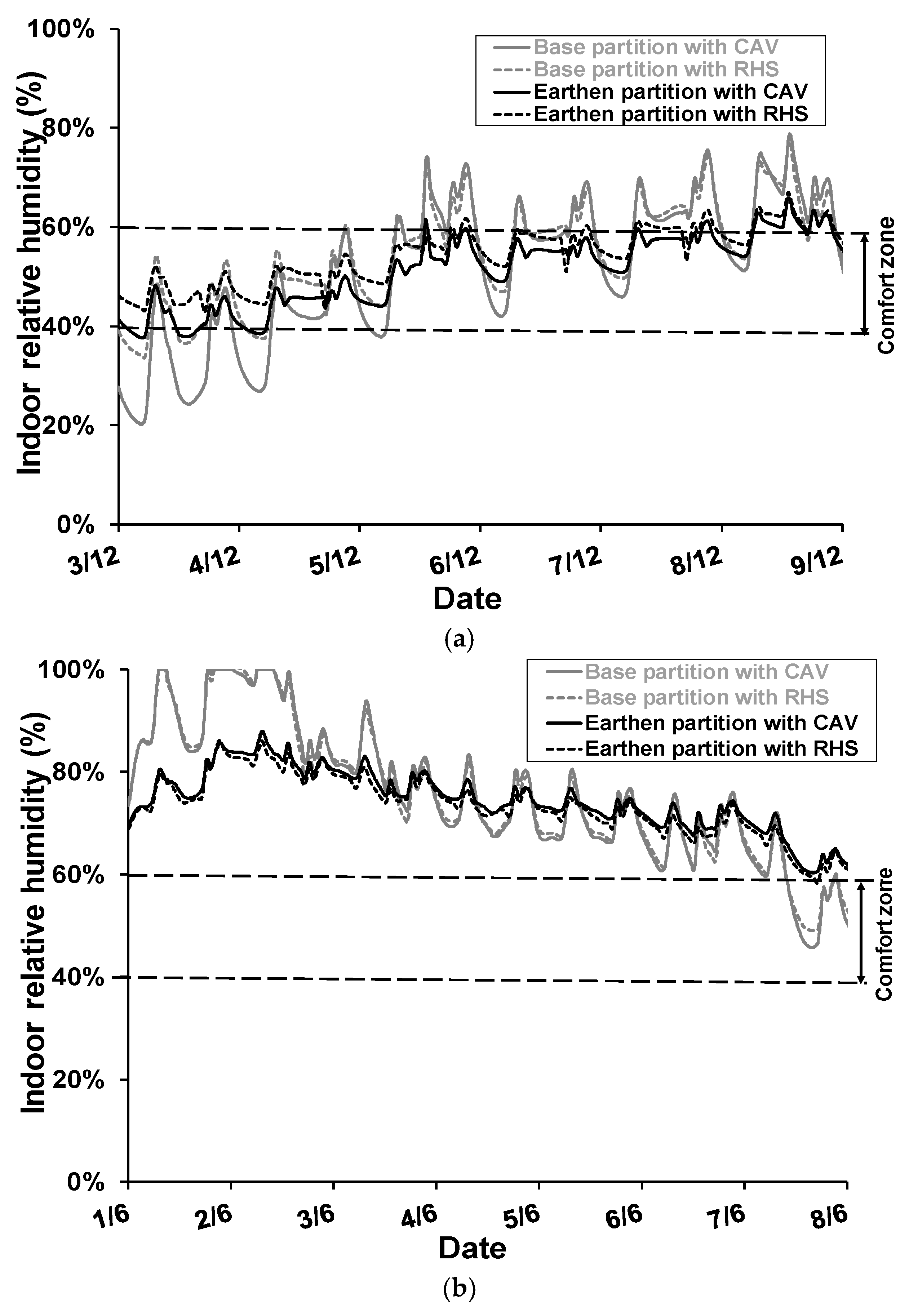
4.1.1. The Regulating Effects of Partition Walls on Indoor Humidity
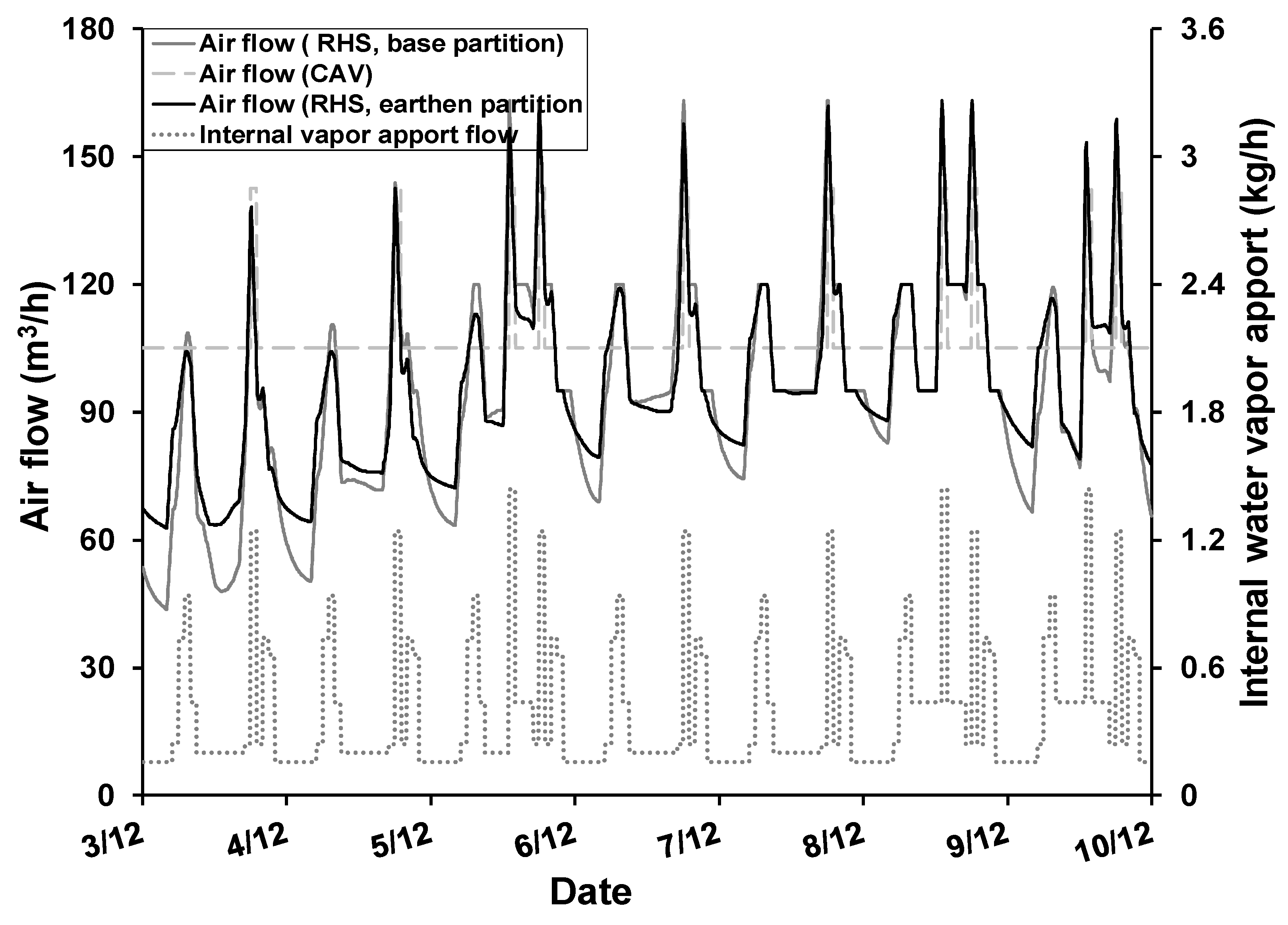
4.1.2. Impact of the Choice of Ventilation on Partition Behavior
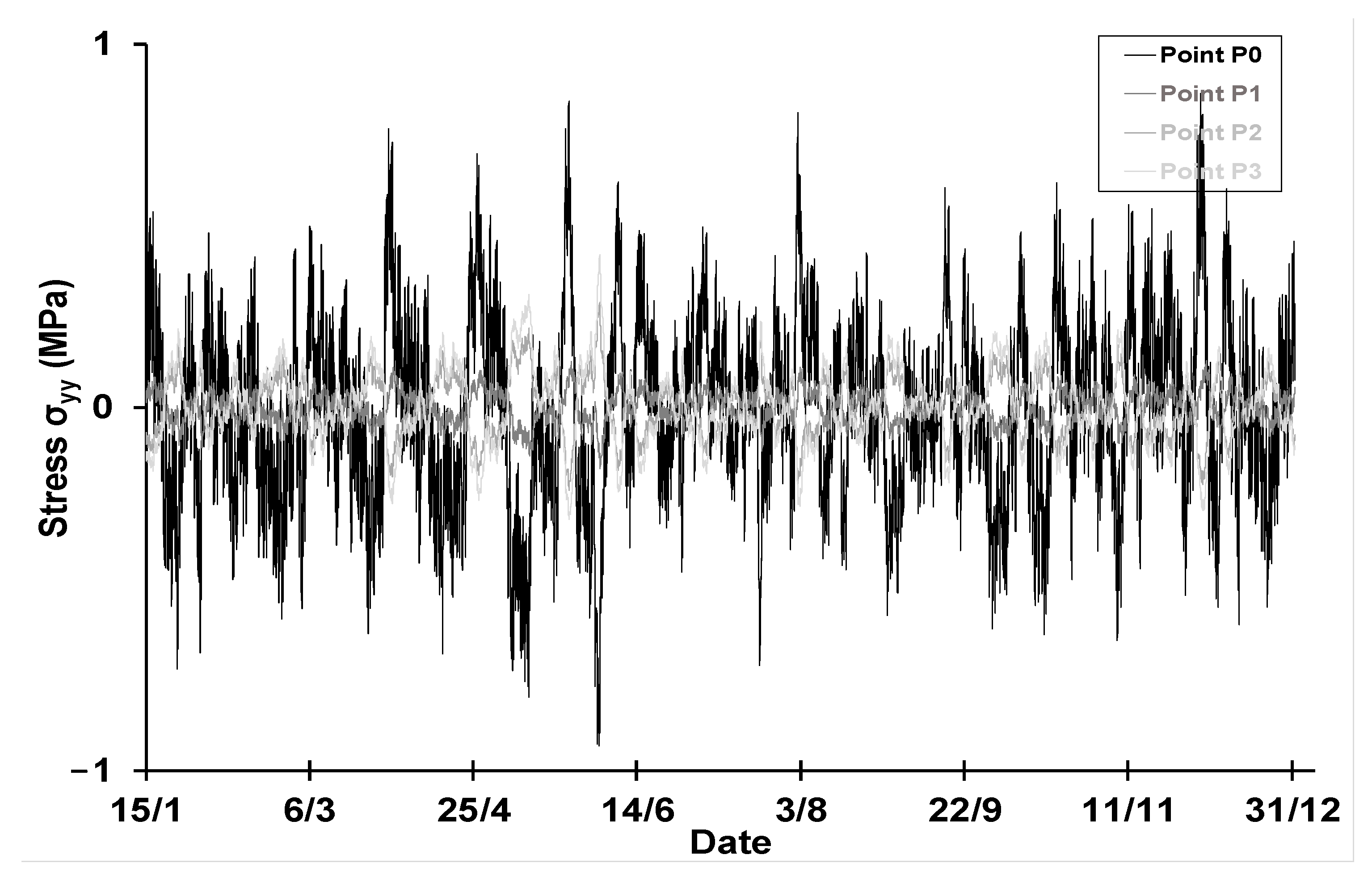
4.1.3. Mechanical Impacts
- Imposition of horizontal displacements Uy parallel to the plane of the wall at an identical but free value.
- Imposition of vertical displacements Uz at an identical but free value.
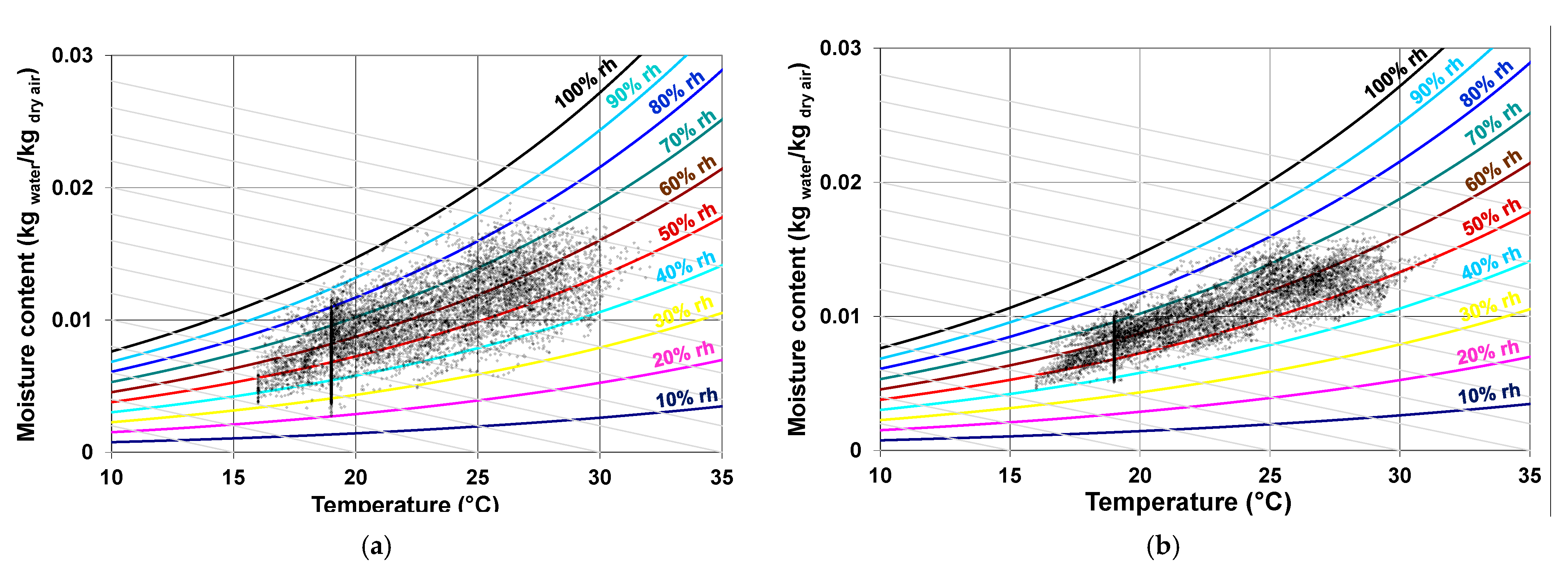
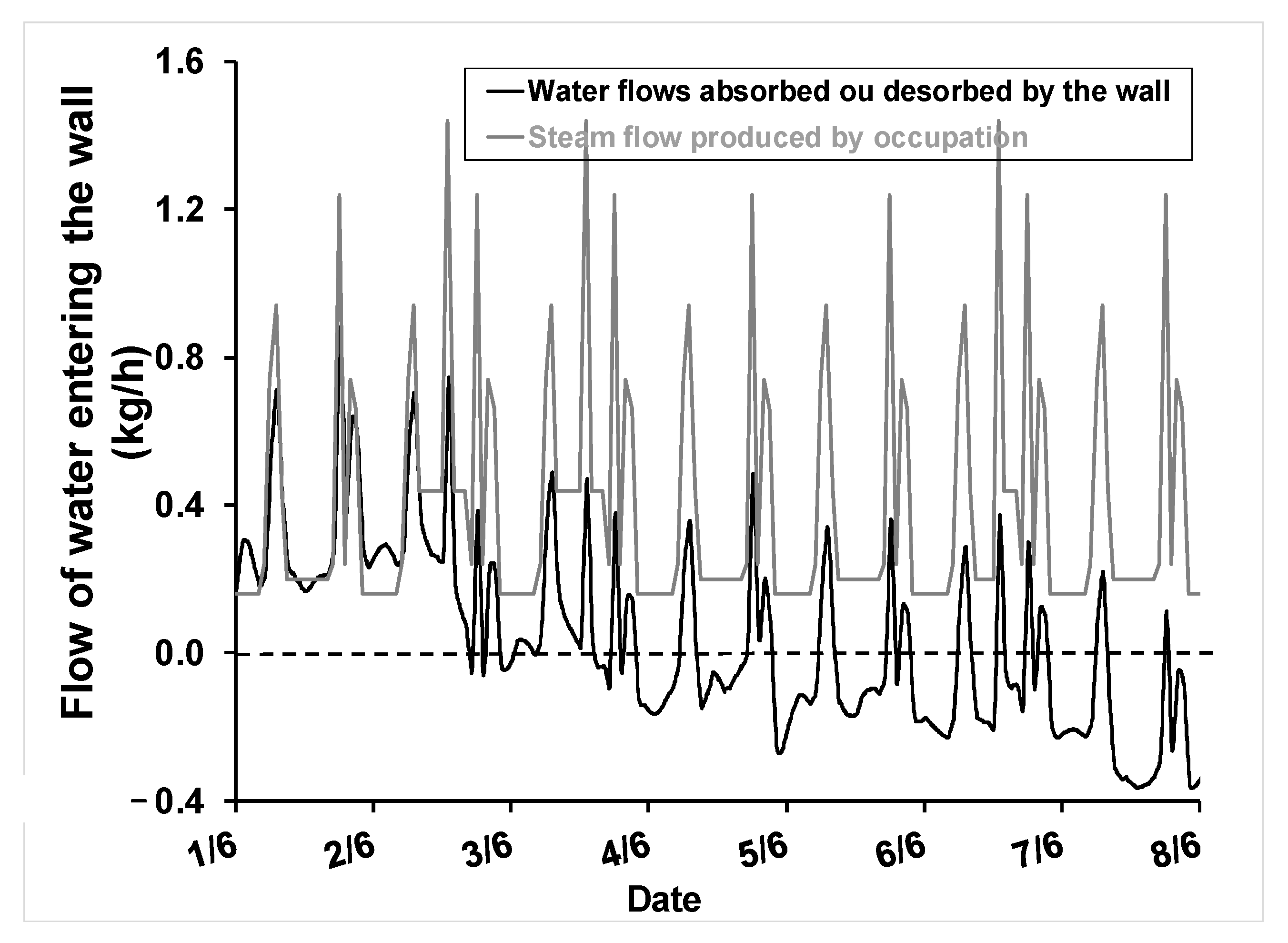
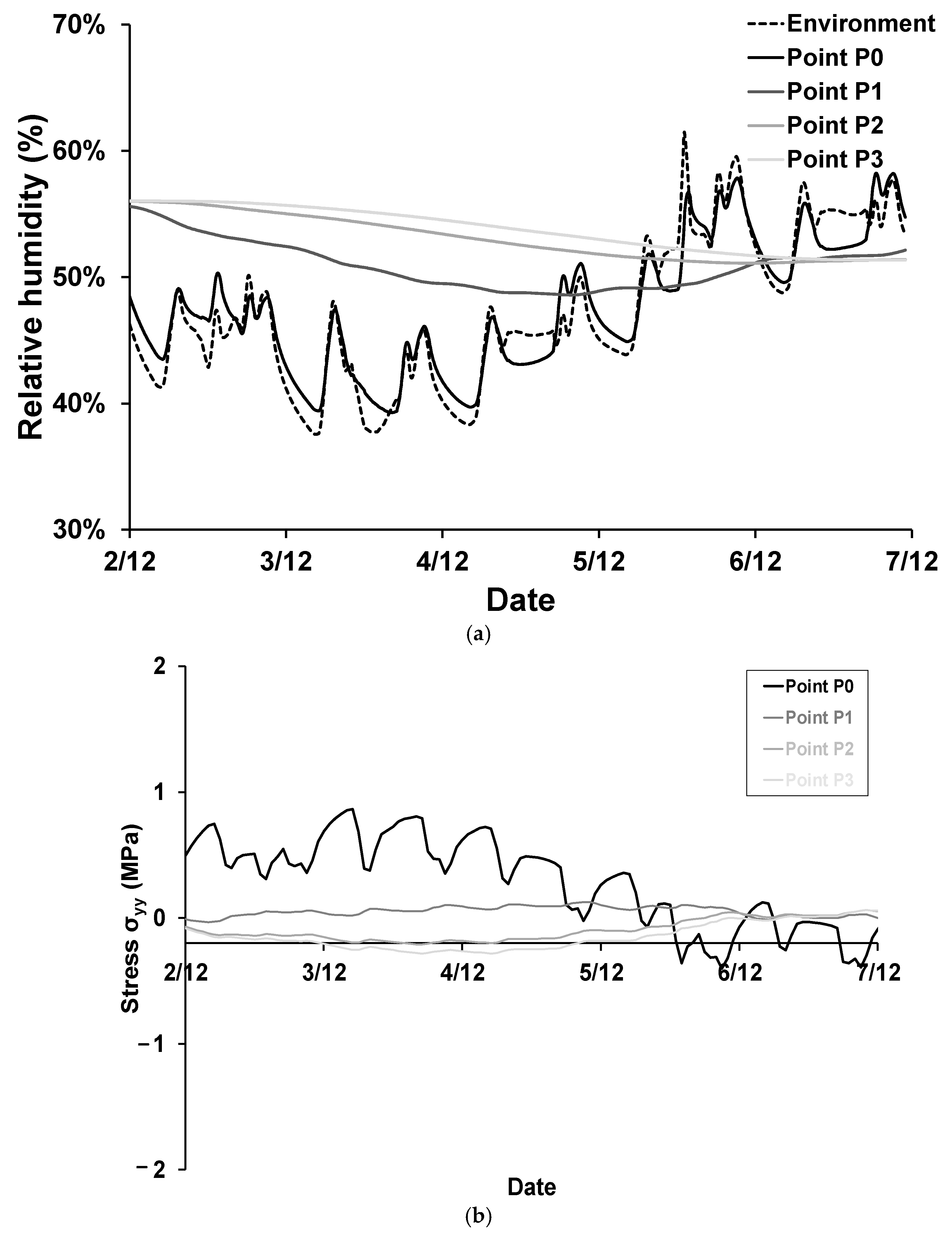
4.2. A Detailed Study of a Critical Week
- i.
- This is one-dimensional behavior, which does not take into account the effects of possible confinement due to the weight of the wall and the stress caused by the expansion of the wall elements on the sides (y direction).
- ii.
- There is a wide dispersion in the experimental results. Also, from a design perspective, while it is sensible to take a characteristic or average value, in the aim of modeling actual wall behavior, a probabilistic approach should be used due to the heterogeneity, which leads to great variability in the physical and mechanical characteristics.
- iii.
- Microcracks could form, though they would ultimately close under the effect of confinement and humidity; they should still be taken into account through damageable behavior.
5. Conclusions
- A 50% reduction in annual humidity amplitude occurs with an earth wall compared to a classical plaster wall;
- The stress variation is maximized at the wall surface, which could lead to crack formation;
- Lastly, from a more general perspective, the conclusions drawn from this work may lead to numerous prospects for future studies, namely:
- Improvement of the numerical model by taking free water transfer into account in order to extend the results obtained in the hygroscopic domain to the capillary domain, in addition to modeling the drying phase during the wall construction phase;
- Characterization of the mechanical behavior of earth bricks in the capillary domain in order to control the wall construction phase;
- Choice of a viscoelastic, or even viscoelastoplastic, approach, which proves to be necessary when incorporating changes in the material submitted to high water content.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Latin symbols | |
| C | specific heat capacity (J × kg−1 × K−1) |
| L | latent heat of sorption (J × kg−1) |
| pv | vapor pressure (Pa) |
| pvs | saturation vapor pressure (Pa) |
| QT | volumetric thermal source (W × m−3) |
| Qw | volumetric water vapor source (kg × s−1 × m−3) |
| rh | relative humidity (0 ≤ rh ≤ 1) |
| T | temperature (K) |
| w | moisture content (kgwater/kgdry material) |
| Dw | liquid diffusion coefficient (m2 × s−1) |
| Vint | internal volume of the area (m3) |
| xint | specific humidity of indoor air (kgwater/kgdry air) |
| xext | specific humidity of outdoor air (kgwater/kgdry air) |
| Greek symbols | |
| δ | vapor permeability (kg × s−1 × m−1 × Pa−1) |
| λ | thermal conductivity (W × m−1 × K−1) |
| ρ | density (kg × m−3) |
| φT | flow density of heat (W × m−2) |
| φlw | flow density of liquid water (kg × s−1 × m−2) |
| φvw | flow density of water vapor (kg × s−1 × m−2) |
| Φw | mass flow of water vapor transferred by the wall to the environment (kg × s−1) |
| Φint | mass flow rate of internal water vapor supply (kg × s−1) |
| Φvent | mass flow of water vapor supplied by the CMV (kg × s−1) |
| Subscripts | |
| * | apparent |
| 0 | anhydrous |
| a | adsorption |
| d | desorption |
| s | saturation |
References
- ADEME. Agence de l’Environnement et de la Maitrise de l’Energie. 2015. Available online: https://www.ademe.fr (accessed on 12 October 2023).
- Colin, S.; Fendrich, Y.; Lefranc, S.; Mathieu, B.; Morel, R.; Nouvellon, Q.; Polard, G.; Rateau, G. Chiffres Clés du Logement; Ministry of Ecological Transition: Paris, France, 2022.
- Jaquin, P.; Augarde, C.; Toll, D.G.; Gallipoli, D. The strength of unstabilised rammed earth materials. Géotechnique 2009, 59, 487–490. [Google Scholar] [CrossRef]
- Kherrouf, S.; Covalet, D. Mieux Comprendre les Transferts de Masse Pour Maitriser les Transferts de Chaleur; EDF R&D Département EnerBAT: Paris, France, 2010. [Google Scholar]
- Courgey, S.; Oliva, J.-P. La Conception Bioclimatique; Editions Terre Vivante: Rhone-Alpes, France, 2006; ISBN 9782914717212. [Google Scholar]
- Pittet, D.; Kotak, T.; Jagadish, K.S.; Kotak, T.; Vaghela, K.; Zaveri, P.; Sareshwala, H.; Gohel, J. Environmental impact of building technologies, a comparative study in Kutch District, Gujarat State, India. In Technologies and Innovations for Development; Springer: Paris, France, 2012. [Google Scholar] [CrossRef]
- Cagnon, H.; Aubert, J.E.; Coutand, M.; Magniont, C. Hygrothermal properties of earth bricks. Energy Build. 2014, 80, 208–217. [Google Scholar] [CrossRef]
- Maillard, P.; Aubert, J.E. Effects of the anisotropy of extrudes earth bricks on their hygrothermal properties. Constr. Build. Mater. 2014, 63, 56–61. [Google Scholar] [CrossRef]
- Minke, G. Building with Earth: Design and Technology of a Sustainable Architecture; Birkhauser: Basel, Switzerland, 2006. [Google Scholar]
- Allinson, D.; Hall, M. Hygrothermal analysis of a stabilished rammed earth test building in the UK. Energy Build 2010, 42, 845–852. [Google Scholar] [CrossRef]
- Guettala, A.; Abibsi, A.; Houari, H. Durability study of stabilized earth concrete under both laboratory and climatic conditions exposure. Constr. Build. Mater. 2006, 20, 119–127. [Google Scholar] [CrossRef]
- McGregor, F.; Heath, A.; Shea, A.; Lawrence, M. The moisture buffering capacity of unfired clay mansonry. Build. Environ. 2014, 82, 599–607. [Google Scholar] [CrossRef]
- Jeannet, J.; Pollet, G. La Thermique du Pisé: Modernité de la Construction en Terre; Actes de Colloque: Paris, France, 1986; ISSN 0246-5612. [Google Scholar]
- Taylor, P.; Luther, M.B. Evaluating rammed earth walls: A case study. Solar Energy 2004, 76, 79–84. [Google Scholar] [CrossRef]
- Soudani, L.; Woloszyn, M.; Fabbri, A.; Morel, J.-C.; Grillet, A.-C. Energy evaluation of rammed earth walls using long term in-situ measurements. Solar Energy 2017, 141, 60–70. [Google Scholar] [CrossRef]
- Khoshbakht, M.; Lin, M.-W. A finite element model for hygro-thermo-mechanical analysis of masonry walls with FRP reinforcement. Finite Elem. Analy Des. 2010, 46, 783–791. [Google Scholar] [CrossRef]
- Steeman, H.-J.; Van Belleghem, M.; Janssens, A.; De Paepe, M. Coupled simulation of heat and moisture transport in air and porous materials for the assessment of moisture related damage. Build. Environ. 2009, 44, 2176–2184. [Google Scholar] [CrossRef]
- Zonno, G.; Aguilar, R.; Boroschek, R.; Lourenço, P.B. Analysis of the long and short-term effects of temperature and humidity on the structural properties of adobe buildings using continuous monitoring. Eng. Struct. 2019, 196, 109299. [Google Scholar] [CrossRef]
- Zonno, G.; Aguilar, R.; Boroschek, R.; Lourenço, P. Experimental analysis of the thermohygrometric effects on the dynamic behavior of adobe systems. Constr. Build. Mater 2019, 208, 158–174. [Google Scholar] [CrossRef]
- Laou, L. Evaluation du Comportement Mécanique sous Sollicitations Thermo-Hydriques d’un mur Multimatériaux (Bois, Terre crue, Liants Minéraux) Lors de sa Construction et de son Utilisation. Ph.D. Thesis, University of Limoges France, Limoges, France, 2017. Available online: https://www.theses.fr/2017LIM00066≠ (accessed on 12 October 2023).
- Laou, L.; Aubert, J.-E.; Yotte, S.; Maillard, P.; Ulmet, L. Hygroscopic and mechanical behaviour of earth bricks. Mater. Struct. 2021, 54, 116. [Google Scholar] [CrossRef]
- TH-b-CE, 2012, Fascicule TH-u Matériaux, Arrêté du 18 May 2011. Available online: https://rt-re-batiment.developpement-durable.gouv.fr/IMG/pdf/thu-ex_5_fascicules.pdf (accessed on 12 October 2023).
- Samson, E.; Marchand, J.; Beaudoin, J. Describing ion diffusion mechanisms in cement based materials using the homogenization technique. Cem. Concr. Res. 1999, 29, 1341–1345. [Google Scholar] [CrossRef]
- Lemaire, T.; Moyne, C.; Stemmelen, D. Modelling of electro-osmosis in clayey materials including pH effects. Phys. Chem. Earth 2007, 32, 441–452. [Google Scholar] [CrossRef]
- Bourbatache, K. Modélisation du Transfert des Ions Chlorures dans les Matériaux Cimentaires par Homogénéisation Périodique. Ph.D. Thesis, University of La Rochelle, La Rochelle, France, 2009. [Google Scholar]
- Moyne, C.; Murad, M. A two-scale model for coupled electro-chemo-mechanical phenomena and onsager’ s reciprocity relations in expansive clays: I homogenization analysis. Trans. Porous Media. 2006, 62, 333–380. [Google Scholar] [CrossRef]
- Luikov, A. Heat and Mass Transfer in Capillary Porous Bodies. Adv. Hea Trans. 1966, 1, 123–184. [Google Scholar] [CrossRef]
- Daïan, J.F. Processus de Condensation et de Transfert d’eau dans un Matériau Méso et Macroporeux. Etude Expérimentale du Mortier de Ciment. Ph.D. Thesis, University of Grenoble, Grenoble, France, 2012. [Google Scholar]
- Janssen, H. Simulation efficiency and accuracy of different moisture transfer potentials. Build. Perform. Simul. 2014, 7, 379–389. [Google Scholar] [CrossRef]
- Medjelekh, D. Caractérisation Multi-Echelle du Comportement Thermo Hydrique des Enveloppes Hygroscopiques. Ph.D Thesis, University of Limoges, Limoges, France, 2015. [Google Scholar]
- Künzel, H.M.; Kiessl, P. Simultaneous Heat and Moisture Transport in Building Components: One-and Two-Dimensional Calculation Using Simple Parameters; Fraunhofer Institue of Building Physics: Stuttgart, Germany, 1995. [Google Scholar]
- Pedersen, C. Prediction of moisture transfer in building constructions. Build. Environ. 1992, 27, 387–397. [Google Scholar] [CrossRef]
- Philip, J.; De Vries, D. Moisture movement in porous material under temperature gradients. Trans. Am. Geophys. Union 1957, 38, 222–232. [Google Scholar] [CrossRef]
- Qin, M.; Belarbi, R.; Aït-Mokhtar, A.; Nilsson, L. Coupled heat and moisture transfer in multi-layer building materials. Constr. Build. Mater. 2009, 23, 967–975. [Google Scholar] [CrossRef]
- Qin, M.; Belarbi, R.; Aït-Mokhtar, A.; Seigneurin, A. An analytical method to calculate the coupled heat and moisture transfer in building materials. Int. Commun. Heat Mass Transf. 2006, 331, 39–48. [Google Scholar] [CrossRef]
- Davie, C.; Pearce, C.; Bicanic, N. A fully generalised, coupled, multi-phase, hygrothermo-mechanical model for concrete. Mater. Struct. 2010, 43, 13–33. [Google Scholar] [CrossRef]
- Thibeault, F.; Marceau, D.; Younsi, R.; Kocaefe, D. Numerical and experimental validation of thermo-hygro-mechanical behaviour of wood during drying process. Int. Commun. Heat Mass Transf. 2010, 37, 756–760. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Jiabin, L.; Ferhun, C.-C. Microplane constitutive model m4lfor concrete. I: Theory. Comput. Struct. 2013, 128, 219–229. [Google Scholar] [CrossRef]
- Gonzalez, I.J.; Scherer, G. Effect of swelling inhibitors on the swelling and stress relaxation of clay bearing stones. Environ. Geol. 2004, 46, 364–377. [Google Scholar] [CrossRef]
- Cast3M. Finite Element Software, Commissariat Français à l’Energie Atomique (CEA). 2017. Available online: https://www.cast3M.cea.fr (accessed on 12 October 2023).
- ISO 12571:2021; Performance Hygrothermique des Matériaux et Produits pour le Bâtiment—Détermination des Propriétés de Sorption Hygroscopique. ISO Standards: Geneva, Switzerland, 2000.
- ISO 12570:2000; Performance Hygrothermique des Matériaux et Produits pour le Bâtiment—Détermination du Taux d’Humidité par Séchage à Chaud. ISO Standards: Geneva, Switzerland, 2013.
- Merakeb, S. Modélisation des Structure en Bois en Environnement Variable. Ph.D. Thesis, University of Limoges, Limoges, France, 2006. [Google Scholar]
- Nguyen, T.-A. Approches Expérimentales et Numériques pour l’Etude des Transferts Hygroscopiques Dans le Bois. Ph.D. Thesis, Université de Limoges, Limoges, France, 2014. [Google Scholar]
- Droin-Josserand, A.; Taverdet, J.L.; Vergnaud, J.M. Modelling the absorption and desorption of moisture by wood in an atmosphere of constant and programmed relative humidity. J. Wood Sci. Technol. 1988, 22, 299–310. [Google Scholar] [CrossRef]
- ISO 12572:2016; Performance Hygrothermique des Matériaux et Produits pour le Bâtiment—Détermination des Propriétés de Transmission de la Vapeur d’eau. ISO Standards: Geneva, Switzerland, 2000.
- Collet, F. Caractérisation Hydrique et Thermique de Matériaux de Génie Civil à Faibles Impacts Environnementaux. Ph.D. Thesis, University of Rennes, Rennes, France, 2004. [Google Scholar]
- Hall, M.; Allinson, D. Assessing the effects of soil grading on the moisture content-dependent thermal conductivity of stabilised rammed earth materials. Appl. Therm. Eng. 2009, 29, 740–747. [Google Scholar] [CrossRef]
- CTMNC. Centre Technique de Matériaux Naturels de Construction (CTMNC), Service Céramique R&D, 11 Avenue d’Ariane, 87068, Limoges Cedex, France. Available online: https://cmtnc.polaris-creations.fr (accessed on 12 October 2023).
- Fontaine, L. Cohésion et Comportement Mécanique de la Terre Comme Matériau de Construction. Ph.D. Thesis, University of Limoges, Limoges, France, 2004. Available online: https://dumas.ccsd.cnrs.fr/dumas-03230968 (accessed on 12 October 2023).
- Aubert, J.; Maillard, P.; Morel, J.C.; Al Rafii, M. Towards a simple compressive strength test for earth bricks? J. Mater. Struct. 2016, 49, 1641–1654. [Google Scholar] [CrossRef]
- Pkla, A.; Mesbah, A.; Rigassi, V.; Morel, J. Comparaison de méthodes d’essais de mesures des caractéristiques mécaniques des mortiers de terre. Mater. Struct. 2003, 36, 108–117. [Google Scholar] [CrossRef]
- NF P94-422; Roches—Détermination de la Résistance à la Traction—Méthode Indirecte—Essai Brésilien. AFNOR: Paris, France, 2001.
- Heath, A.; Walker, P.; Fourie, C.; Lawrence, M. Compressive strength of extruded unfired clay masonry units. J. Constr. Mater. 2009, 162, 105–112. [Google Scholar] [CrossRef]
- Pirat, P.E.; Filloux, R. Etude de l’effet d’échelle sur le matériau terre. In Projet d’Initiation à la Recherche et au Développement; INSA: Lyon, France, 2012. [Google Scholar]
- Jacquin, P.-A.; Augarde, C. Earth Building—History, Science and Conservation; IHS BRE Press: Bracknell, UK, 2012; ISBN 978-1-84806-192-7. [Google Scholar]
- Hakimi, A.; Yamani, N.; Ouissi, H. Résultats d’essais de résistance mécanique sur échantillon de terre comprimé. J. Mater. Struct. 1996, 29, 600–608. [Google Scholar] [CrossRef]
- Givoni, B. L’Homme, le Climat et l’Architecture; Editions du Moniteur: Paris, France, 1978. [Google Scholar]
- Kwiatkowski, L.; Woloszyn, M.; Roux, J.-J. Influence of sorption isotherms hysteresis effect on indoor climate and energy demand for heating. J. Appl. Therm. Engine 2011, 31, 1050–1057. [Google Scholar] [CrossRef]
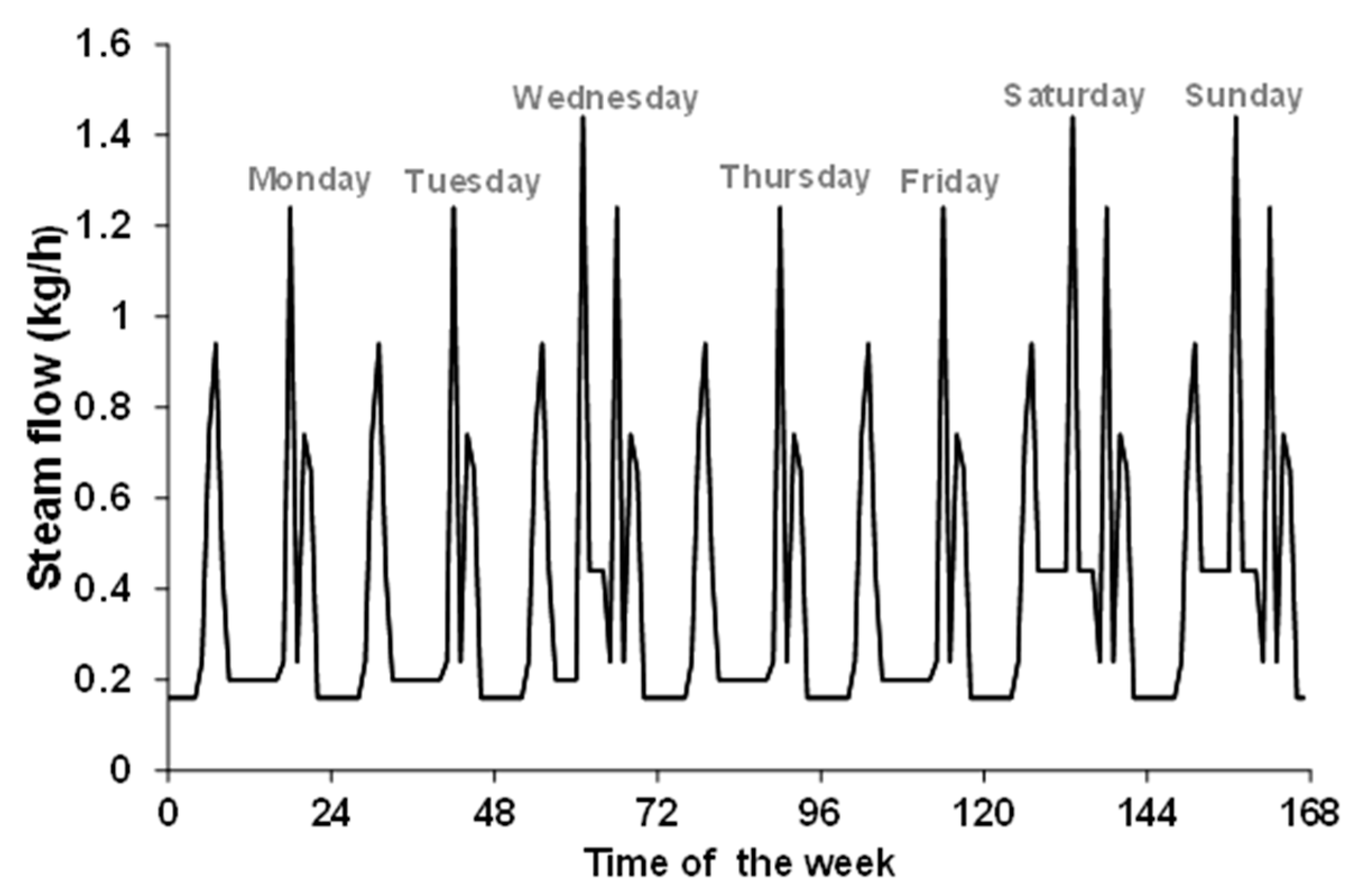



| Type of Input | Amount of Water Vapor |
|---|---|
| Occupant | 4 persons, 40 g/h/person (at rest), 60 g/h/person (during activity) |
| Kitchen | 1 kg/meal, 0.5 kg/breakfast |
| Toilet, showers | 0.5 kg in the morning, 1 kg in the evening |
| Washing and drying/laundry | 2 kg/day, distributed between 7 a.m. and 5 p.m. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laou, L.; Ulmet, L.; Yotte, S.; Aubert, J.-E.; Maillard, P. Simulation of the Hygro-Thermo-Mechanical Behavior of Earth Brick Walls in Their Environment. Buildings 2023, 13, 3061. https://doi.org/10.3390/buildings13123061
Laou L, Ulmet L, Yotte S, Aubert J-E, Maillard P. Simulation of the Hygro-Thermo-Mechanical Behavior of Earth Brick Walls in Their Environment. Buildings. 2023; 13(12):3061. https://doi.org/10.3390/buildings13123061
Chicago/Turabian StyleLaou, Lamyaa, Laurent Ulmet, Sylvie Yotte, Jean-Emmanuel Aubert, and Pascal Maillard. 2023. "Simulation of the Hygro-Thermo-Mechanical Behavior of Earth Brick Walls in Their Environment" Buildings 13, no. 12: 3061. https://doi.org/10.3390/buildings13123061
APA StyleLaou, L., Ulmet, L., Yotte, S., Aubert, J.-E., & Maillard, P. (2023). Simulation of the Hygro-Thermo-Mechanical Behavior of Earth Brick Walls in Their Environment. Buildings, 13(12), 3061. https://doi.org/10.3390/buildings13123061






