Research on Reinforcement Technology of Existing Frame Structure with Externally Attached U-Shaped Steel Plate Sub-Structure
Abstract
:1. Introduction
2. Research on the Seismic Reinforcement Method of Externally Attached U-Shaped Steel Sub-Structures
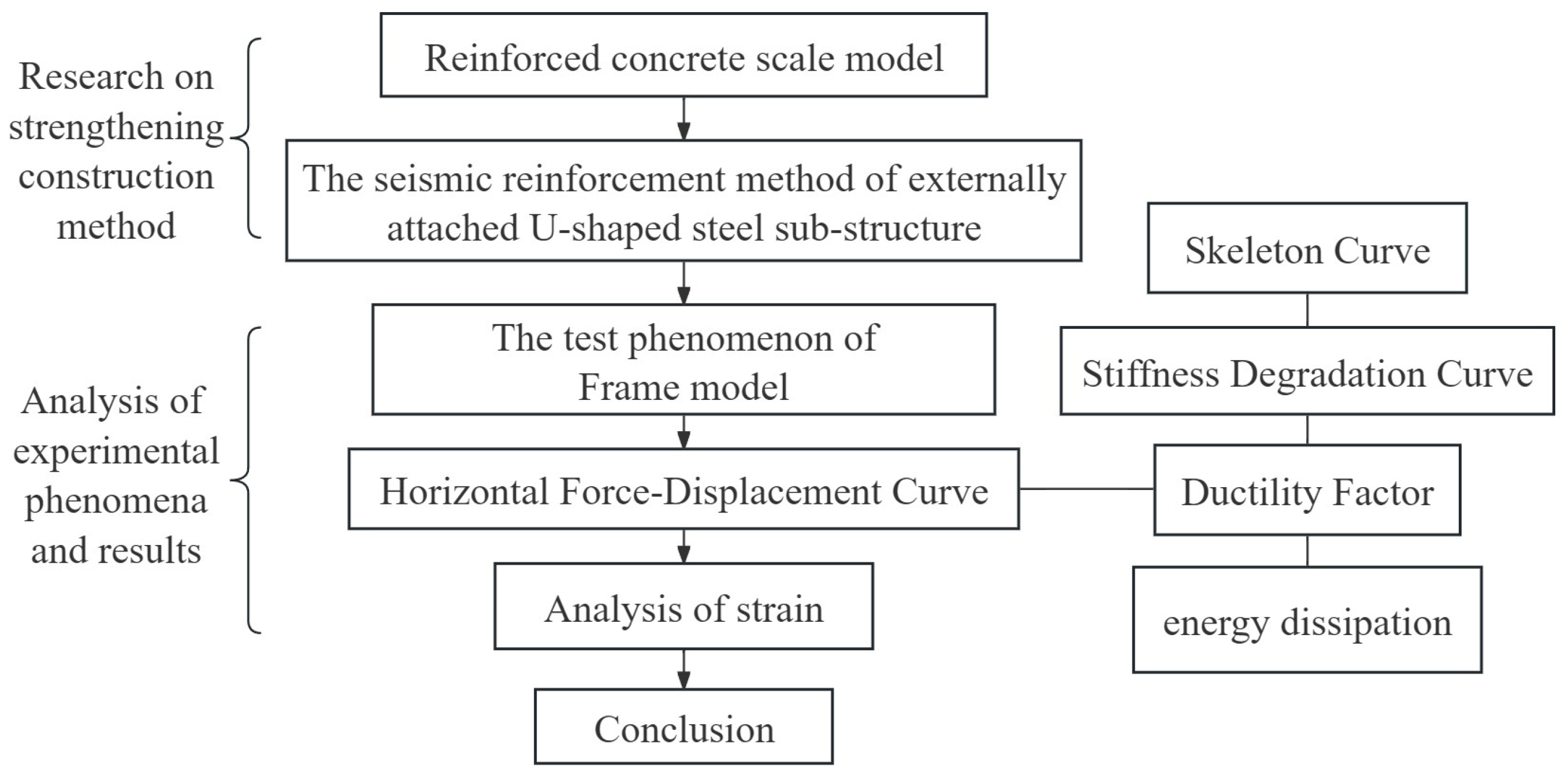
3. Test Scheme Design
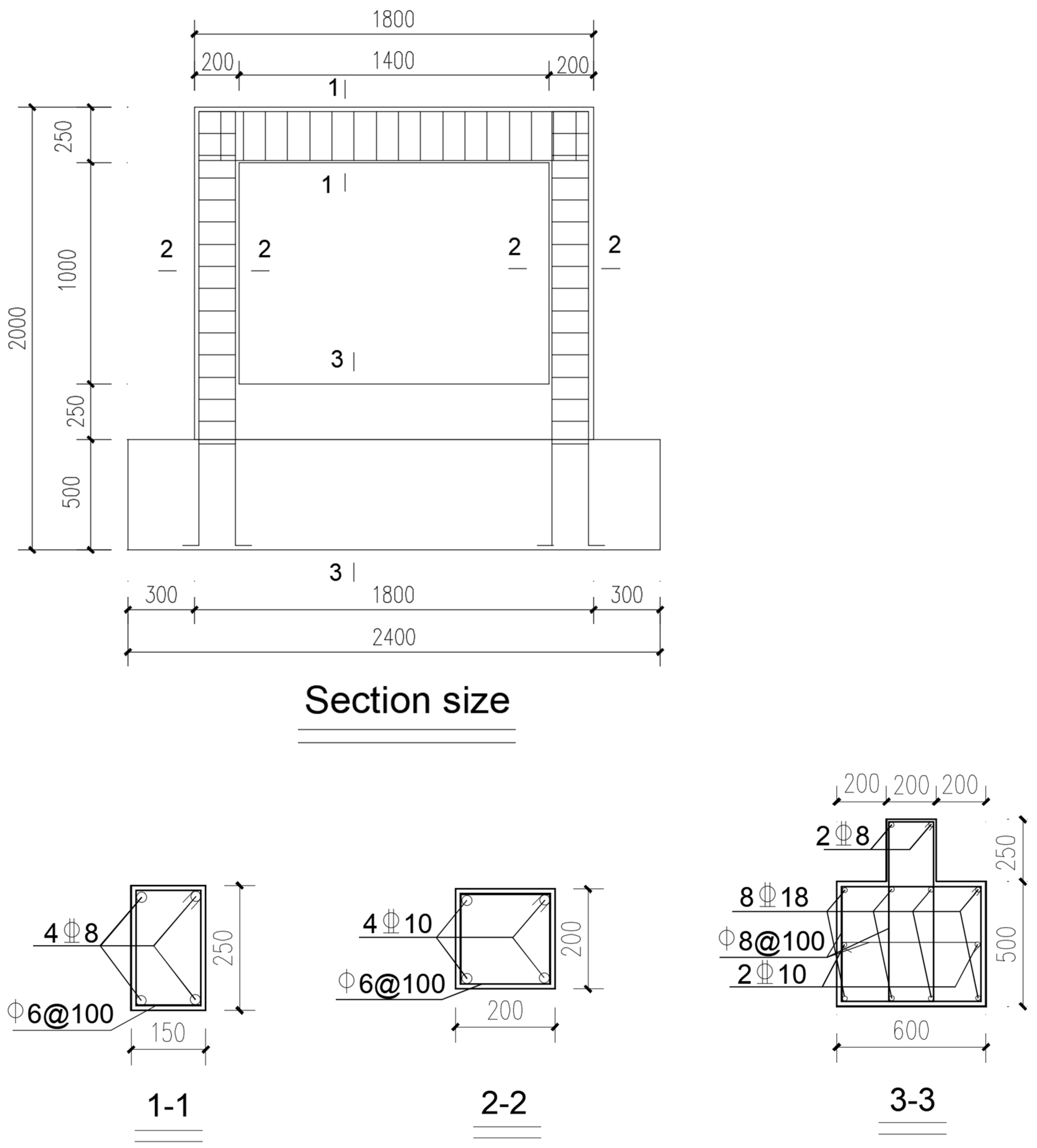
3.1. Concrete Frame Parameters
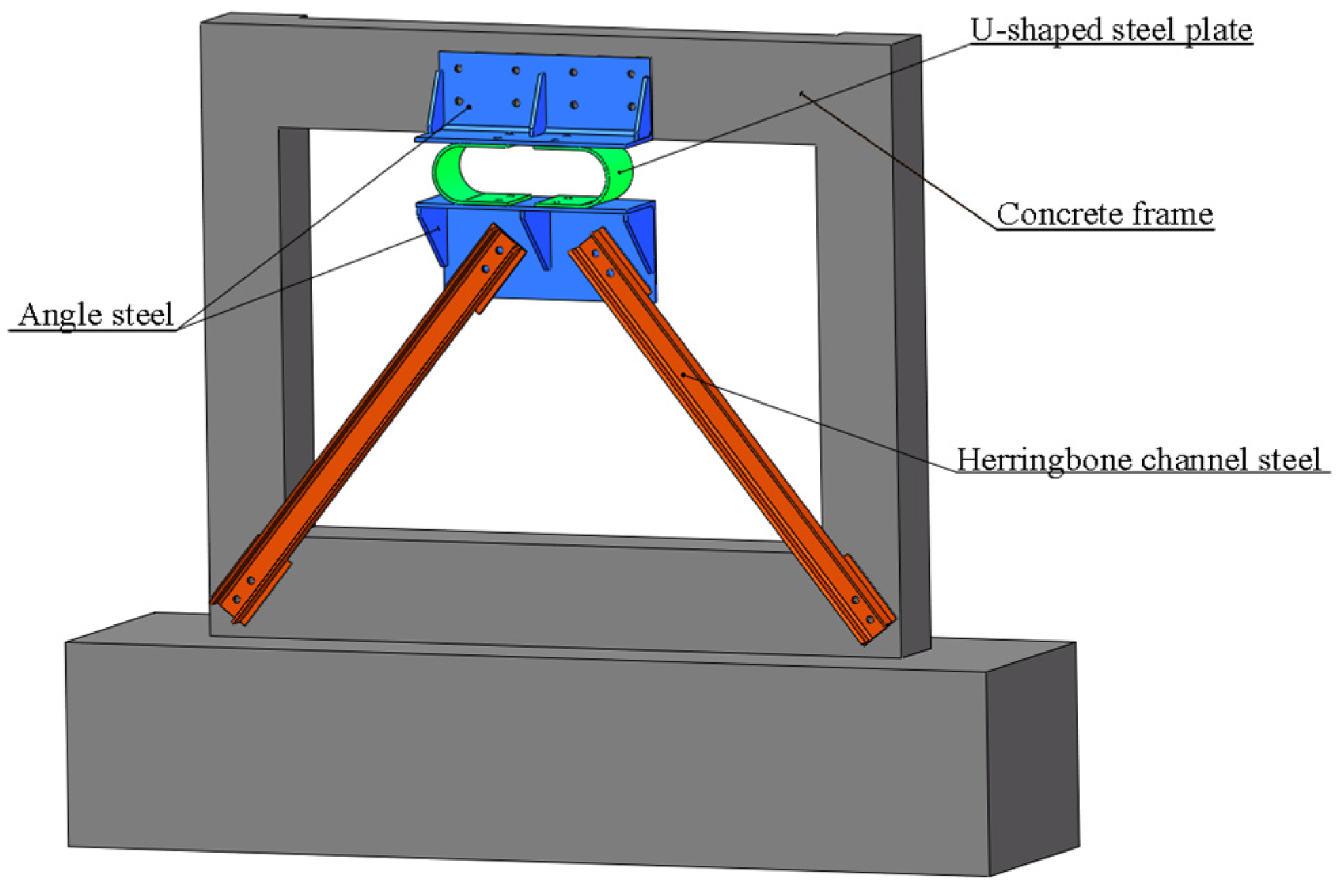
3.2. Design of Attached U-Shaped Steel Plate Sub-Structure
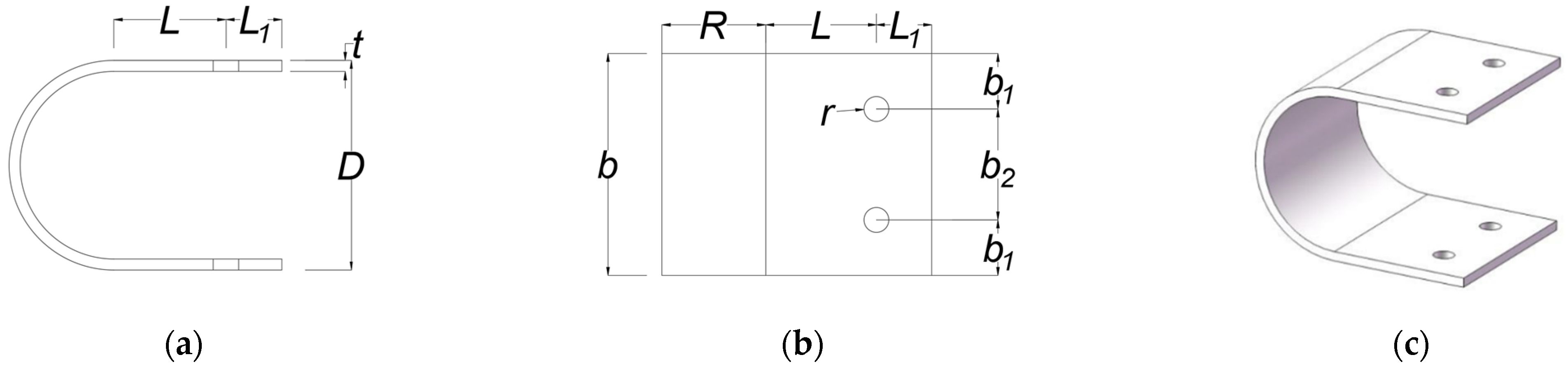
3.2.1. Design of the U-Shape Steel Plate
3.2.2. Connection of the U-Shaped Steel Plate
3.3. Test Loading and Measurement Scheme
3.3.1. Loading Device and Loading Rules
3.3.2. Measurement Scheme
4. Analysis of Pseudo-Static Test Phenomena and Results
4.1. Test Phenomena
4.2. Analysis of Frame Test Results
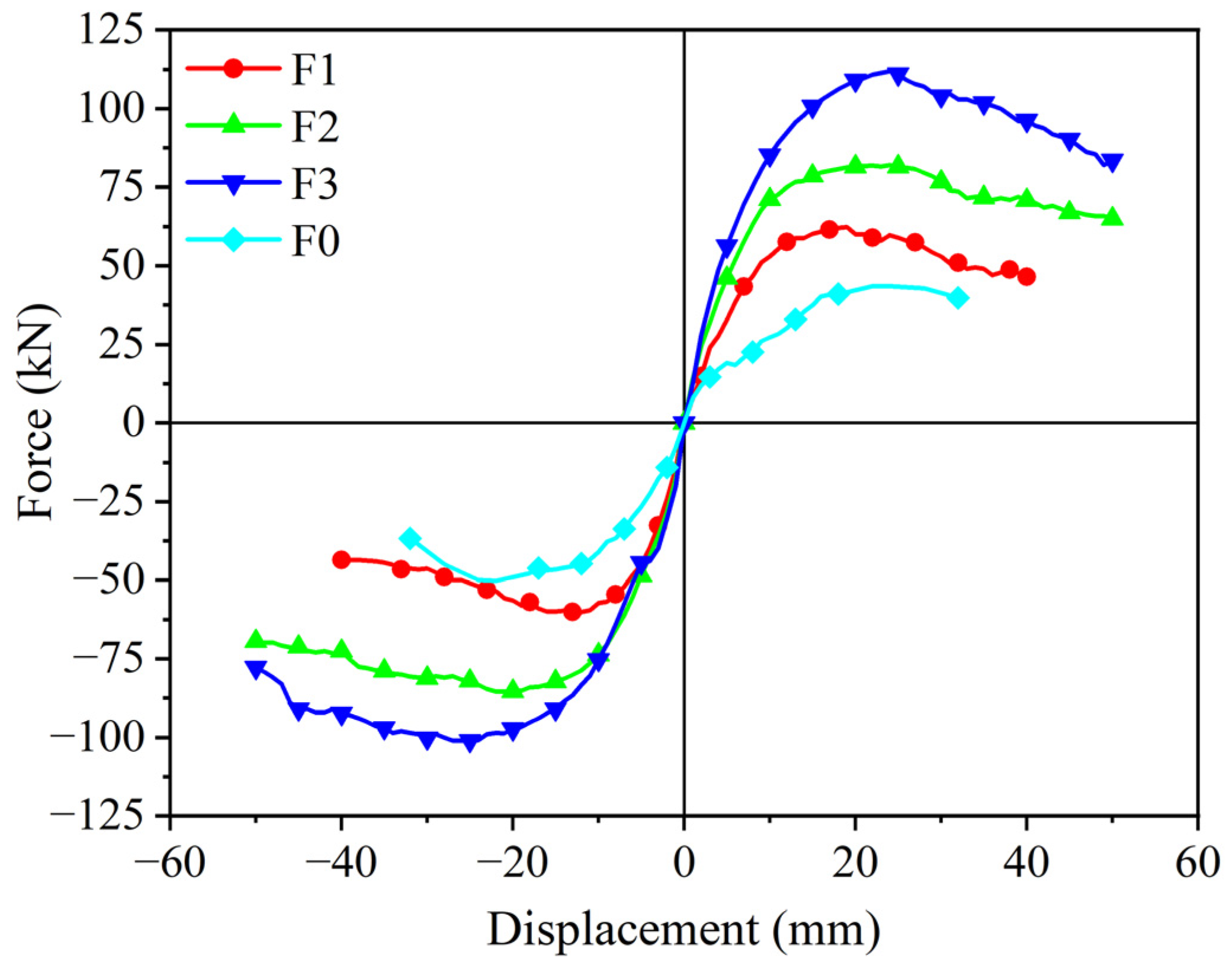
4.2.1. Comparative Analysis of Hysteresis Curve and Skeleton Curve
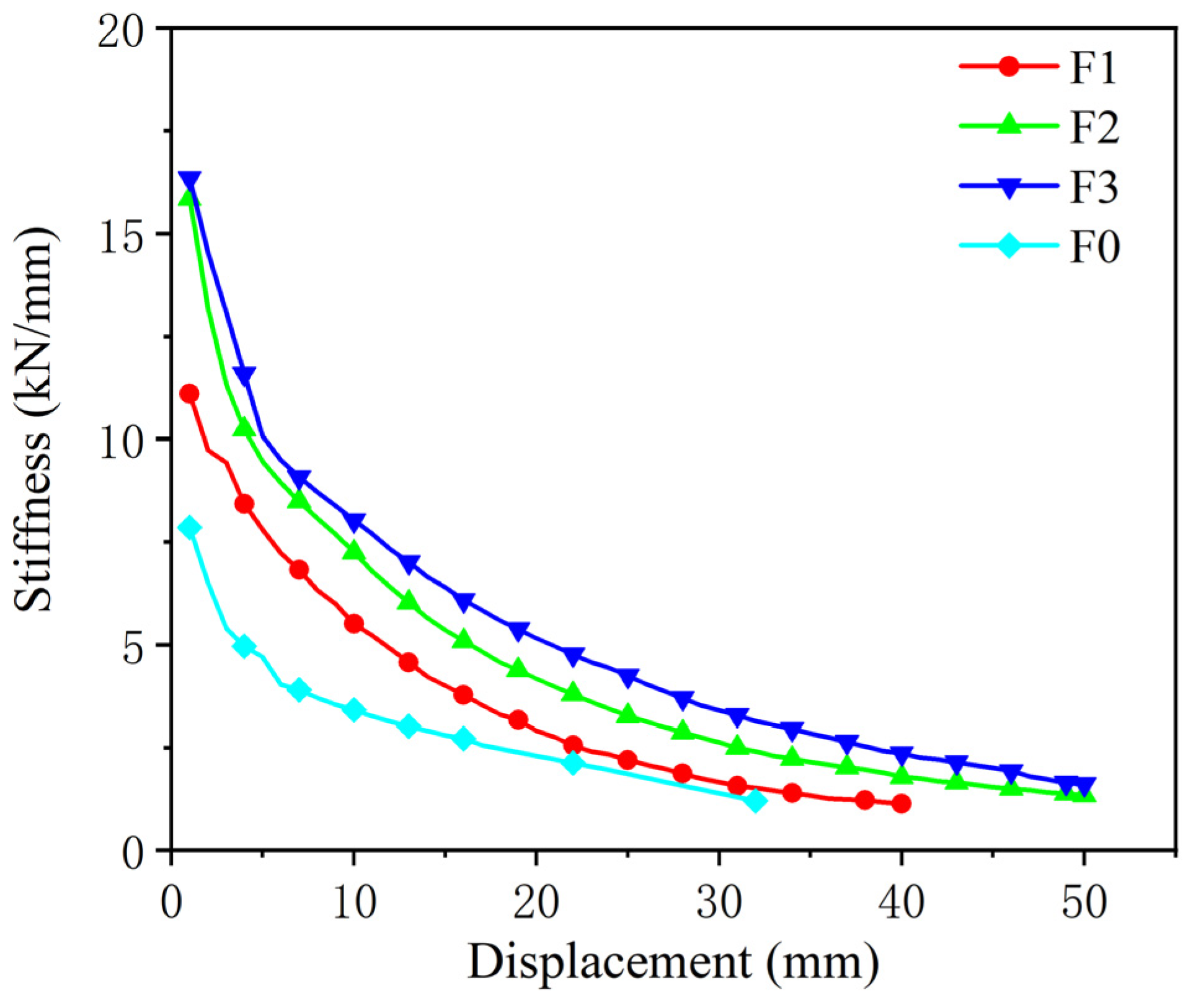
4.2.2. Analysis of Stiffness Degradation
4.2.3. Ductility Factor
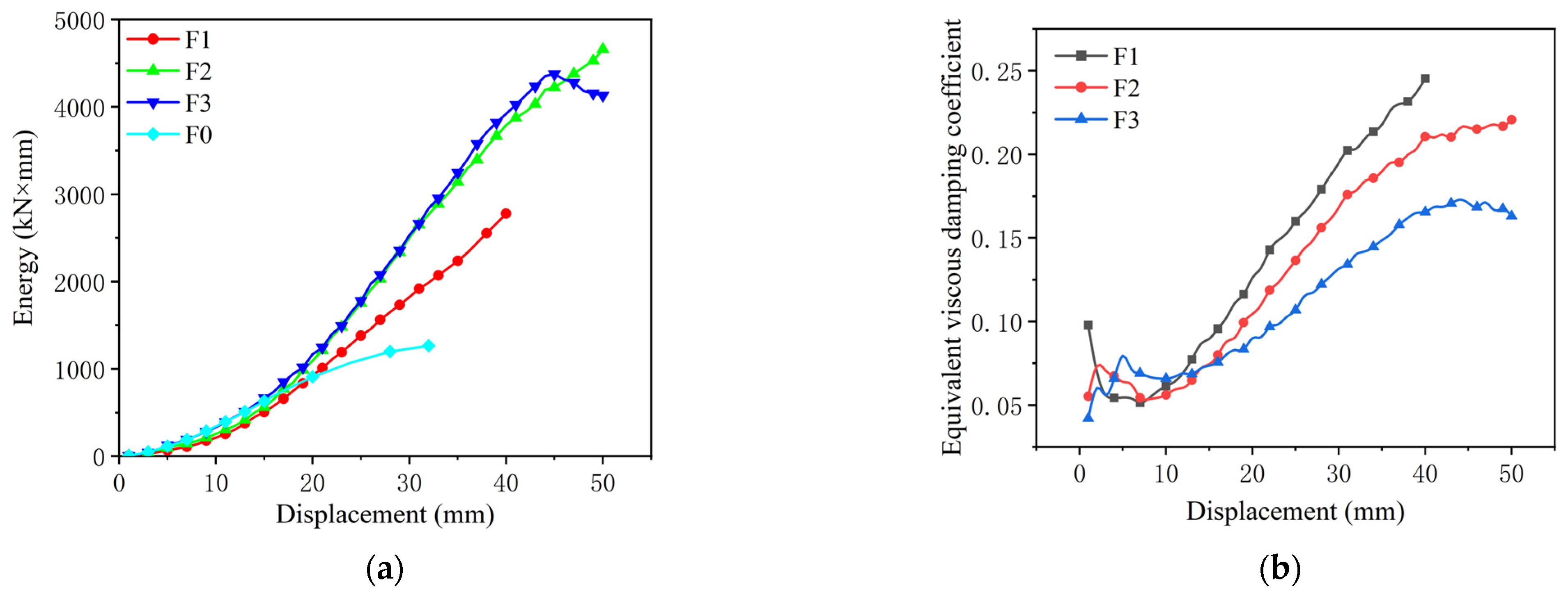
4.2.4. Analysis of Energy Dissipation
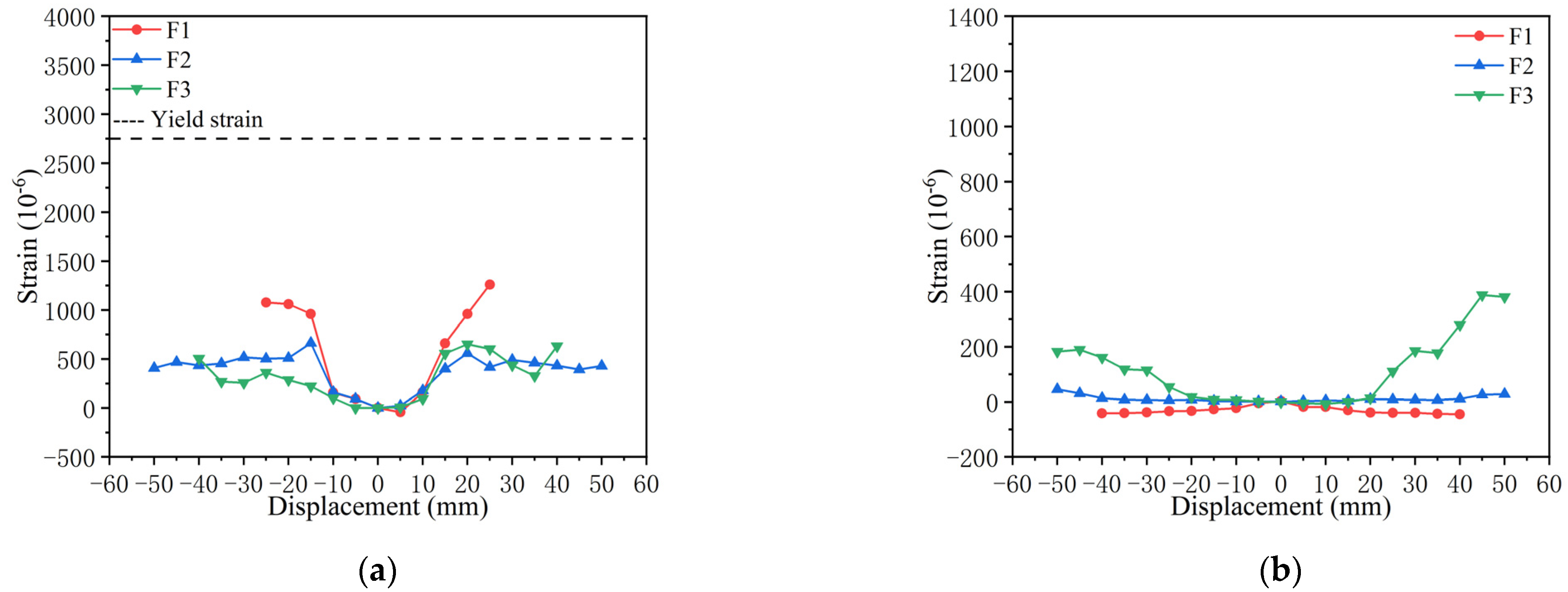
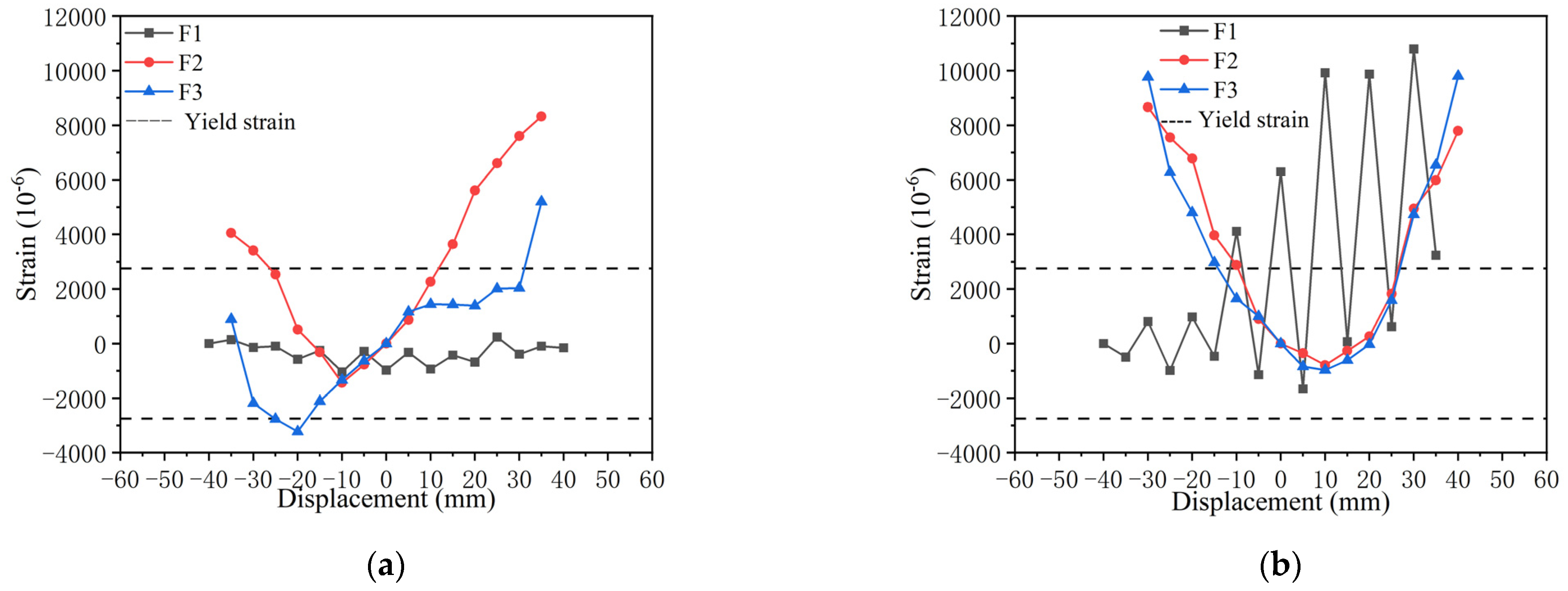
4.2.5. Analysis of Strain
5. Conclusions and Prospects
- (1)
- The test values of bearing capacity and lateral stiffness of test specimens F1, F2, and F3 are close to the theoretical predicted values, showing that the mechanical model of U-shaped steel plates can be effectively applied to the overall design of U-shaped steel plate sub-structures. The bearing capacity of the U-shaped steel plate presents an ideal superposition phenomenon, which makes the design idea clearer and more reliable.
- (2)
- The horizontal carrying capacity of test specimens F1, F2, and F3 strengthened by the external U-shaped steel plate sub-structures was greatly improved, and their maximum horizontal force was 1.43, 1.89, and 2.57 times of that of the unreinforced specimen F0. The initial lateral stiffness of the frame also increased significantly, being 1.41, 2.02, and 2.08 times that of the unreinforced specimen, and the stiffness degradation rate also decreased significantly. The higher the resistance level of the substructure, the lower the stiffness degradation rate.
- (3)
- Comparing the unreinforced test specimen and the reinforced test specimen, the externally attached U-shaped steel plate sub-structure reinforcement has ideal damping and reinforcement ability, which can effectively improve the seismic performance of the existing structure. The failure mode of the original structure did not change in test specimens F1, F2, and F3, and no obvious shear cracks appeared in the frame beam. The deformation of the substructure was concentrated in the U-shaped steel plate, and the sub-structure was stable overall. The failure mode consisted of concrete damage and a plastic hinge appearing at the lower end of the frame column. Failure patterns are also reflected in ductility. The ductility of test specimens F1, F2, and F3 was 1.28 times higher than that of F0, the unreinforced specimen. Due to the stable bending and stretching deformation of the U-shaped steel plates, the overall frame ductility and structural limit displacement were improved, and the hysteresis curves of test specimens F1, F2, and F3 were fuller and had higher energy dissipation capacity. The order of total energy consumption of the frame was F2, F3, and F1, ordered from highest to lowest, and the equivalent viscous damping coefficient decreased with the increase in the thickness and number of U-shaped steel plates. Concerning cumulative energy consumption and energy consumption efficiency, experimental specimen F2 has better energy dissipation performance.
- (4)
- The results of the strain analysis of the steel bars were consistent with the failure mode response of the four specimens of test frames: the U-shaped steel plates in test specimens F1, F2, and F3 yielded, while the other steel members did not show yielding, indicating that the U-shaped steel plate sub-structure design is reasonable and stable overall and that U-shaped steel plates can continue to deform and play a role and, at the same time, provide effective guidance for the enumeration and layout design of U-shaped steel plates.
- (5)
- The externally attached U-shaped steel plate sub-structure was connected to the existing frame through bolts, and the force transmission was clear, forming a lateral force resistance system. The mode of bolt connection reduces the number of wet operations, provides convenience for reinforcement construction, and meets the requirements of multiple reinforcement of in-service concrete structures throughout their life cycles.
- (6)
- At present, there is still insufficient research on the strengthening method applied to externally U-shaped steel plate sub-structures. The mechanical model of a U-shaped steel plate can be further studied to analyze the change in stiffness during the transition from flexural–tensile deformation to tensile deformation under the condition of large displacement and deepen the current two-fold mechanical model to a three-fold mechanical model. The damping potential of the reinforced U-shaped steel plate sub-structure under rare earthquakes in high-intensity areas was further studied.
- (7)
- In this study, we applied pseudo-static tests to scaled models, wherein the conditions are different from the actual situation to some extent. Subsequently, test studies on the reinforcement of external steel substructures of multi-story and multi-span full-scale reinforced concrete frames can be carried out, including pseudo-static tests and shaking table tests, so as to investigate the seismic performance of these two construction methods more comprehensively. The influence of the external steel substructure on the mechanical properties of the main frame has been summarized, and the popularization and application of this substructure in the seismic reinforcement of reinforced concrete frame structures are promoted.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| The yield load of the U-shaped steel plate. | |
| The initial stiffness of the U-shaped steel plate. | |
| The thickness of the U-shaped steel plate. | |
| The radius of the arc section of the U-shaped steel plate. | |
| The elastic modulus of the U-shaped steel plate. | |
| The correction coefficients, which are 1.6 and 0.45, respectively. | |
| The positive and negative peak loads under the same displacement cyclic load | |
| The positive and negative maximum displacements of the vertex under the same displacement cyclic load | |
| Ductility factor | |
| The ultimate deformation of the specimen | |
| The yield displacement of the specimen | |
| Equivalent viscous damping coefficient |
References
- Wang, J. Optimization Design and Reliability Analysis for Reinforced Concrete Frame Structural Member. Master’s Thesis, Xi‘an University of Architecture and Technology, Xi‘an, China, 2016. [Google Scholar]
- Quan, S. Study on Seismic Behavior of Reinforced Concrete Beams and Columns. Master’s Thesis, Tianjin University, Tianjin, China, 2017. [Google Scholar]
- Zhang, M. Research on Reliability and Residual Life of Reinforced Concrete Beam Strengthened by Steel Plate. Master’s Thesis, Tianjin University, Tianjin, China, 2017. [Google Scholar]
- Xun, L.; Shi, W.; Jin, W. Summary and comparison of traditional and innovative seismic strengthening technologies. Struct. Eng. 2012, 28, 101–105. [Google Scholar] [CrossRef]
- Qu, Z.; Zhang, L. State of the art and development tendency of seismic retrofit for reinforced concrete structures in Japan. Earthq. Eng. Eng. Dyn. 2013, 33, 61–74. [Google Scholar]
- Ji, X. Graphic Seismic Strengthening Technology of Reinforced Concrete Structure; China Architecture & Building Press: Beijing, China, 2010. [Google Scholar]
- Cao, X.-Y.; Feng, D.-C.; Wu, G. Seismic Performance Upgrade of RC Frame Buildings Using Precast Bolt-Connected Steel-Plate Reinforced Concrete Frame-Braces. Eng. Struct. 2019, 195, 382–399. [Google Scholar] [CrossRef]
- Yin, B.; Cheng, S.; Ji, F.; Yuan, D.; Lei, C.; Hong, X. Experimental study on seismic performance of frame structure strengthened with attached steel braces. Earthq. Resist. Eng. Retrofit. 2019, 41, 109–113. [Google Scholar] [CrossRef]
- Yongxuan, Z. Research on Seismic Reinforcement Technology of Existing RC Frame Structure Reinforced by Additional Diagonal Bracing. Master’s Thesis, Beijing University of Civil Engineering and Architecture, Beijing, China, 2023. [Google Scholar]
- Yulin, F. Study on Seismic Behaviors of Existing Reinforced Concrete Frame Strengthened with Self-Centering Members. Master’s Thesis, Beijing University of Civil Engineering and Architecture, Beijing, China, 2023. [Google Scholar]
- Jinsheng, S.; Liwei, L.; Shaozhuo, J.; Ningning, P. Experimental study on seismic performance of external energy dissipative swing steel frame structure. Build. Struct. 2022, 52, 92–97. [Google Scholar] [CrossRef]
- Fantao, M.; Xingqun, R.; Jianfeng, Z. Seismic performance of existing RC frame structure retrofitted with external energy dissipation substructure. Earthq. Resist. Eng. Retrofit. 2023, 45, 156–163. [Google Scholar] [CrossRef]
- Qu, B.; Dai, C.; Qiu, J.; Hou, H.; Qiu, C. Testing of Seismic Dampers with Replaceable U-Shaped Steel Plates. Eng. Struct. 2019, 179, 625–639. [Google Scholar] [CrossRef]
- Zhai, Z.; Guo, W.; Yu, Z.; He, C.; Zeng, Z. Experimental and Numerical Study of S-Shaped Steel Plate Damper for Seismic Resilient Application. Eng. Struct. 2020, 221, 111006. [Google Scholar] [CrossRef]
- Wang, H. Study on Seismic Performance and Fragility Analysis of Existing Concrete Frames Upgraded by Metallic Dampers. Master’s Thesis, Hefei University of Technology, Hefei, China, 2023. [Google Scholar]
- Guo, L.; Wang, J.; Wang, W.; Wang, H. Performance-based seismic design and vulnerability assessment of concrete frame retrofitted by metallic dampers. Structures 2023, 57, 105073. [Google Scholar] [CrossRef]
- Lee, C.-H.; Ryu, J.; Oh, J.; Yoo, C.-H.; Ju, Y.K. Friction between a New Low-Steel Composite Material and Milled Steel for SAFE Dampers. Eng. Struct. 2016, 122, 279–295. [Google Scholar] [CrossRef]
- Lee, C.-H.; Ryu, J.; Kim, D.-H.; Ju, Y.K. Improving Seismic Performance of Non-Ductile Reinforced Concrete Frames through the Combined Behavior of Friction and Metallic Dampers. Eng. Struct. 2018, 172, 304–320. [Google Scholar] [CrossRef]
- Hu, B.; Lv, H.; Kundu, T. Experimental study on seismic behavior of reinforced concrete frame in primary and middle schools with different strengthening methods. Constr. Build. Mater. 2019, 217, 473–486. [Google Scholar] [CrossRef]
- TahamouliRoudsari, M.; Entezari, A.; Hadidi, M.; Gandomian, O. Experimental Assessment of Retrofitted RC Frames with Different Steel Braces. Structures 2017, 11, 206–217. [Google Scholar] [CrossRef]
- TahamouliRoudsari, M.; Eslamimanesh, M.B.; Entezari, A.R.; Noori, O.; Torkaman, M. Experimental Assessment of Retrofitting RC Moment Resisting Frames with ADAS and TADAS Yielding Dampers. Structures 2018, 14, 75–87. [Google Scholar] [CrossRef]
- GB50011-2010; Code for Seismic Design of Buildings. China Architecture & Building Press: Beijing, China, 2010.
- Du, H.; Han, M.; Yan, W. Study on the calculation method of mechanical characteristics for constrained U-shaped steel plates. China Civ. Eng. J. 2014, 47, 158–163. [Google Scholar]
- GB 50017-2017; Code for Design of Steel Structures. China Architecture & Building Press: Beijing, China, 2016.
- JGJ/T 101-2015; Specification for Seismic Test of Buildings. China Architecture & Building Press: Beijing, China, 2015.
- Xiong, Z.; Wang, S. Structural Experiment of Civil Engineering; China Architecture & Building Press: Beijing, China, 2014. [Google Scholar]
- Luzhong, G.; Xiangyu, G.; Jianwei, X.; Chuheng, H.U.; Na, W.U. Experimental research on seismic performance of BRB concrete frames. J. Build. Struct. 2011, 32, 101–111. [Google Scholar] [CrossRef]
- Dan, Z.; Yuwen, X. Mechanical Properties and Parameter Analysis of U-shaped Metal Dampers. Pop. Stand. 2022, 372, 148–149. [Google Scholar]


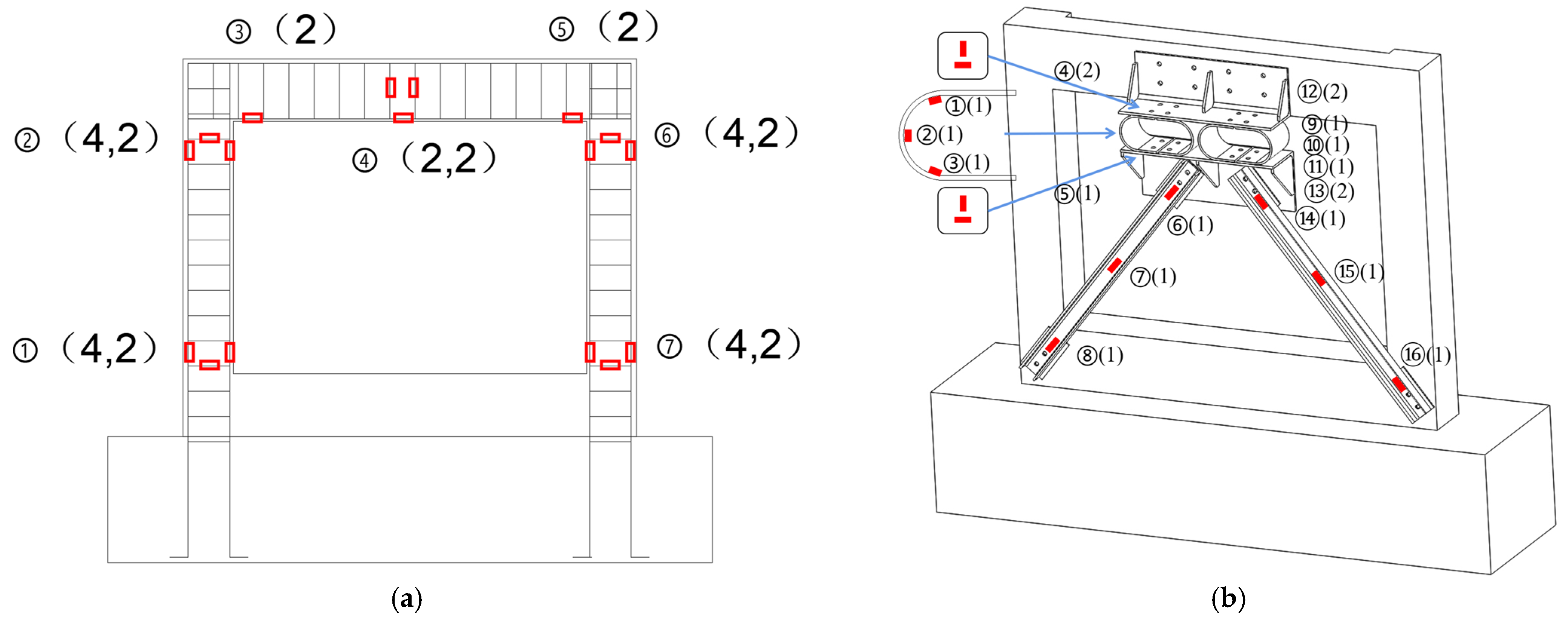


| Component | Section Size/mm | longitudinal Bar (HRB400) | Stirrup (HRB300) |
|---|---|---|---|
| The original model frame column | 400 × 400 | 2C20; 2C20 | A8@100 |
| The original model frame beam | 300 × 500 | 2C16; 2C16 | A8@100 |
| The scale model frame column | 200 × 200 | 2C10; 2C10 | A6@100 |
| The scale model frame beam | 150 × 250 | 2C8; 2C8 | A6@100 |
| Specification | t/mm | b/mm | D/mm | L/mm | L1/mm | r/mm | b1/mm | b2/mm |
|---|---|---|---|---|---|---|---|---|
| 1 | 8 | 160 | 150 | 80 | 40 | 16 | 40 | 80 |
| 2 | 8 | 160 | 150 | 50 | 30 | 16 | 40 | 80 |
| 3 | 10 | 160 | 150 | 50 | 30 | 16 | 40 | 80 |
| Number | Quantity of U-Shaped Steel Plates | Specifications of U-Shaped Steel Plates/mm | Upper-Angle Steel/mm | Lower-Angle Steel/mm | Channel Steel | Yield Force/kN |
|---|---|---|---|---|---|---|
| F1 | 2 | 8 | 200 × 180 × 10 × 550 | 250 × 190 × 10 × 550 | No. 8 | 17.1 |
| F2 | 4 | 8 | 200 × 180 × 10 × 550 | 250 × 190 × 10 × 600 | No. 8 | 34.2 |
| F3 | 4 | 10 | 200 × 180 × 10 × 550 | 250 × 192 × 12 × 660 | No. 8 | 53.5 |
| Number | Original Lateral Force/kN | Additional lateral Force/kN | Theoretical Lateral Force/kN | Positive Peak Value/kN | Negative Peak Value/kN | Peak Mean Value/kN | Difference Ratio | Positive F(X)/F0 | Negative F(X)/F0 |
|---|---|---|---|---|---|---|---|---|---|
| F0 | - | - | - | 43.5 | −50.0 | 46.75 | - | 1.00 | 1.00 |
| F1 | 50 | 17.1 | 67.1 | 62.3 | −60.0 | 61.16 | −8.85% | 1.43 | 1.20 |
| F2 | 50 | 34.2 | 84.2 | 82.0 | −85.4 | 83.70 | −0.59% | 1.89 | 1.71 |
| F3 | 50 | 53.5 | 103.5 | 111.9 | −101 | 106.45 | 2.85% | 2.57 | 2.02 |
| Number | Original Stiffness (kN/mm) | Additional Stiffness (kN/mm) | Theoretical Initial Stiffness (kN/mm) | Initial Stiffness (kN/mm) | Difference Ratio | F(x)/F0 |
|---|---|---|---|---|---|---|
| F0 | 7.85 | - | - | 7.85 | - | 1.00 |
| F1 | 7.85 | 1.95 | 9.80 | 11.10 | 13.27% | 1.41 |
| F2 | 7.85 | 3.90 | 11.75 | 15.85 | 34.89% | 2.02 |
| F3 | 7.85 | 7.60 | 15.45 | 16.35 | 5.83% | 2.08 |
| Number | F0 | F1 | F2 | F3 |
|---|---|---|---|---|
| Ultimate displacement/mm | 32 | 31 | 44 | 41 |
| Yield displacement/mm | 8 | 6 | 8 | 8 |
| Ductility factor | 4.00 | 5.17 | 5.50 | 5.13 |
| F(x)/F(0) | 1.00 | 1.29 | 1.38 | 1.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Liu, Y.; Wang, X.; Li, Z.; Wang, W. Research on Reinforcement Technology of Existing Frame Structure with Externally Attached U-Shaped Steel Plate Sub-Structure. Buildings 2023, 13, 3058. https://doi.org/10.3390/buildings13123058
Xu Z, Liu Y, Wang X, Li Z, Wang W. Research on Reinforcement Technology of Existing Frame Structure with Externally Attached U-Shaped Steel Plate Sub-Structure. Buildings. 2023; 13(12):3058. https://doi.org/10.3390/buildings13123058
Chicago/Turabian StyleXu, Zhiwen, Yulin Liu, Xingchen Wang, Zixuan Li, and Weilun Wang. 2023. "Research on Reinforcement Technology of Existing Frame Structure with Externally Attached U-Shaped Steel Plate Sub-Structure" Buildings 13, no. 12: 3058. https://doi.org/10.3390/buildings13123058
APA StyleXu, Z., Liu, Y., Wang, X., Li, Z., & Wang, W. (2023). Research on Reinforcement Technology of Existing Frame Structure with Externally Attached U-Shaped Steel Plate Sub-Structure. Buildings, 13(12), 3058. https://doi.org/10.3390/buildings13123058





