A Constitutive Model for Circular and Square Cross-Section Concrete Confined with Aramid FRP Laminates
Abstract
1. Introduction
2. Materials and Fabrication of Test Specimens
2.1. Aramid Fiber
2.2. Epoxy Resin
2.3. Concrete Specimen Preparations
2.4. Compressive Test
3. Results
3.1. Unconfined Concrete Specimens (Benchmark)
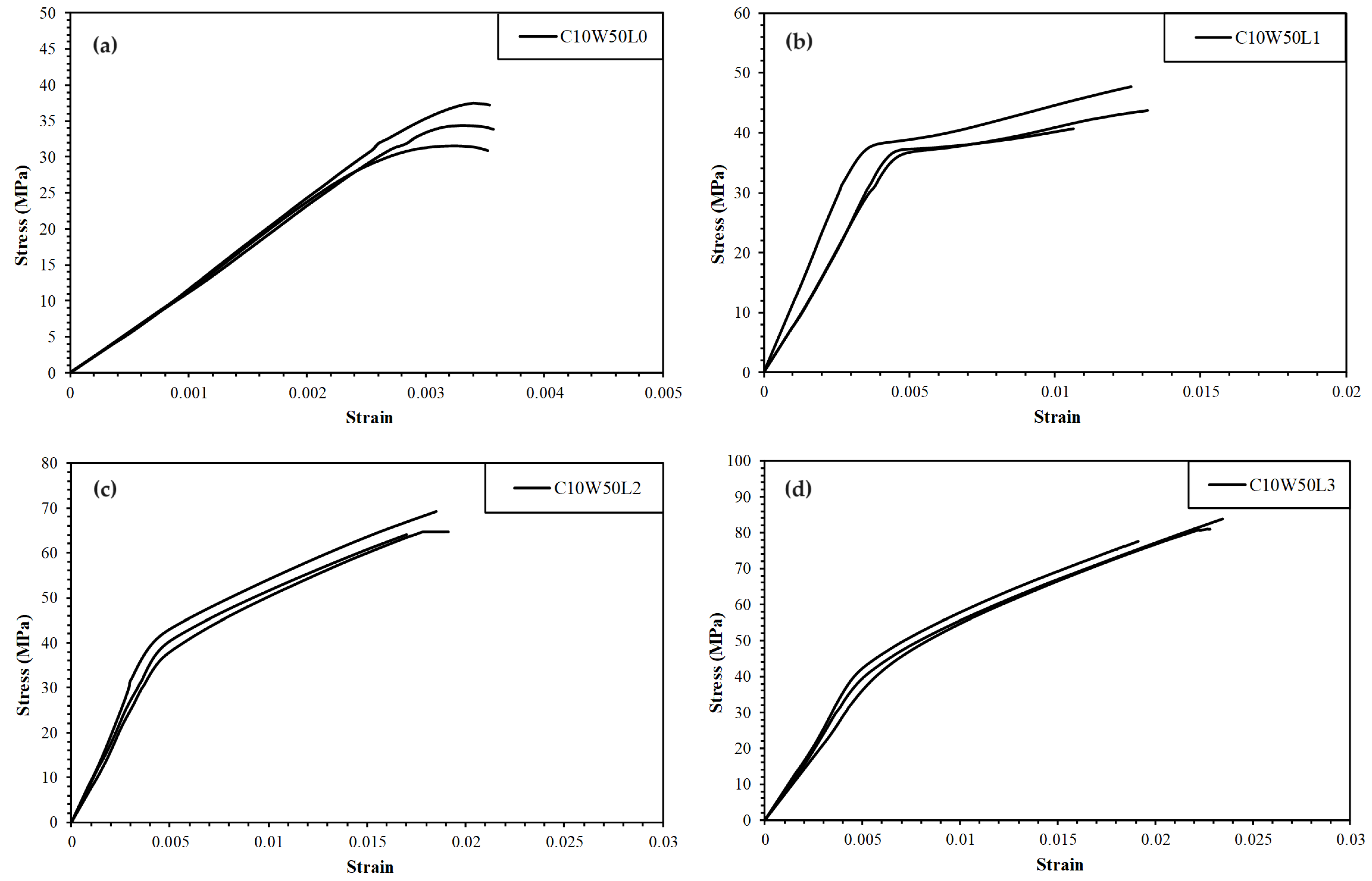
3.2. Confined Concrete Specimens Ø10 × 20
3.3. Confined Concrete Specimens Ø15 × 30
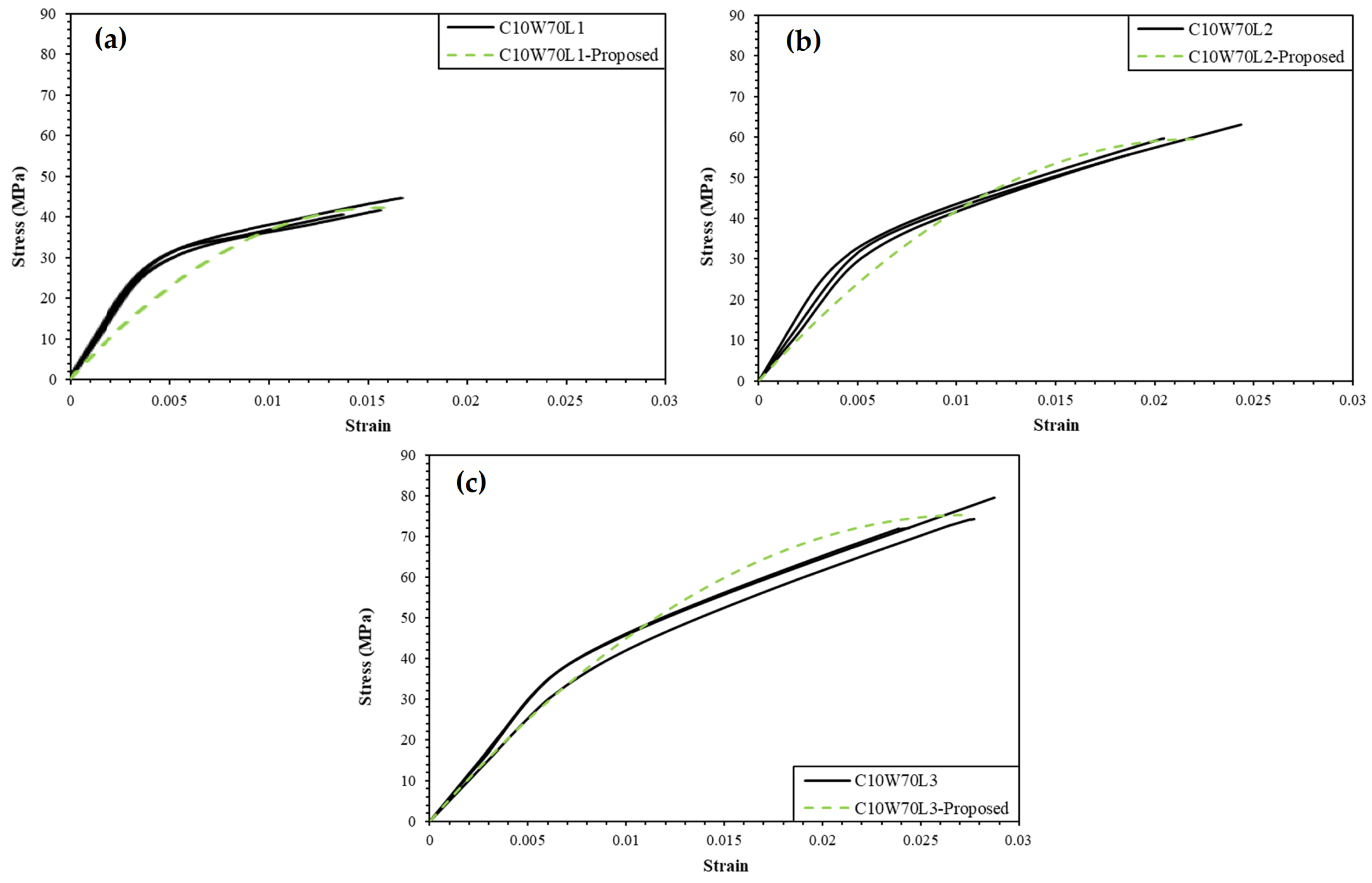
3.4. Confined Square Cross-Section Concrete Specimens
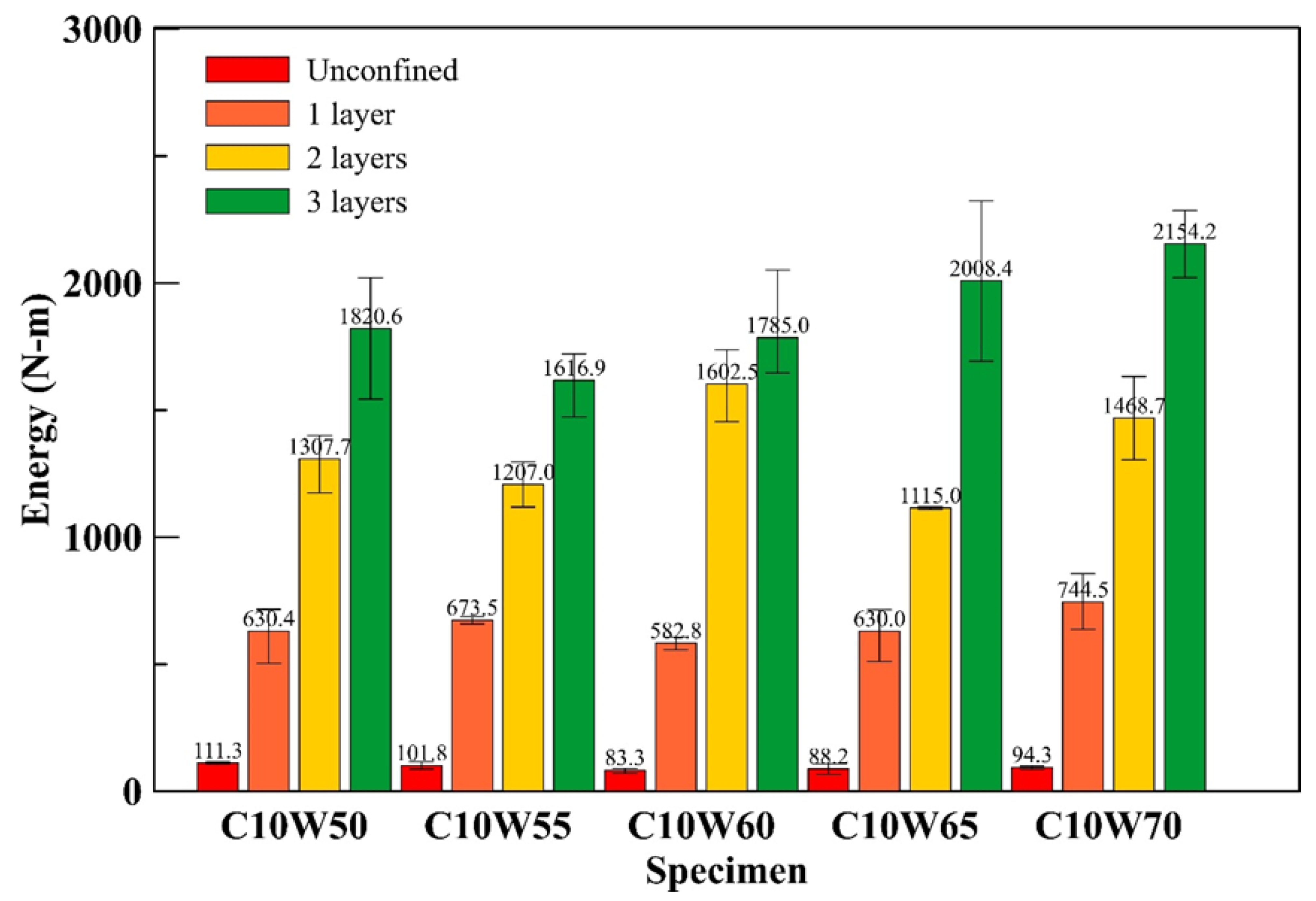
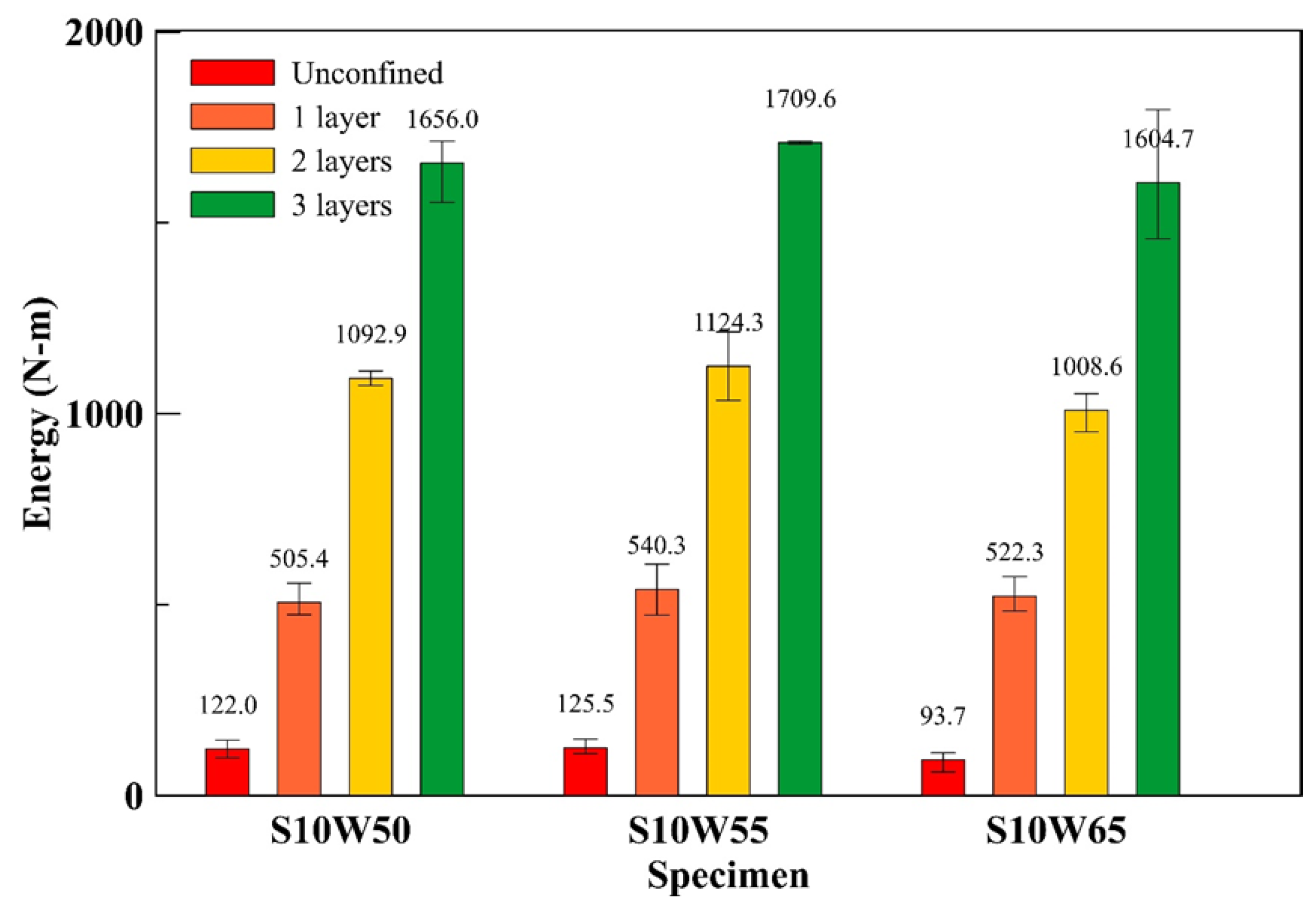
3.5. Strain Energy
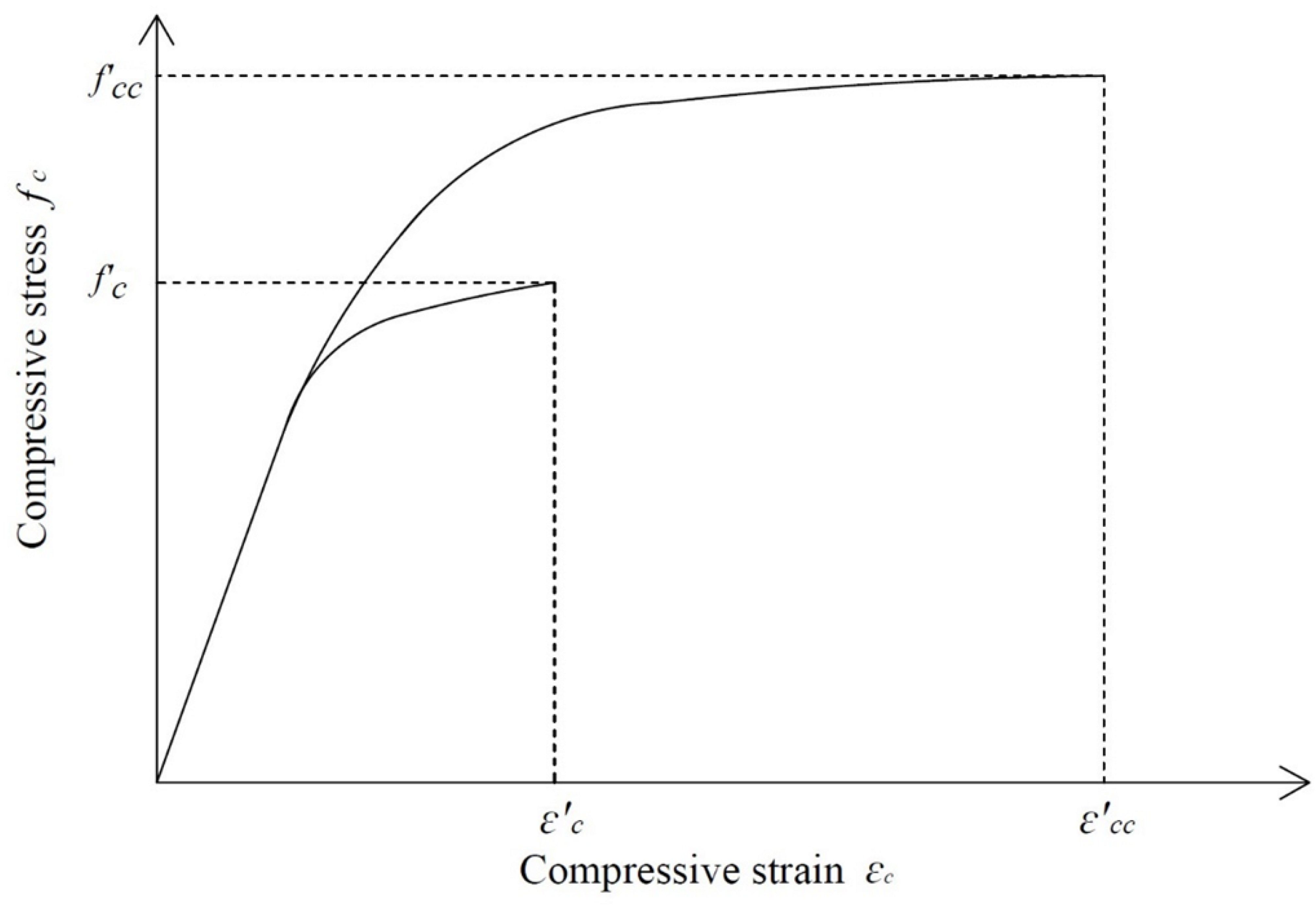
4. Constitutive Model for AFRP-Confined Concrete
4.1. Constitutive Model for Compressive Strength of the Confined Concrete
4.2. Constitutive Model for Axial STRAIN at the compressive Strength
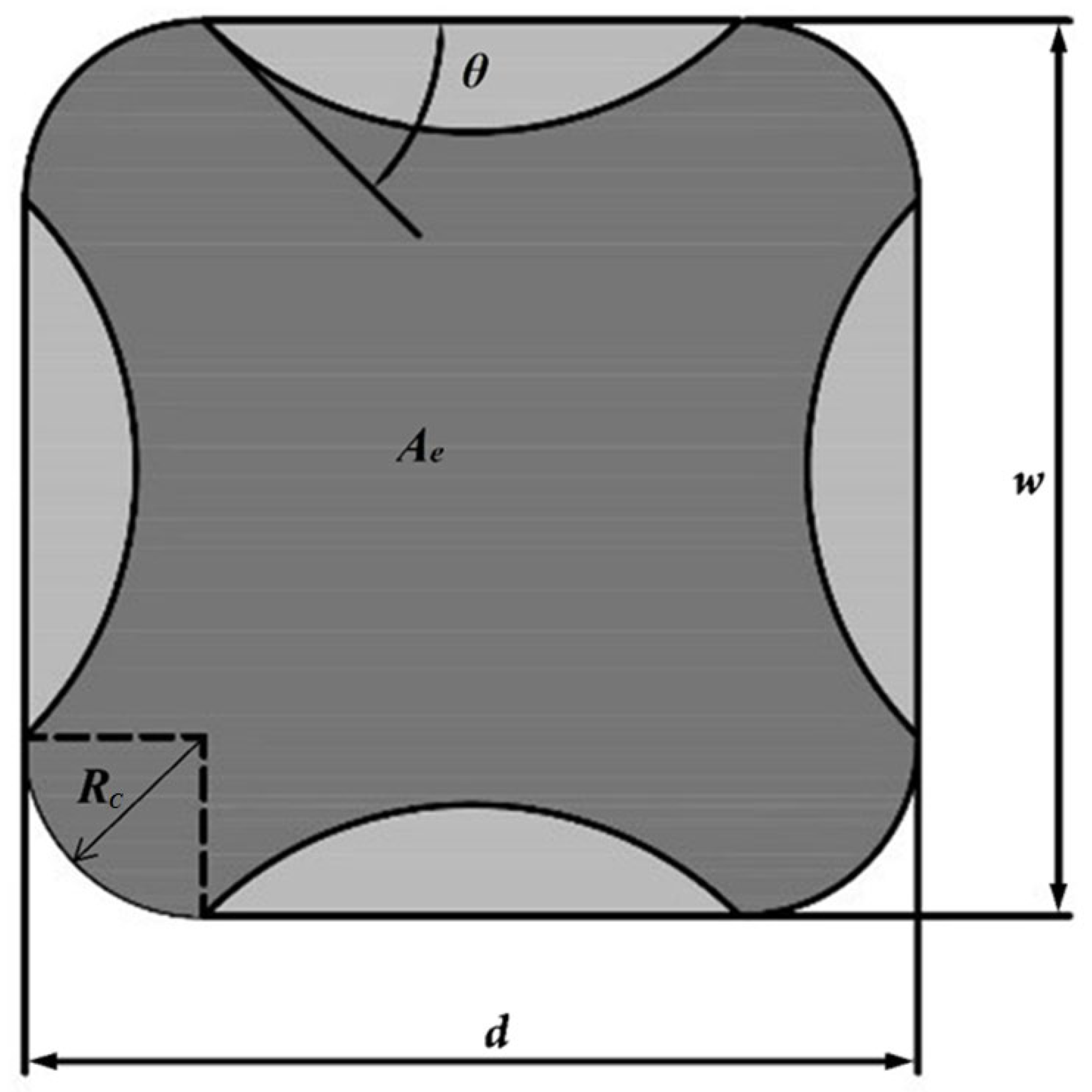
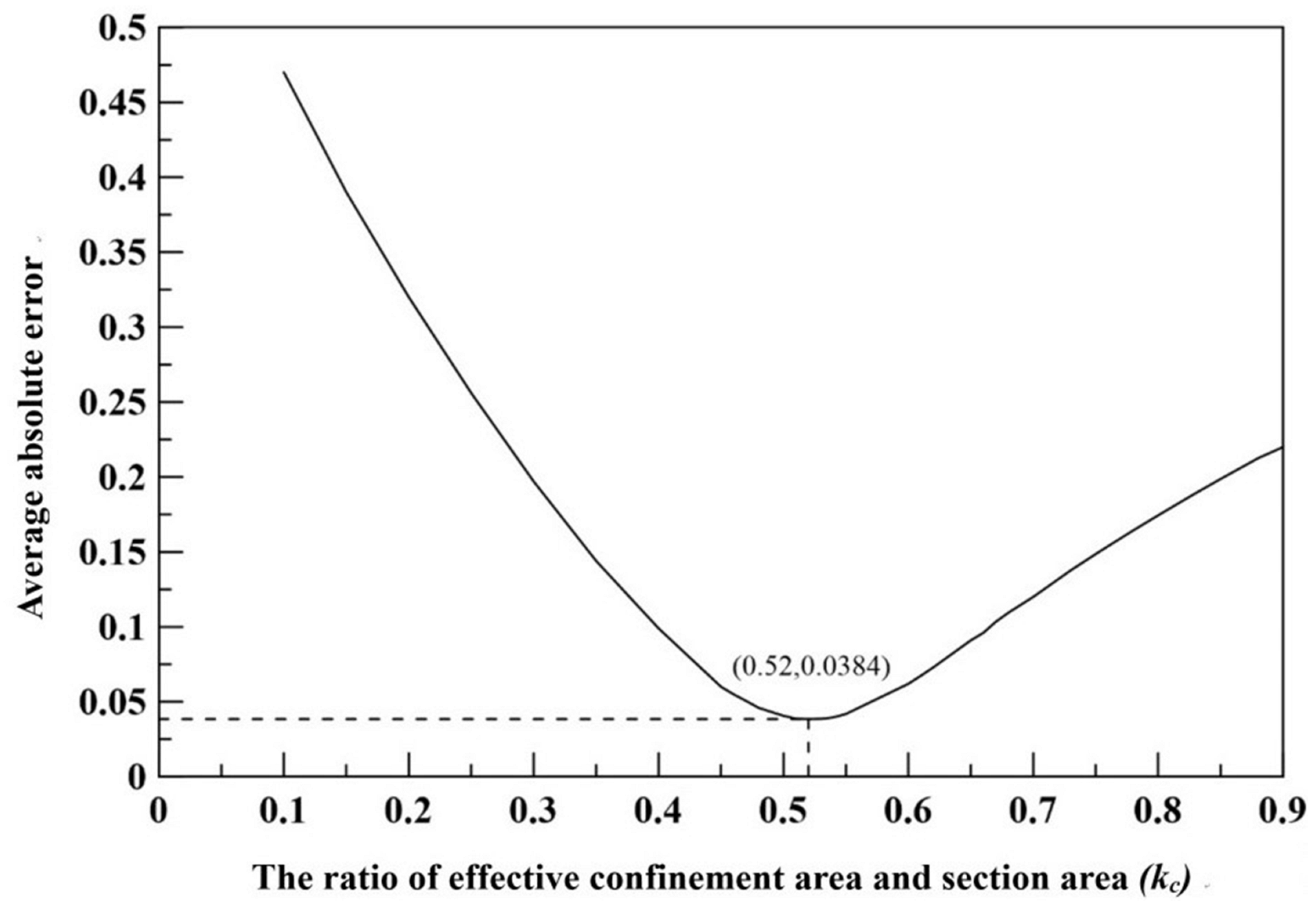
4.3. Shape Factor for Square Cross-Section
4.4. Verification of the Constitutive Model
4.5. Predictions of Compressive Strength for Square Cross-Section Specimens
5. Conclusions
- The experimental data of the specimens confined with one and two layers of AFRP were used to obtain the internal friction angle (ϕ). The average absolute error of compressive strength between the proposed constitutive model and experimental results was 7.01%, and the coefficient of determination (R2) was 0.86;
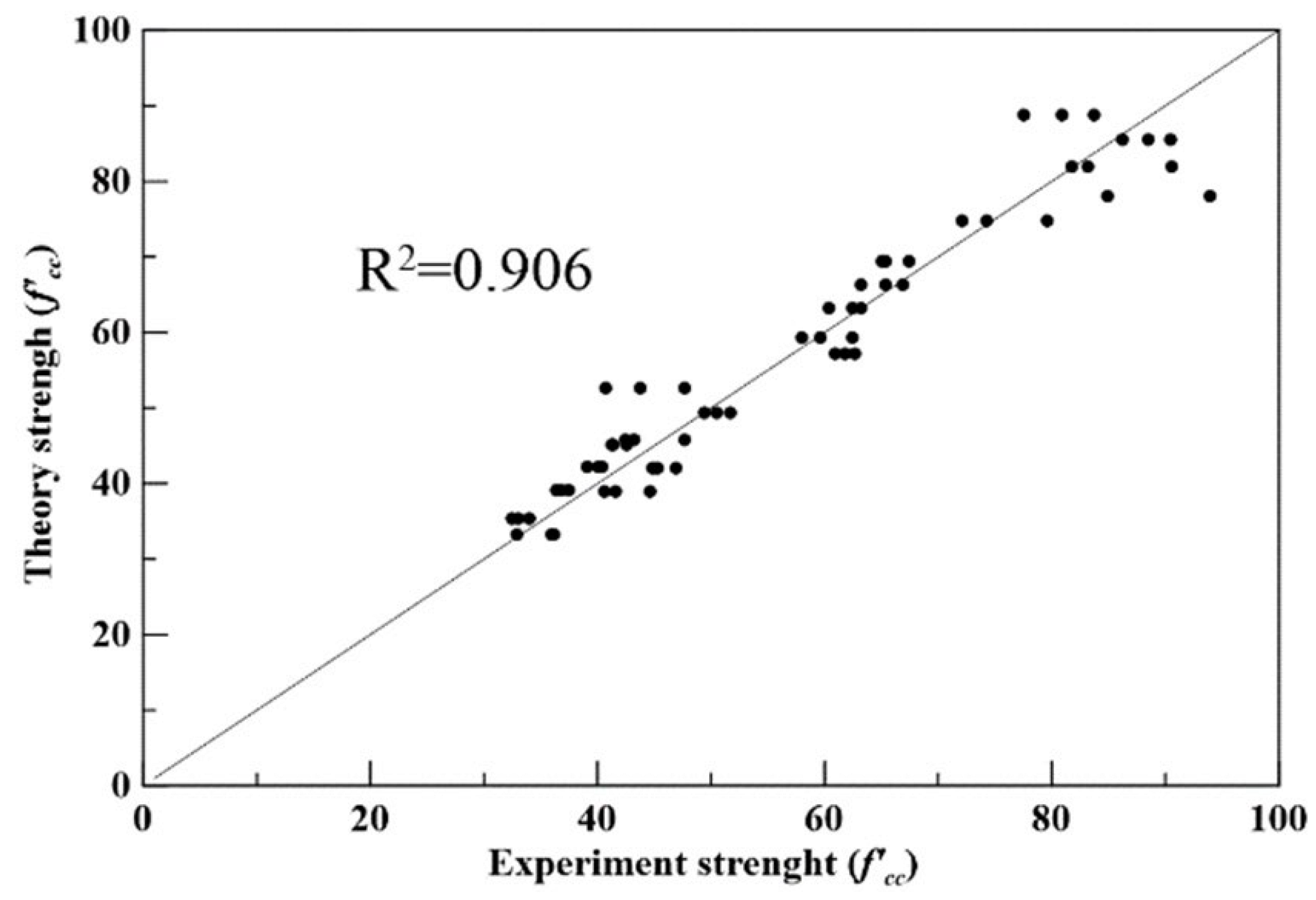
- The compressive strength of concrete specimens confined with three layers of AFRP were predicted using the above constitutive parameters; the absolute average error of cylindrical concrete specimens was less than 4.95%, and its coefficient of determination (R2) was 0.906. Other researchers’ experimental compressive strengths were predicted with the proposed constitutive model in this study, and the average absolute errors were less than 6.38%;
- A cross-sectional shape coefficient for square cross-section concrete specimens was proposed and incorporated into the constitutive model, and the average absolute error for the predicted compressive strength and the experimental results was 3.83%; its coefficient of determination (R2) was 0.93;
- From the experimental results, AFRP confinement can enhance the compressive stress, corresponding compressive strain, and strain energy capacity of concrete specimens. This enhancement is attributed to the confinement effect facilitated via the AFRP;
- The proposed constitutive model can predict the experimental maximum compressive strength for the normal strength concrete confined with AFRP composite materials with good accuracy. The major reason is that the compressive strength of the confined constitutive concrete was derived from the Mohr–Coulomb failure criterion with parameters obtained from the experimental data.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | section area; |
| Ae | effective confinement area; |
| C0 | uniaxial compressive strength without lateral confinement; |
| D | diameter of the specimens; |
| d | length of the square cross-section specimens; |
| Ekf | elastic modulus of AFRP; |
| Er | average absolute error; |
| f′c | compressive strength of the unconfined concretes; |
| f′cc | compressive strength of the confined concretes; |
| fc | compressive stress of the concretes; |
| fl | effective lateral confined stress; |
| kc | cross-section shape coefficient; |
| m | number of the compressive stress data recorded with the universal test machine; |
| n | number of AFRP wrapping layers; |
| ns | number of the specimens; |
| Rc | radius of the chamfer; |
| t | thickness of a single AFRP layer; |
| V | volume of the specimens; |
| x | experimental compressive strength; |
| average of experimental compressive strength; | |
| y | proposed compressive strength; |
| average of proposed compressive strength. | |
| εc | axial strain of AFRP-confined concrete; |
| εcc′ | maximum axial strain of AFRP-confined concrete; |
| εi | compressive strain of the concrete specimens at point i; |
| εkf | ultimate lateral strain of KFRP; |
| θ | intersect angle; |
| σ1 | uniaxial compressive strength of rock; |
| σ3 | lateral confinement stress; |
| σi | compressive stress of the concrete specimens at point i; |
| ϕ | internal friction angle; and |
| Ø | diameter of the specimens. |
References
- Berthet, J.F.; Ferrier, E.; Hamelin, P. Compressive behavior of concrete externally confined by composite jackets. Part A: Experimental study. Constr. Build. Mater. 2005, 19, 223–232. [Google Scholar] [CrossRef]
- Abbasnia, R.; Hosseinpour, F.; Rostamian, M.; Ziaadiny, H. Effect of corner radius on stress–strain behavior of FRP confined prisms under axial cyclic compression. Eng. Struct. 2012, 40, 529–535. [Google Scholar] [CrossRef]
- Saleem, S.; Hussain, Q.; Pimanmas, A. Compressive behavior of PET FRP-confined circular, square, and rectangular concrete columns. J. Compos. Constr. 2017, 21, 04016097. [Google Scholar] [CrossRef]
- Rousakis, T.C.; Panagiotakis, G.D.; Archontaki, E.E.; Kostopoulos, A.K. Prismatic RC columns externally confined with FRP sheets and pretensioned basalt fiber ropes under cyclic axial load. Compos. Part B Eng. 2019, 163, 96–106. [Google Scholar] [CrossRef]
- Ceccato, C.; Teng, J.G.; Cusatis, G. Numerical prediction of the ultimate condition of circular concrete columns confined with a fiber reinforced polymer jacket. Compos. Struct. 2020, 241, 112103. [Google Scholar] [CrossRef]
- Valasaki, M.K.; Papakonstantinou, C.G. Fiber reinforced polymer (FRP) confined circular concrete columns: An experimental overview. Buildings 2023, 13, 1248. [Google Scholar] [CrossRef]
- Shawki Ali, N.K.; Mahfouz, S.Y.; Amer, N.H. Flexural Response of Concrete Beams Reinforced with Steel and Fiber Reinforced Polymers. Buildings 2023, 13, 374. [Google Scholar] [CrossRef]
- Xian, G.; Guo, R.; Li, C. Combined effects of sustained bending loading, water immersion and fiber hybrid mode on the mechanical properties of carbon/glass fiber reinforced polymer composite. Compos. Struct. 2022, 281, 115060. [Google Scholar] [CrossRef]
- Benzaid, R.; Mesbah, H.A. Chapter 6: Circular and Square Concrete Columns Externally Confined by CFRP Composite: Experimental Investigation and Effective Strength Models. In Fiber Reinforced Polymers—The Technology Applied for Concrete Repair; Masuelli, M.A., Ed.; IntechOpen: London, UK, 2013; Section 3; pp. 167–201. Available online: https://hal.science/hal-00782084v1/preview/InTech-Circular_and_square_concrete_columns_externally_confined_by_cfrp_composite_experimental_investigation_and_effective_strength_models.pdf (accessed on 10 October 2023).
- Saeed, H.Z.; Khan, H.A.; Farooq, R. Experimental investigation of stress-strain behavior of CFRP confined Low Strength Concrete (LSC) cylinders. Constr. Build. Mater. 2016, 104, 208–215. [Google Scholar] [CrossRef]
- Li, P.; Sui, L.; Xing, F.; Li, M.; Zhou, Y.; Wu, Y.F. Stress-strain relation of FRP-confined predamaged concrete prisms with square sections of different corner radii subjected to monotonic axial compression. J. Compos. Constr. 2019, 23, 04019001. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, P.; Wang, H.; Xu, C.; Wang, H.; Zhang, L. Constitutive model of FRP tube-confined alkali-activated slag lightweight aggregate concrete columns under axial compression. Buildings 2023, 13, 2284. [Google Scholar] [CrossRef]
- Wu, H.L.; Wang, Y.F.; Yu, L.; Li, X.R. Experimental and computational studies on high-strength concrete circular columns confined by aramid fiber-reinforced polymer sheets. J. Compos. Constr. 2009, 13, 125–134. [Google Scholar] [CrossRef]
- Wang, Y.F.; Wu, H.L. Size effect of concrete short columns confined with aramid FRP jackets. J. Compos. Constr. 2011, 15, 535–544. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T.; Lim, J.C.; Vincent, T. FRP-confined concrete in circular sections: Review and assessment of stress-strain models. Eng. Struct. 2013, 49, 1068–1088. [Google Scholar] [CrossRef]
- Lim, J.C.; Ozbakkaloglu, T. Unified stress-strain model for FRP and actively confined normal-strength and high-strength concrete. J. Compos. Constr. 2015, 19, 04014072. [Google Scholar] [CrossRef]
- Vincent, T.; Ozbakkaloglu, T. Compressive behavior of prestressed high-strength concrete-filled aramid FRP tube columns: Experimental observations. J. Compos. Constr. 2015, 19, 04015003. [Google Scholar] [CrossRef]
- Lobo, P.S.; Faustino, P.; Jesus, M.; Marreiros, R. Design model of concrete for circular columns confined with AFRP. Compos. Struct. 2018, 200, 69–78. [Google Scholar] [CrossRef]
- Sivasankar, S.; Sankar, L.P.; Kumar, A.P.; Shunmugasundaram, M. Compression behavior of cylinder reinforced with aramid fiber reinforced polymer. Mater. Today Proc. 2020, 27, 764–771. [Google Scholar] [CrossRef]
- Product Manual. Zhe Jiang GBF Basalt Fiber Co., Ltd. Available online: http://www.chinagbf.com/product/584.html (accessed on 1 September 2023).
- Li, Y.F.; Hung, J.Y.; Syu, J.Y.; Chang, S.M.; Kuo, W.S. Influence of sizing of basalt fiber on the mechanical behavior of basalt fiber reinforced concrete. J. Mater. Res. Technol. 2022, 21, 295–307. [Google Scholar] [CrossRef]
- Chen, B.; Wu, K.; Yao, W. Conductivity of carbon fiber reinforced cement-based composites. Cem. Concr. Compos. 2004, 26, 291–297. [Google Scholar] [CrossRef]
- Jung, S.H.; Kishimoto, H.; Nakazato, N.; Nakata, D.; Park, J.S.; Kohyama, A. Effect of the fabrication process on the micro-structural evolution of carbon fibers and flexural property on C/SiC composites by the NITE method. Ceram. Int. 2022, 48, 32712–32722. [Google Scholar] [CrossRef]
- Li, C.; Xian, G. Experimental and modeling study of the evolution of mechanical properties of PAN-based carbon fibers at elevated temperatures. Materials 2019, 12, 724. [Google Scholar] [CrossRef] [PubMed]
- Pertuz-Comas, A.D.; Díaz, J.G.; Meneses-Duran, O.J.; Niño-Álvarez, N.Y.; León-Becerra, J. Flexural fatigue in a polymer matrix composite material reinforced with continuous Kevlar fibers fabricated by additive manufacturing. Polymers 2022, 14, 3586. [Google Scholar] [CrossRef] [PubMed]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Observed stress-strain behavior of confined concrete. J. Struct. Eng. 1988, 114, 1827–1849. [Google Scholar] [CrossRef]
- Mirmiran, A.; Shahawy, M. Behavior of concrete columns confined by fiber composites. J. Struct. Eng. 1997, 123, 583–590. [Google Scholar] [CrossRef]
- Razvi, S.; Saatcioglu, M. Confinement model for high-strength concrete. J. Struct. Eng. 1999, 125, 281–289. [Google Scholar] [CrossRef]
- Li, Y.F.; Lin, C.T.; Sung, Y.Y. A constitutive model for concrete confined with carbon fiber reinforced plastics. Mech. Mater. 2003, 35, 603–619. [Google Scholar] [CrossRef]
- Lin, C.T.; Li, Y.F. An effective peak stress formula for concrete confined with carbon fiber reinforced plastics. Can. J. Civ. Eng. 2003, 30, 882–889. [Google Scholar] [CrossRef]
- Li, Y.F.; Fang, T.S. A constitutive model for concrete confined by steel reinforcement and carbon fiber reinforced plastic sheet. Struct. Eng. Mech. 2004, 18, 21–40. [Google Scholar] [CrossRef]
- Li, Y.F.; Sio, W.K.; Tsai, Y.K. A compressive peak strength model for CFRP-confined thermal insulation materials under elevated temperature. Materials 2020, 13, 26. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.F.; Sio, W.K.; Yang, T.H.; Tsai, Y.K. A constitutive model of high-early-strength cement with perlite powder as a thermal-insulating material confined by carbon fiber reinforced plastics at elevated temperatures. Polymers 2020, 12, 2369. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, D.; Smith, S.T.; Lu, D. CFRP-confined square RC columns. I: Experimental investigation. J. Compos. Constr. 2012, 16, 150–160. [Google Scholar] [CrossRef]
- Sadeghian, P.; Rahai, A.R.; Ehsani, M.R. Effect of fiber orientation on compressive behavior of CFRP-confined concrete columns. J. Reinf. Plast. Compos. 2010, 29, 1335–1346. [Google Scholar] [CrossRef]
- Sadeghian, P.; Fam, A. Improved design-oriented confinement models for FRP-wrapped concrete cylinders based on statistical analyses. Eng. Struct. 2015, 87, 162–182. [Google Scholar] [CrossRef]
- Keshtegar, B.; Sadeghian, P.; Gholampour, A.; Ozbakkaloglu, T. Nonlinear modeling of ultimate strength and strain of FRP-confined concrete using chaos control method. Compos. Struct. 2017, 163, 423–431. [Google Scholar] [CrossRef]
- Khorramian, K.; Sadeghian, P. New mechanics-based confinement model and stress–strain relationship for analysis and design of concrete columns wrapped with FRP composites. Structures 2021, 33, 2659–2674. [Google Scholar] [CrossRef]
- Toufigh, V.; Toufigh, V.; Saadatmanesh, H.; Ahmari, S.; Kabiri, E. Behavior of polymer concrete beam/pile confined with CFRP sleeves. Mech. Adv. Mater. Struct. 2019, 26, 333–340. [Google Scholar] [CrossRef]
- Djafar-Henni, I.; Kassoul, A. Stress-strain model of confined concrete with Aramid FRP wraps. Constr. Build. Mater. 2018, 186, 1016–1030. [Google Scholar] [CrossRef]
- Arabshahi, A.; Gharaei-Moghaddam, N.; Tavakkolizadeh, M. Development of applicable design models for concrete columns confined with aramid fiber reinforced polymer using Multi-Expression Programming. Structures 2020, 23, 225–244. [Google Scholar] [CrossRef]
- De Luca, A.; Nanni, A. Single-parameter methodology for the prediction of the stress-strain behavior of FRP-confined RC square columns. J. Compos. Constr. 2011, 15, 384–392. [Google Scholar] [CrossRef]
- Diboune, N.; Benzaid, R.; Berradia, M. New strength–strain model and stress–strain relationship for square and rectangular concrete columns confined with CFRP wraps. Mech. Adv. Mater. Struct. 2022, 30, 2971–2994. [Google Scholar] [CrossRef]
- ASTM C39/C39M-01; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens. ASTM: West Conshohocken, PA, USA, 2021.
- Kent, D.C.; Park, R. Flexural Members with Confined Concrete. J. Struct. Div. ASCE 1971, 97, 1969–1990. [Google Scholar] [CrossRef]
- Al-Salloum, Y.A. Influence of edge sharpness on the strength of square concrete columns confined with FRP composite laminates. Compos. Part B Eng. 2007, 38, 640–650. [Google Scholar] [CrossRef]
- Rousakis, T.C.; Karabinis, A.I.; Kiousis, P.D. FRP-confined concrete members: Axial compression experiments and plasticity modelling. Eng. Struct. 2007, 29, 1343–1353. [Google Scholar] [CrossRef]
- Wang, L.M.; Wu, Y.F. Effect of corner radius on the performance of CFRP-confined square concrete columns: Test. Eng. Struct. 2008, 30, 493–505. [Google Scholar] [CrossRef]
- Wu, H.L.; Wang, Y.F. Experimental study on reinforced high-strength concrete short columns confined with AFRP sheets. Steel Compos. Struct. 2010, 10, 501–516. [Google Scholar] [CrossRef]
- Wu, Y.F.; Wei, Y.Y. Effect of cross-sectional aspect ratio on the strength of CFRP-confined rectangular concrete columns. Eng. Struct. 2010, 32, 32–45. [Google Scholar] [CrossRef]
- Belouar, A.; Laraba, A.; Benzaid, R.; Chikh, N. Structural performance of square concrete columns wrapped with CFRP sheets. Procedia Eng. 2013, 54, 232–240. [Google Scholar] [CrossRef][Green Version]
- Nisticò, N.; Pallini, F.; Rousakis, T.; Wu, Y.F.; Karabinis, A. Peak strength and ultimate strain prediction for FRP confined square and circular concrete sections. Compos. Part B Eng. 2014, 67, 543–554. [Google Scholar] [CrossRef]





| Properties | Fiber | |||
|---|---|---|---|---|
| Aramid | Carbon | Glass | Basalt | |
| Density (g/cm3) | 1.44 | 1.78 | 2.48~2.76 | 2.65 |
| Tensile Strength (MPa) | 2500~3100 | 3500~6000 | 1400~2500 | 3800~4840 |
| Elastic Modulus (GPa) | 60~120 | 230~600 | 70~80 | 93.1~110 |
| Elongation (%) | 2.1~4.5 | 1.5~2.0 | 2.5~3.5 | 3.1 |
| Properties | Value | Test Standard |
|---|---|---|
| Fiber areal weight, FAW (g/m2) | 225.0 | ASTM D3776 |
| Young’s modulus (GPa) | 128.5 | ASTM D3039 |
| Tensile strength (MPa) | 2188.5 | ASTM D3039 |
| Elongation (%) | 3.6 | ASTM D3039 |
| Specimen * | Average Compressive Strength (MPa) | Specimen * | Average Compressive Strength (MPa) | Specimen * | Average Compressive Strength (MPa) |
|---|---|---|---|---|---|
| C10W50 | 34.4 | C15W50 | 33.1 | S10W50 | 33.1 |
| C10W55 | 31.3 | C15W55 | 30.2 | S10W55 | 29.6 |
| C10W60 | 27.8 | C15W60 | 27.1 | S10W65 | 24.4 |
| C10W65 | 24.1 | C15W65 | 23.4 | ||
| C10W70 | 21.0 | C15W70 | 21.3 |
| Specimen * | Compressive Strength (MPa) | Ultimate Compressive Axial Strain | Measured Ultimate Lateral Strain | ||
|---|---|---|---|---|---|
| Test | Avg. Value/ Increment (%) | Test | Avg. Value | ||
| C10W50L1 | 40.7; 47.7; 43.7 | 44.0/28 | 0.0132; 0.0106; 0.0126 | 0.0121 | 0.0135; 0.0147; 0.0181 |
| C10W50L2 | 64.5; 64.0; 69.1 | 65.9/91 | 0.0191; 0.0185; 0.0170 | 0.0182 | 0.0115; 0.0133; 0.0159 |
| C10W50L3 | 77.5; 80.9; 83.8 | 80.7/134 | 0.0228; 0.0235; 0.0191 | 0.0218 | 0.0172; 0.0184; 0.0176 |
| C10W55L1 | 50.5; 51.7; 49.4 | 50.5/61 | 0.0114; 0.0121; 0.0128 | 0.0121 | 0.0158; 0.0135; 0.0148 |
| C10W55L2 | 72.2; 67.1; 73.9 | 71.1/126 | 0.0145; 0.0122; 0.0173 | 0.0147 | 0.0209; 0.0186; 0.0180 |
| C10W55L3 | 88.5; 90.4; 86.2 | 88.4/181 | 0.0171; 0.0187; 0.0189 | 0.0183 | 0.0136; 0.0142; 0.0113 |
| C10W60L1 | 43.3; 47.7 | 45.5/60 | 0.0129; 0.0126 | 0.0128 | - |
| C10W60L2 | 72.1; 74.8; 78.4 | 75.1/170 | 0.0188; 0.0201; 0.0208 | 0.0199 | - |
| C10W60L3 | 83.2; 90.6; 81.7 | 85.2/206 | 0.0205; 0.0218; 0.0191 | 0.0205 | - |
| C10W65L1 | 44.9; 46.9; 45.2 | 45.7/89 | 0.0112; 0.0131; 0.0128 | 0.0124 | 0.0113; 0.0175; 0.0198 |
| C10W65L2 | 65.3; 70.5; 71.6 | 69.1/187 | 0.0161; 0.0186; 0.0153 | 0.0167 | 0.0155; 0.0163; 0.0143 |
| C10W65L3 | 93.9; 84.9 | 89.4/271 | 0.0244; 0.0196 | 0.0220 | 0.0175; 0.0166 |
| C10W70L1 | 40.6; 44.6; 41.6 | 42.3/101 | 0.0142; 0.0161; 0.0171 | 0.0158 | - |
| C10W70L2 | 63.1; 59.7; 55.7 | 59.5/183 | 0.0199; 0.0211; 0.0249 | 0.0220 | - |
| C10W70L3 | 74.3; 79.6; 72.1 | 75.33/259 | 0.0250; 0.0282; 0.0290 | 0.0274 | - |
| Specimen * | Compressive Strength (MPa) | Avg. Compressive Strength (MPa) | Strength Increment (%) | Measured Ultimate Lateral Strain |
|---|---|---|---|---|
| C15W50L1 | 42.6; 41.3; 41.3 | 41.7 | 26 | 0.0200; 0.0258; 0.0247 |
| C15W50L2 | 56.1; 49.4; 54.2 | 53.2 | 61 | 0.0251; 0.0208; 0.0239 |
| C15W50L3 | 65.1; 67.5; 65.4 | 66.0 | 99 | 0.0155; 0.0201; 0.0159 |
| C15W55L1 | 40.4; 39.1; 40.0 | 39.8 | 32 | 0.0193; 0.0200; 0.0189 |
| C15W55L2 | 53.2; 51.6; 51.0 | 51.9 | 72 | 0.0201; 0.0189; 0.0199 |
| C15W55L3 | 63.2; 65.4; 66.9 | 65.2 | 116 | 0.0193; 0.0180; 0.0186 |
| C15W60L1 | 37.5; 36.3; 36.8 | 36.9 | 36 | 0.0113; 0.0189; 0.0136 |
| C15W60L2 | 53.0; 49.0; 50.5 | 50.8 | 87 | 0.0143; 0.0156; 0.0157 |
| C15W60L3 | 63.2; 62.4; 60.3 | 62.0 | 128 | 0.0183; 0.0203; 0.0192 |
| C15W65L1 | 34.0; 33.0; 32.5 | 33.2 | 42 | 0.0140; 0.0230; 0.0185 |
| C15W65L2 | 47.9; 49.4; 49.4 | 48.9 | 109 | 0.0179; 0.0194; 0.0185 |
| C15W65L3 | 62.5; 58.0; 59.6 | 60.0 | 157 | 0.0169; 0.0233; 0.0188 |
| C15W70L1 | 32.9; 35.9; 36.1 | 35.0 | 68 | 0.0199; 0.0201; 0.0257 |
| C15W70L2 | 47.6; 47.7; 45.0 | 46.8 | 119 | 0.0205; 0.0247; 0.0239 |
| C15W70L3 | 60.9; 62.6; 61.8 | 61.8 | 190 | 0.0200; 0.0157; 0.0198 |
| Specimen * | Compressive Strength (MPa) | Ultimate Compressive Axial Strain | Measured Ultimate Lateral Strain | ||
|---|---|---|---|---|---|
| Test | Avg. Value/ Increment (%) | Test | Avg. Value | ||
| S10W50L1 | 41.8; 41.6; 39.7 | 41.0/24 | 0.0106; 0.0104; 0.0114 | 0.0108 | 0.0138; 0.0200; 0.0189 |
| S10W50L2 | 50.8; 51.2; 52.5 | 51.5/56 | 0.0174; 0.0151; 0.0172 | 0.0166 | 0.0188; 0.0165; 0.0123 |
| S10W50L3 | 62.9; 61.5; 62.2 | 62.2/88 | 0.0225; 0.0217; 0.0226 | 0.0223 | 0.0176; 0.0178; 0.0183 |
| S10W55L1 | 41.9; 38.8; 37.6 | 39.4/33 | 0.0119; 0.0114; 0.0105 | 0.0112 | 0.0185; 0.0144; 0.0158 |
| S10W55L2 | 46.8; 48.9; 44.2 | 46.6/57 | 0.0171; 0.0197; 0.0153 | 0.0174 | 0.0128; 0.0168; 0.0166 |
| S10W55L3 | 61.9; 58.3; 62.2 | 60.8/105 | 0.0180; 0.0238; 0.0225 | 0.0214 | 0.0137; 0.0173; 0.0133 |
| S10W65L1 | 34.9; 33.1; 34.1 | 34.0/40 | 0.0128; 0.0127; 0.0113 | 0.0123 | 0.0218; 0.0140; 0.0181 |
| S10W65L2 | 44.2; 42.6; 44.9 | 43.9/80 | 0.0180; 0.0177; 0.0174 | 0.0177 | 0.0141; 0.0108; 0.0153 |
| S10W65L3 | 59.3; 58.3; 57.2 | 58.3/139 | 0.0261; 0.0216; 0.0230 | 0.0236 | 0.0081; 0.0149; 0.0146 |
| Specimen * | Experimental Compressive Strength (MPa) | Proposed Constitutive Model Compressive Strength (Mpa) | Error (%) | |
|---|---|---|---|---|
| Test | Avg. Value | |||
| C10W50L1 | 40.7; 47.7; 43.7 | 44.0 | 52.5 | 28.99; 10.06; 20.14 |
| C10W50L2 | 64.5; 64.0; 69.1 | 65.9 | 70.6 | 9.46; 10.31; 2.17 |
| C10W55L1 | 50.5; 51.7; 49.4 | 50.5 | 49.4 | −2.18; −4.45; 0.0 |
| C10W55L2 | 72.2; 67.1; 73.9 | 71.1 | 67.5 | −6.51; 0.60; −8.66 |
| C10W60L1 | 43.3; 47.7; 42.5 | 44.5 | 45.9 | 6.00; −3.77; 8.00 |
| C10W60L2 | 72.1; 74.8; 78.4 | 75.1 | 66.0 | −8.46; −11.76; −15.82 |
| C10W65L1 | 44.9; 46.9; 45.2 | 45.7 | 42.2 | −6.01; −10.02; −6.64 |
| C10W65L2 | 65.3; 70.5; 71.6 | 69.1 | 60.2 | −7.81; −14.61; −15.92 |
| C10W70L1 | 40.6; 44.6; 41.6 | 42.3 | 39.0 | −3.94; −12.56; −6.25 |
| C10W70L2 | 63.1; 59.7; 55.7 | 59.5 | 57.1 | −9.51; −4.36; 2.51 |
| C15W50L1 | 42.6; 41.3; 41.3 | 41.7 | 45.2 | 6.10; 9.44; 9.44 |
| C15W50L2 | 56.1; 49.4; 54.2 | 53.2 | 57.2 | 1.96; 15.79; 5.54 |
| C15W55L1 | 40.4; 39.1; 40.0 | 39.8 | 42.2 | 4.46; 7.93; 5.50 |
| C15W55L2 | 53.2; 51.6; 51.0 | 51.9 | 54.3 | 2.07; 5.23; 6.47 |
| C15W60L1 | 37.5; 36.3; 36.8 | 36.9 | 39.2 | 4.53; 7.99; 6.52 |
| C15W60L2 | 53.0; 49.0; 50.5 | 50.8 | 51.2 | −3.40; 4.49; 1.39 |
| C15W65L1 | 34.0; 33.0; 32.5 | 33.2 | 35.4 | 4.12; 7.27; 8.92 |
| C15W65L2 | 47.9; 49.4; 49.4 | 48.9 | 47.5 | −0.84; −3.85; −3.85 |
| C15W70L1 | 32.9; 35.9; 36.1 | 35.0 | 33.4 | 1.52; −6.96; −7.48 |
| C15W70L2 | 47.6; 47.7; 45.0 | 46.8 | 45.4 | −4.62; −4.82; 0.89 |
| Average absolute error = 7.01 | ||||
| Specimen * | Experimental Compressive Strength (MPa) | Proposed Constitutive Model Compressive Strength (MPa) | Error (%) | |
|---|---|---|---|---|
| Test | Avg. Value | |||
| C10W50L3 | 77.5; 80.9; 83.8 | 80.7 | 88.7 | 14.45; 9.64; 5.85 |
| C10W55L3 | 88.5; 90.4; 86.2 | 88.4 | 85.6 | 3.28; −5.31; 0.70 |
| C10W60L3 | 83.2; 90.6; 81.7 | 85.2 | 82.0 | −1.44; −9.49; 0.37 |
| C10W65L3 | 93.9; 84.9 | 89.4 | 78.3 | −16.61; 7.77 |
| C10W70L3 | 74.3; 79.6; 72.1 | 75.3 | 75.2 | 1.21; −5.53; 4.30 |
| C15W50L3 | 65.1; 67.5; 65.4 | 66.0 | 69.3 | 6.45; 2.67; 5.96 |
| C15W55L3 | 63.2; 65.4; 66.9 | 65.2 | 66.3 | 4.91; 1.38; −0.90 |
| C15W60L3 | 63.2; 62.4; 60.3 | 62.0 | 63.3 | 0.16; 1.44; 4.98 |
| C15W65L3 | 62.5; 58.0; 59.6 | 60.0 | 59.5 | −4.80; 2.59; −0.17 |
| C15W70L3 | 60.9; 62.6; 61.8 | 61.8 | 57.4 | −5.75; −8.31; −7.12 |
| Average absolute error = 4.95 | ||||
| Specimen * | Experimental Compressive Strength (MPa) | Proposed Constitutive Model Compressive Strength (MPa) | Error (%) | |
|---|---|---|---|---|
| Test | Avg. Value | |||
| S10W50L1 | 41.8; 41.6; 39.7 | 41.0 | 43.0 | 2.81; 3.31; 8.25 |
| S10W50L2 | 50.8; 51.2; 52.5 | 51.5 | 52.9 | 4.04; 3.22; 0.67 |
| S10W50L3 | 63.5; 64.1 | 63.8 | 62.7 | −1.22; −2.15 |
| S10W55L1 | 41.9; 38.8; 37.6 | 39.4 | 39.5 | −5.77; 1.76; 5.01 |
| S10W55L2 | 46.8; 48.9; 44.2 | 46.6 | 49.4 | 5.46; 0.93; 11.66 |
| S10W55L3 | 61.9; 58.3; 62.2 | 60.8 | 59.2 | −4.32; 1.59; −4.78 |
| S10W65L1 | 34.9; 33.1; 34.1 | 34.0 | 34.2 | −1.95; 3.38; 0.35 |
| S10W65L2 | 44.2; 42.7; 44.9 | 43.9 | 44.1 | −0.26; 3.38; −1.81 |
| S10W65L3 | 59.3; 58.3; 57.2 | 58.3 | 54.0 | −9.01; −7.45; −5.67 |
| Average absolute error = 3.85 | ||||
| Reference | FRP Type | Experimental Value | Proposed Constitutive Model | Error (%) | |||||
|---|---|---|---|---|---|---|---|---|---|
| d/h (Length/Height) | f′c (MPa) | f′cc (MPa) | Rc (mm) | Effective Area Ratio (%) | f′l (MPa) | f′cc (MPa) | |||
| Wang and Wu, 2011 [14] | Aramid | 100/300 | 46.4 | 49.5 | 10 | 11.95 | 1.99 | 50.5 | 2.02 |
| 46.4 | 54.2 | 3.97 | 54.6 | 0.74 | |||||
| 46.4 | 59.0 | 5.96 | 58.6 | −0.68 | |||||
| 78.5 | 78.7 | 1.99 | 82.6 | 4.96 | |||||
| 78.5 | 94.3 | 3.97 | 86.7 | −8.06 | |||||
| 78.5 | 96.0 | 5.96 | 90.7 | −5.52 | |||||
| 101.2 | 104.36 | 1.99 | 105.3 | 0.90 | |||||
| 101.2 | 112.06 | 3.97 | 109.4 | −2.37 | |||||
| 101.2 | 110.87 | 5.96 | 113.4 | 2.28 | |||||
| Average absolute error = 3.06 | |||||||||
| Wang and Wu, 2008 [49] | Carbon | 150/300 | 31.9 | 33.6 | 15 | 16.6 | 1.27 | 34.5 | 2.68 |
| 31.9 | 42.2 | 15 | 16.6 | 3.80 | 39.7 | −5.92 | |||
| 32.3 | 39.8 | 30 | 51.9 | 3.95 | 40.4 | 1.51 | |||
| 32.3 | 56.5 | 30 | 51.9 | 11.84 | 56.5 | 0.00 | |||
| 30.7 | 43.7 | 45 | 77.7 | 5.91 | 42.8 | −2.06 | |||
| 30.7 | 68.0 | 45 | 77.7 | 17.72 | 66.9 | −1.62 | |||
| 31.8 | 50.0 | 60 | 93.9 | 7.15 | 46.4 | −7.20 | |||
| 31.8 | 78.9 | 60 | 93.9 | 21.44 | 75.6 | −4.18 | |||
| 54.1 | 55.8 | 15 | 16.6 | 1.26 | 56.7 | 1.61 | |||
| 54.1 | 59.4 | 15 | 16.6 | 3.79 | 61.9 | 4.21 | |||
| 52.0 | 55.9 | 30 | 51.9 | 3.94 | 60.1 | 7.51 | |||
| 52.0 | 63.0 | 30 | 51.9 | 11.81 | 76.2 | 20.95 | |||
| 52.7 | 57.6 | 45 | 77.7 | 5.89 | 64.8 | 12.50 | |||
| 52.7 | 80.3 | 45 | 77.7 | 17.68 | 88.9 | 10.71 | |||
| 52.7 | 62.6 | 60 | 93.9 | 7.13 | 67.3 | 7.51 | |||
| Average absolute error = 6.01 | |||||||||
| Wu and Wei, 2010 [51] | Carbon | 150/300 | 34.1 | 40.5 | 30 | 51.88 | 3.93 | 42.3 | 4.44 |
| 40.7 | 3.93 | ||||||||
| 42.5 | −0.47 | ||||||||
| Average absolute error = 2.95 | |||||||||
| Al-Salloum, 2007 [47] | Carbon | 150/500 | 34.8 | 48.3 | 25 | 41.2 | 7.32 | 49.8 | 3.11 |
| 34.8 | 45.6 | 25 | 41.2 | 7.32 | 49.8 | 9.21 | |||
| 29.0 | 57.0 | 38 | 66.8 | 11.88 | 53.3 | −6.49 | |||
| 29.0 | 55.0 | 38 | 66.8 | 11.88 | 53.3 | −3.09 | |||
| 27.5 | 61.7 | 50 | 84.1 | 14.96 | 58.1 | −5.83 | |||
| 27.5 | 63.7 | 50 | 84.1 | 14.96 | 58.1 | −8.79 | |||
| Average absolute error = 6.09 | |||||||||
| Rousakis et al., 2007 [48] | G-glass | 200/320 | 33.0 | 42.6 | 30 | 35.44 | 2.67 | 38.5 | −9.62 |
| 33.0 | 44.4 | 5.34 | 44.0 | −0.90 | |||||
| 33.0 | 55.5 | 8.01 | 49.4 | −10.99 | |||||
| 38.0 | 40.4 | 2.67 | 43.4 | 7.43 | |||||
| 38.0 | 52.8 | 5.34 | 48.9 | −7.39 | |||||
| 38.0 | 60.2 | 8.01 | 54.4 | −9.63 | |||||
| 39.9 | 43.1 | 2.67 | 45.4 | 5.34 | |||||
| 39.9 | 51.2 | 5.34 | 50.8 | −0.78 | |||||
| 39.9 | 59.5 | 8.01 | 56.3 | −5.38 | |||||
| Average absolute error = 6.38 | |||||||||
| Reference | Aspect Ratio (h/D) | Model |
|---|---|---|
| D. and K. [41] | Any ratio | |
| L. and F. [18] | 3.5 (750/200) | |
| W. and W. [14] | Any ratio | |
| A. and G. [42] | Any ratio | |
| V. and O. [17] | 2 (305/152) |
| Experiment | This Study | D. and K. [41] | L. and F. [18] | W. and W. [14] | A. and G. [42] | V. and O. [17] | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f′c | f′cc | f′cc (MPa) | Error (%) | f′cc (MPa) | Error (%) | f′cc (MPa) | Error (%) | f′cc (MPa) | Error (%) | f′cc (MPa) | Error (%) | f′cc (MPa) | Error (%) |
| 34.44 | 80.75 | 88.69 | 9.83 | 58.50 | −27.55 | 85.71 | 6.14 | −34.79 | −143.09 | 113.07 | 40.03 | 112.68 | 39.54 |
| 31.33 | 88.35 | 85.57 | −3.15 | 56.84 | −35.66 | 73.95 | −16.29 | −53.92 | −161.03 | 115.48 | 30.70 | 105.57 | 19.49 |
| 28.71 | 85.16 | 82.04 | −3.66 | 55.64 | −34.66 | 69.23 | −18.70 | −72.79 | −185.48 | 118.44 | 39.08 | 99.28 | 16.58 |
| 24.09 | 89.41 | 78.30 | −12.43 | 54.12 | −39.47 | 56.48 | −36.84 | −114.84 | −228.44 | 126.70 | 41.71 | 87.40 | −2.25 |
| 20.96 | 75.33 | 75.16 | −0.23 | 53.70 | −28.72 | 54.40 | −27.78 | −152.84 | −302.90 | 135.71 | 80.16 | 78.63 | 4.38 |
| 33.11 | 65.95 | 69.28 | 5.05 | 45.89 | −30.41 | 93.46 | 41.71 | 19.50 | −70.44 | 87.02 | 31.95 | 95.71 | 45.12 |
| 30.15 | 65.16 | 66.31 | 1.76 | 43.70 | −32.94 | 85.77 | 31.63 | 9.39 | −85.59 | 87.84 | 34.81 | 90.07 | 38.23 |
| 27.12 | 61.97 | 63.27 | 2.10 | 41.59 | −32.89 | 79.72 | 28.65 | −2.65 | −104.27 | 89.55 | 44.51 | 84.02 | 35.57 |
| 23.38 | 60.05 | 59.52 | −0.88 | 39.24 | −34.65 | 70.18 | 16.87 | −20.85 | −134.72 | 93.42 | 55.58 | 76.05 | 26.65 |
| 21.31 | 61.76 | 57.44 | −6.99 | 38.11 | −38.29 | 62.78 | 1.66 | −33.17 | −153.71 | 96.78 | 56.70 | 71.36 | 15.55 |
| Avg. absolute error (%) | 4.61 | 35.53 | 25.15 | 156.97 | 45.52 | 24.34 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.-F.; Chen, B.-Y.; Syu, J.-Y.; Ramanathan, G.K.; Lee, W.-H.; Huang, C.-H.; Lok, M.-H. A Constitutive Model for Circular and Square Cross-Section Concrete Confined with Aramid FRP Laminates. Buildings 2023, 13, 2895. https://doi.org/10.3390/buildings13112895
Li Y-F, Chen B-Y, Syu J-Y, Ramanathan GK, Lee W-H, Huang C-H, Lok M-H. A Constitutive Model for Circular and Square Cross-Section Concrete Confined with Aramid FRP Laminates. Buildings. 2023; 13(11):2895. https://doi.org/10.3390/buildings13112895
Chicago/Turabian StyleLi, Yeou-Fong, Bo-Yu Chen, Jin-Yuan Syu, Gobinathan Kadagathur Ramanathan, Wei-Hao Lee, Chih-Hong Huang, and Man-Hoi Lok. 2023. "A Constitutive Model for Circular and Square Cross-Section Concrete Confined with Aramid FRP Laminates" Buildings 13, no. 11: 2895. https://doi.org/10.3390/buildings13112895
APA StyleLi, Y.-F., Chen, B.-Y., Syu, J.-Y., Ramanathan, G. K., Lee, W.-H., Huang, C.-H., & Lok, M.-H. (2023). A Constitutive Model for Circular and Square Cross-Section Concrete Confined with Aramid FRP Laminates. Buildings, 13(11), 2895. https://doi.org/10.3390/buildings13112895









