Elastic Buckling of Prismatic Web Plate under Shear with Simply-Supported Boundary Conditions
Abstract
:1. Introduction
2. Methodology
2.1. Analysis Procedure
- Determined the variables (inputs) that may impact the local shear buckling coefficient (output) estimate. The selected parameters were based on outcomes from previous studies.
- The ANSYS V.2021 software program was used to estimate the theoretical shear buckling stress of the prismatic web plates.
- The elastic buckling load was determined for each model from eigenvalue analysis, and the local shear buckling coefficient was determined using the Timoshenko and Gere formula (Equation (1)).
- Constructed the dependence charts, which revealed the interactions between the input parameters and the local shear buckling coefficient.
- Carried out the regression analysis of the dataset by using MATLAB V.2020 software to obtain a conservative model for design purposes.
2.2. Influencing Parameters
- i.
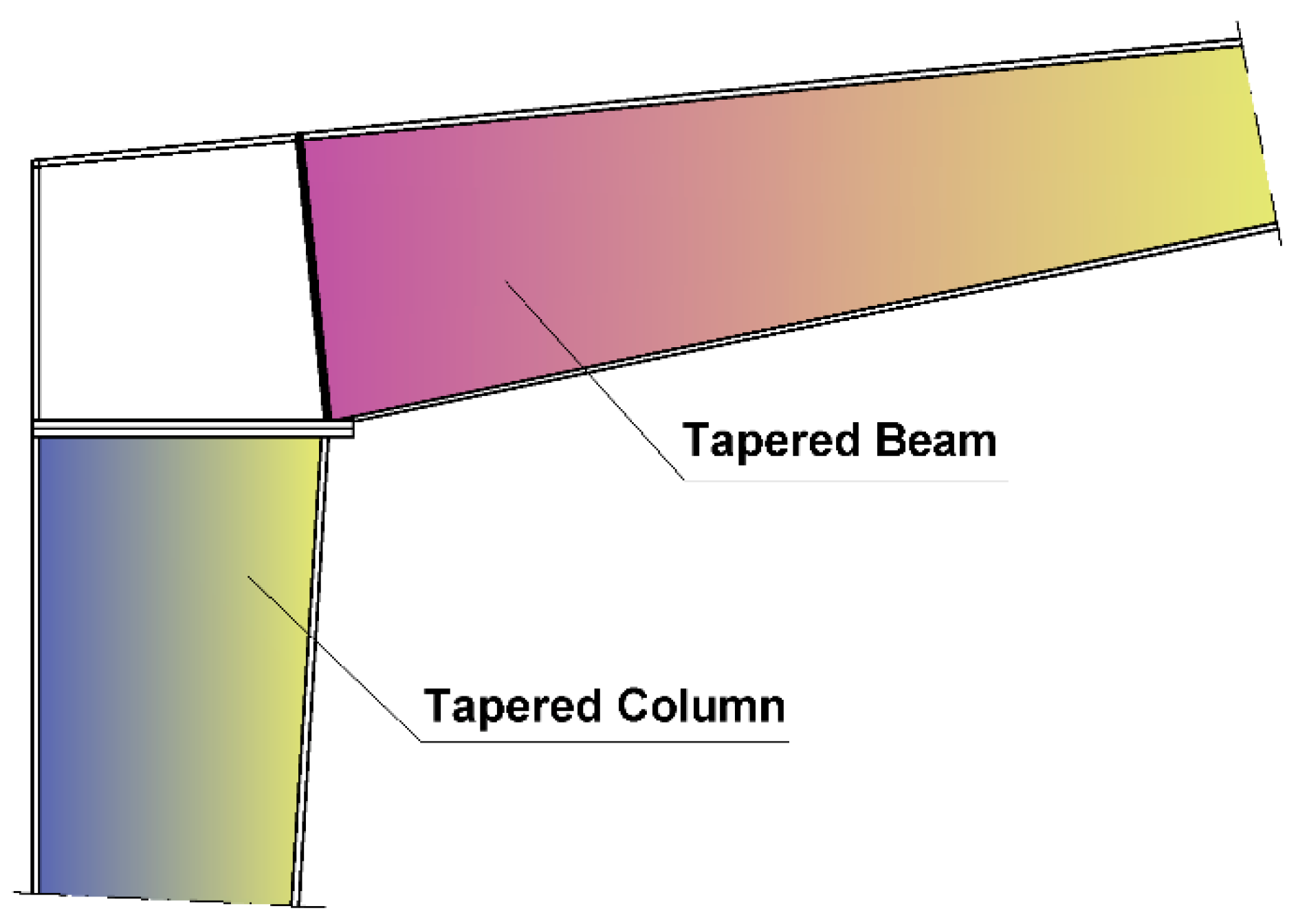
- The geometric characteristics of the web panels include aspect ratio (α = a/h), where is the aspect ratio and h is the larger width, tapering ratio (R = h/h1) or inclination angle, where is the tapering ratio and h1 is the smaller width, and web slenderness ratio , where is the plate thickness, as well as boundary and loading conditions, as illustrated in Figure 2.
- ii.
- Material properties such as modulus of elasticity (E) and Poisson’s ratio (ν).
3. Finite Element Modeling (FEM)
3.1. General
3.2. Boundary Conditions
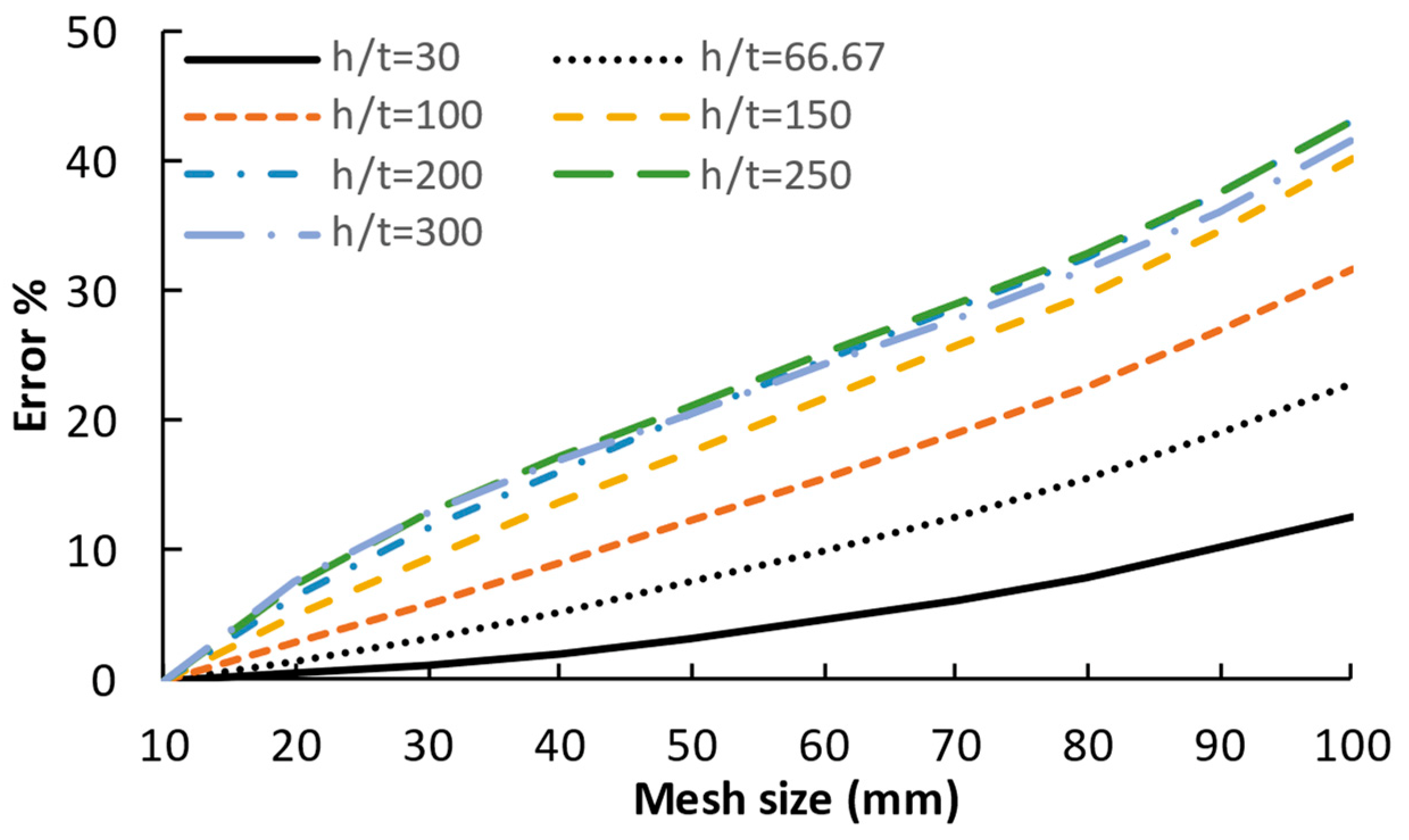
3.3. Mesh Size
4. Validation of the Finite Element Model
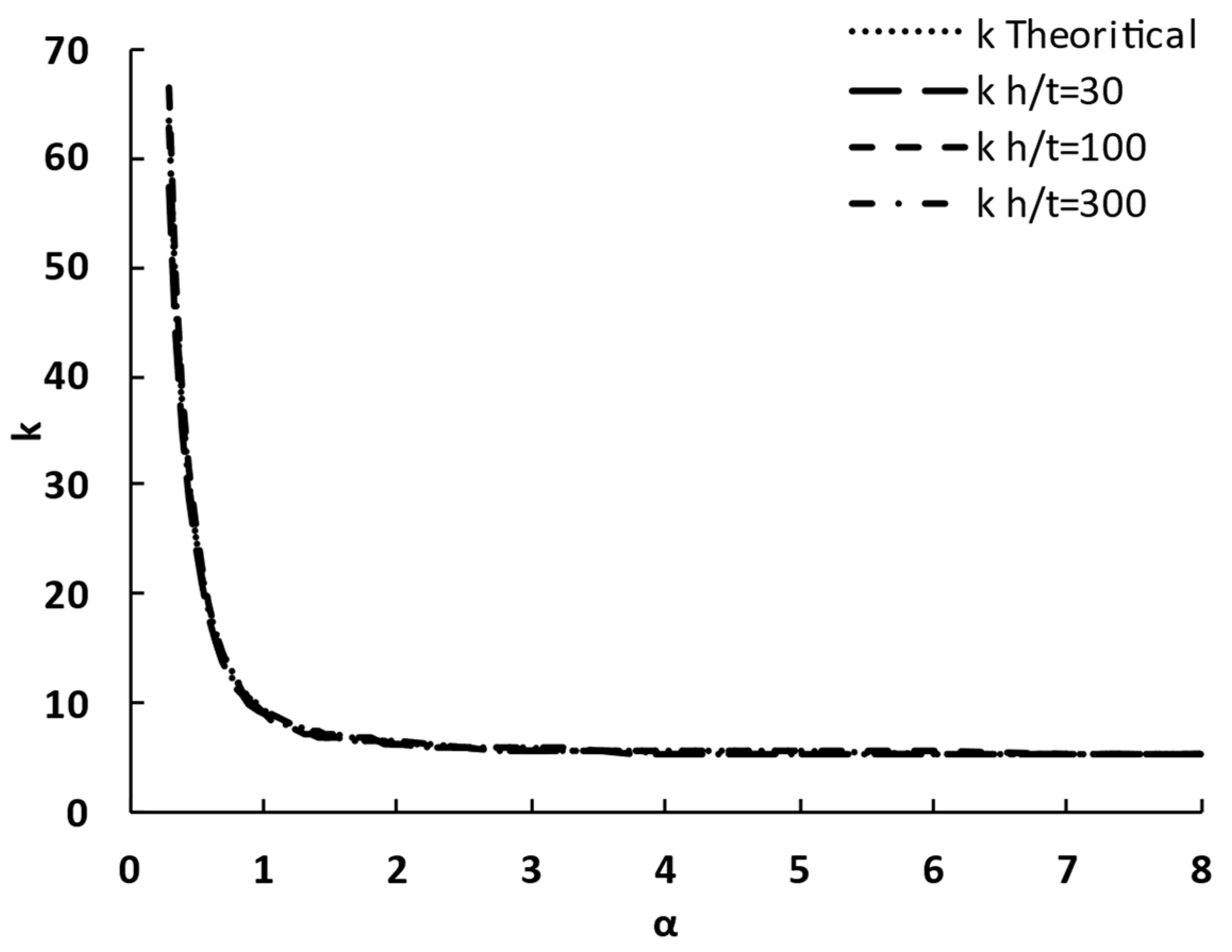
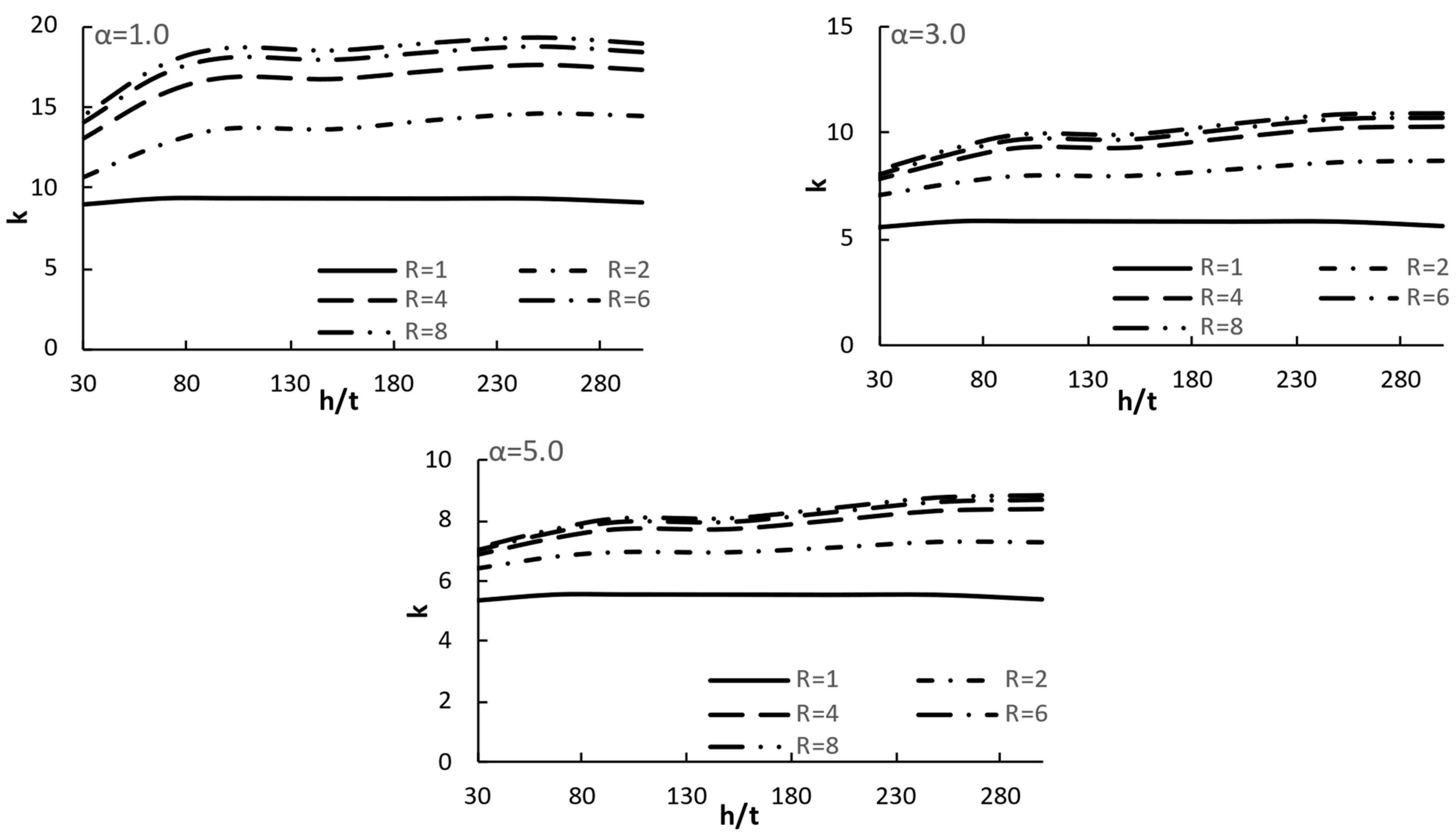
5. Parametric Study and Finite Element Results
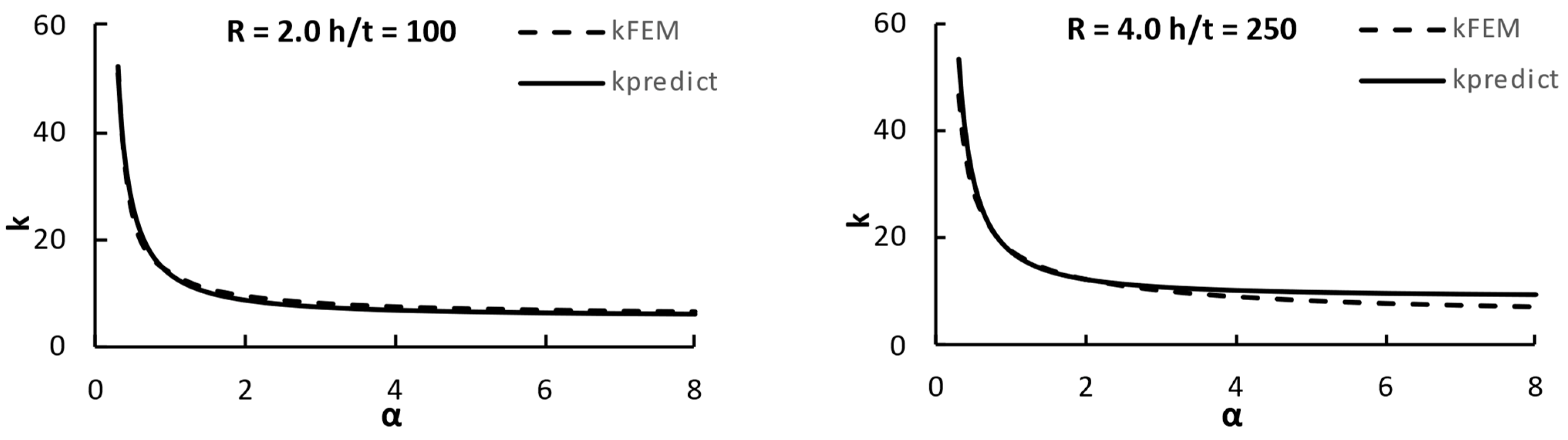
6. Proposed Formula for the Shear Buckling Coefficient
6.1. Development of the Proposed Formula
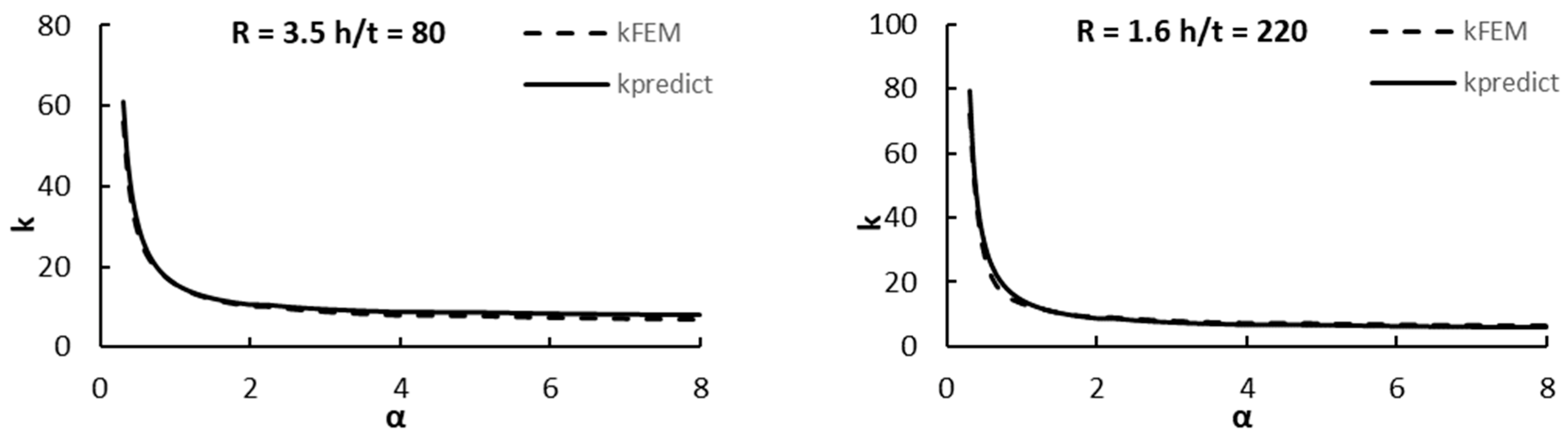
6.2. Validation of the Proposed Formula
- R = 3.5 and h/t = 80.
- R = 1.6 and h/t = 220.
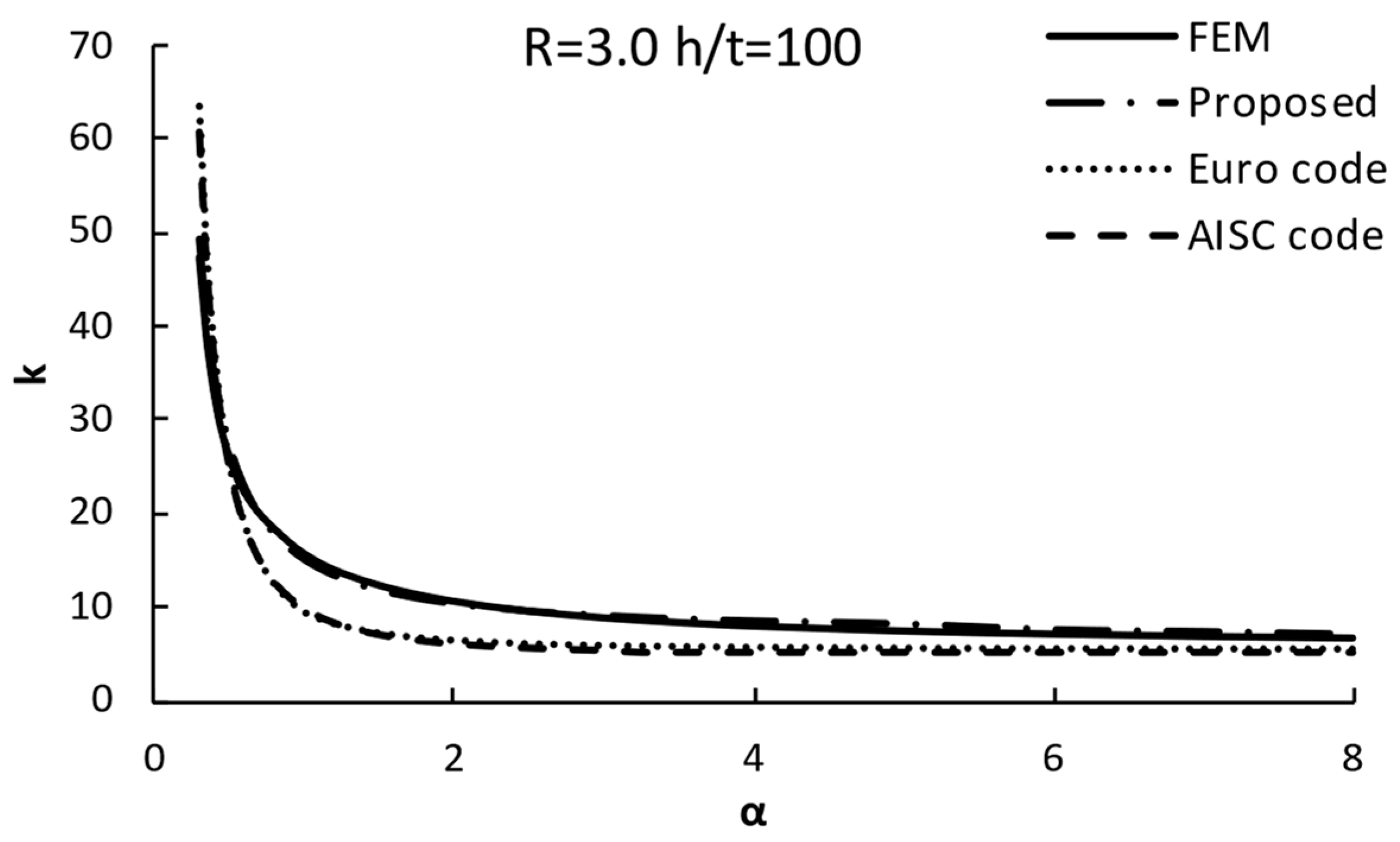
7. Comparisons with Current Code Formulas
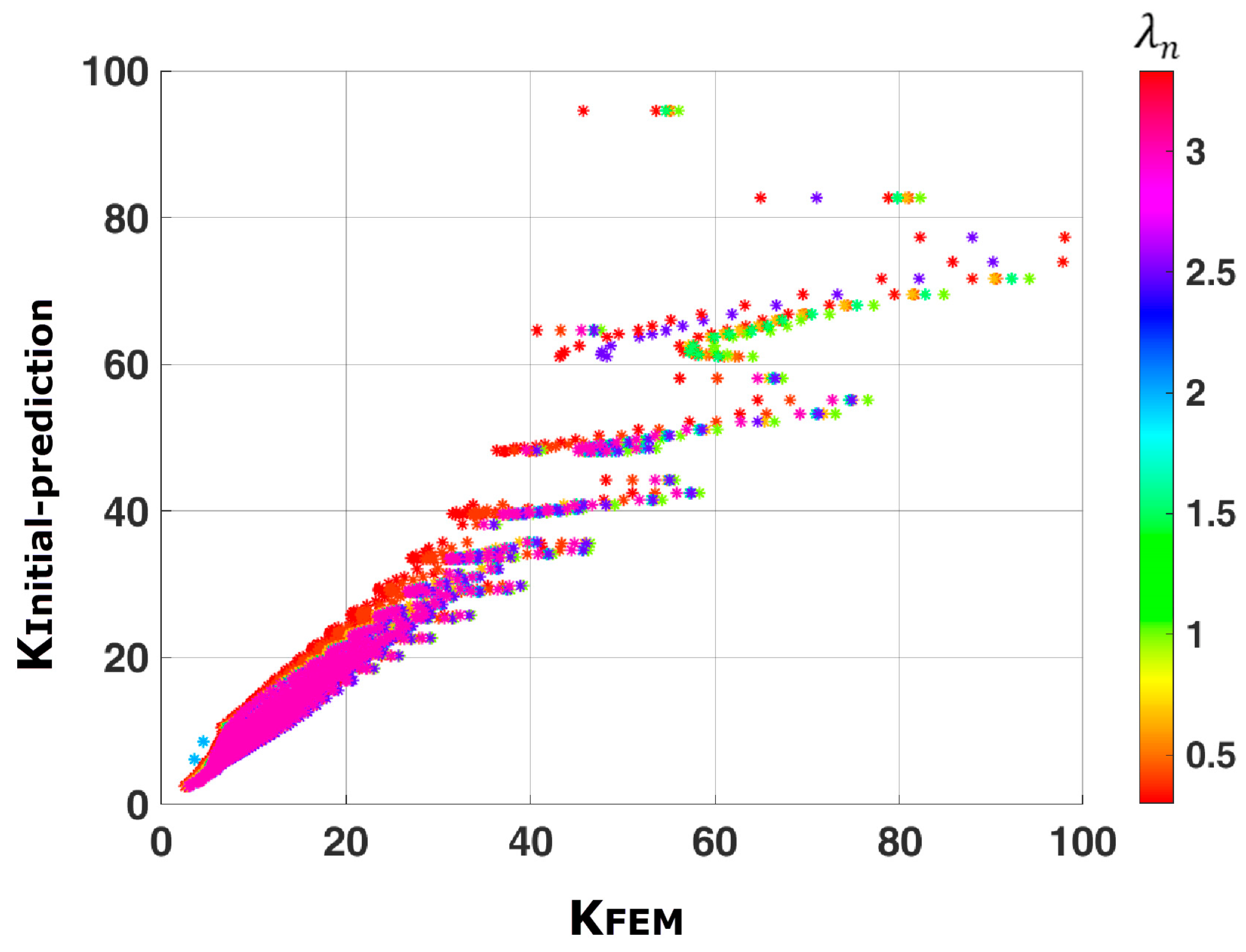
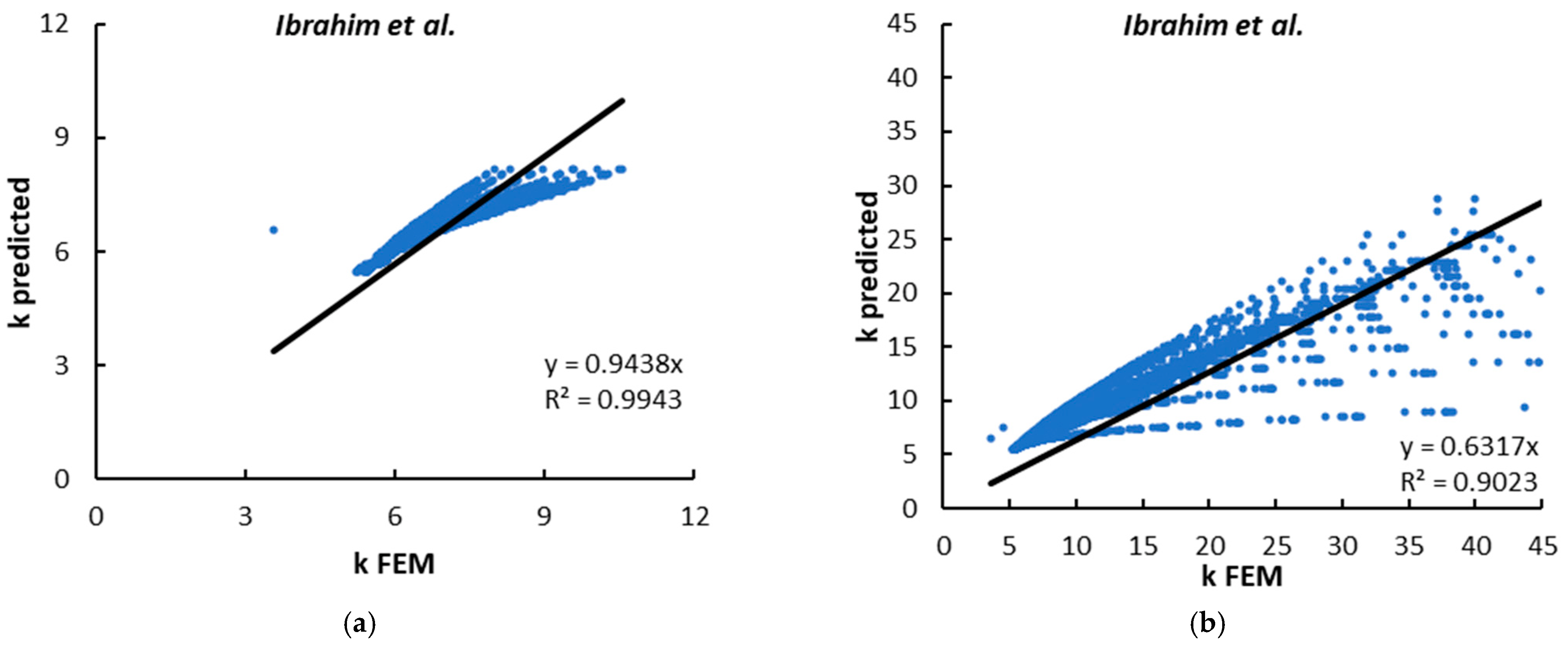
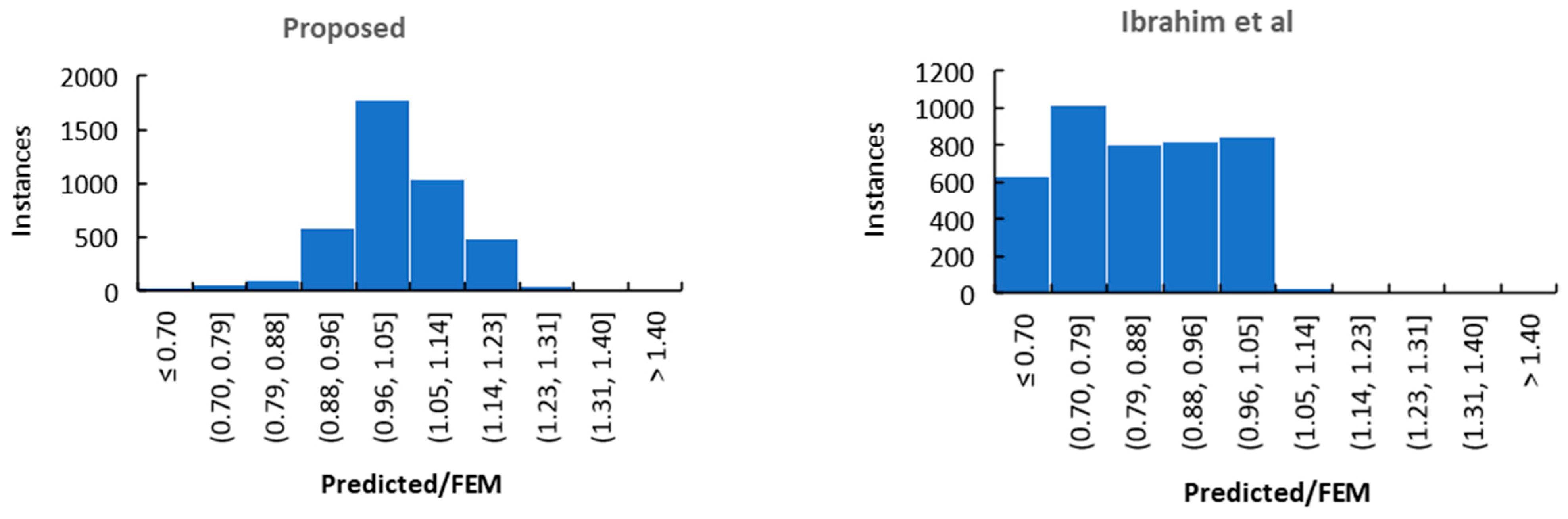
8. Comparisons with the Existing Model Proposed by Ibrahim et al. [26]
9. Conclusions
- Incorporating the impact of the slenderness ratio improves the prediction of the shear buckling coefficient, as the buckling coefficient exhibits sensitivity to slenderness variations. Further examination of this relationship for trapezoidal web plates is recommended.
- As the tapering ratio R increases, the stiffness in the smaller depth region becomes greater than the stiffness in the wider depth region and the geometry becomes closer to a triangle section. This, in turn, leads to an increase in the buckling coefficient. Meanwhile, at higher aspect ratios, the stiffening influence diminishes, likely indicating altered buckling modal behavior.
- The proposed shear buckling coefficient formula enables reliable critical shear buckling evaluation of prismatic webs, advancing design standards.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Plate length | |
| Flexural rigidity | |
| E | Elasticity modulus |
| Axial critical buckling stress | |
| Steel yield stress | |
| h | Larger width |
| Smaller width | |
| Shear buckling coefficient | |
| Shear buckling coefficient as suggested by Timoshinko and Gree | |
| Shear buckling coefficient as suggested by Ibrahim et al. | |
| Shear buckling coefficient according to AISC code | |
| Tapering ratio (h/h1) | |
| Plate thickness | |
| Flange thickness | |
| Standard deviation | |
| α | Aspect ratio (a/h) |
| λ | Slenderness ratio of the web (h/t) |
| normalized slenderness ratio . | |
| ν | Poisson’s ratio |
| Correction factor |
Appendix A


References
- Attaalla, S.A. Inelastic buckling strength of unsymmetrical tapered plates. Adv. Struct. Eng. 2002, 5, 165–171. [Google Scholar] [CrossRef]
- Abu-Hamd, M.; El Dib, F.F. Buckling strength of tapered bridge girders under combined shear and bending. HBRC J. 2016, 12, 163–174. [Google Scholar] [CrossRef]
- Bradford, M.; Azhari, M. Buckling of plates with different end conditions using the finite strip method. Comput. Struct. 1995, 56, 75–83. [Google Scholar] [CrossRef]
- Liang, Q.Q.; Uy, B.; Wright, H.D.; Bradford, M.A. Local buckling of steel plates in double skin composite panels under biaxial compression and shear. J. Struct. Eng. 2004, 130, 443–451. [Google Scholar] [CrossRef]
- Liang, Q.Q.; Uy, B.; Liew, J.Y.R. Local buckling of steel plates in concrete-filled thin-walled steel tubular beam–columns. J. Constr. Steel Res. 2007, 63, 396–405. [Google Scholar] [CrossRef]
- Shi, Y.; Xu, K.; Shi, G.; Li, Y. Local buckling behavior of high strength steel welded I-section flexural members under uniform moment. Adv. Struct. Eng. 2018, 21, 93–108. [Google Scholar] [CrossRef]
- Wan, J.; Cai, J.; Long, Y.-L.; Chen, Q.-J. Local buckling of rectangular concrete-filled steel tubular columns with binding bars under eccentric compression. Adv. Struct. Eng. 2020, 23, 2204–2219. [Google Scholar]
- Ahmed, M.; Tran, V.-L.; Ci, J.; Yan, X.-F.; Wang, F. Computational analysis of axially loaded thin-walled rectangular concrete-filled stainless steel tubular short columns incorporating local buckling effects. Structures 2021, 34, 4652–4668. [Google Scholar] [CrossRef]
- Ahmed, M.; Sheikh, M.N.; Hadi, M.N.S.; Liang, Q.Q. Nonlinear analysis of square spiral-confined reinforced concrete-filled steel tubular short columns incorporating novel confinement model and interaction local buckling. Eng. Struct. 2023, 274, 115168. [Google Scholar] [CrossRef]
- Kim, Y.D. Behavior and Design of Metal Building Frames Using General Prismatic and Web-Tapered Steel I-Section Members; Georgia Institute of Technology: Atlanta, GA, USA, 2010. [Google Scholar]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability; Courier Corporation: Chelmsford, MA, USA, 2009. [Google Scholar]
- Pope, G.G. The Buckling of Plates Tapered in Planform; Report No-3324; Ministry of Aviation: London, UK, 1962. [Google Scholar]
- Prawel, S.; Morrell, M.; Lee, G. Bending and buckling strength of tapered structural members. Weld. Res. Suppl. 1974, 53, 75–84. [Google Scholar]
- Bedynek, A.; Real, E.; Mirambell, E. Tapered plate girders under shear: Tests and numerical research. Eng. Struct. 2013, 46, 350–358. [Google Scholar] [CrossRef]
- Eurocode 3: Design of Steel Structures-Part 1-1: General Rules and Rules for Buildings. 2005. Available online: https://www.unirc.it/documentazione/materiale_didattico/599_2010_260_7483.pdf (accessed on 23 October 2023).
- Lee, S.C.; Davidson, J.; Yoo, C. Shear buckling coefficients of plate girder web panels. Comput. Struct. 1996, 59, 789–795. [Google Scholar] [CrossRef]
- Mirambell, E.; Zarate, A. Web buckling of tapered plate girders. Proc. Inst. Civ. Eng. Struct. Build. 2000, 140, 51–60. [Google Scholar] [CrossRef]
- Abu-Hamd, M.; Abu-Hamd, I. Buckling strength of tapered bridge girders under shear and bending. In Proceedings of the Annual Stability Conference, Pittsburgh, PA, USA, 10–14 May 2011. [Google Scholar]
- Abdelbaset, B.H. Evaluation of Shear Strength of Tapered Plate-Girder Web. Master’s Thesis, Cairo University, Cairo, Egypt, 2015. [Google Scholar]
- Sediek, O.A.; Safar, S.S.; Hassan, M.M. Numerical investigation on shear strength of tapered perfect end web panels. Structures 2020, 28, 354–368. [Google Scholar] [CrossRef]
- Sediek, O. Numerical Investigation on Shear Strength and Design Requirements of Tapered end Web Panels. Ph.D. Thesis, Cairo University, Cairo, Egypt, 2017. [Google Scholar]
- Serror, M.H.; Abdelbaset, B.H.; Sayed, H.S. Shear strength of tapered end web panels. J. Constr. Steel Res. 2017, 138, 513–525. [Google Scholar] [CrossRef]
- Studer, R.P.; Binion, C.D.; Davis, D.B. Shear strength of tapered I-shaped steel members. J. Constr. Steel Res. 2015, 112, 167–174. [Google Scholar] [CrossRef]
- AbdelAleem, B.H.; Ismail, M.K.; Haggag, M.; El-Dakhakhni, W.; Hassan, A.A. Interpretable soft computing predictions of elastic shear buckling in tapered steel plate girders. Thin-Walled Struct. 2022, 176, 109313. [Google Scholar] [CrossRef]
- AISC 360-22; Specification for Structural Steel Buildings. American Institute of Steel Construction: Chicago, IL, USA, 2022.
- Ibrahim, M.M.; El Aghoury, I.M.; Ibrahim, S.A.-B. Finite element investigation on plate buckling coefficients of tapered steel members web plates. Structures 2020, 28, 2321–2334. [Google Scholar] [CrossRef]
- Bedynek, A. Structural Behaviour of Tapered Steel Plate Girders Subjected to Shear; Polytechnic University of Catalonia, Barcelona Tech: Barcelona, Spain, 2014. [Google Scholar]
- Lee, S.C.; Lee, D.S.; Yoo, C.H. Ultimate shear strength of long web panels. J. Constr. Steel Res. 2008, 64, 1357–1365. [Google Scholar] [CrossRef]
- Monjezi, M.; Hasanipanah, M.; Khandelwal, M. Evaluation and prediction of blast-induced ground vibration at Shur River Dam, Iran, by artificial neural network. Neural Comput. Appl. 2013, 22, 1637–1643. [Google Scholar] [CrossRef]
- Ross, T.J. Fuzzy Logic with Engineering Applications; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Chern, C.; Ostapenko, A. Ultimate Strength of Plate Girders under Shear; Rep. No. 328.7; Fritz Laboratory Reports; Lehigh Univiversity: Bethlehem, PA, USA, 1969. [Google Scholar]
- Porter, D.M.; Rockey, K.C.; Evans, H.R. The collapse behaviour of plate girders loaded in shear. Struct. Eng. 1975, 53, 313–325. [Google Scholar]
- Sharp, M.L.; Clark, J.W. Thin aluminum shear webs. J. Struct. Div. 1971, 97, 1021–1038. [Google Scholar] [CrossRef]
- Shahin, R.I.; Ahmed, M.; Yehia, S.A.; Liang, Q.Q. ANN model for predicting the elastic critical buckling coefficients of prismatic tapered steel web plates under stress gradients. Eng. Struct. 2023, 294, 116794. [Google Scholar] [CrossRef]
- Bedynek, A.; Real, E.; Mirambell, E. Shear buckling coefficient: Proposal for tapered steel plates. Proc. Inst. Civ. Eng. Struct. Build. 2014, 167, 243–252. [Google Scholar] [CrossRef]
- Stein, M.; Neff, J. Buckling Stresses of Simply Supported Rectangular Flat Plates in Shear; NACA: Washington, DC, USA, 1947. Available online: https://ntrs.nasa.gov/api/citations/19930082111/downloads/19930082111.pdf (accessed on 23 October 2023).





| Parameter | Prismatic Parameter Values |
|---|---|
| Tapering ratio (R = h/h1) | 1–8 |
| Aspect ratio (α = a/h) | 0.30–8 |
| Web slenderness ratio | 30, 60, 100, 150, 200, 250, and 300 |
| Properties of steel material | modulus of elasticity E = 200 GPa |
| Poisson’s ratio ν = 0.3 |
| Boundary Conditions | Loading Conditions | Edges | Degrees of Freedom | |||||
|---|---|---|---|---|---|---|---|---|
| Ux | Uy | Uz | θx | θy | θz | |||
| Simply-Supported Edges | Pure shear loading | LS | 0 | 1 | 1 | 1 | 0 | 0 |
| SS | 1 | 0 | 1 | 1 | 0 | 1 | ||
| TS | 1 | 0 | 1 | 0 | 1 | 1 | ||
| BS | 1 | 0 | 1 | 0 | 1 | 1 | ||
| No. | h = h1 (m) | a (m) | α | Difference % | ||
|---|---|---|---|---|---|---|
| 1 | 1 | 0.3 | 0.3 | 63.33 | 66.42 | 4.88 |
| 2 | 1 | 0.4 | 0.4 | 37.38 | 38.38 | 2.68 |
| 3 | 1 | 0.5 | 0.5 | 25.36 | 26.5 | 4.5 |
| 4 | 1 | 0.6 | 0.6 | 18.83 | 19.1 | 1.43 |
| 5 | 1 | 0.7 | 0.7 | 14.9 | 14.82 | 0.53 |
| 6 | 1 | 0.8 | 0.8 | 12.34 | 12.19 | 1.24 |
| 7 | 1 | 0.9 | 0.9 | 10.59 | 10.5 | 0.92 |
| 8 | 1 | 1 | 1 | 9.34 | 9.36 | 0.17 |
| 9 | 1 | 1.2 | 1.2 | 8.12 | 8.01 | 1.36 |
| 10 | 1 | 1.3 | 1.3 | 7.71 | 7.6 | 1.34 |
| 11 | 1 | 1.4 | 1.4 | 7.38 | 7.31 | 0.98 |
| 12 | 1 | 1.5 | 1.5 | 7.12 | 7.09 | 0.38 |
| 13 | 1 | 1.6 | 1.6 | 6.9 | 6.93 | 0.36 |
| 14 | 1 | 1.7 | 1.7 | 6.72 | 6.8 | 1.19 |
| 15 | 1 | 1.8 | 1.8 | 6.57 | 6.71 | 2.03 |
| 16 | 1 | 1.9 | 1.9 | 6.45 | 6.63 | 2.84 |
| 17 | 1 | 2 | 2 | 6.34 | 6.57 | 3.56 |
| 18 | 1 | 3 | 3 | 5.78 | 5.86 | 1.26 |
| 19 | 1 | 4 | 4 | 5.59 | 5.64 | 0.91 |
| 20 | 1 | 5 | 5 | 5.5 | 5.55 | 0.84 |
| 21 | 1 | 6 | 6 | 5.45 | 5.49 | 0.8 |
| 22 | 1 | 7 | 7 | 5.42 | 5.46 | 0.63 |
| 23 | 1 | 8 | 8 | 5.4 | 5.43 | 0.51 |
| (α = a/h) | 2.2 | 2.4 | 2.6 | 2.8 | 3.0 | 3.2 |
|---|---|---|---|---|---|---|
| Stein et al. [36] | 6.3 | 6.15 | 6.04 | 5.97 | 5.92 | 5.88 |
| 6.29 | 6.10 | 5.97 | 5.89 | 5.84 | 5.80 | |
| Difference% | 0.16 | 0.81 | 1.16 | 1.34 | 1.35 | 1.36 |
| Beam | Test Results | FEM Proposed | Difference |
|---|---|---|---|
| (kN) | (kN) | % | |
| T600/800L800 × 3.9 − 180 × 15 | 225 | 228.4 | 1.51 |
| T500/800L1200 × 3.9 − 180 × 15 | 220 | 216.60 | 1.55 |
| T480/800L800 × 3.9 − 180 × 15 | 265 | 265.00 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahin, R.I.; Ahmed, M.; Yehia, S.A. Elastic Buckling of Prismatic Web Plate under Shear with Simply-Supported Boundary Conditions. Buildings 2023, 13, 2879. https://doi.org/10.3390/buildings13112879
Shahin RI, Ahmed M, Yehia SA. Elastic Buckling of Prismatic Web Plate under Shear with Simply-Supported Boundary Conditions. Buildings. 2023; 13(11):2879. https://doi.org/10.3390/buildings13112879
Chicago/Turabian StyleShahin, Ramy I., Mizan Ahmed, and Saad A. Yehia. 2023. "Elastic Buckling of Prismatic Web Plate under Shear with Simply-Supported Boundary Conditions" Buildings 13, no. 11: 2879. https://doi.org/10.3390/buildings13112879
APA StyleShahin, R. I., Ahmed, M., & Yehia, S. A. (2023). Elastic Buckling of Prismatic Web Plate under Shear with Simply-Supported Boundary Conditions. Buildings, 13(11), 2879. https://doi.org/10.3390/buildings13112879








