Next Article in Journal
Investigation of Real Estate Tax Leakage Loss Rates with ANNs
Previous Article in Journal
Concrete Modification for Hot Weather Using Crushed Dolomite Stone
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Buildings
Volume 13
Issue 10
10.3390/buildings13102463
buildings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Research on the Distributive Relationship between Bond Force and Bearing Pressure for Anchorage Force by Headed Bars

by
Tianming Miao
1,
Jian Yang
1,
Ying Zhou
1,
Meiqiu Zhan
1,
Lirong Sha
1,* and
Wenzhong Zheng
2,3,4
1
School of Civil Engineering, Jilin Jianzhu University, Changchun 130118, China
2
School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China
3
Key Lab of Structures Dynamic Behavior and Control Ministry of Education, Harbin Institute of Technology, Harbin 150090, China
4
Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters of the Ministry of Industry and Information Technology, Harbin Institute of Technology, Harbin 150090, China
*
Author to whom correspondence should be addressed.
Buildings 2023, 13(10), 2463; https://doi.org/10.3390/buildings13102463
Submission received: 1 September 2023 / Revised: 23 September 2023 / Accepted: 26 September 2023 / Published: 28 September 2023
(This article belongs to the Section Building Structures)
Browse Figures
Versions Notes

Abstract

:
Anchorage force comprises bond force and bearing pressure when headed bars are used. Pull-out tests were conducted on 120 concrete specimens to derive a method for calculating the bond force for reinforcement in straight anchor sections at the yield moment. The parameters include the diameter d, embedded length lae, and yield strength fy of the reinforcement, as well as the strength grade of the concrete fcg. The experimental results indicated that the specimens underwent three failure modes depending primarily on the embedded length lae. The nominal average bond stress τu concept was proposed and the difference between τu and the actual average bond stress τ caused by the headed bars was observed. To reduce the difference between the τu and τ values, the correction coefficient γ was proposed. Analysis indicated that γ increased with an increase in the lae/d (on average, 146% higher than the initial value) and decreased with an increase in the fy/ft (on average, 33% less than the initial value). A formula was developed to calculate γ, and the bond force in the straight anchor sections at the yield moment for the reinforcement was determined. Thus, a distributive relationship was established for the anchorage force, the bond force, and the bearing pressure.

1. Introduction

High-strength reinforcements have recently emerged as a prominent development trend in the construction industry. It is difficult to achieve reliable and effective anchorage when reinforcements with a higher strength and larger diameter are used in concrete structures. The interweaving of the primary and bending reinforcements leads to congestion in the beam–column joint reinforcement arrangement and affects the quality of concrete casting at the joint. Installing headed bars at the end of the reinforcement significantly reduces the anchorage length and resolves interweaving issues to ensure high-quality concrete pouring [1,2,3,4,5,6,7]. Research on reinforcements using headed bars began in the 1960s [8]. Nelson Stud was the first to test the anchorage performance of headed bars, which were later used by a welding company and Lehigh University in the connection between a concrete slab and steel beams. Since then, great progress has been made, and fruitful results have been achieved in this field.
To ensure adequate shear transfer, appropriate connection systems are required for the joints of precast reinforced concrete structures. However, conventional connection methods for precast components are susceptible to damage under seismic loads. To address this issue, Singhal et al. conducted an experimental investigation on a connection system using headed bars. They investigated the anchorage behaviours of the reinforcements with headed bars based on different failure modes, changes in the bond force, and slip values. The test results showed that precast reinforced concrete wall–column connections using headed bars performed significantly better than dowel bar connections [9,10]. To evaluate the effectiveness of T-headed bars as shear reinforcements, Yang et al. conducted 12 tests. Their findings showed that the specimens reinforced with T-headed bars exhibited higher shear strength than those reinforced with conventional stirrups. This observation indicates that T-headed bars have the potential to replace traditional reinforcements [11]. To investigate the impact of joint concrete strength, transverse reinforcement, geometric shape, and out-of-plane tolerance on joint performance, Vella et al. conducted a series of tensile and bending tests on joints featuring headed bars. The reinforcement had a diameter of 25 mm, and the headed bars were square-shaped with a side length of 70 mm. Based on both experimental and numerical results, a design procedure for headed bar joints was established using a model incorporating struts and tie rods [12,13,14].
Headed bars could also be used to reinforce structural members, such as beam–column joints. Paknejadi et al. investigated the anchorage performance of beam–column joints in steel fibre-reinforced concrete using headed bar reinforcement. Their results indicated that headed bars with higher anchorage capacity, better ductility, and good stiffness response could significantly replace conventional reinforcements [15]. Chiu et al. identified six potential failure mechanisms for headed bars embedded in concrete under tensile loads. These mechanisms were reinforcement yield or fracture, bar-to-head connection failure, pull-out failure, concrete breakout failure, side-face blowout failure (SBF), and splitting failure. Experiments were conducted to prevent the occurrence of SBF, which is a critical failure mode. The test results and finite element analysis showed that when the diameter of the headed bar embedded in external beam–column joints was not larger than 35 mm, the minimal net concrete cover could be reduced to the diameter multiplied by 1.5 [16]. Chun and Lee assessed the contribution of headed bars to the anchorage force in external beam–column joints, specifically in the bearing and bond components. They found that the bearing components of the headed bars remained consistent, regardless of their embedded length [17,18,19,20,21]. However, further investigations have been conducted on the relationship between the bond stress and bond slip. Eligehausen et al. developed a constitutive model that included a power function in the rising section and a peak platform based on the analysis on the pull-out test data [22]. This model was ultimately adopted by the CEP-FIP Model Code 2010 [23]. Xu et al. proposed a segmented constitutive model that was in excellent agreement with the measured data, and this model was adopted by the GB50010-2010 Code in China for the design of concrete structures [24,25,26,27].
While some studies have examined headed bars and bonding properties, insufficient attention has been given to the relationship between bond force and bearing pressure. This study addressed this gap by restricting the minimum embedded length and bearing area of the headed bars. However, these restrictions resulted in a longer anchorage length of the reinforcement and a larger bearing area of the headed bars.
Specific standards for headed bars are provided by JGJ 256-2011 (technical specification for the application of headed bars) [28], as follows:
(1)
when using a partial anchorage head for the rebar, the bearing area of the headed bars must be at least nine times as large as the sectional area of the reinforcement;
(2)
when using the full anchorage head for the rebar, the bearing area of the headed bars must be at least 4.5 times as large as the sectional area of the reinforcement, and the reinforcement’s nominal diameter must not exceed 40 mm;
(3)
the thickness of the headed bars should not be less than the nominal reinforcement diameter.
A partial anchorage head refers to a reinforcement bond that partially bears the anchorage force, whereas a full anchorage head indicates that no reinforcement bond bears the anchorage force. These specific standards lead to the inefficient use of resources and can create complications due to overly detailed regulations. If the requirements are not fulfilled, the corresponding inspection methods are not provided. To address this, it is essential to determine the distributive relationship between the bond force and bearing pressure when headed bars are used. Understanding this relationship makes it possible to select appropriate dimensions for the headed bars and an appropriate embedded length for the reinforcement.
This study conducted a total of 120 pull-out tests to address this issue. The influences of the diameter d, embedded length lae, yield strength fy, of the reinforcement, and strength grades of the concrete, fcg were studied. This study established a method for calculating the bond force in straight anchor sections at the yield moment of the reinforcement. This method determined the distributive relationship between the bond force and bearing pressure, shifting the design concept of headed bars from passive checking to active selection.

2. Experimental Program

2.1. Design of the Specimens

A total of 120 concrete specimens with headed bars were prepared according to GB50010-2010. The cross-sectional dimensions of the pull-out specimens were 150 mm × 150 mm, and the longitudinal reinforcement consisted of headed bars positioned at the centroid of the section. HRB500 and HRB600 high-strength reinforcements were selected as the longitudinal reinforcements in the test, and the diameters d were 20, 22, and 25 mm. The various diameters d correspond to different sizes of the headed bars, with dimensions of 40 mm × 40 mm × 16 mm, 45 mm × 45 mm × 16 mm, and 50 mm × 50 mm × 16 mm. Perforated plug welding was utilised to join the reinforcement and headed bars, enabling them to function in unison. In addition, four HPB300 bars with a diameter of 8 mm were used as erection reinforcements to facilitate construction. The stirrup in the concrete specimen was made of an HPB300 steel bar with an 8 mm diameter and a stirrup spacing of 100 mm. In addition, the protective layer thickness c in this study is the distance from the longitudinal reinforcement to the outermost edge of the specimen. Figure 1 shows a representative specimen.
According to GB50010-2010, when the yield strength of the reinforcement fy is at least 400 MPa, the concrete strength grade fcg must not be lower than C25 [24]. The concrete strength grades used in the tests ranged from C30 to C70 and tests included five distinct concrete strength grades. Concrete strength grades ranged from C30 to C60 when HRB500 longitudinal reinforcing bars were used, and from C40 to C70 when HRB600 longitudinal reinforcing bars were used. The specimens were classified into 24 groups based on their identical reinforcement yield strength fy, reinforcement diameter d, and concrete strength grade fcg. Each group consisted of five specimens with different embedded lengths lae. The embedded lengths were calculated based on different ratios to the basic embedded length lab. The basic embedded length of the reinforcement lab was calculated according to Equation (1) in the code for the design of concrete structures (GB50010-2010).
l a b = α f y f t d
The groups and numbers of specimens are listed in Table 1, where β is the ratio of the embedded length lae to the basic embedded length lab. When the reinforcement was HRB500, the diameter of reinforcement was 20 mm, and the concrete strength grade was C30, the group would be named “500-20-30”. The specific specimens were named by adding the embedded length based on the group, such as “500-20-30-140”. The naming principles and numbers for the other groups were the same.

2.2. Properties of Materials

Five specimens from each group were cast in the same batch. Nine concrete cubes with side lengths of 100 mm were used in each group. When the concrete strength grade was C60 or C70, at least three additional concrete cubes with a side length of 150 mm were included. The materials used in this study were silica sand with a mean particle size of 225 µm, Portland cement with a Blaine specific surface area of 4500 cm2, condensed silica fume, slag powder, and crushed stone with a max particle size of 30 mm. The SF had an amorphous SiO2 content of 97.2% and its mean particle size was about 0.1–0.15 µm. Table 2 lists the mix proportions of the concrete, while Table 3 shows the mechanical properties of the concrete, including ft,m derived from fc,m according to the specifications in the GB50010-2010 code for the design of concrete structures. The mechanical properties of HRB500 and HRB600 reinforcements are listed in Table 4.

2.3. Loading and Measurement Scheme

Pull-out tests were performed using a universal testing machine. The pull-out test setup is illustrated in Figure 2. The loading frame in Figure 2a consists of two square steel plates with a 50 mm thickness and a 400 mm side length. Four 8.8-grade high-strength screws with a diameter of 22 mm and matching nuts were used to assemble the loading frame, and the centre of the two square steel plates was provided with a 40 mm diameter round hole. The loading frame is shown in Figure 2b.
Prior to the formal loading, preloading was conducted to ensure the proper functioning of the instrument. The loading process consisted of two stages. In the first stage, the loading rate was controlled according to the load, until the tensile yield of the reinforcement was reached, at a loading rate of 0.15 kN/s. In the second stage, the loading rate was controlled according to the displacement, until the end of the test, at a rate of 1 mm/min. To obtain the strain variations rule for the reinforcement in the straight anchor section, a 4 mm × 4 mm groove was milled along the longitudinal reinforcement, and 1 mm × 2 mm strain gauges were arranged at a spacing of 30 mm. Finally, the grooves were sealed with planting glue. Figure 3 illustrates the arrangement of the strain measurement points.
Based on the number of strain gauges shown in Figure 3, the value of strain gauge 1 indirectly reflected the value of the load applied to the loading end of the reinforcement. i would indirectly reflect the load values of the headed bars. The bond force between the reinforcement and concrete in the straight anchor section can be calculated from the difference between the values of strain gauges 1 and i.

3. Experimental Phenomenon

By observing the test phenomenon, it was found that the bond stress between the reinforcement and concrete always existed before the reinforcement yielded. The presence of the headed bars in the reinforcement limited the slip at the free end. Therefore, most of the bond stresses in the straight anchor section did not reach the ultimate bond stress in the bond–slip constitutive model. Based on Xu’s results, the embedded length lae was divided by the diameter d to create a dimensionless parameter for studying the effect of the relative embedded length lae/d on the observed phenomenon. The average bond stress varied depending on the embedded length, suggesting that altering the relative embedded length lae/d led to distinct failure modes, as demonstrated by the test results.

3.1. First Failure Mode of the Specimen

When the embedded length of the reinforcement lae was short, cracks appeared on the specimen surface and continued to develop as the load increased. These cracks were categorised as transverse and longitudinal ones. Longitudinal cracks emerged at the loading end of the specimen and progressed towards the free end, while transverse cracks appeared at the edge of the specimen and progressed towards its interior. As the load increased, a concrete wedge formed under the headed bars. The test was stopped when the displacement of the headed bars increased, and the load correspondingly decreased, resulting in serious damage to the specimen. For example, the cracks that occurred in the concrete specimen with the identification number No. “500-20-30-180” when the reinforcement yielded are shown in Figure 4a, and when the reinforcement fractured, in Figure 4b.
The smaller the embedded length lae, the larger the average bond stress between the reinforcement and concrete. The radial tensile stress caused by the average bond stress was relatively large. As the radial tensile stress surpassed the tensile strength of the concrete, cracks initially emerged at the loading end of the specimen. With a gradual increase in the radial tensile stress, a longitudinal crack developed towards the free end of the specimen. However, a smaller embedded length lae would cause a larger bearing pressure. The bearing effect of the headed bars primarily bore the anchorage force. The splitting effect of the bearing pressure aggravated the development of the longitudinal crack, leading to its propagation throughout the entire specimen upon fracture. Meanwhile, transverse cracks were caused by compressive strains in the concrete under the headed bars, as well as transverse expansion of the specimen, causing transverse cracks at the edge of the specimen. This failure mode was mainly concentrated in the specimens with β ≈ 0.3 and β ≈ 0.4.

3.2. Second Failure Mode of the Specimen

When the embedded length of the reinforcement lae was long, longitudinal cracks appeared at the loading ends of the specimens, and as the load increased, longitudinal cracks developed towards the free end. Despite the loading and fracture of the longitudinal reinforcement, crack development was slow, and only a few new cracks were created, failing to penetrate the entire specimen. Taking No. “600-20-40-320” concrete specimen as an example, the cracks of the specimen when the reinforcement yielded are shown in Figure 5a, and the cracks of the specimen when the reinforcement fractured are shown in Figure 5b.
The increased embedded length lae resulted in a higher bond force between the reinforcement and concrete. The slip between the reinforcement and concrete at the loading end increased as the load increased. At this point, the radial tensile stress exceeded the tensile strength of the concrete, resulting in longitudinal splitting cracks. The anchorage force was then transmitted along the reinforcement to the free end of the specimen. As the distance from the loading end increased, the slip between the reinforcement and the concrete decreased gradually, and lower bond stresses came with smaller slip values. Due to the insufficient radial tensile stress caused by the bond stress, significant concrete cracking did not develop. However, an increase in the embedded length lae decreased the bearing pressure of the headed bars. Thus, the anchorage force was mainly sustained by the bond force between the reinforcement and the concrete. Any longitudinal or transverse cracks resulting from the bearing pressure of the headed bars remained inconspicuous. Only longitudinal cracks were observed in the specimens, and this failure mode was mainly concentrated in specimens with β ≈ 0.7.

3.3. Third Failure Mode of the Specimen

When the embedded length of the reinforcement lae fell within the aforementioned range, the pattern of crack development was similar to that of the initial failure mode. The cracks primarily developed in the longitudinal and transverse directions. The difference was that the transverse cracks developed slowly before the reinforcement yielded but became more obvious after yielding. However, longitudinal cracks only developed before the reinforcement yielded and progressed more slowly after yielding occurred. Consequently, the longitudinal cracks tended to penetrate the specimen. Taking No.“600-25-50-240” concrete specimen as an example, Figure 6a shows the cracks of the specimen when the reinforcement yielded, while Figure 6b shows the cracks of the specimen when the reinforcement fractured.
The embedded length lae and the average bond stress were moderate. Longitudinal cracks appeared at the loading end and developed towards the free end as the load increased. However, as the reinforcement was pulled, the anchorage force was gradually borne by the bearing pressure of the headed bars, which resulted in the production of longitudinal split cracks. The development of cracks extended significantly between the loading and free ends, owing to the superposition of the longitudinal cracks at both ends. In addition, transverse cracks were observed at the edge of the specimen, owing to the bearing pressure of the headed bars. This failure mode was mainly concentrated in the specimens with β ≈ 0.5 and β ≈ 0.6.

4. Results and Analysis

4.1. Results of Pull-Out Tests

When the longitudinal reinforcement was stressed, the anchorage force Fy was shared by the bond force between the reinforcement and concrete Fb and the bearing pressure of the headed bars Fp. According to the strain gauge numbering principle, Fb can be determined as the difference between Fy and Fp. The specific measured data for the reinforcement anchorage force Fy, the bond force Fb, and the bearing pressure Fp of each specimen when the longitudinal reinforcement at the loading end yielded are listed in Table 5.
Based on Figure 7, the average bond stress τ was computed as the anchorage force Fy divided by the initial surface area of the embedded portion of the reinforcement, as follows:
τ = F y π d l a e
In Equation (2), Fy denotes the anchorage force of the reinforcement. To ensure that the reinforcement reached its yield strength, Fy was set to fyAs, with As being the cross-sectional area of the reinforcement, where lae is equal to βlab. These values are substituted into Equation (2) to derive Equation (3) as follows:
τ = f y A s π d β l a b
Based on the superposition of Equations (1) and (3), the calculation formula for the average bond stress is derived as follows:
τ u = f t 4 α β
In the theoretical derivation, fyAs was introduced above. Moreover, since the actual embedded length of the reinforcement lae was less than the basic embedded length lab, the reinforcement could not reach its yield strength fy when the embedded length was lae. The results calculated using Equation (4) represent the theoretical value τu. However, in this study, the reinforcement could reach its yield strength fy owing to the existence of headed bars, which could share part of the anchorage force. In addition, the headed bars limited the slip value of the free end of the reinforcement. Hence, when the reinforcement yields at the loading end, and the slip value at the free end is limited to 0, the average bond stress is defined as the nominal average bond stress τu and the formula is given in Equation (4). Notably, according to GB50010-2010, the shape factor of the reinforcement α in Equation (4) was set to 0.14.

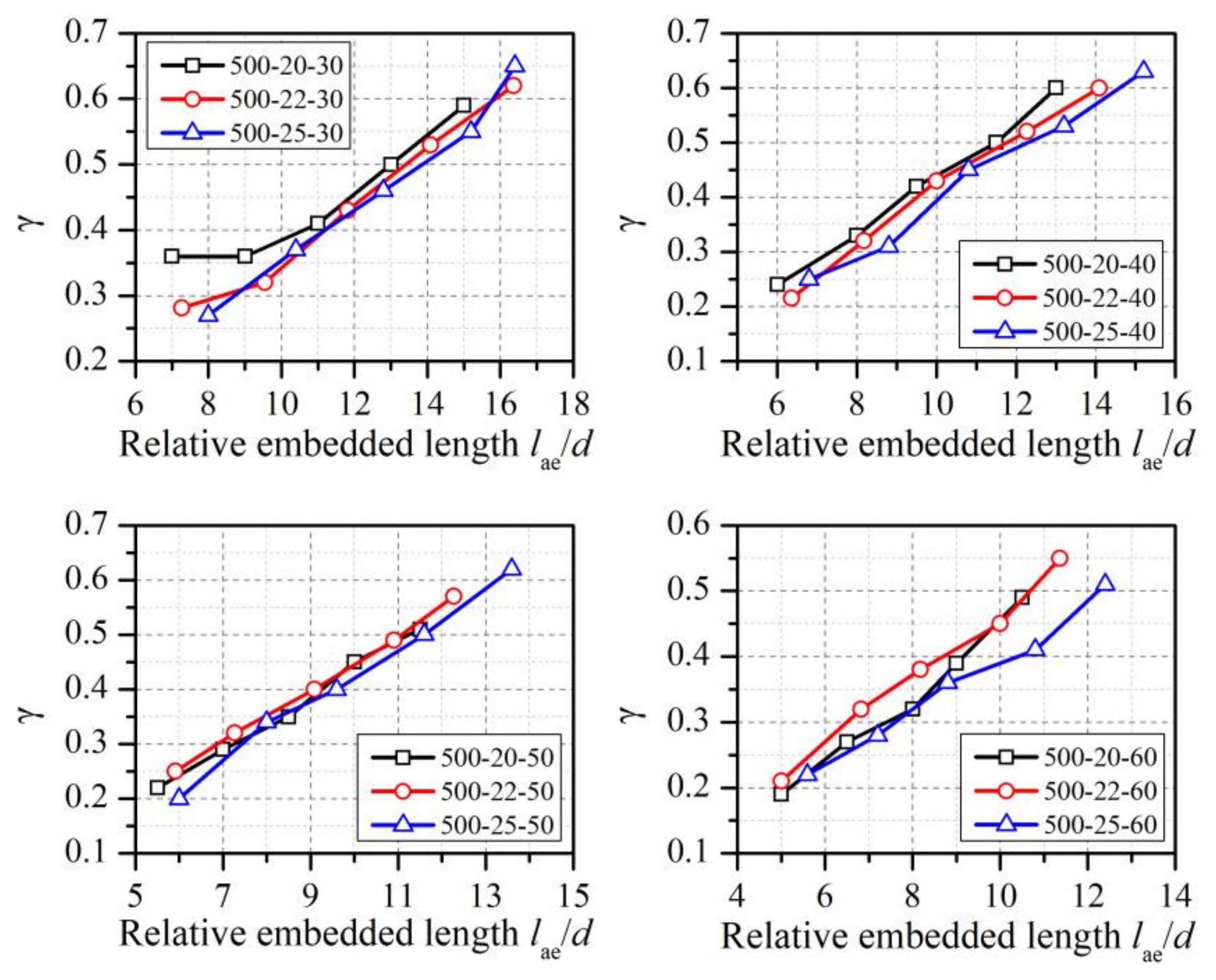
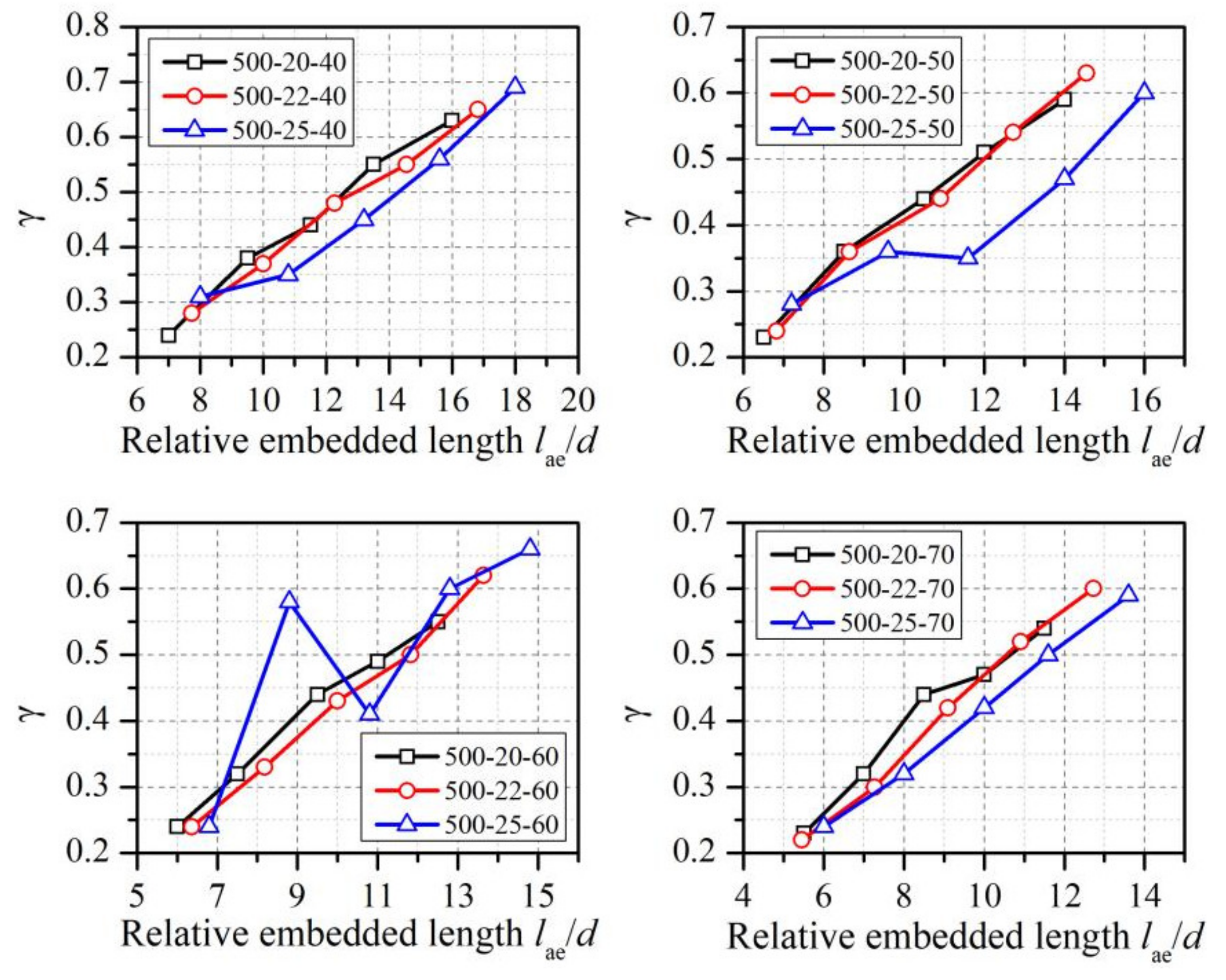
4.2. Analysis of the Influencing Parameters on γ

From the analysis, it can be inferred that there is a certain disparity between the nominal average bond stress τu and the actual average bond stress τ owing to the presence of headed bars. Therefore, a correction coefficient γ was introduced to modify the nominal average bond stress τu.
The correction coefficient γ is the ratio of the actual average bond stress τ to the nominal average bond stress τu, which could reflect the gap caused by the headed bars. Therefore, any factors that affect the bearing pressure of the headed bars Fp would also affect the value of γ.

4.2.1. Effect of the Relative Embedded Length lae/d

The embedded length lae significantly affects the bearing pressure of the headed bar Fp. The bond force between the reinforcement and concrete in the straight anchor section Fb increased proportionally with the embedded length lae. As the embedded length lae increased, the bearing pressure of the headed bars Fp decreased. This lower bearing pressure can result in a closer actual average bond stress τ to the nominal average bond stress τu. Therefore, the value of γ would positively correlate with an increase in the embedded length lae. The influence of the relative embedded length lae/d on γ was analysed under the same diameter d of the reinforcement, concrete strength grade fcg, and reinforcement tensile strength fy as conditions, and the results are presented in Figure 8 and Figure 9.
As shown in Figure 8 and Figure 9, the influence of the diameter d was limited when lae/d remained constant. Additionally, the coefficient γ increased linearly with the relative embedded length lae/d for a given reinforcement diameter d, concrete strength grade fcg, and reinforcement tensile strength fy.

4.2.2. Effect of fy/ft

The tensile strength of the concrete ft is also a crucial parameter for determining the bearing pressure of the headed bars Fp. The bond force between the reinforcement and the concrete Fb decreased with the decrease in the tensile strength of the concrete ft. The decrease in the tensile strength of the concrete ft led to an increase in the bearing pressure of the headed bars Fp. A higher bearing pressure resulted in a greater distance between the actual average bond stress τ and the nominal average bond stress τu, leading to a decrease in the value of γ with the increase in the fy/ft. To analyse the influence of fy/ft on γ under the same diameter d of the reinforcement, the same reinforcement tensile strength fy, and the similar embedded length of the headed bars lae, the test data were fitted, and the results are shown in Figure 10. The maximum discrepancy in the embedded length lae was 20 mm, which was approximated as negligible.
The analysis showed that increases in fy/ft led to similar decreases in γ according to the diameter d of the reinforcement, the reinforcement tensile strength fy, and the embedded length of the headed bars lae. Furthermore, this relationship exhibited approximate linearity.
γ would increase with the increase in lae/d and decrease with the increase in fy/ft when the concrete strength classes were C30–C70, the longitudinal reinforcement was HRB500 or HRB600, and the reinforcement embedded lengths lae were 0.3–0.7 lab. After fitting the curve with a linear equation, the R2 value was 0.916, indicating that the linear formula fit was highly accurate.
Thus, by considering lae/d and fy/ft as independent variables in the test data, Equation (5) is obtained for γ after fitting the curve.
γ = 4.38 × 10 − 2 l a e d − 1.5 × 10 − 3 f y f t + 0.2038
The test value of γ was obtained and compared to the values of γ5 listed in Table 6. In the table, μ is the ratio of the test value to the calculated value γ5 (obtained using Equation (5)). The average value μ, standard deviation, and the coefficient of variation were 0.999, 0.105, and 0.105, respectively.
Figure 11 shows the fitting results when lae/d and fy/ft are the independent variables and γ is the dependent variable.

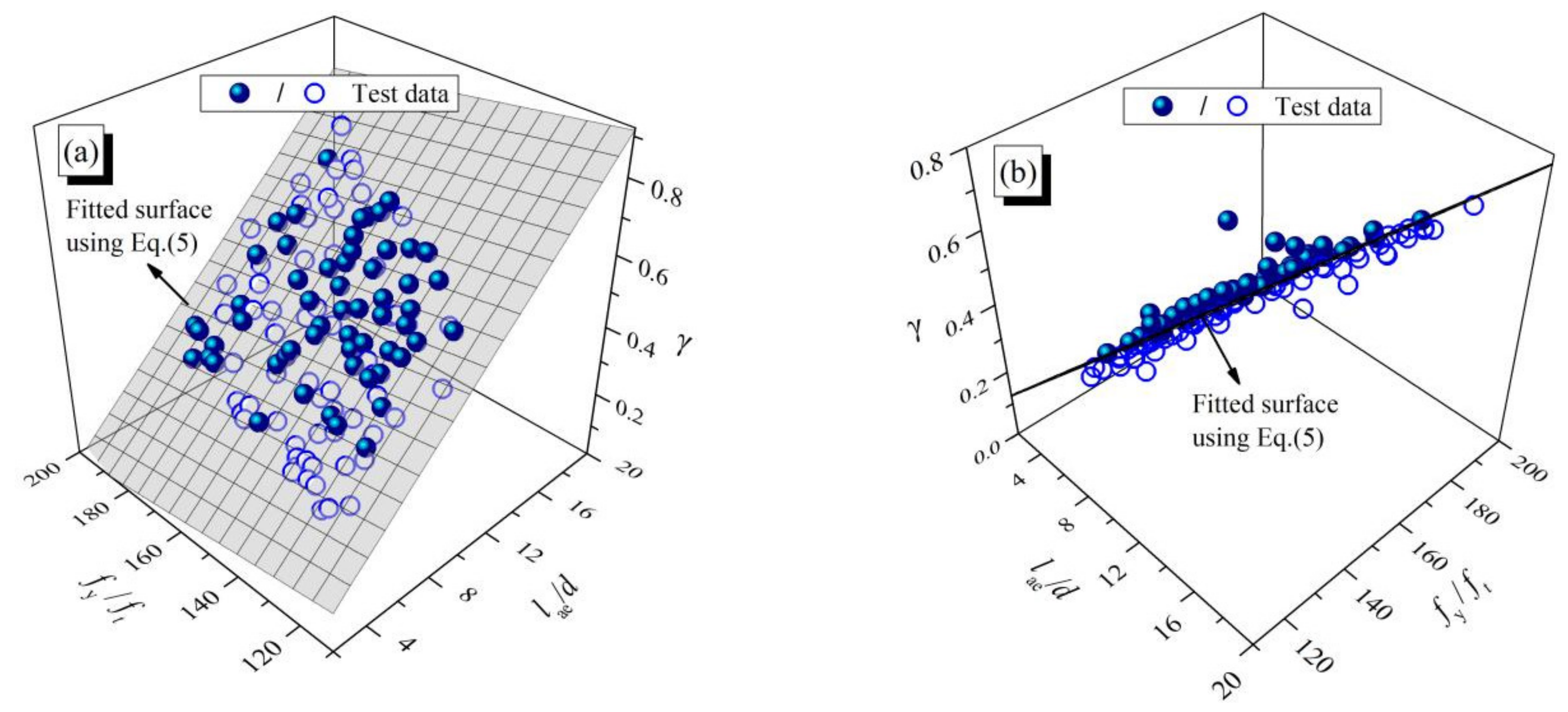
4.3. Determination of the Distributive Relationship

To calculate the bond force between the reinforcement and the concrete Fb, the actual average bond stress τ needs to be determined.
The actual average bond stress τ can be obtained based on the superposition of Equations (4) and (5), as follows:
τ = f t 4 α β 4.38 × 10 − 2 l a e d − 1.5 × 10 − 3 f y f t + 0.2038
The following can be used to calculate Fb at the yield moment of the reinforcement:
F b = f t 4 α β 4.38 × 10 − 2 l a e d − 1.5 × 10 − 3 f y f t + 0.2038 π d l a e
Based on Equation (7), the distributive relationship for the anchoring force between the bond force and bearing pressure can be obtained:
F b F y = f t 4 α β f y A s 4.38 × 10 − 2 l a e d − 1.5 × 10 − 3 f y f t + 0.2038 π d l a e
The test values for Fb/Fy were used to compare the Fb/Fy,8 values listed in Table 7. In this table, λ is the ratio of the test value to the calculated Fb/Fy,8 value (obtained using Equation (8)). The average value of λ is 1.016, the standard deviation is 0.120, and the coefficient of variation is 0.118. The value of Fb/Fy obtained using Equation (8) has a certain accuracy that meets the requirements for calculating the anchorage force of the reinforcement with headed bars.

5. Conclusions

Herein, pull-out tests on 120 reinforced concrete specimens were conducted, with concrete strength grades being within the range of C30–C70, longitudinal reinforcement performed using HRB500 or HRB600 grade steel bars, and the embedded lengths of the reinforcement with headed bars lae being within the range of 0.3–0.7 times the basic embedded length lab. The following conclusions can be obtained by observing the test phenomena and analysing the test data.
  • Different embedded lengths lae led to varying damage results. For small values of lae, failure was mainly due to the bearing pressure of the headed bars, resulting in longitudinal cracks throughout the specimen. For large values of lae, failure was primarily due to reinforcement fracture, and longitudinal crack development was not evident. For moderate values of lae, the joint action of the bearing pressure of the headed bars and the bond force between the reinforcement and concrete caused failure, with longitudinal cracks developing along the specimen but not penetrating it entirely.
  • The concept of a nominal average bond stress τu was proposed. The correction coefficient γ was introduced to correct the difference between the actual average bond stress τ and the nominal average bond stress τu.
  • The correction coefficient γ would increase with an increase in the relative embedded length of the reinforcement lae/d (on average, 146% higher than the initial value) and decrease with an increase in the fy/ft (on average, 33% less than the initial value), with an obvious linear relationship. A formula for γ with lae/d and fy/ft as independent variables was established.
  • A calculation method could be derived for the bond force in straight anchor sections at the yield moment for the reinforcement. A distributive relationship for the anchorage force between the bond force and the bearing pressure was obtained. This enabled the direct and effective consideration and selection of influencing factors such as the dimensions of the headed bars, embedded reinforcement length, and concrete strength grade. Consequently, reinforcement design with headed bars can shift from passive checking to active selection.

Author Contributions

Conceptualization, T.M. and J.Y.; methodology, T.M. and L.S.; software, T.M. and Y.Z.; formal analysis, T.M., J.Y., Y.Z., L.S., M.Z. and W.Z.; investigation, T.M., J.Y., Y.Z., L.S., M.Z. and W.Z.; resources, L.S. and W.Z.; data curation, T.M. and J.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Natural Science Foundation of China (Grant No. 51378146 Funder: Wenzhong Zheng), Science and Technology Research Project of Education Department of Jilin Province (Grant No. JJKH20220281KJ, Funder: Prof. Lirong Sha).

Data Availability Statement

Data will be made available on request.

Conflicts of Interest

The authors declare no conflict of interest and have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Nomenclature

AsCross-sectional area of the reinforcement, mm2
cDistance from the longitudinal reinforcement to the outermost edge of the specimen, mm
dDiameter of reinforcement, mm
FbBond force between the reinforcement and concrete in the straight anchor section, kN
Fb/Fy,8Calculated value using Equation (8)
FpBearing pressure of the headed bars, kN
FyAnchorage force of reinforcement, kN
fcgStrength grade of concrete
fc,mMeasured axial values concrete compressive strength, MPa
ft,mMeasured axial values concrete tensile strength, MPa
fu,mMeasured reinforcement ultimate strength, MPa
fyYield strength of reinforcement, MPa
fyAsYield force of reinforcement, kN
fy/ftRatio of the yield strength of reinforcement to the tensile strength of concrete
fy,mMeasured reinforcement yield strength, MPa
labBasic embedded length of reinforcement, mm
laeEmbedded length of reinforcement, mm
lae/dRelative embedded length
τuNominal average bond stress, MPa
τActual average bond stress, MPa
γCorrection coefficient
βRatio of the actual embedded length to the basic embedded length
γ5Calculated value using Equation (5)
μRatio of the test value to the calculated value γ5
λRatio of the test value to the calculated value Fb/Fy,8

References

  1. Brooker, O. Use of headed bars as anchorage to reinforcement. Struct. Eng. 2013, 91, 49–57. [Google Scholar]
  2. Wright, J.L.; McCabe, S.L. The Development Length and Anchorage Behavior of Headed Reinforcing Bars; SM Report No. 44; University of Kansas Centre for Research: Lawrence, KS, USA, 1997. [Google Scholar]
  3. Wallace, J.W.; McConnell, S.W.; Gupta, P.; Cote, P.A. Use of headed reinforcement in beam-column joints subjected to earthquake loads. ACI Struct. J. 1998, 95, 590–606. [Google Scholar]
  4. Miao, T.M.; Zheng, W.Z. Distributive relationship of anchorage force relative to reinforcement and headed bars. Eng. Struct. 2020, 209, 109961. [Google Scholar] [CrossRef]
  5. Youssf, O.; Hassanli, R.; Mills, J.E.; Elrahman, M.A. An experimental investigation of the mechanical performance and structural application of LECA-Rubcrete. Constr. Build. Mater. 2018, 175, 239–253. [Google Scholar] [CrossRef]
  6. Yi, O.; Zhuge, Y.; Ma, X.; Gravina, R.J.; Mills, J.E.; Youssf, O. Push-off and pull-out bond behaviour of CRC composite slabs—An experimental investigation. Eng. Struct. 2021, 228, 111480. [Google Scholar] [CrossRef]
  7. Gravina, R.J.; Xie, T.Y.; Roychand, R.; Zhuge, Y.; Ma, X.; Mills, J.E.; Youssf, O. Bond behaviour between crumb rubberized concrete and deformed steel bars. Structures 2021, 34, 2115–2133. [Google Scholar] [CrossRef]
  8. Wallace, J.W. Headed reinforcement: A viable option. Concr. Int. 1997, 19, 47–53. [Google Scholar]
  9. Singhal, S.; Chourasia, A.; Parashar, J. Anchorage behaviour of headed bars as connection system for precast reinforced concrete structural components. Structures 2020, 27, 1408–1418. [Google Scholar] [CrossRef]
  10. Singhal, S.; Chourasia, A.; Kajale, Y. Cyclic behaviour of precast reinforced concrete beam-columns connected with headed bars. J. Build. Eng. 2021, 42, 103087. [Google Scholar] [CrossRef]
  11. Yang, Y.Z.; Varma, A.H.; Kreger, M.E.; Wang, Y.; Zhang, K. Shear strength of reinforced concrete beams with T-headed bars for safety-related nuclear structures. Eng. Struct. 2021, 230, 111705. [Google Scholar] [CrossRef]
  12. Vella, J.P.; Vollum, R.L.; Jackson, A. Investigation of headed bar joints between precast concrete panels. Eng. Struct. 2017, 138, 351–366. [Google Scholar] [CrossRef]
  13. Vella, J.P.; Vollum, R.L.; Kotecha, R. Headed bar connections between precast concrete elements: Design recommendations and practical applications. Structures 2018, 15, 162–173. [Google Scholar] [CrossRef]
  14. Sachdeva, P.; Roy, A.B.D.; Kwatra, N. Behaviour of steel fibers reinforced exterior beam-column joint using headed bars under reverse cyclic loading. Structures 2021, 33, 3929–3943. [Google Scholar] [CrossRef]
  15. Paknejadi, A.H.; Behfarnia, K. Performance of reinforced self-consolidating concrete beam-column joints with headed bars subjected to pseudo-static cyclic loading. Ain Shams Eng. J. 2020, 11, 751–765. [Google Scholar] [CrossRef]
  16. Chiu, C.K.; Lays, D.P.; Ricky; Krasna, W.A. Anchorage strength development of headed bars in HSRC external beam-column joints considering side-face blowout failure under monotonic loading. Eng. Struct. 2021, 239, 112218. [Google Scholar] [CrossRef]
  17. Chun, S.C.; Lee, B.S. Components of side-face blowout strengths of headed bars in exterior beam-column joints. ACI Struct. J. 2019, 116, 159–169. [Google Scholar] [CrossRef]
  18. Chourasia, A.; Gupta, S. Influential parameters for headed bars in RC beam-column joint. Curr. Sci. 2019, 116, 1666–1673. [Google Scholar] [CrossRef]
  19. Sachdeva, P.; Roy, A.B.D.; Kwatra, N. Anchorage capacity of headed bars in steel fiber reinforced concrete. Can. J. Civ. Eng. 2021, 49, 134–147. [Google Scholar] [CrossRef]
  20. Sachdeva, P.; Roy, A.B.D.; Kwatra, N. Performance evaluation of different shapes of headed bars in steel fiber reinforced concrete. Adv. Concr. Constr. 2021, 11, 387–396. [Google Scholar]
  21. Zhao, D.B.; Zhou, Y.W.; Xing, F.; Sui, L.L.; Ye, Z.H.; Fu, H.K. Bond behavior and failure mechanism of fiber-reinforced polymer bar-engineered cementitious composite interface. Eng. Struct. 2021, 243, 112520. [Google Scholar] [CrossRef]
  22. Eligehausen, R.; Popov, E.P.; Bertero, V. Local Bond Stress-Slip Relationships of Deformed Bars under Generalized Excitations; College of Engineering, University of California: Berkeley, CA, USA, 1983. [Google Scholar]
  23. CEP-FIP Model Code 2010; The International Federation for Structural Concrete: Lausanne, Switzerland, 2010.
  24. Xu, Y.L.; Shao, Z.M.; Shen, W.D. Bond strength between reinforcement bars and concrete. J. Build. Sci. 1988, 4, 8–14. [Google Scholar]
  25. Xu, Y.L. Experimental Study on Bond Anchorage Performance of Deformed Reinforcement Concrete. Ph.D. Thesis, Tsinghua University, Beijing, China, 1990. [Google Scholar]
  26. Xu, Y.L.; Shen, W.D.; Wang, H. Experimental study on bond anchorage performance of reinforced concrete. J. Build. Struct. 1994, 15, 26–37. [Google Scholar]
  27. GB50010-2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2015.
  28. JGJ 256-2011; Technical Specification for Application of Headed Bars. China Architecture & Building Press: Beijing, China, 2011.
Buildings 13 02463 g001
Figure 1. Representative specimen: (a) Front view of specimen; (b) Top view of specimen; (c) Perforated plug welding between reinforcement and headed bars.
Figure 1. Representative specimen: (a) Front view of specimen; (b) Top view of specimen; (c) Perforated plug welding between reinforcement and headed bars.
Buildings 13 02463 g001
Buildings 13 02463 g002
Figure 2. Test setup: (a) Pull-out test; (b) Load frame.
Figure 2. Test setup: (a) Pull-out test; (b) Load frame.
Buildings 13 02463 g002
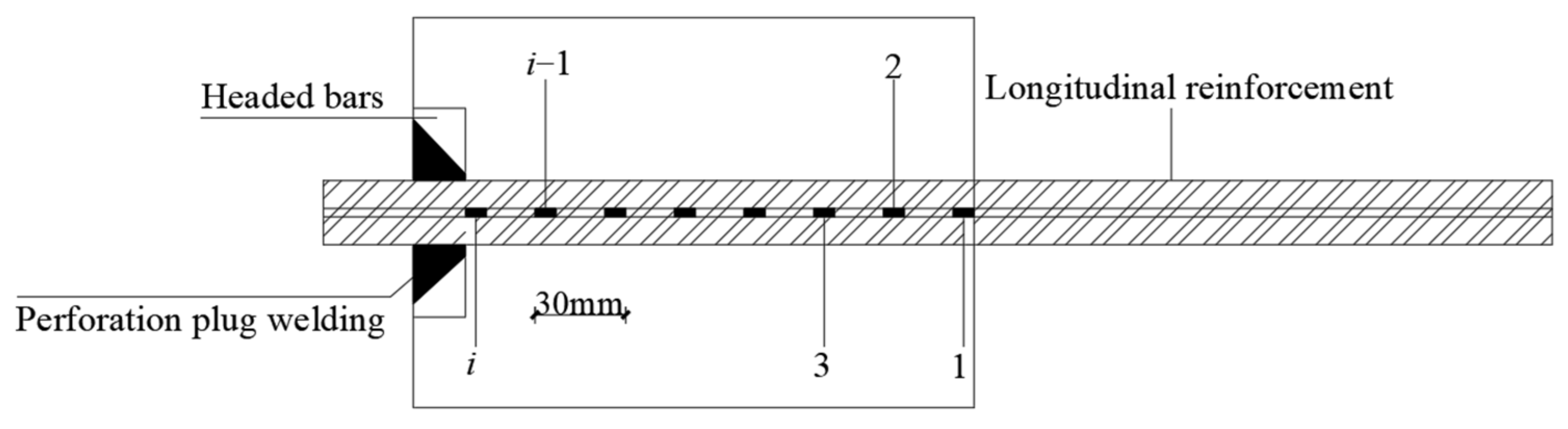
Buildings 13 02463 g003
Figure 3. Arrangement of strain gauges.
Figure 3. Arrangement of strain gauges.
Buildings 13 02463 g003
Buildings 13 02463 g004
Figure 4. Cracks on the side of specimen No. “500-20-30-180”: (a) Cracks of the specimen when the reinforcement yielded; (b) Cracks of the specimen when the reinforcement fractured.
Figure 4. Cracks on the side of specimen No. “500-20-30-180”: (a) Cracks of the specimen when the reinforcement yielded; (b) Cracks of the specimen when the reinforcement fractured.
Buildings 13 02463 g004
Buildings 13 02463 g005
Figure 5. Cracks on the side of specimen No. “600-20-40-320”: (a) Cracks of the specimen when the reinforcement yielded; (b) Cracks of the specimen when the reinforcement fractured.
Figure 5. Cracks on the side of specimen No. “600-20-40-320”: (a) Cracks of the specimen when the reinforcement yielded; (b) Cracks of the specimen when the reinforcement fractured.
Buildings 13 02463 g005
Buildings 13 02463 g006
Figure 6. Cracks on the side of specimen No. “600-25-50-240”: (a) Cracks of the specimen when the reinforcement yielded; (b) Cracks of the specimen when the reinforcement fractured.
Figure 6. Cracks on the side of specimen No. “600-25-50-240”: (a) Cracks of the specimen when the reinforcement yielded; (b) Cracks of the specimen when the reinforcement fractured.
Buildings 13 02463 g006
Buildings 13 02463 g007
Figure 7. Calculation diagram of the average bond stress.
Figure 7. Calculation diagram of the average bond stress.
Buildings 13 02463 g007
Buildings 13 02463 g008
Figure 8. Effect of lae/d on γ for the reinforcement HRB500.
Figure 8. Effect of lae/d on γ for the reinforcement HRB500.
Buildings 13 02463 g008
Buildings 13 02463 g009
Figure 9. Effect of lae/d on γ for the reinforcement HRB600.
Figure 9. Effect of lae/d on γ for the reinforcement HRB600.
Buildings 13 02463 g009
Buildings 13 02463 g010
Figure 10. Effect of fy/ft on γ.
Figure 10. Effect of fy/ft on γ.
Buildings 13 02463 g010
Buildings 13 02463 g011
Figure 11. Fitting results. (a) The front view of test data and fitting surface. (b) The side view of test data and fitting surface.
Figure 11. Fitting results. (a) The front view of test data and fitting surface. (b) The side view of test data and fitting surface.
Buildings 13 02463 g011
Table 1. Groups and numbers for the specimens.
Table 1. Groups and numbers for the specimens.
GroupNo.βGroupNo.βGroupNo.β
500-20-30500-20-30-1400.28500-20-40500-20-40-1200.28500-20-50500-20-50-1100.28
500-20-30-1800.36500-20-40-1600.36500-20-50-1400.36
500-20-30-2200.43500-20-40-1900.44500-20-50-1700.42
500-20-30-2600.50500-20-40-2300.53500-20-50-2000.51
500-20-30-3000.61500-20-40-2600.63500-20-50-2300.58
500-20-60500-20-60-1000.28500-22-30500-22-30-1600.29500-22-40500-22-40-1400.28
500-20-60-1300.36500-22-30-2100.37 500-22-40-1800.37
500-20-60-1600.45 500-22-30-2600.46 500-22-40-2200.46
500-20-60-1800.49500-22-30-3100.56 500-22-40-2700.56
500-20-60-2100.59 500-22-30-3600.65 500-22-40-3100.63
500-22-50500-22-50-1300.31500-22-60500-22-60-1100.28500-25-30500-25-30-2000.33
500-22-50-1600.38 500-22-60-1500.39 500-25-30-2600.43
500-22-50-2000.47 500-22-60-1800.46 500-25-30-3200.52
500-22-50-2400.56 500-22-60-2200.55 500-25-30-3800.62
500-22-50-2700.64 500-22-60-2500.67 500-25-30-4100.67
500-25-40500-25-40-1700.32500-25-50500-25-50-1500.30500-25-60500-25-60-1400.33
500-25-40-2200.41 500-25-50-2000.43 500-25-60-1800.41
500-25-40-2700.51500-25-50-2400.51 500-25-60-2200.50
500-25-40-3300.62500-25-50-2900.61 500-25-60-2700.64
500-25-40-3800.71500-25-50-3400.70 500-25-60-3100.70
600-20-40600-20-40-1400.27600-20-50600-20-50-1300.28600-20-60600-20-60-1200.30
600-20-40-1900.38600-20-50-1700.38 600-20-60-1500.36
600-20-40-2300.45 600-20-50-2100.47 600-20-60-1900.48
600-20-40-2700.53 600-20-50-2400.53 600-20-60-2200.53
600-20-40-3200.63 600-20-50-2800.62 600-20-60-2500.60
600-20-70600-20-70-1100.29600-22-40600-22-40-1700.31600-22-50600-22-50-1500.30
600-20-70-1400.37600-22-40-2200.40600-22-50-1900.39
600-20-70-1700.46 600-22-40-2700.49 600-22-50-2400.49
600-20-70-2000.54 600-22-40-3200.56600-22-50-2800.58
600-20-70-2300.61 600-22-40-3700.67 600-22-50-3200.66
600-22-60600-22-60-1400.32600-22-70600-22-70-1200.29600-25-40600-25-40-2000.30
600-22-60-1800.40600-22-70-1600.38 600-25-40-2700.40
600-22-60-2200.49 600-22-70-2000.49600-25-40-3300.48
600-22-60-2600.61600-22-70-2400.59 600-25-40-3900.59
600-22-60-3000.70600-22-70-2800.69 600-25-40-4500.69
600-25-50600-25-50-1800.29600-25-60600-25-60-1700.29600-25-70600-25-70-1500.31
600-25-50-2400.41600-25-60-2200.40 600-25-70-2000.41
600-25-50-2900.49600-25-60-2700.50600-25-70-2500.51
600-25-50-3500.59 600-25-60-3200.58600-25-70-2900.59
600-25-50-4000.67 600-25-60-3700.68 600-25-70-3400.68
Table 2. Mix proportions of the concrete.
Table 2. Mix proportions of the concrete.
fcg/MPaType of CementWater-Binder RatioSlump of ConcreteMaterial Consumption
CementSilica FumeSlag PowderWaterSandStone
C30P·O 42.50.5270 mm413--2156021169
C40P·O 42.50.4470 mm430--1906101180
C50P·O 42.50.3570 mm542--1905661100
C60P·O 42.50.2675 mm654--1735511025
C70P·O 52.50.2075 mm58850112150513986
Table 3. Mechanical properties of the concrete.
Table 3. Mechanical properties of the concrete.
fcg/MPafc,m/MPaft,m/MPa
C3029.622.96
C4037.883.39
C5046.403.79
C6056.014.14
C7067.024.51
Table 4. Mechanical properties of the reinforcing bars.
Table 4. Mechanical properties of the reinforcing bars.
Steel Graded/mmfy,m/MPafu,m/MPa
HRB3008340400
HRB50020555725
22555716
25560713
HRB60020633825
22612796
25684901
Table 5. Key values of the pull-out specimens.
Table 5. Key values of the pull-out specimens.
No.Fp/kNFb/kNFy/kNNo.Fp/kNFb/kNFy/kN
500-20-30-140107.3660.39167.75500-20-40-120124.7639.40164.16
500-20-30-180104.8558.98163.83500-20-40-160113.0555.68168.73
500-20-30-22099.2969.00168.29500-20-40-19094.8768.70163.57
500-20-30-26085.8485.84171.68500-20-40-23082.8382.83165.66
500-20-30-30067.5297.16164.68500-20-40-26063.0494.56157.60
500-20-50-110130.5136.81167.32500-20-60-100135.5231.79167.31
500-20-50-140118.2548.30166.55500-20-60-130122.2845.23167.51
500-20-50-170111.1159.83170.94500-20-60-160112.9953.17166.16
500-20-50-20092.1675.40167.56500-20-60-180104.3666.72171.08
500-20-50-23082.7986.17168.96500-20-60-21084.4681.15165.61
500-22-30-160144.6656.42201.08500-22-40-140163.2944.71208.00
500-22-30-210142.3566.99209.34500-22-40-180140.1465.95206.09
500-22-30-260118.5989.46208.05500-22-40-220113.3885.53198.91
500-22-30-31095.17107.32202.49500-22-40-27097.42105.54202.96
500-22-30-36077.40126.28203.68500-22-40-31082.04123.06205.10
500-22-50-130147.1449.05196.19500-22-60-110157.1341.77198.90
500-22-50-160134.3963.24197.63500-22-60-150133.0562.61195.66
500-22-50-200120.2080.13200.33500-22-60-180123.3475.60198.94
500-22-50-240102.4598.43200.88500-22-60-220111.9991.63203.62
500-22-50-27085.43113.24198.67500-22-60-25085.58104.60190.18
500-25-30-200184.8268.36253.18500-25-40-170190.0163.34253.35
500-25-30-260158.6693.18251.84500-25-40-220174.6278.45253.07
500-25-30-320136.64116.40253.04500-25-40-270138.26113.12251.38
500-25-30-380115.06140.63255.69500-25-40-330119.02134.21253.23
500-25-30-41089.06165.40254.46500-25-40-38094.53160.96255.49
500-25-50-150211.2852.82264.10500-25-60-140194.8954.97249.86
500-25-50-200164.5184.75249.26500-25-60-180185.1271.99257.11
500-25-50-240151.47100.98252.45500-25-60-220162.8891.62254.50
500-25-50-290125.47125.47250.94500-25-60-270144.61100.49245.10
500-25-50-34098.34160.45258.79500-25-60-310125.63130.76256.39
600-20-40-140148.4746.89195.36600-20-50-130149.4844.65194.13
600-20-40-190118.4672.60191.06600-20-50-170120.5467.80188.34
600-20-40-230109.9086.35196.25600-20-50-210106.9784.05191.02
600-20-40-27086.59105.83192.42600-20-50-24094.3698.21192.57
600-20-40-32071.81122.27194.08600-20-50-28078.45112.89191.34
600-20-60-120139.9444.19184.13600-20-70-110147.8144.15191.96
600-20-60-150129.9961.17191.16600-20-70-140128.9960.70189.69
600-20-60-190103.4481.27184.71600-20-70-170104.5382.13186.66
600-20-60-22097.5893.75191.33600-20-70-20099.6688.38188.04
600-20-60-25087.71107.20194.91600-20-70-23087.13102.28189.41
600-22-40-170166.6664.81231.47600-22-50-150177.3256.00233.32
600-22-40-220144.3284.76229.08600-22-50-190144.9981.56226.55
600-22-40-270118.88109.74228.62600-22-50-240129.24101.55230.79
600-22-40-320106.91130.67237.58600-22-50-280104.53122.71227.24
600-22-40-37080.28149.09229.37600-22-50-32083.89142.84226.73
600-22-60-140172.1554.36226.51600-22-70-120177.7050.12227.82
600-22-60-180152.9975.35228.34600-22-70-160163.3069.99233.29
600-22-60-220130.2098.22228.42600-22-70-200130.4694.47224.93
600-22-60-260109.61109.61219.22600-22-70-240108.91117.99226.90
600-22-60-30082.91135.27218.18600-22-70-28090.05135.08225.13
600-25-40-200216.1897.12313.30600-25-50-180236.4291.94328.36
600-25-40-270207.96111.98319.94600-25-50-240199.79112.38312.17
600-25-40-330179.50146.86326.36600-25-50-290202.47109.02311.49
600-25-40-390139.15177.10316.25600-25-50-350167.41148.46315.87
600-25-40-45096.62215.06311.68600-25-50-400126.83190.25317.08
600-25-60-170256.7781.09337.86600-25-70-150233.1473.62306.76
600-25-60-220132.60183.11315.71600-25-70-200210.6999.15309.84
600-25-60-270185.40128.84314.24600-25-70-250178.90129.55308.45
600-25-60-320128.16192.24320.40600-25-70-290154.78154.78309.56
600-25-60-370107.70209.06316.76600-25-70-340130.32187.53317.85
Table 6. The values of γ and μ.
Table 6. The values of γ and μ.
No.γ
(Test Value)		μNo.γ
(Test Value)		μNo.γ
(Test Value)		μNo.γ
(Test Value)		μ
500-20-30-1400.3601.509500-20-30-1800.3601.083500-20-30-2200.4100.993500-20-30-2600.5001.011
500-20-30-3000.5900.994500-20-60-1000.1900.830500-20-60-1300.2700.917500-20-60-1600.3200.885
500-20-60-1800.3900.976500-20-60-2100.4901.039500-22-50-1300.2500.972500-22-50-1600.3201.014
500-22-50-2000.4001.020500-22-50-2400.4901.040500-22-50-2700.5701.069500-25-40-1700.2500.919
500-25-40-2200.3100.861500-25-40-2700.4501.002500-25-40-3300.5300.959500-25-40-3800.6300.988
600-20-40-1400.2401.026600-20-40-1900.3801.087600-20-40-2300.4401.024600-20-40-2700.5501.052
600-20-40-3200.6301.001600-20-70-1100.2300.956600-20-70-1400.3201.037600-20-70-1700.4401.166
600-20-70-2000.4701.064600-20-70-2300.5401.068600-22-60-1400.2400.904600-22-60-1800.3300.961
600-22-60-2200.4301.017600-22-60-2600.5000.978600-22-60-3000.6201.048600-25-50-1800.2801.106
600-25-50-2400.3600.970600-25-50-2900.3500.762600-25-50-3500.4700.838600-25-50-4000.6000.927
500-20-40-1200.2401.024500-20-40-1600.3301.046500-20-40-1900.4201.082500-20-40-2300.5001.057
500-20-40-2600.6001.091500-22-30-1600.2811.109500-22-30-2100.3200.937500-22-30-2600.4300.971
500-22-30-3100.5300.964500-22-30-3600.6200.958500-22-60-1100.2100.904500-22-60-1500.3201.016
500-22-60-1800.3801.023500-22-60-2200.4501.008500-22-60-2500.5501.059500-25-50-1500.2000.792
500-25-50-2000.3400.965500-25-50-2400.4000.953500-25-50-2900.5000.984500-25-50-3400.6201.052
600-20-50-1300.2300.947600-20-50-1700.3601.066600-20-50-2100.4401.043600-20-50-2400.5101.051
600-20-50-2800.5901.027600-22-40-1700.2801.031600-22-40-2200.3700.990600-22-40-2700.4801.013
600-22-40-3200.5500.977600-22-40-3700.6500.967600-22-70-1200.2200.908600-22-70-1600.3000.946
600-22-70-2000.4201.039600-22-70-2400.5201.079600-22-70-2800.6001.066600-25-60-1700.2400.956
600-25-60-2200.5801.634600-25-60-2700.4100.924600-25-60-3200.6001.139600-25-60-3700.6601.070
500-20-50-1100.2200.945500-20-50-1400.2900.968500-20-50-1700.3500.973500-20-50-2000.4501.048
500-20-50-2300.5101.034500-22-40-1400.2150.898500-22-40-1800.3200.997500-22-40-2200.4301.051
500-22-40-2700.5201.032500-22-40-3100.6001.033500-25-30-2000.2700.926500-25-30-2600.3700.930
500-25-30-3200.4600.917500-25-30-3800.5500.910500-25-30-4100.6500.988500-25-60-1400.2200.834
500-25-60-1800.2800.853500-25-60-2200.3600.899500-25-60-2700.4100.829500-25-60-3100.5100.916
600-20-60-1200.2400.948600-20-60-1500.3201.030600-20-60-1900.4401.084600-20-60-2200.4901.057
600-20-60-2500.5501.047600-22-50-1500.2400.929600-22-50-1900.3601.044600-22-50-2400.4401.000
600-22-50-2800.5401.032600-22-50-3200.6301.044600-25-40-2000.3101.146600-25-40-2700.3500.904
600-25-40-3300.4500.925600-25-40-3900.5600.933600-25-40-4500.6900.972600-25-70-1500.2400.931
600-25-70-2000.3200.932600-25-70-2500.4200.973600-25-70-2900.5000.998600-25-70-3400.5901.012
Table 7. The values of Fb/Fy and λ.
Table 7. The values of Fb/Fy and λ.
No.Fb/Fy
(Test Value)		λNo.Fb/Fy
(Test Value)		λNo.Fb/Fy
(Test Value)		λNo.Fb/Fy
(Test Value)		λ
500-20-30-1400.3601.508500-20-30-1800.3601.082500-20-30-2200.4100.993500-20-30-2600.5001.010
500-20-30-3000.5890.993500-20-60-1001.0041.000500-20-60-1300.2701.109500-20-60-1600.3191.070
500-20-60-1800.3891.180500-20-60-2100.4901.256500-22-50-1300.2500.971500-22-50-1600.3201.013
500-22-50-2000.4001.019500-22-50-2400.4901.039500-22-50-2700.5701.068500-25-40-1700.2500.918
500-25-40-2200.3100.861500-25-40-2700.4501.002500-25-40-3300.5300.959500-25-40-3800.6300.987
600-20-40-1400.2401.025600-20-40-1900.3801.086600-20-40-2300.4401.024600-20-40-2700.5501.052
600-20-40-3200.6301.000600-20-70-1100.2301.157600-20-70-1400.3201.254600-20-70-1700.4401.409
600-20-70-2000.4701.287600-20-70-2300.5401.291600-22-60-1400.2400.903600-22-60-1800.3300.960
600-22-60-2200.4301.016600-22-60-2600.5000.977600-22-60-3000.6201.047600-25-50-1800.2801.105
600-25-50-2400.3600.969600-25-50-2900.3500.761600-25-50-3500.4700.838600-25-50-4000.6000.926
500-20-40-1200.2401.024500-20-40-1600.3301.046500-20-40-1900.4201.081500-20-40-2300.5001.057
500-20-40-2600.6001.090500-22-30-1600.2811.108500-22-30-2100.3200.937500-22-30-2600.4300.971
500-22-30-3100.5300.964500-22-30-3600.6200.957500-22-60-1100.2100.904500-22-60-1500.3201.015
500-22-60-1800.3801.022500-22-60-2200.4501.007500-22-60-2500.5501.059500-25-50-1500.2000.791
500-25-50-2000.3400.965500-25-50-2400.4000.953500-25-50-2900.5000.983500-25-50-3400.6201.051
600-20-50-1300.2300.947600-20-50-1700.3601.066600-20-50-2100.4401.043600-20-50-2400.5101.050
600-20-50-2800.5901.026600-22-40-1700.2801.031600-22-40-2200.3700.989600-22-40-2700.4801.013
600-22-40-3200.5500.977600-22-40-3700.6500.967600-22-70-1200.2200.907600-22-70-1600.3000.945
600-22-70-2000.4201.039600-22-70-2400.5201.078600-22-70-2800.6001.065600-25-60-1700.2400.955
600-25-60-2200.5801.633600-25-60-2700.4100.924600-25-60-3200.6001.139600-25-60-3700.6601.069
500-20-50-1100.2200.944500-20-50-1400.2900.968500-20-50-1700.3500.973500-20-50-2000.4501.047
500-20-50-2300.5101.033500-22-40-1400.2150.898500-22-40-1800.3200.996500-22-40-2200.4301.051
500-22-40-2700.5201.032500-22-40-3100.6001.032500-25-30-2000.2700.926500-25-30-2600.3700.929
500-25-30-3200.4600.916500-25-30-3800.5500.910500-25-30-4100.6500.988500-25-60-1400.2200.834
500-25-60-1800.2800.852500-25-60-2200.3600.899500-25-60-2700.4100.828500-25-60-3100.5100.916
600-20-60-1200.2400.947600-20-60-1500.3201.029600-20-60-1900.4401.084600-20-60-2200.4901.056
600-20-60-2500.5501.047600-22-50-1500.2400.929600-22-50-1900.3601.043600-22-50-2400.4400.999
600-22-50-2800.5401.031600-22-50-3200.6301.043600-25-40-2000.3101.146600-25-40-2700.3500.904
600-25-40-3300.4500.925600-25-40-3900.5600.932600-25-40-4500.6900.972600-25-70-1500.2580.931
600-25-70-2000.3200.932600-25-70-2500.4200.973600-25-70-2900.5000.998600-25-70-3400.5901.012
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Miao, T.; Yang, J.; Zhou, Y.; Zhan, M.; Sha, L.; Zheng, W. Research on the Distributive Relationship between Bond Force and Bearing Pressure for Anchorage Force by Headed Bars. Buildings 2023, 13, 2463. https://doi.org/10.3390/buildings13102463

AMA Style

Miao T, Yang J, Zhou Y, Zhan M, Sha L, Zheng W. Research on the Distributive Relationship between Bond Force and Bearing Pressure for Anchorage Force by Headed Bars. Buildings. 2023; 13(10):2463. https://doi.org/10.3390/buildings13102463

Chicago/Turabian Style

Miao, Tianming, Jian Yang, Ying Zhou, Meiqiu Zhan, Lirong Sha, and Wenzhong Zheng. 2023. "Research on the Distributive Relationship between Bond Force and Bearing Pressure for Anchorage Force by Headed Bars" Buildings 13, no. 10: 2463. https://doi.org/10.3390/buildings13102463

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop