Abstract
Mean radiant temperature (MRT) is one of the six primary factors that determine thermal comfort in a given thermal environment. In this study, the average radiant temperature was determined using a calculation method based on the surrounding surface temperatures and view factors. The present study specifically investigated the use of calculated radiant temperature, compared to measured radiant temperature, for predicting the mean vote (PMV) and percentage of dissatisfied (PPD) comfort parameters. The method was validated by the experimental measurements via the black sphere thermometer at five different reference points in a test room, including radiant panels on the ceiling and walls. By using global thermometer measurements, the proposed approach achieved a high degree of compatibility and an accuracy of 0.17 °C, which was the difference between calculated and measured values. The results demonstrated the reliability of the procedure using view factors and surrounding surface temperatures to calculate the radiant temperature in the designated test room; here, a straightforward method for evaluating the thermal conditions of an office room and determining the optimal location of an air temperature sensor in PMV-controlled radiant systems was also proposed. This study contributes to the increasing field of research on thermal comfort and offers knowledge that is beneficial for the design and optimization of indoor environments.
1. Introduction
Ongoing technological advancements have placed considerable pressure on engineers and architects to design structures that are thermally efficient and cost-effective, with the ultimate goal of enhancing the quality of the indoor thermal environment for occupants. This is particularly important due to the significant energy consumption associated with buildings, which accounts for approximately one third of global carbon emissions [1,2,3]. Using data from the last ten years, it is seen that the building sector in Turkey consumes more energy than the industry and transportation sectors, with a share of 32.3% of total energy consumption, and that heating and cooling account for approximately 70% of total energy consumption in buildings [4]. Many reports at the national, regional, and global levels highlighted the importance of radiant heating and cooling (RHC) over conventional systems in relation to “near-zero” energy consumption in buildings [5,6,7].
Thermal comfort is a sensation that reflects a person’s satisfaction with the thermal environment they are in. The purpose of a heating and cooling system is to provide a suitable environment in terms of thermal comfort standards, which is known as International Organization for Standardization (ISO 7730) and ASHRAE 55 [8,9]. As a new type of air conditioning system, RHC systems have increased in popularity over the past decade and, therefore, can offer improved indoor quality with more energy-saving potential than traditional air conditioning systems [10]. The RHC system uses the surrounding surfaces of the conditioning area as a heating or cooling source (depending on the application type), and heat exchange occurs by radiant and convective heat transfer mechanisms. In an RHC system, radiant heat transfer forms more than 50% of the total heat transfer between occupants and surfaces [11]. Six main parameters affect thermal comfort: metabolic rate, clothing insulation, air temperature, mean radiant temperature (MRT), air velocity, and relative humidity. The MRT is defined as “the temperature of a uniform, the black enclosure that exchanges the same amount of thermal radiation with the occupant as the actual enclosure” [9]. It is a single value representing the entire body and can be considered the average temperature of the surrounding surfaces weighted by their view factors concerning the occupant.
RHC systems can also be defined as hydronic radiant systems and/or water-based surface-embedded heating and cooling systems as they are usually operated by water [12]. RHC systems bring a significant advantage due to their compatibility with renewable energy sources, in particular with solar power. This compatibility results from the alignment of water temperatures provided by solar energy systems with the optimal range for radiant heating systems. Solar thermal collectors produce moderate water temperatures (38 °C to 60 °C) that efficiently integrate with radiant systems, promoting energy efficiency and sustainable heating practices [13]. Stetiu [14] showed that an office with a radiant cooling system had 30% less energy consumption and 27% less peak power demand than traditional all-air conditioning systems in the United States. Le Dreau [15] investigated an office room with four different cooling solutions that were active: chilled beam, radiant floor, radiant wall, and radiant ceiling. It was observed that the radiant floor system was the most efficient way in terms of cooling needs thanks to its bigger view factor between a sitting person and the floor, while the second most efficient solution was the radiant ceiling system that managed to provide the most uniform comfort conditions in the area. One of the critical points was the thickness of insulation for optimized energy performance when the effectiveness of RHC systems is considered. Chen and Li [16] worked on the energy, emission, and economic feasibilities of air-source heat pump-integrated underfloor heating/cooling systems in the summer and winter seasons. Compared to the current system, the radiant system consumed 12.3% less primary energy, emitted 36.9% more carbon dioxide, and saved operating expenses by 26.0%. Cvetkovic and Bojic [17] performed an experimental study in a residential house in Serbia fitted with an RHC system. It was shown that the thickness of thermal insulation should be higher for the locations where the radiant panels were located. When the RHC system was considered in itself, the thermal insulation required for walls was thicker than needed for the radiant floor.
Among all six thermal comfort parameters, the MRT is one of the most challenging parameters to obtain since it does not depend only on the air temperature but also the temperature of surrounding surfaces that radiate heat towards the occupants. Measuring and calculating the MRT require specialized equipment and precise environmental data, which make it more complex compared to other thermal comfort parameters such as air temperature, relative humidity, air velocity, clothing insulation, and metabolic rate. Therefore, several measurement and calculation methods were developed with different equipment to solve this problem. Black globe thermometers, two-sphere radiometers, and constant-air-temperature sensors are commonly used to measure the MRT. Amongst others, the black globe thermometer is the most popular device in indoor environments due to its low cost, compactness, and ease of calculation [18]. It is simply a thin-walled copper sphere painted black with a sensor placed at the center of the sphere [19]. The standard globe has a 150 mm diameter and 0.4 mm thickness of copper. For a reliable measurement, the first globe thermometer needs to reach thermal equilibrium. Reading from the internal thermometer depends on convective and radiant heat transfer mechanisms. One of the severe disadvantages of the globe thermometer is the long-time requirement to reach its equilibrium before reading. To overcome this challenge, various diameters for the globe have been studied. Studies showed that the globe reaches thermal equilibrium quickly for smaller diameters, but this gained time costs its accuracy and causes a higher error incidence than the standard diameter [20,21,22]. Kang et al. [23] assessed the uncertainty of MRT estimates by grouping surfaces with similar temperature behavior. Using a measurement data-based simulation model and the Monte Carlo method, the study inferred that excluding similar surfaces had no significant effect on MRT uncertainty. When an adequate number of input surfaces were used, the difference between MRT and measurements of all surfaces was less than 1%. The study conducted by Tamrakar et al. [24] aimed to evaluate the impact of variations in outdoor temperatures and wall thermal transmittance on the inside thermal environment. The researchers also examined whether the resultant conditions satisfied ergonomic guidelines for the ideal ratio of mean radiant temperature to outdoor temperature. The study found that MRT responses differed across five outdoor temperature scenarios and three types of exterior walls. Seated occupants had consistent MRT, while standing occupants had minor differences when near a window in all scenarios. However, when occupants were not equally positioned near the window, seated occupants experienced larger MRT variations compared to standing occupants.
In the context of large venues such as concert halls and stadiums, attaining uniform heat distribution presents unique challenges compared to smaller indoor spaces. While evaluating thermal conditions in such environments, it is essential to account for the distribution of the MRT. Lee et al. [25] chose a stadium as a case study and made a comparison between the black globe temperature and infrared thermal imaging camera (IR camera) with calculated view factors. Results showed that there might be prominent differences in surface temperatures; thus, using an IR camera was proposed in such environments. Tan et al. [26] investigated radiant temperatures with a 40 mm diameter grey globe thermometer in a tropical urban environment. It was seen that greeneries and trees had a reduction effect on the MRT during daytime while there was not a significant difference in the absence of sunlight. A similar study focused on urban environments was carried out by Park et al. [27]. They investigated how pedestrian MRT varied with tree spacing using a new multilayer MRT model. Large trees were found to be more effective in reducing MRT and could be planted at wider intervals, while small trees showed an exponential MRT reduction as the spacing decreased. Guo et al. [28] carried out a lab-scale experimental study and observed the change of air and mean radiant temperature at 1.3 m height over 48 h. It was deduced that the variation of mean radiant temperatures was up to 8 °C while air temperatures changed about 2 °C during the experiments. The influence of room geometry on mean radiant temperature was studied by Kalmar [29] in rooms with the same width and height but different lengths. The study discovered that mean radiant temperature varies parabolically with room height and length, suggesting an optimal height for the minimal MRT. Occupant position in the room affected the values. Surface heating systems yielded lower MRT values, and thermal refurbishment led to decreased mean radiant temperature. Walikewitz et al. [30] investigated the relation between the air and mean radiant temperatures for four different office rooms in a building located in Berlin/Germany. It was inferred that the difference between the two temperatures was not significant in most cases; however, the room with windows which faced southeast and southwest had the maximum deviation between air and radiant temperatures due to the existence of solar radiation. Hwang et al. [31] investigated the impact of solar radiation on indoor thermal comfort in subtropical climates by conducting field measurements in six test cells with varying types of glass. The study found considerable increases in MRT near windows, reaching up to 50.8 °C for single-pane glass, while indoor temperatures remained stable between 25 °C and 27 °C regardless of glazing type. Another study assessed the effects of solar radiation on the indoor environment and thermal discomfort [32]. The study showed that thermal discomfort and mean radiant temperature increased when the distance from the window decreased in a south-facing room. A comparative study was carried out by Özbey and Turhan [33], which focused on a case study of an office building in a university. Different calculation methods were used to obtain mean radiant temperature compared with results from the black globe thermometer, and the study discovered that the methods based on angle factors and the radiant plane temperatures had similar trends. Also, mean radiant temperatures by these methods overestimated above 20 °C and underestimated below 20 °C due to sharp temperature changes in window temperatures on cloudy days.
There are a variety of measurement and calculation methods for determining MRT in indoor environments. Following the above-mentioned studies, this study aims to propose a calculation method for MRT distribution in a live space. Hereby, to counteract the drawbacks of the globe-based measurements, the method can be used as a reliable way of MRT calculation. To this end, an actively used office space is selected, and then the space is equipped with ground source heat pump (GSHP)-integrated hydronic radiant wall and ceiling panels for heating purposes. By using wall and ceiling panels at the same time, we can also consider the angle factors and compare with the global thermometer measurements. Based on the validation of the calculated and measured mean radiant temperatures, the predicted mean vote (PMV) and predicted percentage dissatisfied (PPD) deviations caused by the calculated mean radiant temperatures are compared with the experimental PMV and PPD. Two main original contributions can be counted for the present work. The first contribution is developing an easier method of monitoring the thermal conditions of the office space to determine the optimal position of the air temperature sensor in radiant systems controlled by PMV. The second is experimentally determining the thermal comfort conditions by implementing radiant systems to the walls and ceilings of a real-sized and actively used office room combined with the ground heat exchanger (GHE) system placed in the ground under the building foundation, which was experimentally validated before [34,35]. Consequently, it can be stated that studies related to energy-saving and sustainable building systems integrated with renewable energy systems are important for researchers and practitioners, especially when considering the approaches of nearly zero-energy buildings and decarbonization gains.
2. Experimental Study
2.1. Test Room
The test room was located on the first floor of the Yildiz Technical University (YTU) Science and Technology Application and Research Center building facing the northeast (NE) direction. Radiant panels were embedded in the walls and ceilings of the test room, which had dimensions of 7 m × 7.5 m × 2.8 m. The room was fitted with 29 radiant panels (1 m × 0.6 m) on the ceiling whereas the southeast (SE) and northwest (NW) walls of the room were equipped with 6 and 9 radiant panels with dimensions of 2 m × 0.6 m, respectively. The schematic and actual views of the radiant panels on the ceiling and walls of the test room are represented in Figure 1, while the detailed geometric specifications can be seen in Table 1. The radiant panels can be operated and controlled separately using control valves. The room had large glazing and an aluminum frame with a heat transfer coefficient of 2.4 W/m2∙K that covers a total area of 18.2 m2. Beneath the window section, there was a wall with a height of 0.2 m and an area of 1.4 m2. The southwest (SW) side looked to the corridor, and as well as the door of the room, it also had a large glazed window area of 17.5 m2 and a wall height of 0.3 m above. The heat transfer coefficient of the corridor window was 5.7 W/m2∙K. The test room was adjacent to the elevator shaft on the NE side and adjacent to an office room on the SE side. The NW wall of the room with a heat transfer coefficient of 0.65 W/m2∙K was near the elevator shaft, while the SE wall with a heat transfer coefficient of 0.53 W/m2∙K was adjacent to an actively used office room. The upstairs and downstairs of the office room were utilized as labs, and the slab between the two mediums had a heat transfer coefficient of 0.42 W/m2∙K. Lighting, active computers, and dummies were utilized in the test room to provide a realistic office environment (see Figure 1). Four cylinders were placed in the room to ensure a sensible heat load, according to the EN 14240 standard [36]. Each cylinder had three luminaires with a capacity of 60 W. The dummies were set to the heating capacity of 80 W during the experiment, which was similar to an office worker’s low metabolic rate [36]. The data obtained from the measurements in the test room were collected and recorded using a 30 W heat-loaded Agilent 34572A datalogger. To simulate a typical office environment, four desktop computers with a 90 W heat load were used within working hours.

Figure 1.
(a) The schematic and (b) actual view of the test room.

Table 1.
The geometric properties of the radiant panels.
2.2. Ground Source Heat Pump (GSHP) System
The real and schematic appearances of the ground source heat pump system, which was integrated into the wall and ceiling radiant panels in the test room, are represented in Figure 2. The ground source heat pump system can be described as three main subgroups: (i) heat pump unit, (ii) measurement system, and (iii) ground heat exchangers (GHE). Firstly, the projected and real views of the heat pump system consisting of circulation pumps, accumulation and expansion tanks, flow switches, and piping systems are indicated in Figure 2. The second subgroup is the measurement system and its equipment is as follows: flow meters, manometers, thermometers, rotameters, RTD sensors, and PLC unit. The last subgroup includes GHE pipes placed under the building foundation and previously tested in Ref. [35]. These pipes, consisting of 10 parallel pipes buried horizontally under the building foundation, are made of high-density polyethylene material. The length of the pipes is 85 m with a distance of 0.5 m from one another. The water circulating through the GHE pipes reached a collector and was circulated to the heat pump from there, and then the room was conditioned by the implemented radiant panels. Further elaboration on this subsection of the experimental setup can be found in our former works [34,35,37].
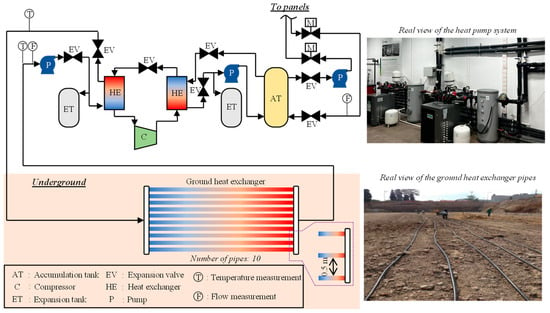
Figure 2.
The real and schematic appearances of the ground source heat pump system.
2.3. Measurement Equipment in the Test Room
To obtain the PMV and MRT values, the parameters of indoor air temperature, surface temperature, air velocity, and relative humidity were required. A total of 51 T-type thermocouples were used for surface temperature measurements, including radiant panel surfaces, unheated walls, inner and outer surfaces of the exterior window, and a glazed window facade to the corridor. For this, five metal stands (trees) with a height of 2.5 m were installed in the places presented in Figure 3a,b. Thermocouples were placed at five different heights on each stand as follows: 0.1 m, 0.6 m, 1.1 m, 1.7 m, and 2.5 m (see Figure 3a). In order to obtain a reliable indoor air temperature, a radiation shield was used as recommended by the ASHRAE 55-2013 standard [9], as indicated in Figure 3c.

Figure 3.
Measurements in the room; (a) placement of thermocouples on each stand, (b) on-site view of stands in the center of the test room, and (c) radiation shield.
PMV values were obtained using relative humidity, globe thermometer, and temperature and turbulence probes attached to the Testo 400 Universal indoor air quality (IAQ) equipment. Table 2 summarizes the key technical details of the instruments used for the measurement of parameters in the test room. With an adjustable tripod, the Testo 400 Universal IAQ equipment, shown in Figure 4a, was used to collect measurements at the height of 1.1 m in the center of the test room. As depicted in Figure 4b,c, the datalogger switch unit was used for all measurements in the test room, while the PLC unit was used for all measurements on the GSHP unit.

Table 2.
Instruments used for the measurement of parameters in the test room (Adapted with permission from [34]. 2023, Elsevier).

Figure 4.
The appearances of (a) Testo 400 Universal IAQ system, (b) PLC system, and (c) datalogger switch unit.
2.4. Measurements
The experiments for five different cases were carried out on 24 February 2022 between 12:12 and 14:59 p.m. The comfort device, which measured radiant temperature, air temperature, air velocity, and humidity, was placed to take measurements from five reference points of the test room over 20 min periods, as shown in Figure 5. The dimensional details of the five different reference points of the comfort device in the test room are also presented in Table 3.

Figure 5.
An overview of the test room and the positions of the reference points.

Table 3.
Dimensional details of reference points in the test room.
2.5. Uncertainty Analysis
The procedure of implementing the uncertainty analysis method, as recommended by Kline and McClintok [38], is systematically carried out to meticulously ascertain and quantify the diverse errors that are specifically relevant to the experimental studies being conducted. The error rates of each independent variable employed in experiments can be calculated by utilizing Equation (1).
The process of assessing the overall uncertainties associated with the indirectly measured parameters related to thermal comfort indexes, specifically the predicted mean vote (PMV) and the percentage of people dissatisfied (PPD), was undertaken by performing calculations as outlined in Equation (1).
where R represents the parameter that is to be determined, whereas w1, w2, w3, …, wn represent the error rates associated with each independent variable. WR represents the overall uncertainty. The R parameter is influenced by a set of independent variables indicated as x1, x2, x3,……, xn.
The uncertainties attributed to the PMV and PPD were established through a meticulous analysis of direct measurements encompassing essential factors such as air temperature, air velocity, humidity levels, surface temperature subjected to heating or cooling, as well as the mean radiant temperature (MRT). The comprehensive examination of these key parameters allowed for a thorough evaluation of the potential variations and errors associated with the determination of the PMV and PPD, thus offering a more robust understanding of the overall reliability of these thermal comfort indices. The total average estimated uncertainty of the PMV and PPD was found to be approximately ±11% and ±8.8%, respectively.
3. Mathematical Model and Experimental Verification
According to the definition of MRT, it should be calculated in relation to the human body surface area and the environment temperature in every orientation, but due to the complex shape of the human body, such a calculation is extremely difficult to perform [39,40,41]. To overcome this challenge, the human body could be reduced to a spherical point located in a room for a more user-friendly calculation, and also, the best approximation to the globe thermometer can be provided. Therefore, in the present study, the view factor is calculated using Equation (2) [42]:
where a and b represent the width and length of the surfaces, respectively, and c represents the distance between the surface and the measurement point. To apply this equation optimally to the test room, each wall in all directions (northwest, southeast, northeast, southwest, floor, and ceiling) was divided into smaller surfaces and a total of 27 surfaces were created, as shown in Figure 6.

Figure 6.
Schematic view of all surfaces determined in the test room.
It can be said that the determination of MRT, which significantly affects the user’s sensation, is more challenging on thermal comfort than the other parameters. The measurement methods used to determine the MRT are as follows: black globe thermometer, two-sphere radiometer, constant-air-temperature sensor, and a method based on the measurement of the effective radiative flow. The central component of the black sphere thermometer is a black sphere that serves as the measuring device. The external surface of the sphere is designed to absorb radiation coming from the room’s walls, which allows for accurate temperature readings. The MRT measurement, when performed using a black sphere thermometer, is expressed as follows [9]:
where hcg is the convection coefficient between the surrounding air and surfaces of the globe thermometer. Tg and Ta are the surface temperature of the globe thermometer and ambient air temperature, respectively. Va, D, and εg denote the air velocity, diameter, and emissivity of the globe thermometer, respectively.
The two-sphere radiometer is a device that uses two spheres with varying emissivity values. There is a difference in the amount of heat that is supplied to the two spheres due to the fact that the emittance of the black sphere is greater than that of the polished sphere, which results in the measurement of radiation. The MRT is formulated as follows:
where Pp and Pb represent the power supplied to the polished and black spheres, respectively. εb and εp are the emissivities of the black and polished spheres. Ts is the surface temperature of spheres. When using the constant air temperature sensor as the measurement method, the MRT is defined as follows:
where Ps, Ts, and εs are the power supplied to the sensor, surface temperature, and emissivity of the sensor, respectively. Another method is the one based on the measurement of the effective radiative flux. Here, the MRT is calculated as follows:
where Eeff represents the effective radiative flow, which is a measure of the net radiant heat exchange between the person or object and its surroundings. Tb is the background temperature.
The MRT is estimated using several calculation methods, each of which takes into consideration different factors and variables. These techniques provide important insights into the radiant heat exchange between the human body or an object and its surrounding surfaces. The first of these methods considers the temperatures of the various surrounding surfaces and the corresponding view factors, which represent the rate of radiation emitted by each surface toward the person or object of interest. The MRT is determined by calculating the weighted sum of temperatures raised to the fourth power based on the view factors. This equation is expressed as follows:
In the second method, assuming that the radiant heat exchange is proportional to the object surface area, the MRT is calculated by considering the surface areas and weighted average temperatures. The equation is given below:
The last method involves estimating temperatures in various planes and applying weighted coefficients to represent the importance of each direction in thermal radiation exposure. This allows for an approximation of the MRT for seated and standing positions. The corresponding MRT equations for the seated and standing person are presented below:
where Tpr denotes the plane radiant temperature. In this study, Equation (7) is specifically adopted for the accurate computation of the mean radiant temperature (MRT). This equation incorporates the temperatures of the surrounding surfaces as well as the view factors, resulting in enhanced precision during the MRT calculation process [20]. Several assumptions were made in order to apply the mathematical model for the resolution of our physical problem:
- ○
- Since the majority of construction materials in the test chamber have a high emissivity (ε > 0.9), it was assumed that all chamber surfaces were black.
- ○
- Measurements were taken from one point on each glass surface on the hallway and the outdoor environment side. The temperature distribution was assumed to be uniform on the glass surfaces.
- ○
- The floor surface temperature was assumed to be the average of temperature measurements obtained from the center of the floor and near the window.
- ○
- In the developed model, MRT calculations were performed in the sitting position of the occupant (at a height of 1.1 m from the floor) in parallel to the ASHRAE standard [9].
Recognizing the importance of surface temperature measurements in MRT calculations, a total of 23 T-type thermocouples were used on both heated and non-heated interior surfaces of the test room. For the surface temperatures within the test room, five thermocouples were placed on each radiant panel of the heated southeast wall and the heated northwest wall, and three thermocouples were used on the heated ceiling radiant panels for measurements. Additionally, surface temperatures of all non-heated surfaces in the test room (wall surfaces, corridor glass surface, external window surface, ceiling, and floor surfaces) were measured using 10 T-type thermocouples. The view factors for the five reference points in Figure 5 were calculated in a three-dimensional coordinate system using Equation (2), and then implemented in the MATLAB environment. The computed view factors are provided in Table 4. The outdoor ambient temperature varied between 5.6 °C and 6.5 °C with an average value of 6.1 °C, so the outside air temperature was almost stable during the experiments. Furthermore, the average, highest, and lowest temperatures measured by thermocouples for the SE, NW, and ceiling radiant panels are provided in Table 5.

Table 4.
Calculated view factors.

Table 5.
Temperature values for radiant panels.
The comparison of the radiant temperature calculated at different points of the test room with the radiant temperature measured using the globe sensor is represented in Figure 7. The variations of the measured and calculated radiant temperature for Ref. Point 1 over time are depicted in Figure 7a. The measured MRT with a globe thermometer changed from 21 °C to 21.3 °C, while the calculated MRT changed from 21.8 °C to 22.4 °C, and the average difference between the calculated and measured MRT was 1 °C. The reason for the significant temperature difference at this point can be attributed to the large size of the window surface, the absence of a homogeneous temperature distribution, and the fact that measurements were taken from a single point. Taking temperature measurements from different points on the window surface and using the average value of these temperatures in MRT calculations was considered to yield more consistent results in comparison to the measured MRT value.
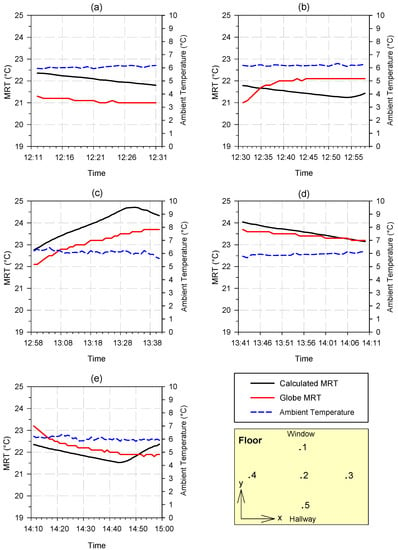
Figure 7.
Measured and calculated MRT values at Ref. Point (a) 1, (b) 2, (c) 3, (d) 4, and (e) 5.
The analysis of mean radiant temperature (MRT) measurements at Ref. Points 1 to 5 resulted in the computation of percentage average deviations between the measured and calculated values. The obtained deviations were found to be 4.7%, 2%, 3.6%, 0.6%, and 1.2%, respectively, for each reference point. These computed values serve as indicators of the discrepancies between the experimental measurements and the calculated MRT values, shedding light on the accuracy and reliability of the applied calculation method in relation to the actual measurements at the specified reference points.
As shown in Figure 7b, the average difference of measured and calculated MRT at Ref. Point 2 was found to be 0.4 °C. Figure 7c,d, representing Ref. Point 3 and Ref. Point 4, show the measured and calculated MRT values at a distance of 0.7 m from the southeast and northwest walls. As these walls contained six and nine radiant heating panels, it was reasonable to expect that the air and MRT would be higher than the other three reference points. The average of 168 air temperatures of these two points were 21.8 °C and 21.6 °C, while the average MRT temperatures were 24 °C and 23.6 °C, respectively. The difference between calculated and measured MRT at Ref. Point 4 was relatively smaller. The reason behind this was the unconditioned elevator shaft and fire escape behind the northeast wall. Figure 7e shows the calculated and measured MRT values at Ref. Point 5 which was 1 m inside from the hallway side of the test room. The temperature differences between the calculated and measured MRT values on the hallway side (Ref. Point 5) were found to be quite low, similar to the values observed at Ref. Point 4. The independent conditioning of the hallway area of the building, resulting in a homogeneous temperature distribution on the hallway glass, contributed to the calculated MRT value closely matching the measured MRT value. The average difference between the calculated and measured MRT at Ref. Point 5 was found to be 0.4 °C.
4. Results and Discussion
In this section, the radiant temperature distribution in the XZ, YZ, and XY sections of the entire room was determined based on the reliability verification of the temperatures of the surrounding surfaces and view factors method. Moreover, the deviations of the calculated MRT in the comfort indices of the PMV and PPD were compared to the measured PMV and PPD.
Figure 7 illustrates the variations in mean radiant temperature along the northwest-southeast and northeast-southwest, at a height of 1.1 m above the floor, precisely determined through the mean radiant temperature calculation method. To facilitate a comparison between the average radiant temperature and the indoor air temperature values, Figure 8 also presents the average air temperature values measured at the height of 1.1 m above the ground in five different locations across the room, using thermocouples on stands. When analyzing the variation in the MRT along a linear path characterized by constant y and z coordinates of 3.75 m and 1.1 m, respectively, the x coordinates were observed to vary within the range of 0.3 m to 6.7 m. Thereby, a total number of 641 points were created, each of which was 0.01 m away from the next point in the x-direction, and then the view factors for all these points according to 27 surfaces was calculated. A total of 107,688 MRT data were created; then, the average MRT for all 641 points was obtained from the created data. As it moved from the NW wall to the SE wall, the MRT first decreased until the bottom value of 22.08 °C at x = 3.33 m. Then, it started to rise as it approached the SE wall and reached the highest value on this line at 23.9 °C. Comparing the MRT in areas close to the wall and in the center of the room with the air temperatures reveals, as expected, that the difference is greater in areas close to the wall. There is a 1.3 °C difference between the air temperature and the MRT, particularly owing to the southwest wall’s high surface temperature. The difference between the average radiant temperature and the atmospheric temperature was observed to be 0.7 °C in the room’s center, where radiant effects were partially diminished. Considering the scale of the room, there are no significant temperature differences between the areas near the radiant panels and the room’s center. The reason for this is that the room can be heated from the ceiling and walls simultaneously.
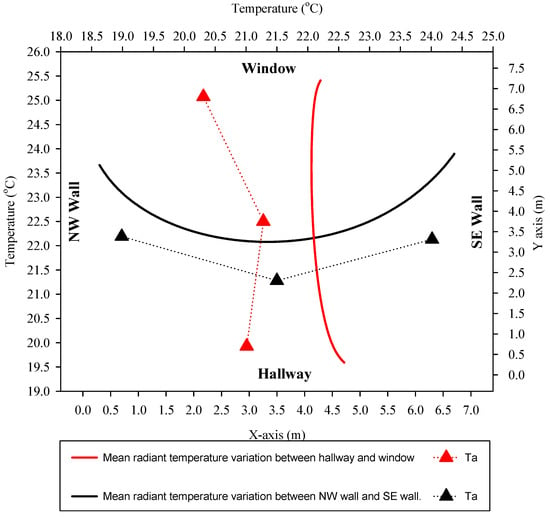
Figure 8.
Variation of the MRT from wall to wall and hallway to window.
As shown in Figure 8, the MRT values were determined from the corridor side of the room to the window side of the room. While the x and z coordinates remained constant at 3.5 m and 1.1 m, respectively, the y coordinate varied between 0.3 m and 7.2 m. As a result, a line was created with 691 points, each of which is 0.01 m away from the next point in the y-direction. As can be seen in Figure 7b, MRT values decreased as it moved from the SW (corridor side) to the NE (window side). At y = 0.3 m, MRT = 22.59 °C; at y = 6.7 m, MRT = 22.21 °C; and its lowest value MRT = 22.06 °C where y = 5.08 m. When examining the differences between MRT and air temperature, particularly near the hallway and window area, notable differences are observed, especially near the window area. At the location of Stand 1 near the window, there is a noticeable 1.8 °C difference between the calculated MRT value and the air temperature. This discrepancy is believed to be attributed to the measurement of temperature data from a single point on the glass surface during MRT computation. It is hypothesized that obtaining surface temperature data from various points on the glass surface could potentially mitigate this discrepancy.
Similarly, on the hallway side, albeit less pronounced than near the window, a difference of 1.4 °C is observed between the air temperature and MRT. It is assumed that acquiring temperature data from multiple points on the glass surfaces may yield improved outcomes, particularly in rooms where radiant effects are more prominent. Thus, the collection of temperature data from multiple points on the glass surfaces is postulated to lead to enhanced results in systems characterized by significant radiant effects.
Before proceeding to PMV-PPD calculations, this approach can be expanded and the MRT distribution observed at any desired plane. As this approach of creating multiple points in an order progresses from a line to a plane, two of the three coordinates change while the third remains constant. Figure 9, Figure 10 and Figure 11 show how the calculated radiant temperature varies at all points of the test room in detail.

Figure 9.
MRT distribution on the XZ plane of the room: (a) y = 0.3 m, (b) y = 3.75 m, (c) y = 7.2 m, and (d) placement of planes in the perspective view of the room.
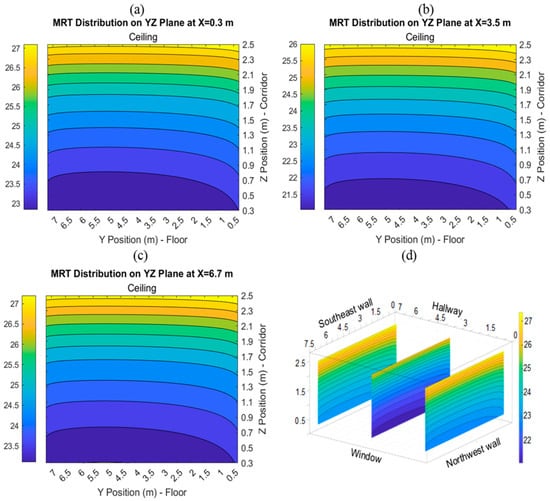
Figure 10.
MRT distribution on the YZ plane of the room: (a) x = 0.3 m, (b) x = 3.5 m, (c) x = 6.7 m, and (d) placement of planes in the perspective view of the room.
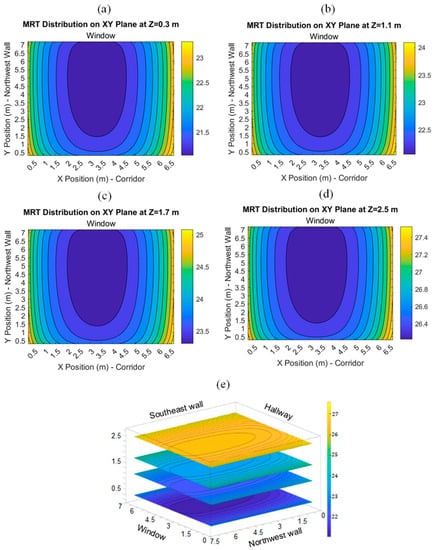
Figure 11.
MRT distribution on the XY plane of the room: (a) z = 0.3 m, (b) z = 1.1 m, (c) z = 1.7 m, (d) z = 2.5, and (e) placement of planes in the perspective view of the room.
Figure 9 illustrates the distribution of mean radiant temperature (MRT) on three XZ planes located at distinct y coordinates: y = 0.3 m, y = 3.75 m, and y = 7.2 m. Each of these planes comprised 641 points in the x-direction, ranging from x = 0.3 m to x = 6.7 m, with an increment of 0.01 m. Similarly, there were 221 points in the z-direction, ranging from z = 0.3 m to z = 2.5 m, with the same 0.01 m increment. Consequently, a total of 141,661 points existed within the XZ planes, with each point corresponding to 168 MRT measurements. The contour lines depicted in Figure 8 represent the MRT averages calculated for the points observed in the time interval between 12:12 and 14:59. The maximum MRT values found in the planes were 27.7 °C, 27.4 °C, and 27.4 °C, corresponding to the y coordinates of 0.3 m, 3.75 m, and 7.2 m, respectively. Conversely, the minimum temperatures observed were 21.6 °C, 21.1 °C, and 21.2 °C for the same y coordinates. The mean MRT values for the three planes (y = 0.3 m, y = 3.75 m, and y = 7.2 m) were 23.8 °C, 23.4 °C, and 23.6 °C, respectively. As predicted, areas proximate to the ceiling panels exhibited a notable prevalence of higher temperature distribution. It is evident that the temperature differentials exhibited a slight decrease when transitioning from the hallway area (y = 0.3 m) towards the window side (y = 7.2 m). Despite the high surface temperatures of the wall panels, it was observed that the MRT values did not exceed the reference temperature values recommended by ISO 7730 [8] and ASHREA 55 [43] standards, even near the panels.
Figure 10 illustrates how MRT changed on the YZ plane as well as the effects of plane positions in the x-direction on MRT. This plane had the same number of points in the z-direction as the XZ plane and 691 points in the y-direction between x = 0.3 m and y = 6.7 m, for a total of 152,711 points. Average MRT values were 24.47 °C, 23.03 °C, and 26.69 °C, with an x of 0.3 m, 3.5 m, and 6.7 m, respectively. When the average MRT values of the three planes were examined, it was found that there was approximately 1.5 °C difference in MRT with radiant wall panel sides compared to the middle of the test room. Based on these results and presuming that the tested room was utilized as a conference room, it can be speculated that the temperature difference perceived by occupants in the room’s center versus those near the room’s walls remains acceptable. As observed in Figure 10, the MRT distribution shows that the sections close to the NW wall have temperature distributions that are lower than those close to the SE wall. That disparity can be attributed to the presence of an actively heated office room situated behind the southeast wall, while an unheated elevator shaft is situated behind the northwest wall. The MRT distribution on XY planes at different heights is shown in Figure 11. There were 442,408 points in one contour where x was between 0.3 m and 6.7 m, and y was between 0.3 m and 7.2 m. While creating these contours, 74,412,408 MRT data points were calculated for each contour. The lowest MRT values calculated at 0.3 m, 1.1 m, 1.7 m, and 2.5 m heights from the test room’s floor were 21.04 °C, 22.06 °C, 23.31 °C, and 26.22 °C, while the maximum MRT values were 21.04 °C, 22.06 °C, 23.31 °C, and 26.22 °C. The highest temperatures were found in the test room’s SW and SE corners, while the lowest temperatures were found in the room’s center near the window area.
The average MRT values at 0.3 m, 1.1 m, 1.7 m, and 2.5 m heights were 21.7 °C, 22.6 °C, 23.8 °C, and 26.6 °C, respectively. The average temperature difference between the height of 0.3 m and the head level of a standing individual at 1.7 m was calculated at 2.1 °C, thereby meeting the comfort criteria outlined in the ISO 7730 Standard A [8]. As expected, the MRT distribution increased as it moved from the floor to the ceiling panels. As mentioned before, the temperature distribution near the SE wall was slightly higher than the NE wall. The reason behind this trend was that the elevator shaft was behind the NE wall, and there was a heated office behind the SE wall.
PMV and PPD were two indices employed for the assessment and prediction of thermal comfort. Both ASHRAE [43] and ISO [8] standards provide equations for calculating the PMV and PPD. In the present study, ISO 7730’s Equations (11)–(15) were utilized for this purpose. To compute the PMV, a MATLAB function was developed, incorporating various input parameters including metabolic rate, mechanical power, clothing surface area factor, air temperature, mean radiant temperature, air velocity, relative humidity, heat transfer coefficient, and clothing surface temperature.
Equations (12) and (13) were solved by iteration and pa was calculated using relative humidity. M and Icl refer to the metabolic rate and clothing insulation. ISO standardizes these parameters and offers tables for different situations. An office in a building was taken as the test room in this study, hence the M value was defined as sedentary activity and taken as 1.2 met. When it came to choosing the Icl parameter, since tests were taking place in February 2022, work clothing that fitted this category was chosen and an Icl of 1.00 clo (for underwear with short sleeves and legs, shirt, trousers, jacket, socks, and shoes) was determined. The effective mechanical power, W, was assumed to be 0 in this study.
The PMV and PPD values were measured every 20 min at five different locations in the test room. Figure 12 shows the changes in heated and unheated surface temperatures, air temperatures, outdoor ambient temperatures, and hallway temperatures in the test room during the experiments. The corridor and outdoor ambient temperatures, which were the important parameters that would affect thermal comfort, almost never changed during the experiments. That was practically very useful when comparing measurements taken at various points throughout the room.
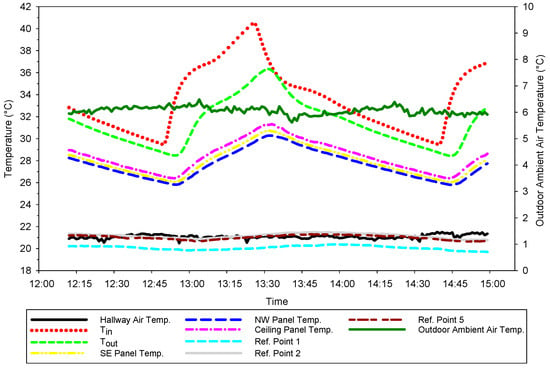
Figure 12.
Temperature measurement of the test room.
Several parameters including air temperature, air velocity, relative humidity, mean radiant temperature, metabolic rate, and clothing insulation were required according to the PMV and PPD equations. The metabolic rate and clothing insulation were predefined from the ISO standard tables; air temperature, relative humidity and air velocity were measured with a comfort device, and the MRT was measured with both a comfort device and Equation (7). The calculated MRTs were compared with globe thermometer measurements and approved in previous sections. Therefore, using the calculated MRT did not result in unacceptable deviations in the results.
When the dimensions of the testing room (7 × 7.5 × 2.8 m) were taken into the account, it might be somewhat challenging to ensure the level of thermal comfort was consistent throughout the entire space. Particularly during the heating seasons, localized disruptions may arise due to lower temperatures on cold wall and glass surfaces. To prevent this, wall and ceiling radiant heating systems have been included in many studies where they can be an alternative to conventional heating systems. Considering the size of the room, it was deemed necessary to measure the PMV and PPD values at various points using a thermal comfort device to ascertain the thermal comfort values in different regions of the test room. The MRT is a crucial factor affecting the radiant heat exchange between the human body and the environment, exerting a preponderant influence on thermal comfort indices like PMV and PPD [44]. Figure 12 shows how the PMV and PPD values would change according to the measurement values, if the MRT value was calculated using Equation (7). The measured and calculated (via ISO 7730 Standard) trends of the PMV and PPD values are presented in Table 6.

Table 6.
ISO 7730 thermal environment categories [8].
Table 7 shows the average parameters during the measurements at five points (see Figure 7) in the test room. During the measurement of comfort at various locations within the test room, it was observed that the air velocity values remained extremely low, predominantly as a result of the occurrence of natural convection, and the average relative humidity was measured to be around 40%.

Table 7.
Average measured values of air temperature, air velocity, and relative humidity.
Figure 13a and Figure 14a show the calculated and measured PMV and PPD values at Ref. Point 1 which was near the window.
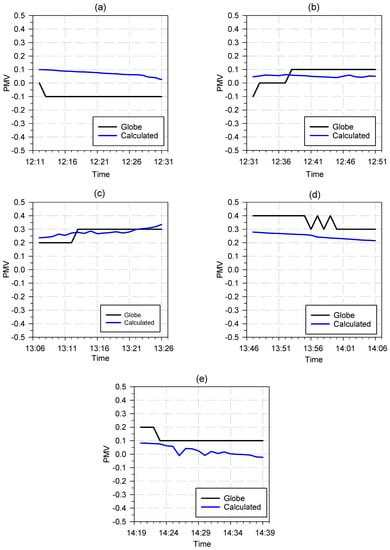
Figure 13.
Measured and calculated PMV at Ref. Point (a) 1, (b) 2, (c) 3, (d) 4 and (e) 5.

Figure 14.
Measured and calculated PPD at Ref. Point (a) 1, (b) 2, (c) 3, (d) 4 and (e) 5.
The mean value average of the calculated and measured PMV are close to each other with 0.073 and −0.095, respectively. Similarly, the average calculated and measured PPD values were almost the same with 5.12% and 5.19%. It was observed that the temperature data taken from a single point on the glass surface resulted in a high error in the MRT calculation method based on the view factor, and, therefore, there was a significant difference between the measured and calculated PMV and PPD values, especially near the glass area (Ref. Point 1). To obtain more accurate results of the comfort indices in buildings with such a high glass ratio, it was necessary to take measurements from various sections of the glass surfaces, particularly during the heating seasons.
Figure 13b and Figure 14b represent Ref. Point 2 that was in the middle of test room. While the calculated PMV and PPD values showed a more consistent pattern with an average of 0.051 PMV and 5.06%, the measured PMV and PPD values increased slightly at 12:37. Figure 13c and Figure 14c and Figure 13d and Figure 14d show a comparison of the measured and calculated PMV and PPD comfort values near the wall where the radiant panels were located. The existence of radiant panels on both walls caused the experimental and calculated PPD and PPV values to be high. The PMV and PPD values near both walls varied from 0.2 to 0.4 and from 5.8% to 7.2%, respectively, not meeting the ISO 7730 comfort standards in the A, B, and C category. The measured and calculated PMV and PPD values on the corridor side (Figure 13e and Figure 14e) were found to be quite well validated and meeting all ISO 7730 comfort standards.
The thermal comfort of living spaces with radiant systems can be controlled using many methods such as air temperature, operating temperature, model predictive control, and PMV. Although the air temperature-based thermostat control is an affordable and established way that has been used in many applications, some of previous efforts [45,46,47,48,49,50] also emphasized that this approach might be insufficient to provide the desired comfort conditions in radiant heating and cooling systems. Figure 14 shows how the PMV comfort parameter varied in different areas of the room by measuring air and surface temperatures of the experimental room solely using T-type thermocouples. Since the test room was conditioned with radiant heating, the humidity value and air velocity were taken as 50% and 0.05 m/s, respectively, in the PMV calculation.
In Figure 15a, when the air temperature parameter was taken from the thermocouple at point 3 or 4, the ISO 7730 category A comfort conditions could not be met. In other words, when the thermostat was set to point 3 or 4, the person sitting in point 1 would feel slightly warmer. The comfort conditions for an individual working at points 2 and 4 (Figure 15b,e) were similar regardless of where the thermostat was located. It was observed that when the thermostat was set to point 3, two of the individuals would feel uncomfortable according to the category A of the ISO 7730 Standard, while it was partially uncomfortable when set to point 4, and comfortable when set to points 1 and 2. A person sitting at points 3 and 4 (Figure 15c,d) naturally would feel warmer and more uncomfortable than other areas. Similarly, if the thermostat was placed in points 3 and 4, it could not meet the category A of the ISO 7730 Standard.
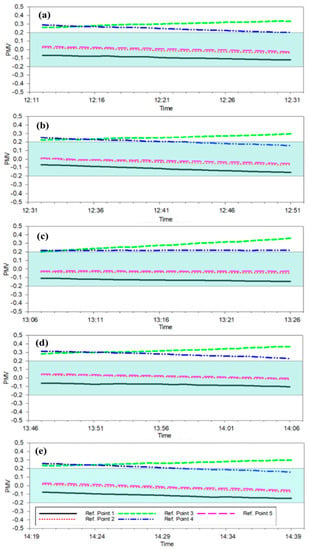
Figure 15.
PMV values at Ref. Point (a) 1, (b) 2, (c) 3, (d) 4, and (e) 5.
When all subfigures in Figure 15 were evaluated, regardless of where an individual would sit in the room, category A could not be achieved when the thermostat is placed at point 3 or 4, whereas categories B and C of the relevant standard (ISO 7730) are achieved. Comfort conditions could be achieved at all points if the air temperature values were taken from points 1, 2, and 5. Figure 15 can work with the help of a made-up scenario as well. For instance, Ref. Point 2 could be designated as a thermostat positioned on a meeting table situated in the central region of the office space, whereas Ref. Point 5 might represent an individual seated on a sofa. Moreover, points 1, 3, and 4 could symbolize individuals engaged in office work while seated at their respective desks. By employing this approach and utilizing data acquired from all the figures, a comprehensive assessment can be formulated.
5. Conclusions
This study aimed to determine the accuracy of a calculation method to obtain MRT and assess the thermal comfort of a test room, that was conditioned using a RHC system, with these temperatures. To prove the reliability of the calculation method, MRT at five different points of a test room with dimensions of 7 m × 7.5 m × 2.8 m was calculated for three hours on 24 February 2022. The calculated temperatures were then compared to the results of a black globe thermometer during the same time. Following the discussion of the results, the PMV and PPD values were included in the study as an index of thermal comfort. These calculated MRT values were examined and validated with readings from a comfort device. According to the given information, some conclusions are given as follows:
- The method based on surface temperatures and angle factors demonstrated a high degree of compatibility and accuracy with globe thermometer measurements. However, the temperature data obtained at a single point on the glass surface caused a high error in the MRT calculation method based on the view factor; consequently, there was a significant discrepancy between the measured and calculated PMV and PPD values, particularly in the nearby region of the glass area. Measurements need to be taken from several sections of the glass surfaces to obtain accurate comfort indices in buildings with a high glass ratio, especially during the heating seasons.
- Comparing MRT values obtained from the globe thermometer (ranging between 21 °C and 23.7 °C) with calculated values (ranging between 21.24 °C and 24.71 °C), Ref. Point 4 showed the closest match, with a mere 0.17 °C difference between calculated and measured values.
- For the next step of the study, two lines at different directions across the test room were created and the change of MRT on these lines were examined. The MRT near the NW side of the test room was lower than the SE side approximately by 0.3 °C. This is because the unheated elevator shaft is located behind the northwest wall of the test room.
- Several planes at different positions were obtained and the MRT distribution on these planes was studied. When the MRT distribution on the XY plane at a 1.1 m height that represented head level for a seated person is considered, the MRT changed from 22.63 °C to 24.30 °C. If an MRT of 23 °C was accepted as a threshold, it is observed that 22.72% of all created 442,931 points on this plane were higher than the threshold and accumulated on the NW and SE sides of the test room.
- The PMV and PPD were also studied to assess thermal comfort in the last section. After the validation of the obtained MRT values using the calculation method that used surface temperatures and view factors, the PMV and PPD values were calculated according to the ISO standards and compared with the results from the indoor air quality equipment.
- Ref. Points 1, 2, and 5 meet ISO 7730 category A conditions while points 3 and 4 that represented points near the radiant heating panels were not able to meet requirements.
In light of the above, the proposed model can be used as a time- and cost-effective approach for thermal comfort measurements instead of conventional globe thermometer measurements. Hereby, the model can increase its applicability in practical use.
Author Contributions
Conceptualization, A.D., N.K. and H.D.; methodology, A.D., N.K. and H.D.; software, A.D. and N.K.; validation, A.D.; formal analysis, A.D.; investigation, A.D.; resources, A.D.; data curation, A.D., N.K., H.D. and B.B.K.; writing—original draft preparation, A.D., N.K. and B.B.K.; writing—review and editing, A.D., N.K. and B.B.K.; visualization, A.D., N.K. and B.B.K.; supervision, N.K. and H.D.; project administration, N.K. and H.D.; funding acquisition N.K. and H.D. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by Yildiz Technical University under the BAP program with GRANT No. FBA-2019-3703. We would like to thank Yildiz Technical University for their financial support during this work.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank Yildiz Technical University for their financial support during this work.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| clo | Clothing insulation [clo] | Abbreviation | |
| D | Diameter of globe thermometer [m] | GSHP | Ground source heat pump |
| Eeff | Effective radiative flow | GHE | Ground heat exchanger |
| fcl | Clothing area factor | IAQ | Universal indoor air quality |
| Fi-j | View factor between the occupant and the surrounding surfaces | MRT | Mean radiant temperature |
| NW | Northwest | ||
| hc | Convective heat transfer coefficient [W/m2∙K] | NE | Northeast |
| RH | Relative humidity | ||
| hcg | Convection coefficient between air and globe thermometer [W/m2∙K] | RHC | Radiant heating and cooling |
| PMV | Predicted mean vote | ||
| Icl | Clothing insulation (m2∙K/W) | PPD | Predicted percentage dissatisfied [%] |
| M | Metabolic rate [W/m2] | SE | Southeast |
| Ta | Indoor air temperature [°C] | SW | Southwest |
| Tb | Background temperature [°C] | Greek letters | |
| Tcl | Clothing surface temperature [°C] | εb | Emissivity of black spheres |
| Tg | Globe temperature [°C] | εp | Emissivity of polished spheres |
| Tin | Water supply temperature [°C] | εs | Emissivity of the sensor |
| Tout | Water return temperature [°C] | εg | Globe emissivity |
| Tpr | Plane radiant temperature [°C] | σ | Stefane Boltzmann’s constant, [W/m2∙K4] |
| Tr | Mean radiant temperature [°C] | ||
References
- International Energy Agency. Statistics Report Key World Energy Statistics 2020; IEA: Paris, France, 2020. [Google Scholar]
- Ministry of Energy and Natural Resources of Türkiye. Türkiye National Energy Plan 2022; Ministry of Energy and Natural Resources of Türkiye: Çankaya, Turkey, 2022.
- Policy Brief Energy Efficiency Trends in Buildings in the EU. In Most European Countries, Buildings Account for the Largest Share of Final Consumption. 2021. Available online: https://www.odyssee-mure.eu/publications/policy-brief/buildings-energy-efficiency-trends.html (accessed on 10 September 2023).
- Energy Market Regulatory Authority of Turkey. Market Development Report, 2020; Energy Market Regulatory Authority of Turkey: Ankara, Türkiye, 2020.
- Hickel, R. Directive 2010/31/Eu of the European Parliament and of the Council of 19 May 2010 on the Energy Performance of Buildings. Off. J. Eur. Union 1955, 63, 619. [Google Scholar]
- Turkish Ministry of Environment and Urbanization. Republic of Turkey Climate Change Action Plan 2011–2023; Turkish Ministry of Environment and Urbanization: Ankara, Turkey, 2011; p. 77.
- Delbeke, J.; Runge-Metzger, A.; Slingenberg, Y.; Werksman, J. The Paris Agreement. In Towards a Climate-Neutral Europe: Curbing the Trend; Routledge: London, UK, 2019; pp. 24–45. [Google Scholar] [CrossRef]
- ISO 7730:2005; Ergonomics of the Thermal Environment. Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the PMV and PPD Indices and Local Thermal Comfort Criteria. International Organization for Standardization: Geneva, Switzerland, 2015; Volume 2015.
- Circle, T. 2013 ASHRAE Handbook—Fundamentals; AbeBooks: Victoria, BC, Canada, 2013; ISBN 1936504472. [Google Scholar]
- Liao, W.; Luo, Y.; Peng, J.; Wang, D.; Yuan, C.; Yin, R.; Li, N. Experimental Study on Energy Consumption and Thermal Environment of Radiant Ceiling Heating System for Different Types of Rooms. Energy 2022, 244, 122555. [Google Scholar] [CrossRef]
- Rhee, K.N.; Kim, K.W. A 50 Year Review of Basic and Applied Research in Radiant Heating and Cooling Systems for the Built Environment. Build. Environ. 2015, 91, 166–190. [Google Scholar] [CrossRef]
- De Carli, M.; Scarpa, M.; Tomasi, R.; Zarrella, A. DIGITHON: A Numerical Model for the Thermal Balance of Rooms Equipped with Radiant Systems. Build. Environ. 2012, 57, 126–144. [Google Scholar] [CrossRef]
- Oravec, J.; Šikula, O.; Krajčík, M.; Arıcı, M.; Mohapl, M. A Comparative Study on the Applicability of Six Radiant Floor, Wall, and Ceiling Heating Systems Based on Thermal Performance Analysis. J. Build. Eng. 2021, 36, 102133. [Google Scholar] [CrossRef]
- Stetiu, C. Energy and Peak Power Savings Potential of Radiant Cooling Systems in US Commercial Buildings. Energy Build. 1999, 30, 127–138. [Google Scholar] [CrossRef]
- Le Dréau, J.; Heiselberg, P. Sensitivity Analysis of the Thermal Performance of Radiant and Convective Terminals for Cooling Buildings. Energy Build. 2014, 82, 482–491. [Google Scholar] [CrossRef]
- Chen, Q.; Li, N. Energy, Emissions, Economic Analysis of Air-Source Heat Pump with Radiant Heating System in Hot-Summer and Cold-Winter Zone in China. Energy Sustain. Dev. 2022, 70, 10–22. [Google Scholar] [CrossRef]
- Cvetković, D.; Bojić, M. Optimization of Thermal Insulation of a House Heated by Using Radiant Panels. Energy Build. 2014, 85, 329–336. [Google Scholar] [CrossRef]
- d’Ambrosio Alfano, F.R.; Dell’Isola, M.; Palella, B.I.; Riccio, G.; Russi, A. On the Measurement of the Mean Radiant Temperature and Its Influence on the Indoor Thermal Environment Assessment. Build. Environ. 2013, 63, 79–88. [Google Scholar] [CrossRef]
- Vernon, H.M. The Measurement of Radiant Heat in Relation to Human Comfort. J. Ind. Hyg. 1932, 14, 95–111. [Google Scholar]
- d’Ambrosio Alfano, F.R.; Dell’isola, M.; Ficco, G.; Palella, B.I.; Riccio, G. On the Measurement of the Mean Radiant Temperature by Means of Globes: An Experimental Investigation under Black Enclosure Conditions. Build. Environ. 2021, 193, 107655. [Google Scholar] [CrossRef]
- Alfano, F.R.D.; Ficco, G.; Frattolillo, A.; Palella, B.I.; Riccio, G. Mean Radiant Temperature Measurements through Small Black Globes under Forced Convection Conditions. Atmosphere 2021, 12, 621. [Google Scholar] [CrossRef]
- Ouyang, W.; Liu, Z.; Lau, K.; Shi, Y.; Ng, E. Comparing Different Recalibrated Methods for Estimating Mean Radiant Temperature in Outdoor Environment. Build. Environ. 2022, 216, 109004. [Google Scholar] [CrossRef]
- Kang, E.; Lee, R.; Yoon, J.; Cho, H.; Kim, D. Uncertainty Assessment of Mean Radiant Temperature Estimation for Indoor Thermal Comfort Based on Clustering Analysis of Reduced-Input Surfaces. Buildings 2023, 13, 342. [Google Scholar] [CrossRef]
- Tamrakar, S.; Chen, L.; Sørensen, B.R. Variation of Mean Radiant Temperature in Rooms for Summer and Winter Conditions. Energies 2023, 16, 5609. [Google Scholar] [CrossRef]
- Lee, D.S.; Kim, E.J.; Cho, Y.H.; Kang, J.W.; Jo, J.H. A Field Study on Application of Infrared Thermography for Estimating Mean Radiant Temperatures in Large Stadiums. Energy Build. 2019, 202, 109360. [Google Scholar] [CrossRef]
- Tan, C.L.; Wong, N.H.; Jusuf, S.K. Outdoor Mean Radiant Temperature Estimation in the Tropical Urban Environment. Build. Environ. 2013, 64, 118–129. [Google Scholar] [CrossRef]
- Park, C.Y.; Lee, D.K.; Krayenhoff, E.S.; Heo, H.K.; Hyun, J.H.; Oh, K.; Park, T.Y. Variations in Pedestrian Mean Radiant Temperature Based on the Spacing and Size of Street Trees. Sustain. Cities Soc. 2019, 48, 101521. [Google Scholar] [CrossRef]
- Guo, H.; Ferrara, M.; Coleman, J.; Loyola, M.; Meggers, F. Simulation and Measurement of Air Temperatures and Mean Radiant Temperatures in a Radiantly Heated Indoor Space. Energy 2020, 193, 116369. [Google Scholar] [CrossRef]
- Kalmár, F.; Kalmár, T. Interrelation between Mean Radiant Temperature and Room Geometry. Energy Build. 2012, 55, 414–421. [Google Scholar] [CrossRef]
- Walikewitz, N.; Jänicke, B.; Langner, M.; Meier, F.; Endlicher, W. The Difference between the Mean Radiant Temperature and the Air Temperature within Indoor Environments: A Case Study during Summer Conditions. Build. Environ. 2015, 84, 151–161. [Google Scholar] [CrossRef]
- Hwang, R.L.; Fang, P.L.; Chen, W.A. Impact of Solar Radiation on Indoor Thermal Comfort near Highly Glazed Façades in a Hot-Humid Subtropical Climate: An Experimental Evaluation. Build. Environ. 2023, 243, 110725. [Google Scholar] [CrossRef]
- Song, B.; Bai, L.; Yang, L. Analysis of the Long-Term Effects of Solar Radiation on the Indoor Thermal Comfort in Office Buildings. Energy 2022, 247, 123499. [Google Scholar] [CrossRef]
- Özbey, M.F.; Turhan, C. A Comprehensive Comparison and Accuracy of Different Methods to Obtain Mean Radiant Temperature in Indoor Environment. Therm. Sci. Eng. Prog. 2022, 31, 101295. [Google Scholar] [CrossRef]
- Kayaci, N.; Demir, H. Comparative Performance Analysis of Building Foundation Ground Heat Exchanger. Geothermics 2020, 83, 101710. [Google Scholar] [CrossRef]
- Kayaci, N.; Demir, H.; Kanbur, B.B.; Atayilmaz, Ş.O.; Agra, O.; Acet, R.C.; Gemici, Z. Experimental and Numerical Investigation of Ground Heat Exchangers in the Building Foundation. Energy Convers Manag. 2019, 188, 162–176. [Google Scholar] [CrossRef]
- EN 14240:2004; Ventilation for Buildings Chilled Ceilings Testing and Rating. CEN: Brussels, Belgium, 2004.
- Doğan, A.; Kayaci, N.; Demİr, H.; Sevİndİr, M.K. Experimental Investigation of Thermal Comfort Performance of a Radiant Wall and Ceiling Panel System. J. Ther. Eng. 2022, 8, 551–561. [Google Scholar] [CrossRef]
- Kline, S.J. Describing Uncertainties in Single-Sample Experiments. Mech. Eng. 1963, 75, 3–8. [Google Scholar]
- Marino, C.; Nucara, A.; Peri, G.; Pietrafesa, M.; Rizzo, G. A Generalized Model of Human Body Radiative Heat Exchanges for Optimal Design of Indoor Thermal Comfort Conditions. Solar Energy 2018, 176, 556–571. [Google Scholar] [CrossRef]
- Marino, C.; Nucara, A.; Peri, G.; Rizzo, G.; Scaccianoce, G. The Spatial Evaluation of the Radiative Human Body Heat Exchanges: An Effective Contribution for Limiting Energy Consumption and Achieving Better Indoor Conditions in Buildings. J. Build. Eng. 2018, 16, 118–128. [Google Scholar] [CrossRef]
- La Gennusa, M.; Nucara, A.; Pietrafesa, M.; Rizzo, G.; Scaccianoce, G. Angle Factors and Projected Area Factors for Comfort Analysis of Subjects in Complex Confined Enclosures: Analytical Relations and Experimental Results. Indoor Built Environ. 2008, 17, 346–360. [Google Scholar] [CrossRef]
- Dong, Q.; Li, S.; Han, C. Numerical and Experimental Study of the Effect of Solar Radiation on Thermal Comfort in a Radiant Heating System. J. Build. Eng. 2020, 32, 101497. [Google Scholar] [CrossRef]
- Standard 55; Thermal Environmental Conditions for Human Occupancy. ANSI/ASHRAE: Atlanta, GA, USA, 1992.
- Catalina, T.; Virgone, J.; Kuznik, F. Evaluation of Thermal Comfort Using Combined CFD and Experimentation Study in a Test Room Equipped with a Cooling Ceiling. Build. Environ. 2009, 44, 1740–1750. [Google Scholar] [CrossRef]
- Joe, J.; Karava, P. A Model Predictive Control Strategy to Optimize the Performance of Radiant Floor Heating and Cooling Systems in Office Buildings. Appl. Energy 2019, 245, 65–77. [Google Scholar] [CrossRef]
- Hassan, M.A.; Abdelaziz, O. Best Practices and Recent Advances in Hydronic Radiant Cooling Systems—Part II: Simulation, Control, and Integration. Energy Build. 2020, 224, 110263. [Google Scholar] [CrossRef]
- Kang, D.H.; Mo, P.H.; Choi, D.H.; Song, S.Y.; Yeo, M.S.; Kim, K.W. Effect of MRT Variation on the Energy Consumption in a PMV-Controlled Office. Build. Environ. 2010, 45, 1914–1922. [Google Scholar] [CrossRef]
- Jia, H.; Pang, X.; Haves, P. Experimentally-Determined Characteristics of Radiant Systems for Office Buildings. Appl. Energy 2018, 221, 41–54. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F. Theory and Applications of HVAC Control Systems—A Review of Model Predictive Control (MPC). Build. Environ. 2014, 72, 343–355. [Google Scholar] [CrossRef]
- Karlsson, H.; Hagentoft, C.E. Application of Model Based Predictive Control for Water-Based Floor Heating in Low Energy Residential Buildings. Build. Environ. 2011, 46, 556–569. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).