Application of GSM-SVM for Forecasting Construction Output: A Case Study of Hubei Province
Abstract
1. Introduction
- (1)
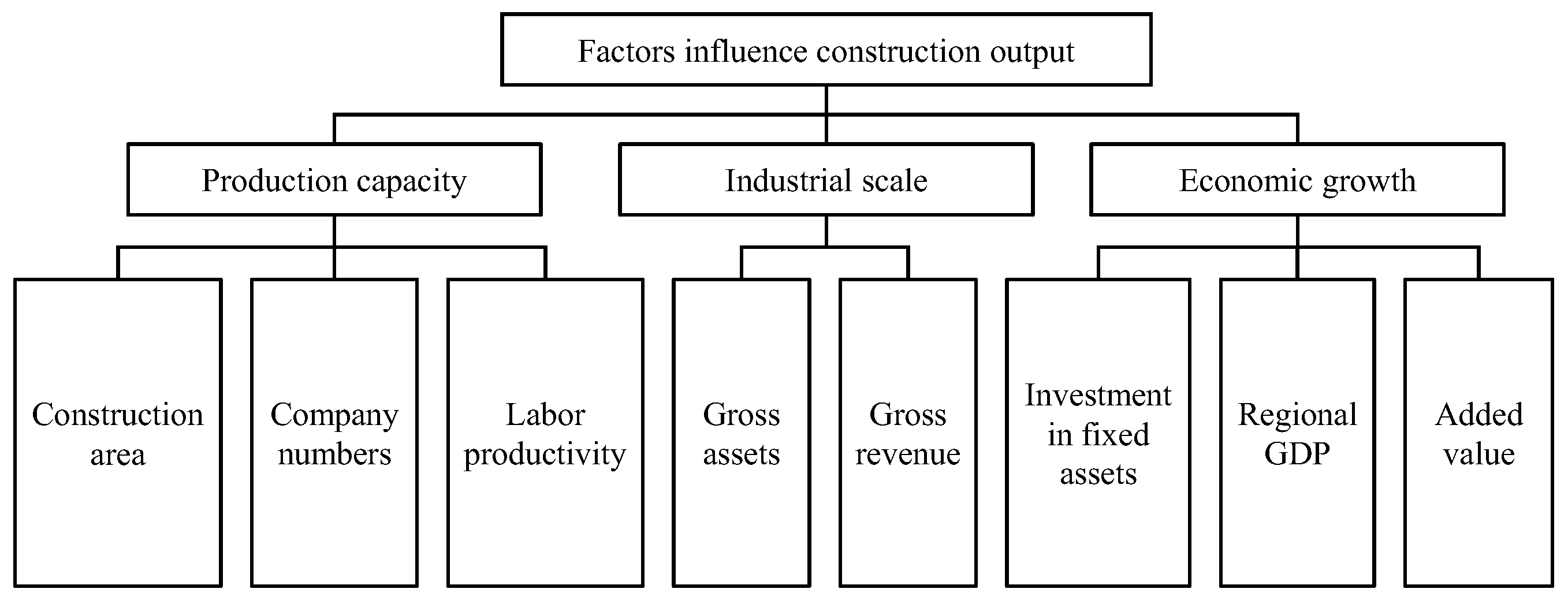
- Screening scientific and practical influencing factor indicators are the basis for construction output to conduct predictive analysis research. Based on the literature and related research, the evaluation index system for influencing factors is proposed by combining it with the current Chinese construction industry development situation to screen out the more scientific influencing factors of construction output.
- (2)
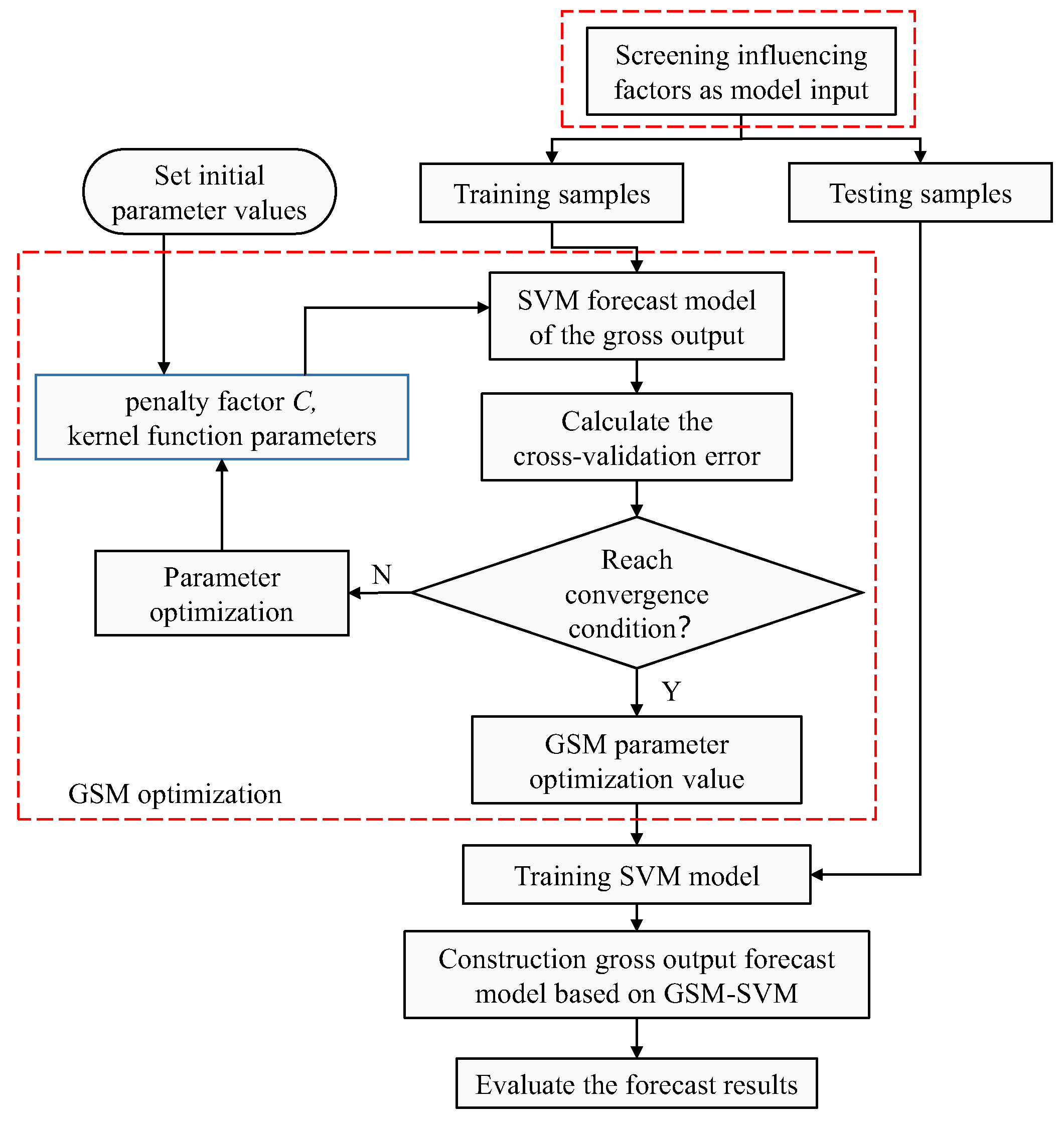
- A grid search method is used to optimize the SVM algorithm to find the optimal combination of values of penalty factor C and kernel function parameters g to improve the recognition accuracy and prediction performance of the SVM prediction model.
- (3)
- The SVM algorithm attempts to apply to Chinese construction output forecasting, and related experiments verify that the GSM-SVM forecasting model has higher accuracy and is a critical extension of the economic forecasting method of the construction industry.
2. Related Works
2.1. Current Status of Research on Factors Influencing Construction Output
2.2. Current Status of Research on Construction Output Forecasting
3. Related Methods
3.1. Definition
3.2. Construction of the Index System
3.3. SVM Prediction Model Based on GSM Optimization
4. Results and Discussion
4.1. Data Sources and Data Pre-Processing
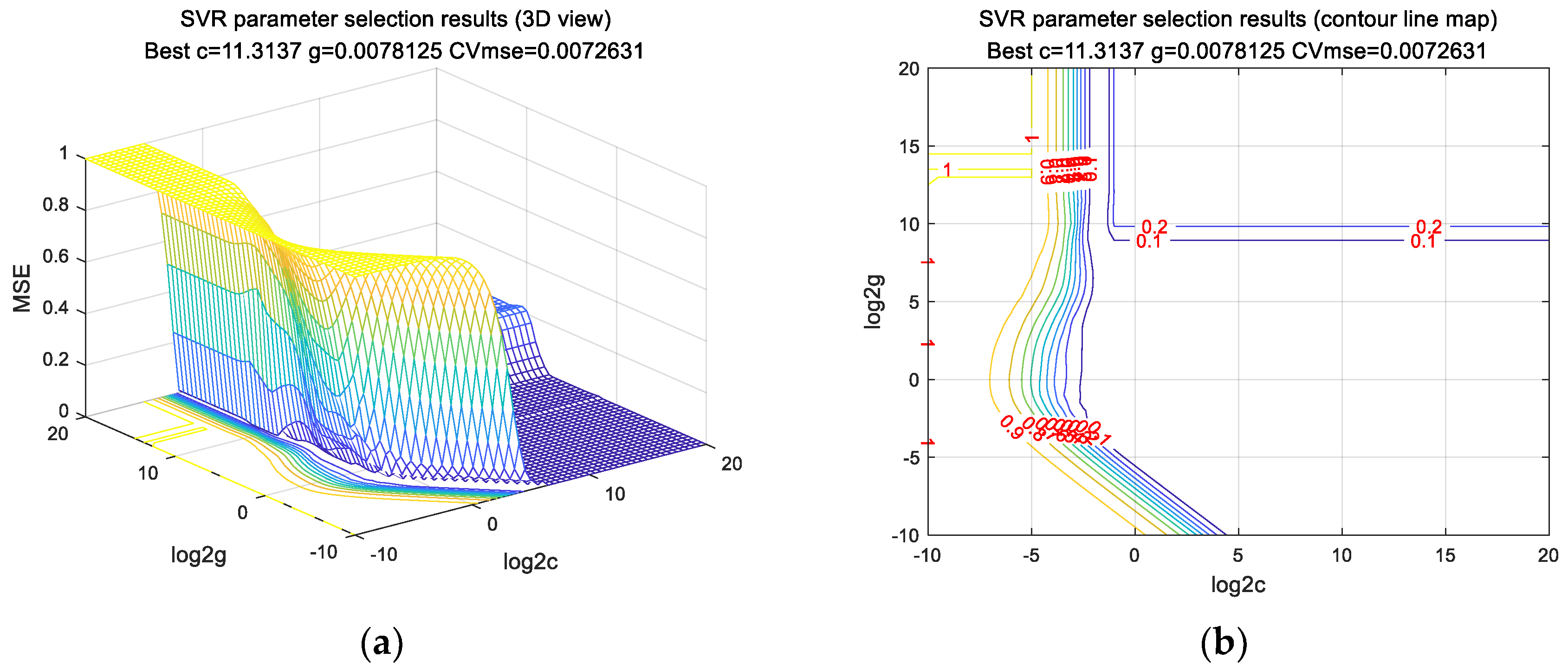
4.2. Model Fitting Based on GSM-SVM
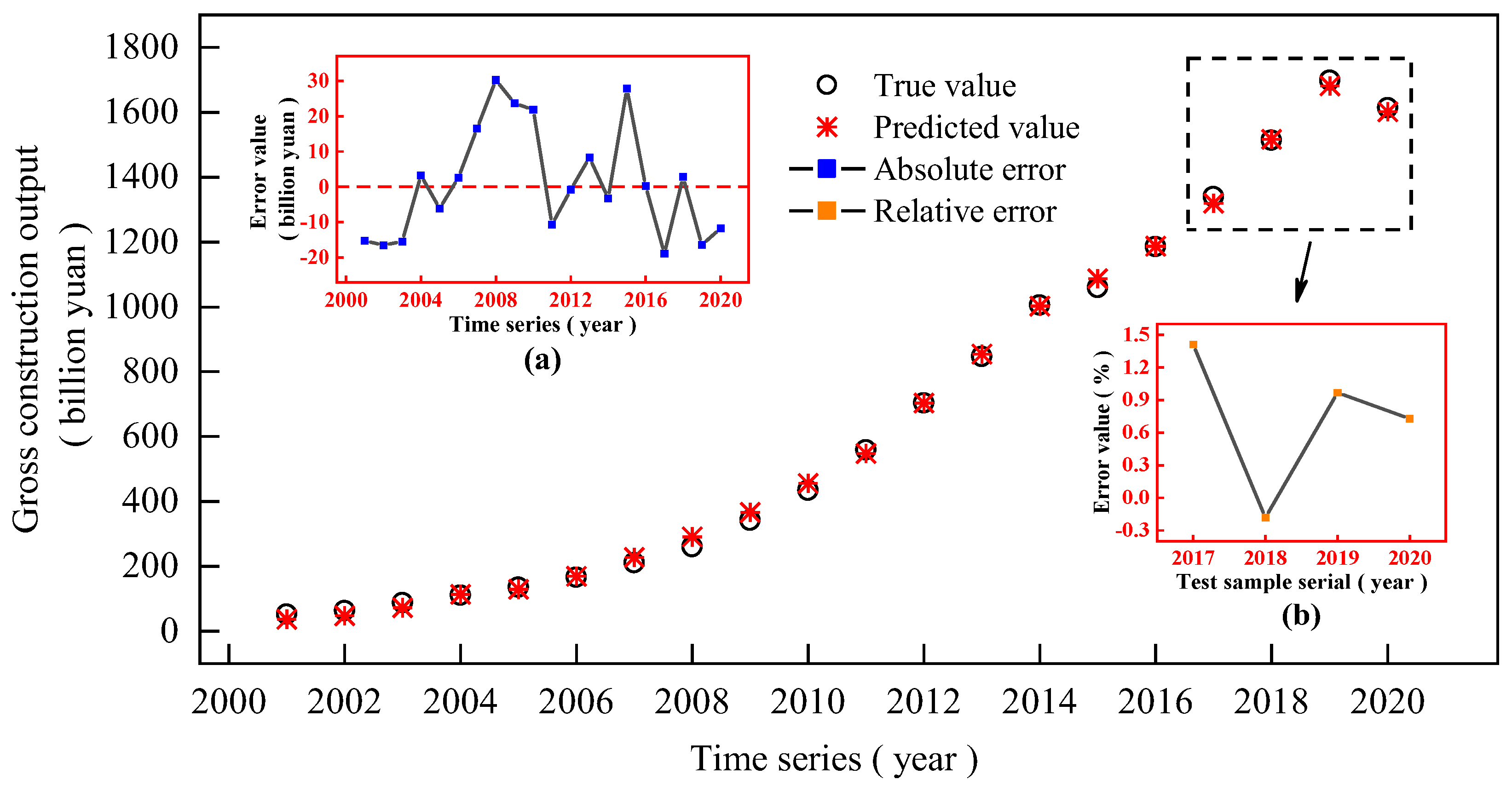
4.3. Model Comparison and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Giang, D.T.; Pheng, L.S. Role of construction in economic development: Review of key concepts in the past 40 years. Habitat Int. 2011, 35, 118–125. [Google Scholar] [CrossRef]
- Anaman, K.A.; Osei-Amponsah, C. Analysis of the causality links between the growth of the construction industry and the growth of the macro-economy in Ghana. Constr. Manag. Econ. 2007, 25, 951–961. [Google Scholar] [CrossRef]
- Yang, X.; Cheng, J. Economic Forecasting: Characteristics and Quantitative Methods. Syst. Sci. Math. 2019, 39, 1553–1582. [Google Scholar]
- Lu, X. The Growth Path and Affecting Factors of Construction Industry in China. Doctoral Dissertation, Xi’an University of Architecture and Technology, Xi’an, China, 2003. [Google Scholar]
- Yi, Z. The Research of the Development Prediction and the Space of Construction Industry’s Growth-Based on the Analysis of Chongqing’s Construction Industry. Master’s Thesis, Chongqing University, Chongqing, China, 2014. [Google Scholar]
- Tang, J.J.; Liang, W.Z.; Hu, S.H.; Zhao, T.S. Present Situation Analysis and Development Trend Forecast of Construction Industry. J. Civ. Eng. Manag. 2012, 121, 84–88. [Google Scholar] [CrossRef]
- Zhang, L.; Li, H. Application of ARIMA model to forecast the total output value of construction industry in China. Enterp. Econ. 2011, 11, 93–96. [Google Scholar] [CrossRef]
- Li, X. Study on the Comprehensive Evaluation and Prediction of Construction Industry in Anhui Province. Master’s Thesis, Anhui University of Construction, Hefei, China, 2017. [Google Scholar]
- Liu, L.; Wu, L. Predicting the output value of assembled buildings based on grey mean model. Math. Pract. Underst. 2019, 15, 104–111. [Google Scholar]
- Li, H. Research on the Evaluation of the Development of Construction Industry in China Based on Multi-Technology. Master’s Thesis, Northeast Forestry University, Harbin, China, 2012. [Google Scholar]
- Guang, H. Research on Forecasting Value Added in Construction Industry Based on GA Optimized Grey Neural Network Model. China Constr. Met. Struct. 2021, 5, 12–13. [Google Scholar]
- Yang, S. The Empirical Research on Factors Affecting the Development of the Construction Industry in Anhui. Master’s Thesis, Anhui University of Finance and Economics, Bengbu, China, 2017. [Google Scholar]
- Zhang, Y. Research on the Economic Status Evaluation and Comparison of the Technical Efficiency for Construction Industry in Guangdong Province. Doctoral Dissertation, South China University of Technology, Guangzhou, China, 2015. [Google Scholar]
- Dai, Y.A.; Chen, C. Technical Efficiency in China’s Construction Industry and Its Influencing Factors. China Soft Sci. 2010, 1, 87–95. [Google Scholar]
- Hua, R. Research on Evaluation and Influencing Factors of High-Quality Development of China’s Construction Industry. Master’s Thesis, Anhui University of Construction, Hefei, China, 2021. [Google Scholar]
- Wang, X.; Wang, Z. Study on the Temporal and Spatial Difference of Construction Efficiency in the Yangtze River Economic Belt. Constr. Econ. 2021, 42, 14–18. [Google Scholar] [CrossRef]
- Jiang, J. Research on the Evaluation System of High-Quality Development of Provincial Construction Industry in China. Master’s Thesis, Guangzhou University, Guangzhou, China, 2021. [Google Scholar]
- Peng, X. Research on the High-Quality Development of the Construction Industry in Anhui Province under the Background of the Integration of the Yangtze River Delta. Master’s Thesis, Anhui University of Construction, Hefei, China, 2022. [Google Scholar]
- Wang, Y.; Wu, X. Research on High-Quality Development Evaluation, Space–Time Characteristics and Driving Factors of China’s Construction Industry under Carbon Emission Constraints. Sustainability 2022, 14, 10729. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Behzad, M.; Asghari, K.; Eazi, M.; Palhang, M. Generalization performance of support vector machines and neural networks in runoff modeling. Expert Syst. Appl. 2009, 36, 7624–7629. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, C.; Zhou, A. Prediction Model for Stability Classification of Roadway Surrounding Rock Based on Grid Search Method and Support Vector Machine. Saf. Coal Mines 2017, 48, 200–203. [Google Scholar] [CrossRef]
- Zhang, C.; Tian, Y.; Deng, N. The new interpretation of support vector machines on statistical learning theory. Sci. China Math. 2010, 53, 151–164. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, S.; Li, J. Time Series Prediction Based on Support Vector Regression. Inf. Technol. J. 2006, 5, 353–357. [Google Scholar]
- Zhang, T. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods. AI Mag. Artif. Intell. 2001, 22, 103. [Google Scholar]
- Raghavendra, N.S.; Deka, P.C. Support vector machine applications in the field of hydrology: A review. Appl. Soft Comput. 2014, 19, 372–386. [Google Scholar] [CrossRef]
- Virmani, J.; Kumar, V.; Kalra, N.; Khandelwal, N. SVM-Based Characterization of Liver Ultrasound Images Using Wavelet Packet Texture Descriptors. J. Digit. Imaging 2012, 26, 530–543. [Google Scholar] [CrossRef]
- Wu, M. Parameter Optimization Method Research and Application of RBF Neural Network and SVM. Master’s Thesis, Central South University, Changsha, China, 2007. [Google Scholar]
- Scholkopf, B.; Sung, K.-K.; Burges, C.; Girosi, F.; Niyogi, P.; Poggio, T.; Vapnik, V. Comparing support vector machines with Gaussian kernels to radial basis function classifiers. IEEE Trans. Signal Process. 1997, 45, 2758–2765. [Google Scholar] [CrossRef]
- Wang, Q.; Zheng, J. Study of network parameter model base on support vector machine. Mod. Electron. Tech. 2015, 12, 23–24+28. [Google Scholar] [CrossRef]
- Boolchandani, D.; Ahmed, A.; Sahula, V. Efficient kernel functions for support vector machine regression model for analog circuits’ performance evaluation. Analog. Integr. Circuits Signal Process. 2011, 66, 117–128. [Google Scholar] [CrossRef]
- Gao, Y. Research on Factors Affecting the Economic Growth of the Construction Industry in Henan Province. Master’s Thesis, Zhengzhou University, Zhengzhou, China, 2014. [Google Scholar]
- Hu, W.; Kong, D.; He, X. Analysis on Influencing Factors of Green Building Development Based on BP-WINGS. Soft Sci. 2020, 34, 75–81. [Google Scholar] [CrossRef]
- Cui, X. Empirical Analysis on Influence Factor of Economic Growth in Henan Construction Industry. Constr. Econ. 2012, 3, 99–101. [Google Scholar] [CrossRef]
- Ding, Z.; Fan, Z.; Tam, V.W.; Bian, Y.; Li, S.; Illankoon, I.C.S.; Moon, S. Green building evaluation system implementation. Build. Environ. 2018, 133, 32–40. [Google Scholar] [CrossRef]
- Chen, C.; Cao, X.; Zhang, S.; Lei, Z.; Zhao, K. Dynamic Characteristic and Decoupling Relationship of Energy Consumption on China’s Construction Industry. Buildings 2022, 12, 1745. [Google Scholar] [CrossRef]
- Li, H.; Han, Z.; Zhang, J.; Philbin, S.P.; Liu, D.; Ke, Y. Systematic Identification of the Influencing Factors for the Digital Transformation of the Construction Industry Based on LDA-DEMATEL-ANP. Buildings 2022, 12, 1409. [Google Scholar] [CrossRef]
- Tian, M.; Liu, S.; Bu, Z. Review of research on grey relational degree algorithm model. Stat. Decis. 2008, 1, 24–27. [Google Scholar]
- Yin, K.; Xu, T.; Li, X.; Cao, Y. A study of the grey relational model of interval numbers for panel data. Grey Syst. Theory Appl. 2020, 11, 200–211. [Google Scholar] [CrossRef]
- Cui, J.; Yuan, W. Optimization of Support Vector Machine Parameters Based on Intelligent Algorithm. J. Hebei Norm. Univ. Sci. Technol. 2017, 1, 34–38. [Google Scholar]
- Gaspar, P.; Carbonell, J.; Oliveira, J.L. On the parameter optimization of Support Vector Machines for binary classification. J. Integr. Bioinform. 2012, 9, 33–43. [Google Scholar] [CrossRef]
- Xu, C.; Cao, H.; Zhao, X. Speaker Recognition Parameter Selection Method Based on SVM. Comput. Eng. 2012, 38, 175–177. [Google Scholar]
- Xu, W.; Liu, C. A Regression Model for Forecasting Regional Annual Water-consumed Quantity Based on GSM and SVM. J. Shenyang Agric. Univ. 2011, 42, 238–240. [Google Scholar]
- Tahyudin, I.; Nambo, H.; Goto, Y. An Optimization of the Autoregressive Model Using the Grid Search Method. Int. J. Eng. Technol. 2018, 7, 84–86. [Google Scholar] [CrossRef][Green Version]
- Wang, X.; Li, Z. Identifying the Parameters of the Kernel Function in Support Vector Machines Based on the Grid-Search Method. Period. Ocean. Univ. China 2005, 35, 859–862. [Google Scholar] [CrossRef]
- Wang, S.; Jin, Z. Intrusion detection classification algorithm based on fuzzy SVM model. Comput. Appl. Res. 2020, 2, 501–504. [Google Scholar] [CrossRef]
- Wang, Y. Research on the Methods of Combining Forecasts Based on Correlativity. Forecasting 2002, 21, 58–62. [Google Scholar]
| Existing Method | Method Limitations | SVM Advantages | |
|---|---|---|---|
| Forecast of gross output of construction industry | linear regression, ARIMA Model | For linear relationships only, it cannot predict unstable data; | Kernel function can be used to solve non-linear, high-dimensional problems; |
| Grey GM (1,1) | Not suitable for non-linear prediction, does not consider the influence of related factors; | Input influencing factors as feature vectors; | |
| BP Neural Network | Converge to a local minimum rather than a global minimum, usually results in overfitting and unstable output data; | Obtained the optimal global solution, low generalization error rate, and more suitable for small sample learning; |
| Evaluation Items | Construction Area | Company Number | Labor Productivity | Gross Assets | Gross Revenue | Investment in Fixed Assets | Regional GDP | Added Value |
|---|---|---|---|---|---|---|---|---|
| Correlation | 0.863 | 0.718 | 0.725 | 0.915 | 0.930 | 0.857 | 0.782 | 0.822 |
| Year | Construction Area (Thousand m2) | Company Number (Unit) | Labor Productivity (Yuan/Person) | Gross Assets (Billion Yuan) | Gross Revenue (Billion Yuan) | Investment in Fixed Assets (Billion Yuan) | Regional GDP (Billion Yuan) | Added Value (Billion Yuan) | Gross Output (Billion Yuan) |
|---|---|---|---|---|---|---|---|---|---|
| 2020 | 852,682.0 | 4633 | 752,079 | 1581.790 | 1480.225 | 2341.263 | 4344.35 | 282.80 | 1613.611 |
| 2019 | 920,422.3 | 4566 | 675,791 | 1488.138 | 1608.693 | 2886.884 | 4542.90 | 307.31 | 1697.967 |
| 2018 | 882,381.0 | 4196 | 595,205 | 1303.266 | 1435.736 | 2603.141 | 4202.20 | 278.14 | 1513.387 |
| 2017 | 792,576.9 | 3692 | 525,908 | 1145.165 | 1248.490 | 2377.298 | 3723.50 | 234.25 | 1339.073 |
| 2016 | 728,350.5 | 3368 | 458,776 | 985.331 | 1165.986 | 2287.658 | 3335.30 | 210.92 | 1186.240 |
| 2015 | 622,047.2 | 3218 | 454,961 | 889.491 | 1113.957 | 2182.603 | 3034.40 | 195.78 | 1059.286 |
| 2014 | 622,278.8 | 3217 | 487,456 | 755.753 | 971.267 | 1818.542 | 2824.21 | 187.54 | 1005.959 |
| 2013 | 489,379.6 | 3197 | 486,265 | 635.188 | 834.340 | 1431.225 | 2537.80 | 165.70 | 846.527 |
| 2012 | 391,139.0 | 2774 | 410,437 | 585.253 | 708.284 | 1105.416 | 2259.09 | 141.79 | 704.342 |
| 2011 | 310,237.5 | 2640 | 261,332 | 487.432 | 568.842 | 805.652 | 1994.25 | 124.68 | 558.645 |
| 2010 | 250,467.0 | 2846 | 268,719 | 375.635 | 465.363 | 670.191 | 1622.69 | 102.27 | 434.520 |
| 2009 | 204,993.3 | 2860 | 234,352 | 311.270 | 364.885 | 502.562 | 1319.21 | 84.23 | 342.189 |
| 2008 | 182,728.6 | 2972 | 193,189 | 225.493 | 264.597 | 356.897 | 1149.75 | 67.57 | 260.508 |
| 2007 | 166,796.8 | 2490 | 167,141 | 196.809 | 215.524 | 285.731 | 945.14 | 54.49 | 211.080 |
| 2006 | 144,782.4 | 2271 | 145,998 | 134.349 | 170.648 | 225.272 | 753.18 | 41.80 | 166.700 |
| 2005 | 120,911.6 | 2072 | 122,576 | 114.010 | 136.572 | 169.68 | 646.97 | 35.74 | 134.932 |
| 2004 | 107,201.3 | 2417 | 96,520 | 106.860 | 113.538 | 140.925 | 554.68 | 32.52 | 111.213 |
| 2003 | 89,334.4 | 1746 | 81,761 | 90.862 | 94.460 | 105.998 | 475.75 | 27.39 | 87.300 |
| 2002 | 72,275.0 | 1579 | 69,478 | 74.870 | 65.506 | 97.473 | 421.28 | 23.69 | 63.655 |
| 2001 | 66,626.0 | 1637 | 63,664 | 60.080 | 52.588 | 89.060 | 388.05 | 21.43 | 52.902 |
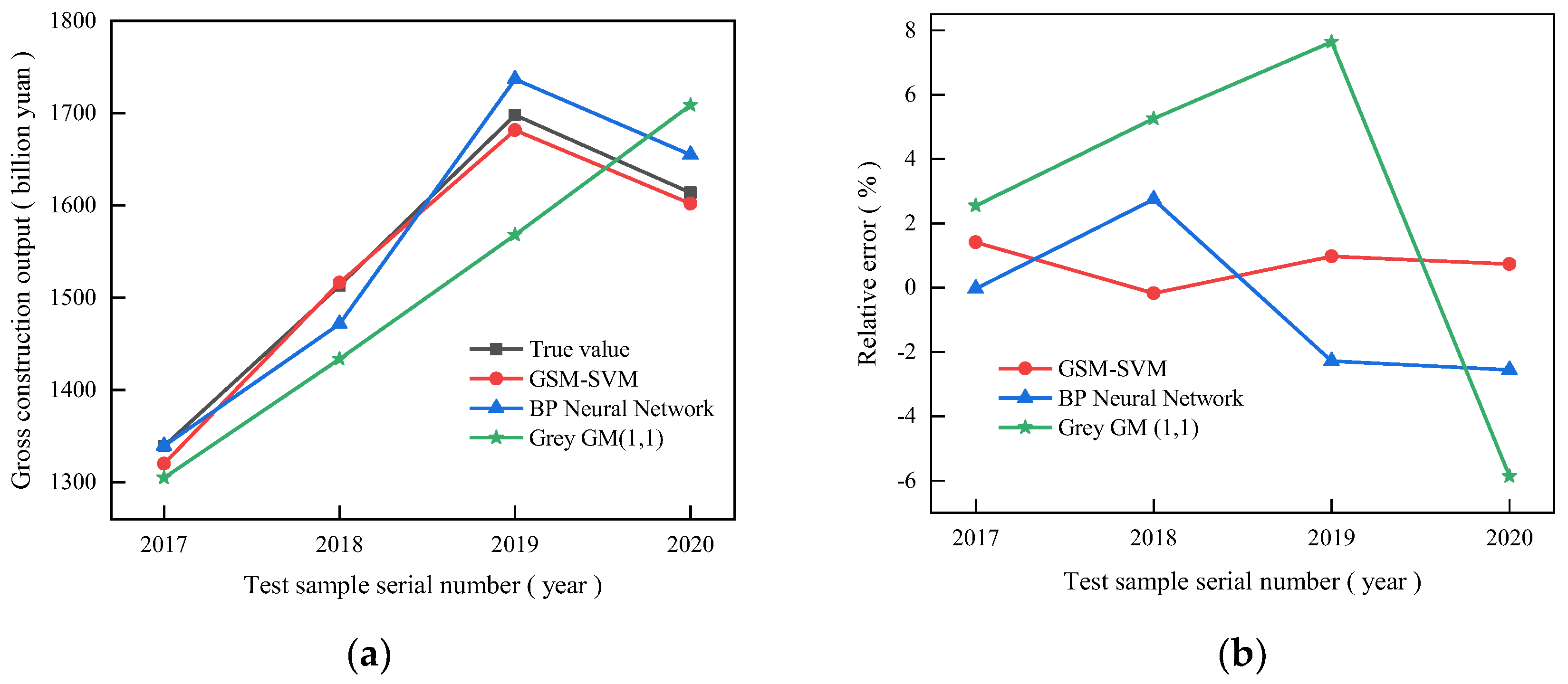
| Year | Actual Value (Billion Yuan) | Value Forecasted by the GSM-SVM Model (Billion Yuan) | Relative Error (%) | Value Forecasted by the BP Neural Network (Billion Yuan) | Relative Error (%) | Value Forecasted by the Grey GM (1,1) (Billion Yuan) | Relative Error (%) |
|---|---|---|---|---|---|---|---|
| 2020 | 1613.611 | 1601.869 | 0.7277 | 1654.968 | −2.5630 | 1708.434 | −5.8764 |
| 2019 | 1697.967 | 1681.539 | 0.9675 | 1736.754 | −2.2843 | 1568.251 | 7.6395 |
| 2018 | 1513.387 | 1516.158 | −0.1831 | 1471.862 | 2.7438 | 1433.838 | 5.2563 |
| 2017 | 1339.073 | 1320.183 | 1.4107 | 1339.562 | −0.0366 | 1304.956 | 2.5478 |
| Value Forecasted by the GSM-SVM Model | Value Forecasted by the BP Neural Network | Value Forecasted by the Grey GM (1,1) | |
|---|---|---|---|
| (MAPE) % | 0.823 | 1.905 | 5.333 |
| (TIC) % | 0.413 | 0.951 | 2.704 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, M.; He, Y.; Wang, D.; He, D.; Feng, Y.; Cheng, L.; Qin, Z. Application of GSM-SVM for Forecasting Construction Output: A Case Study of Hubei Province. Buildings 2023, 13, 48. https://doi.org/10.3390/buildings13010048
Lei M, He Y, Wang D, He D, Feng Y, Cheng L, Qin Z. Application of GSM-SVM for Forecasting Construction Output: A Case Study of Hubei Province. Buildings. 2023; 13(1):48. https://doi.org/10.3390/buildings13010048
Chicago/Turabian StyleLei, Ming, Yuejie He, Dandan Wang, Debin He, Yuhao Feng, Lianhuan Cheng, and Zihao Qin. 2023. "Application of GSM-SVM for Forecasting Construction Output: A Case Study of Hubei Province" Buildings 13, no. 1: 48. https://doi.org/10.3390/buildings13010048
APA StyleLei, M., He, Y., Wang, D., He, D., Feng, Y., Cheng, L., & Qin, Z. (2023). Application of GSM-SVM for Forecasting Construction Output: A Case Study of Hubei Province. Buildings, 13(1), 48. https://doi.org/10.3390/buildings13010048





