Optimal Site Selection for Women University Using Neutrosophic Multi-Criteria Decision Making Approach
Abstract
1. Introduction
1.1. Motivation and Novelties of the Study
- MCDM tools in the neutrosophic environment have been applied in different areas, but the literature survey reflects that minimum work has been done on women’s university site selection problem (any other type of university site selection also). So, this study focuses on this problem and aims to fill the gap in the literature. It provides encouraging results.
- New De-Neutrosophication technique for trapezoidal neutrosophic number is developed and further used in this study model.
- Finding the trapezoidal neutrosophic numbers (TrNNs), weights are constructed in a new way and applied in the proposed application model.
- A model for Women University site selection is proposed by taking important criteria, and ranking of the sites is conducted using an uncertain MCDM method.
- Questionnaires were made regarding different locations and their attributes. Various experts were questioned, such as transportation engineers, architects, environmental engineers, civil engineers, geologists, environmental experts, and municipal officials. Their opinion about the criteria that correspond to different locations has been taken into consideration as the input and has been aggregated to solve the problem.
- AHP technique has been used to obtain the crisp weight of the criteria, and for consistency check, two MCDM tools, namely Neutrosophic TOPSIS and Neutrosophic COPRAS have been applied for ranking of the sites.
- Sensitivity analysis has been calculated to measure the change in ranking and to check the robustness and steadiness of the methods used.
1.2. Structure of the Paper
2. Literature Review
2.1. Multi Criterion Decision Making
2.2. Neutrosophic Set
2.3. Neutrosophic Set with MCDM Techniques
2.4. Site Selection and University Site Selection
- 1.
- Fully research university: This type of university is primarily focused on research. They have few full-time postgraduate courses but with motivation for research. Also, they have mostly focused Ph.D. programs. The establishment of this type of university needs more funding as the number of students are less.
- 2.
- Fully academic university: The primary goal of this type of university is academic purposes. They run undergraduate and postgraduate with several specializations. Research might not be the primary focus of this type of university.
- 3.
- Mixed type university (academic and research): The academic program and research program are both in this type of university. There is a balance between academic and research activity.
- 4.
- Affiliated university: This type of university is for only controlling the affiliated colleges that are under this university. Different work like inspection of college, control of examination, quality improvement of colleges, etc., plays an important role in this type of university.
- 5.
- University for some special purposes: University, which is beneficial for the society, country or an organization.
- A
- Fully government university: University which is run by government funding and direction which is fully controlled by the government.
- B
- Government aided university: Public and private partnerships with government collaboration. A few portions are helped and directed by the government and the rest is executed by the institute’s internal organization.
- C
- Private university: Fully funded and directed by the private sector, i.e., non-governm- ental organization.
| Type of University/Institution | Type | Number of University/Institution |
|---|---|---|
| Institute of national importance | Fully government | 9 |
| Research institutes | Fully government | 15 |
| State universities | Government aided | 36 |
| Private universities | Private | 12 |
| Deemed universities | Government | 2 |
| Central universities | Government | 1 |
| National law university | Government | 1 |

3. Preliminaries
3.1. Neutrosophic Logic
3.2. Neutrosophic Sets
3.3. Single Valued Neutrosophic Set (SVNS)
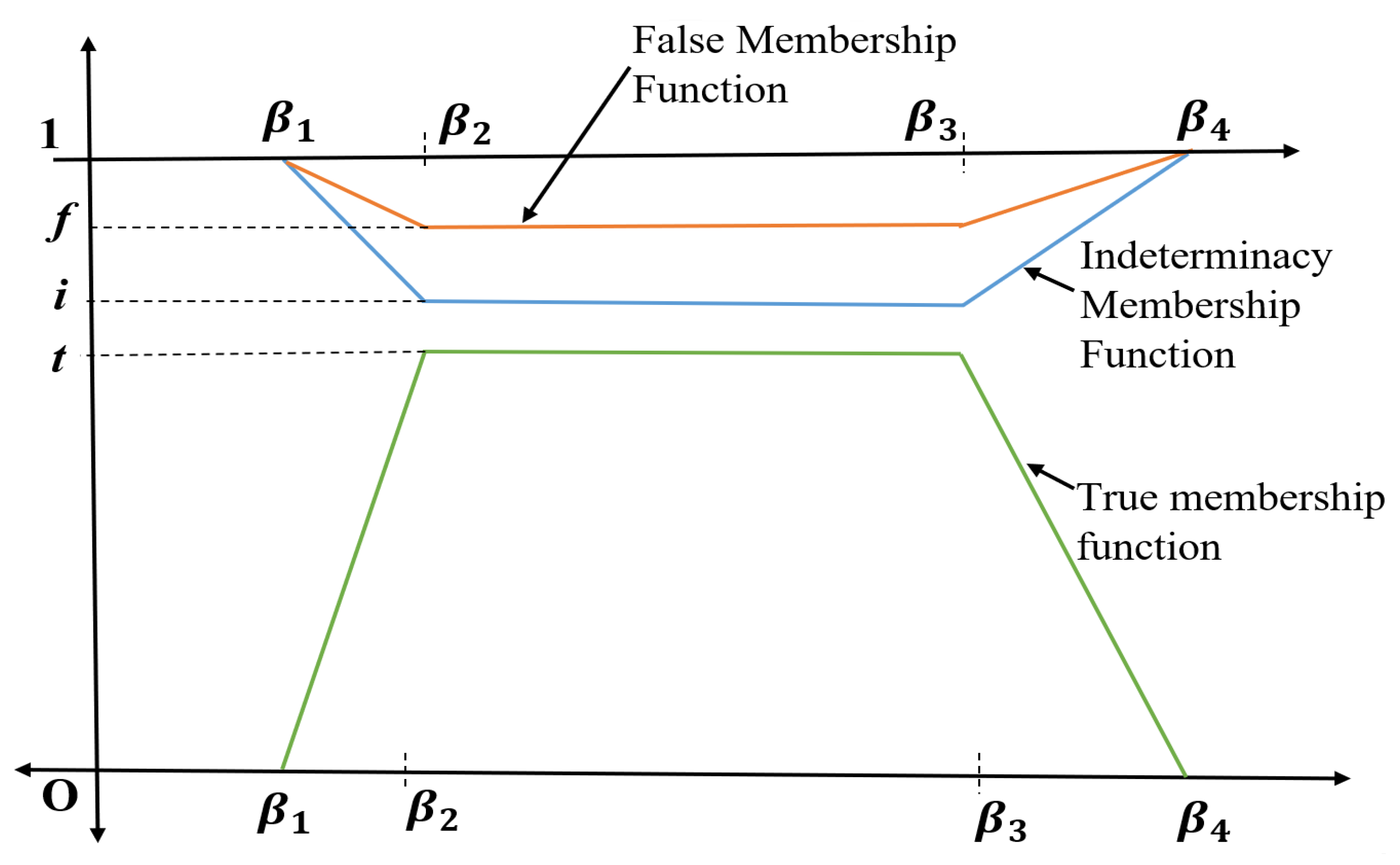
3.4. Trapezoidal Neutrosophic Number
3.5. Arithmetic Operation on TrNN
- Addition of two TrNNs:
- Negation of a TrNN:
- Subtraction of two TrNNs:
- Scalar multiplication of a TrNN by k:
- Multiplication of two TrNNs:
- Inverse of a TrNN:
3.6. Distance between Two TrNN
3.7. De-Neutrosophication of Neutrosophic Number
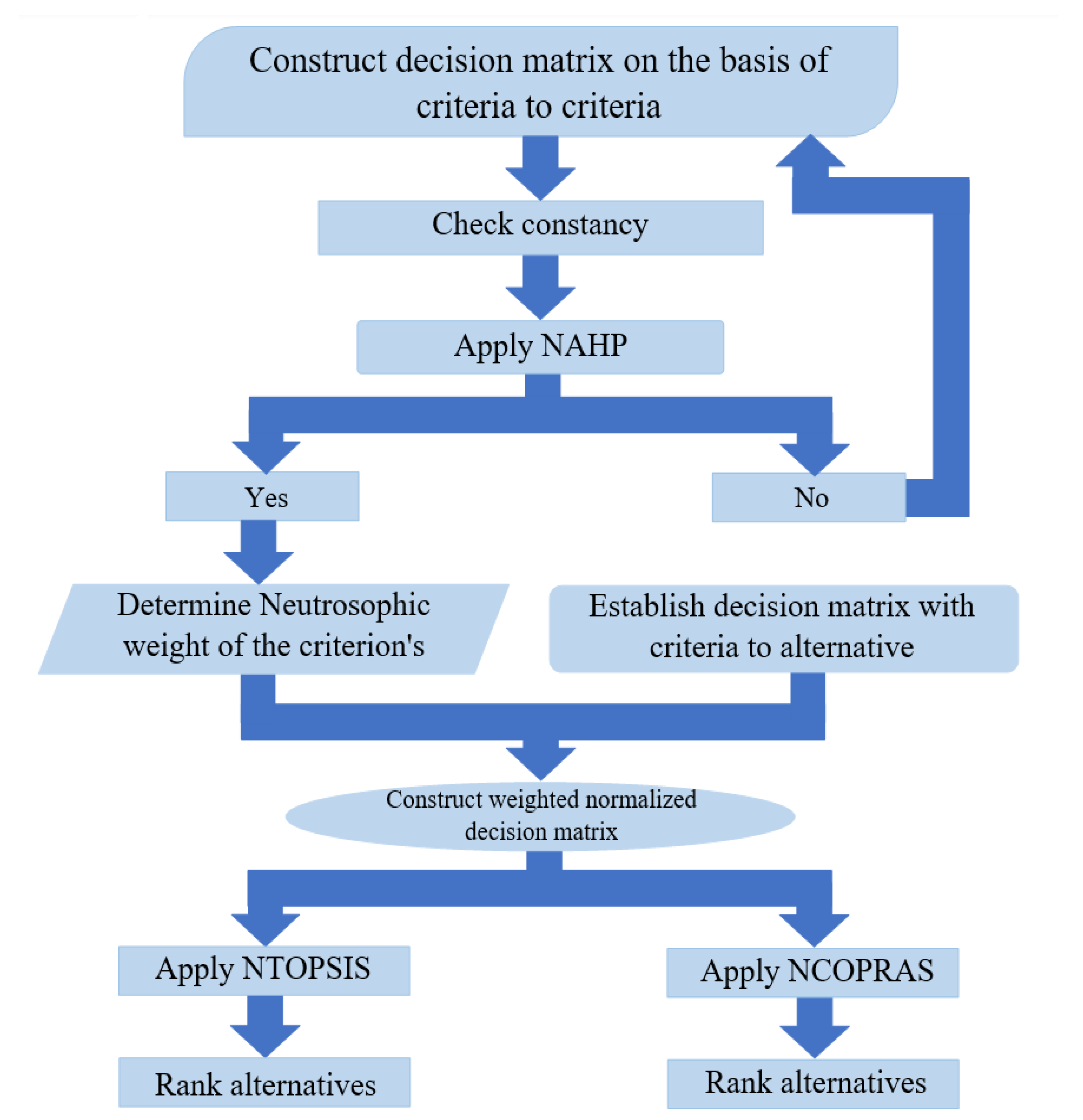
4. Used Multi-Criteria Decision Making Methods
4.1. Analytic Hierarchy Process (AHP)
- I.
- Recognition and study of the criterion’s and their respective sub-criterion’s.
- II.
- On the basis of opinions of DMs, construction of a pairwise comparison matrix with the trapezoidal neutrosophic numbers (TrNNs). Let N number of DMs give their decision. Individual DM reveal their own view in terms of the pairwise comparison matrix of criterion’s. Let us assume t number of criterion’s, then, the comparison matrix has ordered square matrix. Now N set of matrices are obtained where & .Now indicate TrNN of i criteria to j criteria as communicate by the DM ‘c’.
- III.
- De-neutrosophication of TrNN:De-neutrosophication of the TrNN is done by using Equation (18) of the matrixwhere .
- IV.
- Normalization of De-neutrosophication matrix:Normalized the comparison matrix A get from Equation (20) and converted into matrix B. Each entry of B is evaluated asNote: The weighted sum of each column on the normalization matrix is equal to one.
- V.
- Evaluation of criteria weights:Criteria weight of each criteria j is determined using
- VI.
- Determination of weight sum value and :The weight sum value of each criterion j isthen is
- VII.
- Calculation of Consistency Index (CI):The consistency index (CI) of the matrix is estimated. CI of the matrix is computed using the following:where t denotes the number of criteria, which ultimately represents the size of the matrix.
- VIII.
- Finally, the consistency ratio (CR) is calculated.where random index () is the standardised. The values of varies with respect to the order of the matrix (i.e., the number of criterion). The size of the matrix and corresponding values of are shown in Table 7 (values of t vary 1 to 10).
4.2. Determination of Trapezoidal Neutrosophic Numbers (TrNNs) Weights of Criterion’s
- (a)
- Recognition and study of the criterion for MCDM. Construction of pairwise comparison matrix in terms of TrNNs given by the DMs.
- (b)
- Aggregation of the opinions of ‘N’ DMs using the operator followed by the Equation (19).
- (c)
- The geometric mean is calculated of the TrNN in the comparison matrix by using
- (d)
- Addition of trapezoidal numbers and optimization of the membership numbers using the equation
- (e)
- Calculation of the inverse of TrNN getting from the Equation (15) as follows
- (f)
- The TrNN weights of the criteria is calculated by the equation
4.3. The Neutrosophic Technique for Order of Preference by Similarity to Ideal Solution (NTOPSIS)
- I.
- Decision matrices are constructed on the basis of DMs in linguistic ratings. The linguistic assignments are then transformed into TrNNs.
- II.
- Aggregation of the opinions of ‘N’ DMs using the operator follow by the Equation (19).
- III.
- Standardization of the TrNNs, using the formula:where ; ;; and Beneficent Criteria (B.C)and ; and Non-beneficent Criteria (N.B.C).
- IV.
- Weighted standardized matrix is determined by the product of criteria’s TrNNs weight and standardized TrNNs value .where ; and .
- V.
- Determination of TrNNs positive ideal solution and TrNNs negative ideal solution . Here signifies the maximum value of and denotes the minimum value of .where
- VI.
- Relative distance is calculated for each alternative in term of TrNNs (i.e., from positive ideal solution and negative ideal solution respectively).where & denotes the Hamming distance. The distance measure used here is given in Equation (17).
- VII.
- Finally, calculation of relative closeness of the alternativesUltimately, the ranking of the alternatives by the obtained value of . The higher value of denotes the optimal alternative.
4.4. Neutrosophic Complex Proportional Assessment (NCOPRAS) Approach
- i.
- Establish of TrNN comparison matrix by the expert of decision makers. The DMs allocate in linguistic terms depending on criterion’s.
- ii.
- integration of the decision matrix of the viewpoint of ‘N’ DMs using the operator followed by the Equation (19).
- iii.
- Standardization of decision matrix is computed in the same way as computed in the TOPSIS method using Equation (31).
- iv.
- Construction of weighted standardization decision matrix which is done by product of the TrNN criteria weight and standardization decision matrix.
- v.
- Calculation of beneficiary criteria (BC) and non-beneficiary criteria (NBC) denoted as and respectively as follows:where () come from the weighted standardization matrix in Equation (32).
- vi.
- Now, de-neutrosophication of the TrNN using the Equation (18). De-deutrosophication of the Beneficiary Criteria (BC) is denoted by , and de-neutrosophication of the non-beneficiary criteria (NBC) is denoted by .
- vii.
- Calculatewhere and i indicate as alternatives.
- viii.
- Calculation of the value ofwhere .Finally, ranking of the alternative in ascending order on the score.
4.5. Pseudo Code Depicting the Empirical Study Application
- INPUT: Comparison matrix & Decision matrix
- OUTPUT: Ranking the alternatives
- COMPUTE: Consistency ratio, weight of the criteria in TrNN
- INITIALIZE: TrNN
- OPERATION: NAHP, weight in TrNN, NTOPSIS & NCOPRAS
- FOR NAHP
- MERGE merge the N number of DMs inputs of comparison matrix
- IF comparison matrix is inconsistent ()
- THEN reconstruct the comparison matrix
- ELSE comparison matrix is consistent ()
- END FOR
- COMPUTE TrNN weight of the criteria
- CONSTRUCT comparison matrix
- THEN compute the weighted normalized comparison matrix
- FIND determine the weight of the criteria in TrNN
- THEN consider the N decision matrix given by DMs
- MERGE merge the N number of DMs inputs of decision matrix
- COMPUTE determination of the weighted normalised decision matrix
- BEGIN NTOPSIS
- COMPUTE calculation of the ranking of the alternatives using weighted normalizeddecision matrix
- END NTOPSIS
- BEGIN NCOPRAS
- COMPUTE calculation of the ranking of the alternatives using weighted normalizeddecision matrix
- END NCOPRAS
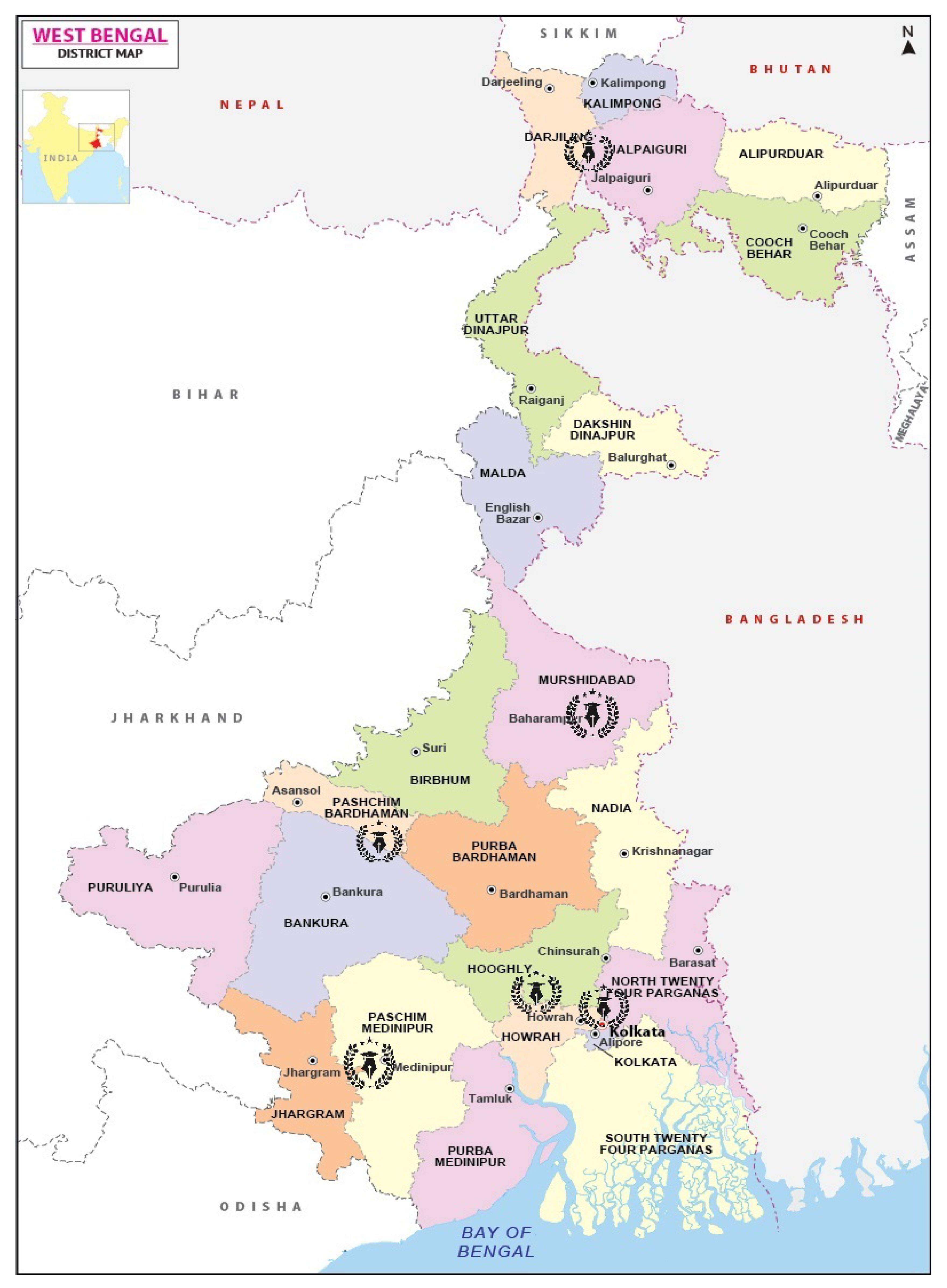
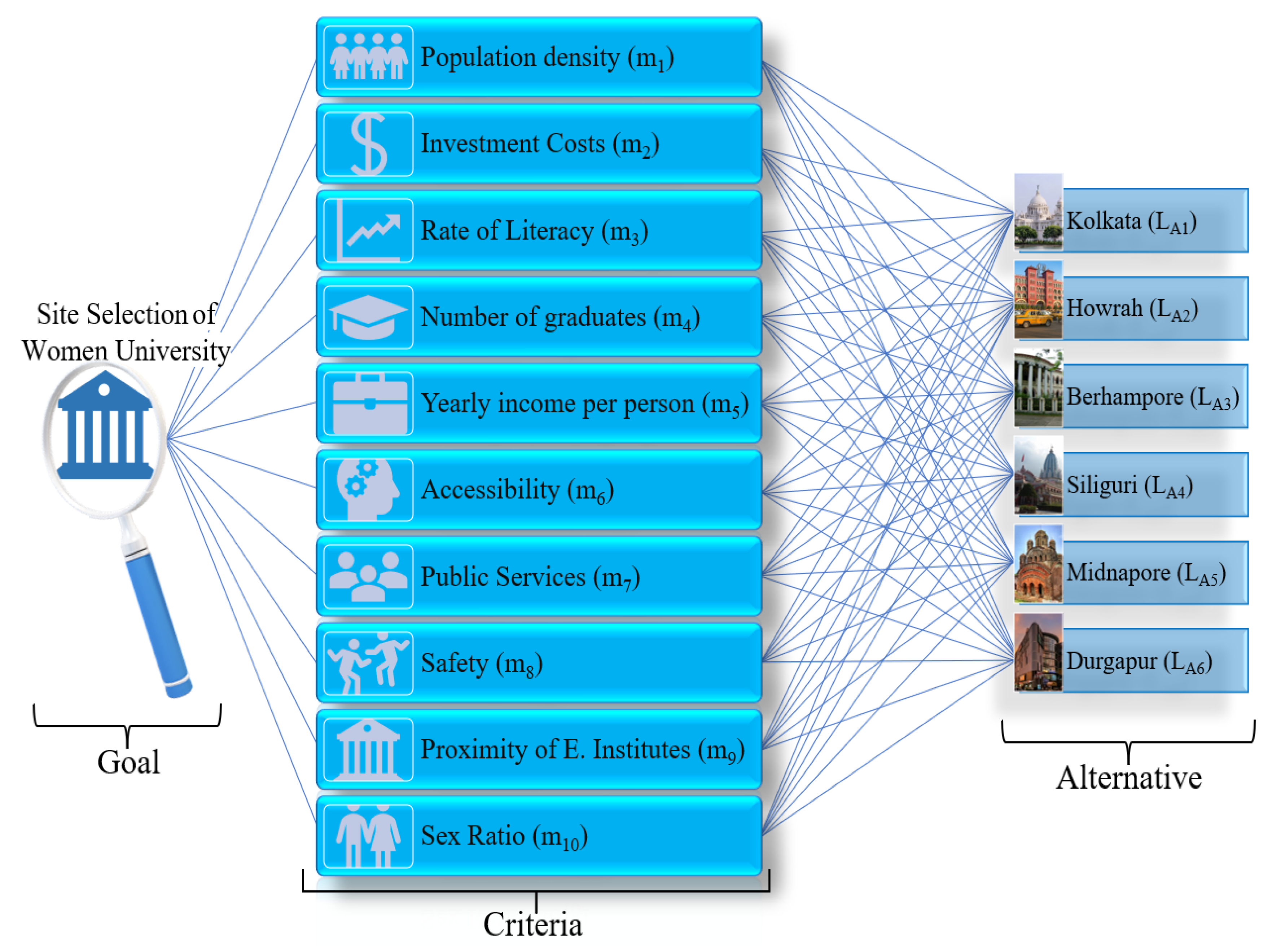
5. Model for Setting Up a Government/Government Aided University for Women (Selection of the Alternatives)
6. Criteria of Women’s University Site Selection
6.1. Population Density () (Fixed Data)
6.2. Investment Costs ()
6.3. Rate of Literacy () (Fixed Data)
6.4. Number of Graduates ()
6.5. Yearly Income per Person ()
6.6. Accessibility ()
6.7. Public Services ()
6.8. Safety ()
6.9. Proximity of Educational Institutes ()
6.10. Sex Ratio () (Fixed Data)
7. Data Collection
| Linguistic Terms | Trapezoidal Neutrosophic Numbers (TrNN) |
|---|---|
| Low priority (LP) | |
| Below Priority (BP) | |
| Medium priority (MP) | |
| Very priority (VP) | |
| Extremely priority (EP) |
| Alternative | Population Density | Rate of Literacy | Sex Ratio |
|---|---|---|---|
| Kolkata () | 24306 | 908 | |
| Howrah () | 3306 | 939 | |
| Berhampore () | 1334 | 958 | |
| Siliguri () | 586 | 970 | |
| Midnapore () | 631 | 966 | |
| Durgapur () | 1099 | 945 |
| Linguistic Terms | Population Density | Rate of Literacy | Sex Ratio |
|---|---|---|---|
| Low priority (LP) | |||
| Below priority (BP) | |||
| Medium priority (MP) | |||
| Very priority (VP) | |||
| Extremely priority (EP) |
| Criteria | |||||||||||
| Decision Maker 1 | Population density () | EI | VSNI | VSNI | SNI | EI | SNI | ANI | ANI | MNI | AI |
| Investment Costs () | VSI | EI | VSNI | SNI | SI | VSNI | SNI | ANI | EI | ANI | |
| Rate of Literacy () | VSI | VSI | EI | EI | AI | EI | MI | EI | SI | SI | |
| Number of graduates () | SI | SI | EI | EI | SI | EI | EI | SNI | EI | SI | |
| Yearly income per person () | EI | SNI | ANI | SNI | EI | ANI | VSNI | ANI | SI | ANI | |
| Accessibility () | SI | VSI | EI | EI | AI | EI | SI | EI | SI | ANI | |
| Public Services () | AI | SI | MNI | EI | VSI | SNI | EI | SNI | EI | ANI | |
| Safety () | AI | AI | EI | SI | AI | EI | SI | EI | AI | AI | |
| Proximity of E. Institutes () | MI | EI | SNI | EI | SNI | SNI | EI | ANI | EI | MNI | |
| Sex Ratio () | ANI | AI | SNI | SNI | AI | AI | AI | ANI | MI | EI | |
| Criteria | |||||||||||
| Decision Maker 2 | Population density () | EI | SNI | ANI | VSNI | MNI | SNI | SNI | ANI | MNI | AI |
| Investment Costs () | SI | EI | ANI | SNI | VSI | SNI | SNI | VSNI | MNI | VSNI | |
| Rate of Literacy () | AI | AI | EI | MI | VSI | EI | SI | EI | EI | VSI | |
| Number of graduates () | VSI | SI | MNI | EI | AI | MI | SI | ANI | MNI | SI | |
| Yearly income per person () | MI | VSNI | VSNI | ANI | EI | ANI | VSNI | ANI | MI | VSNI | |
| Accessibility () | SI | SI | EI | MNI | AI | EI | EI | EI | SI | ANI | |
| Public Services () | SI | SI | SNI | SNI | VSI | EI | EI | SNI | EI | VSNI | |
| Safety () | AI | VSI | EI | AI | AI | EI | SI | EI | VSI | VSI | |
| Proximity of E. Institutes () | MI | MI | EI | MI | MNI | SNI | EI | VSNI | EI | EI | |
| Sex Ratio () | ANI | VSI | VSNI | SNI | VSI | AI | VSI | VSNI | EI | EI | |
| Criteria | |||||||||||
| Decision Maker 3 | Population density () | EI | MNI | MNI | SNI | MI | ANI | ANI | VSNI | EI | VSI |
| Investment Costs () | MI | EI | VSNI | ANI | SNI | MI | VSNI | ANI | SI | ANI | |
| Rate of Literacy () | MI | VSI | EI | MI | AI | SI | EI | EI | MI | MI | |
| Number of graduates () | SI | AI | MNI | EI | AI | SI | EI | EI | SI | VSI | |
| Yearly income per person () | MNI | SI | ANI | ANI | EI | VSNI | SNI | SNI | SNI | VSNI | |
| Accessibility () | AI | MNI | SNI | SNI | VSI | EI | MI | SNI | MI | VSNI | |
| Public Services () | AI | VSI | EI | EI | SI | MNI | EI | EI | SNI | ANI | |
| Safety () | VSI | AI | EI | EI | SI | SI | EI | EI | MNI | AI | |
| Proximity of E. Institutes () | EI | SNI | MNI | SNI | SI | MNI | SI | MNI | EI | MNI | |
| Sex Ratio () | VSNI | AI | MNI | VSNI | VSI | VSI | AI | ANI | MI | EI |
| Criteria | |||||||||||
| Decision Maker 1 | Kolkata () | EP | EP | EP | MP | MP | EP | EP | MP | EP | LP |
| Howrah () | VP | MP | EP | LP | BP | VP | EP | LP | BP | MP | |
| Berhampore () | MP | BP | BP | LP | BP | BP | LP | LP | LP | MP | |
| Siliguri () | BP | MP | VP | LP | BP | MP | BP | BP | LP | VP | |
| Midnapore () | BP | BP | VP | MP | BP | MP | MP | MP | MP | VP | |
| Durgapur () | MP | MP | VP | MP | MP | BP | BP | MP | BP | MP | |
| Criteria | |||||||||||
| Decision Maker 2 | Kolkata () | EP | EP | EP | MP | VP | EP | EP | VP | VP | LP |
| Howrah () | VP | VP | EP | BP | MP | EP | VP | BP | MP | MP | |
| Berhampore () | MP | BP | BP | LP | LP | MP | LP | MP | LP | MP | |
| Siliguri () | BP | BP | VP | LP | MP | VP | MP | BP | LP | VP | |
| Midnapore () | BP | MP | VP | EP | MP | VP | BP | VP | MP | VP | |
| Durgapur () | MP | BP | VP | BP | BP | MP | BP | BP | BP | MP | |
| Criteria | |||||||||||
| Decision Maker 3 | Kolkata () | EP | VP | EP | VP | VP | VP | EP | VP | EP | LP |
| Howrah () | VP | VP | EP | MP | MP | VP | EP | BP | BP | MP | |
| Berhampore () | MP | BP | BP | BP | LP | BP | LP | BP | BP | MP | |
| Siliguri () | BP | MP | VP | LP | BP | MP | BP | MP | BP | VP | |
| Midnapore () | BP | MP | VP | VP | MP | BP | MP | VP | MP | VP | |
| Durgapur () | MP | BP | VP | BP | BP | BP | LP | MP | LP | MP |
8. Numerical Illustration
8.1. Step 1
8.2. Step 2
8.3. Step 3
8.4. Step 4
8.5. Computational Complexity
- For NAHP, the comparison matrix is of entries; therefore, by N DMs gives entries. Finding a comparison matrix has been operations needed. Then De-Neutrosophic process number of operations performed and to get normalized De-Neutrosophic comparison matrix operations conducted. Thereafter to find the nth root and factor weight needed operations. Also, factor weight needs operations. Then factor sum and sum/weight are calculated by operations. Finally, the consistency ratio is calculated by 3 more operations. Total operations conducted for NAHP are .
- For Trapezoidal Neutrosophic Number (TrNN) factor weight calculated on comparison matrix with given N DMs total entries. Calculation of geometric mean by operations. The sum and inverse operations performed by 2 number of operations. Finally, factor weight calculation require operations. Therefore, total calculations performed are .
- For NTOPSIS method, decision matrix is entries therefore N DMs gives entries. The decision matrix has operations needed. Then normalized and weighted normalized decision matrix was calculated using operations. Finding positive and negative ideal solution there are operations. To measure the relative closeness from the positive and negative ideal solutions there are operations performed, and the calculated total sum is by number of operations. Finally, the comparison ratio and ranking of the alternatives need number of operations. The total number of calculations conducted is .
- For NCOPRAS techniques, up to weighted normalized decision matrix operations are performed, which is already done in NTOPSIS. Then calculated sum of beneficial and non-beneficial attributes number of operations needed. For the De-Neutrosophic method, operations were performed. Then find values for k number of operations needed and lastly, k operations performed to rank the alternatives. The total calculation performed are .
- For NAHP, number of calculations are .
- For weight, number of operations are .
- For FTOPSIS, number of operations are .
- For FCOPRAS, number of calculations are .
9. Sensitivity Analysis
9.1. Removing Investment Cost
9.2. Removing Accessibility
- Government has proposed public accessibility.
- The investors might set up its own accessibility.
- Fully residential university need not require accessibility.
9.3. Removing Proximity of Educational Institute
10. Conclusions and Future Research Scope
- Check the consistency of the decision matrix using Neutrosophic AHP.
- Obtain the neutrosophic weight of the criteria to evaluate the weighted decision matrix.
- Calculate the nearest distance from the positive ideal solution, and the farthest distance from the negative ideal solution is calculated using the MCDM method Neutrosophic TOPSIS.
- Determine the maximizing and minimizing index values, and consequently, the attributes of maximizing and minimizing indexes are the assessment of the results examined individually using the Neutrosophic COPRAS method.
- the methodology can be used for setting up a private university, fully research-oriented institute, etc.,
- different sub-criterion may be taken for each criterion,
- different de-neutrosophication techniques associated with different efficient MCDM methods, like MIVES, WASPAS, CoCOSo, PROMETHEE, VIKOR may be applied,
- different uncertain environments may be considered like hesitant neutrosophic environment, Pythagorean fuzzy,
- same methodology may be extended with more alternatives,
- different new distance measures may be used.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Serrai, W.; Abdelli, A.; Mokdad, L.; Hammal, Y. Towards an efficient and a more accurate web service selection using MCDM methods. J. Comput. Sci. 2017, 22, 253–267. [Google Scholar] [CrossRef]
- Jayant, A.; Sharma, J. A comprehensive literature review of MCDM techniques ELECTRE, PROMETHEE, VIKOR and TOPSIS applications in business competitive environment. Int. J. Curr. Res. 2018, 10, 65461–65477. [Google Scholar]
- Zain, Z.M. A Fuzzy TOPSIS Approach for Evaluating the Quality of Breast Cancer Information on the Internet. Int. J. Appl. Eng. Res. 2018, 13, 11267–11271. [Google Scholar]
- Chattopadhyay, A.; Bose, U. An Assessment of Objectivity Convergence of Fuzzy TOPSIS Method Extended with Rank Order Weights in Group Decision Making. Asian J. Manag. Sci. 2018, 7, 26–33. [Google Scholar] [CrossRef]
- Mitra, S.; Kundu, S. Application of TOPSIS for Best Domestic Refrigerator Selection. Int. J. Res. Anal. Rev. 2018, 5, 226–231. [Google Scholar]
- Sa, L.K.; Nhung, N.C.; Chien, L.V.; Tuan, N.A.; Tu, P.V. Green Material Selection Using an Integrated Fuzzy Multi-criteria Decision Making Model. Asian J. Sci. Res. 2018, 11, 195–202. [Google Scholar] [CrossRef]
- Balioti, V.; Tzimopoulos, C.; Evangelides, C. Multi-Criteria Decision Making Using TOPSIS Method under Fuzzy Environment. Application in Spillway Selection. Proceedings 2018, 2, 637. [Google Scholar] [CrossRef]
- Khan, S.A.; Chaabane, A.; Dweiri, F.T. Multi-Criteria Decision-Making Methods Application in Supply Chain Management: A Systematic Literature Review. Multi-Criteria Methods Tech. Appl. Supply Chain. Manag. 2018, 1, 3–31. [Google Scholar] [CrossRef]
- Masum, A.K.M.; Karim, A.N.M.R.; Abid, F.B.A.; Islam, S.; Anas, M. A New Hybrid AHP-TOPSIS Method for Ranking Human Capital Indicators by Normalized Decision Matrix. J. Comput. Sci. 2019, 15, 1746–1751. [Google Scholar] [CrossRef]
- Min Oo, H.; Hnin, S.H. Application of Fuzzy Analytic Hierarchy Process and TOPSIS Methods for Destination Selection. Int. J. Trend Sci. Res. Dev. 2019, 3, 2404–2410. [Google Scholar]
- Gholap, A.B.; Jaybhaye, M.D. Decision Making of Condition Monitoring using AHP and TOPSIS Method. Int. J. Eng. Adv. Technol. 2019, 8, 495–499. [Google Scholar] [CrossRef]
- Negi, N.; Chandra, S. Efficient Selection of QoS Based Web Services using Modified TOPSIS Method. Int. J. Recent Technol. Eng. 2019, 8, 5732–5738. [Google Scholar] [CrossRef]
- Singh, M.; Pant, M.; Godiyal, R.D.; Sharma, A.K. MCDM approach for selection of raw material in pulp and papermaking industry. Mater. Manuf. Process. 2019, 35, 241–249. [Google Scholar] [CrossRef]
- Song, Y.; Peng, Y. A MCDM-based evaluation approach for imbalanced classification methods in Financial Risk Prediction. IEEE Access 2019, 7, 84897–84906. [Google Scholar] [CrossRef]
- Cheng, C.; Ding, W.; Xiao, F.; Pedrycz, W. A majority rule-based measure for Atanassov type intuitionistic membership grades in MCDM. IEEE Trans. Fuzzy Syst. 2020, 30, 121–132. [Google Scholar] [CrossRef]
- Youssef, A.E. An Integrated MCDM Approach for Cloud Service Selection Based on TOPSIS and BWM. IEEE Access 2020, 8, 71851–71865. [Google Scholar] [CrossRef]
- Zulqarnain, R.M.; Saeed, M.; Ahmad, N.; Dayan, F.; Ahmad, B. Application of TOPSIS Method for Decision Making. Int. J. Sci. Res. Math. Stat. Sci. 2020, 7, 76–81. [Google Scholar]
- Abdelli, A.; Mokdad, L.; Hammal, Y. Dealing with value constraints in decision making using MCDM methods. J. Comput. Sci. 2020, 44, 101154. [Google Scholar] [CrossRef]
- Lin, M.; Huang, C.; Xu, Z.; Chen, R. Evaluating IoT Platforms Using Integrated Probabilistic Linguistic MCDM Method. IEEE Internet Things J. 2020, 7, 11195–11208. [Google Scholar] [CrossRef]
- Pangaribuan, I.; Beniyanto, A. Multi-Criteria Decision Making method for procurement of goods and services auction system. Journal of Engineering Science and Technology. INCITEST2020. 2020., 26–32. Available online: https://jestec.taylors.edu.my/Special%20Issue%20INCITEST2020/INCITEST2020_04.pdf (accessed on 20 November 2022).
- Raju, S.S.; Murali, G.B.; Patnaik, P.K. Ranking of Al-CSA composite by MCDM approach using AHP–TOPSIS and MOORA methods. J. Reinf. Plast. Compos. 2020, 39, 721–732. [Google Scholar] [CrossRef]
- Saeed, M.; Ahsan, M.; Abdeljawad, T. A Development of Complex Multi-Fuzzy Hypersoft Set With Application in MCDM Based on Entropy and Similarity Measure. IEEE Access 2021, 9, 60026–60042. [Google Scholar] [CrossRef]
- Lee, W.H.; Tsai, J.H.; Lee, L.C. A New Multiple Criteria Decision Making Approach Based on Intuitionistic Fuzzy Sets, the Weighted Similarity Measure, and the Extended TOPSIS Method. J. Internet Technol. 2021, 22, 645–656. [Google Scholar]
- Trung, D.O.D. Application of EDAS, MARCOS, TOPSIS, MOORA and PIV Methods for Multi-Criteria Decision Making in Milling Process. Strojníckycčasopis J. Mech. Eng. 2021, 71, 69–84. [Google Scholar] [CrossRef]
- Vassoney, E.; Mochet, A.M.; Desiderio, E.; Negro, G.; Pilloni, M.G.; Comoglio, C. Comparing Multi-Criteria Decision-Making Methods for the Assessment of Flow Release Scenarios from Small Hydropower Plants in the Alpine Area. Front. Environ. Sci. 2021, 9, 635100. [Google Scholar] [CrossRef]
- Lata, S.; Sachdeva, A.K.; Paswan, M.K. Selection of machine tool by using FUZZY TOPSIS method. AIP Conf. Proc. 2021, 2341, 020015. [Google Scholar] [CrossRef]
- Basaran, S.; Homsi, F.E. Mobile Mathematics Learning Application Selection using Fuzzy TOPSIS. Int. J. Adv. Comput. Sci. Appl. 2022, 13, 270–282. [Google Scholar] [CrossRef]
- Ukpanyang, D.; Terrados-Cepeda, J.; Hermoso-Orzaez, M.J. Multi-Criteria Selection of Waste-to-Energy Technologies for Slum/Informal Settlements Using the PROMETHEE Technique: A Case Study of the Greater Karu Urban Area in Nigeria. Energies 2022, 15, 3481. [Google Scholar] [CrossRef]
- Olgun, M.; Türkarslan, E.; Ye, J.; Ünver, M. Single and Interval-Valued Hybrid Enthalpy Fuzzy Sets and a TOPSIS Approach for Multicriteria Group Decision Making. Math. Probl. Eng. 2022, 2022, 2501321. [Google Scholar] [CrossRef]
- Boix-Cots, D.; Pardo-Bosch, F.; Blanco, A.; Aguado, A.; Pujadas, P. A systematic review on MIVES: A sustainability-oriented multi-criteria decision-making method. Build. Environ. 2022, 223, 109515. [Google Scholar] [CrossRef]
- Casanovas-Rubio, M.M.; Pablo Pujadas, P.; Pardo-Bosch, F.; Blancod, A.; Aguado, A. Sustainability assessment of trenches including the new eco-trench: A multi-criteria decision-making tool. J. Clean. Prod. 2019, 238, 117957. [Google Scholar] [CrossRef]
- Pujadas, P.; Cavalaro, S.H.P.; Aguado, A. Mives multicriteria assessment of urban-pavement conditions: Application to a case study in Barcelon. Road Mater. Pavement Des. 2019, 20, 1827–1843. [Google Scholar] [CrossRef]
- Pons, O.; Albert De la Fuente, A.D.; Aguado, A. The Use of MIVES as a Sustainability Assessment MCDM Method for Architecture and Civil Engineering Applications. Sustainability 2016, 8, 460. [Google Scholar] [CrossRef]
- Pujadasa, P.; Pardo-Boschb, F.; Aguado-Renterc, A.; Aguado, A. MIVES multi-criteria approach for the evaluation, prioritization, and selection of public investment projects. A case study in the city of Barcelona. Land Use Policy 2017, 64, 29–37. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophic Logic -A Generalization of the Intuitionistic Fuzzy Logic. In Proceedings of the 3rd Conference of the European Society for Fuzzy Logic and Technology, Zittau, Germany, 10–12 September 2003. [Google Scholar]
- Zhang, H.Y.; Wang, J.Q.; Chen, X.H. Interval neutrosophic sets and their application in multicriteria decision making problems. Sci. World J. 2014, 2014, 645953. [Google Scholar] [CrossRef]
- Ren, S. Multicriteria decision-making method under a single valued neutrosophic environment. Int. J. Intell. Inf. Technol. IJIIT 2017, 13, 23–37. [Google Scholar] [CrossRef]
- Garg, H. Multi-criteria decision-making method based on prioritized Muirhead mean aggregation operator under neutrosophic set environment. Symmetry 2018, 10, 280. [Google Scholar] [CrossRef]
- Sodenkamp, M.A.; Tavana, M.; Di Caprio, D. An aggregation method for solving group multi-criteria decision-making problems with single-valued neutrosophic sets. Appl. Soft Comput. 2018, 71, 715–727. [Google Scholar] [CrossRef]
- Nabeeh, N.A.; Abdel-Basset, M.; El-Ghareeb, H.A.; Aboelfetouh, A. Neutrosophic multi-criteria decision making approach for iot-based enterprises. IEEE Access 2019, 7, 59559–59574. [Google Scholar] [CrossRef]
- Wang, L.; Xia, Q.; Li, H.; Cao, Y. Multi-criteria decision making method based on improved cosine similarity measure with interval neutrosophic sets. Int. J. Intell. Comput. Cybern. 2019, 12, 414–423. [Google Scholar] [CrossRef]
- Garg, H. A novel divergence measure and its based TOPSIS method for multi criteria decision-making under single-valued neutrosophic environment. J. Intell. Fuzzy Syst. 2019, 36, 101–115. [Google Scholar]
- Zeng, S.; Luo, D.; Zhang, C.; Li, X. A correlation-based TOPSIS method for multiple attribute decision making with single-valued neutrosophic information. Int. J. Inf. Technol. Decis. Mak. 2020, 19, 343–358. [Google Scholar] [CrossRef]
- Jiao, Y.; Wang, L.; Liu, J.; Ma, G. Multi-criteria decision making based on induced generalized interval neutrosophic Choquet integral. PLoS ONE 2020, 15, e0242449. [Google Scholar] [CrossRef] [PubMed]
- Duong, T.T.T.; Thao, N.X. TOPSIS model based on entropy and similarity measure for market segment selection and evaluation. Asian J. Econ. Bank. 2021, 5, 194–203. [Google Scholar] [CrossRef]
- Ye, J.; Türkarslan, E.; Ünver, M.; Olgun, M. Algebraic and Einstein weighted operators of neutrosophic enthalpy values for multi-criteria decision making in neutrosophic multi-valued set settings. Granul. Comput. 2021, 7, 479–487. [Google Scholar] [CrossRef]
- Hezam, I.M.; Nayeem, M.K.; Foul, A.; Alrasheedi, A.F. COVID-19 Vaccine: A neutrosophic MCDM approach for determining the priority groups. Results Phys. 2021, 20, 103654. [Google Scholar] [CrossRef]
- Jafar, M.N.; Saeed, M.; Saqlain, M.; Yang, M.S. Trigonometric similarity measures for neutrosophic hypersoft sets with application to renewable energy source selection. IEEE Access 2021, 9, 129178–129187. [Google Scholar] [CrossRef]
- Rani, P.; Ali, J.; Krishankumar, R.; Mishra, A.R.; Cavallaro, F.; Ravichandran, K.S. An integrated single-valued neutrosophic combined compromise solution methodology for renewable energy resource selection problem. Energies 2021, 14, 4594. [Google Scholar] [CrossRef]
- Abdullah, L.; Ong, Z.; Mohd Mahali, S. Single-valued neutrosophic DEMATEL for segregating types of criteria: A case of subcontractors’ selection. J. Math. 2021, 2021, 6636029. [Google Scholar] [CrossRef]
- Elhosiny, A.M.; El-Ghareeb, H.; Shabana, B.T.; AbouElfetouh, A. A Hybrid Neutrosophic GIS-MCDM Method Using a Weighted Combination Approach for Selecting Wind Energy Power Plant Locations: A Case Study of Sinai Peninsula, Egypt. Int. J. Fuzzy Log. Intell. Syst. 2021, 21, 12–28. [Google Scholar] [CrossRef]
- Rıdvan, Ş.; Fuat, A.; Gökçe Dilek, K. A single-valued neutrosophic multicriteria group decision approach with DPL-TOPSIS method based on optimization. Int. J. Intell. Syst. 2021, 36, 3339–3366. [Google Scholar] [CrossRef]
- Deveci, M.; Erdogan, N.; Cali, U.; Stekli, J.; Zhong, S. Type-2 neutrosophic number based multi-attributive border approximation area comparison (MABAC) approach for offshore wind farm site selection in USA. Eng. Appl. Artif. Intell. 2021, 103, 104311. [Google Scholar] [CrossRef]
- Nãdãban, S.; Dzitac, S.; Dzitac, I. Fuzzy TOPSIS: A General View. Procedia Computer Science, Elsevier. 2016, 91, 823–831. [Google Scholar] [CrossRef]
- Irvanizam, I.; Zulfan, Z.; Nasir, P.F.; Marzuki, M.; Rusdiana, S.; Salwa, N. An Extended MULTIMOORA Based on Trapezoidal Fuzzy Neutrosophic Sets and Objective Weighting Method in Group Decision-Making. IEEE Access 2022, 10, 47476–47498. [Google Scholar] [CrossRef]
- Bavia, M.S.; Nagarajan, D.; Broumi, S.; Kavikumar, J.; Rajkumar, A. Neutrosophic in Multi-Criteria Decision Making for Location Selection. Neutrosophic Sets Syst. 2022, 48, 142–153. [Google Scholar]
- Abdel-Basset, M.; Mohamed, M.; Mostafa, N.N.; El-Henawy, I.M.; Abouhawwash, M. New multi-criteria decision-making technique based on neutrosophic axiomatic design. Sci. Rep. 2022, 12, 10657. [Google Scholar] [CrossRef]
- Görçün, Ö.F. A novel integrated MCDM framework based on Type-2 neutrosophic fuzzy sets (T2NN) for the selection of proper Second-Hand chemical tankers. Transp. Res. Part E Logist. Transp. Rev. 2022, 163, 102765. [Google Scholar] [CrossRef]
- Özlü, Ş.; Karaaslan, F. Hybrid similarity measures of single-valued neutrosophic type-2 fuzzy sets and their application to MCDM based on TOPSIS. Soft Comput. 2022, 26, 4059–4080. [Google Scholar] [CrossRef]
- Farid, H.M.A.; Riaz, M. Single-valued neutrosophic Einstein interactive aggregation operators with applications for material selection in engineering design: Case study of cryogenic storage tank. Complex Intell. Syst. 2022, 8, 2131–2149. [Google Scholar] [CrossRef]
- Wu, M.; Chen, R.; Fan, J. Application of evidence reasoning algorithm and QUALIFLEX with single-valued neutrosophic set for MCDM. J. Intell. Fuzzy Syst. 2022, 1–16. [Google Scholar] [CrossRef]
- Alzahrani, F.A. Fuzzy Based Decision-Making Approach for Estimating Usable-Security of Healthcare Web Application. Comput. Mater. Contin. 2021, 66, 2599–2625. [Google Scholar] [CrossRef]
- Ansari, M.T.J.; Alzahrani, F.A.; Pandey, D.; Agrawal, A. A fuzzy TOPSIS based analysis toward selection of effective security requirements engineering approach for trustworthy healthcare software development. BMC Med. Inform. Decis. Mak. 2020, 20, 236. [Google Scholar] [CrossRef] [PubMed]
- Sahu, K.; Alzahrani, F.A.; Srivastava, R.K.; Kumar, R. Hesitant Fuzzy Sets Based Symmetrical Model of Decision-Making for Estimating the Durability of Web Application. Symmetry 2020, 12, 1770. [Google Scholar] [CrossRef]
- Alzahrani, F.A. Evaluating the Usable-Security of Healthcare Software Through Unified Technique of Fuzzy Logic, ANP and TOPSIS. IEEE Access 2020, 8, 109905–109916. [Google Scholar] [CrossRef]
- Lin, M.; Huang, C.; Xu, Z. MULTIMOORA based MCDM model for site selection of car sharing station under picture fuzzy environment. Sustain. Cities Soc. 2019, 101873. [Google Scholar] [CrossRef]
- Chatterjee, K.; Zavadskas, E.K.; Tamosčaitien, J.; Adhikary, K.; Kar, S. A Hybrid MCDM Technique for Risk Management in Construction Projects. Symmetry 2018, 10, 46. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Gamal, A.; Chakrabortty, R.K.; Ryan, M.; El-Saber, N. A Comprehensive Framework for Evaluating Sustainable Green Building Indicators under an Uncertain Environment. Sustainability 2021, 13, 6243. [Google Scholar] [CrossRef]
- Asadi, M.; Pourhossein, K. Wind and Solar Farms Site Selection Using Geographical Information System (GIS), Based on Multi Criteria Decision Making (MCDM) Methods: A Case-Study for East-Azerbaijan. In Proceedings of the 2019 Iranian Conference on Renewable Energy & Distributed Generation (ICREDG), Tehran, Iran, 11–12 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, H.; Yan, T. Bidding-Evaluation of Construction Projects Based on VIKOR Method. In Proceedings of the 2007 IEEE International Conference, Jinan, China, 18–21 August 2007. [Google Scholar] [CrossRef]
- Wang, C.N.; Huang, Y.F.; Chai, Y.C.; Nguyen, V.T. A Multi-Criteria Decision Making (MCDM) for Renewable Energy Plants Location Selection in Vietnam under a Fuzzy Environment. Appl. Sci. 2018, 8, 2069. [Google Scholar] [CrossRef]
- Wang, C.N.; Nguyen, V.T.; Thai, H.T.N.; Duong, D.H. Multi-Criteria Decision Making (MCDM) Approaches for Solar Power Plant Location Selection in Viet Nam. Energies 2018, 11, 1504. [Google Scholar] [CrossRef]
- Maghsoodi, A.I.; Rasoulipanah, H.; López, L.M.; Liao, H.; Zavadskas, E.K. Integrating Interval-valued Multi-granular 2-tuple Linguistic BWM-CODAS Approach with Target-based Attributes: Site Selection for a Construction Project. Comput. Ind. Eng. 2019, 139, 106147. [Google Scholar] [CrossRef]
- Zolfani, S.H.; Hasheminasab, H.; Torkayesh, A.E.; Zavadskas, E.K.; Derakhti, A. A Literature Review of MADM Applications for Site Selection Problems—One Decade Review from 2011 to 2020. Int. J. Inf. Technol. Decis. Mak. 2022, 21, 7–57. [Google Scholar] [CrossRef]
- Kharat, M.G.; Kamble, S.J.; Raut, R.D.; Kamble, S.S.; Dhume, S.M. Modeling landfill site selection using an integrated fuzzy MCDM approach. Model. Earth Syst. Environ. 2016, 2, 53. [Google Scholar] [CrossRef]
- Karaşan, A.; Kaya, İ.; Erdogčan, M. Location selection of electric vehicles charging stations by using a fuzzy MCDM method: A case study in Turkey. Neural Comput. Appl. 2020, 32, 4553–4574. [Google Scholar] [CrossRef]
- Boyacı, A.Ç.; Şişman, A. Pandemic hospital site selection: A GIS-based MCDM approach employing Pythagorean fuzzy sets. Environ. Sci. Pollut. Res. 2022, 29, 1985–1997. [Google Scholar] [CrossRef]
- Önüt, S.; Efendigil, T.; Kara, S.S. A combined fuzzy MCDM approach for selecting shopping center site: An example from Istanbul, Turkey. Expert Syst. Appl. 2010, 37, 1973–1980. [Google Scholar] [CrossRef]
- Sennaroglu, B.; Celebi, G.V. A military airport location selection by AHP integrated PROMETHEE and VIKOR methods. Transp. Res. Part D Transp. Environ. 2018, 59, 160–173. [Google Scholar] [CrossRef]
- Rezaeisabzevar, Y.; Bazargan, A.; Zohourian, B. Landfill site selection using multi criteria decision making: Influential factors for comparing locations. J. Environ. Sci. 2020, 93, 170–184. [Google Scholar] [CrossRef]
- Liu, H.C.; Yang, M.; Zhou, M.; Tian, G. An Integrated Multi-Criteria Decision Making Approach to Location Planning of Electric Vehicle Charging Stations. IEEE Trans. Intell. Transp. Syst. 2019, 20, 362–373. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, Y.; Bao, X.T. Methodology of location selection for biofuel refinery based on fuzzy TOPSIS. In Proceedings of the 2012 IEEE International Conference on Automation and Logistics, Zhengzhou, China, 15–17 August 2012. [Google Scholar] [CrossRef]
- Miç, P.; Antmen, Z.F. A Decision-Making Model Based on TOPSIS, WASPAS, and MULTIMOORA Methods for University Location Selection Problem. SAGE Open 2021, 11, 21582440211040115. [Google Scholar] [CrossRef]
- Moussa, M.; Mostafa, Y.; Elwafa Arch, A.A. School Site Selection Process. Procedia Environ. Sci. 2017, 37, 282–293. [Google Scholar] [CrossRef]
- Baser, V. Effectiveness of School Site Decisions on Land Use Policy in the Planning Process. ISPRS Int. J. Geo-Inf. 2020, 9, 662. [Google Scholar] [CrossRef]
- Universities and Colleges of West Bengal. Wikipedia. Available online: https://en.wikipedia.org/wiki/Universities_and_colleges_of_West_Bengal (accessed on 28 October 2022).
- Jana, S.K. Higher Education in West Bengal—An Overview. Artha Beekshan 2017, 26, 21–55. [Google Scholar]
- List of Districts of West Bengal. Wikipedia. Available online: https://en.wikipedia.org/wiki/List_of_districts_of_West_Bengal (accessed on 26 October 2022).
- Smarandache, F.; Vlâdâreanu, L. Applications of Neutrosophic Logic to Robotics: An Introduction. In Proceedings of the 2011 IEEE International Conference on Granular Computing, Kaohsiung, Taiwan, 8–10 November 2011; p. 12459263. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field in Logics: Neutrosophic Field, Multiple-Valued Logic. Int. J. 2002, 8, 385–438. [Google Scholar]
- Li, X.; Dai, X.; Dezert, J.; Smarandache, F. Fusion of imprecise qualitative information. Appl. Intell. 2010, 33, 340–351. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophic Set—A Generalization of the Intuitionistic Fuzzy Set. Int. J. Pure Appl. Math. 2004, 24, 1–29. [Google Scholar]
- Smarandache, F. A unifying field in logics: Neutrosophic logic. neutrosophic, neutrosophic set, neutrosophic probability and statistics. Mult.-Valued Log. Int. J. 2002, 8, 591–604. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophy: Neutrosophic Probability, Set, and Logic: Analytic Synthesis & Synthetic Analysis; American Research Press: Santa Fe, NM, USA, 1998. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.; Sunderraman, R. Single Valued Neutrosophic Sets. Tech. Sci. Appl. Math. 2012, 10, 10–14. [Google Scholar]
- Peng, J.; Wang, J.; Wu, X.; Wang, J.; Chen, X. Multi-valued Neutrosophic Sets and Power Aggregation Operators with Their Applications in Multi-criteria Group Decision-making Problems. Int. J. Comput. Intell. Syst. 2014, 8, 345–363. [Google Scholar] [CrossRef]
- Jin, Q.; Hu, K.; Bo, C.; Li, L. A New Single-Valued Neutrosophic Rough Sets and Related Topology. J. Math. 2021, 5522021. [Google Scholar] [CrossRef]
- Pramanik, S.; Mallick, R. VIKOR Based MAGDM Strategy with Trapezoidal Neutrosophic Numbers. Neutrosophic Sets Syst. 2018, 22, 118–130. [Google Scholar]
- Biswas, P.; Pramanik, S.; Giri, B.C. Distance Measure Based MADM Strategy with Interval Trapezoidal Neutrosophic Numbers. Neutrosophic Sets Syst. 2018, 19, 40–46. [Google Scholar]
- Wang, T. Distance of Single-Valued Neutrosophic Set and Its Application in Pattern Recognition. J. Phys. Conf. Ser. 2021, 2025, 012019. [Google Scholar] [CrossRef]
- Saqlain, M.; Riaz, M.; Saleem, M.A.; Yang, M.S. Distance and Similarity Measures for Neutrosophic HyperSoft Set (NHSS) With Construction of NHSS-TOPSIS and Applications. IEEE Access 2021, 9, 30803–30816. [Google Scholar] [CrossRef]
- Xu, D.; Cui, X.; Peng, L.; Xian, H. Distance measures between interval complex neutrosophic sets and their applications in multi-criteria group decision making. AIMS Math. 2020, 5, 5700–5715. [Google Scholar] [CrossRef]
- Deli, İ. A novel defuzzification method of SV-trapezoidal neutrosophic numbers and multi-attribute decision making: A comparative analysis. Soft Comput. 2019, 23, 12529–12545. [Google Scholar] [CrossRef]
- Chakraborty, A.; Mondal, S.P.; Ahmadian, A.; Senu, N.; Alam, S.; Salahshour, S. Different Forms of Triangular Neutrosophic Numbers, De-Neutrosophication Techniques, and their Applications. Symmetry 2018, 10, 327. [Google Scholar] [CrossRef]
- Satty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Canco, I.; Kruja, D.; Iancu, T. AHP, a Reliable Method for Quality Decision Making: A Case Study in Business. Sustainability 2021, 13, 13932. [Google Scholar] [CrossRef]
- Taherdoost, H. Decision Making Using the Analytic Hierarchy Process (AHP); A Step by Step Approach. Int. J. Econ. Manag. Syst. 2017, 2, 244–246. [Google Scholar]
- Kumar, A.; Kumar, M. Implementation of Analytic Hierarchy Process (AHP) as a Decision-Making Tool for Selection of Materials for the Robot Arm. Int. J. Appl. Eng. Res. 2019, 14, 2727–2733. [Google Scholar]
- Hwang, C.L.; Yoon, K. Methods for Multiple Attribute Decision Making. In Multiple Attribute Decision Making; Springer: Berlin/Heidelberg, Germany, 1981; Volume 186, pp. 58–191. [Google Scholar] [CrossRef]
- Nakhaeinejad, M.; Nahavandi, N. An interactive algorithm for multi-objective flow shop scheduling with fuzzy processingtime through resolution method and TOPSIS. Int. J. Adv. Manuf. Technol. 2013, 66, 1047–1064. [Google Scholar] [CrossRef]
- Handayani, N.U.; Rinawati, D.I.; Wiguna, Y.K. Model of pre-positioning warehouse logistics for disaster eruption of Mount Merapi in Sleman Yogyakarta. In Proceedings of the Joint International Conference on Electric Vehicular Technology and Industrial, Mechanical, Electrical and Chemical Engineering (ICEVT & IMECE), Surakarta, Indonesia, 4–5 November 2015; pp. 401–405. [Google Scholar] [CrossRef]
- Scalia, G.L.; Aiello, G.; Rastellini, C.; Micale, R. Multi-Criteria Decision Making support system for pancreatic islet transplantation. Expert Syst. Appl. 2011, 38, 3091–3097. [Google Scholar] [CrossRef]
- Chamodrakas, I.; Martakos, D. A utility-based fuzzy TOPSIS method for energy efficient network selection in heterogeneous wireless networks. Appl. Soft Comput. 2012, 12, 1929–1938. [Google Scholar] [CrossRef]
- Li, P.; Wu, J.; Qian, H. Groundwater quality assessment based on rough sets attribute reduction and TOPSIS method in a semi-arid area, China. Environ. Monit. Assess. 2012, 184, 4841–4854. [Google Scholar] [CrossRef] [PubMed]
- Ghorui, N.; Ghosh, A.; Algehyne, E.A.; Mondal, S.P.; Saha, A.P. AHP-TOPSIS Inspired Shopping Mall Site Selection Problem with Fuzzy Data. Mathematics 2020, 8, 1380. [Google Scholar] [CrossRef]
- Ghosh, A.; Ghorui, N.; Mondal, S.P.; Kumari, S.; Mondal, B.K.; Das, A.; Gupta, M.S. Application of Hexagonal Fuzzy MCDM Methodology for Site Selection of Electric Vehicle Charging Station. Mathematics 2021, 9, 393. [Google Scholar] [CrossRef]
- Ostad-Ahmad-Ghorabi, M.J.; Attari, M. Advancing environmental evaluation in cement industry in Iran. J. Clean. Prod. 2013, 41, 23–30. [Google Scholar] [CrossRef]
- Biswas, P.; Pramanik, S.; Giri, B.C. TOPSIS Strategy for Multi-Attribute Decision Making with Trapezoidal Neutrosophic Numbers. Neutrosophic Sets Syst. 2018, 19, 29–39. [Google Scholar]
- Zavadskas, E.K.; Kaklauskas, A.; Sarka, V. The new method of multicriteria complex proportional assessment of projects. Technol. Econ. Dev. Econ. 1994, 1, 131–139. [Google Scholar]
- Ayrim, Y.; Atalay, K.D.; Can, G.F. A new stochastic MCDM approach based on COPRAS. Int. J. Inf. Technol. Decis. Mak. 2018, 17, 857–882. [Google Scholar] [CrossRef]
- Seker, S. Site Selection for Solar Power Plants Using Integrated Two-Stage Hybrid Method Based on Intuitionistic Fuzzy AHP and COPRAS Approach. Intell. Fuzzy Tech. Big Data Anal. Decis. Mak. 2020, 1029, 616–624. [Google Scholar] [CrossRef]
- Fouladgar, M.M.; Chamzini, A.Y.; Lashgari, A.; Zavadskas, E.K.; Turskis, Z. Maintenance strategy selection using AHP and COPRAS under fuzzy environment. Int. J. Strateg. Prop. Manag. 2012, 16, 85–104. [Google Scholar] [CrossRef]
- Narayanamoothy, S.; Ramya, L.; Kalaiselvan, S.; Kureethara, J.V.; Kang, D. Use of DEMATEL and COPRAS method to select best alternative fuel for control of impact of greenhouse gas emissions. Socio-Econ. Plan. Sci. 2021, 76, 100996. [Google Scholar]
- Tolga, A.C.; Durak, G. Evaluating Innovation Projects in Air Cargo Sector with Fuzzy COPRAS. Int. Conf. Intell. Fuzzy 2019, 1029, 702–710. [Google Scholar] [CrossRef]
- Ghose, D.; Pradhan, S.; Tamuli, P.; Uddin, S. Optimal material for solar electric vehicle application using an integrated Fuzzy-COPRAS model. Energy Sources Part A Recover. Util. Environ. Eff. 2019, 1556–7230, 1–20. [Google Scholar] [CrossRef]
- Bausys, R.; Zavadskas, E.K.; Kaklauskas, A. Application of neutrosophic set to multicriteria decision making by COPRAS, Economic computation and economic cybernetics studies and research. Acad. Econ. Stud. 2015, 49, 91–106. [Google Scholar]
- Census Population 2022 Data. West Bengal Population 2011–2022. Census 2011. Available online: https://www.census2011.co.in/census/state/west+bengal.html (accessed on 25 October 2022).
- West Bengal District Map. MapsofIndia.com. Available online: https://www.mapsofindia.com/maps/westbengal/westbengal-district.htm (accessed on 25 October 2022).
- Districts of West Bengal, Census2011. 2011. Available online: https://www.census2011.co.in/census/state/districtlist/west+bengal.html (accessed on 26 October 2022).
- List of West Bengal Districts Ranked by Literacy Rate. Wikipedia. Available online: https://en.wikipedia.org/wiki/List_of_West_Bengal_districts_ranked_by_literacy_rate (accessed on 28 October 2022).
- Chakraborty, S.; Saha, A.P. Selection of optimal lithium ion battery recycling process: A multi-criteria group decision making approach. J. Energy Storage 2022, 55, 105557. [Google Scholar] [CrossRef]
- Chakraborty, S.; Saha, A.P. A framework of LR fuzzy AHP and fuzzy WASPAS for health care waste recycling technology. Appl. Soft Comput. 2022, 127, 109388. [Google Scholar] [CrossRef]
- Ghaleb, A.M.; Kaid, H.; Alsamhan, A.; Mian, S.H.; Hidri, L. Assessment and Comparison of Various MCDMA pproaches in the Selection of Manufacturing Process. Adv. Mater. Sci. Eng. 2020, 2020, 4039253. [Google Scholar] [CrossRef]
| Authors | Years | MCDM Methods | Application Area | |
|---|---|---|---|---|
| [1] | Serrai, W. et al. | 2017 | AHP, ANP, SAW, TOPSIS, VIKOR, PROMETHEE, MAUT, ELECTRE, BWM & COPRAS | Web service selection |
| [2] | Jayant, A. et al. | 2018 | ELECTRE, PROMETHEE, VIKOR, TOPSIS | Business competitive environment |
| [3] | Zain, Z.M. | 2018 | Fuzzy TOPSIS | Evaluation of the quality of online information on breast cancer |
| [4] | Chattopadhyay, A. et al. | 2018 | Fuzzy TOPSIS | Supplier selection |
| [5] | Mitra, S. et al. | 2018 | TOPSIS | Best domestic Refrigerator selection |
| [6] | Sa L.K. et al. | 2018 | TOPSIS | Green Material Selection |
| [7] | Balioti, V. et al. | 2018 | TOPSIS | Spillway Selection |
| [8] | Khan, S.A. et al. | 2018 | TOPSIS | Supply Chain Management |
| [9] | Masum, A.K.M. et al. | 2019 | AHP-TOPSIS | Ranking Human Capital |
| [10] | Min Oo, H. et al. | 2019 | Fuzzy AHP, TOPSIS | Destination selection |
| [11] | Gholap, A.B. et al. | 2019 | AHP & TOPSIS | Ranking Condition monitoring |
| [12] | Negi, N. et al. | 2019 | AHP, ARAS, TOPSIS & VIKOR | Quality of Service(QoS) based Web services |
| [13] | Singh, M. et al. | 2019 | TOPSIS, MTOPSIS, FTOPSIS | Raw material selection in pulp and paper making industry |
| [14] | Song, Y. et al | 2019 | TOPSIS | Financial risk prediction |
| [15] | Cheng, C. et al. | 2020 | MCDM | Selecting a supplier |
| [16] | Youssef, A.E. | 2020 | BWM, TOPSIS, AHP | Cloud Service Selection |
| [17] | Zulqarnain, R.M. et al. | 2020 | TOPSIS | Selection of a car |
| [18] | Abdelli, A. et al. | 2020 | TOPSIS | Web services characterized by Quality of service (QoS) |
| [19] | Lin, M. et al. | 2020 | TODIM | Evaluating IoT Platforms |
| [20] | Pangaribuan, I. et al. | 2020 | SAW, TOPSIS, WPM | Auction application |
| [21] | Raju, S.S. et al. | 2020 | AHP, TOPSIS, MOORA | Ranking of Al-CSA |
| [22] | Dr. Kashid, U. et al. | 2021 | AHP, TOPSIS | Players performance evaluation and selection in IPL |
| [23] | Lee, W.H. et al. | 2021 | TOPSIS, WSM | Sustainable building materials supplier selection |
| [24] | Trung, DO D. | 2021 | EDAS, MARCOS, TOPSIS, MOORA & PIV | The weights of surface roughness calculation and finding MRR |
| [25] | Vassoney, E. et al. | 2021 | SAW, WPM, AHP, TOPSIS, VIKOR, ELECTRE III & SHARE MCA | The optimal flow of downstream of a small run of the river HP plant |
| [26] | Lata, S. et al. | 2021 | Fuzzy TOPSIS | Selection of Machine Tool |
| [27] | Basaran, S. et al. | 2022 | Fuzzy TOPSIS | Mobile Mathematics Learning Application Selection |
| [28] | Ukpanyang, D. et al. | 2022 | PROMETHEE | Waste-to-Energy Technologies for Slum/Informal Settlements selection |
| [29] | Olgun, M. et al. | 2022 | TOPSIS | Multicriteria Group Decision Making |
| [30] | Boix-Cots, D. et al. | 2022 | MIVES | Different construction problem (Review paper) |
| [31] | Casanovas-Rubio, M. M. et al. | 2019 | MIVES | Sustainability assessment of trenches |
| [32] | Pujadas, P. et al. | 2018 | MIVES | Urban-pavement conditions evaluation |
| [33] | Pons, O. et al. | 2016 | AHP & MIVES | Sustainability of green building |
| [34] | Pujadasa, P. et al. | 2017 | MIVES | Evaluation, prioritization and selection of public investment projects |
| This paper | 2023 | NAHP, NTOPSIS & NCOPRAS | Women’s university site selection | |
| Authors | Years | Neutrosophic Number/Set Used | MCDM Technique Used | Application Area | |
|---|---|---|---|---|---|
| [36] | Zhang et al. | 2014 | Interval neutrosophic sets | INN Aggregation Operators based MCDM | Money investing problem |
| [37] | Ren et al. | 2017 | Single Valued Neutrosophic Set (SVNS) | Prioritized Weighted Geometric (SVNPWG) Operator based MCDM | Selection of an investment company |
| [38] | Garg & Nancy | 2018 | Single Valued Neutrosophic Number (SVNN) | Prioritized Muirhead Mean based MCDM | Finding an appropriate Information Technology (IT) software company |
| [39] | Sodenkamp et al. | 2018 | Single Valued Neutrosophic Set (SVNS) and Group Decision Making Aggregation | NS-based GMCDM approach | Unequal voting powers be respon-sible for the assessment of ranking alternatives |
| [40] | Nabeeh et al. | 2019 | Triangular Neutrosophic Numbers | AHP | Selection of IoT based Enterprises |
| [41] | Wang et al. | 2019 | Interval Neutrosophic Sets | Improved cosine similarity measure based MCDM method | Supplier selection |
| [42] | Garg & Nancy | 2019 | Single Valued Neutrosophic Set (SVNS), Divergence measure developed | Divergence measure based TOPSIS method | Finding an appropriate Information Technology (IT) software company |
| [43] | Zeng et al. | 2020 | Single Valued Neutrosophic Set (SVNS) | Correlation based TOPSIS | Finding an appropriate Information Technology (IT) software company |
| [44] | Jiao et al. | 2020 | Interval Neutrosophic Number (INN) | Induced Generalized Interval Neutrosophic Choquet Integral based MCDM | Country selection for investment |
| [45] | Duong & Thao | 2021 | Entropy based Neutrosophic Numbers | TOPSIS | Market segment selection and evaluation |
| [46] | Ye et al. | 2021 | Neutrosophic enthalpy set | Aggregation operator and score function based MCDM method using the algebraic and the Einstein t-norms and t-conorms | Car selection |
| [47] | Hezam et al. | 2021 | Generalized triangular neutrosophic number | Neutrosophic AHP-TOPSIS | Prioritized peoples group selection for vaccine |
| [48] | Jafar et al. | 2021 | Neutrosophic Hypersoft Sets | Similarity measures based MCDM | Renewable energy source selection |
| [49] | Rani et al. | 2021 | Single Valued Neutrosophic Set (SVNS) | SWARA & CoCoSo | Renewal Energy Source Selection |
| [50] | Abdullah et al. | 2021 | Single Valued Neutrosophic Set (SVNS) | DEMATEL | Identification of Influential Criteria in Sub- Contractors Selection |
| [51] | Elhosini et al. | 2021 | Single Valued Neutrosophic Set (SVNS) | TOPSIS, PROMETHEE | Selection of Wind Energy Power Plant Location |
| [52] | Ridvan et al. | 2021 | Single Valued Neutrosophic Set (SVNS) | Divergence, Projection, Likelihood (DPL)- TOPSIS | Selection of right mask in COVID-19 |
| [53] | Deveci et al. | 2021 | Type 2 Neutrosophic Sets | MABAC | Site selection of offshore wind farm location |
| [54] | Nãdãban, S. et al. | 2016 | Neutrosophic Set (NS) | Fuzzy TOPSIS | Supplier selection, sustainable and renewable energy location selection |
| [55] | Irvanizam et al. | 2022 | Trapezoidal Fuzzy Neutrosophic Sets | Ordinal Priority Approach (OPA) and MULTIMOORA | Social Aid Distribution Problem |
| [56] | Bavia et al. | 2022 | Single Valued Neutrosophic Set (SVNS) | hybrid score accuracy based MCGDM method | Logistics Centre Location Problem |
| [57] | Abdel-Basset et al. | 2022 | Single Valued Neutrosophic Set (SVNS) | AD principles based MCDM | Selecting the suitable medical image modality |
| This paper | 2023 | Trapezoidal neutrosophic number (TrNN) | NAHP, NTOPSIS & NCOPRAS | Women’s university site selection | |
| Authors | Year | Types of Site | Methodology | Environment | |
|---|---|---|---|---|---|
| [71] | Wang, C. N. et al. | 2018 | Renewable energy plants location | FAHP & TOPSIS | Fuzzy |
| [72] | Wang, C. N. et al. | 2018 | Solar power plant location | DEA, fuzzy AHP & TOPSIS | Fuzzy |
| [73] | Maghsoodi, A. I. et al. | 2019 | Construction project site | BWM, CODAS & T-MADM | Crisp |
| [74] | Zolfani, S. H. et al. | 2022 | Different types of site (Review paper) | Different MADM methodology | Fuzzy & crisp |
| [75] | Kharat, M. G. et al. | 2016 | Landfill site | Fuzzy AHP & Fuzzy TOPSIS | Fuzzy |
| [76] | Karaşan, A. et al. | 2020 | Electric vehicles charging stations | AHP, DEMATEL & TOPSIS | Fuzzy |
| [77] | Boyacı, A. Ç. et al. | 2022 | Pandemic hospital location | Fuzzy AHP & TOPSIS | Fuzzy |
| [78] | Önüt, S. et al. | 2010 | Shopping center site | AHP & TOPSIS | Fuzzy |
| [79] | Sennaroglu, B. et al. | 2018 | Military airport location | AHP, PROMETHEE & VIKOR | Crisp |
| [80] | Rezaeisabzevar, Y. et al. | 2020 | Landfill site | AHP, TODIM & ANP | Fuzzy |
| [81] | Liu, H. C. et al. | 2019 | Electric vehicle charging stations | DEMATEL & MULTIMOORA | Grey |
| [82] | Zhou, S. et al. | 2012 | Biofuel refinery location | Fuzzy TOPSIS | Fuzzy |
| This paper | 2023 | Women’s university site selection | NAHP, NTOPSIS & NCOPRAS | Neutrosophic | |
| TrNNs | Euclidean Distance [100,101,102] | Hausdorff Distance [102] | Chebyshev Distance [100] | Minkowski Distance [100] | Normalized Hamming Distance [100,101,102] & This Paper |
|---|---|---|---|---|---|
| & | 0.2179449472 | 0.10 | 0.01666667 | 0.0687944616 | 0.20 |
| & | 0.0345808227 | 0.01875 | 0.003125 | 0.0329153016 | 0.0375 |
| TrNN | Method 1 [103] | Method 2 [103] | Method 3 [103] | Method 4 [103] | Method 5 [103] | Method 6 [103] | Method 7 [103] | Above Method (18) |
|---|---|---|---|---|---|---|---|---|
| W | 3.6875 | 7 | 3.5 | 3.5 | 3.5 | 0.8333 | 7.5 | 4.2 |
| X | 7.8433 | 13 | 6.7083 | 6.6444 | 6.7374 | 0.2778 | 3.9 | 8.05 |
| Y | 0.3949 | 0.63 | 0.3563 | 0.35 | 0.3607 | 0.6403 | 0.175 | 0.4275 |
| Z | 0.6524 | 0.85 | 0.765 | 0.765 | 0.765 | 0.5344 | 0.8925 | 0.918 |
| Matrix Size (t) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Random Index (RI) | 0 | 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 |
| Location | District | Latitude & Longitude | Location Details |
|---|---|---|---|
| Kolkata () | Kolkata | 22.5726 °N, 88.3639 °E | It is the capital city of West Bengal. |
| Howrah () | Howrah | 22.5958 °N, 88.2636 °E | It is the capital city of Howrah district. |
| Berhampore () | Murshidabad | 24.0983 °N, 88.2684 °E | It is the capital city of Murshidabad district. |
| Siliguri () | Darjeeling | 26.7271 °N, 88.3953 °E | This city is in Darjeeling district base of the Himalaya mountains and the side of Mahananda river. It is second largest city of West Bengal. |
| Midnapore () | Paschim Medinipur | 22.4257 °N, 87.3199 °E | This city beside the Kangsabati river and capital city of Midnapore district. |
| Durgapur () | Paschim Bardhaman | 23.5204 °N, 87.3119 °E | It is the capital city of Burdwan district. |
| Linguistic Terms | Trapezoidal Neutrosophic Numbers (TrNN) |
|---|---|
| Equally Important (EI) | |
| Moderately Important (MI) | |
| Strongly Important (SI) | |
| Very Strongly Important (VSI) | |
| Absolutely Important (AI) | |
| Moderately Not Important (MNI) | |
| Strongly Not Important (SNI) | |
| Very Strongly Not Important (VSNI) | |
| Absolutely Not Important (ANI) |
| Serial No | Criteria | Scales (Units) | Source of Data |
|---|---|---|---|
| 1 | Population density () | This is calculated by average number of population per square kilometer. | This is fixed data collected from Census2011 [129]. |
| 2 | Investment Costs () | In Rupees. | After considering the investment costs different location. |
| 3 | Rate of Literacy () | Divide the number of literates of a given age range by the corresponding age group population and then multiply the result by 100. | This is fixed data collected from Census2011 [129]. |
| 4 | Number of graduates () | Number of people. | Based on literacy rate. |
| 5 | Yearly income per person () | In Rupees. | After considering the average income of the district where the sites are located. |
| 6 | Accessibility () | Linguistics term (good, bad etc.). | After seeing the transport and related system of the sites. |
| 7 | Public Services () | Linguistics term. | After seeing whether there is public service active or not nearby the sites. |
| 8 | Safety () | Linguistics term | After analysing the crime agents women and crime rate nearby the sites. |
| 9 | Proximity of E. Institutes () | Linguistics term | After seeing nearby educational institutes exist or not. |
| 10 | Sex Ratio () | Number of women per 1000 men. | This is fixed data collected from Census2011 [129]. |
| Criteria | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Criteria weight | 0.0696 | 0.0677 | 0.1400 | 0.1197 | 0.0578 | 0.1074 | 0.0989 | 0.1478 | 0.0932 | 0.0979 |
| Criteria | t | i | f | ||||
|---|---|---|---|---|---|---|---|
| Population density () | 0.0000 | 0.0536 | 0.0929 | 0.6438 | 0.7500 | 0.3000 | 0.2000 |
| Investment costs () | 0.0000 | 0.0528 | 0.0925 | 0.6458 | 0.7500 | 0.3000 | 0.2000 |
| Rate of literacy () | 0.0634 | 0.1146 | 0.1647 | 0.9274 | 0.8500 | 0.2000 | 0.1500 |
| Number of graduates () | 0.0000 | 0.0972 | 0.1454 | 0.9104 | 0.7500 | 0.3000 | 0.2000 |
| Yearly income per person () | 0.0000 | 0.0425 | 0.0791 | 0.6024 | 0.7500 | 0.3000 | 0.2000 |
| Accessibility () | 0.0000 | 0.0873 | 0.1340 | 0.8142 | 0.7500 | 0.3000 | 0.2000 |
| Public services () | 0.0000 | 0.0798 | 0.1247 | 0.7703 | 0.7500 | 0.3000 | 0.2000 |
| Safety () | 0.0649 | 0.1228 | 0.1734 | 0.9633 | 0.8000 | 0.2000 | 0.1500 |
| Proximity of E. institutes () | 0.0000 | 0.0751 | 0.1178 | 0.7849 | 0.7500 | 0.3000 | 0.2000 |
| Sex ratio () | 0.0000 | 0.0764 | 0.1222 | 0.7359 | 0.7500 | 0.3000 | 0.2000 |
| Alternatives | Ranking | |||
|---|---|---|---|---|
| Kolkata () | 0.1382 | 0.8824 | 0.8646 | 1 |
| Howrah () | 0.3527 | 0.6680 | 0.6545 | 2 |
| Berhampore () | 0.8321 | 0.1886 | 0.1847 | 6 |
| Siliguri () | 0.6078 | 0.4160 | 0.4063 | 5 |
| Midnapore () | 0.3555 | 0.6656 | 0.6518 | 3 |
| Durgapur () | 0.6058 | 0.4178 | 0.4082 | 4 |
| Alternatives | Ranking | ||||
|---|---|---|---|---|---|
| Kolkata () | 1.807561 | 0.056614 | 2.062153 | 100.0 | 1 |
| Howrah () | 1.58208 | 0.082565 | 1.756652 | 85.18 | 2 |
| Berhampore () | 1.099746 | 0.165103 | 1.187046 | 57.56 | 6 |
| Siliguri () | 1.356608 | 0.159694 | 1.446866 | 70.16 | 5 |
| Midnapore () | 1.653031 | 0.159694 | 1.743288 | 84.53 | 3 |
| Durgapur () | 1.361117 | 0.162181 | 1.44999 | 70.31 | 4 |
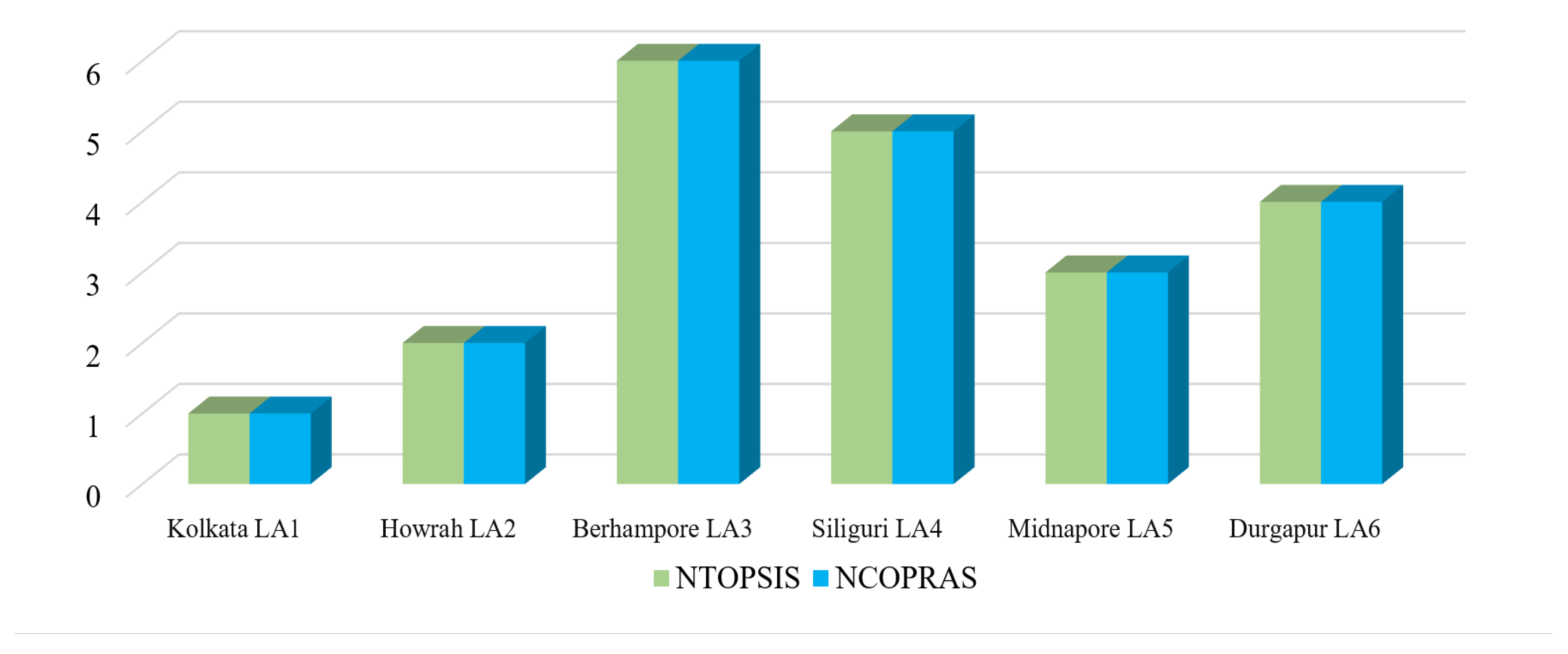
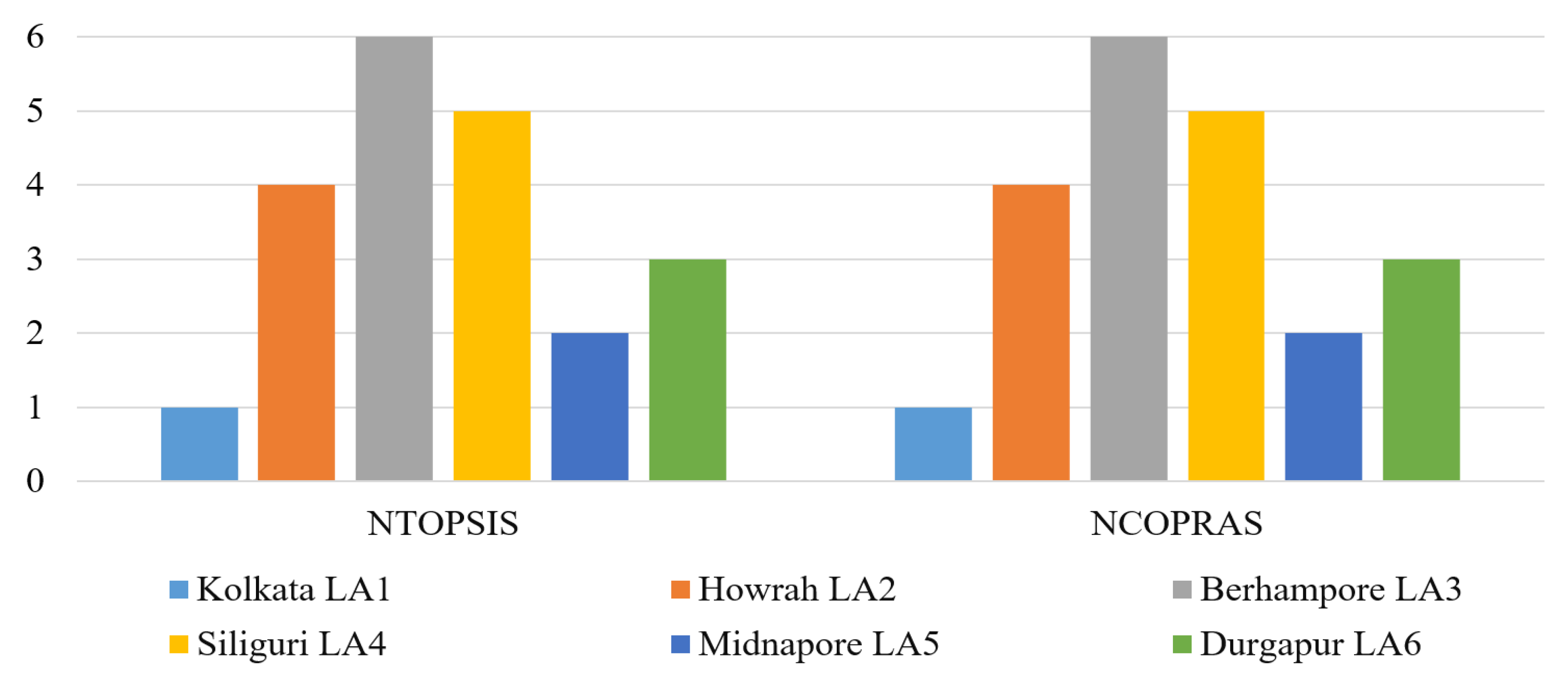
| Alternatives | Ranking Using NTOPSIS | Ranking Using NCOPRAS |
|---|---|---|
| Kolkata () | 1 | 1 |
| Howrah () | 4 | 4 |
| Berhampore () | 6 | 6 |
| Siliguri () | 5 | 5 |
| Midnapore () | 2 | 2 |
| Durgapur () | 3 | 3 |
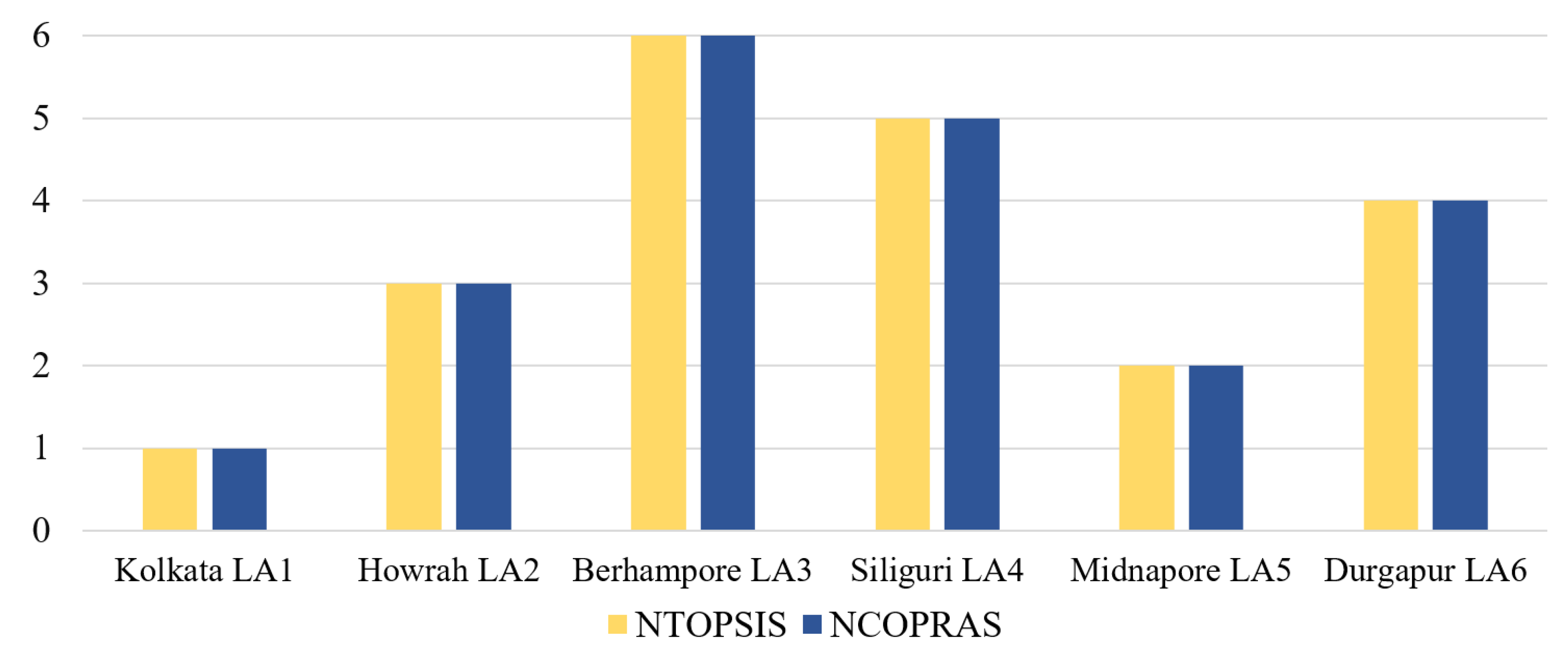
| Alternatives | Ranking Using NTOPSIS | Ranking Using NCOPRAS |
|---|---|---|
| Kolkata () | 1 | 1 |
| Howrah () | 3 | 3 |
| Berhampore () | 6 | 6 |
| Siliguri () | 5 | 5 |
| Midnapore () | 2 | 2 |
| Durgapur () | 4 | 4 |
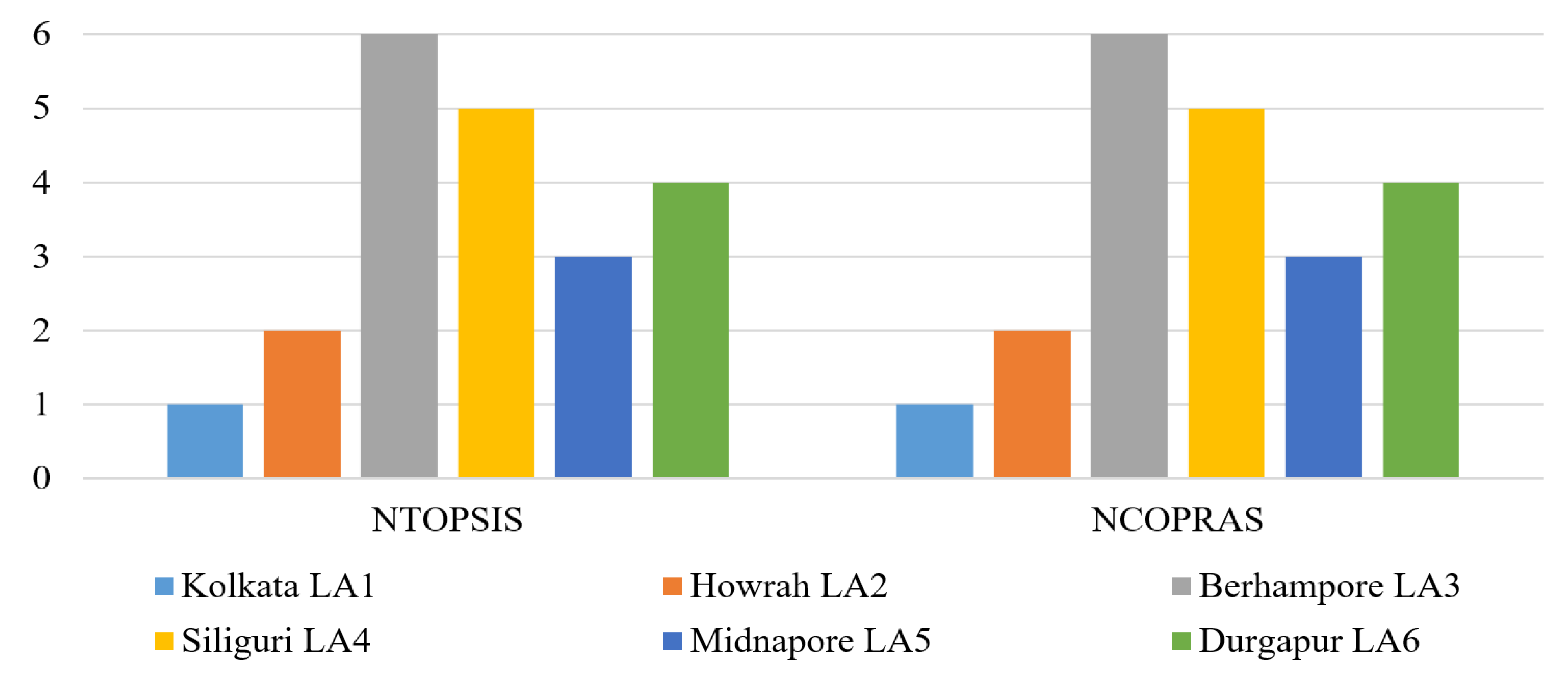
| Alternatives | Ranking Using NTOPSIS | Ranking Using NCOPRAS |
|---|---|---|
| Kolkata () | 1 | 1 |
| Howrah () | 2 | 2 |
| Berhampore () | 6 | 6 |
| Siliguri () | 5 | 5 |
| Midnapore () | 3 | 3 |
| Durgapur () | 4 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alzahrani, F.A.; Ghorui, N.; Gazi, K.H.; Giri, B.C.; Ghosh, A.; Mondal, S.P. Optimal Site Selection for Women University Using Neutrosophic Multi-Criteria Decision Making Approach. Buildings 2023, 13, 152. https://doi.org/10.3390/buildings13010152
Alzahrani FA, Ghorui N, Gazi KH, Giri BC, Ghosh A, Mondal SP. Optimal Site Selection for Women University Using Neutrosophic Multi-Criteria Decision Making Approach. Buildings. 2023; 13(1):152. https://doi.org/10.3390/buildings13010152
Chicago/Turabian StyleAlzahrani, Fahad A., Neha Ghorui, Kamal Hossain Gazi, Bibhas Chandra Giri, Arijit Ghosh, and Sankar Prasad Mondal. 2023. "Optimal Site Selection for Women University Using Neutrosophic Multi-Criteria Decision Making Approach" Buildings 13, no. 1: 152. https://doi.org/10.3390/buildings13010152
APA StyleAlzahrani, F. A., Ghorui, N., Gazi, K. H., Giri, B. C., Ghosh, A., & Mondal, S. P. (2023). Optimal Site Selection for Women University Using Neutrosophic Multi-Criteria Decision Making Approach. Buildings, 13(1), 152. https://doi.org/10.3390/buildings13010152










