Flexural Behavior of GBFS-Based Geopolymer-Reinforced Concrete Beams
Abstract
1. Introduction
2. Material and Methodology
2.1. Materials
2.2. Test Beams Fabrication and Curing
2.3. Test Set-Up
2.4. Cross-Section of Beams
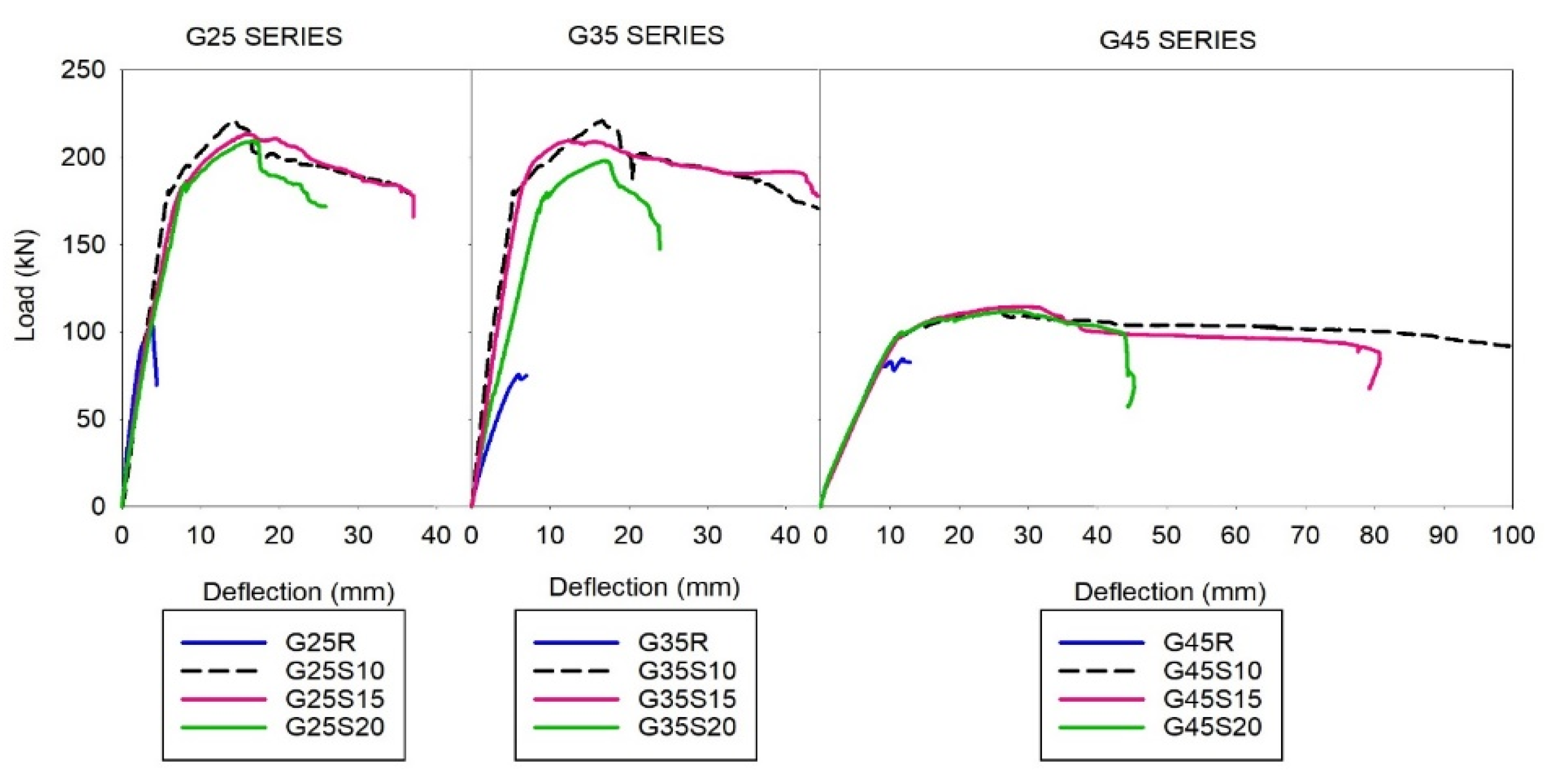
3. Experimental Results
4. Evaluation of the Moment Capacities of the Tested Beams
4.1. Modulus of Rupture of Concrete
4.2. Flexural Moment
4.3. Evaluation of Test Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Maholtra, V. Introduction: Sustainable development and concrete technology. ACI Concr. Int. 2002, 24, 22. [Google Scholar]
- Huntzinger, D.N.; Eatmon, T.D. A life-cycle assessment of Portland cement manufacturing: Comparing the traditional process with alternative technologies. J. Clean. Prod. 2009, 17, 668–675. [Google Scholar] [CrossRef]
- Meyer, C. The greening of the concrete industry. Cem. Concr. Compos. 2009, 31, 601–605. [Google Scholar] [CrossRef]
- Davidovits, J. False Values on CO2 Emission for Geopolymer Cement/Concrete; Technical Paper No. 24; Scientific Papers; Geopolymer Institute Library: Saint-Quentin, France, 2015; pp. 1–9. [Google Scholar]
- Flower, D.J.M.; Sanjayan, J.G. Greenhouse gas emissions due to concrete manufacture. Int. J. Life Cycle Assess. 2007, 12, 282–288. [Google Scholar] [CrossRef]
- Ulugöl, H.; Kul, A.; Yıldırım, G.; Şahmaran, M.; Aldemir, A.; Figueira, D.; Ashour, A. Mechanical and microstructural characterization of geopolymers from assorted construction and demolition waste-based masonry and glass. J. Clean. Prod. 2021, 280, 124358. [Google Scholar] [CrossRef]
- Zhuang, X.Y.; Chen, L.; Komarneni, S.; Zhou, C.H.; Tong, D.S.; Yang, H.M.; Yu, W.H.; Wang, H. Fly ash-based geopolymer: Clean production, properties and applications. J. Clean. Prod. 2016, 125, 253–267. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Y. Hybrid machine learning model and Shapley additive explanations for compressive strength of sustainable concrete. Constr. Build. Mater. 2022, 330, 127298. [Google Scholar] [CrossRef]
- Antiohos, S.K.; Tapali, J.G.; Zervaki, M.; Sousa-Coutinho, J.; Tsimas, S.; Papadakis, V.G. Low embodied energy cement containing untreated RHA: A strength development and durability study. Constr. Build. Mater. 2013, 49, 455–463. [Google Scholar] [CrossRef]
- Oakes, L.; Magee, B.; McIlhagger, A.; McCartney, M. Strength prediction and mix design procedures for geopolymer and alkali-activated cement mortars comprising a wide range of environmentally responsible binder systems. J. Struct. Integr. Maint. 2019, 4, 135–143. [Google Scholar] [CrossRef]
- Juenger, M.C.G.; Winnefeld, F.; Provis, J.L.; Ideker, J.H. Advances in alternative cementitious binders. Cem. Concr. Res. 2011, 41, 1232–1243. [Google Scholar] [CrossRef]
- Tian Sing, N.G.; Voo, Y.L.; Foster, S.J. Sustainability with Ultra-High Performance and Geopolymer Concrete Construction. In Innovative Materials and Techniques in Concrete Construction; Springer: Dordrecht, The Netherlands, 2012; pp. 81–100. [Google Scholar] [CrossRef]
- Hassan, A.; Arif, M.; Shariq, M. Use of geopolymer concrete for a cleaner and sustainable environment–A review of mechanical properties and microstructure. J. Clean. Prod. 2019, 223, 704–728. [Google Scholar] [CrossRef]
- Davidovits, J. Geopolymers: Inorganic polymeric new materials. J. Therm. Anal. Calorim. 1991, 37, 1633–1656. [Google Scholar] [CrossRef]
- Aydın, S.; Baradan, B. Mechanical and microstructural properties of heat cured alkali-activated slag mortars. Mater. Des. 2012, 35, 374–383. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Y. Splitting tensile strength prediction of sustainable high-performance concrete using machine learning techniques. Environ. Sci. Pollut. Res. 2022, 29, 89198–89209. [Google Scholar] [CrossRef]
- Van Jaarsveld, J.G.S.; van Deventer, J.S.J.; Lorenzen, L. The potential use of geopolymeric materials to immobilise toxic metals: Part I. Theory and applications. Miner. Eng. 1997, 10, 659–669. [Google Scholar] [CrossRef]
- Komnitsas, K.; Zaharaki, D. Geopolymerisation: A review and prospects for the minerals industry. Miner. Eng. 2007, 20, 1261–1277. [Google Scholar] [CrossRef]
- Fernández-Jiménez, A.; Garcia-Lodeiro, I.; Palomo, A. Durability of alkali-activated fly ash cementitious materials. J. Mater. Sci. 2007, 42, 3055–3065. [Google Scholar] [CrossRef]
- Feng, K.N.; Ruan, D.; Pan, Z.; Collins, F.; Bai, Y.; Wang, C.M.; Duan, W.H. Effect of strain rate on splitting tensile strength of geopolymer concrete. Mag. Concr. Res. 2014, 66, 825–835. [Google Scholar] [CrossRef]
- Lee, K.M.; Choi, S.; Choo, J.F.; Choi, Y.C.; Yoo, S.W. Flexural and Shear Behaviors of Reinforced Alkali-Activated Slag Concrete Beams. Adv. Mater. Sci. Eng. 2017, 2017, 5294290. [Google Scholar] [CrossRef]
- Kumaravel, S.; Thirugnanasambandam, S. Flexural behaviour of geopolymer concrete beams. Int. J. Adv. Eng. Res. Stud. 2013, 4, 06. [Google Scholar]
- Chang, E.H. Shear and Bond Behavior of Reinforced Fly Ash-Based Geopolymer Concrete Beams. Ph.D. Thesis, Department of Civil Engineering, Curtin University of Technology, Bentley, Australia, 2009. Available online: http://hdl.handle.net/20.500.11937/468 (accessed on 30 January 2009).
- Yacob, N.S.; ElGawady, M.A.; Sneed, L.H.; Said, A. Shear strength of fly ash-based geopolymer reinforced concrete beams. Eng. Struct. 2019, 196, 109298. [Google Scholar] [CrossRef]
- Sanni, S.H. Analytical Modelling and Experimental Validation of Balanced Reinforced Geopolymer Concrete Beams. I-Manag. J. Struct. Eng. 2021, 10, 31–39. [Google Scholar] [CrossRef]
- Wu, C.; Hwang, H.J.; Shi, C.; Li, N.; Du, Y. Shear tests on reinforced slag-based geopolymer concrete beams with transverse reinforcement. Eng. Struct. 2020, 219, 110966. [Google Scholar] [CrossRef]
- Madheswaran, C.K.; Ambily, P.S.; Lakshmanan, N.; Dattatreya, J.K.; Sathik, S.A. Shear Behavior of Reinforced Geopolymer Concrete Thin-Webbed T-Beams. ACI Mater. J. 2014, 111, 89. [Google Scholar]
- ACI 318; Building Code Requirements for Structural Concrete (ACI 318-08) and Commentary. ACI: Farmington Hills, MI, USA, 2008; p. 473.
- AS-3600; Concrete Structures. Standards Australia International: Sydney, Australia, 2009.
- ACI 318-19; Building Code Requirements for Structural Concrete and Commentary. ACI: Farmington Hills, MI, USA, 2019.
- ACI 363; State of the Art Report on High Strength Concrete. ACI363-R. ACI: Farmington Hills, MI, USA, 1992.
- TS500; Requirements for Design and Construction of Reinforced Concrete Structures. Turkish Standards Institute: Ankara, Turkey, 2000; p. 67. (In Turkish)
- Eurocode 2 ENV 1992-1-1; Design of Concrete Structures, Part 1: General Rules and Rules for Buildings. British Standards Institution: London, UK, 1992.
- Ahmad, S.H.; Shah, S.P. Structural properties of high strength concrete and its implications for precast prestressed concrete. PCI J. 1985, 30, 92–119. [Google Scholar]
- Swamy, R.N. Properties of high-strength concrete. Cem. Concr. Aggreg. CCAGDP 1986, 8, 33–41. [Google Scholar]
- Diaz-Loya, E.I.; Allouche, E.N.; Vaidya, S. Mechanical properties of fly-ash-based geopolymer concrete. ACI Mater. J. 2011, 108, 300–306. [Google Scholar]
- Shehab, H.K.; Eisa, A.S.; Wahba, A.M. Mechanical properties of fly ash based geopolymer concrete with full and partial cement replacement. Constr. Build. Mater. 2016, 126, 560–565. [Google Scholar] [CrossRef]
- Phoo-ngernkham, T.; Sata, V.; Hanjitsuwan, S.; Ridtirud, C.; Hatanaka, S.; Chindaprasirt, P. Compressive strength, bending and fracture characteristics of high calcium fly ash geopolymer mortar containing portland cement cured at ambient temperature. Arab. J. Sci. Eng. 2016, 41, 1263–1271. [Google Scholar] [CrossRef]
- Nath, P.; Sarker, P.K. Flexural strength and elastic modulus of ambient-cured blended low-calcium fly ash geopolymer concrete. Constr. Build. Mater. 2017, 130, 22–31. [Google Scholar] [CrossRef]
- Xu, H.; Van Deventer, J.S.J. The geopolymerisation of alumino-silicate minerals. Int. J. Miner. Process. 2000, 59, 247–266. [Google Scholar] [CrossRef]
- Skorina, T. Ion exchange in amorphous alkali-activated aluminosilicates: Potassium based geopolymers. Appl. Clay Sci. 2014, 87, 205–211. [Google Scholar] [CrossRef]
- Shehata, N.; Sayed, E.T.; Abdelkareem, M.A. Recent progress in environmentally friendly geopolymers: A review. Sci. Total Environ. 2021, 762, 143166. [Google Scholar] [CrossRef]
- Ozturk, M.; Arslan, G. Shear Behavior of Granulated Blast Furnace Slag-Based Geopolymer-Reinforced Concrete Beams. Buildings 2022, 12, 2053. [Google Scholar] [CrossRef]
- ASTM C78; Test Method for Flexural Strength of Concrete Using Simple Beam with Third-Point Loading. In Annual Book of ASTM Standards . ASTM: West Conshohocken, PA, USA, 1988.
- ASTM C293; Standard Test Method for Flexural Strength of Concrete (Using Simple Beam with Center-Point Loading). In Annual Book of ASTM Standards. ASTM: West Conshohocken, PA, USA, 2004.
- ASTM C1018; Standard Test Method for Flexural Toughness and Firstcrack Strength of Fiber-Reinforced Concrete (Using Beam with Third-Point Loading). ASTM International: West Conshohocken, PA, USA, 1997.
- AS 1012, 10-2000; Australian: Methods of Testing Concrete-Method for the Determination of Indirect Tensile Strength of Concrete Cylinders (Brasil or Splitting Test). Standards Australia: Sydney, Australia, 2000.
- TS EN 12390-3; Testing Hardened Concrete-Part 3: Compressive Strength of Test Specimen. Turkish Standards Institute: Ankara, Turkey, 2019. (In Turkish)






| Material | Amount (kg/m3) |
|---|---|
| GBFS | 450 |
| NaOH solution | 102 |
| Na2SiO3 solution | 234 |
| Superplasticizer | 4.5 |
| Naturel sand (0–2 mm) | 322 |
| Crushed sand (0–4 mm) | 458 |
| Crushed stone (5–13 mm) | 804 |
| Beams | Beam | fc (MPa) | s (mm) | ρw (%) | L (mm) | a (mm) | a/d |
| G25R # G25S10 # G25S15 # G25S20 # | G25R # | 56.43 | - | - | 1400 | 525 | 2.5 |
| G25S10 # | 69.58 | 100 | 0.67 | ||||
| G25S15 # | 58.49 | 150 | 0.45 | ||||
| G25S20 # | 62.83 | 200 | 0.34 | ||||
| G35R # G35S10 G35S15 G35S20 | G35R # | 48.26 | - | - | 2200 | 735 | 3.5 |
| G35S10 | 46.18 | 100 | 0.67 | ||||
| G35S15 | 51.01 | 150 | 0.45 | ||||
| G35S20 | 54.58 | 200 | 0.34 | ||||
| G45R # G45S10 G45S15 G45S20 | G45R # | 62.39 | - | - | 2200 | 945 | 4.5 |
| G45S10 | 71.00 | 100 | 0.67 | ||||
| G45S15 | 66.40 | 150 | 0.45 | ||||
| G45S20 | 56.14 | 200 | 0.34 |
| Beams | Pcr,Fl (kN) | Pcr (kN) | Pmax (kN) | ⸹Pmax (mm) | Pu (kN) | ⸹u (mm) | Failure Mode |
|---|---|---|---|---|---|---|---|
| G25R # | 37.55 | 70.20 | 103.90 | 3.82 | 69.58 | 4.36 | S * |
| G25S10 # | 38.15 | 69.20 | 221.06 | 16.66 | 178.90 | 39.62 | S-F ** |
| G25S15 # | 36.36 | 65.52 | 213.43 | 16.04 | 165.99 | 37.00 | S * |
| G25S20 # | 40.69 | 72.68 | 209.01 | 15.78 | 171.86 | 25.84 | S * |
| G35R # | 22.79 | 50.16 | 75.74 | 5.98 | 74.92 | 6.98 | S * |
| G35S10 | 23.10 | 47.70 | 221.05 | 16.58 | 170.52 | 44.34 | F & |
| G35S15 | 22.78 | 56.71 | 209.66 | 12.36 | 147.48 | 23.96 | F & |
| G35S20 | 25.93 | 59.58 | 197.06 | 17.5 | 165.29 | 46.62 | F & |
| G45R # | 19.21 | 63.47 | 82.56 | 12.02 | 82.56 | 12.02 | S * |
| G45S10 | 22.49 | 68.59 | 111.54 | 25.57 | 88.29 | 103.24 | F & |
| G45S15 | 24.64 | 66.74 | 114.38 | 28.24 | 68.69 | 79.30 | F & |
| G45S20 | 20.79 | 62.03 | 111.71 | 28.94 | 58.01 | 44.40 | F & |
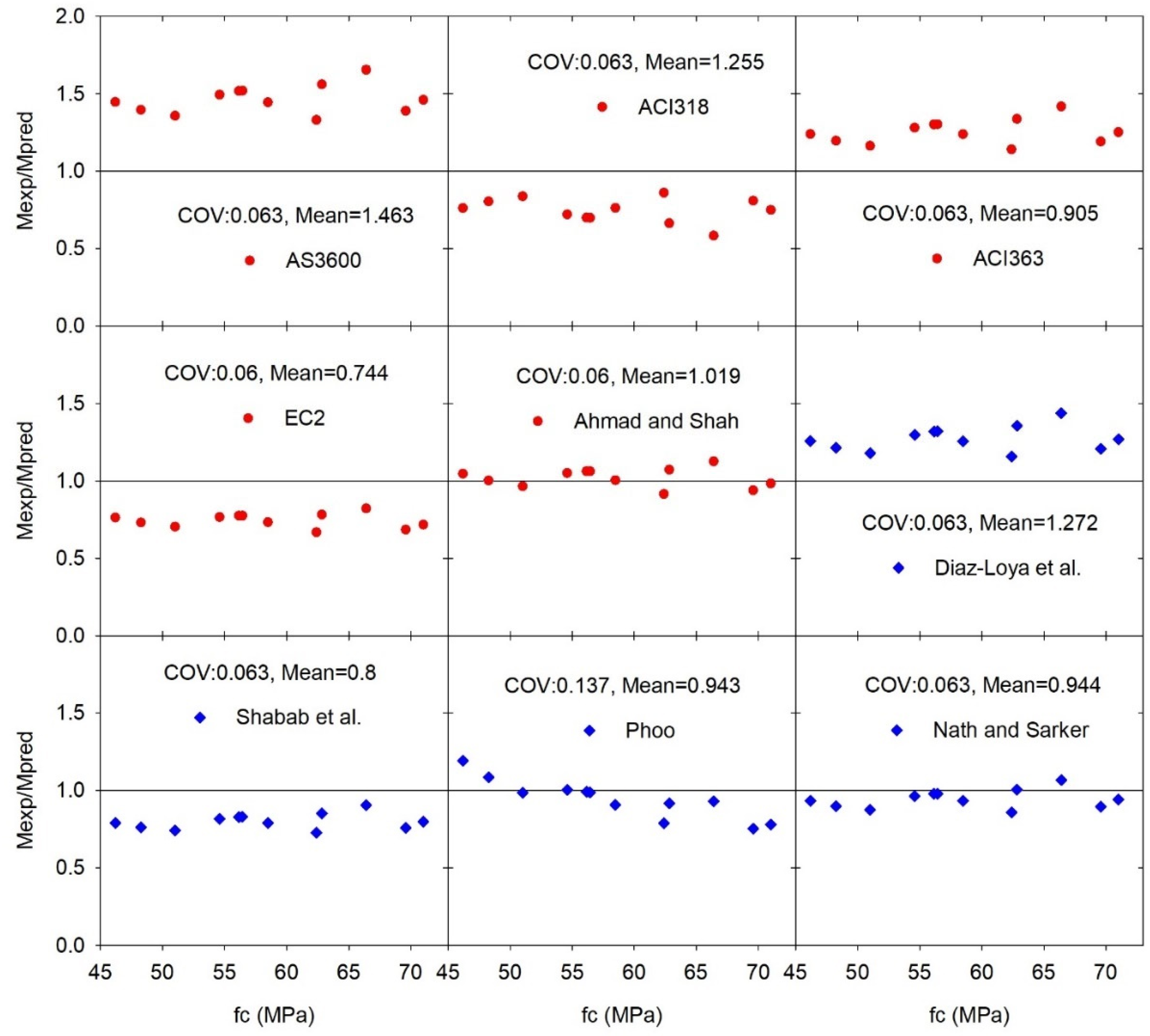
| Beam | AS3600 [29] | ACI318 [30] | ACI363 [31] | EC2 [33] | Ahmad and Shah [34] | Swamy [35] | Diaz-Loya et al. [36] | Shehab et al. [37] | Phoo-ngernkham et al. [38] | Nath and Sarker [39] |
|---|---|---|---|---|---|---|---|---|---|---|
| G25R | 1.519 | 1.302 | 0.939 | 0.775 | 1.062 | 1.069 | 1.321 | 0.830 | 0.987 | 0.980 |
| G25S10 | 1.389 | 1.191 | 0.859 | 0.685 | 0.939 | 0.963 | 1.208 | 0.759 | 0.753 | 0.896 |
| G25S15 | 1.444 | 1.238 | 0.893 | 0.733 | 1.004 | 1.014 | 1.256 | 0.789 | 0.907 | 0.932 |
| G25S20 | 1.560 | 1.337 | 0.965 | 0.782 | 1.072 | 1.089 | 1.356 | 0.852 | 0.917 | 1.006 |
| G35R | 1.395 | 1.196 | 0.863 | 0.731 | 1.002 | 0.996 | 1.213 | 0.763 | 1.085 | 0.900 |
| G35S10 | 1.446 | 1.239 | 0.894 | 0.763 | 1.046 | 1.037 | 1.257 | 0.790 | 1.193 | 0.933 |
| G35S15 | 1.357 | 1.163 | 0.839 | 0.704 | 0.965 | 0.964 | 1.180 | 0.741 | 0.985 | 0.875 |
| G35S20 | 1.493 | 1.280 | 0.923 | 0.766 | 1.050 | 1.054 | 1.298 | 0.816 | 1.004 | 0.963 |
| G45R | 1.330 | 1.140 | 0.823 | 0.668 | 0.915 | 0.929 | 1.157 | 0.727 | 0.787 | 0.858 |
| G45S10 | 1.460 | 1.251 | 0.903 | 0.717 | 0.983 | 1.011 | 1.269 | 0.798 | 0.779 | 0.942 |
| G45S15 | 1.654 | 1.417 | 1.023 | 0.822 | 1.126 | 1.150 | 1.438 | 0.904 | 0.929 | 1.067 |
| G45S20 | 1.517 | 1.301 | 0.939 | 0.775 | 1.062 | 1.069 | 1.319 | 0.829 | 0.992 | 0.979 |
| MV | 1.464 | 1.255 | 0.905 | 0.744 | 1.019 | 1.029 | 1.273 | 0.801 | 0.943 | 0.944 |
| SD | 0.092 | 0.079 | 0.057 | 0.045 | 0.062 | 0.062 | 0.080 | 0.050 | 0.129 | 0.059 |
| COV | 0.063 | 0.063 | 0.063 | 0.060 | 0.060 | 0.060 | 0.063 | 0.063 | 0.136 | 0.063 |
| Beams | MExp. (kNm) | Mn,ACI (kNm) | Mn, TS (kNm) | MExp./Mn,ACI | MExp./Mn,TS500 |
|---|---|---|---|---|---|
| G35S10 | 81.24 | 43.50 | 40.90 | 1.868 | 1.986 |
| G35S15 | 77.05 | 45.00 | 42.10 | 1.712 | 1.830 |
| G35S20 | 72.42 | 45.90 | 42.80 | 1.578 | 1.692 |
| G45S10 | 52.70 | 49.80 | 47.40 | 1.058 | 1.112 |
| G45S15 | 54.04 | 48.70 | 45.80 | 1.110 | 1.180 |
| G45S20 | 52.78 | 46.30 | 43.10 | 1.140 | 1.225 |
| MV | 0.746 | 0.701 | |||
| SD | 0.181 | 0.173 | |||
| COV | 0.243 | 0.247 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozturk, M.; Arslan, G. Flexural Behavior of GBFS-Based Geopolymer-Reinforced Concrete Beams. Buildings 2023, 13, 141. https://doi.org/10.3390/buildings13010141
Ozturk M, Arslan G. Flexural Behavior of GBFS-Based Geopolymer-Reinforced Concrete Beams. Buildings. 2023; 13(1):141. https://doi.org/10.3390/buildings13010141
Chicago/Turabian StyleOzturk, Mehdi, and Guray Arslan. 2023. "Flexural Behavior of GBFS-Based Geopolymer-Reinforced Concrete Beams" Buildings 13, no. 1: 141. https://doi.org/10.3390/buildings13010141
APA StyleOzturk, M., & Arslan, G. (2023). Flexural Behavior of GBFS-Based Geopolymer-Reinforced Concrete Beams. Buildings, 13(1), 141. https://doi.org/10.3390/buildings13010141






