New Fuzzy-Heuristic Methodology for Analyzing Compression Load Capacity of Composite Columns
Abstract
1. Introduction
2. Data Provision
3. Methodology
3.1. ANFIS
3.2. Metaheuristic Algorithms
4. Results and Discussion
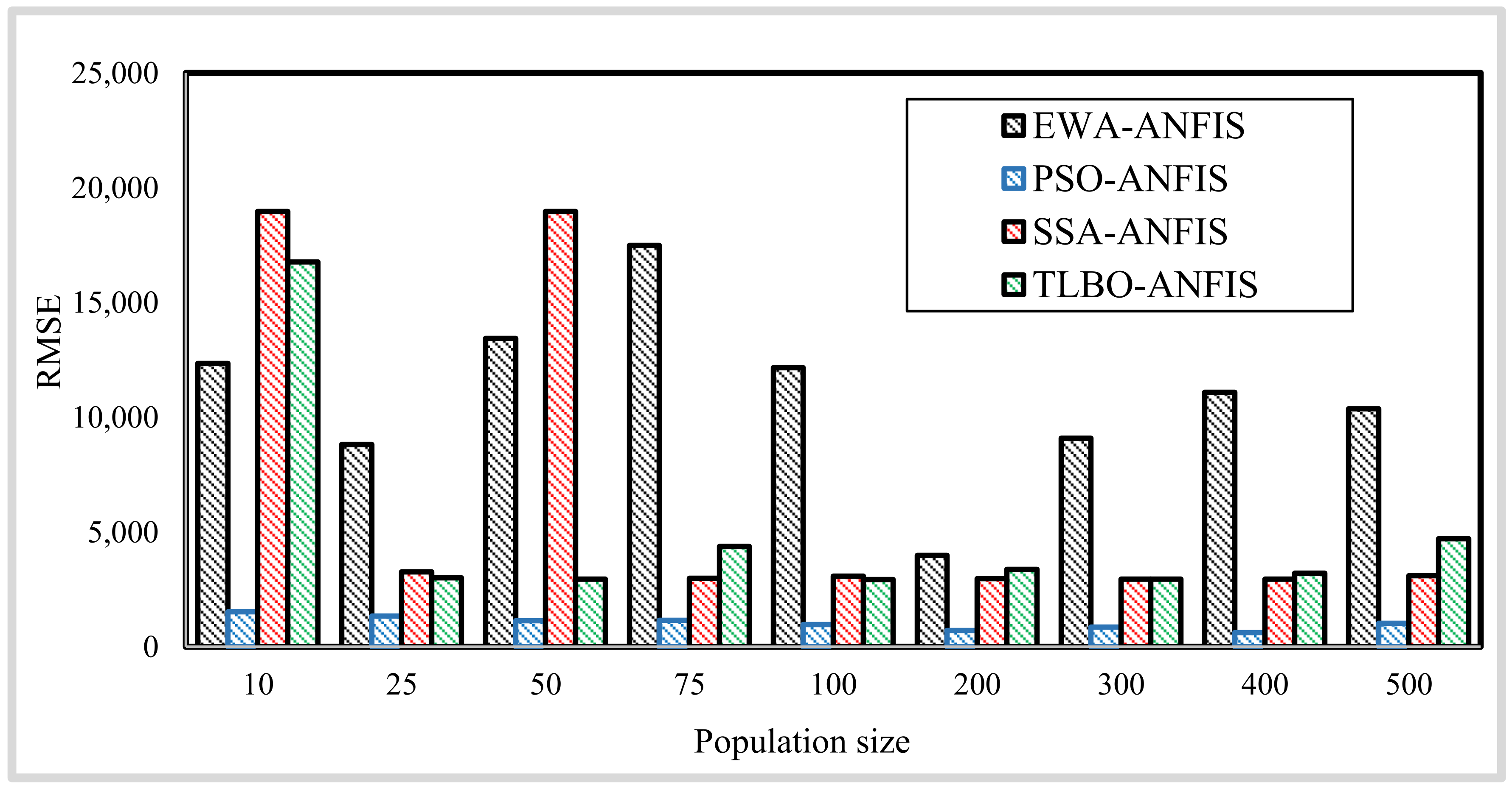
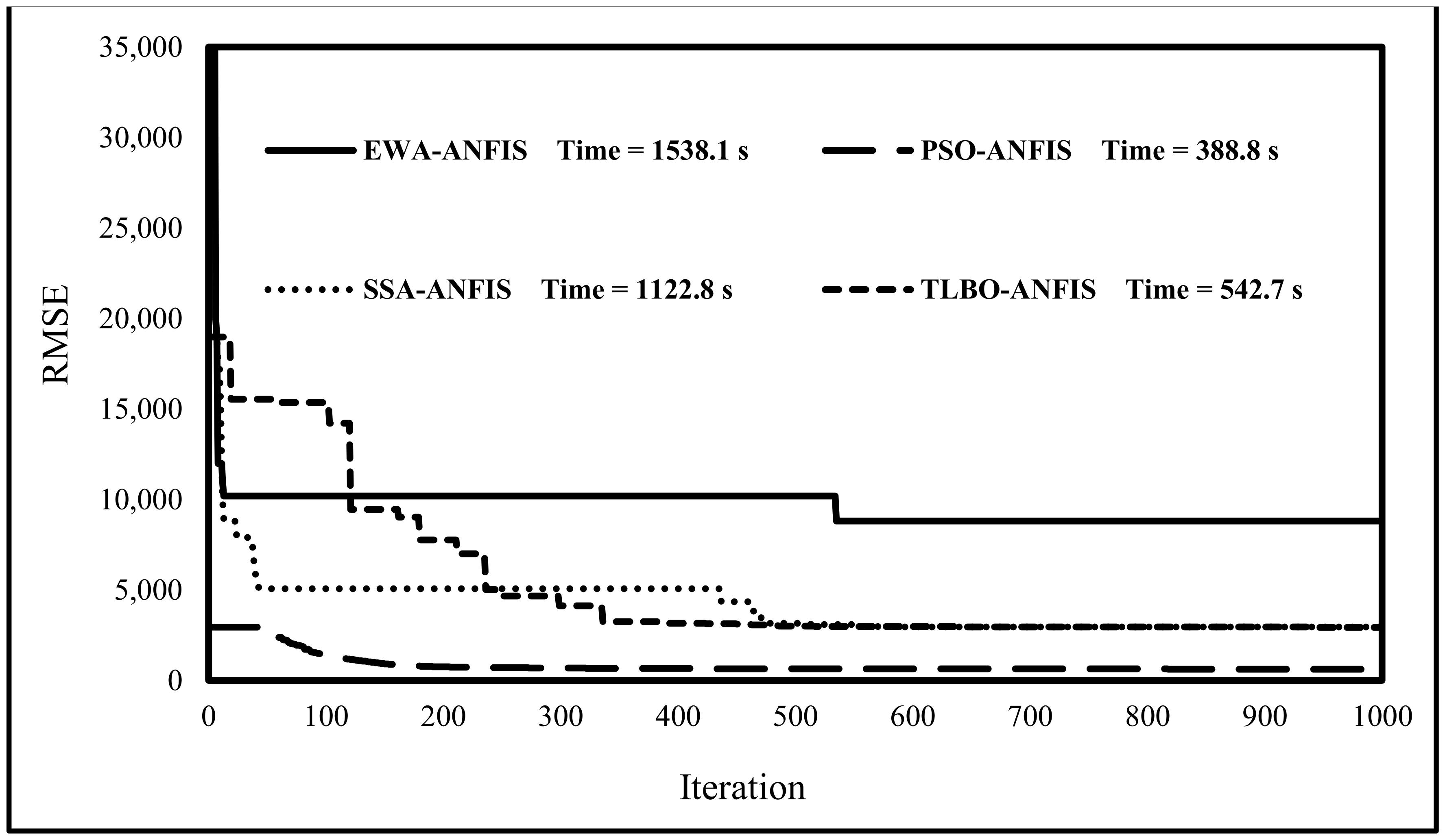
4.1. Metaheuristic Optimization
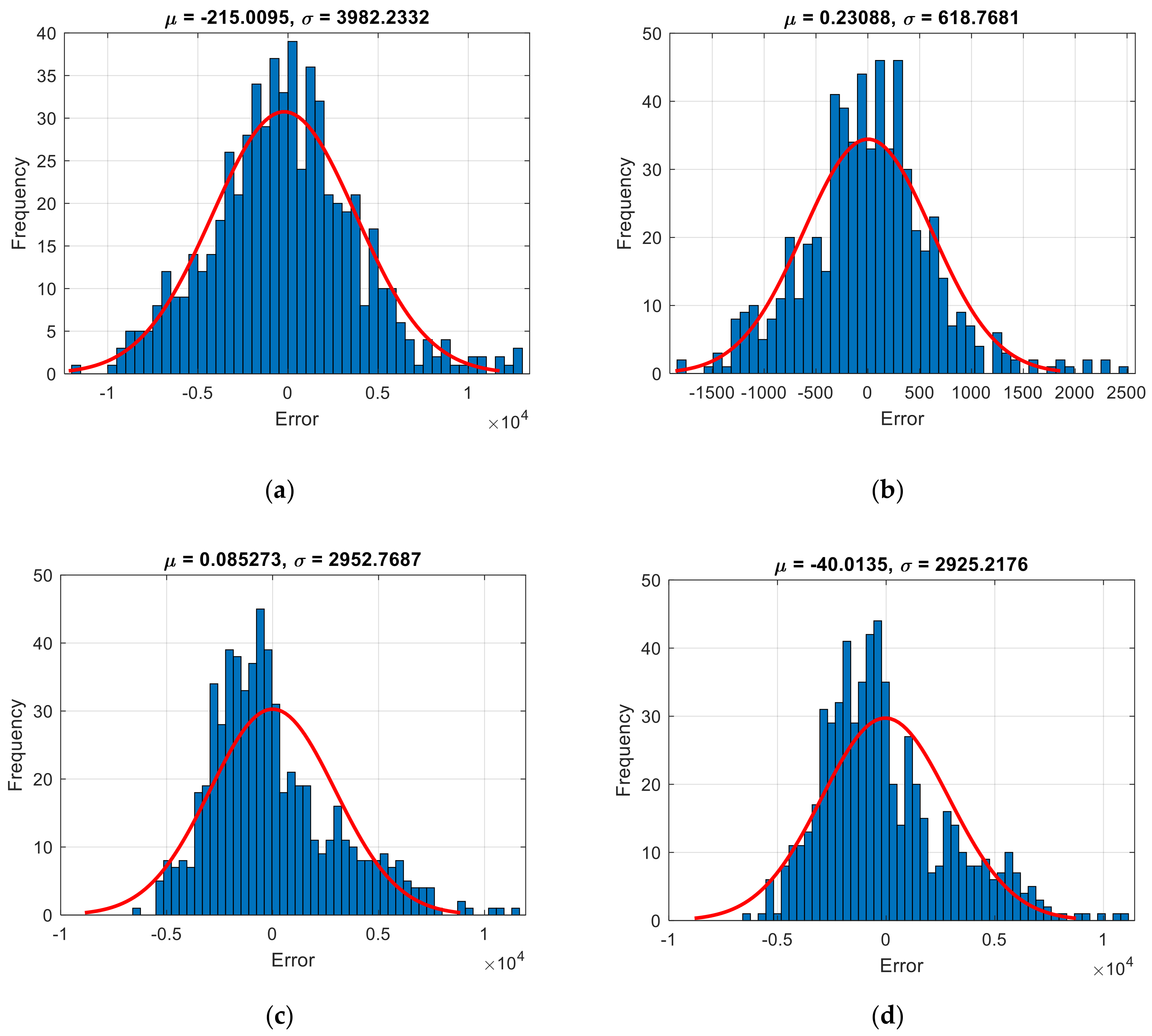
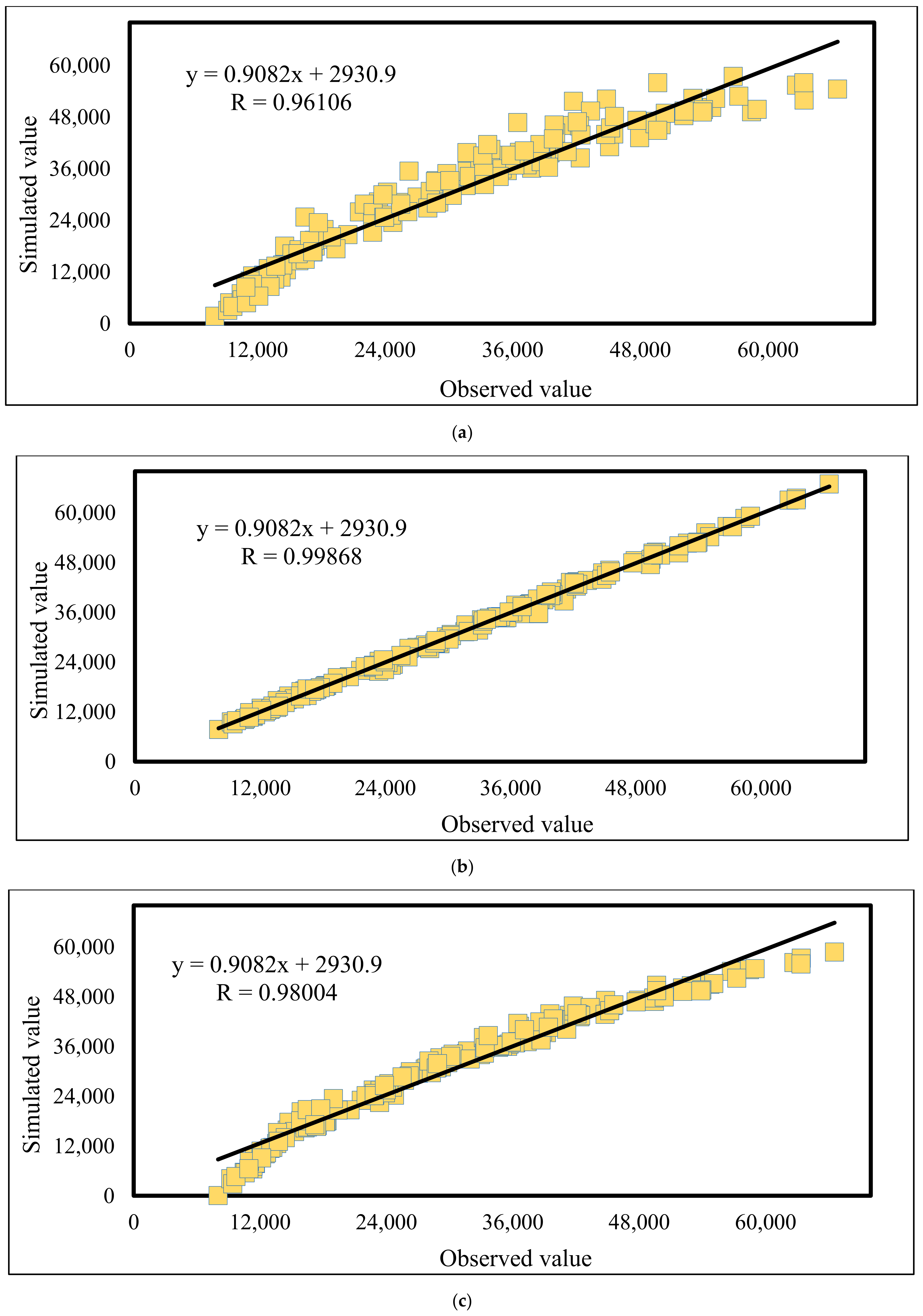
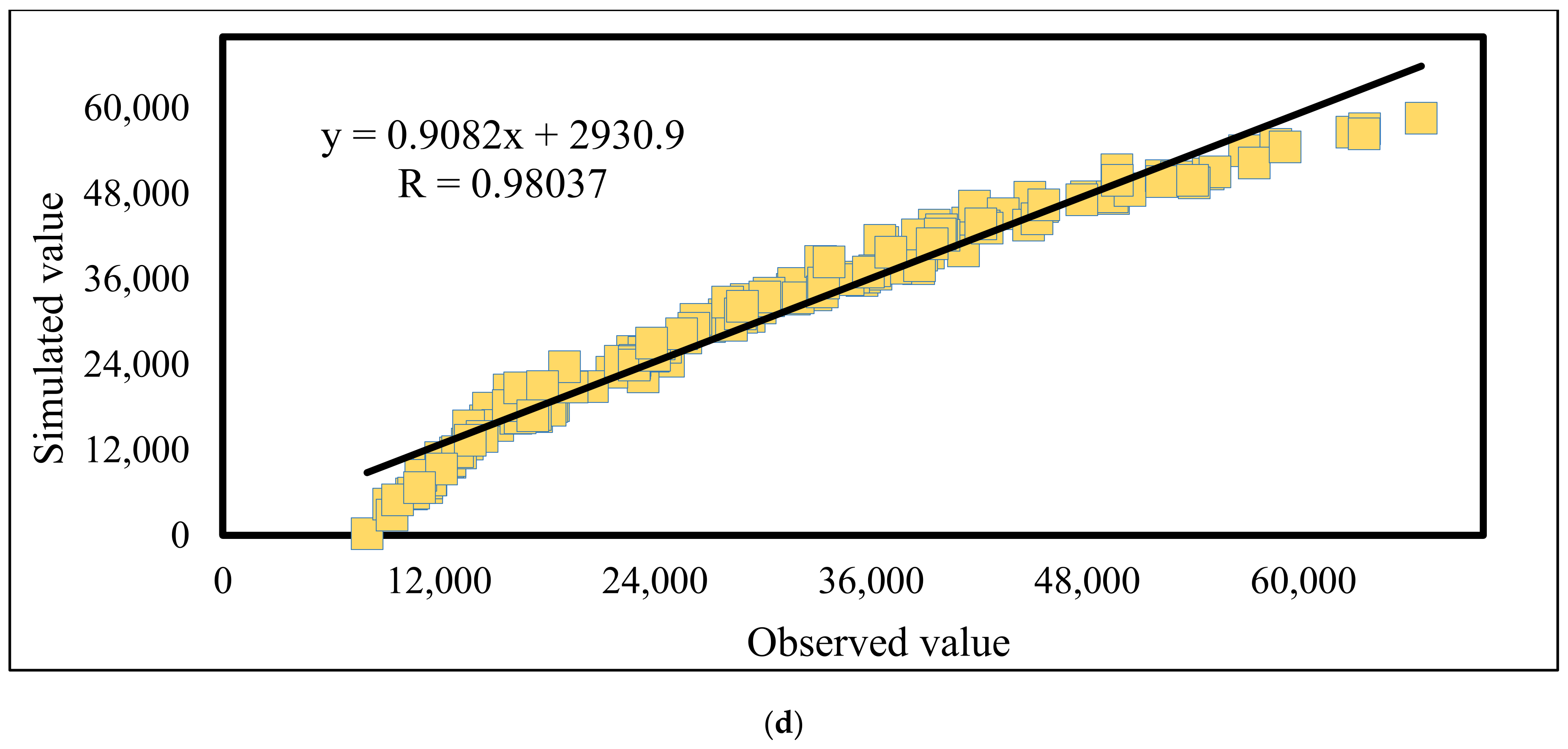
4.2. Prediction Results
4.3. Comparison
5. Conclusions
- Metaheuristic algorithms are suitable options for training neuro-fuzzy systems for the mentioned purpose.
- Referring to the correlation values >0.96, all employed fuzzy-metaheuristic models are capable of both comprehending and generalizing the relationship between the CC and input parameters.
- The PSO algorithm emerged as the most suitable optimizer for the ANFIS. This deduction came up due to the highest accuracy, as well as the most time-efficient optimization behavior observed compared to the three other algorithms.
- The PSO-ANFIS could present a finer prediction of extremum CC values.
- In short, the use of the PSO-ANFIS is recommended for practical applications which pursue efficient cost-competitive design of CCFST columns.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| CCFST | Circular concrete-filled steel tube | CC | Compression capacity |
| ANN | Artificial neural network | ANFIS | Adaptive neuro-fuzzy inference system |
| BART | Bayesian additive regression tree | GA | Genetic algorithm |
| ABC | Artificial bee colony | PSO | Particle swarm optimization |
| EWA | Earthworm algorithm | SSA | Salp swarm algorithm |
| TLBO | Teaching learning-based optimization | fc’ | Compressive strength of UHSC |
| L | Length of column | D | Diameter |
| t | Thickness | fy | Yield stress |
| fu | Ultimate stress of the steel tube | MF | Membership function |
| RMSE | Root mean square error | R | Pearson correlation index |
| MAPE | Mean absolute percentage error | MAE | Mean absolute error |
References
- Zhang, Z.; Liang, G.; Niu, Q.; Wang, F.; Chen, J.; Zhao, B.; Ke, L. A Wiener degradation process with drift-based approach of determining target reliability index of concrete structures. Qual. Reliab. Eng. Int. 2022, 38, 3710–3725. [Google Scholar] [CrossRef]
- Zhang, H.; Li, L.; Ma, W.; Luo, Y.; Li, Z.; Kuai, H. In Effects of welding residual stresses on fatigue reliability assessment of a PC beam bridge with corrugated steel webs under dynamic vehicle loading. Structures 2022, 45, 1561–1572. [Google Scholar] [CrossRef]
- Zhang, C.; Ali, A.; Sun, L. Investigation on low-cost friction-based isolation systems for masonry building structures: Experimental and numerical studies. Eng. Struct. 2021, 243, 112645. [Google Scholar]
- Huang, Y.; Zhang, W.; Liu, X. Assessment of Diagonal Macrocrack-Induced Debonding Mechanisms in FRP-Strengthened RC Beams. J. Compos. Constr. 2022, 26, 04022056. [Google Scholar] [CrossRef]
- Huang, H.; Yao, Y.; Liang, C.; Ye, Y. Experimental study on cyclic performance of steel-hollow core partially encased composite spliced frame beam. Soil Dyn. Earthq. Eng. 2022, 163, 107499. [Google Scholar] [CrossRef]
- Liao, D.; Zhu, S.-P.; Keshtegar, B.; Qian, G.; Wang, Q. Probabilistic framework for fatigue life assessment of notched components under size effects. Int. J. Mech. Sci. 2020, 181, 105685. [Google Scholar]
- He, J.-C.; Zhu, S.-P.; Luo, C.; Niu, X.; Wang, Q. Size effect in fatigue modelling of defective materials: Application of the calibrated weakest-link theory. Int. J. Fatigue 2022, 165, 107213. [Google Scholar] [CrossRef]
- Xu, H.; He, T.; Zhong, N.; Zhao, B.; Liu, Z. Transient thermomechanical analysis of micro cylindrical asperity sliding contact of SnSbCu alloy. Tribol. Int. 2022, 167, 107362. [Google Scholar] [CrossRef]
- Han, L.-H.; Li, W.; Bjorhovde, R. Developments and advanced applications of concrete-filled steel tubular (CFST) structures: Members. J. Constr. Steel Res. 2014, 100, 211–228. [Google Scholar] [CrossRef]
- Yang, M.-G.; Cai, C.; Chen, Y. Creep performance of concrete-filled steel tubular (CFST) columns and applications to a CFST arch bridge. Steel Compos. Struct. 2015, 19, 111–129. [Google Scholar] [CrossRef]
- Lin, L.; Wang, F. A finite element based study on concrete filled steel tube (CFST) pile used in wharf structure. In Proceedings of the 32nd International Ocean and Polar Engineering Conference, Shanghai, China, 6–10 June 2022; OnePetro: Richardson, TX, USA, 2022. [Google Scholar]
- Zhang, J.; Liu, L.; Cao, J.; Yan, X.; Zhang, F. Mechanism and application of concrete-filled steel tubular support in deep and high stress roadway. Constr. Build. Mater. 2018, 186, 233–246. [Google Scholar] [CrossRef]
- Ren, Q.; Li, M.; Zhang, M.; Shen, Y.; Si, W. Prediction of ultimate axial capacity of square concrete-filled steel tubular short columns using a hybrid intelligent algorithm. Appl. Sci. 2019, 9, 2802. [Google Scholar] [CrossRef]
- Dundu, M. Compressive strength of circular concrete filled steel tube columns. Thin-Walled Struct. 2012, 56, 62–70. [Google Scholar] [CrossRef]
- Zhai, Q.; Zhang, J.; Xiao, J.; Du, G.; Huang, Y. Feasibility of Piezoceramic Transducer-Enabled Active Sensing for the Monitoring Cross-shaped Concrete Filled Steel Tubular (CCFST) Columns under Cyclic Loading. Measurement 2021, 182, 109646. [Google Scholar] [CrossRef]
- Fan, J.; Lyu, F.; Ding, F.; Bu, D.; Wang, S.; Tan, Z.; Tan, S. Compatibility Optimal Design of Axially Loaded Circular Concrete-Filled Steel Tube Stub Columns. Materials 2021, 14, 4839. [Google Scholar] [CrossRef]
- Reddy, S.V.B.; Sivasankar, S. Axial behaviour of corroded CFST columns wrapped with GFRP sheets—An experimental investigation. In Advances in Structural Engineering; Springer: Berlin/Heidelberg, Germany, 2020; pp. 15–28. [Google Scholar]
- Teng, J.; Wang, J.; Lin, G.; Zhang, J.; Feng, P. Compressive behavior of concrete-filled steel tubular columns with internal high-strength steel spiral confinement. Adv. Struct. Eng. 2021, 24, 1687–1708. [Google Scholar] [CrossRef]
- Güneyisi, E.M.; Nour, A.I. Axial compression capacity of circular CFST columns transversely strengthened by FRP. Eng. Struct. 2019, 191, 417–431. [Google Scholar] [CrossRef]
- Yu, M.; Zha, X.; Ye, J.; She, C. A unified formulation for hollow and solid concrete-filled steel tube columns under axial compression. Eng. Struct. 2010, 32, 1046–1053. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, Q.; Chen, G. Compressive behavior of thin-walled circular steel tubular columns filled with steel stirrup-reinforced compound concrete. Eng. Struct. 2018, 170, 178–195. [Google Scholar] [CrossRef]
- Abdalla, S.; Abed, F.; AlHamaydeh, M. Behavior of CFSTs and CCFSTs under quasi-static axial compression. J. Constr. Steel Res. 2013, 90, 235–244. [Google Scholar] [CrossRef]
- Xu, L.; Cai, M.; Dong, S.; Yin, S.; Xiao, T.; Dai, Z.; Wang, Y.; Soltanian, M.R. An upscaling approach to predict mine water inflow from roof sandstone aquifers. J. Hydrol. 2022, 612, 128314. [Google Scholar] [CrossRef]
- Seyedashraf, O.; Mehrabi, M.; Akhtari, A.A. Novel approach for dam break flow modeling using computational intelligence. J. Hydrol. 2018, 559, 1028–1038. [Google Scholar] [CrossRef]
- Moayedi, H.; Mehrabi, M.; Mosallanezhad, M.; Rashid, A.S.A.; Pradhan, B. Modification of landslide susceptibility mapping using optimized PSO-ANN technique. Eng. Comput. 2019, 35, 967–984. [Google Scholar] [CrossRef]
- Zhan, C.; Dai, Z.; Soltanian, M.R.; de Barros, F.P. Data-worth analysis for heterogeneous subsurface structure identification with a stochastic deep learning framework. Water Resour. Res. 2022, 58, e2022WR033241. [Google Scholar] [CrossRef]
- Duan, J.; Asteris, P.G.; Nguyen, H.; Bui, X.-N.; Moayedi, H. A novel artificial intelligence technique to predict compressive strength of recycled aggregate concrete using ICA-XGBoost model. Eng. Comput. 2020, 37, 1–18. [Google Scholar] [CrossRef]
- Chandwani, V.; Agrawal, V.; Nagar, R. Modeling slump of ready mix concrete using genetic algorithms assisted training of Artificial Neural Networks. Expert Syst. Appl. 2015, 42, 885–893. [Google Scholar] [CrossRef]
- Nguyen, M.-S.T.; Trinh, M.-C.; Kim, S.-E. Uncertainty quantification of ultimate compressive strength of CCFST columns using hybrid machine learning model. Eng. Comput. 2021, 38, 1–20. [Google Scholar] [CrossRef]
- Tran, V.-L.; Kim, S.-E. Efficiency of three advanced data-driven models for predicting axial compression capacity of CFDST columns. Thin-Walled Struct. 2020, 152, 106744. [Google Scholar] [CrossRef]
- Basarir, H.; Elchalakani, M.; Karrech, A. The prediction of ultimate pure bending moment of concrete-filled steel tubes by adaptive neuro-fuzzy inference system (ANFIS). Neural Comput. Appl. 2019, 31, 1239–1252. [Google Scholar] [CrossRef]
- Ho, N.X.; Le, T.-T. Effects of variability in experimental database on machine-learning-based prediction of ultimate load of circular concrete-filled steel tubes. Measurement 2021, 176, 109198. [Google Scholar] [CrossRef]
- Tran, V.-L.; Thai, D.-K.; Nguyen, D.-D. Practical artificial neural network tool for predicting the axial compression capacity of circular concrete-filled steel tube columns with ultra-high-strength concrete. Thin-Walled Struct. 2020, 151, 106720. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhong, X.; Foong, L.K. Predicting the splitting tensile strength of concrete using an equilibrium optimization model. Steel Compos. Struct. 2021, 39, 81–93. [Google Scholar]
- Lyu, F.; Fan, X.; Ding, F.; Chen, Z. Prediction of the axial compressive strength of circular concrete-filled steel tube columns using sine cosine algorithm-support vector regression. Compos. Struct. 2021, 273, 114282. [Google Scholar] [CrossRef]
- Luat, N.-V.; Shin, J.; Lee, K. Hybrid BART-based models optimized by nature-inspired metaheuristics to predict ultimate axial capacity of CCFST columns. Eng. Comput. 2020, 38, 1–30. [Google Scholar]
- Sarir, P.; Armaghani, D.J.; Jiang, H.; Sabri, M.M.S.; He, B.; Ulrikh, D.V. Prediction of Bearing Capacity of the Square Concrete-Filled Steel Tube Columns: An Application of Metaheuristic-Based Neural Network Models. Materials 2022, 15, 3309. [Google Scholar] [CrossRef] [PubMed]
- Bardhan, A.; Biswas, R.; Kardani, N.; Iqbal, M.; Samui, P.; Singh, M.; Asteris, P.G. A novel integrated approach of augmented grey wolf optimizer and ann for estimating axial load carrying-capacity of concrete-filled steel tube columns. Constr. Build. Mater. 2022, 337, 127454. [Google Scholar] [CrossRef]
- Zheng, Y.; Jin, H.; Jiang, C.; Moradi, Z.; Khadimallah, M.A.; Moayedi, H. Analyzing behavior of circular concrete-filled steel tube column using improved fuzzy models. Steel Compos. Struct. 2022, 43, 625–637. [Google Scholar]
- Jang, J.-S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Ebrahimi-Khusfi, Z.; Taghizadeh-Mehrjardi, R.; Nafarzadegan, A.R. Accuracy, uncertainty, and interpretability assessments of ANFIS models to predict dust concentration in semi-arid regions. Environ. Sci. Pollut. Res. 2021, 28, 6796–6810. [Google Scholar] [CrossRef] [PubMed]
- Alajmi, M.S.; Almeshal, A.M. Prediction and optimization of surface roughness in a turning process using the ANFIS-QPSO method. Materials 2020, 13, 2986. [Google Scholar] [CrossRef]
- Moayedi, H.; Mehrabi, M.; Kalantar, B.; Abdullahi Mu’azu, M.; A. Rashid, A.S.; Foong, L.K.; Nguyen, H. Novel hybrids of adaptive neuro-fuzzy inference system (ANFIS) with several metaheuristic algorithms for spatial susceptibility assessment of seismic-induced landslide. Geomat. Nat. Hazards Risk 2019, 10, 1879–1911. [Google Scholar] [CrossRef]
- Yang, X.-S. Metaheuristic optimization. Scholarpedia 2011, 6, 11472. [Google Scholar] [CrossRef]
- Yang, X.-S. Metaheuristic optimization: Algorithm analysis and open problems. In Proceedings of the International Symposium on Experimental Algorithms, Crete, Greece, 5–7 May 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 21–32. [Google Scholar]
- Moayedi, H.; Mehrabi, M.; Bui, D.T.; Pradhan, B.; Foong, L.K. Fuzzy-metaheuristic ensembles for spatial assessment of forest fire susceptibility. J. Environ. Manag. 2020, 260, 109867. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.-G.; Deb, S.; dos Santos Coelho, L. Earthworm optimisation algorithm: A bio-inspired metaheuristic algorithm for global optimisation problems. IJBIC 2018, 12, 1–22. [Google Scholar] [CrossRef]
- Ghosh, I.; Roy, P.K. Application of earthworm optimization algorithm for solution of optimal power flow. In Proceedings of the 2019 International Conference on Opto-Electronics and Applied Optics (Optronix), Kolkata, India, 18–20 March 2019; IEEE: New York, NY, USA, 2019; pp. 1–6. [Google Scholar]
- Kanna, S.R.; Sivakumar, K.; Lingaraj, N. Development of Deer Hunting linked Earthworm Optimization Algorithm for Solving large scale Traveling Salesman Problem. Knowl. Based Syst. 2021, 227, 107199. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory, MHS’95. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; IEEE: New York, NY, USA, 1995; pp. 39–43. [Google Scholar]
- Nguyen, H.; Mehrabi, M.; Kalantar, B.; Moayedi, H.; Abdullahi, M.a.M. Potential of hybrid evolutionary approaches for assessment of geo-hazard landslide susceptibility mapping. Geomat. Nat. Hazards Risk 2019, 10, 1667–1693. [Google Scholar] [CrossRef]
- Mehrabi, M.; Pradhan, B.; Moayedi, H.; Alamri, A. Optimizing an adaptive neuro-fuzzy inference system for spatial prediction of landslide susceptibility using four state-of-the-art metaheuristic techniques. Sensors 2020, 20, 1723. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Tubishat, M.; Ja’afar, S.; Alswaitti, M.; Mirjalili, S.; Idris, N.; Ismail, M.A.; Omar, M.S. Dynamic salp swarm algorithm for feature selection. Expert Syst. Appl. 2021, 164, 113873. [Google Scholar]
- Ye, X.; Moayedi, H.; Khari, M.; Foong, L.K. Metaheuristic-hybridized multilayer perceptron in slope stability analysis. Smart Struct. Syst. 2020, 26, 263–275. [Google Scholar]
- Rao, R.V.; Savsani, V.J.; Vakharia, D. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Zhao, Y.; Bai, C.; Xu, C.; Foong, L.K. Efficient metaheuristic-retrofitted techniques for concrete slump simulation. Smart Struct. Syst. 2021, 27, 745–759. [Google Scholar]
- Chen, W.; Chen, X.; Peng, J.; Panahi, M.; Lee, S. Landslide susceptibility modeling based on ANFIS with teaching-learning-based optimization and Satin bowerbird optimizer. Geosci. Front. 2021, 12, 93–107. [Google Scholar] [CrossRef]
- Ghoneim, S.S.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M. Enhancing Diagnostic Accuracy of Transformer Faults Using Teaching-Learning-Based Optimization. IEEE Access 2021, 9, 30817–30832. [Google Scholar] [CrossRef]
- Mehrabi, M. Landslide susceptibility zonation using statistical and machine learning approaches in Northern Lecco, Italy. Nat. Hazards 2021, 11, 1–37. [Google Scholar] [CrossRef]
- Mehrabi, M.; Moayedi, H. Landslide susceptibility mapping using artificial neural network tuned by metaheuristic algorithms. Environ. Earth Sci. 2021, 80, 1–20. [Google Scholar] [CrossRef]
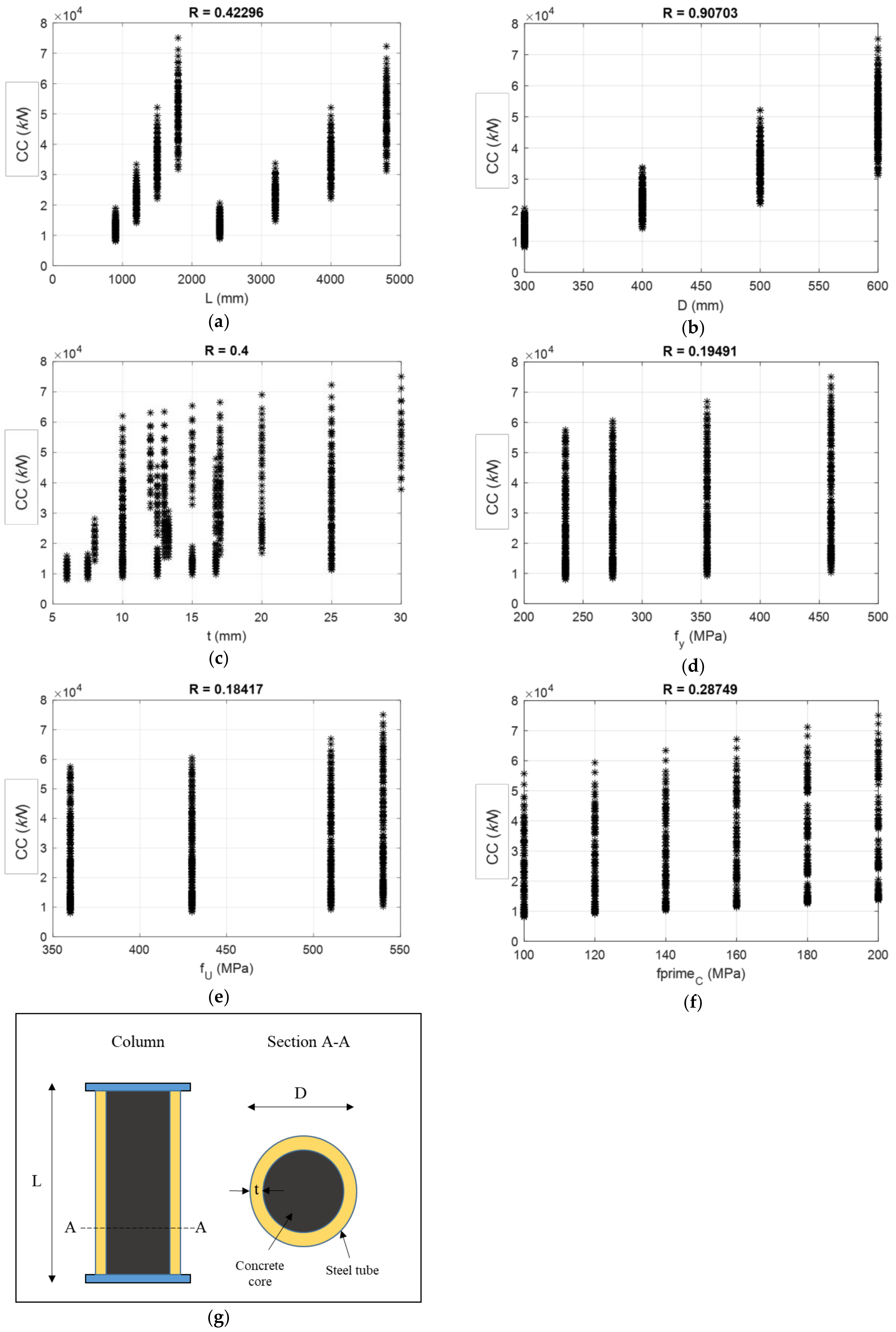
| Indicator | Factor | ||||||
|---|---|---|---|---|---|---|---|
| L [mm] | D [mm] | t [mm] | fy [MPa] | fu [MPa] | fc’ [MPa] | CC [kN] | |
| Mean | 2475.0 | 450.0 | 15.2 | 331.3 | 460.0 | 150.0 | 30,185.3 |
| Std. Error | 47.4 | 4 | 0.2 | 3.1 | 2.5 | 1.2 | 538.3 |
| Std. Deviation | 1313.1 | 111.9 | 6.1 | 86 | 70.4 | 34.2 | 14,918.5 |
| Sample Variance | 1,724,120 | 12,516.3 | 37.3 | 7401.8 | 4956.5 | 1168.2 | 222,561,708.9 |
| Minimum | 900.0 | 300.0 | 6.0 | 235.0 | 360.0 | 100.0 | 8016.3 |
| Maximum | 4800.0 | 600.0 | 30.0 | 460.0 | 540.0 | 200.0 | 75,051.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karimi Sharafshadeh, B.; Ketabdari, M.J.; Azarsina, F.; Amiri, M.; Nehdi, M.L. New Fuzzy-Heuristic Methodology for Analyzing Compression Load Capacity of Composite Columns. Buildings 2023, 13, 125. https://doi.org/10.3390/buildings13010125
Karimi Sharafshadeh B, Ketabdari MJ, Azarsina F, Amiri M, Nehdi ML. New Fuzzy-Heuristic Methodology for Analyzing Compression Load Capacity of Composite Columns. Buildings. 2023; 13(1):125. https://doi.org/10.3390/buildings13010125
Chicago/Turabian StyleKarimi Sharafshadeh, Bizhan, Mohammad Javad Ketabdari, Farhood Azarsina, Mohammad Amiri, and Moncef L. Nehdi. 2023. "New Fuzzy-Heuristic Methodology for Analyzing Compression Load Capacity of Composite Columns" Buildings 13, no. 1: 125. https://doi.org/10.3390/buildings13010125
APA StyleKarimi Sharafshadeh, B., Ketabdari, M. J., Azarsina, F., Amiri, M., & Nehdi, M. L. (2023). New Fuzzy-Heuristic Methodology for Analyzing Compression Load Capacity of Composite Columns. Buildings, 13(1), 125. https://doi.org/10.3390/buildings13010125








