Fracture Behavior of Headed Studs: Ductile Fracture of Cold Heading Steel ML15
Abstract
1. Introduction
2. Characteristics of Stress States
3. Tests and Setup
- smooth round bar η = 1/3, = 1;
- notched round bar with η > 1/3, = 1;
- flat grooved plate with η > 1/3, = 0;
- tensile–shear flat plate.
3.1. Specimen Design
3.2. Experimental Design
4. Test Results
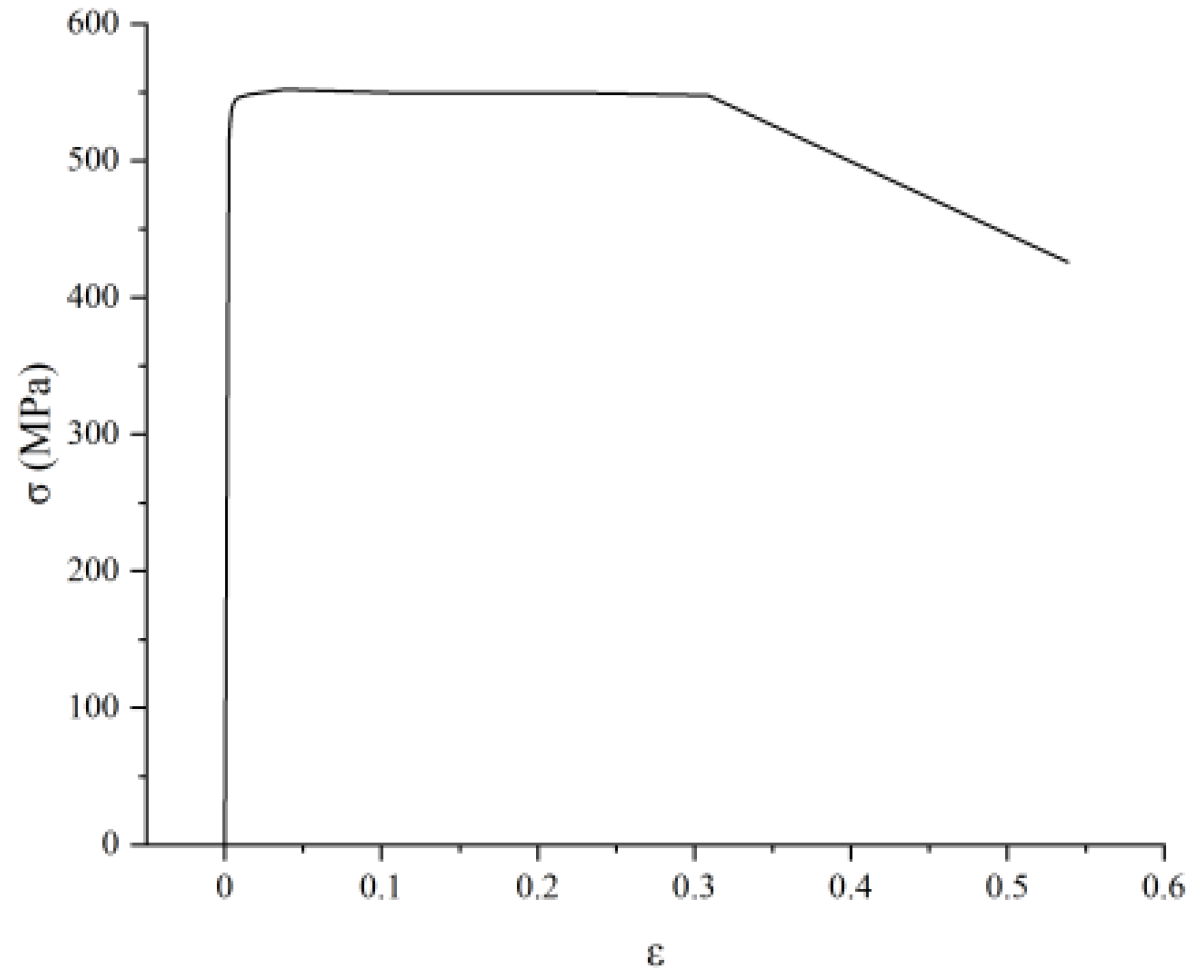
4.1. Smooth Round-Bar Specimens
4.2. Notched Round-Bar Specimens
4.3. Flat Notched Specimens
4.4. Tensile–Shear Flat Specimens
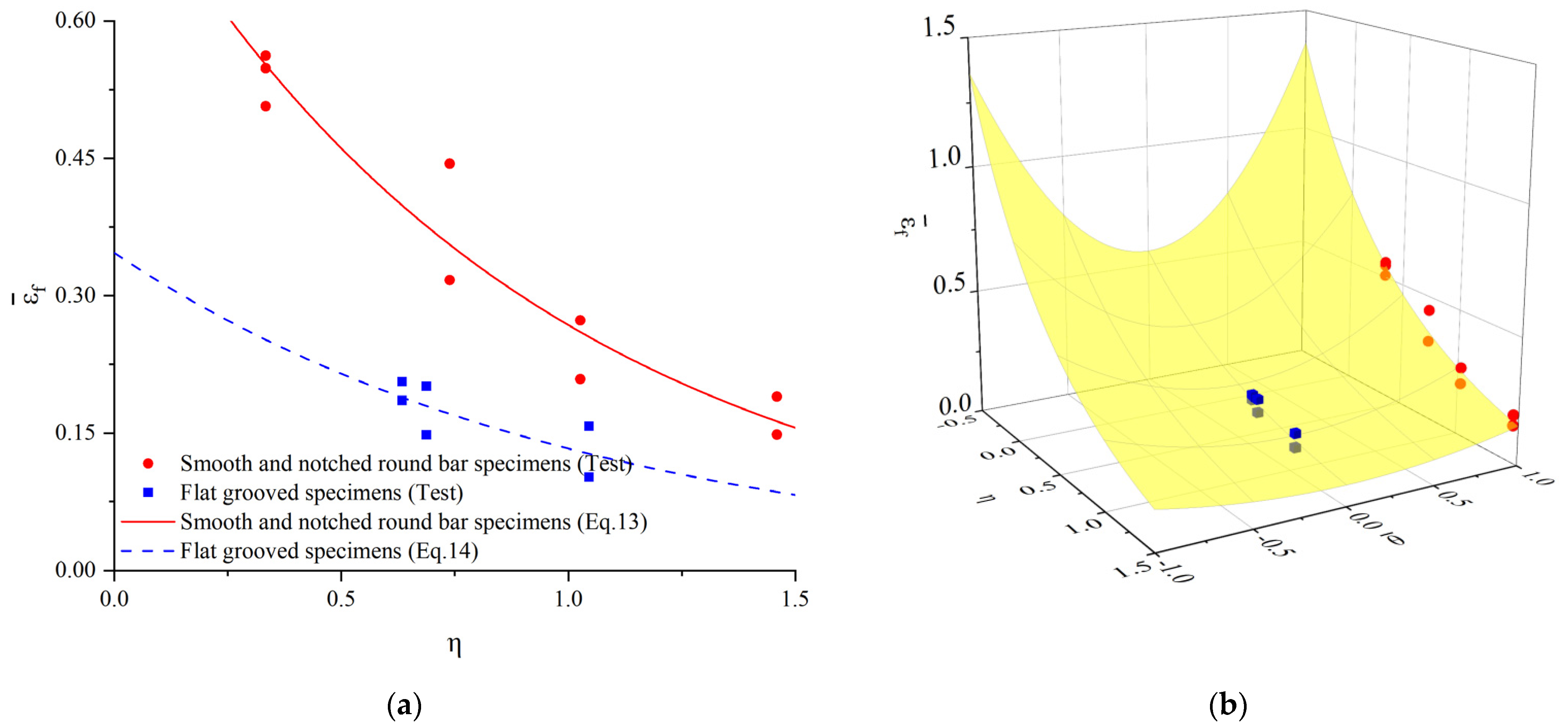
5. Fracture Locus Calibration
6. Microscopic Crack Characteristics of ML15 Steel Specimens
7. Numerical Simulations
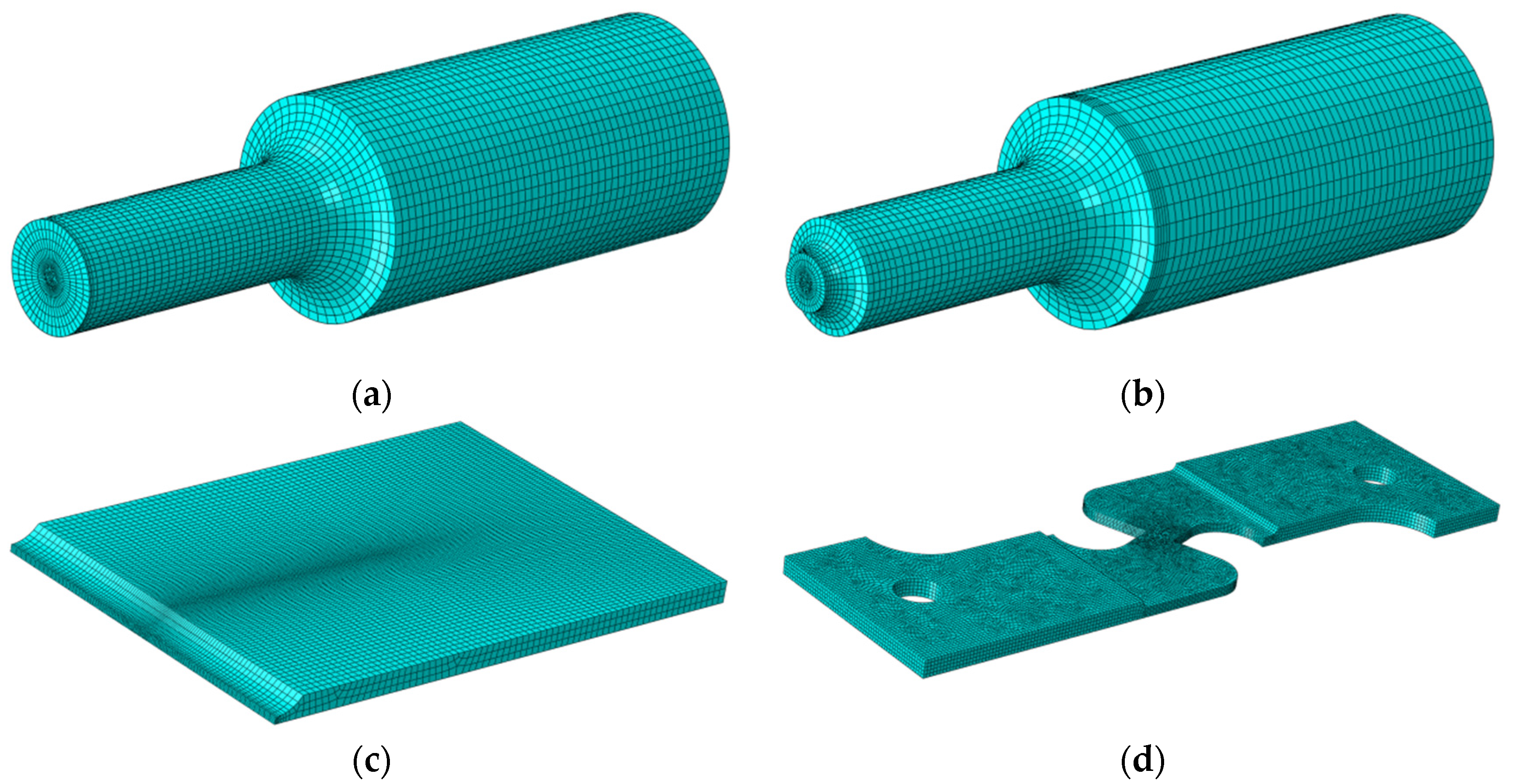
7.1. Finite Element Model
7.2. Numerical Results
8. Conclusions
- (1)
- The true stress–strain curve of ML15 is basically a straight line before the ultimate load, which clearly demonstrated the hardening of cold heading process on steel. The true stress–strain behavior of ML15 includes linear elasticity, non-linear hardening steady deformation, and strain softening, but no obvious yield stage;
- (2)
- The fracture locus of ML15 depends on the stress state, which decreases exponentially when the stress triaxiality increases and has different trends under different Lode angle parameters. The Rice–Tracey 2D criterion, which only considers the stress triaxiality, cannot describe the difference in the fracture properties of structural steels under different deviating stress states. The Bai–Wierzbicki 3D criterion, considering the parameters of stress triaxiality and Lode angle, gives a better description of the fracture locus of ML15;
- (3)
- The microscopic crack characteristics of all round-bar tensile specimens revealed by the scanning electron microscope showed wide and deep dimples, which indicated that the failure mode of all round-bar tensile specimens was ductile fracture. Contrasted with the smooth and notched round round bar specimens, the dimples observed microscopically in the flat notched specimens are smaller and shallower. Microscopic phenomena that change dimple size due to different Lode angle parameters explain why Rice–Tracey model can not accurately predict the fracture strain of ML15 steel. Different microfracture mechanisms were observed in tensile–shear plate specimens including tensile fracture, combined tensile–shear fracture and shear fracture;
- (4)
- The expansion of high strain areas with the increment of stress triaxiality indicates that the deformation of the failure sections become more uniform with the increase in stress triaxiality. It also explains the increment in ultimate load of specimens along with the stress triaxiality increase. As the stress triaxiality decreases, the high strain areas extend towards the direction of tension, which explains the phenomenon that the ductility of the round bar as well as the flat grooved plate specimens change inversely proportional to the stress triaxiality.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- McClintock, F.A. A Criterion for Ductile Fracture by the Growth of Holes. J. Appl. Mech. 1968, 35, 363–371. [Google Scholar] [CrossRef]
- Rice, J.R.; Tracey, D.M. On the ductile enlargement of voids in triaxial stress fields. J. Mech. Phys. Solids 1969, 17, 201–217. [Google Scholar] [CrossRef]
- Kanvinde, A.M. Micro Mechanical Simulation of Earthquake-Induced Fracture in Micro Mechanical Simulation of Earthquake-Induced Fracture in Steel Structures; Stanford University: Stanford, CA, USA, 2004. [Google Scholar]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Bao, Y.; Wierzbicki, T. On fracture locus in the equivalent strain and stress triaxiality space. Int. J. Mech. Sci. 2004, 46, 81–98. [Google Scholar] [CrossRef]
- Bao, Y.; Wierzbicki, T. On the cut-off value of negative triaxiality for fracture. Eng. Fract. Mech. 2005, 72, 1049–1069. [Google Scholar] [CrossRef]
- Xue, L.; Wierzbicki, T. Ductile fracture initiation and propagation modeling using damage plasticity theory. Eng. Fract. Mech. 2008, 75, 3276–3293. [Google Scholar] [CrossRef]
- Bai, Y.; Wierzbicki, T. A new model of metal plasticity and fracture with pressure and Lode dependence. Int. J. Plast. 2008, 24, 1071–1096. [Google Scholar] [CrossRef]
- Bai, Y.; Wierzbicki, T. Application of extended Mohr–Coulomb criterion to ductile fracture. Int. J. Fract. 2010, 161, 1. [Google Scholar] [CrossRef]
- Lou, Y.; Huh, H.; Lim, S.; Pack, K. New ductile fracture criterion for prediction of fracture forming limit diagrams of sheet metals. Int. J. Solids Struct. 2012, 49, 3605–3615. [Google Scholar] [CrossRef]
- Marcadet, S.J.; Mohr, D. Effect of compression-tension loading reversal on the strain to fracture of dual phase steel sheets. Int. J. Plasticity 2015, 72, 21–43. [Google Scholar] [CrossRef]
- Hu, Q.; Li, X.; Han, X.; Chen, J. A new shear and tension based ductile fracture criterion: Modeling and validation. European J. Mech.-A/Solids 2017, 66, 370–386. [Google Scholar] [CrossRef]
- Mu, L.; Zang, Y.; Wang, Y.; Li, X.L.; Stemler, P. Phenomenological uncoupled ductile fracture model considering different void deformation modes for sheet metal forming. Int. J. Mech. Sci. 2018, 141, 408–423. [Google Scholar] [CrossRef]
- Cerik, B.C.; Choung, J. Ductile Fracture Behavior of Mild and High-Tensile Strength Shipbuilding Steels. Appl. Sci. 2020, 10, 7034. [Google Scholar] [CrossRef]
- Cho, Y.; Lee, C.; Yee, J.-J.; Kim, D.-K. Modeling of Ductile Fracture for SS275 Structural Steel Sheets. Appl. Sci. 2021, 11, 5392. [Google Scholar] [CrossRef]
- Peng, J.; Zhou, P.; Wang, Y.; Dai, Q.; Knowles, D.; Mostafavi, M. Stress Triaxiality and Lode Angle Parameter Characterization of Flat Metal Specimen with Inclined Notch. Metals 2021, 11, 1627. [Google Scholar] [CrossRef]
- Panwitt, H.; Heyer, H.; Sander, M. Experimental and Numerical Investigation of the Fracture Behavior of Welded Aluminum Cross Joints under Axial Compression. Materials 2020, 13, 4310. [Google Scholar] [CrossRef]
- Li, W.; Liao, F.; Zhou, T.; Askes, H. Ductile fracture of Q460 steel: Effects of stress triaxiality and Lode angle. J. Constr. Steel Res. 2016, 123, 1–17. [Google Scholar] [CrossRef]
- Yan, S.; Zhao, X.; He, P. Ductility and fracture models of G20Mn5 cast steel. J. Constr. Steel Res. 2020, 175, 106363. [Google Scholar] [CrossRef]
- Wilson-Heid, A.E.; Furton, E.T.; Beese, A.M. Contrasting the Role of Pores on the Stress State Dependent Fracture Behavior of Additively Manufactured Low and High Ductility Metals. Materials 2021, 14, 3657. [Google Scholar] [CrossRef]
- Zhang, S.; Jia, Y.; Ding, Y. Study on the Flexural Behavior of Steel-Concrete Composite Beams Based on the Shear Performance of Headed Stud Connectors. Buildings 2022, 12, 961. [Google Scholar] [CrossRef]
- Alsharari, F.; El-Sisi, A.E.-D.; Mutnbak, M.; Salim, H.; El-Zohairy, A. Effect of the Progressive Failure of Shear Connectors on the Behavior of Steel-Reinforced Concrete Composite Girders. Buildings 2022, 12, 596. [Google Scholar] [CrossRef]
- Bridgman, P.W. Studies in Large Plastic Flow and Fracture: With Special Emphasis on the Effects of Hydrostatic Pressure; McGraw-Hil: New York, NY, USA, 1952. [Google Scholar]
- GB/T 10433-2002; Cheese Head Studs for Arc Stud Welding. China Machinery Industry Federation: Beijing, China, 2002.
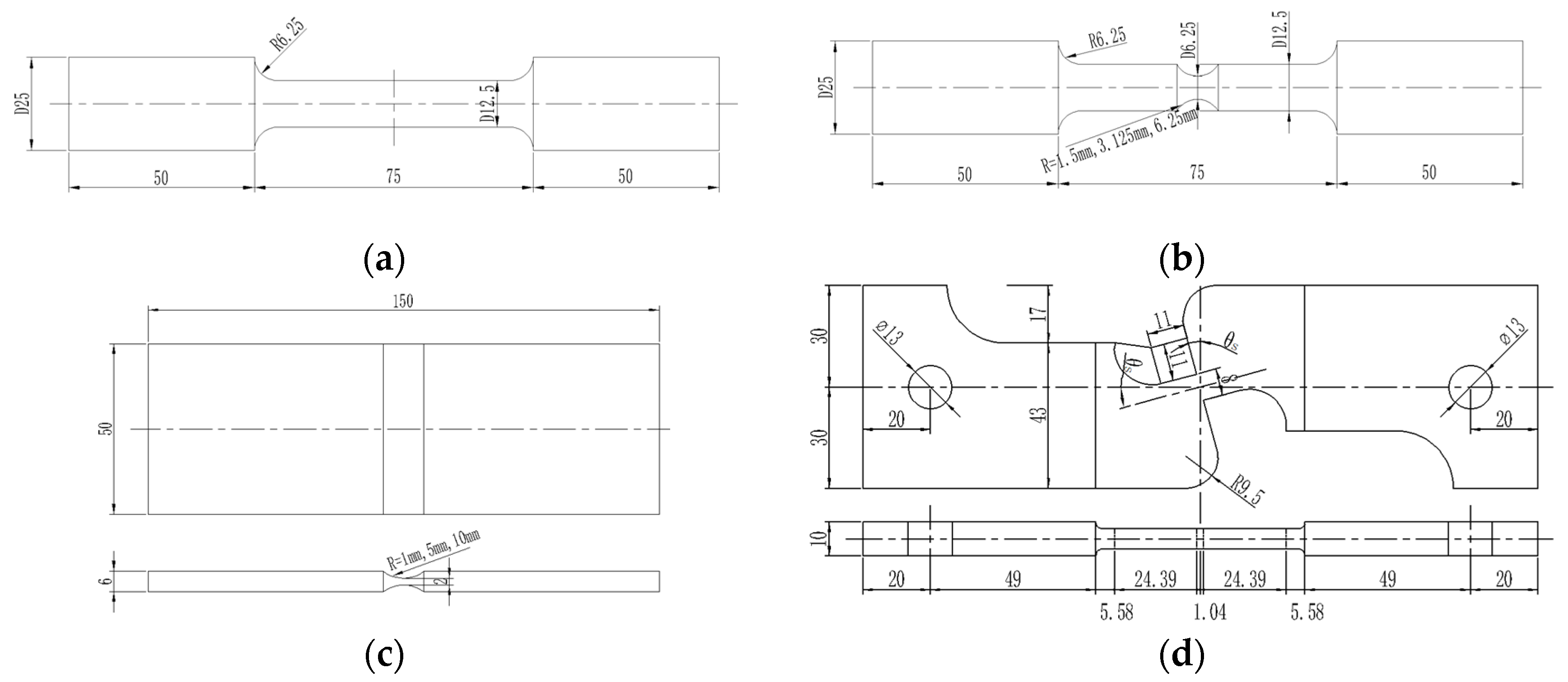







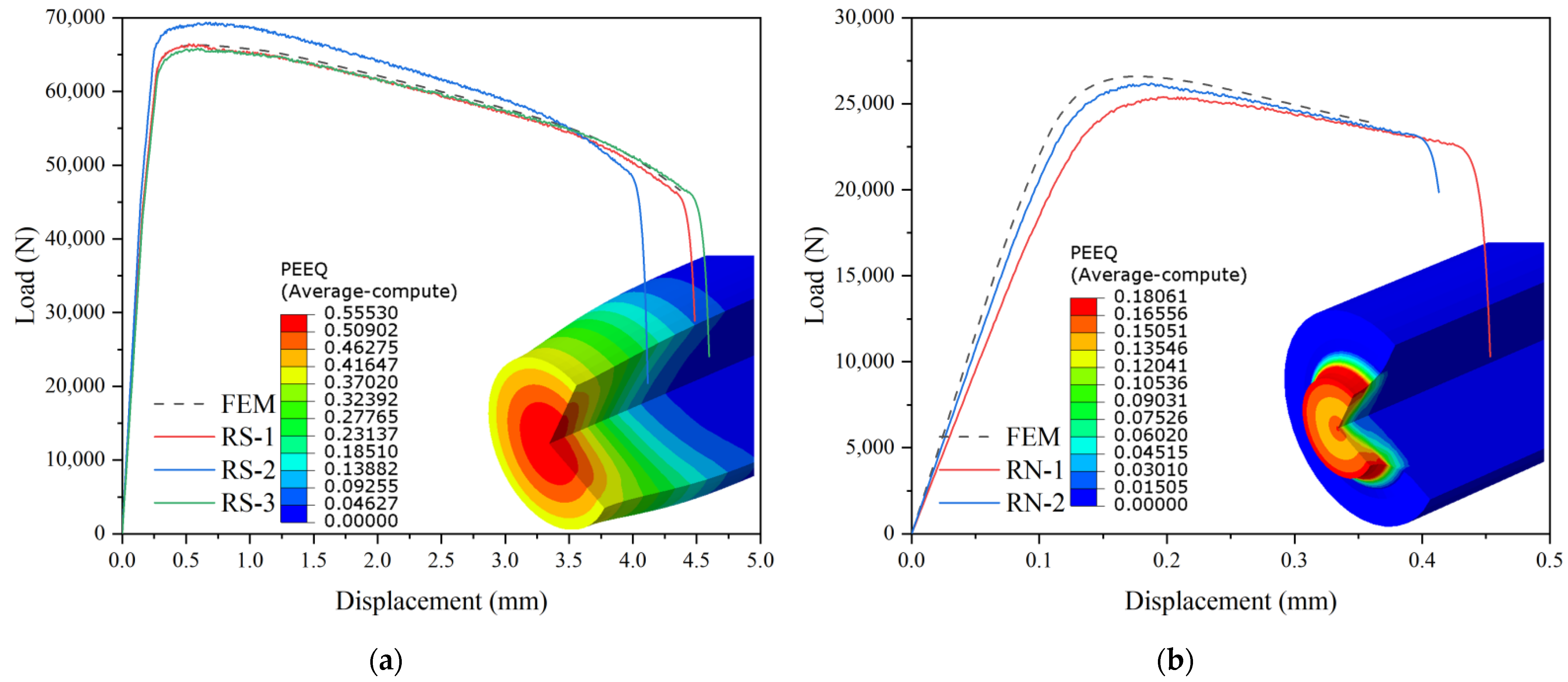
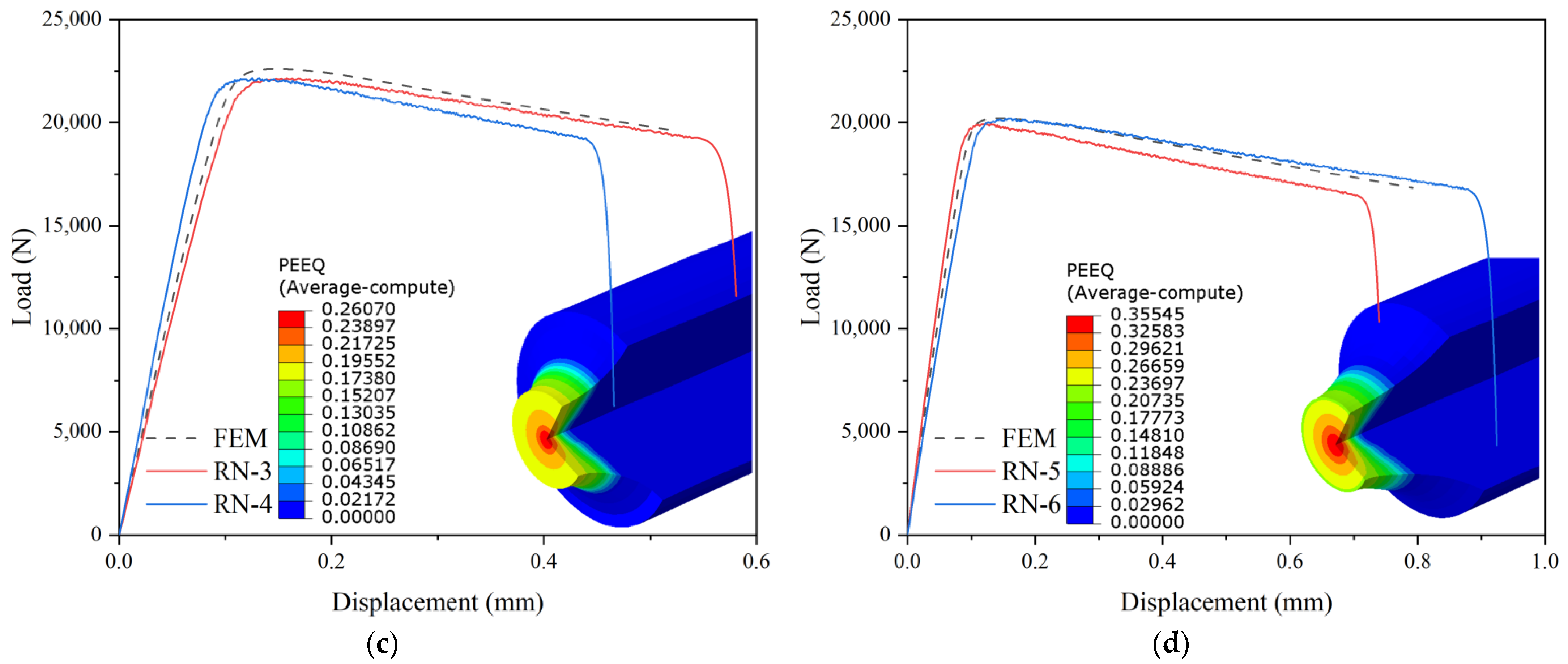
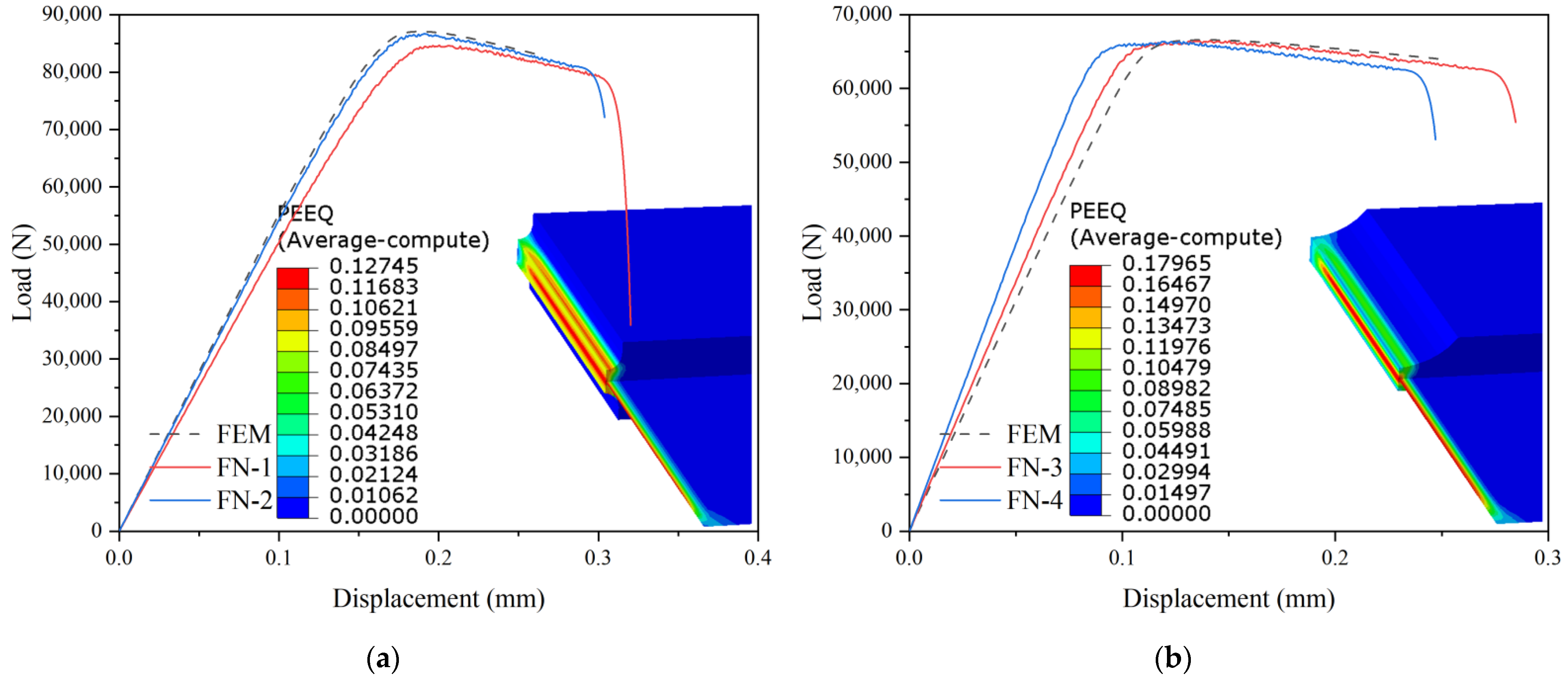

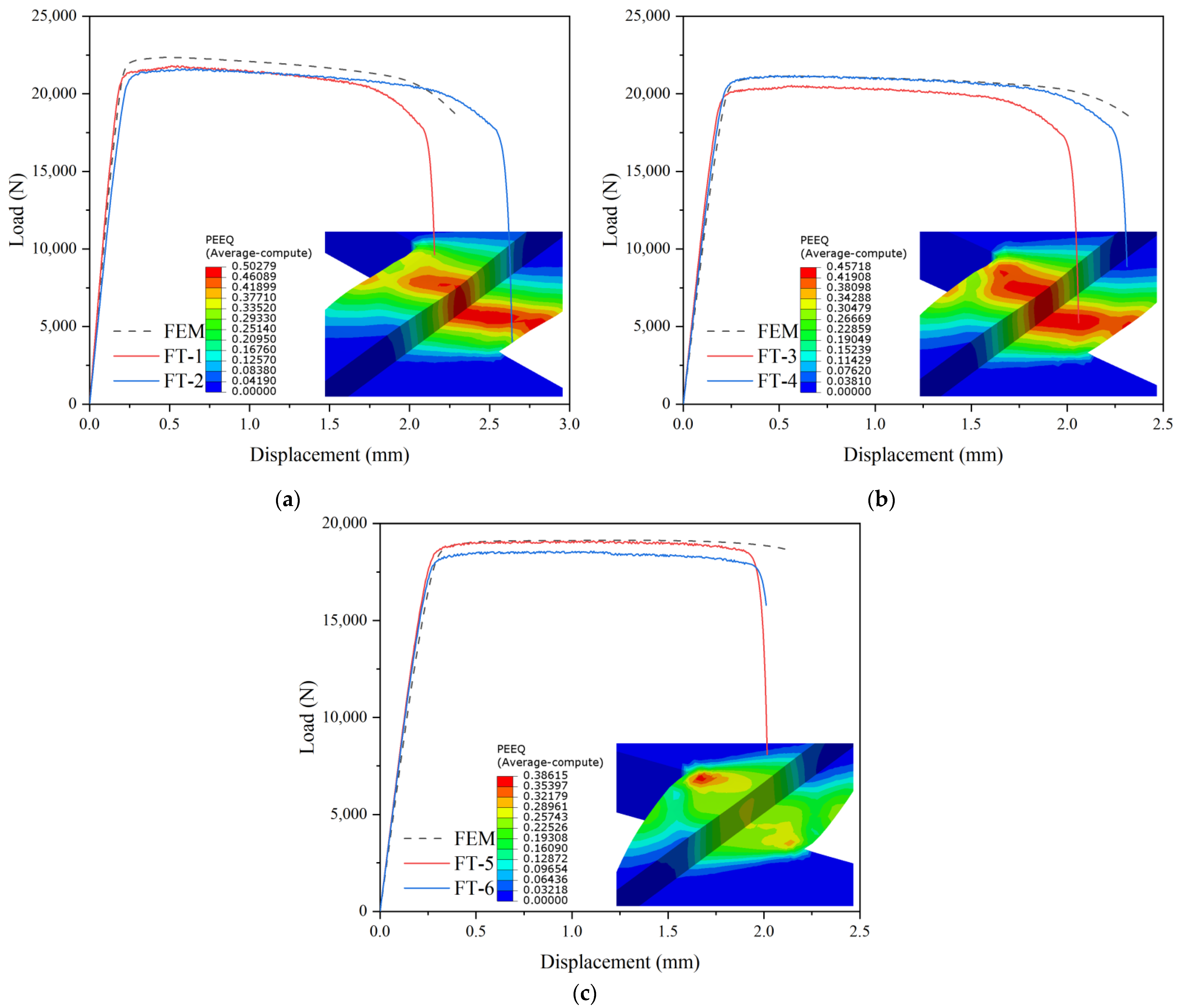
| Specimen | η | Specimen | η | ||||
|---|---|---|---|---|---|---|---|
| RN-1 | 0.74 | 1 | 0.1898 | FN-1 | 1.05 | 0 | 0.1575 |
| RN-2 | 0.74 | 1 | 0.1484 | FN-2 | 1.05 | 0 | 0.1020 |
| RN-3 | 1.03 | 1 | 0.2731 | FN-3 | 0.69 | 0 | 0.2010 |
| RN-4 | 1.03 | 1 | 0.2091 | FN-4 | 0.69 | 0 | 0.1482 |
| RN-5 | 1.46 | 1 | 0.3172 | FN-5 | 0.63 | 0 | 0.2063 |
| RN-6 | 1.46 | 1 | 0.4443 | FN-6 | 0.63 | 0 | 0.1857 |
| RS-1 | 0.33 | 1 | 0.5485 | RS-2 | 0.33 | 1 | 0.5071 |
| RS-3 | 0.33 | 1 | 0.5623 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Y.; Jia, Y. Fracture Behavior of Headed Studs: Ductile Fracture of Cold Heading Steel ML15. Buildings 2022, 12, 2128. https://doi.org/10.3390/buildings12122128
Ding Y, Jia Y. Fracture Behavior of Headed Studs: Ductile Fracture of Cold Heading Steel ML15. Buildings. 2022; 12(12):2128. https://doi.org/10.3390/buildings12122128
Chicago/Turabian StyleDing, Yixing, and Yanmin Jia. 2022. "Fracture Behavior of Headed Studs: Ductile Fracture of Cold Heading Steel ML15" Buildings 12, no. 12: 2128. https://doi.org/10.3390/buildings12122128
APA StyleDing, Y., & Jia, Y. (2022). Fracture Behavior of Headed Studs: Ductile Fracture of Cold Heading Steel ML15. Buildings, 12(12), 2128. https://doi.org/10.3390/buildings12122128





