Numerical Modelling of Timber Beams with GFRP Pultruded Reinforcement
Abstract
1. Introduction
Existing Numerical Modelling Method for Timber
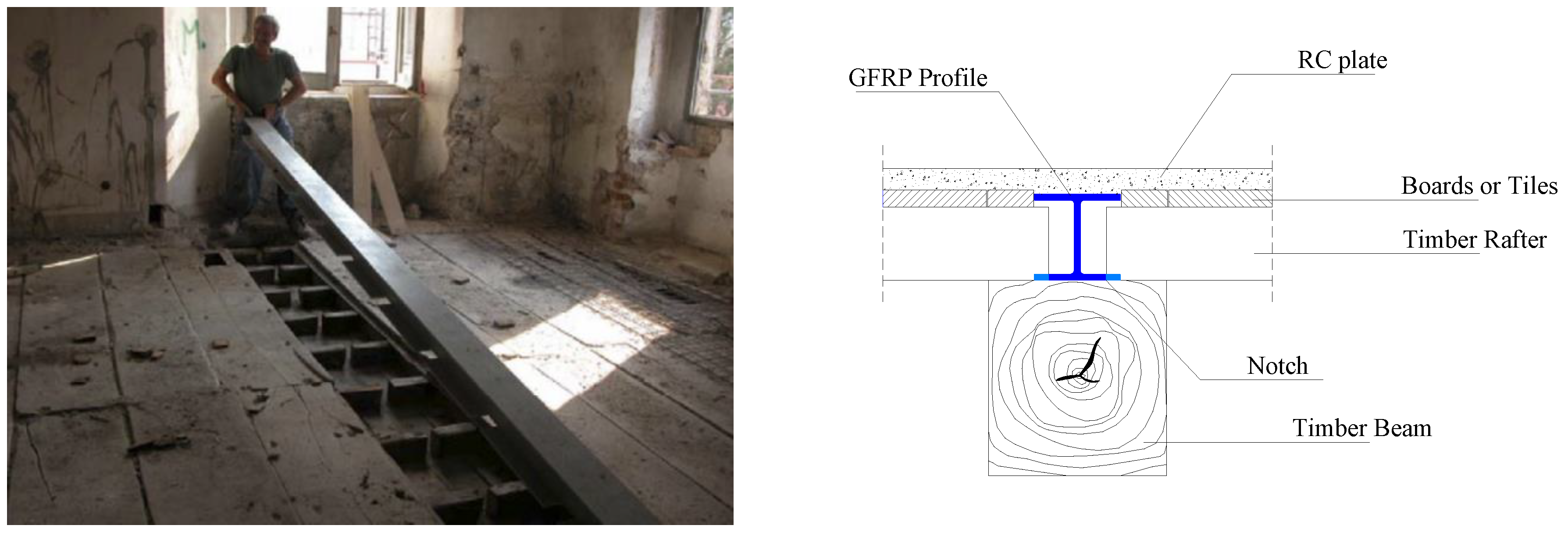
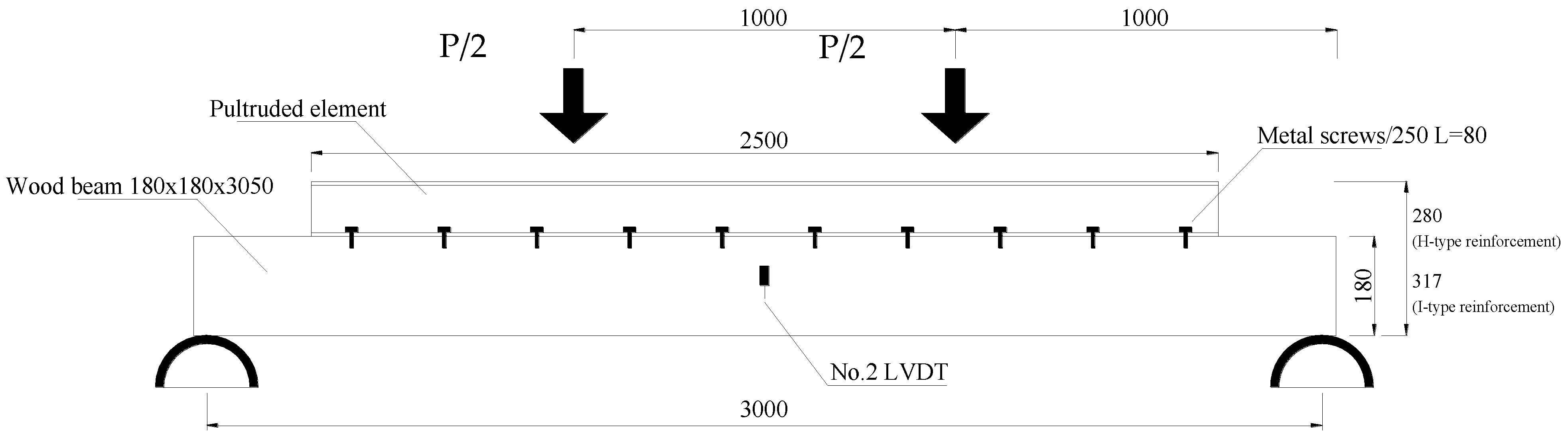
2. Experimental Method
3. FEM Development
3.1. FEM of Timber
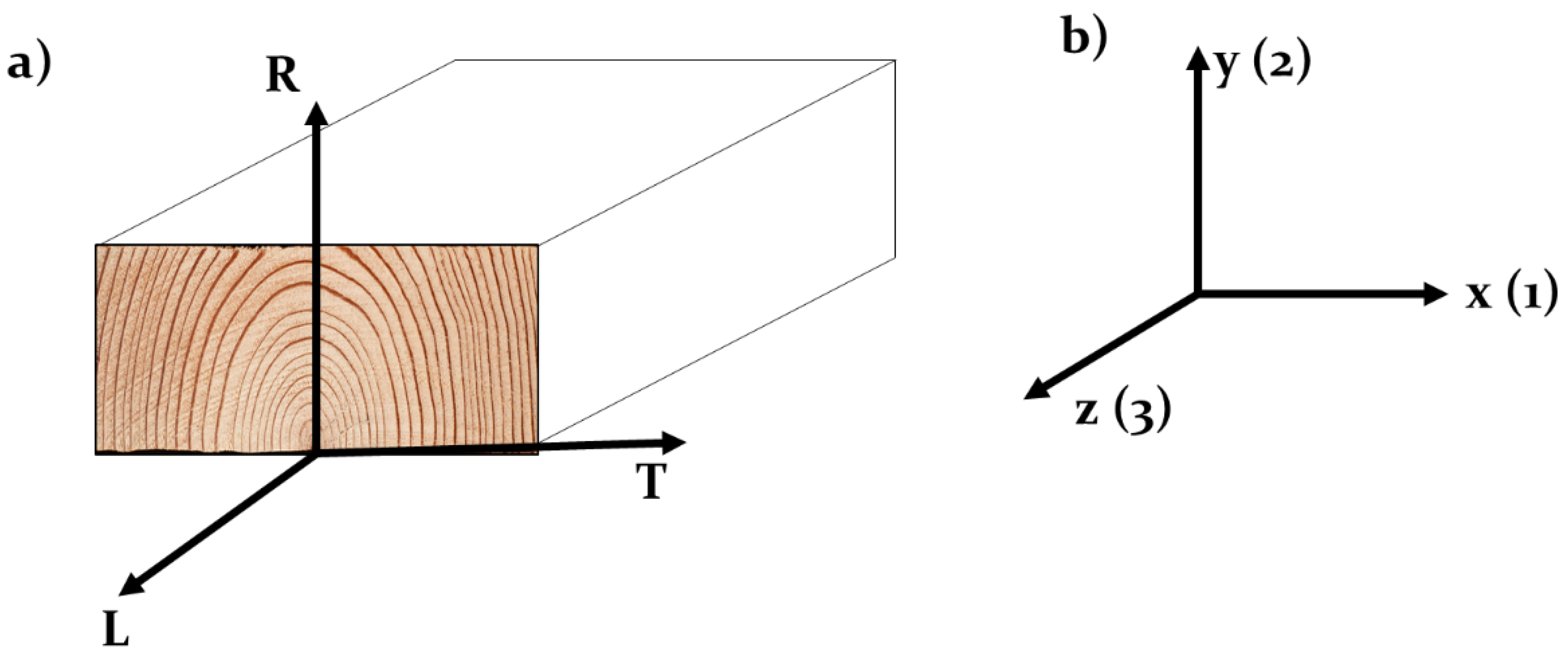
3.1.1. Theoretical Formulation
3.1.2. Model Implementation for Fir Timber Beam
3.2. FEM of GFRP Pultruded Beam
3.3. Contact and Interaction Definition
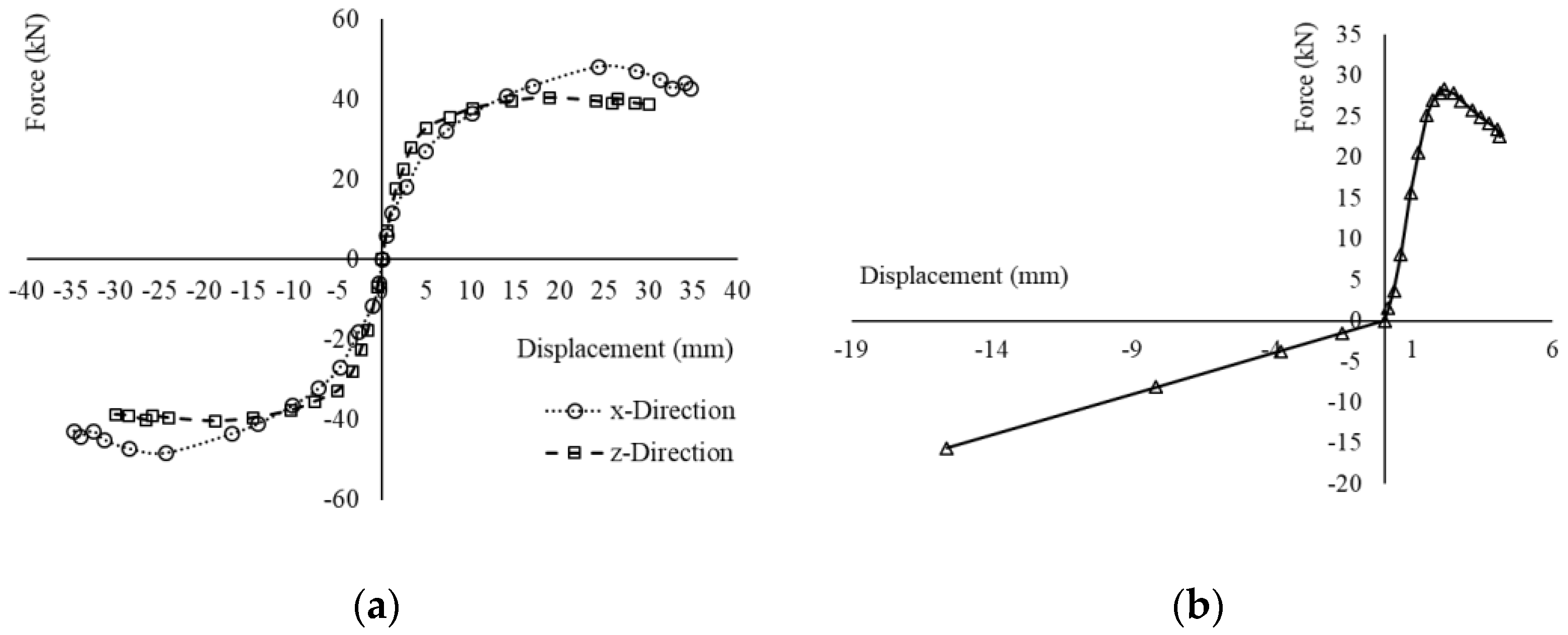
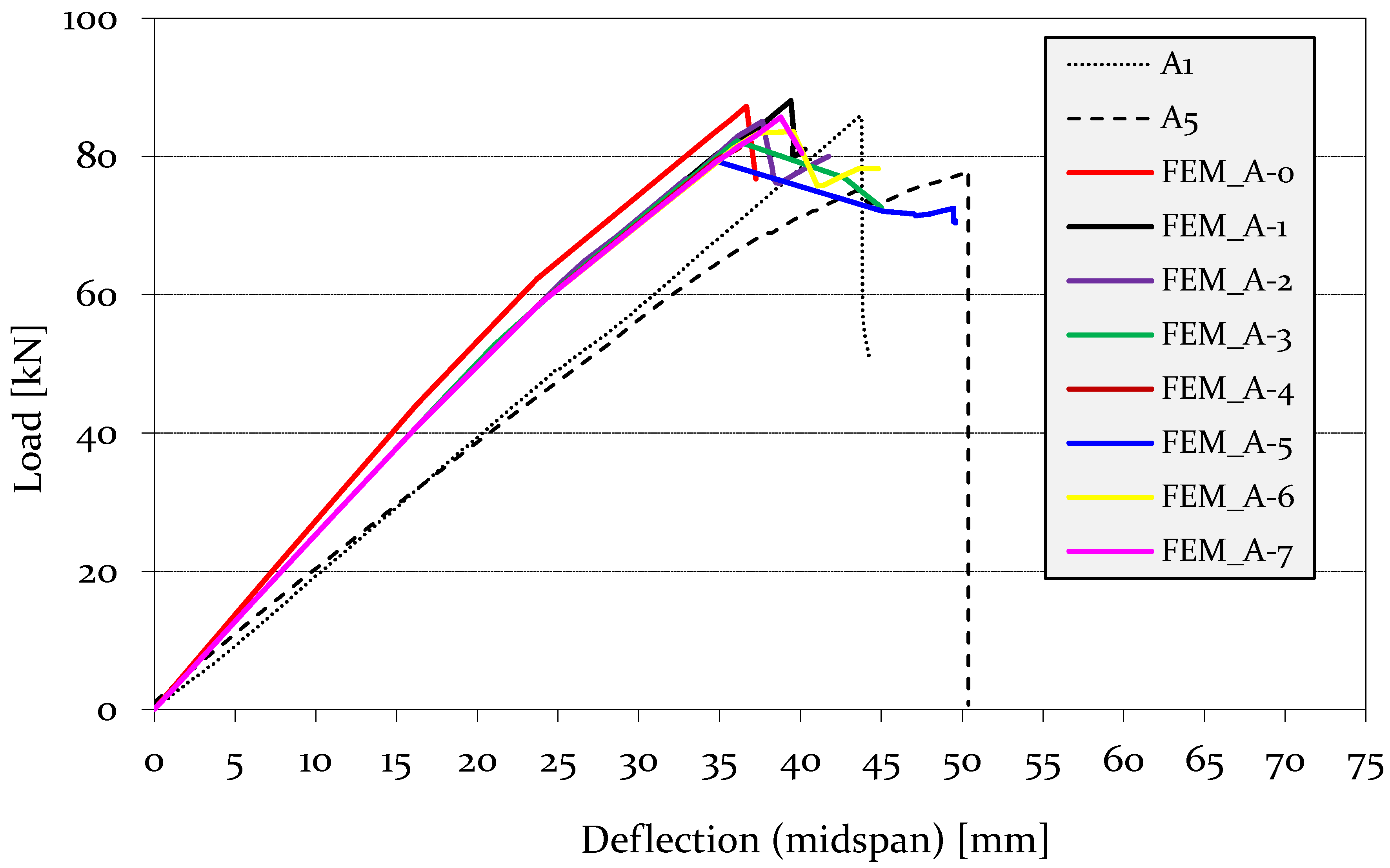
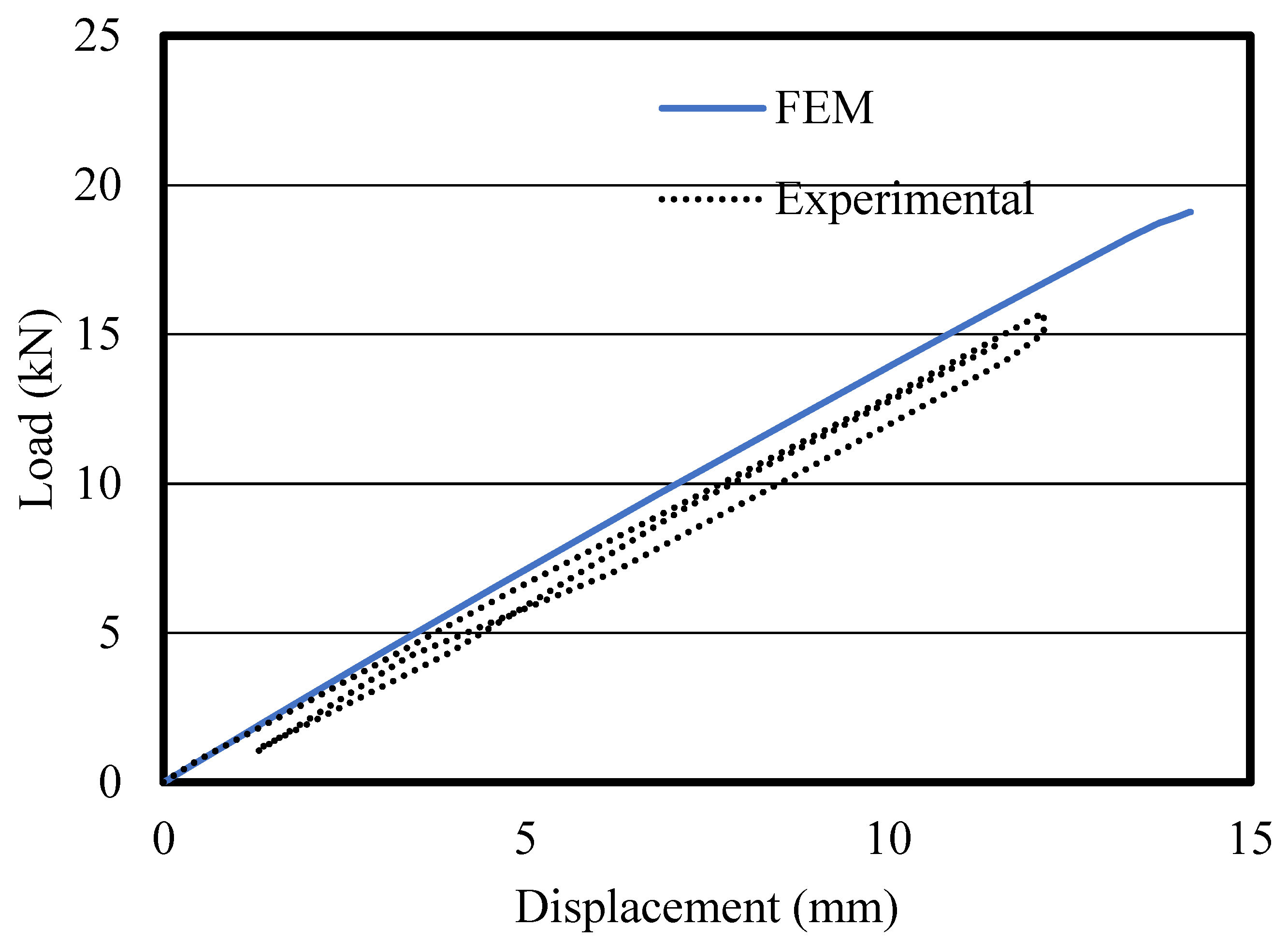
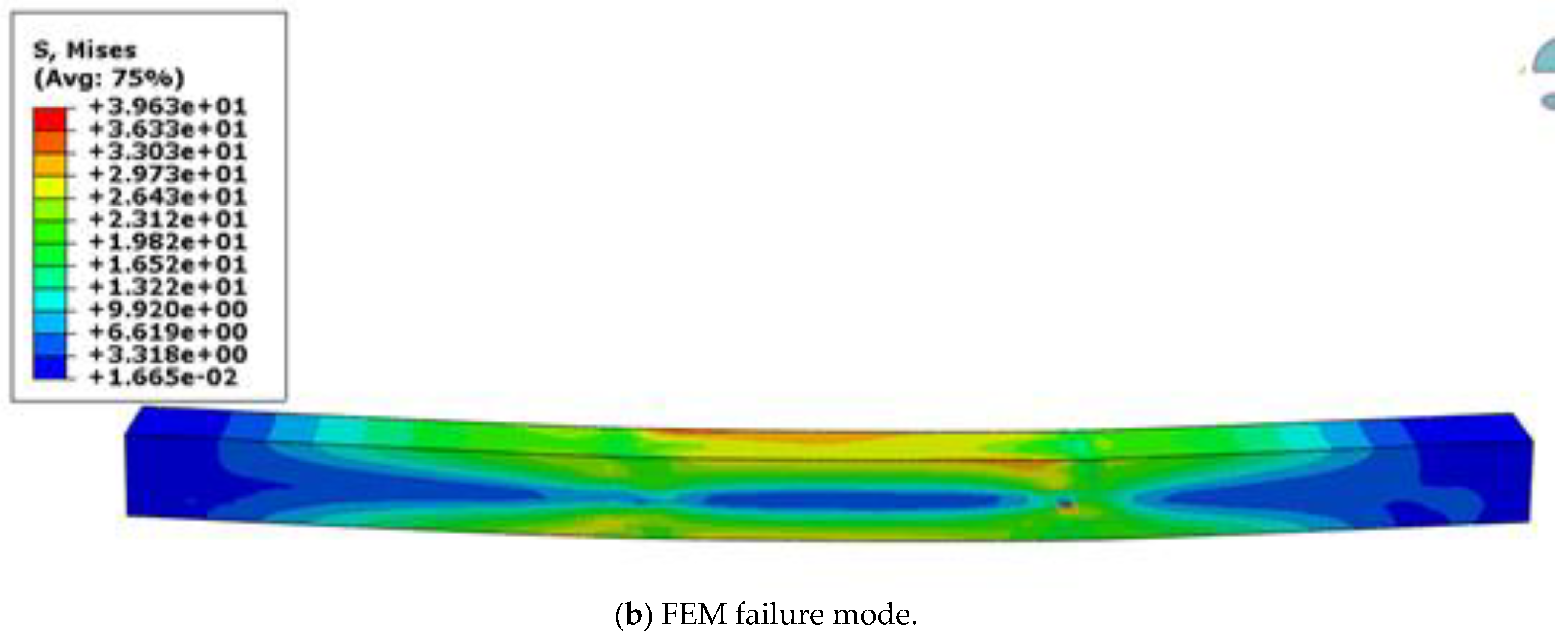
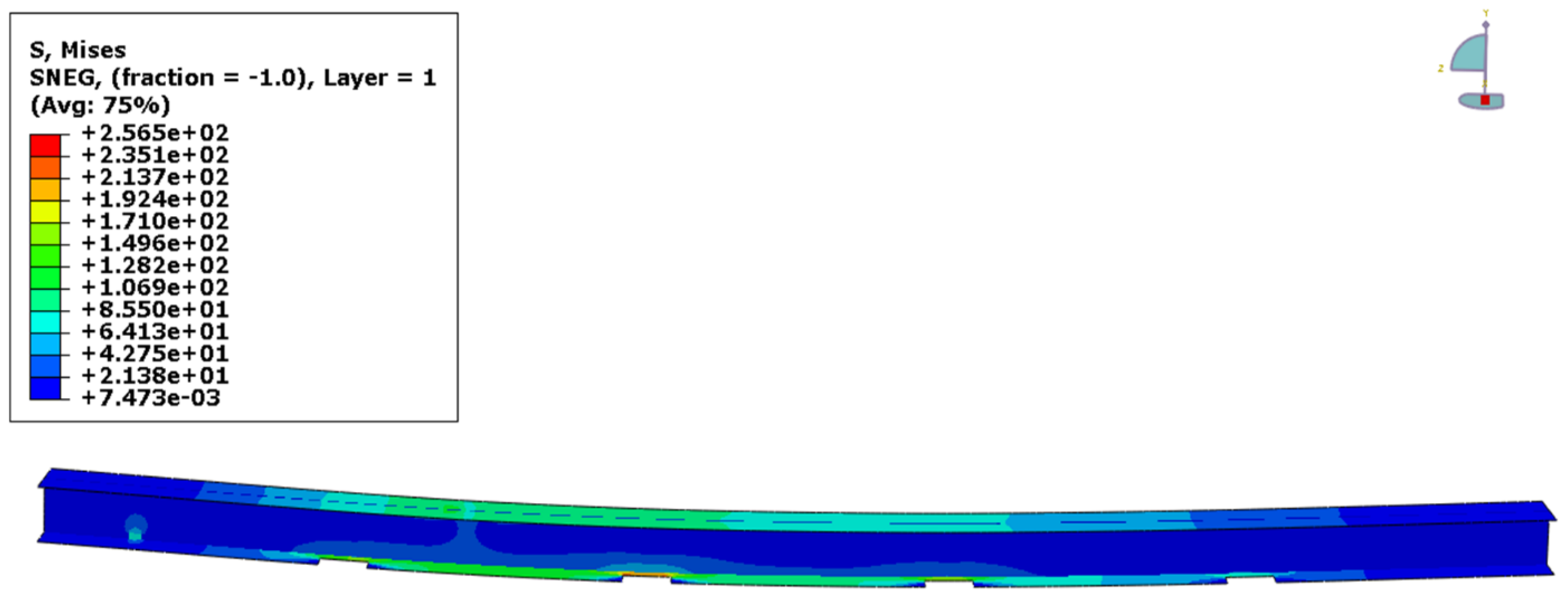
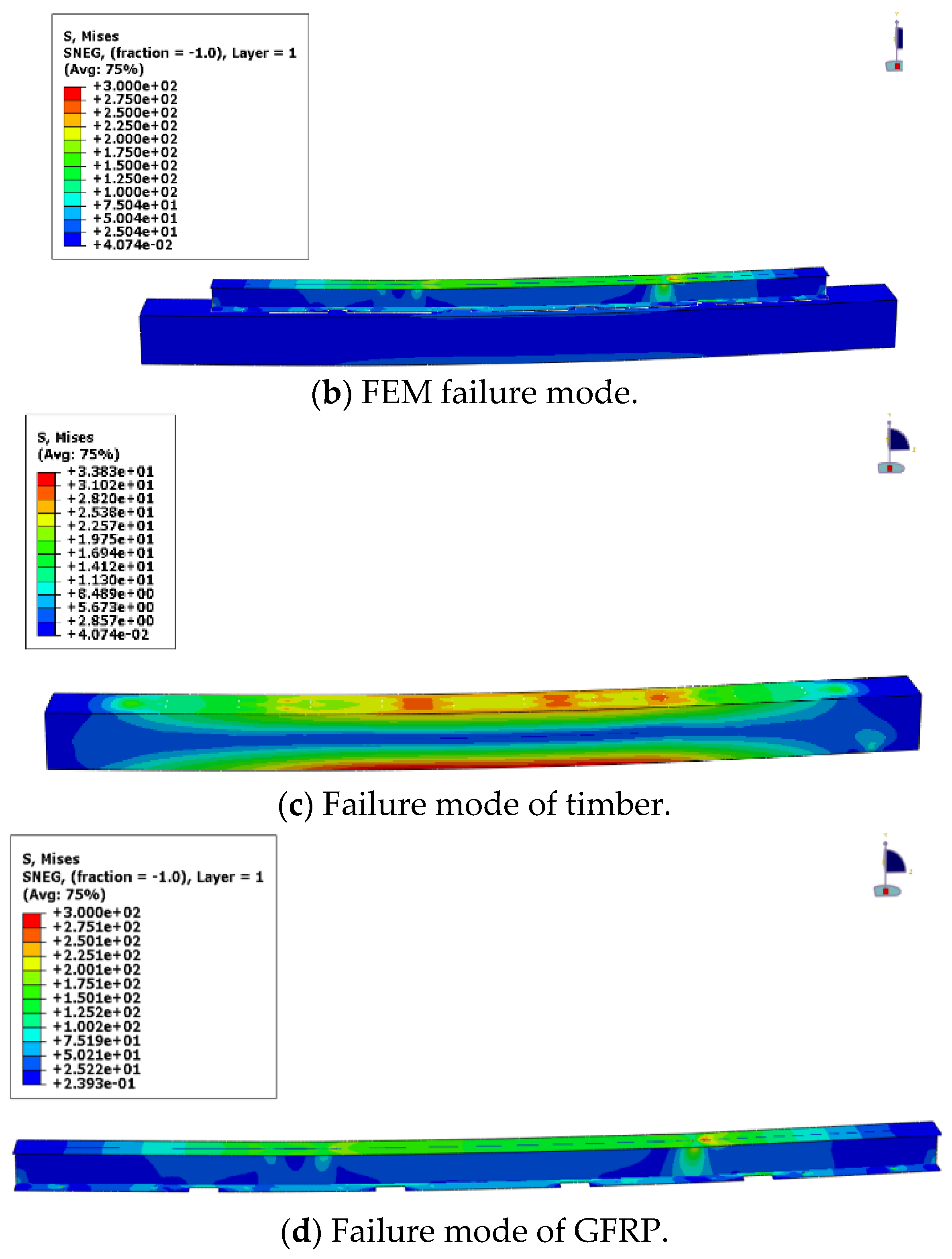
4. Results and Discussion
FEM Validation
5. Conclusions
- The FEM introduced was able to capture flexural strength, load–displacement response, and complex failure modes very similar to those in the experimental results.
- The key point in the modelling procedure is the connection between the timber beam and the GFRP pultruded profiles. The good agreement with the experimental results shows that the proposed spring-based modelling for screws can mobilise the composite action within the system.
- The influence of the grain deviation was also studied by considering different mode angles in the models. The results demonstrate that the grain deviation influenced the flexural strength of timber beams without GFRP pultruded reinforcement.
- It was noticed that there was a lesser effect of the grain deviation on the flexural strength of timber beams with GFRP pultruded reinforcement.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| E | Young’s modulus |
| F, G, H, L, M, N | Hill’s constants |
| GLR, GLT, GRT | Shear modulus |
| Gft, Gfc, Gmt, Gmc | Fracture energy |
| R11, R22, R33, R12, R23, R13 | Anisotropic yield stress ratios |
| v | Poisson’s ratio |
| x (1), y (2), z (3) | Global coordination |
| ft,0° | Tensile strength parallel to grain |
| fc,0° | Compressive strength parallel to grain |
| ft,90° | Tensile strength perpendicular to grain |
| fc,90° | Compressive strength perpendicular to the fibre direction |
| fτ | Shear strength |
| [M] | Transformation matrix |
| Strain tensor | |
| Strains in the local coordinate system | |
| ε | Strain |
| Stress tensor | |
| Reference yield stress | |
| Stresses in the local coordinate system | |
| σ | Normal stress |
| σc,90° | Yield stress under compression in the perpendicular direction |
| α | Cosine for the grain deviation angle |
| τ | Shear stress |
| γ | Shear strain |
| λ | Plastic multiplier |
| Subscripts | |
| c | Compressive |
| f | Fibre |
| t | Tensile |
| m | Matrix |
| L | Longitudinal direction (parallel to grain) |
| R | Radial direction (perpendicular to grain) |
| T | Tangential direction (perpendicular to grain) |
| Abbreviations | |
| CFRP | Carbon fibre-reinforced polymer |
| FEM | Finite element model |
| FRP | Fibre-reinforced polymer |
| GFRP | Glass fibre-reinforced polymer |
| RC | Reinforced concrete |
References
- Thomas, H.; Julius, N.; Roland, S.; Michael, V.; Wolfgang, W. Timber Construction Manual; Birkhäuser: Basel, Switzerland, 2012. [Google Scholar]
- Historic England. Practical Building Conservation: Timber; Routledge: London, UK, 2012. [Google Scholar]
- Ross, P. Appraisal and Repair of Timber Structures; Thomas Telford: London, UK, 2002. [Google Scholar]
- Satheeskumar, N. Wind Load Sharing and Vertical Load Transfer from Roof to Wall in a Timber-Framed House. Ph.D. Thesis, James Cook University, Douglas, Australia, 2016. [Google Scholar]
- European Committee for Standardization. Eurocode 5: Design of Timber Structures; European Committee for Standardization (CEN): Brussels, Belgium, 2004. [Google Scholar]
- Istat, 15° Censimento Generale Della Popolazione e Delle Abitazioni 15th Census of Population and Constructions in Italy, 2011. Available online: https://www.istat.it/it/censimenti-permanenti/censimenti-precedenti/popolazione-e-abitazioni/popolazione-2011 (accessed on 1 November 2022).
- Borri, A.; Corradi, M. Architectural Heritage: A Discussion on Conservation and Safety. Heritage 2019, 2, 631–647. [Google Scholar] [CrossRef]
- Atalić, J.; Uroš, M.; Novak, M.Š.; Demšić, M.; Nastev, M. The Mw5.4 Zagreb (Croatia) earthquake of March 22, 2020: Impacts and response. Bull. Earthq. Eng. 2021, 19, 3461–3489. [Google Scholar] [CrossRef] [PubMed]
- Arslan, M.H.; Korkmaz, H.H.; Gulay, F.G. Damage and failure pattern of prefabricated structures after major earthquakes in Turkey and shortfalls of the Turkish Earthquake code. Eng. Fail. Anal. 2006, 13, 537–557. [Google Scholar] [CrossRef]
- Macabuag, J.; Altheim, C.; Thorvaldsdottir, S.; Perks, D. Damage assessments by International Engineers following the Albania earthquake of November 2019. Int. J. Disaster Risk Reduct. 2022, 72, 102822. [Google Scholar] [CrossRef]
- Jasieńko, J.; Nowak, T.P. Solid timber beams strengthened with steel plates—Experimental studies. Constr. Build. Mater. 2014, 63, 81–88. [Google Scholar] [CrossRef]
- Franke, S.; Franke, B.; Harte, A.M. Failure modes and reinforcement techniques for timber beams—State of the art. Constr. Build. Mater. 2015, 97, 2–13. [Google Scholar] [CrossRef]
- Corradi, M.; Osofero, A.I.; Borri, A. Repair and Reinforcement of Historic Timber Structures with Stainless Steel—A Review. Metals 2019, 9, 106. [Google Scholar] [CrossRef]
- Pavković, K.; Stepinac, M.; Rajčić, V. Brittle failure modes in reinforced and non-reinforced timber joint with large diameter fastener loaded parallel to grain. Eng. Struct. 2020, 222, 111104. [Google Scholar] [CrossRef]
- Alam, P.; Ansell, M.P.; Smedley, D. Mechanical repair of timber beams fractured in flexure using bonded-in reinforcements. Compos. Part B Eng. 2009, 40, 95–106. [Google Scholar] [CrossRef]
- Raftery, G.M.; Harte, A.M. Low-grade glued laminated timber reinforced with FRP plate. Compos. Part B Eng. 2011, 42, 724–735. [Google Scholar] [CrossRef]
- ICOMOS–ISCARSAH Committee. ICOMOS Charter—Principles for the analysis, conservation and structural restoration of architectural heritage. In Proceedings of the ICOMOS 14th General Assembly and Scientific Symposium, Victoria Falls, Zimbabwe, 27–31 October 2003; Volume 2731. [Google Scholar]
- Francesco, M.; Scialpi, V.; Tegola, A.L. Flexural Reinforcement of Glulam Timber Beams and Joints with Carbon Fiber-Reinforced Polymer Rods. J. Compos. Constr. 2005, 9, 337–347. [Google Scholar]
- Gilfillan, J.R.; Gilbert, S.G.; Patrick, G.R.H. The Use of FRP Composites in Enhancing the Structural Behavior of Timber Beams. J. Reinf. Plast. Compos. 2003, 22, 1373–1388. [Google Scholar] [CrossRef]
- Fiorelli, J.; Dias, A.A. Glulam beams reinforced with FRP externally-bonded: Theoretical and experimental evaluation. Mater. Struct. 2011, 44, 1431–1440. [Google Scholar] [CrossRef]
- Vahedian, A.; Shrestha, R.; Crews, K. Experimental and analytical investigation on CFRP strengthened glulam laminated timber beams: Full-scale experiments. Compos. Part B Eng. 2019, 164, 377–389. [Google Scholar] [CrossRef]
- Vedernikov, A.; Gemi, L.; Madenci, E.; Özkılıç, Y.O.; Yazman, Ş.; Gusev, S.; Sulimov, A.; Bondareva, J.; Evlashin, S.; Konev, S.; et al. Effects of high pulling speeds on mechanical properties and morphology of pultruded GFRP composite flat laminates. Compos. Struct. 2022, 301, 116216. [Google Scholar] [CrossRef]
- Correia, J.R.; Cabral-Fonseca, S.; Branco, F.A.; Ferreira, J.G.; Eusébio, M.I.; Rodrigues, M.P. Durability of pultruded glass-fiber-reinforced polyester profiles for structural applications. Mech. Compos. Mater. 2006, 42, 325–338. [Google Scholar] [CrossRef]
- Correia, J.R.; Branco, F.A.; Ferreira, J.G. Flexural behaviour of GFRP–concrete hybrid beams with interconnection slip. Compos. Struct. 2007, 77, 66–78. [Google Scholar] [CrossRef]
- Gemi, L.; Madenci, E.; Özkılıç, Y.O.; Yazman, Ş.; Safonov, A. Effect of Fiber Wrapping on Bending Behavior of Reinforced Concrete Filled Pultruded GFRP Composite Hybrid Beams. Polymers 2022, 14, 3740. [Google Scholar] [CrossRef]
- Lokuge, W.; Otoom, O.; Borzou, R.; Navaratnam, S.; Herath, N.; Thambiratnam, D. Experimental and numerical analysis on the effectiveness of GFRP wrapping system on timber pile rehabilitation. Case Stud. Constr. Mater. 2021, 15, e00552. [Google Scholar] [CrossRef]
- Corradi, M.; Borri, A. Fir and chestnut timber beams reinforced with GFRP pultruded elements. Compos. Part B Eng. 2007, 38, 172–181. [Google Scholar] [CrossRef]
- Ormarsson, S. Numerical Analysis of Moisture-Related Distortions in Sawn Timber. Ph.D. Thesis, Chalmers University of Technology, Gothenburg, Sweden, 1999. [Google Scholar]
- Oudjene, M.; Khelifa, M. Elasto-plastic constitutive law for wood behaviour under compressive loadings. Constr. Build. Mater. 2009, 23, 3359–3366. [Google Scholar] [CrossRef]
- Kim, Y.J.; Harries, K.A. Modeling of timber beams strengthened with various CFRP composites. Eng. Struct. 2010, 32, 3225–3234. [Google Scholar] [CrossRef]
- Navaratnam, S.; Small, D.W.; Gatheeshgar, P.; Poologanathan, K.; Thamboo, J.; Higgins, C.; Mendis, P. Development of cross laminated timber-cold-formed steel composite beam for floor system to sustainable modular building construction. Structures 2021, 32, 681–690. [Google Scholar] [CrossRef]
- Green, D.W.; Winandy, J.E.; Kretschmann, D.E. Mechanical properties of wood. In Wood Handbook: Wood as an Engineering Material; USDA Forest Service, Forest Products Laboratory: Madison, WI, USA, 1999; p. 4. [Google Scholar]
- Navaratnam, S.; Herath, N.; Lokuge, W.; Thamboo, J.; Poologanathan, K. Performance of timber girders with end-notch: Experimental and numerical investigation. Structures 2021, 29, 730–740. [Google Scholar] [CrossRef]
- Satheeskumar, N.; Henderson, D.J.; Ginger, J.D.; Wang, C.H. Finite element modelling of the structural response of roof to wall framing connections in timber-framed houses. Eng. Struct. 2017, 134, 25–36. [Google Scholar] [CrossRef]
- Shekarchi, M.; Oskouei, A.V.; Raftery, G.M. Flexural behavior of timber beams strengthened with pultruded glass fiber reinforced polymer profiles. Compos. Struct. 2020, 241, 112062. [Google Scholar] [CrossRef]
- Korkmaz, H.H.; Dere, Y.; Özkılıç, Y.O.; Bozkurt, M.B.; Ecemiş, A.S.; Özdoner, N. Excessive snow induced steel roof failures in Turkey. Eng. Fail. Anal. 2022, 141, 106661. [Google Scholar] [CrossRef]
- Gatheeshgar, P.; Poologanathan, K.; Thamboo, J.; Roy, K.; Rossi, B.; Molkens, T.; Perera, D.; Navaratnam, S. On the fire behaviour of modular floors designed with optimised cold-formed steel joists. Structures 2021, 30, 1071–1085. [Google Scholar] [CrossRef]
- Navaratnam, S.; Thamboo, J.; Poologanathan, K.; Roy, K.; Gatheeshgar, P. Finite element modelling of timber infilled steel tubular short columns under axial compression. Structures 2021, 30, 910–924. [Google Scholar] [CrossRef]
- Ishqy, M.F.M.; Wanniarachchi, S.; Poologanathan, K.; Gunalan, S.; Gatheeshgar, P.; Suntharalingam, T.; Navaratnam, S. Shear behaviour of cold-formed stainless-steel beams with web openings: Numerical studies. Structures 2021, 31, 127–144. [Google Scholar] [CrossRef]
- Tsai, S.W.; Wu, E.M. A General Theory of Strength for Anisotropic Materials. J. Compos. Mater. 1971, 5, 58–80. [Google Scholar] [CrossRef]
- Hashin, Z. Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Klasztorny, M.; Bondyra, A.; Szurgott, P.; Nycz, D. Numerical modelling of GFRP laminates with MSC.Marc system and experimental validation. Comput. Mater. Sci. 2012, 64, 151–156. [Google Scholar] [CrossRef]
- Gupta, A.K.; Velmurugan, R.; Joshi, M. Numerical and experimental study of multimode failure phenomena in GFRP laminates of different lay-ups. Int. J. Crashworthiness 2018, 23, 87–99. [Google Scholar] [CrossRef]
- Czechowski, L.; Gliszczyński, A.; Bieniaś, J.; Jakubczak, P.; Majerski, K. Failure of GFRP channel section beams subjected to bending-Numerical and experimental investigations. Compos. Part B Eng. 2017, 111, 112–123. [Google Scholar] [CrossRef]
- Ulger, T.; Okeil, A.M. Analysis of thin-walled steel beams retrofitted by bonding GFRP stiffeners: Numerical model and investigation of design parameters. Eng. Struct. 2017, 153, 166–179. [Google Scholar] [CrossRef]
- Hill, R.; Orowan, E. A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 193, 281–297. [Google Scholar]
- Mackenzie-Helnwein, P.; Eberhardsteiner, J.; Mang, H.A. A multi-surface plasticity model for clear wood and its application to the finite element analysis of structural details. Comput. Mech. 2003, 31, 204–218. [Google Scholar] [CrossRef]
- ABAQUS. Theory Manual, Version 6.14; Hibbitt, Karlsson & Sorensen, Inc.: Providence, RI, USA, 2014. [Google Scholar]
- Nouri, F.; Valipour, H.R.; Bradford, M.A. Finite element modelling of steel-timber composite beam-to-column joints with nominally pinned connections. Eng. Struct. 2019, 201, 109854. [Google Scholar] [CrossRef]
- Valipour, H.; Khorsandnia, N.; Crews, K.; Foster, S. A simple strategy for constitutive modelling of timber. Constr. Build. Mater. 2014, 53, 138–148. [Google Scholar] [CrossRef]
- BS EN ISO 898-1:2013; Mechanical Properties of Fasteners Made of Carbon Steel and Alloy Steel Bolts, Screws and Studs with Specified Property Classes. Coarse Thread and Fine Pitch Thread. European Committee for Standardization (CEN): Brussels, Belgium, 2013.
- Guan, Z.W.; Zhu, E.C. Finite element modelling of anisotropic elasto-plastic timber composite beams with openings. Eng. Struct. 2009, 31, 394–403. [Google Scholar] [CrossRef]
- Fernandes, L.A.; Nunes, F.; Silvestre, N.; Correia, J.R.; Gonilha, J. Web-crippling of GFRP pultruded profiles. Part 2: Numerical analysis and design. Compos. Struct. 2015, 120, 578–590. [Google Scholar] [CrossRef]
- Nunes, F.; Correia, J.R.; Silvestre, N. Structural behavior of hybrid FRP pultruded beams: Experimental, numerical and analytical studies. Thin-Walled Struct. 2016, 106, 201–217. [Google Scholar] [CrossRef]
- Fascetti, A.; Feo, L.; Nisticò, N.; Penna, R. Web-flange behavior of pultruded GFRP I-beams: A lattice model for the interpretation of experimental results. Compos. Part B Eng. 2016, 100, 257–269. [Google Scholar] [CrossRef]
- Madenci, E.; Özkılıç, Y.O.; Gemi, L. Experimental and theoretical investigation on flexure performance of pultruded GFRP composite beams with damage analyses. Compos. Struct. 2020, 242, 112162. [Google Scholar] [CrossRef]
- Alhawamdeh, M.; Alajarmeh, O.; Aravinthan, T.; Shelley, T.; Schubel, P.; Kemp, M.; Zeng, X. Modelling hollow pultruded FRP profiles under axial compression: Local buckling and progressive failure. Compos. Struct. 2021, 262, 113650. [Google Scholar] [CrossRef]
- Asiz, A.; Smith, I. Connection System of Massive Timber Elements Used in Horizontal Slabs of Hybrid Tall Buildings. J. Struct. Eng. 2011, 137, 1390–1393. [Google Scholar] [CrossRef]
- Ellingsbø, P.; Malo, K. Withdrawal capacity of long self-tapping screws paralell to grain direction. In Proceedings of the World Conference on Timber Engineering, WCTE 2012, Auckland, New Zealand, 15–19 July 2012; pp. 228–237. [Google Scholar]
- Maik, G. Pull-Out Resistance of Self-Tapping Wood Screws with Continuous Thread. Ph.D. Thesis, The University of British Columbia, Vancouver, BC, Canada, 2011. [Google Scholar]
- Hassanieh, A.; Valipour, H.R.; Bradford, M.A. Experimental and analytical behaviour of steel-timber composite connections. Constr. Build. Mater. 2016, 118, 63–75. [Google Scholar] [CrossRef]
- Masood, S.N.; Viswamurthy, S.R.; Singh, A.K.; Muthukumar, M.; Gaddikeri, K.M. Simulation and validation of disbond growth in co-cured composite skin–stringer specimens using cohesive elements. J. Compos. Mater. 2017, 52, 807–822. [Google Scholar] [CrossRef]
- Ikramullah; Afrizal, A.; Huzni, S.; Thalib, S.; Abdul Khalil, H.P.S.; Rizal, S. Effect of Mesh Sensitivity and Cohesive Properties on Simulation of Typha Fiber/Epoxy Microbond Test. Computation 2020, 8, 2. [Google Scholar] [CrossRef]
- Liu, C.; Zhou, Z.; Wang, X.; Zhang, B. Analysis and determination for the parameters of “cohesive element” in the numerical model of single fiber composites: The elastic parameters. J. Reinf. Plast. Compos. 2012, 31, 1127–1135. [Google Scholar] [CrossRef]








| No. | Pmax (kN) | Increment Pmax Reinforced/ Un-Reinforced | k1/3 (N mm−1) | Increment k1/3 Reinforced/ Un-Reinforced | ku (N mm−1) | Increment ku Reinforced/ Un-Reinforced |
|---|---|---|---|---|---|---|
| C1 | 65.1 | - | 1753 | - | 1491 | - |
| C4 | 67.2 | - | 1829 | - | 1470 | - |
| C3 + I1 | 225.2 | 3.40 | 7591 | 4.24 | 7011 | 4.74 |
| C2 + I2 | 183.5 | 2.77 | 5665 | 3.16 | 5837 | 3.94 |
| C5 + H4 | 137.2 | 2.07 | 3659 | 2.04 | 3102 | 2.10 |
| C6 + H5 | 101.8 | 1.54 | 3190 | 1.78 | 1816 | 1.23 |
| A1 | 85.8 | - | 1975 | - | 1971 | - |
| A5 | 78.0 | - | 1988 | - | 1547 | - |
| A3 + H3 | 173.2 | 2.11 | 3699 | 1.87 | 3187 | 1.81 |
| A2 + H1 | 80.8 | 0.99 | 2393 | 1.21 | 2307 | 1.31 |
| A4 + H2 | 148.3 | 1.81 | 3944 | 1.99 | 2284 | 1.30 |
| A6 + I3 | 193.0 | 2.36 | 6721 | 3.39 | 6535 | 3.72 |
| A7 + I4 | 205.8 | 2.51 | 6827 | 3.45 | 6647 | 3.78 |
| Weight density (kg/m3) | 452 |
| Young’s modulus L direction (MPa) | 11,426 |
| Young’s modulus R direction (MPa) | 888 |
| Young’s modulus T direction (MPa) | 622 |
| Poisson’s ratio LR | 0.053 |
| Poisson’s ratio RT | 0.43 |
| Poisson’s ratio LT | 0.036 |
| Shear modulus LR (MPa) | 616 |
| Shear modulus RT (MPa) | 61.6 |
| Shear modulus LT (MPa) | 616 |
| σc,90° (MPa) | 9.6 |
| F | 0.98 |
| G | 0.04 |
| H | 0.02 |
| L = M | 0.6 |
| N | 0.9 |
| Modulus of elasticity (E1) | 36,000 MPa |
| Modulus of elasticity (E2) | 5100 MPa |
| Shear modulus (G12) | 3000 MPa |
| Shear modulus (G13) | 3000 MPa |
| Shear modulus (G23) | 190 MPa |
| Poisson’s Ratio | 0.28 |
| Tensile strength (ft,0°) | 402 MPa |
| Tensile strength (ft,90°) | 39 MPa |
| Compressive strength (fc,0°) | 389 MPa |
| Compressive strength (fc,90°) | 101 MPa |
| Shear strength (fτ) | 26 MPa |
| Fracture energy (Gft) | 12.5 N/mm |
| Fracture energy (Gfc) | 12.5 N/mm |
| Fracture energy (Gmt) | 1 N/mm |
| Fracture energy (Gmc) | 1 N/mm |
| FEM Type | Details | |
|---|---|---|
| FEM_A-0 | 0° | |
| FEM_A-1 | 1° | |
| FEM_A-2 | 2° | |
| FEM_A-3 | 3° | Unreinforced timber |
| FEM_A-4 | 4° | |
| FEM_A-5 | 5° | |
| FEM_A-6 | 6° | |
| FEM_A-7 | 7° | |
| FEM_A-0-H | 0° | |
| FEM_A-1-H | 1° | |
| FEM_A-2-H | 2° | |
| FEM_A-3-H | 3° | Reinforced timber |
| FEM_A-4-H | 4° | |
| FEM_A-5-H | 5° | |
| FEM_A-6-H | 6° | |
| FEM_A-7-H | 7° | |
| GFRP | GFRP pultruded beam |
| FEM Type | Exp-(kN) | FEM (kN) | Test */FEM | k1/3 (N mm−1) | ku (N mm−1) |
|---|---|---|---|---|---|
| A1 | 85.8 | 1975 | 1971 | ||
| A5 | 78 | 1988 | 1547 | ||
| FEM_A-0 | 87.3 | 0.94 | 2725 | 2380 | |
| FEM_A-1 | 88.1 | 0.93 | 2528 | 2235 | |
| FEM_A-2 | 85.1 | 0.96 | 2529 | 2261 | |
| FEM_A-3 | 82.3 | 1.00 | 2529 | 2280 | |
| FEM_A-4 | 81.4 | 1.01 | 2529 | 2245 | |
| FEM_A-5 | 79.3 | 1.03 | 2529 | 2276 | |
| FEM_A-6 | 83.6 | 0.98 | 2529 | 2114 | |
| FEM_A-7 | 85.7 | 0.96 | 2529 | 2210 |
| FEM Type | Exp. (kN) | FEM (kN) | Test */FEM | k1/3 (N mm−1) | ku (N mm−1) |
|---|---|---|---|---|---|
| A3 + H3 | 173.2 | 3699 | 3187 | ||
| A4 + H2 | 148.3 | 3944 | 2284 | ||
| FEM_A-0-H | 141.6 | 1.14 | 4353 | 4182 | |
| FEM_A-1-H | 141.6 | 1.14 | 4353 | 4114 | |
| FEM_A-2-H | 145.8 | 1.10 | 4350 | 4183 | |
| FEM_A-3-H | 142.1 | 1.13 | 4353 | 4172 | |
| FEM_A-4-H | 148 | 1.09 | 4353 | 4183 | |
| FEM_A-5-H | 142.1 | 1.13 | 4341 | 4172 | |
| FEM_A-6-H | 146.5 | 1.10 | 4354 | 4197 | |
| FEM_A-7-H | 141.8 | 1.13 | 4354 | 4153 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navaratnam, S.; Small, D.W.; Corradi, M.; Gatheeshgar, P.; Poologanathan, K.; Higgins, C. Numerical Modelling of Timber Beams with GFRP Pultruded Reinforcement. Buildings 2022, 12, 1992. https://doi.org/10.3390/buildings12111992
Navaratnam S, Small DW, Corradi M, Gatheeshgar P, Poologanathan K, Higgins C. Numerical Modelling of Timber Beams with GFRP Pultruded Reinforcement. Buildings. 2022; 12(11):1992. https://doi.org/10.3390/buildings12111992
Chicago/Turabian StyleNavaratnam, Satheeskumar, Deighton Widdowfield Small, Marco Corradi, Perampalam Gatheeshgar, Keerthan Poologanathan, and Craig Higgins. 2022. "Numerical Modelling of Timber Beams with GFRP Pultruded Reinforcement" Buildings 12, no. 11: 1992. https://doi.org/10.3390/buildings12111992
APA StyleNavaratnam, S., Small, D. W., Corradi, M., Gatheeshgar, P., Poologanathan, K., & Higgins, C. (2022). Numerical Modelling of Timber Beams with GFRP Pultruded Reinforcement. Buildings, 12(11), 1992. https://doi.org/10.3390/buildings12111992









