Deep Forest-Based DQN for Cooling Water System Energy Saving Control in HVAC
Abstract
1. Introduction
- We extended our previously proposed DF-DQN from the prediction problem to the control problem. The introduction of DF mapped the original DQN output action space into a new smaller action space, which could accelerate the convergence speed of DQN;
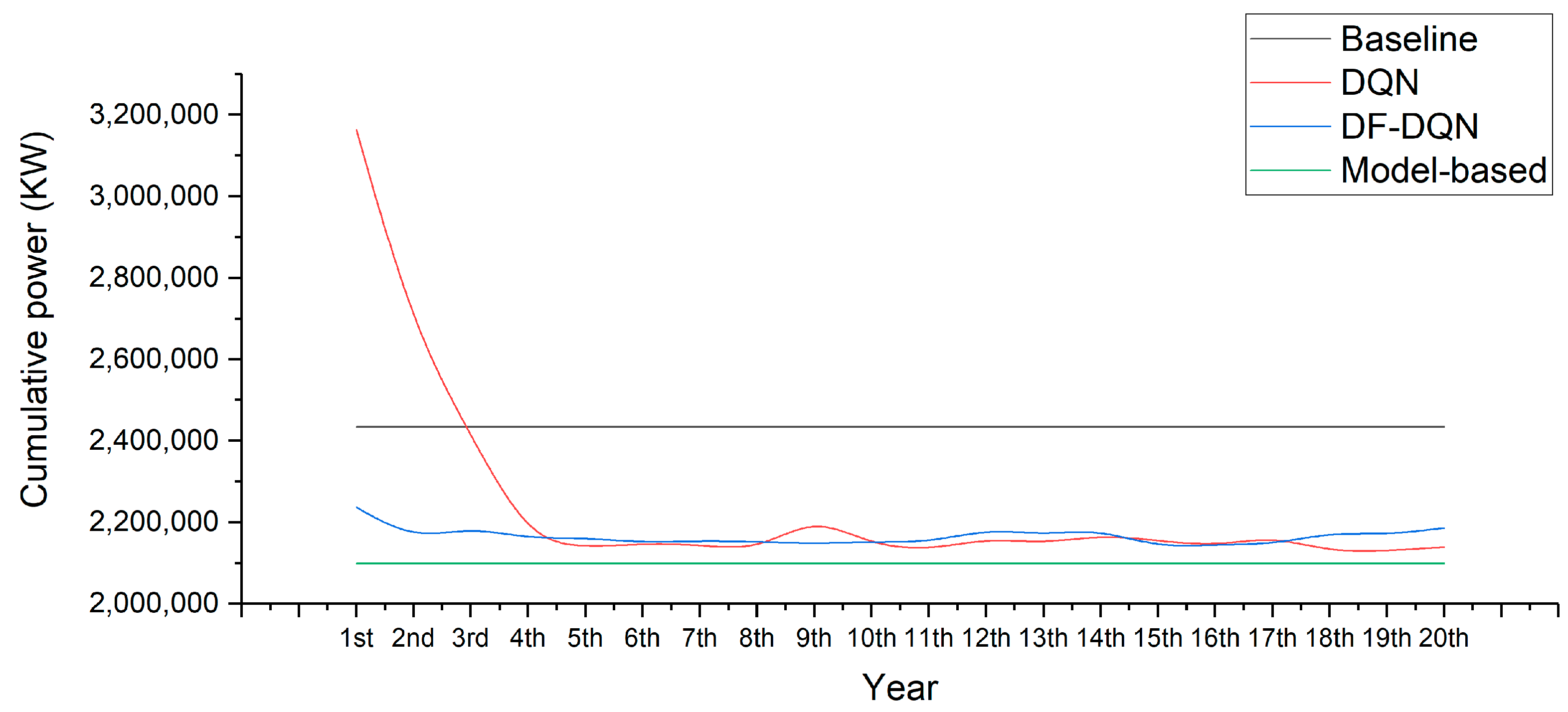
- We used DF-DQN to control a cooling water system in HVAC and to realize energy savings from the early stage. A priori knowledge was introduced as a deep forest classifier, which can not only reduce the action space, but also reduce the exploration of the agent. The experimental results show that DF-DQN can save energy from the first year, while DQN can achieve similar energy saving from the third year;
- We verified the performance of DF-DQN in an environment based on the modeling of a real cooling water system, so as to ensure the credibility of DF-DQN. The data that DF-DQN and other compared methods used were collected from a real-world system, and the simulation environment was built based on this system. The code and the experimental data are available at: https://github.com/H-Phoebe/DF-DQN-for-energy-saving-control (accessed on 20 August 2022).
2. Related Works
3. Preliminaries
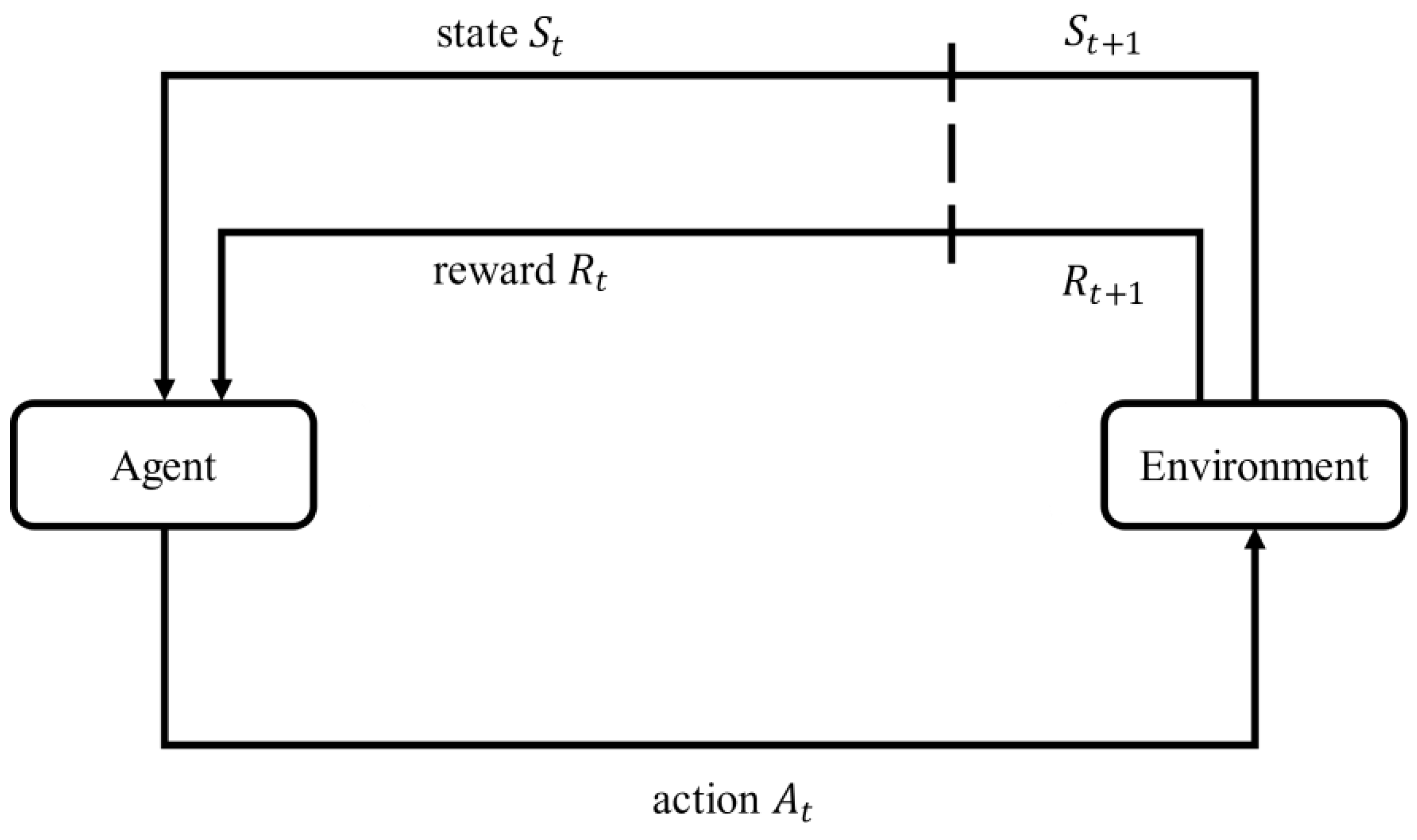
3.1. MDP
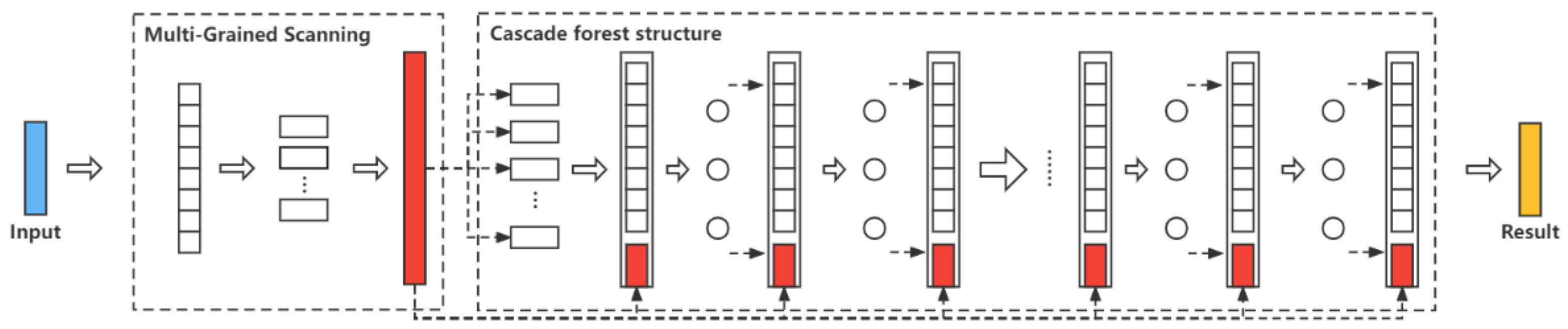
3.2. Deep Forest
3.3. DQN
4. Environment and Modeling
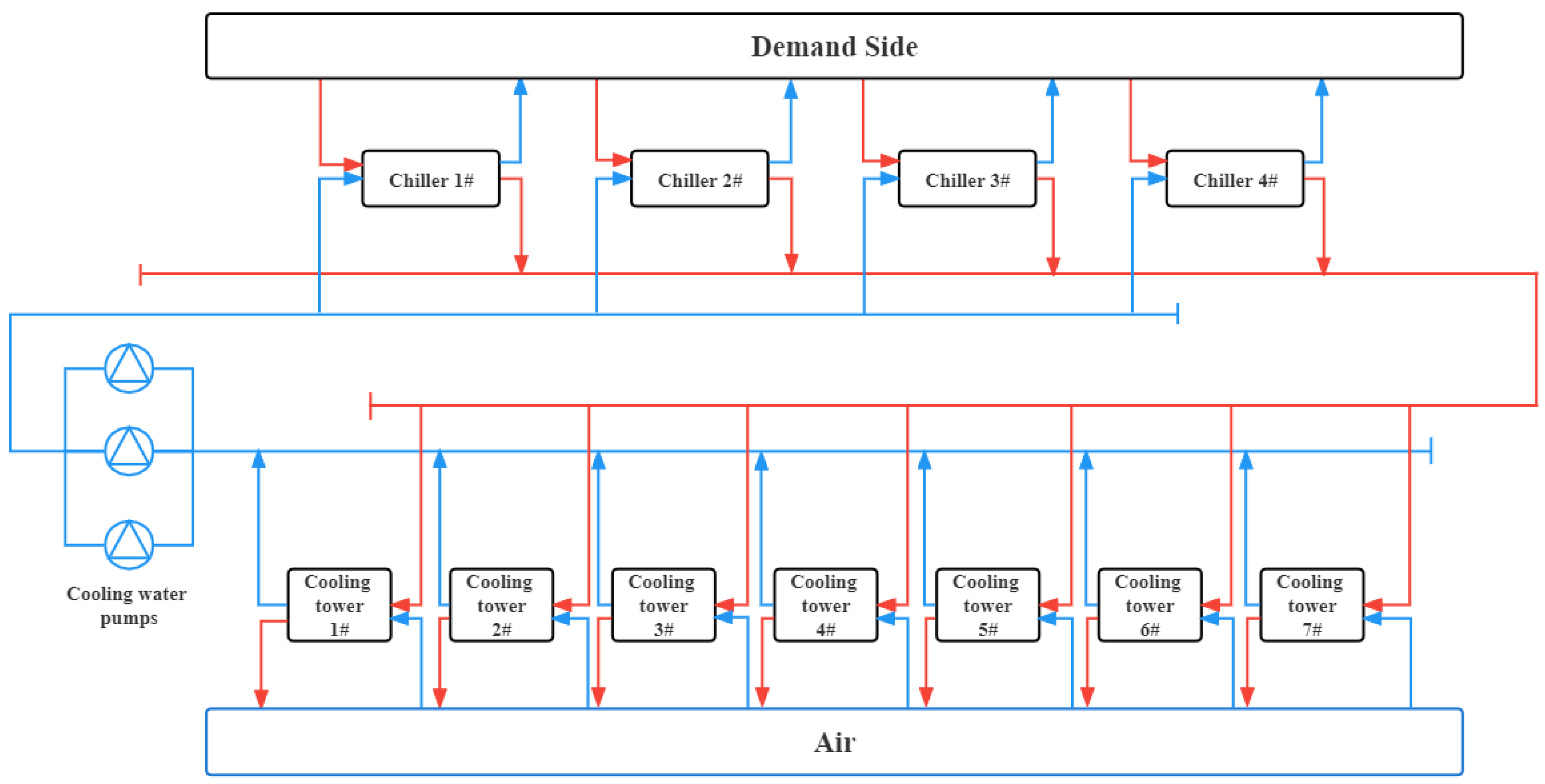
4.1. Cooling Water System Layout
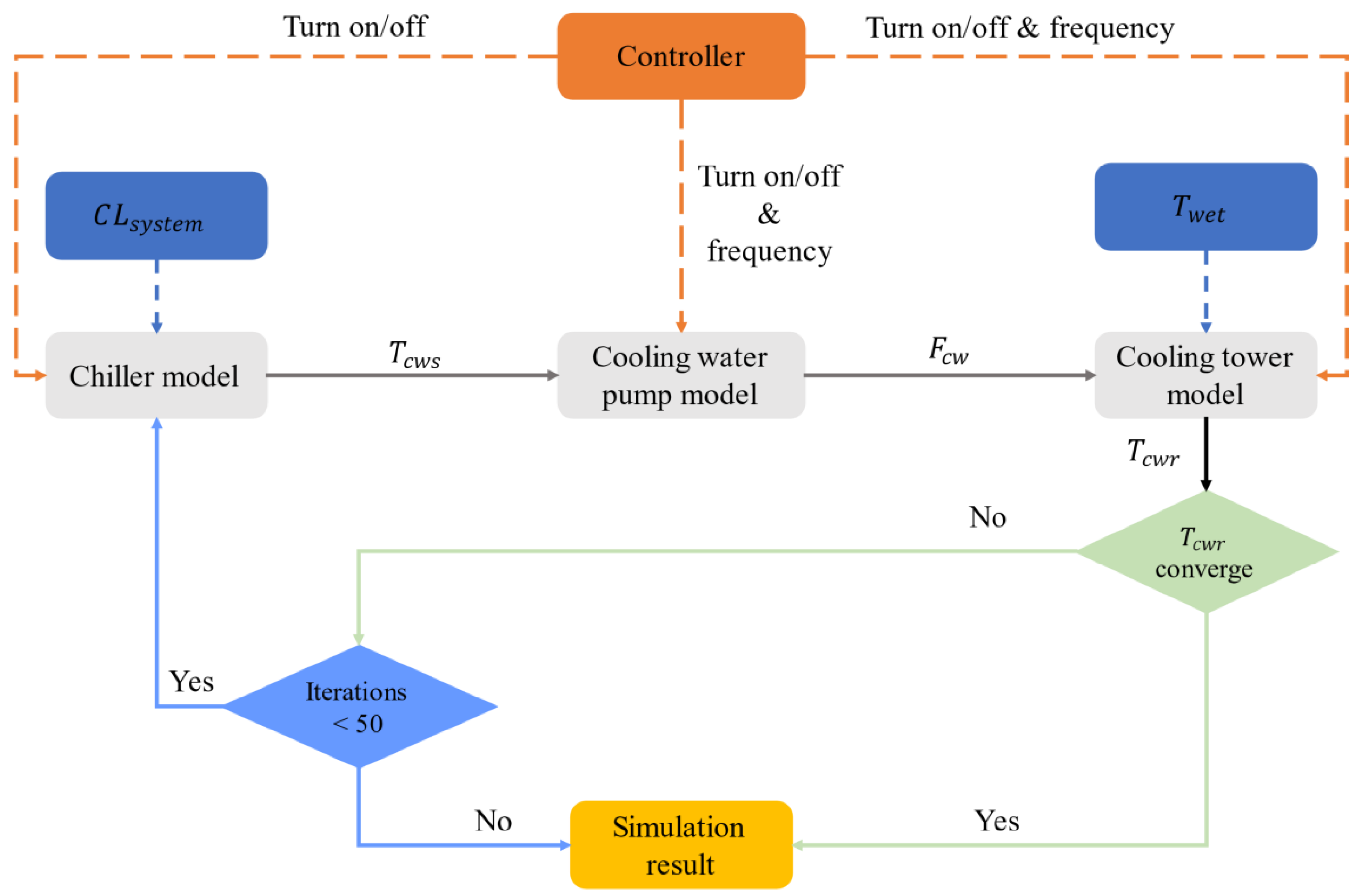
4.2. System Simulation Modeling
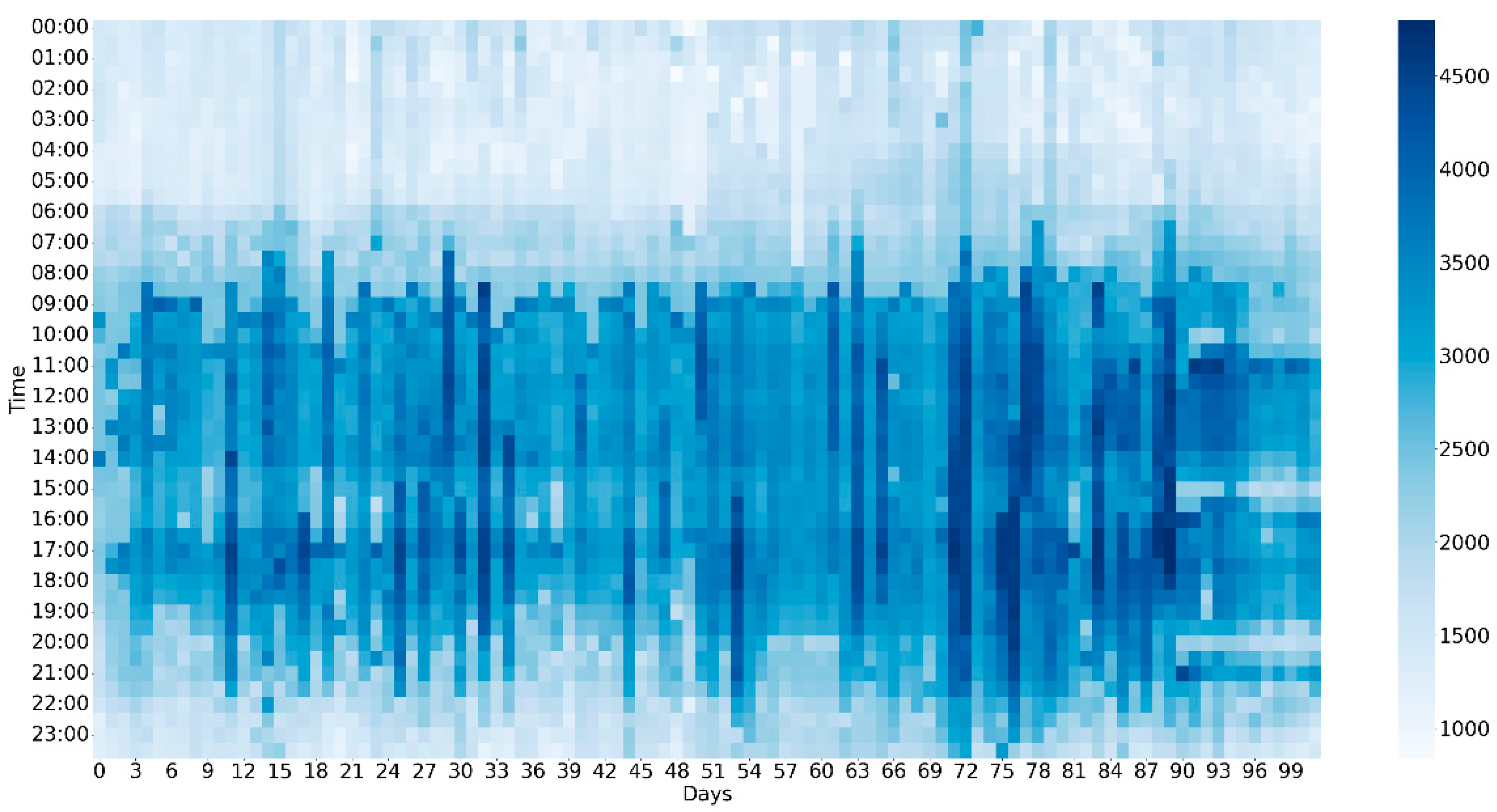
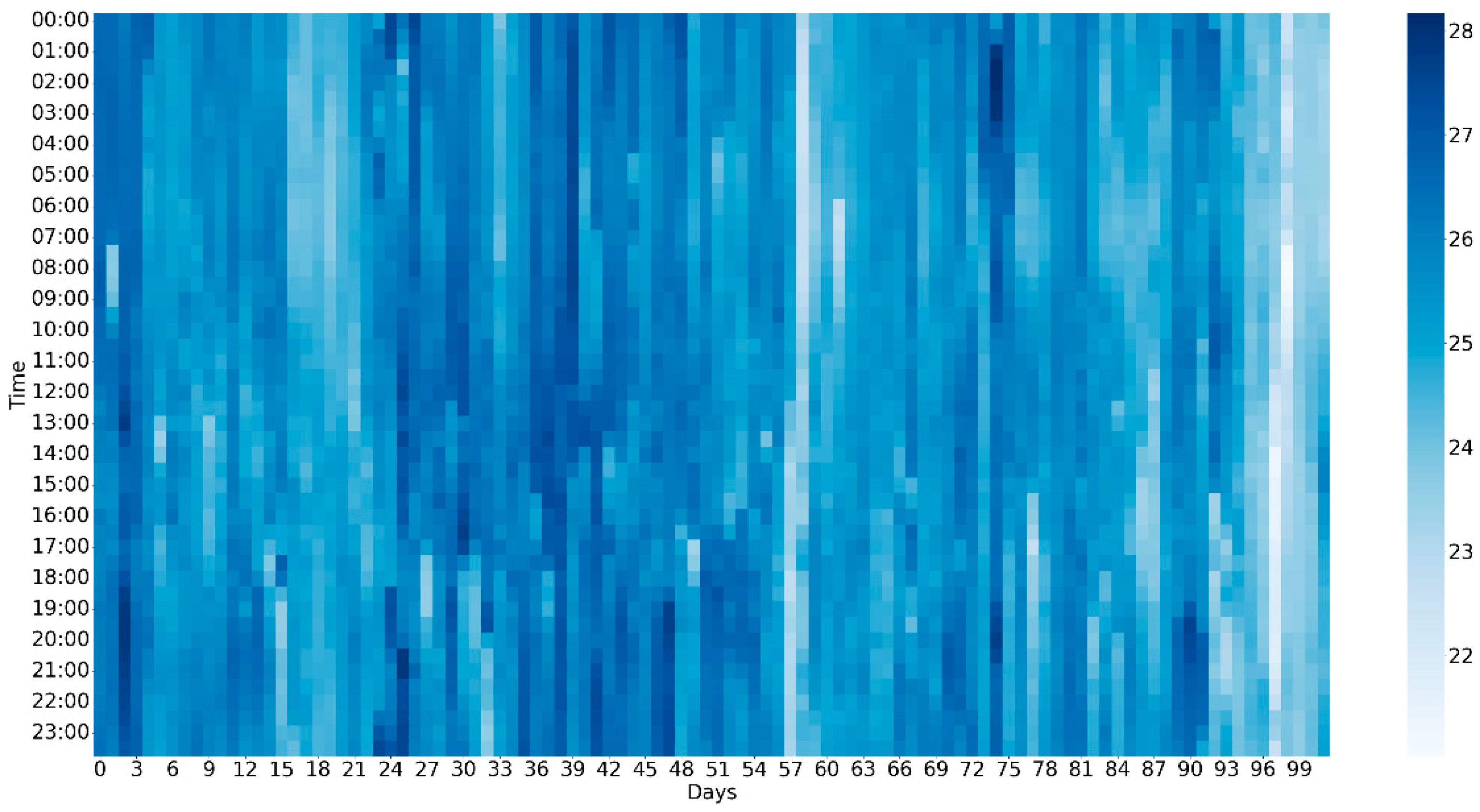
4.3. Data Collection
5. Methodology
5.1. MDP Modeling
- (a)
- StateIn this paper, we took the combination of ambient the wet-bulb temperature () and system cooling load () as state. There were two reasons for using these two variables:
- (1)
- The operation of the system has no influence of these variables;
- (2)
- is a component factor of COP, which is related to the operation of cooling water system.
- (b)
- ActionIn this paper, operating frequencies of cooling tower fans and cooling water pumps were taken as the action (e.g.,). In addition, the action was discretized and the control accuracy was 1 hz. In order to protect the equipment, the action needed to be limited within a reasonable range. We limited the action frequency within [20, 50] for both the cooling tower and cooling water pump, so there were 31 actions in total for each one.
- (c)
- RewardCOP was taken as the reward in this paper. In the case of the same , the higher the COP value is, the sum of power is the lowest, which reflects the purpose of energy saving. The reward is shown in Equation (16).
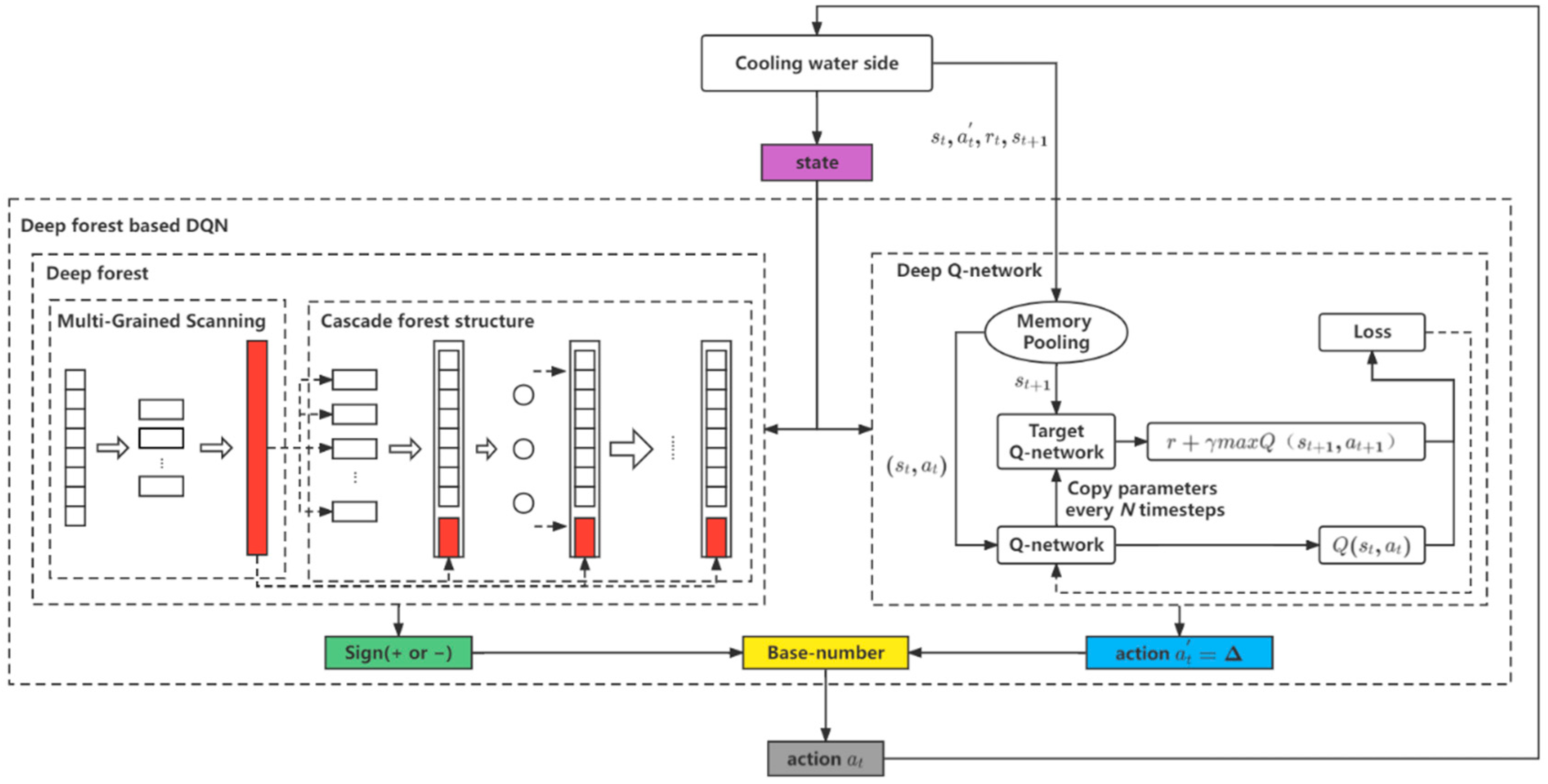
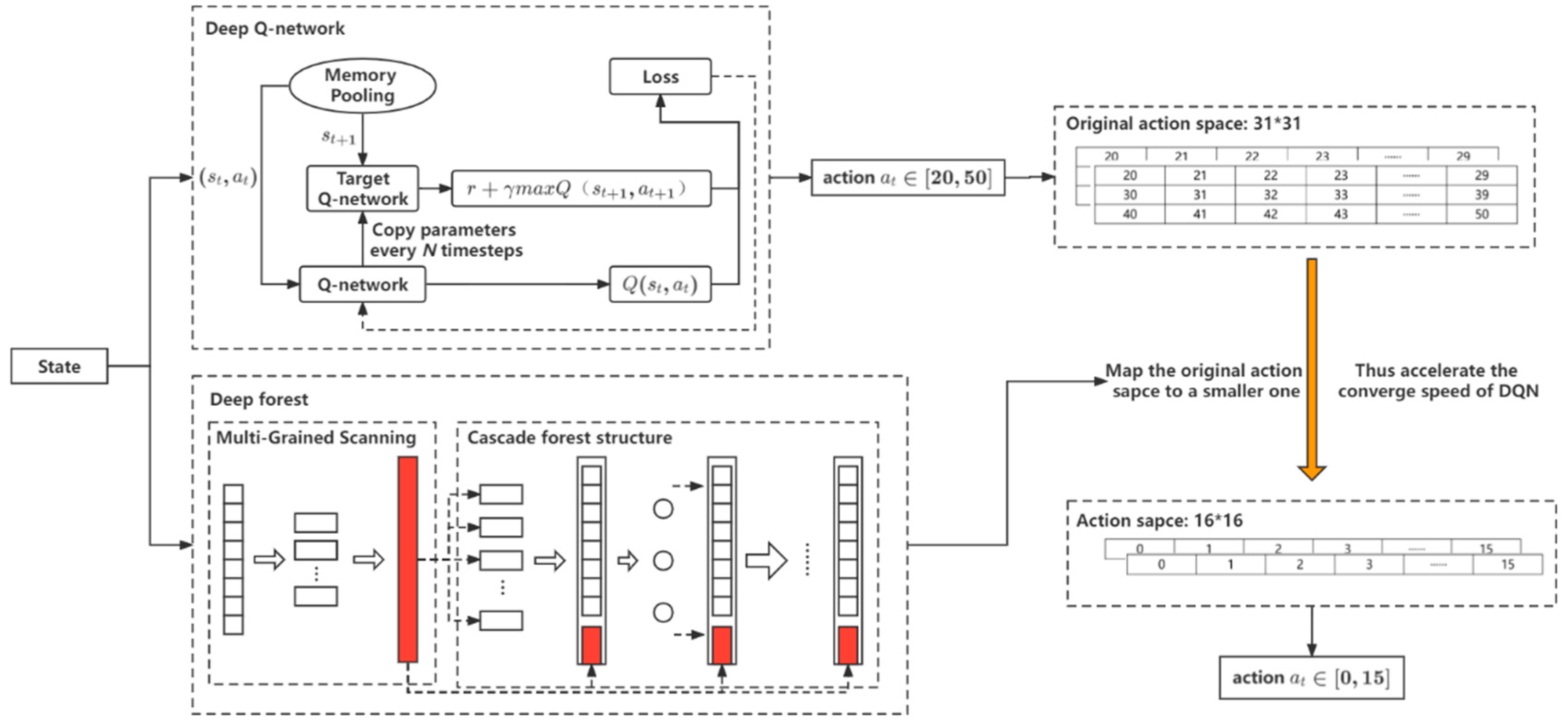
5.2. DF-DQN for Control
5.3. Theoretical Analysis of Shrink Action
5.4. DF-DQN Algorithm
| Algorithm 1. DF-DQN for cooling water system |
| Initialize replay memory to capacity Initialize action value function with random weights Detect and replace outliers in training set Split the training set (80% for training, 20% for testing) Train the deep forest classifier For episode = 1, M do Attain initial state of the cooling water system For t = 1, T do Select a random action with probability , otherwise Attain positive or negative sign through Combine base number, sign (‘+’ or ‘−’), to derive (the true running frequency of cooling water system) Execute action in cooling water system Observe reward and state from the simulation system Store transition () in Sample random minibatch of transitions () from Set Update Q function using Copy parameters every steps Update state End for End for |
6. Experiment and Result
6.1. Compare Methods
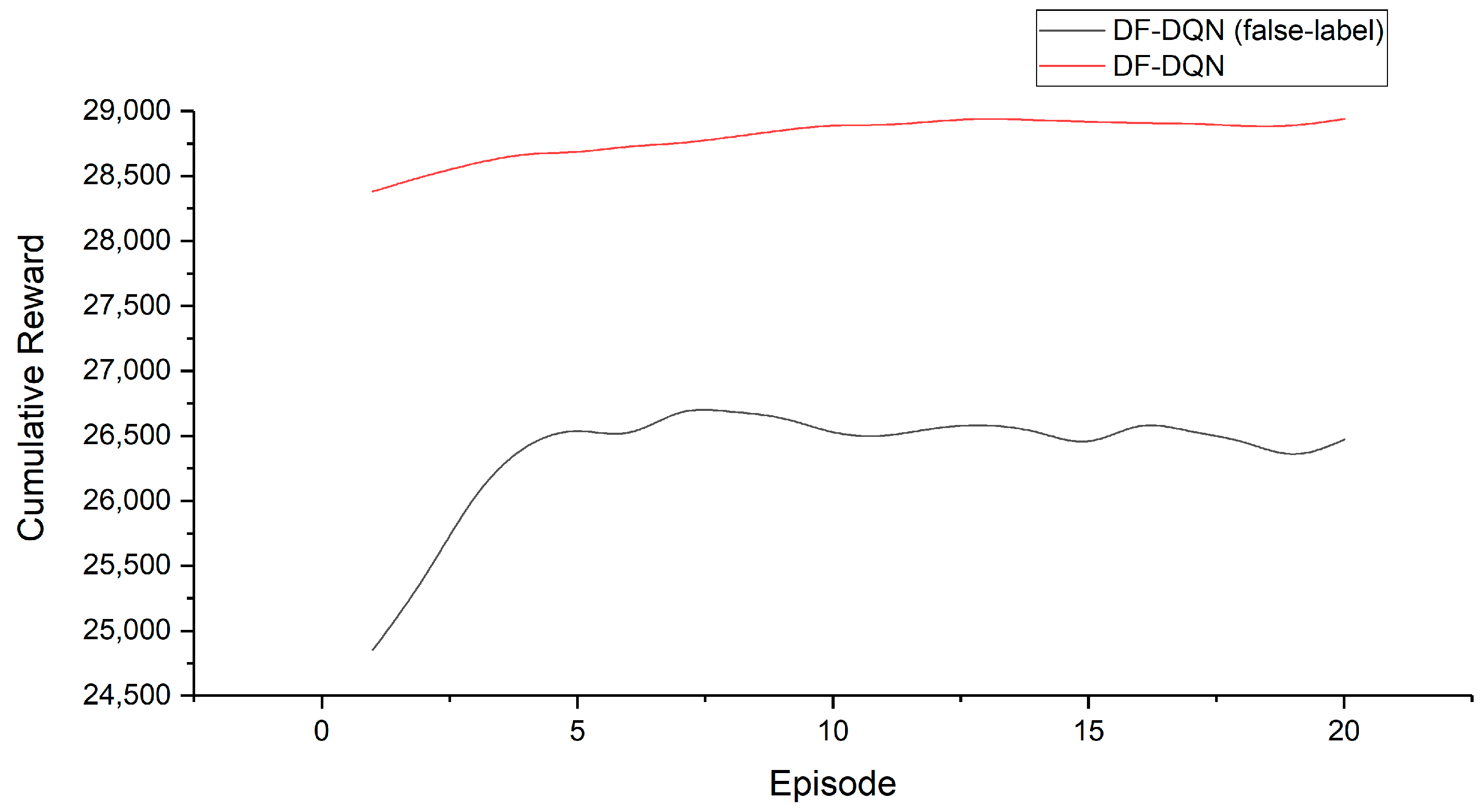
- DF-DQN: DF-DQN is the method we proposed before [25], which has been used to solve prediction problem. We extended DF-DQN to control problems in this paper;
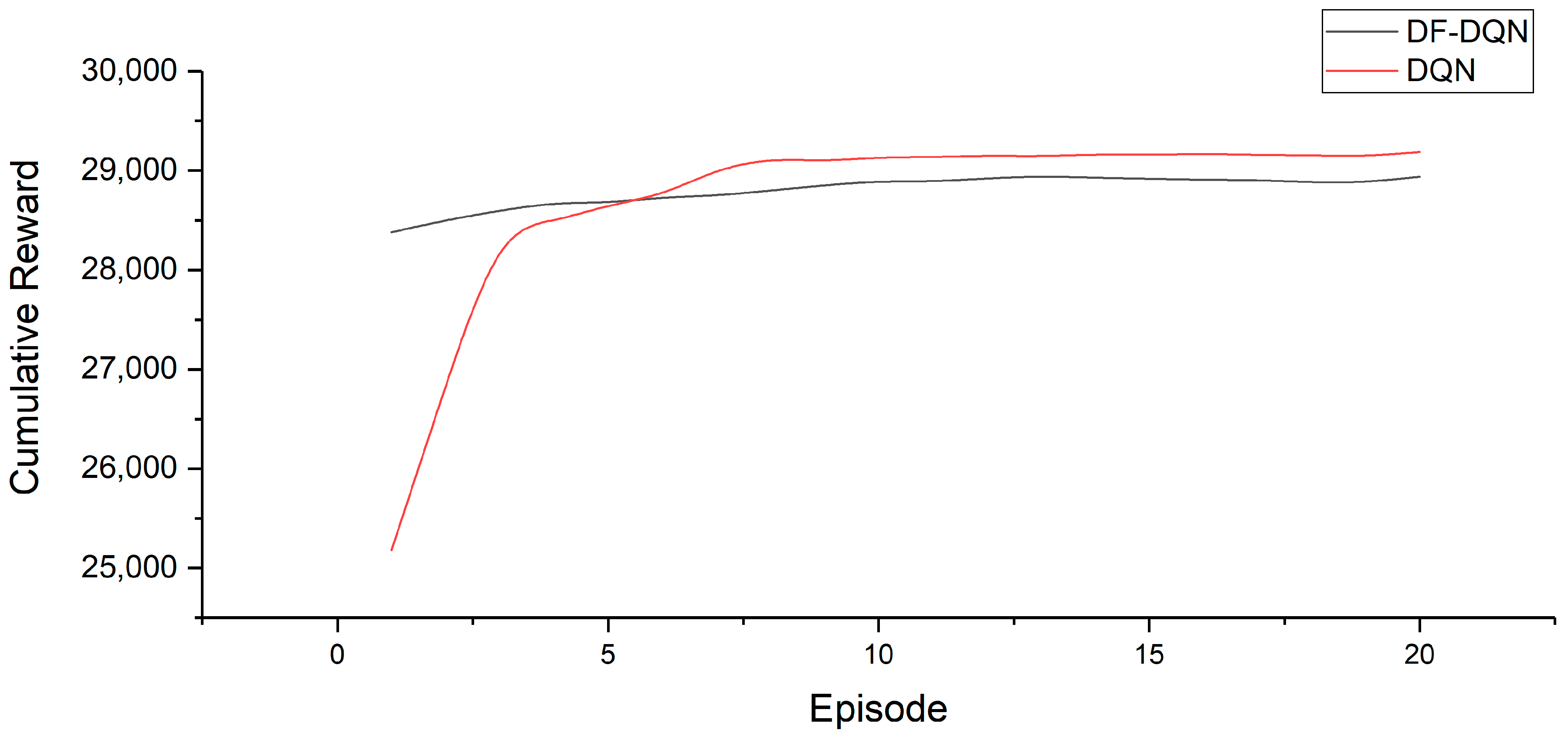
- DQN: In this paper, DQN and DF-DQN share the same parameter settings in the DQN part. For the cooling water system, the action space was small and discrete, and its state space was large enough, so usually DQN can provide a good control policy according to paper [24];
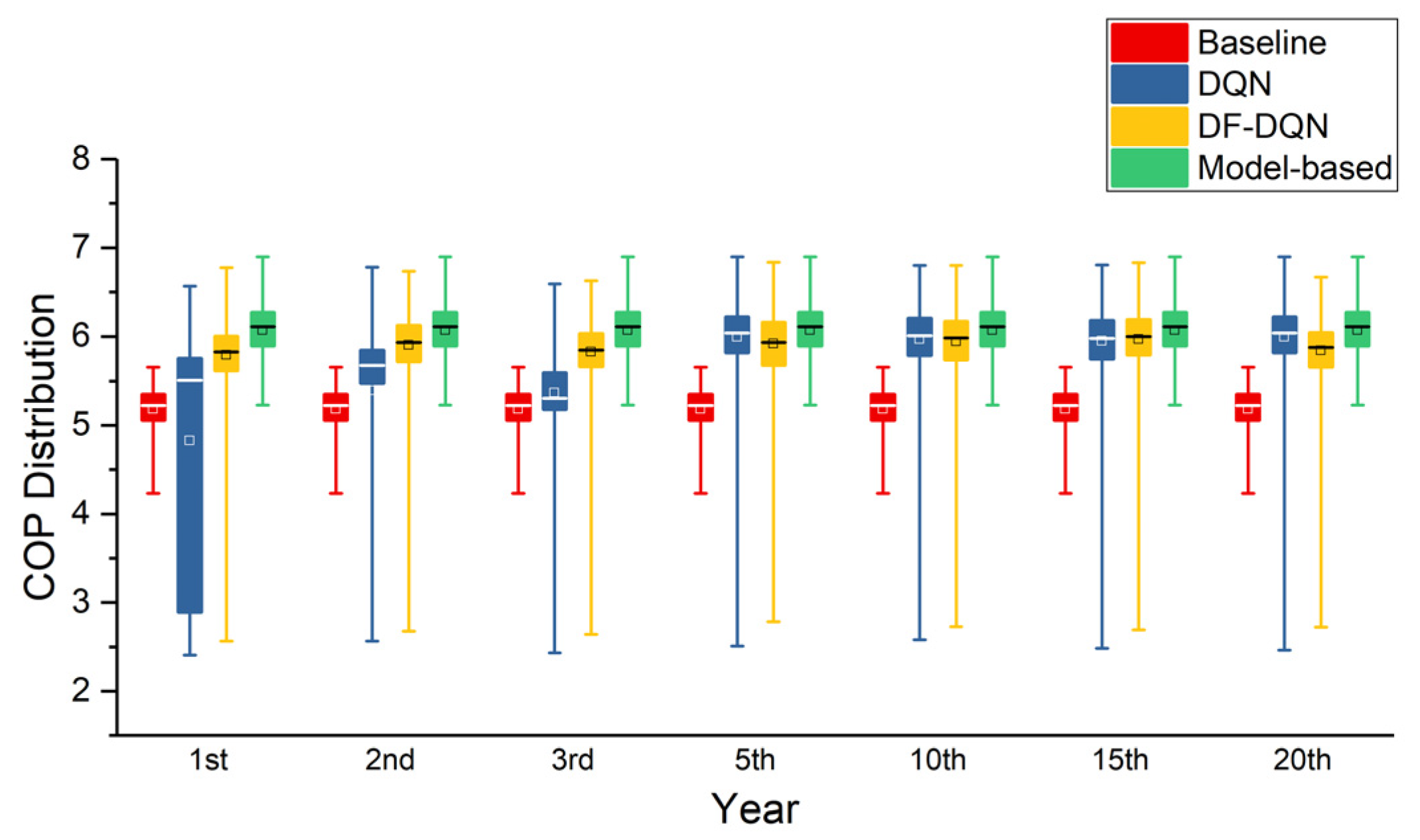
- Baseline control: The PID control was selected as the baseline method, which is often used in real HVAC control applications. This method selects the action by approaching the difference between and . We took the baseline control method for comparison because it is the original control method in this system;
- Model-based control: The model-based control is the best method among all methods, and can select the best action in each situation, but this method is heavily dependent on the model. In this paper, we traversed the best action in each state as the model-based control. Actually, it is often impossible to deploy the model-based control method in real applications, but in this paper, based on our simulation model, the model-based control method provided the best policy. We used the model-based control method for comparison because it has the best control performance of all methods in this system.
6.2. Parameters Setting
6.3. Experimental Result
6.3.1. Influence of DF’s Accuracy on DF-DQN
6.3.2. Performance of DF-DQN Compared with DQN, Baseline Control, and Model-Based Control
- (a)
- COP
- (b)
- Cumulative power
- (c)
- Energy saving
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
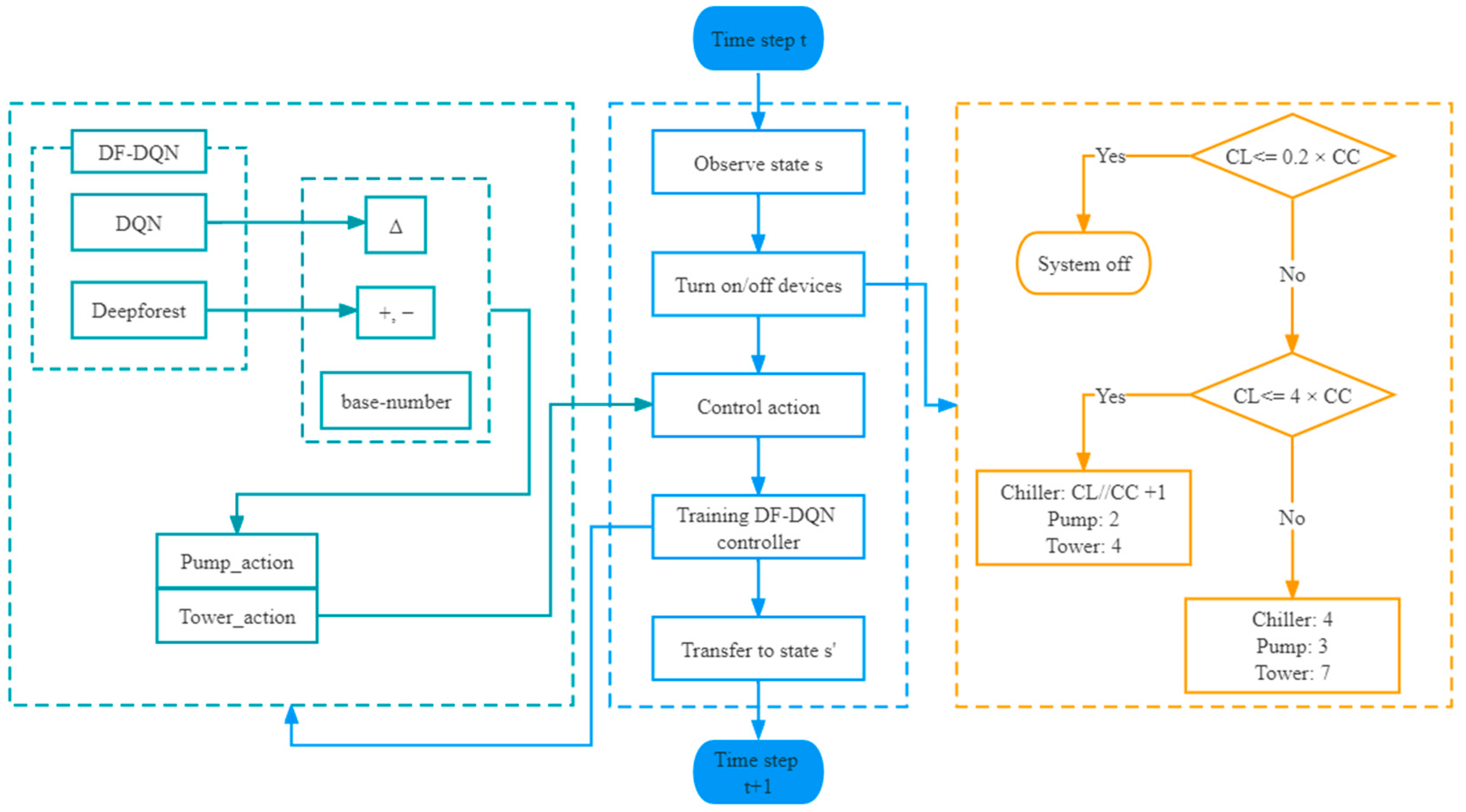
- In time step , the agent observes the state , and decides to turn the system on or off according to . This process is shown in the right-hand part of Figure A1. The details of this process are shown below:Figure A1. The workflow of system.
- (1)
- If is less than 20% of the chiller cooling capacity (CC) that one chiller can offer, the system will be turned off;
- (2)
- If is more than 20% of the rated refrigerating capacity that one chiller can offer and less than the refrigerating capacity that all the chillers can offer, namely 4 × CC, we will turn on the system, and the number of chillers is decided by the minimum , which can make , and is the number of chillers we turn on. can be calculated by Equation (A1).where “” represents exact division. No matter how many chillers we turn on, the assigned to each chiller is the same. As for cooling water pumps and the cooling towers, we turn on 2 and 4, respectively.
- (3)
- If is more than 4 × CC, we turn on all the chillers, cooling water pumps, and cooling towers, namely 4, 3, 7, respectively.
- We use the DF-DQN controller to control cooling water pumps and cooling towers, select the frequency of them, and combine them into an action . The system COP, reward in RL, can be observed after executing the action. The action is selected by policy;
- Then we train our DF-DQN agent;
- Transfer to next state ;
- End the current learning and move to step (A).
Appendix B
| Energy Saving (Compared to Baseline Control) | ||||
|---|---|---|---|---|
| Year | DQN | DF-DQN | DF-DQN (False Label) | Model-Based Control |
| 1st | −29.996% | 8.074% | −10.022% | 13.755% |
| 2nd | −9.843% | 11.337% | −8.037% | 13.755% |
| 3rd | 0.798% | 10.086% | −4.224% | 13.755% |
| 4th | 11.362% | 11.273% | −5.659% | 13.755% |
| 5th | 12.195% | 11.157% | −5.191% | 13.755% |
| 6th | 11.752% | 11.677% | −2.374% | 13.755% |
| 7th | 11.879% | 11.480% | −3.465% | 13.755% |
| 8th | 12.503% | 11.578% | −2.349% | 13.755% |
| 9th | 8.957% | 11.757% | −3.350% | 13.755% |
| 10th | 11.908% | 11.580% | −1.934% | 13.755% |
| 11th | 12.440% | 11.636% | −2.274% | 13.755% |
| 12th | 11.195% | 10.299% | −2.866% | 13.755% |
| 13th | 11.763% | 10.879% | −2.266% | 13.755% |
| 14th | 10.893% | 10.311% | −3.364% | 13.755% |
| 15th | 11.461% | 12.168% | −3.754% | 13.755% |
| 16th | 12.042% | 11.855% | −2.420% | 13.755% |
| 17th | 10.967% | 11.850% | −7.476% | 13.755% |
| 18th | 12.583% | 10.639% | −3.268% | 13.755% |
| 19th | 12.490% | 10.893% | −3.704% | 13.755% |
| 20th | 12.094% | 10.177% | −4.094% | 13.755% |
| Average | 7.972% | 11.035% | −4.104% | 13.755% |
References
- Cao, X.; Dai, X.; Liu, J. Building energy-consumption status worldwide and the state-of-the-art technologies for zero-energy buildings during the past decade. Energy Build. 2016, 128, 198–213. [Google Scholar] [CrossRef]
- Taylor, S.T. Fundamentals of Design and Control of Central Chilled-Water Plants; ASHRAE Learning Institute: Atlanta, GA, USA, 2017. [Google Scholar]
- Wang, S.; Ma, Z. Supervisory and optimal control of building HVAC systems: A review. HVAC&R Res. 2008, 14, 3–32. [Google Scholar] [CrossRef]
- Wang, J.; Hou, J.; Chen, J.; Fu, Q.; Huang, G. Data mining approach for improving the optimal control of HVAC systems: An event-driven strategy. J. Build. Eng. 2021, 39, 102246. [Google Scholar] [CrossRef]
- Gholamzadehmir, M.; Del Pero, C.; Buffa, S.; Fedrizzi, R.; Aste, N. Adaptive-predictive control strategy for HVAC systems in smart buildings–A review. Sustain. Cities Soc. 2020, 63, 102480. [Google Scholar] [CrossRef]
- Zhu, N.; Shan, K.; Wang, S.; Sun, Y. An optimal control strategy with enhanced robustness for air-conditioning systems considering model and measurement uncertainties. Energy Build. 2013, 67, 540–550. [Google Scholar] [CrossRef]
- Heo, Y.; Choudhary, R.; Augenbroe, G.A. Calibration of building energy models for retrofit analysis under uncertainty. Energy Build. 2012, 47, 550–560. [Google Scholar] [CrossRef]
- Qiu, S.; Li, Z.; Li, Z.; Li, J.; Long, S.; Li, X. Model-free control method based on reinforcement learning for building cooling water systems: Validation by measured data-based simulation. Energy Build. 2020, 218, 110055. [Google Scholar] [CrossRef]
- Claessens, B.J.; Vanhoudt, D.; Desmedt, J.; Ruelens, F. Model-free control of thermostatically controlled loads connected to a district heating network. Energy Build. 2018, 159, 1–10. [Google Scholar] [CrossRef]
- Lork, C.; Li, W.T.; Qin, Y.; Zhou, Y.; Yuen, C.; Tushar, W.; Saha, T.K. An uncertainty-aware deep reinforcement learning framework for residential air conditioning energy management. Appl. Energy 2020, 276, 115426. [Google Scholar] [CrossRef]
- Ahn, K.U.; Park, C.S. Application of deep Q-networks for model-free optimal control balancing between different HVAC systems. Sci. Technol. Built Environ. 2020, 26, 61–74. [Google Scholar] [CrossRef]
- Brandi, S.; Piscitelli, M.S.; Martellacci, M.; Capozzoli, A. Deep reinforcement learning to optimise indoor temperature control and heating energy consumption in buildings. Energy Build. 2020, 224, 110225. [Google Scholar] [CrossRef]
- Du, Y.; Zandi, H.; Kotevska, O.; Kurte, K.; Munk, J.; Amasyali, K.; Mckee, E.; Li, F. Intelligent multi-zone residential HVAC control strategy based on deep reinforcement learning. Appl. Energy 2021, 281, 116117. [Google Scholar] [CrossRef]
- Ding, Z.; Fu, Q.; Chen, J.; Wu, H.; Lu, Y.; Hu, F. Energy-efficient control of thermal comfort in multi-zone residential HVAC via reinforcement learning. Connect. Sci. 2022, 34, 2364–2394. [Google Scholar] [CrossRef]
- Qiu, S.; Li, Z.; Li, Z.; Wu, Q. Comparative Evaluation of Different Multi-Agent Reinforcement Learning Mechanisms in Condenser Water System Control. Buildings 2022, 12, 1092. [Google Scholar] [CrossRef]
- Amasyali, K.; Munk, J.; Kurte, K.; Kuruganti, T.; Zandi, H. Deep reinforcement learning for autonomous water heater control. Buildings 2021, 11, 548. [Google Scholar] [CrossRef]
- Li, B.; Xia, L. A multi-grid reinforcement learning method for energy conservation and comfort of HVAC in buildings. In Proceedings of the 2015 IEEE International Conference on Automation Science and Engineering (CASE), Gothenburg, Sweden, 24–28 August 2015; pp. 444–449. [Google Scholar] [CrossRef]
- Yu, Z.; Yang, X.; Gao, F.; Huang, J.; Tu, R.; Cui, J. A Knowledge-based reinforcement learning control approach using deep Q network for cooling tower in HVAC systems. In Proceedings of the 2020 Chinese Automation Congress, CAC 2020, Shanghai, China, 6–8 November 2020; pp. 1721–1726. [Google Scholar] [CrossRef]
- Fu, Q.; Chen, X.; Ma, S.; Fang, N.; Xing, B.; Chen, J. Optimal control method of HVAC based on multi-agent deep reinforcement learning. Energy Build. 2022, 270, 112284. [Google Scholar] [CrossRef]
- Yang, L.; Nagy, Z.; Goffin, P.; Schlueter, A. Reinforcement learning for optimal control of low exergy buildings. Appl. Energy 2015, 156, 577–586. [Google Scholar] [CrossRef]
- Sutton, R.; Barto, A. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA; London, UK, 2018. [Google Scholar]
- Zhou, Z.H.; Feng, J. Deep forest. Natl. Sci. Rev. 2019, 6, 74–86. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Fu, Q.; Han, Z.; Chen, J.; Lu, Y.; Wu, H.; Wang, Y. Applications of reinforcement learning for building energy efficiency control: A review. J. Build. Eng. 2022, 50, 104165. [Google Scholar] [CrossRef]
- Fu, Q.; Li, K.; Chen, J.; Wang, J. A Novel Deep-forest-based DQN method for Building Energy Consumption Prediction. Buildings 2022, 12, 131. [Google Scholar] [CrossRef]
- Li, Z.; Huang, G.; Sun, Y. Stochastic chiller sequencing control. Energy Build. 2014, 84, 203–213. [Google Scholar] [CrossRef]



| Parameters | Value |
|---|---|
| 1 | |
| 0.0001 | |
| 0.01 | |
| 0.01 | |
| 1000 | |
| 100 | |
| 0.01 |
| Energy Saving (Compared to Baseline Control) | ||
|---|---|---|
| Year | DF-DQN | DF-DQN (False Label) |
| 1st | 8.074% | −10.022% |
| 2nd | 11.337% | −8.037% |
| 3rd | 10.086% | −4.224% |
| 5th | 11.157% | −5.191% |
| 10th | 11.580% | −1.934% |
| 15th | 12.168% | −3.754% |
| 20th | 10.177% | −4.094% |
| Average (20 years) | 11.035% | −4.104% |
| Energy Saving (Compared to Baseline Control) | |||
|---|---|---|---|
| Year | DQN | DF-DQN | Model-Based Control |
| 1st | −29.996% | 8.074% | 13.755% |
| 2nd | −9.843% | 11.337% | 13.755% |
| 3rd | 0.798% | 10.086% | 13.755% |
| 5th | 12.195% | 11.157% | 13.755% |
| 10th | 11.908% | 11.580% | 13.755% |
| 15th | 11.461% | 12.168% | 13.755% |
| 20th | 12.094% | 10.177% | 13.755% |
| Average (20 years) | 7.972% | 11.035% | 13.755% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Z.; Fu, Q.; Chen, J.; Wang, Y.; Lu, Y.; Wu, H.; Gui, H. Deep Forest-Based DQN for Cooling Water System Energy Saving Control in HVAC. Buildings 2022, 12, 1787. https://doi.org/10.3390/buildings12111787
Han Z, Fu Q, Chen J, Wang Y, Lu Y, Wu H, Gui H. Deep Forest-Based DQN for Cooling Water System Energy Saving Control in HVAC. Buildings. 2022; 12(11):1787. https://doi.org/10.3390/buildings12111787
Chicago/Turabian StyleHan, Zhicong, Qiming Fu, Jianping Chen, Yunzhe Wang, You Lu, Hongjie Wu, and Hongguan Gui. 2022. "Deep Forest-Based DQN for Cooling Water System Energy Saving Control in HVAC" Buildings 12, no. 11: 1787. https://doi.org/10.3390/buildings12111787
APA StyleHan, Z., Fu, Q., Chen, J., Wang, Y., Lu, Y., Wu, H., & Gui, H. (2022). Deep Forest-Based DQN for Cooling Water System Energy Saving Control in HVAC. Buildings, 12(11), 1787. https://doi.org/10.3390/buildings12111787