Numerical Study on Static and Dynamic Load Response of Temporary Support System for Group Tunnels Excavation
Abstract
1. Introduction
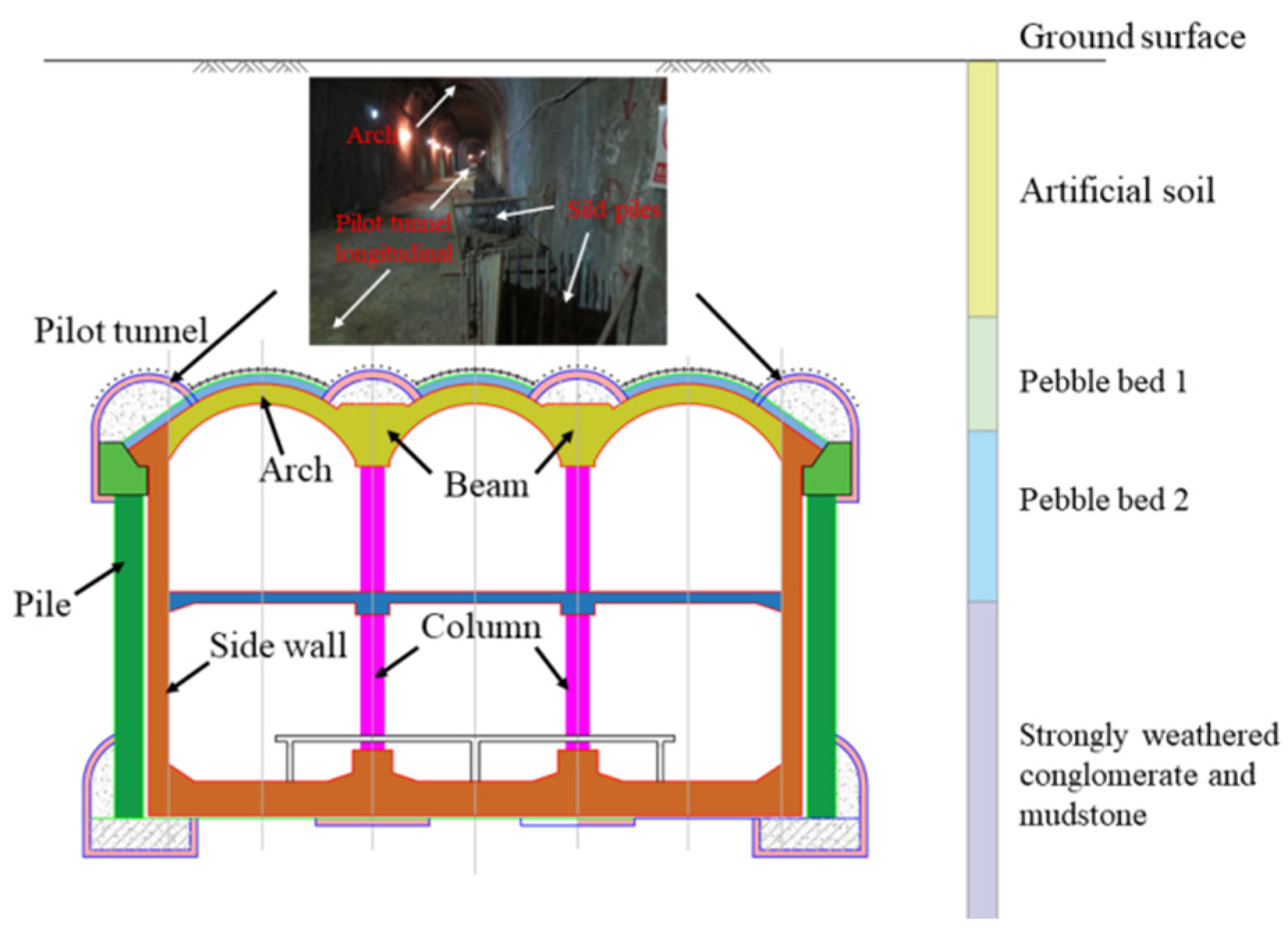
2. Project Overview
3. Static Response of the Pilot Tunnels Excavation
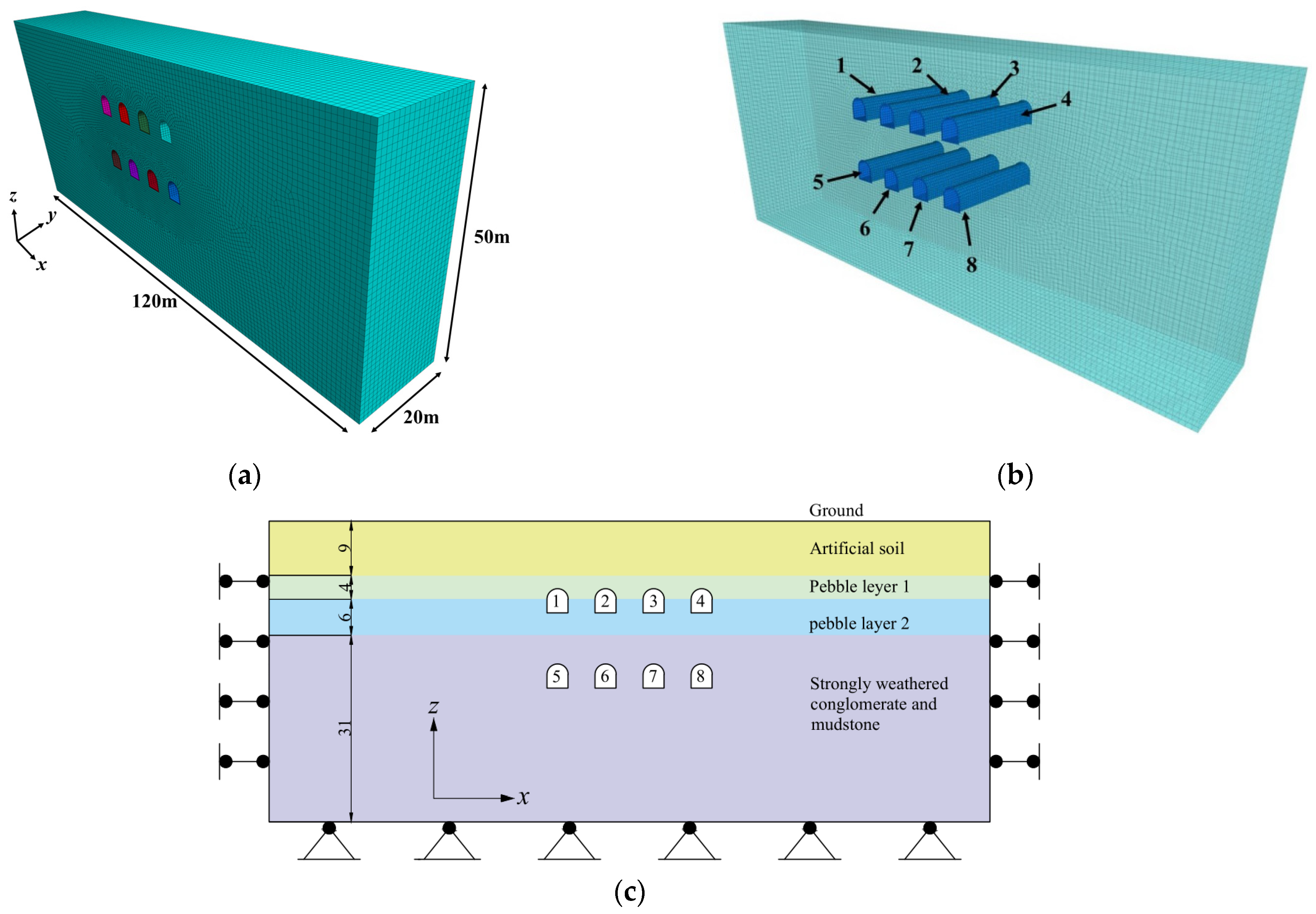
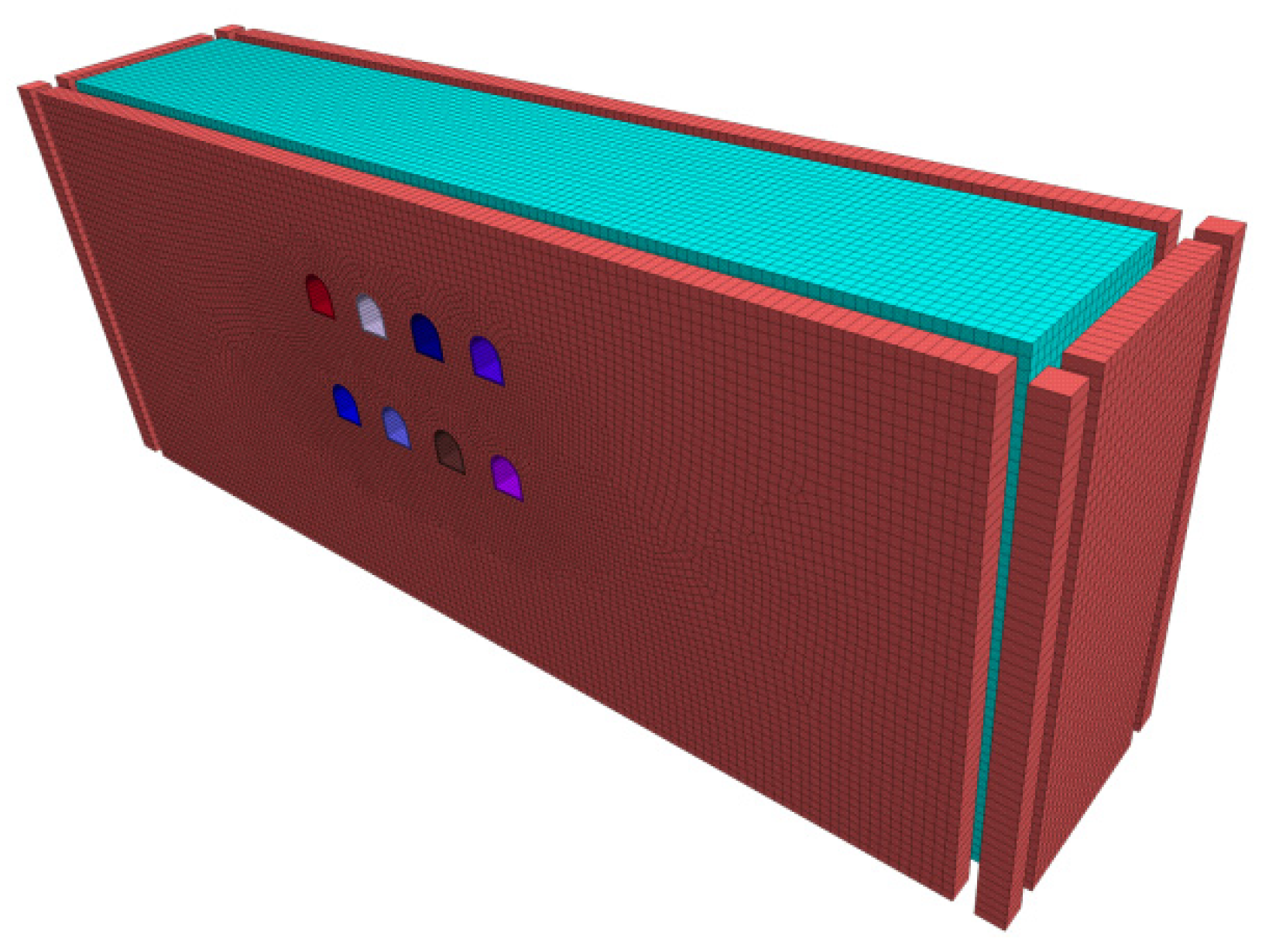
3.1. Numerical Model
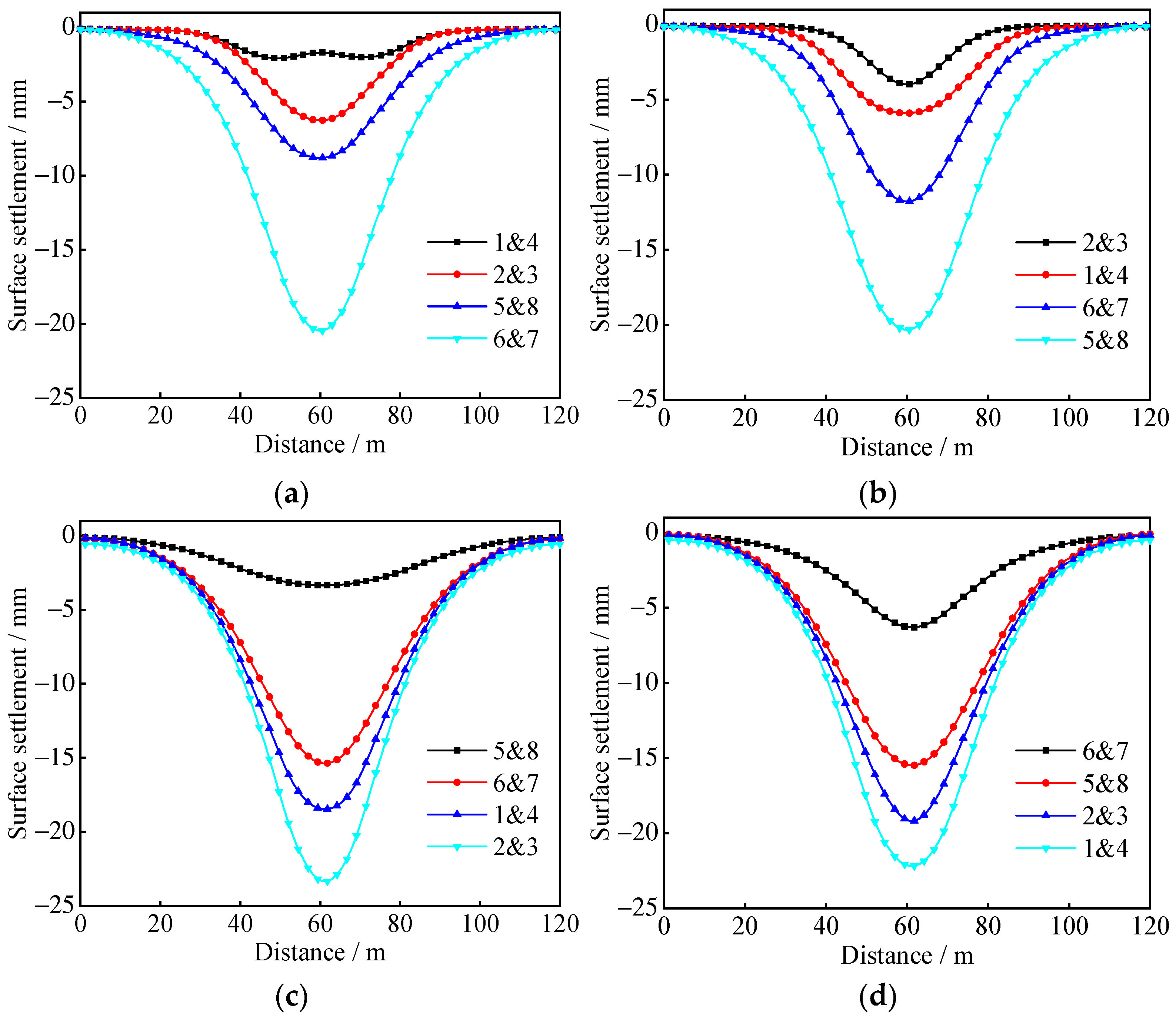
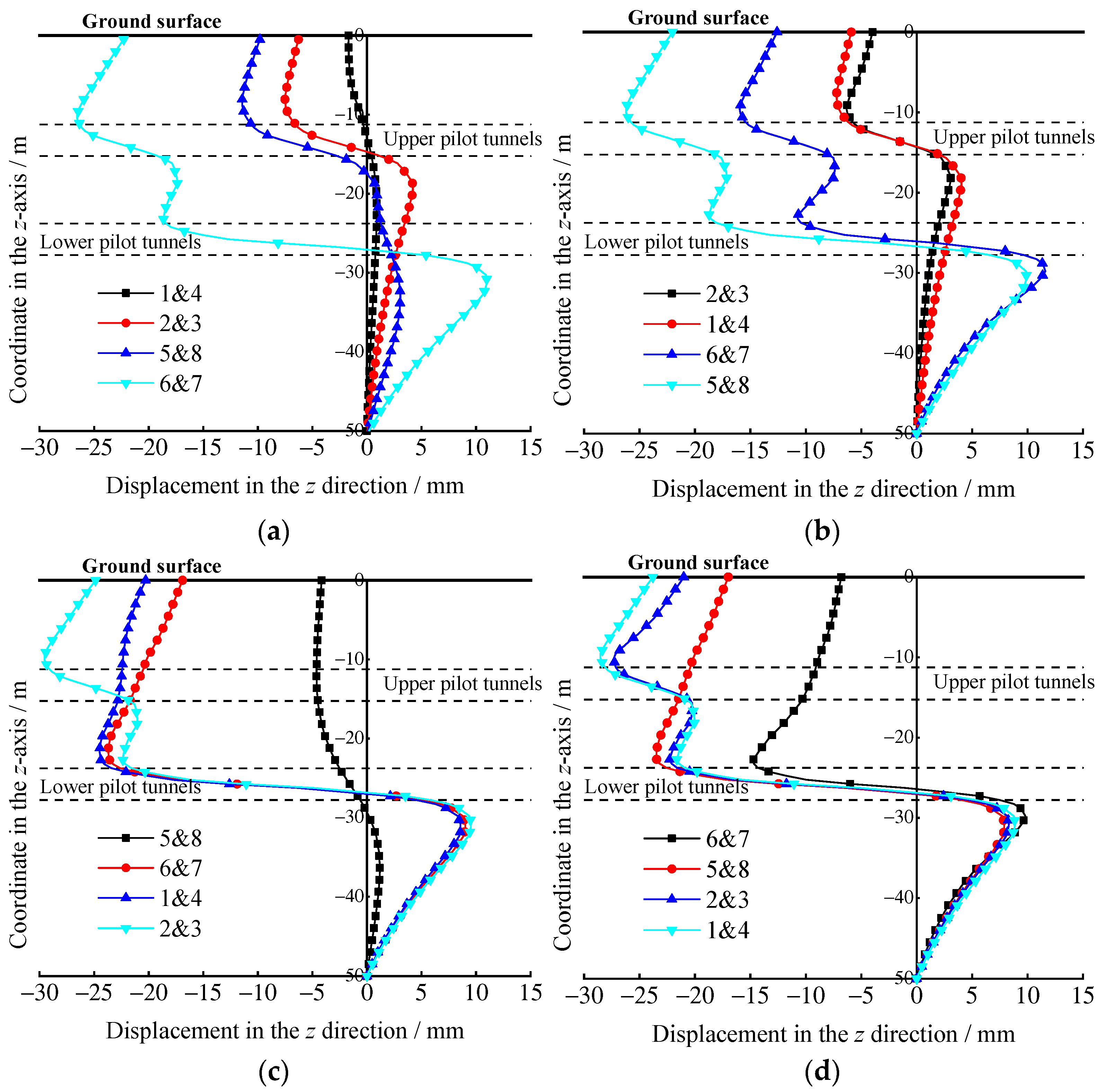
3.2. Selection of Excavation Plan
3.3. Ground Surface Settlement Analysis
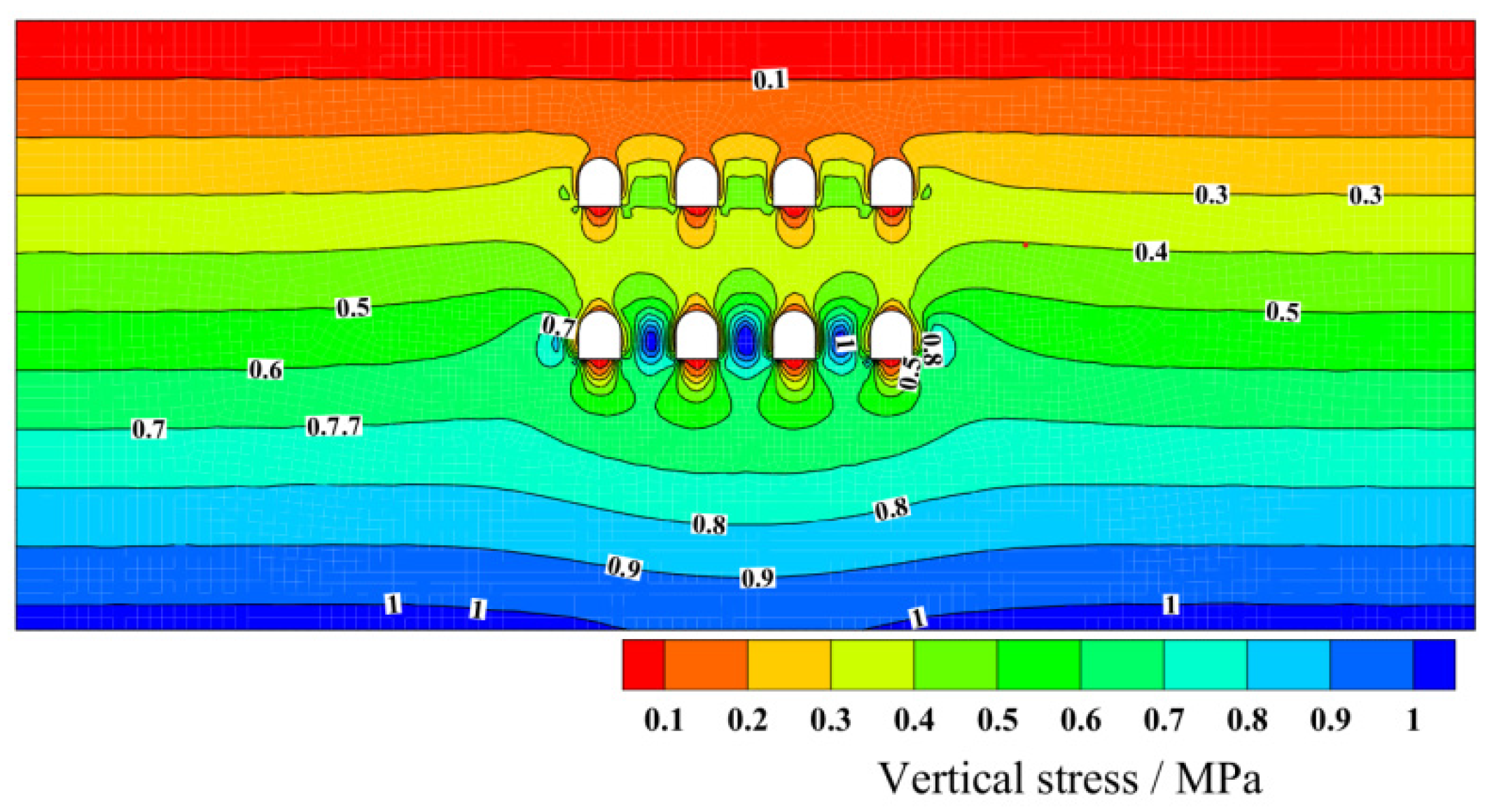
3.4. Ground Settlement Analysis
3.5. Settlement Control Measures
4. Dynamic Response on Group Tunnels
4.1. Establishment of the Dynamic Simulation Model
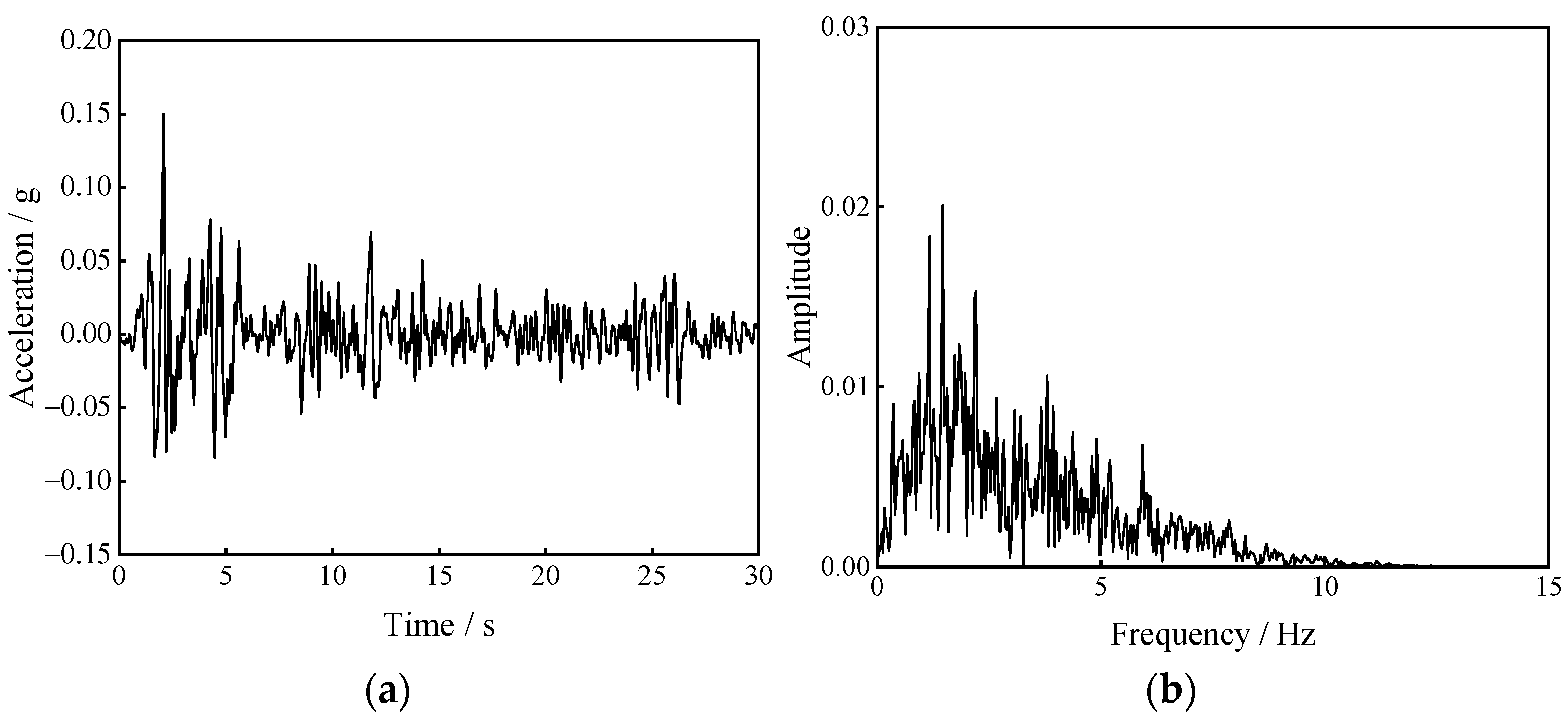
4.2. Dynamic Wave Input
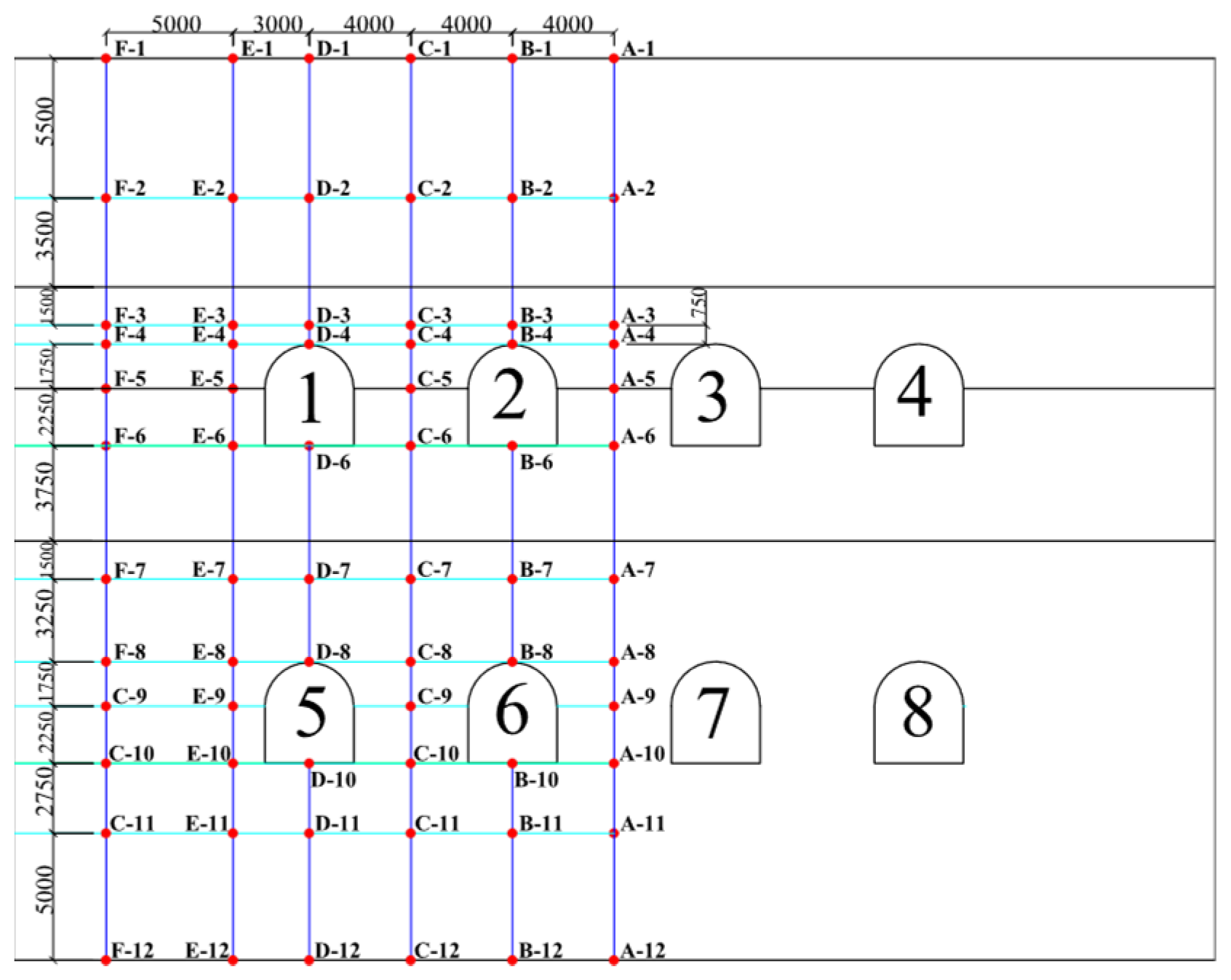
4.3. Setting Monitoring Points
4.4. Simulation Results and Analysis
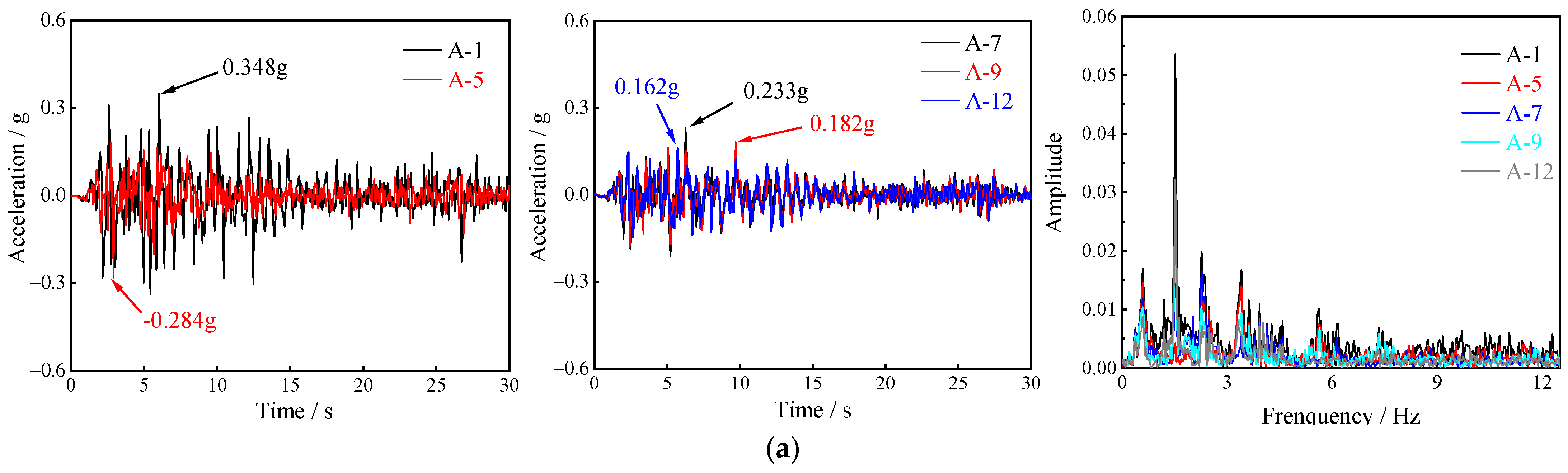
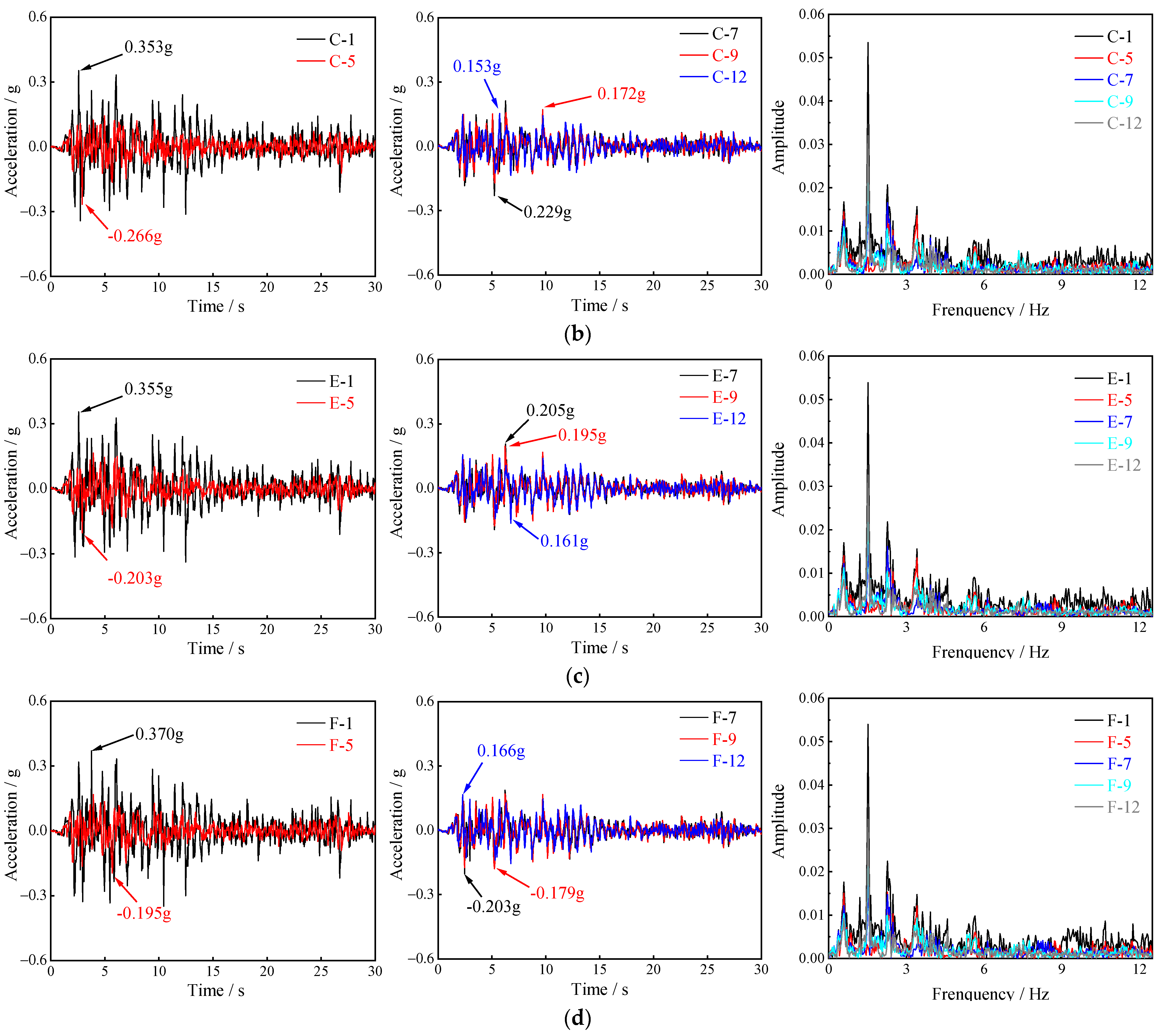
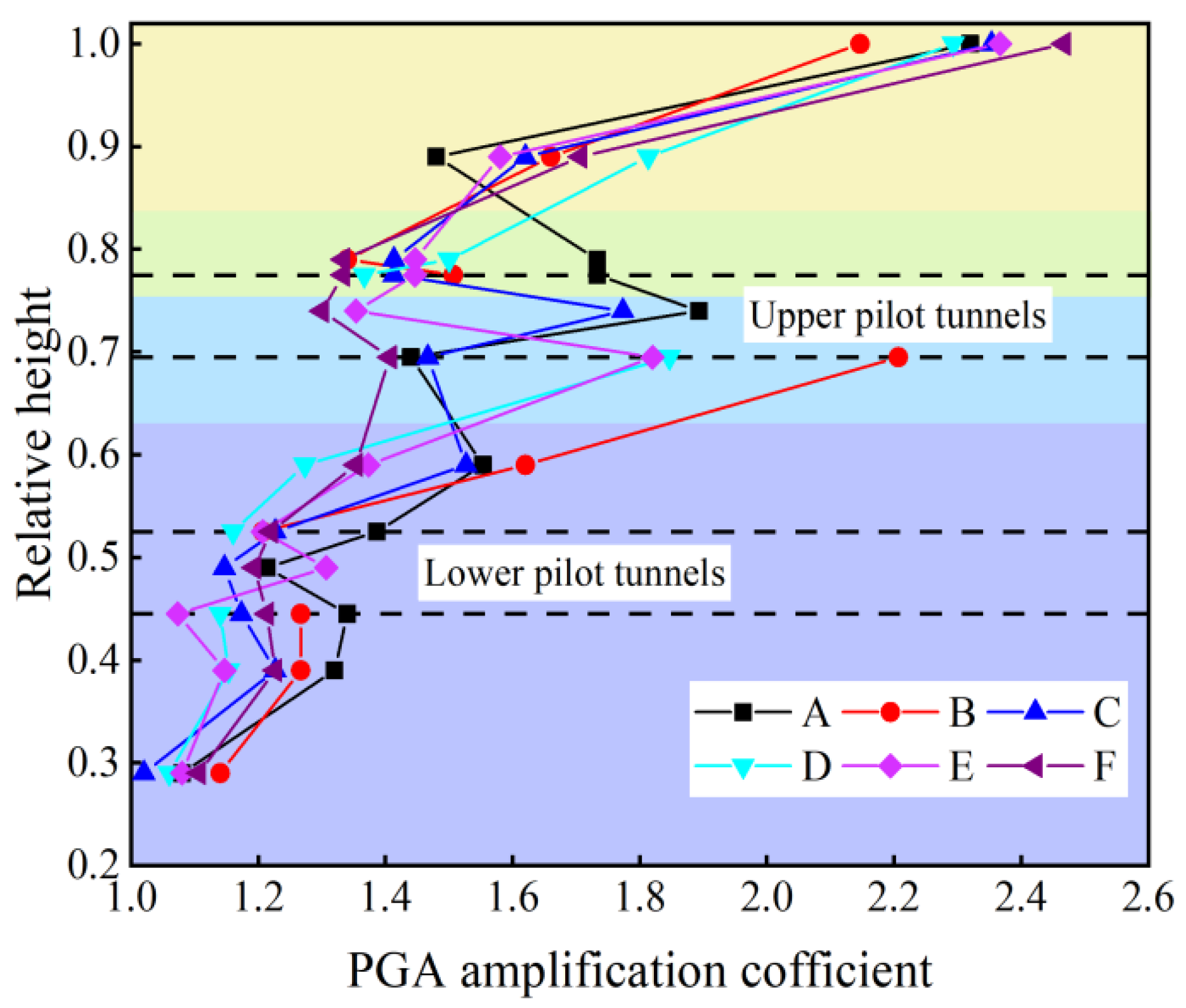
4.4.1. Acceleration Response Analysis
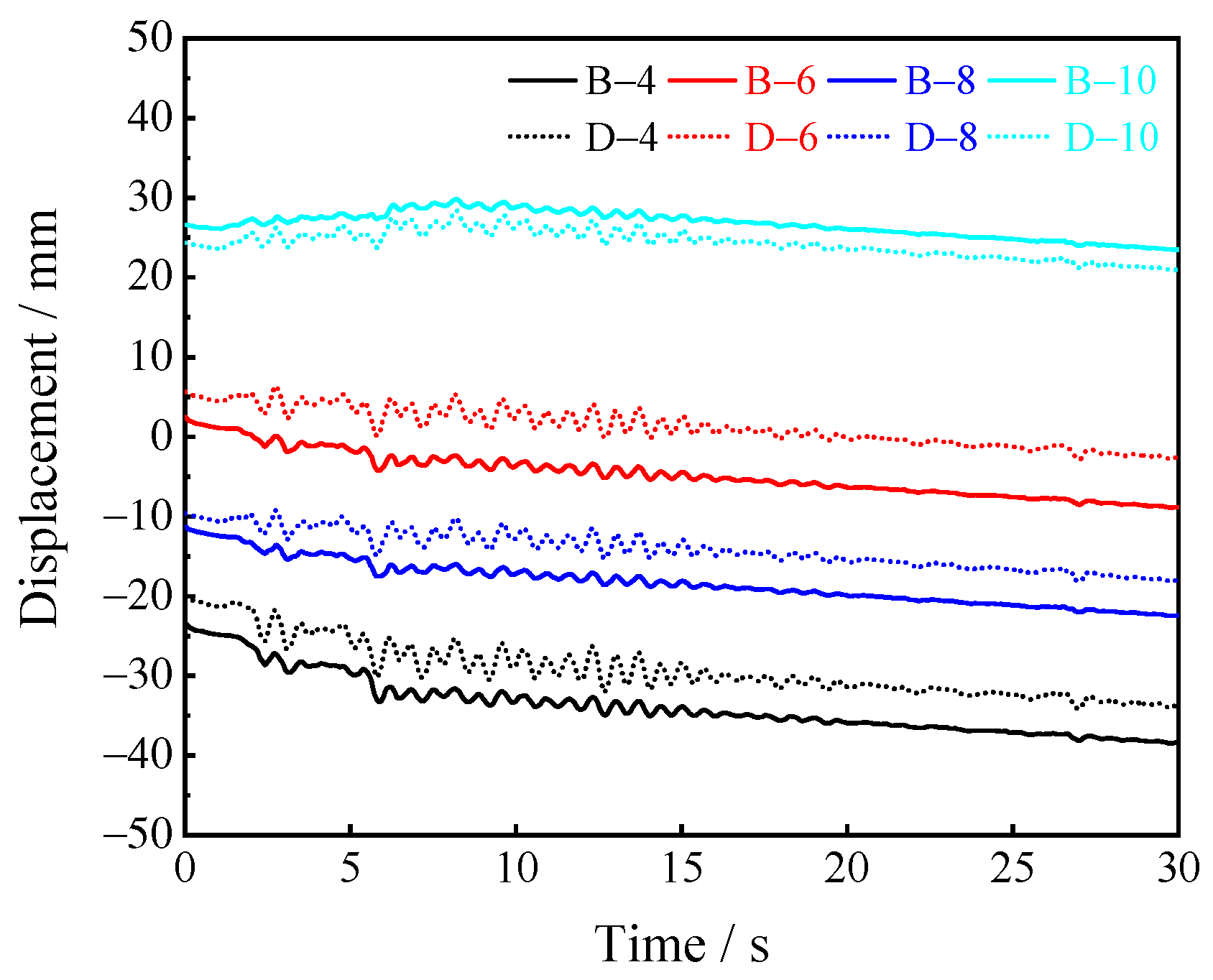
4.4.2. Displacement Response Analysis
5. Conclusions and Discussion
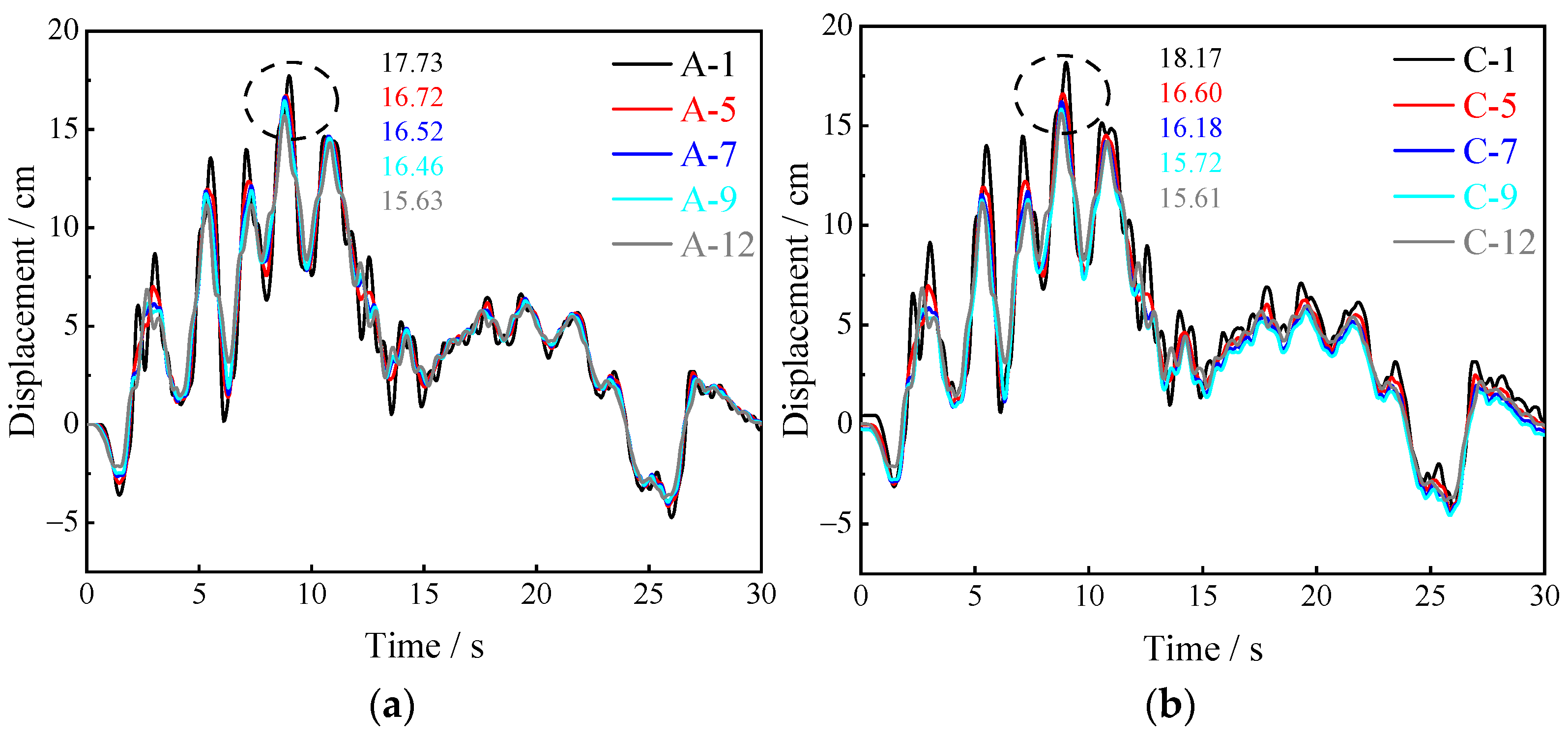
- (a)
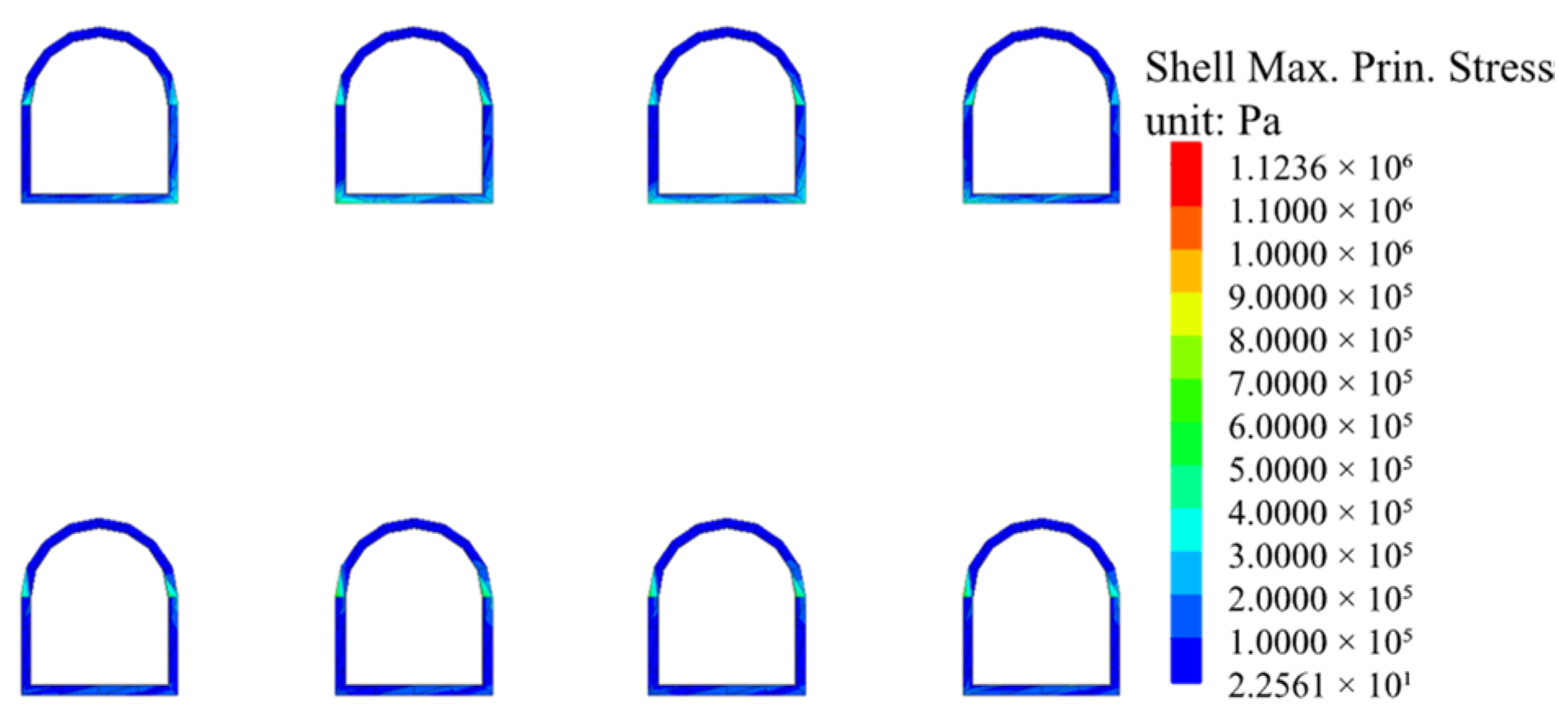
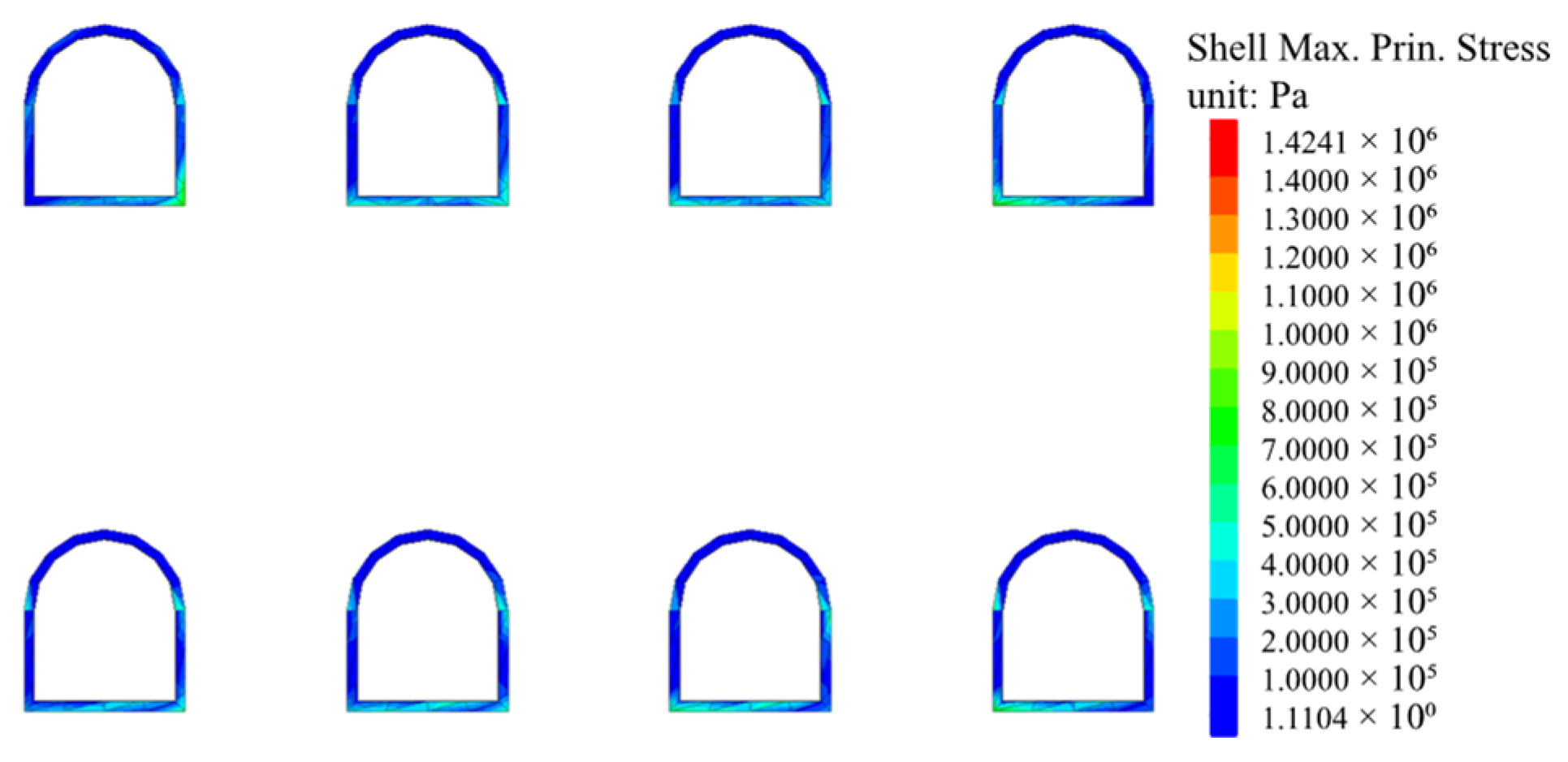
- During the excavation of the pilot tunnels, different excavation sequences cause different ground settlements and ground displacements. For the eight pilot tunnels in this study, the excavation sequence of 2&3→1&4→6&7→5&8 of Plan 2 results in the smallest surface settlement of 20.3 mm. For ground displacement, excavating the upper pilot tunnels first and then the lower pilot tunnels can reduce settlement, which will be larger in the lower pilot tunnels excavation. The maximum principal stress of the lining structure is primarily concentrated at the foot of the arch of the pilot tunnels after the excavation of the pilot tunnels, and the maximum principal stress value is 1.124 MPa. In the construction process, the support strength can be improved, and the soil can be reinforced to reduce the ground displacement.
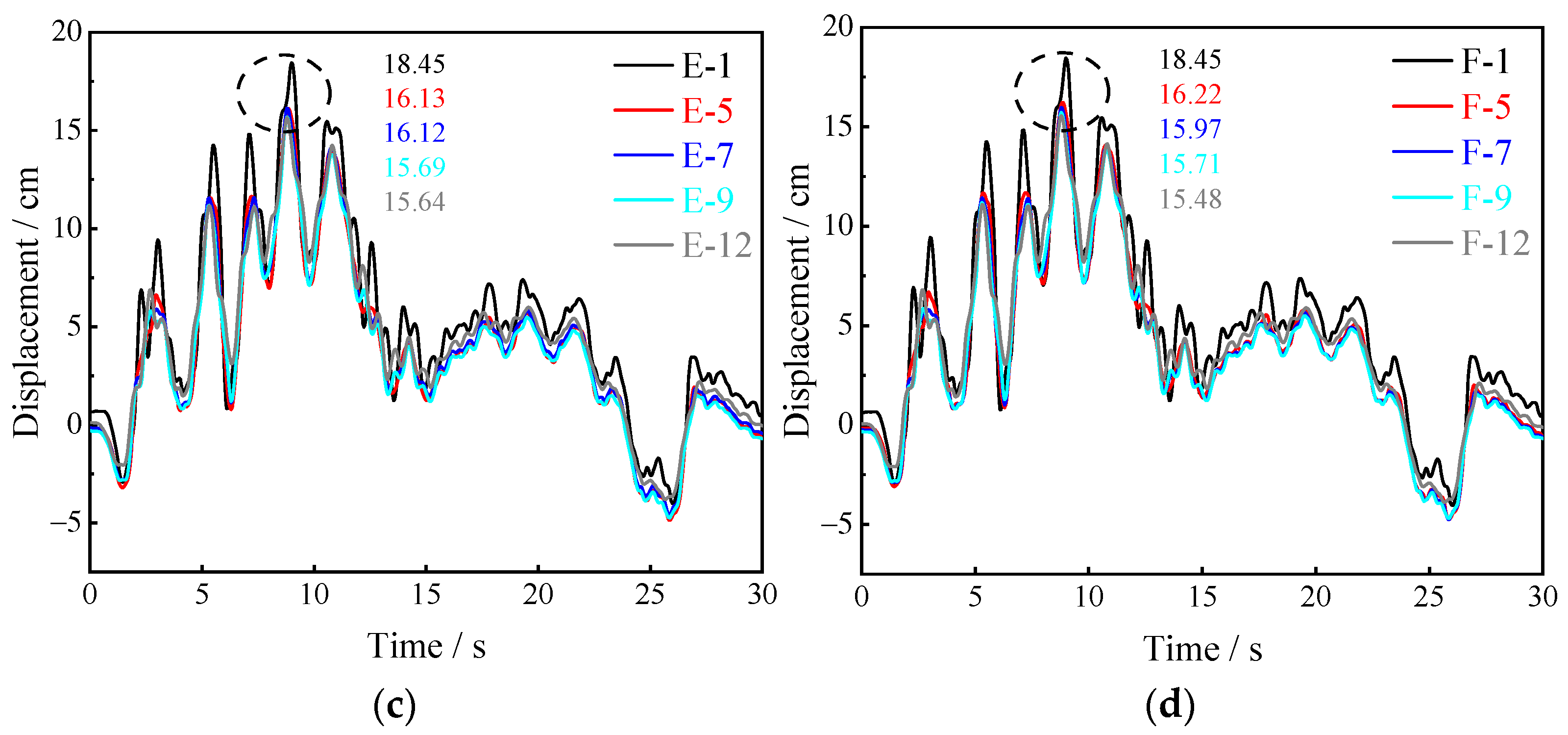
- (b)
- After the excavation of the pilot tunnels is completed, due to the coupling effect of the complex stratum and the pilot tunnel lining structure, the horizontal PGA amplification coefficient propagated along the relative height tends to increase with significant nonlinear characteristics under the 0.15 g EI Centro wave excitation. The same phenomenon exists for the peak horizontal absolute displacements. The amplitude leads to a significant amplification effect at a certain frequency, which is nearly 1.5 Hz. The horizontal PGA amplification coefficient at the surface is the largest, and the upper pilot tunnel is significantly affected by the horizontal acceleration, which should be the vital observed object in the seismic design.
- (c)
- Under seismic excitation, the displacement component will be generated in the vertical direction under the horizontal seismic action, and new surface settlement will be generated continuously. Lastly, a settlement trough similar to that after the excavation will be formed. The ground displacement close to the upper pilot tunnels is even larger. In addition, the maximum principal stress is largely concentrated at the foot of the arch of the pilot tunnels and the bottom corner point of the upper and lower pilot tunnels, and the maximum principal stress value is 1.424 MPa. It is necessary to strengthen the support of the arch foot and bottom corner of the pilot tunnels in the seismic design.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lv, J.; Li, X.; Li, Z.; Fu, H. Numerical simulations of construction of shield tunnel with small clearance to adjacent tunnel without and with isolation pile reinforcement. KSCE J. Civ. Eng. 2020, 24, 295–309. [Google Scholar] [CrossRef]
- Cao, L.; Fang, Q.; Zhang, D.; Chen, T. Subway station construction using combined shield and shallow tunnelling method: Case study of Gaojiayuan station in Beijing. Tunn. Undergr. Space Technol. 2018, 82, 627–635. [Google Scholar] [CrossRef]
- Liu, H.; Song, E. Seismic response of large underground structures in liquefiable soils subjected to horizontal and vertical earthquake excitations. Comput. Geotech. 2005, 32, 223–244. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Qu, W.; Tu, Y. Internal force calculation and supporting parameters sensitivity analysis of side piles in the subway station excavated by Pile-Beam-Arch method. Tunn. Undergr. Space Technol. 2016, 56, 186–201. [Google Scholar] [CrossRef]
- Guan, Y.; Zhao, W.; Li, S.; Zhang, G. Key Techniques and Risk Management for the Application of the Pile-Beam-Arch (PBA) Excavation Method: A case study of Zhongjie subway station. Sci. World J. 2014, 2014, 275362. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Wang, J. Ground movement prediction for tunnels using simplified procedure. Tunn. Undergr. Space Technol. 2011, 26, 462–471. [Google Scholar] [CrossRef]
- Chakeri, H.; Ozcelik, Y.; Unver, B. Effects of important factors on surface settlement prediction for metro tunnel excavated by EPB. Tunn. Undergr. Space Technol. 2013, 36, 14–23. [Google Scholar] [CrossRef]
- Xu, Y.; Tang, B.; Duan, Y. Research on Surface Settlement of Subway Station Construction Using Pile-Beam-Arch Approach. IOP Conf. Ser. Earth Environ. Sci. 2020, 455, 012167. [Google Scholar] [CrossRef]
- Kivi, A.; Sadaghiani, M.; Ahmadi, M. Numerical modeling of ground settlement control of large span underground metro station in Tehran Metro using Central Beam Column (CBC) structure. Tunn. Undergr. Space Technol. 2012, 28, 1–9. [Google Scholar] [CrossRef]
- Zeng, Y.; Bai, Y.; Zou, Y.; Huang, B. Numerical Study on Stratigraphic and Structural Deformation Patterns Considering Surface Load with Pile-Beam-Arch Method Construction. Symmetry 2022, 14, 1892. [Google Scholar] [CrossRef]
- Duenser, C.; Beer, G. Simulation of sequential excavation with the Boundary Element Method. Comput. Geotech. 2012, 44, 157–166. [Google Scholar] [CrossRef]
- Li, B.; Wang, Z. Numerical study on the response of ground movements to construction activities of a metro station using the pile-beam-arch method. Tunn. Undergr. Space Technol. 2019, 88, 209–220. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Yang, Z.; He, C. Numerical analysis on the mechanical performance of supporting structures and ground settlement characteristics in construction process of subway station built by pile-beam-arch method. KSCE J. Civ. Eng. 2017, 21, 1690–1705. [Google Scholar] [CrossRef]
- Guo, X.; Jiang, A.; Wang, S.; Gui, Y. Study on the Applicability of an Improved Pile-Beam-Arch Method of Metro Station Construction in the Upper-Soft and Lower-Hard Stratum. Adv. Civ. Eng. 2021, 2021, 6615016. [Google Scholar] [CrossRef]
- Huang, B.; Du, Y.; Zeng, Y.; Cao, B.; Zou, Y.; Yu, Q. Study on Stress Field Distribution during the Construction of a Group of Tunnels Using the Pile-Beam-Arch Method. Buildings 2022, 12, 300. [Google Scholar] [CrossRef]
- Stepinac, M.; Skokandić, D.; Ožić, K.; Zidar, M.; Vajdić, M. Condition Assessment and Seismic Upgrading Strategy of RC Structures-A Case Study of a Public Institution in Croatia. Buildings 2022, 12, 1489. [Google Scholar] [CrossRef]
- Shao, Q.; Ma, J.; Zhu, S. A System Dynamics Approach for Evaluating the Synergy Degree of Social Organizations Participating in Community and Home-Based Elderly Care Services. Buildings 2022, 12, 1491. [Google Scholar] [CrossRef]
- Jia, H.; Song, Y.; Chen, X.; Liu, S.; Zhang, B. Seismic Performance Evaluation of a High-Rise Building with Structural Irregularities. Buildings 2022, 12, 1484. [Google Scholar] [CrossRef]
- Yue, Y.; Li, C.; Jia, K.; Zhang, Y.; Tian, J. Optimization of the Seismic Performance of a Steel-Concrete Wind Turbine Tower with the Tuned Mass Damper. Buildings 2022, 12, 1474. [Google Scholar] [CrossRef]
- Chen, P.; Wu, X. Investigations on the Dynamic Response of Adjacent Buildings Connected by Viscous Dampers. Buildings 2022, 12, 1480. [Google Scholar] [CrossRef]
- Wang, W.; Wang, T.; Su, J.; Lin, C.; Seng, C.; Huang, T. Assessment of damage in mountain tunnels due to the Taiwan Chi-Chi Earthquake. Tunnelling Underg. Space Technol. 2001, 16, 133–150. [Google Scholar] [CrossRef]
- Miao, Y.; Zhong, Y.; Ruan, B.; Cheng, K.; Wang, G. Seismic response of a subway station in soft soil considering the structure-soil-structure interaction. Tunn. Undergr. Space Technol. 2020, 106, 103629. [Google Scholar] [CrossRef]
- Wang, J. Distribution of earthquake damage to underground facilities during the 1976 Tang-shan earthquake. Earthq. Spectra. 1985, 1, 741–757. [Google Scholar] [CrossRef]
- Yoo, J.; Park, J.; Park, D.; Lee, S. Seismic Response of Circular Tunnels in Jointed Rock. KSCE J. Civ. Eng. 2018, 22, 1121–1129. [Google Scholar] [CrossRef]
- Abate, G.; Massimino, R. Parametric analysis of the seismic response of coupled tunnel-soil-aboveground building systems by numerical modelling. Bull. Earthq. Eng. 2017, 15, 443–467. [Google Scholar] [CrossRef]
- Pitilakis, K.; Tsinidis, G.; Leanza, A.; Maugeri, M. Seismic behaviour of circular tunnels accounting forabove ground structures interaction effects. Soil Dyn. Earthq. Eng. 2014, 67, 1–15. [Google Scholar] [CrossRef]
- Lee, T.; Park, D.; Nguyen, D.; Park, J. Damage analysis of cut-and-cover tunnel structures under seismic loading. Bull. Earthq. Eng. 2016, 14, 413–431. [Google Scholar] [CrossRef]
- Argyroudis, S.; Pitilakis, K. Seismic fragility curves of shallow tunnels in alluvial deposits. Soil Dyn. Earthq. Eng. 2012, 35, 1–12. [Google Scholar] [CrossRef]
- Bobet, A. Effect of pore water pressure on tunnel support during static and seismic loading. Tunn. Undergr. Space Technol. 2003, 18, 377–393. [Google Scholar] [CrossRef]
- Alzabeebee, S. Seismic response and design of buried concrete pipes subjected to soil loads. Tunn. Undergr. Space Technol. 2019, 93, 103084. [Google Scholar] [CrossRef]
- Michael, G. Seismic Design and Analysis of Buried Culverts and Structures. J. Pipeline Syst. Eng. Pract. 2010, 1, 111–119. [Google Scholar] [CrossRef]
- Abuhajar, O.; El Naggar, H.; Newson, T. Seismic soil-culvert interaction. Can. Geotech. J. 2015, 52, 1649–1667. [Google Scholar] [CrossRef]
- Abuhajar, O.; El Naggar, H.; Newson, T. Experimental and numerical investigations of the effect of buried box culverts on earthquake excitation. Soil Dyn. Earthq. Eng. 2015, 79, 130–148. [Google Scholar] [CrossRef]
- Chen, C.; Wang, T.; Jeng, F.; Huang, T. Mechanisms causing seismic damage of tunnels at different depths. Tunn. Underg. Space Technol. 2012, 28, 31–40. [Google Scholar] [CrossRef]
- Xu, Z.; Du, X.; Xu, C.; Jiang, J.; Han, R. Simplified equivalent static methods for seismic analysis of shallow buried rectangular underground structures. Soil Dyn. Earthq. Eng. 2019, 121, 1–11. [Google Scholar] [CrossRef]
- Cilingir, U.; Madabhushi, S. Effect of depth on seismic response of circular tunnels. Can. Geotech. J. 2010, 48, 117–127. [Google Scholar] [CrossRef]
- Cilingir, U.; Madabhushi, S. Effect of depth on the seismic response of square tunnels. Soils Found. 2011, 51, 449–457. [Google Scholar] [CrossRef]
- Gazetas, G.; Psarropoulos, P.; Anastasopoulos, I.; Gerolymos, N. Seismic behaviour of flexible retaining systems subjected to short-duration moderately strong excitation. Soil Dyn. Earthq. Eng. 2004, 24, 537–550. [Google Scholar] [CrossRef]
- Tsinidis, G. Response characteristics of rectangular tunnels in soft soil subjected to transversal ground shaking. Tunn. Undergr. Space Technol. 2017, 62, 1–22. [Google Scholar] [CrossRef]
- Cilingir, U.; Madabhushi, S. A model study on the effects of input motion on the seismic behaviour of tunnels. Soil Dyn. Earthq. Eng. 2011, 31, 452–462. [Google Scholar] [CrossRef]
- Hatzigeorgiou, G.; Beskos, D. Soil-structure interaction effects on seismic inelastic analysis of 3D tunnels. Soil Dyn. Earthq. Eng. 2010, 30, 851–861. [Google Scholar] [CrossRef]
- Ma, C.; Lu, D.; Du, X.; Qi, C.; Zhang, X. Structural components functionalities and failure mechanism of rectangular underground structures during earthquakes. Soil Dyn. Earthq. Eng. 2019, 119, 265–280. [Google Scholar] [CrossRef]
- Ma, M.; Brady, B.H. Analysis of the dynamic performance of an underground excavation in jointed rock under re-peated seismic loading. Geotech. Geol. Eng. 1999, 17, 1–20. [Google Scholar] [CrossRef]
- Amorosi, A.; Boldini, D. Numerical modelling of the transverse dynamic behaviour of circular tunnels in clayey soils. Soil Dyn. Earthq. Eng. 2009, 29, 1059–1072. [Google Scholar] [CrossRef]
- Yang, D.; Naesgaard, E.; Byrne, P.; Adalier, K.; Abdoun, T. Numerical model verification and calibration of George Massey Tunnel using centrifuge models. Can. Geotech. J. 2004, 41, 921–942. [Google Scholar] [CrossRef]

| Items | Elastic Modulus (MPa) | Poisson’s Ratio | Cohesion (kPa) | Internal Friction Angle (°) | Density (kg·m−3) |
|---|---|---|---|---|---|
| Artificial soil | 23 | 0.3 | 10 | 18 | 1950 |
| Pebble bed 1 | 63 | 0.25 | 0.5 | 40 | 2070 |
| Pebble bed 2 | 75 | 0.23 | 0.8 | 32 | 2000 |
| strongly weathered conglomerate and mudstone | 105 | 0.26 | 0 | 35 | 2150 |
| Grid steel frame | 25,000 | 0.3 | - | - | 2300 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Y.; Huang, B.; Zou, Y.; Bai, Y. Numerical Study on Static and Dynamic Load Response of Temporary Support System for Group Tunnels Excavation. Buildings 2022, 12, 1719. https://doi.org/10.3390/buildings12101719
Zeng Y, Huang B, Zou Y, Bai Y. Numerical Study on Static and Dynamic Load Response of Temporary Support System for Group Tunnels Excavation. Buildings. 2022; 12(10):1719. https://doi.org/10.3390/buildings12101719
Chicago/Turabian StyleZeng, Yu, Bo Huang, Yu Zou, and Yao Bai. 2022. "Numerical Study on Static and Dynamic Load Response of Temporary Support System for Group Tunnels Excavation" Buildings 12, no. 10: 1719. https://doi.org/10.3390/buildings12101719
APA StyleZeng, Y., Huang, B., Zou, Y., & Bai, Y. (2022). Numerical Study on Static and Dynamic Load Response of Temporary Support System for Group Tunnels Excavation. Buildings, 12(10), 1719. https://doi.org/10.3390/buildings12101719






