Simplified Models to Capture the Effects of Restraints in Glass Balustrades under Quasi-Static Lateral Load or Soft-Body Impact
Abstract
1. Introduction
2. Research Study
2.1. Methodology and Goal
2.2. Reference Glass Balustrade
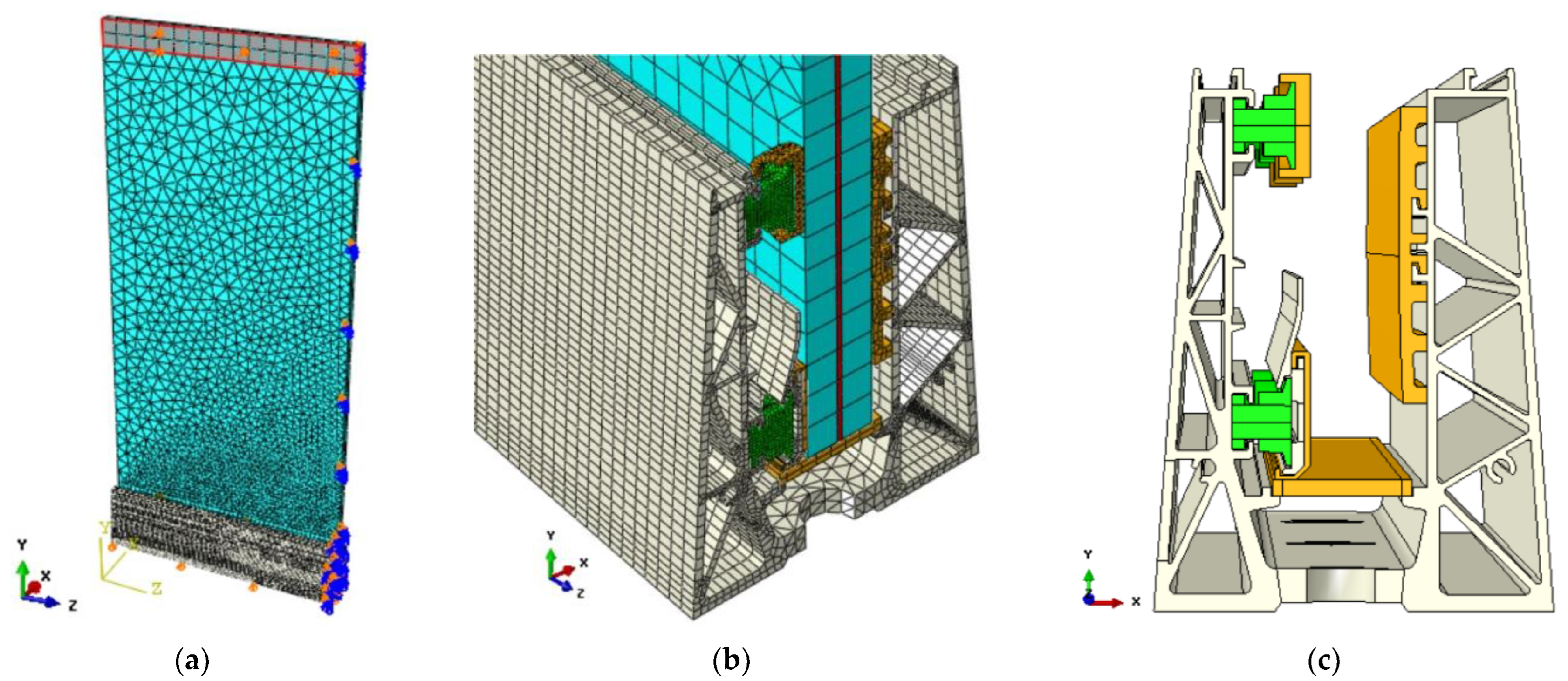
3. Full 3D Refined Numerical Model
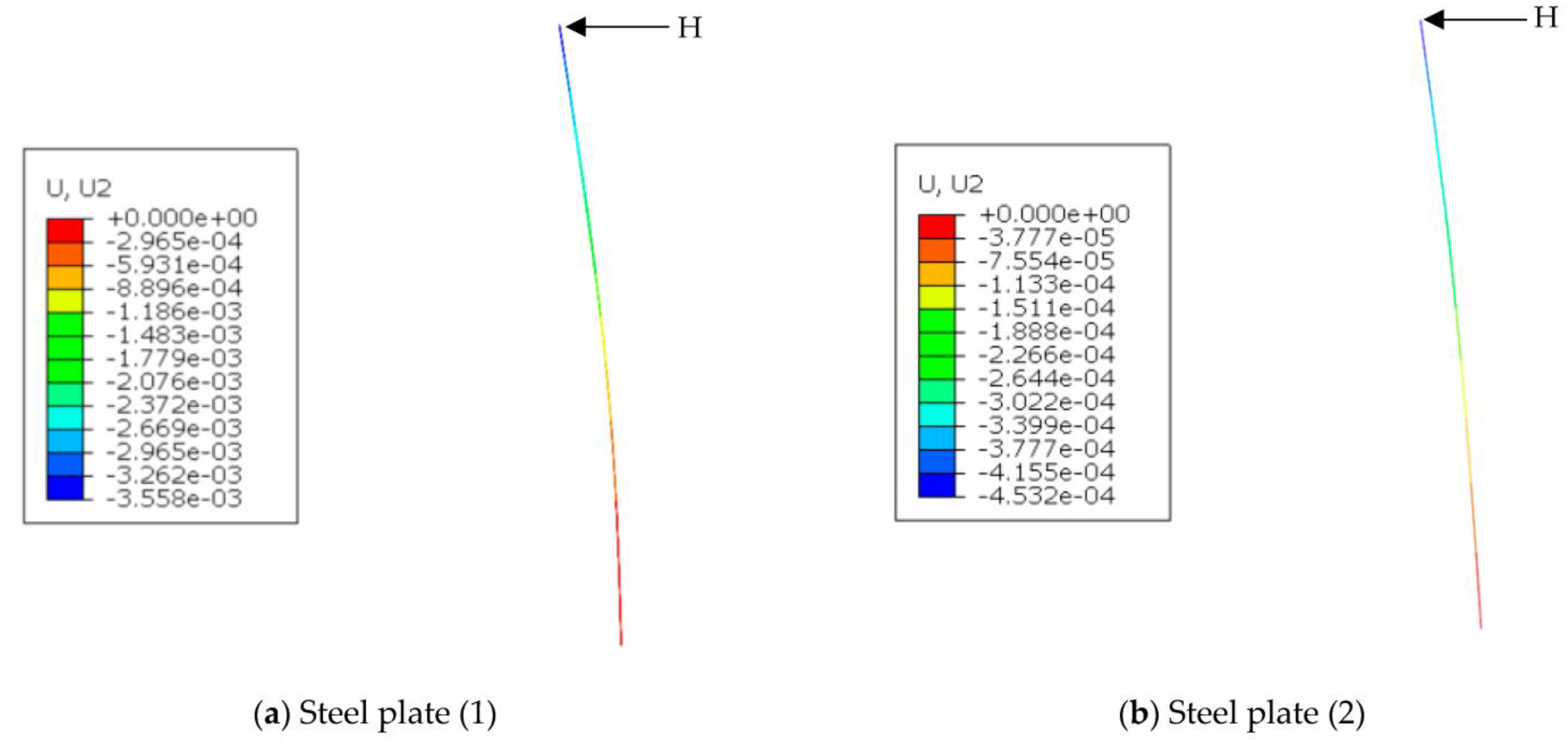
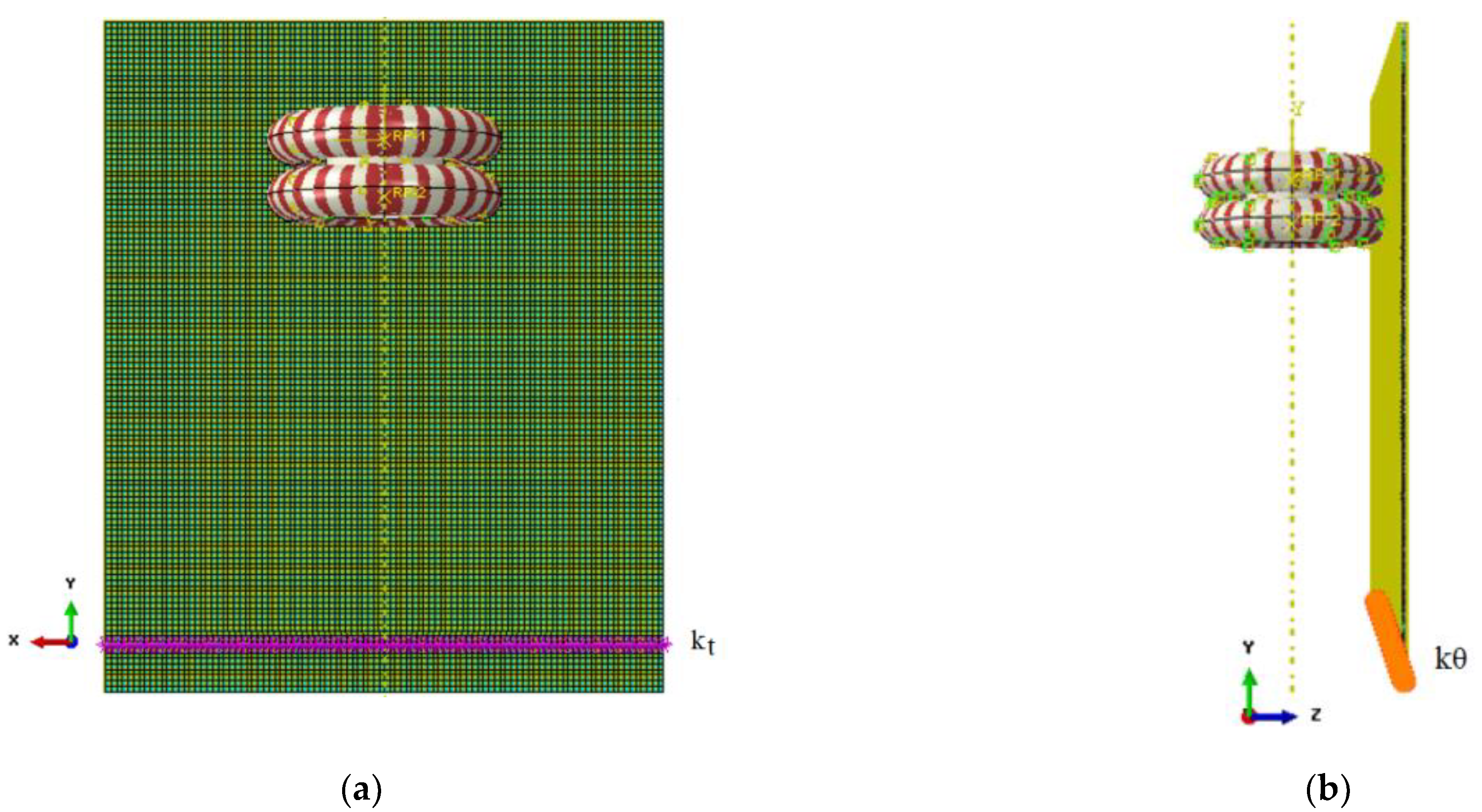
3.1. Model Description
- L1: a quasi-static, monotonically increasing lateral load at the top edge of the glass (until a maximum value P = 4.5 kN/m), and
- L2: a twin-tyre impact loading configuration which was numerically reproduced and calibrated according to the experimental setup summarized in Section 2 (with 300 mm being the drop height).
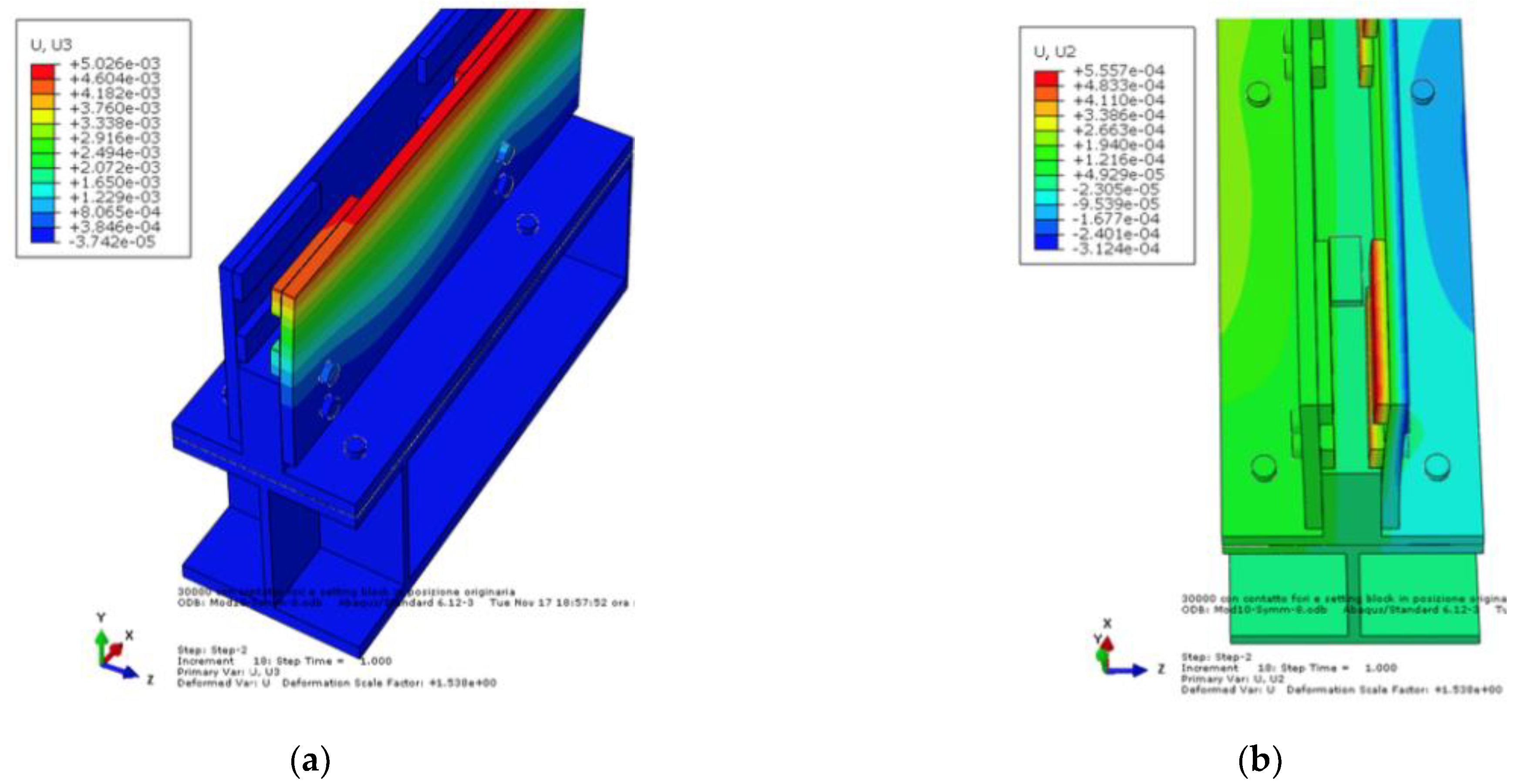
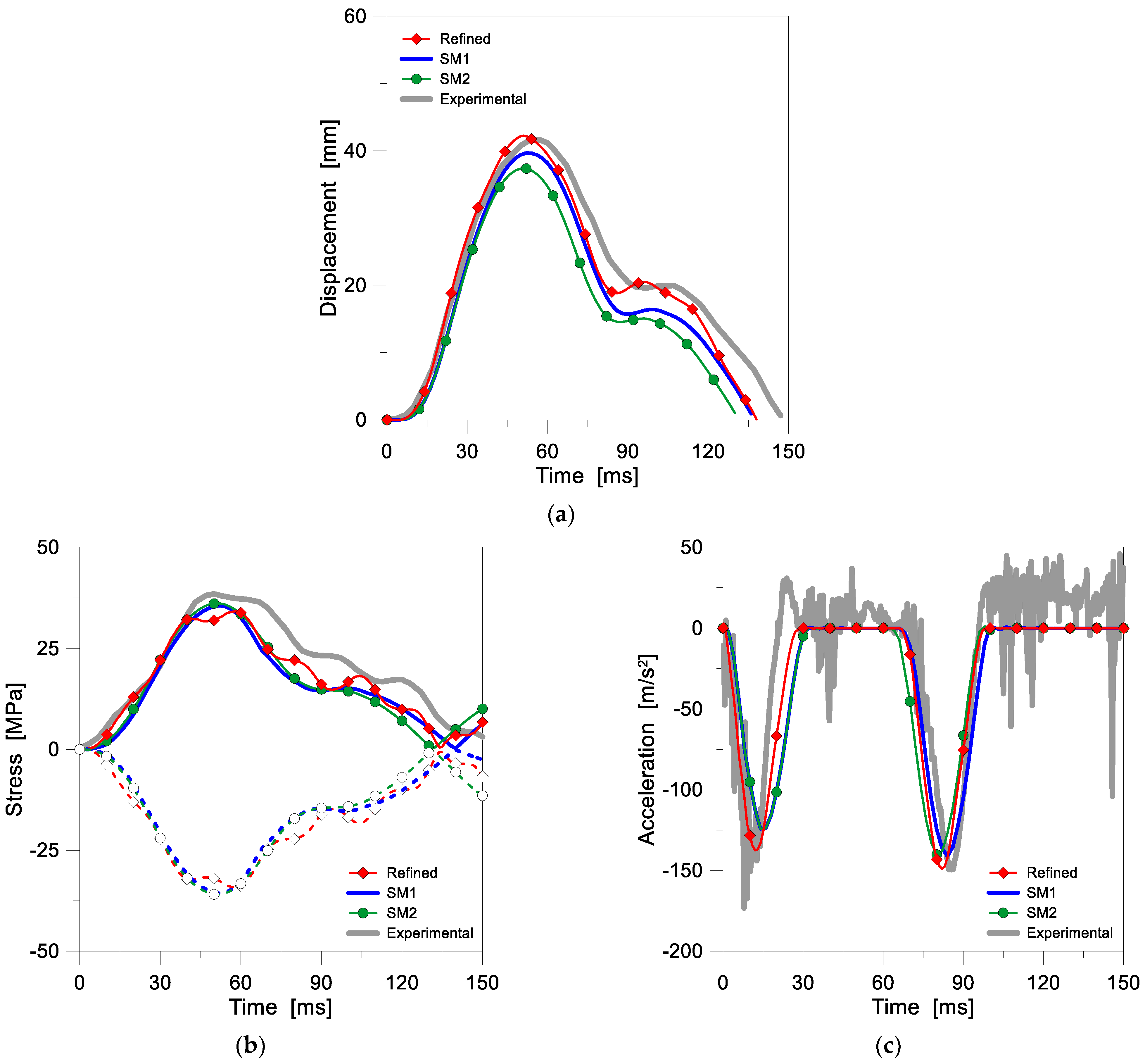
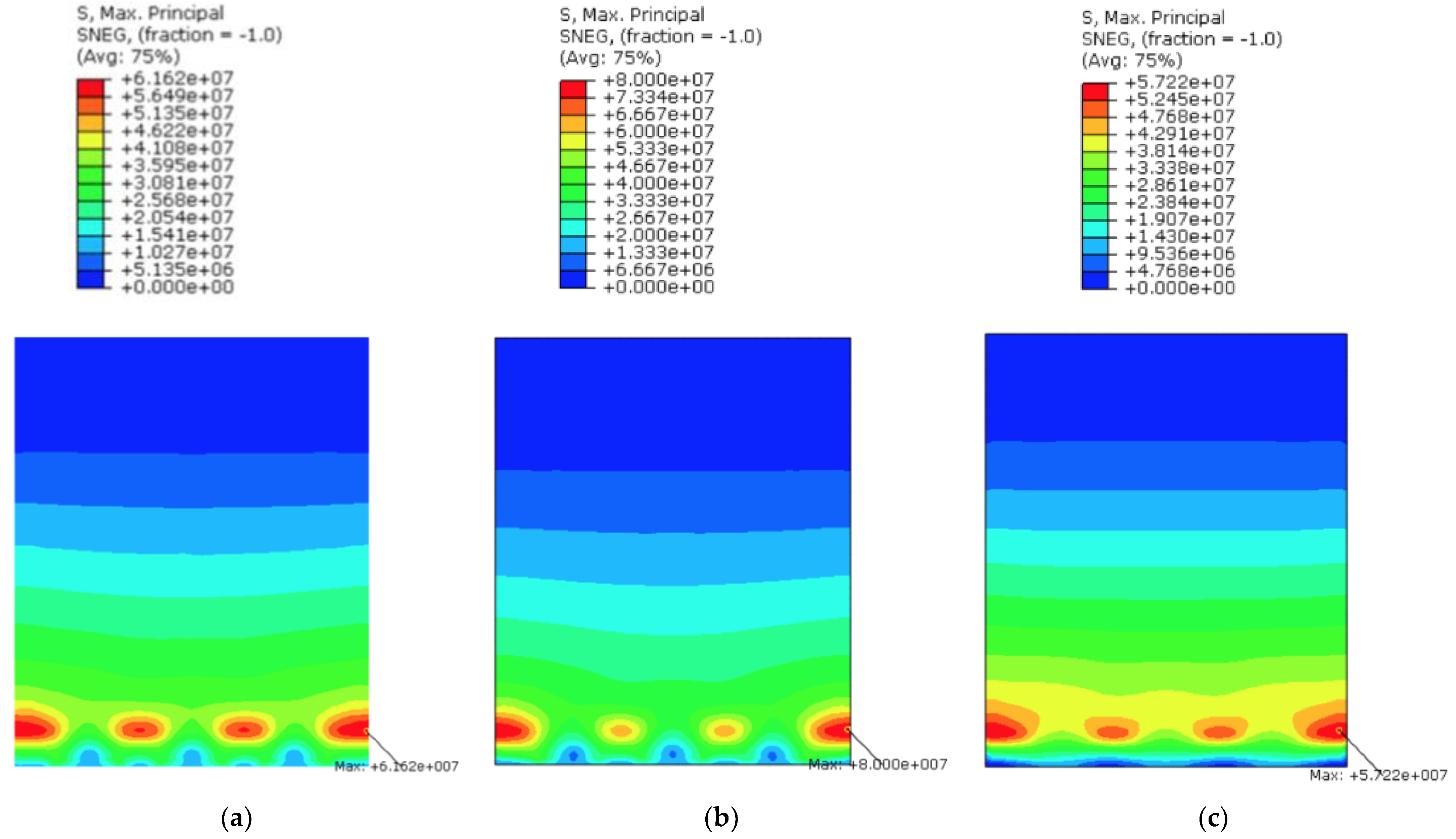
3.2. Results
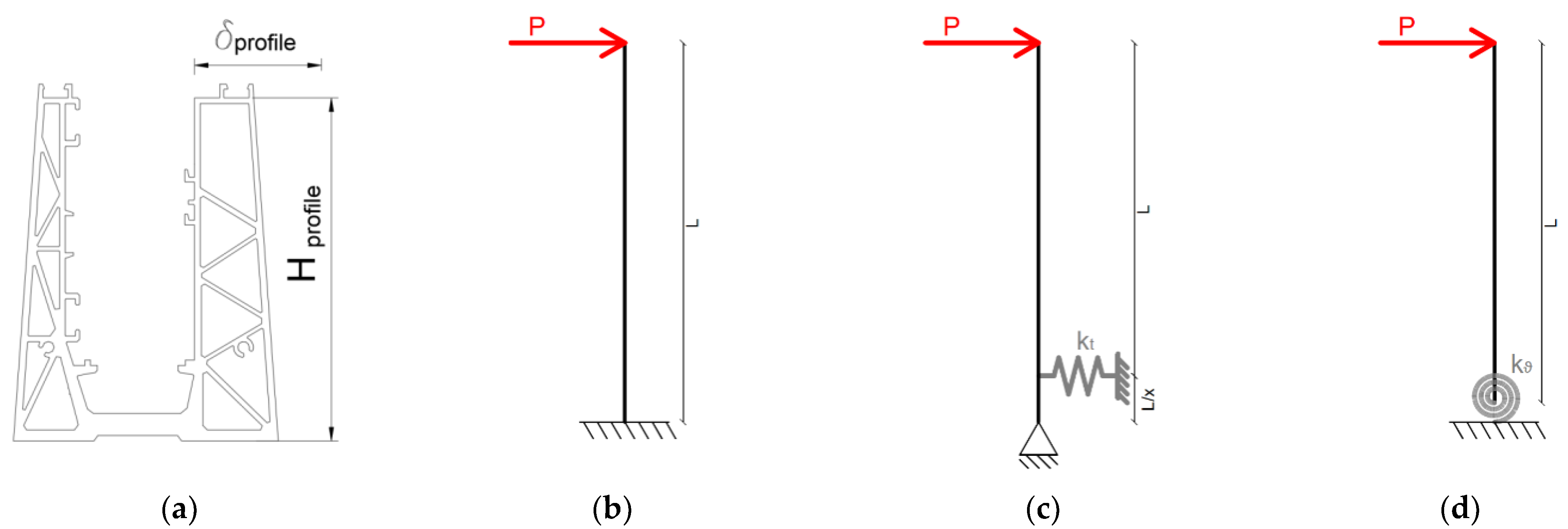
4. Derivation and Calibration of Simplified Numerical Models
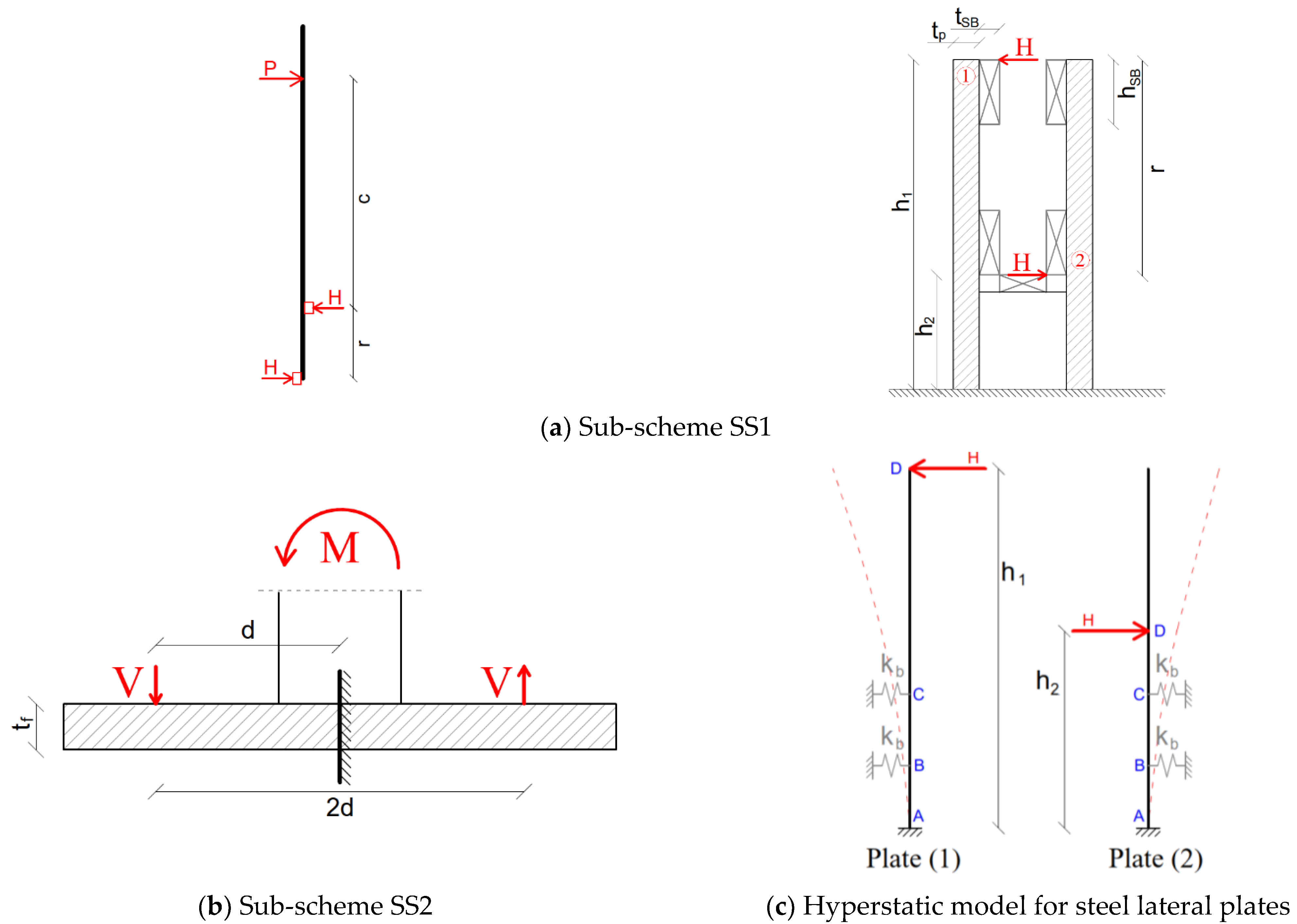
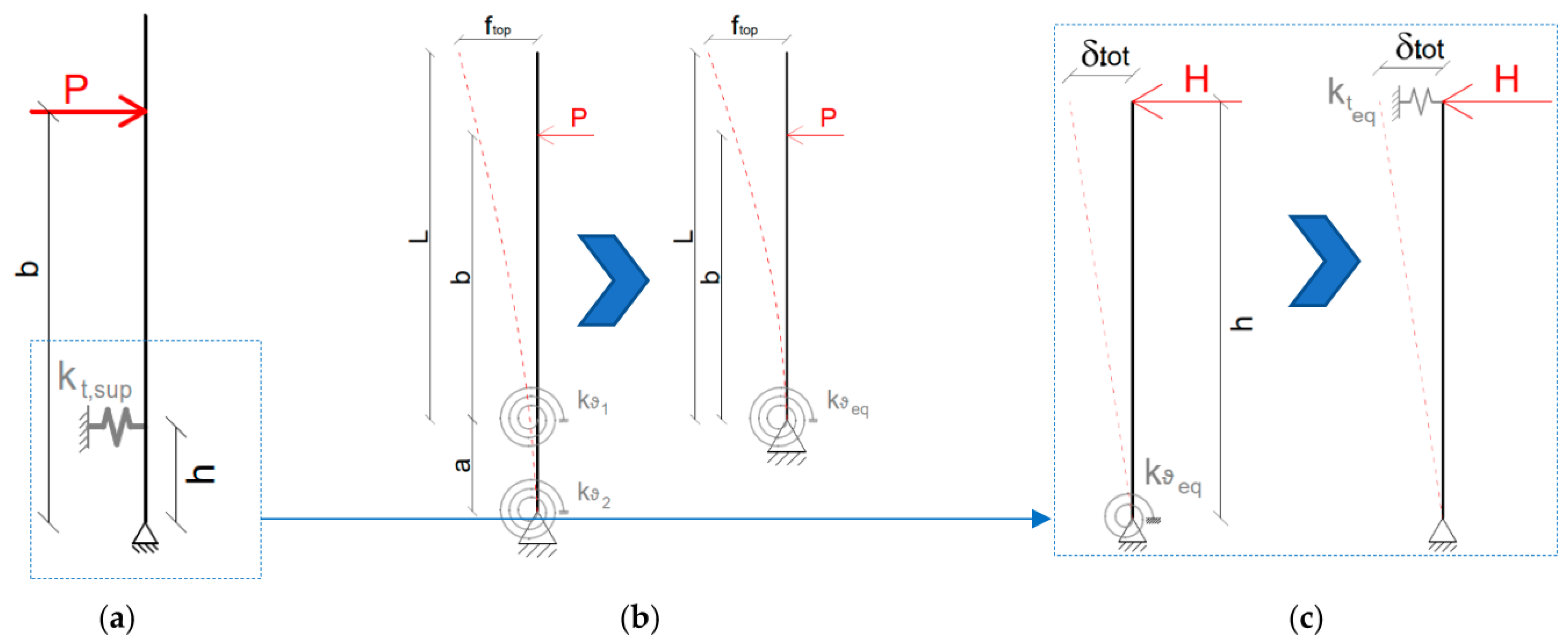
4.1. Simplified Characterization of the Base Restraint—SM1 Model
4.2. Simplified Characterization of the Base Restraint and LG Panel—SM2 Model
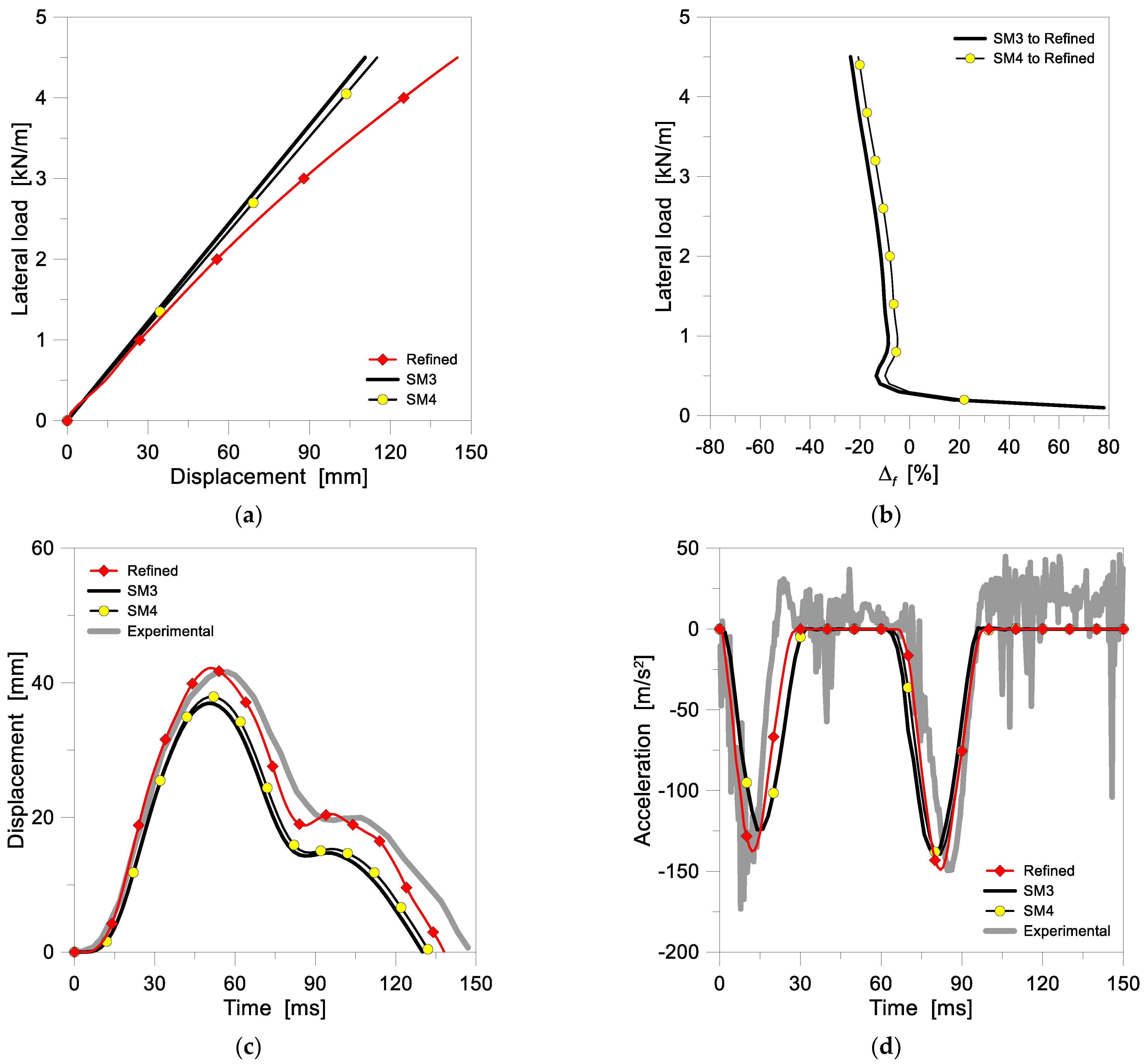
4.3. Linearly Distributed Base Springs—SM3 and SM4 Models
5. Discussion of Numerical Results
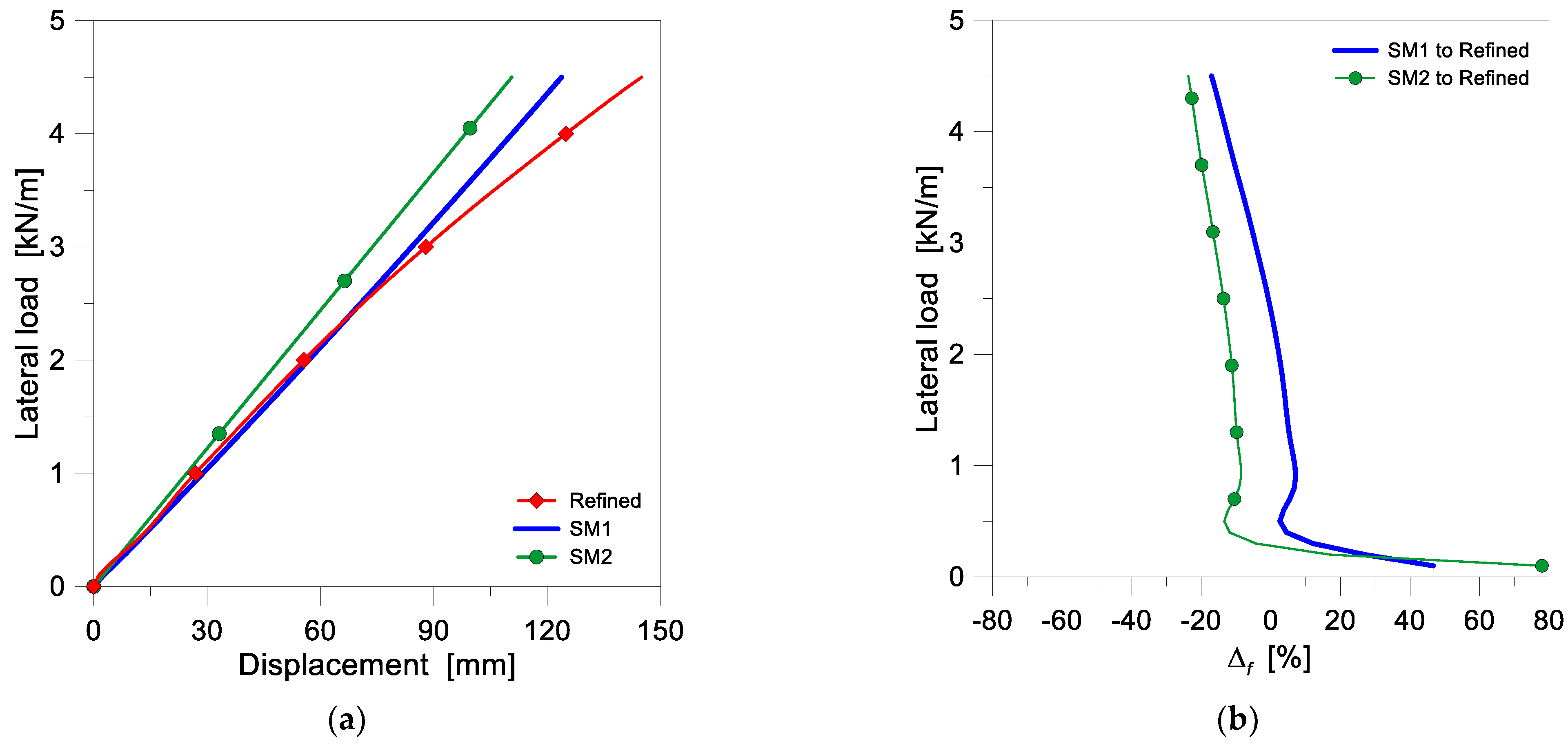
5.1. Simplified Models SM1 and SM2
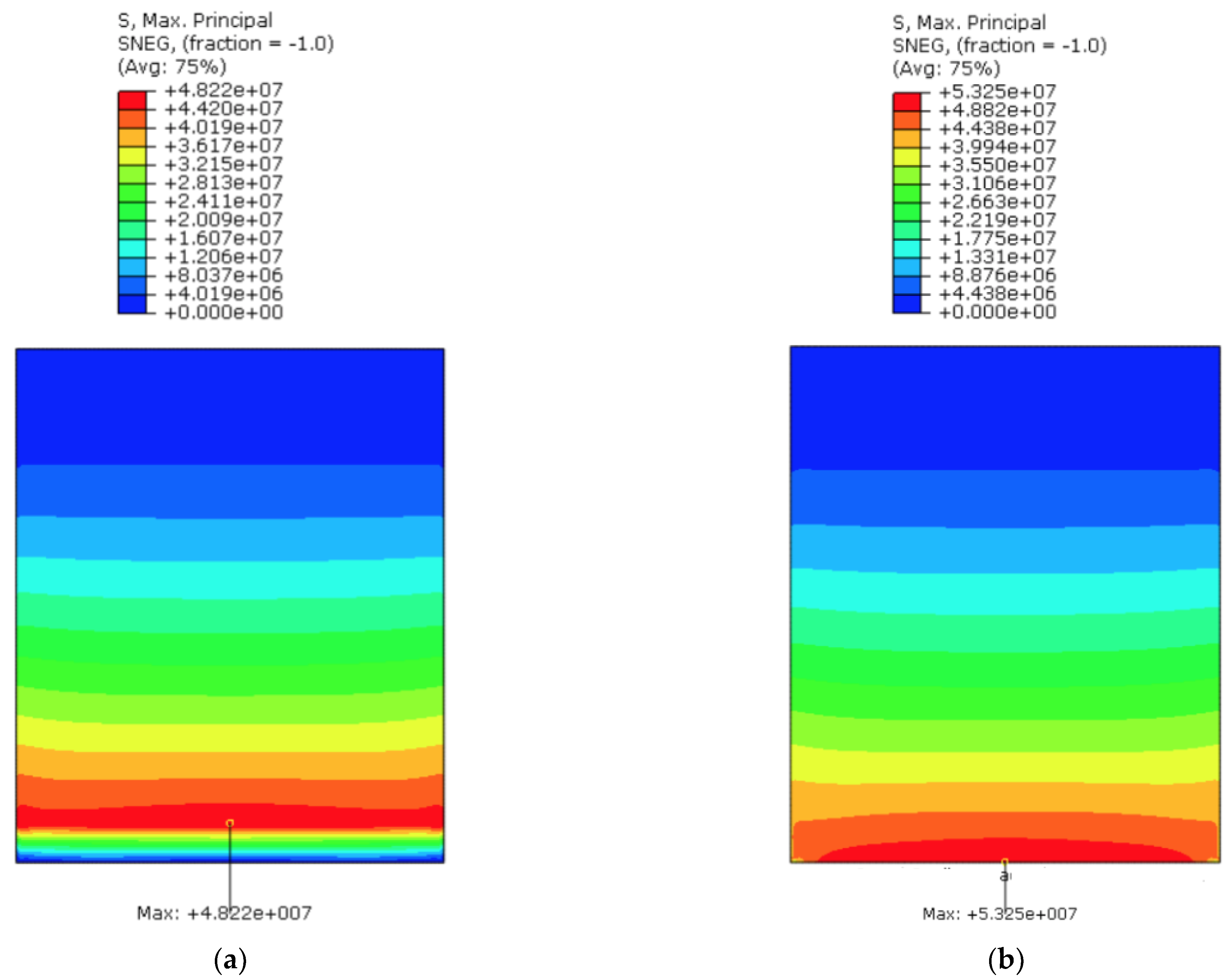
5.2. Effect of Linearly Distributed Equivalent Springs—SM3 and SM4
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feldmann, M.; Kasper, R.; Abeln, B.; Cruz, P.; Belis, J.; Beyer, J. Guidance for European Structural Design of Glass Components—Support to the Implementation, Harmonization and Further Development of the Eurocodes; Report EUR 26439; Dimova, P., Feldmann, D., Eds.; Joint Research Centre–Institute for the Protection and Security of the Citizen: Ispra, Italy, 2014. [Google Scholar] [CrossRef]
- CNR-DT 210/2013; Istruzioni Per la Progettazione, L’esecuzione ed il Controllo di Costruzioni con Elementi Strutturali di Vetro. National Research Council of Italy (CNR): Roma, Italy, 2013; (In Italian–English Version Freely Available).
- Bedon, C.; Santarsiero, M. Transparency in Structural Glass Systems Via Mechanical, Adhesive, and Laminated Connections. Adv. Eng. Mater. 2018, 20, 1700815. [Google Scholar] [CrossRef]
- EN 12600:2002; Glass in Building. Pendulum Test. Impact Test Method and Classification for Flat Glass Method and Classification for Flat Glass. European Committee for Standardization: Brussels, Belgium, 2002.
- DIN 18008-4; Glass in Building—Design and Construction Rules—Part 4: Additional Requirements for Barrier Glazing. DIN: Berlin, Germany, 2013.
- Bedon, C.; Zhang, X.; Santos, F.; Honfi, D.; Kozłowski, M.; Arrigoni, M.; Figuli, L.; Lange, D. Performance of structural glass facades under extreme loads—Design methods, existing research, current issues and trends. Constr. Build. Mater. 2018, 163, 921–937. [Google Scholar] [CrossRef]
- Figuli, L.; Papan, D.; Papanova, Z.; Bedon, C. Experimental mechanical analysis of traditional in-service glass windows subjected to dynamic tests and hard body impact. Smart Struct. Syst. 2021, 27, 365. [Google Scholar]
- Bedon, C.; Santi, M.V. Vulnerability and Structural Capacity Assessment of Historic Glass Facades under Bird-Strike. Math. Probl. Eng. 2022, 2022, 6059466. [Google Scholar] [CrossRef]
- Kalamar, R.; Bedon, C.; Eliasova, M. Experimental investigation for the structural performance assessment of square hollow glass columns. Eng. Struct. 2016, 113, 1–15. [Google Scholar] [CrossRef]
- Bedon, C.; Kalamar, R.; Eliasova, M. Low velocity impact performance investigation on square hollow glass columns via full-scale experiments and Finite Element analyses. Compos. Struct. 2017, 182, 311–325. [Google Scholar] [CrossRef]
- Fröling, M.; Persson, K.; Austrell, P.-E. A reduced model for the design of glass structures subjected to dynamic impulse load. Eng. Struct. 2014, 80, 53–60. [Google Scholar] [CrossRef]
- Andersson, L.; Kozłowski, M.; Persson, P.; Austrell, P.-E.; Persson, K. Reduced order modeling of soft-body impact on glass panels. Eng. Struct. 2022, 256, 113988. [Google Scholar] [CrossRef]
- Bez, A.; Bedon, C.; Manara, G.; Amadio, C.; Lori, G. Calibrated Numerical Approach for the Dynamic Analysis of Glass Curtain Walls under Spheroconical Bag Impact. Buildings 2021, 11, 154. [Google Scholar] [CrossRef]
- Schneider, J.; Schula, S. Simulating soft body impact on glass structures. Proc. Inst. Civ. Eng. Struct. Build. 2016, 169, 416–431. [Google Scholar] [CrossRef]
- Baidjoe, Y.; Van Lancker, B.; Belis, J. Calculation methods of glass parapets in aluminum clamping profiles. Glass Struct. Eng. 2018, 3, 321–334. [Google Scholar] [CrossRef]
- Biolzi, L.; Bonati, A.; Cattaneo, S. Laminated Glass Cantilevered Plates under Static and Impact Loading. Adv. Civil. Eng. 2018, 2018, 7874618. [Google Scholar] [CrossRef]
- Kozłowski, M. Experimental and numerical assessment of structural behaviour of glass balustrade subjected to soft body impact. Compos. Struct. 2019, 229, 111380. [Google Scholar] [CrossRef]
- Bedon, C.; Fasan, M.; Amadio, C. Vibration Analysis and Dynamic Characterization of Structural Glass Elements with Different Restraints Based on Operational Modal Analysis. Buildings 2019, 9, 13. [Google Scholar] [CrossRef]
- Portal, N.W.; Flansbjer, M.; Honfi, D.; Kozłowski, M. The dynamic structural response of a laminated glass balustrade analysed with optical measurements. Ce/papers, Special Issue: Engineered Transparency 2021: Glass in Architecture and Structural Engineering. Glass Struct. Des. 2021, 4, 251–261. [Google Scholar] [CrossRef]
- Galuppi, L.; Royer-Carfagni, G. Effective thickness of laminated glass beams: New expression via a variational approach. Eng. Struct. 2012, 38, 53–67. [Google Scholar] [CrossRef]
- Simulia. ABAQUS Computer Software, Dassault Systémes: Providence, RI, USA, 2021.





| FE Model Features | |||
|---|---|---|---|
| FE Numerical Model | LG Cross-Section (mm) | LG Panel | Base Restraint |
| Refined | 10 + 1.52 PVB + 10 | Full 3D solid brick elements (layered section) | Full 3D solid brick elements |
| SM1 | Same as that of Refined | Lumped equivalent springs in the region of restraints | |
| SM2 | 2D shell elements (equivalent monolithic glass section) | Lumped equivalent springs in the region of restraints | |
| SM3 | Same as that of SM2 | Linearly distributed equivalent springs (translational) at the bottom edge of the glass | |
| SM4 | Same as that of SM2 | Linearly distributed equivalent springs (rotational) at the bottom edge of the glass | |
| Material Properties | ||||
|---|---|---|---|---|
| Material | Constitutive Model | Modulus of Elasticity [N/mm2] | Poisson Ratio | Density [kg/m3] |
| Steel | Linear elastic | 210,000 | 0.3 | 7850 |
| POM | Linear elastic | 2413 | 0.45 | 1250 |
| Glass | Linear elastic | 70,000 | 0.23 | 2500 |
| PVB | Linear elastic | 180 | 0.485 | 1250 |
| Refined Model | |||||
|---|---|---|---|---|---|
| Drop Height [mm] | amax,test [17] [m/s2] | amax,model [17] [m/s2] | amax,Refined [m/s2] | ∆1 [%] | ∆2 [%] |
| 300 | 223 | 216 | 216.38 | −2.97 | 0.18 |
| 400 | 282 | 272 | 269.17 | −4.55 | −1.04 |
| 500 | 332 | 334 | 345.36 | 4.02 | 3.40 |
| FE Model Features | ||
|---|---|---|
| FE Numerical Model | Number of Elements | Number of DOFs |
| Refined | ≈120,000 | ≈505,000 |
| SM1 | ≈76,000 | ≈214,000 |
| SM2 | ≈12,000 | ≈73,000 |
| SM3 and SM4 | ≈12,000 | ≈73,000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rizzi, E.; Bedon, C.; Amadio, C. Simplified Models to Capture the Effects of Restraints in Glass Balustrades under Quasi-Static Lateral Load or Soft-Body Impact. Buildings 2022, 12, 1664. https://doi.org/10.3390/buildings12101664
Rizzi E, Bedon C, Amadio C. Simplified Models to Capture the Effects of Restraints in Glass Balustrades under Quasi-Static Lateral Load or Soft-Body Impact. Buildings. 2022; 12(10):1664. https://doi.org/10.3390/buildings12101664
Chicago/Turabian StyleRizzi, Emanuele, Chiara Bedon, and Claudio Amadio. 2022. "Simplified Models to Capture the Effects of Restraints in Glass Balustrades under Quasi-Static Lateral Load or Soft-Body Impact" Buildings 12, no. 10: 1664. https://doi.org/10.3390/buildings12101664
APA StyleRizzi, E., Bedon, C., & Amadio, C. (2022). Simplified Models to Capture the Effects of Restraints in Glass Balustrades under Quasi-Static Lateral Load or Soft-Body Impact. Buildings, 12(10), 1664. https://doi.org/10.3390/buildings12101664







