Building Geometry as a Variable in Energy, Comfort, and Environmental Design Optimization—A Review from the Perspective of Architects
Abstract
1. Introduction
- What kind of BGDV-s exists in current BECEDO research?
- What are the roles and functions of the different BGDV-s in BECEDO investigations?
- What are the frequently applied simulation engines, optimization algorithms, and software frameworks (including the diverse methods) in BECEDO?
- What kind of space organization and shape defining solutions exist, and what are the pros and cons of each process?
- Which type of building performance is improved through BGDV-s, and how large is the impact on the improvements?
- Is it possible to create a link between the concrete building form and its geometry describing mathematical design variables? Where is the level of achievement in actual research to replicate shape with the use of BGDV-s?
- What is the potential of building shape optimization?
- How can the achieved results and knowledge be applied in further design projects?
- What kind of limitations and/or shortcomings can be detected?
2. Geometry as a Design Variable in BECEDO
2.1. Building Geometry Variables on Basic Level of Complexity
2.2. Building Geometry Variables to Elaborate the Level of Complexity
3. Algorithms in BGDV including BECEDO
4. Discussion
4.1. Prevailing Trends in Building Shape Optimization
4.2. Frequently Applied BGDVs in BECEDO
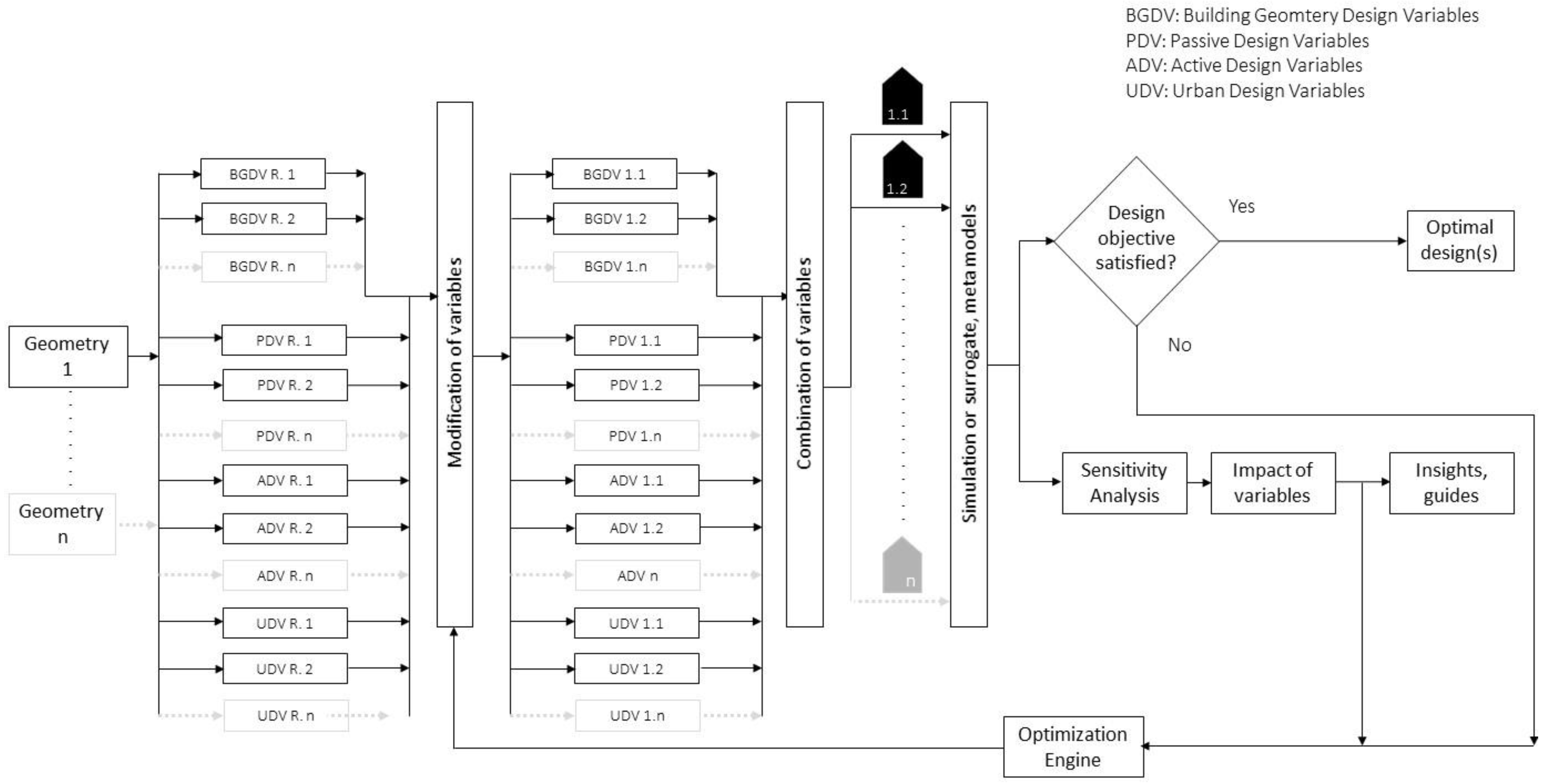
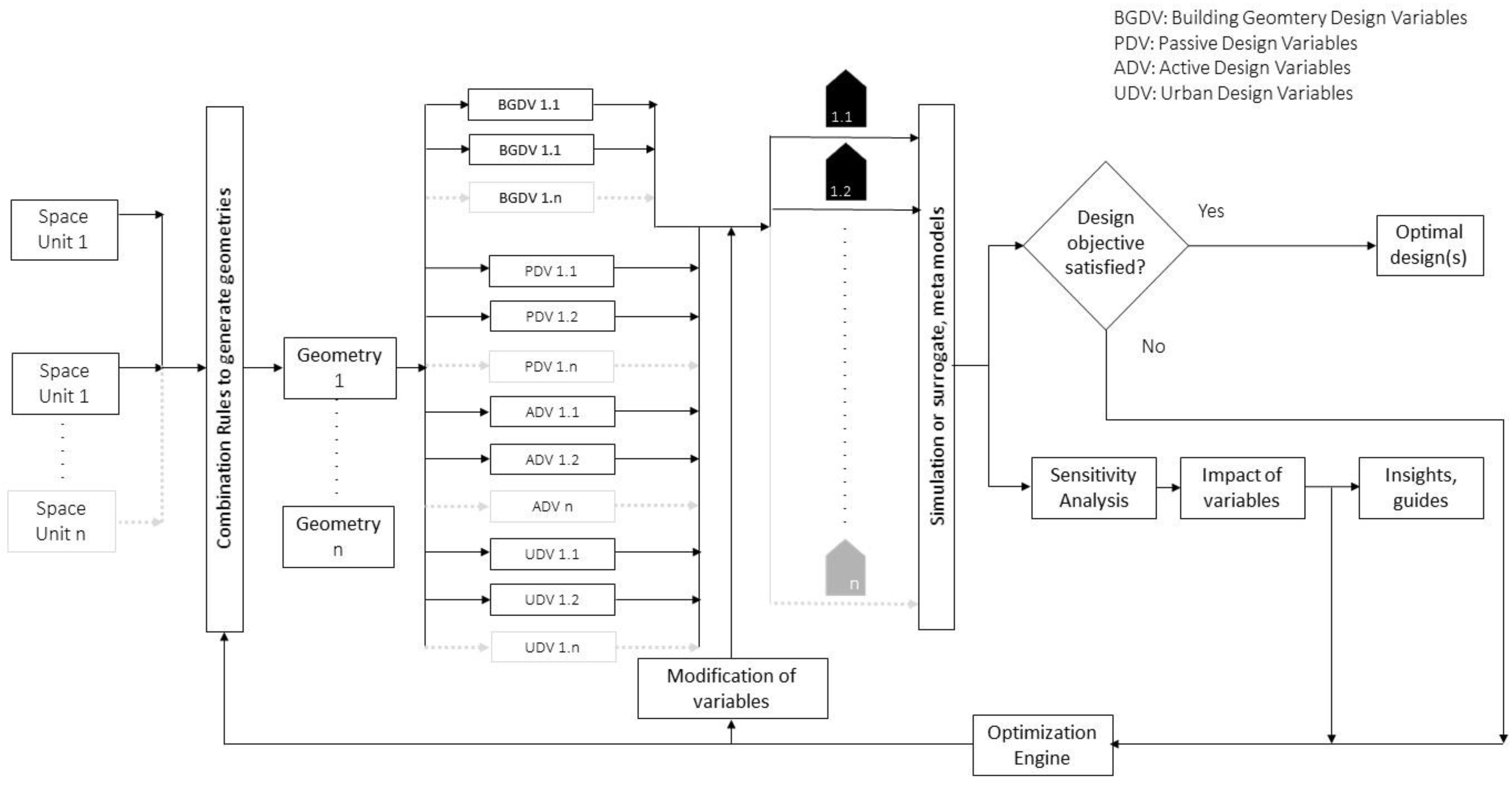
4.3. Principles of Building Geometry Modeling in BECEDO Processes
4.4. Categorization of Building Geometry Modeling in BECEDO
- Shape generation without energy evaluation and optimization.
- An agent-based topology finding system creates layouts as a topology finding process, generating sphere and capsule bubble agents. Interaction rules as attraction, repulsion, swap, and compression help to generate multi-agent systems as layout schemes. The developed software allows connected rooms (agents) to be dragged closer and unconnected rooms push each other away if close enough. A 3D grid-system based on rectangular cells converts the multi-agent layout into a space model [60].
- Shape modification with energy evaluation.
- Changing of diverse BGDVs.
- Modification of geometry and setup arrangement for urban blocks. Four- and eight-story simple prismatic building block morphology versions [63].
- Shape generation with energy evaluation.
- Shape grammar (converted into a parametric system). Variants programming: translating shape transformations (scale, reflection, translation, rotation) into equations and variables. Every room is modeled as a block with changeable aspects ratio, length, width, shape, size, and location. Automated energy evaluation of created forms [54].
- Generation of a large number of building geometry alternatives using “Evolutionary Program for Space Allocation Program” (EPSAP), including GA. A floor plan representation scheme, including total area for each story, construction area, circulation space area, and openings is randomly generated, and then the energy performance is calculated [55].
- “Building Modular Cells” (BMC) geometry generation technique is introduced to generate urban morphology based on a grid raster with various urban density building categories, building height classes, and urban patterns (street area between the building blocks) and a form generating algorithm, including architecturally eligible form selection. Space-units (modular cells) are arranged due to the form generation rules [56].
- Geometry modification with energy evaluation and optimization—simple complexity.
- Changing of diverse BGDVs.
- Geometry modification with energy evaluation and optimization—elaborate complexity.
- Changing of diverse BGDV-s
- Automated generation of 2D-layout and topology. Finding the best location and size of interrelated rectangular spaces. (1) Swapping the positions of two space units, (2) reallocation of positions, and (3) reducing the size of a space unit. Constraining overlapping, regulating connections of spaces, paths and access ways and the building envelope [93].
- Settlement scaled building block morphology optimization for solar energy use (heating, lighting). Diversely oriented building rows and courtyard block arrangements tested [44].
- A hybrid evolutionary algorithm is applied with constraint handling as an optimization method for urban building configurations. Urban block grid density (no. of blocks) and height optimization. Complex extension building and roof shapes adjacent to an existing house); rectangular, planned building’s volume, parametrized by Fourier series [91].
- Optimization of the geometry of simple office building blocks (energy demand) in a city quarter. Optimization of the horizontal and vertical positions of corner points [49].
- Geometry optimization of common linear (I), L- (L), court (O), C- (C), T- (T), H- (H), cross (X), and Y-shaped (Y) buildings (LOD 100). Multiple geometries with shape proportion (depth of the space/wings) modification as a ’gene’ under the same volume [39].
- Geometry generation with energy evaluation and optimization.
- “Building modular cells” (BMC), custom developed geometry generation technique based on a 4 × 4 grid raster to search for optimum solutions in five high-rise office buildings in five urban density (UD) areas. Space-units arranged according to combination rules [40].
- GA generates layouts in two phases: combination of different wings (rotation angle) to form the shape and arrangements of flats into the wings [41].
4.5. Optimization Result Improvements in BGDVs Containing BECEDO
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| AC | Air-Conditioning |
| ACH | Air Change |
| ADV | Active Design Variable |
| AEC | Architecture, Engineering and Construction |
| ANN | Artificial Neural Network |
| ANOVA | Analysis of Variance |
| AR | Aspect Ratio |
| BECED | Building Energy, Comfort and Environmeltal Design |
| BECEDO | Building Energy, Comfort and Environmeltal Design Optimization |
| BEDV | Building Envelope Design Variable |
| BEO | Buiding Energy Optimization |
| BGDV | Building Geomtery Design Variables |
| BIPV | Building Integrated Photovoltaic |
| BMC | Building Modular Cell |
| BOP | Building Optimization Problem |
| CFD | Computational Fluid Dynamics |
| CMA-ES | Covariance Matrix Adaptation Evolution Strategy |
| DAE | Differential-Algebraic Equation |
| DF | Daylight Factor |
| DHW | Domestic Hot Water |
| DOE | Design Of Experiments |
| EA | Evolutionary Algorithm |
| EEF | Efficient Form-finder |
| EPSAP | Evolutionary Program for Space Allocation Program |
| ES | Evolution Strategy |
| EUI | Energy Use Intensity |
| GA | Genetic Algorithm |
| GBM | Gradient Boosting Machine learning |
| GH | GrassHopper |
| GR | Glazing Ratio (e.g., wall-window ratio) |
| GSA | Global Sensitivity Analysis |
| GUI | Graphic User Interface |
| HDE | Hybrid Differential Evolution |
| HJ | Hooke-Jeeves |
| HVAC | Heating, Ventillation, and Air Conditioning |
| LCC | Life Cycle Cost |
| LCCA | Life Cycle Cost Assessment |
| LCEI | Life Cycle Energy Impact |
| MDO | Multidisciplinary Design Optimization |
| MO | Multi-Objective |
| MOGA | Multi-Objective Genetic Algorithm |
| MOO | Multi-Objective Optimization |
| N, NE, E, SE, E, SW, W, NW | North, North-East, East, South-East South, South-West, West, North-West |
| NSGA | Non-dominated Sorting Genetic Algorithm |
| NV | Natural Ventilation |
| ORI | ORIentation |
| PDV | Passive Design Variable |
| PEC | Primary Energy Consumption |
| PSO | Particle Swarm Optimization |
| RC | Relative Compactness |
| SA | Simulated Annealing |
| sDA | spacial Daylight Autonomy |
| SF | Shape Factor |
| SHADE | shading |
| SHC | Stochastic Hill Climbing |
| SHGC | Solar Heat Gain Coefficient |
| SO | Single-Objective |
| STR | Structures, materials |
| TDT | Thermal Discomfort Time |
| TM | Thernal Mass |
| UDI | Useful Daylight Illuminance |
| UDV | Urban Design Varible |
| WWR | Window to Wall Ratio |
References
- IEA; UNEP. 2019 Global Status Report for Buildings and Construction; UN Environment and the International Energy Agency: Nairobi, Kenya; Paris, France, 2019; Volume 224. [Google Scholar]
- Fesanghary, M.; Asadi, S.; Geem, Z.W. Design of low-emission and energy-efficient residential buildings using a multi-objective optimization algorithm. Build. Environ. 2012, 49, 245–250. [Google Scholar] [CrossRef]
- Cao, X.; Dai, X.; Liu, J. Building energy-consumption status worldwide and the state-of-the-art technologies for zero-energy buildings during the past decade. Energy Build. 2016, 128, 198–213. [Google Scholar] [CrossRef]
- Pérez-Lombard, L.; Ortiz, J.; Pout, C. A review on buildings energy consumption information. Energy Build. 2008, 40, 394–398. [Google Scholar] [CrossRef]
- Rullán-Lemke, C. ArchitekturForm & SolarEnergie. Ph.D. Thesis, Hamburg University of Technology, Hamburg, Germany, 2009. [Google Scholar]
- Depecker, P.; Menezo, C.; Virgone, J.; Lepers, S. Design of buildings shape and energetic consumption. Build. Environ. 2001, 36, 627–635. [Google Scholar] [CrossRef]
- AlAnzi, A.; Seo, D.; Krarti, M. Impact of building shape on thermal performance of office buildings in Kuwait. Energy Convers. Manag. 2009, 50, 822–828. [Google Scholar] [CrossRef]
- Nguyen, A.-T.; Reiter, S.; Rigo, P. A review on simulation-based optimization methods applied to building performance analysis. Appl. Energy 2014, 113, 1043–1058. [Google Scholar] [CrossRef]
- Shi, X.; Tian, Z.; Chen, W.; Si, B.; Jin, X. A review on building energy efficient design optimization rom the perspective of architects. Renew. Sustain. Energy Rev. 2016, 65, 872–884. [Google Scholar] [CrossRef]
- U.S. Department of Energy. Buildings energy databook. Energy Effic. Renew. Energy Dep. 2012, 286. Available online: http://buildingsdatabook.eren.doe.gov/DataBooks.aspx (accessed on 17 June 2021).
- Gupta, C. A systematic approach to optimum thermal design. Build. Sci. 1970, 5, 165–173. [Google Scholar] [CrossRef]
- Kheiri, F. A review on optimization methods applied in energy-efficient building geometry and envelope design. Renew. Sustain. Energy Rev. 2018, 92, 897–920. [Google Scholar] [CrossRef]
- Machairas, V.; Tsangrassoulis, A.; Axarli, K. Algorithms for optimization of building design: A review. Renew. Sustain. Energy Rev. 2014, 31, 101–112. [Google Scholar] [CrossRef]
- Rabani, M.; Madessa, H.B.; Nord, N. Achieving zero-energy building performance with thermal and visual comfort enhancement through optimization of fenestration, envelope, shading device, and energy supply system. Sustain. Energy Technol. Assess. 2021, 44, 101020. [Google Scholar] [CrossRef]
- Huang, B.; Gao, X.; Xu, X.; Song, J.; Geng, Y.; Sarkis, J.; Fishman, T.; Kua, H.; Nakatani, J. A Life Cycle Thinking Framework to Mitigate the Environmental Impact of Building Materials. One Earth 2020, 3, 564–573. [Google Scholar] [CrossRef]
- Acar, U.; Kaska, O.; Tokgoz, N. Multi-objective optimization of building envelope components at the preliminary design stage for residential buildings in Turkey. J. Build. Eng. 2021, 42, 102499. [Google Scholar] [CrossRef]
- Al-Saadi, S.N.; Al-Jabri, K.S. Optimization of envelope design for housing in hot climates using a genetic algorithm (GA) computational approach. J. Build. Eng. 2020, 32, 101712. [Google Scholar] [CrossRef]
- Toutou, A.; Fikry, M.; Mohamed, W. The parametric based optimization framework daylighting and energy performance in residential buildings in hot arid zone. Alex. Eng. J. 2018, 57, 3595–3608. [Google Scholar] [CrossRef]
- Gerber, D.J.; Pantazis, E.; Wang, A. A multi-agent approach for performance based architecture: Design exploring geometry, user, and environmental agencies in façades. Autom. Constr. 2017, 76, 45–58. [Google Scholar] [CrossRef]
- Kim, H.; Clayton, M.J. A multi-objective optimization approach for climate-adaptive building envelope design using parametric behavior maps. Build. Environ. 2020, 185, 107292. [Google Scholar] [CrossRef]
- Abdel-Rahman, W.S.M. Thermal performance optimization of parametric building envelope based on bio-mimetic inspiration. Ain Shams Eng. J. 2020, 12, 1133–1142. [Google Scholar] [CrossRef]
- Hromada, E.; Vitasek, S.; Holcman, J.; Heralova, R.S.; Krulicky, T. Residential Construction with a Focus on Evaluation of the Life Cycle of Buildings. Buildings 2021, 11, 524. [Google Scholar] [CrossRef]
- Liu, B.; Rodriguez, D. Renewable energy systems optimization by a new multi-objective optimization technique: A residential building. J. Build. Eng. 2020, 35, 102094. [Google Scholar] [CrossRef]
- Palonen, M.; Hamdy, M.; Hasan, A. Mobo a new software for multi-objective building performance optimization. In Proceedings of the 13th Internationcal Conference of the IBPSA, Chambery, France, 26–28 August 2013; pp. 2567–2574. [Google Scholar]
- Ochoa, C.; Capeluto, I.G. Strategic decision-making for intelligent buildings: Comparative impact of passive design strategies and active features in a hot climate. Build. Environ. 2008, 43, 1829–1839. [Google Scholar] [CrossRef]
- Yu, Z.; Gou, Z.; Qian, F.; Fu, J.; Tao, Y. Towards an optimized zero energy solar house: A critical analysis of passive and active design strategies used in Solar Decathlon Europe in Madrid. J. Clean. Prod. 2019, 236. [Google Scholar] [CrossRef]
- Li, H.; Wang, S. Coordinated optimal design of zero/low energy buildings and their energy systems based on multi-stage design optimization. Energy 2019, 189, 116202. [Google Scholar] [CrossRef]
- Harkouss, F.; Fardoun, F.; Biwole, P. Passive design optimization of low energy buildings in different climates. Energy 2018, 165, 591–613. [Google Scholar] [CrossRef]
- Gunay, H.B.; Ouf, M.; Newsham, G.; O’Brien, W. Sensitivity analysis and optimization of building operations. Energy Build. 2019, 199, 164–175. [Google Scholar] [CrossRef]
- Lee, J.H. Optimization of indoor climate conditioning with passive and active methods using GA and CFD. Build. Environ. 2007, 42, 3333–3340. [Google Scholar] [CrossRef]
- Ferdyn-Grygierek, J.; Grygierek, K. Multi-Variable Optimization of Building Thermal Design Using Genetic Algorithms. Energies 2017, 10, 1570. [Google Scholar] [CrossRef]
- Hong, T.; Kim, J.; Lee, M. A multi-objective optimization model for determining the building design and occupant behaviors based on energy, economic, and environmental performance. Energy 2019, 174, 823–834. [Google Scholar] [CrossRef]
- Hamdy, M. Implementation of pareto-archive NSGA-II algorithms to a nearly-zero-energy building optimisation problem. In Proceedings of the Building Simulation and Optimization Conference, Loughborough, UK, 10–11 September 2012. [Google Scholar]
- Ke, Y.; Xie, J.; Pouramini, S. Utilization of an improved crow search algorithm to solve building energy optimization problems: Cases of Australia. J. Build. Eng. 2021, 38, 102142. [Google Scholar] [CrossRef]
- Ilbeigi, M.; Ghomeishi, M.; Dehghanbanadaki, A. Prediction and optimization of energy consumption in an office building using artificial neural network and a genetic algorithm. Sustain. Cities Soc. 2020, 61, 102325. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; Mauro, G.M.; Napolitano, D.F. Building envelope design: Multi-objective optimization to minimize energy consumption, global cost and thermal discomfort. Application to different Italian climatic zones. Energy 2019, 174, 359–374. [Google Scholar] [CrossRef]
- Saad, M.M.; Araji, M.T. Co-model for urban density permutations and building form optimization with high-performance energy criteria. J. Build. Eng. 2021, 43, 103109. [Google Scholar] [CrossRef]
- Yi, Y.K.; Malkawi, A.M. Optimizing building form for energy performance based on hierarchical geometry relation. Autom. Constr. 2009, 18, 825–833. [Google Scholar] [CrossRef]
- Ciardiello, A.; Rosso, F.; Dell’Olmo, J.; Ciancio, V.; Ferrero, M.; Salata, F. Multi-objective approach to the optimization of shape and envelope in building energy design. Appl. Energy 2020, 280, 115984. [Google Scholar] [CrossRef]
- Javanroodi, K.; Nik, V.M.; Mahdavinejad, M. A novel design-based optimization framework for enhancing the energy efficiency of high-rise office buildings in urban areas. Sustain. Cities Soc. 2019, 49, 101597. [Google Scholar] [CrossRef]
- Gan, V.J.; Wong, H.; Tse, K.; Cheng, J.C.; Lo, I.M.; Chan, C. Simulation-based evolutionary optimization for energy-efficient layout plan design of high-rise residential buildings. J. Clean. Prod. 2019, 231, 1375–1388. [Google Scholar] [CrossRef]
- Gratia, E.; De Herde, A. Design of low energy office buildings. Energy Build. 2003, 35, 473–491. [Google Scholar] [CrossRef]
- Ourghi, R.; Al-Anzi, A.; Krarti, M. A simplified analysis method to predict the impact of shape on annual energy use for office buildings. Energy Convers. Manag. 2007, 48, 300–305. [Google Scholar] [CrossRef]
- Kämpf, J.; Montavon, M.; Bunyesc, J.; Bolliger, R.; Robinson, D. Optimisation of buildings’ solar irradiation availability. Sol. Energy 2010, 84, 596–603. [Google Scholar] [CrossRef]
- Wang, W.; Rivard, H.; Zmeureanu, R. Floor shape optimization for green building design. Adv. Eng. Inform. 2006, 20, 363–378. [Google Scholar] [CrossRef]
- Hemsath, T.L.; Bandhosseini, K.A. Sensitivity analysis evaluating basic building geometry’s effect on energy use. Renew. Energy 2015, 76, 526–538. [Google Scholar] [CrossRef]
- Hachem, C.; Athienitis, A.; Fazio, P. Investigation of solar potential of housing units in different neighborhood designs. Energy Build. 2011, 43, 2262–2273. [Google Scholar] [CrossRef]
- Aksoy, U.T.; Inalli, M. Impacts of some building passive design parameters on heating demand for a cold region. Build. Environ. 2006, 41, 1742–1754. [Google Scholar] [CrossRef]
- Waibel, C.; Evins, R.; Carmeliet, J. Co-simulation and optimization of building geometry and multi-energy systems: Interdependencies in energy supply, energy demand and solar potentials. Appl. Energy 2019, 242, 1661–1682. [Google Scholar] [CrossRef]
- Fang, Y.; Cho, S. Design optimization of building geometry and fenestration for daylighting and energy performance. Sol. Energy 2019, 191, 7–18. [Google Scholar] [CrossRef]
- Hemsath, T.L.; Bandhosseini, K.A. Building Design with Energy Performance as Primary Agent. Energy Procedia 2015, 78, 3049–3054. [Google Scholar] [CrossRef]
- Sibenik, G.; Kovacic, I. Interpreted open data exchange between architectural design and structural analysis models. J. Inf. Technol. Constr. 2021, 26, 39–57. [Google Scholar] [CrossRef]
- Mert, Y.; Saygın, N. Energy efficient building block design: An exergy perspective. Energy 2016, 102, 465–472. [Google Scholar] [CrossRef][Green Version]
- Granadeiro, V.; Duarte, J.; Correia, J.R.; Leal, V. Building envelope shape design in early stages of the design process: Integrating architectural design systems and energy simulation. Autom. Constr. 2013, 32, 196–209. [Google Scholar] [CrossRef]
- Rodrigues, E.; Fernandes, M.; Soares, N.; Gomes, Á.; Gaspar, A.R.; Costa, J.J. The potential impact of low thermal transmittance construction on the European design guidelines of residential buildings. Energy Build. 2018, 178, 379–390. [Google Scholar] [CrossRef]
- Javanroodi, K.; Mahdavinejad, M.; Nik, V.M. Impacts of urban morphology on reducing cooling load and increasing ventilation potential in hot-arid climate. Appl. Energy 2018, 231, 714–746. [Google Scholar] [CrossRef]
- Cao, X.; He, Z.; Pan, Y. Automated design of house-floor layout with distributed planning. Comput. Des. 1990, 22, 213–222. [Google Scholar] [CrossRef]
- Elezkurtaj, T.; Franck, G. Algorithmic support of creative architectural design. Organization 2002, 2, 16. Available online: http://www.iemar.tuwien.ac.at/wp-content/uploads/2011/12/umbau19.pdf (accessed on 17 June 2021).
- Francisco, J.; Costa, R.; Doc, P.; Manuel, V.; Murtinho, B. Development of an Algorithm Which Generates Functional Floor Plans for Residential Buildings Based on Modular Construction. Ph.D. Thesis, University in Coimbra, Coimbra, Portugal, 2015. [Google Scholar]
- Guo, Z.; Li, B. Evolutionary approach for spatial architecture layout design enhanced by an agent-based topology finding system. Front. Arch. Res. 2017, 6, 53–62. [Google Scholar] [CrossRef]
- D’Cruz, N.A.; Radford, A.D. A multicriteria model for building performance and design. Build. Environ. 1987, 22, 167–179. [Google Scholar] [CrossRef]
- Hauglustaine, J.M.; Lema, S.A. Interactive Tool Aiding to Optimise The Building Envelope During The Sketch Design. In Proceedings of the Seventh International IBPSA Conference (BS2001), Rio de Janeiro, Brazil, 13–15 August 2001. [Google Scholar]
- Jedrzejuk, H.; Marks, W. Optimization of shape and functional structure of buildings as well as heat source utilization. Basic theory. Build. Environ. 2002, 37, 1379–1383. [Google Scholar] [CrossRef]
- Coley, D.A.; Schukat, S. Low-energy design: Combining computer-based optimisation and human judgement. Build. Environ. 2002, 37, 1241–1247. [Google Scholar] [CrossRef]
- Caldas, L.G.; Norford, L.K. Genetic Algorithms for Optimization of Building Envelopes and the Design and Control of HVAC Systems. J. Sol. Energy Eng. 2003, 125, 343–351. [Google Scholar] [CrossRef]
- Sisk, G.M.; Miles, J.C.; Moore, C.J. Designer Centered Development of GA-Based DSS for Conceptual Design of Buildings. J. Comput. Civ. Eng. 2003, 17, 159–166. [Google Scholar] [CrossRef]
- Wang, W.; Zmeureanu, R.; Rivard, H. Applying multi-objective genetic algorithms in green building design optimization. Build. Environ. 2005, 40, 1512–1525. [Google Scholar] [CrossRef]
- Choudhary, R.; Malkawi, A.; Papalambros, P. Analytic target cascading in simulation-based building design. Autom. Constr. 2005, 14, 551–568. [Google Scholar] [CrossRef]
- Malkawi, A.M.; Srinivasan, R.S.; Yi, Y.K.; Choudhary, R. Decision support and design evolution: Integrating genetic algorithms, CFD and visualization. Autom. Constr. 2005, 14, 33–44. [Google Scholar] [CrossRef]
- Adamski, M. Optimization of the form of a building on an oval base. Build. Environ. 2007, 42, 1632–1643. [Google Scholar] [CrossRef]
- Geyer, P. Component-oriented decomposition for multidisciplinary design optimization in building design. Adv. Eng. Inform. 2009, 23, 12–31. [Google Scholar] [CrossRef]
- Flager, F.; Welle, B.; Bansal, P.; Soremekun, G.; Haymaker, J. Multidisciplinary process integration and design optimization of a classroom building. Electron. J. Inf. Technol. Constr. 2009, 14, 595–612. [Google Scholar]
- Bucking, S.; Athienitis, A.; Zmeureanu, R. An Optimization Methodology to Evaluate the Effect Size of Incentives on Energy-cost Optimal Curves. In Proceedings of the Thirteenth International IBPSA Conference, Chambéry, France, 26–28 August 2008; pp. 1844–1851. [Google Scholar]
- Nguyen, A.T.; Reiter, S. Passive designs and strategies for low-cost housing using simulation-based optimization and different thermal comfort criteria. J. Build. Perform. Simul. 2013, 7, 68–81. [Google Scholar] [CrossRef]
- Xu, J.; Kim, J.-H.; Hong, H.; Koo, J. A systematic approach for energy efficient building design factors optimization. Energy Build. 2014, 89, 87–96. [Google Scholar] [CrossRef]
- Yu, W.; Li, B.; Jia, H.; Zhang, M.; Wang, D. Application of multi-objective genetic algorithm to optimize energy efficiency and thermal comfort in building design. Energy Build. 2015, 88, 135–143. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; Mauro, G.M.; Vanoli, G.P. A new comprehensive framework for the multi-objective optimization of building energy design: Harlequin. Appl. Energy 2019, 241, 331–361. [Google Scholar] [CrossRef]
- Kiss, B.; Szalay, Z. Modular approach to multi-objective environmental optimization of buildings. Autom. Constr. 2020, 111, 103044. [Google Scholar] [CrossRef]
- Zou, Y.; Zhan, Q.; Xiang, K. A comprehensive method for optimizing the design of a regular architectural space to improve building performance. Energy Rep. 2021, 7, 981–996. [Google Scholar] [CrossRef]
- Yigit, S. A machine-learning-based method for thermal design optimization of residential buildings in highly urbanized areas of Turkey. J. Build. Eng. 2021, 38, 102225. [Google Scholar] [CrossRef]
- Wang, S.; Yi, Y.K.; Liu, N. Multi-objective optimization (MOO) for high-rise residential buildings’ layout centered on daylight, visual, and outdoor thermal metrics in China. Build. Environ. 2021, 205, 108263. [Google Scholar] [CrossRef]
- Lin, B.; Chen, H.; Yu, Q.; Zhou, X.; Lv, S.; He, Q.; Li, Z. MOOSAS—A systematic solution for multiple objective building performance optimization in the early design stage. Build. Environ. 2021, 200, 107929. [Google Scholar] [CrossRef]
- McKeen, P.; Fung, A.S. The Effect of Building Aspect Ratio on Energy Efficiency: A Case Study for Multi-Unit Residential Buildings in Canada. Buildings 2014, 4, 336–354. [Google Scholar] [CrossRef]
- Elshafei, G.; Vilčeková, S.; Zeleňáková, M.; Negm, A.M. An Extensive Study for a Wide Utilization of Green Architecture Parameters in Built Environment Based on Genetic Schemes. Buildings 2021, 11, 507. [Google Scholar] [CrossRef]
- Ansah, M.K.; Chen, X.; Yang, H. Two-Stage Lifecycle Energy Optimization of Mid-Rise Residential Buildings with Building-Integrated Photovoltaic and Alternative Composite Façade Materials. Buildings 2021, 11, 642. [Google Scholar] [CrossRef]
- Duart, P.J.; Rocha, J. A Grammar for the Patio Houses of the Medina of Marrakech Towards a Tool for Housing Design in Islamic Contexts. 2006. Available online: http://cumincad.scix.net/data/works/att/2006_860.content.pdf (accessed on 17 June 2021).
- Guerritore, C.; Duarte, J. Design Computing and Cognition’12; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Tuhus-Dubrow, D.; Krarti, M. Genetic-algorithm based approach to optimize building envelope design for residential buildings. Build. Environ. 2010, 45, 1574–1581. [Google Scholar] [CrossRef]
- Bichiou, Y.; Krarti, M. Optimization of envelope and HVAC systems selection for residential buildings. Energy Build. 2011, 43, 3373–3382. [Google Scholar] [CrossRef]
- Ullrich, T.; Silva, N.; Eggeling, E.; Fellner, D.W. Generative modeling and numerical optimization for energy efficient buildings. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; IEEE: New York, NY, USA, 2013; pp. 4756–4761. [Google Scholar] [CrossRef]
- Kämpf, J.H.; Robinson, D. Optimisation of building form for solar energy utilisation using constrained evolutionary algorithms. Energy Build. 2010, 42, 807–814. [Google Scholar] [CrossRef]
- Duarte, J.P.; Rocha, J.M.; Soares, G.D. Unveiling the structure of the Marrakech Medina: A shape grammar and an interpreter for generating urban form. Artif. Intell. Eng. Des. Anal. Manuf. 2007, 21, 317–349. [Google Scholar] [CrossRef]
- Michalek, J.; Choudhary, R.; Papalambros, P. Architectural layout design optimization. Eng. Optim. 2002, 34, 461–484. [Google Scholar] [CrossRef]
- Junghans, L.; Darde, N. Hybrid single objective genetic algorithm coupled with the simulated annealing optimization method for building optimization. Energy Build. 2015, 86, 651–662. [Google Scholar] [CrossRef]
- Si, B.; Tian, Z.; Jin, X.; Zhou, X.; Tang, P.; Shi, X. Performance indices and evaluation of algorithms in building energy efficient design optimization. Energy 2016, 114, 100–112. [Google Scholar] [CrossRef]
- ANSI/ASHRAE Standard 55-2010; Thermal Environmental Conditions for Human Occupancy. American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2004. Available online: http://arco-hvac.ir/wp-content/uploads/2015/11/ASHRAE-55-2010.pdf (accessed on 25 June 2021).
- Juan, Y.-K.; Gao, P.; Wang, J. A hybrid decision support system for sustainable office building renovation and energy performance improvement. Energy Build. 2010, 42, 290–297. [Google Scholar] [CrossRef]
- Gero, J.S.; D’Cruz, N.; Radford, A.D. Energy in context: A multicriteria model for building design. Build. Environ. 1983, 18, 99–107. [Google Scholar] [CrossRef]
- Eisenhower, B.; O’Neill, Z.; Narayanan, S.; Fonoberov, V.A.; Mezić, I. A methodology for meta-model based optimization in building energy models. Energy Build. 2011, 47, 292–301. [Google Scholar] [CrossRef]
- Chen, J.; Gao, X.; Hu, Y.; Zeng, Z.; Liu, Y. A meta-model-based optimization approach for fast and reliable calibration of building energy models. Energy 2019, 188, 116046. [Google Scholar] [CrossRef]

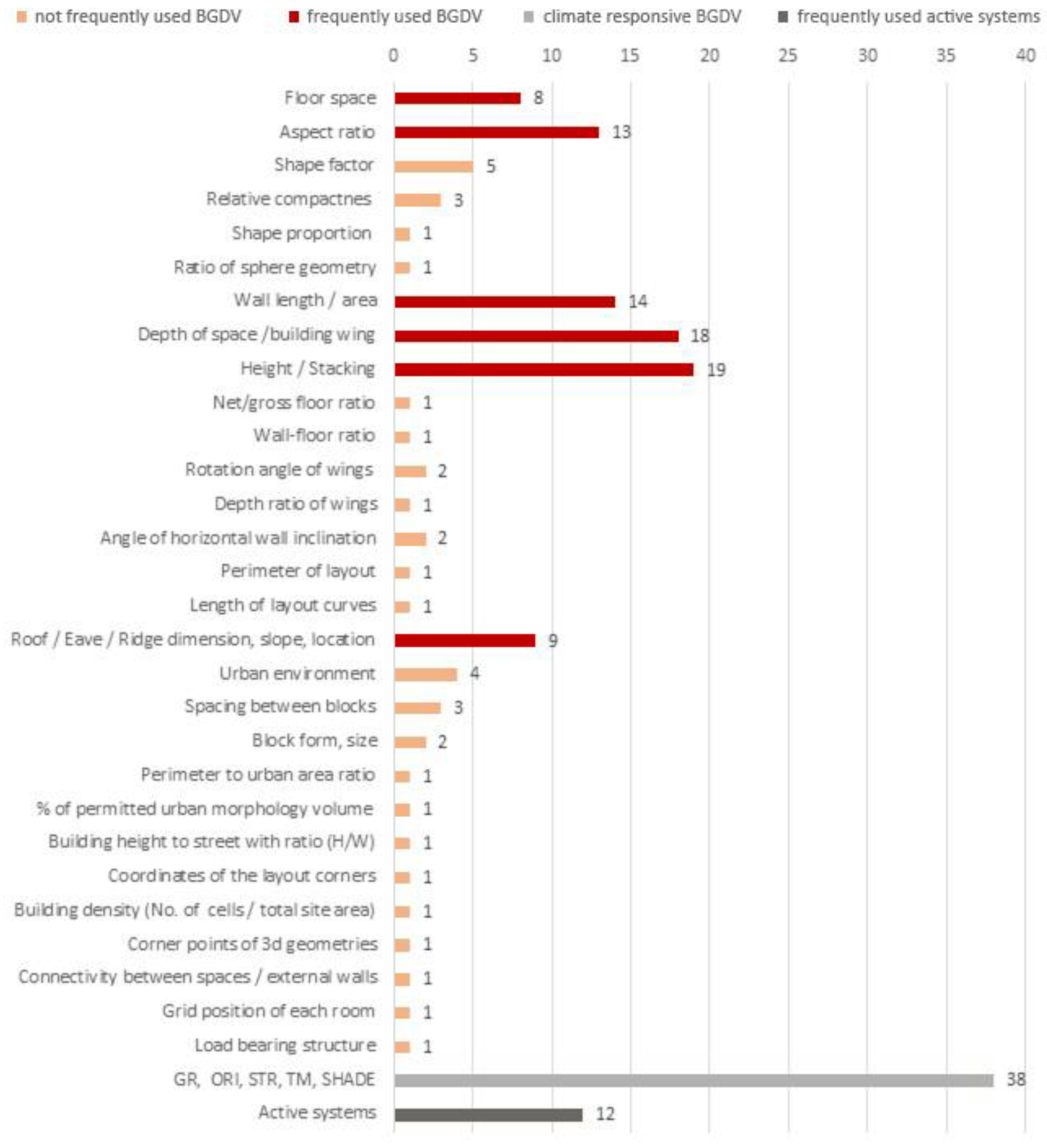



| Ref. No. | Year | Topic and Achievements | Objective Function | Building Geometry Design Variables |
| Limitations |
|---|---|---|---|---|---|---|
| [50] | 2019 | MO optimization of office building energy performance and daylight optimization against DOE commercial reference building template. Climate effect on daylight and energy performance in early-stage design. Depth of the building is greatly influenced by the climate. In hot and mixed climate, larger aspect ratios (1.97) are better, while in cold climates, lower aspect ratios (1–1.37) are advantageous. Roof ridge should be located around the center of the building. Most influencing design variables on EUI and UDI are skylights and windows and some shading properties. Building depth strongly determines the energy demand. |
|
|
| Very limited geometry-related design variables. GA; hence, only near-optimal solutions. Conclusions about building physics performance are not new. Definition of generation and population sizes are not justified. |
| [61] | 1987 | Pioneer study from the 1st authors (1983) investigating building energy optimization including shape and envelope variables. Office (2000 m2). Exemplary demonstration of the method. |
|
|
| Without simulation and advanced optimization algorithm. |
| [62] | 2001 | Building envelope optimization in sketch plan stage for family house in variable size—an interactive tool. Multiple criteria decision aid procedure (MCDA), integrating the client, design team, public authorities and users preferences, requirements, and constraints into the optimization process. (1) Definition of constraints and objectives, (2) feasibility study, (3) sketch design. Iterative intervention/optimization is carried out considering all participants requirements, performance results and design. |
|
|
| GA; hence, only near-optimal solutions. Only theoretical proposal. |
| [63] | 2002 | Three studies about a multicriteria optimization of building shape, internal wall partitions between apartments, and heat source utilization in multifamily housing (2133.3 m2). Decomposition in part-problems: shape, internal partitions, heat sources, and handling of global optimization problem. The shape of the prismatic building was determined in height, proportions of the sides, and ORI. By replacing the rectangular form by a rectangle and 2 trapezoids, an optimum shape was developed. |
|
|
| Very limited geometry related design variables. |
| [64] | 2002 | Low-energy building energy optimization of a community hall, 1 zone (200 m2) based on combined computer algorithm and human judgment. Finding an extensive range of possible near-optimum designs. Instead of the time-consuming process of classifying the architectural appeal of each design case generated by the GA (or to considerably reduce the number of processed designs for time saving), a histogram is proposed for each building variable. Cases can be analyzed and worked up to architectural sketches. Similar annual energy usage performing models possess different designs. Models with minimum heat losses apply insulation and compact shape, while models with maximized solar gains use more free form and greater windows. The combination of the 2 strategies is problematic due to summer overheating issues. |
|
|
| Very limited geometry related design variables. Conclusions about building physics performance are not new. GA; hence, only near-optimal solutions. |
| [65] | 2003 | Multi-objective optimization of schematic rectangle office and apartment building by composition of walls, generation of shapes and define HVAC systems. Pareto experiments: size and roof of each room are modified by the GA. A large diversity of the Pareto front building cases was achieved. Optimal solution for heating is obtained in a single, compact large building body with all-glazed S and W facade. In lighting demand, the optimum case provides small spaces easily penetrated by daylight with S facing large glazed facades. |
|
|
| No interdependencies and energy related logic can be detected in the random generation of the building form. Conclusions about building physics performance are not new. |
| [66] | 2003 | Office, 1092 m2, decision support system (DSS), involving two architects, two structural engineers, and one building services engineer in evaluation. Presenting a mathematical method. |
|
|
| Early stage optimization framework, need further development. Without geometry generation (only calculation). |
| [67] | 2005 | Proposed optimization method with multi-objective genetic algorithms for early design stage, demonstrated through an example (office, 1000 m2). LCEI is 65% reduced and operations within LCEI decrease by 20%. Aspect ratio 1 is preferred for cost reduction, but rectangular shape with long side to the south is better in energy efficiency. Trade-off between optimum aspect ratio for environment or for cost efficiency. Presenting and proofing a mathematical method. |
|
|
| Simple geometry, very limited geometry related variables. |
| [68] | 2005 | Proposing analytic target cascading (ATC), a multidisciplinary hierarchical optimization method. Presenting applicability via a pilot study (office-workshop building 597 m2). Presenting and proofing a mathematical method. |
|
|
| Early-stage optimization framework, need further development. |
| [69] | 2005 | The proposed method allows the designer to explore and visualize design evolution, form generation, and to interact in the optimization process. Through a GUI, the user selects an example from the shapes, and thereafter, the GA continues to search for the best solution. Automated mesh and CFD calculations. Example (generic, simple 1-room) for a continuous evolution of optimization by automatically creating discrete design instances and morphing them in between the process. Compared to conventional design: saving significant computation time, possibility to track relationship between variables and performances, possibility to evaluate trade-off between diverse solutions, possible novel design solution-configurations, because it is not biased by the designer’s view. |
|
|
| GA; hence, only near-optimal solutions. Taking designer’s preferences into consideration in the process means that the selected morph can be a promising solution but may still not be the guaranteed optimum. |
| [70] | 2007 | Optimization of the form of an office building on an oval base. Presenting and proofing a mathematical variational method. Heat losses and gains are reduced by approx. 10%. Optimized oval form performs better than circular or square base. |
|
|
| Simple geometry, very limited geometry-related variables. |
| [71] | 2009 | Presentation of an MDO by breaking down the system into building components (decomposition) using CAD and IFC-codes. Interactive method involving designer for quantitative and qualitative analysis. Presenting and proofing a mathematical method. Optimization of steel and wood frame load bearing structures in an industry hall (1200 m2). |
|
|
| Limited to variables of the structure’s geometry. |
| [72] | 2009 | MDO of a classroom building. Customized factorial design (DOE). Test application of the PIDO software to an AEC task. Investment cost of the structure decreases as the length of the space increases, because beam span reduces and becomes cheaper. Operation cost increases as the length increases due to greater surface area (heat loss), greater WWR with more solar gains and cooling demand. |
|
|
| Conclusions about building physics performance are not new. GA; hence, only near-optimal solutions. |
| [73] | 2013 | Residential house, economic incentives of energy cost optimal curves in net zero energy home (NZEH). MO analysis to find Pareto curves for the objective function. Net-zero energy performance is possible using passive solar design, improved HVAC system efficiency, and renewable sources (PV-panels). The cost-optimal case has an energy performance of approx. 10,000 kWh/a. A NZEH costs approx. the same as the reference building (Building America reference building DOE 2010) over a 30-year life-cycle. |
|
|
| In terms of building physics, the conclusion is not new knowledge. No information is available about the building geometry, size, etc. |
| [74] | 2014 | Multi-objective optimization of low-cost residential housing (LCH) in 3 different climates (China). Exemplary demonstration of the method. Geometry related conclusions as design aid: In tropical monsoon climates, in buildings with NV and/or AC E-W, elongated rectangular shape is recommended. In sub-tropics, the square shape is recommended when NV is operated. Climate has a decisive impact on building operation (passive or active) type. |
|
|
| Very limited geometry related design variables. |
| [75] | 2015 | Office, 1 representative floor (1000–2000 m2). Searching for the set of design variables to minimize heating and cooling load. DOE produced possible design variable configurations. The design variables were obtained statistically in a polynomial equation form to determine the Pareto front. The method uses a subset of all possible combinations of design variables to ease exhaustive full factorial design with a large number of test runs. (1) A large number of variables are modeled and assessed as a screening to find the important ones. (2) Functional relations are explored about the variables’ impact on objective functions. (3) Optimization of the variables. Variables of windows and air leakage affect energy load significantly, while aspect ratio is ineffective. HVAC system affect passive design. |
|
|
| Very limited geometry-related design variables. Shape design variables and enveloped design variables (WWR, materials) are simultaneously examined; hence, importance of geometry as primary architectural-functional premise is overwritten by design technologically subsequent and more expensive design steps. Conclusions do not contain new knowledge. |
| [76] | 2015 | MO optimization of thermal comfort and energy in building design (multi-family house). GA optimizes the back propagation (BP) ANN’s weight and threshold. Simulation-based GA-BP network training and result validation. Thereafter, NSGA-II optimization: evaluation of the potential solutions. Significant (approx. 50%) improvement in energy and insignificant improvement in comfort. |
|
|
| Very limited geometry-related design variables. Limited to a rectangular shape with a known total floor area. There is need for extensive testing results for further building geometry and type training samples. |
| [77] | 2019 | MO BEO. Pareto optimization of geometry, envelope, and energy systems. Proposed optimization framework ’Harlequin’ (unevenness in the diversely oriented facades, materials, colors, WWR, thermal-radiative characteristics): (1) GA generates optimal non dominated solutions; (2) Smart exhaustive sampling of optimal (minimized) PEC, global cost (GC) and investment cost (IC) scenarios. Decision makers can choose the "best" solution according to their needs. Example (office, 2700 m2) modelling and calculations. Recommendations on optimal geometry (aspect ratio 1) and WWR. |
|
|
| Very limited geometry-related design variables. GA; hence, only near-optimal solutions, ’ad hoc’ randomly solution generation. Conclusions about building physics performance are not new. The method is not user-friendly and requires expertise in programming and BEO. Definition of generation and population sizes are not justified. |
| [78] | 2020 | SO and MO environmental optimization of apartment buildings (740 m2). Presented method with LCEI example calculations. Approx. 4–6 story compact, close-to-cube shape with somewhat larger S facade, large WWR (approx. 60%) to the S and small WWR to the N. In optimization of the trade-off between embodied and operational impact, the single objective optimization (SO) preferred compact shape with fully glazed facades and the operational impact optimization resulted in large southern facade (max. solar gains) and extensive insulation (loss reduction). In the case of the optimization of SO + MO: a nearly cubic shape with optimized WWR for solar gains (double glazing) in the S facade and the rest of the facades are optimized for low transmission losses (triple glazing). 60–80% environmental savings achieved in MO environmental impact optimization. Similar results are achieved with significantly diverse solutions. |
|
|
| GA; hence, only a range of near-optimal solutions. GA acts as a ’black box’; hence, the designer cannot follow what is exactly happening in the calculations. Only steady-state energy calculations. |
| [79] | 2021 | MO optimization of a regular classroom space. ANN, a popular type of surrogate models accelerates regular simulation time by factor approx. 2570. 14.2–24.6% average performance improvement in the 3 objective function (integrated solution). |
|
|
| Very limited geometry-related design variables. Randomly generated design cases by parametric tools for ANN training dataset; hence, the optimum may be missed. Unclear distinctions in 3 different cases using alternating geometry, orientation, WWR, shading, solar absorptance. Conclusions about building physics performance are not new. |
| [80] | 2021 | Machine learning-based thermal optimization of residential buildings (2000; 4000; 6000 m2). Latin Hypercube sampling (LHS) generates building configurations. Gradient boosting machine (GBM) is trained by simulation-based dataset for target result prediction. GA optimizes with the surrogate GBM model. Optimal aspect ratio values were found in the 3 alternating locations (climates) and 3 different building heights (5, 10 and 15) ranging 0.67–1.67. |
|
|
| Very limited geometry related design variables. GA; hence, only near-optimal solutions, randomly generated. Conclusions about building physics performance are not new. Definition of generation and population sizes are not justified. |
| [81] | 2021 | The position and the height of residential high-rise buildings has a significant effect on internal and external (urban spaces) visual and thermal comfort. Top 10 optimized cases (urban configurations) were selected. |
|
|
| Limited geometry optimization. Mainly visual comfort optimization only. |
| [82] | 2021 | Geometry-related performance optimization using an automatic recognition and conversion method with a preference based optimization algorithm to help the designers’ decision-making process. (1) Preferences determination by the designer with software assistance. (2) Preference based optimization algorithm searches for optimum solutions. (3) Designer selects the best solution. |
|
|
| Preliminary specific preference model design is required from the designer. |
| Ref. No. | Year | Topic and Achievements | Objective Function | Building Geometry Design Variables |
| Limitations |
|---|---|---|---|---|---|---|
| [38] | 2009 | Proposing an agent-based geometry generation system based on hierarchical geometry relations. Morphing geometries through agent and child points as 3D corner points of geometries. A cuboid reference building geometry (225 m2 redisential building) was modified to an optimal shape with minimal heat loss. Unique geometry generation approach (free forming) to handle complete building geometries in free form. 12% heat load by volume and 6% heat flow per envelope area could be saved. |
|
|
| Simple example of a building with limited geometry variables and impractical and building envelope surfaces, making construction expensive. |
| [39] | 2020 | Multi-objective building shape and envelope optimization of an apartment block (8000 m3, 4–8 levels; 2673 m2, 6 levels). Phase I: geometry optimization of common linear (I), L- (L), court (O), C- (C), T- (T), H- (H), cross (X), and Y-shaped (Y) buildings (LOD 100) with WWR and ORI options. O, T, H, X, and Y-shapes perform as Pareto optimal solutions. Main reason for that is the self-shading effect of these bodies and the minimization of the SF. The optimal building geometry as output from Phase I is input to Phase II, applying passive and active strategies (LOD 300) to further optimization. |
|
|
| Definition of generation and population sizes is not justified (only according to the literature). Geometry optimization of useful floor space and volume, but missing consideration of the different envelope sizes of the diverse shapes and their investment cost. Only single-zone thermal simulation models of multi-story blocks are calculated. This simplification leads to inaccurate or unrealistic results. GA; hence, only near-optimal solutions, randomly generated and therefore hypothesized conclusions. Conclusions about building physics performance are not new. |
| [44] | 2010 | MO optimization of solar energy use (heating, lighting) in an urban district with 18,000 evaluations. ’Terraces Flat Roofs’ (E-W building axis), ’Slabs Sloped Roofs’ (N-S building axis) and ’Terrace Courts’ (courtyards) morphology versions were examined, and the latter performed best in energy gains and losses based on greatest collector surface while the volume remain compact. Medieval settlement morphology has more form-related (compact) structure to minimize losses. Modern settlement morphology requires new forms with less density to utilize solar gain. |
|
|
| EA was used with Pareto optimization to make up for the missing convergence check. This way, only a nearly optimal solution is achievable. |
| [45] | 2006 | Pentagon-shaped office layout optimization. The length-bearing method (polygon represented by the bearing = angle between north and an edge, ORI = 1st edge bearing) perform better than the length–angle method (polygon represented by length of the edges and the angle between two adjacent edges, ORI = 1st edge angle to true north) in the framework of MOGA. Low LCC is performed by close to regular pentagons and low LCEI is caused by larger (wider) south facing facade-shapes. |
|
|
| Demonstration of the method rather than comprehensive geometry generation and optimization. GA; hence, only near-optimum search. |
| [49] | 2019 | Optimization of simple office building blocks’ geometry (energy demand) in an urban environment coupled with renewable energy potentials and concurrent decentralized multi-energy systems (MES). Optimization of the corner points horizontal and vertical positions. In extreme carbon scenarios, the optimal forms are regular, while in the in-between carbon scenarios, the geometries become more irregular (balancing solar and daylight harvesting with available floor space and ORI). Consecutive optimization: 1st geometry optimization, and then energy system and solar potential optimization. Nested optimization: geometry, energy, and solar optimization takes place simultaneously. The consecutive optimal shapes have N-S ORI, while the nested ones have isotropic bodies. Shape and energy systems are mutually dependent and should be simultaneously optimized. |
|
|
| Black-box optimizer because geometrical optimization problem is difficult to solve in an analytical form and simulation programs are complex. Limited simplified geometries. Since shape has a decisive impact on energy demand, system efficiencies and renewable energy potential, as well as HVAC systems may rapidly become obselete compared to a building geometry and structure, certain preliminary choices on energy systems should not influence building densities, ORI and shapes or should be carefully considered with LCA in mind. |
| [88] | 2010 | Different letter-shaped, rectangle, and trapezoid layouts are investigated in 2-story residential homes. Rectangle and trapezoid shapes have best performance. When only shape variable is considered: S facing trapezoid in sunny heating climates, and N facing trapezoid in cooling climates are preferable due to solar gain through windows. When geometry, WWR, and material variables are considered in combination: little difference occurs between the optimal shapes. Lowering U-values decrease the impact of geometry and WWR in colder climate zones, and in warmer climates, overheating inverts this tendency. Architects have great flexibility in form design in cold climates. Results of building shapes with max. LCC (max. surfaces, aspect ratio) show large differentiations, indicating building geometry’s decisive impact on energy efficiency. |
|
|
| This study did not consider that after optimization of the mass shape, significant savings in further passive and active improvements are achievable: shape design modifications have lower initial costs compared to subsequent investments into material and HVAC systems (LCCA); hence, building geometry is not independent from energy design. |
| [89] | 2011 | Different letter-shaped, rectangle, and trapezoid layouts are investigated in 2-storey residential buildings. SO optimization of the HVAC systems, simultaneous (full) optimization of building envelope and HVAC system and in a sequential manner (1st envelop then HVAC optimization). According to different optimization domains (envelope and HVAC) and constraints diverse shapes perform better. In five US cities, the full optimization rectangle shape (AR 1) performs best, while in energy cost full optimization, diverse forms deliver the best results. |
|
|
| No interdependencies between BGDV and optimization results provided. |
| [90] | 2013 | Geometry optimization of a tunnel formed greenhouse (1000 m3) and a 25,000 m2 spherical city-hall inspired by the existing London City-Hall (Arch.: Norman Foster): energy savings roughly estimated. Axes ratio and arch ratio of ellipsoid sphere geometry has greatest effect on energy use, best axes ratio is 1.0–1.2 (almost rotationally symmetric cupola geometries). Orientation does not significantly influence the results. |
|
|
| Limited geometry related variables and poor description of calculations, modelling, and results. |
| [91] | 2010 | Hybrid evolutionary algorithm is applied with constraint handling as a method for urban building configuration optimization. Three applications: cuboid buildings in an urban block; complex extension building roof shapes adjacent to an existing house; rectangular plan building’s volume is parametrized by Fourier series. |
|
|
| Interesting, diverse applications of the method, but demonstrative rather than systematic optimal building generation procedure. |
| Shape Significantly Describing BGDVs | 1987 | 1990 | 2001 | 2002 | 2003 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Floor space | [61] | [57] | [58] | [66] | [75] | [60] | [41] | [82] | ||||||||||||||
| Aspect ratio | [61] | [62] | [67] | [88] | [89] | [73] | [74] | [46,75] | [60] | [77] | [78] | [80] | ||||||||||
| Shape factor | [6] | [42] | [48] | [76] | [55] | |||||||||||||||||
| Relative compactnes | [43] | [7] | [55] | |||||||||||||||||||
| Wall length/area | [57] | [58,63,64] | [65] | [68,69] | [7,72] | [54] | [74] | [60] | [41] | [79] | ||||||||||||
| Depth of space/building wing | [57] | [58,63,64] | [42,65,66] | [69] | [7] | [88] | [54,90] | [74] | [60] | [41,50] | [79,82] | |||||||||||
| Height/Stacking | [61] | [63] | [66] | [69] | [70] | [44,91] | [90] | [46] | [53] | [60] | [56] | [40,41,49] | [37,79,80,81] | |||||||||
| Roof slope/Eave/Ridge location | [62] | [64] | [65] | [45] | [44,91] | [73] | [46] | [50] |
| 1987 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Geometry generation + energy evaluation + optimization | [93] | [40,41] | ||||||||||||||||||||
| Geometry modification (advanced) + energy evaluation + optimization | [1] | [38] | [44,88,91] | [90] | [49] | [39] | ||||||||||||||||
| Geometry modification (basic) + energy evaluation + optimization | [61] | [62] | [63,64] | [65] | [67,68] | [70] | [7] | [73] | [74] | [75,76] | [50,77] | [78] | [37,79,80,81,82] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kistelegdi, I.; Horváth, K.R.; Storcz, T.; Ercsey, Z. Building Geometry as a Variable in Energy, Comfort, and Environmental Design Optimization—A Review from the Perspective of Architects. Buildings 2022, 12, 69. https://doi.org/10.3390/buildings12010069
Kistelegdi I, Horváth KR, Storcz T, Ercsey Z. Building Geometry as a Variable in Energy, Comfort, and Environmental Design Optimization—A Review from the Perspective of Architects. Buildings. 2022; 12(1):69. https://doi.org/10.3390/buildings12010069
Chicago/Turabian StyleKistelegdi, István, Kristóf Roland Horváth, Tamás Storcz, and Zsolt Ercsey. 2022. "Building Geometry as a Variable in Energy, Comfort, and Environmental Design Optimization—A Review from the Perspective of Architects" Buildings 12, no. 1: 69. https://doi.org/10.3390/buildings12010069
APA StyleKistelegdi, I., Horváth, K. R., Storcz, T., & Ercsey, Z. (2022). Building Geometry as a Variable in Energy, Comfort, and Environmental Design Optimization—A Review from the Perspective of Architects. Buildings, 12(1), 69. https://doi.org/10.3390/buildings12010069







