Abstract
The rapid growth of energy consumption in commercial building operations has hindered the pace of carbon emission reduction in the building sector in China. This study used historical data to model the carbon emissions of commercial building operations, the LASSO regression was applied to estimate the model results, and the whale optimization algorithm was used to optimize the nonlinear parameter. The key findings show the following: (1) The major driving forces of carbon emissions from commercial buildings in China were found to be the population size and energy intensity of carbon emissions, and their elastic coefficients were 0.6346 and 0.2487, respectively. (2) The peak emissions of the commercial building sector were 1264.81 MtCO2, and the peak year was estimated to be 2030. Overall, this study analyzed the historical emission reduction levels and prospective peaks of carbon emissions from China’s commercial buildings from a new perspective. The research results are helpful for governments and decision makers to formulate effective emission reduction policies and can also provide references for the low-carbon development of other countries and regions.
1. Introduction
The building sector is one of the top three main drivers of global energy consumption and carbon emissions [1]. According to the report from the 2019 United Nations Climate Conference, carbon emissions caused by the global building sector account for 40% of total emissions [2]. Carbon emissions from commercial buildings have been highly valued worldwide. For the present situation in China, the growing tertiary industry economy and the rising energy demand for commercial buildings have brought severe challenges to China’s low-carbon development [3].
On the other hand, many studies have suggested that targeting carbon emissions from commercial buildings is critical to mitigate the future global climate crisis [4,5,6]. To further advance the process of China’s emission reduction and energy conservation, especially the carbon emissions released by the commercial building sector, efficiently and reasonably assessing historical emission reduction levels and predicting the roadmap for peaking carbon emissions in the future is exceedingly important and should not be delayed. To achieve these tasks, two questions should be considered:
(a) What are the major driving forces of carbon emissions from China’s commercial buildings?
(b) What does the low-carbon development of carbon emissions from commercial buildings in China look like?
In order to answer the above questions and thus tap into the emission reduction potential of China’s commercial building sector, this research first used the LASSO regression model to estimate the coefficients of the carbon emissions model, and then the tunable parameter of the LASSO regression was determined via the popular whale optimization algorithm. The major driving forces of carbon emissions from commercial buildings in China were then determined. Furthermore, combined with the proposed carbon emissions model and scenario analysis, the carbon emissions of commercial buildings in China until 2060 were predicted.
The most outstanding contribution of this work is its use of a new LASSO model approach to estimate the results of the carbon emissions model, thereby identifying the major driving forces of commercial building carbon emissions and analyzing the emission pathway to 2060. To the best of the authors’ knowledge, former research work has not truly reflected the major forces of carbon emissions, and the contribution degrees of different driving forces have not been fully considered when analyzing the peak situation of carbon emissions. As a result, the proposed peaking plan and emission reduction measures may not be sufficiently accurate and feasible, a point which will be further discussed in the following section.
The rest of this study consists of the following four parts: Relevant research on carbon emissions from commercial buildings is reviewed in Section 2. The materials and methods applied in this study are presented in Section 3, which includes the carbon emissions model for commercial buildings in China, the LASSO regression model with the whale optimization algorithm, and the dataset used in this research. In Section 4, three results and the discussion are given: Section 4.1 presents the multicollinearity test results of potential influencing factors, Section 4.2 shows the identification results of the major driving forces of carbon emissions from commercial buildings in China, and Section 4.3 presents the emission roadmap for commercial buildings in China to 2060. Finally, the core findings and upcoming studies are summarized in Section 5.
2. Literature Review
Reliable data sources are an important prerequisite for ensuring the accuracy of results. In this research work, the historical carbon emission data on China’s commercial buildings were derived from the China Building Energy and Emission Database (CBEED) [7,8]. CBEED, a multipurpose database developed by the China Building Energy Conservation Association in 2018, covers energy consumption, emissions, and other related data on China’s construction industry. The database has been recognized in the industry and has provided important support for energy conservation and emission reduction in China’s construction sector. Figure 1 demonstrates the trends of commercial buildings’ carbon emissions in China collected by CBEED from 2000 to 2018. These historical data were utilized to quantify the major driving forces and to obtain the future carbon emission predictions.
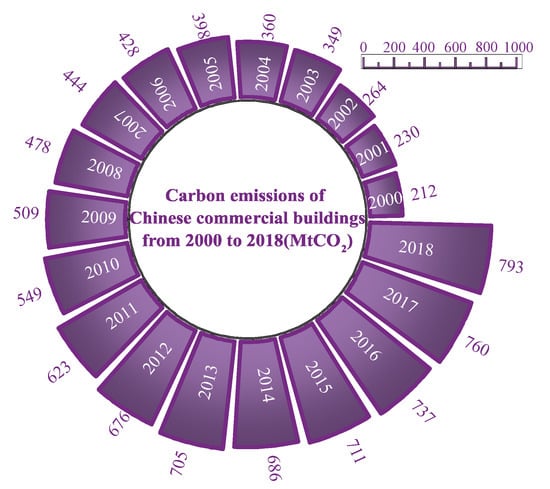
Figure 1.
Carbon emissions from China’s commercial buildings from 2000 to 2018.
In recent years, government officials and research institutions have paid great attention to the importance of identifying the influencing factors of carbon dioxide emissions for carbon emission reduction [9,10,11]. As a result, a number of techniques have been explored to help identify the driving factors of carbon emissions [12,13,14]. The STIRPAT model is a tool used to analyze the influencing factors of carbon emissions and has been widely used in many key emission reduction areas, including the transportation sector [15,16], industrial sector [17,18], and building sector [19,20,21]. However, existing research shows that there are often correlations between potential influencing factors, which reduce the accuracy of model analysis results. Therefore, in exchange for more reasonable results, some methods have been proposed to sacrifice the accuracy of the model, including ridge regression [22,23,24], partial least squares (PLS) [25,26], system-GMM estimator [27,28], and seemingly unrelated regressions (SUR) [29]. On the other hand, scenario analysis, which is used to investigate the change trends of an object in the future under the influence of factors such as social and economic development, technological progress, and policy implementation, is very popular in the analysis of the peak carbon emissions from the construction sector in China [30,31]. Recently, Ma and his collaborators [32] developed a scenario analysis method with uncertain effects, which provides a new way of thinking about emission reduction policies. Given the mentioned analysis, the following two issues need to be addressed:
Regarding the major driving forces of carbon emissions from commercial buildings in China, although these existing efforts have achieved some success, the redundant potential influencing factors cannot be identified and eliminated, which means that high control costs are involved, and policies are difficult to implement due to the interaction of influencing factors.
Regarding the analysis of the carbon emission pathway of commercial buildings, the existing scenario analysis mainly sets scenario assumptions for different impacts based on the KAYA identity, ignoring differences in the importance of different influencing factors. Therefore, this research aims to analyze the future carbon emissions from commercial buildings in China based on carbon emissions models with different influencing factors.
In order to make up for the above-mentioned gaps, the contributions of this study are:
(a) A new tool to assess the historical carbon emissions from China’s commercial buildings is proposed. The LASSO model was first used to estimate the model’s regression coefficients, and the whale optimization algorithm was employed to optimize the nonlinear parameters of the LASSO regression model. LASSO’s feature selection ability is one of its unique advantages. Fewer and more critical factors are identified, further reducing the cost of implementing emission reduction policies.
(b) The pathway of carbon emissions from commercial buildings in China is simulated. Based on the carbon emissions model estimated by the LASSO regression model, this study performed a scenario analysis of Chinese commercial buildings to obtain a carbon emission roadmap for 2060. The analysis results provide guidance for formulating peak plans and reshaping the low-carbon model of China’s commercial buildings.
3. Materials and Methods
3.1. Carbon Emissions Model of Commercial Buildings in China
3.1.1. STIRPAT Model
The stochastic impacts by regression on population, affluence, and technology (STIRPAT) model, initially formulated by Dietz and Rosa in 1971 [33] to meet the needs of statistical testing, was based on the IPAT model, which is an important tool often used to reveal the impacts of human behavior on the environment. After 50 years of development, the IPAT model has been widely recognized and applied in many disciplines such as energy economics [34,35,36], environmental economics [37,38], and climate change economics [39] by virtue of its unique advantages. In addition, a growing number of studies have shown that the IPAT model plays an important role in the study of factors affecting carbon emissions.
In general, the classic IPAT model [40] can be written as:
where represents the constant term, , and represent the parameters to be estimated, and represents the stochastic error term. represents the environmental pressure caused by the influencing factors and , , and represent the total population, affluence, and technical level, respectively. In empirical analysis, Equation (1) is often transformed into a linear logarithmic form, that is, into the STIRPAT model:
The coefficients of the STIRPAT model can be considered as representing the impact of driving forces on environmental pressure. Generally, coefficients greater than zero indicate that the driving forces can enhance carbon dioxide emissions from commercial buildings in China, while coefficients less than zero indicate that the driving forces can curb carbon emissions from China’s commercial buildings. In particular, absolute values of the coefficients equal to 1 indicate that the driving forces and carbon dioxide emissions have the same rates of change, and the coefficients equal to zero indicate that the driving forces have no influence on environmental pressure.
3.1.2. Carbon Emissions Model of Commercial Buildings in China
The environmental pressure of the STIRPAT model can be characterized by different indicators, and additional influencing factors can also be considered as part of the technical impact in order to build the model. In our research work, environmental pressure was represented by the carbon emissions released by the commercial buildings in China. Further, the potential influencing factors are summarized in Figure 2, which includes: population size , GDP per capita , industrial structure , industrial efficiency , energy intensity , and emission factor . In addition, they are defined as follows:
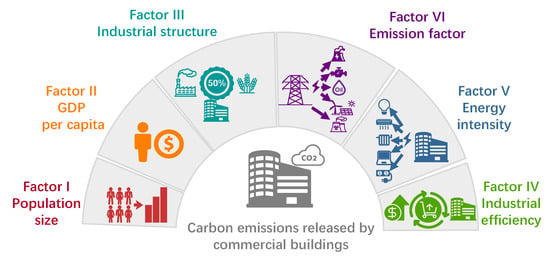
Figure 2.
Potential driving forces of carbon emissions from China’s commercial buildings.
Therefore, the carbon emissions model for commercial buildings in China can be expressed as follows:
3.2. LASSO Regression Model with Whale Optimization Algorithm (WOA)
In the last subsection, we proposed a carbon emissions model for commercial buildings in China according to the classic STIRPAT model. The parameter estimation method of the carbon emissions model will be further introduced in this subsection.
3.2.1. LASSO Regression Model
The proposed carbon emissions model (Equation (4)) can be regarded as a classic multiple linear regression model, and it can be expressed in a vectorized form as follows:
where and represent the independent variable and dependent variable, respectively, and represents the model parameter to be estimated, which reveals the influence of driving forces on the carbon emissions of commercial buildings in China. To our best knowledge, the parameters of the multiple linear regression model can be estimated via the classical least-square regression rule, and the parameter estimation expressions are as follows:
Additionally, we should note that when there is multicollinearity between the driving forces, the calculation of the inverse matrix of the matrix will produce serious errors. As a result, the stability of the estimated value is reduced, and an incorrect estimation result may even be obtained. Pearson correlation coefficient is one of the important criteria for assessing multicollinearity [41], which is defined by the standard deviation and covariance and for which the expression can be written as:
where represents the sample covariance of and , and represents sample variance. Mathematically, the Pearson correlation coefficient takes values between −1 and 1 [42,43]. The larger the absolute value of , the stronger it reveals the correlation between the variables. Conversely, the correlation is weaker. To address this issue, ridge regression has been widely utilized, showing satisfactory results in a large number of studies. The ridge regression model can be given as follows:
where is the L-2 regularization term, and is the nonlinear parameter that constrains the regularization term. The LASSO regression model [44,45] was first proposed by statistician Robert Tibshirani in 1996 and is written as follows:
Unlike the ridge regression model, LASSO regression uses L-1 regularization. Obviously, LASSO can more easily constrain the parameters of the model to 0. Therefore, LASSO regression is good at performing feature selection, that is, at removing irrelevant or redundant features.
3.2.2. Formulating the Nonlinear Optimization Problem for
Once the nonlinear parameter in the model is determined, the linear parameters of the model can be directly estimated. Therefore, the value of the nonlinear parameter of the LASSO regression model directly determines the parameter estimation results of the carbon emissions model for China’s commercial buildings. In this study, the nonlinear parameters of the LASSO regression model were determined by cross-validation. Specifically, the historical carbon emission data were first divided into a training set and a test set. The training set was applied to establish the emission model, and the test set was used to establish a nonlinear constrained optimization problem in order to determine the optimal nonlinear parameters.
For convenience, the mean absolute percent error (MAPE) [46] was employed as the metric for evaluating the performance of the models in this paper, and it can be defined as follows:
After reorganizing the above knowledge, we can formulate the nonlinear optimization problem for as follows:
3.2.3. Whale Optimization Algorithm
Traditional mathematical methods are often faced with the dilemma of a complex and time-consuming solution when dealing with Equation (11). The swarm intelligence optimization algorithm is an alternative scheme that has been widely utilized in many fields, such as in energy [47,48,49,50] and environmental studies [51,52,53,54] and economics [55,56,57], and it has shown outstanding performance due to its advantages of simple operation and fast calculation.
The whale optimization algorithm (WOA) is a popular swarm intelligence optimization algorithm first put forward by Mirjalili et al. in 2016 [58]. The mathematical model of the WOA is established based on three different predation strategies of simulated humpback whales, including the shrinking encircling mechanism, spiral search, and random exploration strategy. For convenience, is used to represent the humpback whale’s current position. Assuming that the prey’s position is the current optimal solution and is represented by , the humpback whale’s shrinking encirclement strategy can be defined as:
where is a random vector in (0, 1), and represents the maximum number of iterations. In addition, humpbacks also spiral in the following way:
where is a random number in (–1, 1), and represents a constant that determines the shape of the spiral. Generally, humpback whales search for prey through random exploration when , and their position update strategy can be mathematically expressed as:
where is the position of a random individual in the herd.
3.3. Dataset
In order to identify the driving forces affecting the carbon dioxide emissions from China’s commercial buildings, the driving forces were calculated according to the time-series cross-section data of China from 2000 to 2018, and the calculation method is introduced in Section 3.1.2. The data on population size () and gross domestic product () were accessed from the Statistical Yearbook of China, which is directly cited in this paper. Data on the carbon emissions (), gross floor space (), and energy consumption () of the commercial building sector were collected from the CBEED database.
4. Results and Discussion
In this work, the carbon emissions from commercial buildings in China from 2000 to 2018 were employed to construct the proposed carbon emissions model. Firstly, the multicollinearity test was performed, and the results are presented in Section 4.1. Subsequently, the major driving forces of historical carbon emissions and the future low-carbon emissions pathway for China’s commercial buildings are presented.
4.1. Multicollinearity Test of Driving Forces
Figure 3 depicts the changing behavior of the potential driving forces of carbon emissions from commercial buildings in China from 2000 to 2018. The potential influencing factors, after taking the logarithm as the dependent variable, were input into the carbon emissions model. Then, the multicollinearity test of the independent variables was performed according to Equation (7); the results are also shown in Figure 3. Most of the P values were lower than 0.001, which reveals that these potential driving forces had a significant correlation. Further, the absolute values of most Pearson correlation coefficients were greater than 0.8. The test results indicate that there was serious multicollinearity among the potential influencing factors, and that the traditional least squares regression parameter estimation method is no longer applicable.
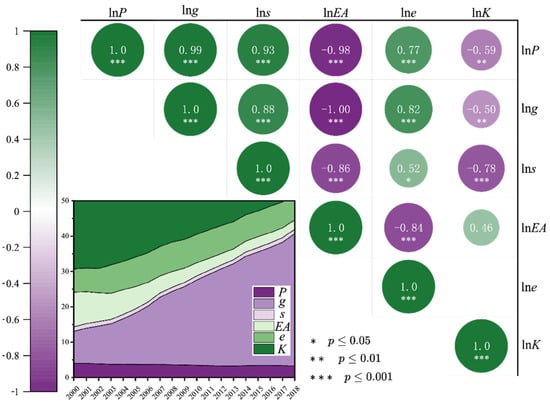
Figure 3.
Multicollinearity test results of potential driving forces of carbon emissions from commercial buildings.
4.2. Major Driving Forces of Historical Carbon Emissions
The commercial buildings’ historical carbon emission data and their potential influencing factors were divided into a training set and a test set. The historical data from 2000 to 2015 were utilized as the training set in order to construct the carbon emissions model of commercial buildings in China, and the historical data from 2016 to 2018 were utilized as the test set to optimize the nonlinear parameter of the LASSO model. Then, the coefficients of the carbon emissions model were estimated via a LASSO regression model optimized by the whale optimization algorithm. In this paper, the maximum number of iterations was set to 100, and the search agents for the whale optimization algorithm were set to 50. The upper and lower bounds of the nonlinear parameters to be optimized were set to 0 and 100, respectively.
Figure 4a shows the convergence curve of the WOA optimization algorithm, which was used to optimize the LASSO regression model, with the curve showing how the training error, test error, and nonlinear parameters changed as the iterations of the algorithm progressed. After about 50 iterations, it can be observed that the optimal nonlinear parameter was 0.1385, and that the training set and the test set eventually converged to 0.6677 and 0.0115, respectively.
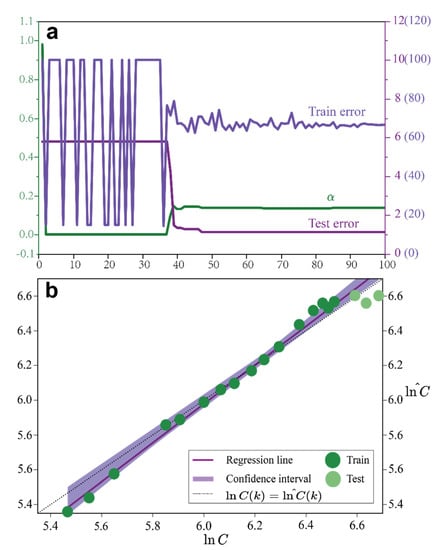
Figure 4.
(a) Convergence curve by the WOA for the LASSO regression model and (b) the comparison of actual carbon emission data and the calculated results of the proposed model.
In addition, the WOA algorithm fell into the local optimum during the early period of the algorithm iteration. Further, the nonlinear parameter was 0 at this moment, which means that the LASSO regression model degenerated back to the ordinary least square multiplicative regression. As mentioned above, the interference of multicollinearity will result in the failure of the classical multiple regression model to accurately estimate the coefficients of the model, which can also be verified by the convergence curve. However, as the nonlinear parameter alpha gradually converged to the optimal value, the model coefficient estimated by the LASSO regression model became more stable, and the training error did not change.
Then, by substituting the optimal nonlinear parameter into Equation (9), the carbon emissions model of the commercial buildings was obtained as follows:
Moreover, the forecast result based on Equation (17) and the actual historical emission data were compared to examine the validity and reliability of the model, with the results illustrated in Figure 4b. It can be noticed that the regression line of the carbon emissions model proposed in this paper was quite close to the ideal regression line, and the overall fitting was very good, which shows that the parameter estimation results of the carbon emissions model based on the LASSO model with the whale optimization algorithm were acceptable. Therefore, the main driving forces of carbon emissions from commercial buildings in China can be interpreted as the population size () and energy intensity ().
According to the results of the commercial carbon emissions model estimated in this study, in the past two decades, the increase in carbon dioxide emissions from commercial buildings was mainly due to changes in population size () and energy intensity (). The size of the population was found to have a significant promoting effect on carbon dioxide emissions. Its elasticity coefficient was 0.6346, which means that for every 1% increase in the population of China, carbon dioxide emissions will increase by 0.6346%. This is because this increase in the size of the population will directly lead to the reduction of space for human activities in commercial buildings, thereby increasing environmental pressure. On the other hand, as the basic prerequisite for economic development, energy consumption is also the main force in the production of carbon dioxide emissions. The results suggested that for every 1% increase in energy consumption intensity, carbon dioxide emissions will increase by 0.2487%. Therefore, in order to reduce the carbon emissions of commercial buildings in China, the population size and energy intensity in China’s commercial buildings must be focused on.
4.3. Low-Carbon Pathway to Future Carbon Emission
Furthermore, the proposed carbon emissions model was also utilized to predict the carbon emission pathway of commercial buildings in China. Similarly, historical data from 2000 to 2015 were utilized as the training set, and the remaining data from 2016 to 2018 were utilized as the test set. The carbon emissions model was also solved by the LASSO regression model with the whale optimization algorithm. The scenario settings in the literature [32] were adopted and input into the carbon emissions model in order to predict the trajectory of carbon emissions from 2019 to 2060.
Figure 5 presents the historical carbon emission data from China’s commercial buildings and their future emissions path. The forecast results indicate that carbon emissions will reach their peak in 2030 and that the peak value will be 1264.81 MtCO2, which reveals that China’s commercial buildings are expected to achieve their carbon peak on time. For the next three decades after the peak, the carbon emissions of commercial buildings in China will no longer increase, declining at an average rate of 34.52 MtCO2 per year. The carbon emissions from commercial buildings in China will drop to 229.31 MtCO2 by 2060, which is still a significant number; therefore, greater determination and effort need to be devoted to help achieve carbon neutrality.
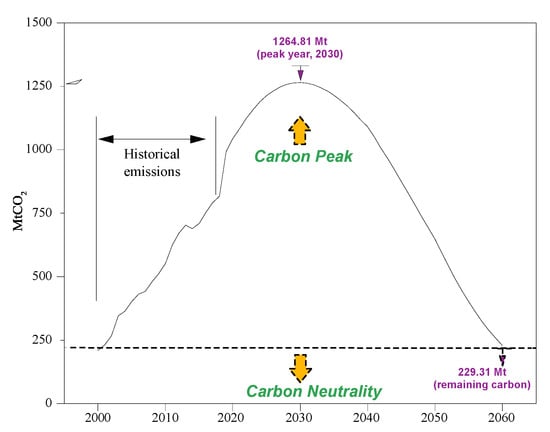
Figure 5.
Historical carbon emissions of and future peak roadmap for commercial buildings in China.
5. Conclusions
This study used the classical STIRPAT model to construct a carbon emissions model for commercial buildings in China, with the LASSO regression model first being applied to estimate the regression coefficients. Then, the whale optimization algorithm was employed to determine the optimal nonlinear parameter of the LASSO regression. Finally, the carbon emissions model was utilized to make historical assessments of carbon emissions from 2000 to 2018 and to further predict the carbon emissions pathway of China’s commercial buildings from 2019 to 2060. In this paper, the properties of LASSO regression are applied to filter out fewer major driver forces and thus reduce decision costs. However, this also means that it becomes more important to build a reasonable carbon emission model; therefore, a more comprehensive consideration of potential influencing factors is needed. Overall, the core findings and upcoming studies can be summarized as follows:
(1) Historical trends show that the major driving forces for carbon emissions of commercial buildings in China were found to be population size and energy intensity, and their elastic coefficients were 0.6346 and 0.2487, respectively. It can be observed that population size plays a crucial role in contributing to carbon emissions from China’s commercial buildings, which are closely related to the accelerated urbanization of China in recent years. The results reveal the importance of controlling the size of the population and raising public awareness of low carbon in the process of urbanization. At present, the frequency of low-carbon participation by the Chinese public is relatively low, and it is worth trying to learn from the advanced international experience. Further, energy consumption intensity is also a critical factor that leads to increases in carbon emissions and adjusting the industrial structure and optimizing the energy structure is the leading solution [59]. Specifically, Chinese commercial buildings should reduce the use of coal and oil, while making full use of open energy.
(2) Carbon emissions in China’s commercial buildings will peak in 2030, with a peak value of 1264.81 MtCO2 estimated to be obtained. Based on historical carbon emissions data and given scenario settings, the proposed carbon emissions model was established and used to further predict the pathway of carbon emissions in China’s commercial building from 2019 to 2060. The results show that China’s commercial buildings’ carbon emissions will peak in 2030. The peak value was estimated to be 1264.81 MtCO2, which is 1.55 times that of 2018. After reaching this peak, the carbon emissions of the commercial buildings will decline at a rate of 34.52 MtCO2 per year, before dropping to 229.31 MtCO2 by 2060. It can be seen that, under the low carbon scenario analysis setting, although China’s commercial buildings can achieve the goal of peaking carbon emissions from China’s commercial buildings in 2030, there is still a certain gap from China’s carbon neutral goal of 2060. In addition, the earlier the peak time is reached, the lower the peak emissions will be, which is more conducive to the goal of long-term carbon neutrality. Therefore, China’s commercial buildings still need to further increase their efforts to take action to reduce emissions in order to reduce the burden of emission reductions faced after 2030 [60].
In order to better promote a reduction in the carbon emissions of China’s commercial buildings to, in turn, achieve carbon neutrality, a few gaps in this study should be covered in future studies:
(1) Historical carbon emissions assessment of commercial buildings from a provincial perspective. This article focuses on historical carbon emissions from China’s commercial buildings, and two major driving forces are identified by the LASSO regression model optimized with the whale optimization algorithm, with the striking differences in the climate environment, population size, and economic models of different provinces in China taken into account. Therefore, future studies should establish emission models for different provinces in order to evaluate the major driving forces of local historical carbon emissions.
(2) Low-carbon pathway for China’s commercial buildings with uncertain impacts. Furthermore, the emission trajectory of commercial buildings in this paper was obtained based on static scenario analysis, ignoring the influence of the uncertainty brought by parameter changes in scenario settings, thus limiting the accuracy and reliability of policy implementation. For this reason, upcoming studies should focus on combining the carbon emissions model with dynamic scenario analysis.
Author Contributions
Conceptualization, M.M. and Z.M.; methodology, M.M.; software, X.X.; validation, X.X. and X.M.; formal analysis, X.X.; investigation, X.X.; resources, M.M.; data curation, X.X.; writing—original draft preparation, X.X.; writing—review and editing, M.M.; visualization, X.X. and M.M.; supervision, Z.M.; project administration, Z.M.; funding acquisition, Z.M. and M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Planning Office of Philosophy and Social Science Foundation of China (21CJY030 and 18BJL034), the Beijing Natural Science Foundation (8224085), the China Postdoctoral Science Foundation (2020M680020), the Shuimu Tsinghua Scholar Program of Tsinghua University (2019SM139), and the Fundamental Research Funds for the Central Universities of China (2020CDJSK03YJ07).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Raw data available at https://www.researchgate.net/project/China-Building-Energy-and-Emission-Database-CBEED (accessed on 1 December 2021).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| CBEED | China Building Energy and Emission Database |
| GDP | Gross domestic product |
| LASSO | Least absolute shrinkage and selection operator |
| MtCO2 | Mega-tons of carbon dioxide |
| MAPE | Mean absolute percent error |
| STIRPAT | Stochastic impacts by regression on population, affluence, and technology model |
| WOA | Whale optimization algorithm |
| Symbols | |
| CO2 emission from commercial buildings | |
| Population size | |
| Gross domestic product (GDP) | |
| Service industry value added | |
| Energy consumption from commercial buildings | |
| Floor space of commercial buildings |
References
- Li, K.; Ma, M.; Xiang, X.; Feng, W.; Ma, Z.; Cai, W.; Ma, X. Carbon reduction in commercial building operations: A provincial retrospection in China. Appl. Energy 2022, 306, 118098. [Google Scholar] [CrossRef]
- UN; IEA. 2019 Global Status Report for Buildings and Construction. 2019. Available online: https://www.iea.org/reports/global-status-report-for-buildings-and-construction-2019 (accessed on 1 December 2021).
- Guillén-Lambea, S.; Rodríguez-Soria, B.; Marín, J.M. Comfort settings and energy demand for residential nZEB in warm climates. Appl. Energy 2017, 202, 471–486. [Google Scholar] [CrossRef]
- Jiang, P.; Dong, W.; Kung, Y.H.; Geng, Y. Analysing co-benefits of the energy conservation and carbon reduction in China’s large commercial buildings. J. Clean. Prod. 2013, 58, 112–120. [Google Scholar] [CrossRef]
- Schäuble, D.; Marian, A.; Cremonese, L. Conditions for a cost-effective application of smart thermostat systems in residential buildings. Appl. Energy 2020, 262, 114526. [Google Scholar] [CrossRef]
- McNeil, M.A.; Feng, W.; du Can, S.R.; Khanna, N.Z.; Ke, J.; Zhou, N. Energy efficiency outlook in China’s urban buildings sector through 2030. Energy Policy. 2016, 97, 532–539. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Ma, M.; Lin, Y.; Ma, Z.; Li, K. Carbon Kuznets curve in China’s building operations: Retrospective and prospective trajectories. Sci. Total Environ. 2021, 803, 150104. [Google Scholar] [CrossRef]
- You, K.; Yu, Y.; Li, Y.; Cai, W.; Shi, Q. Spatiotemporal decomposition analysis of carbon emissions on Chinese residential central heating. Energy Build. 2021, 253, 111485. [Google Scholar] [CrossRef]
- Ren, X.; Cheng, C.; Wang, Z.; Yan, C. Spillover and dynamic effects of energy transition and economic growth on carbon dioxide emissions for the European Union: A dynamic spatial panel model. Sustain. Dev. 2021, 29, 228–242. [Google Scholar] [CrossRef]
- Cheng, C.; Ren, X.; Dong, K.; Wang, Z. How does technological innovation mitigate CO2 emissions in OECD countries? Heterogeneous analysis using panel quantile regression. J. Environ. Manag. 2021, 280, 111818. [Google Scholar] [CrossRef]
- Yan, R.; Ma, M.; Pan, T. Estimating energy savings in Chinese residential buildings from 2001 to 2015: A decomposition analysis. J. Eng. Sci. Technol. Rev. 2017, 10, 107–113. [Google Scholar] [CrossRef]
- Duan, K.; Ren, X.; Shi, Y.; Mishra, T.; Yan, C. The marginal impacts of energy prices on carbon price variations: Evidence from a quantile-on-quantile approach. Energy Econ. 2021, 95, 105131. [Google Scholar] [CrossRef]
- Chen, P.; Wu, Y.; Zhong, H.; Long, Y.; Meng, J. Exploring household emission patterns and driving factors in Japan using machine learning methods. Appl. Energy 2022, 307, 118251. [Google Scholar] [CrossRef]
- Ren, X.; Lu, Z.; Cheng, C.; Shi, Y.; Shen, J. On dynamic linkages of the state natural gas markets in the USA: Evidence from an empirical spatio-temporal network quantile analysis. Energy Econ. 2019, 80, 234–252. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, Z.; Wang, X.; Xue, X. Transportation de-carbonization pathways and effect in China: A systematic analysis using STIRPAT-SD model. J. Clean. Prod. 2021, 288, 125574. [Google Scholar] [CrossRef]
- Liu, J.; Li, S.; Ji, Q. Regional differences and driving factors analysis of carbon emission intensity from transport sector in China. Energy 2021, 224, 120178. [Google Scholar] [CrossRef]
- Yang, L.; Xia, H.; Zhang, X.; Yuan, S. What matters for carbon emissions in regional sectors? A China study of extended STIRPAT model. J. Clean. Prod. 2018, 180, 595–602. [Google Scholar] [CrossRef]
- Xie, H.; Zhai, Q.; Wang, W.; Yu, J.; Lu, F.; Chen, Q. Does intensive land use promote a reduction in carbon emissions? Evidence from the Chinese industrial sector. Resour. Conserv. Recycl. 2018, 137, 167–176. [Google Scholar] [CrossRef]
- Zhu, C.; Chang, Y.; Li, X.; Shan, M. Factors influencing embodied carbon emissions of China’s building sector: An analysis based on extended STIRPAT modeling. Energy Build. 2021, 255, 111607. [Google Scholar] [CrossRef]
- Wu, R.; Wang, J.; Wang, S.; Feng, K. The drivers of declining CO2 emissions trends in developed nations using an extended STIRPAT model: A historical and prospective analysis. Renew. Sustain. Energy Rev. 2021, 149, 111328. [Google Scholar] [CrossRef]
- Xu, G.; Wang, W. China’s energy consumption in construction and building sectors: An outlook to 2100. Energy 2020, 195, 117045. [Google Scholar] [CrossRef]
- Wang, P.; Wu, W.; Zhu, B.; Wei, Y. Examining the impact factors of energy-related CO2 emissions using the STIRPAT model in Guangdong Province, China. Appl. Energy 2013, 106, 65–71. [Google Scholar] [CrossRef]
- Lin, S.; Zhao, D.; Marinova, D. Analysis of the environmental impact of China based on STIRPAT model. Environ. Impact Assess. Rev. 2009, 29, 341–347. [Google Scholar] [CrossRef]
- Ma, M.; Pan, T.; Ma, Z. Examining the Driving Factors of Chinese Commercial Building Energy Consumption from 2000 to 2015: A STIRPAT Model Approach. J. Eng. Sci. Technol. Rev. 2017, 10, 28–34. [Google Scholar] [CrossRef]
- Jia, J.; Deng, H.; Duan, J.; Zhao, J. Analysis of the major drivers of the ecological footprint using the STIRPAT model and the PLS method—A case study in Henan Province, China. Ecol. Econ. 2009, 68, 2818–2824. [Google Scholar] [CrossRef]
- Li, H.; Mu, H.; Zhang, M.; Li, N. Analysis on influence factors of China’s CO2 emissions based on Path–STIRPAT model. Energy Policy 2011, 39, 6906–6911. [Google Scholar] [CrossRef]
- Bargaoui, S.A.; Liouane, N.; Nouri, F.Z. Environmental impact determinants: An empirical analysis based on the STIRPAT model. Procedia-Soc. Behav. Sci. 2014, 109, 449–458. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Zhao, T. Identifying major influencing factors of CO2 emissions in China: Regional disparities analysis based on STIRPAT model from 1996 to 2015. Atmos. Environ. 2019, 207, 136–147. [Google Scholar] [CrossRef]
- Liu, D.; Xiao, B. Can China achieve its carbon emission peaking? A scenario analysis based on STIRPAT and system dynamics model. Ecol. Indic. 2018, 93, 647–657. [Google Scholar] [CrossRef]
- Ma, M.; Ma, X.; Cai, W.; Cai, W. Carbon-dioxide mitigation in the residential building sector: A household scale-based assessment. Energy Convers. Manag. 2019, 198, 111915. [Google Scholar] [CrossRef]
- Olkkonen, V.; Hirvonen, J.; Heljo, J.; Syri, S. Effectiveness of building stock sustainability measures in a low-carbon energy system: A scenario analysis for Finland until 2050. Energy 2021, 235, 121399. [Google Scholar] [CrossRef]
- Ma, M.; Ma, X.; Cai, W.; Cai, W. Low carbon roadmap of residential building sector in China: Historical mitigation and prospective peak. Appl. Energy 2020, 273, 115247. [Google Scholar] [CrossRef]
- Ehrlich, P.R.; Holdren, J.P. Impact of population growth. Science 1971, 171, 1212–1217. [Google Scholar] [CrossRef]
- Song, M.; Wang, S.; Yu, H.; Yang, L.; Wu, J. To reduce energy consumption and to maintain rapid economic growth: Analysis of the condition in China based on expended IPAT model. Renew. Sustain. Energy Rev. 2011, 15, 5129–5134. [Google Scholar] [CrossRef]
- Zaman, K.; Abd-el Moemen, M. Energy consumption, carbon dioxide emissions and economic development: Evaluating alternative and plausible environmental hypothesis for sustainable growth. Renew. Sustain. Energy Rev. 2017, 74, 1119–1130. [Google Scholar] [CrossRef]
- Wang, C.; Wang, F.; Zhang, X.; Yang, Y.; Su, Y.; Ye, Y.; Zhang, H. Examining the driving factors of energy related carbon emissions using the extended STIRPAT model based on IPAT identity in Xinjiang. Renew. Sustain. Energy Rev. 2017, 67, 51–61. [Google Scholar] [CrossRef]
- Yue, T.; Long, R.; Chen, H.; Zhao, X. The optimal CO2 emissions reduction path in Jiangsu province: An expanded IPAT approach. Appl. Energy 2013, 112, 1510–1517. [Google Scholar] [CrossRef]
- York, R.; Rosa, E.A.; Dietz, T. STIRPAT, IPAT and ImPACT: Analytic tools for unpacking the driving forces of environmental impacts. Ecol. Econ. 2003, 46, 351–365. [Google Scholar] [CrossRef]
- Wen, L.; Li, Z. Driving forces of national and regional CO2 emissions in China combined IPAT-E and PLS-SEM model. Sci. Total Environ. 2019, 690, 237–247. [Google Scholar] [CrossRef]
- Wang, M.; Che, Y.; Yang, K.; Wang, M.; Xiong, L.; Huang, Y. A local-scale low-carbon plan based on the STIRPAT model and the scenario method: The case of Minhang District, Shanghai, China. Energy Policy 2011, 39, 6981–6990. [Google Scholar] [CrossRef]
- Khoshbakht, M.; Rasheed, E.O.; Baird, G. Office Distractions and the Productivity of Building Users: The Effect of Workgroup Sizes and Demographic Characteristics. Buildings 2021, 11, 55. [Google Scholar] [CrossRef]
- Kim, J.H.; Han, S.H. Applicability of Preliminary Standards for the Hanok Comfort Evaluation Based on Spatial Indices. Buildings 2021, 11, 497. [Google Scholar] [CrossRef]
- Chen, R.; Tsay, Y.S. An Integrated Sensitivity Analysis Method for Energy and Comfort Performance of an Office Building along the Chinese Coastline. Buildings 2021, 11, 371. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Shi, X.; Wang, K.; Cheong, T.S.; Zhang, H. Prioritizing driving factors of household carbon emissions: An application of the LASSO model with survey data. Energy Econ. 2020, 92, 104942. [Google Scholar] [CrossRef]
- Xiang, X.; Ma, X.; Fang, Y.; Wu, W.; Zhang, G. A novel hyperbolic time-delayed grey model with Grasshopper Optimization Algorithm and its applications. Ain Shams Eng. J. 2021, 12, 865–874. [Google Scholar] [CrossRef]
- Liu, C.; Wu, W.Z.; Xie, W.; Zhang, J. Application of a novel fractional grey prediction model with time power term to predict the electricity consumption of India and China. Chaos Solitons Fractals 2020, 141, 110429. [Google Scholar] [CrossRef]
- Wang, J.; Du, P.; Niu, T.; Yang, W. A novel hybrid system based on a new proposed algorithm—Multi-Objective Whale Optimization Algorithm for wind speed forecasting. Appl. Energy 2017, 208, 344–360. [Google Scholar] [CrossRef]
- Wang, J.; Yang, W.; Du, P.; Niu, T. A novel hybrid forecasting system of wind speed based on a newly developed multi-objective sine cosine algorithm. Energy Convers. Manag. 2018, 163, 134–150. [Google Scholar] [CrossRef]
- Qiao, W.; Lu, H.; Zhou, G.; Azimi, M.; Yang, Q.; Tian, W. A hybrid algorithm for carbon dioxide emissions forecasting based on improved lion swarm optimizer. J. Clean. Prod. 2020, 244, 118612. [Google Scholar] [CrossRef]
- Xiang, X.; Ma, X.; Ma, M.; Wu, W.; Yu, L. Research and application of novel Euler polynomial-driven grey model for short-term PM10 forecasting. Grey Syst. Theory Appl. 2020, 11, 498–517. [Google Scholar] [CrossRef]
- Wu, L.; Huang, G.; Fan, J.; Zhang, F.; Wang, X.; Zeng, W. Potential of kernel-based nonlinear extension of Arps decline model and gradient boosting with categorical features support for predicting daily global solar radiation in humid regions. Energy Convers. Manag. 2019, 183, 280–295. [Google Scholar] [CrossRef]
- Fan, J.; Wang, X.; Wu, L.; Zhou, H.; Zhang, F.; Yu, X.; Lu, X.; Xiang, Y. Comparison of Support Vector Machine and Extreme Gradient Boosting for predicting daily global solar radiation using temperature and precipitation in humid subtropical climates: A case study in China. Energy Convers. Manag. 2018, 164, 102–111. [Google Scholar] [CrossRef]
- Yu, L.; Ma, X.; Wu, W.; Xiang, X.; Wang, Y.; Zeng, B. Application of a novel time-delayed power-driven grey model to forecast photovoltaic power generation in the Asia-Pacific region. Sustain. Energy Technol. Assess. 2021, 44, 100968. [Google Scholar] [CrossRef]
- Kouziokas G, N. A new W-SVM kernel combining PSO-neural network transformed vector and Bayesian optimized SVM in GDP forecasting. Eng. Appl. Artif. Intell. 2020, 92, 103650. [Google Scholar] [CrossRef]
- Liu, C.; Xie, W.; Wu, W.Z.; Zhu, H. Predicting Chinese total retail sales of consumer goods by employing an extended discrete grey polynomial model. Eng. Appl. Artif. Intell. 2021, 102, 104261. [Google Scholar] [CrossRef]
- Cai, Y.; Ma, X. A novel ensemble learning-based grey model for electricity supply forecasting in China. AIMS Math. 2021, 6, 12339–12358. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Zhang, S.; Ma, M.; Li, K.; Ma, Z.; Feng, W.; Cai, W. Historical carbon abatement in the commercial building operation: China versus the US. Energy Econ. 2021, 105, 105712. [Google Scholar] [CrossRef]
- Zhang, S.; Xiang, X.; Ma, Z.; Ma, M.; Zou, C. Carbon Neutral Roadmap of Commercial Building Operations by Mid-Century: Lessons from China. Buildings 2021, 11, 510. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).