Prediction of Shear Strength of Reinforced Recycled Aggregate Concrete Beams without Stirrups
Abstract
:1. Introduction
2. Material and Methods
2.1. Materials Properties
2.2. Concrete Mixture Proportions
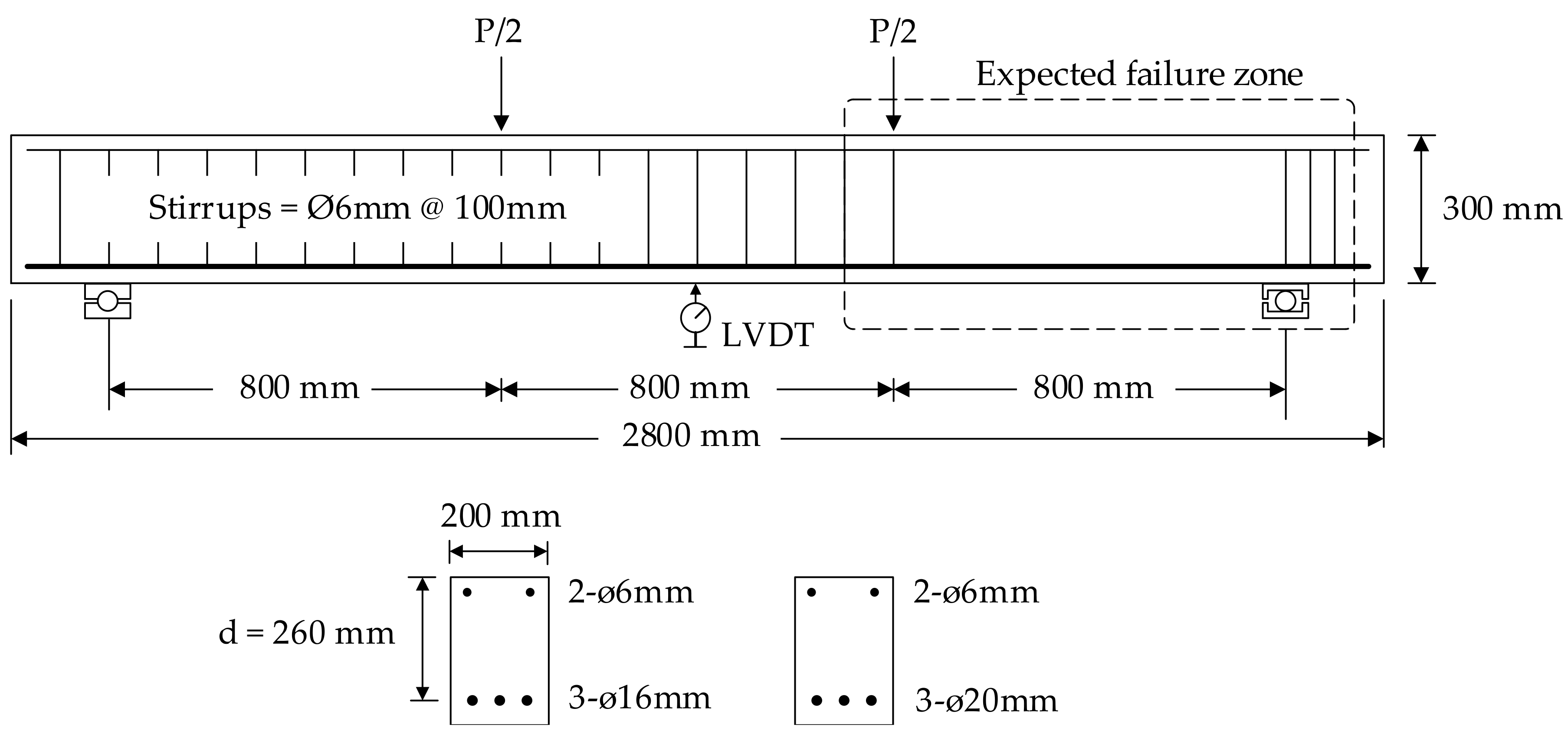
2.3. Details of Test Beams
2.4. Test Setup and Procedure
3. Results and Discussion
3.1. Ultimate Capacity and Failure Behaviour
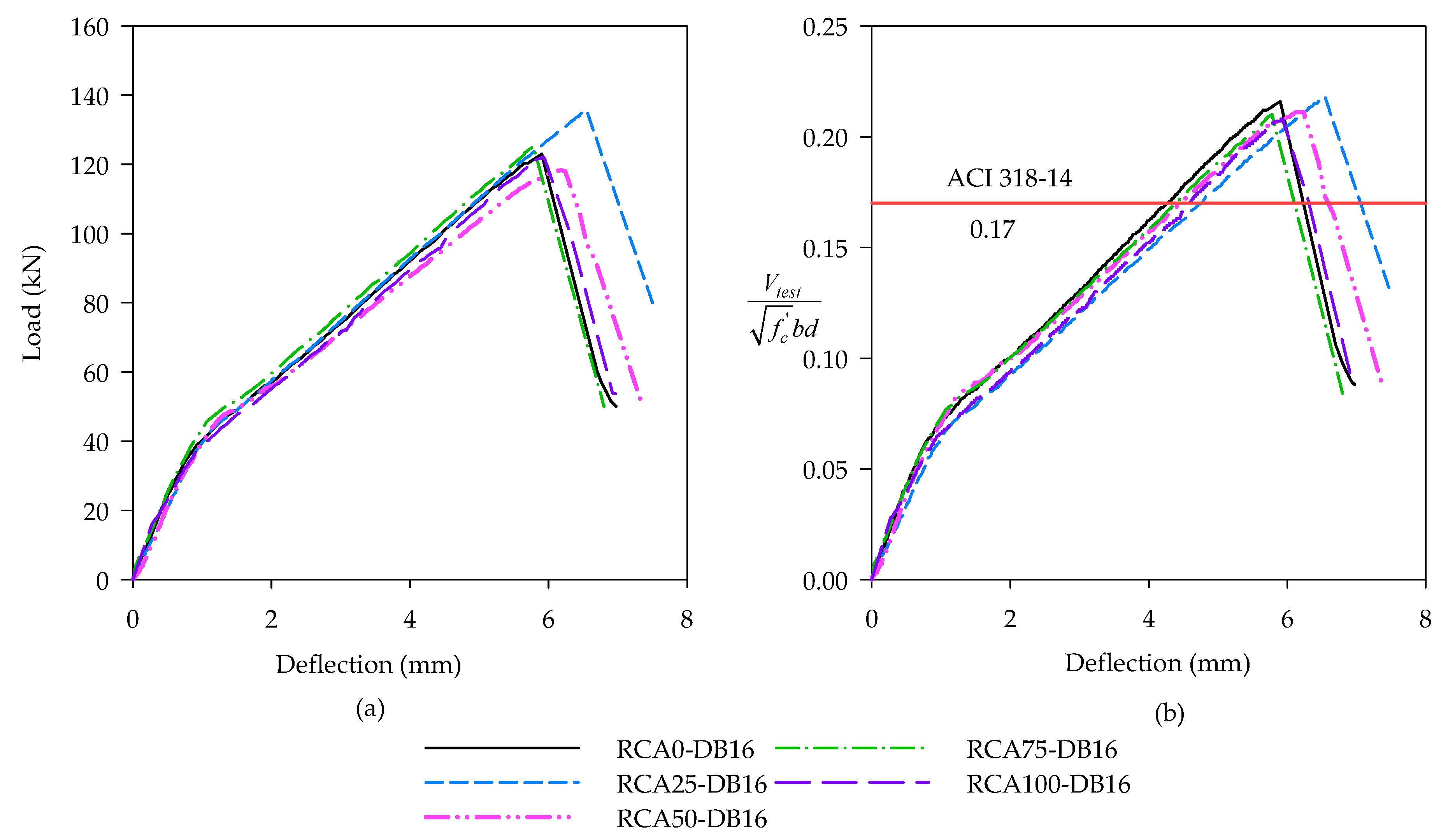
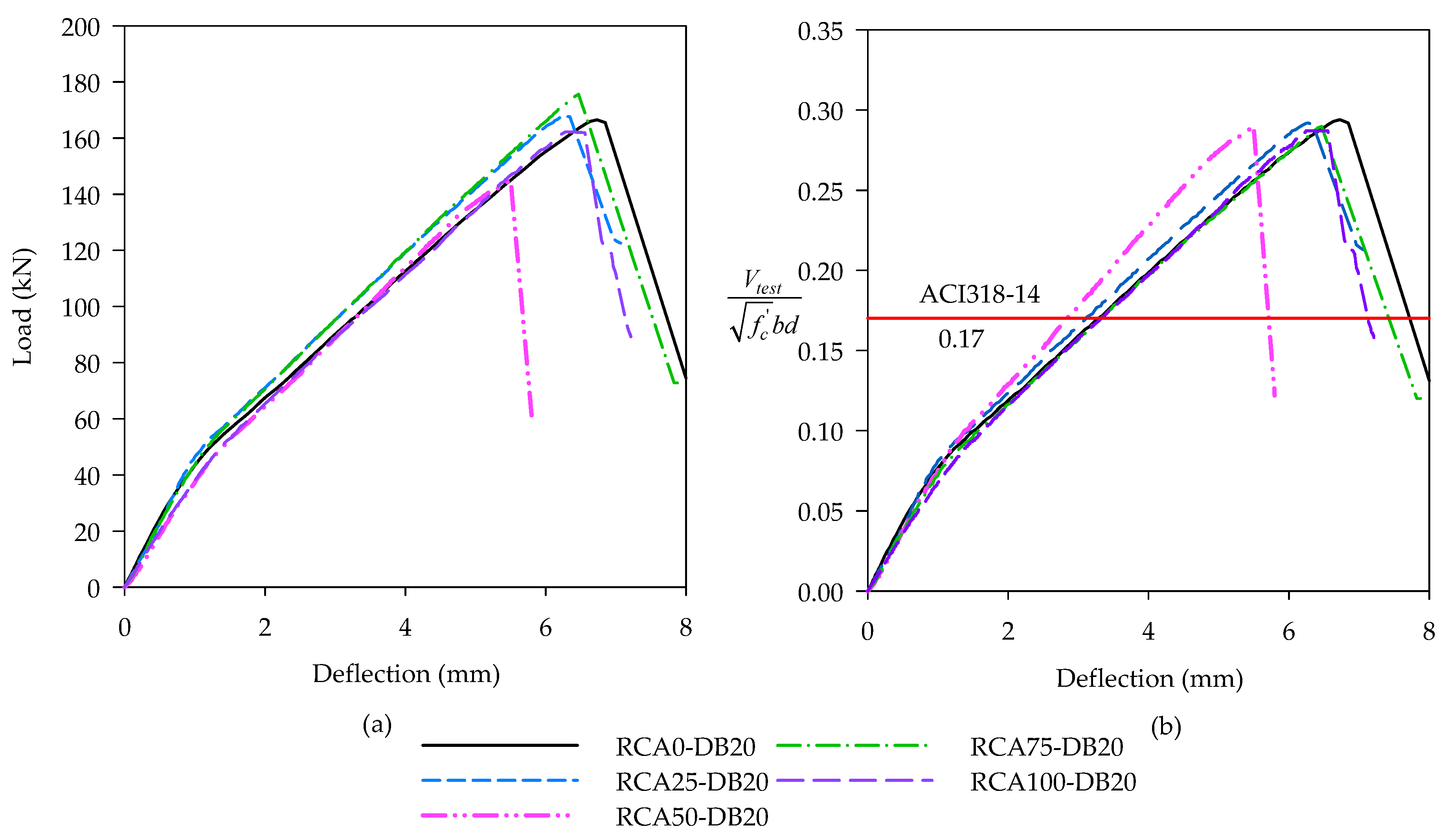
3.2. Load-Deflection Responses
4. Prediction of Concrete Shear Strength
4.1. Ultimate Concrete Shear Strength
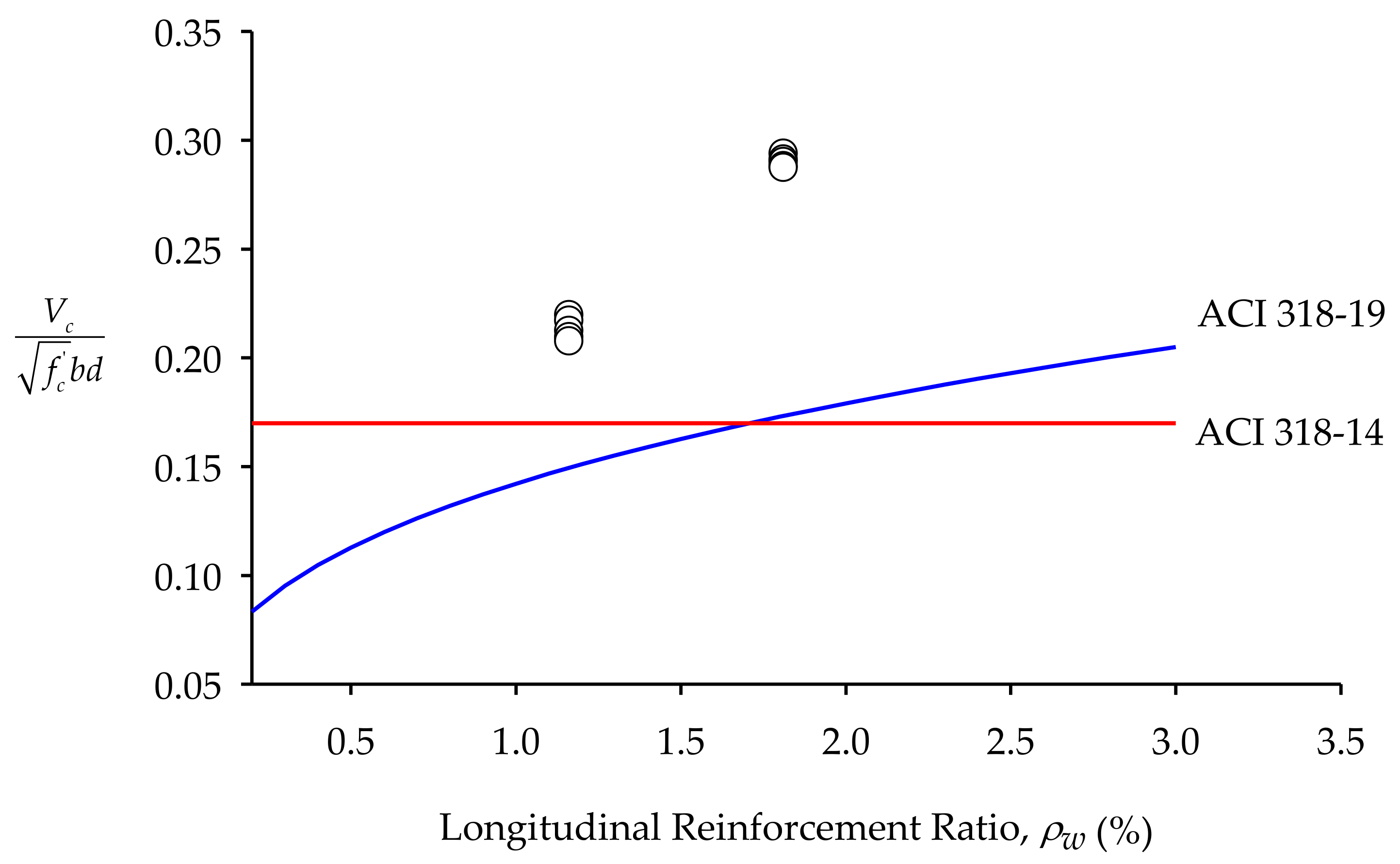
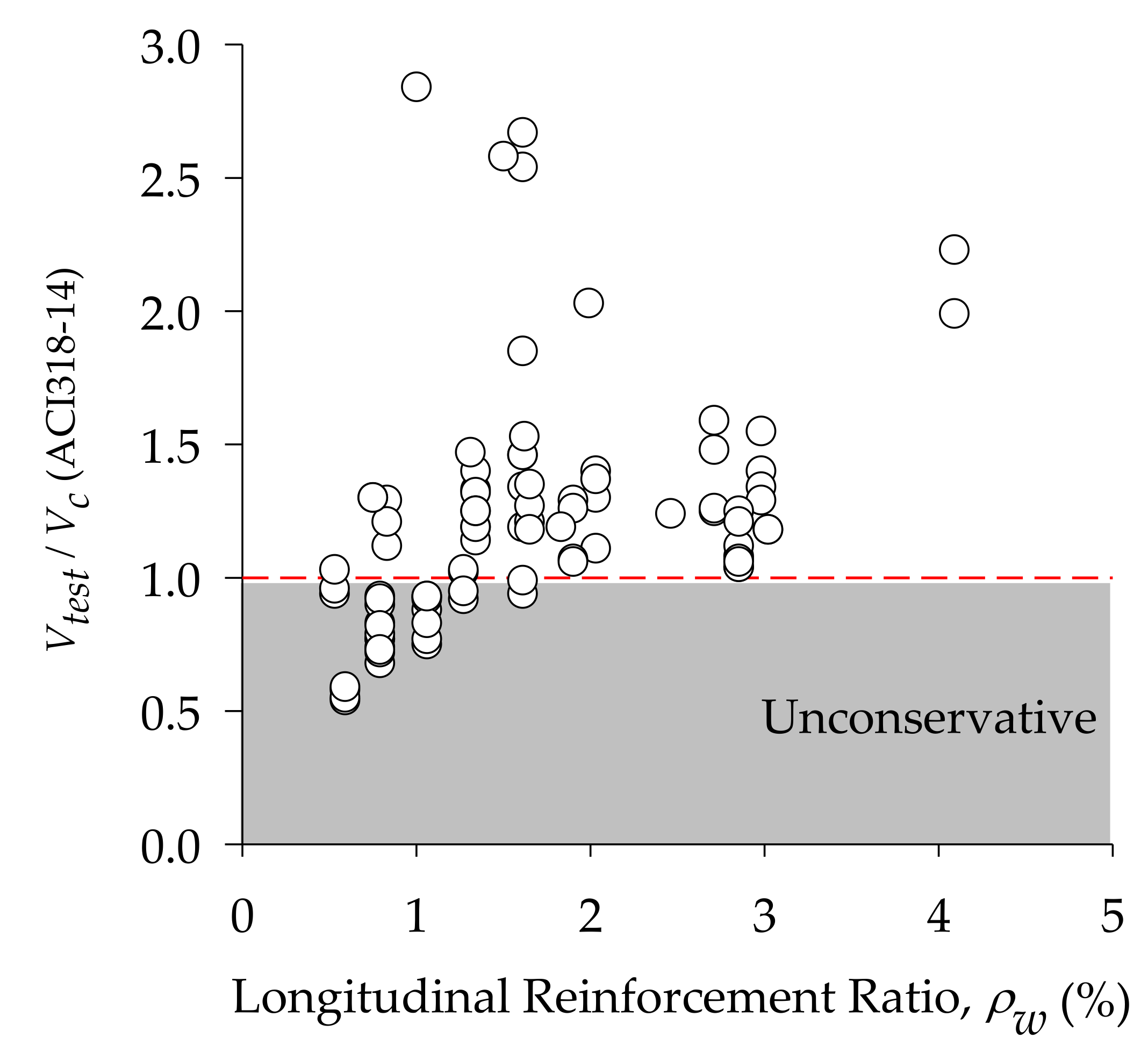
4.2. Effect of Longitudinal Reinforcement
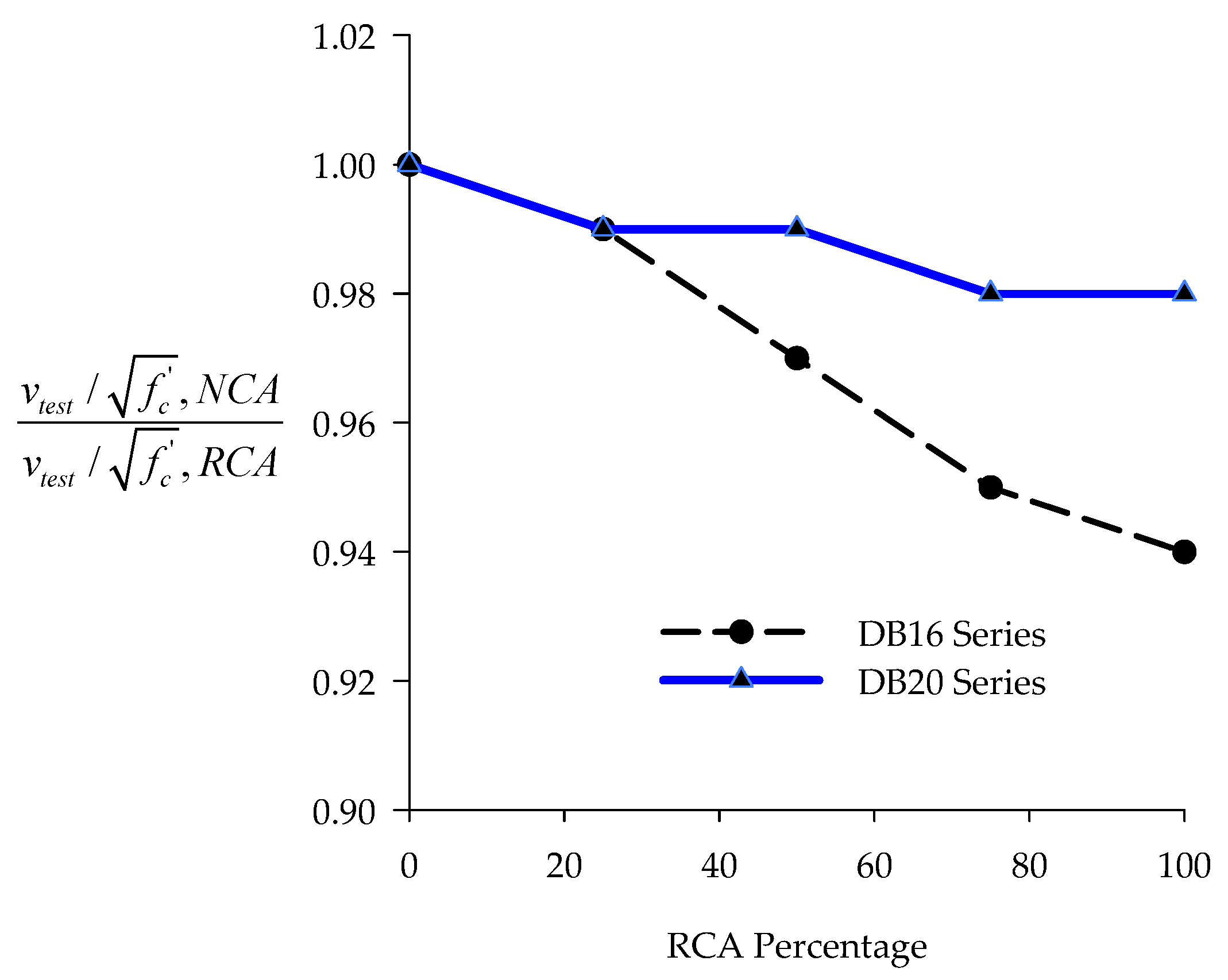
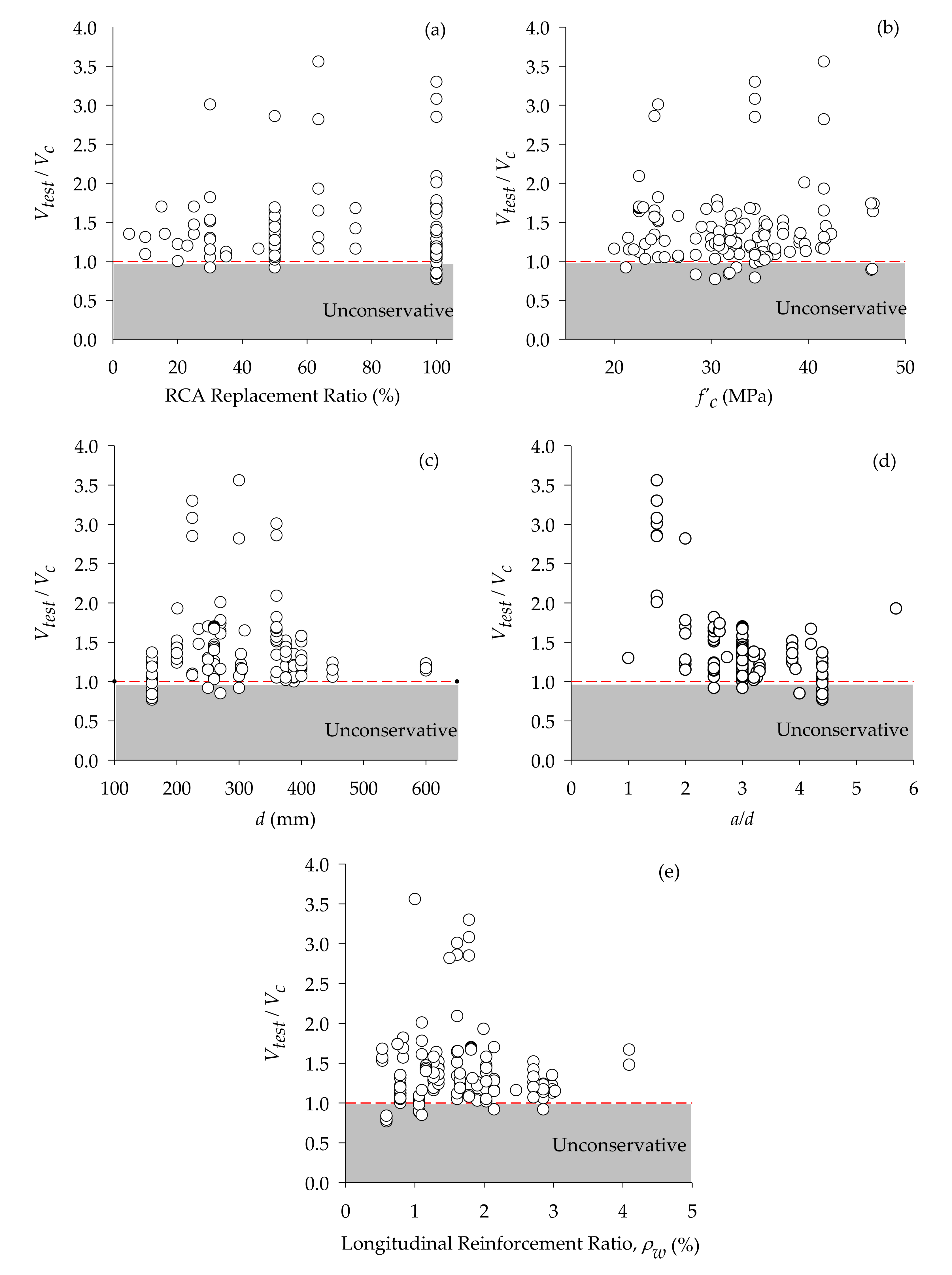
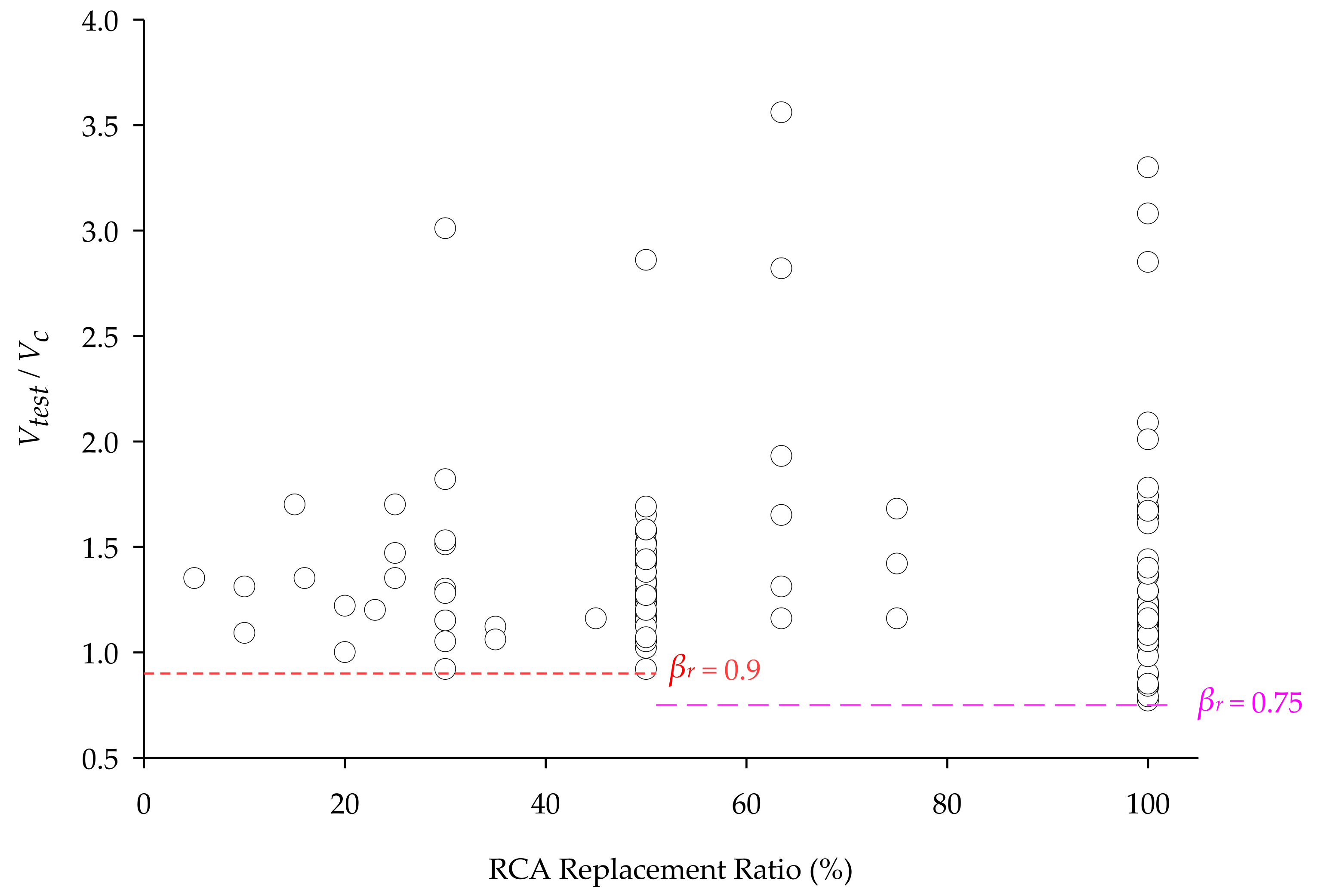
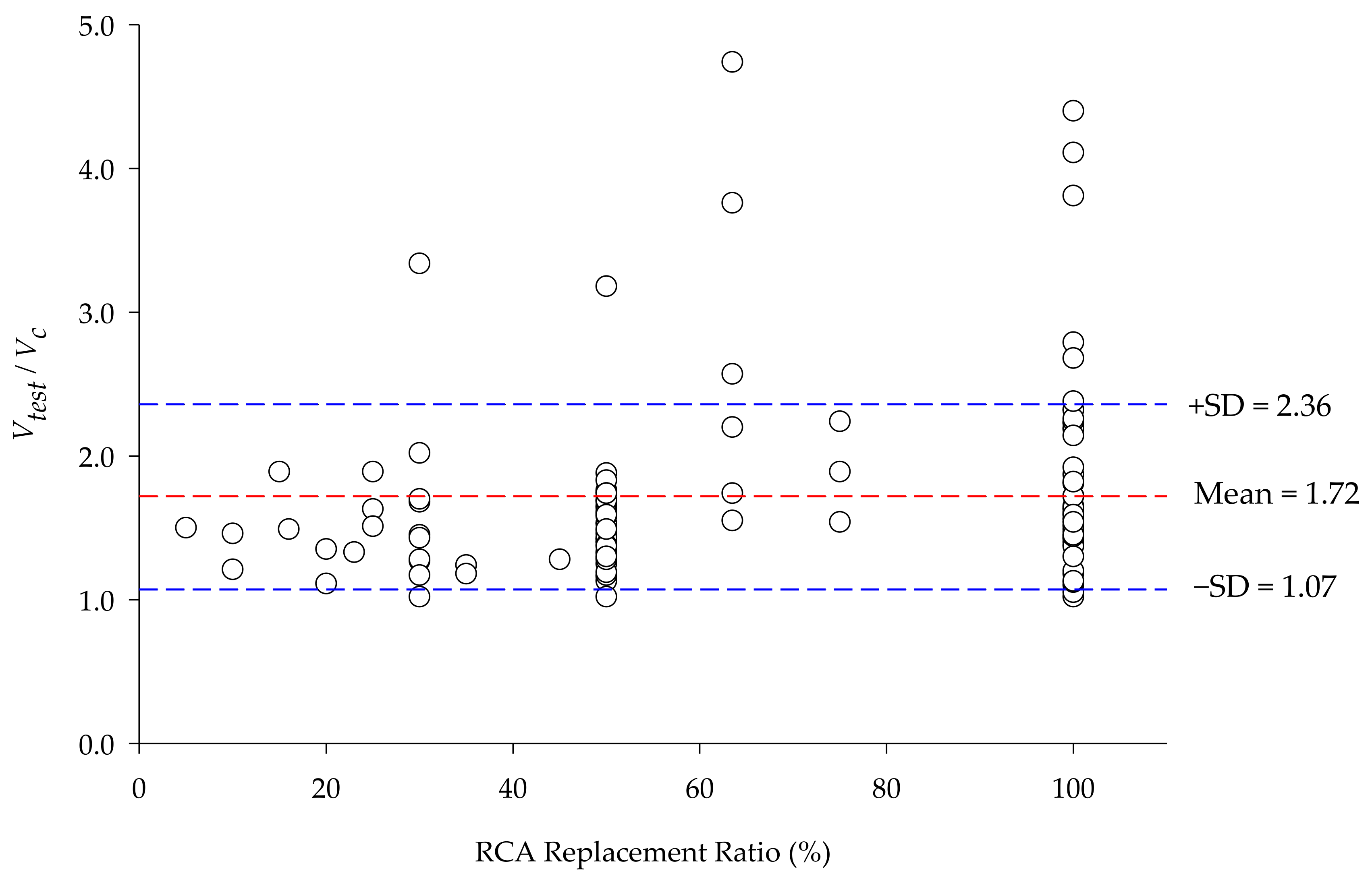
4.3. Effect of RCA Replacement Ratio
5. Modifications to Code Equation to Allow for the Use of RCA
5.1. Proposed RCA Uncertainty Factor to Existing Design Equation
5.2. Model Validation and Compared to Existing Test Data
5.3. Design Recommendations
6. Conclusions and Future Works
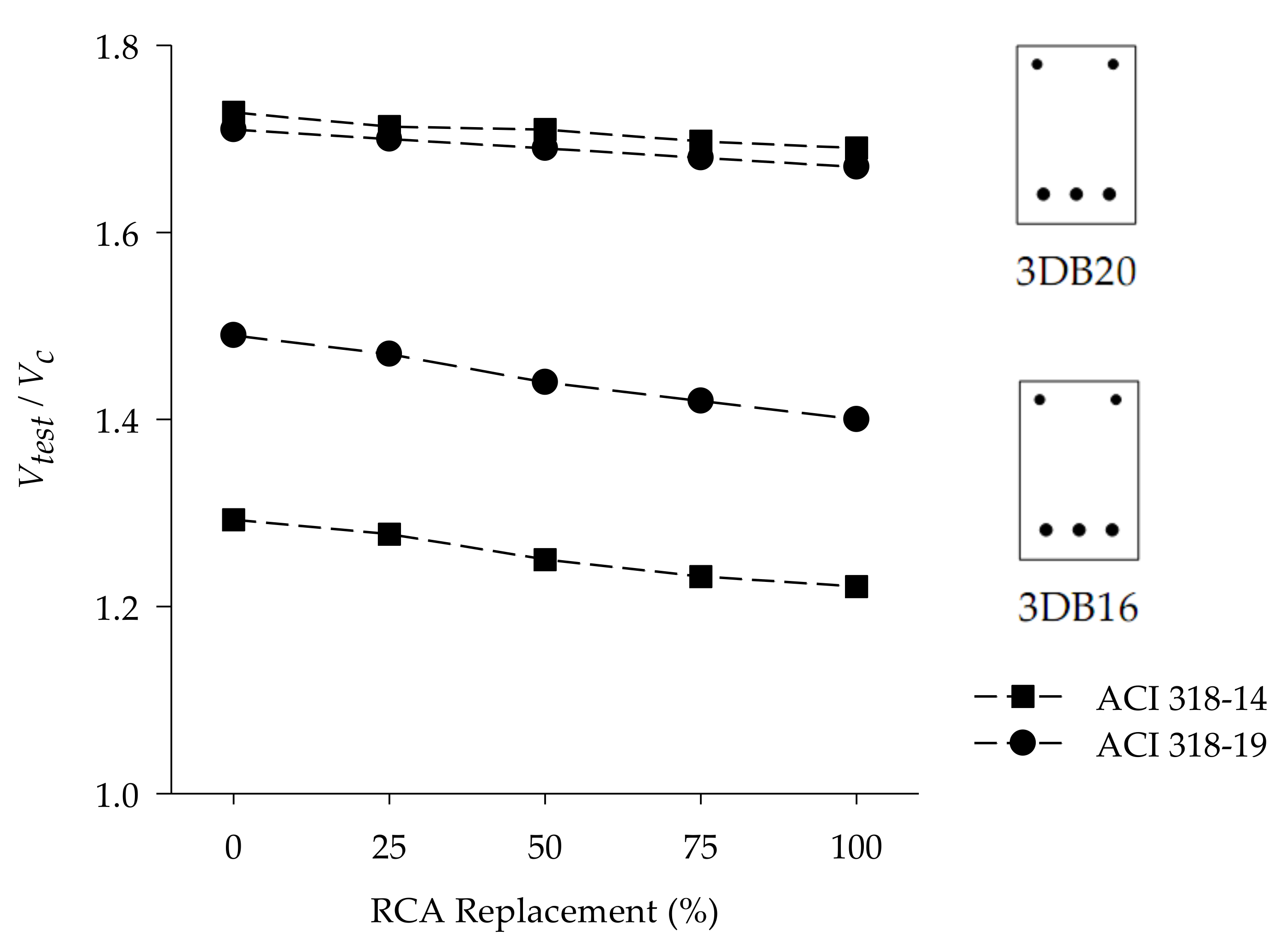
- For beams with a longitudinal reinforcement ratio of 1.16%, the normalized shear stress of the 100% RAC beam was 6% lower than that of the NAC counterpart.
- The normalized shear stress of RAC and NAC beams with a longitudinal reinforcement ratio of 1.81% had a minimal difference.
- The shear failure modes of RAC and NAC beams were similar. However, the crack inclination angles of NAC beams were slightly higher.
- The current ACI 318-19 shear equation conservatively estimates the shear strength of RAC beams when the replacement percentage is less than 75%.
- For a longitudinal reinforcement ratio less than 1.8%, the ACI 318-19 shear equation yielded lower shear strengths (Vc) than the ACI 318-14 simplified equation, thus increasing the safety factor of shear stress ratios found in previous tests in the literature.
- A reduction factor of 0.75 for RCA between 50% and 100% is proposed to the current ACI code provision to account for the physical variations of RCA, such as percentage replacement, source, density, percentage of residual mortar, and physical irregularity.
- The modified ACI equation for predicting the concrete shear strength of RAC beams was calibrated using eight test data carried out by the authors, and then further verified and calibrated against 120 test data from the literature. The use of the modified ACI equation as a design recommendation for predicting the concrete shear strength of RAC beams gives conservative predictions for all levels of RCA up to 100% replacement.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Reference | ID | % RCA | f’c (MPa) | b (mm) | d (mm) | a/d | ρw (%) | Vtest (kN) | Equation (1) | Equation (2) | Equation (4) | Equation (5) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| This study (2021) | 1 | 25 | 35.7 | 200 | 260 | 3.08 | 1.16 | 67.50 | 52.9 | 46.0 | 42.3 | 41.4 |
| 2 | 50 | 29.0 | 200 | 260 | 3.08 | 1.16 | 59.50 | 47.6 | 41.4 | 38.1 | 37.3 | |
| 3 | 75 | 32.9 | 200 | 260 | 3.08 | 1.16 | 62.50 | 50.7 | 44.2 | 40.6 | 33.1 | |
| 4 | 100 | 31.9 | 200 | 260 | 3.08 | 1.16 | 61.00 | 50.0 | 43.5 | 40.0 | 32.6 | |
| 5 | 25 | 30.7 | 200 | 260 | 3.08 | 1.81 | 83.85 | 48.9 | 49.4 | 39.2 | 44.5 | |
| 6 | 50 | 23.0 | 200 | 260 | 3.08 | 1.81 | 72.50 | 42.4 | 42.8 | 33.9 | 38.5 | |
| 7 | 75 | 34.0 | 200 | 260 | 3.08 | 1.81 | 87.50 | 51.6 | 52.0 | 41.2 | 39.0 | |
| 8 | 100 | 29.5 | 200 | 260 | 3.08 | 1.81 | 81.15 | 48.0 | 48.5 | 38.4 | 36.3 | |
| Wardeh and Ghorbel (2019) [35] | 9 | 100 | 34.5 | 200 | 225 | 1.5 | 1.78 | 130.00 | 44.9 | 45.6 | 35.9 | 34.2 |
| 10 | 100 | 34.5 | 200 | 225 | 1.5 | 1.78 | 150.30 | 44.9 | 45.6 | 35.9 | 34.2 | |
| 11 | 100 | 34.5 | 200 | 225 | 1.5 | 1.78 | 140.40 | 44.9 | 45.6 | 35.9 | 34.2 | |
| 12 | 100 | 34.5 | 200 | 225 | 3 | 1.78 | 50.20 | 44.9 | 45.6 | 35.9 | 34.2 | |
| 13 | 100 | 34.5 | 200 | 225 | 3 | 1.78 | 49.00 | 44.9 | 45.6 | 35.9 | 34.2 | |
| Pradhan et al. (2018) [34] | 14 | 100 | 46.7 | 200 | 270 | 2.6 | 1.31 | 92.28 | 62.7 | 56.3 | 50.2 | 42.2 |
| 15 | 100 | 46.8 | 200 | 270 | 2.6 | 0.75 | 81.29 | 62.8 | 46.8 | 50.2 | 35.1 | |
| 16 | 100 | 46.5 | 200 | 270 | 2.6 | 0.75 | 81.10 | 62.6 | 46.6 | 50.1 | 35.0 | |
| Etman et al. (2018) [33] | 17 | 15 | 22.6 | 150 | 250 | 2 | 2.14 | 55.50 | 30.3 | 32.6 | 24.2 | 29.4 |
| 18 | 30 | 21.5 | 150 | 250 | 2 | 2.14 | 36.50 | 29.6 | 31.9 | 23.7 | 28.7 | |
| 19 | 45 | 20.0 | 150 | 250 | 2 | 2.14 | 35.50 | 28.5 | 30.7 | 22.8 | 27.7 | |
| 20 | 30 | 21.4 | 150 | 250 | 1 | 2.14 | 41.50 | 29.5 | 31.8 | 23.6 | 28.6 | |
| 21 | 30 | 21.2 | 150 | 250 | 3 | 2.14 | 29.00 | 29.4 | 31.6 | 23.5 | 28.5 | |
| 22 | 30 | 23.8 | 150 | 250 | 2 | 2.14 | 43.00 | 31.1 | 33.5 | 24.9 | 30.2 | |
| 23 | 30 | 22.0 | 150 | 250 | 2 | 2.14 | 37.00 | 29.9 | 32.2 | 23.9 | 29.0 | |
| Ignjatović et al. (2017) [29] | 24 | 50 | 33.4 | 200 | 235 | 4.2 | 4.09 | 91.75 | 46.2 | 61.8 | 37.0 | 55.6 |
| 25 | 100 | 34.5 | 200 | 235 | 4.2 | 4.09 | 104.75 | 46.9 | 62.8 | 37.5 | 47.1 | |
| Rahal and Alrefaei (2017) [32] | 26 | 10 | 36.6 | 150 | 388 | 3 | 0.79 | 44.50 | 59.9 | 41.0 | 47.9 | 36.9 |
| 27 | 20 | 35.0 | 150 | 388 | 3 | 0.79 | 40.05 | 58.5 | 40.1 | 46.8 | 36.1 | |
| 28 | 20 | 35.3 | 150 | 388 | 3 | 0.79 | 48.90 | 58.8 | 40.2 | 47.0 | 36.2 | |
| 29 | 35 | 35.3 | 150 | 388 | 3 | 0.79 | 45.05 | 58.8 | 40.2 | 47.0 | 36.2 | |
| 30 | 50 | 38.1 | 150 | 388 | 3 | 0.79 | 46.95 | 61.1 | 41.8 | 48.9 | 37.6 | |
| 31 | 75 | 36.6 | 150 | 388 | 3 | 0.79 | 47.40 | 59.9 | 41.0 | 47.9 | 30.7 | |
| 32 | 100 | 35.8 | 150 | 388 | 3 | 0.79 | 42.50 | 59.2 | 40.5 | 47.4 | 30.4 | |
| 33 | 5 | 37.4 | 150 | 388 | 3 | 0.79 | 56.00 | 60.5 | 41.4 | 48.4 | 37.3 | |
| 34 | 10 | 34.8 | 150 | 388 | 3 | 0.79 | 52.50 | 58.4 | 40.0 | 46.7 | 36.0 | |
| 35 | 16 | 35.4 | 150 | 388 | 3 | 0.79 | 54.20 | 58.9 | 40.3 | 47.1 | 36.3 | |
| 36 | 23 | 34.0 | 150 | 388 | 3 | 0.79 | 47.25 | 57.7 | 39.5 | 46.2 | 35.5 | |
| 37 | 35 | 35.1 | 150 | 388 | 3 | 0.79 | 42.50 | 58.6 | 40.1 | 46.9 | 36.1 | |
| Katkhuda and Shatarat (2016) [39] | 38 | 50 | 25.2 | 206 | 260 | 2 | 1.90 | 58.94 | 45.7 | 46.9 | 36.6 | 42.2 |
| 39 | 50 | 25.2 | 206 | 260 | 3 | 1.90 | 49.07 | 45.7 | 46.9 | 36.6 | 42.2 | |
| 40 | 100 | 23.2 | 206 | 260 | 2 | 1.90 | 55.04 | 43.9 | 45.0 | 35.1 | 33.7 | |
| 41 | 100 | 23.2 | 206 | 260 | 3 | 1.90 | 46.45 | 43.9 | 45.0 | 35.1 | 33.7 | |
| Sadati et al. (2016) [38] | 42 | 50 | 32.0 | 305 | 375 | 3.2 | 1.27 | 117.40 | 110.0 | 89.1 | 88.0 | 80.2 |
| 43 | 50 | 35.5 | 305 | 375 | 3.2 | 2.03 | 111.60 | 115.9 | 109.7 | 92.7 | 98.8 | |
| 44 | 50 | 32.0 | 305 | 400 | 3 | 2.71 | 151.20 | 117.3 | 120.0 | 93.9 | 108.0 | |
| 45 | 50 | 35.5 | 305 | 400 | 3 | 1.27 | 148.60 | 123.6 | 98.2 | 98.9 | 88.4 | |
| 46 | 50 | 32.0 | 305 | 400 | 3 | 2.03 | 171.70 | 117.3 | 109.0 | 93.9 | 98.1 | |
| 47 | 50 | 35.5 | 305 | 400 | 3 | 2.71 | 168.60 | 123.6 | 126.4 | 98.9 | 113.8 | |
| 48 | 50 | 30.8 | 305 | 375 | 3.2 | 1.27 | 120.50 | 107.9 | 87.4 | 86.3 | 78.7 | |
| 49 | 50 | 26.6 | 305 | 375 | 3.2 | 2.03 | 99.90 | 100.3 | 95.0 | 80.2 | 85.5 | |
| 50 | 50 | 30.8 | 305 | 400 | 3 | 2.71 | 140.80 | 115.1 | 117.7 | 92.1 | 105.9 | |
| 51 | 50 | 26.6 | 305 | 400 | 3 | 1.27 | 134.60 | 107.0 | 85.0 | 85.6 | 76.5 | |
| 52 | 50 | 30.8 | 305 | 400 | 3 | 2.03 | 136.30 | 115.1 | 106.9 | 92.1 | 96.2 | |
| 53 | 50 | 26.6 | 305 | 400 | 3 | 2.71 | 116.80 | 107.0 | 109.4 | 85.6 | 98.5 | |
| Arezoumandi (2014 & 2015) [30,31] | 54 | 50 | 32.1 | 300 | 400 | 3 | 1.27 | 117.50 | 115.6 | 91.8 | 92.5 | 82.6 |
| 55 | 50 | 32.1 | 300 | 375 | 3 | 2.03 | 151.30 | 108.4 | 102.6 | 86.7 | 92.4 | |
| 56 | 50 | 32.1 | 300 | 375 | 3 | 2.71 | 171.80 | 108.4 | 113.0 | 86.7 | 101.7 | |
| 57 | 50 | 35.5 | 300 | 400 | 3 | 1.27 | 111.70 | 121.6 | 96.6 | 97.2 | 86.9 | |
| 58 | 50 | 35.5 | 300 | 375 | 3 | 2.03 | 148.60 | 114.0 | 107.9 | 91.2 | 97.1 | |
| 59 | 50 | 35.5 | 300 | 375 | 3 | 2.71 | 168.70 | 114.0 | 118.9 | 91.2 | 107.0 | |
| 60 | 100 | 30.0 | 300 | 400 | 3 | 1.27 | 114.80 | 111.7 | 88.8 | 89.4 | 66.6 | |
| 61 | 100 | 30.0 | 300 | 375 | 3 | 2.03 | 143.20 | 104.8 | 99.2 | 83.8 | 74.4 | |
| 62 | 100 | 30.0 | 300 | 375 | 3 | 2.71 | 131.40 | 104.8 | 109.3 | 83.8 | 81.9 | |
| 63 | 100 | 34.1 | 300 | 400 | 3 | 1.27 | 113.00 | 119.1 | 94.6 | 95.3 | 71.0 | |
| 64 | 100 | 34.1 | 300 | 375 | 3 | 2.03 | 124.10 | 111.7 | 105.8 | 89.3 | 79.3 | |
| 65 | 100 | 34.1 | 300 | 375 | 3 | 2.71 | 140.30 | 111.7 | 116.5 | 89.3 | 87.4 | |
| Knaack and Kurama (2014) [28] | 66 | 50 | 41.8 | 150 | 200 | 3.875 | 1.34 | 44.00 | 33.0 | 30.4 | 26.4 | 27.4 |
| 67 | 50 | 41.8 | 150 | 200 | 3.875 | 1.34 | 39.10 | 33.0 | 30.4 | 26.4 | 27.4 | |
| 68 | 50 | 37.4 | 150 | 200 | 3.875 | 1.34 | 43.70 | 31.2 | 28.8 | 25.0 | 25.9 | |
| 69 | 50 | 37.4 | 150 | 200 | 3.875 | 1.34 | 41.20 | 31.2 | 28.8 | 25.0 | 25.9 | |
| 70 | 100 | 39.1 | 150 | 200 | 3.875 | 1.34 | 36.40 | 31.9 | 29.4 | 25.5 | 22.1 | |
| 71 | 100 | 39.1 | 150 | 200 | 3.875 | 1.34 | 38.00 | 31.9 | 29.4 | 25.5 | 22.1 | |
| 72 | 100 | 39.2 | 150 | 200 | 3.875 | 1.34 | 39.90 | 31.9 | 29.4 | 25.5 | 22.1 | |
| 73 | 100 | 39.2 | 150 | 200 | 3.875 | 1.34 | 39.90 | 31.9 | 29.4 | 25.5 | 22.1 | |
| Kim et al. (2013) [40] | 74 | 50 | 32.6 | 200 | 300 | 2.5 | 2.85 | 60.60 | 58.2 | 65.9 | 46.6 | 59.3 |
| 75 | 50 | 32.6 | 200 | 450 | 2.5 | 2.85 | 108.90 | 87.4 | 87.6 | 69.9 | 78.8 | |
| 76 | 50 | 32.6 | 200 | 600 | 2.5 | 2.85 | 126.10 | 116.5 | 105.9 | 93.2 | 95.3 | |
| 77 | 50 | 32.6 | 300 | 450 | 2.5 | 3.02 | 154.20 | 131.0 | 133.9 | 104.8 | 120.5 | |
| 78 | 50 | 32.6 | 400 | 600 | 2.5 | 2.85 | 261.50 | 233.0 | 211.9 | 186.4 | 190.7 | |
| 79 | 100 | 34.9 | 200 | 300 | 2.5 | 2.85 | 72.90 | 60.3 | 68.1 | 48.2 | 51.1 | |
| 80 | 100 | 34.9 | 200 | 450 | 2.5 | 2.85 | 96.40 | 90.4 | 90.6 | 72.3 | 67.9 | |
| 81 | 100 | 34.9 | 200 | 600 | 2.5 | 2.85 | 125.10 | 120.5 | 109.6 | 96.4 | 82.2 | |
| 82 | 100 | 34.9 | 300 | 450 | 2.5 | 3.02 | 159.80 | 135.6 | 138.5 | 108.5 | 103.9 | |
| 83 | 100 | 34.9 | 400 | 600 | 2.5 | 2.85 | 256.60 | 241.0 | 219.2 | 192.8 | 164.4 | |
| Fathifazl et al. (2011) [22] | 84 | 63.5 | 41.6 | 200 | 300 | 1.5 | 1.00 | 186.70 | 65.8 | 52.5 | 52.6 | 39.4 |
| 85 | 63.5 | 41.6 | 200 | 300 | 2 | 1.50 | 169.50 | 65.8 | 60.1 | 52.6 | 45.0 | |
| 86 | 63.5 | 41.6 | 200 | 309 | 2.59 | 1.62 | 103.90 | 67.8 | 63.0 | 54.2 | 47.2 | |
| 87 | 63.5 | 41.6 | 200 | 201 | 5.69 | 1.99 | 89.30 | 44.1 | 46.4 | 35.3 | 34.8 | |
| 88 | 63.5 | 41.6 | 200 | 305 | 3.93 | 2.46 | 83.20 | 66.9 | 71.7 | 53.5 | 53.8 | |
| 89 | 63.5 | 41.6 | 200 | 381 | 2.73 | 1.83 | 99.50 | 83.6 | 76.1 | 66.8 | 57.1 | |
| Choi et al. (2010) [41] | 90 | 30 | 24.5 | 200 | 360 | 1.5 | 1.61 | 161.70 | 60.6 | 53.8 | 48.5 | 48.4 |
| 91 | 30 | 24.5 | 200 | 360 | 2.5 | 1.61 | 81.34 | 60.6 | 53.8 | 48.5 | 48.4 | |
| 92 | 30 | 24.5 | 200 | 360 | 3.25 | 1.61 | 56.70 | 60.6 | 53.8 | 48.5 | 48.4 | |
| 93 | 30 | 24.5 | 200 | 360 | 2.5 | 0.53 | 56.70 | 60.6 | 37.1 | 48.5 | 33.4 | |
| 94 | 30 | 24.5 | 200 | 360 | 2.5 | 0.83 | 78.40 | 60.6 | 43.1 | 48.5 | 38.8 | |
| 95 | 50 | 24.2 | 200 | 360 | 1.5 | 1.61 | 152.88 | 60.2 | 53.4 | 48.1 | 48.1 | |
| 96 | 50 | 24.2 | 200 | 360 | 2.5 | 1.61 | 87.90 | 60.2 | 53.4 | 48.1 | 48.1 | |
| 97 | 50 | 24.2 | 200 | 360 | 3.25 | 1.61 | 71.54 | 60.2 | 53.4 | 48.1 | 48.1 | |
| 98 | 50 | 24.2 | 200 | 360 | 2.5 | 0.53 | 57.82 | 60.2 | 36.9 | 48.1 | 33.2 | |
| 99 | 50 | 24.2 | 200 | 360 | 2.5 | 0.83 | 67.13 | 60.2 | 42.8 | 48.1 | 38.5 | |
| 100 | 100 | 22.6 | 200 | 360 | 1.5 | 1.61 | 107.80 | 58.1 | 51.6 | 46.5 | 38.7 | |
| 101 | 100 | 22.6 | 200 | 360 | 2.5 | 1.61 | 84.77 | 58.1 | 51.6 | 46.5 | 38.7 | |
| 102 | 100 | 22.6 | 200 | 360 | 3.25 | 1.61 | 57.77 | 58.1 | 51.6 | 46.5 | 38.7 | |
| 103 | 100 | 22.6 | 200 | 360 | 2.5 | 0.53 | 59.78 | 58.1 | 35.6 | 46.5 | 26.7 | |
| 104 | 100 | 22.6 | 200 | 360 | 2.5 | 0.83 | 70.07 | 58.1 | 41.4 | 46.5 | 31.0 | |
| González-Fonteboa and Martínez-Abella (2007) [27] | 105 | 100 | 39.7 | 200 | 303 | 3.3 | 2.98 | 90.64 | 64.9 | 74.2 | 51.9 | 55.7 |
| Etxeberria et al. (2007) [26] | 106 | 25 | 42.4 | 200 | 303 | 3.3 | 2.98 | 104.00 | 67.1 | 76.8 | 53.7 | 69.1 |
| 107 | 50 | 41.3 | 200 | 303 | 3.3 | 2.98 | 89.00 | 66.2 | 75.8 | 53.0 | 68.2 | |
| 108 | 100 | 39.8 | 200 | 303 | 3.3 | 2.98 | 84.00 | 65.0 | 74.3 | 52.0 | 55.8 | |
| Sato et al. (2007) [42] | 109 | 100 | 46.5 | 150 | 160 | 4.4 | 1.06 | 21.00 | 27.8 | 23.7 | 22.3 | 17.8 |
| 110 | 100 | 32.9 | 150 | 160 | 4.4 | 1.06 | 21.70 | 23.4 | 20.0 | 18.7 | 15.0 | |
| 111 | 100 | 46.6 | 150 | 160 | 4.4 | 1.06 | 21.40 | 27.9 | 23.8 | 22.3 | 17.8 | |
| 112 | 100 | 30.4 | 150 | 160 | 4.4 | 0.59 | 12.10 | 22.5 | 15.8 | 18.0 | 11.8 | |
| 113 | 100 | 28.4 | 150 | 160 | 4.4 | 0.59 | 12.60 | 21.7 | 15.3 | 17.4 | 11.4 | |
| 114 | 100 | 34.5 | 150 | 160 | 4.4 | 0.59 | 13.20 | 24.0 | 16.8 | 19.2 | 12.6 | |
| 115 | 100 | 31.8 | 150 | 160 | 4.4 | 0.59 | 13.50 | 23.0 | 16.1 | 18.4 | 12.1 | |
| 116 | 100 | 30.4 | 150 | 160 | 4.4 | 1.06 | 19.70 | 22.5 | 19.2 | 18.0 | 14.4 | |
| 117 | 100 | 28.4 | 150 | 160 | 4.4 | 1.06 | 20.00 | 21.7 | 18.5 | 17.4 | 13.9 | |
| 118 | 100 | 34.5 | 150 | 160 | 4.4 | 1.06 | 20.00 | 24.0 | 20.4 | 19.2 | 15.3 | |
| 119 | 100 | 31.8 | 150 | 160 | 4.4 | 1.06 | 21.40 | 23.0 | 19.6 | 18.4 | 14.7 | |
| 120 | 100 | 30.4 | 150 | 160 | 4.4 | 1.65 | 27.30 | 22.5 | 22.2 | 18.0 | 16.7 | |
| 121 | 100 | 28.4 | 150 | 160 | 4.4 | 1.65 | 27.70 | 21.7 | 21.5 | 17.4 | 16.1 | |
| 122 | 100 | 34.5 | 150 | 160 | 4.4 | 1.65 | 28.30 | 24.0 | 23.7 | 19.2 | 17.8 | |
| 123 | 100 | 31.8 | 150 | 160 | 4.4 | 1.65 | 31.10 | 23.0 | 22.7 | 18.4 | 17.1 | |
| Han et al. (2001) [46] | 124 | 100 | 39.6 | 170 | 270 | 1.5 | 1.10 | 83.50 | 49.1 | 41.6 | 39.3 | 31.2 |
| 125 | 100 | 30.6 | 170 | 270 | 2 | 1.10 | 65.20 | 43.2 | 36.6 | 34.5 | 27.4 | |
| 126 | 100 | 32.6 | 170 | 270 | 2 | 1.10 | 60.60 | 44.6 | 37.7 | 35.6 | 28.3 | |
| 127 | 100 | 31.2 | 170 | 270 | 3 | 1.10 | 42.70 | 43.6 | 36.9 | 34.9 | 27.7 | |
| 128 | 100 | 31.9 | 170 | 270 | 4 | 1.10 | 31.70 | 44.1 | 37.3 | 35.3 | 28.0 |
References
- Wu, H.; Xiao, J.; Liang, C.; Ma, Z. Properties of Cementitious Materials with Recycled Aggregate and Powder both from Clay Brick Waste. Buildings 2021, 11, 119. [Google Scholar] [CrossRef]
- Makul, N.; Fediuk, R.; Amran, M.; Zeyad, A.; de Azevedo, A.; Klyuev, S.; Vatin, N.; Karelina, M. Capacity to Develop Recycled Aggregate Concrete in South East Asia. Buildings 2021, 11, 234. [Google Scholar] [CrossRef]
- Tam, V.W.Y.; Soomro, M.; Evangelista, A.C.J. A Review of Recycled Aggregate in Concrete Applications (2000–2017). Constr. Build. Mater. 2018, 172, 272–292. [Google Scholar] [CrossRef]
- Liew, K.M.; Sojobi, A.O.; Zhang, L.W. Green Concrete: Prospects and Challenges. Constr. Build. Mater. 2017, 156, 1063–1095. [Google Scholar] [CrossRef]
- Meddah, M.S.; Al-Harthy, A.; Ismail, M.A. Recycled Concrete Aggregates and Their Influences on Performances of Low and Normal Strength Concretes. Buildings 2020, 10, 167. [Google Scholar] [CrossRef]
- Al Ajmani, H.; Suleiman, F.; Abuzayed, I.; Tamimi, A. Evaluation of Concrete Strength Made with Recycled Aggregate. Buildings 2019, 9, 56. [Google Scholar] [CrossRef] [Green Version]
- Shaikh, F. Mechanical and Durability Properties of Green Star Concretes. Buildings 2018, 8, 111. [Google Scholar] [CrossRef] [Green Version]
- Junak, J.; Sicakova, A. Effect of Surface Modifications of Recycled Concrete Aggregate on Concrete Properties. Buildings 2018, 8, 2. [Google Scholar] [CrossRef] [Green Version]
- Kisku, N.; Joshi, H.; Ansari, M.; Panda, S.; Nayak, S.; Dutta, S. A Critical Review and Assessment for Usage of Recycled Aggregate as Sustainable Construction Material. Constr. Build. Mater. 2017, 131, 721–740. [Google Scholar] [CrossRef]
- de Brito, J.; Ferreira, J.G.; Pacheco, J.; Soares, D.; Guerreiro, M. Structural, Material, Mechanical and Durability Properties and Behaviour of Recycled Aggregates Concrete. J. Build. Eng. 2016, 6, 1–16. [Google Scholar] [CrossRef]
- Kou, S.-C.; Poon, C.S. Effect of the Quality of Parent Concrete on the Properties of High Performance Recycled Aggregate Concrete. Constr. Build. Mater. 2015, 77, 501–508. [Google Scholar] [CrossRef]
- Rao, A.; Jha, K.N.; Misra, S. Use of Aggregates from Recycled Construction and Demolition Waste in Concrete. Resour. Conserv. Recycl. 2007, 50, 71–81. [Google Scholar] [CrossRef]
- Silva, F.; Delgado, J.; Azevedo, A.; Lima, A.; Vieira, C. Preliminary Analysis of the Use of Construction Waste to Replace Conventional Aggregates in Concrete. Buildings 2021, 11, 81. [Google Scholar] [CrossRef]
- Behera, M.; Bhattacharyya, S.; Minocha, A.; Deoliya, R.; Maiti, S. Recycled Aggregate from C&D Waste & Its Use in Concrete—A Breakthrough Towards Sustainability in Construction Sector: A Review. Constr. Build. Mater. 2014, 68, 501–516. [Google Scholar]
- Butler, L.; West, J.S.; Tighe, S.L. Effect of Recycled Concrete Coarse Aggregate from Multiple Sources on the Hardened Properties of Concrete with Equivalent Compressive Strength. Constr. Build. Mater. 2013, 47, 1292–1301. [Google Scholar] [CrossRef]
- Xiao, J.; Li, J.; Zhang, C. Mechanical Properties of Recycled Aggregate Concrete under Uniaxial Loading. Cem. Concr. Res. 2005, 35, 1187–1194. [Google Scholar] [CrossRef]
- Buyle-Bodin, F.; Hadjieva-Zaharieva, R. Influence of Industrially Produced Recycled Aggregates on Flow Properties of Concrete. Mater. Struct. 2002, 35, 504–509. [Google Scholar] [CrossRef]
- Silva, R.; de Brito, J.; Dhir, R. Properties and Composition of Recycled Aggregates from Construction and Demolition Waste Suitable for Concrete Production. Constr. Build. Mater. 2014, 65, 201–217. [Google Scholar] [CrossRef]
- Ismail, S.; Ramli, M. Influence of Surface-Treated Coarse Recycled Concrete Aggregate on Compressive Strength of Concrete. World Acad. Sci. Eng. Technol. Int. J. Civ. Environ. Struct. Constr. Archit. Eng 2014, 8, 862–866. [Google Scholar]
- Tam, V.W.; Tam, C.M.; Le, K. Removal of Cement Mortar Remains from Recycled Aggregate Using Pre-Soaking Approaches. Resour. Conserv. Recycl. 2007, 50, 82–101. [Google Scholar] [CrossRef] [Green Version]
- Kou, S.-C.; Poon, C.S. Properties of Concrete Prepared with Pva-Impregnated Recycled Concrete Aggregates. Cem. Concr. Compos. 2010, 32, 649–654. [Google Scholar] [CrossRef]
- Fathifazl, G.; Razaqpur, A.; Isgor, O.B.; Abbas, A.; Fournier, B.; Foo, S. Shear Capacity Evaluation of Steel Reinforced Recycled Concrete (Rrc) Beams. Eng. Struct. 2011, 33, 1025–1033. [Google Scholar] [CrossRef]
- Katz, A. Treatments for the Improvement of Recycled Aggregate. J. Mater. Civ. Eng. 2004, 16, 597–603. [Google Scholar] [CrossRef]
- Li, J.; Xiao, H.; Zhou, Y. Influence of Coating Recycled Aggregate Surface with Pozzolanic Powder on Properties of Recycled Aggregate Concrete. Constr. Build. Mater. 2009, 23, 1287–1291. [Google Scholar] [CrossRef]
- Sogo, M.; Sogabe, T.; Maruyama, I.; Sato, R.; Kawai, K. Shear Behavior of Reinforced Recycled Concrete Beams. In Proceedings of the International RILEM Conference on the Use of Recycled Materials in Buildings and Structures, Barcelona, Spain, 8–11 November 2004. [Google Scholar]
- Etxeberria, M.; Mari, A.; Vázquez, E. Recycled Aggregate Concrete as Structural Material. Mater. Struct. 2007, 40, 529–541. [Google Scholar] [CrossRef]
- González-Fonteboa, B.; Martínez-Abella, F. Shear Strength of Recycled Concrete Beams. Constr. Build. Mater. 2007, 21, 887–893. [Google Scholar] [CrossRef]
- Knaack, A.M.; Kurama, Y.C. Behavior of Reinforced Concrete Beams with Recycled Concrete Coarse Aggregates. J. Struct. Eng. 2014, 141, B4014009. [Google Scholar] [CrossRef]
- Ignjatović, I.; Marinković, S.B.; Tošić, N. Shear Behaviour of Recycled Aggregate Concrete Beams with and without Shear Reinforcement. Eng. Struct. 2017, 141, 386–401. [Google Scholar] [CrossRef]
- Arezoumandi, M.; Smith, A.; Volz, J.S.; Khayat, K. An Experimental Study on Shear Strength of Reinforced Concrete Beams with 100% Recycled Concrete Aggregate. Constr. Build. Mater. 2014, 53, 612–620. [Google Scholar] [CrossRef]
- Arezoumandi, M.; Drury, J.; Volz, J.S.; Khayat, K. Effect of Recycled Concrete Aggregate Replacement Level on Shear Strength of Reinforced Concrete Beams. ACI Mater. J. 2015, 112, 559. [Google Scholar] [CrossRef]
- Rahal, K.; Alrefaei, Y. Shear Strength of Longitudinally Reinforced Recycled Aggregate Concrete Beams. Eng. Struct. 2017, 145, 273–282. [Google Scholar] [CrossRef]
- Etman, E.E.; Afefy, H.M.; Baraghith, A.T.; Khedr, S.A. Khedr. Improving the Shear Performance of Reinforced Concrete Beams Made of Recycled Coarse Aggregate. Constr. Build. Mater. 2018, 185, 310–324. [Google Scholar] [CrossRef]
- Pradhan, S.; Kumar, S.; Barai, S.V. Shear Performance of Recycled Aggregate Concrete Beams: An Insight for Design Aspects. Constr. Build. Mater. 2018, 178, 593–611. [Google Scholar] [CrossRef]
- Wardeh, G.; Ghorbel, E. Shear Strength of Reinforced Concrete Beams with Recycled Aggregates. Adv. Struct. Eng. 2019, 22, 1938–1951. [Google Scholar] [CrossRef]
- Yun, H.-D.; Choi, W.-C. Shear Strength of Reinforced Recycled Aggregate Concrete Beams without Shear Reinforcements. J. Civ. Eng. Manag. 2017, 23, 76–84. [Google Scholar] [CrossRef]
- Tošić, N.; Marinković, S.; Ignjatović, I. A Database on Flexural and Shear Strength of Reinforced Recycled Aggregate Concrete Beams and Comparison to Eurocode 2 Predictions. Constr. Build. Mater. 2016, 127, 932–944. [Google Scholar] [CrossRef]
- Sadati, S.; Arezoumandi, M.; Khayat, K.; Volz, J.S. Shear Performance of Reinforced Concrete Beams Incorporating Recycled Concrete Aggregate and High-Volume Fly Ash. J. Clean. Prod. 2016, 115, 284–293. [Google Scholar] [CrossRef]
- Katkhuda, H.; Shatarat, N. Shear Behavior of Reinforced Concrete Beams Using Treated Recycled Concrete Aggregate. Constr. Build. Mater. 2016, 125, 63–71. [Google Scholar] [CrossRef]
- Kim, S.-W.; Jeong, C.-Y.; Lee, J.-S.; Kim, K.-H. Size Effect in Shear Failure of Reinforced Concrete Beams with Recycled Aggregate. J. Asian Archit. Build. Eng. 2013, 12, 323–330. [Google Scholar] [CrossRef]
- Choi, H.; Yi, C.; Cho, H.; Kang, K. Experimental Study on the Shear Strength of Recycled Aggregate Concrete Beams. Mag. Concr. Res. 2010, 62, 103–114. [Google Scholar] [CrossRef]
- Sato, R.; Maruyama, I.; Sogabe, T.; Sogo, M. Flexural Behavior of Reinforced Recycled Concrete Beams. J. Adv. Concr. Technol. 2007, 5, 43–61. [Google Scholar] [CrossRef]
- Kanhakorn, P.; Watanee, R.; Rerksamosorn, W.; Inmontien, N.; Tippakdee, S.; Thanongsak, I.; Monthian, S.; Wattanapanich, C. Estimation of Shear Behaviour for Recycled Aggregate Concrete Using Digital Image Correlation (Wu-Dic). J. King Mongkut’s Univ. Technol. North Bangk. 2021, 33, 4. [Google Scholar]
- Imjai, T.; Guadagnini, M.; Garcia, R.; Pilakoutas, K. A Practical Method for Determining Shear Crack Induced Deformation in Frp Rc Beams. Eng. Struct. 2016, 126, 353–364. [Google Scholar] [CrossRef]
- González-Fonteboa, B.; Martínez-Abella, F.; Martínez-Lage, I.; Eiras-López, J. Structural Shear Behaviour of Recycled Concrete with Silica Fume. Constr. Build. Mater. 2009, 23, 3406–3410. [Google Scholar] [CrossRef]
- Han, B.C.; Yun, H.D.; Chung, S.Y. Shear Capacity of Reinforced Concrete Beams Made with Recycled-Aggregate. Spec. Publ. 2001, 200, 503–516. [Google Scholar]


| Properties | FA | NCA | RCA |
|---|---|---|---|
| Bulk Specific Gravity (SSD) | 2.6 | 2.7 | 2.43 |
| Unit Weight (kg/m3) | 1730 | 1397 | |
| Water Absorption (%) | 1.05 | 0.28 | 4.59 |
| Moisture (%) | 1.35 | 0.61 | 2.24 |
| Fineness Modulus | 2.7 | ||
| Max. size (mm) | 4.76 | 19.1 | 18.6 |
| Impact value (%) | 10.15 | 13.4 | |
| Crushing value (%) | 21.77 | 23.12 | |
| Residual mortar (%) | 32.5 |
| Nominal Size (mm) | Yield Stress (MPa) | Ultimate Stress (MPa) | Elongation (%) |
|---|---|---|---|
| 20 | 519 | 668 | 18 |
| 16 | 561 | 658 | 21 |
| 6 | 424 | 639 | 28 |
| Mix Type | Cement | FA | NCA | RCA | Water | SP |
| NCA | 357 | 719 | 1069 | 190 | 1.07 | |
| 25% RCA | 357 | 750 | 802 | 216 | 190 | 1.07 |
| 50% RCA | 357 | 780 | 535 | 432 | 190 | 1.07 |
| 75% RCA | 357 | 810 | 267 | 648 | 190 | 1.07 |
| 100% RCA | 357 | 840 | 864 | 190 | 1.07 |
| Specimen ID | f’c (MPa) | ρw (%) | Pu (kN) | ∆u (mm) | Shear Crack Inclination Angle (Degree) | Vtest (kN) | vtest = Vtest/bd (MPa) | |
|---|---|---|---|---|---|---|---|---|
| RCA0-DB16 | 29.9 | 1.16 | 125 | 5.9 | 38 | 62.5 | 1.20 | 0.220 |
| RCA25-DB16 | 35.7 | 1.16 | 135 | 6.5 | 31 | 67.5 | 1.29 | 0.217 |
| RCA50-DB16 | 29.0 | 1.16 | 119 | 6.2 | 31 | 59.5 | 1.14 | 0.212 |
| RCA75-DB16 | 32.9 | 1.16 | 125 | 5.8 | 31 | 62.5 | 1.20 | 0.209 |
| RCA100-DB16 | 31.9 | 1.16 | 122 | 5.9 | 36 | 61.0 | 1.17 | 0.208 |
| RCA0-DB20 | 29.7 | 1.81 | 166.6 | 6.8 | 38 | 83.3 | 1.60 | 0.294 |
| RCA25-DB20 | 30.7 | 1.81 | 167.8 | 6.2 | 32 | 83.9 | 1.61 | 0.291 |
| RCA50-DB20 | 23.1 | 1.81 | 145 | 5.5 | 31 | 72.5 | 1.39 | 0.290 |
| RCA75-DB20 | 34.1 | 1.81 | 175 | 6.5 | 31 | 87.5 | 1.68 | 0.289 |
| RCA100-DB20 | 29.5 | 1.81 | 162.4 | 6.3 | 30 | 81.2 | 1.56 | 0.287 |
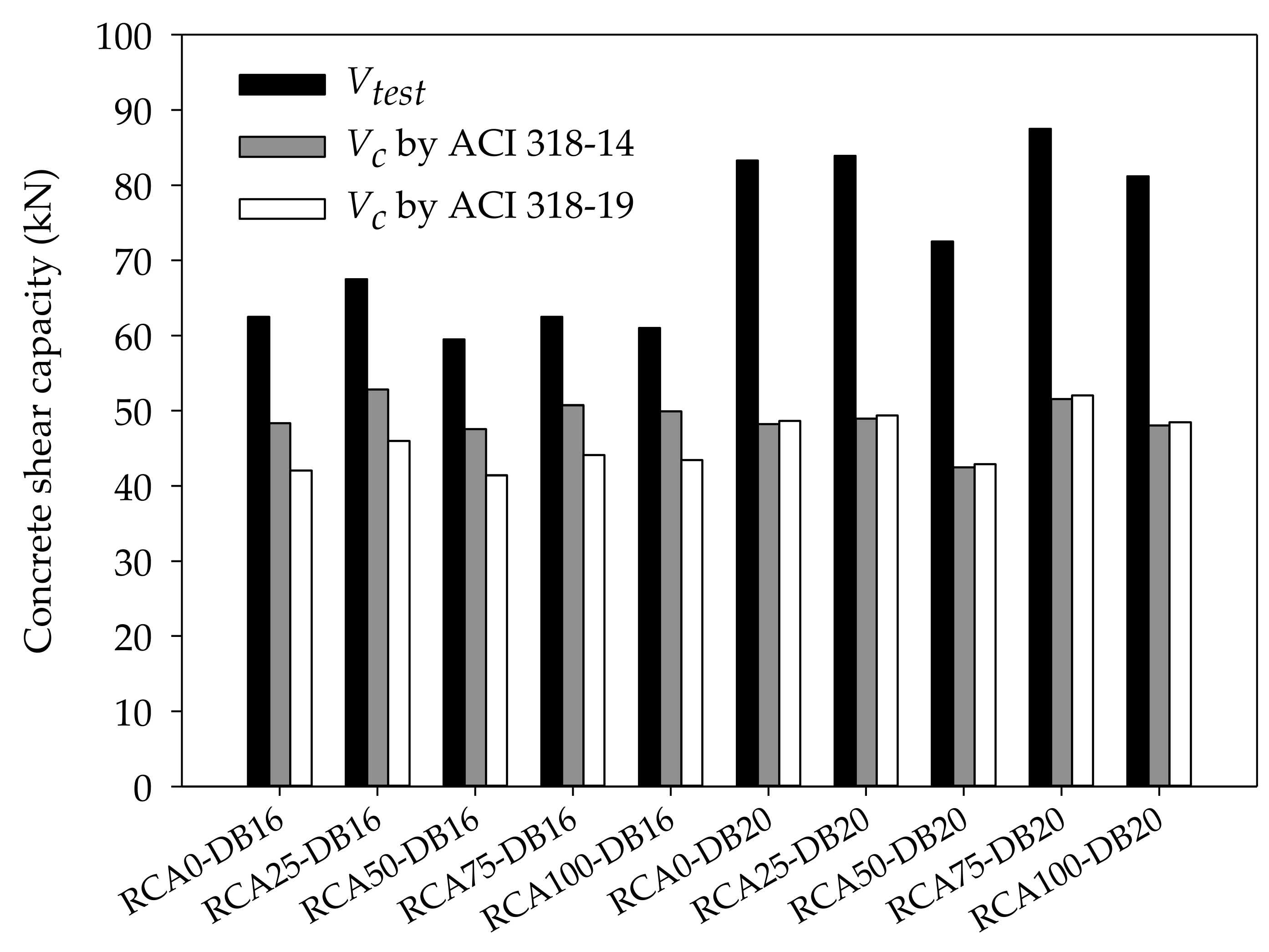
| Specimen ID | f’c (MPa) | ρw (%) | Ultimate Load Pu (kN) | Vtest (kN) | Vc (kN) ACI 318-14 | Vtest/Vc ACI 318-14 | Vc (kN) ACI 318-19 | Vtest/Vc ACI 318-19 |
|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) |
| RCA0-DB16 | 29.9 | 1.16 | 125 | 62.5 | 48.35 | 1.29 | 42.07 | 1.49 |
| RCA25-DB16 | 35.7 | 1.16 | 135 | 67.5 | 52.85 | 1.28 | 45.99 | 1.47 |
| RCA50-DB16 | 29.0 | 1.16 | 119 | 59.5 | 47.60 | 1.25 | 41.42 | 1.44 |
| RCA75-DB16 | 32.9 | 1.16 | 125 | 62.5 | 50.74 | 1.23 | 44.15 | 1.42 |
| RCA100-DB16 | 31.9 | 1.16 | 122 | 61.0 | 49.95 | 1.22 | 43.46 | 1.40 |
| RCA0-DB20 | 29.7 | 1.81 | 166.6 | 83.3 | 48.19 | 1.73 | 48.65 | 1.71 |
| RCA25-DB20 | 30.7 | 1.81 | 167.8 | 83.9 | 48.94 | 1.71 | 49.41 | 1.70 |
| RCA50-DB20 | 23.1 | 1.81 | 145 | 72.5 | 42.49 | 1.71 | 42.89 | 1.69 |
| RCA75-DB20 | 34.1 | 1.81 | 175 | 87.5 | 51.55 | 1.70 | 52.04 | 1.68 |
| RCA100-DB20 | 29.5 | 1.81 | 162.4 | 81.2 | 48.01 | 1.69 | 48.47 | 1.67 |
| Code Provision | Ratios of Vtest/Vc | ||
|---|---|---|---|
| Average | Least Conservative Value | COV | |
| ACI 318-14 | 1.15 | 0.54 | 0.25 |
| ACI 318-19 | 1.28 | 0.77 | 0.30 |
| βr | Number of Unconservative (Vtest/Vc) by Modified ACI 318-19 | Number of Unconservative (Vtest/Vc) by ACI 318-14 |
|---|---|---|
| 0.90 | 6 | 7 |
| 0.85 | 4 | 7 |
| 0.80 | 2 | 7 |
| 0.75 | 0 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Setkit, M.; Leelatanon, S.; Imjai, T.; Garcia, R.; Limkatanyu, S. Prediction of Shear Strength of Reinforced Recycled Aggregate Concrete Beams without Stirrups. Buildings 2021, 11, 402. https://doi.org/10.3390/buildings11090402
Setkit M, Leelatanon S, Imjai T, Garcia R, Limkatanyu S. Prediction of Shear Strength of Reinforced Recycled Aggregate Concrete Beams without Stirrups. Buildings. 2021; 11(9):402. https://doi.org/10.3390/buildings11090402
Chicago/Turabian StyleSetkit, Monthian, Satjapan Leelatanon, Thanongsak Imjai, Reyes Garcia, and Suchart Limkatanyu. 2021. "Prediction of Shear Strength of Reinforced Recycled Aggregate Concrete Beams without Stirrups" Buildings 11, no. 9: 402. https://doi.org/10.3390/buildings11090402
APA StyleSetkit, M., Leelatanon, S., Imjai, T., Garcia, R., & Limkatanyu, S. (2021). Prediction of Shear Strength of Reinforced Recycled Aggregate Concrete Beams without Stirrups. Buildings, 11(9), 402. https://doi.org/10.3390/buildings11090402








