Overview on the Nonlinear Static Procedures and Performance-Based Approach on Modern Unreinforced Masonry Buildings with Structural Irregularity
Abstract
1. Introduction
2. Description of Structural Irregularities: Is It Comprehensive Enough for Masonry Buildings?
3. Performance-Based Approach as a Design/Assessment Tool
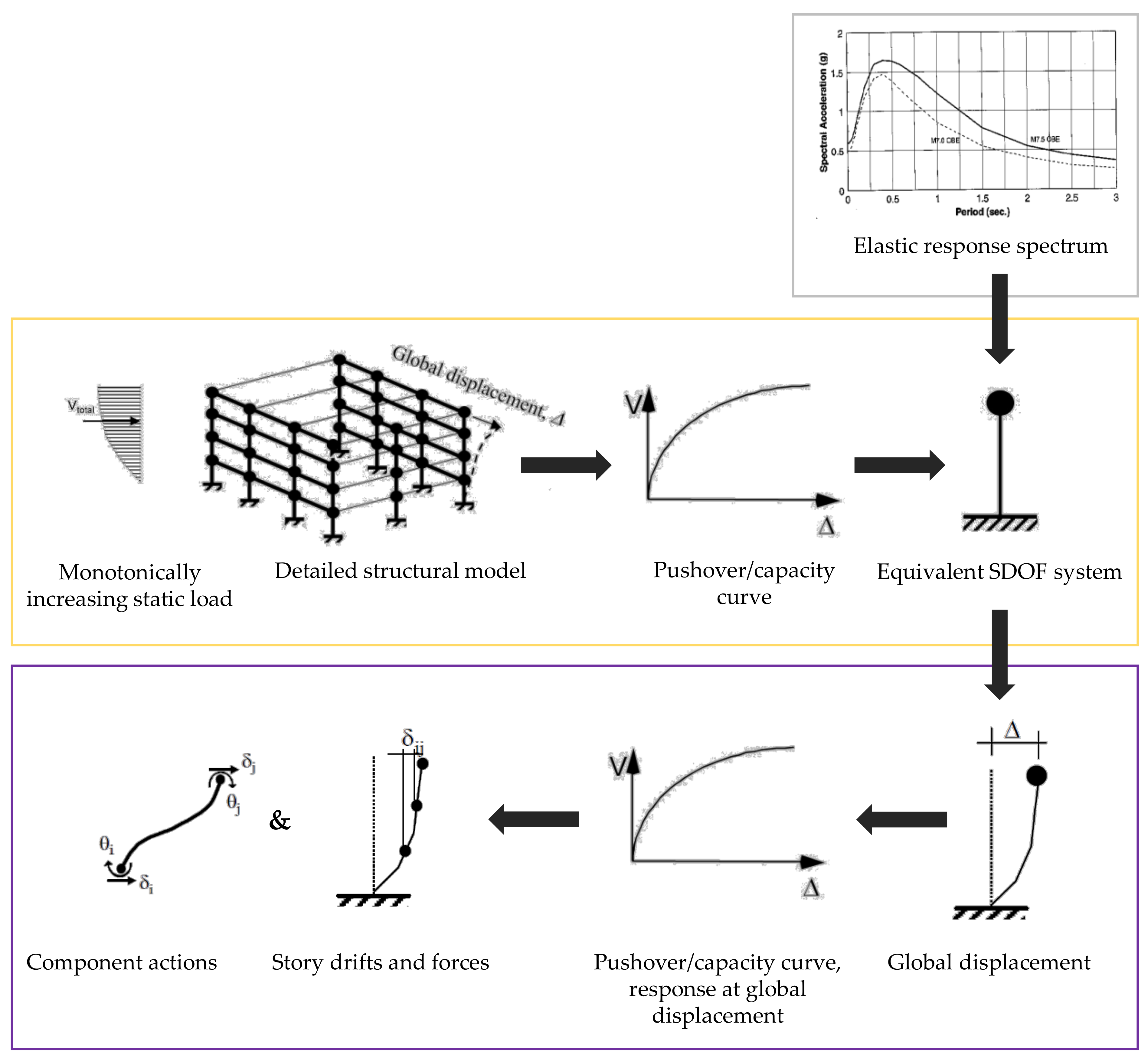
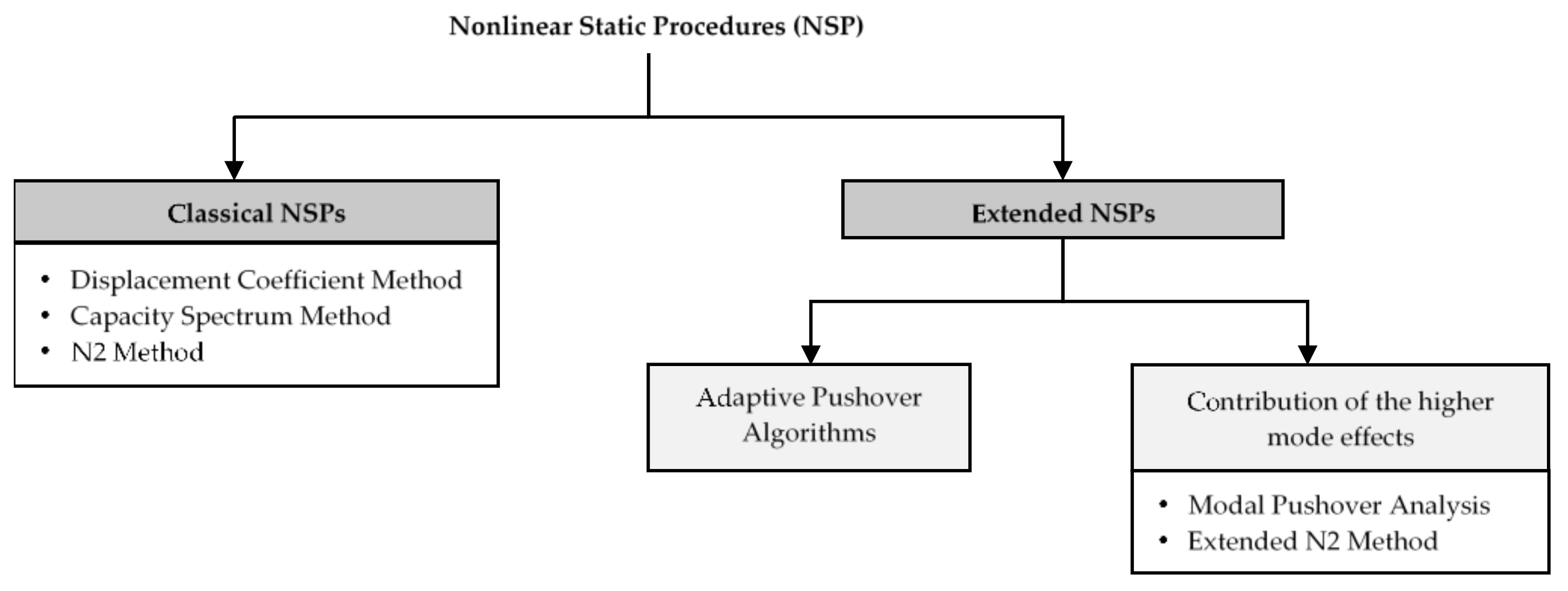
3.1. Classical Nonlinear Static Procedures
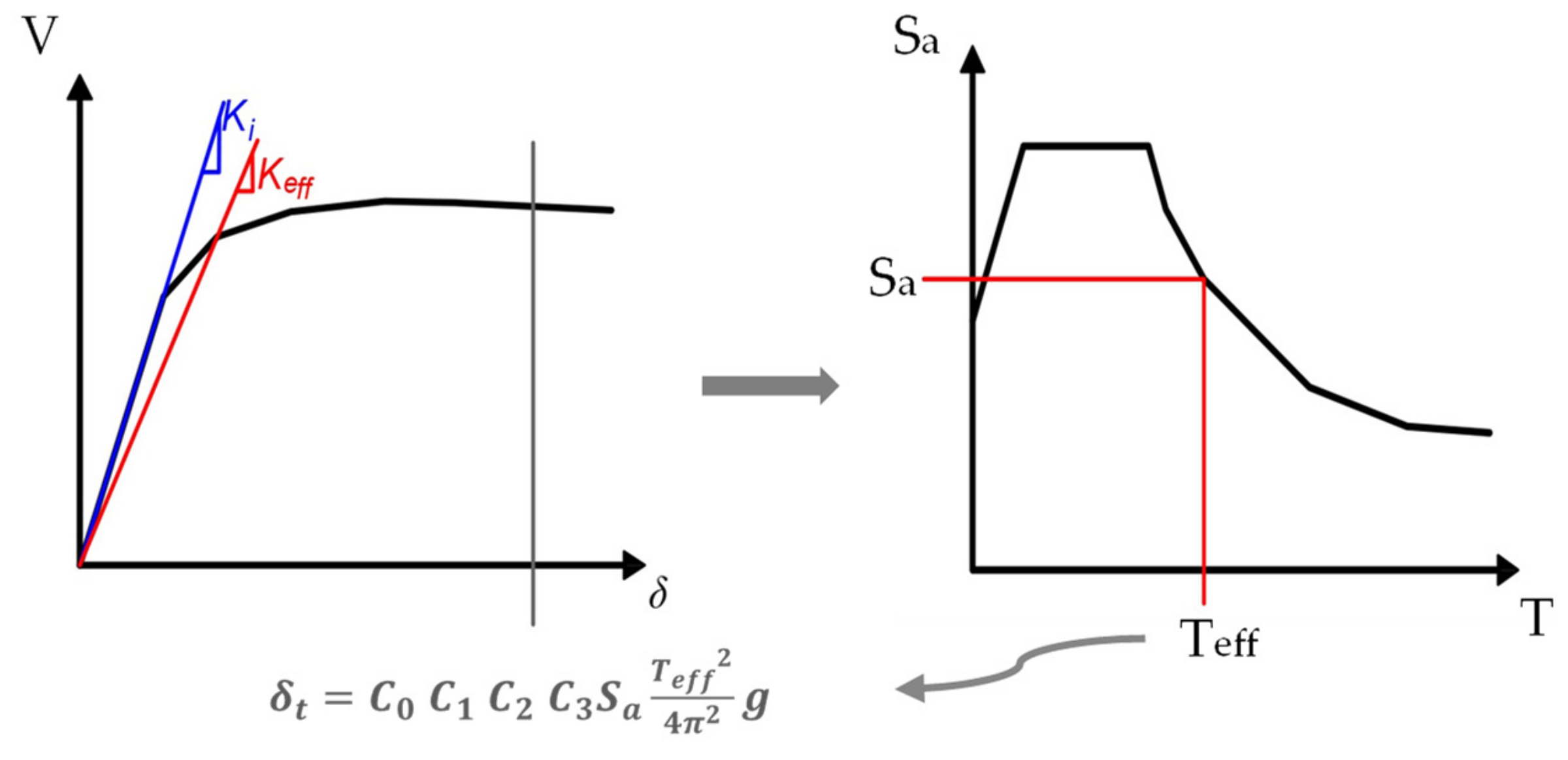
3.1.1. Displacement Coefficient Method
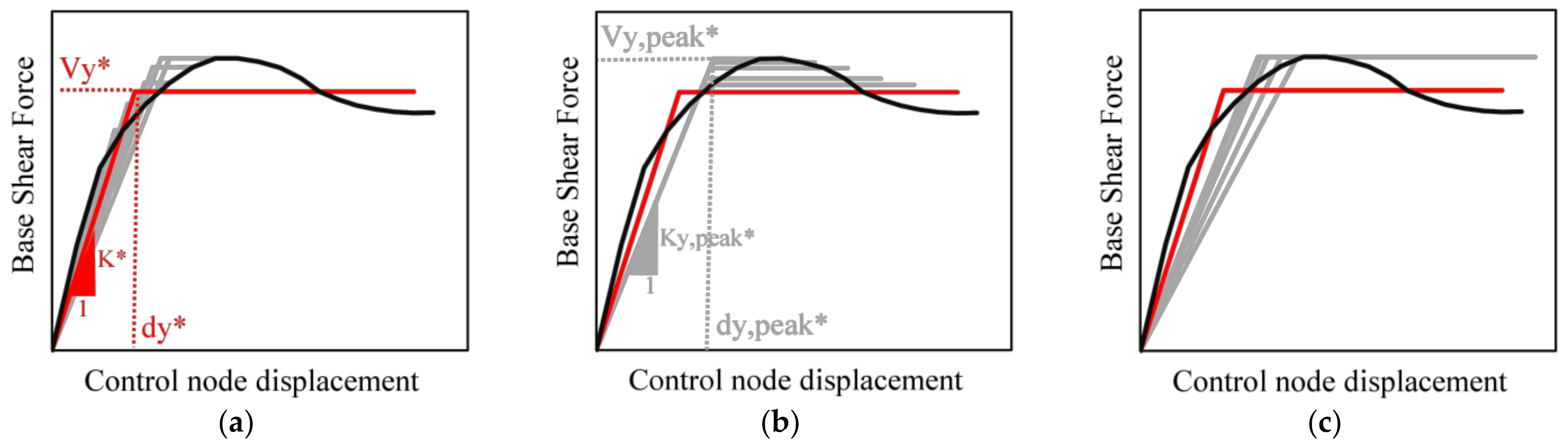
- A pushover curve, which is an idealization of force-deformation relation, is obtained through numerical analysis.
- On the pushover curve, an effective period (Teff) is calculated as a function of the initial period (Ti). In this way, stiffness loss observed during the transition from elastic to inelastic response is taken into account. Thus, an equivalent SDOF system is assumed to have the same elastic stiffness that corresponds to the effective period of the MDOF system obtained previously.
- A maximum acceleration response of the SDOF system is obtained as a function of an effective period on an elastic response spectrum that is representative of the seismic ground motion.
- The maximum global displacement demand is evaluated in terms of spectral displacement that is directly associated with the spectral acceleration through Equation (1).where:
- C0 converts the SDOF spectral displacement to MDOF roof displacement (elastic); it can be considered as the first mode participation factor or an appropriate value given in Table 2.
- C1 is the factor that relates the expected maximum inelastic displacement to elastic displacement.
- C2 represents the effects of pinched hysteretic shape, stiffness degradation and strength deterioration. The values given in Table 2 are associated with different performance limit states.
- C3 adjusts for second-order geometric nonlinearity (P-Δ) effects.
- Sa(Teff) is the spectral acceleration at the effective period.
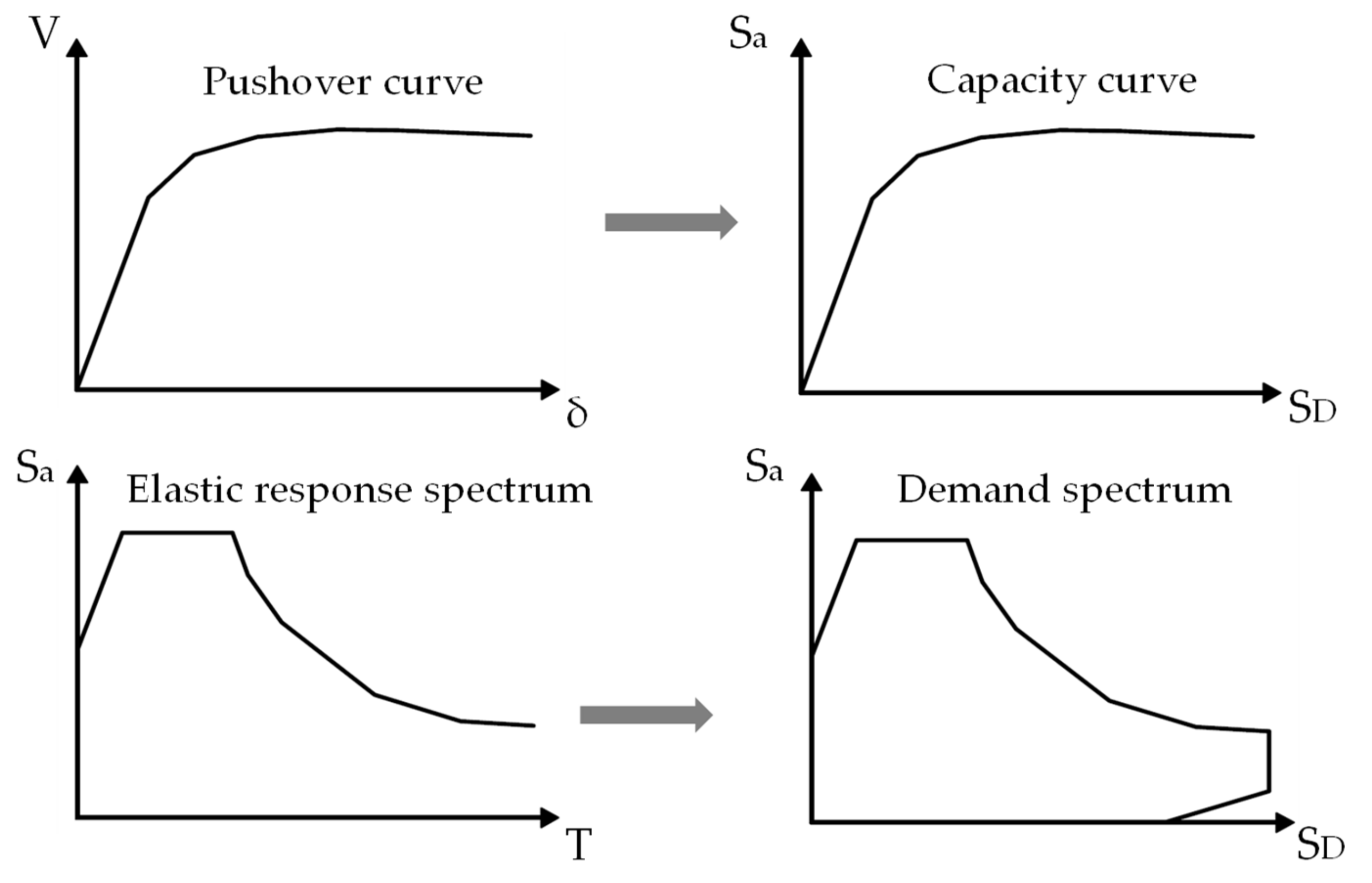
3.1.2. Capacity Spectrum Method of Equivalent Linearization
- Definition of the structural response based on the force–deformation diagram, i.e., pushover curve.
- The pushover curve is transformed into a capacity curve that is a function of spectral acceleration and spectral displacement of an SDOF system by using the modal properties of the structure. This format of the graph is termed as the acceleration–displacement response spectrum (ADRS).
- The elastic response spectrum of representative seismic ground motion is converted into the ADRS format (Figure 9). This enables the drawing and comparison of both seismic capacity and demand curves on the same coordinate system.
- As seen in Figure 9, the secant modulus is used to attain an equivalent inelastic period, and the inelastic displacement demand of the structure is estimated through the intersection of the capacity and overdamped demand curve.
- In order to obtain the overdamped response spectrum, equivalent viscous damping is needed. Two different approaches can be used to estimate the value as follows:
- Analytical expression proposed in [47], according to Equation (2).
- βel is the elastic viscous damping, which is generally considered 5%.
- is a factor, and values of 1.5 and 2.0 are suggested by [48] for buildings with box behavior and existing buildings without box behavior, respectively. This is dependent on the hysteretic behavior of the structure.
- α is the factor representing the asymptote of the hysteretic damping, and values of 25 and 20 are suggested by [48] for buildings with and without box behavior, respectively. This is also dependent on the hysteretic behavior of the structure.
- μ is the ductility.
- b.
- Cyclic pushover curve as a function of displacement (Figure 9).
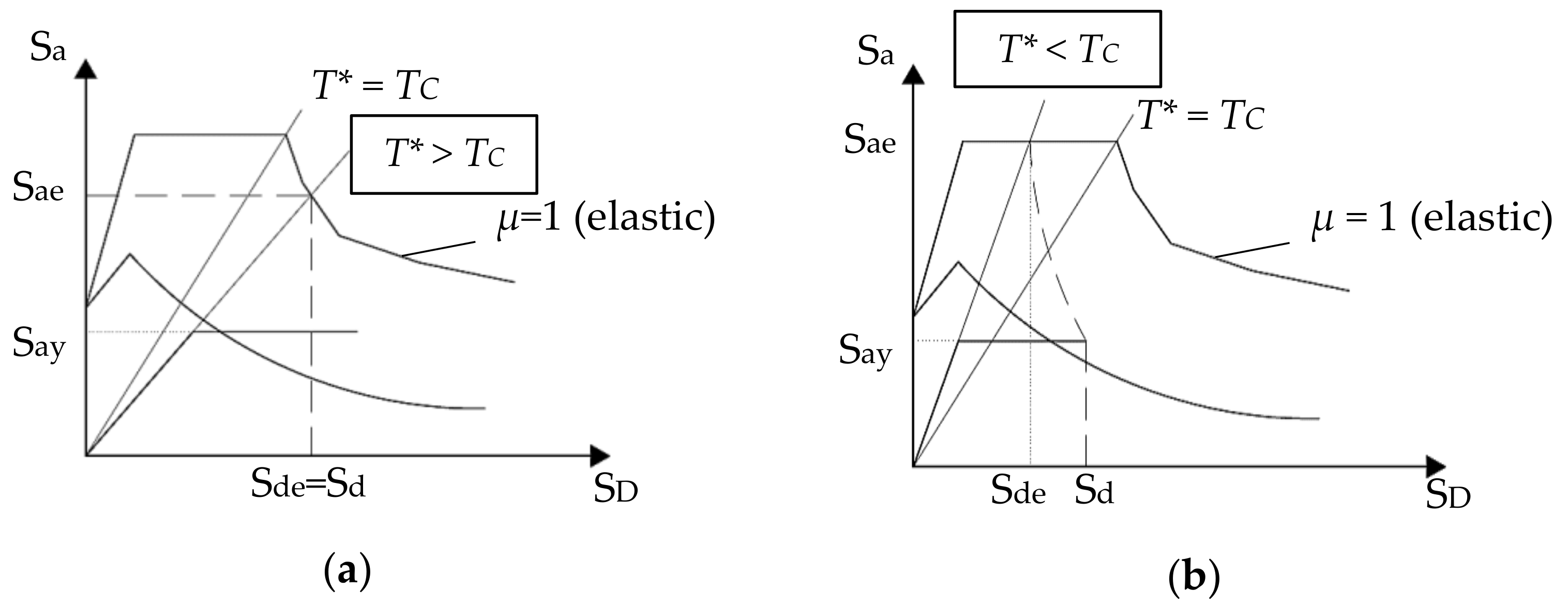
3.1.3. N2 Method
- Eigenvalue analysis to obtain modal properties of the MDOF system structure.
- The representative seismic action is defined in the form of an elastic acceleration spectrum as a function of the natural period of the structure (T), converted to ADRS format (Figure 10).
- The inelastic spectrum for constant ductility is determined by using the relations given in Equations (4) and (5).where μ is the ductility factor, and Rμ is the reduction factor due to hysteretic energy dissipation. It is important to mention that Rμ is different from the reduction factor R, which is used to modify the response of a building by taking into account both energy dissipation and overstrength.
- The mode proportional pushover analysis is performed, and a capacity curve is obtained. The first mode shape of the vibration is assumed, and lateral loads are applied proportional to the 1st mode shape. Note that the displacement profile is assumed to be the initial first mode shape throughout the procedure.
- The capacity curve of the MDOF system is then converted into a bilinear diagram, which represents the capacity of an equivalent SDOF system.
- Seismic demand of the equivalent SDOF system is attained graphically from the demand versus capacity diagram given in ADRS format, as depicted in Figure 10. Alternatively, Equation (6) is used to compute the displacement demand.
3.2. Extended Nonlinear Static Procedures
3.2.1. Modal Pushover Analyses
3.2.2. Extended N2 Method
- Perform the basic N2 method and determine the displacement demand at the center of mass (CM) at the roof level. Neglect the higher mode effects at the roof level.
- Perform the eigenvalue analysis and consider all the relevant modes. Use the SRSS rule to combine the results for both orthogonal directions. Next, obtain displacements and drifts at each level and normalize the results with respect to target displacement being equal to the roof displacement at CM.
- Apply a set of correction factors to take into account both in-plan and elevation irregularities. Displacements are used for in plan, while the drifts are considered for the elevation to evaluate the correction factors for each horizontal direction. These factors are location dependent. In the presence of both in-plan and elevation irregularity, the correction factors are obtained individually and then multiplied to attain the final value.
- Application of the correction factor for displacements due to in-plan irregularity:Firstly, the normalized roof displacement is calculated by dividing the roof displacement at a specific location by the displacement at the roof level at CM. Then, the correction factor applied to displacements is computed as the ratio between the normalized roof displacements obtained by elastic modal analysis and pushover analysis. The correction factor is equal to this ratio if the normalized displacement obtained by modal analysis is higher than 1.0. Otherwise, the value of the coefficient is assumed as 1.0.
- Application of the correction factor for drifts due to vertical irregularity:Similarly, the correction factor applied to drifts in each horizontal direction is calculated as the ratio of elastic to inelastic normalized story drifts. The reduction factor is not considered if the ratio is lower than 1.0.
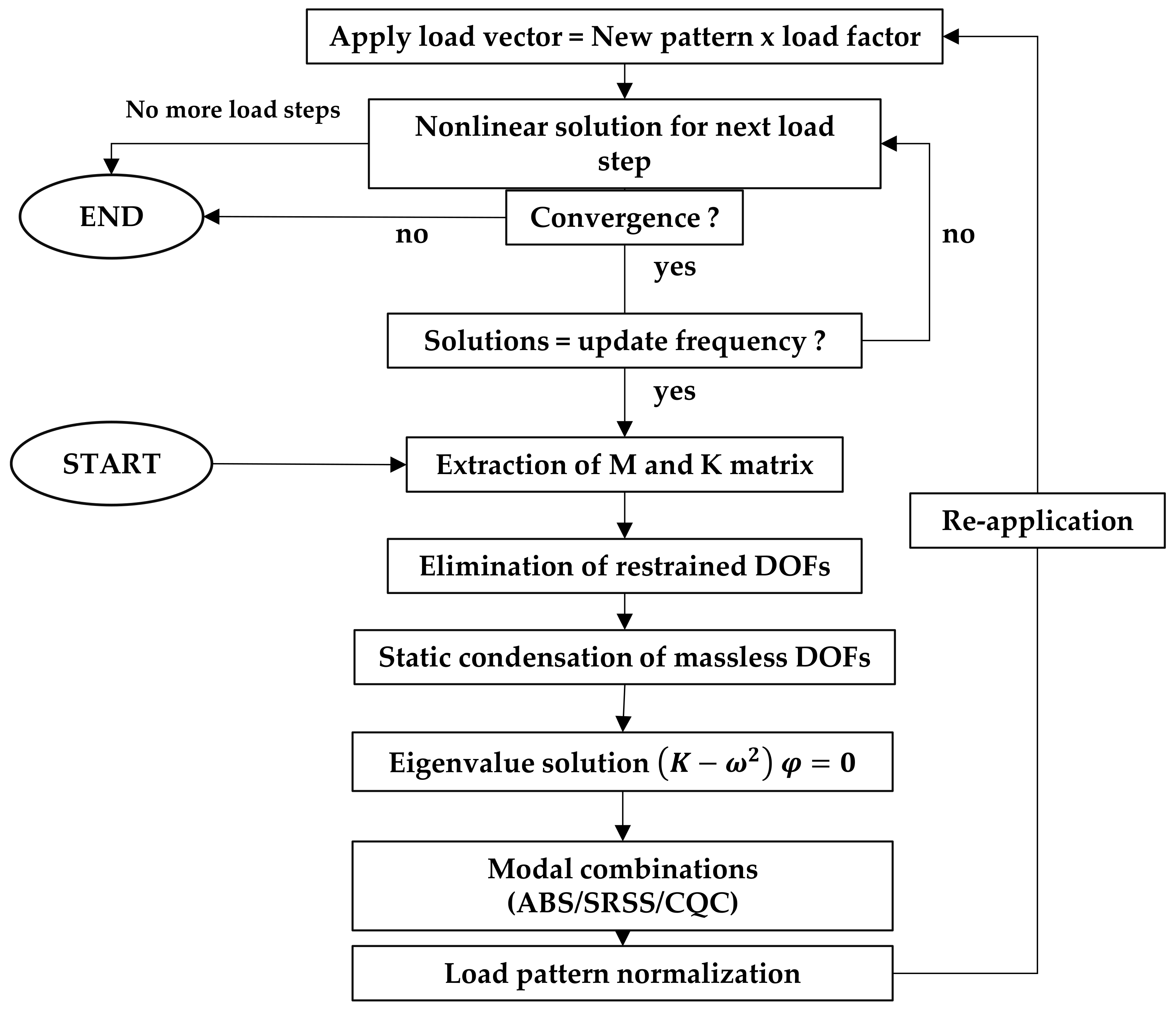
3.2.3. Adaptive Pushover Method
- Perform an eigenvalue analysis before the next incremental displacement.
- Based on the modal response, the displacement profile for the current step is calculated by using Equation (7).where:
- i is the story number.
- j is the mode number.
- ϕj is the modal participation factor for the jth mode.
- Φi,j is the mass normalized mode shape value for the ith story and the jth mode.
- SD(j) is the spectral displacement of the jth mode.
- To keep top displacement proportional to the load factor, displacements obtained by the previous step are normalized (Equation (8)).
- Update the load factor λ, and calculate the displacement vector (Equations (9) and (10)),where:
- Δλ is the load increment factor.
- ui,0 is the nominal displacement in a story i
- n is the pushover step.
- Apply the updated displacement to the model and solve the system of equations.
- Calculate updated stiffness matrix after loading is applied.
- Return to the first step of the loop to proceed with the next step.
4. Applications on Masonry Buildings
4.1. Case Studies Available in the Literature
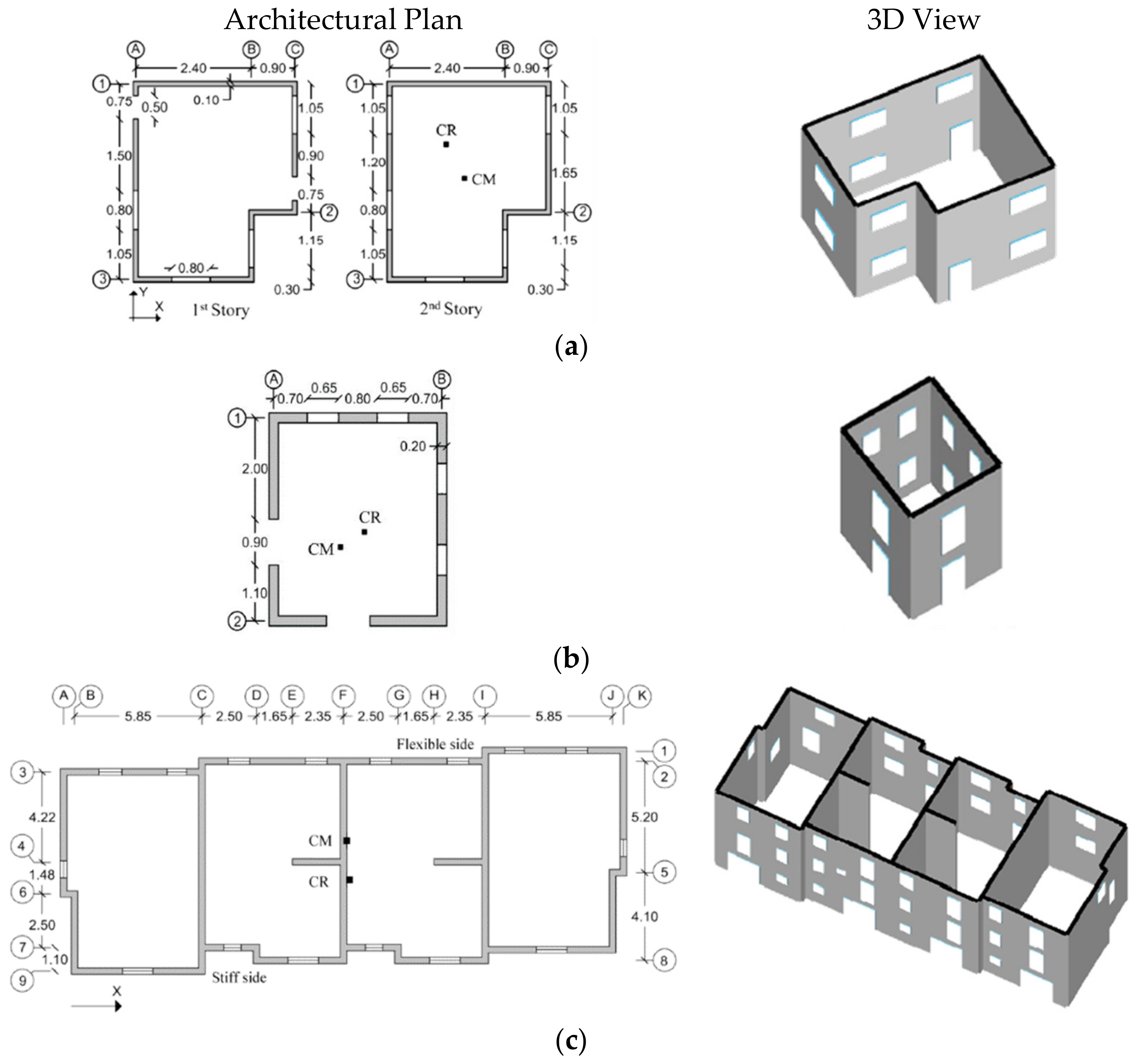
4.1.1. Case Study 1: Marino et al. (2019)
4.1.2. Case Study 2: Azizi (2018)
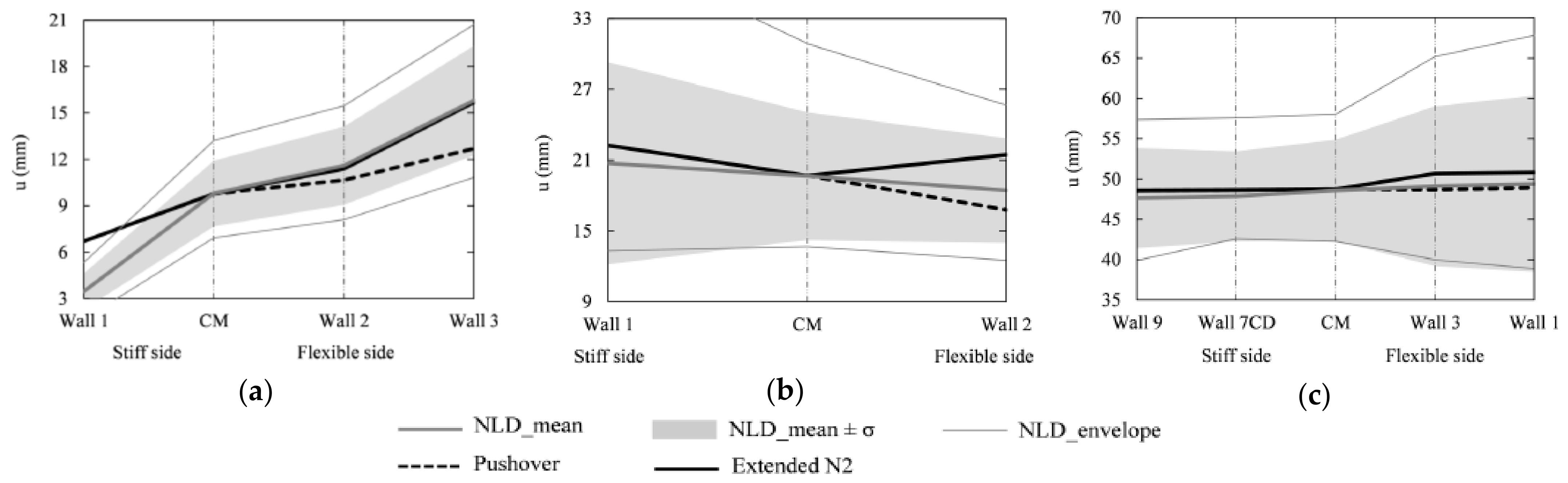
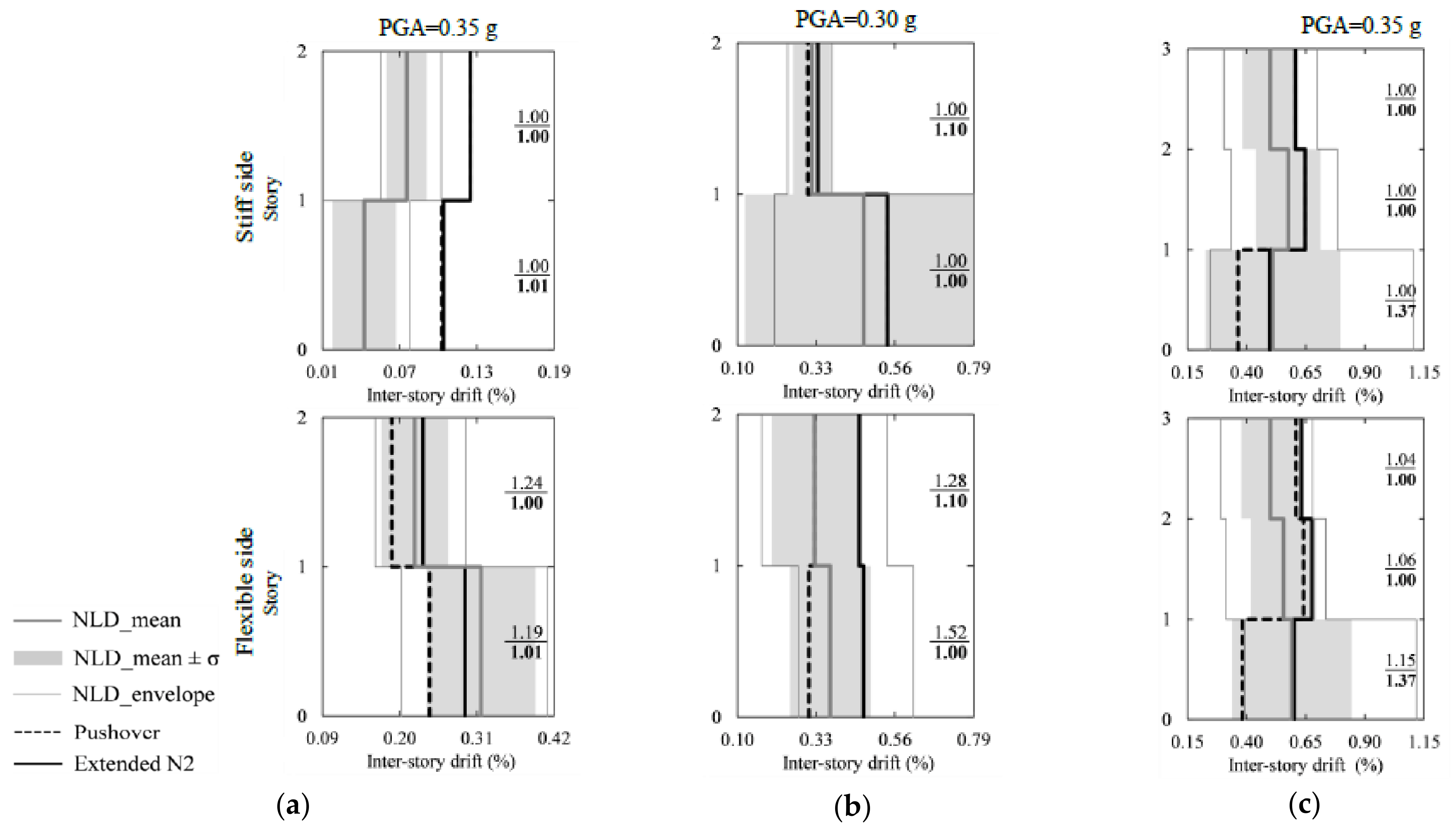
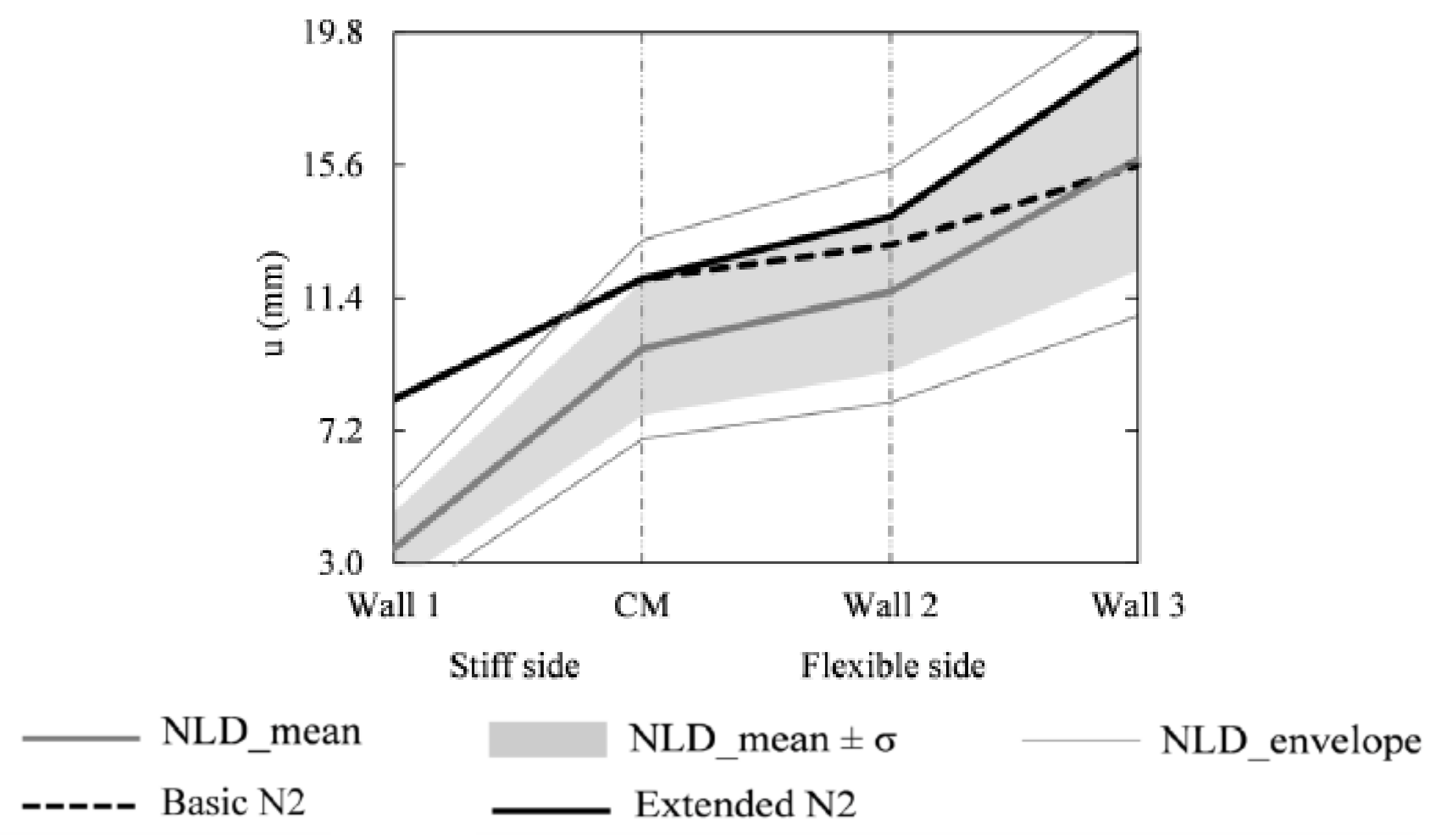
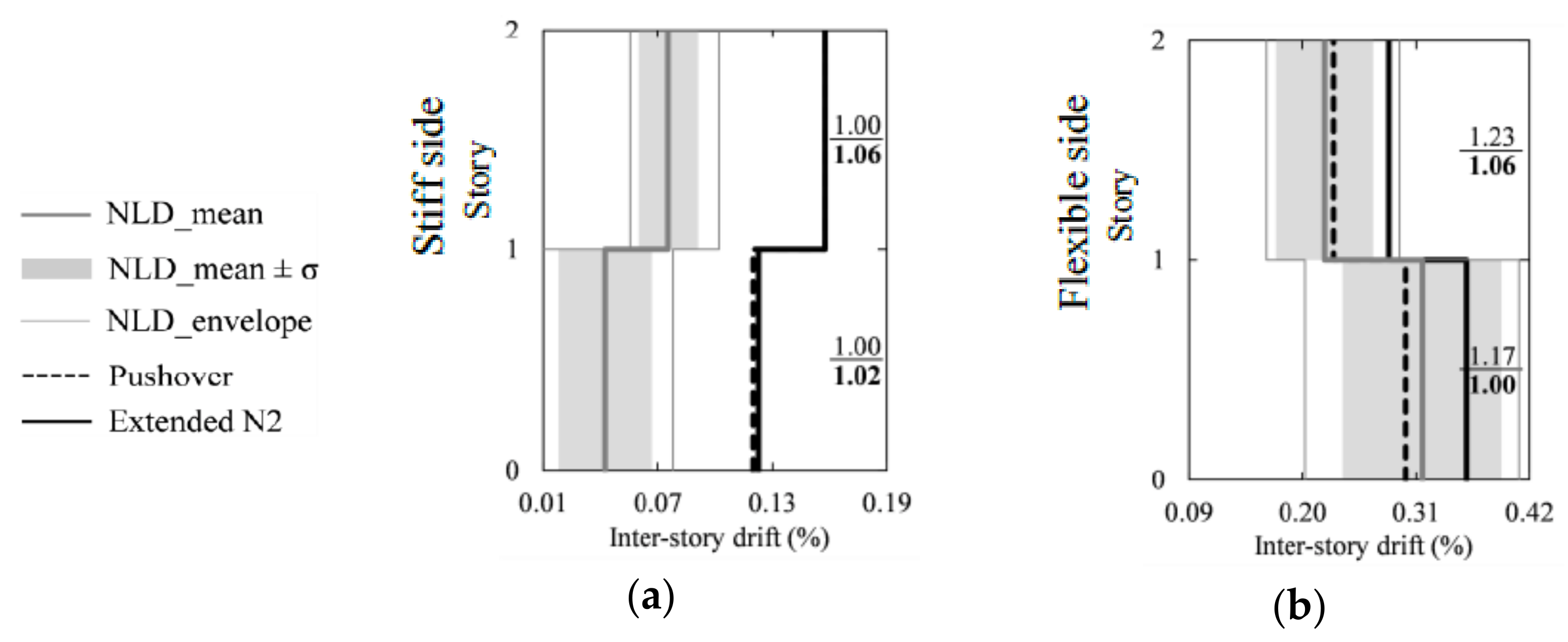
- First approach: The target displacement was computed by considering the mean value of NLD analyses instead of the basic N2 method. Next, pushover analysis was performed until the target displacement value was equal to that obtained from NLD analysis. The response computed in the previous step was updated employing a correction factor considering both torsional and elevation effects (extended N2 method). This method was applied to all models, namely, COM, CLM and ACM.
- Second approach: The target displacement was calculated by the basic N2 method, and then updated using a correction factor to take into account the effects of in-plan and elevation irregularities on the response (extended N2 method). This approach was utilized for COM buildings only.
4.2. Limitations of NSPs in Masonry Buildings
- The selection of load patterns is important, and the structural response is highly influenced by the presence of irregularities. According to [38], neither uniform nor triangular load patterns are suitable for buildings with elevation irregularities. The main reason for this is that the damage is concentrated at the top level as a result of dynamic behavior, but in pushover analysis with a uniform or triangular load pattern, a reduction in internal forces is recorded, as the applied force is a function of mass and height. Therefore, in the case of irregularity, it may be expected to have a reduction in mass, which will lead to a reduction in force. In addition, the mode proportional load pattern is only feasible if the response is governed by the so-called box behavior.
- Another important aspect is the identification of damage levels and the corresponding limit states. According to the codes, the definition of limit states is based on drift values associated with the failure mechanism at the building scale, which can be unconservative [36,38,67,68]. To overcome this issue, a multiscale approach, combining global and microelement scale behavior, was suggested by [48], particularly for buildings with an intermediate or flexible diaphragm.
- It should be mentioned that although IDA and ISA consider different levels of intensity, the major differences found between them are mostly justified by inherent differences found in the static and dynamic behavior of masonry buildings.
4.3. Improvements Proposed
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADRS | Acceleration–displacement response spectrum |
| CM | Center of mass |
| CQC | Complete-Quadratic-Combination |
| CR | Center of rigidity |
| CSM | Capacity spectrum method |
| DAP | Displacement-based adaptive pushover analysis |
| DCM | Displacement coefficient method |
| DL | Damage limit |
| IDA | Incremental dynamic analysis |
| IM | Intensity measure |
| ISA | Incremental static analysis |
| MDOF | Multi-degree-of-freedom |
| MMP | Multi-modal pushover analysis |
| MMPA | Modified modal pushover analysis |
| MPA | Modal pushover analysis |
| NLD | Nonlinear dynamic analysis |
| NSP | Nonlinear static procedures |
| PBD | Performance based design |
| PGA | Peak ground acceleration |
| RS | Response spectrum |
| SDOF | Single-degree-of-freedom |
| SRSS | Square-root-of-sum-of-square |
Appendix A
| Irregularity Type | EC 8 [11] | TEC 2019 [33] | ASCE/SEI 7-16 [72] | NTC 2018 [71] |
|---|---|---|---|---|
| Torsional | N.A | >1.2 | >1.2 >1.4 (extreme) | N.A |
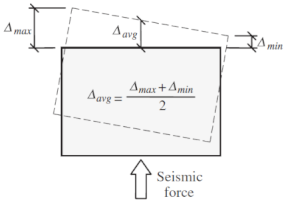 [72] [72] | ||||
| Setback | >0.05 | >0.2 | >0.15 | >0.05 |
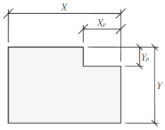 [72] [72]; | ||||
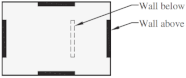
| Diaphragm discontinuity | N.A | > | >0.5 | N.A |
 or or  [72] [72] | ||||
| Out-of-plane offset | N.A | N.A | QL | Not allowed |
 [72] [72] | ||||
| Nonparallel system | N.A | N.A | QL | N.A |
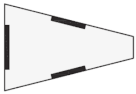 [72] [72] | ||||
| Plan shape regularity | < 4.0 | N.A | N.A | < 4.0 |
where Lmax is larger, Lmin is smaller dimensions of the plan |
| Irregularity Type | EC 8 [11] | TEC 2019 [33] | ASCE/SEI 7-16 [72] | NTC 2018 [71] | |
|---|---|---|---|---|---|
| Soft story (lateral stiffness) | QL | >2.0 * | a < 0.7 or b <
Extreme: a < 0.6 or b < | Reduction: a < 30 ϕ% Increase: a < 10 ϕ% | |
 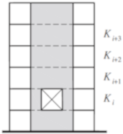 * TEC 2019 considers inter-story drift Δd as a parameter instead of Str. or ϕ NTC 2018 consider reduction or increase from one level to its above. | |||||
| Weak story (lateral strength) | <20 ϕ% | <0.80 * | <0.8 <0.65 (extreme) | N.A | |
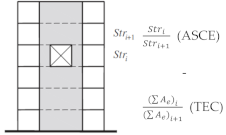 * TEC 2019 considers effective shear area Ae as a parameter instead of Str. ϕ Eurocode 8 considers the difference in shear area between two adjacent stories, specifically defined for masonry. | |||||
| Weight (Mass) | <20 *% | N.A | >1.5 | <25% | |
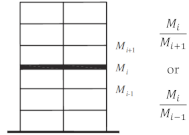 * Eurocode 8 and NTC 2018 consider the difference in mass between two adjacent stories. | |||||
| Geometric | a ≤ 0.20 b ≤ 0.20 c ≤ 0.50 d1 ≤ 0.30 d2 ≤ 0.10 | N.A | >1.3 | <30% at the first level <10% at other levels | |
ASCE/SEI 7-16 (Figure from [72])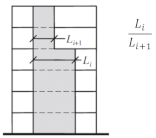 | |||||
| Eurocode 8 (Figures given below from [11]) | |||||
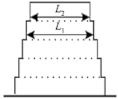 | 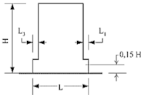 | ||||
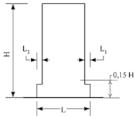 | 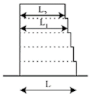 | ||||
| NTC 2018 [71] Setbacks are considered in terms of the plan area. The difference between the levels should be; | |||||
| In-plane discontinuity of lateral force resisting elements (figures from [72]) | QL | QL | >1.0 | QL | |
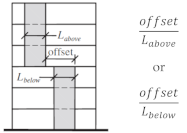 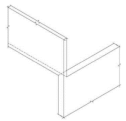  Perpendicular walls, walls with offset | |||||
Appendix B. Nomenclature
| Symbols in Figure 3 and Table 1 | Symbols in Figure 4 and Table 1 | ||
| D | Inter-story height | Regularized opening height at j-th story | |
| G | Centroid | Regularized horizontal alignment at i-th vertical alignment | |
| Ha | Height of the higher opening | Subsequent regularized horizontal alignment at i-th vertical alignment | |
| Hb | Height of the lower opening | Preceding regularized horizontal alignment at i-th vertical alignment | |
| Hmax | Maximum height of the opening | Centroid ordinate of an opening at i-th level j-th opening | |
| Hmin | Minimum height of the opening | Regularized vertical alignment at j-th story | |
| i | Irregularity index | Regularized opening width at i-th vertical alignment | |
| Lmax | Maximum opening length | bij | Opening width |
| Lmin | Minimum opening length | H | Total height of the wall |
| Lw | Overall length of the wall | hij | Opening height |
| tf | Thickness of the slab | L | Total length of the wall |
| XG | Distance of the centroid G | YG,ij | Centroid ordinate of an opening |
| Δ0 | Distance between the upper edges of the two openings | ΔHj | Inter-story height |
| ΔHa | Distance between upper opening edge | ||
| ΔHb | Distance between lower opening edge | ||
| ΔL | Total irregularity, distances between right and left opening edges | ||
| ΔH | Total irregularity, difference between maximum and minimum height | ||
| Nmin | Minimum number of openings per story | ||
| Nmax | Maximum number of openings per story | ||
References
- Battaglia, L.; Ferreira, T.M.; Lourenço, P.B. Seismic fragility assessment of masonry building aggregates: A case study in the old city Centre of Seixal, Portugal. Earthq. Eng. Struct. Dyn. 2021, 50, 1358–1377. [Google Scholar] [CrossRef]
- Valente, M.; Milani, G.; Grande, E.; Formisano, A. Historical masonry building aggregates: Advanced numerical insight for an effective seismic assessment on two row housing compounds. Eng. Struct. 2019, 190, 360–379. [Google Scholar] [CrossRef]
- Formisano, A.; Florio, G.; Landolfo, R.; Mazzolani, F.M. Numerical calibration of an easy method for seismic behaviour assessment on large scale of masonry building aggregates. Adv. Eng. Softw. 2015, 80, 116–138. [Google Scholar] [CrossRef]
- Lourenço, P.; Marques, R. Design of masonry structures (General rules): Highlights of the new European masonry code. In Brick and Block Masonry-From Historical to Sustainable Masonry, Proceedings of the 17th International Brick/Block Masonry Conference, Kraków, Poland, 5–8 July 2020; CRC Press: Boca Raton, FL, USA, 2020; p. 3. [Google Scholar]
- Priestley, M.J.N.; Calvi, G.M.; Kowalsky, M.J. Displacement-Based Seismic Design of Structures; IUSS Press: Pavia, Italy, 2007; ISBN 978-88-6198-0006. [Google Scholar]
- Fajfar, P. A Nonlinear Analysis Method for Performance-Based Seismic Design. Earthq. Spectra 2000, 16, 573–592. [Google Scholar] [CrossRef]
- Fajfar, P.; Marušić, D.; Perus, I. Torsional effects in the pushover-based seismic analysis of buildings. J. Earthq. Eng. 2005, 9, 831–854. [Google Scholar] [CrossRef]
- Kreslin, M.; Fajfar, P. The extended N2 method considering higher mode effects in both plan and elevation. Bull. Earthq. Eng. 2012, 10, 695–715. [Google Scholar] [CrossRef]
- Silva, V.; Crowley, H.; Pinho, R.; Varum, H. Extending displacement-based earthquake loss assessment (DBELA) for the computation of fragility curves. Eng. Struct. 2013, 56, 343–356. [Google Scholar] [CrossRef]
- Eurocode 6. Eurocode 6–Design of Masonry Structures–Part 1-1: General Rules for Reinforced and Unreinforced Masonry Structures; European Committee for Standardization: Brussels, Belgium, 2018. [Google Scholar]
- Eurocode 8. EN 1998-1: Design of Structures for Earthquake Resistance–Part 1: General Rules, Seismic Actions and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- De Stefano, M.; Pintucchi, B. A review of research on seismic behaviour of irregular building structures since 2002. Bull. Earthq. Eng. 2007, 6, 285–308. [Google Scholar] [CrossRef]
- D’Altri, A.; Sarhosis, V.; Milani, G.; Rots, J.; Cattari, S.; Lagomarsino, S.; Sacco, E.; Tralli, A.; Castellazzi, G.; De Miranda, S. A Review of Numerical Models for Masonry Structures; Numerical Modeling of Masonry and Historical Structures; Woodhead Publishing Series in Civil and Structural Engineering; Woodhead Publishing: Cambridge, UK, 2019; pp. 3–53. ISBN 9780081024393. [Google Scholar]
- Aşıkoğlu, A.; Vasconcelos, G.; Lourenço, P.B.; Pantò, B. Pushover analysis of unreinforced irregular masonry buildings: Lessons from different modeling approaches. Eng. Struct. 2020, 218, 110830. [Google Scholar] [CrossRef]
- Silva, L.C.; Lourenço, P.B.; Milani, G. Numerical homogenization-based seismic assessment of an English-bond masonry prototype: Structural level application. Earthq. Eng. Struct. Dyn. 2020, 49, 841–862. [Google Scholar] [CrossRef]
- Lourenço, P.B.; Silva, L.C. computational applications in masonry structures: From the meso-scale to the super-large/super-complex. Int. J. Multiscale Comput. Eng. 2020, 18, 1–30. [Google Scholar] [CrossRef]
- Abbati, S.D.; D’Altri, A.M.; Ottonelli, D.; Castellazzi, G.; Cattari, S.; de Miranda, S.; Lagomarsino, S. Seismic assessment of interacting structural units in complex historic masonry constructions by nonlinear static analyses. Comput. Struct. 2019, 213, 51–71. [Google Scholar] [CrossRef]
- Shehu, R. Implementation of Pushover Analysis for Seismic Assessment of Masonry Towers: Issues and Practical Recommendations. Buildings 2021, 11, 71. [Google Scholar] [CrossRef]
- Clementi, F. Failure Analysis of Apennine Masonry Churches Severely Damaged during the 2016 Central Italy Seismic Sequence. Buildings 2021, 11, 58. [Google Scholar] [CrossRef]
- Saloustros, S.; Pelà, L.; Roca, P. Nonlinear Numerical Modeling of Complex Masonry Heritage Structures Considering History-Related Phenomena in Staged Construction Analysis and Material Uncertainty in Seismic Assessment. J. Perform. Constr. Facil. 2020, 34, 04020096. [Google Scholar] [CrossRef]
- Croce, P.; Landi, F.; Formichi, P. Probabilistic Seismic Assessment of Existing Masonry Buildings. Buildings 2019, 9, 237. [Google Scholar] [CrossRef]
- Rodrigues, H.; Šipoš, T.K. Masonry Buildings: Research and Practice. Buildings 2019, 9, 162. [Google Scholar] [CrossRef]
- Simões, A. Evaluation of the Seismic Vulnerability of the Unreinforced Masonry Buildings Constructed in the Transition between the 19 th and 20 th Centuries in Lisbon, Portugal. Ph.D. Thesis, Universidade de Lisboa Instituto Superior Tecnico, Lisbon, Portugal, 2018. [Google Scholar]
- Cundari, G.; Milani, G.; Failla, G. Seismic vulnerability evaluation of historical masonry churches: Proposal for a general and comprehensive numerical approach to cross-check results. Eng. Fail. Anal. 2017, 82, 208–228. [Google Scholar] [CrossRef]
- Tiberti, S.; Acito, M.; Milani, G. Comprehensive FE numerical insight into Finale Emilia Castle behavior under 2012 Emilia Romagna seismic sequence: Damage causes and seismic vulnerability mitigation hypothesis. Eng. Struct. 2016, 117, 397–421. [Google Scholar] [CrossRef]
- Parisse, F.; Cattari, S.; Marques, R.; Lourenço, P.; Magenes, G.; Beyer, K.; Calderoni, B.; Camata, G.; Cordasco, E.; Erberik, M.; et al. Benchmarking the seismic assessment of unreinforced masonry buildings from a blind prediction test. Structures 2021, 31, 982–1005. [Google Scholar] [CrossRef]
- Asteris, P.; Chronopoulos, M.; Chrysostomou, C.; Varum, H.; Plevris, V.; Kyriakides, N.; Silva, V. Seismic vulnerability assessment of historical masonry structural systems. Eng. Struct. 2014, 62–63, 118–134. [Google Scholar] [CrossRef]
- Parisi, F.; Augenti, N. Seismic capacity of irregular unreinforced masonry walls with openings. Earthq. Eng. Struct. Dyn. 2013, 42, 101–121. [Google Scholar] [CrossRef]
- Augenti, N.; Parisi, F. Learning from Construction Failures due to the 2009 L’Aquila, Italy, Earthquake. J. Perform. Constr. Facil. 2010, 24, 536–555. [Google Scholar] [CrossRef]
- Giordano, A.; Guadagnuolo, M.; Faella, G. Pushover analysis of plan irregular masonry buildings. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Drysdale, R.G.; Hamid, A.A. Masonry Structures Behavior and Design, 3rd ed.; The Masonry Society: Englewood Cliffs, NJ, USA, 2008. [Google Scholar]
- De Stefano, M.; Mariani, V. Pushover analysis for plan irregular building structures. In Perspectives on European Earthquake Engineering and Seismology Geotechnical, Geological and Earthquake Engineering; Springer: Berlin/Heidelberg, Germany, 2014; pp. 8–11. [Google Scholar]
- TEC. Turkish Earthquake Code: Specifications for Building Design under Earthquake Effects; Official Newspaper No 30364; TEC: Ankara, Turkey, 2019. [Google Scholar]
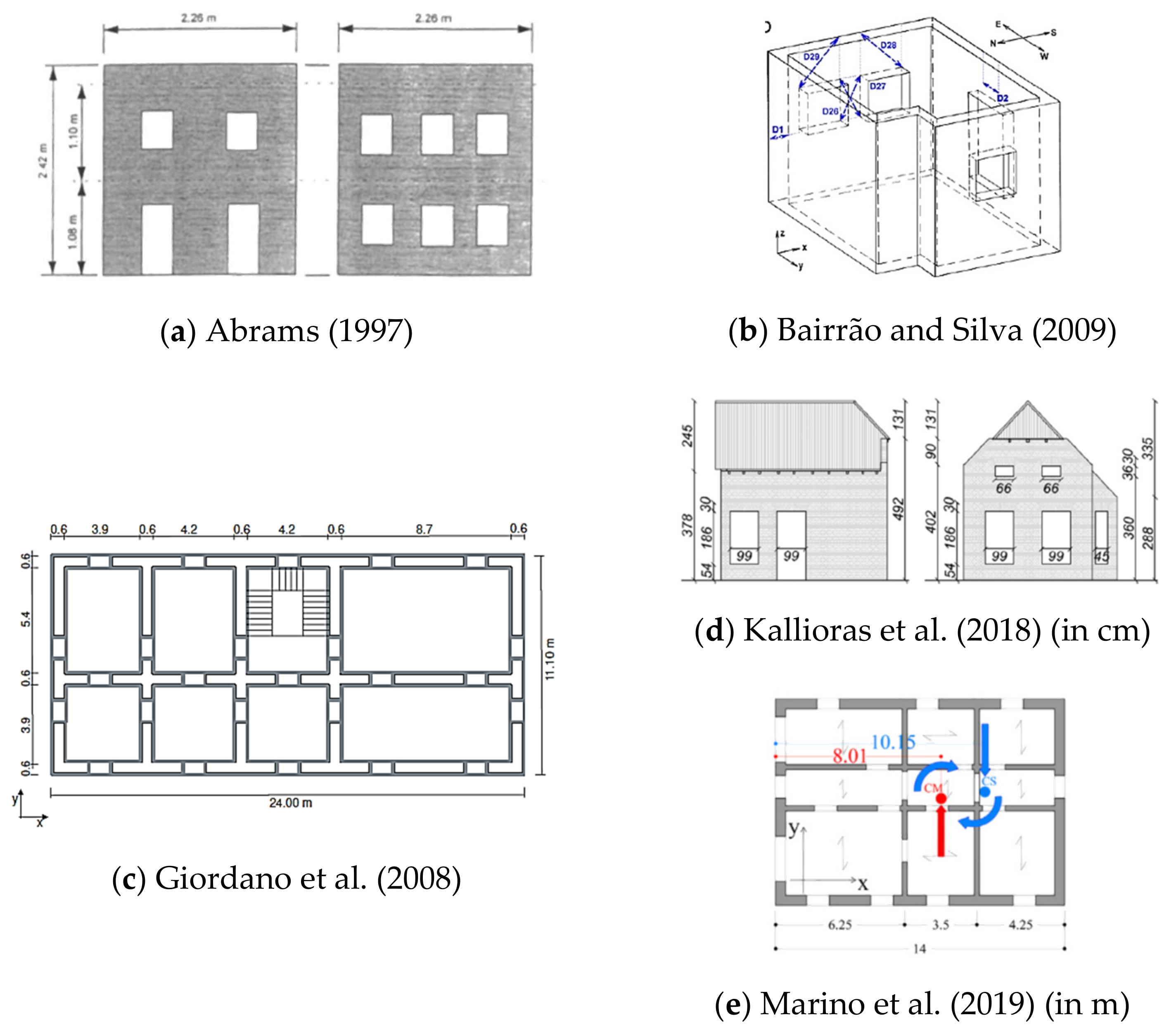
- Abrams, D.P. Response of Unreinforced Masonry Buildings. J. Earthq. Eng. 1997, 1, 257–273. [Google Scholar] [CrossRef]
- Bairrão, R.; Silva, M.F. Shaking table tests of two different reinforcement techniques using polymeric grids on an asymmetric limestone full-scaled structure. Eng. Struct. 2009, 31, 1321–1330. [Google Scholar] [CrossRef]
- Kallioras, S.; Guerrini, G.; Tomassetti, U.; Marchesi, B.; Penna, A.; Graziotti, F.; Magenes, G. Experimental seismic performance of a full-scale unreinforced clay-masonry building with flexible timber diaphragms. Eng. Struct. 2018, 161, 231–249. [Google Scholar] [CrossRef]
- Lagomarsino, S.; Camilletti, D.; Cattari, S.; Marino, S. Seismic Assessment of Existing Irregular Masonry Buildings by Nonlinear Static and Dynamic Analyses. Eurocode Compliant Seism. Anal. Des. R/C Build. 2018, 46, 123–151. [Google Scholar] [CrossRef]
- Marino, S.; Cattari, S.; Lagomarsino, S. Are the nonlinear static procedures feasible for the seismic assessment of irregular existing masonry buildings? Eng. Struct. 2019, 200, 109700. [Google Scholar] [CrossRef]
- Berti, M.; Salvatori, L.; Orlando, M.; Spinelli, P. Unreinforced masonry walls with irregular opening layouts: Reliability of equivalent-frame modelling for seismic vulnerability assessment. Bull. Earthq. Eng. 2017, 15, 1213–1239. [Google Scholar] [CrossRef]
- Grünthal, G. European Macroseismic Scale; European Seismological Commission: Luxembourg, 1998. [Google Scholar]
- SEAOC. Performance Based Seismic Engineering of Buildings; Vision 2000; Structural Engineers Association of California: Sacramento, CA, USA, 1995. [Google Scholar]
- Bilgin, H.; Hysenlliu, M. Comparison of near and far-fault ground motion effects on low and mid-rise masonry buildings. J. Build. Eng. 2020, 30, 101248. [Google Scholar] [CrossRef]
- FEMA 440. Improvement of Nonlinear Static Seismic Analysis Procedures; Department of Homeland Security Federal Emergency Management Agency: Washington, DC, USA, 2005. [Google Scholar]
- Fajfar, P.; Fischinger, M. N2—A Method for Nonlinear seismic analysis of regular buildings. In Proceedings of the Ninth World Conference Earthquake Engineering, Tokyo, Japan, 2–6 August 1988. [Google Scholar]
- Freeman, S.; Nicoletti, J.; Tyrell, J. Evaluation of existing buildings for seismic risk—A case study of Puget Sound Naval Shipyard. In Proceedings of the U.S. National Conference on Earthquake, Bremerton, WA, USA, 18–20 June 1975; pp. 113–122. [Google Scholar]
- FEMA 356. Prestandard and Commentary for the Seismic Rehabilitation of Buildings; Department of Homeland Security Federal Emergency Management Agency: Washington, DC, USA, 2000. [Google Scholar]
- Calvi, G.M. A Displacement-Based Approach for Vulnerability Evaluation of Classes of Buildings. J. Earthq. Eng. 1999, 3, 411–438. [Google Scholar] [CrossRef]
- Lagomarsino, S.; Cattari, S. PERPETUATE guidelines for seismic performance-based assessment of cultural heritage masonry structures. Bull. Earthq. Eng. 2015, 13, 13–47. [Google Scholar] [CrossRef]
- Paret, T.; Sasaki, K.; Elibeck, D.; Freeman, S. Approximate inelastic procedures to identify failure mechanism from higher modes effects. In Proceedings of the 11th World Conference Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996. [Google Scholar]
- Chopra, A.K.; Goel, R.K. A modal pushover analysis procedure for estimating seismic demands for buildings. Earthq. Eng. Struct. Dyn. 2002, 31, 561–582. [Google Scholar] [CrossRef]
- Chopra, A.K.; Goel, R.K. A modal pushover analysis procedure to estimate seismic demands for unsymmetric-plan buildings. Earthq. Eng. Struct. Dyn. 2004, 33, 903–927. [Google Scholar] [CrossRef]
- Fajfar, P.; Kilar, V.; Marusic, D.; Perus, I.; Magliulo, G. The extension of the N2 method to asymmetric buildings. In Proceedings of the 4th European Workshop on the Seismic Behaviour of Irregular and Complex Structures, Thessaloniki, Greece, 26–27 August 2005. [Google Scholar]
- Antoniou, S. Advanced Inelastic Static Analysis for Seismic Assessment of Structures. PhD. Thesis, Imperial College London (University of London), London, UK, 2002. [Google Scholar]
- Papanikolaou, V.K.; Elnashai, A.S. Evaluation of conventional and adaptive pushover analysis I: Methodology. J. Earthq. Eng. 2005, 9, 923–941. [Google Scholar] [CrossRef]
- Minghini, F.; Bertolesi, E.; Del Grosso, A.; Milani, G.; Tralli, A. Modal pushover and response history analyses of a masonry chimney before and after shortening. Eng. Struct. 2016, 110, 307–324. [Google Scholar] [CrossRef]
- Minghini, F.; Milani, G.; Tralli, A. Seismic risk assessment of a 50m high masonry chimney using advanced analysis techniques. Eng. Struct. 2014, 69, 255–270. [Google Scholar] [CrossRef]
- Peña, F.; Lourenço, P.B.; Mendes, N.; Oliveira, D.V. Numerical models for the seismic assessment of an old masonry tower. Eng. Struct. 2010, 32, 1466–1478. [Google Scholar] [CrossRef]
- Ferracuti, B.; Pinho, R.; Savoia, M.; Francia, R. Verification of displacement-based adaptive pushover through multi-ground motion incremental dynamic analyses. Eng. Struct. 2009, 31, 1789–1799. [Google Scholar] [CrossRef]
- Silva, V.; Crowley, H.; Varum, H.; Pinho, R.; Sousa, L. Investigation of the characteristics of Portuguese regular moment-frame RC buildings and development of a vulnerability model. Bull. Earthq. Eng. 2015, 13, 1455–1490. [Google Scholar] [CrossRef]
- Antoniou, S.; Rovithakis, A.; Pinho, R. Development and Verification of a Fully Adaptive Pushover Procedure. In Proceedings of the 12th European Conference Earthquake Engineering, London, UK, 9–13 September 2002. [Google Scholar]
- Yi, T.; Moon, F.L.; Leon, R.T.; Kahn, L.F. Lateral Load Tests on a Two-Story Unreinforced Masonry Building. J. Struct. Eng. 2006, 132, 643–652. [Google Scholar] [CrossRef]
- Galasco, A.; Lagomarsino, S.; Penna, A. On the use of pushover analysis for existing masonry buildings. In Proceedings of the 1st European Conference on Earthquake and Seismology, Geneva, Switzerland, 3–8 September 2006. [Google Scholar]
- Caliò, I.; Cannizzaro, F.; D’Amore, E.; Marletta, M.; Pantò, B. A new discrete-element approach for the assessment of the seismic resistance of composite reinforced concrete-masonry buildings. Fourth Huntsville Gamma Ray Burst Symp. 2008, 1020, 832–839. [Google Scholar] [CrossRef]
- Azizi, H. Analytical and Empirical Seismic Fragility Analysis of Irregular URM Buildings with Box Behavior. Ph.D. Thesis, University of Minho, Guimarães, Portugal, 2018. [Google Scholar]
- Lagomarsino, S.; Penna, A.; Galasco, A.; Cattari, S. TREMURI Program: Seismic Analyses of 3D Masonry Buildings, Release 2.0; University of Genoa: Genoa, Italy, 2012. [Google Scholar]
- Marino, S. Nonlinear Static Procedures for the Seismic Assessment of Irregular URM Buildings. Ph.D. Thesis, University of Genoa, Genoa, Italy, 2018. [Google Scholar]
- Kallioras, S.; Correia, A.A.; Graziotti, F.; Penna, A.; Magenes, G. Collapse shake-table testing of a clay-URM building with chimneys. Bull. Earthq. Eng. 2020, 18, 1009–1048. [Google Scholar] [CrossRef]
- Graziotti, F.; Tomassetti, U.; Kallioras, S.; Penna, A.; Magenes, G. Shaking table test on a full scale URM cavity wall building. Bull. Earthq. Eng. 2017, 15, 5329–5364. [Google Scholar] [CrossRef]
- Graziotti, F.; Penna, A.; Bossi, E.; Magenes, G. Evaluation of displacement demand for unreinforced masonry buildings by equivalent SDOF systems. In Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014, Porto, Portugal, 30 June–2 July 2014; pp. 365–372. [Google Scholar]
- Guerrini, G.; Graziotti, F.; Penna, A.; Magenes, G. Improved evaluation of inelastic displacement demands for short-period masonry structures. Earthq. Eng. Struct. Dyn. 2017, 46, 1411–1430. [Google Scholar] [CrossRef]
- NTC. Norme Tecniche per le Costruzioni; DM 17/1/2018; Gazzetta Ufficiale della Repubblica Italiana n. 42 del 20 febbraio 2018; NTC: Roma, Italy, 2018. [Google Scholar]
- ASCE/SEI 7-16. Minimum Design Loads and Associated Criteria for Buildings and Other Structures; American Society of Civil Engineers: Reston, VA, USA, 2017. [Google Scholar]

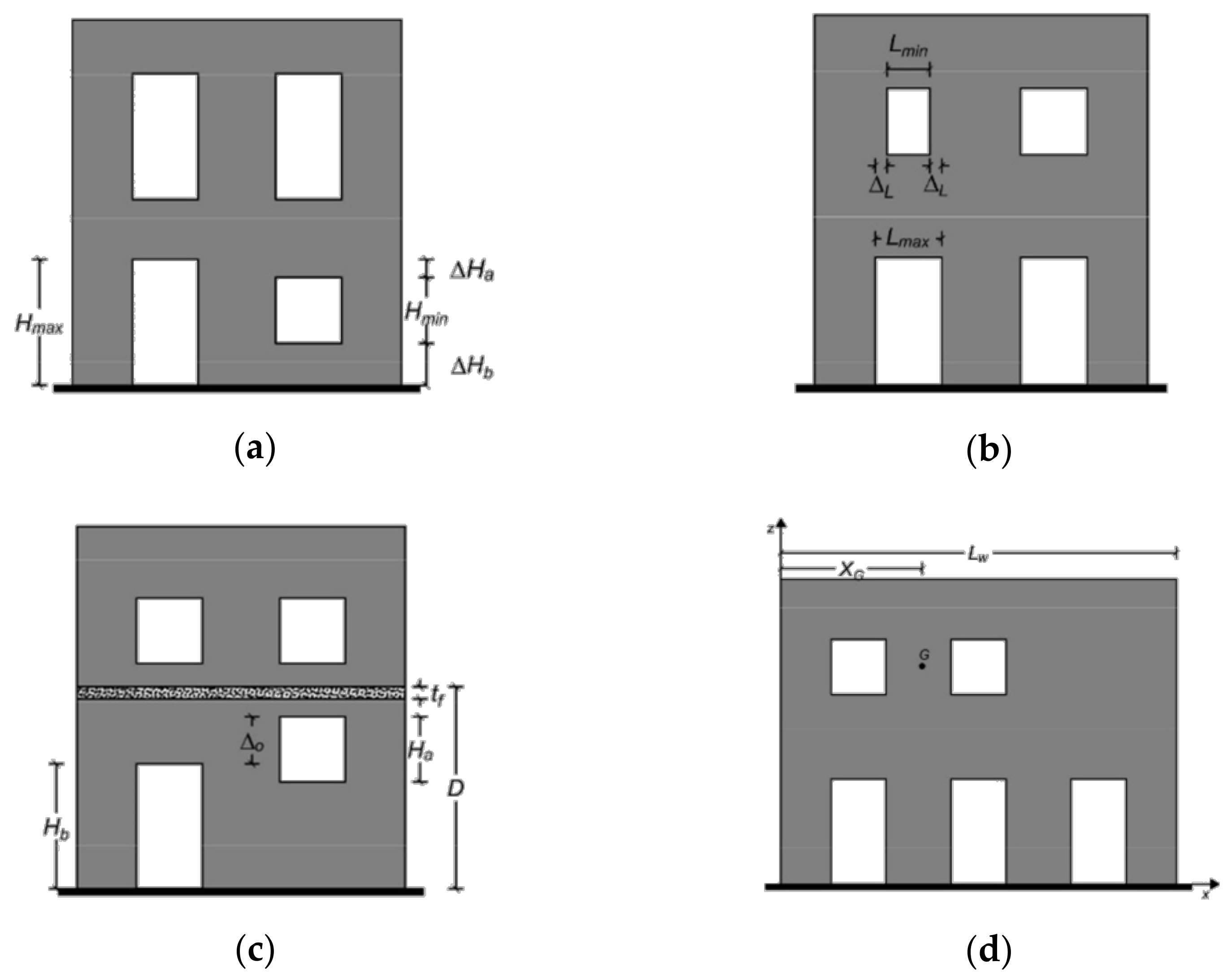
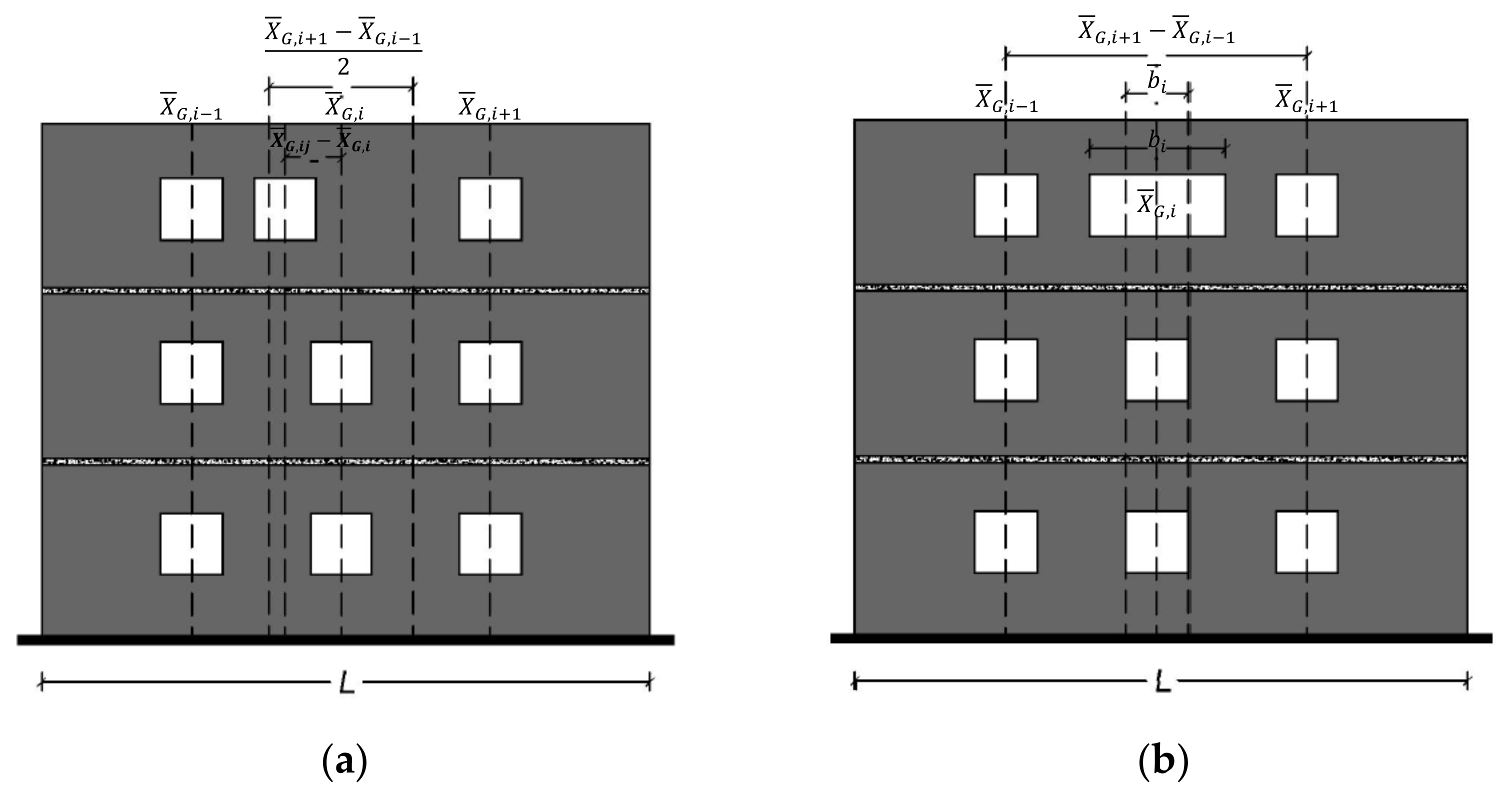
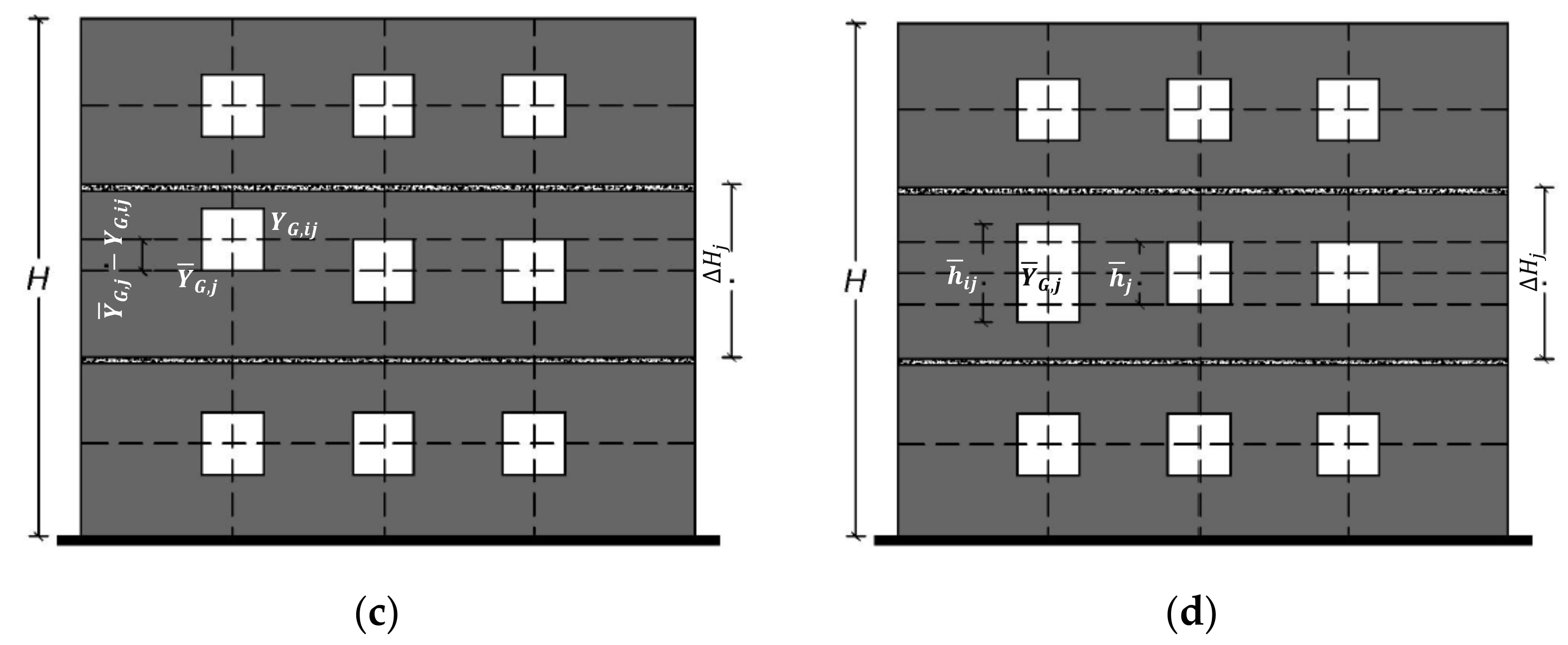




| Definition | Index | ||
|---|---|---|---|
| Authors | Parisi and Augenti (2013) [28] | 1—Horizontal Irregularity | |
| The openings have different heights at the same story while equal lengths among the stories. | |||
| 2—Vertical Irregularity | |||
| The openings have the same height at the same story while different lengths among the stories. | |||
| 3—Offset Irregularity | |||
| The wall has horizontal and/or vertical offsets between openings of equal or different sizes. | |||
| 4—Variable openings number irregularity | ; | ||
| The wall has a different number of openings per story. | |||
| Berti et al. (2017) [39] | 1—Horizontal misalignment | ||
| The centroid abscissa of an opening XG,ij differs from the vertical alignment of the i-th vertical opening array XG,i. | |||
| 2—Vertical misalignment | |||
| The centroid ordinate of an opening YG,ij differs from the horizontal alignment of the j-th story YG,j | |||
| 3—Irregularity in width | |||
| The opening width bij differs from the average one of the i-th vertical opening alignment bi. | |||
| 4—Irregularity in height | |||
| The opening height hij differs from the average one in the j-th story hj. | |||
| 5—Global index | |||
| Global irregularity measure in which the combination of irregularity indexes is obtained. | |||
| Coef. | Number of Stories | Shear Buildings 2 | Other Buildings | |||
|---|---|---|---|---|---|---|
| Triangular Load Pattern | Uniform Load Pattern | Any Load Pattern | ||||
| C0 1 | 1 | 1.00 | 1.00 | 1.00 | ||
| 2 | 1.20 | 1.15 | 1.20 | |||
| 3 | 1.20 | 1.20 | 1.30 | |||
| 5 | 1.30 | 1.20 | 1.40 | |||
| 10+ | 1.30 | 1.20 | 1.50 | |||
| C1 | where Ts is the characteristic period of the response spectrum | However, it should be less than and higher than 1.0. | ||||
| Coef. | T< 0.1 s 5 | T > Tss 5 | ||||
| Structural Performance Level | Framing Type 1 3 | Framing Type 2 4 | Framing Type 1 3 | Framing Type 2 4 | ||
| C2 | Immediate Occupancy | 1.0 | 1.0 | 1.0 | 1.0 | |
| Life Safety | 1.3 | 1.0 | 1.1 | 1.0 | ||
| Collapse Prevention | 1.5 | 1.0 | 1.2 | 1.0 | ||
| C3 | where is the ratio of post-yield stiffness to effective elastic stiffness, and R is the strength ratio. | |||||
| Building | Diaphragm Stiffness | In-Plan Regularity | Elevation Regularity | Constructive Details |
|---|---|---|---|---|
| Ar,rig | Rigid | Yes | Yes | Tie-rods |
| Br,rig | Rigid | Yes | Yes | Ring-beams |
| Airr,rig | Rigid | No | Yes | Tie-rods |
| Birr,rig | Rigid | No | Yes | Ring-beams |
| Cirr,rig | Rigid | No | No | Tie-rods |
| Ar,int | Intermediate | Yes | Yes | Tie-rods |
| Br,int | Intermediate | Yes | Yes | Ring-beams |
| Airr,int | Intermediate | No | Yes | Tie-rods |
| Birr,int | Intermediate | No | Yes | Ring-beams |
| Cirr,int | Intermediate | No | No | Tie-rods |
| Ar,flex | Flexible | Yes | Yes | Tie-rods |
| Airr,flex | Flexible | No | Yes | Tie-rods |
| Cirr,flex | Flexible | No | No | Tie-rods |
| Reference | Improvements Proposed |
|---|---|
| Graziotti et al. (2014) [69] | where |
| Guerrini et al. (2017) [70] | if R > 1 if R < 1 where and |
| Marino et al. (2019) [38] | where |
| Case | ahyst (-) | b (-) | c (-) | Thyst (s) |
|---|---|---|---|---|
| Mainly FD * 13% ≤ ξhyst < 15% | 0.7 | 2.3 | 2.1 | 0.055 |
| Intermediate 15% ≤ ξhyst ≤ 18% | 0.2 | 2.3 | 2.1 | 0.030 |
| Mainly SD * 18% < ξhyst ≤ 20% | 0.0 | 2.3 | 2.1 | 0.022 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aşıkoğlu, A.; Vasconcelos, G.; Lourenço, P.B. Overview on the Nonlinear Static Procedures and Performance-Based Approach on Modern Unreinforced Masonry Buildings with Structural Irregularity. Buildings 2021, 11, 147. https://doi.org/10.3390/buildings11040147
Aşıkoğlu A, Vasconcelos G, Lourenço PB. Overview on the Nonlinear Static Procedures and Performance-Based Approach on Modern Unreinforced Masonry Buildings with Structural Irregularity. Buildings. 2021; 11(4):147. https://doi.org/10.3390/buildings11040147
Chicago/Turabian StyleAşıkoğlu, Abide, Graça Vasconcelos, and Paulo B. Lourenço. 2021. "Overview on the Nonlinear Static Procedures and Performance-Based Approach on Modern Unreinforced Masonry Buildings with Structural Irregularity" Buildings 11, no. 4: 147. https://doi.org/10.3390/buildings11040147
APA StyleAşıkoğlu, A., Vasconcelos, G., & Lourenço, P. B. (2021). Overview on the Nonlinear Static Procedures and Performance-Based Approach on Modern Unreinforced Masonry Buildings with Structural Irregularity. Buildings, 11(4), 147. https://doi.org/10.3390/buildings11040147








