Assessment and Rehabilitation of Culturally Protected Prince Rudolf Infantry Barracks in Zagreb after Major Earthquake
Abstract
:1. Introduction
2. Case Study of Rudolf’s Barracks
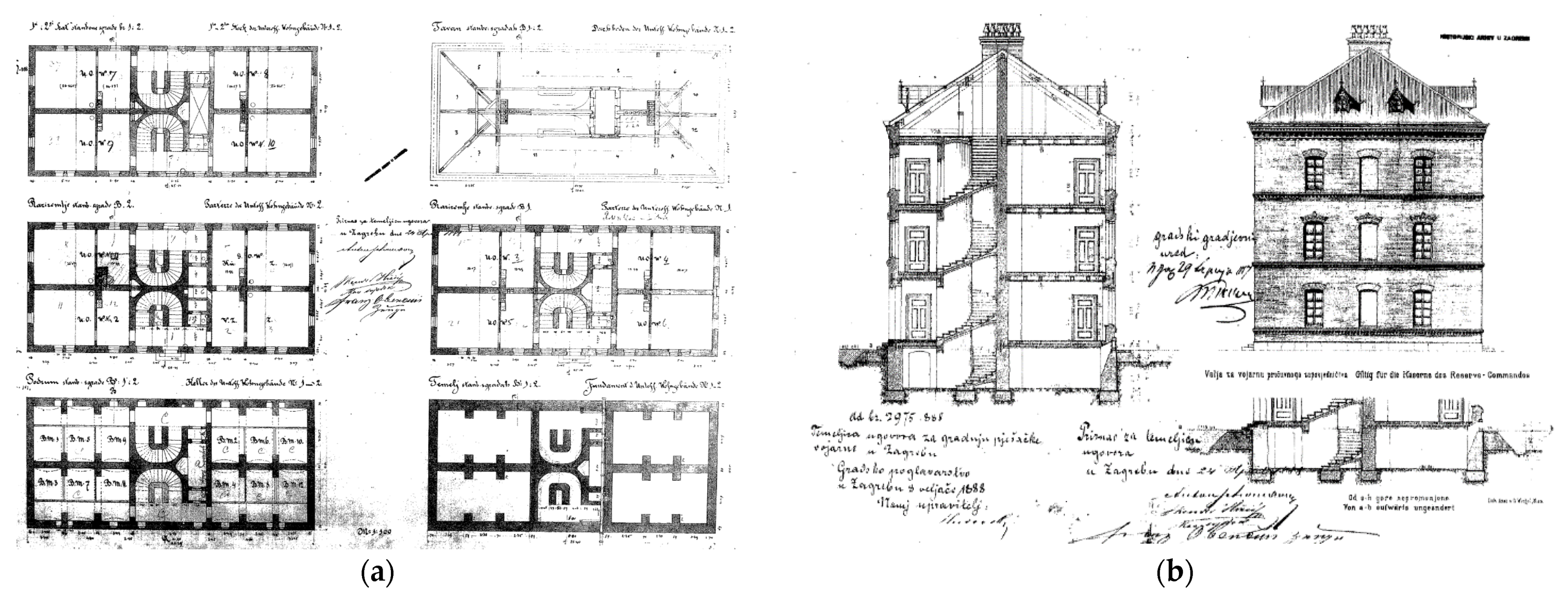
2.1. Historical Background
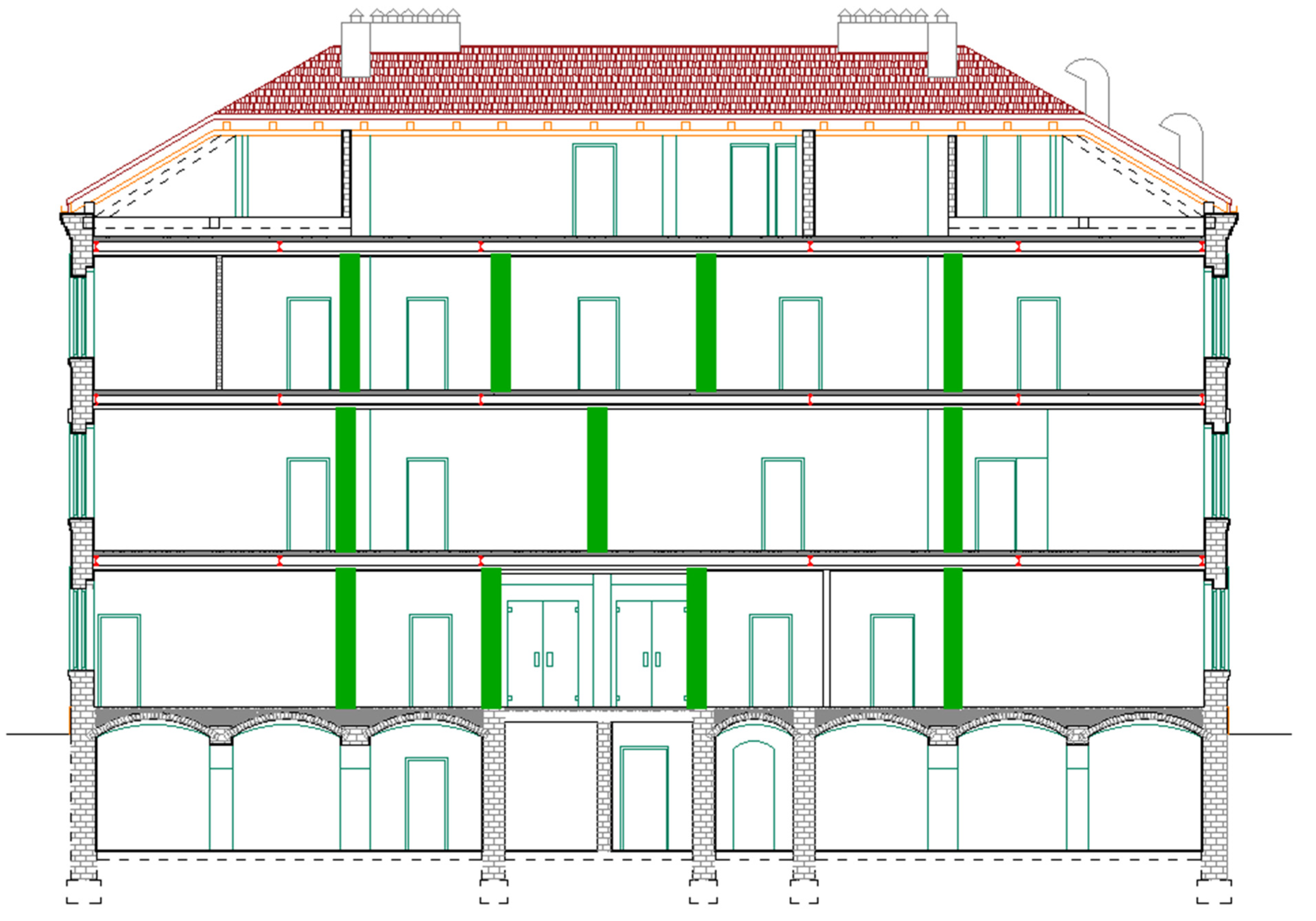
2.2. Today’s Building
2.3. Damage Detection after Earthquake
- Several minor cracks were observed on the façades of the building. Due to their slenderness and low vertical load chimneys failed predominantly by shear sliding and overturning. Additionally, roof displacement and collision with chimneys increased failure occurrences.
- On the ground floor, small cracks were noticed at the places of the lintel and at the connections of the walls and ceiling. Lintels are weakened parts of the masonry walls and are therefore vulnerable since the damage is usually concentrated in them.
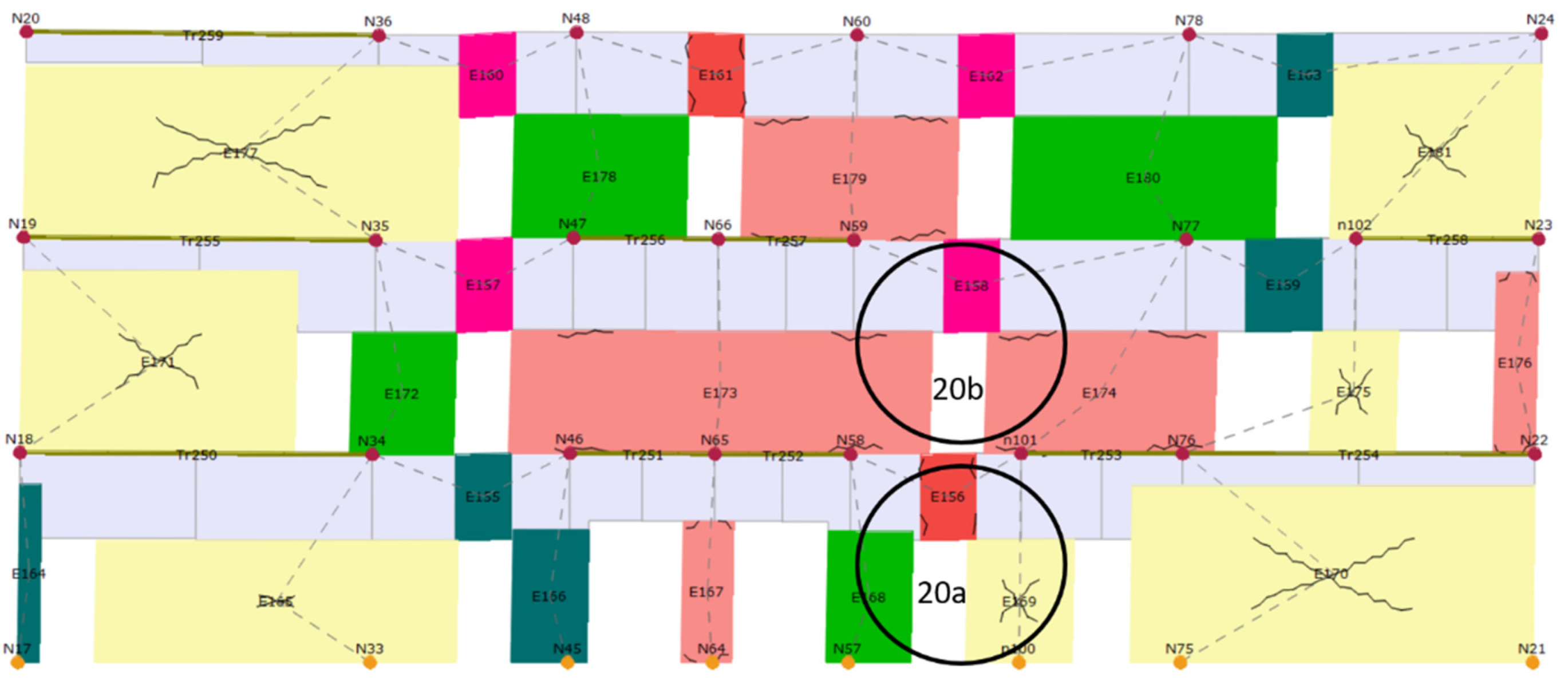
- On the first floor, major damage was noticed at the connection of partition and load-bearing walls and at the connection of walls and ceilings. Observed damage is not surprising because at the partition and load-bearing wall connections and wall and ceiling connections, there is a discontinuity of material and contact of different materials that have different behavior, and thus, there are different displacements that cause cracking. Often, such cracks do not pose a significant hazard.
- The original staircase has not been preserved, and the existing staircase has minor damage that does not indicate a threat to mechanical resistance and stability.
3. Condition Assessment and Moderately Destructive Testing
- Removal of mortar from the horizontal joint of the masonry to partially release the masonry from compressive stress.
- Inserting a flat jack into the hole.
- Establishing the initial state of stress and strain by increasing the pressure in flat jacks.
- The test is performed in the same place as the vertical stress test.
- A second hole is made above the existing opening into which a flat jack is inserted.
- Both openings are horizontal, and they are vertically spaced by 5–7 rows of bricks.
- Inserted flat jacks are connected to one hydraulic pump.
- Displacement and relative deformation measuring devices are placed between flat jacks.
- Simultaneous application of vertical pressure to flat jacks and measurement of relative deformation using the device allows determining the modulus of elasticity.
- The test is performed in the same place as the test of the modulus of elasticity of the masonry.
- One horizontal brick is removed to install the hydraulic press.
- Mortar was removed from the vertical joint of the horizontal test brick.
- A device for measuring displacements and relative deformations is installed over the test brick and the adjacent horizontal brick.
- Using a hydraulic press, horizontal pressure was applied to the test brick to move.
- Flat jacks enable the control of vertical stress to obtain the values of the coefficient of friction and the initial shear strength from the values of the ratio of shear strength and vertical stress.
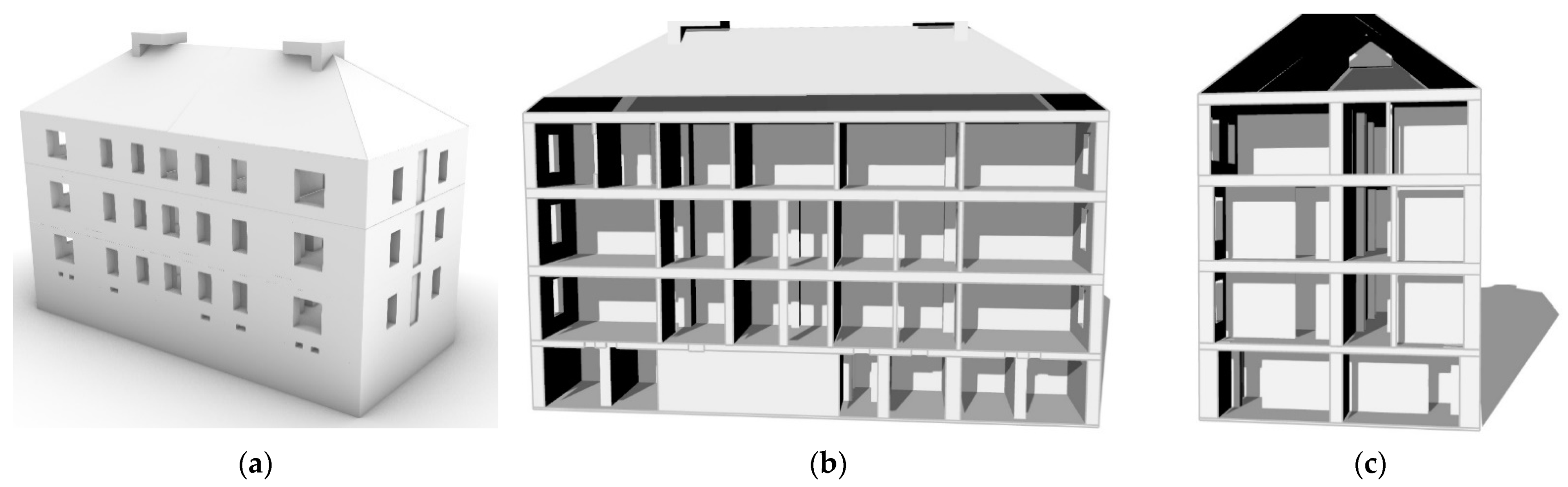
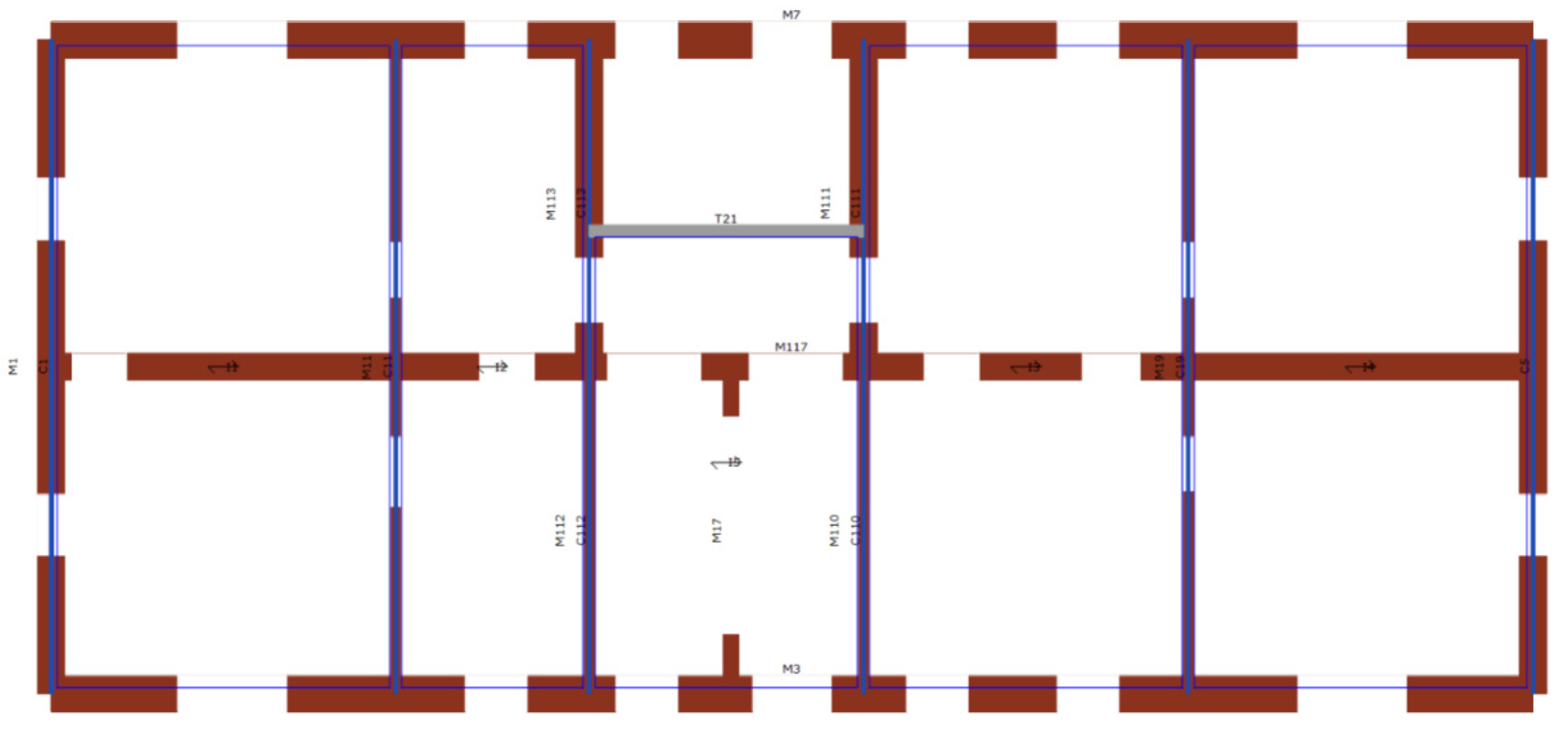
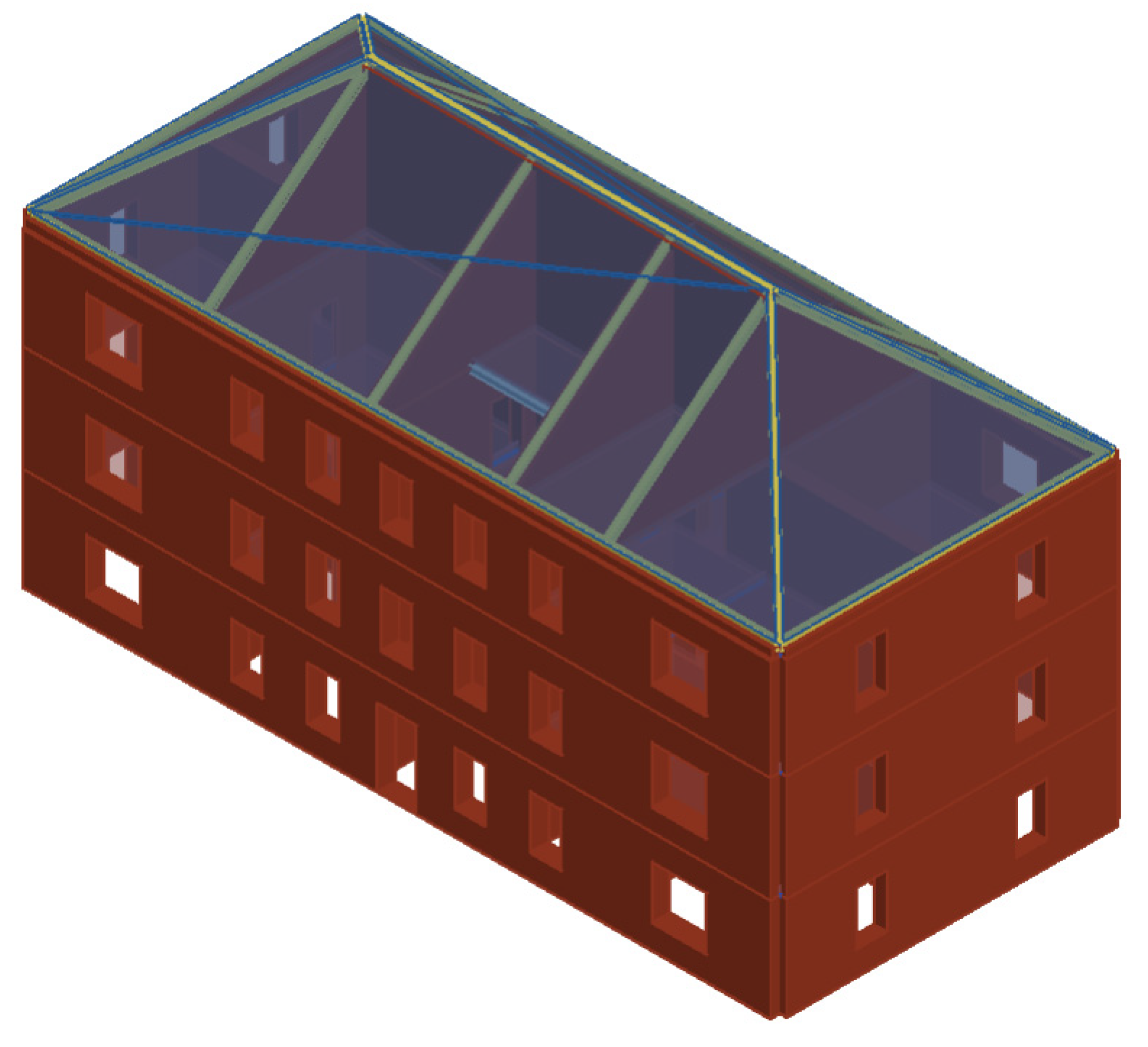
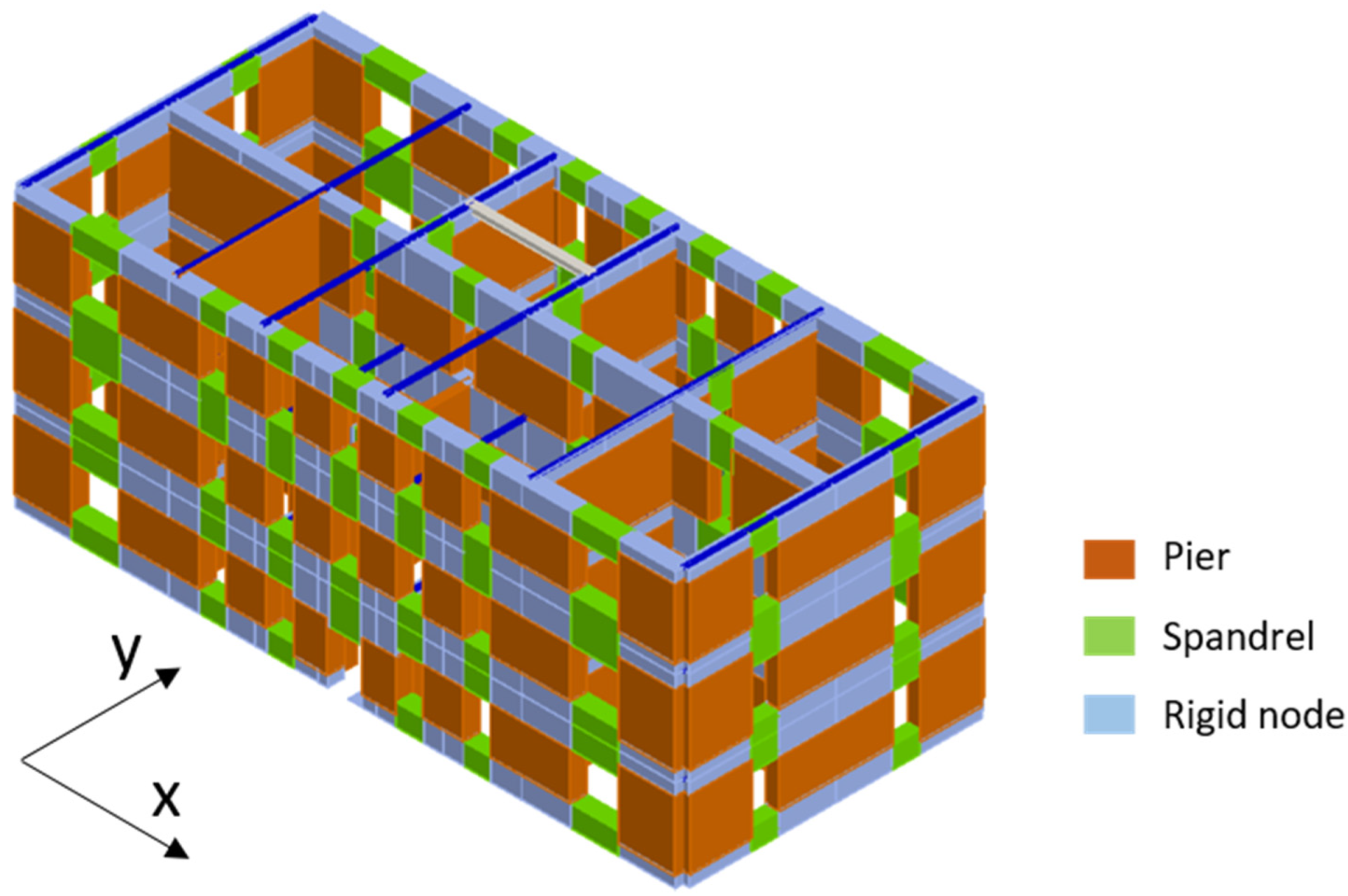
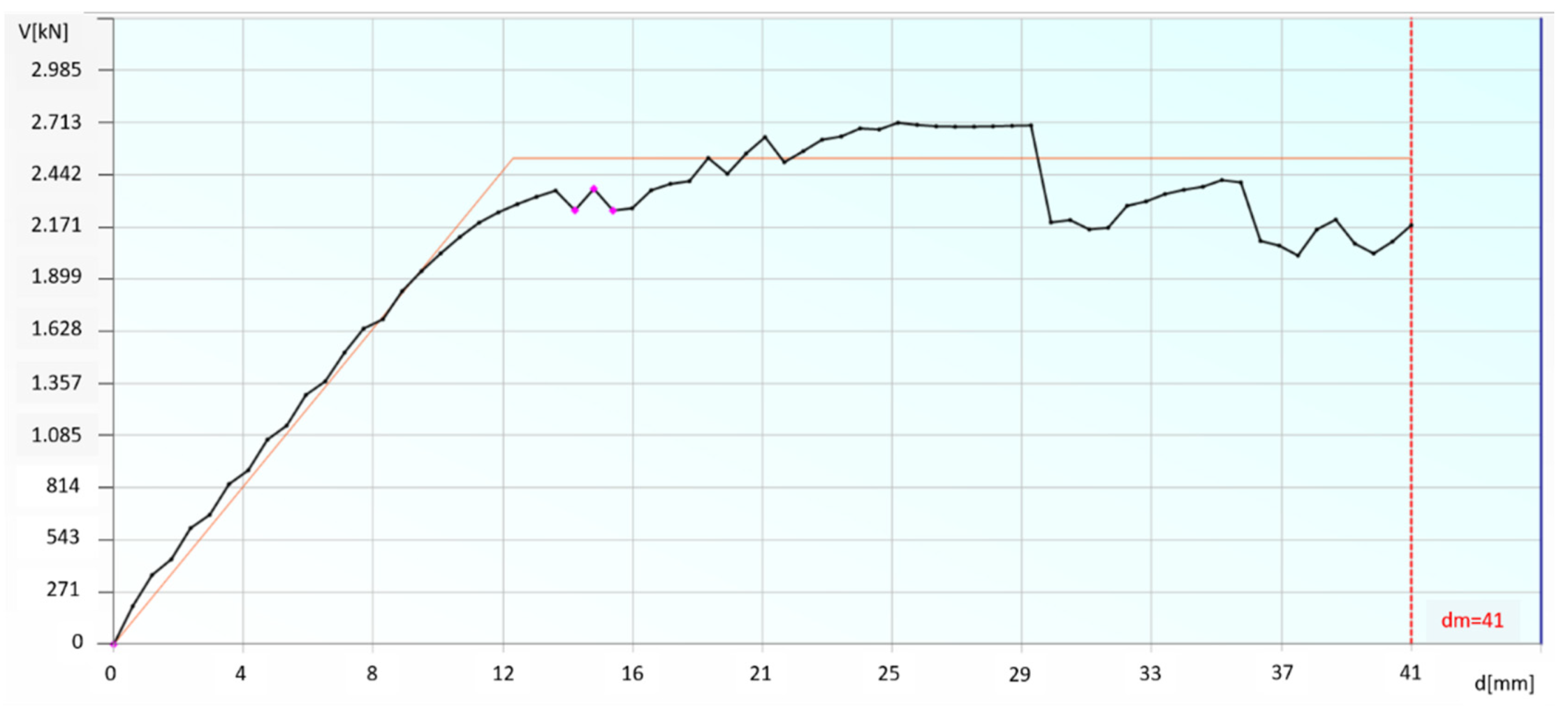
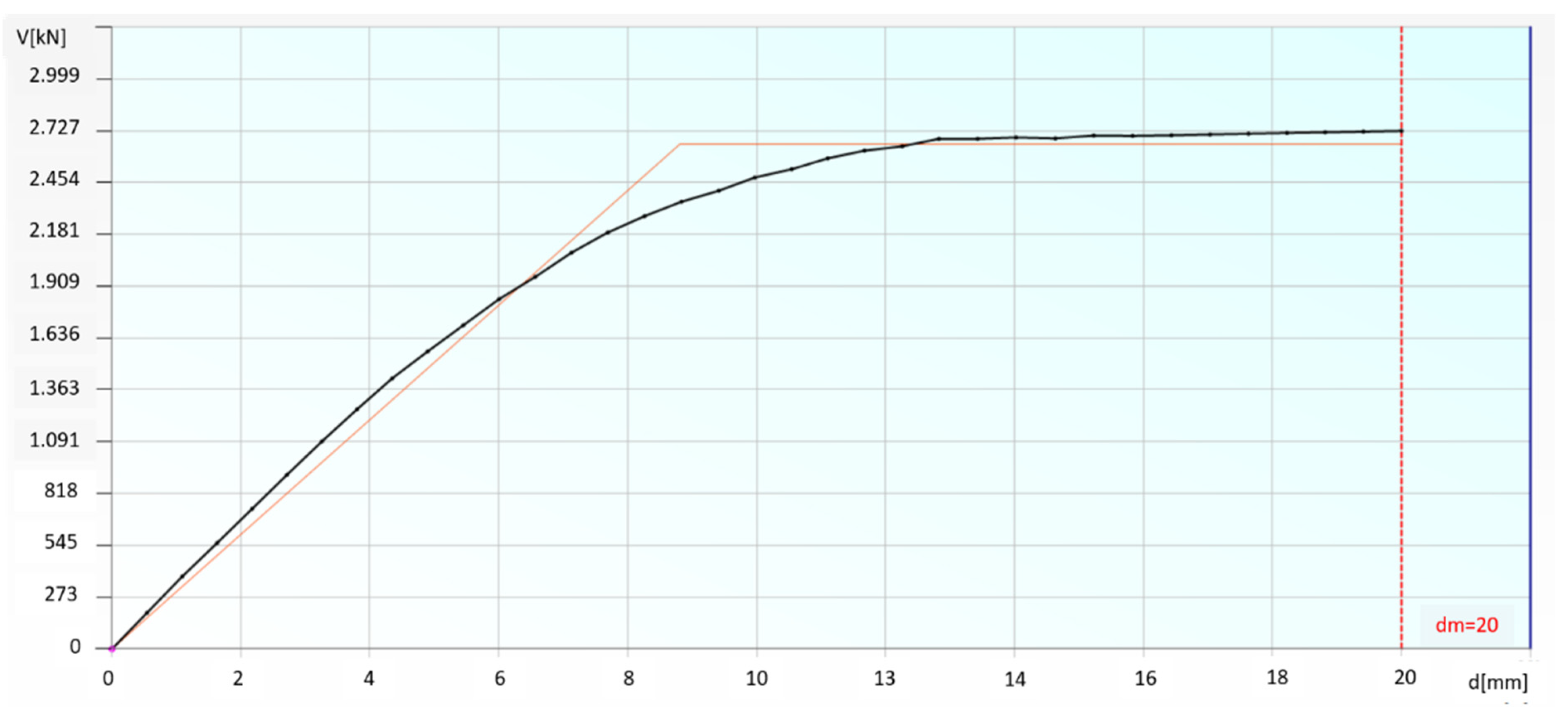
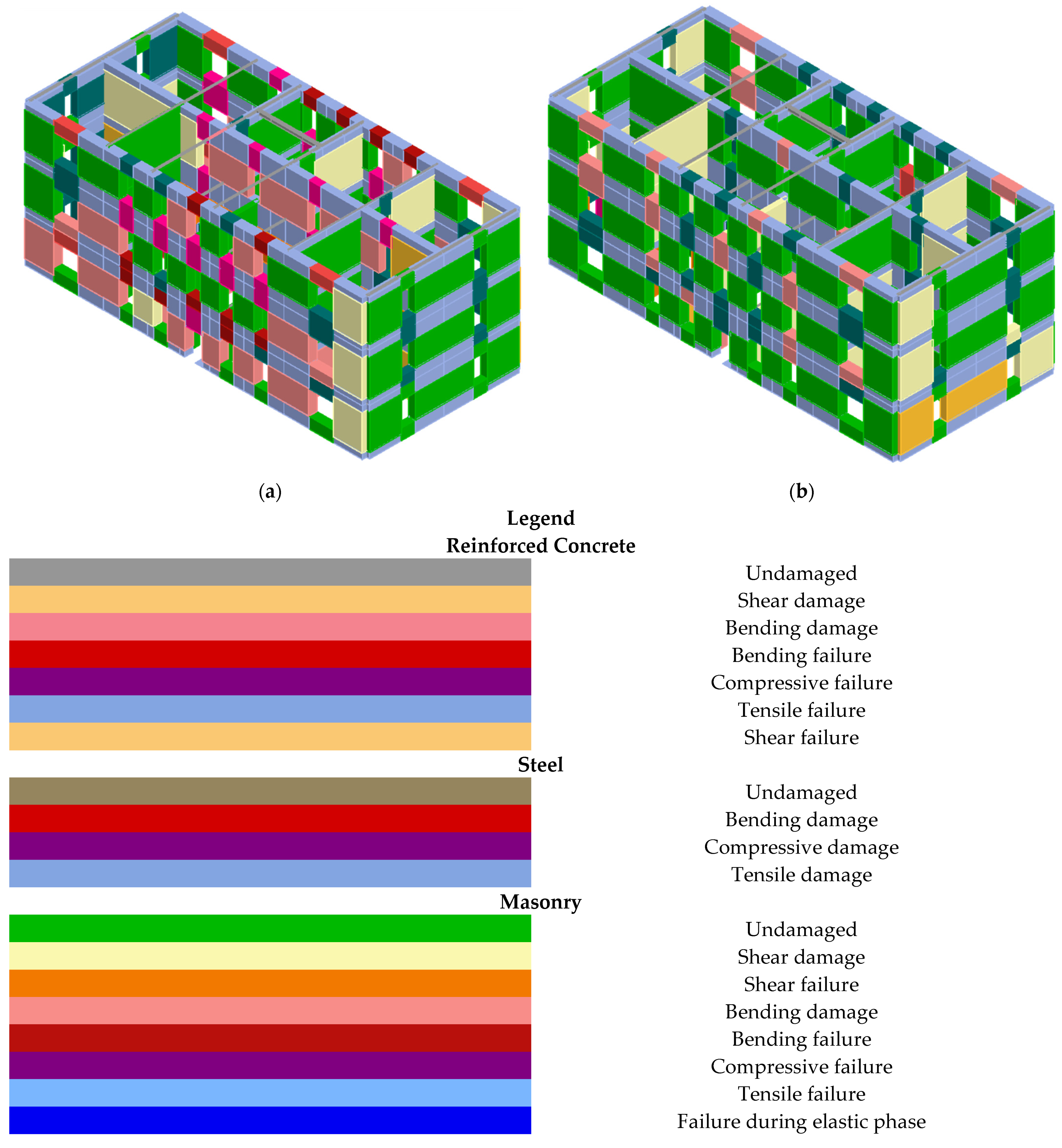
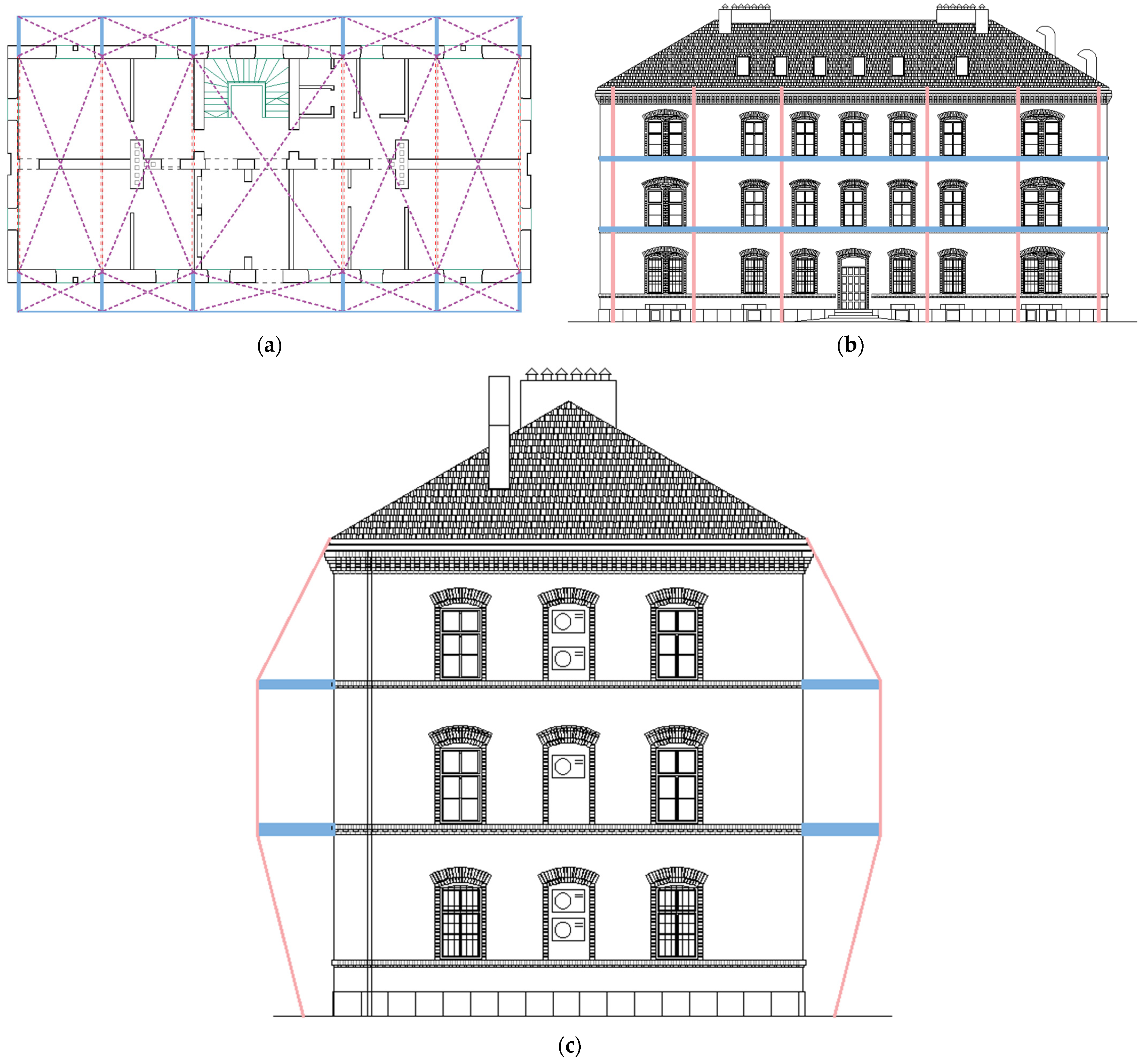
4. Numerical Modeling of the Case Study Building
- Partial safety factor, .
- Modulus of elasticity
- Initial shear strength of masonry obtained from in situ testing, .
- Confidence factor value, according to knowledge level 2.
- Diagonal tensile strength of masonry, .
- Local coefficient of friction of the joint, .
- Clamping coefficient, .
- Mean compressive strength of the units, .
- Value for clay unit from group 1 and general-purpose mortar, .
- Mortar compressive strength, .
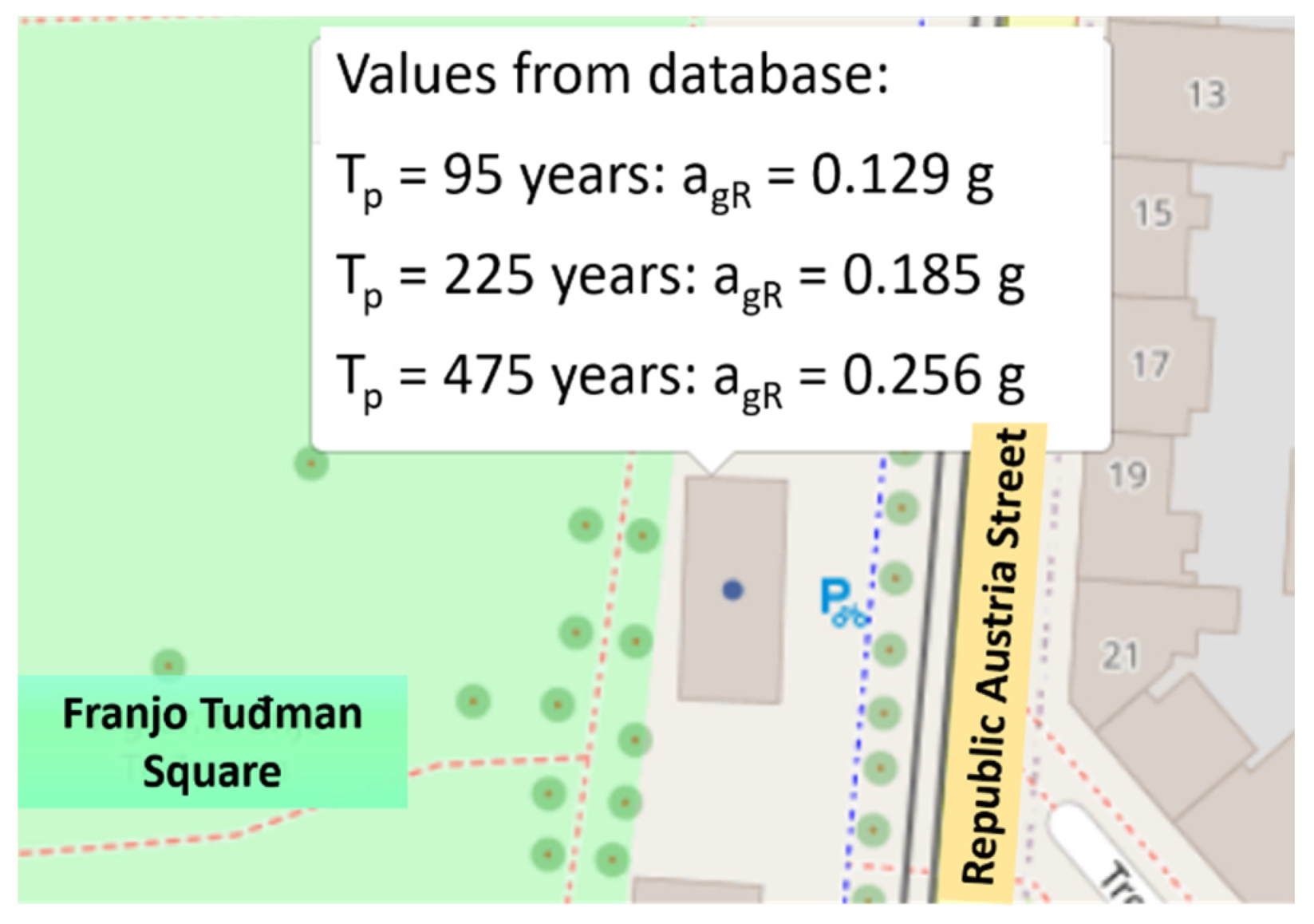
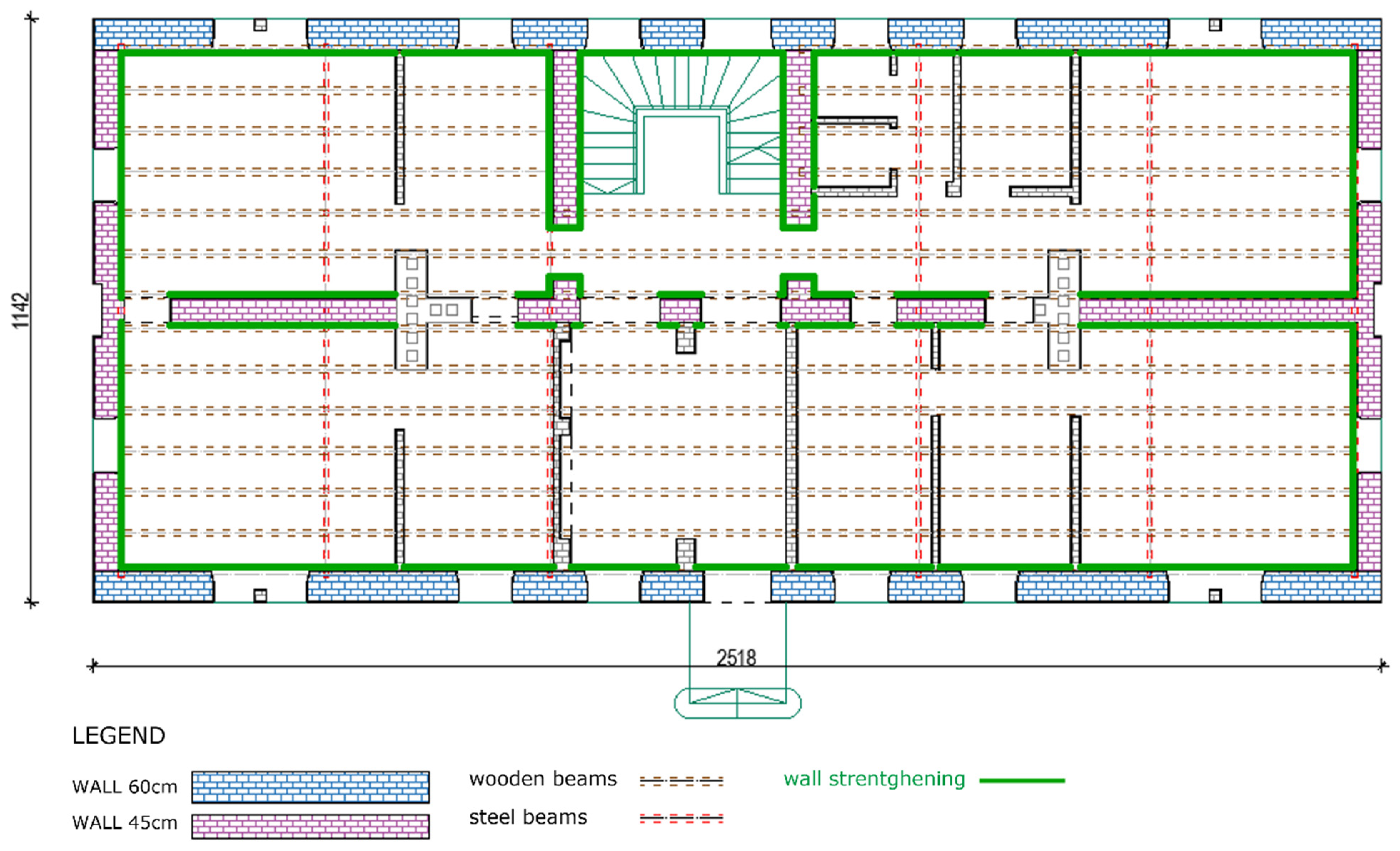
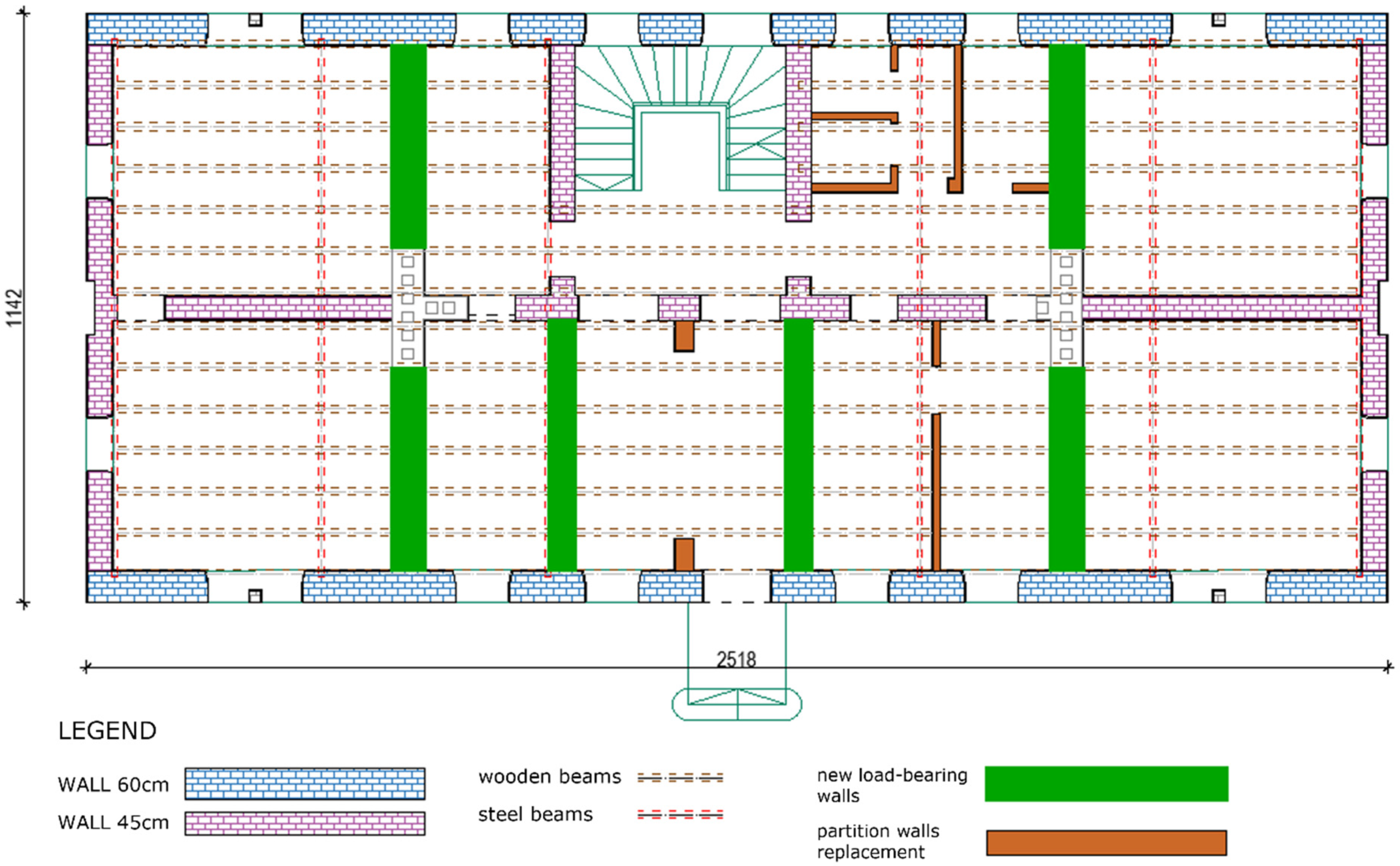
5. Renovation Measures for Existing Masonry Buildings after the Earthquake(s) in Croatia
- Level 1: repair of nonstructural elements.
- Level 2: structural repair to the return period of 95 years.
- Level 3: strengthening to the return period of 225 years.
- Level 4: Complete retrofitting to the return period of 475 years.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- World Bank Report: Croatia Earthquake–Rapid Damage And Needs Assessment, 2020, June 2020; Government of Croatia: Zagreb, Croatia, 2020.
- Lulić, L.; Ožić, K.; Kišiček, T.; Hafner, I.; Stepinac, M. Post-Earthquake Damage Assessment-Case Study of the Educational Building after the Zagreb Earthquake. Sustainability 2021, 13, 6353. [Google Scholar] [CrossRef]
- Saloustros, S.; Pelà, L.; Contrafatto, F.R.; Roca, P.; Petromichelakis, I. Analytical Derivation of Seismic Fragility Curves for Historical Masonry Structures Based on Stochastic Analysis of Uncertain Material Parameters. Int. J. Archit. Herit. 2019, 13, 1142–1164. [Google Scholar] [CrossRef]
- Stepinac, M.; Kisicek, T.; Renić, T.; Hafner, I.; Bedon, C. Methods for the Assessment of Critical Properties in Existing Masonry Structures under Seismic Loads-the ARES Project. Appl. Sci. 2020, 10, 1576. [Google Scholar] [CrossRef] [Green Version]
- Stepinac, M.; Lourenço, P.B.; Atalić, J.; Kišiček, T.; Uroš, M.; Baniček, M.; Šavor Novak, M. Damage Classification of Residential Buildings in Historical Downtown after the ML5.5 Earthquake in Zagreb, Croatia in 2020. Int. J. Disaster Risk Reduct. 2021, 56, 102140. [Google Scholar] [CrossRef]
- Novak, M.Š.; Uroš, M.; Atalić, J.; Herak, M.; Demšić, M.; Baniček, M.; Lazarević, D.; Bijelić, N.; Crnogorac, M.; Todorić, M. Zagreb Earthquake of 22 March 2020–Preliminary Report on Seismologic Aspects and Damage to Buildings. Gradjevinar 2020, 72, 843–867. [Google Scholar] [CrossRef]
- Kišiček, T.; Stepinac, M.; Renić, T.; Hafner, I.; Lulić, L. Strengthening of Masonry Walls with FRP or TRM. Gradjevinar 2020, 72, 937–953. [Google Scholar] [CrossRef]
- The Database of Usability Classification, Croatian Centre of Earthquake Engineering (HCPI-Hrvatski Centar Za Potresno Inženjerstvo); Faculty of Civil Engineering, University of Zagreb and The City of Zagreb: Zagreb, Croatia, 2020.
- Forsyth, M. Structures and Construction in Historic Building Conservation; Blackwell Publishing Ltd.: Hoboken, NJ, USA, 2008. [Google Scholar] [CrossRef]
- Vlachakis, G.; Vlachaki, E.; Lourenço, P.B. Learning from Failure: Damage and Failure of Masonry Structures, after the 2017 Lesvos Earthquake (Greece). Eng. Fail. Anal. 2020, 117, 104803. [Google Scholar] [CrossRef]
- Cruz, H.; Yeomans, D.; Tsakanika, E.; Macchioni, N.; Jorissen, A.; Touza, M.; Mannucci, M.; Lourenço, P.B. Guidelines for On-Site Assessment of Historic Timber Structures. Int. J. Archit. Herit. 2015, 9, 277–289. [Google Scholar] [CrossRef]
- Sánchez Rodríguez, A.; Riveiro Rodríguez, B.; Soilán Rodríguez, M.; Arias Sánchez, P. Laser Scanning and Its Applications to Damage Detection and Monitoring in Masonry Structures. In Long-Term Performance and Durability of Masonry Structures. Degradation Mechanisms. Health Monitoring and Service Life Design; Ghiassi, B., Lourenço, P.B., Eds.; Woodhead Publishing: Cambridge, UK, 2019; pp. 265–285. [Google Scholar] [CrossRef]
- Funari, M.F.; Mehrotra, A.; Lourenço, P.B. A Tool for the Rapid Seismic Assessment of Historic Masonry Structures Based on Limit Analysis Optimisation and Rocking Dynamics. Appl. Sci. 2021, 11, 942. [Google Scholar] [CrossRef]
- Endo, Y.; Pelà, L.; Roca, P. Review of Different Pushover Analysis Methods Applied to Masonry Buildings and Comparison with Nonlinear Dynamic Analysis. J. Earthq. Eng. 2017, 21, 1234–1255. [Google Scholar] [CrossRef] [Green Version]
- Ortega, J.; Vasconcelos, G.; Rodrigues, H.; Correia, M. Assessment of the Influence of Horizontal Diaphragms on the Seismic Performance of Vernacular Buildings. Bull. Earthq. Eng. 2018, 16, 3871–3904. [Google Scholar] [CrossRef]
- Stepinac, M.; Rajčić, V.; Barbalić, J. Inspection and Condition Assessment of Existing Timber Structures. Gradjevinar 2017, 69, 861–873. [Google Scholar] [CrossRef] [Green Version]
- Fortunato, G.; Funari, M.F.; Lonetti, P. Survey and Seismic Vulnerability Assessment of the Baptistery of San Giovanni in Tumba (Italy). J. Cult. Herit. 2017, 26, 64–78. [Google Scholar] [CrossRef]
- Malcata, M.; Ponte, M.; Tiberti, S.; Bento, R.; Milani, G. Failure Analysis of a Portuguese Cultural Heritage Masterpiece: Bonet Building in Sintra. Eng. Fail. Anal. 2020, 115, 104636. [Google Scholar] [CrossRef]
- CIB 335. Guide for the Structural Rehabilitation of Heritage Buildings; CIB Commission W023: Ottawa, ON, Canada, 2010. [Google Scholar]
- Lourenço, P.B. Conservation of Cultural Heritage Buildings: Methodology and Application to Case Studies. Rev. ALCONPAT 2013, 3, 98–110. [Google Scholar] [CrossRef] [Green Version]
- Betti, M.; Bonora, V.; Galano, L.; Pellis, E.; Tucci, G.; Vignoli, A. An Integrated Geometric and Material Survey for the Conservation of Heritage Masonry Structures. Heritage 2021, 4, 585–611. [Google Scholar] [CrossRef]
- Stepinac, M.; Gašparović, M. A Review of Emerging Technologies for an Assessment of Safety and Seismic Vulnerability and Damage Detection of Existing Masonry Structures. Appl. Sci. 2020, 10, 5060. [Google Scholar] [CrossRef]
- Ortega, J.; Vasconcelos, G.; Rodrigues, H.; Correia, M. Seismic Vulnerability and Loss Assessment of Vila Real de Santo António, Portugal: Application of a Novel Method. Int. J. Archit. Herit. 2020, 15, 1585–1607. [Google Scholar] [CrossRef]
- Saloustros, S.; Pelà, L.; Roca, P.; Portal, J. Numerical Analysis of Structural Damage in the Church of the Poblet Monastery. Eng. Fail. Anal. 2015, 48, 41–61. [Google Scholar] [CrossRef]
- Giordano, E.; Ferrante, A.; Clementi, F.; Milani, G.; Formisano, A. Cultural Heritage and Earthquake: The Case Study of San Francesco’s Church in Amandola (Central Italy). In Proceedings of the 2019 IMEKO TC4 International Conference on Metrology for Archaeology and Cultural Heritage, MetroArchaeo 2019, Florence, Italy, 4–6 December 2019. [Google Scholar]
- Formisano, A.; Vaiano, G.; Fabbrocino, F. A Seismic-Energetic-Economic Combined Procedure for Retrofitting Residential Buildings: A Case Study in the Province of Avellino (Italy). In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2019. [Google Scholar] [CrossRef]
- Capanna, I.; Aloisio, A.; Di Fabio, F.; Fragiacomo, M. Sensitivity Assessment of the Seismic Response of a Masonry Palace via Non-Linear Static Analysis: A Case Study in l’aquila (Italy). Infrastructures 2021, 6, 8. [Google Scholar] [CrossRef]
- Kneževicć, S. Zagrebaćke Planirane Vojarne Iz Doba Habsburške Monarhije (Zagreb Planned Barracks From the Age of the Habsburg Monarchy); Institut Za Povijest Umjetnosti: Zagreb, Croatia, 2007. [Google Scholar]
- Knežević, S. Povijest Područja Bivše Rudolfove Vojarne i Trga Francuske Republike u Zagrebu (History of the Area of the Former Rudolf Barracks and the Square of the French Republic in Zagreb). Godišnjak Zaštite Spomenika Kult. Hrvat. 1996–1997, 22–23, 57–72. [Google Scholar]
- Digital Collections of the National and University Library in Zagreb [Internet]. Available online: Https://Digitalna.Nsk.Hr/Pb/?Object=list&mr%5B553362%5D=a (accessed on 28 June 2021).
- Borri, A.; Corradi, M.; De Maria, A.; Sisti, R. Calibration of a Visual Method for the Analysis of the Mechanical Properties of Historic Masonry. Procedia Struct. Integr. 2018, 11, 418–427. [Google Scholar] [CrossRef]
- EN 1998-1. Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings. Eur. Comm. Norm. Brussels 2004. Available online: https://www.phd.eng.br/wp-content/uploads/2015/02/en.1998.1.2004.pdf (accessed on 17 September 2021).
- HRN EN 1998-3:2011 Eurocode 8: Design of Structures for Earthquake Resistance—Part 3: Assessment and Retrofitting of Buildings (EN 1998-3:2005+AC:2010). Available online: https://www.phd.eng.br/wp-content/uploads/2014/07/en.1998.3.2005.pdf (accessed on 17 September 2021).
- Lagomarsino, S.; Penna, A.; Galasco, A.; Cattari, S. TREMURI Program: An Equivalent Frame Model for the Nonlinear Seismic Analysis of Masonry Buildings. Eng. Struct. 2013, 56, 1787–1799. [Google Scholar] [CrossRef]
- S.T.A. DATA, 3Muri Program 12.5.0.2. Available online: http://www.stadata.com/ (accessed on 14 September 2021).
- Herak, M.; Allegretti, I.; Herak, D.; Kuk, V.; Marić, K.; Markušić, S.; Sović, I. Maps of Seismic Areas of the Republic of Croatia. Available online: http://seizkarta.gfz.hr/hazmap/ (accessed on 21 September 2021).
- Uroš, M.; Todorić, M.; Crnogorac, M.; Atalić, J.; Šavor Novak, M.; Lakušić, S. (Eds.) Potresno Inženjerstvo-Obnova Zidanih Zgrada; Građevinski Fakultet, Sveučilišta u Zagrebu: Zagreb, Croatia, 2021. [Google Scholar]
- Law on the Reconstruction of Earthquake-Damaged Buildings in the City of Zagreb, Krapina-Zagorje County and Zagreb County (NN 102/2020). Available online: https://www.zakon.hr/z/2656/Zakon-o-obnovi-zgrada-o%C5%A1te%C4%87enih-potresom-na-podru%C4%8Dju-Grada-Zagreba,-Krapinsko-zagorske-%C5%BEupanije,-Zagreba%C4%8Dke-%C5%BEupanije,-Sisa%C4%8Dko-moslava%C4%8Dke-%C5%BEupanije-i-Karlova%C4%8Dke-%C5%BEupanije (accessed on 10 September 2021).
- Tehnički Propis o Izmjeni i Dopunama Tehničkog Propisa Za Građevinske Konstrukcije (Technical Regulation on Amendments to the Technical Regulation for Building Structures) [Internet]. Available online: Https://Narodne-Novine.Nn.Hr/Clanci/Sluzbeni/2020_07_75_1448.Html (accessed on 29 June 2021).










| 1786 | 2520 | 4.07 | 6.44 | 0.06 | 0.10 | 440 | 648 | 0.14 | 0.27 |
| Material | Color | Norm |
|---|---|---|
| Masonry | According to the experimental results | |
| Reinforced concrete | EN 1992-1-1:2005 | |
| Structural steel | EN1993-1-1:2005 | |
| Timber | EN 338:2002 |
| Return Period [Years] | ||
|---|---|---|
| 95 | 0.373 | 3012 |
| 225 | 0.518 | 4183 |
| 475 | 0.748 | 6040 |
| Mode | T (s) | mx (kg) | Mx (%) | my (kg) | My (%) | mz (kg) | Mz (%) |
|---|---|---|---|---|---|---|---|
| 1 | 0.2934 | 85 | 0.01 | 973,618 | 81.78 | 13 | 0.00 |
| 2 | 0.2293 | 209,897 | 17.63 | 150 | 0.01 | 0 | 0.00 |
| 3 | 0.2214 | 835,847 | 70.21 | 334 | 0.03 | 34 | 0.00 |
| Type of Analyses | x-Direction | y-Direction |
|---|---|---|
| Simplified hand calculation | 92% | 44% |
| Seismic load distribution according to equivalent static forces method | 66% | 71% |
| Modal distribution of seismic load | 69% | 78% |
| Uniform distribution of seismic load | 81% | 83% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Milić, M.; Stepinac, M.; Lulić, L.; Ivanišević, N.; Matorić, I.; Čačić Šipoš, B.; Endo, Y. Assessment and Rehabilitation of Culturally Protected Prince Rudolf Infantry Barracks in Zagreb after Major Earthquake. Buildings 2021, 11, 508. https://doi.org/10.3390/buildings11110508
Milić M, Stepinac M, Lulić L, Ivanišević N, Matorić I, Čačić Šipoš B, Endo Y. Assessment and Rehabilitation of Culturally Protected Prince Rudolf Infantry Barracks in Zagreb after Major Earthquake. Buildings. 2021; 11(11):508. https://doi.org/10.3390/buildings11110508
Chicago/Turabian StyleMilić, Mija, Mislav Stepinac, Luka Lulić, Nataša Ivanišević, Ivan Matorić, Boja Čačić Šipoš, and Yohei Endo. 2021. "Assessment and Rehabilitation of Culturally Protected Prince Rudolf Infantry Barracks in Zagreb after Major Earthquake" Buildings 11, no. 11: 508. https://doi.org/10.3390/buildings11110508
APA StyleMilić, M., Stepinac, M., Lulić, L., Ivanišević, N., Matorić, I., Čačić Šipoš, B., & Endo, Y. (2021). Assessment and Rehabilitation of Culturally Protected Prince Rudolf Infantry Barracks in Zagreb after Major Earthquake. Buildings, 11(11), 508. https://doi.org/10.3390/buildings11110508








