Abstract
This study investigates Smart Grid Optimised Buildings (SGOBs) which can respond to real-time electricity prices by utilising battery storage systems (BSS). Different building design characteristics are assessed to evaluate the impact on energy use, the interaction with the battery, and potential for peak load shifting. Two extreme cases based on minimum and maximum annual energy consumption were selected for further investigation to assess their capability of utilising BSS to perform arbitrage, under real-time pricing. Three operational dispatch strategies were modelled to allow buildings to provide such services. The most energy-efficient building was capable of shifting a higher percentage of its peak loads and export more electricity, when this is allowed. When using the biggest battery (220 kWh) to only meet the building loads, the energy-efficient building was able to shift 39.68% of its original peak loads in comparison to the 33.95% of the least efficient building. With exports allowed, the shifting percentages went down to 31.76% and 29.46%, respectively, while exports of 18.08 and 16.34 kWh/m2 took place. The formation of a regulatory framework is vital in order to establish proper motives for buildings to undertake an active role in the smart grid.
1. Introduction
The building sector is responsible for a significant percentage of energy consumption and greenhouse gas emissions, worldwide [1]. When it comes to the sector’s electricity needs, the electricity demand is expected to increase in the future depending on many parameters, including the extent of electrification of space heating in buildings, utilisation of heat pumps and electric vehicles. Further adoption of these technologies will result in higher peak loads and put pressure on the grid infrastructure [1,2].
The ramifications of peak electrical loads are significant for the environment and the economy as expensive carbon intensive power generation is needed, often creating serious issues for the low voltage distribution networks and their capacity. Peak loads can lead to imbalances between supply and demand which consequently cause electricity price fluctuations in the wholesale markets. These imbalances will likely be present even in a decarbonised network due to the intermittency introduced by renewable energy sources (RES), seasonal weather conditions and the utilisation of the emerging technologies mentioned previously [3]. More specifically, because of the stochastic nature of RES and the uncertainty around their output characteristics, the grid operators are not able to control that energy output; therefore, scheduling and distributing their energy is not as flexible as with the traditional electric generators such as thermal power plants and hydropower. This effect has the potential to introduce frequency and voltage fluctuations which can affect the balance and the stability of the network [4]. Mechanisms that will provide temporal flexibility through peak demand management are urgently needed for the future operation of the electricity network.
At the building level, optimised peak demand reductions can take place through coordinated control of building loads, often called demand response (DR), local electricity generation (e.g., photovoltaics) and energy storage. By controlling their heating, ventilation and air conditioning (HVAC) loads over time, buildings can become demand-responsive following demand reduction signals from the electrical grid and result in significant savings [5,6,7,8,9,10]. DR can also be conducted in synergy with other energy technologies, such as combined heat and power (CHP), storage and RES [11,12,13]. Temporally, it can be classified as day-ahead (slow), intra-day or ancillary (fast) DR, indicating how much in advance its specifications are arranged. The DR framework can be applied in both existing and new buildings [14].
DR is usually delivered through incentive-based and price-based programs [15]. To implement DR, it is vital to know and understand the energy amount used by a building, on a daily and hourly basis. The ability of a building to modify its demand and how quickly this response can take place varies from building to building and depends on different parameters, including the HVAC configuration [16], domestic hot water (DHW) production method as well as the presence of battery storage and renewables [17]. It is essential to recognise and understand the peak demand reduction potential and the capabilities presented under different DR strategies for various building types, in different climates and occupancy profiles [18].
Building integrated energy storage, such as batteries, can allow buildings to manage their demand and reduce their peak loads, relieving pressure on the electrical network [2]. Additionally, they are able to store electricity when excess generation from RES takes place. Furthermore, energy storage can provide grid services such as reserve power, ancillary services for frequency response and regulation, facilitate the integration of RES into the system and offer more control to the final consumers [19]. The main balancing services are currently procured by the National Grid in Great Britain in order to achieve a balance between supply and demand. They are open to generators, big consumers or both. For each service, there are specifications regarding the response time needed, minimum duration and power provided. Rewards include availability (GBP/MW/h), utilisation (GBP/MWh) and nomination fee (GBP/hour) [20]. Therefore, it is important to understand the potential that can be unlocked by deploying an energy storage system (ESS) at the building level and providing services to the grid.
A summary of selected energy technologies for buildings along with their applications can be seen in Table 1. Energy storage is capable of providing a wide variety of services in various parts of the network and combining it with other technologies has been evaluated extensively in [21,22,23]. While many options are available for buildings, a techno-economic assessment is required on a case-to-case basis to evaluate the cost-effectiveness of any suggested scheme. There are many case studies investigating energy technologies in buildings; however, the literature is scarce on the utilisation of battery storage in buildings with different design characteristics.
It can be concluded that the building sector as the major energy consumer is expected to play a critical role in the development of future smart energy systems and the future smart grid through a variety of different mechanisms such as real-time trade of energy, DR, self-generation, decentralised renewable energy and energy storage [24,25]. These mechanisms will allow buildings to shift from passive elements to active players by cooperating in the network operation. However, this cooperation will require a closer relationship between the building and the energy sector [5,14,26] as well as the ability of the building to store energy, for instance with batteries [27]. A recent case study highlighted that establishing a proper regulatory framework and financial motives was deemed to be of the essence towards making battery storage attractive and cost-effective to potential investors [28]. Currently, there are many important barriers under the current regulatory and economic regimes that prevent ES from participating in the electricity markets and contributing towards technological innovations. These have been well summarised by [29,30,31].

Table 1.
Studied energy technologies in buildings and their applications in selected publications.
Table 1.
Studied energy technologies in buildings and their applications in selected publications.
| Technologies | Application(s) in Buildings and/or the Grid | Comments/Conclusions |
|---|---|---|
| Batteries | Peak-shaving [32] | Residential Battery energy storage systems can reduce peak electricity loads by >40%. |
| Time-of-Use (ToU) Energy management [33] | Medium-scale batteries can reduce the electricity bills of consumers through ToU energy management. They are economically beneficial for medium-scale buildings if there is an important difference between the max. and the min. electricity prices. | |
| Balancing Services, RES Integration, Customer Energy Management [34,35] | Batteries can provide several services, including balancing services, such as voltage support, black start and load following, as well as customer energy management (power quality/reliability). RES Integration can be achieved through time-shifting and capacity firming. | |
| Optimisation of energy dispatch schedule in a PV/storage system [36] | Batteries are important for providing peak-shaving and load shifting. The cost-effectiveness of the system depends on the electricity rates and battery technology used (lithium-ion, lead acid, etc.) | |
| Hydrogen Storage | Self-sufficient energy buildings and cost minimisation [37] | There is an increasing interest in combined battery and hydrogen storage. Domestic hydrogen storage can render a building self-sufficient for an annual premium of 52% when compared to buying electricity from the grid by 2030. It can also lead to annualised cost reductions of 72–80% for the supply of heat and electricity when compared to Li-ion batteries. |
| Integration of RES and balancing of the grid [38] | Electrochemical and mechanical storage are not sufficient to balance the grid; therefore, hydrogen is expected to play a major role in the energy transition. Evaluating hydrogen is very challenging while a detailed techno-economic assessment is required on a case-to-case basis. | |
| Thermal mass | Energy flexible buildings [39] | Using the building’s thermal mass as thermal storage through preheating, precooling and night ventilation can lead to a maximum of 3.2% savings for heating and 8.5% for cooling. |
| HVAC | Fast DR [40] | Turning off part of the HVAC is an efficient way for buildings to respond quickly to notifications issued by the Smart Grid, provide fast DR and achieve considerable power reduction (39%). |
| Peak-shaving [41] | An HVAC energy management system can minimise cooling loads by altering thermostat settings, leading to a reduction in the daily peak loads by 25.5% in domestic buildings. | |
| Hybrid System | Meeting loads, minimisation of costs and emissions [42] | Considering several energy systems (wind turbines, PVs, hydrogen storage, batteries), many optimal combinations include high levels of solar and wind power. As high costs are associated with hydrogen storage, priority is given to batteries. |
| CHP | Emissions reductions [43] | CHP can reduce emissions (CO2, NOx, CH4) as well as the carbon equivalent in commercial buildings. |
| Primary Energy Savings [44] | CHP can lead to the reduction in electricity and gas consumption by 56% and 43%, respectively. Results are considered to be dependent on climate conditions and building types. |
The concept of SGOBs was first mentioned in [45], while [28] presented initial results for one building scenario, showing how battery arbitrage can change the building’s electricity profile. The current paper recognises the potential of building integrated storage for the benefits of both the building and the electrical network. The combination of energy storage and renewables as well as optimisation algorithms for pumped-hydro energy storage (PHES) arbitrage are often encountered in the literature. However, the majority of PHES studies have focused on the financial aspect of storage operation by maximising the revenue streams, and therefore the profitability of such schemes. According to the literature review, utilising BSS in buildings in order to perform peak-shaving based on different technical (both building design and BSS sizes) and arbitrage scenarios has not been investigated before. Therefore, this study evaluates the utilisation of the battery as a standalone technology, without the concurrent use of renewables in buildings, to reduce peak loads. In this way, different buildings are taken into account in terms of glazing and insulation as building design affects daily and annual load profiles. To accomplish this, the developed arbitrage algorithms use the hourly electricity demand of different buildings, hourly electricity prices from the grid and the BSS technical specifications. Moreover, a cost-benefit analysis is studied for 10- and 20-year periods to quantify the financial motive required to make BSS economically attractive to building owners. The novelties of this study form the interaction between the building’s dynamic requirements for power and the cost of electricity while using a battery to reduce peak load requirements.
Summing up, this research article examines a combination of unique parameters that include building design, operational dispatch strategies, BSS sizes and long-term economics to compare the SGOB potential of different buildings. This work takes the first vital step towards the establishment of a regulatory framework for battery arbitrage in the building sector to understand the suitability of buildings to become SGOBs.
2. Methodology
Three operational (dispatch) strategies are presented techno-economically, under which BSS are deployed at the building level to conduct energy arbitrage by responding to real-time electricity prices, shifting their daily electricity profile and providing in this way a service to the grid. The objective function of the arbitrage model is lowest operational costs; buying electricity when costs are low to use within the building or sell back to the grid at a later time. The results are finally evaluated in respect of total electricity consumption, peak hours shaved and net cost based on the relative impact of building design, battery and inverter sizing and dispatch strategies.
Building simulations are used to estimate hourly electricity loads across a full year. The output results of the building simulations include the building’s electricity consumption on an hourly basis (kWh) while the output of the real-time electricity pricing includes retail hourly electricity prices (GBP/kWh); these data are used as the input of the BSS. The three main elements along with their examined characteristics are summarised below, in Figure 1, while Figure 2 demonstrates the modelling process and the software used along with the key inputs and outputs.
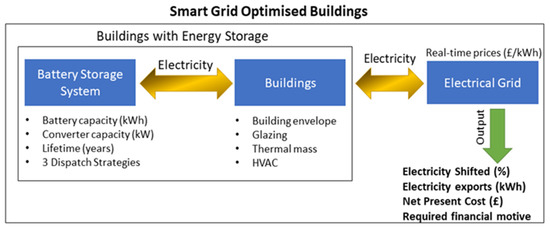
Figure 1.
Main research elements and their characteristics.
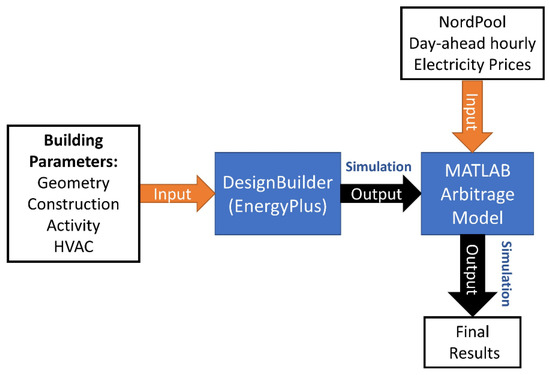
Figure 2.
Modelling Methodology, inputs and outputs.
2.1. Building Specifications
In this section, the chosen building key parameters along with their characteristics and values are explained, regarding design, structure, HVAC configuration, building loads and simulations.
2.1.1. Design and Structure
One common commercial building geometry of four storeys, each one occupying 625 m2 of total floor area. Each floor includes two zones: open-plan office (Zone 1) and a small generic reception/stairwell/lift area, located at the centre of the floor (Zone 2). Zone 2 is separated from the rest of the storey through an internal partition. The buildings vary in terms of three key design characteristics, as shown in Table 2:

Table 2.
Properties of Building Scenarios.
- Building envelope. This characteristic refers to the thermal transmittance of the envelope elements and their airtightness. The first category meets the building regulations as described in Part L [46] while Best Practice is more energy-efficient with lower envelope U-values, along with less external infiltration. Concerning the airtightness, crack templates are used to calculate the external infiltration that takes place due to surface cracks or by general fabric porosity, as explained in [47]. The envelope determines the interior climate conditions and consequently the additional heating and cooling demand required. The envelope parameters are presented in Table 3;
 Table 3. Building Envelope properties for the simulated buildings.
Table 3. Building Envelope properties for the simulated buildings. - Thermal mass. Lightweight buildings are assumed to include metallic cladding with plastering while heavyweight buildings consist of brickwork, concrete and plastering at their respective external walls. Thermal mass is responsible for a time delay in the heat exchange (thermal lag) between the building interior and the outside environment, depending on the properties of the building materials used [48];
- Window-to-Wall ratio. For this category, 30% and 80% glazed buildings are considered. Glazing is considered to be one of the weakest control points in the thermal performance of buildings as heating losses and solar gain take place through the windows [49].
Finally, concerning their occupancy, the buildings are occupied between 8 a.m. and 6 p.m., on weekdays only, while environmental control settings follow the CIBSE guidelines [50].
2.1.2. HVAC Configuration and Building Loads
The buildings are fully electric as ground source heat pumps (GSHPs) are used for both heating and cooling purposes. The heat pump’s coefficient of performance (CoP) values (3.5 and 5, respectively) are considered to be constant and equal to the seasonal COPs. Mechanical ventilation is used to meet the minimum air requirements of the occupants (10 L/s·person) as well as deliver free cooling whenever the indoor temperature is higher than the cooling set-point. An economiser is used to provide free cooling during the occupied hours, at a maximum rate of two air changes per hour. Night cooling only takes place between 31 May and 30 September, for the heavyweight buildings. The auxiliary energy is assumed to be constant throughout the year. The set-point and set-back temperatures are 22 °C and 12 °C for heating, while the respective values used for cooling are 27 °C and 23 °C. Finally, equipment loads from desktop workstations are 9.06 W/m2 while recessed LED with linear control is used for lighting purposes, with 10.6 W/m2 and 7.4 W/m2 for the office and the reception area, respectively, in order to meet the 500 and 200 lux illuminance targets.
2.1.3. Building Simulations
The building loads were calculated using DesignBuilder, which utilises the integrated EnergyPlus simulation engine which is a well-recognised and accepted building energy simulation software tool, capable of modelling HVAC as well as other energy flows in a building and therefore widely used to estimate building energy performance [51,52]. Figure 3 demonstrates the interoperation between DesignBuilder Graphical User Interface (GUI), and EnergyPlus Simulation engine. Regarding temperature control and the used indoor set-point and set-back temperatures, the operative temperature and therefore equal ambient and radiant fractions are considered for the simulations. The thermal comfort of the occupants is maintained, even in the highly glazed buildings. The discomfort hours, based on the ASHRAE 55 Simple Standard, were normalised per floor area and four time steps per hour were chosen for the Zone heat balance model calculations [53].
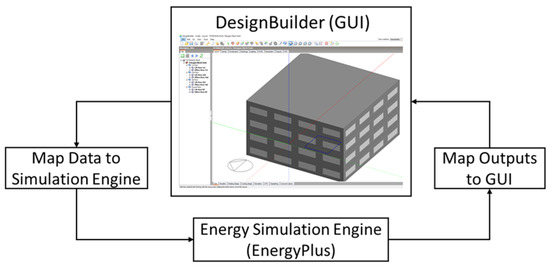
Figure 3.
Interoperation between DesignBuilder Graphical User Interface and EnergyPlus (Adapted from [51]).
The location chosen is Birmingham Airport, United Kingdom (UK) with an ASHRAE Climate Zone 5C. The location weather data from IWEC were used. Daylight Saving Time is not observed to avoid any temporal changes on the electricity profile of the buildings.
2.2. Real-Time Electricity Pricing Data
Wholesale electricity prices were obtained from NordPool, for the day-ahead market [54,55]. The wholesale cost of domestic electricity constituted only 33.6% of the total domestic electricity bill, in 2017 [56]. Other parameters include operating costs, the supplier pre-tax margin, network costs, environmental and social obligation costs, as well as VAT. For non-domestic electricity prices, there are no readily available values provided from Ofgem and therefore, the wholesale percentage had to be calculated, based on the data reported by the Consolidated Segmental Statements of the six largest UK electricity suppliers.
In order to be able to convert wholesale costs to the retail level, it is assumed that the wholesale percentage remains constant throughout the year. The real contribution of the wholesale cost to the final electricity bill might vary hourly, depending on the circumstances. Therefore, Equation (1) is used for the wholesale-to-retail conversion.
Finally, it must also be taken into account that while the reduced VAT rate of 5% applies for consumption of domestic electricity, non-domestic power is taxed at the standard rate of 20% [57]. The wholesale contribution to the non-domestic electricity price, reported by Ofgem as “direct fuel costs”, was calculated by the current study to be 36.6%, which is around 3% higher than its respective value for domestic electricity [58]. Figure 4 presents the maximum, minimum and average values per day for 2017 for the calculated retail electricity prices. It is shown that the daily difference between the lowest and the highest prices constitute the foundations of electricity arbitrage.
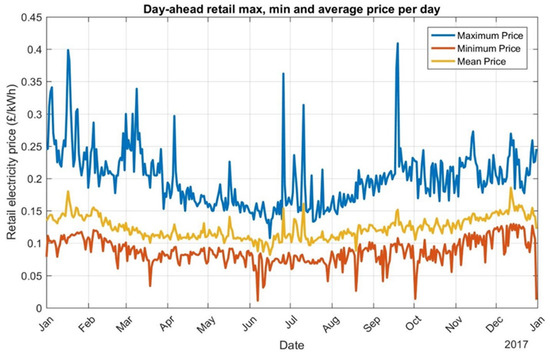
Figure 4.
Real-time day-ahead hourly electricity retail prices for 2017.
2.3. Battery Storage Model
The BSS model consists of the battery bank, one inverter, one rectifier and the controller. The battery can be discharged to meet building loads or export electricity back to the grid. The rectifier and inverter are combined in a bidirectional inverter, also called a bi-directional converter [59]. The input of the model includes the values of the building which have been generated from the building simulations and the hourly electricity retail prices in order to configure the BSS operation, based on the applied control algorithm strategy. Regarding the sizing of the BSS components, it is assumed that the BSS is able to discharge the total usable battery capacity in a maximum of 2 h and charge it under 3 h. Ten battery sizes between 40 and 220 kWh were considered, with a 20 kWh step.
This study has adopted an arbitrage algorithm, originally designed for the utilisation of large scale PHES, as presented in detail and used in [60,61,62]. In this study, significant changes have been made in order for the algorithm to adapt to the unique characteristics of the building scale. Their common objective is to make the algorithm take into account the hourly building loads towards deciding whether to operate the battery or not. The model variables are listed in Table 4 along with their units.

Table 4.
Battery Storage Model key variables and their units.
2.3.1. Control Algorithm Strategies
The BSS model operates on an hourly basis and the algorithm takes into account day-ahead real-time electricity prices. It is assumed that the prices of the following day are announced at midnight and that it is possible to perfectly predict the building energy consumption for the following day, in advance. Using all the data mentioned above, the routine takes place 365 times, each covering one day of the year. The principle of the algorithm is to preschedule the charging and discharging operations of the battery; therefore, charging cannot take place without discharging and vice versa.
When discharging, the operation of the battery can have one of the following two forms: (a) meeting the local building loads or (b) exporting back to the grid. In this direction, a total of three operational strategies have been considered, each one examining at least one form of the battery operation. Furthermore, it is important to examine the impact of the battery operation and the additional exports that take place, during non-working days, when no building loads are present; therefore, combinations of the above elements led to the formulation of three individual strategies: E7, E5 and E0. Under E7, both forms of the battery operation are allowed during the entire week, including exports to the grid when there is excess electricity stored in the battery. Additionally, E0 uses all stored electricity towards meeting building loads, during the working days of the week, with no exports allowed. Finally, as a middle-ground scenario, E5 allows both forms, but only during the working days of the week. An overview of the operational strategies is shown below, in Table 5.

Table 5.
Overview of the Operational Strategies.
2.3.2. Operational Strategy E7: Exports Allowed with Retail Revenues
The first operational strategy identifies the cheapest and most expensive hours of the day and schedules the BSS to take advantage of the price difference. The process refers to a day and is repeated until the end of one calendar year and until all periods (8760 h) have been examined for their suitability for battery operation. No distinction is made between working and non-working days (NWDs) and therefore the algorithm operates the battery as many times as technically possible. The combined flow chart for both operational strategies E7 and E5 is presented in Figure 5.
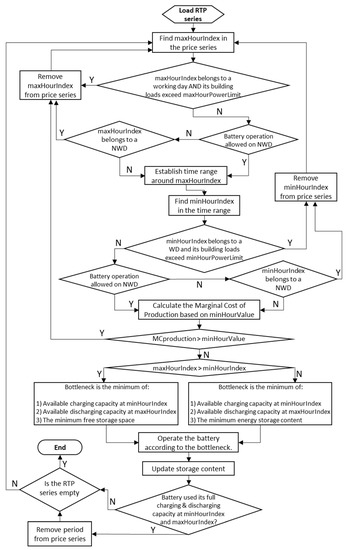
Figure 5.
Flow chart for Arbitrage with Exports for Strategies E7 and E5. If the battery operation is not allowed on NWDs, minHourIndex is removed from the price series (E5); otherwise, the algorithm proceeds directly with the calculation of the marginal cost of production (E7) based on the respective minHourValue.
Discharging hours (maxHourIndex) and their respective prices (maxHourPrice) are identified and given priority. However, if the corresponding building loads exceed a specific value (maxHourPowerLimit), the hours in question are removed from the time series and the algorithm moves on to the next iteration to identify the next suitable maxHourIndex. This is necessary in order to avoid discharging the battery during hours when the building loads are insignificant. This threshold is calculated as the average value of the building loads of the first day, which is always a non-working day, plus an optional margin of 5 kW to allow for error.
Afterwards, a range around maxHourIndex where charging might occur is established. The earliest hour the battery can charge is after the most recent period to maxHourIndex when the battery was full (minRangeIndex). Likewise, the latest hour when charging can happen after maxHourIndex is the hour before the battery has reached its minimum state of charge (maxRangeIndex). Then, the minimum electricity price in this range is identified (minHourIndex) along with its respective price (minHourPrice). If the building loads that take place during minHourIndex exceed a specified limit (minHourPowerLimit), which is set equal to maxHourPowerLimit, then the period is removed from the price series and the next iteration starts again to identify a new period for charging. This ensures that charging does not take place during the building’s operation, as it would result in higher peak loads.
The total cost of operating the BSS is based on the buying electricity price and the roundtrip efficiency in order to ensure that the energy discharged by the battery to meet the building loads is less expensive than directly buying electricity from the grid. The marginal operational costs of charging and discharging the ESS, often used in PHES arbitrage, are assumed to be zero and therefore the marginal cost of production is equal to maxHourPrice. The battery only operates if the condition of Equation (2) is met, which takes into account the roundtrip efficiency that consists of four different efficiencies that are present in charging and discharging:
Finally, operational bottlenecks are in place and will instruct the BSS with the exact amount of power to charge and discharge, depending on the amount of the energy stored in the battery. More specifically, constraints for the charging and discharging capacities of the battery will also apply to avoid charging above a state of charge of 100% and discharging below the minimum percentage required (10%). The storage content is then updated, and the process is complete when all the time periods have been evaluated.
2.3.3. Operational Strategy E5: Exports Allowed Only on Working Days
This version of the algorithm excludes the non-working days (NWDs) from the battery operation; therefore, 52 weekends and four public holidays, a total of 108 days and the equivalent of 2592 h during which the battery is not allowed to charge or discharge. This number of hours constitute approximately 30% of a calendar year and when combined with the technical capability of the BSS to cycle more than once daily can have an enormous impact on the energy exports and consequent revenues, which are massively reduced. It should be noted that a significantly less frequent battery usage leads to a higher battery life.
Operational Strategies E7 and E5 make use of all the available battery and inverter capacities, trying to discharge as much as possible during the most expensive hour(s), with any excess electricity being exported back to the electrical grid.
2.3.4. Operational Strategy E0: No Exports Allowed
The third version of the algorithm introduces one additional constraint to ensure that all the discharged energy from the battery is only used locally to cover the local building loads. Therefore, the maximum power discharged in any given hour is never greater than the building’s electricity demand. The roundtrip efficiency is also considered in order to avoid any additional grid purchases for remaining loads (Figure 6).
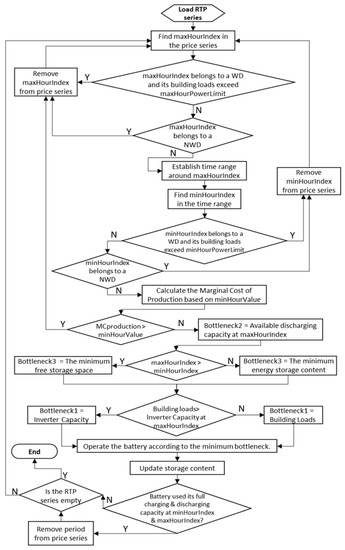
Figure 6.
Flowchart for Arbitrage without exports (Strategy E0). The algorithm presents structural differences compared to Figure 5 as building loads are now taken into account in the calculation of the bottlenecks. Bottleneck1 is set equal to either the building loads or the inverter capacity in kW based on the comparison of their values.
2.4. Economics and Cost–Benefit Analysis (CBA)
The battery used was based on a nominal lithium-ion lifecycle of 5000 cycles with a depth of discharge (DOD) of 90%, the equivalent of 4500 full cycles [63]. For the operation strategies that allow exports to the grid, the annual revenues are calculated by multiplying the hourly retail prices with the amount of the respective exported electricity. The total annual net costs of the electricity are considered to be equal to the electricity grid purchases, minus any export revenues. The calculated (annual) electricity cost is given in Equation (3), with its revenues and net cost given in Equations (4) and (5), respectively. Operation and maintenance (O&M) costs for the BSS are calculated through Equation (6) with the lifetime referring to the duration of the study period (life of the system in years). The replacement costs are calculated in Equation (7) with Nrepj representing the number of the replacements needed for a component j, such as the battery and the converter, and lifej referring to the estimated lifetime of a component j. The last part of the equation is used to consider the revenues due to the remaining lifespan of the components.
Regarding the CBA conducted, the BSS prices used are calculated per kWh and kW, based on a high-end commercial power pack [64]. The exact capital costs have been calculated to be around GBP 371/kWh and GBP 162/kW [65,66]; slightly higher values of GBP 390/kWh and GBP 170/kW are considered to adjust for error and inflation. The costs of cabling and other hardware are included in the total battery cost and are estimated to be approximately GBP 28/kWh.
In order to calculate the net present costs (NPCs) for each scenario, an annual inflation rate of 2% and an interest rate of 5% were taken into account, for 10-year and 20-year periods (Equations (8) and (9)). The levelised costs of electricity (LCOE) were calculated by dividing each NPC by the respective amounts of energy involved, as shown in Equations (10) and (11), excluding any battery losses for charging and discharging. Finally, the financial reward needed is introduced in Equation (12) to represent the economic benefit that a building must receive per kWh shifted in order to make the two NPCs equal and consequently render the scheme cost-effective, for the entire lifetime of the project. It should be noted that Equation (2) is based on [60,61] and Equations (3)–(11) on [59,67], adjusted for the needs of the current research.
The lifetime of the battery will differ depending on the operational strategy, as shown in Table 6 along with key technical and economic parameters considered in the modelling process. For strategy E7, the estimated battery lifetime is approximately 10 years, whereas for E5 and E0 the lifetime is higher, around 20 years. Moreover, the converter lifetime is assumed to be 10 years for all strategies. The economic analysis for this study is considered over 10- and 20-year periods; therefore, while there are no replacements required for the former period, an additional battery and converter is needed under strategy E7 while E5 and E0 require only the addition of a replacement converter, for the 20-year period.

Table 6.
Technical and economic parameters used for modelling purposes.
3. Results
3.1. Breakdown Electricity Consumption
The electricity consumption results per sector for all the simulated buildings are presented in Figure 7. All buildings have demonstrated satisfactory thermal comfort for the occupants, based on the ASHRAE 55 Standard. Electricity loads for room equipment, auxiliary energy and DHW are equal for all building scenarios as they are based on the same assumptions and occupant needs. Heating loads are significantly higher for the Part L Compliant buildings compared to best practice due to the higher U-Values and infiltration. Higher levels of glazing reduced both electricity for heating and lighting, but increased cooling requirements due to higher solar gain. Higher levels of thermal mass reduced electricity required for cooling as they took advantage of passive night cooling; however, this value is small in comparison to the total building energy consumption.
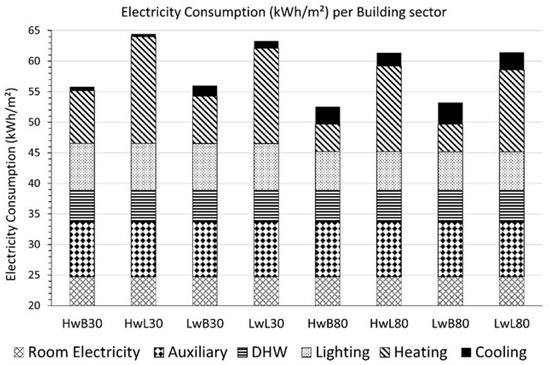
Figure 7.
Annual Electricity Consumption per sector for the simulated buildings.
In conclusion, Buildings HwL30 and HwB80 have the highest and lowest electricity consumption values, respectively, and at the same time they provide very good thermal comfort for their occupants. Therefore, as the two extreme cases, they are selected to be further analysed and compared, using several BSS and operational strategies E7, E5 and E0.
3.2. Battery Storage
The sizing of BSS is based on the “three hours to charge” and “two hours to discharge” rules. However, for the biggest systems, the first results indicated that the inverters rated power were oversized when compared with the average or even the maximum hourly building loads. Therefore, instead of using the stored electricity towards shifting building loads, all the excess electricity would be exported back to the grid (for the E7 and E5 scenarios). More specifically, when batteries larger than 160 kWh are used, the differences in the shifted peak loads would be insignificant. Consequently, the BSS components were revised and presented in Table 7.

Table 7.
BSS Components Sizing.
3.2.1. Exports Allowed with Retail Revenues (E7)
The results from the Battery Storage model are presented in Table 8, for the Operational Strategy E7, which allows exports to take place every day. The peak loads shifted refer to the loads directly met by the battery instead of buying electricity from the grid, between the building’s opening hours (8 a.m.–6 p.m.) while the electricity net cost includes the revenues from selling back to the grid. The operation of the BSS and its impact on the building’s electricity profile can be seen in Figure 8, for a Sunday and two working days.

Table 8.
Annual BSS Results for Operational Strategy E7.
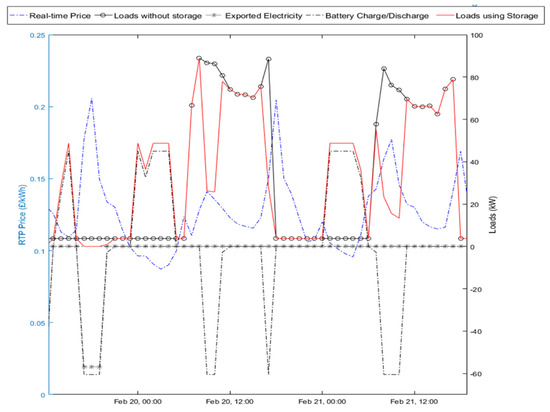
Figure 8.
Arbitrage E7 Results for Building HwL30 using Battery Storage (220 kWh, 45/−65 kW).
It is clear that the utilisation of battery storage which is adaptable to dynamic electricity prices leads to different results every day of the year. These results are always a function of the daily variation in both the electricity prices (GBP/kWh) and the building loads (kW). Potential applications of BSS include load-shifting and peak-shaving which can take place either in terms of reducing the highest load of the day or by reducing the number of hours during peak loads. Additionally, it can also be seen that during non-working days, the battery has the capacity to cycle more than once in order to export back to the grid as much as possible, during the most expensive prices, and take advantage of the price difference.
Regarding the comparison of the two buildings investigated, it is clear that Building HwB80 can shift more loads when using the same BSS. The difference is also dependent on the BSS size and specifications, varying between 1.66% and 2.92%. For the smallest BSS sizes (40–80 kWh), both buildings are able to shift their peak loads by a considerable percentage that varies between 7.68 and 17%. Concerning the electricity exports, the comparison between the two buildings is negligible for the smaller battery sizes as the entire stored electricity is used to meet building loads and there is no excess energy left to be sent back to the grid. However, as the BSS size increases and excess electricity is generated, it is evident that Building HwB80 is able to export higher amounts of electricity. For the BSS of 220 kWh, Building HwB80 exports 18.08 kWh/m2, which is 1.74 kWh/m2 more than Building HwL30.
Finally, regarding the electricity economics and the annual net costs (GBP/m2), as Building HwL30 is less energy-efficient, it consumes more electricity to meet its loads and therefore its total electricity purchases from the grid increase even more when utilising battery storage. For all scenarios and BSS sizes, Building HwB80 costs 1.67 GBP/m2 less, which translates into GBP 4175 of annual savings. Additionally, as the BSS size increases, the excess electricity also grows, resulting in higher electricity exports, increasing amount of revenues and a consequent lower net cost. The differences between the no storage scenario and the biggest BSS size are shown to identify the maximum benefits introduced by the battery. The net cost of electricity can be reduced from 8.68 to 7.06 and from 7.01 to 5.40 GBP/m2 for Buildings HwL30 and HwB80, respectively.
3.2.2. Exports Allowed on Working Days with Retail Revenues (E5)
The impact of the BSS regarding the Operational Strategy E5 which allows exports to take place on working days can be seen in Figure 9, for a Sunday and two working days. The BSS results are identical to E7 when it comes to working days and the shifting of peak loads; however, the battery does not run on weekends.
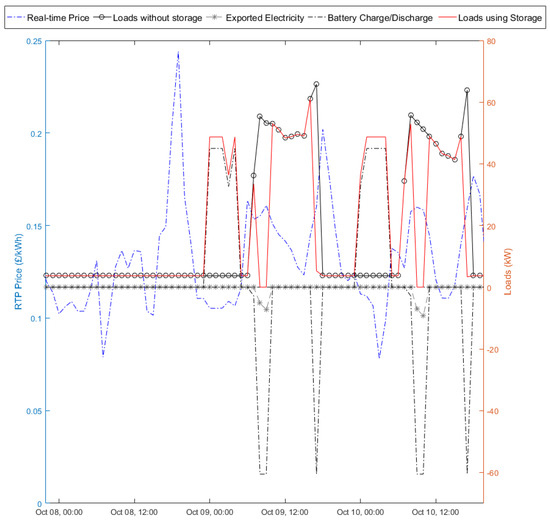
Figure 9.
Arbitrage E5 Results for Building HwL30 using Battery Storage (220 kWh, 45/−65 kW).
Building HwB80 can shift a higher percentage of its peak loads, in comparison with Building HwL30. Once using the same BSS, Building HwB80 shifts 2% more than HwL30 on average, which is not significant. It should be pointed out that all peak load shifts have been decreased when compared with Table 8 and Operational Strategy E7. The battery operation for both E7 and E5 strategies is the same for working days; however, E7 allows load-shifting during weekends as well. While the buildings’ activity is minimal at weekends, there is a small constant electricity load (~4 kW), representing the auxiliary (parasitic) energy consumption. Therefore, E7 leads to higher load-shifting around 2% more when compared to the E5 respective results.
Revenue-wise, the most important parameter when comparing E5 and E7 is the electricity exported back to the grid. Under E5, the battery is idle on non-working days and exports can only take place in cases of excess electricity, on weekdays. For the different battery sizes, export ranges of 0–3.79 and 0–5.53 kWh/m2 can be achieved for Buildings HwL30 and HwB80, respectively. For comparison purposes, the respective export ranges under the E7 strategy were 2.23–16.34 and 2.23–18.08 kWh/m2. In addition, as the E5 export values are smaller, they also lead to consequent lower revenue streams and therefore higher net costs. Under E5, the electricity net costs are in the range 7.74–8.46 for HwL30 and 6.07–6.79 kWh/m2 for HwB80. The respective values for the E7 strategy were previously shown to be 7.06–8.30 and 5.40–6.63 kWh/m2.
3.2.3. No Exports (E0)
The absence of exports and the excess stored electricity under E0 have led to higher amounts of energy being available and used towards meeting the local building loads. Consequently, from an electricity footprint perspective, buildings implementing E0 have been able to change their daily profile significantly (Figure 10). For the first time, the peak loads-shifting has now established a linear relationship with the battery capacity of the system; this was not the case for E7 and E5 strategies.
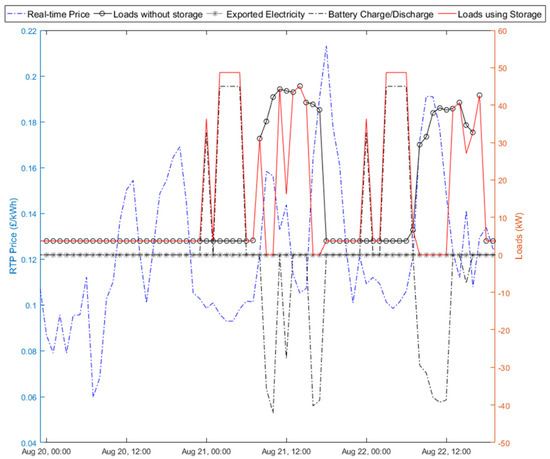
Figure 10.
Arbitrage E0 Results for Building HwL30 using Battery Storage (220 kWh, 45/−65 kW).
Quantitively, the potential for load-shifting has been significantly increased when compared with the E7 and E5 strategies, as the battery operation now focuses exclusively on this objective. More specifically, the peak load-shifting percentage ranges are now 6.38–33.95% and 7.79–39.68% for Buildings HwL30 and HwB80, respectively. The peak load-shifting of the two buildings for the larger 220 kWh battery, under the E7 strategy, was respectively 4.5 and 8% lower than with No Exports.
Finally, the total absence of exports and the relevant revenue streams also result in higher annual net costs, when compared with E7; however, net cost differences between E5 and E0 are insignificant, reflecting the low amount of E5 exports. In terms of cost-effectiveness, Building HwB80 still appears to be more attractive, as for every BSS size, it is always GBP 1.6/m2 cheaper than HwL30.
3.3. Cost–Benefit Analysis
A CBA for a 10- and 20-year period was conducted for the two final buildings in order to evaluate the long-term economics, taking into account parameters that have the potential to affect the cost-effectiveness of the suggested SGOB scheme, including the inflation and interest rates that are assumed to be constant. Two batteries (120 and 240 kWh) were used along with a common inverter size (60 kW). The rectifier capacity was chosen in order to be able to fully charge the battery within 3 h (40 and 80 kW). The CBA focusses on the BSS and does not consider costs for the building construction, as they are deemed to be outside the scope of this article and the suggested scheme can also be applied to existing buildings.
3.3.1. CBA for a 10-Year Period
The NPCs for all operational strategies can be seen per building, in Figure 11. The difference between the no storage case and the rest of the scenarios is due to the introduced BSS capital cost which is dependent on the battery and converter sizes. When not using storage, Building HwL30 has an NPC over 10 years of GBP 185,661 which is approximately GBP 35,000 more expensive than Building HwB80. This GBP 35,000 NPC difference between the two buildings appears to be consistent throughout all operational strategies and BSS sizes, indicating that HwB80 is more economical for all the scenarios presented. This is in accordance with the results presented in Section 3.1, where the buildings’ total electricity consumption was 64.45 kWh/m2 for HwL30 and 52.57 kWh/m2 for HwB80.
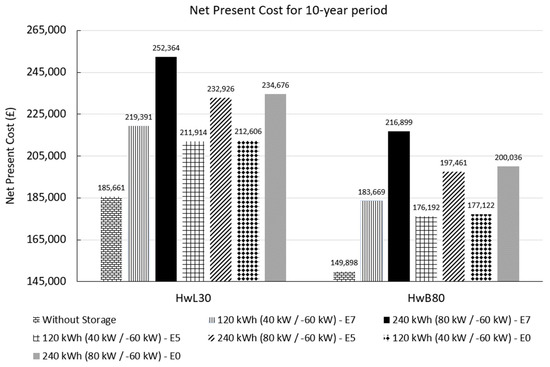
Figure 11.
Net Present Cost for 10-year period (all operational strategies).
From the three suggested operational strategies, E7 appears to incur the highest NPCs, despite the additional revenue stream of exports that is introduced during weekends. It should be highlighted that at the end of the 10-year period, E7 is the only operational strategy under which the lifetime of the battery reaches its end. In contrast, under E5 and E0, the battery has a remaining lifespan of 10 additional years and therefore has 50% of its lifetime intact, as previously shown in Table 6, leading to the reduction in the battery’s NPCs. Furthermore, the second highest NPC values are observed under E0 where no exports take place, followed by E5 that allows exports only on working days. For both buildings, the results for E5 and E0 strategies appear to be very similar for both scenarios, forming a separate group from E7 and demonstrating that the impact of the minimal number of exports under E5 is insignificant, resulting in a marginal difference between E0 and E5 of just GBP 1000–3000, depending on the battery size.
Under E7, the NPC is around GBP 8000 or GBP 20,000 higher than the respective values under E5 for the 120 kWh and 240 kWh battery, respectively. It is important to point out that while the primary objective of the three operational strategies is to shift electricity demand from peak to off-peak periods of the day and occasionally perform peak-shaving, exports are of vital economic importance for the viability and the cost-effectiveness of the SGOB scheme. Reviewing the results per building and beginning with HwB80, E7 adds a GBP 34,000 cost when using the 120 kWh battery, compared to the no storage case, while the 240 kWh battery brings the total extra cost to GBP 67,000. The exact same trends are observed for HwL30.
It is vital to highlight that under the E7 and E5 scenarios, it is assumed that building-exported energy is rewarded with the retail electricity price. As explained, there is no current mechanism or financial motive for buildings to provide such a service to the electrical grid. This is also one of the reasons that made the distinction between E7 and E5 necessary.
In this direction, a financial reward is necessary in order to encourage commercial buildings to participate in this suggested enterprise and become SGOBs. This reward may at least cover the difference between the (business as usual) NPC without storage and the NPC when using a BSS. Essentially, this will create an additional revenue stream that will render the two NPCs equal. Concerning the structure of this SGOB reward, the authors of this paper support that it should be based on the amount of electricity shifted and/or exported by the BSS. For the needs of the current article, emphasis will be given only on the electricity shifted as this is present in all three operational strategies.
If financial motives are to be calculated based on the amount of electricity shifted during the building’s working hours, as presented in Chapter 2.4, the reward range is GBP 0.0966–0.1432 for HwL30 and GBP 0.1031–0.1575 for HwB80, as shown in Figure 12. Shifting electricity is of benefit to the grid; however, for an individual building more energy shifted is usually due to the building having a higher energy consumption due to poor energy efficiency. It is therefore necessary that any incentive does not incentivise lower energy efficiency in the building stock. In this case, this is tackled by using energy shifted in the denominator of the calculation for incentives. This can also be achieved with incentives only applied to buildings when they reach a certain level of energy efficiency.
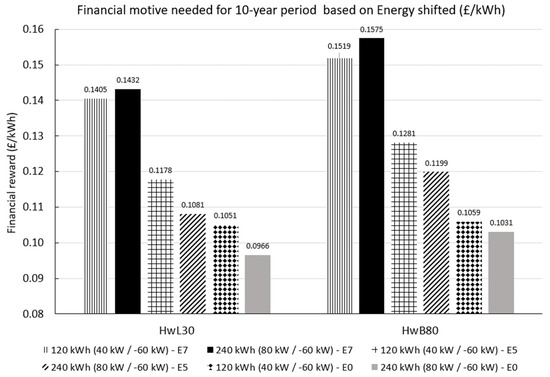
Figure 12.
Required financial motive for a 10-year period (all operational strategies).
Operational strategy E7 requires the highest financial rewards, followed by E5 and E0. In descending order, the financial motive establishes a range between GBP 0.1405–0.1575 for E7, GBP 0.1081–0.1281 for E5 and finally GBP 0.0966–0.1059 for E0. The highest numbers observed under E7 can be explained due to the reduced lifetime of the battery, which leads to comparatively higher NPCs and therefore to a greater NPC difference which needs to be covered by the financial motive (Equation (12)). The reward needed under E0 appears to be slightly lower than the respective values under E5 due to the entirety of the E0 battery operation being dedicated to load shifting while there is a combination of load shifting and minor electricity exports, under E5.
Finally, the levelised cost of electricity (LCOE) is presented below, in Table 9. The cost is almost the same for buildings without storage, around GBP 0.1146/kWh. For the smaller BSS size (120 kWh), it can be seen for both buildings that, under operational strategy E7, the cost of purchasing electricity is similar to the no storage scenario, while the value increases to approximately GBP 0.1289 for E5 and reaches its maximum price for E0, with a mean value of GBP 0.1334. When utilising the bigger BSS (240 kWh), the LCOE has a mean value of GBP 0.1225 under E7, marginally higher than the respective value of the smaller battery. The electricity costs for E5 and E0 strategies are higher, with respective mean values of GBP 0.1382 and GBP 0.1489.

Table 9.
Levelised Cost of Electricity (LCOE) for 10-year period.
In conclusion, despite some minor differences, the LCOE results are similar for both buildings. The parameters that affect the electricity costs are the operational strategy and the size of the BSS while the LCOE under E7 appears to be similar to the no storage scenario value. It should be reminded that this is also related to the LCOE calculation methodology followed as the NPCs are divided by sum of the electricity demand and any present exports. It can be argued that the inclusion of exports can potentially lead to an underestimation of the LCOE, for the E7 and E5 strategies. However, the additional electricity is purchased from the grid to only be later exported back, resulting in a subsequent profit and at the same time providing an important service to the electrical grid.
3.3.2. CBA for a 20-Year Period
The 20-year CBA results are shown, in detail, in Table 10, along with the number of replacements needed, for the bidirectional converter and the battery. It should be noted that, as a result of increasing the study period from 10 to 20 years, all the NPC values, including the no-storage scenario, have increased due to the higher amounts of electricity purchased by the grid to cover the local building loads. More specifically, when not using storage, Building HwL30 has an NPC over 20 years of GBP 324,602, which is around GBP 62,000 more expensive than Building HwB80. Similarly to the 10-year period results, this GBP 62,000 NPC difference between the two buildings is present throughout all strategies and BSS sizes, confirming that HwB80 is indeed more economical. Furthermore, the additional costs introduced by the capital expenditure of the replacements has led to an increase of the NPCs for all storage scenarios. At the same time, as all the BSS components do not have any remaining lifespan at the end of the study period, there are no deductions from their respective NPC values. Nevertheless, the 20-year results and their trends are consistent with the 10-year period results, as presented in Section 3.3.1.

Table 10.
LCOE, NPC and financial motive needed for 20-year period.
At this point, it is important to present a brief comparison between the 10- and 20-year results in order to evaluate how the NPC values affect the financial motives needed to render the SGOB scheme cost-effective (Figure 13). For both buildings and study periods, it can be seen that, with the exception of some minor variations, the financial motive values are largely the same for both BSS sizes used; this is expected due to their normalisation (GBP/kWh shifted). In terms of the financial motive values per operational strategy, the same trends are observed, as in Section 3.3.1, with E7 requiring the highest financial reward, followed by E5 and finally E0. In addition, it is clear that for the 20-year period, the financial motive needed is reduced by GBP 0.02/kWh, for both buildings and all operational strategies, when compared to the respective values of the 10-year period. Consequently, the BSS operation is not just able to compensate the additional capital costs needed for the replacement components of the 20-year period, but it also results in a reduction in the financial reward needed when increasing the study period from 10 to 20 years. In more detail, for the smaller 120 kWh BSS and both buildings, the reduction reaches 13% for E7 and 21% for E5 and E0, while the respective values for the 240 kWh BSS (13%, 22%, 21%) remain largely consistent.
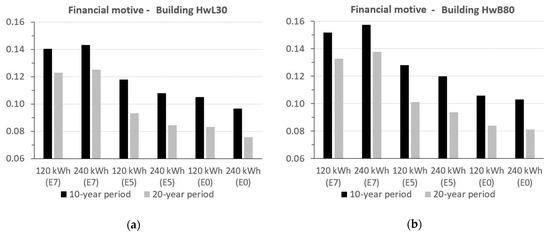
Figure 13.
Financial reward needed for a 10-year and 20-year period, based on the electricity shifted (GBP/kWh), for buildings (a) HwL30 and (b) HwB80.
4. Conclusions
From a total of eight simulated buildings with different design characteristics, the two extreme cases, energy-wise, were selected for further investigation in order to assess their capability to utilise BSS to perform arbitrage under real-time electricity prices. When assuming the biggest battery size of 220 kWh, the most energy-efficient building (HwB80), in terms of the envelope U-values, has proven to be capable of shifting a higher percentage of its peak loads (31.76% for E7, 29.51% for E5 and 39.68% for E0) and at the same time export more electricity (18.08 kWh/m2 for E7 and 5.53 kWh/m2 for E5) when this is available as an option. In addition, HwB80 has been proven to have the lowest annual net costs (5.40 GBP/m2 for E7, 6.07 GBP/m2 for E5 and 6.20 GBP/m2 for E0) which are significantly lower when compared with the no-storage scenario cost of 7.01 GBP/m2, for the same building. It is clear that the building design affects the energy as well as the arbitrage performance.
Regarding the long-term economics and the CBA conducted for a 10-year period, Building HwB80 proved to be the most economical, incurring GBP 35,000 less costs under all scenarios, including no storage. The lowest NPCs were observed under the E5 strategy due to the remaining lifetime of the battery (50%) at the end of the 10-year period, and the small amount of revenues. The E0 results are very similar to E5′s, indicating that the E5 operational strategy leads to an insignificant revenue stream from exports. Finally, strategy E7 has the highest NPC values for all scenarios as the export revenues are not sufficient to compensate for the fact that the remaining battery lifespan is non-existent, leading to zero NPC deductions at the end of the study period. When a 20-year period is considered, HwB80 is still the most economical building, incurring GBP 62,000 less in costs under all scenarios, including no storage. Increasing the study period from 10 to 20 years leads to a reduction in the financial motive by GBP 0.02 per kWh shifted, despite the introduction of the additional capital costs needed for the system replacements.
The results regarding the financial rewards needed to make the building-arbitrage scheme cost-effective were remarkably interesting, as the energy-efficient building (HwB80) proved to require a higher amount of extra revenues (GBP/kWh shifted). The problematic nature of the financial reward definition was explained; therefore, the authors of this article believe that the monetisation of building-provided services to the grid by BSS utilisation should be based on the percentage of the building loads shifted (%) rather than the total amount of electricity shifted. The latter constitutes a much fairer criterion that is able to reflect the energy efficiency of the buildings and indirectly their design and HVAC configuration.
Regarding limitations of this study, it should be noted that the majority of the end-users do not have access to real-time electricity prices and there is no current mechanism enabling battery arbitrage at the building scale. However, this paper makes the case for methods to enable this to happen towards wider building-level storage utilisation.
It is clear that the formation of a proper regulatory framework is of fundamental importance in order to establish motives for buildings to undertake an active role in the future smart grid by utilising battery storage and evolving gradually into SGOBs. This will be possible only if all the associated market players and stakeholders recognise the peak demand reduction potential and the capabilities presented under different DR strategies for various building types, in different climates and occupancy profiles. They have to come together to discuss and create such a framework, including the electricity utilities, the government, the public and building owners.
The current article made the first vital step by examining how building design and BSS characteristics affect the performance of commercial buildings conducting arbitrage by introducing three operational strategies and examining the techno-economic implications in the long term. Further work should be carried out towards defining and examining potential financial motives and subsidy mechanisms, not only for arbitrage but for other balancing services as well. These motives could be structured similarly to the services procured by the National Grid, mentioned previously, and could include availability fee (GBP/hour), utilisation (GBP/MWh) and nomination fee (GBP/hour).
Regarding future work, it is important to examine additional building design and HVAC configurations, especially naturally ventilated buildings which could demonstrate a different behaviour in terms of their daily electricity profile, especially in the summer period. Further development to incorporate building scale renewables should also follow.
Author Contributions
Conceptualization, A.D.G., B.V., E.A.H. and M.M.; formal analysis, A.D.G., B.V., E.A.H. and M.M.; investigation, A.D.G., B.V., E.A.H. and M.M.; methodology, A.D.G., B.V., E.A.H. and M.M.; software, A.D.G.; supervision, B.V., E.A.H. and M.M.; Writing—original draft, A.D.G.; Writing—review and editing, A.D.G. All authors have read and agreed to the published version of the manuscript.
Funding
The authors gratefully acknowledge support from the EPSRC via grant EP/L016818/1 which funds the Centre for Doctoral Training in Energy Storage and its Applications.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- D’Agostino, D.; Cuniberti, B.; Bertoldi, P. Energy consumption and efficiency technology measures in European non-residential buildings. Energy Build. 2017, 153, 72–86. [Google Scholar] [CrossRef]
- Warwicker, B.; Cash, D. The building services relationship to the national grid. In Proceedings of the CIBSE ASHRAE Technical Symposium, London, UK, 18–19 April 2012. [Google Scholar]
- Anderson, B.; Torriti, J. Explaining shifts in UK electricity demand using time use data from 1974 to 2014. Energy Policy 2018, 123, 544–557. [Google Scholar] [CrossRef]
- Das, P.; Mathur, J.; Bhakar, R.; Kanudia, A. Implications of short-term renewable energy resource intermittency in long-term power system planning. Energy Strat. Rev. 2018, 22, 1–15. [Google Scholar] [CrossRef]
- Sehar, F.; Pipattanasomporn, M.; Rahman, S. An energy management model to study energy and peak power savings from PV and storage in demand responsive buildings. Appl. Energy 2016, 173, 406–417. [Google Scholar] [CrossRef]
- Palensky, P.; Dietrich, D. Demand side management: Demand response, intelligent energy systems, and smart loads. IEEE Trans. Ind. Inform. 2011, 7, 381–388. [Google Scholar] [CrossRef]
- Brandt, T.; Feuerriegel, S.; Neumann, D. Modeling interferences in information systems design for cyberphysical systems: Insights from a smart grid application. Eur. J. Inf. Syst. 2018, 27, 207–220. [Google Scholar] [CrossRef]
- Valogianni, K.; Ketter, W. Effective demand response for smart grids: Evidence from a real-world pilot. Decis. Support Syst. 2016, 91, 48–66. [Google Scholar] [CrossRef]
- Alimohammadisagvand, B. Influence of Demand Response Actions on Thermal Comfort and Electricity Cost for Residential House. Ph.D. Thesis, Aalto University, Espoo, Finland, 2018. [Google Scholar]
- Alimohammadisagvand, B.; Jokisalo, J.; Siren, K. The potential of predictive control in minimizing the electricity cost in a heat-pump heat residential house. In Proceedings of the 3rd IBPSA-England Conference BSO 2016, Great North Museum, Newcastle, UK, 12–14 September 2016. [Google Scholar]
- Hemmati, M.; Mirzaei, M.A.; Abapour, M.; Zare, K.; Mohammadi-Ivatloo, B.; Mehrjerdi, H.; Marzband, M. Economic-environmental analysis of combined heat and power-based reconfigurable microgrid integrated with multiple energy storage and demand response program. Sustain. Cities Soc. 2021, 69, 102790. [Google Scholar] [CrossRef]
- Korkas, C.D.; Baldi, S.; Michailidis, I.; Kosmatopoulos, E.B. Occupancy-based demand response and thermal comfort optimization in microgrids with renewable energy sources and energy storage. Appl. Energy 2016, 163, 93–104. [Google Scholar] [CrossRef]
- Gholinejad, H.R.; Loni, A.; Adabi, J.; Marzband, M. A hierarchical energy management system for multiple home energy hubs in neighborhood grids. J. Build. Eng. 2020, 28, 101028. [Google Scholar] [CrossRef]
- Kiliccote, S.; Piette, M.A.; Ghatikar, G.; Hafemeister, D.; Kammen, D.; Levi, B.G.; Schwartz, P. Smart buildings and demand response. AIP Conf. Proc. 2011, 1401, 328–338. [Google Scholar] [CrossRef]
- Derakhshan, G.; Shayanfar, H.A.; Kazemi, A. The optimization of demand response programs in smart grids. Energy Policy 2016, 94, 295–306. [Google Scholar] [CrossRef]
- Lee, Y.M.; Horesh, R.; Liberti, L. Optimal HVAC control as demand response with on-site energy storage and generation system. Energy Procedia 2015, 78, 2106–2111. [Google Scholar] [CrossRef]
- Lorenzi, G.; Silva, C.A.S. Comparing demand response and battery storage to optimize self-consumption in PV systems. Appl. Energy 2016, 180, 524–535. [Google Scholar] [CrossRef]
- Lawrence Berkeley National Laboratory. Introduction to Commercial Building Control Strategies and Techniques for Demand Response. 2007. Available online: https://buildings.lbl.gov/publications/introduction-commercial-building (accessed on 18 March 2021).
- Winfield, M.; Shokrzadeh, S.; Jones, A. Energy policy regime change and advanced energy storage: A comparative analysis. Energy Policy 2018, 115, 572–583. [Google Scholar] [CrossRef]
- National Grid ESO. Balancing Services. 2021. Available online: https://www.nationalgrideso.com/balancing-services/list-all-balancing-services (accessed on 10 March 2021).
- Heris, M.-N.; Mirzaei, M.A.; Asadi, S.; Mohammadi-Ivatloo, B.; Zare, K.; Jebelli, H.; Marzband, M. Evaluation of hydrogen storage technology in risk-constrained stochastic scheduling of multi-carrier energy systems considering power, gas and heating network constraints. Int. J. Hydrogen Energy 2020, 45, 30129–30141. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Asadi, S. Optimal operation of multi-carrier energy networks with gas, power, heating, and water energy sources considering different energy storage technologies. J. Energy Storage 2020, 31, 101574. [Google Scholar] [CrossRef]
- Mirzaei, M.A.; Nazari-Heris, M.; Zare, K.; Mohammadi-Ivatloo, B.; Marzband, M.; Asadi, S.; Anvari-Moghaddam, A. Evaluating the impact of multi-carrier energy storage systems in optimal operation of integrated electricity, gas and district heating networks. Appl. Therm. Eng. 2020, 176, 115413. [Google Scholar] [CrossRef]
- Bulut, M.B.; Odlare, M.; Stigson, P.; Wallin, F.; Vassileva, I. Buildings in the future energy system—Perspectives of the Swedish energy and buildings sectors on current energy challenges. Energy Build. 2015, 107, 254–263. [Google Scholar] [CrossRef]
- Bulut, M.B.; Wallin, F. Buildings as components of smart grids—Perspectives of different stakeholders. Energy Procedia 2014, 61, 1630–1633. [Google Scholar] [CrossRef][Green Version]
- Agarwal, Y.; Weng, T.; Gupta, R.K. Understanding the role of buildings in a smart microgrid. In Proceedings of the 2011 Design, Automation & Test in Europe, Grenoble, France, 14–18 March 2011. [Google Scholar]
- Niu, J.; Tian, Z.; Lu, Y.; Zhao, H. Flexible dispatch of a building energy system using building thermal storage and battery energy storage. Appl. Energy 2019, 243, 274–287. [Google Scholar] [CrossRef]
- Georgakarakos, A.D.; Mayfield, M.; Hathway, E.A. Battery storage systems in smart grid optimised buildings. Energy Procedia 2018, 151, 23–30. [Google Scholar] [CrossRef]
- Gissey, G.C.; Dodds, P.; Radcliffe, J. Market and regulatory barriers to electrical energy storage innovation. Renew. Sustain. Energy Rev. 2018, 82, 781–790. [Google Scholar] [CrossRef]
- Forrester, S.P.; Zaman, A.; Mathieu, J.; Johnson, J. Policy and market barriers to energy storage providing multiple services. Electr. J. 2017, 30, 50–56. [Google Scholar] [CrossRef]
- Zame, K.K.; Brehm, C.A.; Nitica, A.T.; Richard, C.L.; Schweitzer III, G.D. Smart grid and energy storage: Policy recommendations. Renew. Sustain. Energy Rev. 2018, 82, 1646–1654. [Google Scholar] [CrossRef]
- Leadbetter, J.; Swan, L. Battery storage system for residential electricity peak demand shaving. Energy Build. 2012, 55, 685–692. [Google Scholar] [CrossRef]
- Graditi, G.; Ippolito, M.; Telaretti, E.; Zizzo, G. Technical and economical assessment of distributed electrochemical storages for load shifting applications: An Italian case study. Renew. Sustain. Energy Rev. 2016, 57, 515–523. [Google Scholar] [CrossRef]
- Palizban, O.; Kauhaniemi, K. Energy storage systems in modern grids—Matrix of technologies and applications. J. Energy Storage 2016, 6, 248–259. [Google Scholar] [CrossRef]
- Gür, T.M. Review of electrical energy storage technologies, materials and systems: Challenges and prospects for large-scale grid storage. Energy Environ. Sci. 2018, 11, 2696–2767. [Google Scholar] [CrossRef]
- Parra, D.; Gillott, M.; Norman, S.A.; Walker, G.S. Optimum community energy storage system for PV energy time-shift. Appl. Energy 2015, 137, 576–587. [Google Scholar] [CrossRef]
- Knosala, K.; Kotzur, L.; Röben, F.T.; Stenzel, P.; Blum, L.; Robinius, M.; Stolten, D. Hybrid hydrogen home storage for decentralized energy autonomy. Int. J. Hydrogen Energy 2021, 46, 21748–21763. [Google Scholar] [CrossRef]
- Elberry, A.M.; Thakur, J.; Santasalo-Aarnio, A.; Larmi, M. Large-scale compressed hydrogen storage as part of renewable electricity storage systems. Int. J. Hydrogen Energy 2021, 46, 15671–15690. [Google Scholar] [CrossRef]
- Ramos, J.S.; Moreno, M.P.; Delgado, M.G.; Domínguez, S.Á.; Cabeza, L.F. Potential of energy flexible buildings: Evaluation of DSM strategies using building thermal mass. Energy Build. 2019, 203, 109442. [Google Scholar] [CrossRef]
- Wang, S.; Gao, D.-C.; Tang, R.; Xiao, F. Cooling supply-based HVAC system control for fast demand response of buildings to urgent requests of smart grids. Energy Procedia 2016, 103, 34–39. [Google Scholar] [CrossRef]
- Perez, K.X.; Baldea, M.; Edgar, T.F. Integrated HVAC management and optimal scheduling of smart appliances for community peak load reduction. Energy Build. 2016, 123, 34–40. [Google Scholar] [CrossRef]
- Dufo-López, R.; Agustín, J.L.B. Multi-objective design of PV–wind–diesel–hydrogen–battery systems. Renew. Energy 2008, 33, 2559–2572. [Google Scholar] [CrossRef]
- Mago, P.J.; Smith, A.D. Evaluation of the potential emissions reductions from the use of CHP systems in different commercial buildings. Build. Environ. 2012, 53, 74–82. [Google Scholar] [CrossRef]
- Jung, Y.; Kim, J.; Lee, H. Multi-criteria evaluation of medium-sized residential building with micro-CHP system in South Korea. Energy Build. 2019, 193, 201–215. [Google Scholar] [CrossRef]
- Georgakarakos, A.D.; Mayfield, M.; Buckman, A.H.; Jubb, S.A.; Wootton, C. What are smart grid optimised buildings? In Proceedings of the Living and Sustainability: An Environmental Critique of Design and Building Practices, Locally and Globally, London, UK, 9–10 February 2017. [Google Scholar]
- HM Government. The Building Regulations 2010: Conservation of Fuel and Power (L1A). 2016. Available online: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/540326/BR_PDF_AD__L1A__2013_with_2016_amendments.pdf (accessed on 5 March 2021).
- International Energy Agency. Numerical Data for Air Infiltration & Natural Ventilation Calculations. 1998. Available online: https://www.aivc.org/sites/default/files/members_area/medias/pdf/Technotes/TN44%20NUMERICAL%20DATA%20FOR%20AIR%20INFILTRATION.PDF (accessed on 10 February 2021).
- Florides, G.; Tassou, S.; Kalogirou, S.; Wrobel, L. Measures used to lower building energy consumption and their cost effectiveness. Appl. Energy 2002, 73, 299–328. [Google Scholar] [CrossRef]
- Pacheco-Torres, R.; Ordóñez, J.; Martínez, G. Energy efficient design of building: A review. Renew. Sustain. Energy Rev. 2012, 16, 3559–3573. [Google Scholar] [CrossRef]
- CIBSE. Environmental Design: CIBSE Guide A, 8th ed.; The Lavenham Press: Suffolk, UK, 2015. [Google Scholar]
- Kamel, E.; Memari, A.M. Review of BIM’s application in energy simulation: Tools, issues, and solutions. Autom. Constr. 2018, 97, 164–180. [Google Scholar] [CrossRef]
- Boyano, A.; Hernandez, P.; Wolf, O. Energy demands and potential savings in European office buildings: Case studies based on EnergyPlus simulations. Energy Build. 2013, 65, 19–28. [Google Scholar] [CrossRef]
- DesignBuilder. Calculation Options. 2019. Available online: https://designbuilder.co.uk//helpv5.4/#Calculation_Options.htm%3FTocPath%3DBuilding%2520Models%7CModel%2520Options%7CSimulation%2520Calculation%2520Options%7C_____2 (accessed on 5 January 2021).
- Nord Pool. Nord Pool Spot Annual Report 2018. 2018. Available online: http://www.nordpoolspot.com/globalassets/download-center/annual-report/annual-report_nord-pool-spot_2013.pdf (accessed on 15 December 2020).
- Nord Pool. Historical Market Data. 2019. Available online: https://www.nordpoolgroup.com/historical-market-data/ (accessed on 20 November 2020).
- Ofgem. Breakdown of an Electricity Bill. 2018. Available online: https://www.ofgem.gov.uk/data-portal/breakdown-electricity-bill (accessed on 12 December 2020).
- HM Government. Fuel and Power (VAT Notice 701/19). 2016. Available online: https://www.gov.uk/guidance/vat-on-fuel-and-power-notice-70119 (accessed on 11 November 2020).
- Ofgem. Energy Companies’ Consolidated Segmental Statements. 2018. Available online: https://www.ofgem.gov.uk/system/files/docs/2018/08/css_-_energy_companies_consolidated_segmental_statements_css_-_2018.pdf (accessed on 25 November 2020).
- Dufo-López, R.; Bernal-Agustín, J.L. Techno-economic analysis of grid-connected battery storage. Energy Convers. Manag. 2015, 91, 394–404. [Google Scholar] [CrossRef]
- Connolly, D.; Lund, H.; Finn, P.; Mathiesen, B.; Leahy, M. Practical operation strategies for pumped hydroelectric energy storage (PHES) utilising electricity price arbitrage. Energy Policy 2011, 39, 4189–4196. [Google Scholar] [CrossRef]
- Staffell, I.; Rustomji, M. Maximising the value of electricity storage. J. Energy Storage 2016, 8, 212–225. [Google Scholar] [CrossRef]
- Barbour, E.; Wilson, G.; Hall, P.; Radcliffe, J.; Wilson, I. Can negative electricity prices encourage inefficient electrical energy storage devices? Int. J. Environ. Stud. 2014, 71, 1–15. [Google Scholar] [CrossRef]
- TESVOLT. The Lithium Storage System for Business and Industry. 2016. Available online: http://www.solfex.co.uk/uploads/downloads/TESVOLT_ENG_Li_Datasheet_Version_2016_06.pdf (accessed on 3 November 2020).
- Tesla. Tesla Powerpack. 2020. Available online: https://www.tesla.com/en_GB/powerpack (accessed on 8 October 2020).
- Pimm, A.J.; Cockerill, T.T.; Taylor, P.G.; Bastiaans, J. The value of electricity storage to large enterprises: A case study on Lancaster University. Energy 2017, 128, 378–393. [Google Scholar] [CrossRef]
- Yang, L.; Ribberink, H. Investigation of the potential to improve DC fast charging station economics by integrating photovoltaic power generation and/or local battery energy storage system. Energy 2019, 167, 246–259. [Google Scholar] [CrossRef]
- Dufo-López, R. Optimisation of size and control of grid-connected storage under real time electricity pricing conditions. Appl. Energy 2015, 140, 395–408. [Google Scholar] [CrossRef]
- Dehghani-Sanij, A.; Tharumalingam, E.; Dusseault, M.; Fraser, R. Study of energy storage systems and environmental challenges of batteries. Renew. Sustain. Energy Rev. 2019, 104, 192–208. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).