Numerical Modelling and Validation of the Response of Masonry Infilled RC Frames Using Experimental Testing Results
Abstract
:1. Introduction
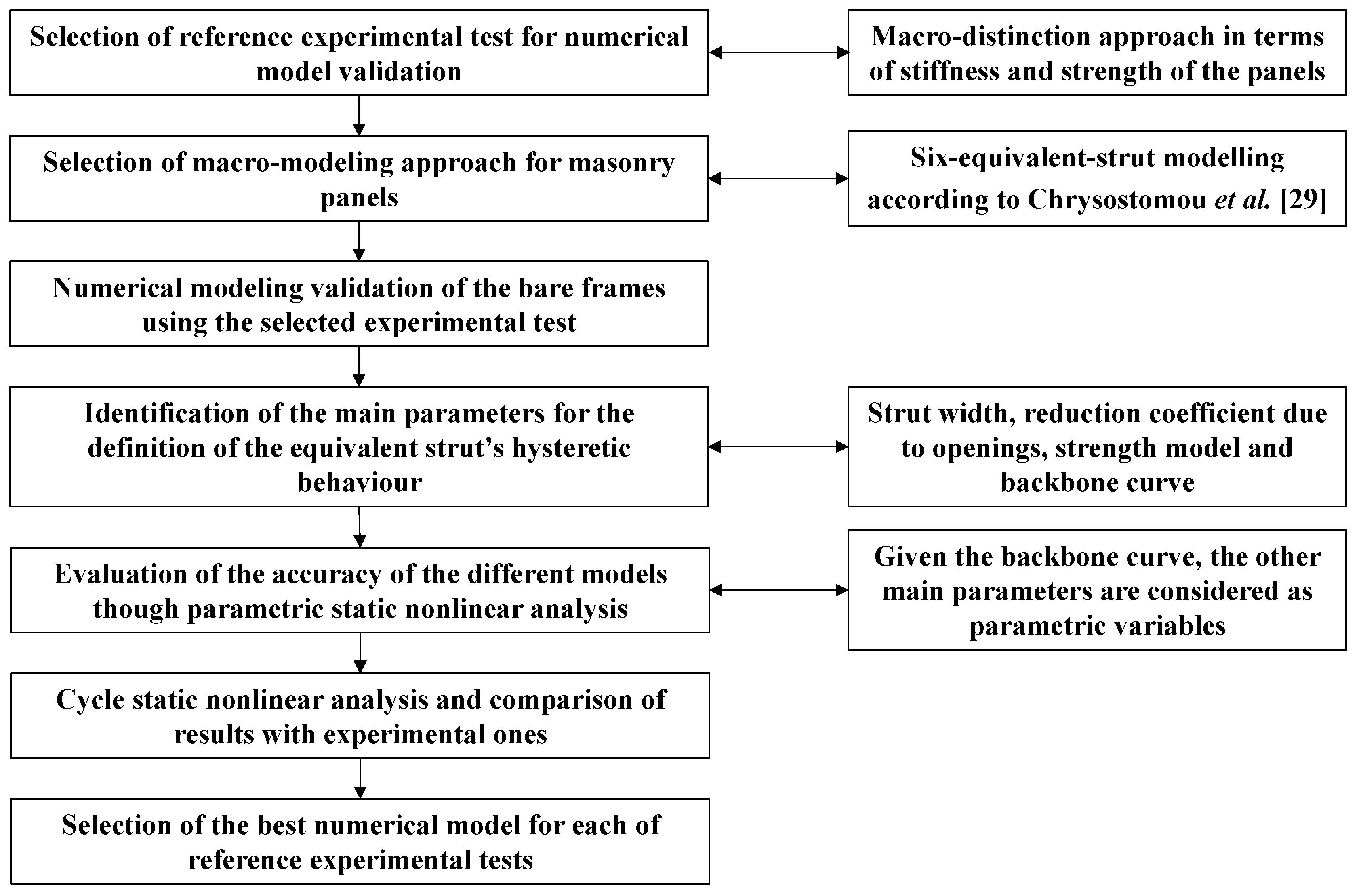
2. Research Methodology
- Classify the typologies of masonry infills representative of the typical configurations adopted in Italy and other Mediterranean countries based on experimental data. The results of in-plane pseudostatic cyclic tests, carried out on single-storey and single-bay masonry-infilled RC frames, with and without openings, are analysed to identify the most common configurations. The masonry infill typologies are defined based on the masonry infills strength; this parameter was found to be the most suitable for future analytical applications on the seismic performance assessment of masonry infilled RC building portfolios accounting for infill variability [20];
- Define the most accurate numerical modelling approach to simulate the experimental lateral response of masonry-infilled RC frames. If the frames are not designed according to modern seismic provisions, then the numerical modelling should also be able to account for the typical phenomena observed in existing buildings, such as material and geometrical nonlinearity, bar slippage, joint flexibility, behaviour of poorly detailed and non-ductile RC frame members, among others;
- The main parameters affecting the numerical modelling of masonry infills are investigated. The hysteretic behaviour of the masonry infill panel depends on several parameters, such as the strut width, reduction coefficient to account for the presence of openings, failure mechanism model or formulations to define the backbone curve. For each of these parameters, the main formulations available in the literature are analysed to undertake parametric static pushover analysis;
- In order to define the most reliable numerical modelling approach, for each masonry infill typology identified in point 1, a set of parametric static pushover analyses are carried out combining all the formulations defined in point 3. The comparison is then performed in terms of capacity curves. In specific, given a selected backbone curve, different models could be employed to predict the failure mechanism and strut width; hence, for each of the selected strength models, the impact and accuracy of all the strut width equations is investigated and the same procedure is repeated for all the parameters investigated;
- Finally, once the most accurate numerical model is identified, cyclic pushover analysis (according to the loading protocol used for the corresponding testing) is performed to investigate the effectiveness of the proposed numerical models, when it comes to predicting the hysteretic response of the masonry infilled RC frames.
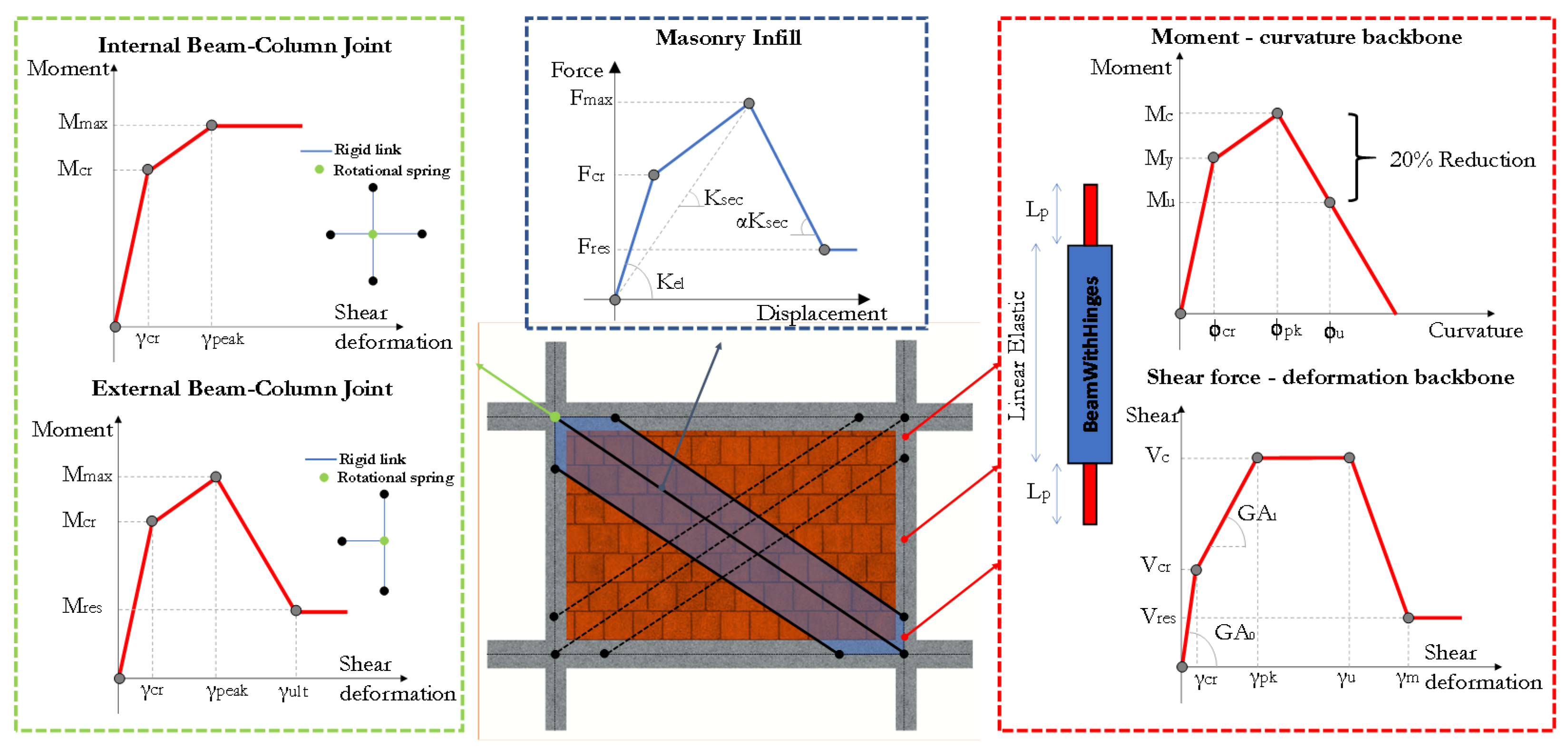
3. Numerical Modelling and Structural Response of Masonry Infills
3.1. Macro-Modelling Approaches
3.1.1. Approaches for Full-Height Solid Infill Panels
3.1.2. Approaches for Infill Panels with Openings
3.1.3. Infill-Frame Contact Length
3.2. Failure Modes and Backbone Curves
- Surrounding frame: this failure mode is associated with the development of plastic hinges in the RC elements. The collapse mechanism could be due to flexure, shear, beam-column joint failure or high axial load. The location of flexural plastic hinges is strongly related to the features of the frame-infill systems and may occur (very rarely) in the beams and/or columns, where the maximum bending moment demand is reached. Shear failure in the columns is due to high shear stress in the contact length zones and depends on the amount of transverse reinforcement, concrete strength and efficiency of the concrete confinement. Especially in existing RC frames built according to old codes and prescriptions, the panel may cause wide diagonal cracks along the beam-columns joints and, consequently, their failure. Finally, even though it is very rare, due to concrete strength effect, an axial failure might take place as consequence of high axial load transmitted by a truss mechanism;
- Shear sliding: this mode produces horizontal sliding failure through several bed joints; it is related to the aspect ratio of the masonry units and the infill panel, as well as the poor mechanical properties of the mortar in the bed joints. This failure mode is associated with a strong frame and weak mortar joints. The crack pattern starts a few courses beneath the upper loaded corner and continues along the diagonal direction until reaching the centre of the panel, where finally the cracks spread horizontally;
- Corner crushing: this failure mode produces compression failure (due to a biaxial compression state) of the infill panels with crushing of the units near the beam-column joints; later on, it might produce out-of-plane (OOP) failure and eventually collapse. It normally occurs if the contact length is very or the contact length may be reduces increasing the lateral displacement and the infilled frame is characterized by weak infill panel, combined with strong columns/beams and weak joints;
- Diagonal compression: it is another compression failure mode however, in contrast with the previous failure mode, the crushing of masonry units appears in the centre of the panel. This failure mode is due to the geometry of panel, that is, when the infill is slender, with a subsequent OOP failure;
- Diagonal tension or cracking: this is related to the failure of the compressed diagonal strut, which consists of widespread cracking along the panel; as highlighted in El-Dakhakhni [15], this failure mode occurs when the RC frame is weak or is characterized by weak joints and strong elements, combined with a rather strong infill.
4. Classification of Masonry Infills According to Test Data
5. Numerical Modelling Results and Validation with Experimental Data
5.1. Bare Frames
5.2. Masonry-Infilled Frames
6. Discussion and Influence of Modelling Assumptions
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Manfredi, G.; Prota, A.; Verderame, G.M.; De Luca, F.; Ricci, P. Emilia earthquake, Italy: Reinforced concrete buildings response. Bull. Earthq. Eng. 2014, 12, 2275–2298. [Google Scholar] [CrossRef] [Green Version]
- Cardone, D.; Perrone, G. Damage and Loss Estimation of Pre-70 Reinforced Concrete Frame Buildings with FEMA P-58: A Case Study. J. Earthq. Eng. 2016, 21, 23–61. [Google Scholar] [CrossRef]
- El-Dakhakhni, W.W.; Hamid, A.A.; Hakam, Z.H.R.; Elgaaly, M. Hazard mitigation and strengthening of unreinforced masonry walls using composites. Compos. Struct. 2006, 73, 458–477. [Google Scholar] [CrossRef]
- Calvi, G.M.; Bolognini, D. Seismic response of RC frames infilled with weakly reinforced masonry panels. J. Earthq. Eng. 2001, 5, 153–185. [Google Scholar] [CrossRef]
- Morandi, P.; Hak, S.; Magenes, G. Performance-based interpretation of in-plane cyclic tests on RC frames with strong masonry infills. Eng. Struct. 2018, 156, 503–521. [Google Scholar] [CrossRef]
- Cavaleri, L.; Di Trapani, F. Cyclic response of masonry infilled RC frames: Experimental results and simplified modeling. Soil Dyn. Earthq. Eng. 2014, 65, 224–242. [Google Scholar] [CrossRef]
- Verderame, G.M.; Ricci, P.; Del Gaudio, C.; De Risi, M.T. Experimental tests on masonry infilled gravity- and seismic-load designed RC frames. In Proceedings of the 16th International Brick and Block Masonry Conference—IB2MAC, Padova, Italy, 26–30 June 2016. [Google Scholar]
- Ricci, P.; Di Domenico, M.; Verderame, G.M. Experimental assessment of the in-plane/out-of-plane interaction in unreinforced masonry infill walls. Eng. Struct. 2018, 173, 960–978. [Google Scholar] [CrossRef]
- Hak, S.; Morandi, P.; Magenes, G. Out-of-plane experimental response of strong masonry infills. In Proceedings of the Advances in Civil Engineering 17 Proceedings of the Presented at the Second European Conference on Earthquake Engineering and Seismology—2ECEES, Istanbul, Turkey, 25–29 August 2014. [Google Scholar]
- Akhoundi, F.; Vasconcelos, G.; Lourenço, P.; Silva, B. Out-of-plane response of masonry infilled RC frames: Effect of workamnship and opening. In Proceedings of the 16th International Brick and Block Masonry Conference—IB2MAC, Padova, Italy, 26–30 June 2016. [Google Scholar]
- Furtado, A.; Rodrigues, H.; Arˆede, A.; Varum, H. Effect of the panel width support and columns axial load on the infill masonry walls out-of-plane behavior. J. Earth. Eng. 2018, 24, 653–681. [Google Scholar] [CrossRef]
- Ricci, P.; Di Domenico, M.; Verderame, G.M. Experimental investigation of the influence of slenderness ratio and of the in-plane/out-of-plane interaction on the out-of plane strength of URM infill walls. Constr. Build. Mater. 2018, 191, 507–522. [Google Scholar] [CrossRef]
- De Luca, F.; Morciano, E.; Perrone, D.; Aiello, M.A. MID1.0: Masonry Infilled RC Frame Experimental Database. In Proceedings of the Italian Concrete Days, Rome, Italy, 27–28 October 2016; Lecture Notes in Civil Engineering. Springer: Cham, Switzerland, 2016; Volume 10. [Google Scholar]
- De Risi, M.T.; Del Gaudio, C.; Ricci, P.; Verderame, G.M. In-plane behaviour and damage assessment of masonry infills with hollow clay bricks in RC frames. Eng. Struct. 2018, 168, 257–275. [Google Scholar] [CrossRef]
- Crisafulli, F.J.; Carr, A.J.; Park, R. Analytical modelling of infilled frame structures—A general review. Bull. N. Z. Soc. Earthq. Eng. 2000, 33, 30–47. [Google Scholar]
- Asteris, P.G. Finite Element Micro-Modeling of Infilled Frames. Elect. J. Struct. Eng. 2008, 8, 1–11. [Google Scholar]
- Asteris, P.G.; Cotsovos, D.M.; Chrysostomou, C.Z.; Mohebkhah, A.; Al-Chaar, G.K. Mathematical micromodeling of infilled frames: State of the art. Eng. Struct. 2013, 56, 1905–1921. [Google Scholar] [CrossRef]
- Bertoldi, S.H.; Decanini, L.D.; Gavarini, C. Telai tamponati soggetti ad azioni sismiche, un modello semplificato: Confronto sperimentale e numerico. In Proceedings of the 6 Convegno Nazionale L’ingegneria sismica in Italia, Perugia, Italy, 13–15 October 1993. [Google Scholar]
- Panagiotakos, T.B.; Fardis, M.N. Seismic response of infilled RC frames structures. In Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996. [Google Scholar]
- Mucedero, G.; Perrone, D.; Monteiro, R. Nonlinear static characterisation of masonry-infilled RC building portfolios accounting for variability of infill properties. Bull. Earth. Eng. (under review).
- Rivero, C.E.; Walker, W.H. An analytical study of the interaction of frames and infill masonry walls. In Proceedings of the 11th World Conference on Earthquake Engineering, San Francisco, CA, USA, 21–28 July 1984. [Google Scholar]
- Mehrabi, A.; Shing, P.B. Finite Element Modeling of Masonry-Infilled RC Frames. ASCE J. Struct. Eng. 1997, 123, 604–613. [Google Scholar] [CrossRef]
- Lotfi, H.R.; Shing, P.B. Interface model applied to fracture of masonry structures. ASCE J. Struct. Eng. 1994, 120, 63–80. [Google Scholar] [CrossRef]
- Lourenço, P.B. Computational Strategies for Masonry Structures. Ph.D. Thesis, Delft University, Delft, The Netherlands, 1996. [Google Scholar]
- Al-Chaar, G.L.; Mehrabi, A. Constitutive Models for Nonlinear Finite Element Analysis of Masonry Prisms and Infill Walls, No. ERDC/CERL-TR-08-19; Engineer Research and Development Center, Construction Engineering Research Lab: Champaign, IL, USA, 2008. [Google Scholar]
- Holmes, M. Steel frames with brickwork and concrete filling. In Proceedings of the Institution of Civil Engineers, London, UK, August 1961; Volume 19, pp. 473–478. Available online: https://www.icevirtuallibrary.com/doi/abs/10.1680/iicep.1961.11305?journalCode=jpric (accessed on 12 October 2020).
- Furtado, A.; Rodrigues, H.; Arêde, A.; Varum, H. Simplified macro-model for infill masonry walls considering the out-of-plane behaviour. Earth. Eng. Struct. Dyn. 2015, 45, 507–524. [Google Scholar] [CrossRef]
- Crisafulli, F.J. Seismic Behaviour of Reinforced Concrete Structures with Masonry Infills. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 1997. [Google Scholar]
- Chrysostomou, C.Z.; Gergely, P.; Abel, J.F. A six-strut model for nonlinear dynamic analysis of steel infilled frames. Int. J. Struct. Stab. Dyn. 2002, 2, 335–353. [Google Scholar] [CrossRef]
- El-Dakhakhni, W.W.; Elgaaly, M.; Hamid, A.A. Three-strut model for concrete masonry infilled steel frames. J. Struct. Eng. 2003, 129, 177–185. [Google Scholar] [CrossRef]
- Polyakov, S.V. Masonry in Framed Buildings (An Investigation into the Strength and Stiffness of Masonry Infilling); Translated from the Russian by Cairns, G.L., Moscow, 1956; National Lending Library for Science and Technology: Boston Spa, Yorkshire, 1963. [Google Scholar]
- Kligner, R.E.; Bertero, V.V. Eartquake Resistance of Infilled Frames. Reinforced Concrete Structures Subjected to Wind and Eartquakes Forces. Am. Concr. Inst. 1980, 63, 1–25. [Google Scholar]
- Stafford Smith, B. Behaviour of square infilled frames. ASCE J. Struct. Div. 1966, 92, 381–403. [Google Scholar]
- FEMA 306. Evaluation of Earthquake Damaged Concrete and Masonry Wall Buildings—Basic Procedures Manual; Federal Emergency Management Agency: Washington, DC, USA, 1998.
- Leuchars, J.M.; Scrivener, J.C. Masonry Infill Panels Subjected to Cyclic In-Plane Loading. In Proceedings of the South Pacific Regional Earthquake Engineering Conference, Wellington, New Zealand, 13–15 May 1975. [Google Scholar]
- Mainstone, R.J. Supplementary Note on the Stiffnesses and Strengths of Infilled Frames; Building Research Establishment, Building Research Station: Watford, UK, 1974. [Google Scholar]
- Liauw, T.C.; Kwan, K. Nonlinear behaviour of non-integral infilled frames. Comput. Struct. 1984, 18, 551–560. [Google Scholar]
- Decanini, L.D.; Fantin, G.E. Modelos Simplificados de la Mamposteria Incluida en Porticos. Caractreisticas de Rigidez y Resistencia Lateral en Estrado Limite (in spanish). J. Argent. Ing. Estruct. 1987, 2, 817–836. [Google Scholar]
- Paulay, T.; Priestley, M.J. Seismic Design of Reinforced Concrete and Masonry Buildings; John Wiley & Sons: New York, NY, USA, 1992. [Google Scholar]
- Papia, M.; Cavaleri, L.; Fossetti, M. Infilled frames: Developments in the evaluation of the stiffening effect of infills. Struct. Eng. Mech. 2003, 16, 675–693. [Google Scholar] [CrossRef]
- Benjamin, J.E.; Williams, H.A. The behaviour of one story brick shear walls. ASCE J. Struct. Div. 1958, 84, 1–30. [Google Scholar]
- Imai, H.; Miyamoto, M. Seismic behavior of reinforced masonry walls with small opening. In Proceedings of the 5 Jornadas Chilenas de Sismología e Ingeniería Antisísmica, Santiago, Chile, 7–11 August 1989; Volume 2, pp. 965–973. [Google Scholar]
- Tasnimi, A.A.; Mohebkhah, A. Investigation on the behavior of brick-infilled steel frames with openings, experimental and analytical approaches. Eng. Struct. 2011, 33, 968–980. [Google Scholar] [CrossRef]
- Asteris, P.G. Lateral stiffness of brick masonry infilled plane frames. ASCE J. Struct. Eng. 2003, 129, 1071–1079. [Google Scholar] [CrossRef] [Green Version]
- Dawe, J.L.; Seah, C.K. Lateral load resistance of masonry panels in flexible steel frames. In Proceedings of the 8th International Brick and Block Masonry Conference, Dublin, Ireland, 19–21 September 1988; Elsevier Applied Science: London, UK, 1988; Volume 2, pp. 606–616. [Google Scholar]
- Decanini, L.D.; Liberatore, L.; Mollaioli, F. Strength and stiffness reduction factors for infilled frames with openings. Earthq. Eng. Eng. Vib. 2014, 13, 437–454. [Google Scholar] [CrossRef]
- Al-Chaar, G. Evaluating Strength and Stiffness of Unreinforced Masonry Infill Structures. Rep. No. ERDC/CERL TR-02-1; U.S. Army Corps of Engineers: Champaign, IL, USA, 2002. [Google Scholar]
- Asteris, P.G.; Antoniou, S.T.; Sophianopoulos, D.S.; Chrysostomou, C.Z. Mathematical macromodeling of infilled frames: State of the art. J. Struct. Eng 2011, 137, 1508–1517. [Google Scholar] [CrossRef]
- CEN Eurocode 6 EN 1996-1-1. Design of Masonry Structures, Part 1—1. Common Rules for Reinforced and Unreinforced Masonry Structures; European Committee for Standardisation: Brussels, Belgium, 2004. [Google Scholar]
- CEN Eurocode 8 EN 1998-1. Design of Structures for Earthquake Resistance, Part 1. General Rules, Seismic Actions and Rules for Buildings; European Committee for Standardisation: Brussels, Belgium, 2004. [Google Scholar]
- Sassun, K.; Sullivan, T.J.; Morandi, P.; Cardone, D. Characterising the In-Plane Seismic Performance of Infill Masonry. Bull. N. Z. Soc. Earthq. Eng. 2015, 49, 98–115. [Google Scholar] [CrossRef]
- De Sortis, A.; Bazzurro, P.; Mollaioli, F.; Bruno, S. Influenza delle tamponature sul rischio sismico degli edifici in calcestruzzo armato. In Proceedings of the ANIDIS Conference L’ingegneria Sismica in Italia, Pisa, Italy, 10–14 June 2007. (In Italian). [Google Scholar]
- Pires, F.; Carvalho, E.C. The behaviour of infilled reinforced concrete frames under horizontal cyclic loading. In Proceedings of the 10th World Conference on Earthquake Engineering, Madrid, Spain, 9–24 July 1992. [Google Scholar]
- Stylianides, K.C. Cyclic Behaviour of Infilled R/C Frames. Brick and Block Masonry (8th IBMAC); Elsevier Applied Science: London, UK, 1988; Volume 2, pp. 792–799. [Google Scholar]
- Hak, S.; Morandi, P.; Magenes, G.; Sullivan, T. Damage control for clay masonry infills in the design of RC frame structures. J. Earth. Eng. 2012, 16, 1–35. [Google Scholar] [CrossRef]
- Ministero delle Infrastrutture e dei Trasporti. Circolare n.7 C.S.LL.PP 21 January 2019 “Istruzioni per L’applicazione dell’Aggiornamento delle Norme Tecniche per le Costruzioni di cui al Decreto Ministeriale 17 gennaio 2018”; Ministero delle Infrastrutture e dei Trasporti: Rome, Italy, 2018. (In Italian)
- NPR 9998:2017. Assessment of Structural Safety of Buildings in Case of Erection, Reconstruction and Disapproval—Basic Rules for Seismic Actions: Induced Earthquakes; Nederlands Normalisatie Instituut: Delft, The Netherlands, 2017. [Google Scholar]
- Mohammad, A.F.; Faggella, M.; Gigliotti, R.; Spacone, E. Probabilistic seismic response sensitivity of nonlinear frame bending-shear and infill model parameters for an existing infilled reinforced concrete structure. In Proceedings of the Twelfth International Conference on Computational Structures Technology, Naples, Italy, 2–5 September 2014; Topping, B.H.V., Iványi, P., Eds.; Civil-Comp Press: Stirlingshire, UK, 2014. [Google Scholar]
- CEN Eurocode 2 EN 1992-1-1. Design of Concrete Structures, Part 1—1 General Rules and Rules for Buildings; ECS: Brussels, Belgium, 2004. [Google Scholar]
- McKenna, F.; Fenves, G.L.; Scott, M.H. Open System for Earthquake Engineering Simulation; University of California: Berkeley, CA, USA, 2000; Available online: http://opensees.berkeley.edu (accessed on 13 October 2020).
- O’Reilly, G.J.; Sullivan, T.J. Modeling techniques for the seismic assessment of the existing Italian RC Frame Structures. J. Earth. Eng. 2017, 23, 1262–1296. [Google Scholar] [CrossRef]
- O’Reilly, G.J. Performance-Based Seismic Assessment and Retrofit of Existing RC Frame Buildings in Italy. Ph.D. Thesis, IUSS, Pavia, Italy, 2016. [Google Scholar]
- Scott, M.H.; Fenves, G.L. Plastic hinge integration methods for force-based beam–column elements. ASCE J. Struct. Eng. 2006, 132, 244–252. [Google Scholar] [CrossRef]
- Zimos, D.K.; Mergos, P.E.; Kappos, A.J. Shear hysteresis model for reinforced concrete elements including the post-peak range. In Proceedings of the 5th Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete Island, Greece, 25–27 May 2015. [Google Scholar]
- Bosi, A.; Marazzi, F.; Pinto, A.; Tsionis, G. The L’Aquila (Italy) Earthquake of 6 April 2009: Report and Analysis from a Field Mission; EUR—Scientific and Technical Research Reports; Publications Office of the European Union: Luxembourg, 2011. [Google Scholar]
- Pampanin, S.; Magenes, G.; Carr, A. Modelling of shear hinge mechanism in poorly detailed RC beam column joints. In Proceedings of the FIB Symp. Concrete Structures in Seismic Regions, Federation International du Beton, Athens, Grece, 6–8 May 2003. [Google Scholar]
- Braga, F.; Gigliotti, R.; Laterza, M. R/C Existing Structures with Smooth Reinforcing Bars: Experimental Behaviour of Beam-Column Joints Subject to Cyclic Lateral Loads. Open Constr. Build. Technol. J. 2009, 3, 52–67. [Google Scholar] [CrossRef] [Green Version]
- Melo, J.; Varum, H.; Rossetto, T.; Costa, A. Cyclic response of RC beam-column joints reinforced with plain bars: An experimental testing campaign. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Beschi, C.; Riva, P.; Metelli, G.; Meda, A. HPFRC Jacketing of Non Seismically Detailed RC Corner Joints. J. Earth. Eng. 2014, 19, 25–47. [Google Scholar] [CrossRef]
- CEN Eurocode 1 EN 1991-1-1. Actions on Structures, Part 1—1 General Actions—Densities, Selfweight, Imposed Loads for Buildings; ECS: Brussels, Belgium, 2002. [Google Scholar]
- NTC08. Norme Tecniche per le Costruzioni, D.M. 14 Gennaio 2008; S.O. No. 30 alla G.U. del 4.2.2008, No. 29; Ministero delle Infrastrutture: Rome, Italy, 2008. (In Italian) [Google Scholar]
- Morandi, P.; Hak, S.; Magenes, G. Comportamento sismico delle tamponature in laterizio in telai in c.a.: Analisi numeriche su edifici ed implicazioni progettuali. In Proceedings of the XIV Convegno ANIDIS, Bari, Italy, 18–22 September 2011. [Google Scholar]
- Jeon, J.S.; Park, J.H.; DesRoches, R. Seismic fragility of lightly reinforced concrete frames with masonry infills. Earthq. Eng. Struct. Dyn. 2015, 44, 783–1803. [Google Scholar] [CrossRef]













| Diagonal Infill Strut Width According to Different Models | ||
|---|---|---|
| Bertoldi et al. [18] | (Stafford Smith [33]) : elastic modulus of masonry (inclined direction) : elastic modulus of concrete : elastic modulus of concrete : thickness of the infill : strut width of the infill : diagonal length of the infill | |
| Paulay and Priestley [39] | ||
| Holmes [26] | ||
| Liauw and Kwan [37] | ||
| Mainstone [36] | ||
| Stafford Smith [33] | ||
| Decanini and Fantin [38] | Uncracked: Cracked: | |
| Papia et al. [40] | c, β: accounting for Poisson’s ratio k: accounting for vertical load z: geometrical parameter | According to Papia et al. [40] L: frame centreline span h: centreline storey height. : column cross section : beam cross section |
| Reduction Coefficients of Stiffness and Strength due to the Presence of Openings | ||
| Dawe and Seah [45] | : opening length : opening height : infill length : infill height | |
| Imai and Miyamoto [42] | ||
| Tasnini and Mohebkhan [43] | ||
| Decanini et al. [46] | ||
| Asteris [44] | ||
| Infill Strength According to Different Models | ||
|---|---|---|
| Paulay and Priesley [39] | Sliding shear failure: Compression failure: | : initial shear strength of bed-joints; friction coefficient (; : according to (Stafford Smith [33]. |
| Bertoldi et al. [18] | Compression at the centre: Compression at the corners: Sliding shear failure: Diagonal cracking: | : shear strength under diagonal compression; compression strength in vertical direction; : initial shear strength of bed-joints; vertical stress; : according to Stafford Smith [33]. : according to Bertoldi et al. [18]. |
| EC6/EC8 [49,50] | : initial shear strength of bed-joints; vertical stress. | |
| FEMA 306 [34] | Sliding shear failure: Compression failure: Diagonal cracking failure: | : initial shear strength of bed-joints; : cracking strength of masonry; friction coefficient (; vertical stress; compression strength in horizontal direction of masonry; compression strength in vertical direction; : according to Mainstone [36]; : according to Stafford Smith [33]. |
| Backbone Curve according to Different Models | ||
| Bertoldi et al. [18] | cracking strength: residual strength: elastic stiffness: softening-to-peak stiffness: | : peak strength, defined according to the selected infill strength model; secant stiffness according to Mainstone [36]. |
| Panagiotakos and Fardis [19] | cracking strength: residual strength elastic stiffness softening-to-peak stiffness | : cracking strength, defined according to the selected infill strength model; α: [0.5%, 10%]; β: [1%, 2%]; secant stiffness according to Mainstone [36]. |
| De Risi et al. [14] | cracking strength: residual strength: elastic stiffness: secant stiffness: softening-to-peak stiffness: | : peak strength, defined according to the selected infill strength model; secant stiffness according to Mainstone ( [36]. |
| Sassun et al. [51] | Backbone according to Bertoldi et al. [18] modified with prefixed values of drift capacity ϑ (or equivalently in terms of strain capacity ε [55]) | DS1 (Operational): DS2 (Damage Limitation): DS3 (Life Safety): DS4 (Ultimate): |
| References | Type | Macro Classification | tw [mm] | Ewv [MPa] | Ewh [MPa] | Gw [MPa] | fwv [MPa] | fwlat [MPa] | fwu [MPa] |
|---|---|---|---|---|---|---|---|---|---|
| Calvi and Bolognini [4] | 1 | Weak | 80 | 1873 | 991 | 1089 | 2.02 | 1.18 | 0.44 |
| Hak et al. [55] | 2 | Weak-Medium | 240 | 1873 | 991 | 1873 | 1.5 | 1.11 | 0.25 |
| Hak et al. [55] | 3 | Medium-Strong | 300 | 3240 | 1050 | 1296 | 3.51 | 1.5 | 0.3 |
| Morandi et al. [5] | 4 | Medium-Strong | 350 | 5299 | 494 | 2120 | 4.64 | 1.08 | 0.359 |
| Cavaleri and Di Trapani [6] | 5 | Strong | 150 | 6401 | 5038 | 2547 | 8.66 | 4.18 | 1.07 |
| Type | Macro Classification | Strut Width | Reduction Coefficient | Failure Mechanism | Backbone Curve |
|---|---|---|---|---|---|
| 1 | Weak | Bertoldi et al. [18] | - | Bertoldi et al. [18] | Sassun et al. [51] (modified) |
| 2 | Weak-Medium | Bertoldi et al. [18] | - | Bertoldi et al. [18] | Sassun et al. [51] (modified) |
| 3 | Medium-Strong | Bertoldi et al. [18] | - | Bertoldi et al. [18] | Sassun et al. [51] (modified) |
| 4 | Medium-Strong | Mainstone [36] | Decanini et al. [46] | Paulay and Priestley [39] | Bertoldi et al. [18] |
| 5 | Strong | Mainstone [36] | - | Paulay and Priestley [39] | Bertoldi et al. [18] |
| Numerical Modelling ID | Backbone Curve | Strut Width | Strength Model | μ | σ |
|---|---|---|---|---|---|
| Model-1 | Bertoldi et al. [18] | Mainstone [36] | Bertoldi et al. (fwu/2) [18] | 1.00 | 2.46 |
| Model-2 | Bertoldi et al. [18] | Stafford Smith [33] | Bertoldi et al. (fwu/2) [18] | 1.02 | 2.64 |
| Model-3 | Bertoldi et al. [18] | Bertoldi et al. [18] | Paulay and Priestley [39] | 0.86 | 1.29 |
| Model-4 | Bertoldi et al. [18] | Mainstone [36] | Paulay and Priestley (fwu/2) [39] | 1.00 | 2.46 |
| Model-5 | Bertoldi et al. [18] | FEMA 306 [34] | Bertoldi et al. [18] | 0.93 | 1.35 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mucedero, G.; Perrone, D.; Brunesi, E.; Monteiro, R. Numerical Modelling and Validation of the Response of Masonry Infilled RC Frames Using Experimental Testing Results. Buildings 2020, 10, 182. https://doi.org/10.3390/buildings10100182
Mucedero G, Perrone D, Brunesi E, Monteiro R. Numerical Modelling and Validation of the Response of Masonry Infilled RC Frames Using Experimental Testing Results. Buildings. 2020; 10(10):182. https://doi.org/10.3390/buildings10100182
Chicago/Turabian StyleMucedero, Gianrocco, Daniele Perrone, Emanuele Brunesi, and Ricardo Monteiro. 2020. "Numerical Modelling and Validation of the Response of Masonry Infilled RC Frames Using Experimental Testing Results" Buildings 10, no. 10: 182. https://doi.org/10.3390/buildings10100182
APA StyleMucedero, G., Perrone, D., Brunesi, E., & Monteiro, R. (2020). Numerical Modelling and Validation of the Response of Masonry Infilled RC Frames Using Experimental Testing Results. Buildings, 10(10), 182. https://doi.org/10.3390/buildings10100182








