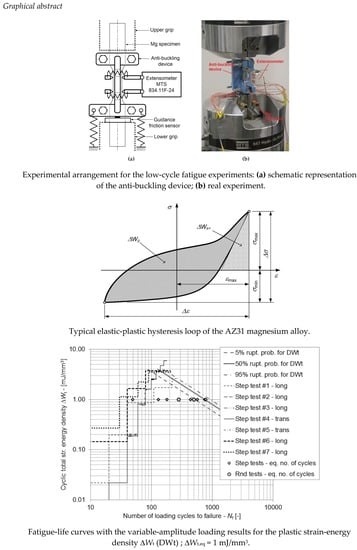
A Durability Prediction for the Magnesium Alloy AZ31 based on Plastic and Total Energy
Abstract
:1. Introduction
2. Materials and Methods
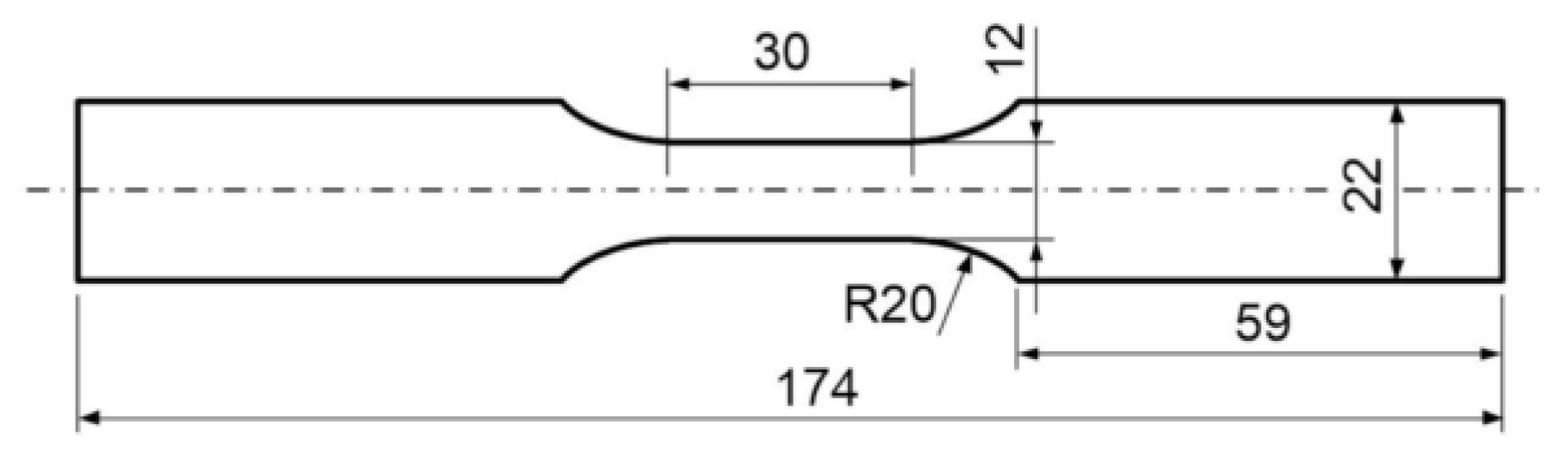
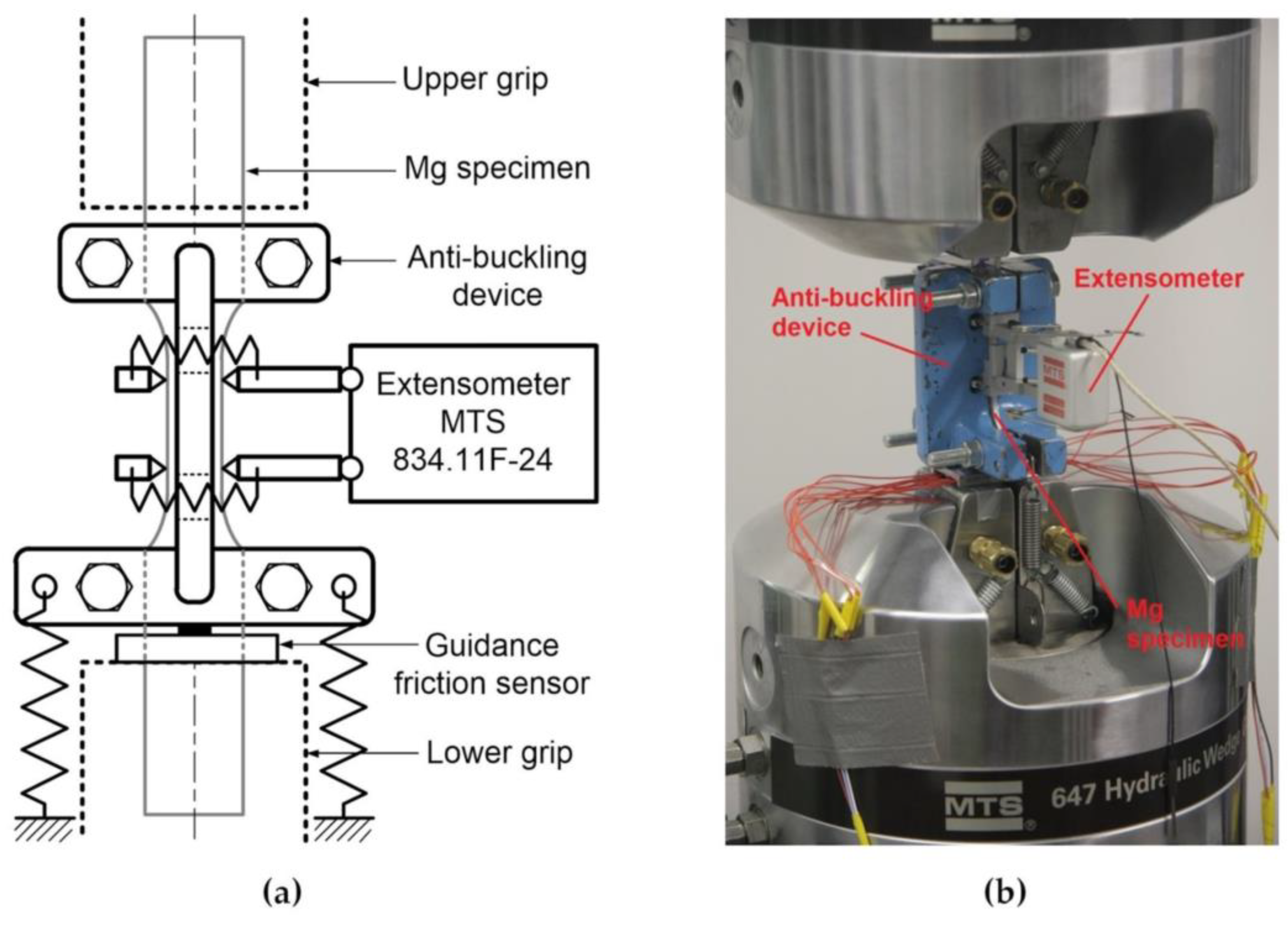
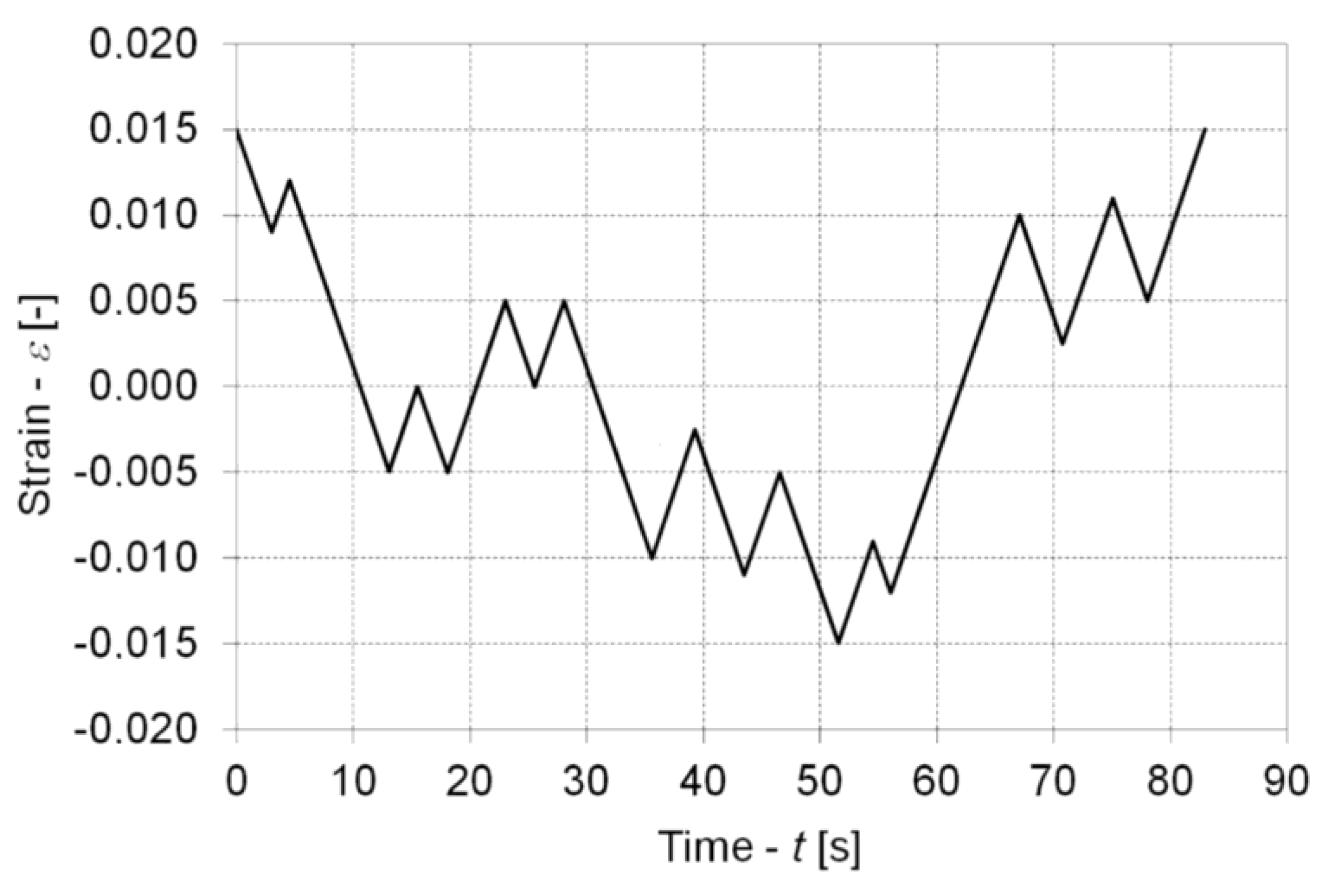
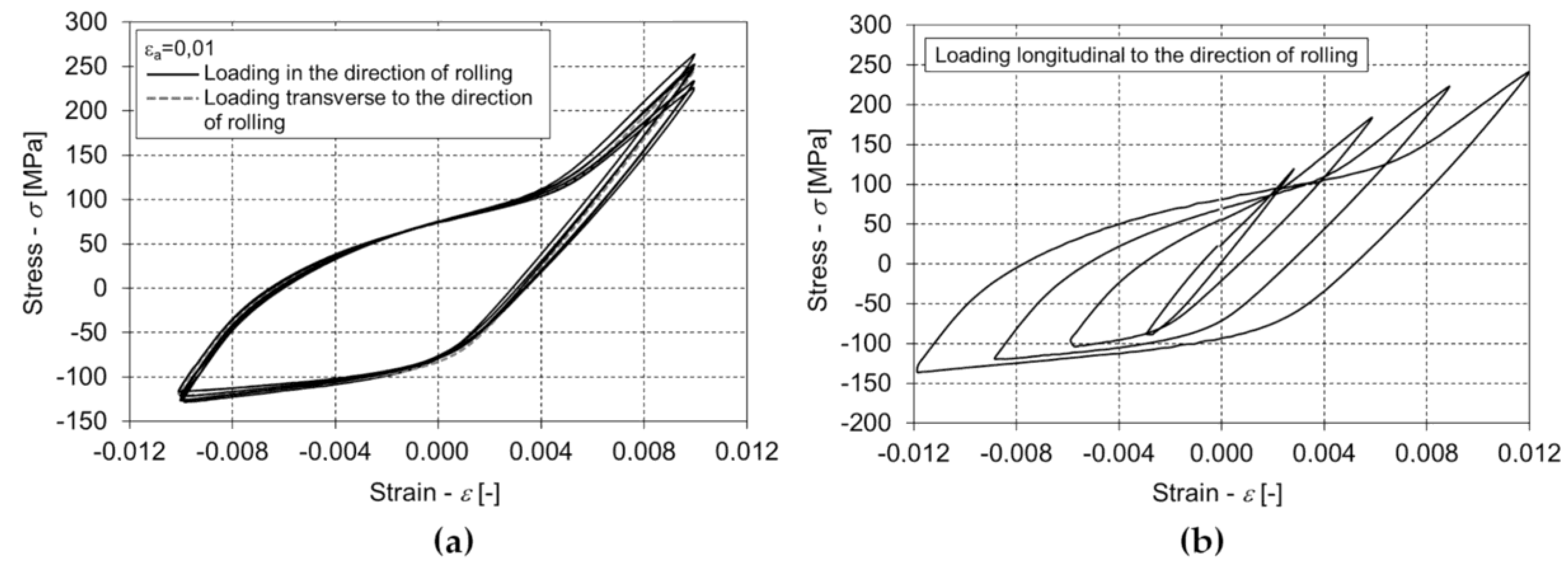
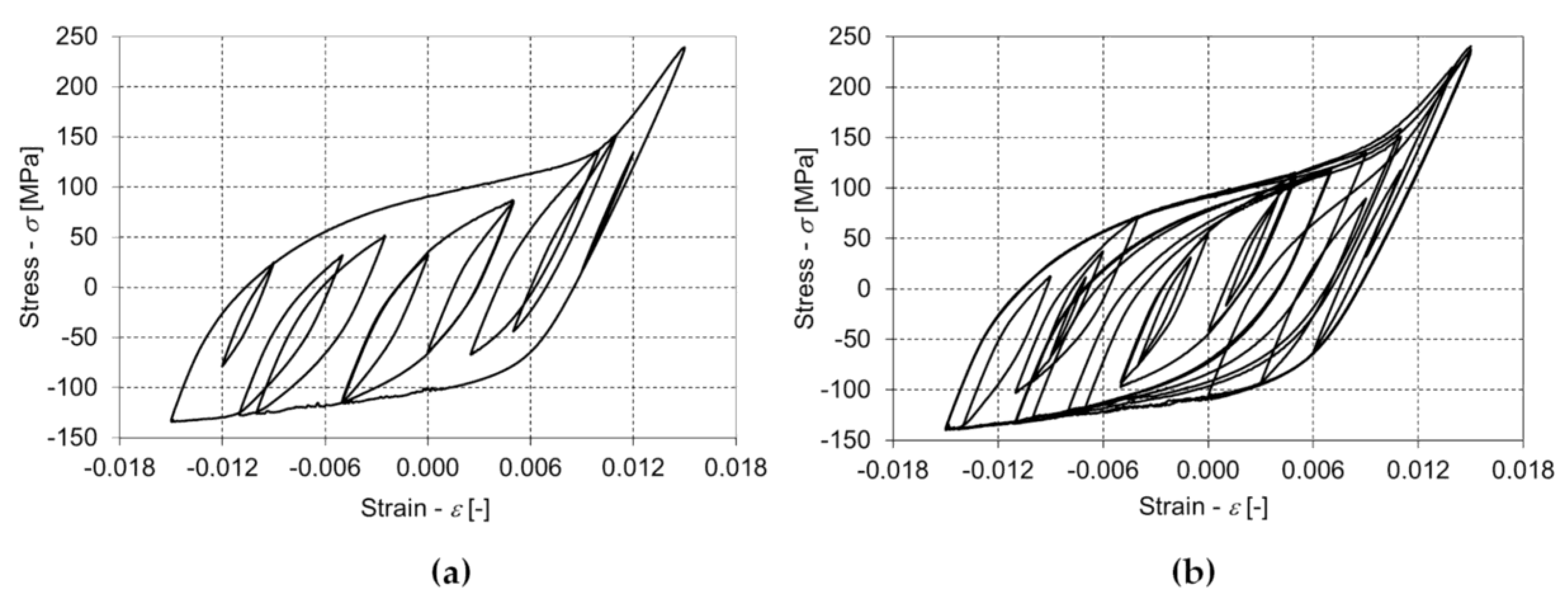
2.1. The Magnesium Alloy AZ31 and the Low-Cycle Fatigue Experiments
2.2. Calculating the Fatigue Damage on the Basis of the Strain-Energy Density
2.3. Modeling the Strain-Energy-Density Fatigue-Life Curve and Its Scatter
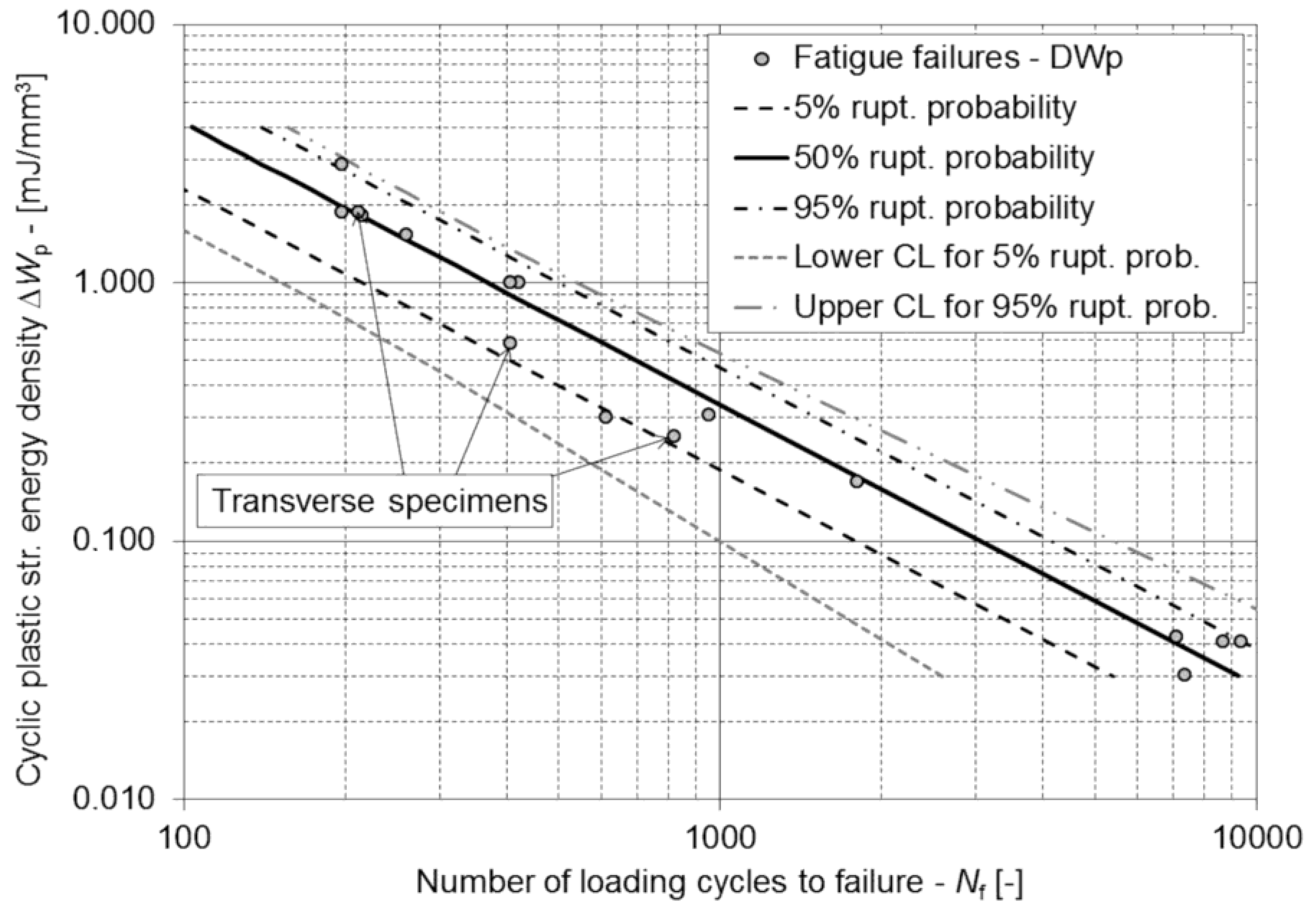
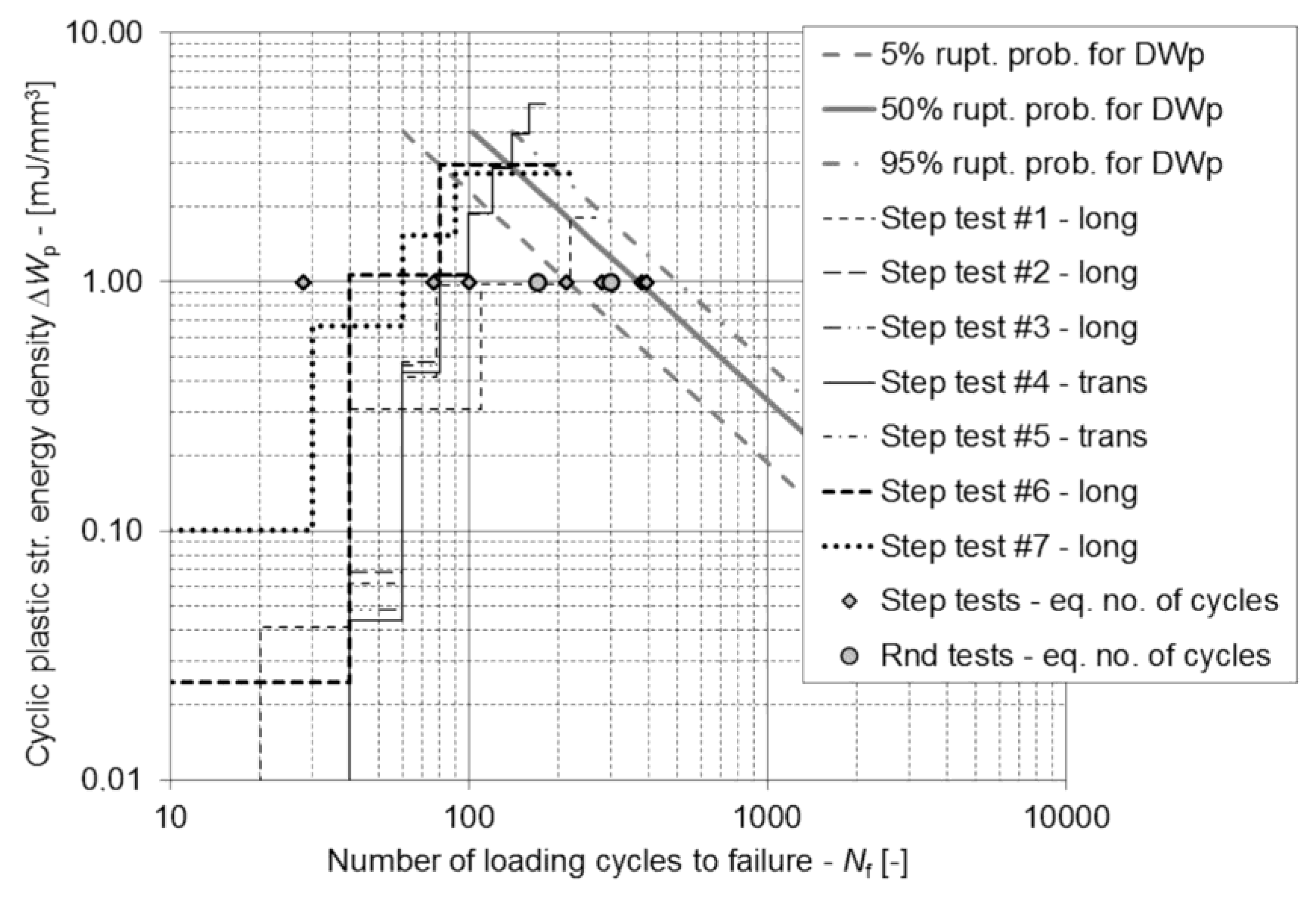
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Klemenc, J.; Seruga, D.; Nagode, M. Plastic and total energy as the basis of durability prediction for magnesium alloy AZ31. In Proceedings of the 27th International Conference on Processing and Fabrication of Advanced Materials (PFAM-XXVII), Jönköping, Sweden, 27–29 May 2019. [Google Scholar]
- Lukac, P.; Kocich, R.; Greger, M.; Padalka, O.; Szaraz, Z. Microstructure of AZ31 and AZ61 Mg alloys prepared by rolling and ECAP. Kovove Mater. 2007, 45, 115–120. [Google Scholar]
- Kocich, R.; Kursa, M.; Macháčková, A. FEA of Plastic Flow in AZ63 Alloy during ECAP Process. Acta Phys. Pol. A 2012, 122, 581–587. [Google Scholar] [CrossRef]
- Smith, K.N.; Watson, P.; Topper, T.H. A stress-strain function for the fatigue of metals. J. Mater. 1970, 5, 767–778. [Google Scholar]
- Ellyin, F.; Kujawski, D. Plastic strain energy in fatigue failure. J. Press. Vessel Technol. 1984, 106, 342–347. [Google Scholar] [CrossRef]
- Golos, K.M.; Ellyin, F. A total strain energy density theory for cumulative fatigue damage. J. Press. Vessel. Technol. 1988, 110, 36–41. [Google Scholar] [CrossRef]
- Golos, K.M. Multiaxial fatigue criterion with mean stress effect. Int. J. Press. Vessel Pip. 1996, 69, 263–266. [Google Scholar] [CrossRef]
- Koh, S.K. Fatigue damage evaluation of high pressure tube steel using cyclic strain energy density. Int J Press. Vessel Pip. 2002, 79, 791–798. [Google Scholar] [CrossRef]
- Park, S.H.; Hong, S.G.; Lee, B.H.; Bang, W.; Lee, C.S. Low-cycle fatigue characteristics of rolled Mg-3Al-1Zn alloy. Int. J. Fatigue 2010, 32, 1835–1842. [Google Scholar] [CrossRef]
- Dallmeier, J.; Huber, O.; Saage, H.; Eigenfeld, K. Uniaxial cyclic deformation and fatigue behavior of AK50 magnesium alloy sheet metals under symmetric and asymmetric loadings. Mater. Des. 2015, 70, 10–30. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.M.; Liu, Z.H.; Chen, J. Investigation of uniaxial low-cycle fatigue failure behavior of hot-rolled AZ91 magnesium alloy. Int. J. Fatigue 2013, 48, 122–132. [Google Scholar] [CrossRef]
- Roostaei, A.; Pahlevanpour, A.; Behravesh, S.B.; Jahed, H. On the definition of elastic strain energy density in fatigue modeling. Int. J. Fatigue 2019, 121, 237–242. [Google Scholar] [CrossRef]
- Zhu, S.P.; Lei, Q.; Huang, H.Z.; Yang, Y.J.; Peng, W. Mean stress effect correction in strain-energy based fatigue life prediction of metals. Int. J. Damage Mech. 2017, 26, 1219–1241. [Google Scholar] [CrossRef]
- Jahed, H.; Varvani-Farahani, A.; Noban, M.; Khalaji, I. An energy-based fatigue life assessment model for various metallic materials under proportional and non-proportional loading conditions. Int. J. Fatigue 2007, 29, 647–655. [Google Scholar] [CrossRef]
- Park, J.; Nelson, D. Evaluation of an energy-based approach and a critical plane approach for predicting constant amplitude multiaxial fatigue life. Int. J. Fatigue 2000, 22, 23–39. [Google Scholar] [CrossRef]
- Ince, A. A generalized mean stress correction model based on distortional strain energy. Int. J. Fatigue 2017, 104, 273–282. [Google Scholar] [CrossRef]
- Ince, A. A mean stress correction model for tensile and compressive mean stress fatigue loadings. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 939–948. [Google Scholar] [CrossRef]
- Park, S.H.; Hong, S.-G.; Lee, B.H.; Lee, C.S. Fatigue life prediction of rolled AZ31 magnesium alloy using an energy-based model. Int. J. Mod. Phys. B 2008, 22, 5503–5508. [Google Scholar] [CrossRef]
- Letcher, T.; Shen, M.H.H.; Scott-Emuakpor, O.; George, T.; Cross, C. An energy-based critical fatigue life prediction method for Al6061-T6. Fatigue Fract. Eng. Mater. Struct. 2012, 35, 861–870. [Google Scholar] [CrossRef]
- Ozaltun, H.; Shen, M.H.H.; George, T. An energy based fatigue life prediction framework for in-service structural components. Exp. Mech. 2011, 51, 707–718. [Google Scholar] [CrossRef]
- Kabir, S.M.H.; Yeo, T. Evaluation of an energy-based fatigue approach considering mean stress effects. J. Mech. Sci. Tech. 2014, 28, 1265–1275. [Google Scholar] [CrossRef]
- Jahed, H.; Albinmousa, J. Multiaxial behaviour of wrought magnesium alloys – A review and suitability of energy-based fatigue life model. Theor. Appl. Fract. Mech. 2014, 73, 97–108. [Google Scholar] [CrossRef]
- Wang, C.; Luo, T.J.; Zhou, J.X.; Yang, Y.S. Anisotropic cyclic deformation behaviour of extruded ZA81M magnesium alloy. Int. J. Fatigue 2017, 96, 178–184. [Google Scholar] [CrossRef]
- Dallmeier, J.; Denk, J.; Huber, O.; Saage, H.; Eigenfeld, K. A phenomenological stress-strain model for wrought magnesium alloys under elastoplastic strain-controlled variable amplitude loading. Int. J. Fatigue 2015, 80, 306–323. [Google Scholar] [CrossRef]
- Klemenc, J.; Fajdiga, M. Estimating S-N curves and their scatter using a differential ant-stigmergy algorithm. Int. J. Fatigue 2012, 43, 90–97. [Google Scholar] [CrossRef]
- Klemenc, J. Influence of fatigue–life data modelling on the estimated reliability of a structure subjected to a constant-amplitude loading. Reliab. Eng. Syst. Saf. 2015, 142, 238–247. [Google Scholar] [CrossRef]
- Klemenc, J.; Fajdiga, M. Joint estimation of E-N curves and their scatter using evolutionary algorithms. Int. J. Fatigue 2013, 56, 42–53. [Google Scholar] [CrossRef]
- Goodfellow – your global supplier for materials. Available online: https://www.goodfellow.com/catalogue/GFCat2H.php?ewd_token=28skhnCrjhctQ0VRfphfvd6PniE1Vm&n=wFtvXD7C9WyVocNzf9Oip0qnk2dP9i&ewd_urlNo=GFCat2L3&Head=MG01 (accessed on 30 August 2019).
- Seruga, D.; Nagode, M.; Klemenc, J. Measurement of stress-strain response during cyclic tests. In Proceedings of the 27th International Conference on Processing and Fabrication of Advanced Materials (PFAM-XXVII), Jönköping, Sweden, 27–29 May 2019. [Google Scholar]
- Seruga, D.; Nagode, M.; Klemenc, J. Eliminating friction between flat specimens and an antibuckling support during cyclic tests using a simple sensor. Meas. Sci. Technol 2019. [Google Scholar] [CrossRef]





| Test No. | Specimen Orientation | Strain Levels - εa (Number Of Loading Cycles in Blocks - N) | ||||
|---|---|---|---|---|---|---|
| 1 | longitudinal | () | () | () | () | ( rest) |
| 2 | longitudinal | () | () | ()1 | ||
| 3 4 5 6 | longitudinal longitudinal transversal transversal | () | () | () | ()1 | |
| 7 | longitudinal | () | () | ( rest) | ||
| 8 | longitudinal | () | () | () | ( rest) | |
| Parameter | Plastic Strain-Energy Density Model f(Nf |ΔWp) | Total Strain-Energy Density Model f(Nf |ΔWt) |
|---|---|---|
| Parameter C for 50% probability of rupture | 625.41 | 176.45 |
| Parameter C for η | 679.26 | 183.83 |
| Parameter m | 1.089 | 0.781 |
| Parameter β | 4.833 | 6.986 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klemenc, J.; Seruga, D.; Nagode, M. A Durability Prediction for the Magnesium Alloy AZ31 based on Plastic and Total Energy. Metals 2019, 9, 973. https://doi.org/10.3390/met9090973
Klemenc J, Seruga D, Nagode M. A Durability Prediction for the Magnesium Alloy AZ31 based on Plastic and Total Energy. Metals. 2019; 9(9):973. https://doi.org/10.3390/met9090973
Chicago/Turabian StyleKlemenc, Jernej, Domen Seruga, and Marko Nagode. 2019. "A Durability Prediction for the Magnesium Alloy AZ31 based on Plastic and Total Energy" Metals 9, no. 9: 973. https://doi.org/10.3390/met9090973
APA StyleKlemenc, J., Seruga, D., & Nagode, M. (2019). A Durability Prediction for the Magnesium Alloy AZ31 based on Plastic and Total Energy. Metals, 9(9), 973. https://doi.org/10.3390/met9090973