Abstract
Multivariable analytical models provide a descriptive (albeit approximate) mathematical relationship between a set of independent variables and one or more dependent variables. The current work develops an analytical model that extends a design of experiments for the leaching of manganese from marine nodules, using sulfuric acid (H2SO4) in the presence of iron-containing tailings, which are both by-products of conventional copper extraction. The experiments are configured to address the effect of time, particle size, acid concentration, Fe2O3/MnO2 ratio, stirring speed and temperature, under typical industrial conditions. The recovery of manganese has been modeled using a first order differential equation that accurately fits experimental results, noting that Fe2O3/MnO2 and temperature are the most critical independent variables, while the particle size is the least influential (under typical conditions). This study obtains representative fitting parameters, that can be used to explore the incorporation of Mn recovery from marine nodules, as part of the extended value chain of copper sulfide processing.
1. Introduction
Deposits of ferromanganese (Fe–Mn) are present in all of the world′s oceans, on marine ridges and plateaus, where currents have released sediments for ages [1]. They originate from the accumulation of iron and manganese oxides, deposited over volcanic and sedimentary rocks that act as substrates [2]. These deposits were discovered for the first time in the Arctic Ocean of Siberia in 1968 [3]. They form concentric layers of oxide and intermetallic compounds scattered in the sedimentary zone of the seabed [4]. They are located in the Pacific, Atlantic and Indian Oceans, at depths of 4,500 m, reaching reserves that range between 1 and 3 billion tons [5].
There is generally a shortage of high-grade sources of manganese on the planet′s surface [4,6], which has driven the search for alternatives. The marine nodules represent an alternative that has economic potential [7], having an average Mn grade of approximately 24% [8]. The nodules may be further processed so that the resulting manganese may to be incorporated into steel alloys [9].
In addition, the nodules represent large reserves of other metals, such as Cu, Ni, Co and Fe, along with potentially high concentrations of Te, Ti, Pt and rare earth elements [10].
For the dissolution of MnO2 in acidic media, it is necessary to maintain the system in potential and pH ranges of −0.4 to 1.4 V and −2 to 0.1, respectively [9]. This indicates that the use of a reducing agent is necessary to extract Mn from marine nodules [11]. Due to its low cost, abundance and good results in previous studies [4,12,13,14,15,16,17], Fe is an attractive additive for the reductive leaching of manganese nodules. Toro et al. [4] performed leaching tests of marine nodules at the laboratory level by adding smelting slags with high Fe2O3 contents, where it was discovered that Fe2O3, when reacting with H2SO4, forms FeSO4, which is a good reducing agent of MnO2, achieving extractions of 68% of the manganese in 5 min. In addition, in the same study previously mentioned, it was concluded that an MnO2/Fe2O3 ratio of 1/2 is suitable for dissolving MnO2 in an acidic medium. Later, Toro et al. [16] conducted tests using the Fe2O3 present in tailings, obtaining even better results than with the slag, as the tailings were observed to be even more reactive. When exposed to H2SO4, Fe2O3 generates ferrous sulfate (FeSO4), that acts as a reducing agent for MnO2, as described by the following reactions:
Fe2O3(s) + 3 H2SO4(aq) = Fe2(SO4)3(s) + 3 H2O(l)
Fe3O4(s) + 4H2SO4(l) = FeSO4(aq) + Fe2(SO4)3(s) + 4 H2O(l)
Fe2(SO4)3(s) + 6 H2O(l) = 2 Fe(OH)3(s) + 3 H2SO4(l)
2 FeSO4(aq) + 2 H2O(l) = 2 Fe(s) + 2 H2SO4(l) + O2(g)
2 FeSO4(aq) + 2 H2SO4(aq) + MnO2(s) = Fe2(SO4)3(s) + 2 H2O(l) + MnSO4(aq)
The leaching process has been modeled by many authors. However, the validation, verification and implementation of these models are difficult, since there is uncertainty about the operating conditions and parameters of the leaching model [18]. Mellado et al. [19] developed analytical models that describe leaching, and are based upon the Bernoulli Equation, using constitutive equations for different levels, particles and heaps, over different scales of operation. Further work by Mellado et al. [20] extends beyond heap leaching. These more recent models are based on first-order ordinary differential equations in time, incorporating constitutive relationships derived from a combination of ordinary and partial differential equations and other relations, in combination with empirical observations. The resulting models are nonetheless simple (elegant), and are thus especially well-suited for the analysis, design, control and optimization of leaching processes [21]. Another way to describe the mechanisms that govern the leaching process was developed by Yaghobi et al. [22] through non-linear differential equations. Alternatively, Hernández et al. used a non-linear mixed-integer programming approach [23].
Other leaching studies have used the multilevel factorial design (MFD) of experiments, generating a predictive quadratic exponential regression model [24]. Liu et al. developed a leaching experiment in the laboratory, and presented an analytical model of the concentration of the leaching solution [25] using a neural network; they established a prediction model of the concentration of the leaching solution, whose maximum error was less than 2%. Other works studied the recovery of nickel and the dissolution of iron using the response surface methodology [26] to find the optimal leaching conditions for nickel laterite ores [27]. In similar work, Botane et al. [28] used linear regression to generate analytical models of continuous bioleaching in stirred tank reactors. Simulation experiments of the leaching process were carried out by Mellado et al. [29], based on analytical models and Monte Carlo simulation, concluding that there is a significant influence of the uncertainty in the input variables.
The analytical models have the advantage of being tractable, featuring algebraic parameters that can be readily fit to operational data, and extrapolated to apply them to similar operational situations. These mathematical models can be applied with enough reliability in order to technically and economically evaluate initial projects of small and medium-scale mining, where economic resources are scarce, and mineralogical knowledge is limited.
Only a few studies have tested the reduction of manganese nodules within a sulfuric acid medium, in the presence of iron-containing tailings or slag [4,16,17]. Toro et al. [16] related Mn recovery to the MnO2/Fe2O3 ratio and the sulfuric acid concentration, but only under time-independent (static) conditions. This approach involved a three-level factorial design, ignoring the potential impact of particle size distribution and agitation velocity, which are likely to have a dynamic effect upon Mn recovery. Interestingly, iron-containing tailings have been observed to be more reactive than smelter slags within the context of leaching [30]. Moreover, the previous work of Toro et al. [4,16,17] considered neither temperature, nor its interactions with other critical variables that control the effect of iron-containing reducing agents on the leaching of Mn from MnO2 [12,13,14,15].
Finally, the objective of this work is to demonstrate the development of an analytical model based on a first order differential equation, which represents the extraction of manganese from marine nodules, under the set of parameters sampled, together with a factorial design of experiments and a multiple regression model. This approach is indeed capable of representing complex systems through relatively simple analytical models.
2. Materials and Methods
2.1. Manganese Nodule Samples
The marine nodules used in this work were the same as those previously used in Toro et al. [16]. The sample was analyzed by means of atomic emission spectrometry by induction-coupled plasma (ICP-AES), developed in the applied geochemistry laboratory of the Department of Geological Sciences of the Universidad Católica del Norte (Chile). They were composed of 15.96% Mn and 0.45% Fe, where the Mn presented in the nodules has been found to be 29.85% MnO2.
2.2. Tailings Samples
The tailings used for the present investigation were the same as those used in Toro et al. [16]. The methods used to determine its chemical and mineralogical composition are the same as those used with the manganese nodule. Table 1 shows the chemical species determined by QEMSCAN (Quantitative Evaluation of Minerals by SCANning). There were several phases that contained iron (mainly magnetite (58.52%) and hematite (4.47%)), while the content of Fe was estimated at 41.90%.

Table 1.
Mineralogical composition of tailings, as determined by QEMSCAN.
2.3. Reagents and Leaching Parameters
The sulfuric acid used for the leaching tests was obtained from Sigma-Aldrich Chemie, GmbH (Schnelldorf, Germany), with 95–97% purity, and a density of 1.84 kg/L. The leaching tests were carried out in a 50 mL glass reactor with a 0.01 solid/liquid ratio. A total of 200 mg of Mn nodules were maintained in suspension with the use of a 5-position magnetic stirrer (IKA ROS, CEP 13087-534, Campinas, Brazil). The parameters studied were time, particle size, acid concentration, F2O3/MnO2 ratio, stirring speed and temperature.
2.4. Experimental Design
Design of experiments (DOE) can be used to investigate the simultaneous effects of input variables (factors) on an output variable (response). 729 experimental tests were carried out, studying the effects of time, particle size, sulfuric acid (H2SO4) concentration, Fe2O3/MnO2 ratio, agitation speed, and temperature on Mn recovery. The operational parameters considered in the factorial design of six factors and three levels by factor are presented in the Table 2.

Table 2.
Experimental values for operational parameters.
The general form of the experimental model is described by:
in which x1 corresponds to time, x2 to the size of the particle, x3 to the concentration of sulfuric acid, x4 to the ratio Fe2O3/MnO2, x5 to the speed of agitation and x6 to the temperature.
2.5. Adjustment of an Analytical Model
The following is the analytical model for leaching [31,32], where it is considered that leaching behavior could generally be modeled using a system of first order equations as shown in Equation (1):
In which y is a dynamic quantity, such as concentration or recovery , is the kinetic constant and is the order of the reaction. The subscript τ represents a time scale that depends on the phenomenon to be modeled. To solve Equation (1), an initial condition is required, introducing a delay. The general solution for this problem for (see Mellado et al. [19], for example), is given by:
is the maximum expected recovery in operational conditions, and ω is the delay of the reaction.
Dixon and Hendrix [31,33] considered that the leaching phenomenon occurs at different scales (mainly related to characteristics such as heap height) and time, and that different phenomena participate in the leaching process. However, the current study assumes only a single time scale, with the understanding that additional time scales could be developed as a result of future experiments. Modifying the equation to fit a model to the experimental design, it is possible to explain the recovery of manganese from marine nodules according to the equation:
For simplicity, has been taken to be the maximum expected recovery of ore under the experimental conditions (laboratory conditions), and g(X) is a polynomial equation, which is explained by the independent variables’ time, particle size, sulfuric acid and potentially other variables, such as temperature and the Fe2O3/MnO2 ratio. The analytical model presented in Equation (3) can be expressed as:
To ensure the fulfillment of an initial condition for the development of the first-order differential equation, the exponent must be directly proportional to the difference between time and delay ω, which is,. Adjusting a multiple linear regression model for the function presented in terms of y, and considering the proportionality of g(y), the recovery of Mn can be modeled by the equation:
in which,
The substituting Equation (6) into Equation (3) gives:
Considering that H2SO4 concentration μ and stirring speed v are proportional to Mn recovery, and that the square of particle size r is inversely linear to Mn recovery [32,34], the following model is proposed:
in which λ and β are mathematical fitting parameters.
The goodness of fit statistics used to study the fitted model are: The mean absolute deviation (MAD, Equation (9)), a statistic that measures the dispersion of forecast error; the mean square error (MSE, Equation (10)), measuring of error dispersion, which penalizes the periods where the error is larger than the average value; and the absolute average percentage error (MAPE, Equation (11)), a statistic that gives the deviation in percentage terms, calculating the averages of the absolute values between the real value and fitted (forecast) values [35].
R software environment (Version 3.6.0) [36] was used to develop the experimental design transformations presented in Equations (4) and (5), while the version 18 of Minitab software [37] was used to adjust a multiple linear regression of the independent variables (excluding time) to the mathematical model presented in Equation (6).
3. Results and Discussion
3.1. Multilinear Regression of Experimental Data
The analysis of this experimental data shows that only three factors have a significant effect upon the response variable (Figure 1). The factor with the greatest impact is the Fe2O3/MnO2 ratio.
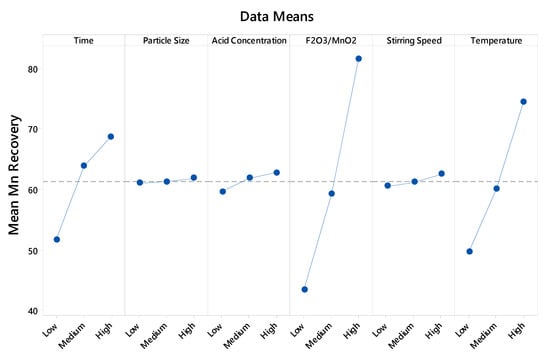
Figure 1.
Graph of the main effects for manganese extraction (Figure created with Minitab 18).
Considering only the static variables (i.e., excluding the time x1), to the following quadratic regression considers only and , which are the Fe2O3/MnO2 ratio and the temperature, respectively. This, response variable y is hence approximated by:
A subsequent Analysis of Variance (ANOVA) analysis indicates that the regression is adequate to represent the extraction of Mn under the range of parameters sampled, including an R2 value of 85.93% (Figure 2); this implies that 85.93% of the total variation is represented by Equation (12). The ANOVA analysis further confirms the significance of the model, as the computed F score greatly exceeds the 95% level, 539.87 > 1.9512. Equivalently, the p-value (Figure 3) of the model represented by the equation also indicates that the model is statistically significant.

Figure 2.
R2 Statistic (Figure created with Minitab 18).

Figure 3.
Statistic p (Figure created with Minitab 18).
The value of the predictive R2 is 85.35%, indicating that the model has a good capacity for predicting responses to new observations. The small difference between the value of R2 and the predictive R2 is an indicator that the model is not over fitted. Moreover, the residuals fall relatively close to the adjusted normal distribution line, and it is not possible to reject the normality assumption with α = 0.05. Equation (12) will be further developed in the following section. Figure 4 describes the full quadratic behavior, in which all three critical variables are maintained: Time, MnO2/Fe3O4 and temperature. As expected, the manganese recovery increases with the passage of time. Figure 4a,b show that Fe2O3/MnO2 and temperature have a qualitatively similar effect over time, although the former is more pronounced. Indeed, Figure 4c confirms the scalable equivalence between Fe2O3/MnO2 and temperature, showing recovery as an approximately linear function, increasing in both temperature and Fe2O3/MnO2. Nonetheless, the full dynamic behavior is not well-represented by such a function, as it does not capture the asymptotic tendency of reaction kinetics [30,31].
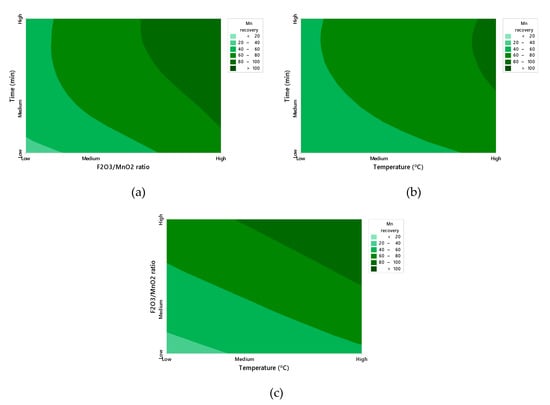
Figure 4.
Contour plot of the independent variables Fe2O3/MnO2 ratio, Time (a); Temperature, Time (b); and Temperature, Fe2O3/MnO2 ratio (c) in Mn recovery (%) (Figures created with Minitab 18).
3.2. Fitting of the Exponential Function
Substituting Equation (12) into Equation (5), the following equation represents the exponent of Equation (3):
Thus, the recovery is given by:
In which r, v and µ are taken to be 64 µm, 600 rpm and 0.5 M, respectively. The fitting of parameters results in the following expression, which is supported by the goodness of fit statistics of Table 3.

Table 3.
Statistics of analytical model of the leaching of marine nodules.
On the other hand, Figure 5 shows that the assumption of residue normality is reached, because the p-value of the test is greater than the level of significance (p > 0.05), indicating that the mathematical model is relatively accurate in representing the experimental design, although some points away from the line imply a distribution with outliers.
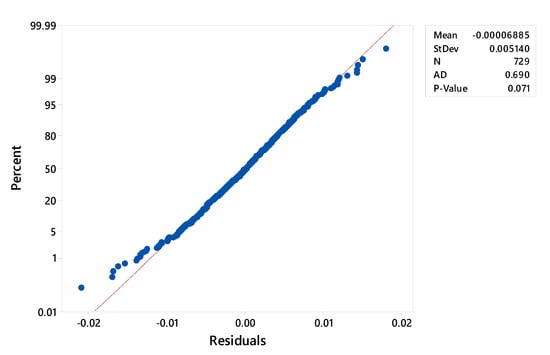
Figure 5.
Probability plot of residuals values (Figure created with Minitab 18).
Following the example of Saldaña et al. [38], Equation (15) can be incorporated into a simulation framework that can quantify benefits, potentially leading to pilot tests and the implementation of nodule processing within copper producing regions [16,17]. Furthermore, there are several mines in Chile that have significant reserves of so-called black copper minerals, including Spence Mine, Mina Sur, Lomas Bayas Mine and Centinela Mine [39]. These black copper minerals are usually excluded from extraction processes, and may be stockpiled for long periods without being treated [40]. These minerals exhibit a semi-crystalline or amorphous structure that is similar to that of manganese nodules; indeed, the extraction of Cu from these black minerals by conventional hydrometallurgical processes is affected by this structure [41], and is therefore comparable to the extraction of Mn from marine nodules. The development of novel methods that may be applicable to both black copper minerals and manganese nodules is thus especially relevant for the Chilean context. Experiment-based parameterization of analytical models is a necessary step to developing alternative leaching methods for potential feeds that are not currently being treated.
4. Conclusions
In the present investigation, the fitting of an analytical model for the extraction of manganese from marine nodules results in an exponential function, which considers the most critical static variables: MnO2/Fe2O3 ratio and temperature. This work demonstrates the use of laboratory-level testing for the extraction of manganese from marine nodules in an acid medium at different temperatures, and with the use of iron-containing tailings, as a potential step toward industrialization of the process. This source of iron is indeed an effective reducing agent. Future experimental work will be carried out to characterize the constants in Equation (15) better through more batch tests, and to represent the effects of different time scales [30,32]. From the modelling perspective, future work will be to simulate an industrial implementation, and test potential operational responses to feed variations and related risks [38].
On the other hand, the form of developing an analytical model can be extended to other scales of time, and can be modified according to the kinetics that describe or dominate the operation. The Dixon and Hendrix′s model [31,33] was used to identify the dimensionless times, but the fit to experimental design can be applied to other models proposed within the literature, considering operational scales how pile height [18,19,20,29]. The generation of analytical models to represent complex processes such as mineral leaching could be used for analysis, scale-up, and in optimization tasks, given that they capture the essence of the process to be modeled, they are rapid and relatively precise, and could be used to predict interpolations and extrapolations of Mn recuperation, at least with regard to time, particle size, H2SO4 concentration, Fe2O3/MnO2 ratio, stirring speed and temperature.
Author Contributions
M.S. and N.T. contributed in the methodology, conceptualization and modeling; J.C. and P.H. investigation and resources and E.T. and A.N. contributed with supervision and validation.
Funding
This research received no external funding.
Acknowledgments
The authors are grateful for the contribution of the Scientific Equipment Unit- MAINI of the Universidad Católica del Norte for aiding in generating data by automated electronic microscopy QEMSCAN®, and for facilitating the chemical analysis of the solutions. We are also grateful to the Altonorte Mining Company for supporting this research and providing slag for this study, and we thank Marina Vargas Aleuy, María Barraza Bustos and Carolina Ossandón Cortés of the Universidad Católica del Norte for supporting the experimental tests.
Conflicts of Interest
The authors declare they have no conflict of interest.
References
- Marino, E.; González, F.J.; Somoza, L.; Lunar, R.; Ortega, L.; Vázquez, J.T.; Reyes, J.; Bellido, E. Strategic and rare elements in Cretaceous-Cenozoic cobalt-rich ferromanganese crusts from seamounts in the Canary Island Seamount Province (northeastern tropical Atlantic). Ore Geol. Rev. 2017, 87, 41–61. [Google Scholar] [CrossRef]
- Nishi, K.; Usui, A.; Nakasato, Y.; Yasuda, H. Formation age of the dual structure and environmental change recorded in hydrogenetic ferromanganese crusts from Northwest and Central Paci fi c seamounts. Ore Geol. Rev. 2017, 87, 62–70. [Google Scholar] [CrossRef]
- Lenoble, J.P. Polymetallic Nodules; International Seabed Authority: Kingston, CA, USA, 2000. [Google Scholar]
- Toro, N.; Herrera, N.; Castillo, J.; Torres, C.; Sepúlveda, R. Initial Investigation into the Leaching of Manganese from Nodules at Room Temperature with the Use of Sulfuric Acid and the Addition of Foundry Slag—Part I. Minerals 2018, 8, 565. [Google Scholar] [CrossRef]
- Premchand, P.; Jana, R.K. Processing of Polymetallic Sea Nodules: An Overview. In Proceedings of the Ocean Mining Symposium, Goa, India, 8–10 November 1999; p. 3. [Google Scholar]
- Hein, J.R.; Cherkashov, G.A. Preface for Ore Geology Reviews Special Issue: Marine mineral deposits: New resources for base, precious, and critical metals. Ore Geol. Rev. 2017, 100, 1–2. [Google Scholar] [CrossRef]
- Konstantinova, N.; Cherkashov, G.; Hein, J.R.; Mirão, J.; Dias, L.; Madureira, P.; Kuznetsov, V.; Maksimov, F. Composition and characteristics of the ferromanganese crusts from the western Arctic Ocean. Ore Geol. Rev. 2017, 87, 88–99. [Google Scholar] [CrossRef]
- Sharma, R. Environmental Issues of Deep-Sea Mining. Procedia Earth Planet. Sci. 2015, 11, 204–211. [Google Scholar] [CrossRef]
- Senanayake, G. Acid leaching of metals from deep-sea manganese nodules—A critical review of fundamentals and applications. Miner. Eng. 2011, 24, 1379–1396. [Google Scholar] [CrossRef]
- Usui, A.; Nishi, K.; Sato, H.; Nakasato, Y.; Thornton, B.; Kashiwabara, T. Continuous growth of hydrogenetic ferromanganese crusts since 17 Myr ago on Takuyo-Daigo Seamount, NW Pacific, at water depths of 800–5500 m. Ore Geol. Rev. 2017, 87, 71–87. [Google Scholar] [CrossRef]
- Randhawa, N.S.; Hait, J.; Jana, R.K. A brief overview on manganese nodules processing signifying the detail in the Indian context highlighting the international scenario. Hydrometallurgy 2016, 165, 166–181. [Google Scholar] [CrossRef]
- Kanungo, S.B. Rate process of the reduction leaching of manganese nodules in dilute HCl in presence of pyrite. Part I. Dissolution behaviour of iron and sulphur species during leaching. Hydrometallurgy 1999, 52, 313–330. [Google Scholar] [CrossRef]
- Kanungo, S.B. Rate process of the reduction leaching of manganese nodules in dilute HCl in presence of pyrite. Part II: Leaching behavior of manganese Hydrometallurgy 1999, 52, 331–347. [Google Scholar]
- Zakeri, A.; Bafghi, M.S.; Shahriari, S.; Das, S.C.; Sahoo, P.K.; Rao, P.K. Dissolution kinetics of manganese dioxide ore in sulfuric acid in the presence of ferrous ion. Hydrometallurgy 2007, 8, 22–27. [Google Scholar]
- Bafghi, M.S.; Zakeri, A.; Ghasemi, Z.; Adeli, M. Reductive dissolution of manganese ore in sulfuric acid in the presence of iron metal. Hydrometallurgy 2008, 90, 207–212. [Google Scholar] [CrossRef]
- Toro, N.; Saldaña, M.; Castillo, J.; Higuera, F.; Acosta, R. Leaching of Manganese from Marine Nodules at Room Temperature with the Use of Sulfuric Acid and the Addition of Tailings. Minerals 2019, 9, 289. [Google Scholar] [CrossRef]
- Toro, N.; Saldaña, M.; Gálvez, E.; Cánovas, M.; Trigueros, E.; Castillo, J.; Hernández, P.C. Optimization of Parameters for the Dissolution of Mn from Manganese Nodules with the Use of Tailings in An Acid Medium. Minerals 2019, 9, 387. [Google Scholar] [CrossRef]
- Mellado, M.; Cisternas, L.; Lucay, F.; Gálvez, E.; Sepúlveda, F. A Posteriori Analysis of Analytical Models for Heap Leaching Using Uncertainty and Global Sensitivity Analyses. Minerals 2018, 8, 44. [Google Scholar] [CrossRef]
- Mellado, M.E.; Cisternas, L.A.; Gálvez, E.D. An analytical model approach to heap leaching. Hydrometallurgy 2009, 95, 33–38. [Google Scholar] [CrossRef]
- Mellado, M.E.; Casanova, M.P.; Cisternas, L.A.; Gálvez, E.D. On scalable analytical models for heap leaching. Comput. Chem. Eng. 2011, 35, 220–225. [Google Scholar] [CrossRef]
- Mellado, M.E.; Gálvez, E.D.; Cisternas, L.A. On the optimization of flow rates on copper heap leaching operations. Int. J. Miner. Process. 2011, 101, 75–80. [Google Scholar] [CrossRef]
- Moghaddam, M.Y.; Tonkaboni, S.Z.S.; Noaparast, M.; Ardejani, F.D. A mathematical model to simulate Heap (bio)-leaching process: An exact conceptual model, Homotopy theory and comparative insights with conventional methods. Int. J. Model. Simul Sci. Comput. 2017, 8, 1750018. [Google Scholar] [CrossRef]
- Hernández, I.F.; Ordóñez, J.I.; Robles, P.A.; Gálvez, E.D.; Cisternas, L.A. A Methodology for Design and Operation of Heap Leaching Systems. Miner. Process. Extr. Metall. Rev. 2017, 38, 180–192. [Google Scholar] [CrossRef]
- Fekete, V.; Deconinck, E.; Bolle, F.; van Loco, J. Modelling aluminium leaching into food from different foodware materials with multi-level factorial design of experiments. Food Addit. Contam. Part A Chem. Anal. Control. Exp. Risk Assess. 2012, 29, 1322–1333. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Wu, A.X.; Yin, S.H.; Chen, X. Nonlinear chaotic characteristic in leaching process and prediction of leaching cycle period. J. Cent. South Univ. 2016, 23, 2935–2940. [Google Scholar] [CrossRef]
- Bezerra, M.A.; Santelli, R.E.; Oliveira, E.P.; Villar, L.S.; Escaleira, L.A. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar] [CrossRef] [PubMed]
- Çetintaş, S.; Bingöl, D. Response surface methodology approach to leaching of nickel laterite and evaluation of different analytical techniques used for the analysis of leached solutions. Anal. Methods 2016, 8, 3075–3087. [Google Scholar] [CrossRef]
- Botane, P.; Brochot, S.; D’Hugues, P.; Spolaore, P. Material size distribution in concurrent bio-leaching and precipitation: Experimental procedure and modelling. Hydrometallurgy 2013, 133, 7–14. [Google Scholar] [CrossRef]
- Mellado, M.E.; Gálvez, E.D.; Cisternas, L.A. Stochastic analysis of heap leaching process via analytical models. Miner. Eng. 2012, 33, 93–98. [Google Scholar] [CrossRef]
- Komnitsas, K.; Manousaki, K.; Zaharaki, D. Assessment of reactivity of sulphidic tailings and river sludges. Geochem. Explor. Environ. Anal. 2009, 9, 313–318. [Google Scholar] [CrossRef]
- Dixon, D.G.; Hendrix, J.L. A general model for leaching of one or more solid reactants from porous ore particles. Metall. Trans. B 1993, 24, 157–169. [Google Scholar] [CrossRef]
- Schlesinger, M.; King, M.; Sole, K.; Davenport, W. Extractive Metallurgy of Copper, 5th ed.; Elsevier: Amsterdam, The Netherlands, 2011; ISBN 978-0-08-096789-9. [Google Scholar]
- Dixon, D.G.; Hendrix, J.L. A mathematical model for heap leaching of one or more solid reactants from porous ore pellets. Metall. Trans. B 1993, 24, 1087–1102. [Google Scholar] [CrossRef]
- Free, M. Hidrometallurgy: Fundamentals and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2013; ISBN 978-1-118-23077-0. [Google Scholar]
- Devore, J. Probability & Statistics for Engineering and the Sciences, 8th ed.; Cengage Learning: Boston, MA, USA, 2010; ISBN 0-538-73352-7. [Google Scholar]
- R Core Team. R: The R Project for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Minitab, LLC. Getting Started with Minitab 18; Minitab Inc.: State College, PA, USA, 2017; p. 73. [Google Scholar]
- Saldaña, M.; Toro, N.; Castillo, J.; Hernández, P.; Navarra, A. Optimization of the Heap Leaching Process through Changes in Modes of Operation and Discrete Event Simulation. Minerals 2019, 9, 421. [Google Scholar] [CrossRef]
- Riquelme, R.; Tapia, M.; Campos, E.; Mpodozis, C.; Carretier, S.; González, R.; Muñoz, S.; Fernández-Mort, A.; Sanchez, C.; Marquardt, C. Supergene and exotic Cu mineralization occur during periods of landscape stability in the Centinela Mining District, Atacama Desert. Basin Res. 2018, 30, 395–425. [Google Scholar] [CrossRef]
- Benavente, O.; Hernández, M.C.; Melo, E.; Núñez, D.; Quezada, V.; Zepeda, Y. Copper Dissolution from Black Copper Ore under Oxidizing and Reducing Conditions. Metals 2019, 9, 799. [Google Scholar] [CrossRef]
- Helle, S.; Pincheira, M.; Jerez, O.; Kelm, U. Sequential extraction to predict the leaching potential of refractory. In Proceedings of the Mineral Processing Congress, Sozopol, Bulgaria, 12–16 June 2013; pp. 109–111. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).