Selective Milling and Elemental Assay of Printed Circuit Board Particles for Their Recycling Purpose
Abstract
:1. Introduction
- To further understand selective milling and the effect of different operational parameters (i.e., feed mass, milling time) in the global recovery and selective enrichment of different metals in comparison with the non-metallic fractions when milling PCB particles with the hammer mill;
- To apply non-destructive characterization of heterogeneous feeds and products in order to capture the metal deportment/concentration and liberation/association for optimizing/maximizing the metal recovery by pre-concentration unit operations; and
- To develop a predictive model to estimate the metal recovery as a function of important milling process parameters, i.e., feed mass and milling time.
2. Materials and Methods
2.1. Material Preparation
2.2. Hammer Milling
2.3. Non-Destructive Elemental Assay
Feed Elemental Composition
2.4. Calculation of Metal Recovery and Enrichment
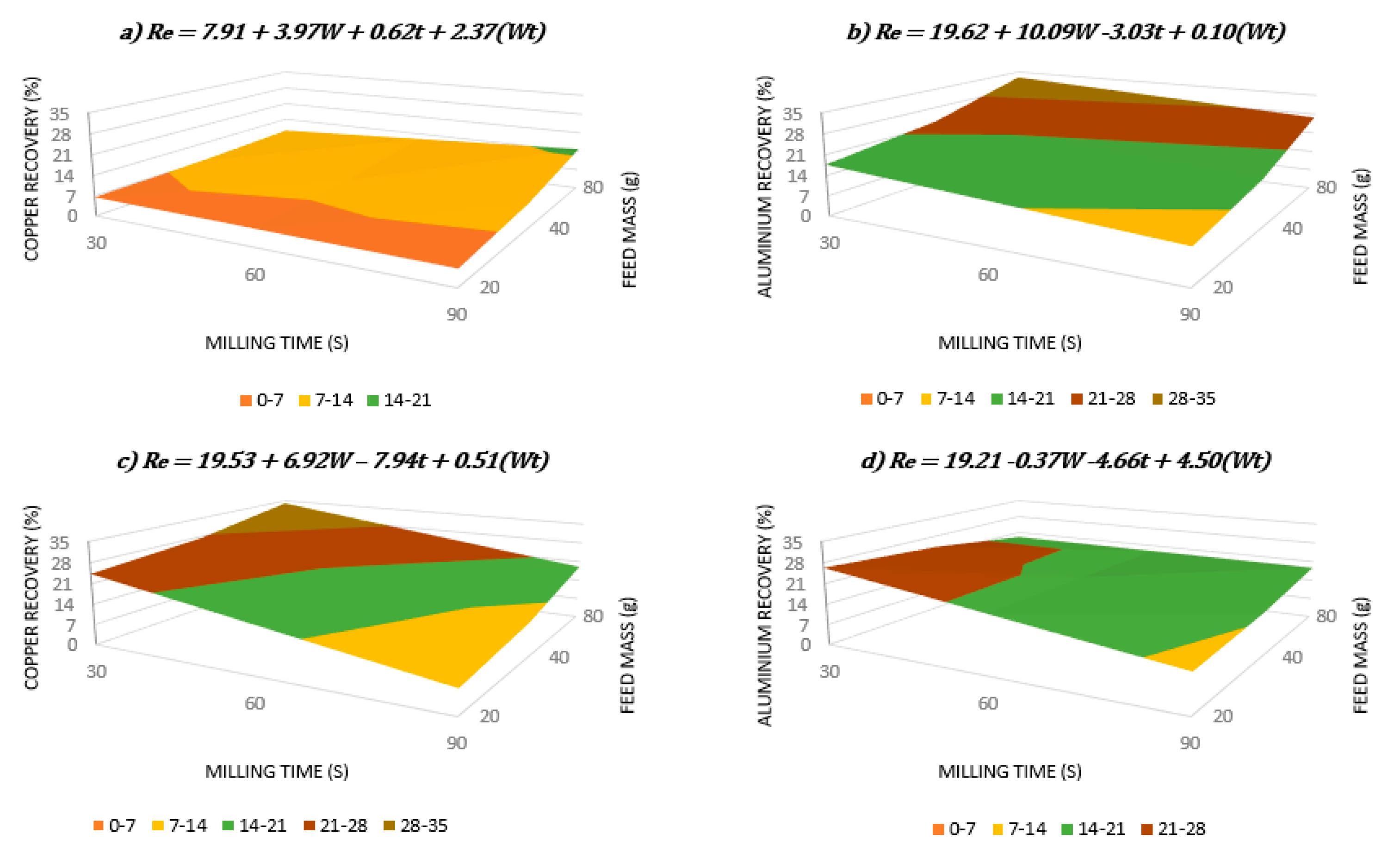
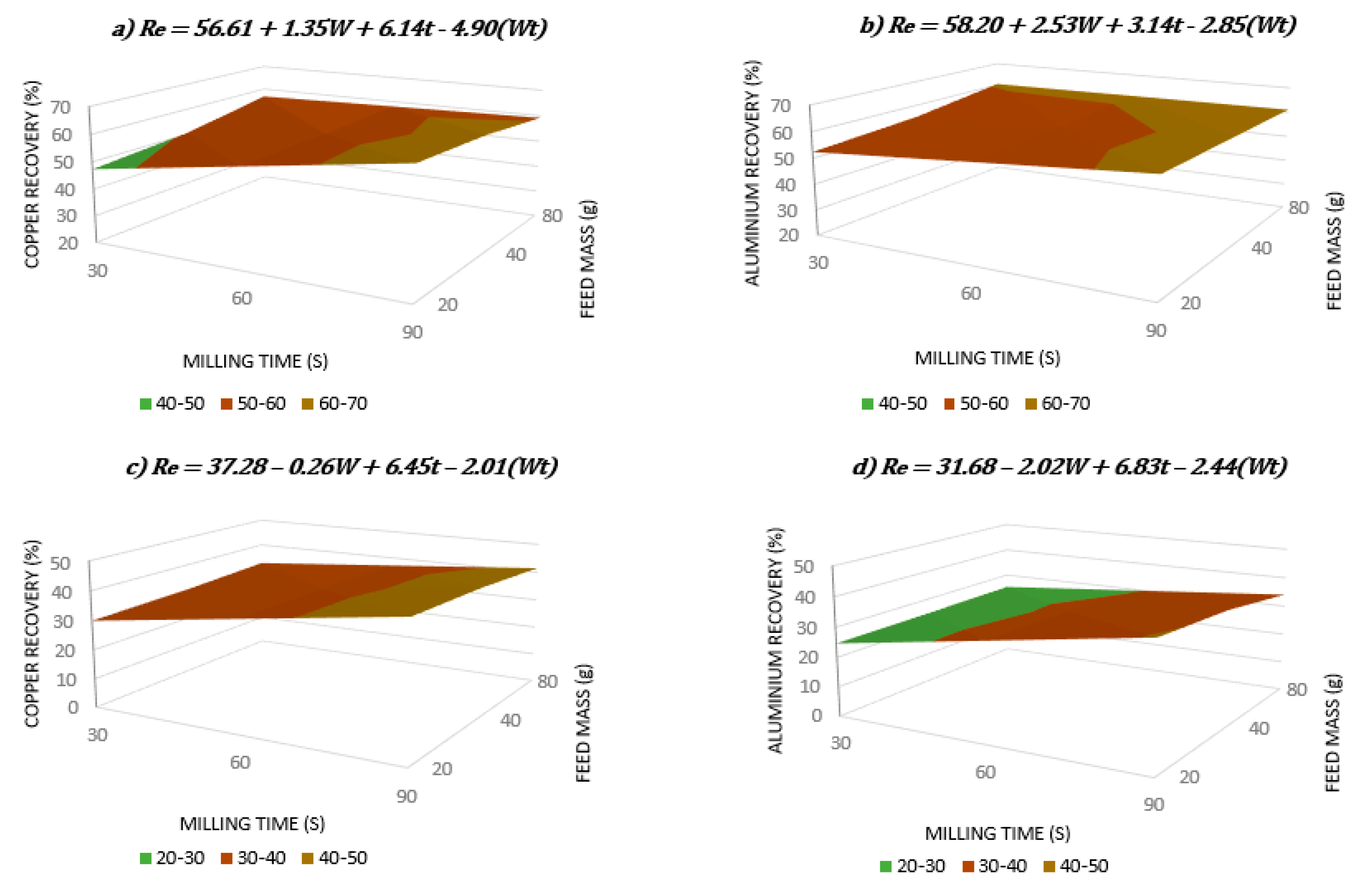
2.5. Modeling the Metal Recovery
3. Results and Discussion
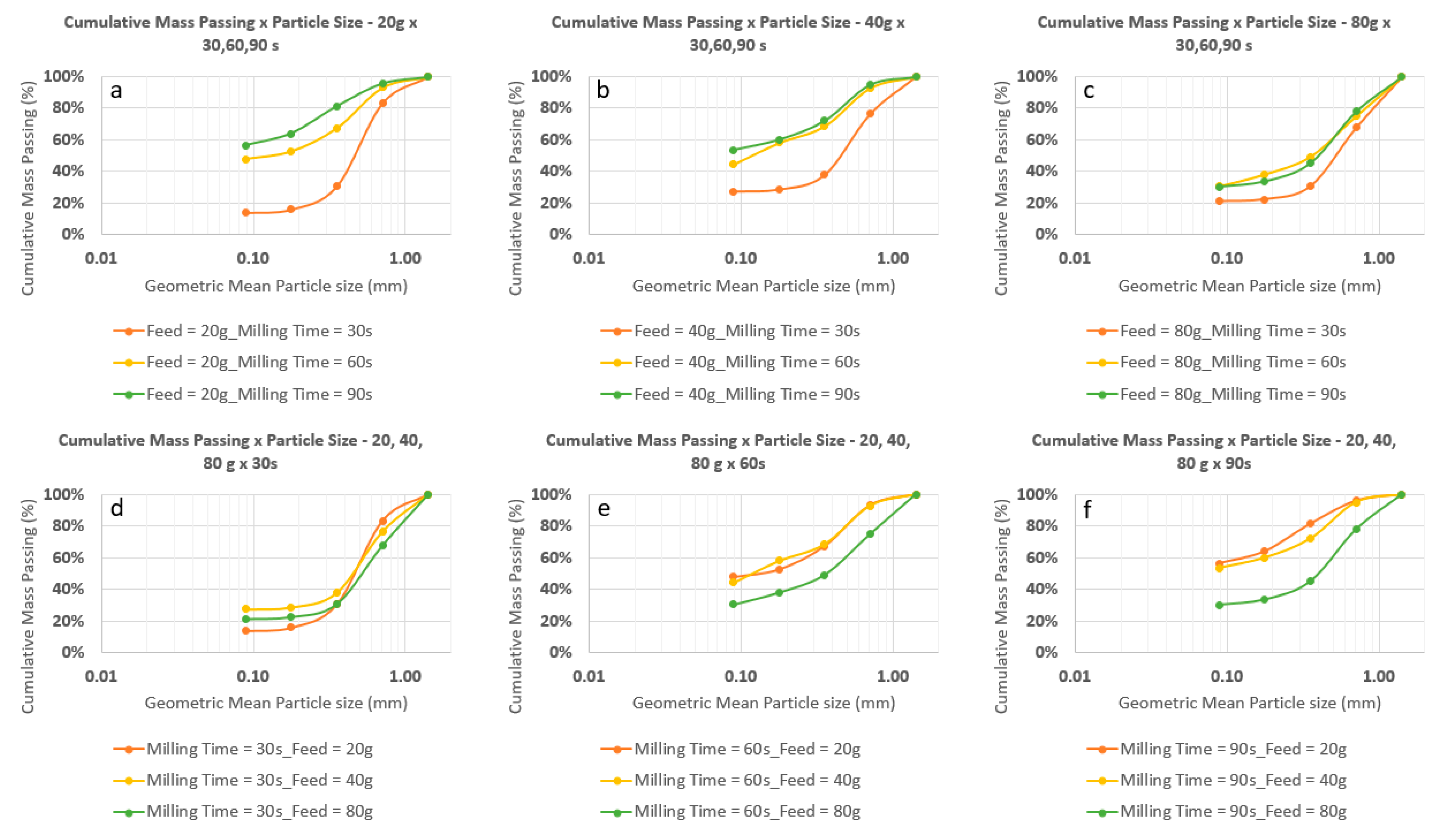
3.1. Particle Size Distribution (PSD) of Mill Products
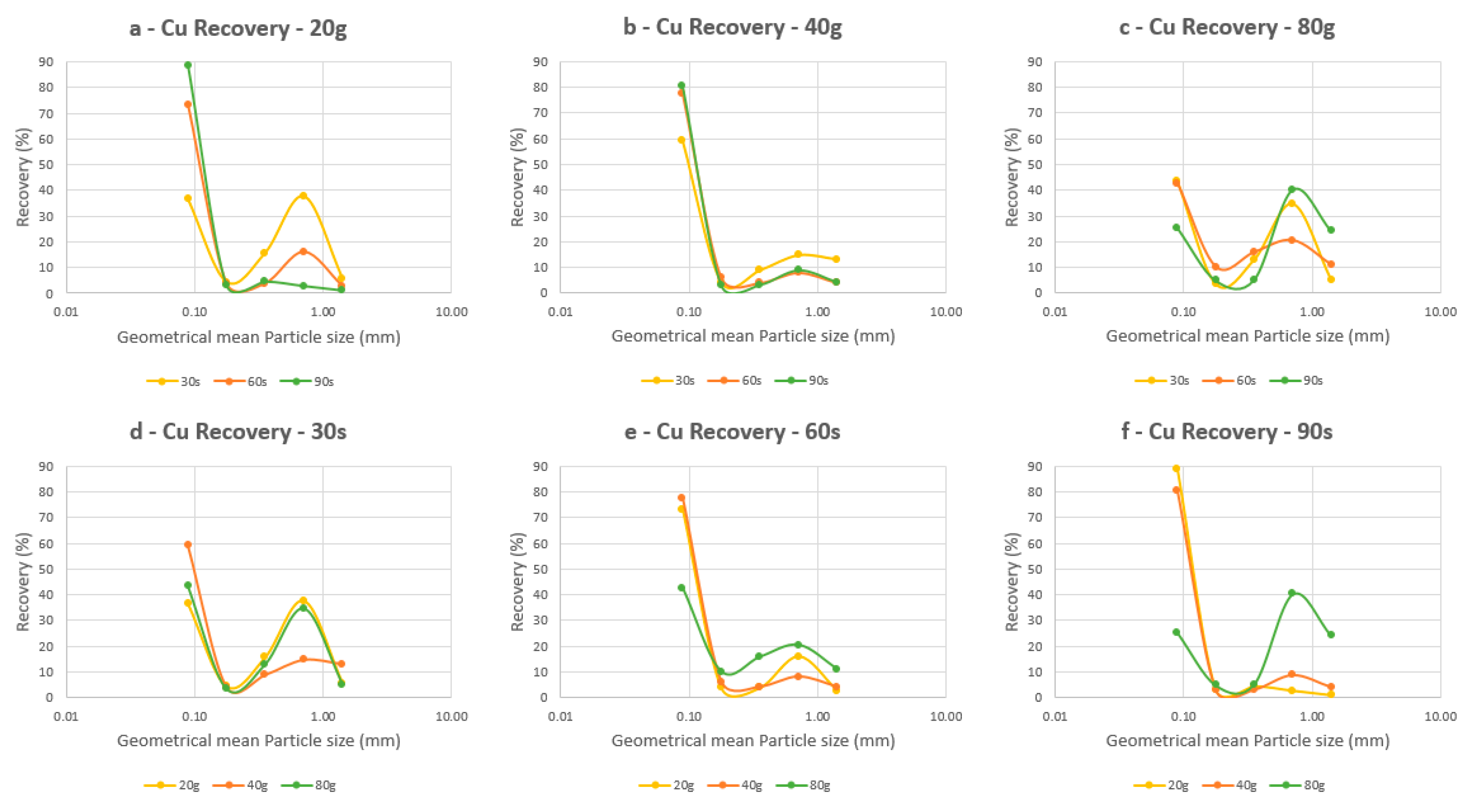
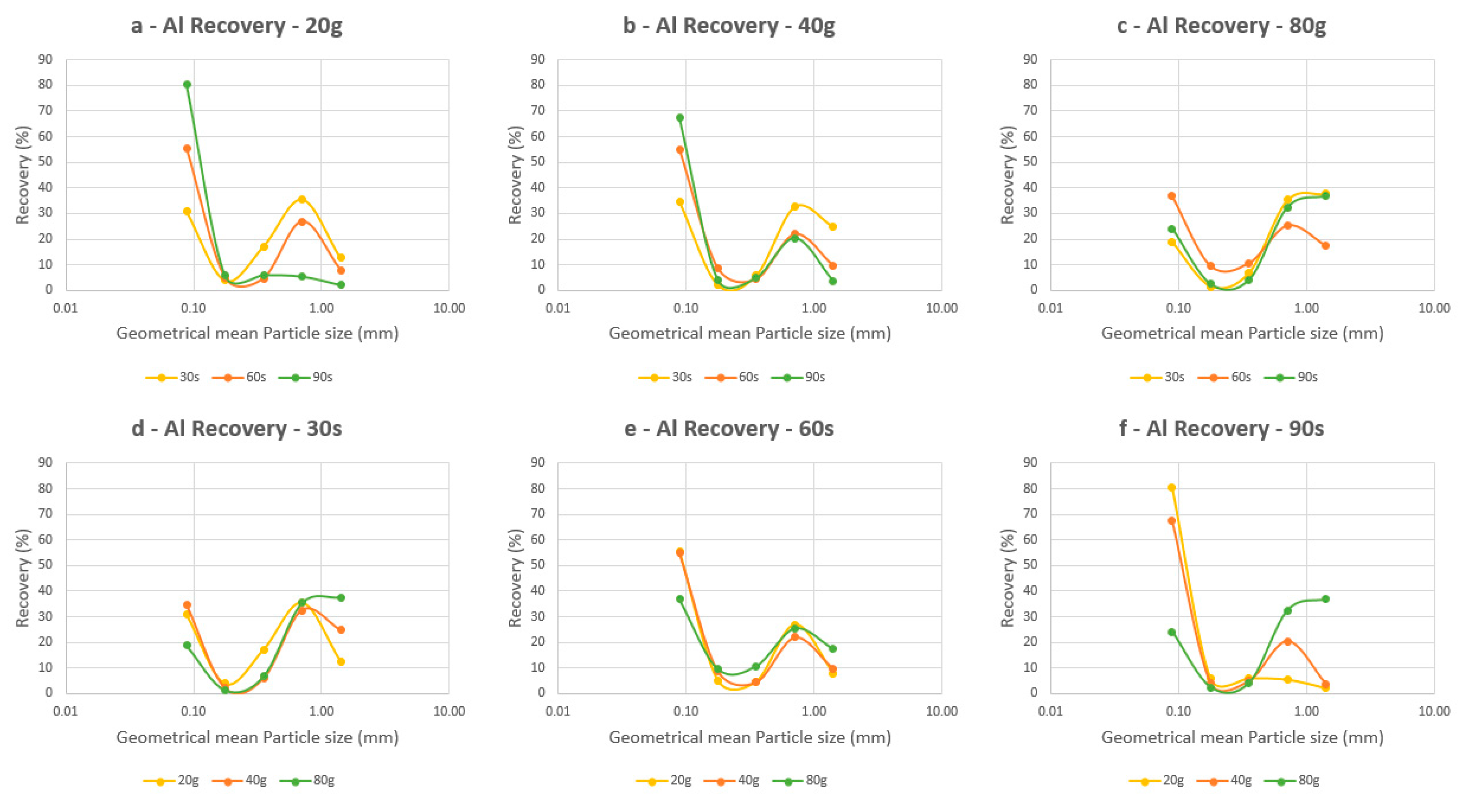
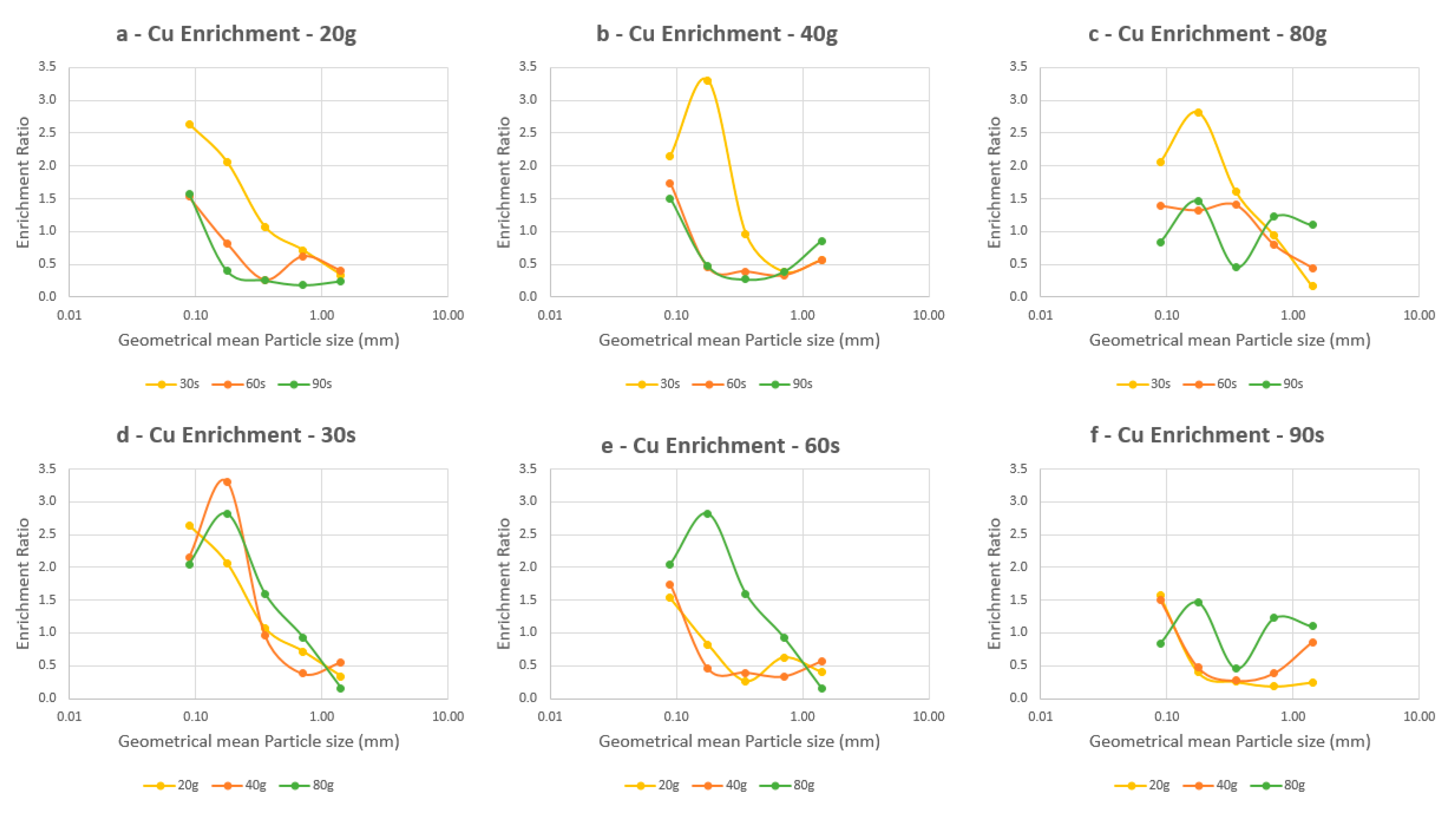
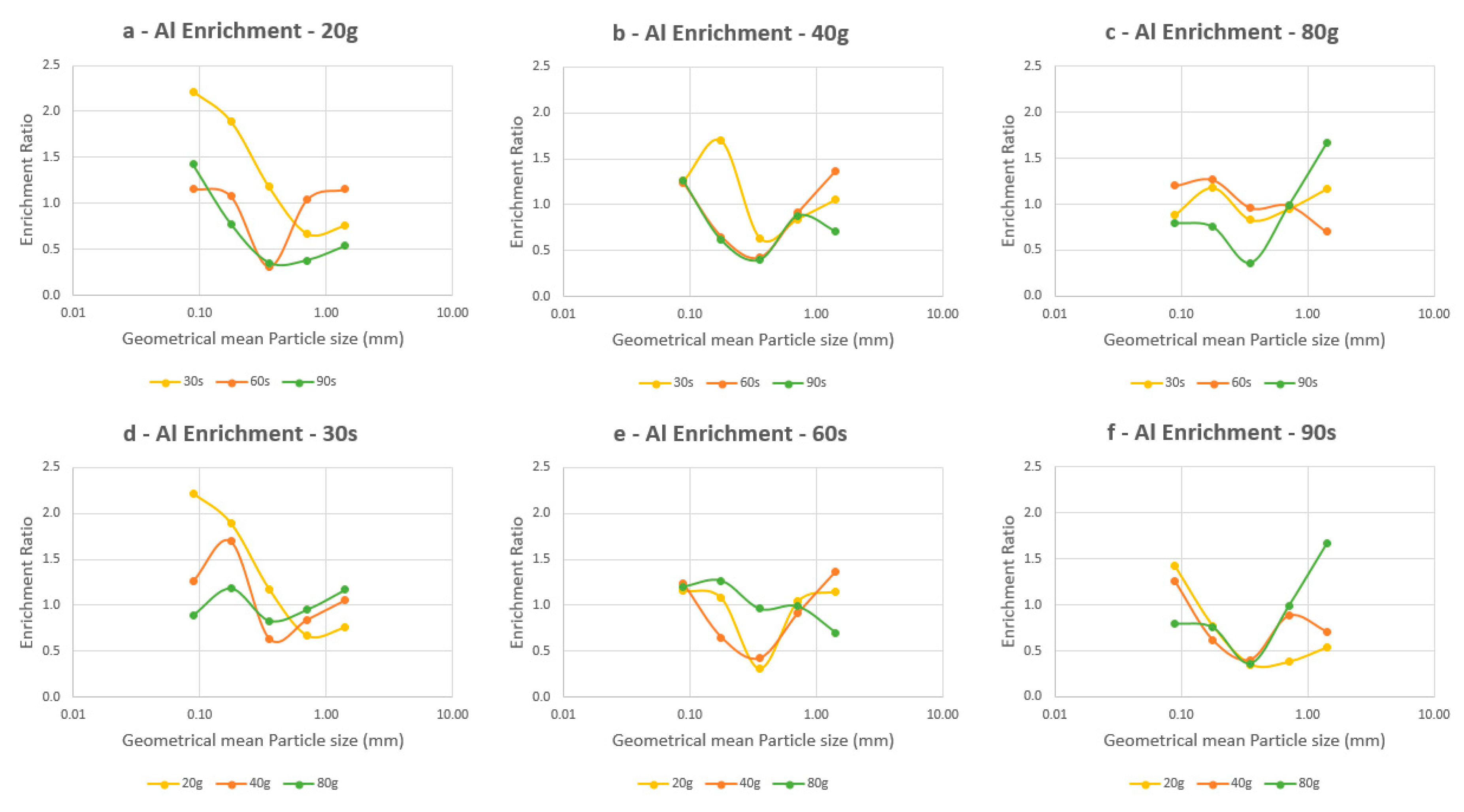
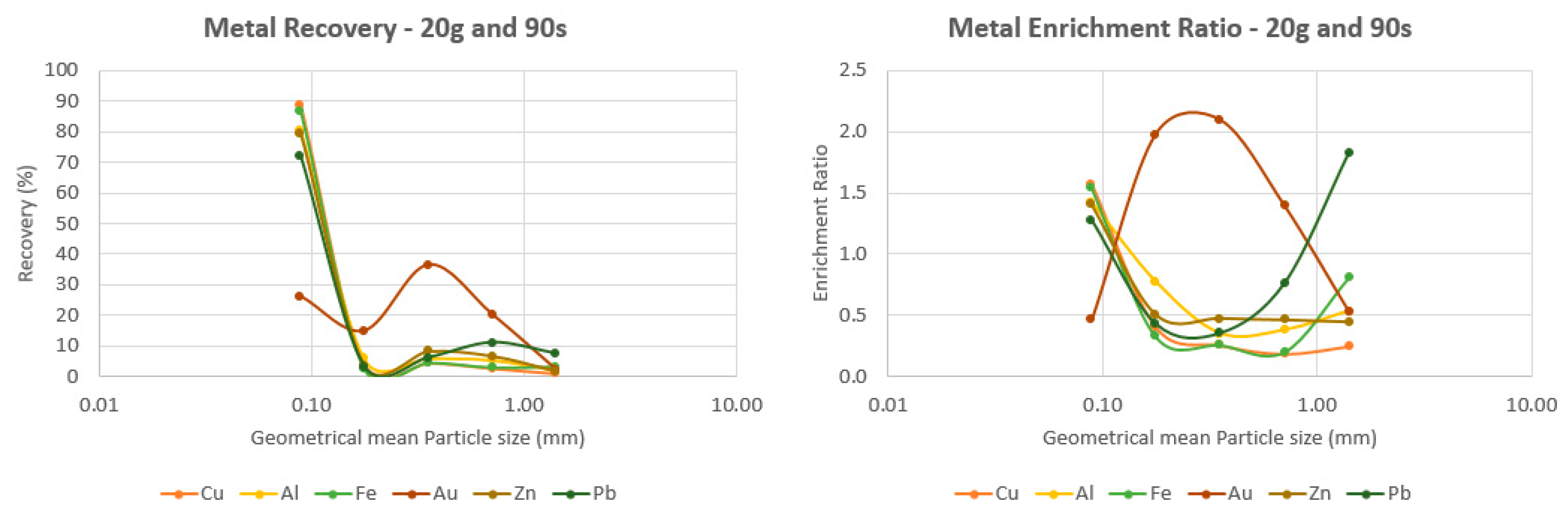
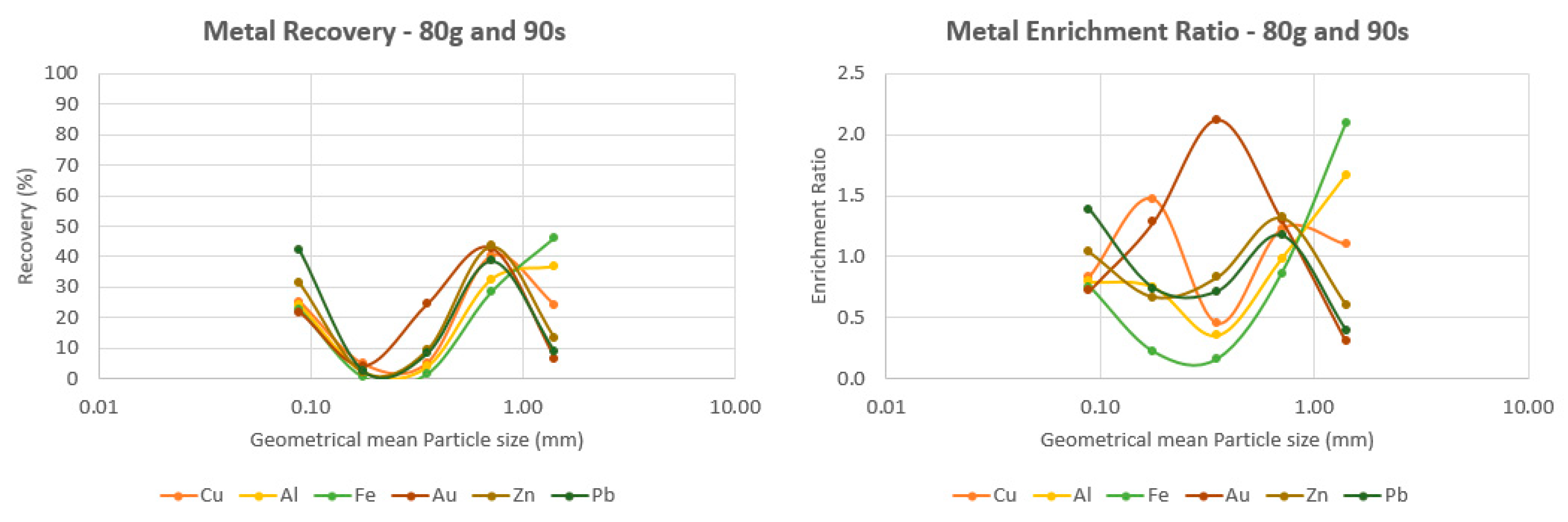
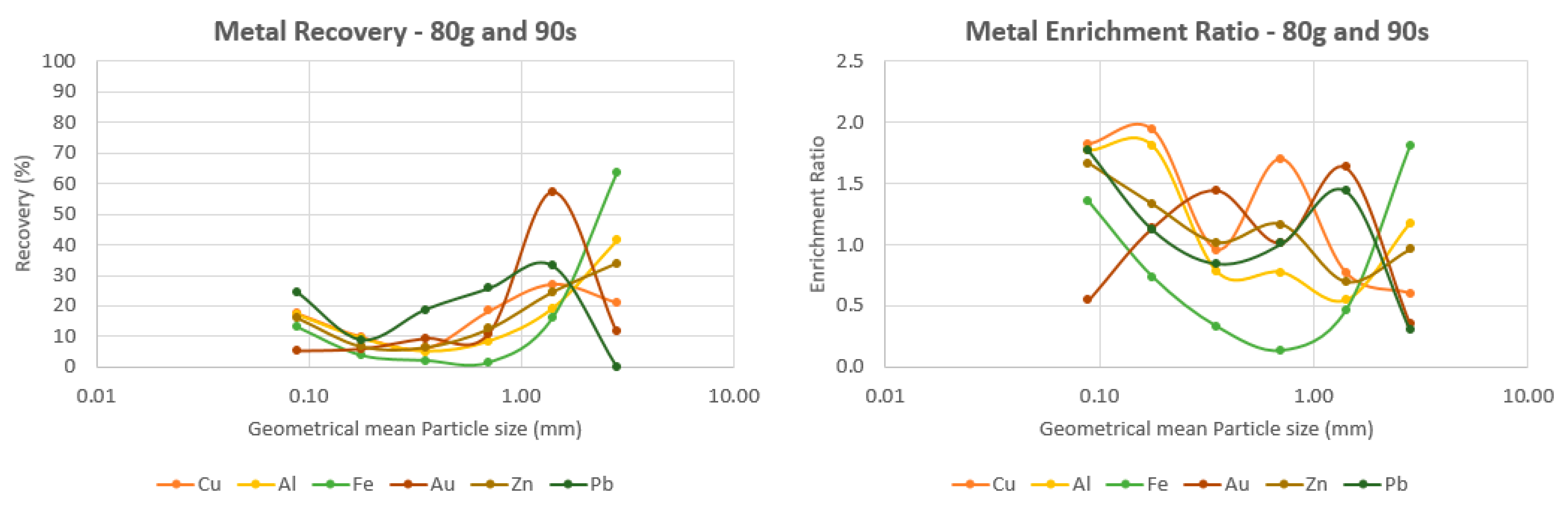
3.2. Metal Recovery and Enrichment Ratio
3.2.1. Behavior of Cu and Al
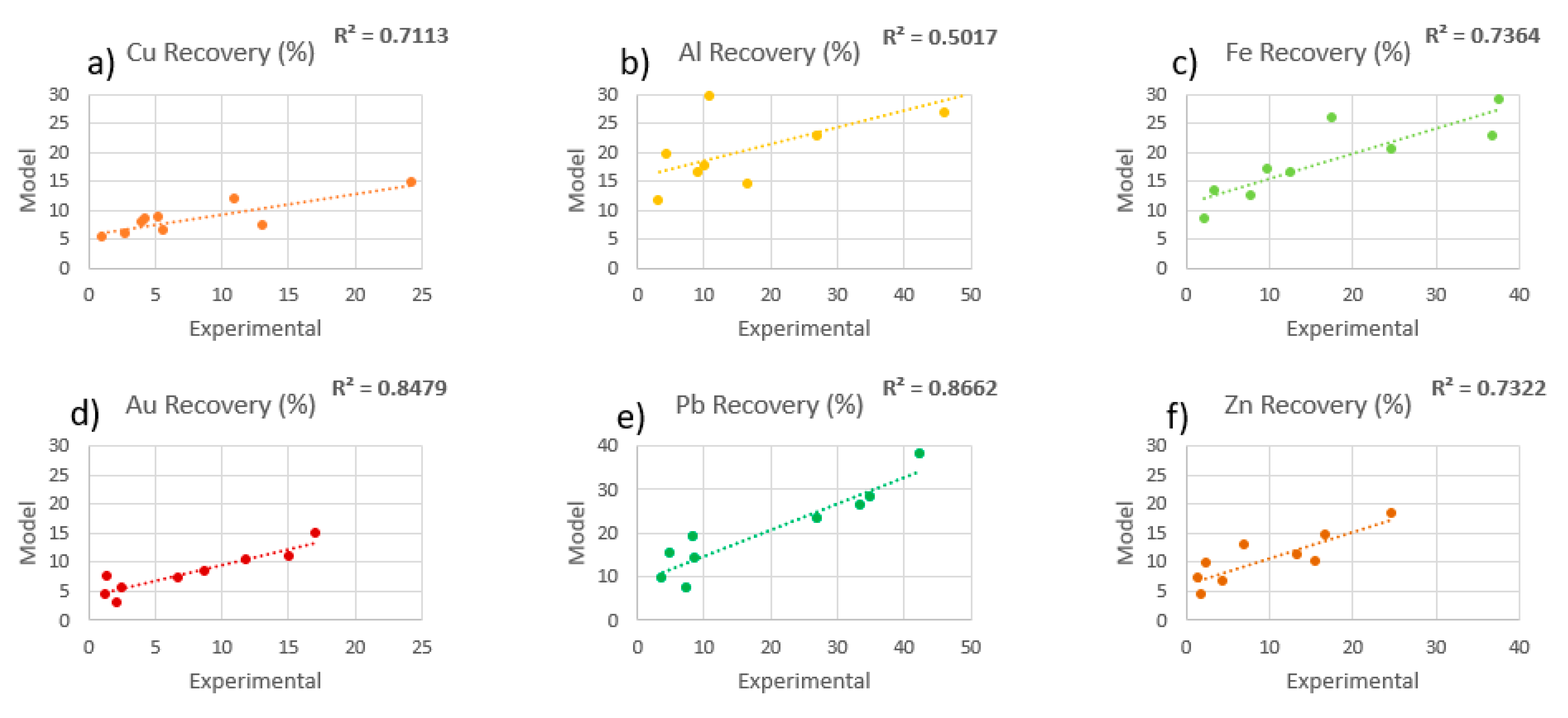
3.2.2. Behavior of all the Six Elements
3.3. Modeling the Metal Recovery
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Eurostat. Available online: http://ec.europa.eu/eurostat/web/waste/key-waste-streams/weee (accessed on 18 May 2018).
- Fujita, T.; Ono, H.; Dodbiba, G.; Yamaguchi, K. Evaluation of a recycling process for printed circuit board by physical separation and heat treatment. Waste Manag. 2014, 34, 1264–1273. [Google Scholar] [CrossRef] [PubMed]
- Koyanaka, S.; Endoh, S.; Ohya, H. Effect of impact velocity control on selective grinding of waste printed circuit boards. Adv. Powder Technol. 2006, 17, 113–126. [Google Scholar] [CrossRef]
- Otsuki, A.; Gonçalves, P.P.; Stieghorst, C.; Révay, Z. Non-destructive characterization of mechanically processed waste printed circuit boards: X-ray fluorescence spectroscopy and prompt gamma activation analysis. J. Compos. Sci. 2019, 3, 54. [Google Scholar] [CrossRef]
- Otsuki, A. Non-destructive liberation analysis of printed circuit board. In Proceedings of the 16th International Waste Management and Landfill Symposium, Sardinia Italy, 2–6 October 2017. [Google Scholar]
- Otsuki, A.; Chen, Y.; Zhao, Y. Characterization and beneficiation of complex ores for sustainable use of mineral resources: Refractory gold ore beneficiation as an example. Int. J. Soc. Mater. Eng. Resour. 2014, 20, 126–135. [Google Scholar] [CrossRef]
- Otsuki, A.; Dodbiba, G.; Shibayama, A.; Sadaki, J.; Mei, G.; Fujita, T. Separation of rare earth fluorescent powders by two-liquid flotation using organic solvents. Jpn. J. Appl. Phys. 2008, 47, 5093–5099. [Google Scholar] [CrossRef]
- Otsuki, A.; Dodbiba, G.; Fujita, T. Two-liquid flotation: Heterocoagulation of fine particles in polar organic solvent. Mater. Trans. 2007, 48, 1095–1104. [Google Scholar] [CrossRef]
- Otsuki, A.; Mei, G.; Yuren, J.; Matsuda, M.; Shibayama, A.; Sadaki, J.; Fujita, T. Solid-Solid separation of fluorescent powders by liquid-liquid extraction using aqueous and organic phases. Resour. Process. 2006, 53, 121–133. [Google Scholar] [CrossRef]
- Otsuki, A.; Shibayama, A.; Sadaki, J.; Fujita, T.; Watanabe, M. Removal of nickel, zinc and phosphorus from wastewater of industrial factories. Resour. Process. 2004, 51, 14–19. [Google Scholar] [CrossRef]
- Shibayama, A.; Matsuda, M.; Otsuki, A.; Dodbiba, G.; Fujita, T.; Jeyadevan, B.; Takahashi, K. The recovery and life cycle assessment of nickel particles in a multi-solenoid open-gradient magnetic separator. Magn. Electr. Sep. 2002, 11, 127–139. [Google Scholar] [CrossRef]
- Leroy, E.; Otsuki, A. ENSG, University of Lorraine, Vandoeuvre-lès-Nancy, France. Unpublished work. 2018. [Google Scholar]
- Thermo Fisher Scientific Inc. NITON XL3t 900Analyzer with GOLDD Technology, User’s Guide. Available online: https://www.thermoscientic.com/niton (accessed on 22 March 2019).
- Hadi, P.; Xu, M.; Lin, C.S.K.; Hui, C.-W.; Mckay, G. Waste printed circuit board recycling techniques and product utilization. J. Hazard. Mater. 2015, 283, 234–243. [Google Scholar] [CrossRef] [PubMed]
- Yamane, L.H.; de Moraes, V.T.; Espinosa, D.C.R.; Tenório, J.A.S. Recycling of WEEE: Characterization of spent printed circuit boards from mobile phones and computers. Waste Manage. 2011, 31, 2553–2558. [Google Scholar] [CrossRef] [PubMed]
- Duan, C.; Wen, X.; Shi, C.; Zhao, Y.; Wenet, B.; He, Y. Recovery of metals from waste printed circuit boards by a mechanical method using a water medium. J. Hazard. Mater. 2009, 166, 478–482. [Google Scholar] [CrossRef] [PubMed]
- Abouzeid, A.Z.M. Mineral Processing Laboratory Manual. Trans. Tech. Publ. 1990, 9, 23–27. [Google Scholar]
- Bouajila, A.; Bartolacci, G.; Kock, N.; Cayouette, J.; Coté, C. Toward the improvement of primary grinding productivity and energy consumption efficiency. Part 1: Investigation of the feed ore size effects. IFAC Proc. Volumes 2000, 33, 267–272. [Google Scholar] [CrossRef]
- Zhang, Q.; Kano, J.; Saito, F. Mechanochemical technology: Application to material synthesis and to the separation and processing of recyclable materials from wastes. KONA Powder Part. J. 2001, 19, 7–15. [Google Scholar] [CrossRef]
- Physical Ductility of the Elements. Available online: http://www.failurecriteria.com/physicalductilit.html (accessed on 23 June 2019).
- Zhang, S.; Forssberg, E. Intelligent liberation and classification of electronic scrap. Powder Technol. 1999, 105, 295–301. [Google Scholar] [CrossRef]





| Sample/Element % | Au% | Pb% | Zn% | Cu% | Fe% | Al% |
|---|---|---|---|---|---|---|
| FEED 2–4 mm | 0.03 | 0.54 | 0.62 | 4.40 | 5.25 | 7.33 |
| FEED 1–2 mm | 0.04 | 0.86 | 0.49 | 8.39 | 2.33 | 5.34 |
| Data from [14] | 0.03 | 0.2–3.0 | 0.5–3.0 | 7.0–36.0 | 2.0–12.0 | 1.0–22.0 |
| Data from [15] | 0.10 | 2.40 | 2.30 | 22.0 | 5.70 | 3.90 |
| R2 (Determination Coefficient)–Experimental x Modeled Metal Recovery | |||||||
|---|---|---|---|---|---|---|---|
| Feed Size | Product Size Fraction | Au | Pb | Zn | Cu | Al | Fe |
| 1–2 mm | 1–2 mm | 0.85 | 0.87 | 0.73 | 0.71 | 0.50 | 0.74 |
| 0.5–1 mm | 0.63 | 0.41 | 0.57 | 0.50 | 0.35 | 0.65 | |
| 0.25–0.5 mm | 0.52 | 0.15 | 0.09 | 0.57 | 0.31 | 0.19 | |
| 0.125–0.25 mm | 0.28 | 0.09 | 0.07 | 0.26 | 0.02 | 0.01 | |
| −0.125 mm | 0.44 | 0.34 | 0.31 | 0.22 | 0.00 | 0.46 | |
| 2–4 mm | 2–4 mm | 0.60 | 0.54 | 0.80 | 0.33 | 0.15 | 0.02 |
| 1–2 mm | 0.67 | 0.58 | 0.61 | 0.41 | 0.39 | 0.46 | |
| 0.5–1 mm | 0.00 | 0.01 | 0.14 | 0.00 | 0.00 | 0.01 | |
| 0.25–0.5 mm | 0.17 | 0.20 | 0.21 | 0.00 | 0.18 | 0.03 | |
| 0.125–0.25 mm | 0.35 | 0.28 | 0.12 | 0.01 | 0.46 | 0.27 | |
| −0.125 mm | 0.51 | 0.28 | 0.46 | 0.31 | 0.54 | 0.51 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otsuki, A.; Pereira Gonçalves, P.; Leroy, E. Selective Milling and Elemental Assay of Printed Circuit Board Particles for Their Recycling Purpose. Metals 2019, 9, 899. https://doi.org/10.3390/met9080899
Otsuki A, Pereira Gonçalves P, Leroy E. Selective Milling and Elemental Assay of Printed Circuit Board Particles for Their Recycling Purpose. Metals. 2019; 9(8):899. https://doi.org/10.3390/met9080899
Chicago/Turabian StyleOtsuki, Akira, Pedro Pereira Gonçalves, and Emilien Leroy. 2019. "Selective Milling and Elemental Assay of Printed Circuit Board Particles for Their Recycling Purpose" Metals 9, no. 8: 899. https://doi.org/10.3390/met9080899
APA StyleOtsuki, A., Pereira Gonçalves, P., & Leroy, E. (2019). Selective Milling and Elemental Assay of Printed Circuit Board Particles for Their Recycling Purpose. Metals, 9(8), 899. https://doi.org/10.3390/met9080899





