Analytical Modeling of the Mixed-Mode Growth and Dissolution of Precipitates in a Finite System
Abstract
1. Introduction
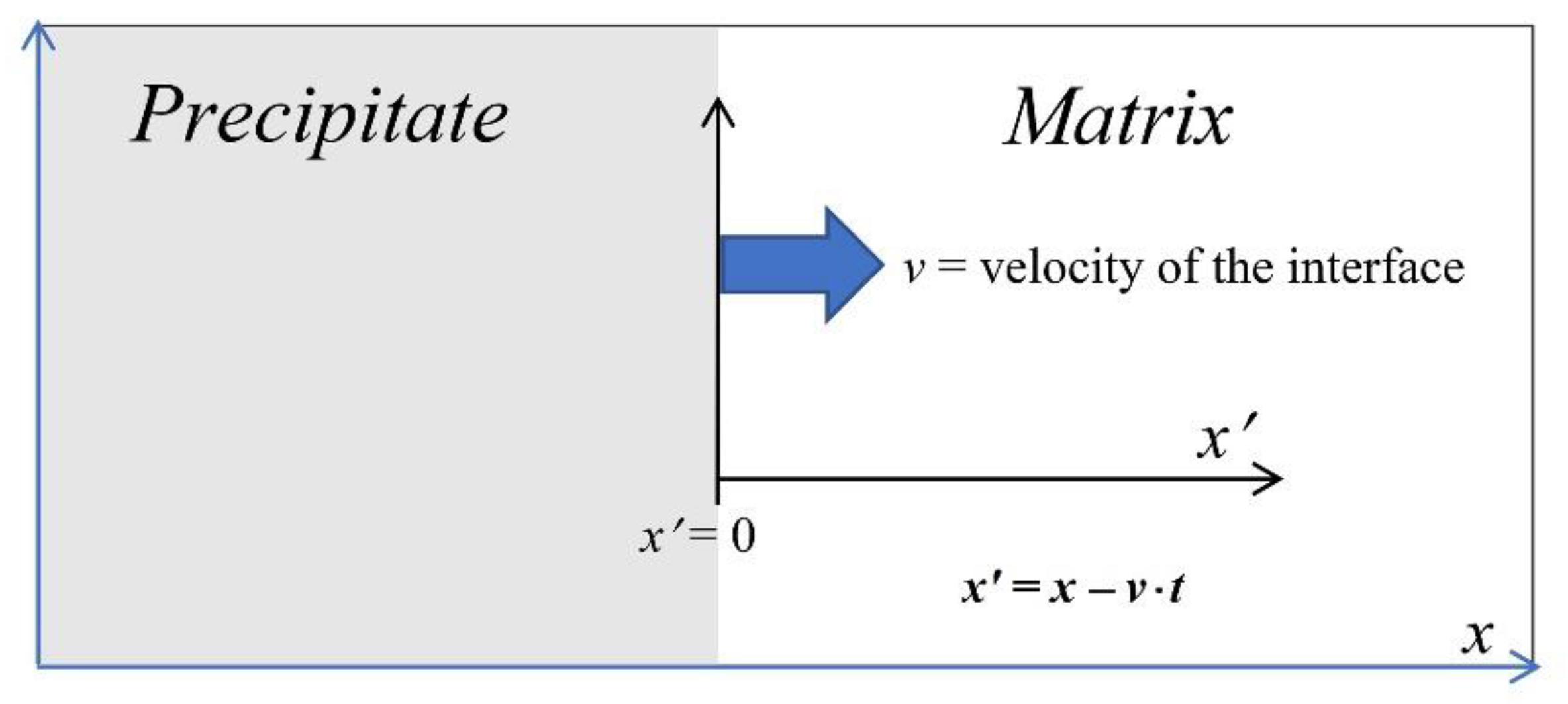
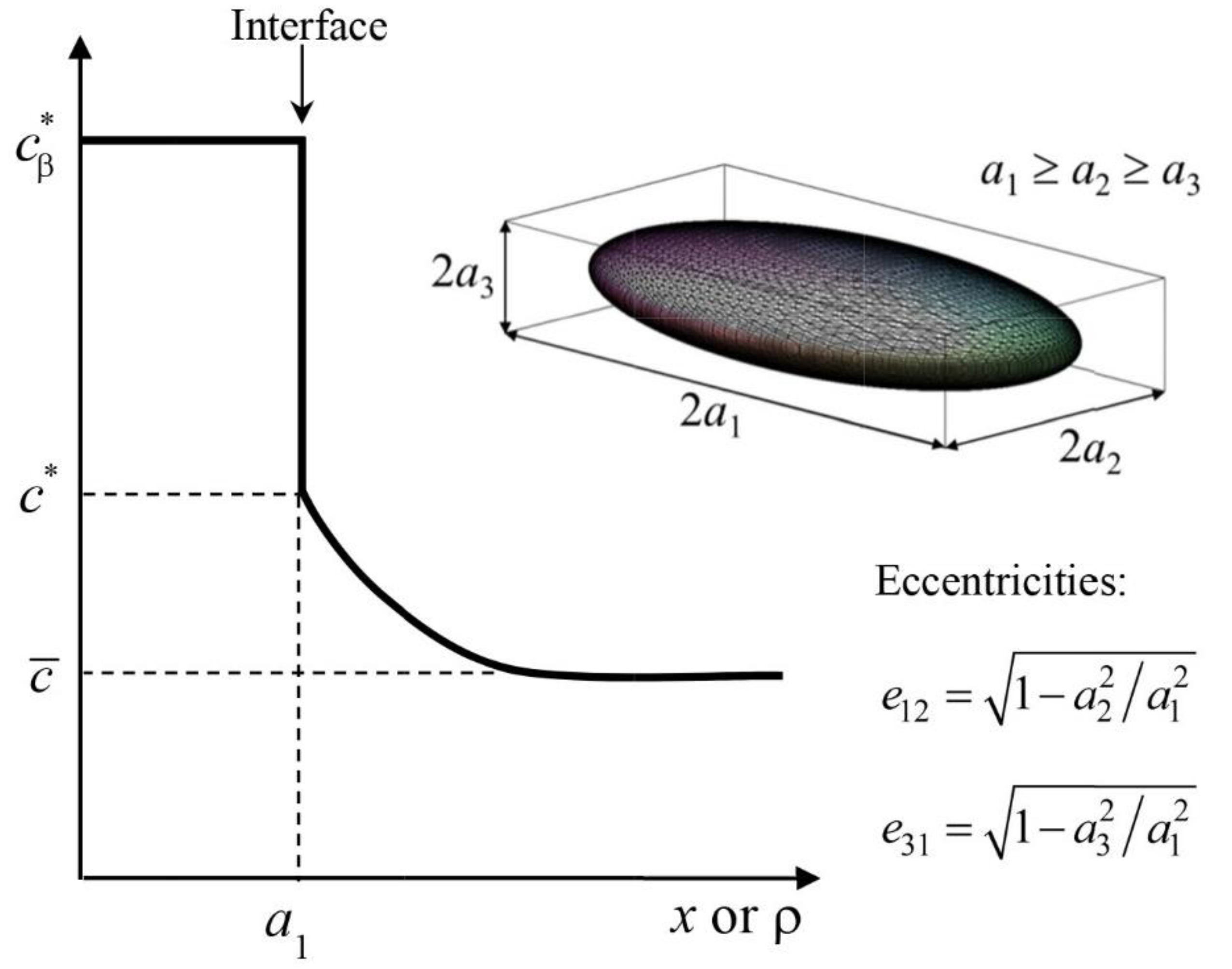
2. Dissolution in the Quasi-Stationary Regime of an Ellipsoidal Precipitate
3. Application of the Dissolution Model
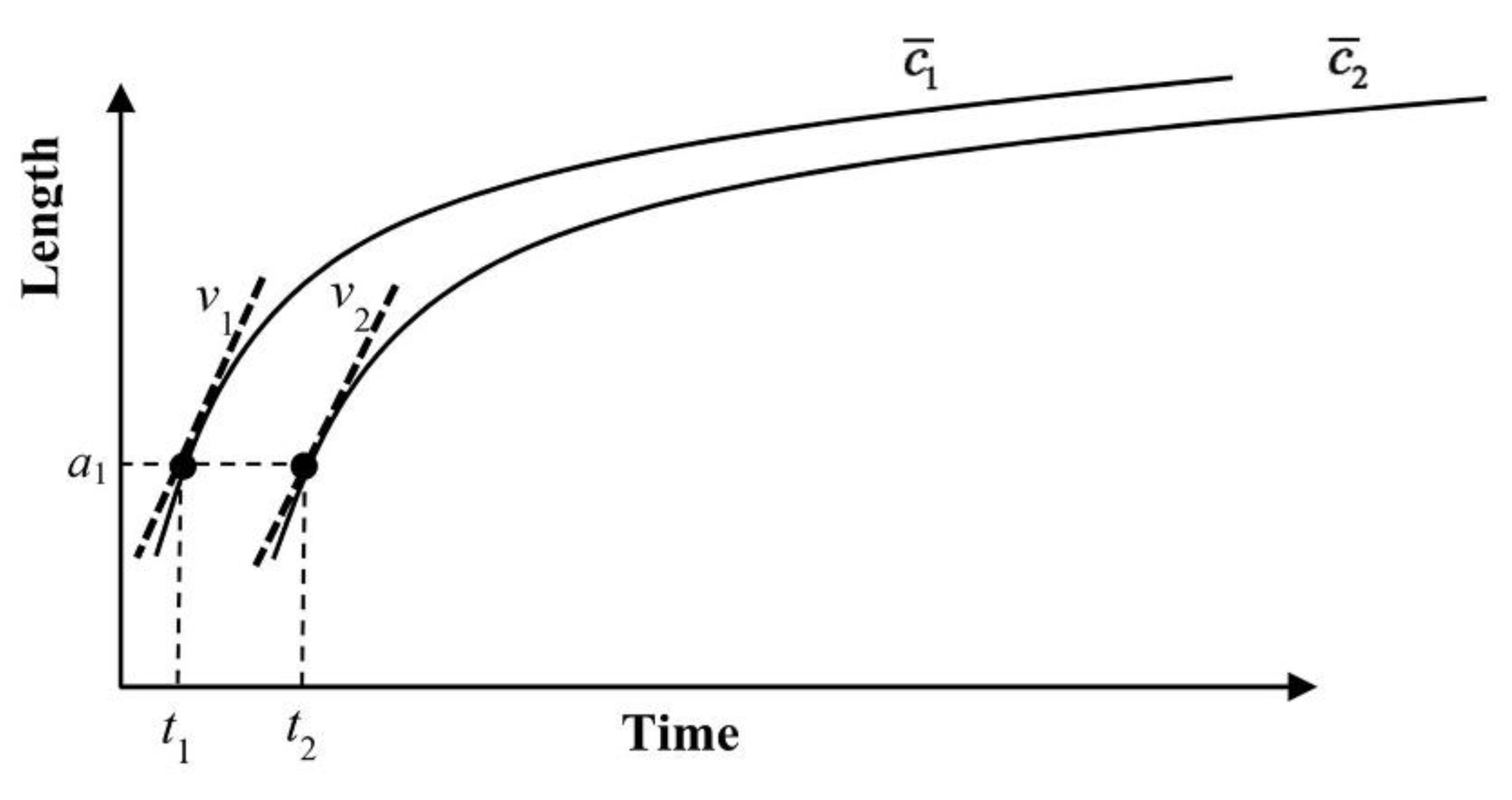
4. Growth and Dissolution in a Finite System
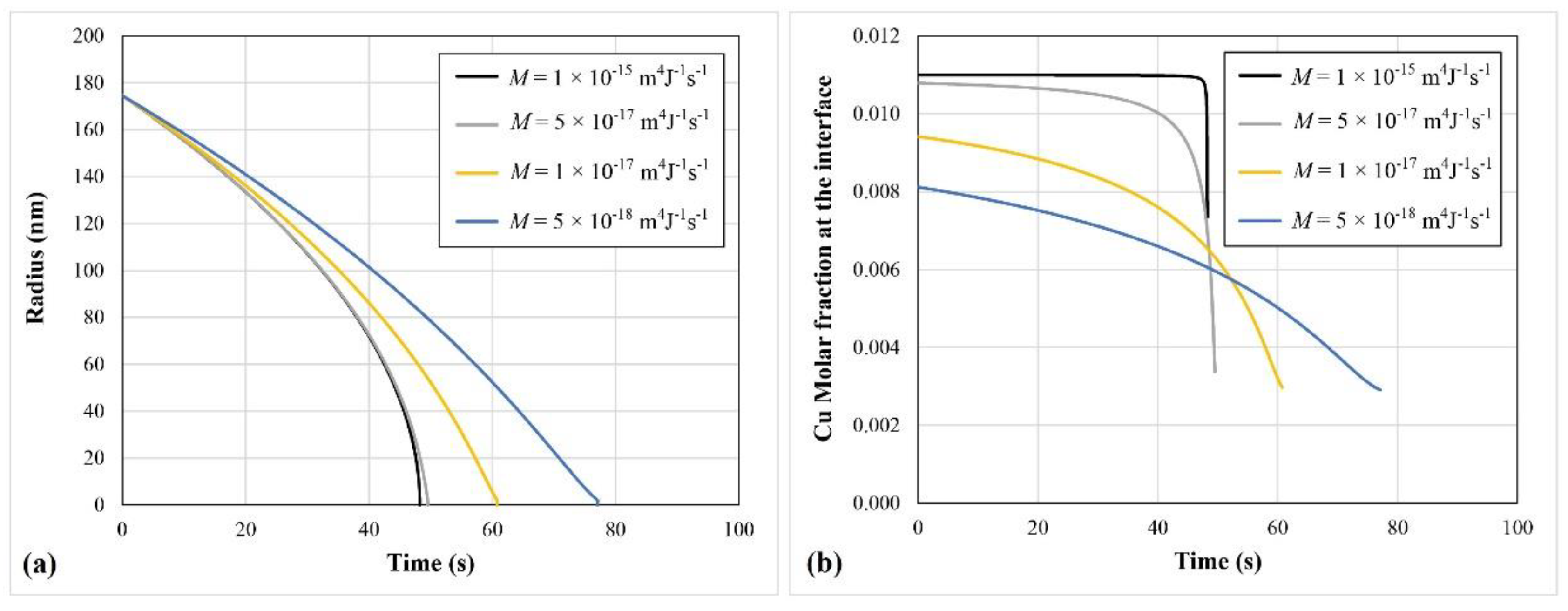
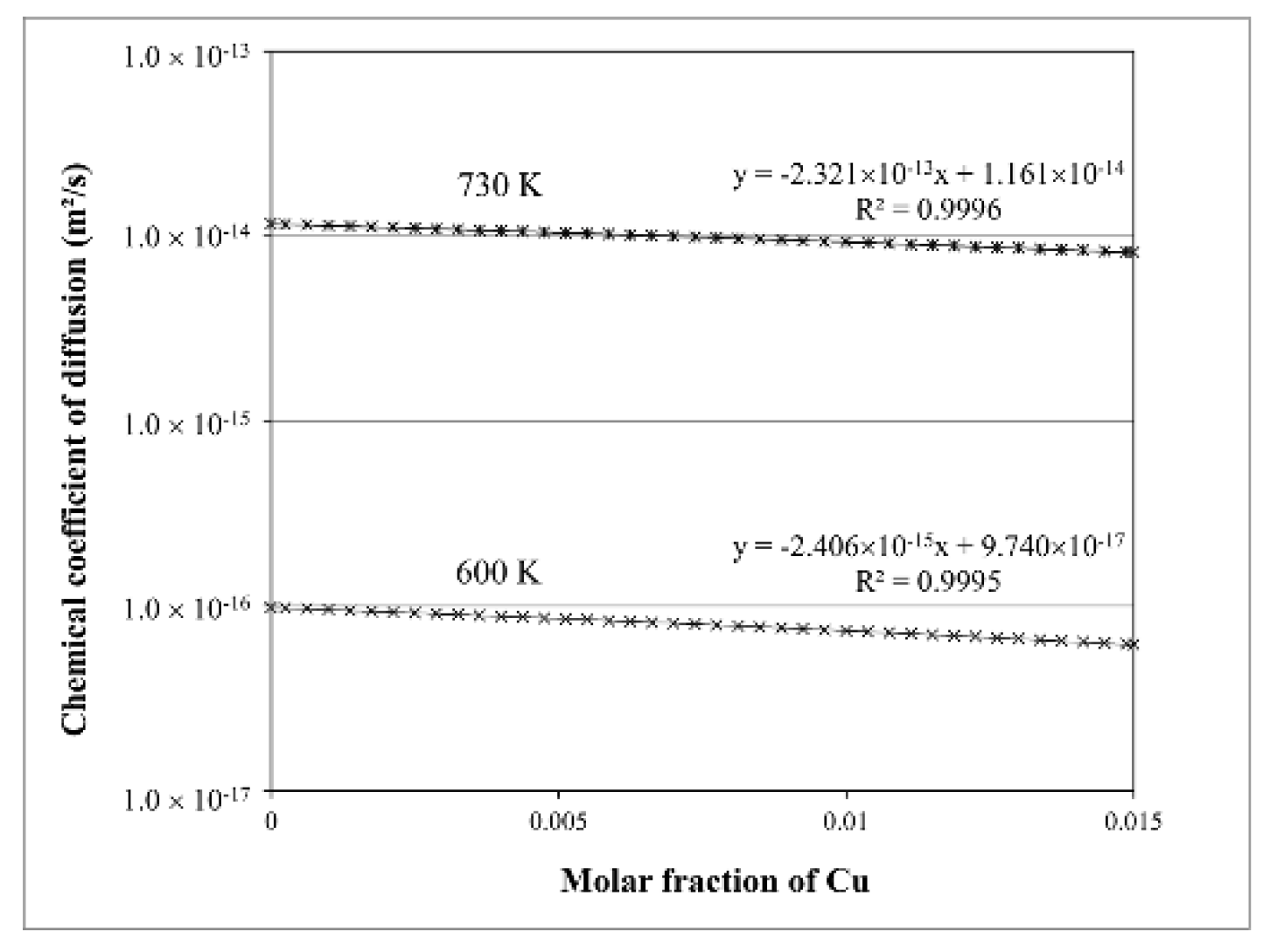
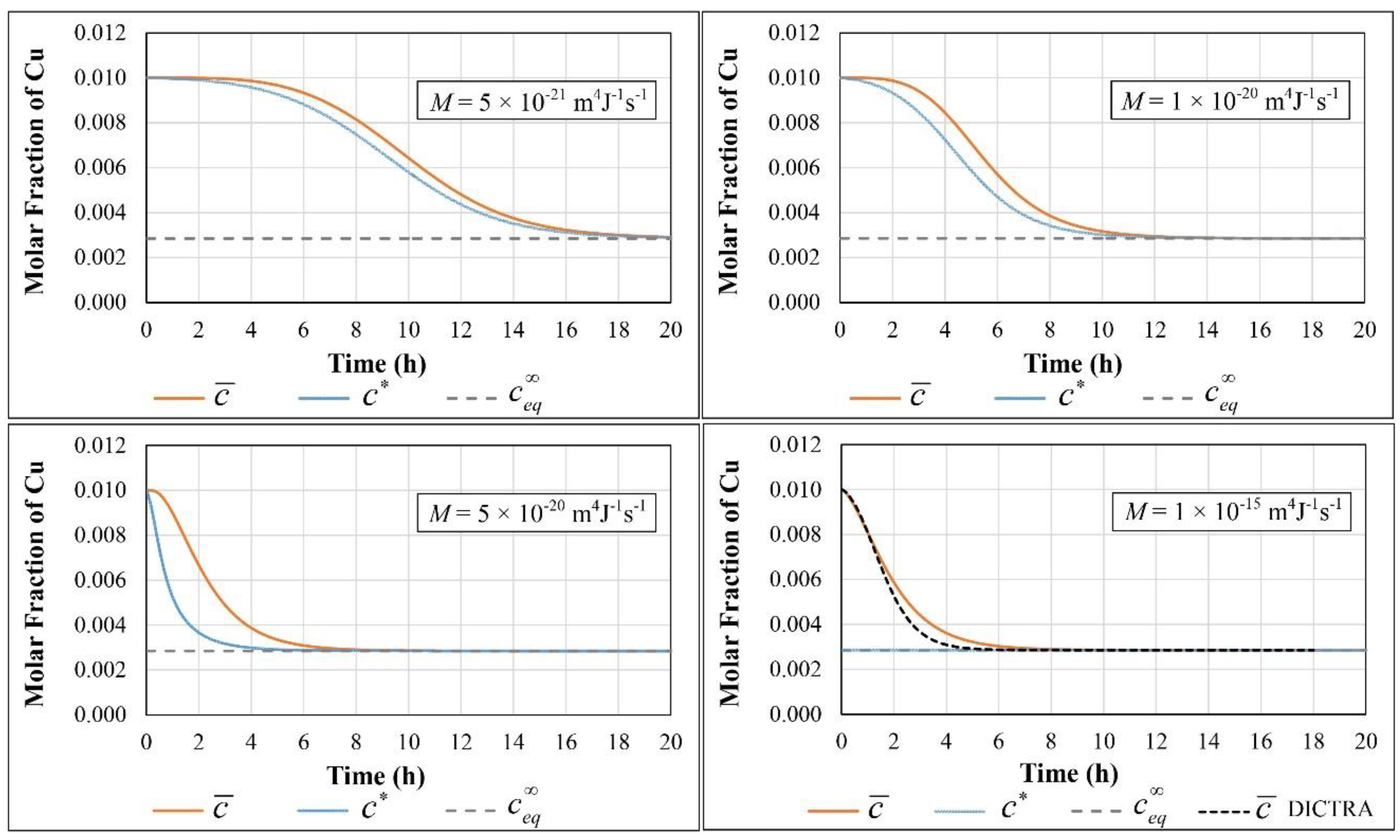
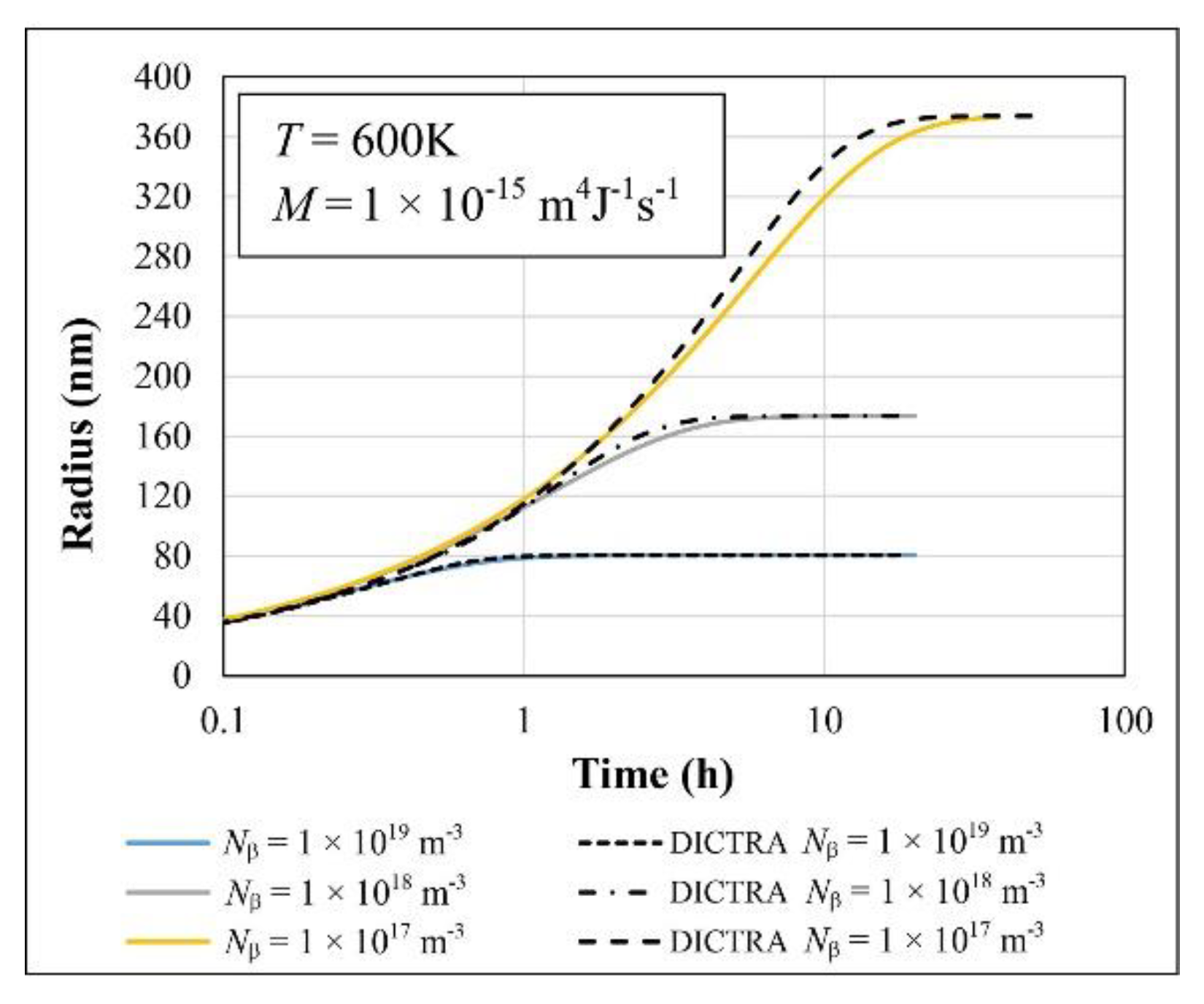
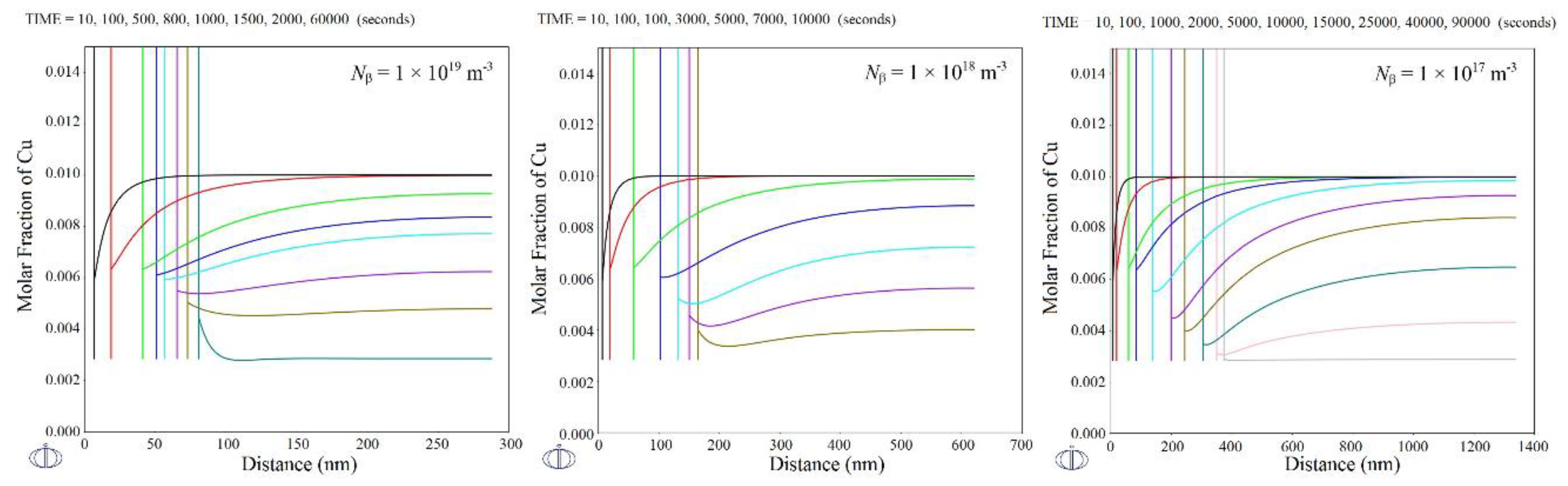
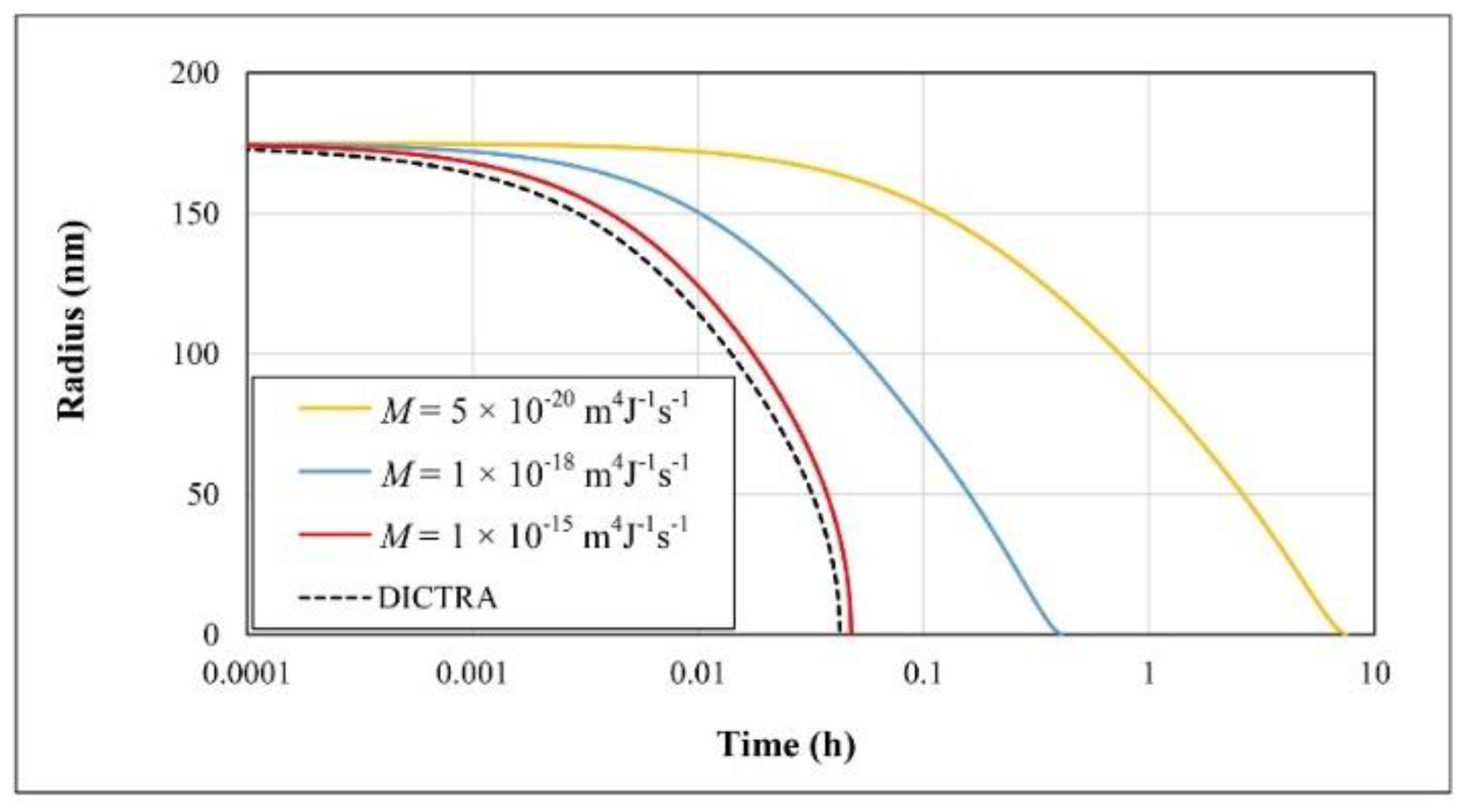
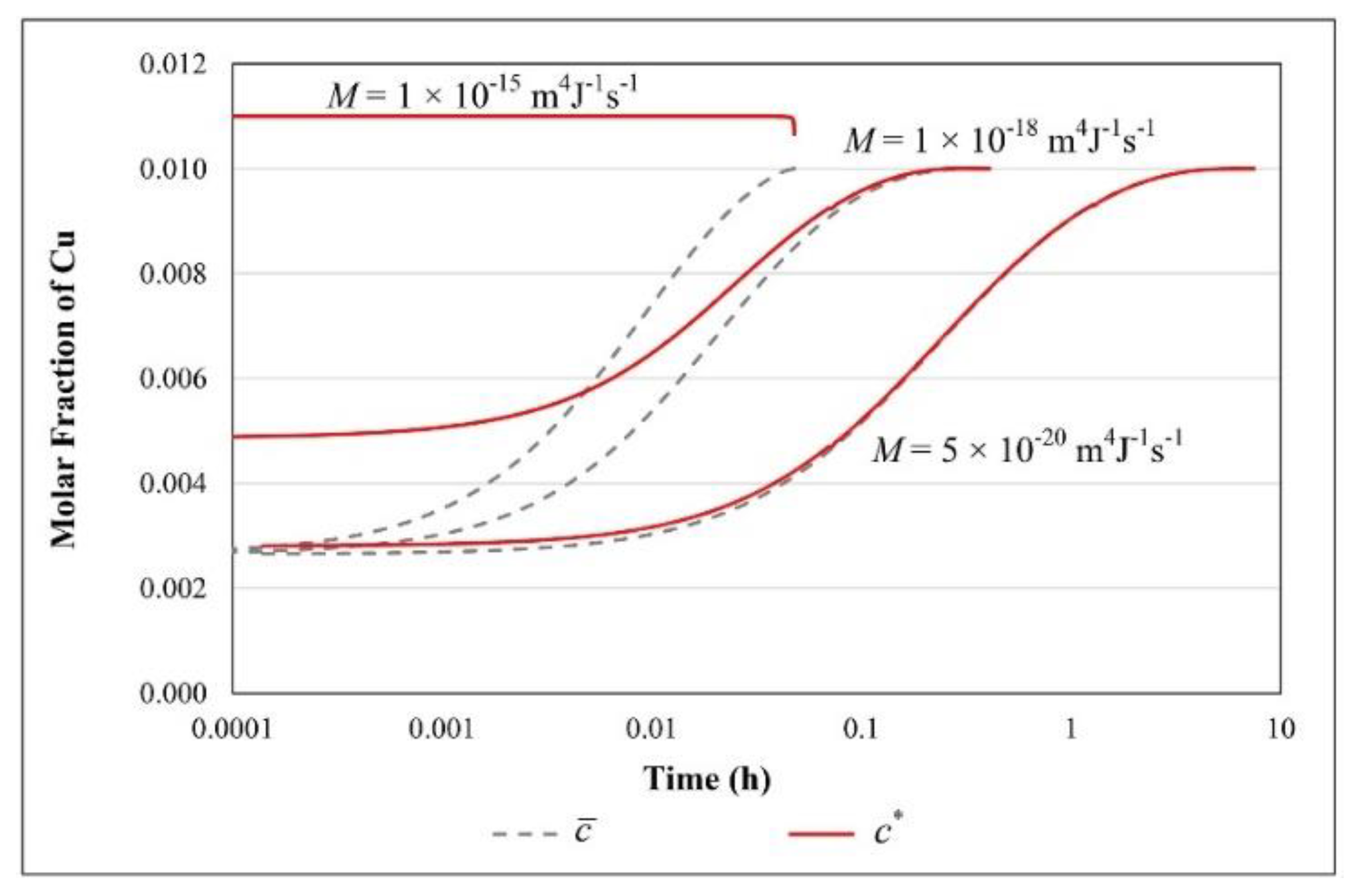
5. Application of the Model
6. Discussion
7. Conclusion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Reversed-Growth Solution of the Mass Conservation Equation in the Mixed-Mode Regime for an Ellipsoidal Precipitate
References
- Jou, H.J.V.; Peter, W.; Olson, B. Computer simulations for the prediction of microstructure/property variation in aeroturbine disks. In Proceedings of the SUPERALLOYS 2004–Proceedings of the Tenth International Symposium on Superalloys, Champion, PA, USA, 19–23 September 2004; pp. 877–886. [Google Scholar]
- Svoboda, J.; Fischer, F.D.; Fratzl, P.; Kozeschnik, E. Modelling of kinetics in multi-component multi-phase systems with spherical precipitates: I: Theory. Mater. Sci. Eng. A 2004, 385, 166–174. [Google Scholar] [CrossRef]
- Morral, J.E.; Purdy, G.R. Particle coarsening in binary and multicomponent alloys. Scr. Metall. Mater. 1994, 30, 905–908. [Google Scholar] [CrossRef]
- Chen, Q.; Jeppsson, J.; Ågren, J. Analytical treatment of diffusion during precipitate growth in multicomponent systems. Acta Mater. 2008, 56, 1890–1896. [Google Scholar] [CrossRef]
- Guillemot, G.; Gandin, C.-A. An analytical model with interaction between species for growth and dissolution of precipitates. Acta Mater. 2017, 134, 375–393. [Google Scholar] [CrossRef]
- Aaron, H.B.; Fainstein, D.; Kotler, G.R. Diffusion-Limited Phase Transformations: A Comparison and Critical Evaluation of the Mathematical Approximations. J. Appl. Phys. 1970, 41, 4404–4410. [Google Scholar] [CrossRef]
- Guo, X.; Sietsma, J.; Yang, Y.; Sun, Z.; Guo, M. Diffusion-limited dissolution of spherical particles: A critical evaluation and applications of approximate solutions. AIChE J. 2017, 63, 2926–2934. [Google Scholar] [CrossRef]
- Precipitation Module (TC-PRISMA) User Guide. Available online: https://www.thermocalc.com/media/40970/precipitation-module-tc-prisma-user-guide.pdf (accessed on 31 January 2019).
- Larouche, D. Mixed mode growth of an ellipsoidal precipitate: Analytical solution for shape preserving growth in the quasi-stationary regime. Acta Mater. 2017, 123, 188–196. [Google Scholar] [CrossRef][Green Version]
- Naseri, T.; Larouche, D.; Martinez, R.; Breton, F. Mixed-mode growth of a multicomponent precipitate in the quasi-steady state regime. Mater. Theor. 2018, 2, 4. [Google Scholar] [CrossRef]
- Bird, R.B.; Lightfoot, E.N.; Stewart, W.E. Transport phenomena, Rev., 3nd ed.; John Wiley: New York, NY, USA, 2007. [Google Scholar]
- Andersson, J.O.; Helander, T.; Höglund, L.; Shi, P.; Sundman, B. Thermo-Calc & DICTRA, computational tools for materials science. Calphad 2002, 26, 273–312. [Google Scholar] [CrossRef]
- TCAL5. TCS Al-based Alloys Database, version 5.0; Thermo-Calc Software AB: Solna, Sweden, 2018.
- MOBAL1. TCS Al-alloys Mobility Database, version 1.0; Thermo-Calc Software AB: Solna, Sweden, 2016.
- Povoden-Karadeniz, E. Thermodynamic Data from MatCalc Database ‘mc_al.tdb’, version 2.030. 2015.

| Parameter | Value |
|---|---|
| Temperature (K) | 600 |
| Nominal molar fraction of Cu, | 0.01 |
| Radius of the precipitate at the start of the mixed-mode model, ac | 2 nm |
| Number density of precipitate, | 1 × 1018 m−3 |
| Radius of the precipitate at the start of simulation | 2 nm |
| Initial layer thickness of the matrix in the DICTRA model | 618.4 nm |
| Molar volume of the precipitate, Vm | 1 × 10−5 m3/mol |
| Parameter | Value |
|---|---|
| The maximum molar fraction of Cu in the matrix at 600 K, | 0.00285 |
| Molar fraction of Cu in the precipitate | 0.33 |
| Molar fraction of Al in the precipitate | 0.67 |
| Surface energy, γ | 0 |
| Parameter | Value |
|---|---|
| Temperature (K) | 730 |
| The maximum molar fraction of Cu in the matrix | 0.011 |
| Radius of the precipitate at the end of the mixed-mode model, ac | 2 nm |
| Radius of the precipitate at the start of simulation | 175 nm |
| Initial layer thickness of the matrix in the DICTRA model | 445.4 nm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naseri, T.; Larouche, D.; Martinez, R.; Breton, F.; Massinon, D. Analytical Modeling of the Mixed-Mode Growth and Dissolution of Precipitates in a Finite System. Metals 2019, 9, 889. https://doi.org/10.3390/met9080889
Naseri T, Larouche D, Martinez R, Breton F, Massinon D. Analytical Modeling of the Mixed-Mode Growth and Dissolution of Precipitates in a Finite System. Metals. 2019; 9(8):889. https://doi.org/10.3390/met9080889
Chicago/Turabian StyleNaseri, Tohid, Daniel Larouche, Rémi Martinez, Francis Breton, and Denis Massinon. 2019. "Analytical Modeling of the Mixed-Mode Growth and Dissolution of Precipitates in a Finite System" Metals 9, no. 8: 889. https://doi.org/10.3390/met9080889
APA StyleNaseri, T., Larouche, D., Martinez, R., Breton, F., & Massinon, D. (2019). Analytical Modeling of the Mixed-Mode Growth and Dissolution of Precipitates in a Finite System. Metals, 9(8), 889. https://doi.org/10.3390/met9080889





