Numerical Modeling of Open-Eye Formation and Mixing Time in Argon Stirred Industrial Ladle
Abstract
1. Introduction
2. Materials and Methods
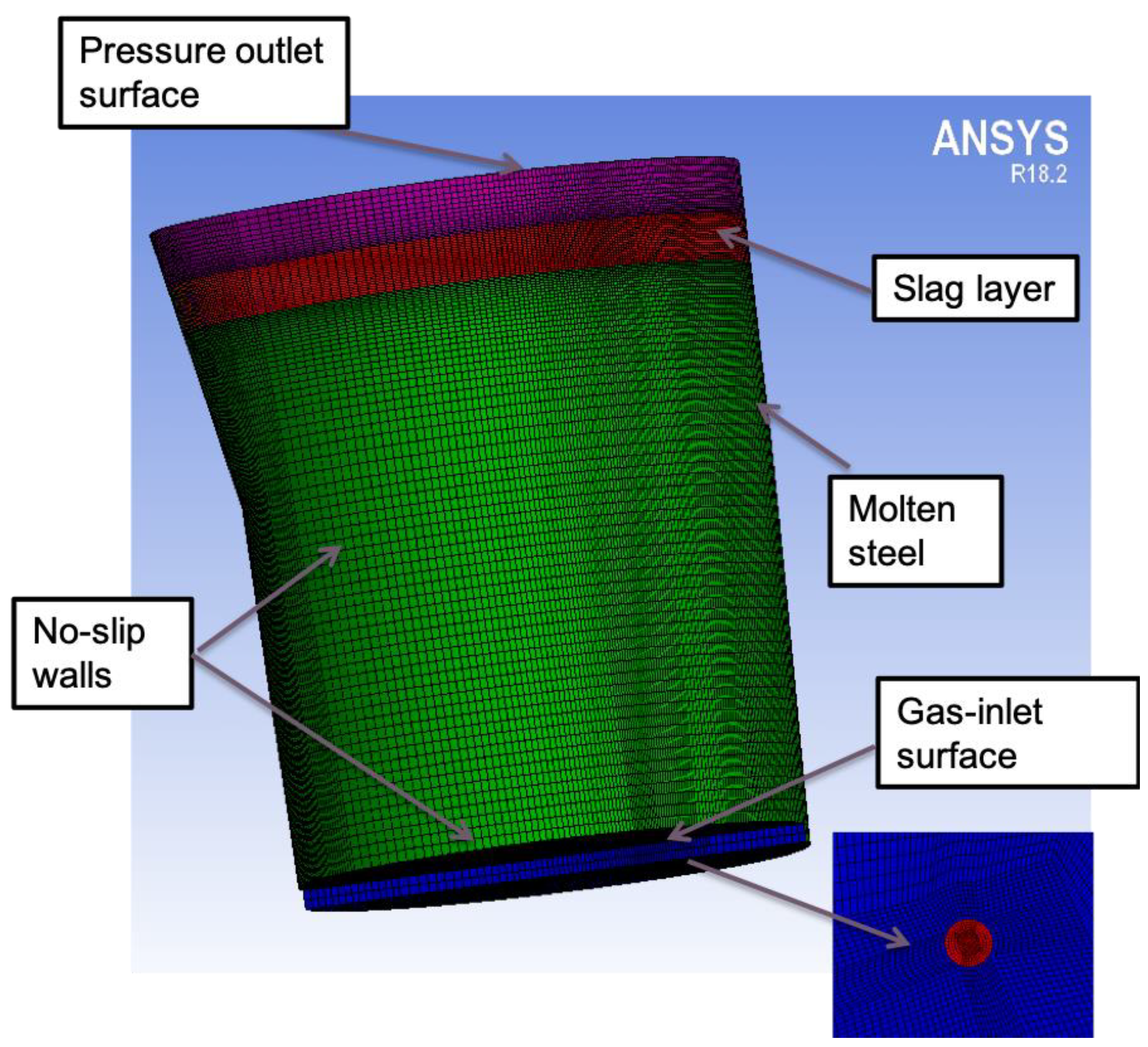
2.1. Model Description
2.2. Experimental Details
2.3. Numerical Details
3. Results and Discussion
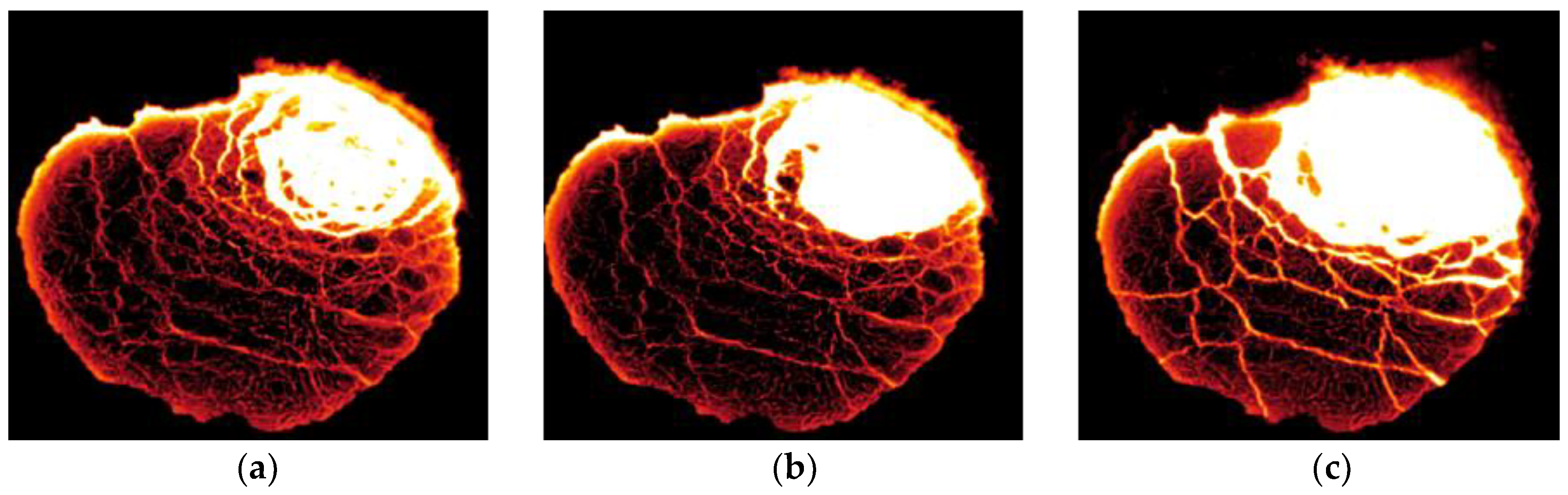
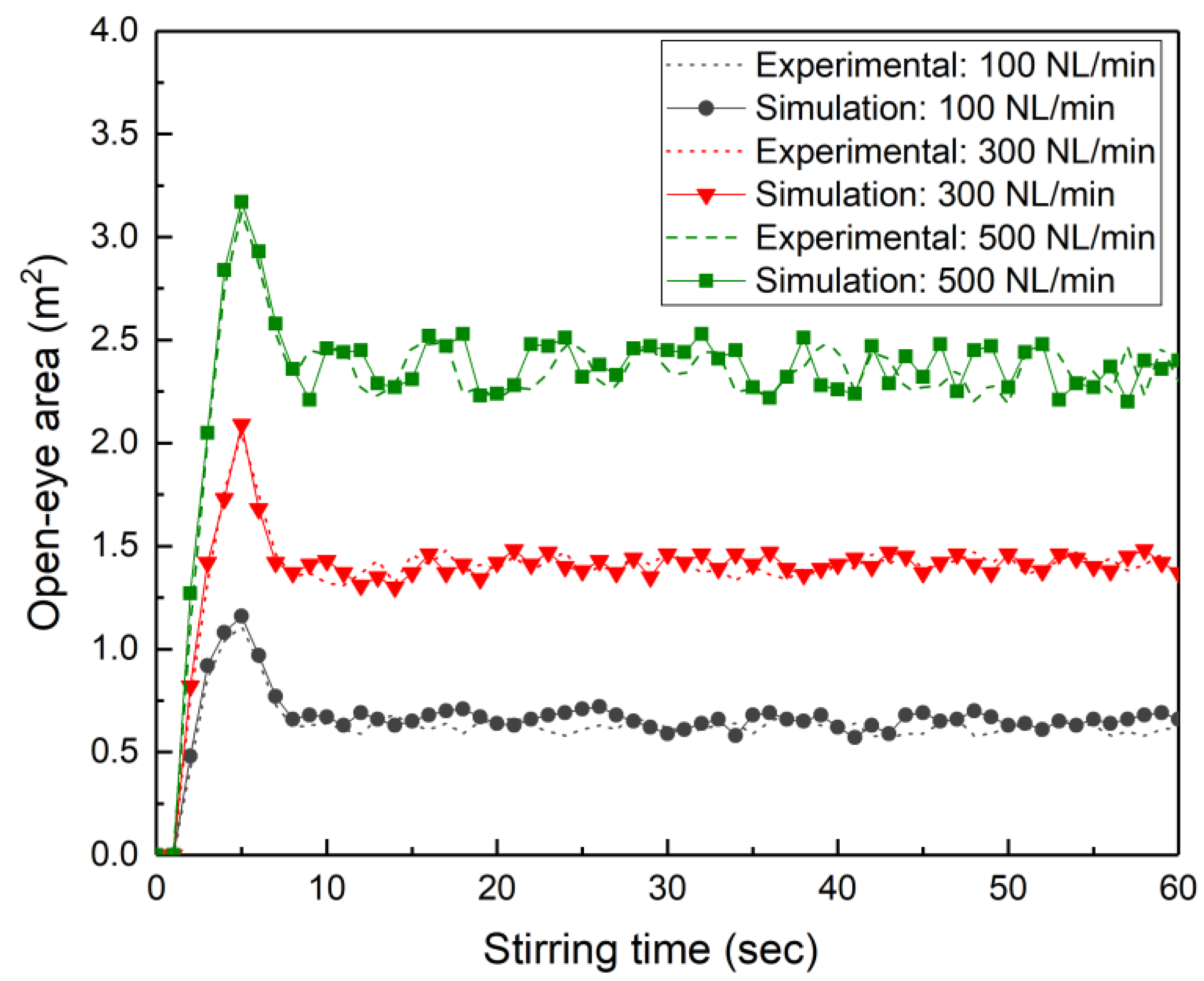
3.1. Effect of Gas Flow Rate on Open-Eye Formation
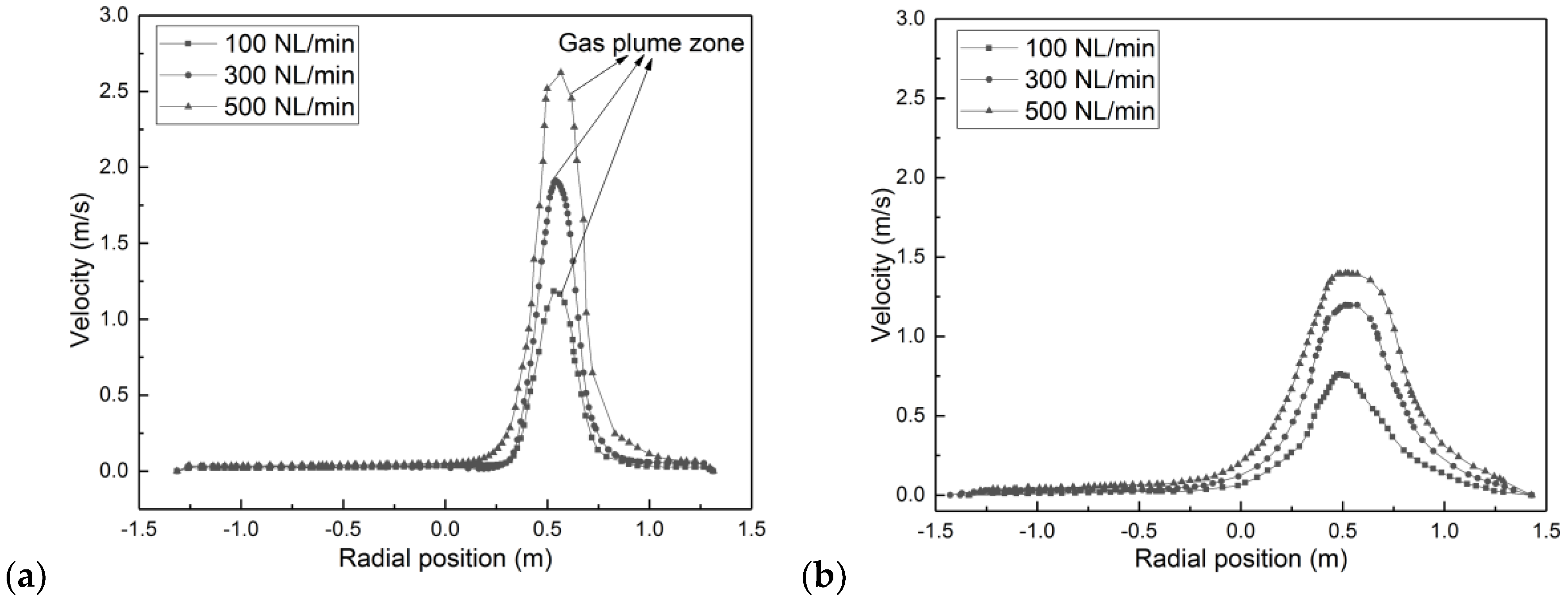
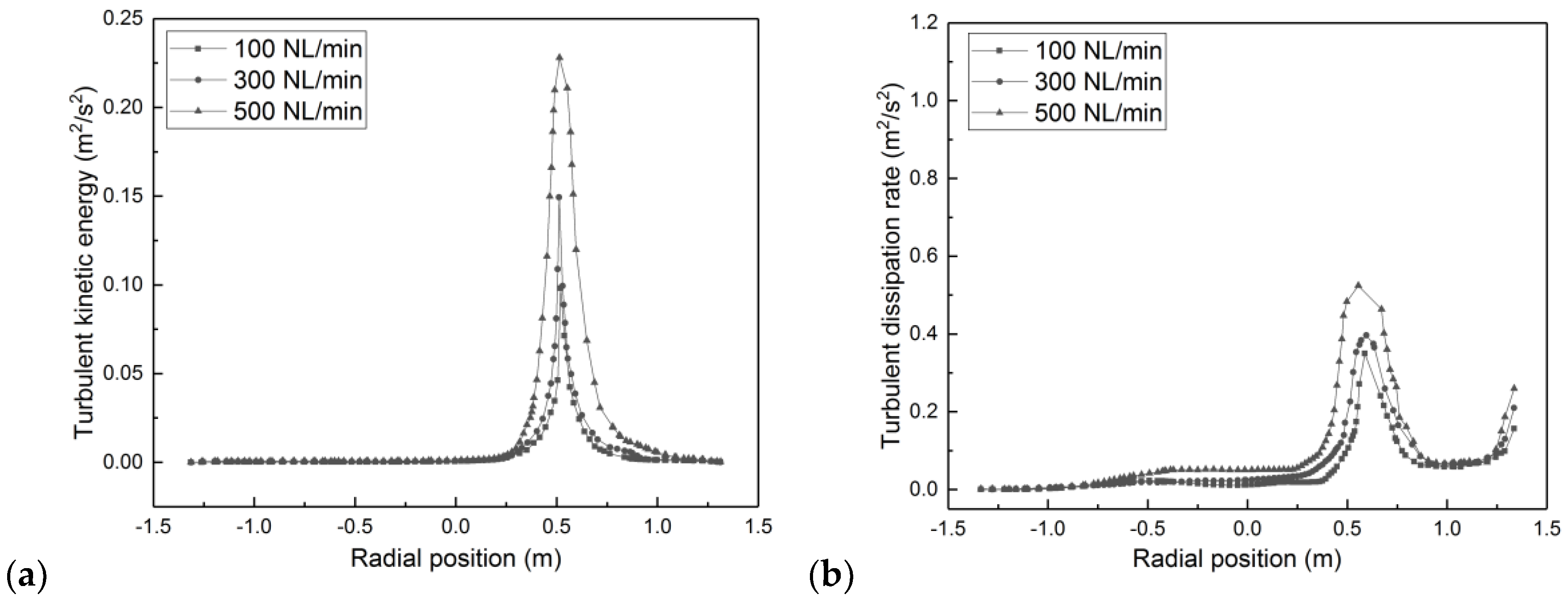
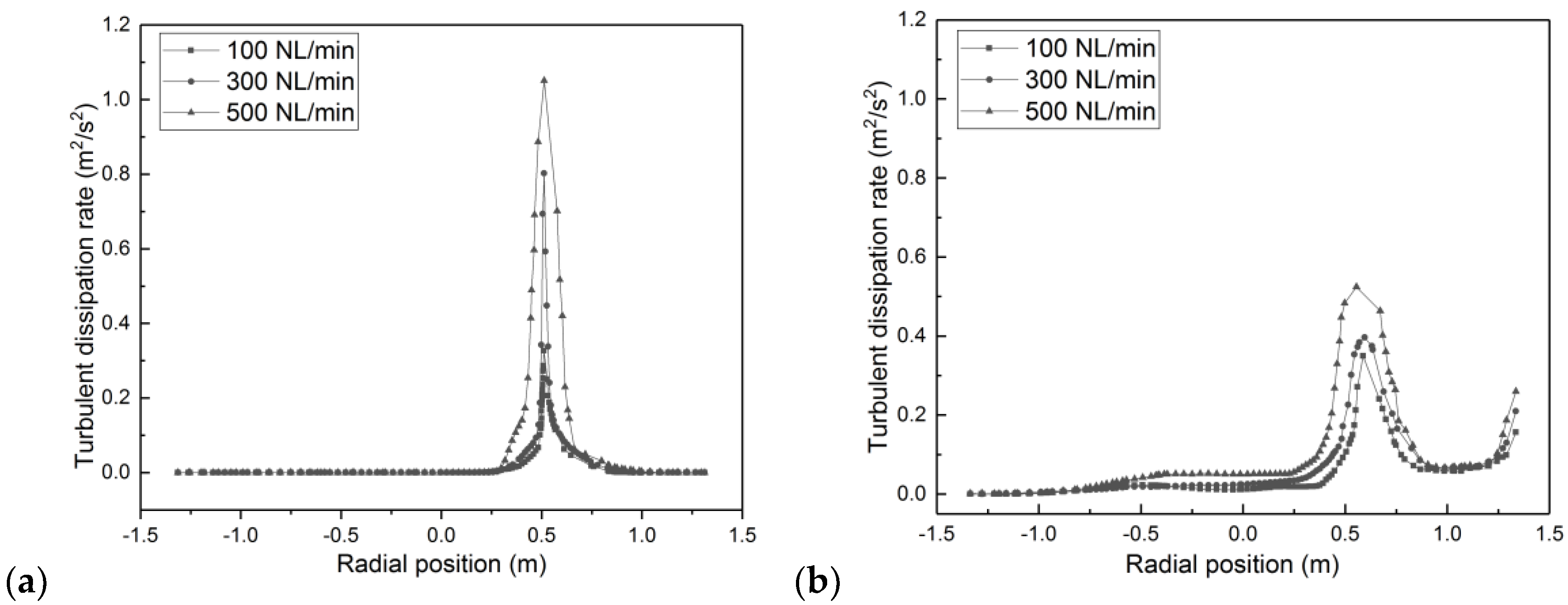
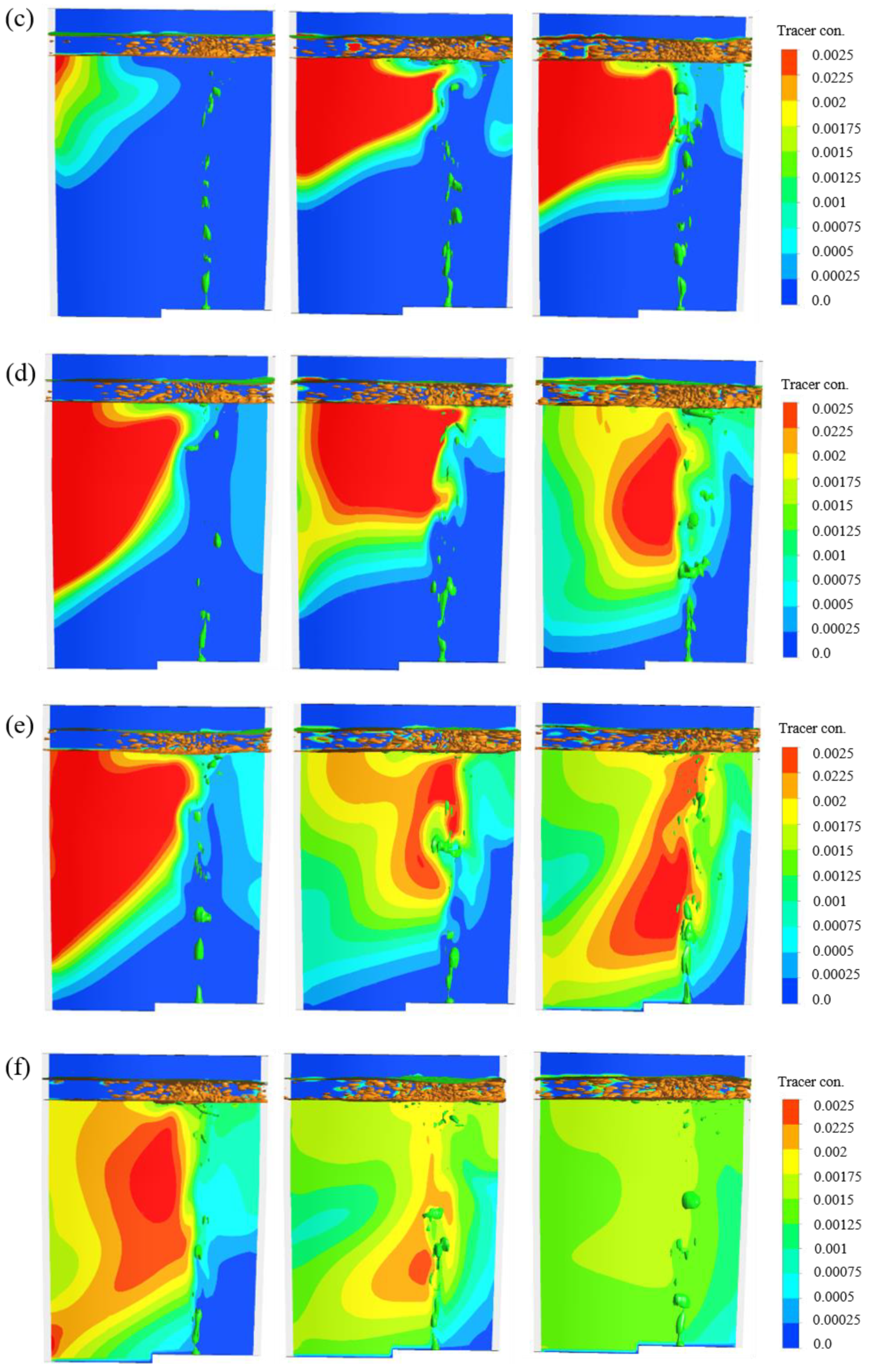
3.2. Flow Field Distribution
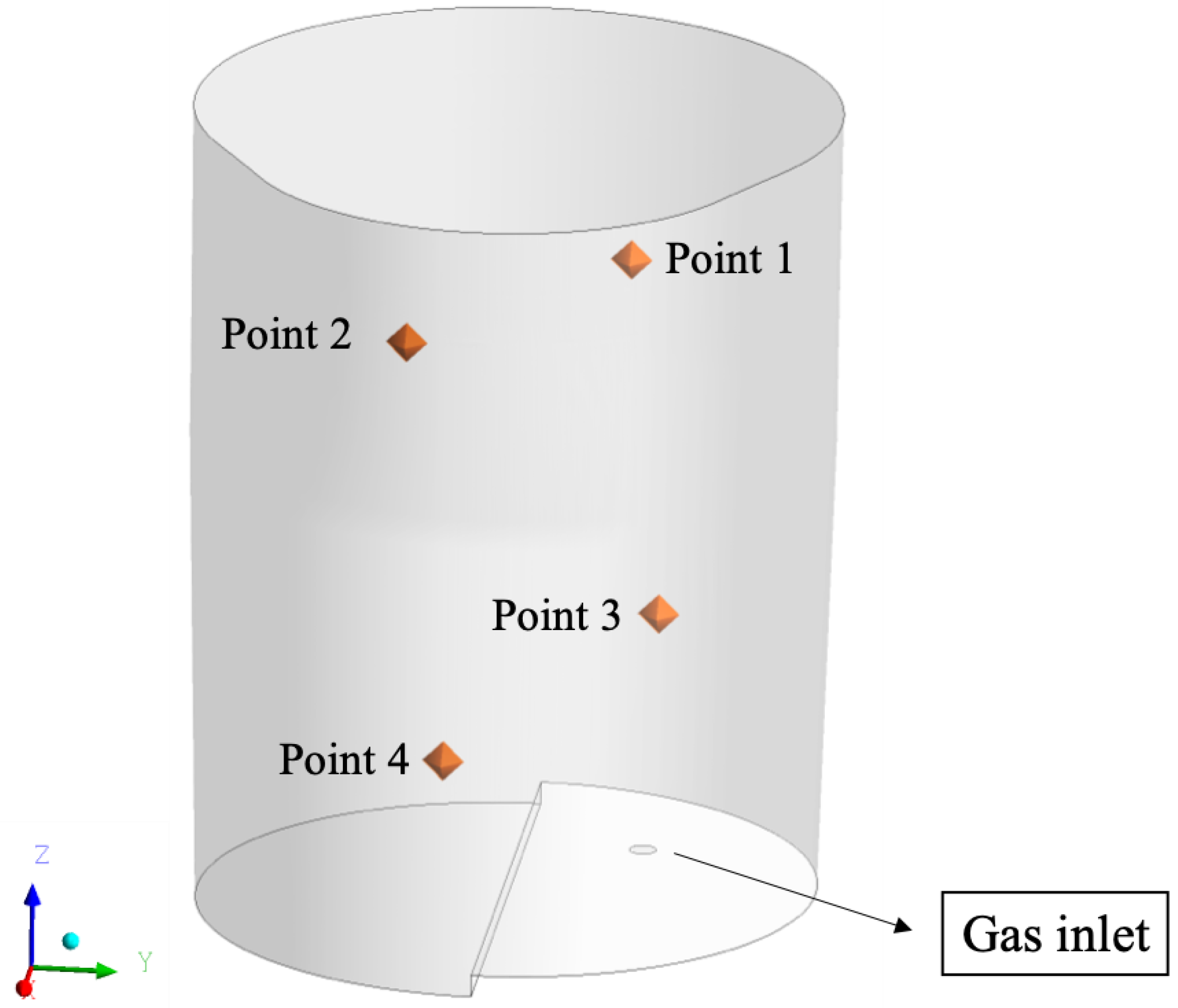
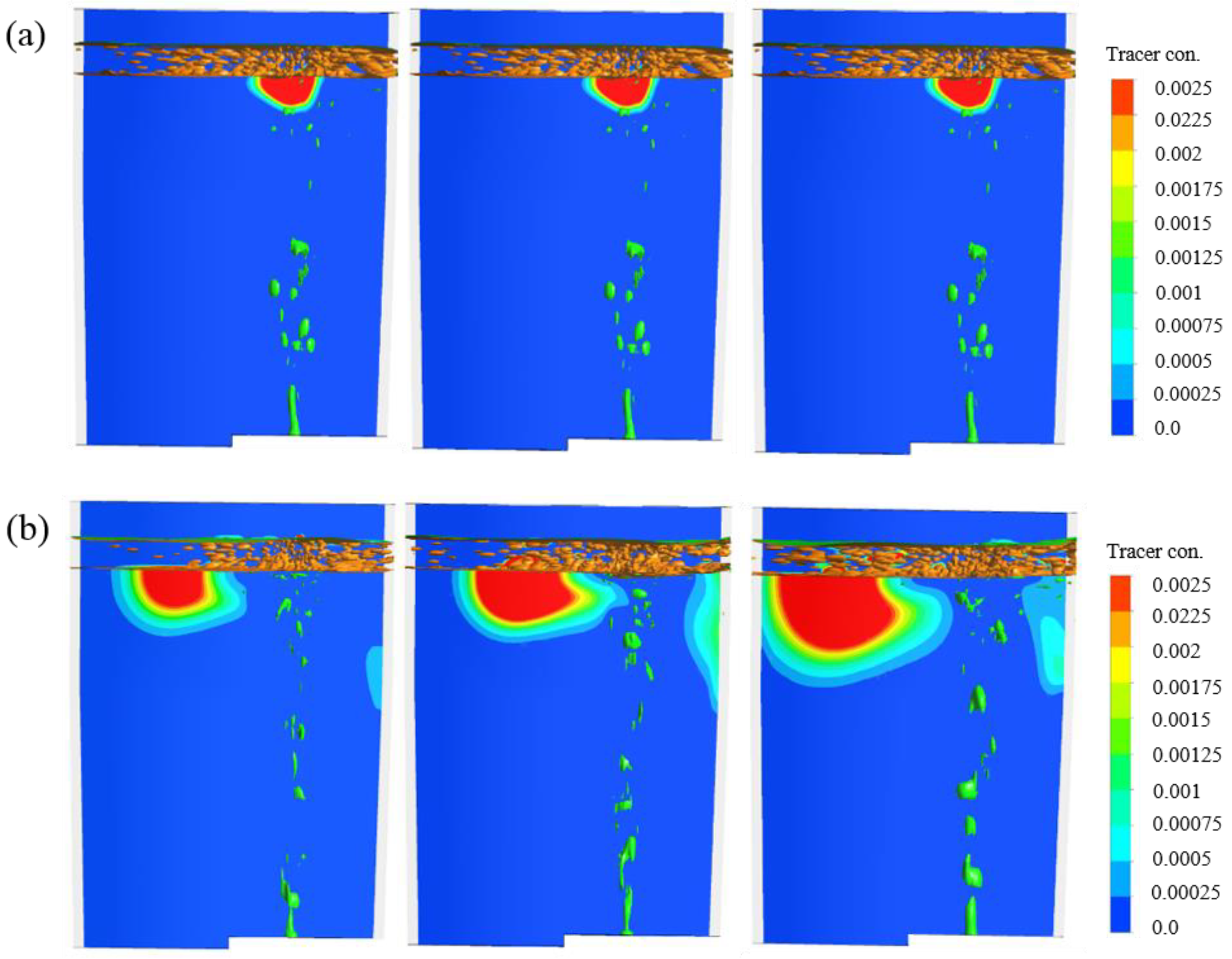
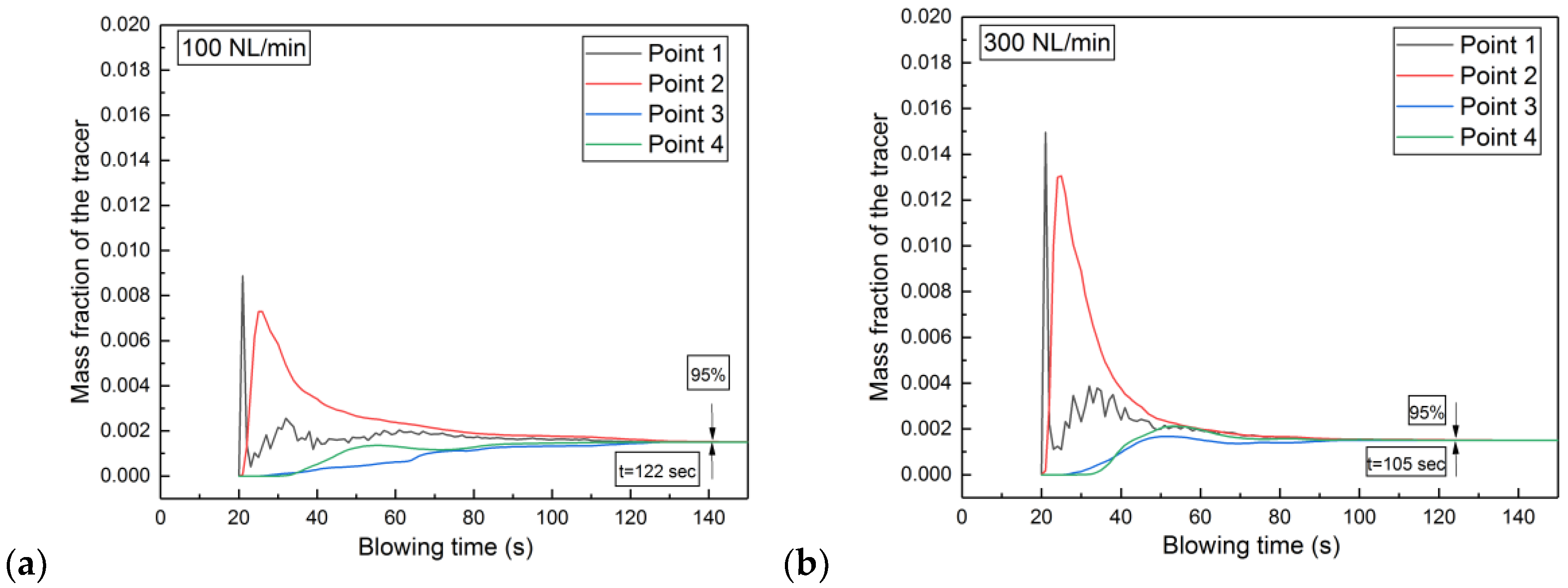
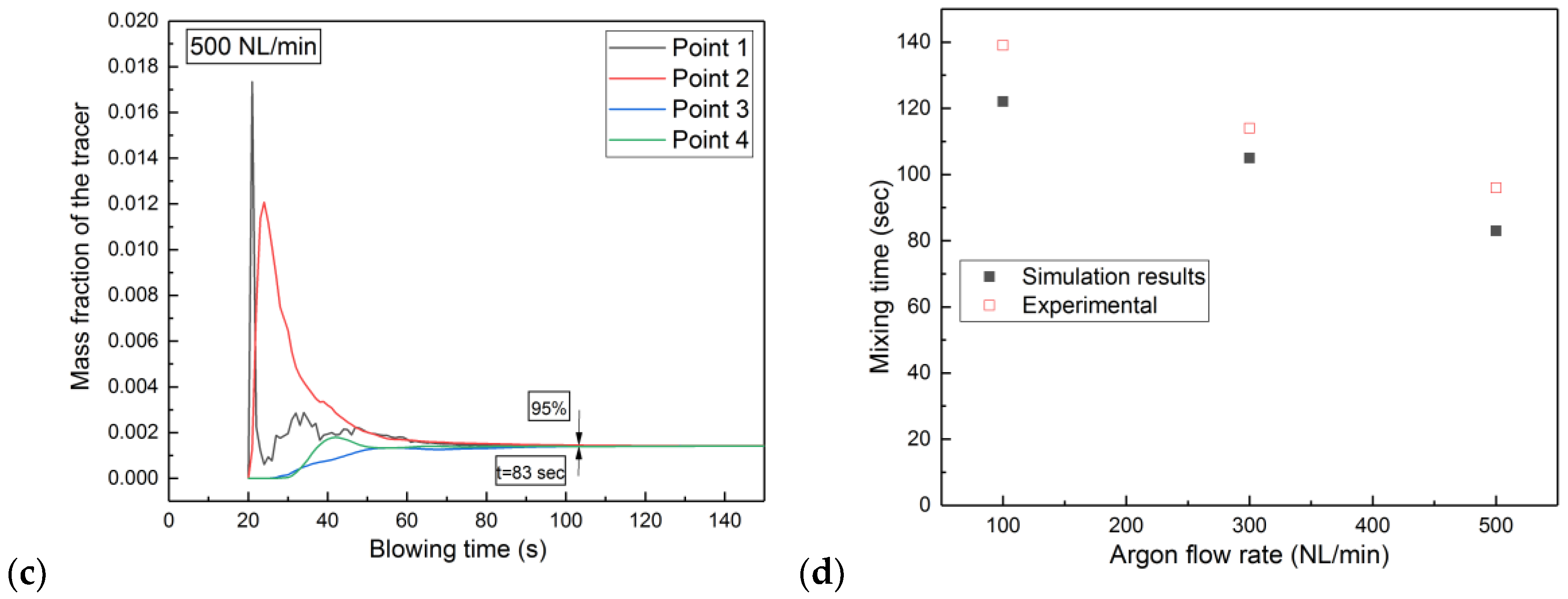
3.3. Mixing Behavior
4. Conclusions
- The flow patterns of the molten steel inside the ladle furnace are largely dependent on the argon flow rate. The flow velocity is very high at heights near to the bottom of the ladle furnace, and it tends to decrease as the flow moves upwards.
- The increase in the flow rate of argon gas from 100 to 500 NL/min enlarges the open-eye size from 0.66 to 2.36 m2.
- The simulated mixing time (95% criterion) of tracer addition into the metal bath decreased from 139 s to 96 s when the argon flow rate was increased from 100 to 500 NL/min.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Peranandhanthan, M.; Mazumdar, D. Modeling of Slag Eye Area in Argon Stirred Ladles. ISIJ Int. 2010, 50, 1622–1631. [Google Scholar] [CrossRef]
- Patil, S.P.; Satish, D.; Peranadhanathan, M.; Mazumdar, D. Mixing Models for Slag Covered, Argon Stirred Ladles. ISIJ Int. 2010, 50, 1117–1124. [Google Scholar] [CrossRef]
- Mandal, J.; Patil, S.; Madan, M.; Mazumdar, M. Mixing Time and Correlations for Ladles Stirred with Dual Plugs. Metall. Mater. Trans. B 2005, 36, 479–487. [Google Scholar] [CrossRef]
- Cao, Q.; Nastac, L. Mathematical Investigation of Fluid Flow, Mass Transfer, and Slag-steel Interfacial Behavior in Gas Stirred Ladles. Metall. Mater. Trans. B 2018, 49, 1388–1404. [Google Scholar] [CrossRef]
- Cao, Q.; Nastac, L. Mathematical Modeling of the Multiphase Flow and Mixing Phenomena in a Gas-Stirred Ladle: The Effect of Bubble Expansion. JOM 2018, 70, 2071–2081. [Google Scholar] [CrossRef]
- Cao, Q.; Nastac, L. Numerical Modelling of the Transport and Removal of Inclusions in an Industrial Gas-Stirred Ladle. Ironmak. Steelmak. 2018, 45, 984–991. [Google Scholar] [CrossRef]
- Valentin, P.; Bruch, C.; Kyrylenko, Y.; Köchner, H.; Dannert, C. Influence of the Stirring Gas in a 170-t Ladle on Mixing Phenomena- Formation and On-line Control of Open-eye at an Industrial LD Steel Plant. Steel Res. Int. 2009, 80, 552–558. [Google Scholar]
- Cloete, S.W.P.; Eksteen, J.J.; Bradshaw, S.M. A Mathematical Modelling Study of Fluid Flow and Mixing in Full-Scale Gas-Stirred Ladles. Prog. Comput. Fluid Dyn. 2009, 9, 345–356. [Google Scholar] [CrossRef]
- Cloete, S.W.P.; Eksteen, J.J.; Bradshaw, S.M. A Numerical Modelling Investigation into Design Variables Influencing Mixing Efficiency in Full Scale Gas Stirred Ladles. Miner. Eng. 2013, 46–47, 16–24. [Google Scholar] [CrossRef]
- Li, L.; Liu, Z.; Li, B.; Matsuura, H.; Tsukihashi, F. Water Model and CFD-PBM Coupled Model of Gas-Liquid-Slag Three Phase Flow in Ladle Metallurgy. ISIJ Int. 2015, 55, 1337–1346. [Google Scholar] [CrossRef]
- Li, L.; Li, B. Investigation of Bubble-Slag Layer Behaviors with Hybrid Eulerian-Lagrangian Modeling and Large Eddy Simulation. JOM 2016, 68, 2160–2169. [Google Scholar] [CrossRef]
- Li, L.; Liu, Z.; Cao, M.; Li, B. Large Eddy Simulation of Bubble Flow and Slag Layer Behavior in Ladle with Discrete Phase Model (DPM)-Volume of Fluid (VOF) Coupled Model. JOM 2015, 67, 1459–1467. [Google Scholar] [CrossRef]
- Gonzalez, H.; Ramos-Banderas, J.A.; Torress-Alonso, E.; Solorio-Diaz, G.; Hernandez-Bocanegra, C.A. Multiphase Modeling of Fluid Dynamic in Ladle Steel Operations Under Non-isothermal Conditions. J. Iron Steel Res. Int. 2017, 24, 888–900. [Google Scholar] [CrossRef]
- Amaro-Villeda, A.M.; Ramirez-Argaez, M.A.; Conejo, A.N. Effect of Slag Properties on Mixing Phenomena in Gas-stirred Ladles by Physical Modeling. ISIJ Int. 2014, 54, 1–8. [Google Scholar] [CrossRef]
- Zhu, M.Y.; Inomoto, T.; Sawada, I.; Hsiao, T.C. Fluid Flow and Mixing Phenomena in the Ladle Stirred by Argon through Multi-Tuyere. ISIJ Int. 1995, 35, 472–479. [Google Scholar] [CrossRef]
- Lou, W.; Zhu, M. Numerical Simulations of Inclusion Behaviour and Mixing Phenomena in Gas-stirred Ladles with Different Arrangement of Tuyeres. ISIJ Int. 2014, 54, 9–18. [Google Scholar] [CrossRef]
- Rodriguez-Avila, J.; Morales, R.D.; Najera-Bastida, A. Numerical Study of Multiphase Flow Dynamics of Plunging Jets of Liquid Steel and Trajectories of Ferroalloys Additios in a Ladle during Tapping Operations. ISIJ Int. 2012, 52, 814–822. [Google Scholar] [CrossRef]
- Liu, Z.; Li, L.; Li, B. Modeling of Gas-Steel-Slag Three-Phase Flow in Ladle Metallurgy: Part I. Physical Modeling. ISIJ Int. 2017, 57, 1971–1979. [Google Scholar] [CrossRef]
- Li, L.; Li, B.; Liu, Z. Modeling of Gas-Steel-Slag Three-Phase Flow in Ladle Metallurgy: Part II. Multi-scale Mathematical Model. ISIJ Int. 2017, 57, 1980–1989. [Google Scholar] [CrossRef]
- Liu, W.; Tang, H.; Yang, S.; Wang, M.; Li, J.; Liu, Q.; Liu, J. Numerical Simulation of Slag Eye Formation and Slag Entrapment in a Bottom-Blown Argon-Stirred Ladle. Metall. Mater. Trans. B 2018, 49, 2681–2691. [Google Scholar] [CrossRef]
- Haiyan, T.; Xiaochen, G.; Guanghui, W.; Yong, W. Effect of Gas Blown Modes on Mixing Phenomena in a Bottom Stirring Ladle with Dual Plugs. ISIJ Int. 2016, 56, 2161–2170. [Google Scholar] [CrossRef]
- Madan, M.; Satish, D.; Mazumdar, D. Modeling of Mixing in Ladles Fitted with Dual Plugs. ISIJ Int. 2005, 45, 677–685. [Google Scholar] [CrossRef]
- Wu, L.; Valentin, P.; Sichen, D. Study of Open Eye Formation in an Argon Stirred Ladle. Steel Res. Int. 2010, 81, 508–515. [Google Scholar] [CrossRef]
- Thunman, M.; Eckert, S.; Hennig, O.; Björkvall, J.; Sichen, D. Study of the Formation of Open-eye and Slag Entrainment in Gas Stirred Ladle. Steel Res. Int. 2010, 78, 849–856. [Google Scholar]
- Li, B.; Yin, H.; Zhou, C.Q.; Tsukihashi, F. Modeling of Three-phase Flows and Behavior of Slag/Steel Interface in an Argon Gas Stirred Ladle. ISIJ Int. 2008, 48, 1704–1711. [Google Scholar] [CrossRef]
- Liu, H.; Qi, Z.; Xu, M. Numerical Simulation of Fluid Flow and Interfacial Behavior in Three-Phase Argon-Stirred Ladles with One Plug and Dual Plugs. Steel Res. Int. 2011, 82, 440–458. [Google Scholar] [CrossRef]
- Singh, U.; Anapagaddi, R.; Mangal, S.; Padmanabhan, K.A.; Singh, A.K. Multiphase Modeling of Bottom-Stirred Ladle for Prediction of Slag-Steel Interface and Estimation of Desulfurization Behavior. Metall. Mater. Trans. B 2016, 47, 1804–1816. [Google Scholar] [CrossRef]
- Ramasetti, E.K.; Visuri, V.V.; Sulasalmi, P.; Mattila, R.; Fabritius, T. Modeling of the Effect of the Gas Flow Rate on the Fluid Flow and Open-Eye Formation in a Water Model of a Steel Making Ladle. Steel Res. Int. 2019, 90, 1–12. [Google Scholar] [CrossRef]
- Ramasetti, E.K.; Visuri, V.V.; Sulasalmi, P.; Gupta, A.K.; Palovaara, T.; Fabritius, T. Physical and CFD Modelling of the Effect of Top Layer Properties on the Formation of Open-eye in Gas-stirred Ladles with Single and Dual-plugs. Steel Res. Int. 2019. [Google Scholar] [CrossRef]
- Valencia, J.J.; Quested, P.N. ASM Handbook; ASM International: Geauga County, OH, USA, 2008; Volume 15, p. 468. [Google Scholar]
- Xie, Y.; Oeters, F. Experimental Studies on the Flow Velocity of Molten Metals in a Ladle Model at Centric Gas Blowing. Steel Res. Int. 1992, 3, 93–104. [Google Scholar] [CrossRef]
- Xie, Y.; Orsten, S.; Oeters, F. Behaviour of Bubbles at Gas Blowing into Liquid Wood’s Metal. ISIJ Int. 1992, 1, 66–75. [Google Scholar] [CrossRef]

| Physical Properties at 1812 K | Value | Unit |
|---|---|---|
| Density of liquid steel [30] | 6913 | kg/m3 |
| Viscosity of liquid steel [30] | 0.005281 | Pa s |
| Density of slag | 2746 | kg/m3 |
| Viscosity of slag | 0.081 | Pa s |
| Density of argon gas | 0.8739 | kg/m3 |
| Viscosity of argon gas | 2.2616 × 10−5 | Pa s |
| Temperature of bath | 1812 | K |
| Flow rate of argon gas | 100, 300 and 500 | NL/min |
| Slag layer height | 35 | cm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramasetti, E.K.; Visuri, V.-V.; Sulasalmi, P.; Fabritius, T.; Saatio, T.; Li, M.; Shao, L. Numerical Modeling of Open-Eye Formation and Mixing Time in Argon Stirred Industrial Ladle. Metals 2019, 9, 829. https://doi.org/10.3390/met9080829
Ramasetti EK, Visuri V-V, Sulasalmi P, Fabritius T, Saatio T, Li M, Shao L. Numerical Modeling of Open-Eye Formation and Mixing Time in Argon Stirred Industrial Ladle. Metals. 2019; 9(8):829. https://doi.org/10.3390/met9080829
Chicago/Turabian StyleRamasetti, Eshwar Kumar, Ville-Valtteri Visuri, Petri Sulasalmi, Timo Fabritius, Tommi Saatio, Mingming Li, and Lei Shao. 2019. "Numerical Modeling of Open-Eye Formation and Mixing Time in Argon Stirred Industrial Ladle" Metals 9, no. 8: 829. https://doi.org/10.3390/met9080829
APA StyleRamasetti, E. K., Visuri, V.-V., Sulasalmi, P., Fabritius, T., Saatio, T., Li, M., & Shao, L. (2019). Numerical Modeling of Open-Eye Formation and Mixing Time in Argon Stirred Industrial Ladle. Metals, 9(8), 829. https://doi.org/10.3390/met9080829








