1. Introduction
For crash-relevant components of the body-in-white design of vehicles, a combination of high strength and high plasticity is necessary to guarantee passenger safety and lightweight construction at the same time. This combination of mechanical material properties is provided by high manganese steels (HMnS). Due to the additional deformation mechanism of twinning, the group of TWIP (twinning-induced plasticity) steels exhibit the possibility of forming complex geometries in combination with a high impact-energy-absorption potential [
1]. Strain hardening engineering can be applied on HMnS to adjust the hardening mechanism for ideal hardening behavior for specific applications. Bambach et al. [
2] argued that a good crash performance for a crash box, built for frontal impact, is achieved by a high initial strength of HMnS. The works of Haase et al. [
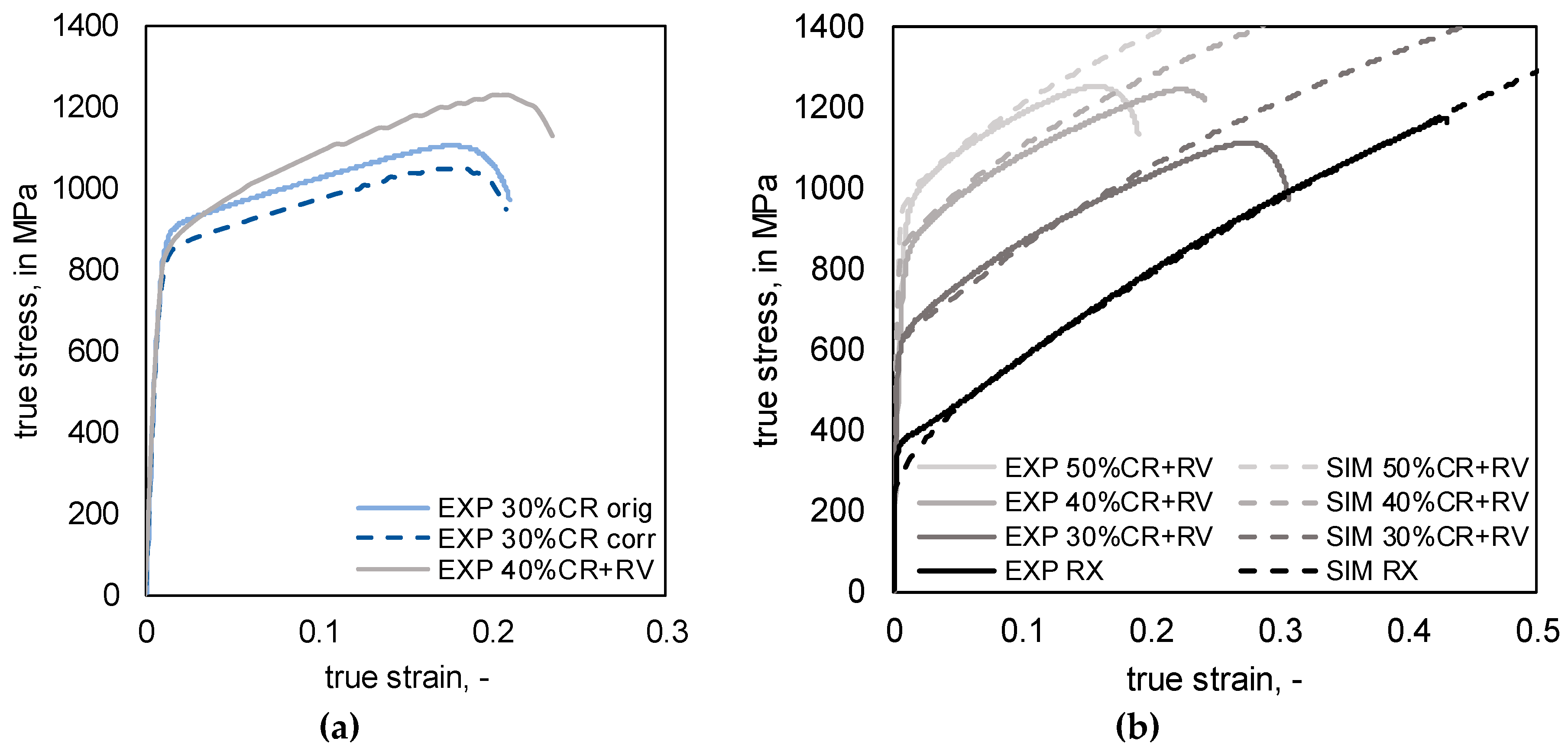
3,
4] showed that recovery (RV) annealing is a simple, promising processing route to overcome the shortcoming of low yield strength usually associated with TWIP steels in recrystallized (RX) condition. While dislocation density of the cold rolled (CR) condition of a Fe-23Mn-1.5Al-0.3C is reduced during the RV annealing, the twin fraction remains constant, resulting in high yield strength with moderate formability. The material condition after RV annealing of Fe-23Mn-1.5Al-0.3C has been applied to the experimental crash test by drop tower tests and successfully increased the specific energy absorption of the crash box [
2,
5]. Due to the higher yield strength compared to the fully RX material condition, an increase of the energy absorption per mass was achieved and resulted in a shorter crash distance. In addition to material strength, the crash behavior and especially the buckling stress, which is necessary for initiation of the folds, is depending on the geometry of the crash boxes. Bambach et al. showed in their work [
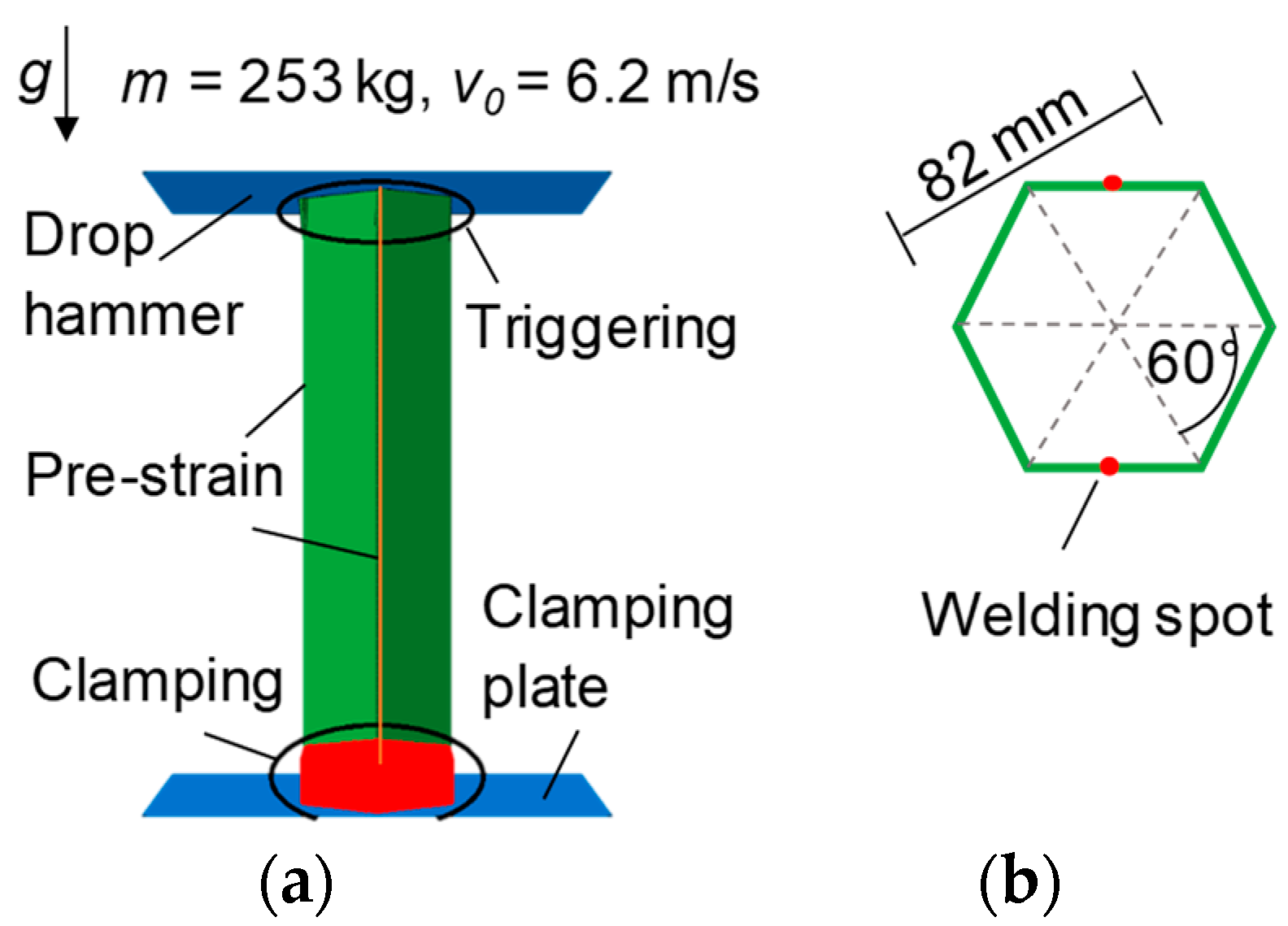
2] that the cross-section geometry of a crash box of the same material has a significant influence on the crashworthiness. While a square cross section needs a higher crash distance, the hexagon shape showed a performance nearly as good as a circular shape with the same cross-sectional area. Therefore, an additional degree of freedom exists in the design of a crash box in the form of the geometry. In this work, only a hexagonal cross section with constant diameter is used and the influence of geometry is only considered by a variation of the sheet thickness.
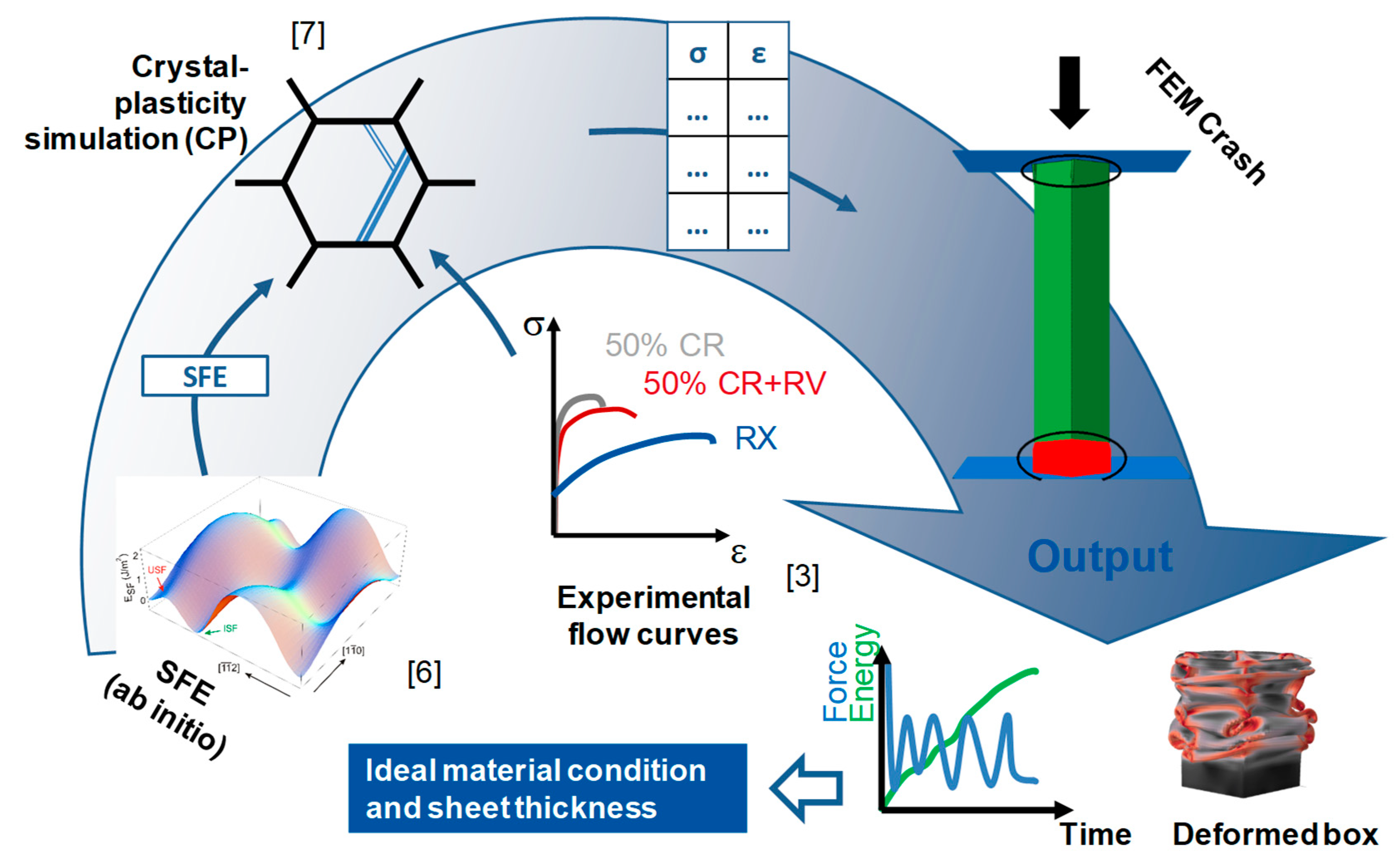
Experimental crash tests are very time consuming and expensive. In order to save costs, a computer-aided design of the ideal material condition and geometry design can be realized by finite element (FE) simulation in combination with sophisticated material models. In this work, an ICME (integrated computational material engineering) approach, depicted in
Figure 1, is used to reduce the experimental effort of the crash box design. Material parameters of HMnS were calculated at different scales and used to predict the hardening behavior of different material conditions, which is finally used to simulate the crash behavior of a crash box. On the atomistic scale, the stacking fault energy of the HMnS was calculated by a combination of thermodynamic and ab initio calculations and was taken from [
6]. The stacking fault energy (SFE) influences the activation of different deformation mechanisms, which are considered during the simulation of hardening behavior with a physics-based crystal plasticity (CP) model, which is described in detail in [
7]. The flow curves of different material conditions are then used in FE simulation to predict the crash behavior. The consideration of the microstructure during FE simulation is necessary because the hardening behavior is significantly correlated to the microstructure and deformation mechanisms. Due to high deformation rates and high dissipation during the crash, the deformation mechanism can change. With the help of the ICME approach, different initial microstructures can be analyzed with respect to their influence on the crash behavior and give a direct insight into promising microstructure-design strategies.
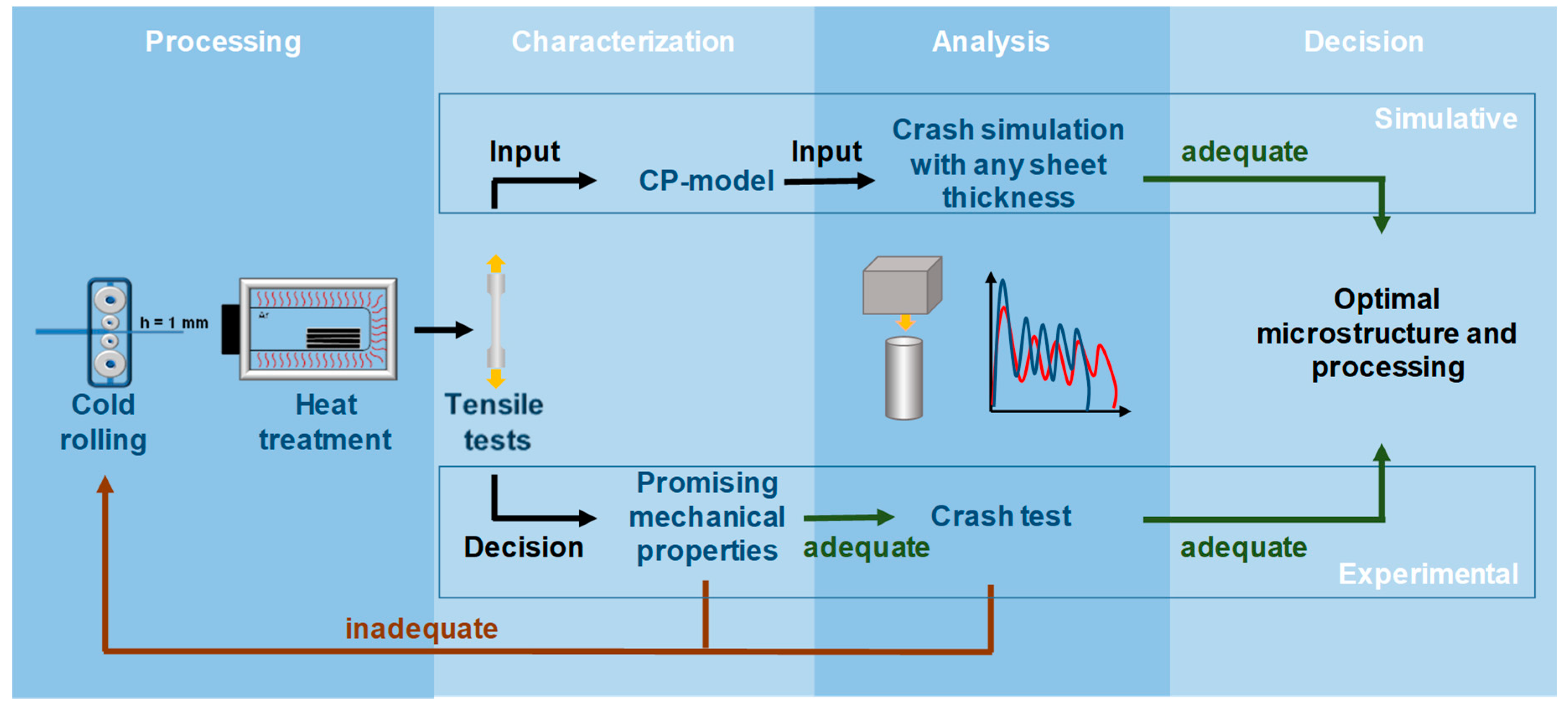
From an economic point of view, a successfully validated simulation chain enables the reduction of experimental effort.
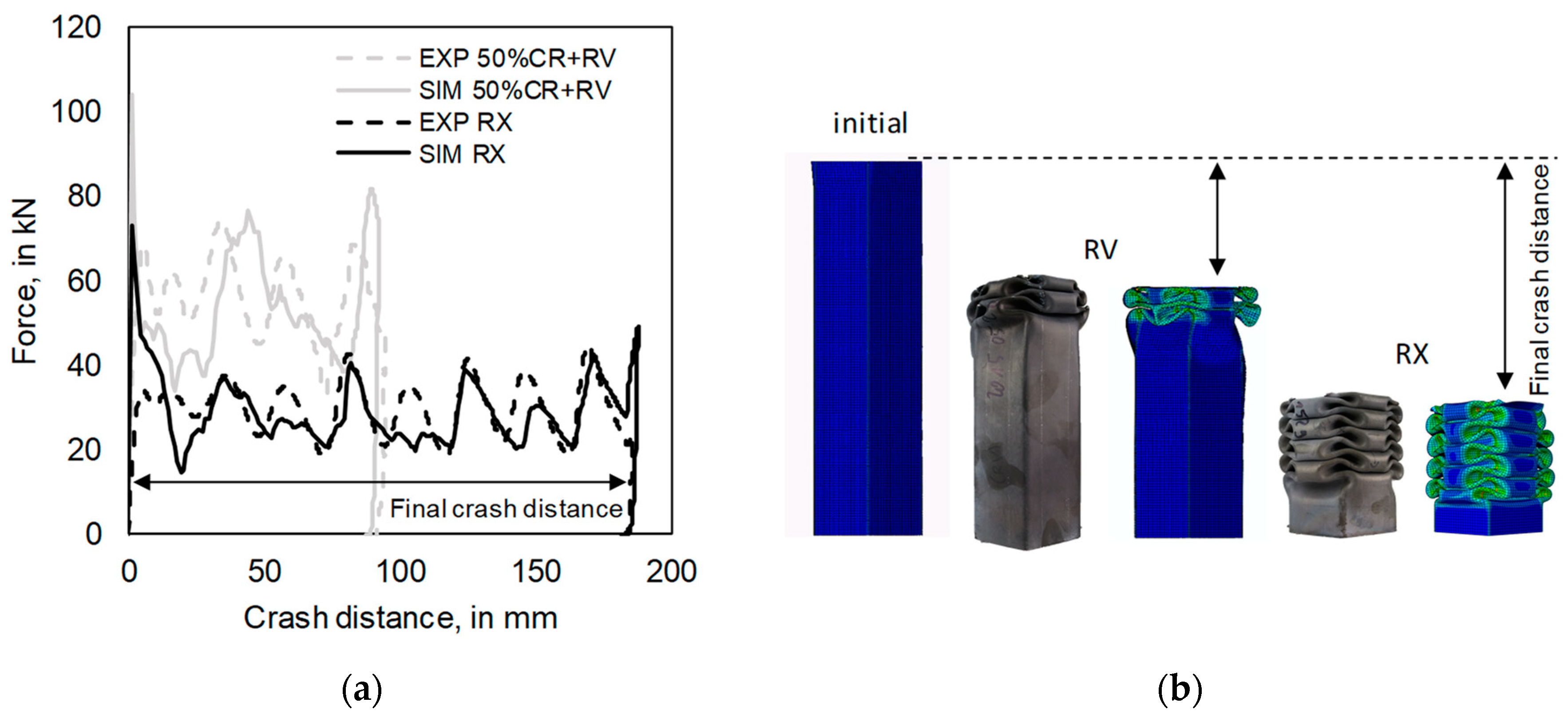
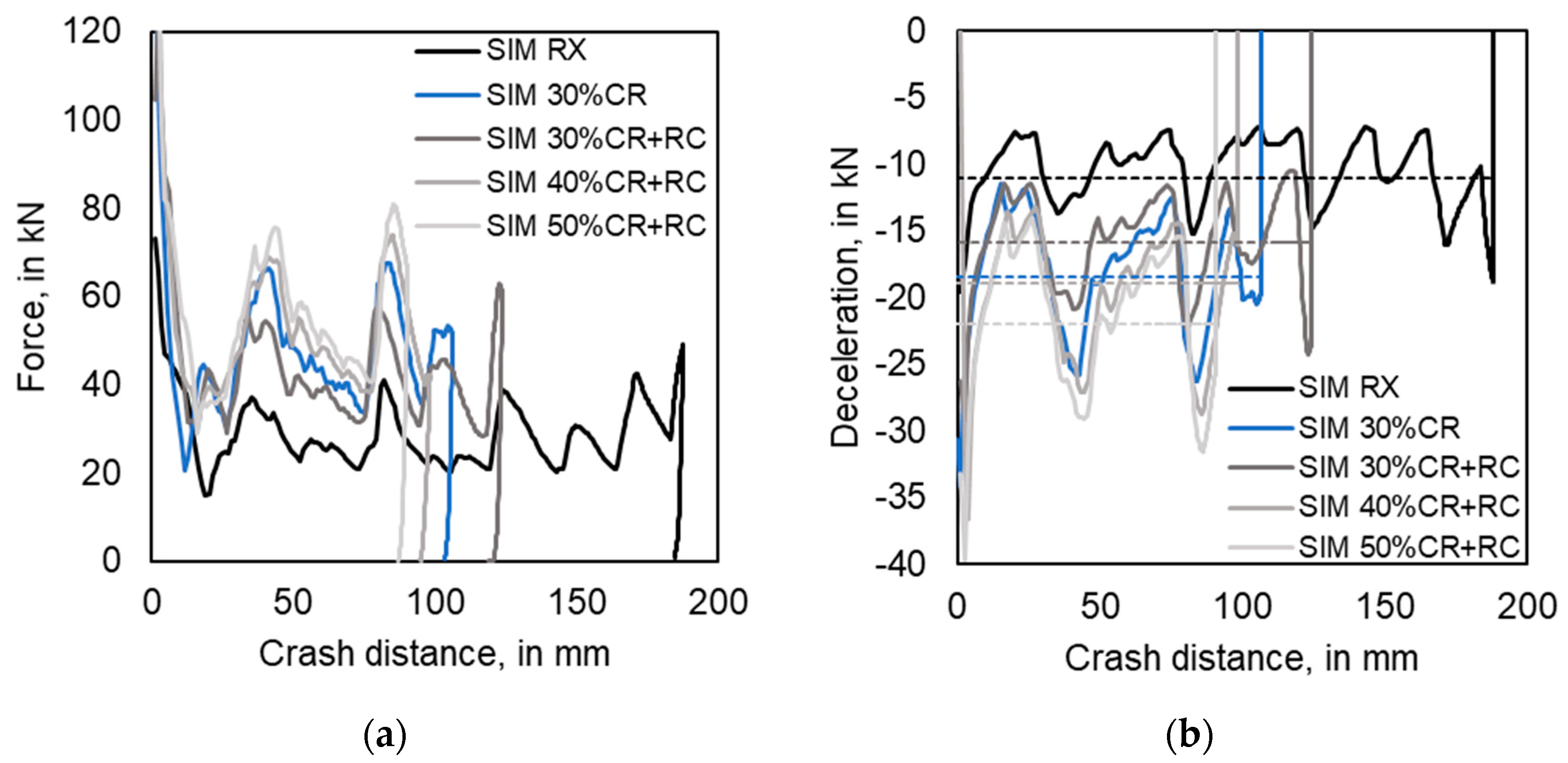
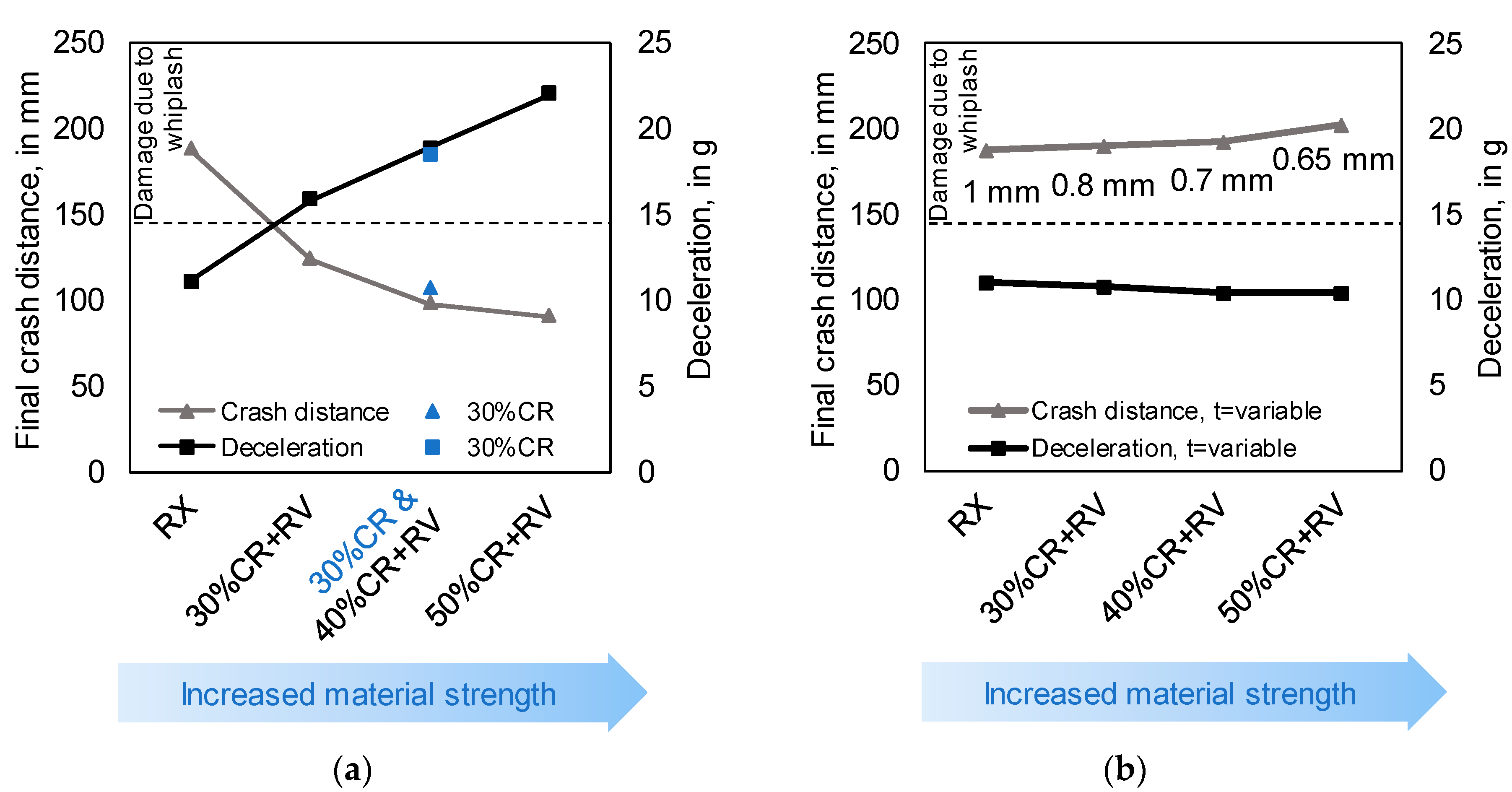
Figure 2 compares the steps for an experimental and a more simulation-based design of a crash box. The traditional experimental-based design process is coupled to a high number of crash experiments for the different material conditions. In the process chain of a crash box, cold rolling and heat treatment are the relevant process steps to define the sheet thickness as well as the material condition and therefore, the mechanical properties. Additionally, all different material conditions have to be tested in tensile tests to make a first choice based on simplified criteria like ECO-index, the product of ultimate tensile strength and uniform elongation, or buckling stress [
2]. Both criteria allow for a first approximation of the energy absorption of different materials, while the buckling stress also considers the simplified geometry of a crash box. However, both criteria cannot replace the analysis of crash behavior under all boundary conditions. Another criterion, for example, is the mean deceleration to ensure passenger safety. A maximum value of 15 g (gravitational acceleration) for deceleration was identified as a limit by biomechanics specialists to avoid long-term damages due to whiplash in [
8]. In order to be able to evaluate the crash behavior of the different material conditions, it is necessary establish their performance in drop tower tests.
The simulation-based design of a crash box should reduce the effort of drop tower tests and should give a direct correlation between crash behavior and microstructure. Based on that, a suggestion for the optimal processing strategy can be given. Also, for the simulation-based design, experimental tensile tests are necessary to validate the material model. However, the decision of which material conditions are suitable for the crash, can be made without further experimental crash tests. For the simulation-based design, only specific material conditions have to be tested in tensile tests to set up the material model, which can then simulate the plastic behavior of other material conditions. The optimal combination of material condition and box geometry can then be identified by simulation and, if necessary, validated for selected conditions with drop tower tests. In contrast, the experimental-based design needs an iterative adaption of the processing during the design process to identify an adequate material condition for the crash behavior.
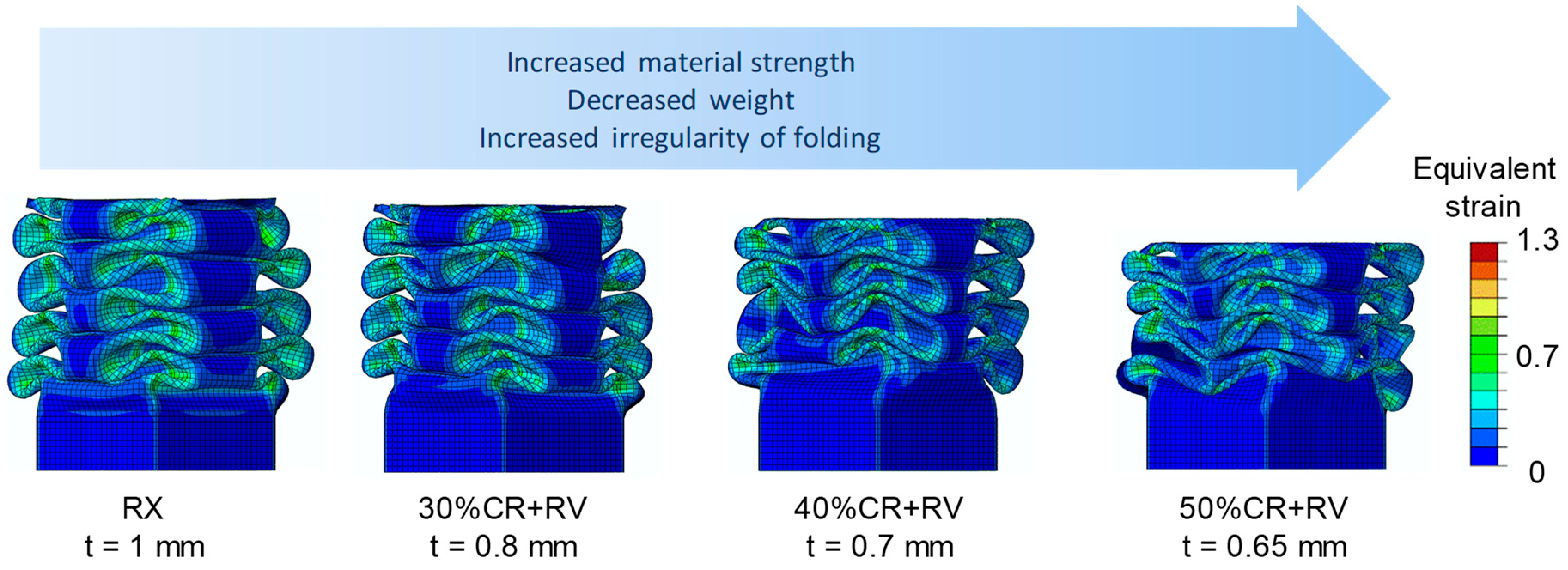
In this work, the crash behavior of high manganese TWIP steel is optimized combining multi-scale simulation tools as well as knowledge from different material science and engineering disciplines to an ICME approach. Within this ICME approach, the crash behavior of the different material conditions was analyzed using flow curves of HMnS subjected to different degrees of cold rolling and additional RV annealing in FE simulation of drop tower tests. In addition to the previously mentioned criteria of crash distance, passenger safety in terms of deceleration was considered as a criterion for ideal crash performance. The aim of the work was to identify the ideal combination of material strength and sheet thickness of crash boxes to fulfill the criteria of passenger safety and lightweight construction at the same time.
Author Contributions
Conceptualization, A.Q., C.H., F.R. and M.T.; software, F.R.; methodology, A.Q. and M.M.; investigation, A.Q., and M.M.; writing—original draft preparation, A.Q.; writing—review and editing, M.T., C.H., F.R., M.M., and G.H.; visualization, A.Q.; supervision, M.T., and G.H.; project administration, G.H. and M.T.; funding acquisition, G.H.
Funding
This research was funded by the “Deutsche Forschungsgemeinschaft” (DFG) within the Sonderforschungsbereich (Collaborative Research Center) 761 “Steel–ab initio” with project number 29898171 within a collaboration of part project B2, B4, A7, and C6.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- De Cooman, B.C.; Kwon, O.; Chin, K.-G. State-of-the-knowledge on TWIP steel. Mater. Sci. Technol. 2012, 28, 513–527. [Google Scholar] [CrossRef]
- Bambach, M.; Conrads, L.; Daamen, M.; Güvençb, O.; Hirt, G. Enhancing the crashworthiness of high-manganese steel by strain-hardening engineering and tai-lored folding by local heat-treatment. Mater. Des. 2015, 110, 157–168. [Google Scholar] [CrossRef]
- Haase, C.; Barrales-Mora, L.A.; Molodov, D.A.; Roters, F.; Gottstein, G. Applying the texture analysis for optimizing thermomechanical treatment of high manganese twinning-induced plasticity steel. Acta Mater. 2014, 80, 327–340. [Google Scholar] [CrossRef]
- Haase, C.; Barrales-Mora, L.A.; Molodov, D.A.; Gottstein, G. Tailoring the Mechanical Properties of a Twinning-Induced Plasticity Steel by Retention of Deformation Twins During Heat Treatment. Metall. Mater. Trans. A 2013, 44, 4445–4449. [Google Scholar] [CrossRef]
- Haase, C.; Ingendahl, T.; Güvenc, O.; Bambach, M.; Bleck, W.; Molodova, D.A.; Barrales-Mora, L.A. On the applicability of recovery-annealed Twinning-Induced Plasticity steels: Potential and limitations. Mater. Sci. Eng. A 2015, 649, 74–84. [Google Scholar] [CrossRef]
- Güvenç, O.; Roters, F.; Hickel, T.; Bambach, M. ICME for Crashworthiness of TWIP Steels: From Ab Initio to the Crash Performance. JOM 2015, 67, 120–128. [Google Scholar] [CrossRef]
- Wong, S.L.; Madivala, M.; Prahl, U.; Roters, F.; Raabe, D. A crystal plasticity model for twinning- and transformation-induced plasticity. Acta Mater. 2016, 118, 140–151. [Google Scholar] [CrossRef]
- Schmidt, G. Grundlegendes zum Unfallmechanismus. In Die Beschleunigungsverletzung der Halswirbelsäule; Moorahrend, U.: Stuttgart, Germany, 1993; pp. 25–37. [Google Scholar]
- Roters, F.; Diehl, M.; Shanthraj, P.; Eisenlohr, P.; Reuber, C.; Wong, S.L.; Maitic, T.; Ebrahimid, A.; Hochrainere, T.; Fabritiusa, H.-O.; et al. DAMASK-The Düsseldorf Advanced Material Simulation Kit for modeling multi-physics crystal plasticity, thermal, and damage phenomena from the single crystal up to the component scale. Comput. Mater. Sci. 2019, 158, 420–478. [Google Scholar] [CrossRef]
- Diehl, M.; Groeber, M.; Haase, C.; Molodov, D.A.; Roters, F.; Raabe, D. Identifying Structure–Property Relationships Through DREAM.3D Representative Volume Elements and DAMASK Crystal Plasticity Simulations: An Integrated Computational Materials Engineering Approach. JOM 2017, 69, 848–855. [Google Scholar] [CrossRef]
- Haase, C.; Kühbach, M.; Barrales-Mora, L.A.; Wong, S.L.; Roters, F.; Molodova, D.A.; Gottstein, G. Recrystallization behavior of a high-manganese steel: Experiments and simulations. Acta Mater. 2015, 100, 155–168. [Google Scholar] [CrossRef]
- Gauss, W. Unfallrekonstruktion und biomechanische Begutachtung bei HWS-Verletzungen durch Heckaufprall. In Beschleunigungsverletzung der Halswirbelsäule; Graf, M., Grill, C., Eds.; Wedig, H.-D.: Darmstadt, Germany, 2009; pp. 78–91. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).